Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent-induced single-chain conformations of a linear synthetic polymer
Susil
Baral
 * and
Binod
Gautam
* and
Binod
Gautam
Department of Chemistry, Illinois State University, Normal, IL 61790, USA. E-mail: sbaral1@ilstu.edu
First published on 8th December 2025
Abstract
In this study, we investigate the solvent-induced single-chain conformations of a model linear synthetic polymer using magnetic tweezers microscopy. We synthesize surface-grafted polynorbornene in situ via ring-opening metathesis polymerization and generate the single-chain elasticity profiles in different solvent environments by scanning the pulling force. The single-chain data demonstrate the sensitivity of the polymer conformations to the solvent, and the polymer undergoes a transition from a swollen chain behavior in toluene to a collapsed chain with increasing proportion of ethanol in the solvent mixture. Moreover, we observe hysteresis in the single-chain elasticity profiles in solvents containing a higher proportion of ethanol, suggesting that the chain may adapt different conformations under relaxation and stretching in poor solvents. Our results provide molecular-level fundamental insights into the mechanical behavior of synthetic polymers and their stimuli-induced conformations.
1. Introduction
The mechanical properties of synthetic polymers are critical in many real-world applications, such as plastics, rubbers, adhesives, coatings, biomimetic materials, implant devices, etc.1–6 Making synthetic polymers with a controlled mechanical response is one of the primary goals of synthetic chemistry. The advances in robust catalysts, monomer design, and polymerization chemistry have significantly contributed to this frontier.1,7–13 While the macroscopic mechanical properties of synthetic polymers are governed by the collective properties of an ensemble of molecules, the properties of individual molecules lay the foundation. Single-chain elasticity or force-extension measurements are, therefore, an ideal platform for studying the mechanical response of heterogeneous systems such as synthetic polymers.Polymer physics models have predicted the single-chain mechanics of a linear polymer under different force regimes and solvent conditions.14 Classically, the entropic spring model was formulated and demonstrated success in predicting rubber elasticity at a relatively low tension.15 The fundamental drawback of infinitely extensible chain length in the classical entropic spring model was later addressed with the freely jointed chain (FJC) model, which considered a polymer to be made of rigid, independent links joined by free joints and was successful in accounting for rubber elasticity at higher tensions. Marko and Siggia further addressed experimental deviations in the elasticity of double-stranded DNA from the FJC model by modeling the polymer as a worm-like chain (WLC), where a chain is treated as an isotropic, homogeneous elastic rod with a bending stiffness.14–17 They formulated the force-extension relation in the high force regime 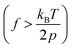 as,
as, 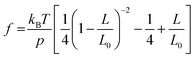 , where kBT is the thermal energy, L is the polymer end-to-end extension, L0 is the polymer counter length, and p is the persistence length of the polymer, which is a characteristic length of exponential decay of the polymer's orientation correlation function, and quantifies its bending stiffness.14–18
, where kBT is the thermal energy, L is the polymer end-to-end extension, L0 is the polymer counter length, and p is the persistence length of the polymer, which is a characteristic length of exponential decay of the polymer's orientation correlation function, and quantifies its bending stiffness.14–18
While Marko-Siggia's WLC model has been successful in describing the experimentally observed elasticity of various bio- and synthetic polymers at high force,14,19–23 where the chain is highly aligned, semiflexible and flexible polymers can exhibit a range of elastic regimes and scaling behavior at lower forces resulting from the interplay between intra-chain and chain-solvent interactions. Here, the transition from one elastic regime to another is predicted based on the applied force and the structural length scale of the polymers.15,19 Based on these predictions, an ideal chain is expected to follow entropic spring behavior with a linear response of the polymer extension to the applied force at lower forces as, 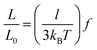 , where l (≈2p) is the polymer Kuhn length.14,15 For real chains, on lowering the force, intra-chain repulsions start to dominate and lead to a positive excluded volume. This causes the chain to swell and occupy a larger space than an ideal chain (i.e., in the absence of excluded-volume interactions). The single chain elasticity of a swollen chain follows Pincus’ prediction with a scaling exponent of 2/3 as,
, where l (≈2p) is the polymer Kuhn length.14,15 For real chains, on lowering the force, intra-chain repulsions start to dominate and lead to a positive excluded volume. This causes the chain to swell and occupy a larger space than an ideal chain (i.e., in the absence of excluded-volume interactions). The single chain elasticity of a swollen chain follows Pincus’ prediction with a scaling exponent of 2/3 as, 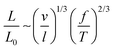 , where v is the excluded volume.14,15 The limit of chain swelling for real chains (i.e., either immediately after the WLC regime or after a linear response following the WLC regime at lower forces) depends on the quality of the solvent.15 Furthermore, for a real chain in a poor solvent, the intra-chain attractions overcome the chain–solvent interactions, resulting in negative excluded volume, and the polymer collapses to a compact conformation at lower forces.14,22
, where v is the excluded volume.14,15 The limit of chain swelling for real chains (i.e., either immediately after the WLC regime or after a linear response following the WLC regime at lower forces) depends on the quality of the solvent.15 Furthermore, for a real chain in a poor solvent, the intra-chain attractions overcome the chain–solvent interactions, resulting in negative excluded volume, and the polymer collapses to a compact conformation at lower forces.14,22
Recent advancements in single-molecule approaches have enabled the experimental study of the elasticity of various polymers at the single-chain level.15,24–34 While atomic force microscopy (AFM) measurements have been extensively used to probe the high force enthalpic elasticity of polymers,32 magnetic tweezers measurements are ideal for probing the entropic elasticity of polymers, as many theoretically predicted single-chain elasticity and scaling behaviors for a flexible polymer exist at the lower force end (e.g., 0.1–4 pN for a flexible polymer with a persistence length, p = 0.5 nm). Several single-chain scaling predictions have been observed experimentally in the magnetic tweezers measurements of various polymers in an aqueous medium.15,19,20 An ideal chain elastic response at lower forces has been experimentally observed under theta solvent conditions,20 where chain–chain interactions cancel out chain–solvent interactions, resulting in net zero excluded volume, while the swollen chain elastic response at lower forces has been experimentally observed for polymers under good solvent conditions.19,20 More recent magnetic tweezers measurements on synthetic polymers in an organic medium further revealed unprecedentedly diverse single-chain scaling behavior for chemically similar polymers under similar solvent conditions.22 The latter observations are theoretically not predicted and highlight the complexity of the single-chain conformations of synthetic polymers. Polynorbornene is a flexible17 synthetic polymer with a chain persistence length (p) of ∼0.7 nm,21,23 and typical magnetic tweezers measurements with a force range of 0.1–20 pN are therefore ideal to probe the single-chain elasticity and scaling behavior in both high force 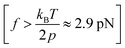 and low force
and low force  regimes.
regimes.
The conformations and elasticity of the synthetic polymers in solution depend on chain rigidity15 and environmental conditions, including the nature of the solvent,14,19,20,35 temperature,36–38 and pH.39,40 Any variations in these conditions act as external stimuli and lead to changes in polymer conformation. These stimuli-induced conformational changes affect the mechanical response of a polymer, which in turn determines the stability and deformation of polymer materials in their real-world applications. Solvent variations are routine stimuli in the application of synthetic polymers, and understanding the interplay between polymer conformations and solvent variations can provide fundamental knowledge that can aid in the design of polymer materials with the desired mechanical response and stability in their respective applications.
Here, we report a single-molecule study of solvent-induced single-chain conformations of a model linear synthetic polymer using magnetic tweezers force microscopy. We use ring-opening metathesis polymerization (ROMP) of the cyclic olefin norbornene to grow surface-grafted polynorbornene polymers in situ. We generate the relaxation and stretching profiles of a single polynorbornene by scanning the pulling force to observe single-chain elasticity and scaling behavior in different solvent environments. We visualize the transition from a swollen-chain conformation in toluene to a collapsed-chain conformation at lower forces as the proportion of ethanol in the solvent mixture increases. Moreover, we observe that solvent-induced conformational changes lead to hysteresis in the single-chain elasticity profiles in solvents with a higher ethanol content. As polymers in real-world applications experience continuous variations in their solvent environments, our single-molecule study of solvent-induced conformations of synthetic polymers will address a molecular-level understanding of stimuli-induced deformation of polymer materials and contribute fundamental knowledge toward developing polymer materials with desired mechanical responses. Our study represents the first force microscopy study of solvent-induced low-force elasticity of a synthetic polymer in an organic medium at the single-chain level. We anticipate that our results will be broadly relevant and will advance the field of polymer physics.
2. Experimental
2.1. Synthesis of surface-grafted polymers
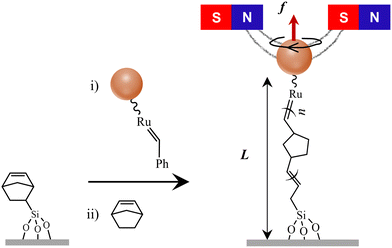
Our approach to single-chain manipulations of a synthetic polymer involves the in situ synthesis of surface-grafted polynorbornene molecules via ROMP of a norbornene monomer catalyzed by a second-generation Grubbs catalyst (G2) immobilized onto the magnetic particles, as illustrated in Fig. 1. Briefly, the G2 catalyst was first immobilized onto magnetic particles. The catalyst-immobilized magnetic particles were then tethered to the glass surface, and surface-grafted polynorbornene polymers were synthesized using a norbornene monomer in toluene. The polymerization reaction was stopped by flushing out the norbornene monomer, resulting in polynorbornenes with one end tethered to the glass coverslip surface and the other end attached to the magnetic particles for magnetic tweezers manipulations (refer to the SI, S1–S3 and Fig. S1–S4 for the detailed synthetic scheme and control measurements to validate the scheme). The synthetic scheme for surface-grafted polymers presented in this manuscript is distinct from those in previously reported schemes21–23,41 that required synthetic modification of the G2 catalyst.2.2. Single-chain force-extension measurements
Single-chain measurements were performed using a custom-built magnetic tweezers (MT) setup based on an inverted microscope21,42–44 (SI, S4, Fig. S5 and S6). A pair of permanent magnets was used to stretch the polymer by exerting a pulling force on the magnetic particle [Fig. 1] and the polymer extension was measured by tracking the axial (z) position of the magnetic particle. The vertical force exerted on the polymer was determined in advance using the fluctuation–dissipation theorem21,43,44 (SI, S5, Fig. S7). Single polynorbornene tethers were first identified by rotating the magnets (SI, S5, Fig. S7), and the force-extension measurements were performed in a cycle to generate the relaxation profile by decreasing the force stepwise from 13 pN to 0.1 pN and the stretching profile by increasing the force from 0.1 pN to 13 pN in the same force steps. This force range is adequate to probe both the high and low force elasticity of a flexible polymer such as polynorbornene, but not sufficient to break the covalent attachment points in our tethering scheme (SI, S6). All single-chain measurements reported here were performed at room temperature (∼21 °C).3. Results and discussion
3.1. Single-chain elasticity under varying solvent conditions
To probe the role of the solvent environment on the single-chain conformations, we examined the force-extension behavior of a single polynorbornene under varying solvent conditions. For these measurements, we varied the solvent environment by using a solvent that consists of a mixture of toluene and ethanol (EtOH). The rationale for the choice of the toluene–ethanol solvent system is: (i) toluene readily dissolves polynorbornene and is regarded as a good solvent for polynorbornene, (ii) EtOH precipitates polynorbornene and is regarded as a poor solvent/non-solvent for polynorbornene21 and (iii) toluene and EtOH are completely miscible at all proportions, and their mixtures at different proportions could behave as a cross-over regime between good and poor solvents. We examined the ensemble solubility of polynorbornene in toluene, ethanol, and toluene–ethanol mixtures in advance with volume ratios of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 7
2, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 6
3, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, and noticed polynorbornene precipitation in all solvent mixtures except for the toluene and 9
4, and noticed polynorbornene precipitation in all solvent mixtures except for the toluene and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
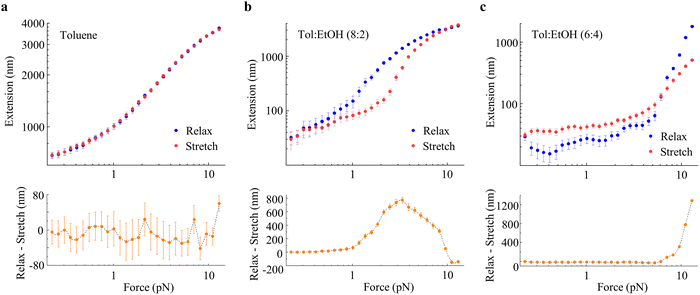
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol mixture. Fig. 2 shows the single-chain force-extension profiles of the single polynorbornene chain under force relaxation under varying solvent conditions. The sensitivity of the single-chain elasticity of the polymer to the solvent environment is very apparent from the data. In the subsequent sections, we will focus on the molecular description of the results and quantification of single-chain parameters from the data.
1 toluene–ethanol mixture. Fig. 2 shows the single-chain force-extension profiles of the single polynorbornene chain under force relaxation under varying solvent conditions. The sensitivity of the single-chain elasticity of the polymer to the solvent environment is very apparent from the data. In the subsequent sections, we will focus on the molecular description of the results and quantification of single-chain parameters from the data.
It is important to note that the polymer solubility depends on the theta temperature. The theta temperature of polynorbornene in toluene is not specified in the literature. Therefore, we only state that toluene is regarded as a good solvent for polynorbornene here and note the results of our ensemble measurements, where we observe complete dissolution of polynorbornene in toluene at room temperature. The goodness of the solvent will be further evaluated from the single-chain scaling behavior in the next section.
The single-chain elasticity of polynorbornene in toluene displays multiple distinct scaling regimes [Fig. 2(a), maroon data and Fig. 2(c)]. The high-force region 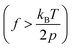 of the force-extension data fits well with Marko-Siggia's worm-like chain (WLC) model,
of the force-extension data fits well with Marko-Siggia's worm-like chain (WLC) model, 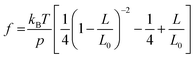 , quantifying the persistence length (p) and the contour length (L0) of the polymer. The p of the polymer is 0.79 ± 0.05 nm, consistent with its expected single-chain rigidity from experimental and computational studies,21,23,45 and L0 is 5650 ± 115 nm. The low-force
, quantifying the persistence length (p) and the contour length (L0) of the polymer. The p of the polymer is 0.79 ± 0.05 nm, consistent with its expected single-chain rigidity from experimental and computational studies,21,23,45 and L0 is 5650 ± 115 nm. The low-force 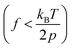 region of the data deviates from the WLC model and transitions to the swollen chain regime as previously observed for single-stranded DNA in a good solvent.19 While the scaling behavior of the polymer agrees with the Pincus prediction of L/L0 ∼ f2/3 in the force range from 2.57 pN to 1.17 pN with the experimental scaling exponent (γ) of 0.59 ± 0.06, a much lower scaling exponent of 0.29 ± 0.03 is observed below a force of 1.17 pN. Scaling exponents lower than 2/3 were observed in previous studies on model brush polymers46 and linear synthetic polymers,22 and the behavior was attributed to sidechain-induced repulsions and polymers interacting with the surface, respectively, at lower forces. We designate the observed f0.29 region as an additional regime of the swollen chain, as polynorbornene is a simple linear polymer without side chains, and the behavior is observed at significant polymer extensions, though we cannot completely rule out this regime being a swollen chain interacting with the surface, as previously assigned.22 The single-chain data, in general, suggest that the polynorbornene chain exhibits a good solvent behavior in toluene, consistent with ensemble observations. In terms of the Pincus blob model,20,47 the size of the Pincus blob (ξ = kBT/f) at the first transition from WLC to the swollen chain regime is ∼1.6 nm. Since this blob size is larger than the Kuhn length of the polymer, excluded volume interactions become dominant, and the chain starts to swell. As the tension is further lowered, the role of excluded-volume interactions becomes more dominant, and the chain swells further below 1.1 pN (blob size ∼3.7 nm).
region of the data deviates from the WLC model and transitions to the swollen chain regime as previously observed for single-stranded DNA in a good solvent.19 While the scaling behavior of the polymer agrees with the Pincus prediction of L/L0 ∼ f2/3 in the force range from 2.57 pN to 1.17 pN with the experimental scaling exponent (γ) of 0.59 ± 0.06, a much lower scaling exponent of 0.29 ± 0.03 is observed below a force of 1.17 pN. Scaling exponents lower than 2/3 were observed in previous studies on model brush polymers46 and linear synthetic polymers,22 and the behavior was attributed to sidechain-induced repulsions and polymers interacting with the surface, respectively, at lower forces. We designate the observed f0.29 region as an additional regime of the swollen chain, as polynorbornene is a simple linear polymer without side chains, and the behavior is observed at significant polymer extensions, though we cannot completely rule out this regime being a swollen chain interacting with the surface, as previously assigned.22 The single-chain data, in general, suggest that the polynorbornene chain exhibits a good solvent behavior in toluene, consistent with ensemble observations. In terms of the Pincus blob model,20,47 the size of the Pincus blob (ξ = kBT/f) at the first transition from WLC to the swollen chain regime is ∼1.6 nm. Since this blob size is larger than the Kuhn length of the polymer, excluded volume interactions become dominant, and the chain starts to swell. As the tension is further lowered, the role of excluded-volume interactions becomes more dominant, and the chain swells further below 1.1 pN (blob size ∼3.7 nm).
When the solvent is changed to a 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol mixture [Fig. 2(a), gray data], the high-force region of the force-extension data looks identical to that in toluene. The WLC fitting of the data yields the p and L0 values within the fitting error of those obtained in toluene (SI, S7, Fig. S8). The experimental data suggest that the high force conformations of the polymer are mostly unaffected in this solvent system. The low-force region of the data shows a deviation from that in toluene, with the scaling exponent of 0.73 ± 0.04 from 2.35 pN to 0.87 pN and 0.40 ± 0.04 from 0.87 pN to 0.2 pN (Fig. S8). These scaling exponents are slightly higher than those in toluene but still consistent with swollen chain behavior as observed in toluene. Overall, the single-molecule data in 9
1 toluene–ethanol mixture [Fig. 2(a), gray data], the high-force region of the force-extension data looks identical to that in toluene. The WLC fitting of the data yields the p and L0 values within the fitting error of those obtained in toluene (SI, S7, Fig. S8). The experimental data suggest that the high force conformations of the polymer are mostly unaffected in this solvent system. The low-force region of the data shows a deviation from that in toluene, with the scaling exponent of 0.73 ± 0.04 from 2.35 pN to 0.87 pN and 0.40 ± 0.04 from 0.87 pN to 0.2 pN (Fig. S8). These scaling exponents are slightly higher than those in toluene but still consistent with swollen chain behavior as observed in toluene. Overall, the single-molecule data in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol solvent still show good solvent behavior, consistent with ensemble observation.
1 toluene–ethanol solvent still show good solvent behavior, consistent with ensemble observation.
When the solvent is changed to an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol mixture [Fig. 2(a), pink data and Fig. 2(d)], the high force-region of the force-extension data only satisfactorily fits with the WLC model, resulting in larger errors in the quantified p (0.55 ± 0.11 nm) and L0 (6180 ± 570 nm). Here, the polymer extension at high forces is also decreased compared to that in toluene, and at lower forces (f < 3.68 pN), the polymer chains undergo rapid extension decay with a scaling exponent of 1.60 ± 0.08. This is a typical poor solvent behavior where the scaling exponent is expected to be greater than 1 (i.e., L/L0 ∼ f>1).14,22 In this regime, the chain–chain interactions overcome the chain–solvent interactions, resulting in negative excluded volume, and the polymer collapses to a compact conformation. In our experimental observation, the polymer attains a compact globule conformation with end-to-end extension approaching 10's of nm and the relative extension, L/L0, approaching zero (i.e., ∼0.006) at a 0.2 pN force.
2 toluene–ethanol mixture [Fig. 2(a), pink data and Fig. 2(d)], the high force-region of the force-extension data only satisfactorily fits with the WLC model, resulting in larger errors in the quantified p (0.55 ± 0.11 nm) and L0 (6180 ± 570 nm). Here, the polymer extension at high forces is also decreased compared to that in toluene, and at lower forces (f < 3.68 pN), the polymer chains undergo rapid extension decay with a scaling exponent of 1.60 ± 0.08. This is a typical poor solvent behavior where the scaling exponent is expected to be greater than 1 (i.e., L/L0 ∼ f>1).14,22 In this regime, the chain–chain interactions overcome the chain–solvent interactions, resulting in negative excluded volume, and the polymer collapses to a compact conformation. In our experimental observation, the polymer attains a compact globule conformation with end-to-end extension approaching 10's of nm and the relative extension, L/L0, approaching zero (i.e., ∼0.006) at a 0.2 pN force.
In the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 toluene–ethanol mixture [Fig. 2(a), purple data], the polymer extension is significantly decreased even at the highest force [Fig. 2(a), inset in linear scale] and undergoes even rapid decay with force. Here, the polymer attains a compact globule conformation with relative extension approaching zero at around 1 pN force, and the polymer extension becomes unresponsive to any further decrease in the force. The force-extension data under these conditions do not fit with any polymer physics model to quantify the physical parameters, except for the qualitative observation of an even higher slope of extension decay (i.e., higher scaling exponent) than in the 8
3 toluene–ethanol mixture [Fig. 2(a), purple data], the polymer extension is significantly decreased even at the highest force [Fig. 2(a), inset in linear scale] and undergoes even rapid decay with force. Here, the polymer attains a compact globule conformation with relative extension approaching zero at around 1 pN force, and the polymer extension becomes unresponsive to any further decrease in the force. The force-extension data under these conditions do not fit with any polymer physics model to quantify the physical parameters, except for the qualitative observation of an even higher slope of extension decay (i.e., higher scaling exponent) than in the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol mixture. As the proportion of ethanol is further increased to a 6
2 toluene–ethanol mixture. As the proportion of ethanol is further increased to a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol mixture [Fig. 2(a), dark cyan data], the extension of the polymer decreases more rapidly with an even higher scaling exponent and attains a compact conformation at a relatively higher force of around 5 pN. It is important to note that as the polymer extension becomes very small with decreasing force in 8
4 toluene–ethanol mixture [Fig. 2(a), dark cyan data], the extension of the polymer decreases more rapidly with an even higher scaling exponent and attains a compact conformation at a relatively higher force of around 5 pN. It is important to note that as the polymer extension becomes very small with decreasing force in 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 7
2, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 6
3, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol mixtures, the magnetic particle may approach and interact with the surface. This interaction at very low extensions could also result in a lack of extension responsiveness at lower forces in these solvents. However, the scaling behavior can still be interpreted from data at higher forces, where the extension remains hundreds of nanometers.
4 toluene–ethanol mixtures, the magnetic particle may approach and interact with the surface. This interaction at very low extensions could also result in a lack of extension responsiveness at lower forces in these solvents. However, the scaling behavior can still be interpreted from data at higher forces, where the extension remains hundreds of nanometers.
From additional experiments, we note that the higher proportions of ethanol beyond 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol sometimes result in a complete collapse of the magnetic particle onto the surface, preventing force-extension measurements. Though the solvent changes are performed at the highest force to avoid the collapse of the magnetic particle onto the surface, the measurements at higher ethanol contents (7
2 toluene–ethanol sometimes result in a complete collapse of the magnetic particle onto the surface, preventing force-extension measurements. Though the solvent changes are performed at the highest force to avoid the collapse of the magnetic particle onto the surface, the measurements at higher ethanol contents (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 6
3 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol mixture) are not always achieved. The data resulting from the measurements involving toluene and a lower proportion of ethanol (i.e., 9
4 toluene–ethanol mixture) are not always achieved. The data resulting from the measurements involving toluene and a lower proportion of ethanol (i.e., 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 8
1 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol mixture) display the behavior consistent with that presented in Fig. 2 (SI, S8.1, Fig. S9). Likewise, single-chain measurements at even higher proportions of ethanol and pure ethanol were not feasible as the magnetic bead collapses onto the surface and becomes unresponsive to the force (i.e., behaves as a particle immobilized onto the surface), likely resulting from the polymer tether instantaneously collapsing upon the addition of these solvents.
2 toluene–ethanol mixture) display the behavior consistent with that presented in Fig. 2 (SI, S8.1, Fig. S9). Likewise, single-chain measurements at even higher proportions of ethanol and pure ethanol were not feasible as the magnetic bead collapses onto the surface and becomes unresponsive to the force (i.e., behaves as a particle immobilized onto the surface), likely resulting from the polymer tether instantaneously collapsing upon the addition of these solvents.
3.2. Diverse single-chain scaling behavior
The single-chain elasticity of the synthetic polymers in organic solvents has been previously observed to exhibit heterogeneity among individual molecules even under identical solvent conditions.22 To examine any heterogeneity, we performed additional measurements probing the single-chain elasticity of several independent polynorbornene polymers in toluene and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 8
1 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol mixtures. The observations are summarized in Fig. 3 and can be broadly regarded as consistent with the behavior shown in Fig. 2 with some degree of dispersion among individual molecules. In general, the single-chain elasticity of polynorbornene in toluene [Fig. 3(a)] displays good solvent behavior, with the majority of the polymers transitioning from the WLC (black data) to the swollen chain regime at lower forces. The transition from the WLC to the ideal chain (purple data) to the swollen chain regime was rare, with a single observation out of 10 measurements. Also, most polymers display two distinct swollen chain regimes as shown in Fig. 2(a), one with the scaling exponent (γ) in agreement with Pincus’ prediction of 2/3 (blue data) after the WLC regime, and one with a scaling exponent much smaller than 2/3 (green data) at the low force end.
2 toluene–ethanol mixtures. The observations are summarized in Fig. 3 and can be broadly regarded as consistent with the behavior shown in Fig. 2 with some degree of dispersion among individual molecules. In general, the single-chain elasticity of polynorbornene in toluene [Fig. 3(a)] displays good solvent behavior, with the majority of the polymers transitioning from the WLC (black data) to the swollen chain regime at lower forces. The transition from the WLC to the ideal chain (purple data) to the swollen chain regime was rare, with a single observation out of 10 measurements. Also, most polymers display two distinct swollen chain regimes as shown in Fig. 2(a), one with the scaling exponent (γ) in agreement with Pincus’ prediction of 2/3 (blue data) after the WLC regime, and one with a scaling exponent much smaller than 2/3 (green data) at the low force end.
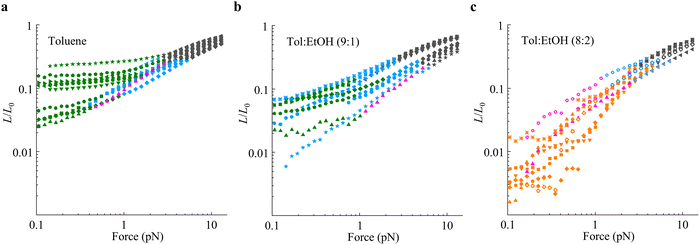 | ||
Fig. 3 Single-chain elasticity of polynorbornene polymers in (a) toluene, (b) 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol, and (c) 8 1 toluene–ethanol, and (c) 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol solvents. Different symbols represent individual polymers and different colors represent different scaling regimes divided by the scheme shown in Fig. 2(c) and (d) and described in the SI, S7. Black data: WLC region, blue data: swollen chain regime with a scaling exponent of ≈0.67 ± 0.17, green data: swollen chain regime with a scaling exponent of <0.50, purple data: ideal chain regime with a scaling exponent of ≈1.00 ± 0.15, orange data: collapsed chain regime with a scaling exponent of >1.15. The scaling exponent limits for different regimes are set for the consistent division of data displaying heterogeneity among individual polymers. 2 toluene–ethanol solvents. Different symbols represent individual polymers and different colors represent different scaling regimes divided by the scheme shown in Fig. 2(c) and (d) and described in the SI, S7. Black data: WLC region, blue data: swollen chain regime with a scaling exponent of ≈0.67 ± 0.17, green data: swollen chain regime with a scaling exponent of <0.50, purple data: ideal chain regime with a scaling exponent of ≈1.00 ± 0.15, orange data: collapsed chain regime with a scaling exponent of >1.15. The scaling exponent limits for different regimes are set for the consistent division of data displaying heterogeneity among individual polymers. | ||
In the 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol solvent, the single-chain elasticity still follows good solvent behavior with a transition from WLC to the swollen chain regime at low forces [Fig. 3(b)]. The ideal-chain regime is still rare as in toluene, with only one observation out of 10 measurements. Here, the observations can be divided into two categories: (i) about half of the polymers display one scaling regime consistent with the Pincus exponent at low force, as previously observed in ss-DNA in a good solvent,19 and (ii) the other half display two distinct swollen chain regimes as in toluene. In the 8
1 toluene–ethanol solvent, the single-chain elasticity still follows good solvent behavior with a transition from WLC to the swollen chain regime at low forces [Fig. 3(b)]. The ideal-chain regime is still rare as in toluene, with only one observation out of 10 measurements. Here, the observations can be divided into two categories: (i) about half of the polymers display one scaling regime consistent with the Pincus exponent at low force, as previously observed in ss-DNA in a good solvent,19 and (ii) the other half display two distinct swollen chain regimes as in toluene. In the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol solvent, the majority of the polymers display a scaling exponent >1 at low force and attain compact conformation as reflected by very small relative extension [Fig. 3(c)]. The transition from WLC to this poor solvent behavior occurs either with or without the intermediate ideal-chain or swollen chain regime. Here, the ideal-chain regime is observed more frequently than in toluene and 9
2 toluene–ethanol solvent, the majority of the polymers display a scaling exponent >1 at low force and attain compact conformation as reflected by very small relative extension [Fig. 3(c)]. The transition from WLC to this poor solvent behavior occurs either with or without the intermediate ideal-chain or swollen chain regime. Here, the ideal-chain regime is observed more frequently than in toluene and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol solvent, suggesting a condition closer to theta solvent. Overall, these observations suggest that the goodness of the solvent decreases with the addition of ethanol and approaches a crossover condition between good and poor solvents in the 8
1 toluene–ethanol solvent, suggesting a condition closer to theta solvent. Overall, these observations suggest that the goodness of the solvent decreases with the addition of ethanol and approaches a crossover condition between good and poor solvents in the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol system.
2 toluene–ethanol system.
The heterogeneity in the single-chain scaling behavior of individual polynorbornene polymers, even in identical solvent environments, is consistent with previous observations in polycyclooctene and polycyclooctatetraene (polyacetylene).22 The observed heterogeneity does not show any clear correlation with polymer contour length (SI, S8.2, Fig. S10), suggesting that this behavior is not a consequence of their chain length/molecular weight dispersion, which is ubiquitous in synthetic polymers. We can also rule out the possibility of the observed heterogeneity in single-chain scaling behavior of individual polynorbornenes even under good solvent conditions (i.e., toluene) as a consequence of our scheme for growing surface-grafted polynorbornenes under confinement (SI, S8.3, Fig. S11). Our results further highlight the unique elastic response of the synthetic polymers compared to the biopolymers, which demonstrate consistent single-chain elasticity under identical solvent conditions. The differences in synthetic polymers are most likely due to the varied microstructures of individual chains, whereby they exhibit different compositions and sequences of cis and trans conformations along the polymer backbone. This varied microstructure is expected to result in individual chains adapting different conformations during single-chain elasticity measurements. While the role of these variations may not be significant when the polymer is stretched at higher forces, their role is expected to be more pronounced under excluded-volume interactions at lower forces.
3.3. Single-chain conformations under relaxation and stretching
Single-chain conformation and mechanical response of a polymer to external force are regarded as fundamental properties, and the resulting behavior is expected to be similar irrespective of how the force is applied (i.e., force applied from one end or both ends, shearing force, sonication, etc.). In this regard, one would also expect the single-chain elasticity to display a similar response irrespective of whether the polymer is relaxed from high force to low force or stretched from low force to high force in a good solvent. However, the behavior of the polymer conformations under stimuli such as solvent variations and any directional nature of the resulting single-chain elasticity is not addressed in polymer physics theories. Modeling such behavior is theoretically challenging due to the complexity resulting from an interplay of various interactions co-occurring within the chain and its surrounding medium (i.e., solvent). Therefore, the experimental study of single-chain conformations under relaxation and stretching measurements under varied solvent conditions can provide valuable insights to advance the field. To this end, we examined any hysteresis in the single-chain elasticity of single polynorbornene polymers under stretching and relaxation measurements in different solvent environments (Fig. 4). For consistency, we evaluate any hysteresis based on the extension difference of 2σ (σ = standard deviation in the extension determined from the z noise of the extension data, and varies from 10 to 40 nm depending on the force and solvent conditions) over more than two consecutive data points that results in distinct differences in their single chain rigidity (i.e., p) and scaling behavior (i.e., γ).To probe the hysteresis in single-chain measurements, we first perform chain relaxation from high force (13 pN) to low force (0.2 pN), followed by subsequent stretching from low force to high force in the same force steps. Solvent changes are performed at high force (13 pN) after completing a relaxation and stretching cycle in toluene, which is followed by the additional relaxation and stretching cycle in the new solvent. Subsequent solvent changes are also performed at high force. In toluene, the relaxation and stretching profiles overlap within the experimental error of extension measurement [Fig. 4(a)] reflecting no hysteresis in single-chain elasticity and scaling behavior. Several independent measurements further support the absence of distinct hysteresis in toluene and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol solution (Fig. S12 and S13) and suggest that the polymer conformations are equilibrated at each force position during the force-extension measurements in a good solvent.
1 toluene–ethanol solution (Fig. S12 and S13) and suggest that the polymer conformations are equilibrated at each force position during the force-extension measurements in a good solvent.
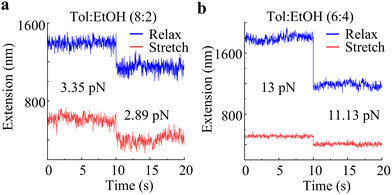
Surprisingly, a distinct hysteresis covering the majority of the force range is discovered in single-chain elasticity in the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol mixture [Fig. 4(b)]. Here, the profiles almost overlap at forces below 1 pN; the stretching profile lags by 100's of nm from 1 pN to 8.2 pN and attains similar extensions at the next force step (i.e., 9.58 pN). This is followed by the stretching profile slightly exceeding in the next higher force steps. In the 7
2 toluene–ethanol mixture [Fig. 4(b)]. Here, the profiles almost overlap at forces below 1 pN; the stretching profile lags by 100's of nm from 1 pN to 8.2 pN and attains similar extensions at the next force step (i.e., 9.58 pN). This is followed by the stretching profile slightly exceeding in the next higher force steps. In the 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 toluene–ethanol solvent, the profiles overlap mostly at forces lower than 5 pN, and a less pronounced hysteresis with no systematic trend is observed for forces above 5 pN [Fig. S15(a)]. Another distinct and more directional hysteresis is observed in the 6
3 toluene–ethanol solvent, the profiles overlap mostly at forces lower than 5 pN, and a less pronounced hysteresis with no systematic trend is observed for forces above 5 pN [Fig. S15(a)]. Another distinct and more directional hysteresis is observed in the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvent, where the profiles overlap below 6.11 pN, and the stretching profile lags exponentially behind the relaxation profile at higher forces [Fig. 4(c)]. An extension difference of ∼1300 nm is observed at the highest applied force (i.e., 13 pN).
4 toluene–ethanol solvent, where the profiles overlap below 6.11 pN, and the stretching profile lags exponentially behind the relaxation profile at higher forces [Fig. 4(c)]. An extension difference of ∼1300 nm is observed at the highest applied force (i.e., 13 pN).
We can rule out the possibility of the observed hysteresis, shown in Fig. 4, being a result of an experimental or data analysis artifact, (i) as it is not observed under good solvent behavior in toluene and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene–ethanol solvent, and (ii) since the measurements are performed on the same magnetic particle/polymer tether in the same force steps, any uncertainties in the estimated force and extension would only result in a lateral shift of the curves with no changes in their shape (and the resulting elasticity behavior). Hysteretic elasticity with tethers exhibiting slowly increasing extensions at high force (up to 100 pN) was previously reported48 in the magnetic tweezers study of single-stranded DNA and was attributed to the tether peeling off the surface due to non-specific attachment. In our scheme, the tethers are attached via a specific interaction (i.e., covalent bonding), and the high force (13 pN) in our measurements is much smaller. Furthermore, our hysteresis evaluation focuses on the extension differences between the relaxation and stretching profiles at relatively longer polymer extensions of several hundred nanometers to microns (Fig. 4(b) and (c) and Fig. S14–S16) at intermediate to higher forces. At these extensions, the magnetic bead is far from the surface, and we can rule out hysteresis originating from any magnetic particle–surface interactions. Although it is difficult to entirely rule out chain interactions with the surface in force-extension measurements, as the hysteresis is only observed under poor solvent behavior, it is more likely to result from the directional nature of single-chain elasticity in poor solvents.
1 toluene–ethanol solvent, and (ii) since the measurements are performed on the same magnetic particle/polymer tether in the same force steps, any uncertainties in the estimated force and extension would only result in a lateral shift of the curves with no changes in their shape (and the resulting elasticity behavior). Hysteretic elasticity with tethers exhibiting slowly increasing extensions at high force (up to 100 pN) was previously reported48 in the magnetic tweezers study of single-stranded DNA and was attributed to the tether peeling off the surface due to non-specific attachment. In our scheme, the tethers are attached via a specific interaction (i.e., covalent bonding), and the high force (13 pN) in our measurements is much smaller. Furthermore, our hysteresis evaluation focuses on the extension differences between the relaxation and stretching profiles at relatively longer polymer extensions of several hundred nanometers to microns (Fig. 4(b) and (c) and Fig. S14–S16) at intermediate to higher forces. At these extensions, the magnetic bead is far from the surface, and we can rule out hysteresis originating from any magnetic particle–surface interactions. Although it is difficult to entirely rule out chain interactions with the surface in force-extension measurements, as the hysteresis is only observed under poor solvent behavior, it is more likely to result from the directional nature of single-chain elasticity in poor solvents.
We believe that these observations are unprecedented, as we are unaware of any reports demonstrating such hysteresis in the single-chain elasticity of synthetic polymers. The observation of hysteresis in single-chain elasticity under poor solvent behavior further suggests that the polymer conformations are either not equilibrated at each force position during the measurements or that the polymer chain exhibits different conformations along the relaxation or stretching pathways under poor solvent conditions. Our force-extension measurements are relatively slow and take 15–30 seconds between changing the force and the subsequent extension measurements at each force position. Also, the force steps in these measurements are small. At these time scales and force steps, we believe that the chain extensions are equilibrated at each force position in our measurements. To validate this, we examined the extension versus time trajectories of force-extension measurements. Fig. 5(a) and (b) show extension vs. time trajectories of the data shown in Fig. 4(b) and (c) for the force steps with the highest extension difference between the relaxation and the stretching profiles. The extensions are relatively stable and rule out the possibility of hysteresis resulting from non-equilibrated chain extensions during force-extension measurements.
 | ||
| Fig. 5 Extension vs. time trajectories of single-chain force-extension data presented in (a) Fig. 4(b) and (c) for the force steps resulting in the highest extension difference between the relaxation and the stretching profiles. | ||
To verify the observed hysteresis in single-chain elasticity, we performed several independent measurements focusing on toluene, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol, and 6
2 toluene–ethanol, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvent systems. These additional measurements support our observation in Fig. 4, displaying no distinct hysteresis in toluene and frequent hysteresis in 8
4 toluene–ethanol solvent systems. These additional measurements support our observation in Fig. 4, displaying no distinct hysteresis in toluene and frequent hysteresis in 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 6
2 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvents (SI, S8). Overall, the hysteresis observed in the solvent with the highest proportion of a poor solvent (i.e., 6
4 toluene–ethanol solvents (SI, S8). Overall, the hysteresis observed in the solvent with the highest proportion of a poor solvent (i.e., 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol) appears to be consistent over several single polymers, where the profiles mostly overlap when the polymer is in a completely collapsed state (as reflected by very short extensions) and the polymer extension does not reach the relaxation values upon subsequent stretching for the majortity of the individual polymers (11/14 individual polymers show this behavior, SI, S8.8). Meanwhile, the hysteresis observed in the 8
4 toluene–ethanol) appears to be consistent over several single polymers, where the profiles mostly overlap when the polymer is in a completely collapsed state (as reflected by very short extensions) and the polymer extension does not reach the relaxation values upon subsequent stretching for the majortity of the individual polymers (11/14 individual polymers show this behavior, SI, S8.8). Meanwhile, the hysteresis observed in the 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol solvent appears to be more stochastic (11/15 individual polymers display distinct hysteresis, SI, S8.6) and difficult to interpret.
2 toluene–ethanol solvent appears to be more stochastic (11/15 individual polymers display distinct hysteresis, SI, S8.6) and difficult to interpret.
We further performed additional measurements with multiple relaxation and stretching cycles in toluene, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol, and 6
2 toluene–ethanol, and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvent systems. The exemplary data in toluene (i.e., a good solvent) show reproducible single-chain elasticity profiles with no hysteresis under multiple relaxation and stretching cycles (SI, Fig. S17). However, the profiles in 8
4 toluene–ethanol solvent systems. The exemplary data in toluene (i.e., a good solvent) show reproducible single-chain elasticity profiles with no hysteresis under multiple relaxation and stretching cycles (SI, Fig. S17). However, the profiles in 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 toluene–ethanol display diverse behavior, with some chains exhibiting consistent hysteresis in multiple cycles and some chains exhibiting hysteresis in the first cycle, followed by reproducible relaxation and stretching in the subsequent cycles (SI, Fig. S18). In the 6
2 toluene–ethanol display diverse behavior, with some chains exhibiting consistent hysteresis in multiple cycles and some chains exhibiting hysteresis in the first cycle, followed by reproducible relaxation and stretching in the subsequent cycles (SI, Fig. S18). In the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvent, the profiles mostly display hysteresis in the first cycle, where the extension does not reach relaxation values upon subsequent stretching, followed by the reproducible profiles in subsequent cycles (SI, Fig. S19). In our measurements, the solvent is changed at high force to prevent the magnetic particle from collapsing onto the surface. This force may prevent the polymer from undergoing complete conformational relaxation, and the polymer chain remains only at local equilibrium (as suggested by the stable extension). As the force is lowered, the polymer undergoes complete relaxation and attains overall equilibrium conformation. Consequently, the chain does not reach initial extensions upon subsequent stretching. This rationale can explain the majority of hysteresis behavior observed in the 6
4 toluene–ethanol solvent, the profiles mostly display hysteresis in the first cycle, where the extension does not reach relaxation values upon subsequent stretching, followed by the reproducible profiles in subsequent cycles (SI, Fig. S19). In our measurements, the solvent is changed at high force to prevent the magnetic particle from collapsing onto the surface. This force may prevent the polymer from undergoing complete conformational relaxation, and the polymer chain remains only at local equilibrium (as suggested by the stable extension). As the force is lowered, the polymer undergoes complete relaxation and attains overall equilibrium conformation. Consequently, the chain does not reach initial extensions upon subsequent stretching. This rationale can explain the majority of hysteresis behavior observed in the 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 toluene–ethanol solvent system.
4 toluene–ethanol solvent system.
Fundamentally, intra-chain interactions are more favorable than chain–solvent interactions in poor solvents. In addition, when the solvent is changed from good to poor, the elimination of favorable polymer–solvent interactions could also lead to polymer–surface interactions, especially at lower stretching forces. These interactions could also contribute to hysteretic elasticity but are difficult to solely account for or rule out in experimental measurements. In general, the observed hysteresis in our measurements should originate from the interplay of polymer conformations and the chain–chain and chain–solvent interactions induced by the solvent variations. This is further supported by the fact that hysteretic elasticity is observed only in poor solvents, while reversible elasticity is observed in good solvents, even under multiple cycles. Overall, our observations suggest that polymer conformations under poor solvent conditions may exhibit a directional nature that depends on solvent quality and whether the polymer is stretched or relaxed. Our results provide first-of-its-kind experimental data and point to the complex single-chain conformations of synthetic polymers in poor solvents. While our current work sets the benchmark, future work, including experiments on various polymeric systems and solvents, theoretical modeling, and molecular-level simulations, can shed additional insights into this unique behavior.
4. Conclusions
In summary, we have demonstrated the application of single-molecule measurements to probe solvent-induced conformations on a model synthetic polymer. We have directly observed the variations in single-chain elasticity and scaling behavior of polynorbornene in different solvent environments by scanning the stretching force using magnetic tweezers microscopy. Single-chain conformations are very sensitive to the solvent environment, and the polymer undergoes rapid collapse at lower stretching forces with increasing proportion of a poor solvent, which further appears to result in hysteresis in the single-chain elasticity profiles. Besides solvent variations, many other physical changes (such as temperature and pH of the medium) can perturb single-chain conformations of a polymer, which is critical for the mechanical stability of the synthetic polymers. Our study sets a benchmark for the application of magnetic tweezers to probe the low-force elastic response of synthetic polymers under environmental variations to acquire molecular-level fundamental knowledge of synthetic polymer mechanics and stimuli-induced polymer deformations.Author contributions
S. B. designed and directed the research. B. G. contributed to experimentation and data collection. S. B. analyzed the data and wrote the main text and SI.Conflicts of interest
The authors have no conflicts to disclose.Data availability
The data supporting the findings of this study are included in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00962f.Acknowledgements
This research was supported by the start-up funds from Illinois State University. The authors thank Prof. Jun-Hyun Kim (ISU) for the assistance with SEM imaging, Prof. Jeremy Driskell (ISU) and Prof. George Barnes (ISU) for insightful discussion, and James Dunham (Physics Model Shop, ISU) for assistance with machining parts for the MT setup.References
- M. L. Gardel, Nature, 2013, 493, 619 CrossRef PubMed.
- I. M. Alarifi, Adv. Ind. Eng. Polym. Res., 2023, 6, 451–464 CAS.
- K. Jung, N. Corrigan, E. H. H. Wong and C. Boyer, Adv. Mater., 2022, 34, 2105063 CrossRef CAS PubMed.
- C. Li, C. Guo, V. Fitzpatrick, A. Ibrahim, M. J. Zwierstra, P. Hanna, A. Lechtig, A. Nazarian, S. J. Lin and D. L. Kaplan, Nat. Rev. Mater., 2020, 5, 61–81 CrossRef.
- C. Verma, M. A. Quraishi, A. Alfantazi and K. Y. Rhee, Adv. Ind. Eng. Polym. Res., 2023, 6, 407–435 CAS.
- G. Raos and B. Zappone, Macromolecules, 2021, 54, 10617–10644 CrossRef CAS.
- H. Tian, Z. Tang, X. Zhuang, X. Chen and X. Jing, Prog. Polym. Sci., 2012, 37, 237–280 CrossRef CAS.
- J.-F. Lutz, M. Ouchi, D. R. Liu and M. Sawamoto, Science, 2013, 341, 1238149 CrossRef PubMed.
- J.-F. Lutz, J.-M. Lehn, E. W. Meijer and K. Matyjaszewski, Nat. Rev. Mater., 2016, 1, 16024 CrossRef CAS.
- A. Anastasaki, B. Oschmann, J. Willenbacher, A. Melker, M. H. C. Van Son, N. P. Truong, M. W. Schulze, E. H. Discekici, A. J. McGrath, T. P. Davis, C. M. Bates and C. J. Hawker, Angew. Chem., 2017, 56, 14483–14487 CrossRef CAS PubMed.
- M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Nature, 2017, 549, 497–501 CrossRef PubMed.
- K. Matyjaszewski, Adv. Mater., 2018, 30, 1706441 CrossRef PubMed.
- O. M. Ogba, N. C. Warner, D. J. O’Leary and R. H. Grubbs, Chem. Soc. Rev., 2018, 47, 4510–4544 RSC.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- O. A. Saleh, J. Chem. Phys., 2015, 142, 194902 CrossRef PubMed.
- X. Li, C. M. Schroeder and K. D. Dorfman, Soft Matter, 2015, 11, 5947–5954 RSC.
- F. Meng and E. M. Terentjev, Polymers, 2017, 9, 52 CrossRef PubMed.
- C. M. Schroeder, J. Rheol., 2018, 62, 371–403 CrossRef CAS.
- O. A. Saleh, D. B. McIntosh, P. Pincus and N. Ribeck, Phys. Rev. Lett., 2009, 102, 068301 CrossRef CAS PubMed.
- A. Dittmore, D. B. McIntosh, S. Halliday and O. A. Saleh, Phys. Rev. Lett., 2011, 107, 148301 CrossRef PubMed.
- C. Liu, K. Kubo, E. Wang, K.-S. Han, F. Yang, G. Chen, F. A. Escobedo, G. W. Coates and P. Chen, Science, 2017, 358, 352–355 CrossRef CAS PubMed.
- S. Baral, C. Liu, U. K. Chakraborty, K. Kubo, X. Mao, G. W. Coates and P. Chen, Chem, 2021, 7, 2175–2189 CAS.
- S. Baral, C. Liu, X. Mao, G. W. Coates and P. Chen, ACS Cent. Sci., 2022, 8, 1116–1124 CrossRef CAS PubMed.
- H. Li, W. Zhang, W. Xu and X. Zhang, Macromolecules, 2000, 33, 465–469 CrossRef CAS.
- H. Li and Y. Cao, Acc. Chem. Res., 2010, 43, 1331–1341 CrossRef CAS PubMed.
- Y. Bao and S. Cui, Langmuir, 2023, 39, 3527–3536 CrossRef CAS PubMed.
- P. Shrestha, T. Emura, D. Koirala, Y. Cui, K. Hidaka, W. J. Maximuck, M. Endo, H. Sugiyama and H. Mao, Nucleic Acids Res., 2016, 44, 6574–6582 CrossRef PubMed.
- D. Karna, W. Pan, S. Pandey, Y. Suzuki and H. Mao, Nanoscale, 2021, 13, 8425–8430 RSC.
- A. Janshoff, M. Neitzert, Y. Oberdörfer and H. Fuchs, Angew. Chem., 2000, 39, 3212–3237 CrossRef CAS.
- Y. Song, Z. Ma and W. Zhang, Macromolecules, 2022, 55, 4177–4199 CrossRef CAS.
- P. Yang, Y. Song, W. Feng and W. Zhang, Macromolecules, 2018, 51, 7052–7060 CrossRef CAS.
- Y. Bao, Z. Luo and S. Cui, Chem. Soc. Rev., 2020, 49, 2799–2827 RSC.
- S. Lu, W. Cai, S. Zhang and S. Cui, Macromolecules, 2023, 56, 3204–3212 CrossRef CAS.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS PubMed.
- F. Tenopala-Carmona, S. Fronk, G. C. Bazan, I. D. W. Samuel and J. C. Penedo, Sci. Adv., 2018, 4, eaao5786 CrossRef PubMed.
- Y. Kotsuchibashi, Polymer J., 2020, 52, 681–689 CrossRef CAS.
- Y. Yuan, K. Raheja, N. B. Milbrandt, S. Beilharz, S. Tene, S. Oshabaheebwa, U. A. Gurkan, A. C. S. Samia and M. Karayilan, RSC Appl. Polym., 2023, 1, 158–189 RSC.
- F. D. Jochum and P. Theato, Chem. Soc. Rev., 2013, 42, 7468–7483 RSC.
- S.-i Yusa, Polym. J., 2022, 54, 235–242 CrossRef CAS.
- G. Kocak, C. Tuncer and V. Bütün, Polym. Chem., 2017, 8, 144–176 RSC.
- U. K. Chakraborty, M. Yang, S. Baral, C. Liu, A. Chen and P. Chen, Proc. Nat. Acad. Sci. U. S. A., 2025, 122, e2418844122 CrossRef CAS PubMed.
- J. Lipfert, X. Hao and N. H. Dekker, Biophys. J., 2009, 96, 5040–5049 CrossRef CAS PubMed.
- A. J. W. te Velthuis, J. W. J. Kerssemakers, J. Lipfert and N. H. Dekker, Biophy. J., 2010, 99, 1292–1302 CrossRef CAS PubMed.
- Y. Seol and K. C. Neuman, in Single Molecule Analysis: Methods and Protocols, ed. E. J. G. Peterman and G. J. L. Wuite, Humana Press, Totowa, NJ, 2011, pp. 265–293 DOI:10.1007/978-1-61779-282-3_15.
- D. F. Sunday, A. Chremos, T. B. Martin, A. B. Chang, A. B. Burns and R. H. Grubbs, Macromolecules, 2020, 53, 7132–7140 CrossRef CAS PubMed.
- S. N. Innes-Gold, J. P. Berezney and O. A. Saleh, Biophys. J., 2020, 119, 1351–1358 CrossRef CAS PubMed.
- P. Pincus, Macromolecules, 1976, 9, 386–388 CrossRef CAS.
- Dustin B. McIntosh, G. Duggan, Q. Gouil and Omar A. Saleh, Biophy. J., 2014, 106, 659–666 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |