DOI:
10.1039/D5SM00882D
(Paper)
Soft Matter, 2026,
22, 589-603
Electrokinetic and electro-elastic instabilities in viscoelastic microfluidic flows: suppression and augmentation in mixing efficiency
Received
31st August 2025
, Accepted 11th December 2025
First published on 16th December 2025
Abstract
Viscoelastic fluids, such as polymer solutions, surfactant mixtures, colloidal suspensions, emulsions, and biological fluids like blood, are frequently transported in microfluidic systems using external electric fields. In such flows, two distinct types of instabilities can emerge, namely, electro-elastic instabilities (EEI), arising from the interaction between elastic stresses and streamline curvature, and electrokinetic instabilities (EKI), triggered by electrical conductivity gradients once the external electric field exceeds a critical value. Both instabilities can promote fluid mixing by inducing chaotic flow structures; however, their roles are not always complementary. Recent experimental and numerical studies have shown that increasing fluid viscoelasticity can suppress EKI, leading to reduced mixing efficiency in a microfluidic T-junction. However, this study demonstrates that while viscoelasticity initially hinders mixing by damping EKI, a further increase in the Weissenberg number (a measure of fluid elasticity) leads to the onset of EEI, which in turn again increases mixing. Therefore, a non-monotonic relationship between mixing efficiency and Weissenberg number is found in the present study. Furthermore, although both EEI and EKI promote mixing, they differ significantly in their coherent flow structures and regions of origin within the microdevice. To elucidate these differences, we employ the data-driven dynamic mode decomposition (DMD) technique to characterise the underlying instability modes and their influence on the mixing dynamics. Overall, this study provides fundamental insights into how viscoelasticity modulates flow instabilities in electrokinetically driven microflows and offers strategies to optimise mixing by tuning fluid properties and operating conditions.
1 Introduction
The transport of fluids in micro and nanofluidic systems is predominantly governed by electrokinetic (EK) transport mechanisms, such as electroosmosis and electrophoresis, rather than conventional pressure-driven approaches. This preference arises due to several advantages of the EK transport mechanism for small-scale devices. For instance, electroosmotic flow (EOF) exhibits a uniform, plug-like velocity profile in contrast to the parabolic velocity distribution for pressure-driven flows. The former velocity profile seen in the EK-driven transport mechanism significantly mitigates Taylor dispersion, increasing solute transport efficiency and preserving sample integrity in miniaturised fluidic environments.1 Additionally, the flow rate in the EK-driven transport mechanism can be precisely modulated by adjusting the magnitude and polarity of the applied electric field, eliminating the need for mechanical components such as pumps or valves, which are essential in pressure-driven systems. This allows for precise manipulation of small fluid volumes with minimal mechanical complexity. Consequently, extensive research over the past three decades or so has focused on EK-driven transport mechanisms, encompassing a wide range of scientific and engineering disciplines.2,3 This stems from the fact that electrokinetically driven fluid transport plays a pivotal role in the development of micro total analysis systems (μTAS) and lab-on-a-chip (LOC) devices, where it facilitates critical functions such as sample pretreatment, separation, mixing, chemical reactions, and the detection of specific analytes.4,5 Therefore, the EK-driven transport mechanisms are essential in advancing microfluidic and nanofluidic technologies for various analytical, chemical, and biomedical applications.
The EK-driven transport mechanisms have garnered significant attention within the research community not only due to their numerous advantages over conventional pressure-driven flows but also because these transport mechanisms can give rise to complex flow phenomena, particularly electrokinetic instabilities (EKI), which do not typically appear in purely pressure-driven systems.6,7 EKI arises when heterogeneous fluid samples, e.g., with electrical conductivity gradients, are subjected to an electric field exceeding a critical threshold.7 Depending on the application, these instabilities can either hinder precise flow control or increase mixing through chaotic advection. Numerous studies have highlighted the role of EKI in mixing enhancement. Lin et al.8 first demonstrated rapid mixing in straight microchannels with conductivity gradients. Huang et al.9 showed that mixing efficiency in a cross-shaped micromixer increased sharply beyond a critical electric field. Luo10 further revealed that mixing strongly depends on the spatial arrangement of high- and low-conductivity solutions. Li et al.11 conducted systematic numerical studies showing the effects of conductivity ratio, field strength, and microchannel depth on EKI onset and mixing. More recently, Hadidi et al.12 reported that microchannel confinement suppresses EKI and that mixing efficiency depends non-monotonically on electric field strength. Additional works have demonstrated similar effects across various microchannel designs, including T-shaped,13 Y-shaped,14 and other microchannels, with a comprehensive review provided by Chang and Yang.15
Apart from operating conditions such as applied electric field strength and conductivity ratio, the geometry and dimensions of the microchannel and the rheological properties of the fluid also play a crucial role in governing the onset and evolution of the electrokinetic instability phenomenon. Despite this, most early studies on EKI primarily focused on Newtonian fluids, where the relationship between applied stress and deformation is linear. However, many fluids commonly encountered in μTAS and LOC devices for biomedical applications, such as blood, saliva, synovial fluid, cerebrospinal fluid, and mucus, exhibit a spectrum of complex non-Newtonian behaviours.16–23 These fluids display non-linear rheological responses, including shear-thinning, shear-thickening, viscoplasticity, viscoelasticity, and thixotropy, making their electrokinetic behaviour significantly more intricate than that of Newtonian fluids.24,25 Similarly, various industrially relevant fluids, including foams, suspensions, emulsions, polymer solutions, and polymer melts, also deviate from Newtonian behaviour and instead follow complex non-Newtonian rheological responses.26,27 These fluids are widely used in chemical, pharmaceutical, and food processing industries, where electrokinetically driven transport and mixing are critical. Given the prevalence of non-Newtonian fluids in these diverse applications, only recently has research begun to explore their influence on the EKI phenomenon. For instance, Hamid and Sasmal28 conducted a comprehensive numerical study investigating EKI in non-Newtonian fluids. Their findings revealed that the critical electric field strength required for EKI onset is lower for shear-thinning fluids than for Newtonian fluids, whereas it is higher for shear-thickening fluids. Additionally, they observed that the degree of mixing is increased in shear-thinning fluids but suppressed in shear-thickening fluids relative to their Newtonian counterparts. Expanding upon these numerical insights, Chen et al.29 performed an experimental investigation using xanthan gum polymer solutions, which exhibit shear-thinning behaviour. Their experimental findings corroborated those of Hamid and Sasmal, further demonstrating that the propagation speed, amplitude, and frequency of EKI waves in shear-thinning fluids are higher than in Newtonian fluids under identical operating conditions. Further investigations into the role of fluid elasticity in the onset and progression of the electrokinetic instability phenomenon have emerged only recently. For instance, Song et al.30 conducted an experimental study in a T-shaped microchannel using polyethylene oxide (PEO) polymer solutions and observed a significant modulation of the EKI characteristics. Specifically, they reported a reduction in both the amplitude and frequency of the EKI waves, alongside an increase in the critical electric field strength required for instability onset, compared to a Newtonian solvent (water). Moreover, their findings revealed a non-monotonic relationship between polymer concentration and the threshold electric field strength for EKI initiation. As the polymer concentration increased, the threshold electric field strength initially decreased before subsequently increasing. In a very recent experimental study, this suppression of EKI intensity was further established by the same research group with a viscoelastic Boger fluid.31 In alignment with these experimental findings, our recent numerical investigation32 corroborated the observed suppression of EKI intensity and its consequent impact on mixing dynamics. Furthermore, our study provided an in-depth mechanistic explanation for the attenuation of instability intensity.
Expanding upon our earlier work, the present study provides a more detailed investigation into the complex interplay between fluid elasticity and mixing dynamics, revealing that the influence of elasticity on instability behaviour is far richer than a simple suppressive effect. This study shows that with a gradual increase in fluid elasticity, the intensity of electrokinetic instability is initially diminished, leading to a reduction in mixing efficiency, consistent with prior experimental29,30 and numerical studies.32 However, beyond a critical threshold of elasticity, quantified by the Weissenberg number, an additional instability emerges in electrokinetic viscoelastic flows, known as the electro-elastic instability (EEI).25 This instability arises from the interplay between elastic stresses and streamline curvature within the flow. Prior studies, both experimental and computational, have demonstrated the role of EEI in increasing mixing across a variety of microfluidic configurations, including contraction–expansion microchannels,33 cross-slot geometries,34 microchannels with embedded obstacles,35 model porous media,36 and even straight microchannels.37 Consequently, the mixing efficiency exhibits a non-monotonic dependence on elasticity, for which the present study provides a comprehensive explanation through extensive numerical simulations. Although both EKI and EEI promote fluid mixing by generating chaotic flow structures, they differ fundamentally in their coherent structures and spatial regions of origin, leading to distinct mixing dynamics. To uncover these differences, this study further employs a data-driven dynamic mode decomposition (DMD) framework,38 which serves as a powerful tool for analysing chaotic flow fields and their role in scalar transport. By decomposing high-dimensional spatiotemporal data into modes characterised by distinct frequencies, growth or decay rates, and spatial patterns, DMD captures the hidden coherent structures associated with each instability. This enables the identification of persistent, growing, and decaying modes, thereby revealing the dynamical origins of EKI and EEI and their relative contributions to mixing efficiency. Overall, the insights gained from this study are particularly relevant for microfluidic applications such as μTAS and LOC devices, where viscoelastic fluids, including biofluids, colloidal suspensions, and emulsions, are routinely transported under external electric fields, and flow instabilities play a pivotal role in their transport and mixing.
2 Problem statement and governing equations
The schematic of the problem considered in this study is shown in Fig. 1. The geometry corresponds to a microfluidic T-junction device with two converging inlets and a single outlet. The lengths of the inlets are fixed at 5.25H, while the outlet length is 20H with H = 100 µm. The microchannel heights are H in the inlet arms and 2H in the outlet section. Leaky dielectric viscoelastic fluids with high and low electrical conductivities are introduced through the south (S) and north (N) inlets, respectively, as schematically illustrated in Fig. 1. The choice of a viscoelastic constitutive equation depends on the rheological response of the fluid under standard homogeneous flows, such as simple shear or uniaxial extension. In the present work, we employ the Oldroyd-B model for several reasons,39 namely, (i) it is a relatively simple model relying on a single conformation tensor to describe stress evolution, governed by only two parameters, the polymer concentration and relaxation time; (ii) it originates from the simplest kinetic theory of polymers, wherein a molecule is modeled as a dumbbell with two beads connected by an infinitely extensible spring; and (iii) it captures the rheological characteristics of Boger fluids, i.e., viscoelastic liquids with constant shear viscosity.40,41 Thus, the model enables explicit investigation of elasticity-driven effects on flow dynamics. To capture electrokinetic instabilities arising from conductivity gradients, we adopt the modified Ohmic model of Lin et al.,8 which extends the classical formulation by Melcher.42 This model is built upon three main assumptions, namely, electroneutrality, negligible diffusive current, and a symmetric electrolyte. The full derivation has been reported by Lin et al.8 and discussed further by Chen et al.43 and Posner et al.44 Hence, only the governing equations relevant to the present flow are first presented here in a dimensional form:| |  | (1) |
Momentum equation:| | 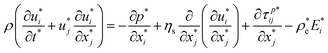 | (2) |
Ohmic model equation:| |  | (3) |
| |  | (4) |
| | 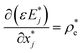 | (5) |
Oldroyd-B viscoelastic constitutive equation:| |  | (6) |
| |  | (7) |
Dye transport equation:| |  | (8) |
In the above equations, ρ is the fluid density (1000 kg m−3), ηs is the solvent viscosity (ηs = 0.0005 Pa s), ηp is the polymeric viscosity (ηp = 0.0005 Pa s), σ is the electrical conductivity, ε is the electrical permitivity, E* is the electric field, ρe is the charge density, x* is the position, u* is the velocity vector, t* is the time, p* is the pressure, τp* is the polymeric stress tensor, and λ is the polymer relaxation time. Deff is the effective diffusivity, which can be calculated for a binary and monovalent fully dissociated electrolyte as  . Here D+ and D− are the diffusivities of positive and negative ions, respectively. Aij = 〈RiRj〉 is the conformation tensor where Ri is the dimensionless end-to-end vector of a polymer molecule, δij is the Kronecker delta, C* is the dye concentration and D is the diffusivity of the dye molecule. Note that here ()* denotes a dimensional variable. The corresponding non-dimensional forms of the above governing equations are written as below:
. Here D+ and D− are the diffusivities of positive and negative ions, respectively. Aij = 〈RiRj〉 is the conformation tensor where Ri is the dimensionless end-to-end vector of a polymer molecule, δij is the Kronecker delta, C* is the dye concentration and D is the diffusivity of the dye molecule. Note that here ()* denotes a dimensional variable. The corresponding non-dimensional forms of the above governing equations are written as below:| |  | (9) |
Momentum equation:| |  | (10) |
Ohmic model equation:| |  | (11) |
| |  | (12) |
| |  | (13) |
Oldroyd-B viscoelastic constitutive equation:| |  | (14) |
| |  | (15) |
Dye transport equation:| |  | (16) |
Note that the following scaling variables are used to non-dimensionalize the governing equations: position with H, velocity with Uev, time with  pressure and polymeric stress tensor with
pressure and polymeric stress tensor with  electric field with Ea, and charge density with
electric field with Ea, and charge density with  . Here Uev is the electroviscous velocity defined as
. Here Uev is the electroviscous velocity defined as  and Ea is the apparent applied electric field calculated as
and Ea is the apparent applied electric field calculated as  , where η0 is the zero-shear rate viscosity of the polymer solution, and VE and VN are the voltages applied at the east and north sides of the device, respectively. It can be seen that the present electrokinetic flow phenomena will be governed by several dimensionless numbers. The first is the Reynolds number defined as
, where η0 is the zero-shear rate viscosity of the polymer solution, and VE and VN are the voltages applied at the east and north sides of the device, respectively. It can be seen that the present electrokinetic flow phenomena will be governed by several dimensionless numbers. The first is the Reynolds number defined as  which is small in the present study so that the effect of the inertial forces on the flow dynamics can be neglected. The second is the electric Rayleigh number defined as
which is small in the present study so that the effect of the inertial forces on the flow dynamics can be neglected. The second is the electric Rayleigh number defined as  which is the ratio of the electroviscous velocity to the diffusive velocity. The third is the Weissenberg number defined as
which is the ratio of the electroviscous velocity to the diffusive velocity. The third is the Weissenberg number defined as  which is the ratio of the polymer relaxation time to the time scale of flow. Note that for a Newtonian fluid, this number is essentially zero. The fourth is the polymer viscosity ratio defined as
which is the ratio of the polymer relaxation time to the time scale of flow. Note that for a Newtonian fluid, this number is essentially zero. The fourth is the polymer viscosity ratio defined as  which is the ratio of the solvent viscosity to the zero-shear rate viscosity of a polymeric fluid. The Peclet number appearing in eqn (16) is defined as
which is the ratio of the solvent viscosity to the zero-shear rate viscosity of a polymeric fluid. The Peclet number appearing in eqn (16) is defined as  , and a high value of the Peclet number (∼106) was utilised to omit any sort of diffusion of the dye molecule in the present problem. Apart from these dimensionless numbers, additionally, the following two dimensionless numbers are also present in this study, namely, conductivity ratio
, and a high value of the Peclet number (∼106) was utilised to omit any sort of diffusion of the dye molecule in the present problem. Apart from these dimensionless numbers, additionally, the following two dimensionless numbers are also present in this study, namely, conductivity ratio  and voltage ratio
and voltage ratio  where VS and VN are the applied voltages at the south and north sides of the microfluidic device, respectively, as depicted in Fig. 1. Furthermore, the present system size is of the order of O ∼ 10−4 m, whereas the Debye length is of the order of O ∼ 10−9 m. The charge-relaxation time is of the order of O ∼ 10−10 s, whereas the present flow time scale is of the order of O ∼ 10−1 s. Both these orders of magnitude analyses further justify the use of the present modified Ohmic electroosmotic flow model in this study.
where VS and VN are the applied voltages at the south and north sides of the microfluidic device, respectively, as depicted in Fig. 1. Furthermore, the present system size is of the order of O ∼ 10−4 m, whereas the Debye length is of the order of O ∼ 10−9 m. The charge-relaxation time is of the order of O ∼ 10−10 s, whereas the present flow time scale is of the order of O ∼ 10−1 s. Both these orders of magnitude analyses further justify the use of the present modified Ohmic electroosmotic flow model in this study.
 |
| | Fig. 1 Schematic of the microfluidic T-junction device used in this study. The inlet microchannels have heights of H, while the outlet microchannel has a height of 2H. The lengths of the upper and bottom inlets are LI,U = 5.25H and LI,B = 5.25H, respectively, and the outlet length is LO = 20H. Applied voltages at the north (N), south (S), and east (E) boundaries are denoted as VN, VS, and VE, respectively. Here, H = 100 µm. | |
Finally, the problem statement was completed by employing the following boundary conditions. For the pressure field, atmospheric exposure at all inlets and outlets was modeled using a fixed-value condition (p = 0), while impermeable solid boundaries were treated with a homogeneous Neumann condition  where ni denotes the outward unit normal vector. For the electric potential, a prescribed constant value (ψ = C) was imposed at the inlet and outlet planes, with C determined by the apparent electric field strength Ea and the applied voltage ratio VR. At all solid surfaces, an insulating condition
where ni denotes the outward unit normal vector. For the electric potential, a prescribed constant value (ψ = C) was imposed at the inlet and outlet planes, with C determined by the apparent electric field strength Ea and the applied voltage ratio VR. At all solid surfaces, an insulating condition  was enforced. The velocity field was specified by applying a zero-gradient condition
was enforced. The velocity field was specified by applying a zero-gradient condition  at the inlet and outlet boundaries, while electroosmotic slip was enforced along the walls through
at the inlet and outlet boundaries, while electroosmotic slip was enforced along the walls through  following Chen et al.43 Here, the reference mobility is defined as
following Chen et al.43 Here, the reference mobility is defined as  with ζ0 representing the reference wall zeta potential, σ0 the reference electrical conductivity, and η0 the zero-shear viscosity of the polymeric fluid. The exponent m accounts for the experimentally observed power-law dependence of the zeta potential on conductivity, and consistent with prior work,43 a value of m = −0.3 was adopted in the present study. However, other values of m, such as 0 and −0.1, were also used, and it has been found that it has hardly any influence on the flow dynamics and mixing efficiency.
with ζ0 representing the reference wall zeta potential, σ0 the reference electrical conductivity, and η0 the zero-shear viscosity of the polymeric fluid. The exponent m accounts for the experimentally observed power-law dependence of the zeta potential on conductivity, and consistent with prior work,43 a value of m = −0.3 was adopted in the present study. However, other values of m, such as 0 and −0.1, were also used, and it has been found that it has hardly any influence on the flow dynamics and mixing efficiency.
3 Computational details
3.1 Numerical solution procedure
In this work, the governing equations describing mass conservation, momentum transport, charge conservation (Ohmic law), and the Oldroyd-B constitutive relation were solved with the help of the rheoEFoam solver from the RheoTool package of version 5.45 This solver is built upon the open-source CFD platform OpenFOAM46 (version 7). Since a comprehensive description of rheoEFoam can be found in Pimenta et al.,47 only some salient features mostly related to discretisation strategies relevant to the present study are presented here. The advective contributions were handled using the high-resolution CUBISTA scheme (Convergent and Universally Bounded Interpolation Scheme for Treatment of Advection), chosen for its favourable convergence behaviour. Diffusive fluxes were approximated by the second-order Gauss linear orthogonal scheme, while gradients were evaluated with the Gauss linear method. For temporal discretisation, a backward implicit scheme was adopted. Regarding the solution of the linear systems, the fields of pressure, velocity, and electric potential were computed using the Geometric-Algebraic Multi-Grid (GAMG) solver with a DIC (Diagonal-based Incomplete Cholesky) preconditioner, whereas the viscoelastic stress, dye concentration, and electrical conductivity equations were treated with the Preconditioned Bi-Conjugate Gradient (PBiCG) solver in combination with a DILU (Diagonal-based Incomplete Lower-Upper) preconditioner. The SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm was employed to achieve pressure–velocity coupling. The numerical stability in the viscoelastic constitutive equations was ensured through the log-conformation tensor approach. As per this approach, a new tensor (Θ) is introduced, which is the natural logarithm of the conformation tensor A, defined as Θ = ln(A) = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(E)BT. Since A is a positive-definite tensor, it is diagonalized as A = BEBT, where B is a matrix consisting of eigenvectors of A in its columns and the diagonal elements of matrix E contain the corresponding eigenvalues, which result from the decomposition of A. The transformation of a variable from A to Θ results in the following constitutive relation:
ln(E)BT. Since A is a positive-definite tensor, it is diagonalized as A = BEBT, where B is a matrix consisting of eigenvectors of A in its columns and the diagonal elements of matrix E contain the corresponding eigenvalues, which result from the decomposition of A. The transformation of a variable from A to Θ results in the following constitutive relation:| |  | (17) |
where| |  | (18) |
| |  | (19) |
| |  | (20) |
| |  | (21) |
The solution of the constitutive equation (eqn (17)) would lead to the diagonalized form of Θ, wherein the recovery of the conformation tensor is attained using the inverse relation: A = exp(Θ) = B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(EΘ)BT. Finally, the relation given in eqn (15) is utilized to evaluate the polymeric stress tensor τpij, which is ultimately used in the momentum equation to solve the concerned governing equations.
exp(EΘ)BT. Finally, the relation given in eqn (15) is utilized to evaluate the polymeric stress tensor τpij, which is ultimately used in the momentum equation to solve the concerned governing equations.
Furthermore, the convergence was monitored by imposing a stringent relative tolerance of 10−10 for all solved fields. A grid independence study was conducted to select the optimum grid, which, on the one hand, would not require excessive computational resources and, on the other hand, would not compromise the final results. Three different grids, namely, G1, G2, and G3, with varying numbers of total cells (see Table 1), were created, and simulations were performed at the highest value of the Weissenberg number (i.e., at Wi = 50) for all these grids. Special care was taken in making each computational grid in this study. In particular, the cell size was kept smaller near the wall region to capture the steep gradients in velocity, stress, pressure, etc.Fig. 2 shows the variation of the time-averaged mixing index along the microchannel outlet length at three different grids, and one can see that they almost coincide with each other, particularly for grids G2 and G3. It is also evident in Table 1 wherein Mmt values at the microchannel outlet are provided. Therefore, grid G2 was selected to carry out the present study for all combinations of Wi and γ values. Likewise, a time step independence study was also performed by carrying out simulations at two different time step size values, namely, Δt* = 1 × 10−4 s and Δt* = 5 × 10−5 s, again at the highest Weissenberg number used in this study. Fig. 3 depicts the temporal variation of the instantaneous mixing index at the microchannel outlet for these two time step size values. Once again, it can be seen that the difference in mixing index values is negligible between the two time step size values, particularly at later times. Furthermore, the corresponding time-averaged mixing index values shown in the legend of the same figure also become almost indistinguishable from each other, leading to the use of Δt* = 1 × 10−4 s in the present study for all simulations.
Table 1 Grid details for carrying out the grid independence study. Here, Nt is the total number of cells in the computational domain and Mmt is the time-averaged mixing index evaluated at the microchannel outlet
| Grid |
N
t
|
M
m
t
|
| G1 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
0.633 |
| G2 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
0.641 |
| G3 |
86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
0.641 |
 |
| | Fig. 2 Variation of the time-averaged mixing index along the microchannel outlet length at three different grids at Wi = 50 and γ = 10. | |
 |
| | Fig. 3 Variation of the instantaneous mixing index at the microchannel outlet at two different time step sizes at Wi = 50 and γ = 10. The time-averaged values of the mixing index at the microchannel outlet are also specified in the legend of this figure. | |
Finally, the accuracy and reliability of the present rheoEFoam solver used in this study have been verified through a validation study against prior results available in the literature. Fig. 4 shows the validation of the variation of the streamwise electroosmotic velocity in a straight microchannel between the present numerical and the analytical results provided by Zhao and Yang.48 An excellent agreement is evident between the two results. In addition, extensive validations of the present rheoEFoam numerical solver against prior experimental and numerical results are also available in our earlier studies.28,37 All simulations were run in parallel using the MPI (Message Passing Interface) facility available in OpenFOAM, with 8 to 15 cores on an Intel Xeon Gold 5218 2.30 GHz 16-core server processor. The various post-processing analyses of the results were mainly performed using the open-source ParaView software.49
 |
| | Fig. 4 Comparison of the streamwise velocity component in a straight microchannel obtained with the present rheoEFoam numerical solver with the analytical results provided by Zhao and Yang48 for Newtonian fluids at a particular value of  where where  . Here c0 is the ionic density, z is the valency, e is the elementary charge, kB is the Boltzmann constant, T is the temperature, and H is the channel height. The streamwise velocity and spanwise direction are non-dimensionalised using the Helmholtz-Smoluchowski velocity us and channel height, respectively. . Here c0 is the ionic density, z is the valency, e is the elementary charge, kB is the Boltzmann constant, T is the temperature, and H is the channel height. The streamwise velocity and spanwise direction are non-dimensionalised using the Helmholtz-Smoluchowski velocity us and channel height, respectively. | |
3.2 Dynamic mode decomposition analysis
As mentioned earlier, the present study examines two distinct instabilities (EEI and EKI) that generate dynamic flow structures within the flow system. These flow structures need to be analysed thoroughly to better understand the origin and evaluation of these instabilities and their subsequent influence on the corresponding mixing dynamics. Therefore, in this study, we employ the data-driven dynamic mode decomposition algorithm28,38,50 to decompose the dynamically significant regions of the flow field into distinct modes, each associated with a particular flow structure. To ensure convergence and accurate representation of both fast and slow dynamics, a sufficiently large set of high-frequency snapshots is required. Accordingly, we collect and vectorise 1000 snapshots of the concentration field sampled at uniform temporal intervals of 0.01 s, arranged in the following form:| |  | (22) |
where  are state snapshots at equally spaced times. DMD seeks a linear operator A such thatSince A is high-dimensional, a reduced operator is computed via the singular value decomposition (SVD) of X:and the low-rank projection of A is given byThe eigen-decomposition of Ãprovides the Ritz values λj (DMD eigenvalues) on the diagonal of Λ = diag(λ1, λ2, …, λr), with eigenvectors W. The DMD modes in the original space are reconstructed asEach DMD mode ϕj evolves in time according to
are state snapshots at equally spaced times. DMD seeks a linear operator A such thatSince A is high-dimensional, a reduced operator is computed via the singular value decomposition (SVD) of X:and the low-rank projection of A is given byThe eigen-decomposition of Ãprovides the Ritz values λj (DMD eigenvalues) on the diagonal of Λ = diag(λ1, λ2, …, λr), with eigenvectors W. The DMD modes in the original space are reconstructed asEach DMD mode ϕj evolves in time according to| |  | (28) |
where the continuous-time eigenvalues are obtained from the Ritz values as| |  | (29) |
and bj are mode amplitudes determined from the initial condition.
4 Results and discussion
First, the results are presented and discussed for the following sets of parameters: VR = 1, Rae = 2773.07, Re = 2.7, γ = 1 and 10, β = 0.5, and for a range of values of Wi between 0 and 50. Note that the case with Wi = 0 and β = 1 represents the results for a Newtonian fluid. We begin the discussion of the results by presenting the instantaneous streamline and dye concentration profiles within the microdevice, which can be particularly useful for understanding the flow pattern, including the flow transition in the present system. Fig. 5 shows the corresponding results for the case where no electrical gradients persist between the fluids entering the microdevice from the south and north inlets, i.e., at a value of γ = 1. For a Newtonian fluid, streamlines are seen to be very ordered, straight and parallel to each other in the outlet port of the device, suggesting the presence of a steady and laminar flow field (Fig. 5(a)). This results in the flow being perfectly symmetric along the horizontal plane passing through the origin of the present flow system. On the other hand, under the same operating conditions, the viscoelastic fluid with Wi = 15 shows a different trend in the streamline profiles compared to the Newtonian fluid. Notably, it can be seen that the streamlines become distorted for this fluid, particularly in the entry region of the outlet port of the microdevice, as can be seen from Fig. 5(b). Therefore, the streamlines no longer remain straight and symmetric along the horizontal plane passing through the origin of the microdevice. The existence of such a flow pattern suggests the onset of some kind of instability within the present microdevice. As the Weissenberg number further increases to 50, the streamlines are found to be more distorted, particularly in the downstream region of the microdevice (Fig. 5(c)). Not only distortion but also vortices adhering to the microchannel wall are observed to be present in viscoelastic fluids with this Weissenberg number. The presence of such a flow situation suggests that the flow becomes chaotic and irregular under these conditions, and the instability triggered at Wi = 15 now becomes further intensified at Wi = 50. The corresponding dye concentration profiles also clearly indicate this flow transition as the Weissenberg number increases gradually. For Newtonian fluids (Fig. 5(d)), the interface between the dyed and undyed fluids remains almost straight, suggesting the presence of a steady and ordered flow. For viscoelastic fluids with Wi = 15 (Fig. 5(e)), almost the same trend is observed. In contrast, at Wi = 50, the interface becomes highly wavy in nature, particularly at the downstream of the outlet microchannel, as can be seen from Fig. 5(f).
 |
| | Fig. 5 Representative streamline (first column) and dye (second column) patterns inside the microdevice with no electrical conductivity gradients (γ = 1) for different fluids, namely, (a) and (d) Newtonian fluids, (b) and (e) viscoelastic fluids with Wi = 15, and (c) and (f) viscoelastic fluids with Wi = 50. | |
This instability is not caused by the electrical conductivity gradient within the system, as the value of γ is kept constant at 1. Instead, it is caused by the elastic stresses present within the viscoelastic fluid, and it is particularly known as the electro-elastic instability.25 As mentioned in the Introduction section, EEI is generated due to the interaction between the normal elastic stresses and the streamline curvature present within the flow system. To characterise this instability and chaotic nature of the flow field, we have further depicted the surface distribution of the spanwise velocity component fluctuation  in Fig. 6 for different fluids. Here,
in Fig. 6 for different fluids. Here,  is defined as
is defined as  where ui2 is the instantaneous spanwise velocity component value and 〈u2〉 is its time-averaged value at a point in the flow domain. The reason for showing the spanwise velocity component fluctuation is that this component can facilitate the mixing of two fluids flowing side by side inside the microdevice. It can be seen that the velocity fluctuation shows almost zero value for Newtonian (Fig. 6(a)) and viscoelastic fluids with Wi = 15 (Fig. 6(b)), whereas a region of high velocity fluctuation is present in the central part of the outlet microchannel of the microdevice for viscoelastic fluids with Wi = 50, as observed in Fig. 6(c). Moreover, the intensity of velocity fluctuation is seen to be notably higher near the end of the outlet microchannel.
where ui2 is the instantaneous spanwise velocity component value and 〈u2〉 is its time-averaged value at a point in the flow domain. The reason for showing the spanwise velocity component fluctuation is that this component can facilitate the mixing of two fluids flowing side by side inside the microdevice. It can be seen that the velocity fluctuation shows almost zero value for Newtonian (Fig. 6(a)) and viscoelastic fluids with Wi = 15 (Fig. 6(b)), whereas a region of high velocity fluctuation is present in the central part of the outlet microchannel of the microdevice for viscoelastic fluids with Wi = 50, as observed in Fig. 6(c). Moreover, the intensity of velocity fluctuation is seen to be notably higher near the end of the outlet microchannel.
 |
| | Fig. 6 Spanwise velocity fluctuation component  inside the microdevice with no electrical conductivity gradients (γ = 1) for different fluids, namely, (a) Newtonian fluids, (b) viscoelastic fluids with Wi = 15, and (c) viscoelastic fluids with Wi = 50. Here, the fluctuation value is normalised with the maximum value seen among the three fluid types. inside the microdevice with no electrical conductivity gradients (γ = 1) for different fluids, namely, (a) Newtonian fluids, (b) viscoelastic fluids with Wi = 15, and (c) viscoelastic fluids with Wi = 50. Here, the fluctuation value is normalised with the maximum value seen among the three fluid types. | |
To further analyse the unsteadiness and fluctuation in the flow field, we plot the temporal variation of the streamwise velocity component  at a probe location near the entry of the outlet microchannel of the microdevice for different fluids in Fig. 7(a). For a Newtonian fluid, this velocity component reaches a steady value with time, whereas it shows almost a regular periodic type fluctuation for viscoelastic fluids at around Wi ∼ 18. At Wi = 50, this fluctuation is further increased and becomes aperiodic in nature. It suggests a gradual transition in the flow field from a steady and laminar state to a periodic unsteady state, and finally, to an aperiodic and chaotic turbulent-like state, known as the electro-elastic turbulent flow state, as the Weissenberg number gradually increases.25 The corresponding power spectrum of velocity fluctuations for viscoelastic fluids with Wi = 50 is plotted in Fig. 7(b). First of all, it can be seen that velocity fluctuations exist over a wide range of the frequency spectrum. A plateau with high PSD magnitude is observed in the low-frequency regime, corresponding to the large-scale fluctuations in the flow domain. In the high-frequency regime, an exponential decay persists, corresponding to the small-scale fluctuation in the flow domain. This is a typical trend in the PSD plot, which has also been seen in earlier studies dealing with electrokinetic flows of viscoelastic fluids at high Weissenberg numbers.33–35 The slope of the decay has a value of approximately −4.46, whereas earlier studies, comprising experiments and simulations, have found values around −4. Nevertheless, it is well-established that a slope equal to or greater than 3.5 (in magnitude) confirms the presence of elastic turbulence, which is true also in the present case.51–53
at a probe location near the entry of the outlet microchannel of the microdevice for different fluids in Fig. 7(a). For a Newtonian fluid, this velocity component reaches a steady value with time, whereas it shows almost a regular periodic type fluctuation for viscoelastic fluids at around Wi ∼ 18. At Wi = 50, this fluctuation is further increased and becomes aperiodic in nature. It suggests a gradual transition in the flow field from a steady and laminar state to a periodic unsteady state, and finally, to an aperiodic and chaotic turbulent-like state, known as the electro-elastic turbulent flow state, as the Weissenberg number gradually increases.25 The corresponding power spectrum of velocity fluctuations for viscoelastic fluids with Wi = 50 is plotted in Fig. 7(b). First of all, it can be seen that velocity fluctuations exist over a wide range of the frequency spectrum. A plateau with high PSD magnitude is observed in the low-frequency regime, corresponding to the large-scale fluctuations in the flow domain. In the high-frequency regime, an exponential decay persists, corresponding to the small-scale fluctuation in the flow domain. This is a typical trend in the PSD plot, which has also been seen in earlier studies dealing with electrokinetic flows of viscoelastic fluids at high Weissenberg numbers.33–35 The slope of the decay has a value of approximately −4.46, whereas earlier studies, comprising experiments and simulations, have found values around −4. Nevertheless, it is well-established that a slope equal to or greater than 3.5 (in magnitude) confirms the presence of elastic turbulence, which is true also in the present case.51–53
 |
| | Fig. 7 (a) Temporal variation of the streamwise velocity component at a probe location near the T-junction for various fluids. (b) The corresponding power spectrum of velocity fluctuations for viscoelastic fluids with Wi = 50. Here, the red dotted line represents a fit of the exponential decay f−α to the power spectrum in the high-frequency region. | |
As the electrical conductivity ratio is increased to γ = 10, the flow dynamics undergoes a fundamental transition, particularly in the case of Newtonian fluids, compared to the behaviour observed at γ = 1. At this higher conductivity ratio, the flow field becomes highly chaotic for Newtonian fluids, as evidenced by the strongly distorted and irregular streamline patterns shown in Fig. 8(a). This is in stark contrast to the highly ordered and symmetric flow structure observed at γ = 1 in Fig. 5(a). The onset of such chaotic behaviour can be attributed to the development of electrokinetic instabilities, which are driven by the strong conductivity gradients present at γ = 10. The intensity of these chaotic fluctuations is further confirmed in Fig. 9(a), where the surface distribution of the spanwise velocity fluctuation, represented by  , exhibits a significant increment. For viscoelastic fluids at low Weissenberg numbers (e.g., at Wi = 1), a similar trend is observed; the flow field also displays chaotic fluctuations, resembling those of Newtonian fluids (not shown here), which are evident from both the streamline distortions and the pronounced spanwise velocity fluctuations. The underlying mechanism remains the same, namely, the presence of EKI induced by the conductivity gradients. However, as the Weissenberg number is further increased to Wi = 15, the behaviour of the viscoelastic fluid markedly changes. At this Wi, the flow fluctuations are strongly suppressed, and the system reverts to a more ordered and streamlined flow state. This suppression is clearly illustrated by the nearly symmetric streamline patterns in Fig. 8(b), along with the almost negligible values of
, exhibits a significant increment. For viscoelastic fluids at low Weissenberg numbers (e.g., at Wi = 1), a similar trend is observed; the flow field also displays chaotic fluctuations, resembling those of Newtonian fluids (not shown here), which are evident from both the streamline distortions and the pronounced spanwise velocity fluctuations. The underlying mechanism remains the same, namely, the presence of EKI induced by the conductivity gradients. However, as the Weissenberg number is further increased to Wi = 15, the behaviour of the viscoelastic fluid markedly changes. At this Wi, the flow fluctuations are strongly suppressed, and the system reverts to a more ordered and streamlined flow state. This suppression is clearly illustrated by the nearly symmetric streamline patterns in Fig. 8(b), along with the almost negligible values of  shown in Fig. 9(b). These results indicate that viscoelastic stresses act to dampen the instability at higher Wi, thereby stabilising the flow.29,30,54 A detailed explanation of the underlying mechanism responsible for this suppression of EKI in viscoelastic fluids has been provided in our earlier work.32
shown in Fig. 9(b). These results indicate that viscoelastic stresses act to dampen the instability at higher Wi, thereby stabilising the flow.29,30,54 A detailed explanation of the underlying mechanism responsible for this suppression of EKI in viscoelastic fluids has been provided in our earlier work.32
 |
| | Fig. 8 Representative streamline (first column) and dye (second column) patterns inside the microdevice with the presence of electrical conductivity gradients (γ = 10) for different fluids, namely, (a) and (d) Newtonian fluids, (b) and (e) viscoelastic fluids with Wi = 15, and (c) and (f) viscoelastic fluids with Wi = 50. | |
 |
| | Fig. 9 Spanwise velocity fluctuation component  inside the microdevice with the presence of electrical conductivity gradients (γ = 10) for different fluids, namely, (a) Newtonian fluids, (b) viscoelastic fluids with Wi = 15, and (c) viscoelastic fluids with Wi = 50. Here, the fluctuation value is normalised with the maximum value seen among the three fluid types. inside the microdevice with the presence of electrical conductivity gradients (γ = 10) for different fluids, namely, (a) Newtonian fluids, (b) viscoelastic fluids with Wi = 15, and (c) viscoelastic fluids with Wi = 50. Here, the fluctuation value is normalised with the maximum value seen among the three fluid types. | |
However, with the same value of electrical conductivity ratio, i.e., γ = 10, when the extent of fluid elasticity is further increased by increasing the Weissenberg number to Wi = 50, the flow field once again transits into a chaotic and strongly fluctuating state. This behaviour is clearly evident from the highly distorted streamline patterns shown in Fig. 8(c) as well as from the finite values of the spanwise velocity fluctuation component  illustrated in Fig. 9(c). Interestingly, both the streamline configurations and the distributions of velocity fluctuations under this condition closely resemble those obtained at γ = 1 for the same Weissenberg number, as presented in Fig. 5(c) and 6(c), respectively. This similarity indicates that while the electrokinetic instability is progressively suppressed in viscoelastic fluids with increasing Wi, the electro-elastic instability can emerge at sufficiently high Weissenberg numbers irrespective of the values of the electrical conductivity ratio. The onset of EEI destabilises the flow field once again, giving rise to chaotic and turbulence-like flow dynamics. Therefore, in viscoelastic fluids subject to conductivity gradients, both instability mechanisms, EKI and EEI, can manifest depending on the elasticity level of the system. Specifically, at low values of Wi, the flow is predominantly governed by EKI, whereas at high values of Wi, the dynamics are controlled by EEI. The corresponding dye concentration profiles also clearly display the non-monotonicity in the flow field fluctuation. For both Newtonian (Fig. 8(d)) and viscoelastic fluids with Wi = 50 (Fig. 8(f)), the interface between the dyed and undyed fluids becomes wavy in nature, suggesting the presence of strong flow field fluctuation arising from the EKI and EEI phenomena, respectively. In contrast, it remains almost straight for viscoelastic fluids with Wi = 15 (Fig. 8(e)), due to the presence of an almost steady and ordered flow.
illustrated in Fig. 9(c). Interestingly, both the streamline configurations and the distributions of velocity fluctuations under this condition closely resemble those obtained at γ = 1 for the same Weissenberg number, as presented in Fig. 5(c) and 6(c), respectively. This similarity indicates that while the electrokinetic instability is progressively suppressed in viscoelastic fluids with increasing Wi, the electro-elastic instability can emerge at sufficiently high Weissenberg numbers irrespective of the values of the electrical conductivity ratio. The onset of EEI destabilises the flow field once again, giving rise to chaotic and turbulence-like flow dynamics. Therefore, in viscoelastic fluids subject to conductivity gradients, both instability mechanisms, EKI and EEI, can manifest depending on the elasticity level of the system. Specifically, at low values of Wi, the flow is predominantly governed by EKI, whereas at high values of Wi, the dynamics are controlled by EEI. The corresponding dye concentration profiles also clearly display the non-monotonicity in the flow field fluctuation. For both Newtonian (Fig. 8(d)) and viscoelastic fluids with Wi = 50 (Fig. 8(f)), the interface between the dyed and undyed fluids becomes wavy in nature, suggesting the presence of strong flow field fluctuation arising from the EKI and EEI phenomena, respectively. In contrast, it remains almost straight for viscoelastic fluids with Wi = 15 (Fig. 8(e)), due to the presence of an almost steady and ordered flow.
Both electrokinetic and electro-elastic instabilities render the flow field inside the microdevice chaotic and turbulent-like in appearance. However, their underlying physical origins and the associated fluctuation patterns are distinct from one another. For instance, in the case of EKI, the distortion of streamlines and the formation of vertical structures primarily occur at the interface between the two fluids, most prominently in the entry region of the outlet microchannel of the microdevice (Fig. 8(a)). In contrast, for EEI, these distorted structures and vortices predominantly develop further downstream along the outlet microchannel, where they are observed to be strongly wall-bounded (Fig. 8(c)). The velocity fluctuation fields corresponding to the two instabilities also exhibit pronounced differences. In the case of EKI, the intensity of velocity fluctuations is highest near the junction of the inlet and outlet sections, after which the fluctuations gradually decay toward the end of the outlet microchannel (Fig. 9(a)). On the other hand, for EEI, the opposite spatial trend is observed. The velocity fluctuation intensity is relatively weak in the upstream portion of the outlet microchannel but becomes significantly stronger toward its downstream end (Fig. 9(c)). This contrast strongly suggests that the coherent structures associated with EKI and EEI differ in nature, implying that the mixing dynamics induced by these instabilities may also be fundamentally distinct.
To quantify these differences, we employ the dynamic mode decomposition analysis of the evolving dye concentration field inside the microdevice under both instability conditions, as outlined in Section 3.2. This data-driven technique is particularly powerful for extracting dominant coherent structures and their temporal dynamics from complex flow fields.38 For both EKI and EEI cases, a total of 1000 snapshots of the dye concentration field are collected with a uniform time spacing of 0.01 s for the analysis. The corresponding Ritz values associated with the leading 100 modes for EKI and EEI are illustrated in Fig. 10(a) and (b), representing Newtonian and viscoelastic fluids, respectively. It is observed that a majority of the Ritz values lie on the unit circle in the complex plane for both instabilities. This indicates the existence of oscillatory modes or coherent structures that neither grow nor decay, but instead persist with nearly constant amplitude. Additionally, certain Ritz values are located inside the unit circle, corresponding to decaying modes, whereas others lie outside the unit circle, signifying growing modes. Hence, both instabilities are characterised by a rich modal spectrum containing persistent, decaying, and growing modes simultaneously. This highlights the dynamic richness of both EKI and EEI, exhibiting physics operating over multiple time scales, with a mixture of strong transient behaviours, sustained oscillations, and the possibility of undergoing or approaching transitions or bifurcations.
 |
| | Fig. 10 Ritz values λj for (a) Newtonian (Wi = 0) and (b) viscoelastic fluids with Wi = 50. A close-up of these values near the circumference is presented in the zoomed-in figures. | |
Fig. 11 presents the first three dominant modes (coherent structures) together with the mean mode of the flow system, obtained through dynamic mode decomposition for both the electrokinetic instability (EKI, first column) and the electro-elastic instability (EEI, second column). The mean mode represents the time-averaged dye concentration field inside the microdevice and serves as a baseline against which the fluctuating modes can be compared. It is observed that in the case of EKI, dispersion and fluctuations in the dye concentration field emerge near the entry of the outlet section of the microdevice (Fig. 11(a)). In contrast, for EEI, the onset of dispersion and fluctuations occurs much further downstream, approximately in the middle of the outlet section (Fig. 11(b)). This spatial difference in the onset location provides direct confirmation of the distinct origins of the two instabilities, namely, EKI originates in the vicinity of the T-junction, whereas EEI develops downstream of the junction. These findings are consistent with the streamline profiles and spanwise velocity fluctuation fields discussed earlier in Fig. 8 and 9, respectively, which also showed near-junction distortions for EKI and far-downstream disturbances for EEI. Another key difference in the degree of mixing is that in the case of EEI, the dye appears to be more uniformly dispersed in the outlet section compared to EKI. This qualitative observation suggests a more effective mixing process under EEI-dominated flow, a point that will be quantified and analysed in detail subsequently.
 |
| | Fig. 11 Representative DMD modes inside the microdevice for Newtonian (first column) and viscoelastic (second column) fluids with Wi = 50. The associated frequencies  are mentioned for each mode and fluid type. Here, the colour bar represents the DMD mode values corresponding to the real part of the eigenvector. The negative or positive sign in the values indicates whether the structures will oscillate (or move) together, in opposite directions, or not at all. Specifically, the blue colour (negative values) represents the structures that will move in opposite directions or out-of-phase, whereas the red colour (positive values) represents the structures that will move together or in-phase. The mean mode in DMD represents the baseline steady field (average over time), which, for the present physical variable, namely, the dye concentration, is always non-negative. Negative values correspond to fluctuations around that mean, and hence they only appear in the higher (oscillatory) DMD modes. are mentioned for each mode and fluid type. Here, the colour bar represents the DMD mode values corresponding to the real part of the eigenvector. The negative or positive sign in the values indicates whether the structures will oscillate (or move) together, in opposite directions, or not at all. Specifically, the blue colour (negative values) represents the structures that will move in opposite directions or out-of-phase, whereas the red colour (positive values) represents the structures that will move together or in-phase. The mean mode in DMD represents the baseline steady field (average over time), which, for the present physical variable, namely, the dye concentration, is always non-negative. Negative values correspond to fluctuations around that mean, and hence they only appear in the higher (oscillatory) DMD modes. | |
Examining the modal structures in detail, Mode-1 for EKI is characterised by alternating, counter-rotating coherent structures that span nearly the entire microchannel height as well as length (Fig. 11(c)). In contrast, under EEI conditions, Mode-1 is confined to the fluid–fluid interface region near the entry of the outlet microchannel, thereby localising dye dispersion close to the interface rather than across the entire microchannel height (Fig. 11(d)). However, at the far downstream, the coherent structures fill the whole microchannel height, and they seem to be more distorted compared to those in the case of the EKI phenomenon, suggesting a more chaotic flow field and hence greater mixing in the case of the EEI phenomenon. These distributions of coherent structures explain why dye spreading begins near the entry region for EKI but is delayed until further downstream for EEI. The same trend in the differences is also observed for Mode-2, albeit the structures become larger in size for both cases (Fig. 11(e) and (f)). In contrast, in Mode-3, the coherent structures are broken, particularly in the case of the EKI phenomenon (see Fig. 11(g)). Furthermore, the frequency associated with these modes is higher in the case of EEI than in the case of EKI for Mode-1 and Mode-2, suggesting a faster evaluation of these modes in the domain of the former instability than in the latter. This eventually facilitates more mixing of the fluids in the case of the electro-elastic instability phenomenon.
Therefore, it is evident that the dynamical coherent structures originating from the EKI and EEI phenomena differ significantly in both their geometric form and spatial location of origin, and these differences can have a profound impact on the efficiency of mixing between the two fluids. To illustrate this effect, we first examine the time-averaged dye concentration distribution along the outlet plane of the microchannel for three different Weissenberg numbers, namely, Wi = 0, Wi = 15, and Wi = 50, while keeping the conductivity ratio fixed at γ = 10, as shown in Fig. 12(a). For the case of Wi = 0, corresponding to Newtonian fluids where the EKI mechanism is active, the dye concentration decreases gradually from its maximum value at the lower half of the microchannel to its minimum at the upper half. This gradient indicates partial mixing of the two fluid streams, with the chaotic fluctuations introduced by EKI promoting some degree of dispersion. However, when the Weissenberg number is increased to Wi = 15, a very different picture emerges. The dye field becomes almost completely segregated into two distinct regions, a dyed lower half and an undyed upper half, with minimal interfacial mixing. This is manifested in the time-averaged profile by a very steep slope near the microchannel centerline, reflecting the suppression of EKI at this elasticity level and the absence of significant instability-driven mixing.
 |
| | Fig. 12 (a) Time-averaged dye concentration profiles after 50 s at the outlet plane of the microfluidic T-junction at different Weissenberg numbers. (b) The corresponding probability density function of the dye concentration field. Here, the vertical dashed line indicates the value of the mean concentration field (i.e., 0.5) for perfectly mixed fluids. (c) Temporal evaluation of the mixing efficiency parameter for Newtonian and viscoelastic fluids with Wi = 50. (d) Variation of the maximum achievable mixing efficiency with the Weissenberg number. In part (d), the vertical dashed line shows an approximate value of the Weissenberg number for the onset of the electro-elastic instability. | |
As the Weissenberg number is further increased to Wi = 50, the mixing characteristics change once again. In this case, the dye concentration decreases from the lower to the upper half of the microchannel, but with the appearance of a plateau region near the mid-plane. Moreover, the maximum concentration near the lower wall and the minimum concentration near the upper wall are both closer to each other compared to the previous two cases. This indicates a more uniform distribution of the dye, consistent with the onset of the EEI phenomenon at high elasticity. The stronger downstream coherent structures generated by EEI enhance the interfacial stretching and folding of fluid elements, thereby promoting a more effective mixing process. This interpretation is further corroborated in Fig. 12(b), where the probability density function (PDF) of the dye concentration is plotted for different Weissenberg numbers. For Wi = 50, where EEI dominates, the PDF exhibits a sharp peak centred at approximately C ∼ 0.33. In contrast, for Wi = 0, corresponding to the EKI regime, the peak occurs around C ∼ 0.25. Since the perfectly mixed state corresponds to C = 0.5 (as shown by the vertical dashed line in this figure), the distribution at Wi = 50 lies closer to this ideal value, thereby confirming quantitatively that EEI leads to more efficient mixing than EKI.
To assess the mixing process more quantitatively, we evaluate a temporal mixing efficiency parameter, defined in the present study as
| |  | (30) |
Here,
Ct represents the local dye concentration at a given point and time
t,
C* denotes the dye concentration in the case of perfectly mixed fluids (with
C* = 0.5), and
C0 is the initial dye concentration of the unmixed fluids. Since
C0 can take values of either 0 or 1, the denominator in the above expression simplifies to a constant value of 0.5. The parameter
Mt therefore provides a normalised measure of mixing efficiency, ranging from 0 (completely unmixed) to 1 (perfectly mixed). The temporal evolution of
Mt for two representative cases, Wi = 0 and Wi = 50, corresponding to the EKI- and EEI-dominated regimes, respectively, is shown in
Fig. 12(c). In both cases,
Mt increases monotonically with time and eventually approaches a plateau value at approximately
t* = 5 s, indicating the establishment of a quasi-steady mixing state. Importantly, the plateau value of
Mt is significantly higher for Wi = 50 than for Wi = 0, implying that EEI enhances the overall mixing efficiency more effectively than EKI. To further illustrate this behaviour, the plateau (maximum) values of
Mt are plotted as a function of the Weissenberg number in
Fig. 12(d). The trend reveals a clear non-monotonic dependence of the mixing efficiency on Wi. At Wi = 0, the mixing process is facilitated by the EKI mechanism, which induces chaotic fluctuations at the fluid–fluid interface. However, as the Weissenberg number increases from 0 to intermediate values (
e.g., Wi ≈ 15), the EKI phenomenon becomes progressively suppressed by elastic effects, resulting in a sharp decline in mixing efficiency. Beyond a critical Wi (as shown by the vertical dashed line in
Fig. 12(d)), the EEI mechanism emerges, reintroducing strong instabilities into the flow. This leads to renewed mixing, with efficiency surpassing that of the Newtonian case (Wi = 0). With further increase in Wi, the intensity of EEI grows and the system eventually transits into the regime of electro-elastic turbulence (as demonstrated in
Fig. 7), which significantly amplifies fluid stretching and folding, thereby achieving increased mixing beyond that produced by EKI alone. Thus, the overall variation of mixing efficiency with the Weissenberg number exhibits a non-monotonic trend. It is strong at low Wi due to EKI, weak at intermediate Wi due to suppression of EKI, and strong again at high Wi owing to the onset and intensification of EEI, which ultimately transits to the electro-elastic turbulence regime.
In Fig. 12, the mixing efficiency parameter is particularly evaluated at the exit of the outlet microchannel. However, it can be seen from the mean dye concentration field that it varies along the length of the outlet microchannel (see Fig. 11(a) and (b)), and hence the location at which the mixing efficiency parameter is evaluated is very important. Fig. 13 depicts the maximum values of the mixing efficiency parameter along with the non-dimensional length of the outlet microchannel at two values of the Weissenberg number, namely, Wi = 0, at which only EKI exists, and Wi = 50, at which EEI appears. In both cases, the mixing efficiency parameter increases as one traverses towards the exit of the outlet microchannel. However, this increment is more pronounced in the case of Wi = 50 than in the case of Wi = 0, due to the appearance of chaotic flow behaviour resulting from the EEI phenomenon, particularly at the downstream side of the outlet microchannel, as pointed out and discussed earlier. Furthermore, a crossover length of the outlet microchannel is present (x1 ∼ 16), beyond which mixing due to the EEI phenomenon is more effective compared to the EKI phenomenon. Therefore, the outlet microchannel length should be sufficiently long for the EEI phenomenon to be superior in mixing the two fluids compared to the EKI phenomenon.
 |
| | Fig. 13 Variation of the mixing efficiency parameter along the non-dimensional length of the outlet microchannel at Wi = 0 and 50. | |
So far, in this study, the results at different Weissenberg numbers were obtained by varying the relaxation time λ while keeping all other parameters constant. Although computationally convenient, this approach implicitly assumes different viscoelastic fluids possessing distinct relaxation times but otherwise identical material properties. This assumption may become difficult to realise and follow, particularly in the context of experiments. In the case of experiments, generally, a given viscoelastic fluid with a fixed λ is typically used, and Wi is varied by altering the electroosmotic velocity Uev through modulation of the applied electric field strength Ea. However, varying Ea simultaneously changes the electric Rayleigh and Reynolds numbers in addition to the Weissenberg number, making it difficult to isolate the direct influence of fluid elasticity on the flow dynamics and mixing behaviour. Nevertheless, to address this experimentally relevant scenario, we also performed simulations wherein the relaxation time was fixed at λ = 0.1 s, and Wi was varied by changing Ea and/or Rae. The chosen λ value ensures that the Reynolds number remains small throughout the investigated range of electric field strengths so that the effect of the inertial forces remains negligible. Fig. 14 presents the instantaneous dye concentration fields at two representative values of Rae for both Newtonian and viscoelastic fluids. For the Newtonian case, electrokinetic instabilities appear at Rae = 2000, which are further intensified at Rae = 3000. In contrast, for the viscoelastic fluid with Wi = 20, no instability is observed even at Rae = 2000, suggesting suppression of EKI due to fluid elasticity. At a higher Rae = 3000 (corresponding to Wi = 30), the dye concentration field exhibits pronounced spatial fluctuations, signifying the onset of an electro-elastic instability. The observed wavy concentration patterns, particularly downstream near the outlet region, are consistent with the characteristics of electro-elastic instability, as discussed earlier. Overall, these results reaffirm that increasing fluid elasticity, quantified by the Weissenberg number, initially suppresses the electrokinetic instability observed in Newtonian fluids but eventually promotes the emergence of electro-elastic instability at sufficiently high Weissenberg numbers, thereby increasing mixing within the microdevice, as also observed in the first approach for obtaining the Weissenberg number by varying the relaxation time λ.
 |
| | Fig. 14 Instantaneous dye concentration profiles inside the microdevice for Newtonian fluids (a) and (c), viscoelastic fluids with Wi = 20 (b) and viscoelastic fluids with Wi = 30 (d) for two values of Rae, namely, 2000 and 3000. | |
5 Conclusions
This study conducted a comprehensive numerical investigation of electrokinetic flows involving viscoelastic fluids with electrical conductivity gradients in a microfluidic T-junction, focusing on the interplay between fluid instabilities and mixing dynamics. Two distinct instability mechanisms were identified within the system, namely, electrokinetic instability (EKI), originating from conductivity gradients, and electro-elastic instability (EEI), driven by elastic stresses inherent to the viscoelastic fluid. Our results reveal a non-monotonic dependence of mixing efficiency on the Weissenberg number (Wi), which quantifies the extent of elasticity in a fluid. At low to moderate values of Wi, the increasing elasticity suppresses the EKI, reducing the chaotic nature of the flow and consequently diminishing mixing efficiency. This observation aligns with recent experimental29,30,54 and numerical findings.32 However, beyond a critical Wi, the flow undergoes a transition marked by the emergence of EEI, which introduces new flow instabilities and restores and increases mixing efficiency. Although both EEI and EKI induce chaotic structures that facilitate mixing, they differ fundamentally in their spatial origin, flow topology, and temporal dynamics. Using the data-driven dynamic mode decomposition (DMD) technique, this study systematically decomposed the flow fields to extract coherent modes associated with each instability. This analysis provided new insights into the distinct mechanisms and modal structures governing the onset and evolution of EEI and EKI. In summary, the study highlights the crucial role of viscoelasticity in modulating flow instabilities and mixing behaviour in electrokinetically driven microflows. By identifying the conditions under which each instability dominates and how they impact mixing, the findings offer a scientific framework for controlling and optimising mixing performance in microfluidic applications involving complex fluids under electric fields. This work paves the way for designing next-generation microdevices that exploit tailored instabilities for increased mixing and transport processes.
Conflicts of interest
There is no conflict to declare.
Data availability
Data for this article are available within the article.
Acknowledgements
CS acknowledges the financial support from the Anusandhan National Research Foundation (ANRF), Government of India, through a core research grant (CRG/2023/001908) and AC thanks the Ministry of Education, Government of India, for the financial support provided by the PMRF (Cycle-9).
Notes and references
-
J. H. Masliyah and S. Bhattacharjee, Electrokinetic and colloid transport phenomena, John Wiley & Sons, 2006 Search PubMed.
- S. Wall, Curr. Opin. Colloid Interface Sci., 2010, 15, 119–124 CrossRef CAS.
-
D. Li, Electrokinetics in microfluidics, Elsevier, 2004, vol. 2 Search PubMed.
- G. J. Bruin, Electrophoresis, 2000, 21, 3931–3951 Search PubMed.
- L. Bousse, C. Cohen, T. Nikiforov, A. Chow, A. R. Kopf-Sill, R. Dubrow and J. W. Parce, Annu. Rev. Biophys. Biomol. Struct., 2000, 29, 155–181 CrossRef CAS PubMed.
- M. H. Oddy, J. G. Santiago and J. C. Mikkelsen, Anal. Chem., 2001, 73, 5822–5832 CrossRef CAS PubMed.
- H. Lin, Mech. Res. Commun., 2009, 36, 33–38 CrossRef.
- H. Lin, B. D. Storey, M. H. Oddy, C.-H. Chen and J. G. Santiago, Phys. Fluids, 2004, 16, 1922–1935 CrossRef CAS.
- M.-Z. Huang, R.-J. Yang, C.-H. Tai, C.-H. Tsai and L.-M. Fu, Biomed. Microdevices, 2006, 8, 309–315 CrossRef CAS PubMed.
- W.-J. Luo, Microfluid. Nanofluid., 2009, 6, 189–202 CrossRef CAS.
- Q. Li, Y. Delorme and S. H. Frankel, Microfluid. Nanofluid., 2016, 20, 1–12 CrossRef CAS.
- H. Hadidi, E. Zandi, M. Al-Bahrani and R. Kamali, Chem. Eng. Process., 2024, 199, 109745 CrossRef CAS.
- J. Park, S. Shin, K. Y. Huh and I. Kang, Phys. Fluids, 2005, 17, 118101 CrossRef.
- Z. Jin and H. Hu, J. Visualization, 2010, 13, 229–239 CrossRef CAS.
- C.-C. Chang and R.-J. Yang, Microfluid. Nanofluid., 2007, 3, 501–525 CrossRef CAS.
- S. Gupta, W. S. Wang and S. A. Vanapalli, Biomicrofluidics, 2016, 10, 043402 CrossRef PubMed.
-
A. Borzacchiello, L. Ambrosio, P. Netti and L. Nicolais, Tissue engineering and novel delivery systems, CRC Press, 2003, pp. 341–361 Search PubMed.
- S. J. Haward, V. Sharma and J. A. Odell, Soft Matter, 2011, 7, 9908–9921 RSC.
- G. B. Thurston, Biophys. J., 1972, 12, 1205–1217 CrossRef CAS PubMed.
- S. S. Davis, Rheol. Acta, 1971, 10, 28–35 CrossRef CAS.
- M. Brust, C. Schaefer, R. Doerr, L. Pan, M. Garcia, P. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS.
- E. Nader, S. Skinner, M. Romana, R. Fort, N. Lemonne, N. Guillot, A. Gauthier, S. Antoine-Jonville, C. Renoux and M.-D. Hardy-Dessources,
et al.
, Front. Physiol., 2019, 10, 1329 CrossRef.
- A. N. Beris, J. S. Horner, S. Jariwala, M. J. Armstrong and N. J. Wagner, Soft Matter, 2021, 17, 10591–10613 RSC.
- C. Zhao and C. Yang, Adv. Colloid Interface Sci., 2013, 201, 94–108 CrossRef PubMed.
- C. Sasmal, Micromachines, 2025, 16, 187 CrossRef.
-
R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids. Fluid Mechanics, John Wiley and Sons Inc., New York, NY, 1987, vol. 1 Search PubMed.
-
R. P. Chhabra and J. F. Richardson, Non-Newtonian Flow and Applied Rheology: Engineering Applications, Butterworth-Heinemann, 2011 Search PubMed.
- F. Hamid and C. Sasmal, Phys. Fluids, 2023, 35, 013107 Search PubMed.
- T.-L. Chen, M. K. Raihan, S. M. Tabarhoseini, C. T. Gabbard, M. M. Islam, Y.-H. Lee, J. B. Bostwick, L.-M. Fu and X. Xuan, Soft Matter, 2025, 21, 699–707 Search PubMed.
- L. Song, P. Jagdale, L. Yu, Z. Liu, D. Li, C. Zhang and X. Xuan, Phys. Fluids, 2019, 31, 082001 Search PubMed.
- T.-L. Chen, M. M. Islam, C. T. Gabbard, Y.-H. Lee, M. K. Raihan, J. B. Bostwick, L.-M. Fu and X. Xuan, Phys. Fluids, 2025, 37, 062016 CrossRef CAS.
- C. Sasmal, Phys. Fluids, 2022, 34, 082011 CrossRef CAS.
- S. H. Sadek, F. T. Pinho and M. A. Alves, J. Non-Newtonian Fluid Mech., 2020, 283, 104293 Search PubMed.
- F. Pimenta and M. Alves, J. Non-Newtonian Fluid Mech., 2018, 259, 61–77 CrossRef CAS.
- M. B. Khan, F. Hamid, N. Ali, V. Mehandia and C. Sasmal, Phys. Fluids, 2023, 35, 083101 CrossRef CAS.
- M. B. Khan and C. Sasmal, Eur. J. Mech. B, 2023, 97, 173–186 CrossRef.
- C. Sasmal, Sci. Rep., 2022, 12, 1–13 CrossRef PubMed.
- P. J. Schmid, J. Fluid Mech., 2010, 656, 5–28 CrossRef CAS.
- E. S. G. Shaqfeh and B. Khomami, J. Non-Newtonian Fluid Mech., 2021, 298, 104672 Search PubMed.
- D. F. James, Annu. Rev. Fluid Mech., 2009, 41, 129–142 CrossRef.
-
R. B. Bird, C. F. Curtiss, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Kinetic Theory, Wiley, 1987, vol. 2 Search PubMed.
-
J. R. Melcher, Continuum electromechanics, MIT Press, Cambridge, 1981, vol. 2 Search PubMed.
- C.-H. Chen, H. Lin, S. K. Lele and J. G. Santiago, J. Fluid Mech., 2005, 524, 263–303 CrossRef.
- J. D. Posner and J. G. Santiago, J. Fluid Mech., 2006, 555, 1–42 CrossRef.
-
F. Pimenta and M. Alves, rheoTool, https://github.com/fppimenta/rheoTool, 2016.
- H. G. Weller, G. Tabor, H. Jasak and C. Fureby, Comput. Phys., 1998, 12, 620–631 CrossRef.
-
F. Pimenta and M. A. Alves, arXiv, 2018, preprint, arXiv:1802.02843, DOI: 10.48550/arXiv.1802.02843.
- C. Zhao and C. Yang, J. Non-Newtonian Fluid Mech., 2011, 166, 1076–1079 CrossRef CAS.
- ParaView Development Team, ParaView, https://www.paraview.org, 2018, Version 5.6.0.
- F. Hamid, C. Sasmal and R. Chhabra, Phys. Fluids, 2022, 34, 103114 CrossRef CAS.
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding and A. Frishman,
et al.
, Phys. Rev. Fluids, 2022, 7, 080701 CrossRef.
- C. Sasmal, J. Non-Newtonian Fluid Mech., 2025, 105393 Search PubMed.
- A. Groisman and V. Steinberg, Nature, 2000, 405, 53–55 CrossRef CAS PubMed.
- L. Song, L. Yu, D. Li, P. P. Jagdale and X. Xuan, Electrophoresis, 2020, 41, 588–597 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  *,
T.
Waghmare
and
A.
Chauhan
*,
T.
Waghmare
and
A.
Chauhan


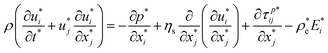


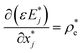



 . Here D+ and D− are the diffusivities of positive and negative ions, respectively. Aij = 〈RiRj〉 is the conformation tensor where Ri is the dimensionless end-to-end vector of a polymer molecule, δij is the Kronecker delta, C* is the dye concentration and D is the diffusivity of the dye molecule. Note that here ()* denotes a dimensional variable. The corresponding non-dimensional forms of the above governing equations are written as below:
. Here D+ and D− are the diffusivities of positive and negative ions, respectively. Aij = 〈RiRj〉 is the conformation tensor where Ri is the dimensionless end-to-end vector of a polymer molecule, δij is the Kronecker delta, C* is the dye concentration and D is the diffusivity of the dye molecule. Note that here ()* denotes a dimensional variable. The corresponding non-dimensional forms of the above governing equations are written as below:







 pressure and polymeric stress tensor with
pressure and polymeric stress tensor with  electric field with Ea, and charge density with
electric field with Ea, and charge density with  . Here Uev is the electroviscous velocity defined as
. Here Uev is the electroviscous velocity defined as  and Ea is the apparent applied electric field calculated as
and Ea is the apparent applied electric field calculated as  , where η0 is the zero-shear rate viscosity of the polymer solution, and VE and VN are the voltages applied at the east and north sides of the device, respectively. It can be seen that the present electrokinetic flow phenomena will be governed by several dimensionless numbers. The first is the Reynolds number defined as
, where η0 is the zero-shear rate viscosity of the polymer solution, and VE and VN are the voltages applied at the east and north sides of the device, respectively. It can be seen that the present electrokinetic flow phenomena will be governed by several dimensionless numbers. The first is the Reynolds number defined as  which is small in the present study so that the effect of the inertial forces on the flow dynamics can be neglected. The second is the electric Rayleigh number defined as
which is small in the present study so that the effect of the inertial forces on the flow dynamics can be neglected. The second is the electric Rayleigh number defined as  which is the ratio of the electroviscous velocity to the diffusive velocity. The third is the Weissenberg number defined as
which is the ratio of the electroviscous velocity to the diffusive velocity. The third is the Weissenberg number defined as  which is the ratio of the polymer relaxation time to the time scale of flow. Note that for a Newtonian fluid, this number is essentially zero. The fourth is the polymer viscosity ratio defined as
which is the ratio of the polymer relaxation time to the time scale of flow. Note that for a Newtonian fluid, this number is essentially zero. The fourth is the polymer viscosity ratio defined as  which is the ratio of the solvent viscosity to the zero-shear rate viscosity of a polymeric fluid. The Peclet number appearing in eqn (16) is defined as
which is the ratio of the solvent viscosity to the zero-shear rate viscosity of a polymeric fluid. The Peclet number appearing in eqn (16) is defined as  , and a high value of the Peclet number (∼106) was utilised to omit any sort of diffusion of the dye molecule in the present problem. Apart from these dimensionless numbers, additionally, the following two dimensionless numbers are also present in this study, namely, conductivity ratio
, and a high value of the Peclet number (∼106) was utilised to omit any sort of diffusion of the dye molecule in the present problem. Apart from these dimensionless numbers, additionally, the following two dimensionless numbers are also present in this study, namely, conductivity ratio  and voltage ratio
and voltage ratio  where VS and VN are the applied voltages at the south and north sides of the microfluidic device, respectively, as depicted in Fig. 1. Furthermore, the present system size is of the order of O ∼ 10−4 m, whereas the Debye length is of the order of O ∼ 10−9 m. The charge-relaxation time is of the order of O ∼ 10−10 s, whereas the present flow time scale is of the order of O ∼ 10−1 s. Both these orders of magnitude analyses further justify the use of the present modified Ohmic electroosmotic flow model in this study.
where VS and VN are the applied voltages at the south and north sides of the microfluidic device, respectively, as depicted in Fig. 1. Furthermore, the present system size is of the order of O ∼ 10−4 m, whereas the Debye length is of the order of O ∼ 10−9 m. The charge-relaxation time is of the order of O ∼ 10−10 s, whereas the present flow time scale is of the order of O ∼ 10−1 s. Both these orders of magnitude analyses further justify the use of the present modified Ohmic electroosmotic flow model in this study.
 where ni denotes the outward unit normal vector. For the electric potential, a prescribed constant value (ψ = C) was imposed at the inlet and outlet planes, with C determined by the apparent electric field strength Ea and the applied voltage ratio VR. At all solid surfaces, an insulating condition
where ni denotes the outward unit normal vector. For the electric potential, a prescribed constant value (ψ = C) was imposed at the inlet and outlet planes, with C determined by the apparent electric field strength Ea and the applied voltage ratio VR. At all solid surfaces, an insulating condition  was enforced. The velocity field was specified by applying a zero-gradient condition
was enforced. The velocity field was specified by applying a zero-gradient condition  at the inlet and outlet boundaries, while electroosmotic slip was enforced along the walls through
at the inlet and outlet boundaries, while electroosmotic slip was enforced along the walls through  following Chen et al.43 Here, the reference mobility is defined as
following Chen et al.43 Here, the reference mobility is defined as  with ζ0 representing the reference wall zeta potential, σ0 the reference electrical conductivity, and η0 the zero-shear viscosity of the polymeric fluid. The exponent m accounts for the experimentally observed power-law dependence of the zeta potential on conductivity, and consistent with prior work,43 a value of m = −0.3 was adopted in the present study. However, other values of m, such as 0 and −0.1, were also used, and it has been found that it has hardly any influence on the flow dynamics and mixing efficiency.
with ζ0 representing the reference wall zeta potential, σ0 the reference electrical conductivity, and η0 the zero-shear viscosity of the polymeric fluid. The exponent m accounts for the experimentally observed power-law dependence of the zeta potential on conductivity, and consistent with prior work,43 a value of m = −0.3 was adopted in the present study. However, other values of m, such as 0 and −0.1, were also used, and it has been found that it has hardly any influence on the flow dynamics and mixing efficiency.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(E)BT. Since A is a positive-definite tensor, it is diagonalized as A = BEBT, where B is a matrix consisting of eigenvectors of A in its columns and the diagonal elements of matrix E contain the corresponding eigenvalues, which result from the decomposition of A. The transformation of a variable from A to Θ results in the following constitutive relation:
ln(E)BT. Since A is a positive-definite tensor, it is diagonalized as A = BEBT, where B is a matrix consisting of eigenvectors of A in its columns and the diagonal elements of matrix E contain the corresponding eigenvalues, which result from the decomposition of A. The transformation of a variable from A to Θ results in the following constitutive relation:




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(EΘ)BT. Finally, the relation given in eqn (15) is utilized to evaluate the polymeric stress tensor τpij, which is ultimately used in the momentum equation to solve the concerned governing equations.
exp(EΘ)BT. Finally, the relation given in eqn (15) is utilized to evaluate the polymeric stress tensor τpij, which is ultimately used in the momentum equation to solve the concerned governing equations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400

 where
where  . Here c0 is the ionic density, z is the valency, e is the elementary charge, kB is the Boltzmann constant, T is the temperature, and H is the channel height. The streamwise velocity and spanwise direction are non-dimensionalised using the Helmholtz-Smoluchowski velocity us and channel height, respectively.
. Here c0 is the ionic density, z is the valency, e is the elementary charge, kB is the Boltzmann constant, T is the temperature, and H is the channel height. The streamwise velocity and spanwise direction are non-dimensionalised using the Helmholtz-Smoluchowski velocity us and channel height, respectively.
 are state snapshots at equally spaced times. DMD seeks a linear operator A such that
are state snapshots at equally spaced times. DMD seeks a linear operator A such that

 in Fig. 6 for different fluids. Here,
in Fig. 6 for different fluids. Here,  is defined as
is defined as  where ui2 is the instantaneous spanwise velocity component value and 〈u2〉 is its time-averaged value at a point in the flow domain. The reason for showing the spanwise velocity component fluctuation is that this component can facilitate the mixing of two fluids flowing side by side inside the microdevice. It can be seen that the velocity fluctuation shows almost zero value for Newtonian (Fig. 6(a)) and viscoelastic fluids with Wi = 15 (Fig. 6(b)), whereas a region of high velocity fluctuation is present in the central part of the outlet microchannel of the microdevice for viscoelastic fluids with Wi = 50, as observed in Fig. 6(c). Moreover, the intensity of velocity fluctuation is seen to be notably higher near the end of the outlet microchannel.
where ui2 is the instantaneous spanwise velocity component value and 〈u2〉 is its time-averaged value at a point in the flow domain. The reason for showing the spanwise velocity component fluctuation is that this component can facilitate the mixing of two fluids flowing side by side inside the microdevice. It can be seen that the velocity fluctuation shows almost zero value for Newtonian (Fig. 6(a)) and viscoelastic fluids with Wi = 15 (Fig. 6(b)), whereas a region of high velocity fluctuation is present in the central part of the outlet microchannel of the microdevice for viscoelastic fluids with Wi = 50, as observed in Fig. 6(c). Moreover, the intensity of velocity fluctuation is seen to be notably higher near the end of the outlet microchannel. at a probe location near the entry of the outlet microchannel of the microdevice for different fluids in Fig. 7(a). For a Newtonian fluid, this velocity component reaches a steady value with time, whereas it shows almost a regular periodic type fluctuation for viscoelastic fluids at around Wi ∼ 18. At Wi = 50, this fluctuation is further increased and becomes aperiodic in nature. It suggests a gradual transition in the flow field from a steady and laminar state to a periodic unsteady state, and finally, to an aperiodic and chaotic turbulent-like state, known as the electro-elastic turbulent flow state, as the Weissenberg number gradually increases.25 The corresponding power spectrum of velocity fluctuations for viscoelastic fluids with Wi = 50 is plotted in Fig. 7(b). First of all, it can be seen that velocity fluctuations exist over a wide range of the frequency spectrum. A plateau with high PSD magnitude is observed in the low-frequency regime, corresponding to the large-scale fluctuations in the flow domain. In the high-frequency regime, an exponential decay persists, corresponding to the small-scale fluctuation in the flow domain. This is a typical trend in the PSD plot, which has also been seen in earlier studies dealing with electrokinetic flows of viscoelastic fluids at high Weissenberg numbers.33–35 The slope of the decay has a value of approximately −4.46, whereas earlier studies, comprising experiments and simulations, have found values around −4. Nevertheless, it is well-established that a slope equal to or greater than 3.5 (in magnitude) confirms the presence of elastic turbulence, which is true also in the present case.51–53
at a probe location near the entry of the outlet microchannel of the microdevice for different fluids in Fig. 7(a). For a Newtonian fluid, this velocity component reaches a steady value with time, whereas it shows almost a regular periodic type fluctuation for viscoelastic fluids at around Wi ∼ 18. At Wi = 50, this fluctuation is further increased and becomes aperiodic in nature. It suggests a gradual transition in the flow field from a steady and laminar state to a periodic unsteady state, and finally, to an aperiodic and chaotic turbulent-like state, known as the electro-elastic turbulent flow state, as the Weissenberg number gradually increases.25 The corresponding power spectrum of velocity fluctuations for viscoelastic fluids with Wi = 50 is plotted in Fig. 7(b). First of all, it can be seen that velocity fluctuations exist over a wide range of the frequency spectrum. A plateau with high PSD magnitude is observed in the low-frequency regime, corresponding to the large-scale fluctuations in the flow domain. In the high-frequency regime, an exponential decay persists, corresponding to the small-scale fluctuation in the flow domain. This is a typical trend in the PSD plot, which has also been seen in earlier studies dealing with electrokinetic flows of viscoelastic fluids at high Weissenberg numbers.33–35 The slope of the decay has a value of approximately −4.46, whereas earlier studies, comprising experiments and simulations, have found values around −4. Nevertheless, it is well-established that a slope equal to or greater than 3.5 (in magnitude) confirms the presence of elastic turbulence, which is true also in the present case.51–53 , exhibits a significant increment. For viscoelastic fluids at low Weissenberg numbers (e.g., at Wi = 1), a similar trend is observed; the flow field also displays chaotic fluctuations, resembling those of Newtonian fluids (not shown here), which are evident from both the streamline distortions and the pronounced spanwise velocity fluctuations. The underlying mechanism remains the same, namely, the presence of EKI induced by the conductivity gradients. However, as the Weissenberg number is further increased to Wi = 15, the behaviour of the viscoelastic fluid markedly changes. At this Wi, the flow fluctuations are strongly suppressed, and the system reverts to a more ordered and streamlined flow state. This suppression is clearly illustrated by the nearly symmetric streamline patterns in Fig. 8(b), along with the almost negligible values of
, exhibits a significant increment. For viscoelastic fluids at low Weissenberg numbers (e.g., at Wi = 1), a similar trend is observed; the flow field also displays chaotic fluctuations, resembling those of Newtonian fluids (not shown here), which are evident from both the streamline distortions and the pronounced spanwise velocity fluctuations. The underlying mechanism remains the same, namely, the presence of EKI induced by the conductivity gradients. However, as the Weissenberg number is further increased to Wi = 15, the behaviour of the viscoelastic fluid markedly changes. At this Wi, the flow fluctuations are strongly suppressed, and the system reverts to a more ordered and streamlined flow state. This suppression is clearly illustrated by the nearly symmetric streamline patterns in Fig. 8(b), along with the almost negligible values of  shown in Fig. 9(b). These results indicate that viscoelastic stresses act to dampen the instability at higher Wi, thereby stabilising the flow.29,30,54 A detailed explanation of the underlying mechanism responsible for this suppression of EKI in viscoelastic fluids has been provided in our earlier work.32
shown in Fig. 9(b). These results indicate that viscoelastic stresses act to dampen the instability at higher Wi, thereby stabilising the flow.29,30,54 A detailed explanation of the underlying mechanism responsible for this suppression of EKI in viscoelastic fluids has been provided in our earlier work.32 illustrated in Fig. 9(c). Interestingly, both the streamline configurations and the distributions of velocity fluctuations under this condition closely resemble those obtained at γ = 1 for the same Weissenberg number, as presented in Fig. 5(c) and 6(c), respectively. This similarity indicates that while the electrokinetic instability is progressively suppressed in viscoelastic fluids with increasing Wi, the electro-elastic instability can emerge at sufficiently high Weissenberg numbers irrespective of the values of the electrical conductivity ratio. The onset of EEI destabilises the flow field once again, giving rise to chaotic and turbulence-like flow dynamics. Therefore, in viscoelastic fluids subject to conductivity gradients, both instability mechanisms, EKI and EEI, can manifest depending on the elasticity level of the system. Specifically, at low values of Wi, the flow is predominantly governed by EKI, whereas at high values of Wi, the dynamics are controlled by EEI. The corresponding dye concentration profiles also clearly display the non-monotonicity in the flow field fluctuation. For both Newtonian (Fig. 8(d)) and viscoelastic fluids with Wi = 50 (Fig. 8(f)), the interface between the dyed and undyed fluids becomes wavy in nature, suggesting the presence of strong flow field fluctuation arising from the EKI and EEI phenomena, respectively. In contrast, it remains almost straight for viscoelastic fluids with Wi = 15 (Fig. 8(e)), due to the presence of an almost steady and ordered flow.
illustrated in Fig. 9(c). Interestingly, both the streamline configurations and the distributions of velocity fluctuations under this condition closely resemble those obtained at γ = 1 for the same Weissenberg number, as presented in Fig. 5(c) and 6(c), respectively. This similarity indicates that while the electrokinetic instability is progressively suppressed in viscoelastic fluids with increasing Wi, the electro-elastic instability can emerge at sufficiently high Weissenberg numbers irrespective of the values of the electrical conductivity ratio. The onset of EEI destabilises the flow field once again, giving rise to chaotic and turbulence-like flow dynamics. Therefore, in viscoelastic fluids subject to conductivity gradients, both instability mechanisms, EKI and EEI, can manifest depending on the elasticity level of the system. Specifically, at low values of Wi, the flow is predominantly governed by EKI, whereas at high values of Wi, the dynamics are controlled by EEI. The corresponding dye concentration profiles also clearly display the non-monotonicity in the flow field fluctuation. For both Newtonian (Fig. 8(d)) and viscoelastic fluids with Wi = 50 (Fig. 8(f)), the interface between the dyed and undyed fluids becomes wavy in nature, suggesting the presence of strong flow field fluctuation arising from the EKI and EEI phenomena, respectively. In contrast, it remains almost straight for viscoelastic fluids with Wi = 15 (Fig. 8(e)), due to the presence of an almost steady and ordered flow.















