Equilibrium scaling of phase separated elastin-like polypeptides for engineered condensates
Adam
Quintana
 ,
Gabriel P.
López
,
Gabriel P.
López
 and
Nick J.
Carroll
and
Nick J.
Carroll
 *
*
Department of Chemical and Biological Engineering, University of New Mexico, Albuquerque, NM, USA. E-mail: ncarroll@unm.edu
First published on 24th November 2025
Abstract
The interaction parameter of the Flory–Huggins free-energy of two phase separating components was experimentally determined and fit to a semi-empirical model. This model captures the temperature and chain length dependence, quantitatively describing phase equilibria and critical temperatures in elastin-like polypeptide systems of VPGVG pentameric repeats. We show temperature driven turbidity measurements of phase separation will recapitulate equilibrium through a simple temperature translation. This integrates both experiment and theory of liquid–liquid phase separation, offering a predictive tool for the ability to engineer ELP condensates and coacervates by tuning number of pentamers, temperature and concentration.
1 Introduction
Programmable biomolecular condensates formed by liquid–liquid phase separation (LLPS) replicate the spatial control of membraneless organelles.1 They furnish biomolecular nanoreactors and molecular capture vessels for on-demand chemistry.2–4 Their assembly is commonly mediated by intrinsically disordered proteins (IDPs), biopolymers which lack tertiary structure that can be genetically engineered for sequence-specific interactions.5–7 By concentrating substrates or selectively excluding reactants, IDP condensates regulate reaction rates through mesh size and internal concentration.8–12 However, LLPS is sensitively dependent on chain length (N) and temperature (T).13 Rational design of programmable, biomimetic, condensates for chemistry-specific reactions therefore requires phase diagrams that relate N and T to equilibrium composition.Quantitative mapping that connects N an T to equilibrium composition remains challenging. In one of the first instances of mapping the phase behavior of simple bio-engineered proteins, Sciortino et al.14 used temperature-ramped turbidity measurements to fit the Flory–Huggins (FH) free-energy to capture the equilibrium phase diagram. However, they used only one chain length and didn't find a relationship for χ(N). Also, their approach is difficult to replicate as it requires large concentrations, and, in the non-dilute regime, these protein samples require millimolar concentrations which are viscous and prone to sample loss.15 Furthermore, attaining the amount of protein required for these high concentration measurements typically requires weeks of cell growth, expression and purification of protein. McDaniel et al.16 characterized the transition temperature with a variable hydrophobic residue, yet only in the dilute regime and did not utilize FH theory. More recently, our group used transition temperatures and polymer surface tension theory to estimate the FH interaction parameter implying a description of the phase diagram.15 Yet, this work also didn't include chain length dependence and in addition we systematically overestimated the transition temperatures while using the typical convention for determining transition temperatures. Our measurements reveal that cloud-point temperatures systematically overestimate equilibrium temperatures by ≈0.5 °C when the heating rate is 1 °C min−1, because phase separation from spinodal decomposition evolves kinetically.17 Models calibrated to such non-equilibrium and therefore kinetically biased data therefore fail to capture the true equilibrium phase diagrams of phase separated condensates.
We address this gap with an integrated theoretical and easily deployable experimental strategy that enables rapid determination of equilibrium phase diagrams derived from low polymer concentrations confined in microfluidic droplets. We use an archetypal IDP for analysis, elastin-like polypeptides (ELPs), which are genetically engineered biopolymers that exhibit a well-defined lower critical solution temperature (LCST) and share the low-complexity architecture of cellular IDPs.16 Their monodispersity offers greater fidelity to theoretical models, making them particularly well-suited for quantitative investigation. We develop a semi-empirical model that generalizes the Flory interaction parameter χ13,18 to simultaneously capture temperature and chain length dependence. By coupling this model with a mass balance analysis from optical microscopy of coacervates in droplets in thermal equilibrium, we reconcile turbidity-derived cloud points with true thermodynamic equilibrium conditions and predict critical temperatures and condensate concentrations of different chain lengths. This quantitative framework enables rational engineering of thermoresponsive IDP condensates by providing predictive control over phase behavior, allowing for the design of systems with tailored transition temperatures and concentrations.
2 Experimental
Elastin like polypeptides with pentameric repeats of sequence (VPGVG)n with n of 40, 80, and 160 were analyzed. Consolidating data of transition temperature with respect to concentration from both Simon et al.15 and Mcdaniel et al.16 provides the dilute branch of the phase diagram for these proteins. We assume that the quoted concentrations are provided as moles of solute per volume of solvent, as there was no mention of ELP molar volume.To quantify the phase equilibrium phase fractions we performed measurements on water-in-oil (w/o) emulsions containing the mentioned ELP with 80 pentameric repeats. Emulsions were produced using a PDMS-based microfluidic device, as previously described by Simon et al.15 ELPs were expressed in E. coli and purified as described in a previous work.15 A stock solution with 114 mg ELP in 1 mL phosphate buffered saline (PBS) was prepared with approximately 3 percent by mass of the protein fluorescently labeled with Alexa Fluor 488 from Thermo Fisher Scientific. This labeling enabled improved optical characterization of the condensed phase (coacervate) during imaging.
Dilution of the stock solution to 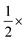 with PBS was used inside monodisperse w/o emulsions. Samples were transferred to a temperature-controlled heating stage mounted on an inverted fluorescence microscope (Olympus IX83).
with PBS was used inside monodisperse w/o emulsions. Samples were transferred to a temperature-controlled heating stage mounted on an inverted fluorescence microscope (Olympus IX83).
3 Results and discussion
3.1. Chain length and temperature dependence of FH interaction parameter
According to Flory,18 Ch. XII, eqn (21) the interaction energy of mixing a solute monomer and a solvent molecule (χ) is the difference in energy between a solvent molecule immersed in pure polymer and the pure solvent.| χkBT = zxΔw12 | (1) |
In the absence of a deeper model of molecular configuration, let us make a generalization of eqn (1) that will be useful in coupling this theory with experimental measurements. Observing that zx is primarily concerned with the configuration of solvation,19 and Δw12 is primarily concerned with the energy change from solvation; we make an empirical assumption that χ is proportional to the product of two factorized quantities.
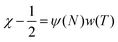 | (2) |
The polymeric chain length N must also be generalized from a coarse-grain assumption. Instead of the assumption that a monomer and solvent have equivalent molar volumes, we assume that one unit of N is coarse-grained such that it represents multiple solvated units of the polymer. This is done by allowing the monomer molar volume, and hence N, to be a fitted parameter. Such a scaling of N will primarily affect the entropic terms of the mixing free-energy and secondarily the interaction term through ψ(N). This assumption is not unfounded, as Sciortino et al.14 found the best fitting Flory chain lengths to be different from the expected values determined through molar weight ratios. Furthermore, we can be sure that allowing N to be an open parameter would not affect the critical or theta conditions of χ as derived by Flory20 and validated by Delmas et al.19 Hence, the interpretation of χ is the interaction energy density of a solvated Flory-monomer which is distinct from the actual monomer in size.
By taking specific derivatives and coupling with polymer theory, we can find expressions for the two factorized quantities ψ(N) and w(T). Starting with the intensive Flory–Huggins free-energy of mixing F:
| βF = χ〈ϕ(1 −ϕ)〉 − 〈s(ϕ,N)〉. | (3) |
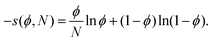 | (4) |
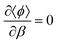 , then taking the partial derivative of eqn (3) with respect to β gives the mixing contribution to the internal energy
, then taking the partial derivative of eqn (3) with respect to β gives the mixing contribution to the internal energy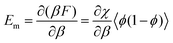 | (5) |
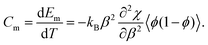 | (6) |
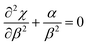 | (7) |
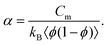 | (8) |
The parameter α is interpreted as the scaling factor for the mixing contribution to heat capacity; further discussion is available in the SI. The heat capacity of phase separating proteins is not generally available a-priori, likely capturing molecular properties that govern the tendency for folding21 and involving complex inter- and intra-molecular interactions.22 Furthermore, the dependence of ϕ within α makes the analytical solution of eqn (7) unsolvable if Cm is a constant with respect to temperature; the term 〈ϕ(1 − ϕ)〉 requires an analytical expression of the equilibrium values of the dilute ϕ′ and dense ϕ″ volume fractions with respect to χ, yet none exist without numerical inversion.23
With these limitations, assuming 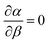 is a first step at attempting a general solution which leads eqn (7) to an integrable second-order differential equation. We also require two known values of χ(T) for a full solution. We will take from polymer physics theory that χ(Tθ) = 1/2 and χ(Tc) = χc(N), where Tθ is the theta temperature and Tc is the critical temperature for each value of N.13 The first condition can be controlled with only w(T), yet the second condition requires coupling with ψ(N). After integrating we find for w(T):
is a first step at attempting a general solution which leads eqn (7) to an integrable second-order differential equation. We also require two known values of χ(T) for a full solution. We will take from polymer physics theory that χ(Tθ) = 1/2 and χ(Tc) = χc(N), where Tθ is the theta temperature and Tc is the critical temperature for each value of N.13 The first condition can be controlled with only w(T), yet the second condition requires coupling with ψ(N). After integrating we find for w(T):
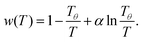 | (9) |
Here we normalize temperature with Tθ, the theta-temperature. In brief, the solvent–monomer and monomer–monomer interactions will equalize at Tθ such that there is no excluded volume and χ = 1/2.13 Furthermore, eqn (9) provides the typical phenomenological form for χ(T) (i.e. ∼1/T) with an additional ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T term tuned by α. In fact, a ln
T term tuned by α. In fact, a ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T term in the temperature dependence of the interaction parameter has been previously proposed when considering the heat capacities of liquid mixtures.24 This term introduces curvature in a plot of χ versus 1/T with a maximum at T = Tθ/α.
T term in the temperature dependence of the interaction parameter has been previously proposed when considering the heat capacities of liquid mixtures.24 This term introduces curvature in a plot of χ versus 1/T with a maximum at T = Tθ/α.
With an adequate temperature dependence, we can find the necessary functional form of ψ(N) by solving to confirm the value of χ at the critical temperature Tc, which is the apex of a binary phase equilibrium plot giving ϕ′ = ϕ″.13
 | (10) |
We choose a generalized form for the critical temperature as a power function of N with a limit of Tθ as N approaches infinity as proposed by Panagiotopoulos et al.,25 or
| Tc(N) = Tθ + δTN−γ, | (11) |
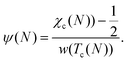 | (12) |
 | (13) |
Determination of N is also needed for a full description of a general phase separating polymer. Flory's original description of N was a molecular weight ratio of the polymer to solvent.20 However, for a coarse grained approach where we allow multiple repeating units to be considered a Flory-monomer, the definition of the monomer molecular weight is undefined. Hence, we will assume the original description with an unknown scaling dependence on molecular weight or
 | (14) |
 | (15) |
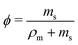 | (16) |
 | (17) |
With this semi-empirical derivation, it is now possible to couple experimentally determined measurements of phase separation with the parameterized χ(N,T). However, careful consideration must be made to find the best chain length and polymer melt density which best match experimental data.
3.2. Determination of phase diagrams using equilibrated coacervates in droplets
We produce monodisperse water-in-oil emulsions containing phase separating ELP of 80 pentameric repeats. We imaged the emulsions and determined the diameters of both the overall droplets and the phase separated coacervate after sufficient time allowed for complete coarsening. Shown in Fig. 1 is a representative image used for such a measurement at 34 °C.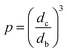 | (18) |
A fitting process was carried out on the acquired transition temperature data. Solving for the equilibrium volume fractions of eqn (3)23 provides the equilibrium χ at the experimental volume fractions, assuming values for Mm and ρm. The extracted χ versus N and T data was then applied to a multi-variable fitting routine to obtain the underlying parameters: Tθ, α, and each Tc.
The fitted function χ(N80,T), where N80 is the chain length for the ELP with 80 pentameric repeats, was used to determine the expected p to match the equilibrium measurements. By similarly finding the equilibrium phase volume fractions for the dilute ϕ′ and dense ϕ″ branches of the phase diagram, the expected phase volume ratio can be calculated from a total volume balance.
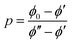 | (19) |
Compatibility of the fitted χ with the measured p was accomplished by altering two parameters. Firstly, the value for N80 must be adjusted to capture the correct range of p, thus giving a correction to the assumed Mm. Secondly, a systemic temperature shift was necessary, which was accomplished by altering Tθ. With the corrected Mm, and consequently a corrected Nn, the above steps were repeated until all parameters converged. Finally, this process was repeated for a range of ρm ∈ [1,1.5] g mL−1 to ascertain the best fitting ρm from the equilibrium measurements. This range of ρm was chosen as it provided the best fitting α ∈ (0,1), and we expect ρm > 1 g mL−1 as the condensed phase is observed to be less buoyant than the solvent.
Shown in Fig. 2, the red dashed line is the expected p from the fitted parameters obtained through only the transition temperature data with the correctly adjusted Mm and the ρm = 1.06 g mL−1 which gave the least error from the equilibrium measurements. The black solid line used a Tθ reduced by ≈0.55 °C.
The refinement to Tθ was motivated by the recognition that turbidity-based transition temperature measurements are inherently subject to kinetic artifacts. During turbidity measurements, phase separation occurs through spinodal decomposition which has been described kinetically by DeGennes17 as concentration fluctuations increasing exponentially in time. Thus, microscale phase separation likely begins prior to the macroscopic increase in turbidity that is detectable. Due to the temperature ramp rate employed in these experiments (≈1 °C per minute), this results in a systematic overestimation of the true equilibrium temperature for turbidity-based transition temperature experiments.
Assuming values within the range of ρm ∈ [1,1.5] provided estimates for the underlying parameters as a function of ρm. It was found that the best fitting Tθ and each Tc varied nominally within this range of ρm. ΔT being the offset temperature had a mean value of −0.47 °C with a variance of 12%. However, α, and Mm vary significantly through the range of assumed ρm. Padé approximations were found to best fit the dependence with ρm.
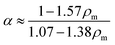 | (20) |
 | (21) |
Although these empirical functions will objectively fit both the transition temperature and phase fraction data simultaneously, ρm ≈ 1.06 g mL−1 produces the least error for the equilibrium experiments. This value corresponds to the parameters α ≈ 0.58, Mm = 944 g mol−1, ΔT ≈ −0.55 °C, and Tθ = 19 °C. This value for Mm suggests the FH chain length dependence of pentameric repeats to be Nn = 0.78 + 0.43n. Taking an average of Nn/n on the interval 40 < n < 160, one FH monomer is ≈2.25 pentameric repeats.
The critical temperatures and corresponding chain lengths for this best fit are given in Table 1. The corresponding critical temperature chain length dependence parameters are δT = 68 K and γ = 0.71.
| n | N n | T c [°C] |
|---|---|---|
| 160 | 70.1 | 22.3 |
| 80 | 35.4 | 24.5 |
| 40 | 18.1 | 27.6 |
From these parameters, we give the phase diagrams overlaid with the transition temperature data in Fig. 3a. Shown in Fig. 3b is the extracted interaction parameters, χ shifted and scaled to show the chain length invariant temperature dependence. Fig. 3c gives the extracted critical temperatures vs. number of pentameric repeats with an asymptote of Tθ.
4. Conclusion
Stimuli-responsive polymers that undergo reversible phase separation are essential in engineering functionally responsive materials. Among these, elastin-like polypeptides (ELPs) are valuable biopolymers due to their relative non-toxicity27 and ability to undergo phase separation near physiological temperatures. This phase behavior, driven by liquid–liquid phase separation (LLPS), enables their use in applications such as targeted drug delivery,28 tissue engineering,29 cancer therapy,30 and metal-ion encapsulation.31 However, generalizing the phase behavior of ELPs quantitatively remains a challenge; phase separation depends sensitively on temperature, concentration, and chain length. Furthermore, widely used characterization methods, such as temperature ramped turbidity or calorimetry measurements, are kinetically dependent and may not capture true equilibrium behavior.The semi-empirical model developed in this work captures the temperature and chain length dependence of the interaction parameter χ which quantitatively describes phase equilibrium in ELP systems of VPGVG pentameric repeats. Due to kinetic limitations inherent in turbidity-based transition temperature measurements, which detect macroscopic changes after microscopic phase separation has already commenced, it was necessary to apply a systematic temperature shift to align these data with equilibrium phase fractions. This adjustment ensures consistency between model predictions and experimental observations. Overall, the framework integrates configurational and energetic contributions, offering a predictive tool for rational design of temperature-responsive biomaterials.
Conflicts of interest
There are no conflicts to declare.Data availability
This study was carried out using available turbidity measurement data from the following two journal articles with DOI numbers: https://doi.org/10.1021/bm4007166 and https://doi.org/10.1038/nchem.2715. Microfluidic droplet images and measurement data can be provided upon request.Supplementary information contains the derivation of the critical temperature chain length dependence for a chain length invariant interaction parameter with analytical approximation to the general form and a deeper explanation of the heat capacity factor α. See DOI: https://doi.org/10.1039/d5sm00873e.
Acknowledgements
N. J. C. received funding for this work from the National Science Foundation's (NSF) CAREER program (CBET-2048051). We are grateful for support for this work provided under the following NSF grants: EF-2318897, MCB-2123465 and EFMA-2421209.References
- Y. Shin and C. P. Brangwynne, Science, 2017, 357, eaaf4382 CrossRef PubMed.
- B. R. Sabari, A. Dall'Agnese, A. Boija, I. A. Klein, E. L. Coffey, K. Shrinivas, B. J. Abraham, N. M. Hannett, A. V. Zamudio, J. C. Manteiga, C. H. Li, Y. E. Guo, D. S. Day, J. Schuijers, E. Vasile, S. Malik, D. Hnisz, T. I. Lee, I. I. Cisse, R. G. Roeder, P. A. Sharp, A. K. Chakraborty and R. A. Young, Science, 2018, 361, eaar3958 CrossRef PubMed.
- A. S. Lyon, W. B. Peeples and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2021, 22, 215–235 CrossRef CAS PubMed.
- X. Wu, Q. Cai, Z. Feng and M. Zhang, Dev. Cell, 2020, 55, 18–29 CrossRef CAS PubMed.
- R. van der Lee, M. Buljan, B. Lang, R. J. Weatheritt, G. W. Daughdrill, A. K. Dunker, M. Fuxreiter, J. Gough, J. Gsponer, D. T. Jones, P. M. Kim, R. W. Kriwacki, C. J. Oldfield, R. V. Pappu, P. Tompa, V. N. Uversky, P. E. Wright and M. M. Babu, Chem. Rev., 2014, 114, 6589–6631 CrossRef CAS PubMed.
- F. G. Quiroz, N. K. Li, S. Roberts, P. Weber, M. Dzuricky, I. Weitzhandler, Y. G. Yingling and A. Chilkoti, Sci. Adv., 2019, 5, eaax5177 CrossRef CAS PubMed.
- X. Zeng, K. M. Ruff and R. V. Pappu, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2200559119 CrossRef CAS PubMed.
- E. M. Zhao, N. Suek, M. Z. Wilson, E. Dine, N. L. Pannucci, Z. Gitai, J. L. Avalos and J. E. Toettcher, Nat. Chem. Biol., 2019, 15, 589–597 CrossRef CAS PubMed.
- A. Boija, I. A. Klein, B. R. Sabari, A. Dall'Agnese, E. L. Coffey, A. V. Zamudio, C. H. Li, K. Shrinivas, J. C. Manteiga, N. M. Hannett, B. J. Abraham, L. K. Afeyan, Y. E. Guo, J. K. Rimel, C. B. Fant, J. Schuijers, T. I. Lee, D. J. Taatjes and R. A. Young, Cell, 2018, 175, 1842–1855 CrossRef CAS PubMed.
- J. E. Henninger, O. Oksuz, K. Shrinivas, I. Sagi, G. LeRoy, M. M. Zheng, J. O. Andrews, A. V. Zamudio, C. Lazaris, N. M. Hannett, T. I. Lee, P. A. Sharp, I. I. Cisse, A. K. Chakraborty and R. A. Young, Cell, 2021, 184, 207–225 CrossRef CAS PubMed.
- S. Elbaum-Garfinkle, Y. Kim, K. Szczepaniak, C. C.-H. Chen, C. R. Eckmann, S. Myong and C. P. Brangwynne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7189–7194 CrossRef CAS PubMed.
- M. V. Garabedian, W. Wang, J. B. Dabdoub, M. Tong, R. M. Caldwell, W. Benman, B. S. Schuster, A. Deiters and M. C. Good, Nat. Chem. Biol., 2021, 17, 998–1007 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, New York, 2003, vol. 23 Search PubMed.
- F. Sciortino, K. U. Prasad, D. W. Urry and M. U. Palma, Biopolymers, 1993, 33, 743–752 CrossRef CAS PubMed.
- J. R. Simon, N. J. Carroll, M. Rubinstein, A. Chilkoti and G. P. López, Nat. Chem., 2017, 9, 509–515 CrossRef CAS PubMed.
- J. R. McDaniel, D. C. Radford and A. Chilkoti, Biomacromolecules, 2013, 14, 2866–2872 CrossRef CAS PubMed.
- P. G. de Gennes, J. Chem. Phys., 1980, 72, 4756–4763 CrossRef CAS.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- G. Delmas, D. Patterson and T. Somcynsky, J. Polym. Sci., 1962, 57, 79–98 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- A. Shakya, N. Rana, R. Kodirov and J. King, Biophys. J., 2024, 123(3), 445 CrossRef.
- Nicy, R. Collepardo-Guevara, J. A. Joseph and D. J. Wales, QRB discovery, 2023, 4, e7 CrossRef CAS PubMed.
- J. P. de Souza and H. A. Stone, J. Chem. Phys., 2024, 161, 044902 CrossRef CAS PubMed.
- R. Koningsveld, W. H. Stockmayer and E. Nies, Polymer Phase Diagrams: A Textbook, Oxford University Press, 2001 Search PubMed.
- A. Z. Panagiotopoulos, V. Wong and M. A. Floriano, Macromolecules, 1998, 31, 912–918 CrossRef CAS.
- D. W. Urry, C. H. Luan, T. M. Parker, D. C. Gowda, K. U. Prasad, M. C. Reid and A. Safavy, J. Am. Chem. Soc., 1991, 113, 4346–4348 CrossRef CAS.
- G. L. Bidwell, Physiology, 2021, 36, 367–381 CrossRef CAS PubMed.
- Y. Guo, S. Liu, D. Jing, N. Liu and X. Luo, J. Nanobiotechnol., 2023, 21, 418 CrossRef CAS PubMed.
- D. Jiang, Y. Yang, X. Yang, B. Wang, W. Fan, Y. Liu, X. Xin and L. Yin, OpenNano, 2023, 9, 100113 CrossRef CAS.
- A. Yi, D. Sim, S.-B. Lee, V. Sarangthem and R.-W. Park, Biomater. Biosyst., 2022, 6, 100050 CAS.
- M. B. van Eldijk, L. Schoonen, J. J. L. M. Cornelissen, R. J. M. Nolte and J. C. M. van Hest, Small, 2016, 12, 2476–2483 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |



