 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Geometry-dependent transmission of externally imposed shear stress in confined microtubule–kinesin active fluids
Joshua H. Dickiea,
Tianxing Weng a,
Yen-Chen Chena,
Haoran Wangb,
Yutian Hec,
Saloni Saxena†
d,
Robert A. Pelcovits
a,
Yen-Chen Chena,
Haoran Wangb,
Yutian Hec,
Saloni Saxena†
d,
Robert A. Pelcovits d,
Thomas R. Powers
d,
Thomas R. Powers de and
Kun-Ta Wu
de and
Kun-Ta Wu *af
*af
aDepartment of Physics, Worcester Polytechnic Institute, Worcester, Massachusetts 01609, USA. E-mail: kwu@wpi.edu
bDepartment of Chemistry and Biochemistry, Worcester Polytechnic Institute, Worcester, Massachusetts 01609, USA
cDepartment of Physics, University of Massachusetts, Amherst, MA 01002, USA
dDepartment of Physics, Brown University, Providence, RI 02912, USA
eSchool of Engineering, Brown University, Providence, RI 02912, USA
fThe Martin Fisher School of Physics, Brandeis University, Waltham, Massachusetts 02454, USA
First published on 30th December 2025
Abstract
Active fluids generate internal active stress and exhibit unique responses to external forces such as superfluid-like flow and self-yielding transitions. However, how confinement geometry influences these responses remains poorly understood. Here, we investigate microtubule–kinesin active fluids under external shear stresses in three geometries. In a thin slab-like container with a translating wall, we observed a kinematic transition from activity-dominated chaotic flow to lid-driven cavity flow when the applied shear stress exceeds ∼1.5 mPa, comparable to the intrinsic active stress magnitude. Simulations supported the conclusion that this transition arises from competition between internal active stress and imposed shear stress. In contrast, in a ratcheted toroidal confinement, the imposed shear remains localized near the driven boundary and does not propagate through the bulk. Nevertheless, this localized perturbation cooperatively couples with internal active stress to reverse the global circulation. This cooperative mechanism is further demonstrated in a connected-toroid geometry: driving one toroid reorganizes flow in a second, indirectly connected toroid, while no such influence occurs in a passive fluid. Together, these findings show that the response of active fluids to external forcing depends not only on the magnitude of applied stress but also on how confinement geometry mediates whether stresses interact through bulk competition or local-to-global cooperative reorganization, revealing a new approach to combining static geometrical design with dynamic external stimuli for real-time modulation of flow patterns. Such strategies may be applied to microfluidics, where micromechanical actuators dynamically tune active fluid behavior within fixed geometries, enabling transitions between chaotic and coherent flows for mixing, sorting, or transport.
Introduction
Active fluids consist of dynamic entities that locally consume fuel to power their motion. The individual motions interact and accumulate, giving rise to large-scale phenomena reminiscent of flocking and swarming in biological systems.1–5 The study of these collective dynamics has provided insights into how order can emerge from microscopic chaos. For instance, when active fluids are confined within ring-like geometries, their collective behavior can be directed to create coherent flow motion.6–10 However, what distinguishes active fluids from their passive counterparts is their dynamic response to moving boundaries.11–13 Active fluids can undergo a rheological transformation to a superfluid with reduced viscosity14–16 or exhibit more complex rheological transitions like self-yielding active networks that transition from fluid-like to gel-like, and then back to a fluid-like state.17 These transitions emphasize the dynamic and adaptive characteristics of active fluids when subjected to external mechanical stress, revealing how the internal active stresses can compete with and respond to external forces.While the rheological properties of active fluids have been extensively studied, particularly in terms of viscosity and fluidity,15–18 the role of confinement geometry in shaping an active fluid's response to external driving forces has remained poorly understood. Previous studies have mainly focused on how confinement affects the self-organization of active fluids6–10,19–21 rather than how confinement can modify active fluid's response to external forces. In this work, we investigate how microtubule–kinesin active fluids respond to external driving in three distinct geometries—a thin cuboidal cavity, a ratcheted toroidal loop, and a connected-toroid geometry that couples two toroidal rings. These geometries are selected to contrast open, slab-like boundaries with closed, ring-like confinements, allowing us to probe how topology governs the pathways by which externally imposed shear interacts with internally generated active stress. In open geometries, external and active stresses compete throughout the bulk, whereas in closed and connected geometries, the imposed shear remains localized and influences the system only through a cooperative coupling with internal activity. Together, these complementary geometries reveal how confinement topology fundamentally mediates stress transmission in active fluids, offering new insights into how such systems can be controlled and manipulated in complex, interconnected environments.
Materials and methods
Microtubule polymerization
To study the response of the microtubule–kinesin active fluid to external shear forces, we prepared this fluid using two key ingredients: microtubules and kinesin motor proteins (Fig. 1B). Microtubules were polymerized from α- and β-tubulin dimers purified from bovine brains.22,23 To polymerize the microtubules, we mixed 8 mg mL−1 of tubulins with 600 µM guanosine-5′[(α,β)-methyleno]triphosphate (GMPCPP, Jena Biosciences, NU-4056) and 1 mM dithiothreitol (DTT, Fisher Scientific, AC165680050) in microtubule buffer [80 mM PIPES, 2 mM MgCl2, 1 mM ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid, pH 6.8].22,24,25 The mixture was incubated at 37 °C for 30 minutes and then annealed at room temperature for 6 hours. For long-term storage, the polymerized microtubules were aliquoted, snap frozen with liquid nitrogen, and stored at −80 °C.Kinesin motor protein preparation
To generate the internal active stress necessary for our microtubule–kinesin active fluid to oppose external influences, we prepared kinesin motor proteins, which are essential for powering the sliding motion of microtubule bundles (Fig. 1B).24,26 We expressed kinesin motor proteins in Escherichia coli–derived Rosetta 2 (DE3) pLysS cells (Novagen, 71403) transformed with DNA plasmids encoding Drosophila melanogaster kinesin genes from fruit flies. For our experiments, we used processive motors consisting of the first 401 N-terminal amino acids (K401).27 The kinesin motors were tagged with six histidines, allowing purification via immobilized metal ion affinity chromatography using gravity nickel columns (Cytiva, 11003399). To enable kinesin motors to slide adjacent microtubule pairs, they need to be dimerized (Fig. 1B), so the kinesin motors were tagged with a biotin carboxyl carrier protein at their N terminals, enabling binding with biotin molecules (Alfa Aesar, A14207).22,24 These biotinylated motors were dimerized by mixing 1.5 µM K401 motors with 1.8 µM streptavidin (Invitrogen, S-888) and 120 µM DTT in microtubule buffer. This mixture was incubated for 30 minutes at 4 °C, snap frozen with liquid nitrogen, and stored at −80 °C.Microtubule–kinesin active fluid preparation
To prepare the microtubule–kinesin active fluid for our study, we mixed 1.3 mg mL−1 microtubules with 60 nM kinesin motor dimers.22,24 Microtubules were bundled using 0.8% polyethylene glycol (Sigma, 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) as a depleting agent (Fig. 1B). The bundled microtubules allowed motor dimers to slide pairs of anti-parallel microtubules apart, creating extensile bundles, which are the primary source of activity in the active fluid.28 This motion required motors to hydrolyze ATP into adenosine diphosphate (ADP), so we added 1.4 mM ATP.29,30 As ATP was hydrolyzed over time, the ATP concentration decreased, leading to a reduction in the active fluid's activity level.25,29–31 Therefore, to maintain ATP concentrations and sustain the active fluid's activity, we included 2.8% v/v pyruvate kinase/lactate dehydrogenase (Sigma, P-0294) and 26 mM phosphenol pyruvate (BeanTown Chemical, 129745) to regenerate ATP from ADP, thereby maintaining the ATP concentration.24 To stabilize the proteins in our active fluid system, we added 5.5 mM DTT. To visualize and track fluid flows during our experiments, we doped the active fluid with 0.0016% v/v fluorescent tracer particles (Alexa 488-labeled [excitation: 499 nm; emission: 520 nm] 3-µm polystyrene microspheres, Polyscience, 18861). Since prolonged fluorescent microscopy can lead to photobleaching, we included 2 mM Trolox (Sigma, 238813) and an oxygen-scavenging system comprising 0.038 mg mL−1 catalase (Sigma, C40), 0.22 mg mL−1 glucose oxidase (Sigma, G2133), and 3.3 mg mL−1 glucose (Sigma, G7528) to reduce photobleaching effects.24 Mixing these ingredients resulted in a microtubule–kinesin active fluid, which formed a self-rearranging microtubule network that continually generated internal active stress to drive flow without the need for external influences.24,32
300) as a depleting agent (Fig. 1B). The bundled microtubules allowed motor dimers to slide pairs of anti-parallel microtubules apart, creating extensile bundles, which are the primary source of activity in the active fluid.28 This motion required motors to hydrolyze ATP into adenosine diphosphate (ADP), so we added 1.4 mM ATP.29,30 As ATP was hydrolyzed over time, the ATP concentration decreased, leading to a reduction in the active fluid's activity level.25,29–31 Therefore, to maintain ATP concentrations and sustain the active fluid's activity, we included 2.8% v/v pyruvate kinase/lactate dehydrogenase (Sigma, P-0294) and 26 mM phosphenol pyruvate (BeanTown Chemical, 129745) to regenerate ATP from ADP, thereby maintaining the ATP concentration.24 To stabilize the proteins in our active fluid system, we added 5.5 mM DTT. To visualize and track fluid flows during our experiments, we doped the active fluid with 0.0016% v/v fluorescent tracer particles (Alexa 488-labeled [excitation: 499 nm; emission: 520 nm] 3-µm polystyrene microspheres, Polyscience, 18861). Since prolonged fluorescent microscopy can lead to photobleaching, we included 2 mM Trolox (Sigma, 238813) and an oxygen-scavenging system comprising 0.038 mg mL−1 catalase (Sigma, C40), 0.22 mg mL−1 glucose oxidase (Sigma, G2133), and 3.3 mg mL−1 glucose (Sigma, G7528) to reduce photobleaching effects.24 Mixing these ingredients resulted in a microtubule–kinesin active fluid, which formed a self-rearranging microtubule network that continually generated internal active stress to drive flow without the need for external influences.24,32
Design of microfluidic devices
We confined the active fluid within 3 different geometries: a thin cuboid, a ratcheted toroid, and connected toroids. All geometries were designed using SolidWorks 2021 to create a 3D model followed by 3D printing to fabricate the chips. The thin cuboid has dimensions of 3 mm × 3 mm × 0.4 mm (Fig. 1A). To study the lid-driven flow of an active fluid, the cuboid abutted a 440 µm-wide driving channel, which was 420 µm deep at the center and 220 µm deep at the sides. This driving channel contained a thread which was a microtube (Scientific Commodities, BB31-695-PE/C) towed by a motor, serving as a moving boundary. The microtube has a diameter of 355.6 µm, which was slightly smaller than the channel width, causing the thread to wobble while being towed. To minimize wobbling and ensure a stable moving boundary, we placed vertical pillars with a radius of 64 µm in the driving channel near the corners of the cuboidal cavity to clamp and stabilize the thread motion. The driving channel led to a 9.4 mm-in-diameter cylindrical well on each side, with a 3.4 mm-in-diameter cylindrical hole in the center to allow the thread to enter and exit the chip. To prevent the thread from being pulled in or out at a right angle, causing jiggling, the hole edges were rounded. Additionally, the thread motion could inadvertently drag fluid from one side of the well to the other, leading to a pressure difference between the ends of the driving channel. This pressure difference could cause a backflow into the cavity, altering the fluid dynamics. To minimize this effect, we added a parallel backflow channel (400 µm in width and depth) connecting the two wells, directing the dragged fluid back to the other side to minimize the pressure buildup and backflow. Finally, to confine the active fluid in the chip, we used the clamping method developed previously,6 which involved sandwiching the active fluid between the chip and a glass slide and clamping them tightly. However, this method created a gap between the chip and the glass slide, which could lead the fluid to evaporate. To prevent this evaporation, we surrounded the active fluid with a gutter (1 mm wide and 400 µm deep), which allowed the fluid within it to evaporate first, thereby minimizing the evaporation impact on the active fluid in the cavity.Fabrication of microfluidic devices
To fabricate the chips described above, we exported the 3D model from SolidWorks to a 3D printer (Phrozen Sonic Mini 8K Resin 3D Printer). For imaging fluorescent tracers in the active fluid through the 3D printed chips, we used transparent resin (Formlabs, RS-F2-GPCL-04). To minimize foam formation during the 3D printing process, the resin was first placed in a vacuum for 1 hour to remove dissolved oxygen and water. To facilitate chip removal after printing, we attached a removable magnetic build plate (Koyofei, KYF-3D-150) to the printer's build plate. After the chips were printed and removed from the 3D printer, they were sonicated in isopropyl alcohol for 10 minutes, rinsed with water, and air-dried. To harden and smoothen the chip surface, the chips were clamped between two clean glass slides, heated to 60 °C for 20 minutes, exposed to ultraviolet light for 5 minutes, and then allowed to cool on the tabletop to room temperature. After these post-printing processes, the chips were ready to be loaded with the microtubule–kinesin active fluid.Sample preparation and imaging
To prepare the samples for studying the active fluid's response to external driving, we first passed the driving thread through the two wells and into the driving channel of the fabricated chips (Fig. 1A), followed by loading 20 µL of the microtubule–kinesin active fluid into the central cavity and clamping it between the chip and polyacrylamide-coated glass slide using our previously developed clamping method.6,33 After clamping, both wells were loaded with an additional 20 µL of the active fluid to serve as reservoirs, thereby reducing the impact of evaporation on the fluid in the central cavity.The assembled chip was mounted onto the optical microscope (Nikon Ti2-E Inverted Microscope, MEA54000); the thread was attached to the edge of a spool rotated by a 5 V brushless DC motor (Great Artisan, X001HN17JB). The motor's power was tuned with an Arduino Uno board (Arduino, Uno R3) connected to a computer, which allowed us to program the spool's rotation speed and thereby the thread's speed. Initially, the thread was kept stationary for 30 minutes to allow the active fluid to reach a steady flowing state (chaotic, turbulence-like flows for the thin cuboid and coherent flows for the toroids); then the motor was programmed to tow the thread for a targeted duration (5–60 minutes) before stopping (Fig. 1D inset).
To characterize the flows of the active fluid in response to the thread motion, we imaged the suspended Alexa 488-labeled tracers using a 4× objective lens (CFI Plan Apo Lambda 4× Obj, Nikon, MRD00045, NA 0.2). To excite the Alexa 488 dye on the tracer particles, we applied blue light (401–500 nm) to the sample and collected the dye-emitted light with a multiband pass filter cube (Multi LED set, Chroma, 89402-ET).34 The collected light was captured with a camera (Andor Zyla, Nikon, ZYLA5.5-USB3) controlled by commercial image acquisition software (Nikon NIS Elements version 5.11.03). All images were acquired at the chamber's mid-plane to capture the fluid motion projected onto the two-dimensional plane. This choice follows our previous observations under similar confinement, which showed that horizontal motion of the active fluid remains ballistic while vertical motion is diffusive, indicating quasi-two-dimensional dynamics.35
Particle tracking and flow field reconstruction
To characterize the influence of the thread motion on the active fluid flow, measuring the thread speed was indispensable, so we doped fluorescent tracer particles inside the thread, which was a tube with inner boundaries to which the tracers adhered (Movies S1–S3). These tracers moved with the thread, allowing us to manually track their trajectories to determine the thread speed.To characterize the flow of the active fluid in response to the thread motion, we tracked the suspended tracer particles in the active fluid in sequential images using a Lagrangian tracking algorithm,36 revealing the trajectories ri(t) and corresponding instantaneous velocities vi(t) ≡ dri/dt of the tracers, where i denotes the tracer index. Since the tracer positions were scattered, the particle tracking provided scattered velocity data points for each frame.
To generate a flow field and vorticity map, these scattered velocities were interpolated onto the grid over the region of interest (cavity), which allowed us to construct a velocity field on a defined grid, V(r,t) and subsequently determine the vorticity distributions as ω(r,t) ≡ [∇ × V(r,t)]z. To visualize the flow structure in the thin cuboid, we normalized the vorticity distribution by three times the standard deviation of the vorticity6,19 and then plotted the instantaneous velocity field and normalized vorticity maps (Fig. 1C and E).
Analysis of Okubo–Weiss field and vortex core density
To quantify vortex core density and identify vortex-dominated regions in the active fluid, we analyzed the Okubo–Weiss field,37–39 which characterizes the balance between shear strain and vorticity and is defined as II ≡ (∂xVy)(∂yVx) − (∂xVx)(∂yVy), where V is the flow velocity field. The Okubo–Weiss field highlights rotational and strain-dominated regions, with negative II indicating vorticity-dominated areas and positive II indicating strain-dominated areas (Fig. S1). To identify vortex cores and analyze vortex core density, we first discarded positive II values, and among the remaining negative II values, we selected the 10th percentile closest to zero as the vortex-defining threshold and further excluded the II's above this threshold. This thresholding ensures that only the significant vortex regions are identified while excluding low-magnitude II values that may arise from measurement noise. Regions where II was below this threshold were classified as vortex cores. These regions were segmented using a connected-component labeling algorithm, and the total number of detected vortices was normalized by the physical area of the domain to obtain the vortex core density (Fig. 1D).Analysis of flow velocity correlation length
To characterize the flow patterns of the active fluid in the thin cuboid upon external driving (Fig. 1C), we analyzed the flow velocity correlation length to gain insight into the sizes of vortices in the fluid.40 To extract the correlation length, we first determined the velocity autocorrelation function:
 | (1) |
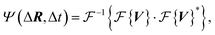 | (2) |
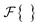 represents the Fourier transform,
represents the Fourier transform,  represents the inverse Fourier transform, and
represents the inverse Fourier transform, and 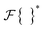 denotes the complex conjugate of
denotes the complex conjugate of  .34 The correlation function was then normalized as
.34 The correlation function was then normalized as 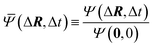 , which allowed us to determine the normalized equal-time velocity autocorrelation function as
, which allowed us to determine the normalized equal-time velocity autocorrelation function as  . In our correlation analysis, we excluded grid points within 150 µm of the boundaries (both stationary and moving) due to tracking algorithm limitations near the moving thread and lower statistics of tracer data near the stationary side walls. This exclusion was implemented to maintain consistent statistics across our analyses for correlation length in the bulk of the active fluid.
. In our correlation analysis, we excluded grid points within 150 µm of the boundaries (both stationary and moving) due to tracking algorithm limitations near the moving thread and lower statistics of tracer data near the stationary side walls. This exclusion was implemented to maintain consistent statistics across our analyses for correlation length in the bulk of the active fluid.
To analyze the correlation length, we first averaged the correlation function over the orientation of ΔR:
 | (3) |
 | (4) |
Numerical simulations of active fluid in a cavity flow system
To gain deeper insight into the observed kinematic transition (Fig. 2C) and test our hypothesis that the transition arises from stress competition rather than network rupture, we developed a 2D numerical model of an active fluid confined in a cavity flow system. Although the experimental system is three-dimensional, the flows occur in a thin layer where the gap height h = 0.4 mm is much smaller than the lateral dimension L = 3 mm (h ≪ L; Fig. 1A). In this regime, the fluid motion is quasi-two-dimensional with most of the dynamics taking place in-plane, with minor vertical fluctuations (see Materials and methods–Sample preparation and imaging).35 In such confined geometries, the top and bottom plates introduce a wall friction (Brinkman term) that effectively introduces a uniform hydrodynamic damping proportional to the local velocity.41–44 We estimated this frictional stress to be ∼1 mPa in our experimental system (Section S3), which is comparable to the estimated active stress of 1.5 mPa from the experiments (Section S2). Because this term acts primarily as a linear dissipation that reduces the overall flow speed without altering the main flow patterns (Fig. S4), we adopted a purely two-dimensional model that neglects such wall friction for computational efficiency, while acknowledging this approximation as a limitation of the present model.To capture how the balance between internal active stress and external shear stress influences the flow behavior of the active fluid, we adopted the minimal continuum active nematic model previously used by Varghese et al.,20,34,40 which treats the microtubule network as a continuous active nematic field where the local orientation of microtubules is represented by the traceless symmetric nematic order tensor Q. The evolution of Q is governed by a kinetic equation that accounts for rotational diffusion and flow-induced reorientation of microtubules:
 | (5) |
| η∇2v − ∇p − α∇·Q = 0, | (6) |
 , characteristic time scale t0 = 1/γ, and characteristic pressure scale p0 = ηγ. If we model the microtubule bundles as long thin rods, then ξ = 1 and the dimensionless equations are
, characteristic time scale t0 = 1/γ, and characteristic pressure scale p0 = ηγ. If we model the microtubule bundles as long thin rods, then ξ = 1 and the dimensionless equations are
 | (7) |
| ∇2v − ∇p − α*∇·Q = 0, | (8) |
 at the top wall, and v = 0 at all other walls. Note that the dimensionless side length of the square cavity is
at the top wall, and v = 0 at all other walls. Note that the dimensionless side length of the square cavity is  . The boundary conditions for the order parameter tensor are n·∇Q = 0 at all walls, where n represents a unit vector normal to boundaries. Although we know the shear viscosity and have an estimate for α, we do not have good estimates for γ and κ. Therefore, we choose an activity value comparable to what Varghese et al.34,40 used in their study, α* = 5, and study the flow as a function of
. The boundary conditions for the order parameter tensor are n·∇Q = 0 at all walls, where n represents a unit vector normal to boundaries. Although we know the shear viscosity and have an estimate for α, we do not have good estimates for γ and κ. Therefore, we choose an activity value comparable to what Varghese et al.34,40 used in their study, α* = 5, and study the flow as a function of  . We assume the length scale l0 is small compared to L, arbitrarily taking L* = 45.
. We assume the length scale l0 is small compared to L, arbitrarily taking L* = 45.
The system was initialized with a quiescent solvent (v = 0) and an isotropic state [Qxx = −Qyy = 2.5 × 10−4 rn(r) and Qxy = Qyx = 5 × 10−4 rn(r), where rn(r) is a spatially uniform random number between −1 and +1] under uniform pressure (p = 0). To enhance numerical stability in solving these governing equations (eqn (7) and (8)), we reformulated them into their weak forms for numerical implementation in COMSOL Multiphysics.34 The system evolved from t = 0 to 40 using a time-dependent solver with adaptive time-stepping to ensure numerical stability.
To quantify the competition between internal active stress and externally imposed shear stress, we defined a dimensionless stress ratio Λ ≡ σth/α, where σth ≡ ηvth/(L/3) represents the characteristic shear stress. Expressed in dimensionless form, this ratio becomes  . This parameter allows us to compare the effects of shear stress relative to active stress and determine how their relative strength governs the transition in flow behavior.
. This parameter allows us to compare the effects of shear stress relative to active stress and determine how their relative strength governs the transition in flow behavior.
To assess how externally imposed shear stress affects flow structure, we performed a correlation analysis similar to that in the experiments (eqn (1)) to extract the normalized equal-time autocorrelation function  , where the simulated velocity field v corresponds to the experimental flow field V. Since the boundary moves in the +x direction, we further extracted the correlation function along the x-dimension,
, where the simulated velocity field v corresponds to the experimental flow field V. Since the boundary moves in the +x direction, we further extracted the correlation function along the x-dimension,  (Fig. 3C). To extract the characteristic correlation length scale, the correlation function was fit to an exponential function:
(Fig. 3C). To extract the characteristic correlation length scale, the correlation function was fit to an exponential function:  with lx as the fitting parameter representing the decay length scale of the correlation function. This analysis was performed across different boundary speeds
with lx as the fitting parameter representing the decay length scale of the correlation function. This analysis was performed across different boundary speeds  from 0 to 134, corresponding to stress ratios in the range of 0 ≤ Λ ≤ 1.8, allowing us to examine how externally imposed shear influences the correlation length (Fig. 3D).
from 0 to 134, corresponding to stress ratios in the range of 0 ≤ Λ ≤ 1.8, allowing us to examine how externally imposed shear influences the correlation length (Fig. 3D).
Externally driven active fluid in ratcheted toroidal geometries
To further investigate how the active fluid responds to external forces in a different geometrical confinement, we explored a toroid (outer radius: 1 mm; inner radius: 500 µm; depth: 400 µm) where the active fluid could form a spontaneous coherent flow before being driven (Fig. 4A).6 We chose this geometry based on our prior study showing that spontaneous coherent circulation occurs only when the aspect ratio of the toroidal cross section lies between 1/3 and 3.6 Accordingly, we selected a channel width of 0.5 mm and height of 0.4 mm (aspect ratio ≈1) to ensure robust coherent flow before the onset of external driving. The height of the toroid (h = 0.4 mm) was chosen to match that of the thin cuboidal geometry (Fig. 1A), enabling comparison between the two confinements with different topologies. To apply external driving to the toroidal system, the toroid intersected with the driving channel, creating an opening width of 485 µm. To ensure that the coherent flow developed in the opposite direction of the driving, the outer boundary of the toroid was decorated with 1–3 ratchet teeth.6 Each tooth had a triangular structure with one edge perpendicular to the outer boundary of the toroid and 500 µm long, and the other edge tangent to the toroidal outer boundary. Apart from the shape change to a toroid, the rest of the design was identical to the one for the thin cuboid.To further examine how external shear stress propagated through loopy confinements, we also designed a connected-toroid geometry consisting of two laterally overlapping toroids (Fig. 6A). Each toroid had the same inner/outer radii, channel width, and height as the single toroidal system (Fig. 4A), and the two toroids overlapped by 10% of their channel widths. The upper toroid included a small opening along its outer boundary to couple to the translating thread and did not contain ratchet teeth, whereas the lower toroid contained three ratchet teeth to bias circulation clockwise.
Analysis of mean tangential velocity
To reveal the net flow of the active fluid in the toroid, we analyzed the mean tangential velocity of the flow 〈vt〉 as a function of distance from the inner boundary di (Fig. 4B). The 〈vt〉 vs. di relationship was determined by first binning the tangential component of the tracer velocities based on their distances from the inner boundary, followed by averaging these components over the period within each phase: before driving, during driving, and after driving. This analysis provided insights into how the net flow of the active fluid in the toroid was influenced by the external driving stresses.Results and discussion
Flow response to an external stimulus in a narrow-gap cavity
To investigate the response of active fluid to external stimuli, we designed a thin cuboidal cavity with an open side covered by a moving thread (Fig. 1A). The thread served as both a dynamic boundary and an external source of shear force. To visualize and quantify how the active fluid responded to external driving, the fluid was doped with fluorescent tracer particles and imaged at the chamber's mid-plane to obtain a projected two-dimensional velocity field (Movie S1; Fig. 1C). Note that although the system is inherently three-dimensional, the fluid motion is predominantly horizontal with small out-of-plane fluctuations;35 accordingly, we treat the fluid dynamics in this study as quasi-two-dimensional (see Materials and methods). Our data shows that at the lowest thread speeds, the active fluid exhibited turbulence-like, chaotic flows, forming 100-µm vortex patches of either sign (Fig. 1C, left panel; Movie S1), consistent with previous studies.6,34,35 As the thread moved, these vortex patches merged into fewer and larger patches, with the counterclockwise bias induced by the thread's motion (the dark blue region in the upper left of the middle panel of Fig. 1C). Above 120 µm s−1 the activity-driven vorticity became less apparent (Fig. 1C, right panel), with the overall flow resembling conventional cavity flow in water (Fig. 1E; Movie S2). To quantify this transition, we analyzed the Okubo–Weiss field to count vortex cores (Fig. S1).37–39 At low thread speeds (vth ≲ 60 µm s−1), vortex core density remained at ∼2 mm−2 but decreased monotonically as thread speed increased, saturating at ∼0.4 mm−2 (Fig. 1D, red dots), matching the baseline vortex core density observed in (passive) water (blue horizontal line).The mean flow speed also increased with thread speed. For the active fluid (Fig. 2A, red dots), the flow speed was ∼10 µm s−1 when the thread was stationary. As thread speed increased, external shear stress combined with active stress, causing the active fluid to flow faster. Moreover, beyond a thread speed of 120 µm s−1, the mean flow speed became indistinguishable from that of water (blue dots), suggesting that external driving dominated the fluid motion. This flow behavior is only possible in the presence of ATP, which allows the kinesin motors to transiently bind and detach, enabling the microtubule network to flow (Fig. 1B).29,30 Without ATP, the motors acted as static crosslinkers, forming an elastic gel that remained immobile at low thread speeds and failed to fully fluidize even at the highest thread speeds (Section S1; Movie S3).
To characterize the pattern transformation from chaotic active fluid flow to ordered cavity flow,45 we analyzed the equal-time velocity autocorrelation function  as a function of separation ΔR (see Methods for analysis details), which revealed that the correlation function decayed exponentially, with correlation length l increasing as thread speed increased (Fig. 2B). To extract l, we fit the correlation function to an exponential function:
as a function of separation ΔR (see Methods for analysis details), which revealed that the correlation function decayed exponentially, with correlation length l increasing as thread speed increased (Fig. 2B). To extract l, we fit the correlation function to an exponential function:  with l as the fitting parameter. When the thread was stationary, l measured ∼200 µm (Fig. 2C, red dots), reflecting the intrinsic vortex size in confined active fluids.6,34,35 As the thread speed increased, l grew almost linearly, reflecting the formation of a cavity-wide vortex (Fig. 1C; Movie S1). Beyond 120 µm s−1, l saturated at ∼600 µm, marking a critical transition where external stresses dominated, making the flow indistinguishable from passive fluids (Fig. 2C, blue dots; Movie S2).
with l as the fitting parameter. When the thread was stationary, l measured ∼200 µm (Fig. 2C, red dots), reflecting the intrinsic vortex size in confined active fluids.6,34,35 As the thread speed increased, l grew almost linearly, reflecting the formation of a cavity-wide vortex (Fig. 1C; Movie S1). Beyond 120 µm s−1, l saturated at ∼600 µm, marking a critical transition where external stresses dominated, making the flow indistinguishable from passive fluids (Fig. 2C, blue dots; Movie S2).
Characterizing the critical shear stress at the transition
We analyzed the kinematics of the active fluid in the thin cuboidal cavity flow system using three quantitative analyses: vortex core density, mean speed, and correlation length (Fig. 1D, 2A and C). These analyses all revealed 120 µm s−1 as the critical thread speed where the active fluid dynamics shifted from being dominated by active stress to being dominated by the thread-driven viscous shear stress. At the critical thread speed we estimated the thread-driven viscous stress as σth ≈ 1.5 mPa (Section S2). Since we expect the thread-driven viscous stress to be comparable to the active stress at the critical thread speed, we estimate the active stress under our experimental conditions to be ∼1.5 mPa. Since the active stress is given by −αQ, where α is the activity coefficient and Q is the liquid crystal order parameter tensor, of order unity, our estimate also implies that the activity in our experimental conditions is α ≈ 1.5 mPa. This estimate aligns with an independent measurement of ∼3 mPa by Adkins et al.13To compare this result with prior findings, we note that Gagnon et al. reported a rheological phase transition from solid-like to fluid-like behavior at an applied shear stress of ∼2.2 mPa.17 While this threshold differs from our estimated value of 1.5 mPa, our estimate is intended as an order-of-magnitude approximation and is likely an underestimate due to the simplified velocity gradient calculation (Section S2). Nevertheless, the similarity between our estimate and Gagnon et al.'s threshold suggests that our observed kinematic transition in the thin cuboidal cavity flow system may result not simply from the external shear overwhelming internally generated active fluid flow, but also from disruption of the microtubule network. However, upon analyzing the orientational distribution of microtubule bundles under confocal microscopy, we found that the external shear enhanced microtubule alignment, rather than fragmenting the network as originally expected (Section S5; Movie S4), which leads us to hypothesize that the kinematic transition observed in our active fluid's flow behavior (Fig. 2C) arises primarily from the competition between internal active stress and external shear stress, rather than from network rupture.
Numerical simulation of active fluid confined in a cavity flow system
To test our hypothesis and further study the competition between the activity-driven flow and the externally driven flow, we adopted the minimal continuum model developed by Varghese et al.34,40 and computed the flow in the classic two-dimensional lid-driven flow geometry (Fig. 1; see the Materials and methods for details of the simulation). Our computation is only meant to be illustrative, since the experiment is a three-dimensional Hele–Shaw geometry while the computation is purely two dimensional.46 This model excludes network fragmentation but includes active stress and external shear stress, so reproducing the kinematic transition similar to what we observed in experiments would support the hypothesis that the transition is governed by stress competition alone without requiring network rupture.In the simulation, the flow field evolved from an initial quiescent state, after which internal active stress generated spontaneous flow while the motion of boundary imposed external shear stress, driving additional flow. To quantify the stress competition, we defined a dimensionless stress ratio Λ ≡ σth/α where α represents active stress and σth is the characteristic shear stress imposed by the moving boundary. When all boundaries were stationary (vth = 0; Λ = 0), the system exhibited chaotic, turbulence-like flow driven by active stress (Fig. 3A, left panel; Movie S5). At low values of imposed shear stress (Λ = 0.38), chaotic flow coexisted with shear-driven flow (middle panel). At higher shear stress (Λ = 1.8), the active turbulence was suppressed, and the flow became predominantly shear-driven (right panel), resembling cavity flow in passive fluids (Fig. 3B).
To characterize the flow structure, we analyzed the equal-time velocity autocorrelation function  and plotted it as a function of normalized displacement Δx/L (with Δy = 0), where +x is the direction of thread motion (Fig. 3C). We found that
and plotted it as a function of normalized displacement Δx/L (with Δy = 0), where +x is the direction of thread motion (Fig. 3C). We found that  decayed nearly exponentially, with the decay length scale lx. As Λ increased, lx grew monotonically and saturated, converging with the passive fluid case at Λ = 1 (Fig. 3D), consistent with experiments (Fig. 2C). This consistency supports our hypothesis that the kinematic transition observed in experiments arises primarily from the competition of internal active stress and external shear stress and does not require the involvement of network rupture.
decayed nearly exponentially, with the decay length scale lx. As Λ increased, lx grew monotonically and saturated, converging with the passive fluid case at Λ = 1 (Fig. 3D), consistent with experiments (Fig. 2C). This consistency supports our hypothesis that the kinematic transition observed in experiments arises primarily from the competition of internal active stress and external shear stress and does not require the involvement of network rupture.
The simulations demonstrate that the flow dynamics of the active fluid confined in a lid-driven cavity are governed by the competition between internally generated active stress and externally imposed shear stress. However, it remains unclear how these two stresses interact and collectively give rise to the net flow observed in the simulation (Fig. 3A). Intuitively, one might expect that the total flow could be represented as a linear superposition of the intrinsic active fluid flow (without external driving) and the passive cavity flow (with driving). In contrast, our simulations show that this expectation fails: the flow of the active fluid under external shear cannot be decomposed into independent active and passive components (Section S4). This finding highlights that active and external shear stresses are coupled, with the imposed shear reorganizing the nematic order and active stress to produce emergent flow structures—either chaotic mixing flows, a cavity-wide single vortex, or coexistence of both (see Section S4 for details).15–17
Response of active fluid to external driving in a toroidal confinement
Our study in a cuboidal space revealed an active fluid transitioning from active stress–dominated to shear stress–dominated flow under external driving. However, confinement influences active fluid self-organization,6,10,19,20,47 raising the question of whether modifying the confinement would alter this transition. In the cuboidal system, externally imposed shear propagated throughout the bulk, enabling system-wide stress competition. To test whether modifying the confinement affects this competition, we examined a toroidal system, where the absence of side walls and the presence of a central hole could alter shear propagation.The toroidal confinement consisted of a circular channel with a segment of the outer boundary replaced by a moving thread to impose shear (Fig. 4A). Unlike in the cuboidal system, where shear propagated throughout the domain, the toroidal geometry was expected to constrain shear to the vicinity of the moving boundary, enabling direct comparison of how confinement affects shear propagation and flow response. In our previous study,6 active fluid confined in this toroidal geometry spontaneously developed a coherent flow. To ensure that this pre-existing flow opposed external driving, we decorated the toroid's outer boundary with ratcheted teeth,6 guiding spontaneous flow counterclockwise before driving (Fig. 4A, left panel).
To observe how the coherent flow responds to external driving in this ring-like confinement, we drove the thread at 52 µm s−1 for 20 minutes, which temporarily reversed the flow direction to clockwise (Fig. 4A, middle panel). This driving also induced a localized vortex patch spanning the toroidal channel. This “mini cavity flow” contrasts with the system-spanning flows observed in slab-like geometry (Fig. 1C), and the induced flow was sufficient to override the pre-existing counterclockwise coherent flow, reorganizing the active network into the opposite direction. After driving ceased, the fluid continued to flow clockwise for 10 minutes before reverting back to its pre-driving counterclockwise state (Fig. 4A, right panel). This reversion demonstrates that the ratcheted teeth established a counterclockwise flow preference in the active fluid system, with external driving inducing only a temporary reversal of the active fluid flow (Movie S6).
To explore how tooth count influences the post-driving reversion, we varied the number of ratcheted teeth. With 2 or 3 teeth, the flow always reverted after the driving stopped (Movie S7). However, with only one tooth, reversion depended on thread speed: at low speeds (40 µm s−1), the flow reverted (Movie S8), but at higher speeds (130 µm s−1), the reversal persisted (Fig. 4C inset; Movie S9). These results indicate that the reversion process is sensitive to both the confinement geometry (number of teeth) and the driving speeds.
The externally driven flow may appear similar to the spontaneous coherent flow because both exhibited circulatory motion, but their velocity profiles differ (Fig. 4B). The spontaneous flow showed a Poiseuille-like profile (gray and blue curves) with localized counter-vortices near the teeth (di ≳ 0.6 mm).6 In contrast, the externally driven flow (red curve) lacked these counter-vortices, highlighting how shear not only reverses flow direction but also alters flow structure.
To further quantify the effect of external driving, we analyzed the circulation order parameter (COP), defined as  , where vt is the tangential velocity of each tracer particle and |v| is its speed (Fig. 4B inset). Before driving, the COP remained stable at ∼0.5 for 30 minutes, demonstrating a persistent spontaneous counterclockwise flow (Fig. 4C). Once external driving began, the COP dropped and plateaued at −0.5, indicating an external force–triggered reversal to clockwise circulation (shaded pink area). The reversal took ∼5 minutes, in contrast to the water/heavy water control where it occurred within 30 seconds (Fig. S7). This slower response in active fluid reflects the resistance from internal active stress as well as the time required for the microtubule network to reorganize during the reversal. After the driving stopped, the reversed flow persisted for ∼10 minutes before gradually reverting to counterclockwise, with COP rising to ∼0.6. This post-driving recovery time is comparable to the timescale over which microtubule–kinesin active fluids develop spontaneous coherent flow after sample preparation6 or recover flow coherence after external perturbation,19 suggesting that these processes are governed by the self-reorganization of the microtubule network from one state into another. While the post-driving reversion behavior raises intriguing questions about network memory and flow state recovery, it is beyond the scope of this study. Here, we focus on the response of the active fluid to external driving.
, where vt is the tangential velocity of each tracer particle and |v| is its speed (Fig. 4B inset). Before driving, the COP remained stable at ∼0.5 for 30 minutes, demonstrating a persistent spontaneous counterclockwise flow (Fig. 4C). Once external driving began, the COP dropped and plateaued at −0.5, indicating an external force–triggered reversal to clockwise circulation (shaded pink area). The reversal took ∼5 minutes, in contrast to the water/heavy water control where it occurred within 30 seconds (Fig. S7). This slower response in active fluid reflects the resistance from internal active stress as well as the time required for the microtubule network to reorganize during the reversal. After the driving stopped, the reversed flow persisted for ∼10 minutes before gradually reverting to counterclockwise, with COP rising to ∼0.6. This post-driving recovery time is comparable to the timescale over which microtubule–kinesin active fluids develop spontaneous coherent flow after sample preparation6 or recover flow coherence after external perturbation,19 suggesting that these processes are governed by the self-reorganization of the microtubule network from one state into another. While the post-driving reversion behavior raises intriguing questions about network memory and flow state recovery, it is beyond the scope of this study. Here, we focus on the response of the active fluid to external driving.
To quantify the effect of thread speed on COP reversal, we analyzed the initial COP drop after the onset of driving and fit the data to a line function: COP ∼ −λt, with the reversal rate λ as the fitting parameter (Fig. 5A, middle panel). To explore how the reversal rate depends on thread speed, we measured λ across thread speeds from 20 to 220 µm s−1 while varying the number of teeth on the outer boundary (1, 2, and 3 teeth; Fig. 5A). Our data showed that below 30 µm s−1, no reversal occurred; λ remained zero (Fig. 5B). Above this threshold, λ increased nearly linearly with thread speed (red dashed line). This critical speed corresponded to an externally imposed shear stress on the order of 1 mPa (Section S2), comparable to the intrinsic active stress (∼1.5 mPa) identified in the cuboidal geometry where the flow became externally dominated (Section S2), suggesting that for flow reversal to occur, the externally imposed shear stress must locally overcome the active stress before reversal of the global flow can be triggered.
Despite sharing a common stress threshold with the cuboidal system, the toroidal system exhibited no sharp kinematic transition. Instead of switching from active stress–dominated to shear stress–dominated flow, the reversal rate increased nearly linearly with thread speed across explored tooth counts (1–3 teeth) even when λ measurements were extended to the maximum achievable thread speed (530 µm s−1; Fig. 5B inset). This lack of a kinematic transition supports our hypothesis that confinement geometry governs an active fluid's response, potentially shifting or even eliminating transitions observed in other geometries. This contrasting result also suggests that externally imposed shear influences the active fluid in a fundamentally different way from the cuboidal system. In the cuboidal system, shear propagates throughout the bulk and enables system-wide stress competition, whereas in the toroidal system, the externally imposed shear remains localized near the moving boundary, producing a small cavity-like vortex patch (Fig. 4A, middle panel) rather than directly reorganizing the system-wide flow field. Thus, global reversal in the toroid appeared to result from a reorganization of the active fluid driven by the cooperative interplay between internal active stress and externally imposed shear.
Cooperative flow response in connected toroidal geometries
To test whether global flow reversal in the toroidal system arose from a cooperative interplay between internal active stress and externally imposed shear, we designed a connected-toroid geometry where two toroids partially overlapped their channel width (Fig. 6A).6,48,49 The two toroids had identical dimensions to the single-toroid system, but only the upper toroid was coupled to the translating thread, while the lower toroid contained three ratchet teeth to bias spontaneous circulation clockwise. This configuration allowed us to test whether external driving applied to one toroid could reorganize the flow in a second, indirectly connected toroid.Before external driving, the lower ratcheted toroid developed a spontaneous clockwise circulation, which induced counterclockwise flow in the upper toroid through the overlapping region (Fig. 6B; Movie S10). When the thread began to move at 120 ± 12 µm s−1, the upper toroid reversed circulation almost immediately (within ∼4 minutes), reflecting its direct coupling to the moving boundary. In contrast, the lower toroid reversed much more slowly, requiring ∼20 minutes to complete its transition from clockwise to counterclockwise circulation. This difference in timescales indicated that the lower toroid did not experience the external shear directly; instead, its reorganization occurred through the influence of the circulation change in the upper toroid.
To examine whether this influence on the second toroid required the cooperation of external shear stress and internal active stress, we repeated the experiment under a comparable driving condition (thread speed vth = 136 ± 10 µm s−1) using a water/heavy-water mixture (Fig. 6C; Movie S11). Our data showed that in this passive system, only the upper toroid developed clockwise circulation during driving, while the lower toroid remained nearly quiescent. The absence of flow in the lower toroid indicated that external shear alone did not propagate through the overlapping region and could not reorganize the flow in the second toroid when active stress was absent. Thus, the reversal of the lower toroid in the active fluid system reflected a process that went beyond direct mechanical forcing, supporting our inference from the single-toroid system that flow reversal in the toroidal geometry was driven by a cooperative reorganization involving both internal active stress and the externally imposed shear (Fig. 5B). Such cooperation was required to complete the reversal process in loopy confinements such as the toroid.
After the driving stopped, the active fluid system remained in the counter-rotating state for ∼1.5 hours, after which the lower toroid reverted to its ratchet-preferred clockwise circulation and subsequently the upper toroid returned to counterclockwise flow (Fig. 6B). This reversion behavior matched that of the single-toroid system, where toroids containing three ratchet teeth consistently recovered their pre-driving state after being transiently reversed (Movie S7), indicating that the connected-toroid geometry preserved the intrinsic flow preference of the ratcheted toroid, albeit on a longer timescale than in the single-toroid system (∼1 hour vs. ∼10 minutes). This longer reversion time scale may reflect the additional hydrodynamic complexity introduced by the coupling between the two toroids which could slow the self-organization of the ratcheted toroid back to its intrinsically preferred state.
Conclusions
We investigated how a microtubule–kinesin active fluid responds to external shear stress across three distinct confinement geometries: a thin cuboidal cavity, a ratcheted toroid, and a connected-toroid system. Together, these geometries revealed that confinement topology fundamentally shapes how external forcing interacts with internally generated active stresses, producing qualitatively different flow responses.In the cuboidal cavity, we observed a sharp kinematic transition at a thread speed of 120 µm s−1, where the system switched from active stress–dominated dynamics to externally imposed shear–dominated flow (Fig. 2C). Simulations suggested that this transition arose from competition between internal active stress and external shear stress rather than microtubule network rupture (Fig. 3D). At the transition speed, the externally imposed shear stress reached ∼1.5 mPa (Section S2), comparable to the intrinsic active stress, yielding an activity coefficient of α ≈ 1.5 mPa. This estimate agrees with previous independent measurements using an interfacial tension-based method (∼3 mPa)13 and provides an experimentally grounded activity scale that can be incorporated into active fluid models.40,50–53
In contrast, the toroidal geometry exhibited no such transition. Instead, the flow reversal rate increased smoothly with thread speed (Fig. 5B), and the flow map analysis showed that the shear in the toroidal system remained localized near the moving boundary (Fig. 4A, middle panel). These observations indicate that reversal did not occur through bulk shear domination as in the cuboidal system, but through a reorganization of the active fluid driven by the cooperation of internal active stress and externally imposed shear. The connected-toroid geometry provided direct evidence for this cooperative mechanism: external driving applied to one toroid reorganized flow in a second, indirectly connected toroid, but only when internal active stress was present (Fig. 6B; Movie S10). Without active stress, the second toroid remained nearly quiescent (Fig. 6C; Movie S11). Together, these results demonstrate that in toroidal confinement, flow reorganization requires the cooperative action of external shear and internal active stress.
Despite these geometric differences, these systems shared a common stress scale governing the onset of externally influenced flow. In both the cuboidal and toroidal geometries, the applied shear stress needed to reach ∼1 mPa (Section S2)—comparable to the intrinsic active stress (∼1.5 mPa)—to elicit a measurable response from the active fluid. Beyond this threshold, confinement determined whether the response proceeded through bulk stress competition (cuboid; Fig. 1C) or local-to-global stress cooperation (toroid; Fig. 4A middle panel). Together, these results indicate that the balance between external and internal stresses sets the fundamental condition for active fluids to respond to external forcing, while confinement geometry dictates how the applied stress is transmitted and whether the response emerges through competition or cooperation of stresses. These findings reveal that confinement topology governs not only spontaneous self-organization of active fluids6–10,19–21 but also the modes by which active fluids respond to external stimuli.
Our work has several limitations. First, only three confinement geometries were explored; given the vast range of possible geometries, further investigation is needed to understand how different confinement geometries influence the active fluid response to external forces. Second, driving conditions were constrained: in the toroidal system, only a small portion of the outer boundary was driven, which localized the shear stress (Fig. 4A middle panel). Further studies can explore how varying the extent of the driven boundary affects the active fluid's response, potentially leading to a transition similar to what was observed in the cuboidal system.
Third, although this paper focuses on the active fluid's response to external driving, the post-driving reversion process in the toroidal system deserves further study to investigate under what conditions (tooth configuration, driving speed, and driving duration) the post-driving reversion process can happen (Fig. 4A right panel). Our data show that under the same tooth configuration, the reversion depends on driving speed (Movies S8 and S9), suggesting that the system retains a form of memory after the cessation of external forcing, likely originating from microtubule network alignment driven by the externally imposed shear. Stronger or longer shear driving may reinforce this alignment throughout the toroidal system, making reversion less probable, whereas weaker driving induces weaker alignment, making the network more likely to relax back to its original state. Unraveling the principles behind this reversion process will enable “set-it-and-forget-it” fluid systems, where active fluids autonomously restore flow direction after perturbation, minimizing the need for continuous mechanical control.
Finally, our numerical model adopts a purely two-dimensional formulation that neglects wall friction from top and bottom plates, whereas in experiments, such friction provides an additional hydrodynamic damping comparable in magnitude to the active stress (Section S3). While this effect primarily reduces the overall flow amplitude without changing the qualitative flow structures, incorporating it into the model (or performing full three-dimensional simulations) will refine quantitative predictions and offer a more complete description of active fluid dynamics confined in a Hele–Shaw-like geometries.
Overall, this work demonstrates the crucial role of confinement geometry in governing active fluid response to external forces. Confinement can serve as a critical design parameter for controlling active fluid behavior under external forces, enabling the development of adaptive biomaterials that self-organize and recover after mechanical perturbations.54 Additionally, our work highlights that coherent flow patterns in active fluids can be programmed through external driving. Systems can be engineered to support multiple flow states with specific patterns activated by external forces (Fig. 4A). This force-activated pattern control can be applied to biomimetic microfluidic networks, which require dynamically regulated transport. More broadly, these findings connect to cellular systems, where confinement and external forces regulate intracellular flows such as cytoplasmic streaming.55 Understanding how confinement modulates active stress interactions can provide new insights into biological processes driven by force-sensitive self-organization.
Author contributions
J. H. D., T. W., Y.-C. C., and K.-T. W. performed the research and designed the experiments; Y.-C. C. initiated the experiments; J. H. D. and H. W. prepared microtubules and kinesin motor proteins; J. H. D., T. W., and Y.-C. C. collected experimental data; J. H. D., T. W., Y.-C. C., and K.-T. W. organized and analyzed the data; T. W., Y. H., S. S., R. A. P., and T. R. P. established the continuum simulation platform on modeling active fluid systems under external driving; J. H. D. and K.-T. W. wrote the manuscript; and K.-T. W. supervised the research. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting this study are in the main text and supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00871a.Acknowledgements
J. H. D., T. W., Y.-C. C., H. W., and K.-T. W. acknowledge support from the National Science Foundation (NSF-CBET-2045621). R. A. P. and T. R. P. acknowledge support in part from National Science Foundation grant NSF-CBET-2227361, and T. R. P. acknowledges support in part from National Science Foundation grants NSF-MRSEC-DMR-2011846 and NSF-PHY-2309135 to the Kavli Institute for Theoretical Physics (KITP), where some of this work was completed. This research was performed with computational resources supported by the Academic & Research Computing Group at Worcester Polytechnic Institute. We acknowledge the Brandeis Materials Research Science and Engineering Center (NSF-MRSEC-DMR-2011846) for use of the Biological Materials Facility. We thank Victoria M. Bicchieri for her assistance in collecting confocal data with the Leica Microsystems Stellaris 8 confocal microscope in the Life Sciences and Bioengineering Center at Worcester Polytechnic Institute, and Wan Luo and Kenneth Breuer for important discussion.Notes and references
- T. Vicsek and A. Zafeiris, Collective motion, Phys. Rep., 2012, 517, 71–140 CrossRef.
- J. Toner, Y. Tu and S. Ramaswamy, Hydrodynamics and phases of flocks, Ann. Phys., 2005, 318, 170–244 Search PubMed.
- C. L. Hueschen, A. R. Dunn and R. Phillips, Wildebeest herds on rolling hills: Flocking on arbitrary curved surfaces, Phys. Rev. E, 2023, 108, 024610 CrossRef CAS.
- M. Scandolo, J. Pausch and M. E. Cates, Active Ising models of flocking: A field-theoretic approach, Eur. Phys. J. E:Soft Matter Biol. Phys., 2023, 46, 103 CrossRef CAS PubMed.
- A. Sokolov and I. S. Aranson, Physical properties of collective motion in suspensions of bacteria, Phys. Rev. Lett., 2012, 109, 248109 CrossRef.
- K.-T. Wu, J. B. Hishamunda, D. T. N. Chen, S. J. DeCamp, Y.-W. Chang, A. Fernández-Nieves, S. Fraden and Z. Dogic, Transition from turbulent to coherent flows in confined three-dimensional active fluids, Science, 2017, 355, eaal1979 Search PubMed.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Confinement stabilizes a bacterial suspension into a spiral vortex, Phys. Rev. Lett., 2013, 110, 268102 Search PubMed.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Emergence of macroscopic directed motion in populations of motile colloids, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- H. Wioland, E. Lushi and R. E. Goldstein, Directed collective motion of bacteria under channel confinement, New J. Phys., 2016, 18, 075002 Search PubMed.
- A. Opathalage, M. M. Norton, M. P. N. Juniper, B. Langeslay, S. A. Aghvami, S. Fraden and Z. Dogic, Self-organized dynamics and the transition to turbulence of confined active nematics, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 4788–4797 Search PubMed.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Topology and dynamics of active nematic vesicles, Science, 2014, 345, 1135–1139 CrossRef CAS PubMed.
- T. D. Ross, H. J. Lee, Z. Qu, R. A. Banks, R. Phillips and M. Thomson, Controlling organization and forces in active matter through optically defined boundaries, Nature, 2019, 572, 224–229 CrossRef CAS PubMed.
- R. Adkins, I. Kolvin, Z. You, S. Witthaus, M. C. Marchetti and Z. Dogic, Dynamics of active liquid interfaces, Science, 2022, 377, 768–772 Search PubMed.
- J. Słomka and J. Dunkel, Geometry-dependent viscosity reduction in sheared active fluids, Phys. Rev. Fluids, 2017, 2, 043102 CrossRef.
- H. M. López, J. Gachelin, C. Douarche, H. Auradou and E. Clément, Turning bacteria suspensions into superfluids, Phys. Rev. Lett., 2015, 115, 028301 CrossRef.
- A. Sokolov and I. S. Aranson, Reduction of viscosity in suspension of swimming bacteria, Phys. Rev. Lett., 2009, 103, 148101 CrossRef PubMed.
- D. A. Gagnon, C. Dessi, J. P. Berezney, R. Boros, D. T. N. Chen, Z. Dogic and D. L. Blair, Shear-induced gelation of self-yielding active networks, Phys. Rev. Lett., 2020, 125, 178003 CrossRef CAS.
- D. Saintillan, Rheology of active fluids, Annu. Rev. Fluid Mech., 2018, 50, 563–592 CrossRef.
- Y.-C. Chen, B. Jolicoeur, C.-C. Chueh and K.-T. Wu, Flow coupling between active and passive fluids across water–oil interfaces, Sci. Rep., 2021, 11, 13965 CrossRef CAS PubMed.
- M. M. Norton, A. Baskaran, A. Opathalage, B. Langeslay, S. Fraden, A. Baskaran and M. F. Hagan, Insensitivity of active nematic liquid crystal dynamics to topological constraints, Phys. Rev. E, 2018, 97, 012702 Search PubMed.
- K. Suzuki, M. Miyazaki, J. Takagi, T. Itabashi and S. Ishiwata, Spatial confinement of active microtubule networks induces large-scale rotational cytoplasmic flow, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2922–2927 CrossRef CAS.
- T. E. Bate, E. J. Jarvis, M. E. Varney and K.-T. Wu, Controlling flow speeds of microtubule-based 3D active fluids using temperature, J. Visualized Exp., 2019, e60484 Search PubMed.
- M. Castoldi and A. V. Popov, Purification of brain tubulin through two cycles of polymerization–depolymerization in a high-molarity buffer, Protein Expression Purif., 2003, 32, 83–88 Search PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Spontaneous motion in hierarchically assembled active matter, Nature, 2012, 491, 431–434 CrossRef CAS.
- G. Henkin, S. J. DeCamp, D. T. N. Chen, T. Sanchez and Z. Dogic, Tunable dynamics of microtubule-based active isotropic gels, Philos. Trans. R. Soc., A, 2014, 372, 20140142 CrossRef.
- F. J. Nédélec, T. Surrey, A. C. Maggs and S. Leibler, Self-organization of microtubules and motors, Nature, 1997, 389, 305–308 CrossRef PubMed.
- D. S. Martin, R. Fathi, T. J. Mitchison and J. Gelles, FRET measurements of kinesin neck orientation reveal a structural basis for processivity and asymmetry, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5453–5458 CrossRef CAS PubMed.
- B. Lemma, L. M. Lemma, S. C. Ems-McClung, C. E. Walczak, Z. Dogic and D. J. Needleman, Structure and dynamics of motor-driven microtubule bundles, Soft Matter, 2024, 20, 5715–5723 RSC.
- M. J. Schnitzer and S. M. Block, Kinesin hydrolyses one ATP per 8-nm step, Nature, 1997, 388, 386–390 CrossRef CAS.
- D. L. Coy, M. Wagenbach and J. Howard, Kinesin takes one 8-nm step for each ATP that it hydrolyzes, J. Biol. Chem., 1999, 274, 3667–3671 CrossRef CAS.
- T. E. Bate, E. J. Jarvis, M. E. Varney and K.-T. Wu, Collective dynamics of microtubule-based 3D active fluids from single microtubules, Soft Matter, 2019, 15, 5006–5016 Search PubMed.
- B. Najma, W.-S. Wei, A. Baskaran, P. J. Foster and G. Duclos, Microscopic interactions control a structural transition in active mixtures of microtubules and molecular motors, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2300174121 Search PubMed.
- A. W. C. Lau, A. Prasad and Z. Dogic, Condensation of isolated semi-flexible filaments driven by depletion interactions, Europhys. Lett., 2009, 87, 48006 CrossRef.
- T. E. Bate, M. E. Varney, E. H. Taylor, J. H. Dickie, C.-C. Chueh, M. M. Norton and K.-T. Wu, Self-mixing in microtubule-kinesin active fluid from nonuniform to uniform distribution of activity, Nat. Commun., 2022, 13, 6573 Search PubMed.
- Y. Fan, K.-T. Wu, S. A. Aghvami, S. Fraden and K. S. Breuer, Effects of confinement on the dynamics and correlation scales in kinesin-microtubule active fluids, Phys. Rev. E, 2021, 104, 034601 CrossRef CAS PubMed.
- N. T. Ouellette, H. Xu and E. Bodenschatz, A quantitative study of three-dimensional Lagrangian particle tracking algorithms, Exp. Fluids, 2005, 40, 301–313 Search PubMed.
- L. Giomi, Geometry and topology of turbulence in active nematics, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- R. Benzi, S. Patarnello and P. Santangelo, Self-similar coherent structures in two-dimensional decaying turbulence, J. Phys. A: Math. Gen., 1988, 21, 1221 CrossRef CAS.
- J. Weiss, The dynamics of enstrophy transfer in two-dimensional hydrodynamics, Phys. D, 1991, 48, 273–294 Search PubMed.
- M. Varghese, A. Baskaran, M. F. Hagan and A. Baskaran, Confinement-induced self-pumping in 3D active fluids, Phys. Rev. Lett., 2020, 125, 268003 Search PubMed.
- D. J. Acheson, Elementary fluid dynamics, Clarendon Press: Oxford University Press, Oxford, 2009 Search PubMed.
- H. C. Brinkman, A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles, Appl. Sci. Res., 1949, 1, 27–34 Search PubMed.
- Y. Almoteri and E. Lushi, Microswimmer collective dynamics in Brinkman flows, Phys. Rev. Fluids, 2025, 10, 083102 CrossRef.
- H. Liu, P. R. Patil and U. Narusawa, On Darcy-Brinkman equation: viscous flow between two parallel plates packed with regular square arrays of cylinders, Entropy, 2007, 9, 118–131 Search PubMed.
- J. M. Ottino, Mixing, chaotic advection, and turbulence, Annu. Rev. Fluid Mech., 1990, 22, 207–254 Search PubMed.
- X. Wang, B. Klaasen, J. Degrève, A. Mahulkar, G. Heynderickx, M.-F. Reyniers, B. Blanpain and F. Verhaeghe, Volume-of-fluid simulations of bubble dynamics in a vertical Hele-Shaw cell, Phys. Fluids, 2016, 28, 053304 CrossRef.
- J. Hardoüin, C. Doré, J. Laurent, T. Lopez-Leon, J. Ignés-Mullol and F. Sagués, Active boundary layers in confined active nematics, Nat. Commun., 2022, 13, 6675 CrossRef.
- H. Wioland, F. G. Woodhouse, J. Dunkel and R. E. Goldstein, Ferromagnetic and antiferromagnetic order in bacterial vortex lattices, Nat. Phys., 2016, 12, 341 Search PubMed.
- J. Hardoüin, J. Laurent, T. Lopez-Leon, J. Ignés-Mullol and F. Sagués, Active microfluidic transport in two-dimensional handlebodies, Soft Matter, 2020, 16, 9230–9241 RSC.
- W. Luo, A. Baskaran, R. A. Pelcovits and T. R. Powers, Flow states of two dimensional active gels driven by external shear, Soft Matter, 2024, 20, 738–753 RSC.
- S. Bhattacharyya and J. M. Yeomans, Phase ordering in binary mixtures of active nematic fluids, Phys. Rev. E, 2024, 110, 024607 CrossRef CAS.
- D. Saintillan and M. J. Shelley, Instabilities, pattern formation, and mixing in active suspensions, Phys. Fluids, 2008, 20, 123304 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys., 2013, 85, 1143–1189 Search PubMed.
- N. De Alwis Watuthanthrige, B. Ahammed, M. T. Dolan, Q. Fang, J. Wu, J. L. Sparks, M. B. Zanjani, D. Konkolewicz and Z. Ye, Accelerating dynamic exchange and self-healing using mechanical forces in crosslinked polymers, Mater. Horiz., 2020, 7, 1581–1587 RSC.
- R. E. Goldstein, I. Tuval and J.-W. van de Meent, Microfluidics of cytoplasmic streaming and its implications for intracellular transport, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 3663–3667 CrossRef CAS PubMed.
Footnote |
| † Present address: Department of Neuroscience, University of Pittsburg, Pittsburgh, PA 15260, USA. |
| This journal is © The Royal Society of Chemistry 2026 |








