Upstream motion of oil droplets in co-axial Ouzo flow due to Marangoni forces
Steffen
Bisswanger
 a,
Duarte
Rocha
a,
Duarte
Rocha
 b,
Sebastian
Dehe
b,
Sebastian
Dehe
 ac,
Christian
Diddens
ac,
Christian
Diddens
 b,
Tobias
Baier
b,
Tobias
Baier
 a,
Detlef
Lohse
a,
Detlef
Lohse
 bd and
Steffen
Hardt
bd and
Steffen
Hardt
 *a
*a
aTechnische Universität Darmstadt, Fachbereich Maschinenbau, Fachgebiet Nano- und Mikrofluidik, Peter-Grünberg-Str. 10, 64287 Darmstadt, Germany. E-mail: hardt@nmf.tu-darmstadt.de
bPhysics of Fluids Department, Max Planck Center Twente for Complex Fluid Dynamics and J. M. Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500AE, Enschede, The Netherlands
cLinac Coherent Light Source SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
dMax Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany
First published on 18th November 2025
Abstract
To explore the physicochemical hydrodynamics of phase-separating ternary liquids (“Ouzo-type”), a binary oil–ethanol mixture is introduced into a co-flowing stream of water. Oil droplets nucleate at the interface between the two liquids, leading to a larger oil droplet interacting with the ethanol-rich jet. Although buoyancy forces and hydrodynamic drag forces push the droplet in downstream direction, we observe an upstream motion. Using computational fluid dynamics simulations of a simplified model system, we identify the nucleation zone for oil droplets and uncover Marangoni forces to be responsible for the upstream motion of the droplet. A semi-analytical model allows us to identify the key parameters governing this effect. A general conclusion is that Marangoni stresses can reverse the motion of droplets through channels, where the surrounding liquid is a multi-component mixture. The insights from this work are not only relevant for channel flow, but more generally, for the physicochemical hydrodynamics of multiphase, multi-component systems.
1. Introduction
A vast number of technical applications involve flows of a liquid that consists of multiple components. Owing to differences in inter-molecular forces for different components, miscibility and interfacial tension heavily depend on the ratio of the different components. In single-phase systems, concentration gradients of dissolved components may influence the flow through changes in bulk properties (e.g., density), but they usually do not directly induce a flow. If, however, an interface is subject to a concentration gradient that results in an interfacial tension gradient, the tangential momentum balance at the interface tells us that it is inevitable that a flow is induced, commonly known as Marangoni flow.1,2 Depending on the cause of the interfacial tension gradient, this flow is categorized into thermal or solutal Marangoni flow. In turn, it can result in a deformation of the interface as is the case, e.g., for sessile droplets that spread or contract due to evaporation-induced solutal or thermal Marangoni stresses,3–5 or in complex advection of droplets that are freely suspended in a stratified liquid.6–9 As mentioned above, the composition of a liquid does not only affect interfacial tension, but also its miscibility. Probably the most famous and most studied example of such a system is a ternary mixture of water, ethanol and transanethole: For compositions with relatively large ethanol mass fraction and small water fraction, the three components are miscible. However, if we increase the water content, the three components will cease to remain fully miscible at some point, resulting in the nucleation of oil droplets. This spontaneous emulsification is often referred to as the “Ouzo effect”,2,10 since the Greek spirit Ouzo (among many others) is one example of such a ternary system with a miscibility gap where emulsification can be observed. Typical droplet radii for “Ouzo type” emulsions are in the range of a few 100 nm, depending on the component ratios, temperature and time.11 The resulting light scattering gives the emulsion its opaque appearance. The dynamics of this system is especially interesting if we have large concentration gradients, as the creation of new interfacial area is particularly rapid. Additionally, large concentration gradients imply large interfacial tension gradients that can act on these interfaces. In combination, these two points imply the emergence of an emulsion in which the characteristic force (surface integral of the Marangoni stresses) per unit volume is relatively large, especially on small length scales.12 This results in the occurrence of phenomena that are rich in dynamics, and to some extent counter-intuitive. In the context of applications in chemical analysis, the large ratio of interfacial area per unit volume in such “Ouzo-type” systems is leveraged in methods like dispersive liquid–liquid microextraction,13–15 where it enables a fast transfer of an analyte from the continuous aquous phase into the dispersed oil phase.In this paper, we study such an “Ouzo-type” system experimentally, numerically, and using analytical models: we create large concentration gradients by injecting an oil–ethanol mixture into a stream of pure water, following a similar approach as used by Hajian and Hardt16 (see Section 2). Capturing the complex multi-scale dynamics occurring in this system through numerical simulations poses a substantial challenge. Resolving the three-dimensional multiphase advection-diffusion problem, including growth and coalescence of droplets ranging from a few 100 nm to about 100 µm in diameter, is impractical. Instead, we are able to shine light onto specific aspects of the experimentally observed phenomena by making simplifying assumptions that preserve the system's fundamental physics (see Section 3). Using even further simplifying assumptions, we then rationalize the observations from the simulations with a semi-analytical model (see Section 4). The paper ends with conclusions and an outlook (see Section 5).
2. Experiments
The experiment takes place in a vertical coaxial flow configuration (see Fig. 1). A mixture of transanethole and ethanol (ratio of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88 by weight) is injected into a capillary with a sheath flow of water. Due to the radial gradients in concentration of the individual components where the sheath flow meets the jet, water diffuses inward, while ethanol and transanethole diffuse outward. While the binary mixture of the jet (ethanol–transanethole) is miscible for arbitrary ratios, the ternary mixture of water, ethanol, and transanethole is only fully miscible for compositions with small water fraction and large ethanol fraction. This means that there has to be an interval along the radial direction where we obtain a composition of the ternary mixture which at that point is not fully miscible anymore. This is qualitatively illustrated in the ternary diagram, as predicted by UNIFAC,17 in Fig. 2: the composition along the center axis of the flow is given by the point near the top corner on the edge of the triangle, representing a binary mixture of ethanol and oil. As we move radially outward, the water content monotonically increases (ternary mixture). Very far outwards, the water fraction will eventually be unity (bottom left corner in Fig. 2). However, as the composition enters the two-phase region (green area in Fig. 2), the continuous phase follows the binodal curve along the water-rich side, while the excess oil separates into droplets. The corresponding composition of the oil-rich phase is then given by the point on the other side of the binodal connected by the corresponding tie-line (see Fig. 2). The radial extent of this two-phase region surrounding the jet depends on the time available to diffusion to smear out the concentration field. Since we prescribe the concentration profile at some upstream position where we inject the binary mixture, the diffusion time can be mapped to the downstream position where the flow is observed. For this reason, further downstream the two-phase region is expected to become wider.16
88 by weight) is injected into a capillary with a sheath flow of water. Due to the radial gradients in concentration of the individual components where the sheath flow meets the jet, water diffuses inward, while ethanol and transanethole diffuse outward. While the binary mixture of the jet (ethanol–transanethole) is miscible for arbitrary ratios, the ternary mixture of water, ethanol, and transanethole is only fully miscible for compositions with small water fraction and large ethanol fraction. This means that there has to be an interval along the radial direction where we obtain a composition of the ternary mixture which at that point is not fully miscible anymore. This is qualitatively illustrated in the ternary diagram, as predicted by UNIFAC,17 in Fig. 2: the composition along the center axis of the flow is given by the point near the top corner on the edge of the triangle, representing a binary mixture of ethanol and oil. As we move radially outward, the water content monotonically increases (ternary mixture). Very far outwards, the water fraction will eventually be unity (bottom left corner in Fig. 2). However, as the composition enters the two-phase region (green area in Fig. 2), the continuous phase follows the binodal curve along the water-rich side, while the excess oil separates into droplets. The corresponding composition of the oil-rich phase is then given by the point on the other side of the binodal connected by the corresponding tie-line (see Fig. 2). The radial extent of this two-phase region surrounding the jet depends on the time available to diffusion to smear out the concentration field. Since we prescribe the concentration profile at some upstream position where we inject the binary mixture, the diffusion time can be mapped to the downstream position where the flow is observed. For this reason, further downstream the two-phase region is expected to become wider.16
 | ||
| Fig. 2 Ternary diagram of the Ouzo system in terms of mass fraction, as predicted by UNIFAC.17 The solid black line denotes the binodal, and the dark green lines denote tie lines. The change in composition in the radial direction inside the flow is indicated with the magenta arrows, starting at a mixture of 12% transanethole and 88% ethanol by weight. | ||
2.1. Setup
In order to implement the coaxial flow, we use a cell as depicted in Fig. 1. The setup is oriented vertically so that buoyancy effects do not disturb the axisymmetry of the flow. It consists of an outer glass capillary with square cross-section (2 mm × 2 mm inner dimensions) and an inner glass capillary with circular cross-section that tapers down to a tip of 30 µm inner diameter. A closed-loop volume-flow-controlled pressure pump (Elveflow, model OB1 MkII equipped with two microthermal flow sensors) connected to the bottom of the cell creates a sheath flow of water (typically approx. 200 µL min−1) and at the same time injects an ethanol–transanethole mixture through the inner capillary, thus creating a jet centered inside the sheath flow, rising as a buoyant plume. The ternary mixture exits the cell at the top (z ≈ 4 cm) and is directed into a waste container at atmospheric pressure. The flow inside the cell is imaged using a high-speed camera (Photron Fastcam Mini AX200) equipped with a long-distance microscope lens (Navitar 1-60191, 0.7-4x and Mitutoyo M Plan Apo 10x/0.28). Illumination (by means of an LED Panel) is provided from the backside. For cleaning the cell from transanethole droplets and from dust particles that can obstruct the flow inside the inner capillary nozzle, we flush the system with ethanol or immerse the dismantled system in 2% Hellmanex III-water solution. Since the cleaning effect of the latter relies on surfactants that strongly affect interfacial tension, we thoroughly flush the cell with ethanol and water after using the Hellmanex III solution. The droplet growth in the freshly cleaned Ouzo system afterwards indicates the absence of surfactants.182.2. Creation and motion of nanodroplets
In Fig. 3, a typical recording of the flow inside the experimental cell is shown. Along the entire length of the cell we observe a “dark mist” that surrounds the jet, which we interpret as nanodroplets nucleating in this region. As we go downstream, the thickness of this “misty region” does not vary much. The overall radial position, however, shifts inward at a typical speed of 80 µm s−1 (cf. (SI)). At the same time, the jet velocity remains constant with respect to the axial position so that mass conservation implies that there is no radial net flow. Therefore, we interpret this as a relative motion between the nanodroplets and the surrounding continuous phase. Haijan and Hardt16 discussed this relative radial inward motion of nanodroplets in detail and identified Marangoni stresses as the driving force. As a result, the dispersed oil phase is focused close to the center axis.2.3. Formation of large droplets
At positions sufficiently far downstream (z > 6 mm, for the flow conditions studied here) the jet undergoes an instability that results in the periodic creation of droplets. While this system is without any doubt more complex than a single-component jet inside a second immiscible fluid, the droplet-shedding process is visually similar to the Rayleigh–Plateau instability, as shown in the detail view (I) of Fig. 3. It is not easily observed when and how exactly the dense envelope of nanodroplets surrounding the jet coalesces and forms a continuous interface that separates the oil-rich inner phase and the water-rich outer phase, which could then be subject to the Rayleigh–Plateau instability. The diameter of the largest droplets formed in this process is approximately the same as the diameter of the jet. Between the larger droplets we observe smaller droplets that stay aligned with the center axis and subsequently coalesce into larger droplets (II).2.4. Upstream motion and instability
Once a droplet is shed from the end of the jet, we often observe that its axial velocity is reduced to values below the centerline velocity of the surrounding flow, so that it moves relative to the jet in upstream direction. This effect quickly dies off if the jet upstream of the droplet is too unstable and fragments into more droplets. If, however, the droplet manages to move fast enough relative to the jet, as is the case in Fig. 3, we can observe the droplet hovering at a fixed position (III), where it grows and eventually moves upstream (negative z-direction), while it keeps growing (IV). Since the end of the jet is then occupied by the droplet, no other large droplets can form behind the jet. Instead, a tail of small droplets can be observed downstream of the droplet. Further downstream, these droplets coalesce to form microdroplets that become individually visible. Once the oil droplet attached to the jet has become sufficiently large, it is notably deformed into an oblate shape (V). Up to this point, the configuration has remained fairly axisymmetric, at least with respect to the larger features of the flow. However, now the upstream-traveling droplet undergoes a second instability: first, we notice slight radial oscillations in the tail behind the droplet, indicating that the north pole of the droplet shifts in a rotational mode. These oscillations grow until eventually the droplet not only rotates but also translates in the radial direction (VI). As a result, the droplet describes an upstream meandering motion. The whole process can be observed in SI Movie S1, where also the flow inside the droplet is qualitatively visible due to water-rich droplets that are trapped inside the oil droplet. The upstream motion of the droplet continues until it reaches the tip of the inner capillary where it becomes pinned. Notably, we only observe a radial translational motion of the droplet (VI) in the focus plane, or at an angle 90° relative to the focus plane. This means that the plane of translation is always aligned with the sidewalls of the outer capillary. A potentially similar aligning behavior is also known in the context of inertial focusing of particles inside microchannels with square cross-section.19 However, the similarity in terms of the alignment does not allow for conclusions on the cause of the instability. The instability could still be caused by mechanisms unrelated to inertial focusing.2.5. Auxiliary experiment: upstream motion of a gas bubble
In order to better understand the conditions that are essential to the phenomenon of upstream motion of the oil droplet in the Ouzo system, we conduct a simplified variant of the experiment. We replace the oil–ethanol mixture in the Ouzo experiment with pure ethanol that is saturated with CO2 at an overpressure of approximately 1 bar as the jet flow. By adding a large flow resistance into the inner capillary a bit upstream of where the ethanol is injected into the sheath flow of water, we create a large pressure drop that allows the dissolved CO2 to start to come out of solution only as it exits the nozzle. The outer flow is pure water as in the original Ouzo experiment. Depending on the nucleation sites at the inner capillary wall, bubbles of various sizes can be produced that are flushed with the ethanol into the sheath flow of water. In Fig. 4 time series images of this experiment is shown where a CO2 bubble rises inside the ethanol jet that is comparable in size to the oil droplet in the Ouzo system. Similar as the oil droplet in the Ouzo system, the gas bubble grows due to coalescence with small gas bubbles from the upstream side and due to the mass flow of CO2 through the surface of the bubble. As for the oil droplet, this coincides with a downstream motion of the bubble (I), followed by hovering (II) and an upstream motion (III), a sequence of processes during which the bubble increases in size. This suggests that the explanation for the upstream motion of the droplet in the Ouzo system can be found by resorting to simplified two-phase models. In a more general context, this auxiliary experiment demonstrates that the motion reversal is also possible in a system where not only drag forces but also buoyancy forces have to be overcome.3. Numerical simulations
The numerical simulations were designed to show the fundamental mechanisms behind some key findings from the experiments. Given the system's inherent complexity – which includes nanodroplet nucleation, Marangoni stresses at the complex boundaries between different phases, as well as mass transfer within the ternary mixture – fully transient, full-scale simulations are impractical. Instead, we isolate distinct phenomena by employing simplified models that facilitate a focused investigation.3.1. Methods
The simulations are performed with the open-source sharp-interface arbitrary Lagrangian–Eulerian (moving mesh) finite element software package pyoomph,20 which builds on oomph-lib21 and GiNaC.22 All domains are meshed using unstructured triangular Lagrangian elements.We model a cylindrical domain with a cross-sectional area equal to that of the outer square capillary used in the experiments. This approximation is justified, as the outer wall is sufficiently distant from the region of interest such that the flow dynamics is insensitive to the precise cross-sectional shape. A central tapered capillary, with 30 µm diameter, injects a jet of fluid – at a volumetric flow rate Qjet – into a surrounding sheath of pure water, maintained at a constant flow rate of Qwater = 175 µL min−1, as in the experiments. All calculations are performed on a 2D mesh using a cylindrical coordinate system, assuming axisymmetry.
The fluid motion is governed by mass conservation and the Navier-Stokes equation
| ∂tρ + ∇·(ρu) = 0 | (1) |
 | (2) |
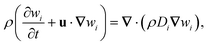 | (3) |
In Section 3.2, we first perform a single-phase simulation under the experimental conditions to identify regions where the Ouzo effect triggers nanodroplet nucleation. For these simulations, the inner jet has a flow rate of Qjet = 5 µL min−1 and an ethanol mass fraction of wEtOH = 88%. The quasi-stationary solution of the composition allows us to identify the regions where the Ouzo effect is expected to occur, based on the binodal curve (cf.Fig. 2).
In Section 3.3, we consider a simplified two-phase model where a pure transanethole droplet is suspended in a binary ethanol–water mixture. Focusing solely on hydrodynamic interactions and neglecting mass transfer in between the two phases, we study the regime in which the net force on a droplet – arising from Marangoni stresses, buoyancy, and advection – vanishes, keeping the droplet fixed at zdrop = 6.5 mm. By assuming no mass transfer, we consider that once the system is close to hydrodynamic equilibrium, it is also near chemical equilibrium, and the limited mass exchange between phases has a negligible effect on the overall flow behavior. By varying the droplet radius Rdrop and the ethanol jet flow rate Qjet, we determine the conditions that drive the droplet upstream or downstream. We compute the critical flow rate Qcritjet, defined via a Lagrange multiplier enforcing zero net force, that leads to a quasi-stationary equilibrium of the system.
At the interface between a droplet and the continuous phase (host fluid), the dynamic boundary condition reads
τh·n − τd·n = γ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) n + ∇tγ n + ∇tγ | (4) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) is the curvature of the interface, and n and t are the unit normal and tangential vectors, respectively. The interface is allowed to deform depending on the local interfacial tension. The interfacial tension is made composition-dependent according to a fit to the experimental data (see Fig. 5 in ref. 25). We assume that although a high ethanol mass fraction could in principle dissolve the transanethole droplet, the droplet remains intact and its interfacial tension is set by the fit to the experimental data of Archer et al.25
is the curvature of the interface, and n and t are the unit normal and tangential vectors, respectively. The interface is allowed to deform depending on the local interfacial tension. The interfacial tension is made composition-dependent according to a fit to the experimental data (see Fig. 5 in ref. 25). We assume that although a high ethanol mass fraction could in principle dissolve the transanethole droplet, the droplet remains intact and its interfacial tension is set by the fit to the experimental data of Archer et al.25
 | ||
| Fig. 5 Quasi-stationary solution for the single-phase system under the experimental conditions. (a) Composition and jet development, with gravity acting from top to bottom. At the left, the ethanol mass fraction (wt%) is shown, at the right the regions prone to nucleation (green) based on the binodal curve from Fig. 2 are indicated. At the nozzle, an ethanol–transanethole mixture enters through the inflow boundary, while water flows in at the outer boundary. (b) Regions prone to nucleation due to Ouzo effect (right) and ethanol wt% (left) within an area between 6 mm and 7 mm away from the nozzle. (c) Ethanol wt% (left) and velocity magnitude (right) close to the nozzle. | ||
Overall, this model framework enables us to capture the essential physics of the axial motion of oil droplets in the jet under a range of conditions. Again, naturally, the simplified models do not account for all the complexities of the experimental system, which prevents quantitative comparisons.
3.2. Nucleation zones around the Ouzo jet
Under the experimental conditions, the injected ethanol–transanethole jet gradually diffuses into the surrounding water as it travels downstream, creating peripheral regions where nucleation is favored according to the binodal curve (see Fig. 2). Fig. 5a illustrates the evolving ethanol concentration in the whole domain (left), while highlighting the zones prone to nucleation in green (right). In Fig. 5b, we show the areas susceptible to the Ouzo effect at a distance from 6 mm to 7 mm from the nozzle. Fig. 5c shows further details on the ethanol mass fraction (left) and the velocity magnitude (right) in the region close to the nozzle.3.3. Axial motion of a droplet in the ethanol jet
Using the simplified two-phase model, we study the axial motion of the droplet within the ethanol jet. By varying the droplet radius, Rdrop, from 15 µm to 120 µm, we determine the critical flow rate, Qcritjet, at which the droplet remains at a constant downstream position zdrop = 6.5 mm. Fig. 6 shows the numerical results (markers) alongside a theoretical estimate (solid line) which will be derived in Section 4 from a force balance between Marangoni forces and viscous drag. In our analysis, the critical flow rate is non-dimensionalized by 4πDminzdrop, where Dmin is the minimum diffusivity of ethanol in water and zdrop is the fixed axial position of the droplet. Detailed justification for this scaling is provided in Section 4, where we also discuss the stability of the equilibrium position with respect to axial perturbations. In the SI's Section S2, the flow features of four selected sets of parameters within the phase space of Fig. 6 are shown. | ||
| Fig. 6 Critical jet flow rate Qcritjet/4πDminzdrop as function of droplet radius Rdrop where the droplet remains stationary at a fixed position with zdrop = 6.5 mm and Dmin = 0.365 × 10−9 m2 s−1. The circular markers represent the numerical results (see Section 3). The solid black line corresponds to the estimate from the further simplified model described in Section 4, where the color gradient around the line indicates the mass fraction of ethanol approaching the droplet. The dashed lines correspond to the limiting cases described by eqn (19) (coarse dashed) and eqn (18) (fine dashed, see Section 4). The colorbar indicates the ethanol mass fraction of the liquid approaching the droplet (taken at r = 0 and z = zdrop − 2Rdrop). The hatched region indicates the region where the droplet is expected to move upstream, according to the numerical simulation results. In the solid white region it moves downstream. The star symbols correspond to the flow rate and droplet growth in the experiment shown in Fig. 3, with corresponding Roman numbering, for general orientation only, without the intent to imply a quantitative comparison or to indicate the axial motion in the experiment. | ||
Notably, the results reveal two distinct branches corresponding to small and large flow rates. The presence of multiple equilibrium flow rates for a given droplet radius is linked to variations in the ethanol concentration, as indicated by the color gradient of the markers in Fig. 6.
4. Discussion and a simple theoretical model
Qualitatively, the nucleation zone around the jet (see Section 3.2) looks similar to the “dark mist” around the jet from the experiments, indicating that what we see are in fact nanodroplets. One aspect that the numerical single-phase simulations do not capture by design is the fact that the nanodroplets that nucleate migrate radially inward due to Marangoni stresses.The simulations on the axial motion of the droplet (see Section 3.3) show that droplets can hover at a fixed axial position, as observed in the experiments. In this context, we can identify the experimental regime as belonging to the top branch shown in Fig. 6, as indicated with the star symbols. We do not observe the bottom branch in experiments. This is due to two reasons: first, the equilibrium of the droplet in the bottom branch is unstable with respect to axial perturbations, as we will soon see. Second, the observation of a hovering droplet requires the creation of a sufficiently large droplet in the first place. This however only happens for large flow rates. Irrespective of that, we can rationalize why we observe these two branches in the simulations.
4.1. Equilibrium configuration of the hovering droplet
The fact that we observe two different equilibrium configurations for a single droplet size indicates that the explanation for this has to be found in the approaching jet that is independent of the hovering droplet. According to Crank,26 the mass fraction of ethanol at the centerline of the jet is approximately given by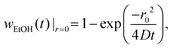 | (5) |
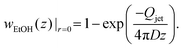 | (6) |
The agreement of this expression with the simulations is shown in Fig. 7, revealing that wEtOH at z = zdrop is well-described for small Qjet using the maximum diffusion coefficient Dmax, while for large Qjet it is well-described using the minimum diffusion coefficient Dmin. Generally, the diffusion coefficient of ethanol in water is concentration-dependent. In our case, the concentration does vary across the entire possible range, since the local ethanol mass fraction in our problem can vary between zero (outer flow of pure water) and unity (inner flow of pure ethanol). This, in turn, affects how the centerline concentration at a specific axial position z varies with the flow rate, which is evident in the comparison. One aspect to note here is that even though the diffusion coefficient is only minimal for an ethanol mass fraction of approx. 0.5 (see small plot in Fig. 7), the minimum diffusion coefficient also determines the centerline concentration for large flow rates, where the centerline concentration itself is close to unity. This is due to the fact that the radial diffusion problem is dominated by the minimum diffusivity along the radial direction, which for centerline concentrations above 0.5 is the global minimum of the diffusivity. We use this minimum diffusivity to non-dimensionalize the flow rate, as shown in Fig. 6. The magnitude of the non-dimensional flow rate in relation to unity is what we refer to as large or small jet flow rates.
 | ||
| Fig. 7 Mass fraction of ethanol at the centerline wEtOH|r=0 as a function of the jet flow rate Qjet (left) and diffusion coefficient of a binary water–ethanol mixture as function of the ethanol mass fraction (bottom right). The markers (left) represent the numerical results, with the colormap being identical to that of Fig. 6. The solid black lines (left) correspond to eqn (6), with z = zdrop, and the cases of maximum and minimum diffusion coefficient of water–ethanol mixtures Dmin = 0.365 × 10−9 m2 s−1 and Dmax = 1.255 × 10−9 m2 s−1. The dashed line (left) represents Qjet·4πDminzdrop. | ||
In order to further explain the two different branches of equilibrium we now employ a force balance between the Marangoni force and the viscous force. Due to the complexity of the system, we do not aim at quantitative predictions, but instead at preserving the fundamental physics while making strongly simplifying assumptions. Based on a conservative estimate (1.46 mm s−1 ≥ uc ≥ 8 mm s−1, 8 µm ≥ Rdrop ≥ 120 µm, 1 mPa s ≥ µ ≥ 2 mPa s and 800 kg m−3 ≥ ρ ≥ 998 kg m−3), the range of the Reynolds number is 0.009 < Re < 2. We approximate the viscous force as Stokes drag27
| Fdrag = 6πµβucRdrop | (7) |
A comparison of the magnitude of the drag force with the magnitude of the buoyancy force acting on the droplet shows that we can neglect the effect of buoyancy: The ratio of these two forces can be approximated as
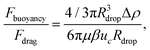 | (8) |
 | (9) |
In order to estimate the Marangoni force and in order to simplify the diffusion problem, we approximate the droplet as a cylinder with the same radius and height as the droplet radius, as shown in Fig. 8. This constrains the cylinder to have the same surface area as the droplet, which is the relevant parameter in the context of interfacial tension and diffusion. Assuming this cylinder to be surrounded by a constant interfacial-tension gradient, we write the Marangoni force acting in negative z-direction as
| FMarangoni = 2πRdropΔγ | (10) |
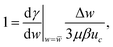 | (11) |
![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) is the mean ethanol mass fraction at the surface of the droplet. Mass conservation for the purely radial diffusion problem around the periphery of the cylindrical droplet gives
is the mean ethanol mass fraction at the surface of the droplet. Mass conservation for the purely radial diffusion problem around the periphery of the cylindrical droplet gives | (12) |
 | (13) |
Next, we approximate the radial gradient in the ethanol mass fraction as
 | (14) |
The thickness of the ethanol layer around the cylindrical droplet can be expressed as (see SI Section S3.1)
 | (15) |
 | (16) |
While the thickness of the ethanol layer does in general vary along the droplet surface, here we assume δr to be constant, which can be interpreted as a zeroth-order approximation with respect to the coordinate along the droplet surface. Inserting eqn (6) and (12–16) into eqn (11) and using the same material models as in the simulations as well as β = 1, we can numerically solve for Rdrop. The result is plotted as the solid black line in Fig. 6 for zdrop = 6.5 mm. For varying axial positions zdrop the result is plotted in Fig. 9. In both cases, the centerline velocity is approximated as uc = 1.46 × 10−3 m s−1 based on the assumption of a purely pressure-driven flow for Qtotal = 175 µL min−1. Again, the actual centerline velocity can be larger than this approximated value due to the buoyancy of the ethanol jet (see SI Section S3.3). However, uc does not affect the two limiting cases that correspond to the two branches that we can see in Fig. 6. In both of these two cases we assume that the droplet radius is large compared to the jet radius
| Rdrop ≫ rjet. | (17) |
 | ||
| Fig. 9 Equilibrium configurations of a hovering droplet. The vertical axis shows the droplet position zdrop, the horizontal axis shows the jet flow rate Qjet, and the colors/contours indicate the radius Rdrop of a droplet that is in equilibrium according to eqn (12–16) and eqn (11). The equilibrium configurations that are stable according to eqn (20) are enclosed by the two solid black lines. Outside of this area, the equilibrium is unstable. The black dashed line indicates where the non-dimensional jet flow rate is unity (Qjet/(4πDminzdrop) = 1). The circular markers show the results from the numerical simulations (zdrop = 6.5 mm), where the color of the marker represents the radius Rdrop of the stationary droplet. The stars correspond the upstream motion (arrow) in the experiment shown in Fig. 3 (between the 4th frame and last frame) for general orientation only, without the intent to imply a quantitative comparison. | ||
The solution shown in Fig. 9 does not depend, qualitatively and order-of-magnitude-wise, on the (arbitrary) choice of β as long as β ∼ 1. Next, we calculate the limiting cases for small flow rates (see SI Section S3.2)
 | (18) |
 | (19) |
These two limiting cases are indicated in Fig. 6 as thin dashed lines. Note that eqn (18) and (19) are independent of uc and β. In retrospect, this justifies the assumption that uc is approximated by assuming a purely pressure-driven flow that only affects the proposed equilibrium configuration for intermediate jet flow rates. For a more detailed outline of the semi-analytical model we refer the reader to the SI Section S3.
4.2. Axial stability of the hovering droplet
From the numerical simulations we know that within the hatched area in Fig. 6 we obtain upstream motion of the droplet, and downstream motion otherwise. However, this information does not allow conclusions on the stability of the equilibrium under small variations of the axial position, since the numerical simulations cover only a single value zdrop. Instead, we can use the dependence of the semi-analytical model on zdrop to determine the stability: the equilibrium will be stable, if and only if a deflected droplet is pushed back to its original position | (20) |
Due to the material properties that (through wEtOH and eqn (6)) implicitly depend on zdrop, the generality of this equilibrium and stability map is limited. The non-monotonic dependence of zdrop on Qjet that we see in Fig. 9 in the unstable region for large Qjet is due to the specific material model for interfacial tension: In the limiting case where Qcritjet ≫ 4πDzdrop, the critical flow rate does not depend explicitly on zdrop anymore (cf.eqn (19)). If the equilibrium configuration was actually independent of zdrop, we would expect that all of the contour lines (Rdrop= const.) are vertical for large jet flow rates. However, this is not the case, as we can see in Fig. 9. Therefore, we attribute all deviations from vertical contour lines in Fig. 9 for large jet flow rates to the material model for interfacial tension that implicitly depends on zdrop.
Based on the axisymmetric model employed in the semi-analytical approach, no direct conclusions on the stability of radial or azimuthal modes are possible. The meandering instability that we observed in the experiments could indicate that in many cases, the axisymmetric configuration is unstable. The azimuthal stability of the axisymmetric base solutions can be determined numerically by applying the method outlined by Diddens and Rocha,20 in which the eigenvalue problem of the system perturbed with an azimuthal mode m is solved. In our calculations, only when artificially manipulating the interfacial tension in between the phases, we obtained the onset of a meandering instability. Therefore, at this stage, drawing conclusions on the origin of the meandering instability does not appear to be justified.
5. Conclusions and outlook
A droplet that is suspended in a coaxial flow with radial concentration gradients can defy advection and buoyancy and hover at a fixed axial position due to Marangoni stresses. We demonstrated this in an experiment, in which we used a coaxial flow of ethanol and oil on the inside, and water on the outside. Due to the partial immiscibility of these components, droplets spontaneously form downstream of the jet. Using numerical simulations, we showed that a growing nucleation zone of oil droplets forms around the jet, and that droplets suspended inside the jet can hover at a fixed position for a wide range of flow rates. They can even experience a net force in opposite direction of buoyancy and advection that drives them upstream. In some cases, we obtained an azimuthally unstable configuration, hinting at the fact that the exact material model for interfacial tension might play a pivotal role in this context. We then rationalized the resulting flow-regime map using a semi-analytical model that agrees qualitatively with the numerical simulations. For large and small flow rates, the semi-analytical model simplifies to two explicit expressions demonstrating how the critical jet flow rate depends on the droplet radius. For intermediate flow rates, the droplet is stable with respect to variations of its axial position, implying that this mechanism can be used to capture or direct droplets inside a channel flow. The capturing of these droplets can be selective for specific droplet sizes, depending on the applied jet flow rate that is easily controlled in a practical application.One additional degree of freedom that has not been explored in this context is the variation of the cross-sectional area of outer capillary: forcing the co-axial flow through converging or diverging sections of the outer capillary, the flow velocity and the jet radius can be modulated locally. In principle, a repeated arrangement of such necks could be used to build a microfluidic system to fractionate droplets of different sizes. In the application context of dispersive liquid–liquid microextraction, this could enable a continuous process that is easier to scale up since it removes the need for using individual spin tubes and centrifuging of an emulsion to obtain a macroscopic liquid volume containing the analyte. Instead, a macroscopic oil droplet that has grown to a specific size could simply be retained at a specific downstream position and further processed subsequently. In a more general context, the upstream motion allows for a novel approach on pipetting small amounts of liquids or gases from emulsions or dispersions. A corresponding example is a pipette from which a coaxial flow of water (outer flow) and ethanol (jet flow) discharges into a bath of an aqueous emulsion/dispersion. While droplets (or bubbles) are pulled into the jet flow coming from the pipette, the continuous outer phase is flushed away by the outer flow, leaving a clean sample of the dispersed phase inside the pipette. For dispensing the sample, the jet flow is then switched off. Furthermore, the axial motion inside the jet can have implications in the context of process engineering: droplets and bubbles in a multiphase reactor, e.g., in a bubble column, are often not in chemical equilibrium with the continuous phase. A droplet (or bubble) moving relative to the continuous phase can leave a tail of dissolved species behind30 that interacts with other close-by droplets (or bubbles) and possibly entrains them. This could lead to Marangoni-stress-mediated interactions analogous to the interactions studied in the present work with possible implications for rise velocities, mass transfer and coalescence behavior.
As indicated, the stability of the equilibrium position of the droplets is sensitive to the material model for the interfacial tension. While this limits the choice of specific liquids to use for droplet capturing, one could also exploit this fact for developing an experimental method for characterizing interfacial tension. One main challenge for using this in systems that are not of the “Ouzo type” lies in introducing small droplets into the co-flow, without disturbing it too much. It is also worth noting that conceptually the hovering and upstream motion phenomenon does not require a liquid–liquid system. The same phenomenon can be expected for the case of gas bubbles inside a low interfacial tension liquid jet, surrounded by a high interfacial tension outer liquid. Considering specifically the co-axial Ouzo flow system, other aspects remain to be explored in more detail. These include the detailed process of the formation of the large droplets that detach from the jet, involving complex configurations that sometimes lead to multiple levels of nested droplets, and an explanation for the cause of the azimuthal meandering instability of the oil droplet.
Author contributions
S. B.: investigation, methodology, writing – original draft, visualization, data curation D. R.: investigation, software, writing – original draft, visualization, data curation S. D.: investigation, writing – original draft C. D.: investigation, software, writing – original draft T. B.: methodology, writing – original draft D. L.: conceptualization, writing – original draft S. H.: conceptualization, project administration, supervision, writing – original draft.Conflicts of interest
There are no conflicts to declare.Data availability
Data used in this study will be made available upon request to the corresponding author.Supplementary information (SI) includes one video corresponding to Fig. 3, one video corresponding to Fig. 4, as well as additional notes on the radial migration of nanodroplets in the Ouzo jet, the flow around the droplet in the two-phase model of the numerical simulations, and on the derivation of the semi-analytical model. The latter notes also include a discussion of the buoyancy effects on the centerline velocity. See DOI: https://doi.org/10.1039/d5sm00848d.
Acknowledgements
The authors thank Joachim Groß, Clemens Hansemann, Alexander May and Leon Schuhmann for helping to establish the experimental setup. Funding by the Deutsche Forschungsgemeinschaft (German Research Foundation), Project ID 455566770 is greatly acknowledged. This work was also supported by an Industrial Partnership Programme of the Netherlands Organisation for Scientific Research (NWO) & High Tech Systems and Materials (HTSM), co-financed by Canon Production Printing Netherlands B.V., University of Twente, and Eindhoven University of Technology (project TKI HTSM - CANON - P1 - PRINTHEAD & DROPLET FORMATION, grant no. PPS2107).References
- L. Scriven and C. Sternling, Nature, 1960, 187, 186–188 CrossRef.
- D. Lohse and X. Zhang, Nat. Rev. Phys., 2020, 2, 426–443 CrossRef.
- D. A. Baumgartner, S. Shiri, S. Sinha, S. Karpitschka and N. J. Cira, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2120432119 CrossRef CAS.
- S. Karpitschka, F. Liebig and H. Riegler, Langmuir, 2017, 33, 4682–4687 CrossRef CAS.
- P. Kant, M. Souzy, N. Kim, D. Van Der Meer and D. Lohse, Phys. Rev. Fluids, 2024, 9, L012001 CrossRef.
- J. G. Meijer, Y. Li, C. Diddens and D. Lohse, J. Fluid Mech., 2023, 966, A14 CrossRef CAS.
- Y. Li, C. Diddens, A. Prosperetti, K. L. Chong, X. Zhang and D. Lohse, Phys. Rev. Lett., 2019, 122, 154502 CrossRef CAS PubMed.
- Y. Li, C. Diddens, A. Prosperetti and D. Lohse, Phys. Rev. Lett., 2021, 126, 124502 CrossRef CAS.
- Y. Li, J. G. Meijer and D. Lohse, J. Fluid Mech., 2022, 932, A11 CrossRef CAS.
- S. A. Vitale and J. L. Katz, Langmuir, 2003, 19, 4105–4110 CrossRef CAS.
- I. Grillo, Colloids Surf., A, 2003, 225, 153–160 CrossRef CAS.
- H. Tan, C. Diddens, A. A. Mohammed, J. Li, M. Versluis, X. Zhang and D. Lohse, J. Fluid Mech., 2019, 870, 217–246 CrossRef CAS.
- M. Rezaee, Y. Assadi, M.-R. M. Hosseini, E. Aghaee, F. Ahmadi and S. Berijani, J. Chromatogr. A, 2006, 1116, 1–9 CrossRef CAS.
- M. Rezaee, Y. Yamini and M. Faraji, J. Chromatogr. A, 2010, 1217, 2342–2357 CrossRef CAS PubMed.
- A. Zgoła-Grześkowiak and T. Grześkowiak, TrAC, Trends Anal. Chem., 2011, 30, 1382–1399 CrossRef.
- R. Hajian and S. Hardt, Microfluid. Nanofluid., 2015, 19, 1281–1296 CrossRef CAS.
- D. Constantinescu and J. Gmehling, J. Chem. Eng. Data, 2016, 61, 2738–2748 CrossRef CAS.
- E. Nazarzadeh, T. Anthonypillai and S. Sajjadi, J. Colloid Interface Sci., 2013, 397, 154–162 CrossRef CAS PubMed.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 RSC.
- C. Diddens and D. Rocha, J. Comput. Phys., 2024, 518, 113306 CrossRef.
- M. Heil and A. L. Hazel, Fluid-structure interaction: Modelling, simulation, optimisation, 2006, pp. 19–49 Search PubMed.
- C. Bauer, A. Frink and R. Kreckel, J. Symb. Comput., 2002, 33, 1–12 CrossRef.
- B. González, N. Calvar, E. Gómez and Á. Domnguez, J. Chem. Thermodyn., 2007, 39, 1578–1588 CrossRef.
- S. Pa
![[r with combining breve]](https://www.rsc.org/images/entities/char_0072_0306.gif) ez, G. Guevara-Carrion, H. Hasse and J. Vrabec,
et al.
, Phys. Chem. Chem. Phys., 2013, 15, 3985–4001 RSC.
ez, G. Guevara-Carrion, H. Hasse and J. Vrabec,
et al.
, Phys. Chem. Chem. Phys., 2013, 15, 3985–4001 RSC. - A. J. Archer, B. D. Goddard, D. N. Sibley, J. T. Rawlings, R. Broadhurst, F. F. Ouali and D. J. Fairhurst, Soft Matter, 2024, 20, 5889–5903 RSC.
- J. Crank, The Mathematics of Diffusion, Oxford university press, 1979 Search PubMed.
- G. G. Stokes, Proc. Cambridge Philos. Soc., 1851, 9, 8 Search PubMed.
- J. S. Hadamard, C. R. Seances Acad. Sci., Vie Acad., 1911, 152, 1735–1738 Search PubMed.
- W. Rybczynski, Bull. Int. Acad. Sci. Cracovie, 1911, 1, 40–46 Search PubMed.
- M. Falcone, D. Bothe and H. Marschall, Chem. Eng. Sci., 2018, 177, 523–536 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |




