 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the limits of effective temperature consistency in actively driven systems
Dima
Boriskovsky
 a,
Rémi
Goerlich
a,
Rémi
Goerlich
 b,
Benjamin
Lindner
b,
Benjamin
Lindner
 cd and
Yael
Roichman
cd and
Yael
Roichman
 *ab
*ab
aRaymond & Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv 6997801, Israel. E-mail: roichman@tauex.tau.ac.il
bRaymond & Beverly Sackler School of Chemistry, Tel Aviv University, Tel Aviv 6997801, Israel
cBernstein Center for Computational Neuroscience Berlin, Philippstr. 13, Haus 2, 10115 Berlin, Germany
dPhysics Department of Humboldt University Berlin, Newtonstr. 15, 12489 Berlin, Germany
First published on 15th December 2025
Abstract
We investigate the thermodynamic properties of a single inertial probe driven into a nonequilibrium steady state by random collisions with self-propelled active walkers. The probe and walkers are confined within a gravitational harmonic potential. We evaluate the robustness of the effective temperature concept in this active system by comparing values of distinct, independently motivated definitions: a generalized fluctuation–dissipation relation, a kinetic temperature, and via a work fluctuation relation. Our experiments reveal that, under specific conditions, these independent measurements coincide over a wide range of system configurations, yielding a remarkably consistent effective temperature. Furthermore, we also identify regimes where this consistency breaks down, which delineates the fundamental limits of extending equilibrium-like thermodynamic concepts to athermal, actively driven systems.
I. Introduction
A single colloidal particle confined within a harmonic potential and immersed in a thermal fluid offers a fundamental realization of a microscopic statistical thermometer.1,2 In thermal equilibrium, the particle's random displacements follow a Boltzmann (Gaussian) distribution, allowing the thermodynamic temperature, T, of the surrounding environment to be directly determined by its mean potential energy via the principle of equipartition.3Near and at equilibrium, T can be equivalently defined through various thermodynamic relations, which can be applied to and measured by a colloidal thermometer. Static relations, measured in stationary states, include canonical distributions and energy equipartition, as well as configurational definitions of temperature.4,5 Dynamic relations, measured by probing the system's response properties, are given by the fluctuation–dissipation theorem,6–10 which rigorously connects the effects of thermal noise and energy dissipation. In addition, fluctuation theorems also relate temperature to fluctuations in thermodynamic quantities such as heat, work, and entropy.11–14
Colloidal thermometers have thus been widely employed in experiments, both to validate theoretical measures of equilibrium temperature and to identify deviations from it.15–18 Crucially, various definitions of absolute temperature must yield consistent, measurement-independent values in accordance with the zeroth law of thermodynamics.
In stark contrast, no universal definition for temperature exists for many natural and engineered systems that operate far from thermal equilibrium. Nonetheless, the notion of effective temperature has frequently arisen as a heuristic extension of equilibrium statistical mechanics to diverse systems operating far from equilibrium, including glassy materials,19–23 biological suspensions,15,16,24–28 driven granular media,29–43 and active matter.18,44–58
In particular, under well-separated timescales, an equilibrium-like fluctuation–dissipation relation (FDR) can become applicable, leading to a definition of an effective temperature, Teff. While the FDR-based Teff has proven useful in various fields of physics,17,59–62 its thermodynamic interpretation and range of applicability remain subjects of ongoing research.63–67
A remaining key challenge lies in identifying under which conditions distinct theoretical definitions of effective temperatures yield mutually consistent values far from equilibrium.68,69 Further examples of nonequilibrium definitions that capture meaningful physical behavior in their statistical formulation include equipartition-based approaches, such as granular temperatures,29,30 and those derived from fluctuation-relations (FR), applicable to both long-time nonequilibrium steady states (NESS) and nonequilibrium transitions.12,38,70 Such definitions typically require stable steady states, the coexistence of stochastic and deterministic dynamics, and access to distinct NESS observables – conditions that are often difficult to achieve experimentally. Although no theoretical principle ensures the coincidence of these definitions far from equilibrium, our experiments indicate a range of conditions in which a consistent effective temperature can emerge in NESS, driven by active or athermal fluctuations (cf.16,20,42).
In this work, a statistical thermometer is realized experimentally, based on a macroscopic tracer particle confined in a harmonic trap and driven into a NESS by random inelastic collisions with self-propelled walkers (see Section 2 and Fig. 1). Previously,71 it was shown that, with a large enough number of walkers, this system satisfies a linear (dynamic) FDR. Here, we assess the consistency of the FDR-based Teff by comparing it to three independent measures: the tracer's potential energy and modified kinetic energy (in an unperturbed NESS), and a temperature based on a steady state work FR, in a NESS under a strong external perturbation. Our main result is displayed in Fig. 2: all three independent measurements of Teff agree across a range of active bath parameters. We further compare our results with theoretical predictions and discuss conditions under which the consistency of Teff breaks down.
 | ||
Fig. 2 Thermometer consistency: Nb = {3, 4, 6, 10, 12, 15, 17} bbots. Effective temperature measurements obtained using three independent methods: the potential temperature Tpot = Teff (circles, eqn (4)), the modified kinetic temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin (squares, eqn (6)), and a constant temperature TFR derived from a work FR (diamonds, eqn (7)). Notably, these static temperatures validate the FDR of eqn (2) (for Nb > 3) and define a consistent effective temperature Teff. kin (squares, eqn (6)), and a constant temperature TFR derived from a work FR (diamonds, eqn (7)). Notably, these static temperatures validate the FDR of eqn (2) (for Nb > 3) and define a consistent effective temperature Teff. | ||
II. Experimental setup and basic characterization
Our experimental setup is illustrated in Fig. 1(A): a lightweight styrofoam ball (the tracer) is confined within a parabolic plastic arena and is subjected to random collisions with an assembly of vibration-driven self-propelled particles (bristlebots, or bbots, specifically Hexbug™). The system is imaged from above using a standard webcam (Brio 4k, Logitech), and particle trajectories in the horizontal plane (XY) are extracted using a custom image analysis algorithm. The confining potential is approximately harmonic, with constant stiffness κ = mga = 28.2 ± 3 g s−2, set by the substrate curvature a, the gravitational acceleration g, and the tracer mass m = 1 ± 0.1 g.An external airflow can be applied via a fan (in the x direction) and abruptly switched-off by a physical shutter, affecting primarily the tracer particle. Stationary probability densities of the tracer's position along the x-axis for different intensities of air streams are shown in Fig. 1(B). The main effect of the air stream is a shift of the mean value of the histograms in the potential well, i.e., an unperturbed state (a), a weakly perturbed state (b), and a strongly perturbed state (c). This mechanism is used to test the validity of both FDRs and FRs, as detailed in Sections 3.1 and 3.3 respectively (see SI, Fig. S1 and S2 for further details). We assume independent statistics along all axes and focus on analyzing the tracer's position and velocity components projected onto the x-axis, where the perturbation occurs.
A. Nonequilibrium properties of the active bath
In this setting, a single bbot with sufficient inertia typically performs circular motion around the trap center,72 with a preferred chirality (clockwise for Hexbugs). As the number of bbots Nb increases, frequent collisions with other bbots (and the tracer) randomize their propulsion direction and result in an active gas-like state (see SI, Movie S1). In particular, the bbot velocity distribution remains independent of Nb whereas its position distribution deviates from the original circular path with large Nb, as seen in Fig. 1(C) and (D).Typical bbot trajectories are shown in Fig. 1(E) and (F). For Nb = 3, collisions are rare, and bbots follow long-lived circular paths; for Nb = 10, frequent collisions yield erratic, stochastic motion. In general, these self-propelled particles exhibit rich dynamics, including alignment with boundaries and emergent collective motion.73 Here, the passive tracer primarily experiences random inelastic collisions with the active bbots (lower panels). These interactions introduce both noise and dissipation, which result in a collision-induced stochastic motion reaching a steady state within the harmonic potential. In this work, we focus on the properties of the tracer particle, as detailed below.
B. Nonequilibrium properties of the tracer
The NESS statistics and the dynamics of the tracer particle (in unperturbed conditions) are shown in Fig. 3, with the number of bbots Nb used as a control parameter. These results were obtained by averaging 375 particle trajectories of 1-minute duration and a time interval of Δt = 1/30 s. | ||
| Fig. 3 NESS dynamics and statistics: data were obtained for active bath configurations with Nb = {3, 4, 6, 10, 12, 15, 17} bbots, using a tracer of mass m = 1 ± 0.1 g confined in a potential of stiffness κ = 28.2 ± 3 g s−2. Results are obtained from combined time and ensemble averages over an ensemble of 375 one-minute-long tracer trajectories recorded at 30 fps for each Nb. (A) Rescaled position (x) distributions. Dashed line show fits to exponential (Nb = 3) and Gaussian (Nb = 15) functions. (B) Rescaled velocity (vx) distributions. An exponential fit is shown for Nb = 3 and a stretched exponential fit for Nb = 15. (C), (D) Position (C) and velocity (D) autocorrelation functions (ACFs), showing increasingly damped dynamics with higher Nb. (E) Position and velocity ACFs for Nb = 10, fitted with eqn (1) using γ and Ω as fitting parameters, yielding consistent descriptions for both Cxx and Cvv. (F) Extracted relaxation rate (γ) and trapping frequency (Ω) as functions of Nb (upper panel). The impact of under-sampling on the observed dynamics is pronounced for large Nb (15 and 17). Hollow markers (dashed lines) show measurements at 30 fps, while colored markers correspond to 60 fps. The lower frame rate leads to apparent overdamped behavior, whereas the higher frame rate reveals dynamics consistent with a critically-damped regime. The collision frequency (τc−1) is plotted versus Nb (lower panel), where τc is the measured mean-free time between tracer-bbot collisions. | ||
Both the stationary position (x) and velocity (vx) distributions of the tracer generally deviate from Gaussian behavior. As shown in Fig. 3(A), the position distribution evolves with increasing Nb, transitioning from an exponential form toward a Gaussian-like profile, particularly within the harmonic trap boundary |x| < 10 cm (for |x| > 10 cm the arena possesses a steeper curvature, i.e., soft boundary for the trapped tracer and bbots). The velocity distributions (Fig. 3(B)) exhibit an exponential decay for small Nb = 3, with reliable statistics within |vx| < 50 cm s−1. At larger Nb, the velocity distributions converge to a distinct non-Gaussian shape that is well described by a stretched exponential function.
The stationary dynamics of the tracer are further characterized in Fig. 3(C) and (D)via the position and velocity autocorrelation functions (ACF). An increase in the rate of dissipative collisions upon adding more bbots, leads to more strongly damped tracer motion. This is reflected in a suppression of oscillations in the relaxation dynamics, and in the reduction of the relaxation time.
The position and velocity ACFs are well fit by the generic solution of a noisy damped harmonic oscillator (Fig. 3(E)). We focus on the velocity ACF that is given by,2,74
 | (1) |
Fitting the ACF to eqn (1) provides system-specific values of the effective inverse timescales: the damping rate, γ, and the harmonic frequency, Ω. These inverse timescales are displayed in Fig. 3(F) as a function of Nb, showing a transition between underdamped (Ω < γ/2) towards critically-damped (Ω ≈ γ/2) dynamics as Nb increases. A reduction in the relaxation time, 2γ−1, corresponds to an increase in collision frequency, evaluated by image analysis as the frequency of tracer-bbot collisions, τc−1 (black line).
At high densities (Nb = 15 and 17), fast sequential collisions require a higher temporal resolution to capture the tracer's inertial dynamics. In these cases, we perform and use additional recordings with Δt = 1/60 s to extract the effective inverse timescales (solid lines). At this sampling rate the fit parameters are consistent with the critical regime, whereas Δt = 1/30 s results in overdamped behavior (dashed lines). These measurements of velocity fluctuations and their corresponding system-specific inverse timescales are further discussed in the context of the kinetic temperature in Section 3.2.
III. Effective temperatures
In the following sections, we aim to assess whether three independent definitions of effective temperatures can yield mutually consistent values across different conditions and observables. Specifically, we examine the FDR for position and velocity observables under a step-perturbation (3.1), effective equipartition between kinetic and potential energies (3.2), and a work FR in a perturbed NESS (3.3).A. FDR temperature
By subjecting the tracer to a small step-perturbation (an abrupt arrest of a constant force F0 at t = 0), a linear FDR can be expressed for both position and velocity observables as74,75 (setting kB = 1):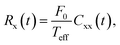 | (2) |
 | (3) |
Notably, a static FDR can be recovered in eqn (2) at t = 0, with Cxx(0) → 〈x2〉0 and Rx(0) → Δxε, where 〈x2〉0 is the position variance in the unperturbed NESS, and Δxε = 〈x〉ε − 〈x〉0 is the mean displacement between the average position in the two steady states, perturbed (sub-index ε) and unperturbed (sub-index 0). Considering that F0 = κΔxε, the effective temperature Teff coincides with the definition of potential energy equipartition,
| Tpot = κ〈x2〉0. | (4) |
Thus, Teff = Tpot is always fulfilled when the system obeys the dynamic FDR in eqn (2), even in the presence of non-Gaussian steady state distributions.
Fig. 4(A) illustrates the experimental protocol designed to measure the system's linear response (see also ref. 71,76). The tracer is subjected to a small mechanical perturbation (external fan, 10 V operating voltage, F0 ≈ 62 µN on average). During an experiment, every two minutes, the fan is turned on for a minute and abruptly turned off at t0 = 60 s for the following minute. In Fig. 4(B) we show the time-dependent ensemble averages 〈x(t)〉 and 〈vx(t)〉, obtained with Nb = 10. These trajectories capture the relaxation dynamics towards a steady state following the force removal (a), as well as a perturbed steady state (b), characterized by a shifted mean Δxε (see also Fig. 1(B)).
 | ||
| Fig. 4 FDR test of the full-response to a step-perturbation: results for mean values are obtained from pure ensemble averages over 375 two-minute step-perturbation sequences (at t0 = 60 s), under weak external airflow applied by a fan at an operating voltage 10 V; correlation functions are computed in the steady state by a combined time and ensemble average. (A) Example of a typical perturbation sequence x(t), where the fan is turned on for one minute and abruptly turned off for the subsequent minute. (B) Time-dependent mean velocity 〈vx(t)〉 and mean position 〈x(t)〉. The shown interval captures the transient response following perturbation arrest (red line) and the unperturbed steady state (a), from which correlation functions are computed. The perturbed steady state is displaced from the trap center by Δxε = 2.2 cm (b). (C) FDR analysis using eqn (2) (lower panel) and eqn (3) (upper panel). These results were obtained with Nb = 10. (D) Parametric plot of position FDRs for Nb = {2, 3, 4, 6, 10, 12, 15, 17} realizations, where the effective temperature Teff determines the linear slope. In equilibrium-like behavior, all FDR data collapse onto a single line with slope Teff ∼ κ〈x2〉0. Clear deviations from this equality are observed for the lowest densities (Nb = 2 and 3, triangles), indicating FDR violations. | ||
Fig. 4(C) presents the corresponding FDR tests for both position and velocity observables. The system's full response to the abrupt force arrest at time t1 = t − t0 is evaluated as Rx(t1) = 〈x(t1)〉 − 〈x〉0 and Rv(t1) = 〈vx(t1)〉 − 〈vx〉0, and compared with the unperturbed correlation functions, Cxx and Cxv. Within measurement error, these results validate the FDRs given in eqn (2) and (3), with an effective temperature determined by eqn (4). Thereby, in this system the tracer's potential temperature satisfies a dynamic FDR in both position and velocity observables. We note that the signal-to-noise ratio in Rv diminishes with increasing Nb, rendering the velocity response experimentally inaccessible for larger values (Nb > 10). The individual FDR tests of the experimental setups are further provided in the SI (see Fig. S4 and S5 therein).
Fig. 4(D) presents a parametric plot of the position FDR, showing normalized fluctuation and response quantities across different Nb configurations. Specifically, the solid linear line represents validation of eqn (2) with Teff = Tpot. Violations of eqn (2) are mainly observed with the lowest Nb = 2 and 3, indicating a breakdown of the effective temperature description (as detailed in ref. 71). In contrast, with larger Nb, the tracer's potential temperature Tpot satisfies a dynamic FDR and is therefore consistent with Teff.
B. Kinetic and potential energy partition
To probe deviations from equilibrium behavior, we define the tracer's kinetic temperature as,| Tkin = m〈vx2〉0. | (5) |
As seen in Fig. 5, this definition seems to result in a contradiction between the kinetic and potential temperatures, since deviations from the potential temperature Tpot (eqn (4)) are observed for all Nb configurations (solid gray line in Fig. 5(A)). Namely, Tkin saturates and becomes largely independent of Nb in the high-density limit. This clear mismatch is further supported by direct measurements of the effective trapping frequencies Ω, extracted from the tracer's velocity ACFs (see Fig. 3(F)). Across all system setups, Ω yields values lower than the natural frequency κ/m ≈ 5.3 s−1, even in an underdamped dynamic regime.
 | ||
Fig. 5 The modified kinetic temperature: data are presented for configurations with Nb = {3, 4, 6, 10, 12, 15, 17} bbots, averaged over 375 one-minute tracer trajectories recorded in unperturbed conditions. (A) Comparison of the standard kinetic temperature Tkin (solid gray line), calculated using the tracer mass m ≈ 1 g (eqn (5)), the modified kinetic temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin (solid red line), evaluated using eqn (6), and the potential temperature Tpot (dashed blue line). Error bars indicate standard deviations. Dot-dashed red lines show deviations in kin (solid red line), evaluated using eqn (6), and the potential temperature Tpot (dashed blue line). Error bars indicate standard deviations. Dot-dashed red lines show deviations in ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin arising from increasing the measurement time interval Δt. (B) Separate contributions to kin arising from increasing the measurement time interval Δt. (B) Separate contributions to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin: (upper panel) the velocity variance σv = 〈vx2〉0, and (lower panel) the effective mass kin: (upper panel) the velocity variance σv = 〈vx2〉0, and (lower panel) the effective mass ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) , evaluated from stationary ACF dynamics using eqn (1) and (6). Gray dot-dashed lines indicate deviations due to increasing Δt in both panels. , evaluated from stationary ACF dynamics using eqn (1) and (6). Gray dot-dashed lines indicate deviations due to increasing Δt in both panels. | ||
We note, however, that for tracer particles embedded in active or driven granular media, an effective mass emerges as a consequence of persistent athermal fluctuations and memory effects.77–79 Accordingly, we define an effective mass, ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) = κΩ−2, derived from the velocity correlations. Mapping the dynamics onto a linear Langevin equation, consistent with the ACF solution in eqn (1), relies on short persistence times and typically necessitates a modification of system parameters.80,81 Consequently, the definition of the kinetic temperature is modified to,
= κΩ−2, derived from the velocity correlations. Mapping the dynamics onto a linear Langevin equation, consistent with the ACF solution in eqn (1), relies on short persistence times and typically necessitates a modification of system parameters.80,81 Consequently, the definition of the kinetic temperature is modified to,
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin = kin = ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) 〈vx2〉0, 〈vx2〉0, | (6) |
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) is defined as a Nb-specific effective mass, under a constant potential stiffness κ. Using the effective mass to compute the kinetic temperature yields agreement between the two effective temperatures (solid red line in Fig. 5(A)). We note that the effective mass correction is derived from the correlation function of the unperturbed NESS, independent of both the step-response measurement and the FDR result (previous section).
is defined as a Nb-specific effective mass, under a constant potential stiffness κ. Using the effective mass to compute the kinetic temperature yields agreement between the two effective temperatures (solid red line in Fig. 5(A)). We note that the effective mass correction is derived from the correlation function of the unperturbed NESS, independent of both the step-response measurement and the FDR result (previous section).
Deviations of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin measurements resulting from low measurement rates are shown as red dashed lines in Fig. 5(A). Fig. 5(B) shows the separate contributions to
kin measurements resulting from low measurement rates are shown as red dashed lines in Fig. 5(A). Fig. 5(B) shows the separate contributions to ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin: the velocity variance 〈vx2〉0 (upper panel) and the effective mass
kin: the velocity variance 〈vx2〉0 (upper panel) and the effective mass ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (lower panel), across different Nb. We note that
(lower panel), across different Nb. We note that ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) deviates from the tracer's actual mass (m = 1 g) and results in values that monotonically increase with Nb. Both measurements show a dependence on the sampling rate (Δt−1), particularly for large Nb > 10 systems where 〈vx2〉0 saturates. Nevertheless, under well-resolved velocity fluctuations, the associated modified kinetic temperature
deviates from the tracer's actual mass (m = 1 g) and results in values that monotonically increase with Nb. Both measurements show a dependence on the sampling rate (Δt−1), particularly for large Nb > 10 systems where 〈vx2〉0 saturates. Nevertheless, under well-resolved velocity fluctuations, the associated modified kinetic temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin is consistent with the potential temperature Tpot, linking tracer dynamics with its linear response through Teff = Tpot.
kin is consistent with the potential temperature Tpot, linking tracer dynamics with its linear response through Teff = Tpot.
C. Effective temperature based on work FR
Here we investigate a work FR in a NESS subjected to a constant force F0 = κΔxε (applied at time t → −∞). An asymmetric work distribution is obtained by the energetic fluctuation around the steady state, defined as δW(t) = F0 [xε(t) − 〈xε〉]. A steady state work FR can then be expressed as,14,82,83 | (7) |
Fig. 6(A) presents a work FR test conducted with Nb = 10. The upper panel shows the work distribution in a strongly perturbed steady state (state (c) in Fig. 1(B)). The red and blue lines correspond to positive and negative work fluctuations, respectively. In the lower panel, the left-hand side of eqn (7) is plotted as a function of δW. For small enough values of δW < 80 µJ, the probabilities are sufficiently sampled, and TFR can be extracted from the slope of the linear relation (solid line). For large δW, deviations from linearity stem from limited sampling of these rare fluctuations.
 | ||
| Fig. 6 Steady state work FR test: results present averages over 375 one-minute perturbed tracer trajectories, under a strong external airflow applied by a fan at an operating voltage 13.5 V. (A) Work FR test for Nb = 10. The upper panel shows an asymmetric work (δW) distribution in a NESS under a strong continuous perturbation (airflow). The temperature measurement of TFR, extracted from a fit to eqn (7) (small δW, solid line), is consistent with the potential temperature (Tpot, dashed line) determined from the unperturbed definition in eqn (4). (B) Normalized plot of work FR tests across various Nb = {2, 3, 4, 6, 10, 12, 15, 17} configurations. The solid (black) line indicates an ideal agreement between the effective temperatures obtained from the work FR and from the equipartition definition (Tpot = TFR), demonstrating thermodynamic-like consistency. | ||
The dashed linear line represents TFR = Tpot, where Tpot is obtained independently in the unperturbed state (a). Namely, the two temperature measures agree, providing an experimental validation of the work FR (eqn (7)). This result can be extended to different Nb, as shown in Fig. 6(B). Here, the solid linear line represents TFR = Tpot. Deviations for large values of the work fluctuations are expected due to under-sampling. Clear violations of eqn (7) are mainly observed for Nb = 2–4. For larger Nb systems, TFR is also consistent with the FDR-based measure Teff. Notably, these temperatures were measured in independent measurements under different perturbations. This result shows that, for a broad range of parameters (Nb = 6–17), the same effective temperature that governs static (equipartition) and dynamic (FDR) properties of the system also rules the irreversibility of energy exchanges.
IV. Limitations of a consistent effective temperature
To further assess the range of consistency of effective temperature measures, we repeated the experiments from Section 3 for other system configurations. The standard experimental setup (detailed in Fig. 1 and shown in Fig. 7(A)) was modified by varying both the passive tracer and the surrounding active particles. Specifically, these modifications included: using a smaller styrofoam tracer particle (Fig. 7(B)); employing faster active bbots (Fig. 7(C)); and introducing a heavy tracer particle (Fig. 7(D)), i.e., heavier than the bbots (mbot = 7.1 g). Further system details are provided in the SI (see Fig. S6 and S8 therein). | ||
Fig. 7 Experimental applicability of effective temperature consistency. (A) Standard experimental setup as presented in Fig. 1 and detailed in Sections 2 and 3. (B) Configuration using a smaller Styrofoam tracer particle (m = 0.8 g, diameter 3.5 cm). (C) Configuration with faster self-propelled bbots (see SI for details). (D) Configuration employing a heavy tracer particle (m = 8.2 g, diameter 3.8 cm). (E) Comparison of energy partitioning between the modified kinetic temperature ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin (eqn (6)) and potential temperature Tpot (eqn (4)) as functions of Nb for configurations (i), (ii), and (iii). (F) Systematic violations of effective equipartition observed for configuration (D) with the heavy tracer, indicating the breakdown of thermodynamic-like consistency in this regime. kin (eqn (6)) and potential temperature Tpot (eqn (4)) as functions of Nb for configurations (i), (ii), and (iii). (F) Systematic violations of effective equipartition observed for configuration (D) with the heavy tracer, indicating the breakdown of thermodynamic-like consistency in this regime. | ||
Fig. 7(E) and (F) compare the tracer's modified kinetic temperature (![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin) and potential temperature (Tpot) as a function of the number of bbots (Nb) for these configurations. The solid linear line represents the condition:
kin) and potential temperature (Tpot) as a function of the number of bbots (Nb) for these configurations. The solid linear line represents the condition: ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin = Tpot. In the alternative experimental setups that include a light tracer (Fig. 7(B) and (C)),
kin = Tpot. In the alternative experimental setups that include a light tracer (Fig. 7(B) and (C)), ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin and Tpot coincide within measurement error and increase with Nb, consistent with our previous findings (Fig. 5). These systems can also yield consistent Teff measurements whether via FDR (eqn 2) or work FR (eqn 7) tests (see details in SI). However, when replacing the lightweight tracers with a heavy tracer, we observe differences between the measured Tpot and
kin and Tpot coincide within measurement error and increase with Nb, consistent with our previous findings (Fig. 5). These systems can also yield consistent Teff measurements whether via FDR (eqn 2) or work FR (eqn 7) tests (see details in SI). However, when replacing the lightweight tracers with a heavy tracer, we observe differences between the measured Tpot and ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) kin (see Fig. 7(F)).
kin (see Fig. 7(F)).
Ultra-high-speed videos (SI, Movie S2) reveal the mechanical origin of this deviation. For lightweight tracers, interactions with the self-propelled bbots occur as discrete impacts, yielding a measurable ballistic regime between collisions. In contrast, heavy tracers can experience rapid recurrent collisions with the bbots, occurring on timescales shorter than the experimental sampling interval (Δt). Upon strong collisions the tracer visibly changes the bbot propulsion dynamics. In addition, the heavy tracer remains embedded among the bbots, whereas a lighter tracer may be kicked upwards, escaping entrapment.
These effects modify the coupling between tracer and environment and may thus lead to the observed discrepancy. We note that the external air-driven perturbation is generally too weak to induce a significant perturbation to the heavy tracer. Due to both effects, the FDR and FR tests fail for all considered Nb systems.
V. Summary and discussion
In this work, we have experimentally demonstrated that a passive granular tracer, confined in a harmonic potential and driven by an active fluctuating medium, can sustain a NESS that is well-characterized by a single effective temperature Teff. This effective temperature serves as a unifying parameter that encapsulates both the system's dynamic response properties and its stationary fluctuations (as detailed in Fig. 2). We find that introducing an effective mass is essential to properly define the tracer's kinetic temperature, ensuring its consistency with the effective temperature of the NESS.We identify three key features that appear essential to this equilibrium-like behavior of effective temperature consistency. First, both the spontaneous fluctuations of the tracer and its response to weak external perturbations are governed by the same physical mechanism, i.e. random collisions with the active medium.71 This is manifested in the validity of a linear FDR.10,62 Second, the light tracer is only weakly coupled to the environment, which minimizes the chance of physical entrapment or caging by bath particles, an effect known to induce long-term memory in the tracer's dynamics.84,85 Finally, the bath dynamics (bbot motion) and the fluctuations they induce are largely unaffected by the external driving (airflow) that acts mainly on the tracer particle.41,65,69
The agreement between different definitions of effective temperatures observed here is unexpected for two reasons. First, the noise is a result of non-exponential collision times with the bath particles that show temporal correlation due to active self-propulsion. Under these conditions, the system exhibits non-trivial steady state distributions, in variance with the Poisson shot noise conditions leading to Boltzmann-like steady states under which such agreement has been predicted.28,86,87 Second, the use of an inertial tracer introduces memory effects in active matter, often breaking Markovian dynamics and precluding a single consistent effective temperature.69,85,88,89 That this agreement persists despite these deviations from the idealized theoretical framework suggests a broader robustness of effective temperature concepts than previously recognized.
Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are available from the corresponding author, Y. R., upon reasonable request.Supplementary information (SI) including supporting measurements and two movies is available. See DOI: https://doi.org/10.1039/d5sm00840a.
Acknowledgements
DB, RG and YR acknowledge support from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 101002392). BL would like to thank Deutsche Forschungsgemeinschaft for their support (DFG grant LI 1046/10-1).References
- G. E. Uhlenbeck and L. S. Ornstein, On the theory of the brownian motion, Phys. Rev., 1930, 36, 823 CrossRef CAS.
- M. C. Wang and G. E. Uhlenbeck, On the theory of the brownian motion ii, Rev. Mod. Phys., 1945, 17, 323 CrossRef.
- H. Risken, Fokker-planck equation, Springer, 1996 Search PubMed.
- Y. Han and D. G. Grier, Configurational temperature of charge-stabilized colloidal monolayers, Phys. Rev. Lett., 2004, 92, 148301 CrossRef.
- H. H. Rugh, Dynamical approach to temperature, Phys. Rev. Lett., 1997, 78, 772 CrossRef CAS.
- A. Einstein, On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat, Ann. Phys., 1905, 17, 208 Search PubMed.
- P. Langevin, On the theory of brownian motion, C. R. Acad. Sci., 1908, 146, 530 Search PubMed.
- H. B. Callen and T. A. Welton, Irreversibility and generalized noise, Phys. Rev., 1951, 83, 34 Search PubMed.
- R. Kubo, The fluctuation-dissipation theorem, Rep. Prog. Phys., 1966, 29, 255 CrossRef CAS.
- R. Kubo, Brownian motion and nonequilibrium statistical mechanics, Science, 1986, 233, 330 Search PubMed.
- G. Gallavotti and E. G. D. Cohen, Dynamical ensembles in nonequilibrium statistical mechanics, Phys. Rev. Lett., 1995, 74, 2694 Search PubMed.
- G. Gallavotti and E. Cohen, Nonequilibrium stationary states and entropy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 035104 CrossRef CAS.
- P. Jop, A. Petrosyan and S. Ciliberto, Work and dissipation fluctuations near the stochastic resonance of a colloidal particle, Europhys. Lett., 2008, 81, 50005 CrossRef.
- J. R. Gomez-Solano, L. Bellon, A. Petrosyan and S. Ciliberto, Steady-state fluctuation relations for systems driven by an external random force, Europhys. Lett., 2010, 89, 60003 CrossRef.
- K. C. Leptos, J. S. Guasto, J. P. Gollub, A. I. Pesci and R. E. Goldstein, Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms, Phys. Rev. Lett., 2009, 103, 198103 CrossRef PubMed.
- C. Maggi, M. Paoluzzi, N. Pellicciotta, A. Lepore, L. Angelani and R. Di Leonardo, Generalized energy equipartition in harmonic oscillators driven by active baths, Phys. Rev. Lett., 2014, 113, 238303 CrossRef CAS PubMed.
- S. Ciliberto, Experiments in stochastic thermodynamics: Short history and perspectives, Phys. Rev. X, 2017, 7, 021051 Search PubMed.
- R. Goerlich, L. B. Pires, G. Manfredi, P.-A. Hervieux and C. Genet, Harvesting information to control nonequilibrium states of active matter, Phys. Rev. E, 2022, 106, 054617 CrossRef CAS.
- L. F. Cugliandolo, D. S. Dean and J. Kurchan, Fluctuation-dissipation theorems and entropy production in relaxational systems, Phys. Rev. Lett., 1997, 79, 2168 CrossRef CAS.
- I. K. Ono, C. S. O’Hern, D. J. Durian, S. A. Langer, A. J. Liu and S. R. Nagel, Effective temperatures of a driven system near jamming, Phys. Rev. Lett., 2002, 89, 095703 CrossRef.
- L. Berthier and J.-L. Barrat, Shearing a glassy material: Numerical tests of nonequilibrium mode-coupling approaches and experimental proposals, Phys. Rev. Lett., 2002, 89, 095702 CrossRef.
- S. Joubaud, B. Percier, A. Petrosyan and S. Ciliberto, Aging and effective temperatures near a critical point, Phys. Rev. Lett., 2009, 102, 130601 CrossRef CAS.
- E. Bouchbinder and J. Langer, Linear response theory for hard and soft glassy materials, Phys. Rev. Lett., 2011, 106, 148301 CrossRef PubMed.
- X.-L. Wu and A. Libchaber, Particle diffusion in a quasi-two-dimensional bacterial bath, Phys. Rev. Lett., 2000, 84, 3017 CrossRef CAS PubMed.
- A. Argun, A.-R. Moradi, E. Pinçe, G. B. Bagci, A. Imparato and G. Volpe, Non-boltzmann stationary distributions and nonequilibrium relations in active baths, Phys. Rev. E, 2016, 94, 062150 CrossRef.
- C. Maggi, M. Paoluzzi, L. Angelani and R. Di Leonardo, Memory-less response and violation of the fluctuation-dissipation theorem in colloids suspended in an active bath, Sci. Rep., 2017, 7, 17588 CrossRef.
- R. Wiese, K. Kroy and V. Holubec, Modeling the efficiency and effective temperature of bacterial heat engines, Phys. Rev. E, 2024, 110, 064608 CrossRef CAS.
- C. Di Bello, R. Majumdar, R. Marathe, R. Metzler and É. Roldán, Brownian particle in a poisson-shot-noise active bath: exact statistics, effective temperature, and inference, Ann. Phys., 2024, 536, 2300427 CrossRef.
- A. Puglisi, V. Loreto, U. M. B. Marconi and A. Vulpiani, Kinetic approach to granular gases, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 59, 5582 CrossRef CAS.
- T. Pöschel and S. Luding, Granular gases, Springer Science & Business Media, 2001 Search PubMed.
- J. Van Zon and F. MacKintosh, Velocity distributions in dissipative granular gases, Phys. Rev. Lett., 2004, 93, 038001 CrossRef CAS.
- R. Ojha, P.-A. Lemieux, P. Dixon, A. Liu and D. Durian, Statistical mechanics of a gas-fluidized particle, Nature, 2004, 427, 521 CrossRef CAS.
- D. Villamaina, A. Puglisi and A. Vulpiani, The fluctuation-dissipation relation in sub-diffusive systems: the case of granular single-file diffusion, J. Stat. Mech., 2008, 2008, L10001 CrossRef.
- D. Villamaina, A. Baldassarri, A. Puglisi and A. Vulpiani, The fluctuation-dissipation relation: how does one compare correlation functions and responses?, J. Stat. Mech., 2009, 2009, P07024 CrossRef.
- Y. Shokef and D. Levine, Energy distribution and effective temperatures in a driven dissipative model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051111 Search PubMed.
- G. Bunin, Y. Shokef and D. Levine, Frequency-dependent fluctuation-dissipation relations in granular gases, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051301 CrossRef.
- A. Puglisi, A. Baldassarri and V. Loreto, Fluctuation-dissipation relations in driven granular gases, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061305 Search PubMed.
- K. Feitosa and N. Menon, Fluidized granular medium as an instance of the fluctuation theorem, Phys. Rev. Lett., 2004, 92, 164301 CrossRef.
- A. R. Abate and D. J. Durian, Effective temperatures and activated dynamics for a two-dimensional air-driven granular system on two approaches to jamming, Phys. Rev. Lett., 2008, 101, 245701 Search PubMed.
- S. Joubaud, D. Lohse and D. Van Der Meer, Fluctuation theorems for an asymmetric rotor in a granular gas, Phys. Rev. Lett., 2012, 108, 210604 Search PubMed.
- A. Gnoli, A. Puglisi, A. Sarracino and A. Vulpiani, Nonequilibrium brownian motion beyond the effective temperature, PLoS One, 2014, 9, e93720 CrossRef.
- J.-Y. Chastaing, J.-C. Géminard and A. Naert, Two methods to measure granular gas temperature, J. Stat. Mech., 2017, 2017, 073212 CrossRef.
- Z. Zeng, S. Zhang, X. Zheng, C. Xia, W. Kob, Y. Yuan and Y. Wang, Equivalence of fluctuation-dissipation and edwards’ temperature in cyclically sheared granular systems, Phys. Rev. Lett., 2022, 129, 228004 Search PubMed.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Sedimentation and effective temperature of active colloidal suspensions, Phys. Rev. Lett., 2010, 105, 088304 CrossRef.
- I. A. Martinez, E. Roldán, J. M. Parrondo and D. Petrov, Effective heating to several thousand kelvins of an optically trapped sphere in a liquid, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032159 Search PubMed.
- D. Levis and L. Berthier, From single-particle to collective effective temperatures in an active fluid of self-propelled particles, Europhys. Lett., 2015, 111, 60006 Search PubMed.
- E. Dieterich, J. Camunas-Soler, M. Ribezzi-Crivellari, U. Seifert and F. Ritort, Single-molecule measurement of the effective temperature in non-equilibrium steady states, Nat. Phys., 2015, 11, 971 Search PubMed.
- F. Ginot, I. Theurkauff, D. Levis, C. Ybert, L. Bocquet, L. Berthier and C. Cottin-Bizonne, Nonequilibrium equation of state in suspensions of active colloids, Phys. Rev. X, 2015, 5, 011004 Search PubMed.
- I. Petrelli, L. F. Cugliandolo, G. Gonnella and A. Suma, Effective temperatures in inhomogeneous passive and active bidimensional Brownian particle systems, Phys. Rev. E, 2020, 102, 012609 Search PubMed.
- E. Flenner and G. Szamel, Active matter: Quantifying the departure from equilibrium, Phys. Rev. E, 2020, 102, 022607 CrossRef CAS.
- É. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. Van Wijland, How far from equilibrium is active matter?, Phys. Rev. Lett., 2016, 117, 038103 Search PubMed.
- M. Han, J. Yan, S. Granick and E. Luijten, Effective temperature concept evaluated in an active colloid mixture, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7513 CrossRef CAS.
- A. Solon and J. M. Horowitz, On the einstein relation between mobility and diffusion coefficient in an active bath, J. Phys. A, 2022, 55, 184002 CrossRef.
- S. Ye, P. Liu, F. Ye, K. Chen and M. Yang, Active noise experienced by a passive particle trapped in an active bath, Soft Matter, 2020, 16, 4655 RSC.
- J. T. Park, G. Paneru, C. Kwon, S. Granick and H. K. Pak, Rapid-prototyping a Brownian particle in an active bath, Soft Matter, 2020, 16, 8122 Search PubMed.
- J. F. Boudet, J. Jagielka, T. Guerin, T. Barois, F. Pistolesi and H. Kellay, Effective temperature and dissipation of a gas of active particles probed by the vibrations of a flexible membrane, Phys. Rev. Res., 2022, 4, L042006 CrossRef CAS.
- J. Shea, G. Jung and F. Schmid, Passive probe particle in an active bath: can we tell it is out of equilibrium?, Soft Matter, 2022, 18, 6965 RSC.
- G. Geva, T. Admon, M. Levin and Y. Roichman, Diffusive contact between randomly driven colloidal suspensions, Phys. Rev. Lett., 2025, 134, 218201 Search PubMed.
- U. M. B. Marconi, A. Puglisi, L. Rondoni and A. Vulpiani, Fluctuation-dissipation: response theory in statistical physics, Phys. Rep., 2008, 461, 111 Search PubMed.
- M. Baiesi, C. Maes and B. Wynants, Fluctuations and response of nonequilibrium states, Phys. Rev. Lett., 2009, 103, 010602 CrossRef PubMed.
- C. Maes, Response theory: a trajectory-based approach, Front. Phys., 2020, 8, 229 CrossRef.
- M. Baldovin, L. Caprini, A. Puglisi, A. Sarracino and A. Vulpiani, The many faces of fluctuation-dissipation relations out of equilibrium, Springer, 2022, pp. 29–57 Search PubMed.
- K. Martens, E. Bertin and M. Droz, Dependence of the fluctuation-dissipation temperature on the choice of observable, Phys. Rev. Lett., 2009, 103, 260602 CrossRef PubMed.
- L. F. Cugliandolo, The effective temperature, J. Phys. A: Math. Theor., 2011, 44, 483001 CrossRef.
- A. Puglisi, A. Sarracino and A. Vulpiani, Temperature in and out of equilibrium: A review of concepts, tools and attempts, Phys. Rep., 2017, 709, 1 CrossRef.
- V. Holubec and R. Marathe, Underdamped active brownian heat engine, Phys. Rev. E, 2020, 102, 060101 CrossRef CAS.
- B. Sorkin, H. Diamant, G. Ariel and T. Markovich, Second law of thermodynamics without einstein relation, Phys. Rev. Lett., 2024, 133, 267101 CrossRef CAS PubMed.
- J. Casas-Vázquez and D. Jou, Temperature in non-equilibrium states: a review of open problems and current proposals, Rep. Prog. Phys., 2003, 66, 1937 CrossRef.
- L. Hecht, L. Caprini, H. Löwen and B. Liebchen, How to define temperature in active systems?, J. Chem. Phys., 2024, 161, 1 CrossRef.
- A. Puglisi, P. Visco, A. Barrat, E. Trizac and F. van Wijland, Fluctuations of internal energy flow in a vibrated granular gas, Phys. Rev. Lett., 2005, 95, 110202 CrossRef PubMed.
- D. Boriskovsky, B. Lindner and Y. Roichman, The fluctuation-dissipation relation holds for a macroscopic tracer in an active bath, Soft Matter, 2024, 20, 8017 Search PubMed.
- O. Dauchot and V. Démery, Dynamics of a self-propelled particle in a harmonic trap, Phys. Rev. Lett., 2019, 122, 068002 Search PubMed.
- L. Giomi, N. Hawley-Weld and L. Mahadevan, Swarming, swirling and stasis in sequestered bristle-bots, Proc. R. Soc. London, Ser. A, 2013, 469, 20120637 Search PubMed.
- M. Yaghoubi, M. E. Foulaadvand, A. Bérut and J. Luczka, Energetics of a driven brownian harmonic oscillator, J. Stat. Mech.: Theory Exp., 2017, 2017, 113206 CrossRef.
- T. Haga, Nonequilibrium langevin equation and effective temperature for particle interacting with spatially extended environment, J. Stat. Phys., 2015, 159, 713 CrossRef.
- K. Engbring, D. Boriskovsky, Y. Roichman and B. Lindner, A nonlinear fluctuation-dissipation test for markovian systems, Phys. Rev. X, 2023, 13, 021034 CAS.
- C. Maes, Fluctuating motion in an active environment, Phys. Rev. Lett., 2020, 125, 208001 CrossRef CAS PubMed.
- A. Seguin and P. Gondret, Added-mass force in dry granular matter, Phys. Rev. E, 2022, 105, 054903 CrossRef CAS PubMed.
- M. Giona, G. Procopio and C. Pezzotti, Fluid-particle interactions and fluctuation-dissipation relations iii–correlated fluctuations, regularity and added mass, arXiv, preprint, 2024, arXiv:2412.19170 DOI:10.48550/arXiv:2412.19170.
- M. Wiśniewski, J. Łuczka and J. Spiechowicz, Effective mass approach to memory in non-Markovian systems, Phys. Rev. E, 2024, 109, 044116 CrossRef.
- J. Shea, G. Jung and F. Schmid, Force renormalization for probes immersed in an active bath, Soft Matter, 2024, 20, 1767 Search PubMed.
- G. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Experimental demonstration of violations of the second law of thermodynamics for small systems and short time scales, Phys. Rev. Lett., 2002, 89, 050601 CrossRef CAS PubMed.
- O. Narayan and A. Dhar, Reexamination of experimental tests of the fluctuation theorem, J. Phys. A: Math. Gen., 2003, 37, 63 Search PubMed.
- L. Berthier and J. Kurchan, Non-equilibrium glass transitions in driven and active matter, Nat. Phys., 2013, 9, 310 Search PubMed.
- L. Caprini, A. Ldov, R. K. Gupta, H. Ellenberg, R. Wittmann, H. Löwen and C. Scholz, Emergent memory from tapping collisions in active granular matter, Commun. Phys., 2024, 7, 52 Search PubMed.
- B. Dybiec, E. Gudowska-Nowak and I. M. Sokolov, Underdamped stochastic harmonic oscillator driven by lévy noise, Phys. Rev. E, 2017, 96, 042118 Search PubMed.
- K. Kanazawa, T. G. Sano, T. Sagawa and H. Hayakawa, Minimal model of stochastic athermal systems: Origin of non-Gaussian noise, Phys. Rev. Lett., 2015, 114, 090601 CrossRef PubMed.
- L. Caprini, R. K. Gupta and H. Löwen, Role of rotational inertia for collective phenomena in active matter, Phys. Chem. Chem. Phys., 2022, 24, 24910 RSC.
- A. R. Sprenger, L. Caprini and H. Lo, wen, and R. Wittmann, Dynamics of active particles with translational and rotational inertia, J. Phys.: Condens. Matter, 2023, 35, 305101 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |

