 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transient grating spectroscopy nondestructively characterizes the mechanics of rubbery polymers and soft gels
Melanie C.
Adams
a,
Allison L.
Chau
b,
Bolin
Liao
a,
Angela A.
Pitenis
 *b and
Christopher W.
Barney
*b and
Christopher W.
Barney
 *c
*c
aDepartment of Mechanical Engineering, University of California, Santa Barbara, Santa Barbara, California, 93106, USA
bMaterials Department, University of California, Santa Barbara, USA. E-mail: apitenis@ucsb.edu
cSchool of Polymer Science and Polymer Engineering, University of Akron, Akron, Ohio, USA. E-mail: barneyc@uakron.edu
First published on 21st January 2026
Abstract
Designing efficient mechanisms for moving mechanical assemblies requires the use of materials with well-defined mechanical responses. Appropriate methods are needed to characterize these mechanical responses. Mechanical characterization of soft materials is critical in the high strain rate regime where intuition from manipulating a material at low rates fails to translate to applications including impact protection, tire traction, and sound damping. Here, transient grating spectroscopy (TGS) is used to measure wave propagation for soft elastomers and hydrogels. TGS is a non-destructive and non-contact optoacoustic technique that enables high strain rate measurements of the bulk modulus, a measure of a material's resistance to changing volume. The bulk modulus of elastomers and hydrogels is measured using TGS and its conversion to Young's modulus is discussed. This data is used to resolve values of Poisson's ratio in nearly incompressible gels to high degrees of precision.
1. Introduction
Mechanics aims to control the dynamics of systems that provide useful action by understanding the storage, transfer, recovery, and dissipation of energy. Materials are the conduit through which this action occurs and are inherent sources of dissipated energy. Thus, characterizing and controlling the dynamic mechanical response of materials is key to developing efficient mechanisms. Nowhere is this characterization more important than in the high strain rate regime (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) > 106 Hz)1 where materials, such as rubbery crosslinked polymers and soft gels, display behavior that is markedly different from their low strain rate response. This contrast means that any intuition researchers can glean from characterizing a soft material at low strain rates does not necessarily translate to the high strain rate regime. Accordingly, high strain rate characterization is vital to designing soft materials for impact protection,2 sound damping,3 tire traction,1 and the dynamic motion of small robots and organisms.4,5
> 106 Hz)1 where materials, such as rubbery crosslinked polymers and soft gels, display behavior that is markedly different from their low strain rate response. This contrast means that any intuition researchers can glean from characterizing a soft material at low strain rates does not necessarily translate to the high strain rate regime. Accordingly, high strain rate characterization is vital to designing soft materials for impact protection,2 sound damping,3 tire traction,1 and the dynamic motion of small robots and organisms.4,5
While the high strain rate response of soft materials is important in applications, characterizing this behavior is challenging. Common mechanical characterization techniques (e.g., dynamic mechanical analysis,6,7 shear rheometry,8–11 and atomic force microscopy)9,12 that rely upon applying a deformation and measuring the stress response are fundamentally limited to timescales above the time it takes a wave to propagate across the sample to the other end and back. As shown in the SI, this wave speed limit can be estimated and is shown in Fig. 1. In practice, such measurements become unreliable at much lower frequencies in the kHz range where inertial effects overwhelm the signal from the material.13–15 Here, strain rates higher than the inertial limit line are only accessible through time-temperature superposition (TTS) methods, which tend not to work with gels due to evaporation and solvent ejection at rising temperatures. Fig. 1 highlights the divide between low and high strain rate characterization methods that may be bridged through TTS.
 | ||
| Fig. 1 Comparison of techniques and the relationship between sample size and achievable strain rates.16–19 | ||
High strain rate techniques such as quartz crystal rheometry,20 cavitation rheometry,16,21–23 and Split-Hopkinson (Kolsky) bar measurements24 all overcome this limit by imposing deformation and then measuring the wave speed to quantify material behavior. These techniques have been very successful for high strain rate characterization yet have potential shortcomings such as the need for a thin film geometry, destructive test nature, and need to contact the sample, respectively. The recent development of transient grating spectroscopy (TGS) provides another pathway to high strain rate characterization that is not subject to these shortcomings.25
Transient grating spectroscopy (TGS) is an optoacoustic technique that creates a temporary interference pattern within a sample by crossing two laser beams causing a periodic modulation in sample properties. Through probing the evolution of this interference pattern over time, transient grating spectroscopy can provide insights into various dynamic processes, such as diffusion, energy transfer, and structural changes in materials. Its ability to capture ultrafast phenomena in real-time, from femtosecond to microsecond timescales, has positioned TGS as a powerful tool for understanding fundamental processes in chemistry, physics, and materials science.25–28 Based on this, we aim to exploit TGS to explore the altered mechanical behavior of soft materials at high strain rates.
This paper addresses this goal by combining high strain rate TGS measurements with low strain rate indentation to characterize the elasticity of soft materials. The materials examined in this study range from rubbery crosslinked silicone elastomers to soft, biocompatible hydrogels. The use of low and high strain rate techniques provides complementary perspectives on the mechanical response of soft materials. Particular attention is paid towards exploring the manner in which these two perspectives can be related to one another. The results presented below have clear implications for predicting and controlling the mechanical behavior of soft materials in high strain rate applications.
2. Materials and methods
A. Polymer gels
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by mass, and Rhodamine B dye was added to achieve a final concentration of 0.025 wt%. A speed mixer (FlackTek SpeedMixer DAC 150.1 FVZ-K) was used to evenly mix all constituents together at 2000 rpm for 40 s, and the mixture was dispensed into a polystyrene or glass dish and cured at room temperature for five days or at 120 °C for 3 h. Note that the sol fraction was not extracted and the samples were tested in the as-formed state. The samples for indentation were prepared by punching out disks with a 16 mm diameter and ∼3 mm thickness.
1 by mass, and Rhodamine B dye was added to achieve a final concentration of 0.025 wt%. A speed mixer (FlackTek SpeedMixer DAC 150.1 FVZ-K) was used to evenly mix all constituents together at 2000 rpm for 40 s, and the mixture was dispensed into a polystyrene or glass dish and cured at room temperature for five days or at 120 °C for 3 h. Note that the sol fraction was not extracted and the samples were tested in the as-formed state. The samples for indentation were prepared by punching out disks with a 16 mm diameter and ∼3 mm thickness.
B. Techniques
 | (1) |
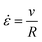 | (2) |
The maximum confinement ratio observed in this work is  (a is contact radius and h is sample height) suggesting that finite thickness effects should not significantly impact this measurement.
(a is contact radius and h is sample height) suggesting that finite thickness effects should not significantly impact this measurement.
 | ||
| Fig. 2 (a) Schematic of TGS used for polymer measurements. Reproduced with permission from ref. 28. Polyacrylamide sample with 17.5 wt% AAm: (b) TGS trace, or signal, for one grating period. (c) Fourier transform of the resulting trace to determine frequencies of oscillation at each grating period. (d) Dispersion of grating period vs. frequency to find the bulk longitudinal wave speed. The wave speed for this sample of 17.5 wt% AAm was approximately 1571 ± 3.4 m s−1. | ||
Since the wavelength of the launched acoustic waves match the grating period L on the sample (which is half of the grating period on the phase mask based on optical parameters used in our system; see SI for more details), dispersion relations of the acoustic waves can be mapped by measuring the frequencies of the oscillations in the TGS signal at a range of grating periods (Fig. 2c). For the polymers studied here, a Fourier transform of each output was used to determine the frequency of oscillation. Note that the sharpness of these peaks indicates that the error in the measurement of oscillation frequencies is at largest 0.01 GHz (from the width of the peaks), which is an order of magnitude below the observed peak values. Depending on the stiffness of the material, the acoustic wave frequency detected by optical TGS is typically in the MHz to GHz range (Fig. 2d). The frequency of these acoustic waves can then be translated to a bulk modulus through eqn (3),
 | (3) |
 .27 This relationship is helpful in characterizing the mechanical properties of a given material.
.27 This relationship is helpful in characterizing the mechanical properties of a given material.
To estimate the strain rate, it is necessary to estimate the thermal strain during the measurements. The absorption coefficient of the Rhodamine B dye at 532 nm can be estimated as 105 M−1 cm−1. Combining this with the molarity of the dye in the gels, 5.2 × 104 M, gives an absorption depth of approximately 0.02 cm. Assuming the pulse energy is absorbed within this depth, the temperature rise can be estimated from the pump laser fluence of 158 mJ cm−2 and the specific heat of water 4.2 J cm−3 K−1. Combining these values gives an estimated temperature rise of 2 K during the TGS measurement. This temperature rise can be combined with the thermal volume expansion coefficient of a hydrogel 2 × 10−4 1/K to predict a volumetric thermal stretch of 1.0004. Assuming an isotropic expansion, the strain in one direction can be estimated by taking the cubic root of the stretch and subtracting 1 to get a strain value of 1 × 10−4. The strain rate can then be estimated by taking this strain value and dividing by the 10−8 s each oscillation takes to get an estimated strain rate of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 1/s.
000 1/s.
3. Results and discussion
The output of TGS shows the time-domain signals that represent the intensity of light as a function of time (Fig. 2b). This is in the form of acoustic waves oscillations that are characteristic of the material behavior. In the case of one hydrogel sample, PAAm with 17.5 wt% AAm (Fig. 2), it is apparent both that the observed frequency of oscillation, f, can be simply extracted through a fast Fourier transform and that f varies as the grating period is altered. When this frequency is compared across all grating periods, a bulk acoustic wave speed can be determined from the slope in Fig. 2D. The values of each of the gels tested are shown below in Table 1. For PAAm, there is a slight, systematic increase in the observed wave speed as the initial polymer content increases. The wave speed values measured here for PAAm hydrogels span values from 1523 m s−1 to 1571 m s−1 and are consistent with the 1500–1650 m s−1 values measured by Gorman and McNeil through Brillouin Light Scattering (BLS).30 For PDMS, the bulk acoustic wave speed is constant within the error of the measurement. For the stiffer formulations of PDMS, the variation is larger due to more scattered light, impacting the wave speed measurements of the samples. The agreement of values across PDMS samples suggests that the measured wave speed is insensitive to the crosslinking density and sol fraction. To ensure consistency across samples, the same power, as discussed in more detail in the SI, was used for the same grating periods as increasing the power can lead to heating that modifies the local properties of the spot being measured. The reported 1072 ± 311 m s−1 value measured here for PDMS agrees well with a reference value of 1319 m s−1 measured with BLS in the work of Stevens et al.31 PHEMA shows a marked difference in wave speed for the gel as the solvent is altered to contain more water. Due to increased light scattering, the PHEMA sample in 100% water was not reliably measurable.| Polymer | Bulk longitudinal wave speed (m s−1) |
|---|---|
| PAAm | |
| 3.75 wt% | 1523 ± 2.17 |
| 7.5 wt% | 1551 ± 10.2 |
| 10 wt% | 1561 ± 4.64 |
| 12.5 wt% | 1570 ± 5.01 |
| 17.5 wt% | 1571 ± 3.37 |
| PDMS | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–25 °C 1–25 °C |
1072 ± 311 |
| 10: −120 °C | 1093 ± 306 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–25 °C 1–25 °C |
1062 ± 8.5 |
| 20: −120 °C | 1073 ± 69.9 |
| PHEMA | |
| Swelled in 100% ethanol | 1225 ± 37.2 |
| Swelled in 65% ethanol | 1482 ± 95.1 |
| Swelled in 0% ethanol | Not measurable |
As is apparent from eqn (3), the wave speed can be converted to the bulk modulus when the density of the sample is known. This calculation has been undertaken and the moduli are plotted in Fig. 3 against variables relating to the formulation of each type of gel. The x-axes for the PAAm hydrogels, PDMS elastomers, and PHEMA gels are the initial concentration of reagents before network formation and swelling, weight ratio of base:curing agent, and the water content of the ethanol/water swelling solvent, respectively. E from indentation is shown in the first row and K from TGS is shown in the second row. For the PAAm hydrogels in Fig. 3a and d, it is apparent that the slight sensitivity of K to the initial polymer concentration is much less pronounced than that of E. This difference in sensitivity is likely due to the different physical origin of the two moduli. K results from the intermolecular forces that resist volumetric changes in rubbery polymer networks.32 In contrast, E in rubbery polymer networks results from the entropic penalty of stretching chains.33 Since K is related to intermolecular forces, which should not change overly much for the highly swollen PAAm hydrogels (mainly composed of water), the relative insensitivity of K to initial polymer concentration makes sense. By similar reasoning, since E is related to the stretching of polymer chains, which is directly affected by the amount of polymer in the hydrogels, their sensitivity to the initial polymer volume fraction is reasonable.
In looking at the PDMS elastomers in Fig. 3b and e, it is apparent that E is sensitive to the cure temperature and crosslink density while K is not. Note that E is measured from indentation and is characterized at much lower strain rates than the TGS method used to characterize K. This is expected as K derives from intermolecular forces and is mainly sensitive to compositional variations instead of structure variations.32 The main difference in the PDMS elastomers at different mixing ratios and cure temperatures is in structure, namely in the network crosslinking density and sol fractions, while the samples are all composed of the same silicone molecules. The agreement between values is consistent with the understanding that, while E is sensitive to the structural features of the network, K is only sensitive to the intermolecular interactions present in the material which are unaltered by changing the crosslinking density and sol fraction. This results in significant changes in E despite a constant observed value of K. The PHEMA gels in Fig. 3c and f are subject to additional compositional effects. Here both E and K show marked differences in value with respect to the swelling solvent composition. E shifts in this case because using mixed solvents alters the solvent quality and changes the equilibrium polymer volume fraction after swelling. In addition to changing the solvent quality, mixing solvents alters the intermolecular forces that determine K. Ethanol has a lower K than water which explains the decrease in K observed in Fig. 3f when the gel is swollen in 100% ethanol.
Notably, the observed K value for the PDMS elastomers is less than that for both the PAAm hydrogels and the PHEMA gels despite the fact that E is an order of magnitude greater in the PDMS elastomers. This difference shows how the mechanical intuition that researchers can gain by manipulating a soft solid by hand does not necessarily translate to the high strain rate regime. In other words, when designing for high strain rate applications, it is critical that researchers make decisions informed by high strain rate measurements.
While the comparisons between moduli and structural parameters presented above makes qualitative sense, each of these moduli are measured at extremely different strain rates. The indentation measurements were performed at strain rates of approximately 3 Hz while TGS probed the materials at 104 Hz. Bridging these two strain rate regimes to connect these moduli measurements would be very impactful to our understanding of design in high strain rate applications. An initial attempt at doing so by compiling literature data collected at various frequencies is contained in Fig. 4. This figure shows E values for the PAAm hydrogels and PDMS elastomers measured at increasing frequencies. As is apparent in Fig. 4a, data for the PAAm hydrogel is relatively sparse. This is likely due to the ill-suited nature of PAAm hydrogels to the application of a TTS analysis. Specifically, shifting temperature is difficult in hydrogels swollen to equilibrium because doing so will both shift the swelling equilibrium and lead to an increase in sample drying rates.34 The only high strain rate data on PAAm hydrogels is from laser-induced cavitation and is in the GPa range compared to the 10–100 kPa values observed at low strain rates.16 For the PDMS elastomers, TTS can be applied and thus more data is available; however, as a commercial product whose final properties depend heavily on mixing and curing procedure, data compiled in this manner should not be considered authoritative. The trends for this system show an increase in E with frequency for the PDMS elastomers. For both materials, measurements of E do not exceed 107 Hz which is close to the frequency range accessible by TGS.
 | ||
Fig. 4 (a) Frequency-dependent storage moduli in PAAm gels with 6–8 wt% AAm (square,35 circle,8 triangle,10 pentagon: indentation). (b) Frequency-dependent Young's modulus for different curing temperatures of PDMS (Sylgard 184) in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monomer: crosslinker ratio. The colors map the temperatures while symbols indicate sources. (circle,36 right triangle,37 up triangle,38 left triangle,39 down triangle,40 filled pentagon,41 pentagon,41 diamond42). These values may be more qualitatively compared since there are a combination of techniques that calculate modulus values in different ways. The target range that TGS measures is indicated on each plot. 1 monomer: crosslinker ratio. The colors map the temperatures while symbols indicate sources. (circle,36 right triangle,37 up triangle,38 left triangle,39 down triangle,40 filled pentagon,41 pentagon,41 diamond42). These values may be more qualitatively compared since there are a combination of techniques that calculate modulus values in different ways. The target range that TGS measures is indicated on each plot. | ||
The gap in available data on E in the high strain rate regime is interesting as TGS can potentially measure this quantity in that regime. As illustrated in Fig. 5, the only real hurdle in quantifying E in the high strain rate regime is the need to convert measurements of K to E. From the mechanics perspective, this is a problem with a straightforward solution where E = 3K(1 − 2v) and v is Poisson's ratio.43 Note that the relationship between these quantities is derived using a linear elastic constitutive relationship. Thus, the problem becomes a question of having a high strain rate value of v. Unfortunately, to the best of the authors’ knowledge, measurements of v in these nearly incompressible systems have been limited to quasi-static measurements. While K is relatively insensitive to strain rate when compared to E,44v is sensitive to strain rate due to its dependence on E. Since v varies at different strain rates this precludes the conversion of K to E when v is not quantified at the same strain rate as K. Thus, high strain rate measurements of v are needed to extract high strain rate values of E from TGS.
One potentially interesting result that comes from considering the interconversion of these moduli is that while the conversion between E and K is sensitive to the value of v used, the calculation of v from E and K is largely insensitive to errors in these two moduli. The experimental error in calculating v from E and K is given by eqn (4),
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–120 °C PDMS elastomer samples have a value of K = 1.4 GPa from TGS performed at 104 Hz while indentation gives E = 2 MPa at about 3 Hz. When combined these moduli give a calculated ν value of 0.49976 which is close to a quasi-static reference value of 0.4998.43 This suggests that high strain rate values of K can be combined with low strain rate values of E to quantify low strain rate values of v.
1–120 °C PDMS elastomer samples have a value of K = 1.4 GPa from TGS performed at 104 Hz while indentation gives E = 2 MPa at about 3 Hz. When combined these moduli give a calculated ν value of 0.49976 which is close to a quasi-static reference value of 0.4998.43 This suggests that high strain rate values of K can be combined with low strain rate values of E to quantify low strain rate values of v.
While the conversion of K to E is stymied by the lack of available literature data on high strain rate v, it is clear that TGS can be used to estimate low strain rate values of v. Values from this analysis have been calculated and are shown in Fig. 5 for the different gels plotted against variables relating to the formulation of the gels. For the PAAm samples, v decreases with increasing E values which increase at higher initial concentration of reagents. The values for PDMS decrease in stiffer samples also indicating an inverse relationship with E. A similar trend is observed for PHEMA where v decreases in gels swollen with pure ethanol when E is highest. Notably, the values of v for PAAm hydrogels are significantly higher than those previously measured in the literature by applying optical strain gauge analysis to uniaxial extension measurements.45,46 The confidence in the measurements presented in this work derive from arguments quantifying the propagation of errors and the sensitivity to the presence of cumulative errors.47 As presented above in the discussion of eqn (4), the propagation of errors shows that incredibly precise values of v can be calculated from combining E and K when they are at least three orders of magnitude apart. Beyond precision, the accuracy of the mean reported values of v is sensitive to the presence of cumulative errors that propagate from the individual measurements of E and K. The sensitivity to such errors was recently quantified by Nedoluha et al.47 and it was found that, of the four v calculation methods analyzed, inferring v from E and K was the method with the lowest sensitivity to cumulative errors. These results highlight the strength of TGS as an accurate and precise method to characterize the Poisson's ratio of nearly incompressible gels and elastomers.
While TGS was ultimately unable to estimate high strain rate values of E without a high strain rate value of v, TGS still provides value to the soft materials community by characterizing low strain rate values of v in difficult to measure samples. Note that the combination of low strain rate and high strain rate data used to calculate low strain rate v values in this work is only appropriate due to both the relative insensitivity of K to strain rate when compared to E and the insensitivity of v to errors in E and K measurements when the two moduli are at least three orders of magnitude apart. Future researchers should be cautious when attempting to combine data measured at different strain rates as is done in this work. Developing high strain rate testing methods capable of quantifying Poisson's ratio remains an open question. TGS is advantageous in this space as it provides a non-contact, non-destructive means of quantifying K for hydrogels that are difficult to manipulate in other techniques. This capability unlocks current and future measurements of v in soft gels where existing methods lack the resolution to meaningfully distinguish nearly incompressible values from the incompressible limit.
4. Conclusion
Transient grating spectroscopy is a nondestructive and noncontact technique that has potential to measure high frequency responses of soft materials, particularly in the context of hydrogels like polyacrylamide (PAAm) and elastomers such as polydimethylsiloxane (PDMS), both of which are commonly used and generally well-characterized. While the output can directly be used to calculate the bulk acoustic wave speed and the bulk modulus for polymers, there is a lack of information about Poisson's ratio (v) at higher frequencies that can bridge the gap to finding dynamic Young's modulus values. Here, in conjunction with a quasistatic method such as indentation, a low stain rate v can be reliably calculated which provides more information on quasistatic properties. While the current body of research has primarily focused on Poisson's ratio values at lower frequencies, there exists a promising avenue for future studies to expand our understanding of higher frequency regimes by focusing on analysis of high frequency values of v. Knowledge of dynamic Poisson's ratio values will lead to enhanced precision in characterizing material behavior under various conditions. In turn, this information can pave the way for the development of innovative materials and structures that can withstand and adapt to dynamic and high-frequency or high strain rate mechanical environments. This study also underscores how transient grating spectroscopy holds significant promise for being a dynamic test platform of polymers provided they meet the constraints of the technique.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information includes further details on the indentation and TGS methods, estimates of polymer mesh sizes, a reporting of the densities used during calculations, and the arguments used to estimate the limits in Fig. 1. See DOI: https://doi.org/10.1039/d5sm00835b.Acknowledgements
This work was supported by the MRSEC Program of the National Science Foundation under Award No. DMR 2308708. Development of the TGS setup at UCSB was supported by an ARO DURIP grant under Award No. W911NF-20-1-0161. A.L.C. acknowledges suppport from the University of California President's Dissertation Year Fellowship.References
- C. M. Roland, Mechanical Behavior of Rubber at High Strain Rates, Rubber Chem. Technol., 2006, 79(3), 429–459, DOI:10.5254/1.3547945.
- R. Zhang, W. Huang, P. Lyu, S. Yan, X. Wang and J. Ju, Polyurea for Blast and Impact Protection: A Review, Polymers, 2022, 14(13), 2670, DOI:10.3390/polym14132670.
- Sound and Vibration Damping with Polymers, 424, ed R. D. Corsaro and L. H. Sperling, in ACS Symposium Series, American Chemical Society, Washington, DC, vol. 424, 1990 DOI:10.1021/bk-1990-0424.
- J. C. Case, E. L. White and R. K. Kramer, Soft Material Characterization for Robotic Applications, Soft Robot., 2015, 2(2), 80–87, DOI:10.1089/soro.2015.0002.
- M. Ilton, et al., The principles of cascading power limits in small, fast biological and engineered systems, Science, 2018, 360(6387), eaao1082, DOI:10.1126/science.aao1082.
- A. D. Mulliken and M. C. Boyce, Mechanics of the rate-dependent elastic–plastic deformation of glassy polymers from low to high strain rates, Int. J. Solids Struct., 2006, 43(5), 1331–1356, DOI:10.1016/j.ijsolstr.2005.04.016.
- R. Esmaeeli, H. Aliniagerdroudbari, S. R. Hashemi, C. Jbr and S. Farhad, Designing a New Dynamic Mechanical Analysis (DMA) System for Testing Viscoelastic Materials at High Frequencies, Model. Simul. Eng., 2019, 2019, 1–9, DOI:10.1155/2019/7026267.
- K. Kumar, M. E. Andrews, V. Jayashankar, A. K. Mishra and S. Suresh, Measurement of Viscoelastic Properties of Polyacrylamide-Based Tissue-Mimicking Phantoms for Ultrasound Elastography Applications, IEEE Trans. Instrum. Meas., 2010, 59(5), 1224–1232, DOI:10.1109/TIM.2009.2038002.
- Y. Abidine, V. M. Laurent, R. Michel, A. Duperray, L. I. Palade and C. Verdier, Physical properties of polyacrylamide gels probed by AFM and rheology, EPL Europhys. Lett., 2015, 109(3), 38003, DOI:10.1209/0295-5075/109/38003.
- R. E. Mahaffy, C. K. Shih, F. C. MacKintosh and J. Käs, Scanning Probe-Based Frequency-Dependent Microrheology of Polymer Gels and Biological Cells, Phys. Rev. Lett., 2000, 85(4), 880–883, DOI:10.1103/PhysRevLett.85.880.
- A. L. Chau, et al., Aqueous surface gels as low friction interfaces to mitigate implant-associated inflammation, J. Mater. Chem. B, 2020, 8(31), 6782–6791, 10.1039/D0TB00582G.
- M. Zhang, Y. Li, P. V. Kolluru and L. C. Brinson, Determination of Mechanical Properties of Polymer Interphase Using Combined Atomic Force Microscope (AFM) Experiments and Finite Element Simulations, Macromolecules, 2018, 51(20), 8229–8240, DOI:10.1021/acs.macromol.8b01427.
- L. Boeckx, P. Leclaire, P. Khurana, C. Glorieux, W. Lauriks and J. F. Allard, Investigation of the phase velocities of guided acoustic waves in soft porous layers, J. Acoust. Soc. Am., 2005, 117(2), 545–554, DOI:10.1121/1.1847848.
- L. Jaouen, A. Renault and M. Deverge, Elastic and damping characterizations of acoustical porous materials: Available experimental methods and applications to a melamine foam, Appl. Acoust., 2008, 69(12), 1129–1140, DOI:10.1016/j.apacoust.2007.11.008.
- A. L. Kelly, T. Gough, B. R. Whiteside and P. D. Coates, High shear strain rate rheometry of polymer melts, J. Appl. Polym. Sci., 2009, 114(2), 864–873, DOI:10.1002/app.30552.
- C. W. Barney, et al., Cavitation in soft matter, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(17), 9157–9165, DOI:10.1073/pnas.1920168117.
- J. E. Field, S. M. Walley, W. G. Proud, H. T. Goldrein and C. R. Siviour, Review of experimental techniques for high rate deformation and shock studies, Int. J. Impact Eng., 2004, 30(7), 725–775, DOI:10.1016/j.ijimpeng.2004.03.005.
- N. N. Dioh, P. S. Leevers and J. G. Williams, Thickness effects in split Hopkinson pressure bar tests, Polymer, 1993, 34(20), 4230–4234, DOI:10.1016/0032-3861(93)90181-9.
- C. R. Siviour and J. L. Jordan, High Strain Rate Mechanics of Polymers: A Review, J. Dyn. Behav. Mater., 2016, 2(1), 15–32, DOI:10.1007/s40870-016-0052-8.
- D. E. Delgado, L. F. Sturdy, C. W. Burkhart and K. R. Shull, Validation of quartz crystal rheometry in the megahertz frequency regime, J. Polym. Sci., Part B: Polym. Phys., 2019, 57(18), 1246–1254, DOI:10.1002/polb.24812.
- S. Tiwari, et al., Seeded laser-induced cavitation for studying high-strain-rate irreversible deformation of soft materials, Soft Matter, 2020, 16(39), 9006–9013, 10.1039/D0SM00710B.
- L. Mancia, et al., Acoustic cavitation rheometry, Soft Matter, 2021, 17(10), 2931–2941, 10.1039/D0SM02086A.
- J. B. Estrada, C. Barajas, D. L. Henann, E. Johnsen and C. Franck, High strain-rate soft material characterization via inertial cavitation, J. Mech. Phys. Solids, 2018, 112, 291–317, DOI:10.1016/j.jmps.2017.12.006.
- W. W. Chen and B. Song, Split Hopkinson (Kolsky) bar: design, testing and applications, Springer, New York, 2011 Search PubMed.
- U. Choudhry, T. Kim, M. Adams, J. Ranasinghe, R. Yang and B. Liao, Characterizing microscale energy transport in materials with transient grating spectroscopy, J. Appl. Phys., 2021, 130, 231101, DOI:10.1063/5.0068915.
- J. A. Rogers, A. A. Maznev, M. J. Banet and K. A. Nelson, Optical Generation and Characterization of Acoustic Waves in Thin Films: Fundamentals and Applications, Annu. Rev. Mater. Sci., 2000, 30(1), 117–157, DOI:10.1146/annurev.matsci.30.1.117.
- F. Hofmann, M. P. Short and C. A. Dennett, Transient grating spectroscopy: An ultrarapid, nondestructive materials evaluation technique, MRS Bull., 2019, 44(5), 392–402, DOI:10.1557/mrs.2019.104.
- A. A. Maznev, K. A. Nelson and J. A. Rogers, Optical heterodyne detection of laser-induced gratings, Opt. Lett., 1998, 23(16), 1319, DOI:10.1364/OL.23.001319.
- J. M. Urueña, A. A. Pitenis, R. M. Nixon, K. D. Schulze, T. E. Angelini and W. G. Sawyer, Mesh Size Control of Polymer Fluctuation Lubrication in Gemini Hydrogels, Biotribology, 2015, 1–2, 24–29, DOI:10.1016/j.biotri.2015.03.001.
- B. Gorman and L. McNeil, Effect of polymerization on free water in polyacrylamide hydrogels observed with Brillouin spectroscopy, Soft Matter, 2024, 20(26), 5164–5173, 10.1039/D4SM00250D.
- L. Stevens, E. Orler, D. Dattelbaum, M. Ahart and R. Hemley, Brillouin-scattering determination of the acoustic properties and their pressure dependence for three polymeric elastomers, J. Chem. Phys., 2007, 127(10) DOI:10.1063/1.2757173.
- D. Tabor, The bulk modulus of rubber, Polymer, 1994, 35(13), 2759–2763, DOI:10.1016/0032-3861(94)90304-2.
- C. W. Barney, et al., Fracture of model end-linked networks, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(7), e2112389119, DOI:10.1073/pnas.2112389119.
- P. J. Flory and J. Rehner, Statistical Mechanics of Cross-Linked Polymer Networks I. Rubberlike Elasticity, J. Chem. Phys., 1943, 11(11), 512–520, DOI:10.1063/1.1723791.
- M. A. Caporizzo, et al., Strain-Rate Dependence of Elastic Modulus Reveals Silver Nanoparticle Induced Cytotoxicity, Nanobiomedicine, 2015, 2, 9, DOI:10.5772/61328.
- A. Mata, A. J. Fleischman and S. Roy, Characterization of Polydimethylsiloxane (PDMS) Properties for Biomedical Micro/Nanosystems, Biomed. Microdevices, 2005, 7(4), 281–293, DOI:10.1007/s10544-005-6070-2.
- K. Khanafer, A. Duprey, M. Schlicht and R. Berguer, Effects of strain rate, mixing ratio, and stress–strain definition on the mechanical behavior of the polydimethylsiloxane (PDMS) material as related to its biological applications, Biomed. Microdevices, 2009, 11(2), 503–508, DOI:10.1007/s10544-008-9256-6.
- G. Xu, et al., Acoustic Characterization of Polydimethylsiloxane for Microscale Acoustofluidics, Phys. Rev. Appl., 2020, 13(5), 054069, DOI:10.1103/PhysRevApplied.13.054069.
- F. Schneider, T. Fellner, J. Wilde and U. Wallrabe, Mechanical properties of silicones for MEMS, J. Micromech. Microeng., 2008, 18(6), 065008, DOI:10.1088/0960-1317/18/6/065008.
- V. Placet and P. Delobelle, Mechanical properties of bulk polydimethylsiloxane for microfluidics over a large range of frequencies and aging times, J. Micromech. Microeng., 2015, 25(3), 035009, DOI:10.1088/0960-1317/25/3/035009.
- E. Rubino and T. Ioppolo, Young's modulus and loss tangent measurement of polydimethylsiloxane using an optical lever, J. Polym. Sci., Part B: Polym. Phys., 2016, 54(7), 747–751, DOI:10.1002/polb.23972.
- S. Gupta, F. Carrillo, C. Li, L. Pruitt and C. Puttlitz, Adhesive forces significantly affect elastic modulus determination of soft polymeric materials in nanoindentation, Mater. Lett., 2007, 61(2), 448–451, DOI:10.1016/j.matlet.2006.04.078.
- C. W. Barney, M. E. Helgeson and M. T. Valentine, Network structure influences bulk modulus of nearly incompressible filled silicone elastomers, Extreme Mech. Lett., 2022, 52, 101616, DOI:10.1016/j.eml.2022.101616.
- N. W. Tschoegl, W. G. Knauss and I. Emri, Poisson's Ratio in Linear Viscoelasticity – A Critical Review, Mech. Time-Depend. Mater., 2002, 6(1), 3–51, DOI:10.1023/A:1014411503170.
- T. Takigawa, Y. Morino, K. Urayama and T. Masuda, Poisson's Ratio of Polyacrylamide (PAAm) Gels, Polym. Gels Networks, 1996, 4(1), 1–5 CrossRef CAS.
- A. M. Smith, D. G. Inocencio, B. M. Pardi, A. Gopinath and R. C. Andresen Eguiluz, Facile Determination of the Poisson's Ratio and Young's Modulus of Polyacrylamide Gels and Polydimethylsiloxane, ACS Appl. Polym. Mater., 2024, 6(4), 2405–2416, DOI:10.1021/acsapm.3c03154.
- R. D. Nedoluha, M. N. Saadawi and C. W. Barney, Errors matter when measuring Poisson’s ratio of nearly incompressible elastomers, Soft Matter, 2025, 21(34), 6689–6696, 10.1039/D5SM00535C.
| This journal is © The Royal Society of Chemistry 2026 |


