Open Access Article
Open Access ArticleIndependent measurement of Young's modulus and Poisson's ratio of transparent thin films using indentation and surface deformation measurements
M. J.
Wald
ab,
J. M.
Considine
 c and
K. T.
Turner
c and
K. T.
Turner
 *a
*a
aDepartment of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA, USA. E-mail: kturner@seas.upenn.edu
b3M Company, St. Paul, MN, USA
cUSDA, Forest Service, Forest Products Laboratory, Madison, WI, USA
First published on 18th December 2025
Abstract
Instrumented indentation is a common technique for measuring the elastic properties of thin materials, including elastomers, gels, and biological materials. Traditional indentation analysis yields a reduced modulus, which is a function of Young's modulus and Poisson's ratio, thus requiring one of the parameters to be estimated or independently measured to decouple the properties. It is difficult in some cases to know the true deformation of the surface due to substrate deformations, machine compliance, and thermal drift. To address these issues, a new technique is demonstrated in which 3D displacements are measured at discrete points along the surface of a transparent specimen during indentation tests using microscopy and fluorescent micrometer-scale particles embedded in the specimen. The out-of-plane displacements of the particles are measured using a defocused imaging technique, taking advantage of the change in spherical aberration ring radius with distance from the focal plane. A technique for tracking the motion of the particles and calibrating the system is described, and experimental measurements on a silicone elastomer are presented. Two optimization algorithms were developed to extract Young's modulus and Poisson's ratio from the experimental measurements. The first algorithm uses radial and normal displacements measured along the surface of the specimen. The second algorithm uses a combination of traditional indentation analysis and radial surface displacements. The elastic properties of polydimethylsiloxane (PDMS) were calculated from experimental data using both algorithms. The results from both methods were in agreement with each other, as well as with values of Young's modulus reported in the literature.
1 Introduction
Soft thin layers, such as pressure sensitive adhesives, polymer thin films, and biological materials, are often cast on or supported by comparably stiff substrates. While accurate measurement of the elastic properties of these materials is necessary for a variety of applications,1–3 it is often difficult to measure them using traditional mechanical testing techniques, due to the small volumes of the specimens and their low moduli. Because of these challenges, instrumented indentation testing has become a common technique for evaluating the elastic properties of soft thin films on substrates. Instrumented indentation allows for relatively small sample sizes and thin layers supported on substrates to be tested.4Previous experimental techniques have been proposed to obtain both Young's modulus, E, and Poisson's ratio, ν, from indentation measurements. Chippada, et al.5 characterized Young's modulus, shear modulus, and Poisson's ratio of hydrogels by tracking the displacement and rotation of embedded nonspherical magnetic microneedles due to a prescribed force or torque. Gross and Kress6 embedded fluorescent microparticles in a gel and determined indentation depth by tracking the particle displacement in an image stack through the thickness of the gel. Balakrishnan and Socrate7 developed an instrumented indentation apparatus that included additional displacement sensors near the primary indenter. A computational analysis was completed to illustrate the implementation of the proposed technique, but no experimental results were reported. Zheng, et al.8 developed a numerical method for simultaneously extracting E and ν from cylindrical flat punch indentation measurements on a thin film bonded to a rigid substrate. This method extends a model developed by Hayes, et al.9 to account for the substrate effect when finite deformations are considered. This model is limited to analyzing thin films where indentation depth is large relative to film thickness, and it is not applicable to the more common testing regime in which indentation depth is small relative to film thickness. Lucas, et al.10 described an indentation method with a 3-axis load cell which uses in-plane and out-of-plane stiffness measurements to calculate both E and ν for bulk materials and thin films using an analytical model.
Traditional instrumented indentation analysis is also sensitive to errors in measuring true deformation of the specimen caused by factors such as machine compliance, thermal drift, and surface detection errors. The effect of machine compliance is commonly modeled as two springs combined in series, representing the compliance of the indenter and the compliance of the material.11,12 Machine compliance is calculated by indenting a material with known elastic properties, typically fused silica, and subtracting the theoretical compliance of the material from the compliance measured in the indentation test. While this technique often provides a good estimate of the machine compliance, it can be sensitive to errors in the assumed contact area. In the case of flat punch indentation, errors in the alignment between the face of the indenter and the specimen surface may lead to incomplete contact.4,13,14 For indenter geometries with cross-sectional areas that vary with indentation depth, calculating the contact area requires accurate detection of the surface, which is done by assessing the initial contact between the indenter and specimen. This can be particularly problematic for soft materials, and surface detection errors can lead to significant errors in the modulus values extracted from tests.15,16 Thermal drift, or the change in measured displacement due to small changes in temperature, is often minimized by conducting tests in a temperature-controlled environment or performing tests quickly.17 However, when measuring time-dependent properties, decreasing the duration of the tests is not always an option.
To address these limitations of standard instrumented indentation, a new technique is introduced here in which the in-plane and out-of-plane displacements along the surface of a specimen are measured independently of the indenter. Specifically, the displacements of fluorescent particles placed near the surface of a transparent specimen are measured using microscopy during an instrumented indentation test. The in-plane and out-of-plane particle displacements are measured using quantitative defocusing (QD).18 From the measured in-plane and out-of-plane displacements near the indenter and a finite element (FE) based inverse method, both E and ν can be determined. In addition, by measuring the displacements of the surface directly, the deformation measurements are independent of machine compliance, substrate effects, and thermal drift. While the general approach used here is applicable to a wide range of materials, the specific implementation presented in this paper has been developed for testing linear-elastic polymeric and soft materials with Young's moduli less than approximately 10 MPa. The experimental protocols and analysis techniques as presented here are not directly applicable to viscoelastic materials where the properties are time-dependent.
The overall objective of this work is to evaluate approaches that use a combination of instrumented indentation and surface deformation measurements to independently characterize both E and ν of soft transparent thin films on stiff substrates. A particle tracking technique was developed and applied to measure surface deformation during a cylindrical flat punch indentation test. The resolution of the particle tracking technique was characterized. A parametric FE analysis was completed to examine the in-plane and normal displacements along the surface of films of varying thickness, t, to determine the range of thicknesses where the particle tracking technique is applicable. Two FE-based optimization algorithms were developed to extract the film E and ν from measured force and surface displacements. Experimental results from indentation tests on a silicone elastomer, polydimethylsiloxane (PDMS), were analyzed with both optimization algorithms and compared with each other and values in the literature.
2 Background
2.1 Quantitative defocusing (QD)
QD is a three-dimensional particle tracking technique that uses wide-field fluorescence microscopy to image micrometer-scaled particles. Out-of-plane displacement is correlated with the change in the radius of the spherical aberration ring that forms around the particle image as the particle moves out of the focal plane.18,19 In-plane displacement is measured by tracking the position of the particle center. This method is advantageous because the entire field-of-view can be captured in a single image, and particles in the focal plane, as well as particles located away from the focal plane, are visible in the frame. This allows for faster data acquisition compared to scanning confocal microscopy, which scans a field point by point.20QD has been used previously to measure displacement fields in soft materials. Long et al.21 investigated the effect of specimen thickness on E of polyacrylamide gels by measuring the out-of-plane displacements of fluorescent particles in the specimen before and after a spherical mass was placed on the surface and assuming ν was 0.5. The z-position of each particle was located by scanning the stage in the z-direction to determine the position at which each particle had the greatest intensity. The z-resolution of this implementation of QD was limited by the stage resolution, which was ±1 µm. A similar method was used to map three-dimensional stress and strain fields in a thin polyacrylamide gel layer indented by a sphere.22 Yoon et al.23 used QD to investigate the swelling kinetics of thin hydrogel layers. Displacements were measured by tracking the particle center and radius. An in-plane resolution of ±1.8 µm and an out-of-plane displacement resolution of ±3.6 µm were reported for a 76 µm-thick hydrogel film.
In experiments, particles are often viewed through multiple media with varying refractive indices. These non-ideal optical conditions limit the usefulness of diffraction models. As such, it is common to compare the aberration rings measured during experiments to an experimentally developed calibration curve. The calibration curve is created by collecting images at known z-displacements from the focal plane. The size of the ring is correlated with the distance from the focal plane.24 The calibration curve depends on the objective, the particle size, and the optical properties of the system and cannot be used universally.24 Zhang and Menq25 developed a method in which the in-plane position of a particle was found using a weighted centroid method and the out-of-plane position was measured by comparing the intensity profile of each particle image as a function of radial distance from the particle center with the intensity profile of the calibration images. To assess the noise in the measured displacements, the particles were simultaneously displaced in the x-, y-, and z-directions following a square wave with an amplitude of 2 nm for in-plane displacements and 5 nm for out-of-plane displacements and a period of 1 s. The measurements showed a standard deviation of 0.35 nm for in-plane displacements and 0.9 nm for out-of-plane displacements for 4.5 µm particles and a 60× water immersion objective with a numerical aperture, NA, of 1.20. Hall et al.22 developed a particle tracking algorithm to measure displacements of particles in a polyacrylamide gel by fitting a circle to each particle and using the center of the circle to track the in-plane displacements and the diameter of the circle to track the out-of-plane displacements. The center and diameter calculated by the algorithm had a resolution of 1 pixel. With a 20× objective (NA = 0.4), this resulted in an in-plane resolution of 0.4 µm and an out-of-plane resolution of 0.8 µm.
2.2 Instrumented indentation
A schematic of cylindrical flat punch indentation of a thin film on a rigid substrate is shown in Fig. 1. A rigid indenter with contact radius, a, is displaced into a specimen. The applied force, P, and normal displacement of the indenter, uz, are measured. In most indentation analysis methods, an approach based on Sneddon's solution26 for an elastic halfspace is used to calculate a reduced modulus, Ē, using P, uz, and a.27Ē = E/(1 − ν2), where E is the Young's modulus and ν is the Poisson's ratio. For film-substrate systems in which the film thickness, t, is small relative to a, an effective modulus, Eeff, which depends on the elastic properties of the film and substrate and a/t, is calculated. Several models for extracting film properties from flat punch indentation tests on film-substrate systems yield reduced modulus of the material.4,9,28,29 To independently determine E, ν must be estimated or measured separately, which is often difficult. | ||
| Fig. 1 A rigid cylindrical indenter with radius, a, indenting an elastic film with Young's modulus, E, and Poisson's ratio, ν, and thickness, t. | ||
In the present work, displacements are measured at various locations on the surface. The in-plane and out-of-plane displacements on the surface of an elastic film are a function of E, ν, t, a, P, and the radial position, r. An FE model was constructed to quantify the effect of a/t on radial displacement, ur, and uz for a range of t. The film was meshed with 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 8-node axisymmetric continuum elements. 200 axisymmetric infinite elements were used along the lateral boundary beginning at a radius of 2.5 mm from the center of the indenter. The number of elements was determined through a convergence study. E = 2 MPa and ν = 0.499 were assumed in the initial simulations. The rigid substrate was modeled by fixing all degrees of freedom along the bottom boundary of the film. The 250 µm-radius cylindrical indenter was modeled as a rigid surface. The film thickness was varied from 10 µm to 1 mm (a/t from 25 to 0.25).
000 8-node axisymmetric continuum elements. 200 axisymmetric infinite elements were used along the lateral boundary beginning at a radius of 2.5 mm from the center of the indenter. The number of elements was determined through a convergence study. E = 2 MPa and ν = 0.499 were assumed in the initial simulations. The rigid substrate was modeled by fixing all degrees of freedom along the bottom boundary of the film. The 250 µm-radius cylindrical indenter was modeled as a rigid surface. The film thickness was varied from 10 µm to 1 mm (a/t from 25 to 0.25).
In many indentation analyses for soft materials, the contact between the indenter and specimen is assumed to be frictionless; however, there is often friction and adhesion between the indenter and specimen. This is permissible for bulk soft materials when ν is near 0.5 because ur is approximately 030 in this special case. However, ur ≠ 0 for thin film systems when ν is near 0.5. To account for this in the analysis, two cases were considered in the simulations: (1) the indenter was in frictionless contact with the film, and (2) the indenter was perfectly bonded to the film (i.e. no-slip). Perfectly bonded contact between the indenter and film was modeled by enforcing ur = 0 on the surface nodes in contact with the indenter. A 40 mN maximum compressive load was assumed in initial simulation cases because it is similar to the maximum loads reported in Wald et al.31 The model was solved using Abaqus 6.9 (SIMULIA, Providence, RI).
FE-calculated ur and uz for the frictionless and bonded cases for three film thicknesses are shown in Fig. 2a–d. As film thickness decreases, the maximum uz also decreases, showing that the effective stiffness of the specimen is increasing due to the substrate effect. uz for the 10 µm thick film in this example case is too small to measure using the particle tracking technique. For the 100 µm film, uz is negative immediately outside of the contact area, indicating that the surface deforms away from the substrate. This occurs because the film is nearly incompressible and is constrained by the substrate and the indenter. ur is nonzero and positive for each of the films. Of the cases examined, the 100 µm thick film has the largest ur and has measurable uz, suggesting that the particle tracking technique is well suited for testing specimens with a/t of approximately 2.5.
3 Methods
3.1 Specimen fabrication
Polydimethysiloxane (PDMS) films cast on glass substrates were fabricated and used for validation experiments. 6.3 µm diameter fluorescent polystyrene microspheres (Bangs Laboratories, Fishers, IN) were used as surface markers. The particles had excitation and emission wavelengths of 480 nm and 520 nm, respectively. 16 µL of the particles were diluted in 1 mL of isopropyl alcohol. A 2 µL drop of the particle solution was placed on a silicon wafer. The alcohol was allowed to evaporate completely, leaving the particles randomly distributed on the wafer surface. Glass coverslips with thicknesses of 145 µm were placed on either side of the particle droplet. PDMS was prepared by mixing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratios of base elastomer to curing agent (Sylgard 184, Dow Corning Corporation, Midland, MI). Drops of the PDMS were placed on the wafer where the particles were distributed. The PDMS was degassed in a vacuum for 1 hour. A 1 mm thick glass microscope slide was placed over the PDMS drop such that the coverslips acted as spacers to control the film thickness. A weight was placed on the glass slide. Both PDMS specimens were cured in an oven at 85 °C for 4 hour. After curing, the slide and PDMS were separated from the wafer. The PDMS surface with the beads, which was in contact with the wafer during molding, was used for curing. The glass slide was the stiff substrate that supports the film. The 10
1 weight ratios of base elastomer to curing agent (Sylgard 184, Dow Corning Corporation, Midland, MI). Drops of the PDMS were placed on the wafer where the particles were distributed. The PDMS was degassed in a vacuum for 1 hour. A 1 mm thick glass microscope slide was placed over the PDMS drop such that the coverslips acted as spacers to control the film thickness. A weight was placed on the glass slide. Both PDMS specimens were cured in an oven at 85 °C for 4 hour. After curing, the slide and PDMS were separated from the wafer. The PDMS surface with the beads, which was in contact with the wafer during molding, was used for curing. The glass slide was the stiff substrate that supports the film. The 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS film was 165 µm thick and the 20
1 PDMS film was 165 µm thick and the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS film was 186 µm thick.
1 PDMS film was 186 µm thick.
3.2 Microscope objective selection
While particles below the diffraction limit of the microscope are often used in conjunction with defocused imaging,19 6.3 µm particles were chosen for this study because larger particles have a higher intensity, resulting in better defined spherical aberration rings. Fig. 3 shows images of two particles on a glass microscope slide at z-displacements of 0, 20, 40, 60, and 80 µm relative to the focal plane, zfocal, obtained with objectives with different NA and working distance (WD). The particle in the left column was imaged with a 20× Zeiss LD EC Epiplan-Neofluar objective (NA = 0.22, WD = 12.1 mm) and the particle in the right column was imaged with a 20× Zeiss EC Plan-Neofluar objective (NA = 0.5, WD = 2 mm). This demonstrates that an objective with higher NA yields a more well-defined aberration ring and that the radius of the ring is more sensitive to changes in z-displacement relative to objectives with lower NA. Thus, high NA objectives provide better z-resolution in QD. However, in general, objectives with larger numerical apertures have shorter working distances. This presents a tradeoff between out-of-plane position resolution and the need for the working distance of the objective to be greater than the combined thickness of the film and substrate. Specifically, in the present work, the working distance of the objective must be greater than 1.2 mm (the combined thickness of the thickest film and the glass substrate). The NA = 0.5 objective described above has a working distance of 2 mm, which was sufficiently large for use in this study. However, the NA = 0.22 objective may be more appropriate if this technique were applied to thicker specimens.3.3 Experimental setup
The cylindrical flat punch indentation apparatus shown in Fig. 4 was developed to implement the surface displacement tracking technique. A simple wide-field fluorescence inverted microscope based on an Infinitube (Infinity Photo-Optical Company, Boulder, CO) was built to image the particles during an indentation test. A 470 nm wavelength LED spot light (Advanced Illumination, Rochester, VT) was used to illuminate the particles. Images were collected with a CMOS (1024 × 1280) camera (Pixelink A741, Ottawa, Canada). The specimen was placed on a three-axis closed-loop nanopositioning stage (nPoint, Middleton, WI) with 100 µm of travel in x, y, and z. The stage is calibrated and has a precision in x, y, and z of 0.5 nm. The nanopositioning stage was mounted on a tip-tilt stage to allow for alignment between the specimen and the indenter to be adjusted. The tip-tilt and nanopositioning stages both had apertures to allow for imaging of the specimen via the microscope. The specimen was positioned over a 19.1 mm diameter aperture. Based on an analytical plate theory calculation, the deformation of the glass substrate over the aperture at the maximum loads in the tests is approximately 22 nm, which is orders of magnitude less than the deformations in the test material. The cylindrical flat punch indenter was made from a 248 ± 0.5 µm radius glass rod with an end that was polished flat. The indenter radius was measured by imaging in an optical microscope, manually selecting points along the circumference of the indenter in the digital image, and fitting a circle to the points. Force was measured with a commercial load cell with a full-scale range of ±1 N (Cooper Instruments and Systems, Warrenton, VA). The entire system was supported on a vibration isolation table (TMC, Peabody, MA).3.4 Image processing and particle tracking procedure
Despite the axisymmetric nature of the system, the camera's sensor lends itself to initially measuring displacements in Cartesian coordinates and transforming the in-plane displacements into cylindrical coordinates. The x-coordinate was defined in the 1280 pixel direction of the camera and the y-coordinate was defined in the 1024 pixel direction. A spatial bandpass filter described in ref. 32 was applied to all images to remove the effects of pixel noise and long wavelength variations due to uneven background illumination. Spatial wavelength cutoffs of 3 and 31 pixels (1.0 µm and 10.3 µm, respectively) were used. The filtered images were then normalized so that the pixel intensities spanned 0 to 255.To identify particles, the first image of each experiment was analyzed to locate intensity peaks. To accomplish this, the image was first converted to binary. Bright regions were identified as potential particle locations. The potential particles were filtered based on area and maximum intensity to exclude regions of the image that were not particles. Minimum area, maximum area, and minimum peak height were adjustable parameters meant to allow the analyst to distinguish particles of interest from surface contamination or background noise that were not removed during image preprocessing. The particles that met these criteria were then located in the grayscale image. A bounding box was created around each particle. The width and height of the bounding box were initially 1.2 times greater than the width and height of the particle, but the dimensions were allowed to vary based on the size of the particle's aberration ring in subsequent images. The area inside each bounding box was processed further using the spatial bandpass filter with spatial cutoff frequencies of 1 and 15 pixels (0.3 µm and 5.0 µm, respectively) and the pixel intensities were then renormalized.
The in-plane and out-of-plane displacements were found using the center and aberration ring radius of the particle images, respectively. The pixels identified as part of the aberration ring were fit with a circle using a nonlinear least squares algorithm to determine the location of the center of the particle to track the in-plane displacements. Out-of-plane displacement was calculated using the radius of the aberration rings in the particle images. While the circle-fitting algorithm also calculates a radius, the fitted radius was found to be sensitive to the thickness of the ring, which varies with distance from the focal plane. Instead, the radius of the ring was determined by calculating the distance between the center of the particle and the outermost intensity peak. To do this, each bounding box was collapsed into a 1-D intensity profile as a function of radius using the method described by Zhang and Menq.25 The intensity peak located furthest from the center of the particle was located using Matlab's findpeaks function (Matlab 2013a, The MathWorks, Natick, MA). The resolution of the peak location was limited by the pixel density of the image. To improve the resolution of the measured radius, the intensity of the pixel identified as the peak along with the intensities of the 4 nearest pixels to the left and right of the peak were fit with a Gaussian distribution. The radius of the aberration ring was then defined as the radial distance from the particle center to the peak of the Gaussian fit.
3.5 Calibration and noise measurement
Displacements were calibrated by measuring the position of the center of the particle and the change of the aberration ring radius as a function of known stage displacements. The calibration data were collected for 6.3 µm particles embedded in the surface of the PDMS films prior to testing. The appearance of the particles in the images depends on the optical properties of the specimen; thus, the calibration curve must be developed for each particle tracked during the indentation tests. Displacement was calibrated using the nanopositioning stage to move the specimen systematically in the x-, y-, and z-directions and measure the position of the particle center and radius at each location. For both x- and y-calibration, the specimen was displaced a total of 5 µm in 0.1 µm increments. z-displacements were calibrated by translating the stage a total of 100 µm away from the microscope objective in 1 µm increments. After each increment, the stage was allowed to settle for 1 s, at which point an image was captured.The in-plane displacements of the particle centers were observed to be linearly related to the stage displacement, as expected. The x- and y-calibration data were fit with a linear relationship to determine the in-plane calibration factor. The change in aberration ring radius as the specimen was displaced away from the focal plane was nonlinear. The relationship between particle radius and distance from the focal plane was determined using linear interpolation between each calibration point over the range of particle radii measured in each experiment. The change in radius as a function of z-displacement is very small until the aberration ring forms around the particle.33 Using the QD technique described above, before the aberration ring forms, the peak intensity is located at the particle center, resulting in a measured ring radius of 0. This occurs from zfocal = 0 to approximately zfocal = 40 µm in Fig. 3. The microscope position was initially adjusted such that the particles were sufficiently far (∼40 µm) from the focal plane that the aberration rings were fully formed at the beginning of the calibration and experiments (i.e., the particles are out of focus when the test begins). The z-position in the experiments was subsequently referenced from this starting plane and referred to as zstage. The focal plane was adjusted manually, but zstage = 0 µm was typically near zfocal = 40 µm. The stage was then displaced away (in the negative z-direction) from the focal plane.
The noise in the displacement measurements was quantified as a function of particle position relative to the focal plane. The stage was displaced 0, 20, 40, and 60 µm in the z-direction. 50 images were collected at each stage position over a period of 128 s. The standard deviations of ux, uy, and uz at each stage position were calculated to assess the noise floor of the technique. The results are shown in Fig. 5. The noise in each component of displacement did not vary significantly with respect to stage displacement. This is likely because the NA = 0.5 objective produces aberration rings that have high intensity relative to background noise over the displacement range examined. Due to the sensitivity of ring radius to z-displacement, when the stage displacement was greater than 60 µm, portions of the aberration rings overlapped with one another or moved out of the field of view. In these cases, the particle tracking technique was unable to accurately track the particles. This limited the out-of-plane measurement range of this technique to approximately 60 µm when using this objective. An objective with a smaller NA could potentially allow larger displacement measurements, but would also increase the noise in the uz measurement.
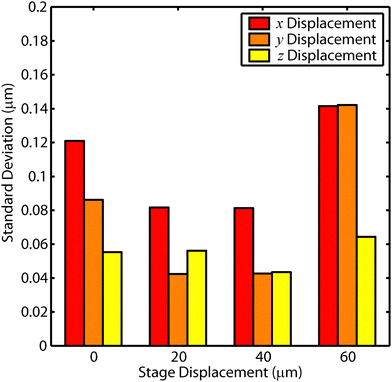 | ||
| Fig. 5 Standard deviation of x-, y-, and z-displacements of 7 particles at zstage = 0, 20, 40, 60, and 80 µm. 50 images were collected over a period of 128 s at each position. | ||
3.6 Indentation experiment procedure
Displacement-controlled indentation tests on the PDMS films were completed using the experimental setup described above. Displacement was controlled using the closed-loop nanopositioning stage. Tests were completed at two different locations on both the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS specimens. All tests were completed at an ambient temperature of 22 ± 1 °C. Each specimen was displaced in the z-direction to a maximum indentation depth of 10 µm. This indentation depth was chosen because it produced measurable force, in-plane displacement, and out-of-plane displacement using the experimental setup and particle tracking procedure described above, while also remaining within the linear elastic regime of the PDMS films. The maximum displacement was held for 10 s. The specimen was then displaced 20 µm away from the indenter in the z-direction. The additional displacement in the unloading portion of the test from the specimen even when adhesion is present. The loading and unloading rates were 1 µm s−1 for all tests. 10 tests were completed at each location. 8 particles were tracked for measurement of ur and uz at Position 1 on both the 10
1 PDMS specimens. All tests were completed at an ambient temperature of 22 ± 1 °C. Each specimen was displaced in the z-direction to a maximum indentation depth of 10 µm. This indentation depth was chosen because it produced measurable force, in-plane displacement, and out-of-plane displacement using the experimental setup and particle tracking procedure described above, while also remaining within the linear elastic regime of the PDMS films. The maximum displacement was held for 10 s. The specimen was then displaced 20 µm away from the indenter in the z-direction. The additional displacement in the unloading portion of the test from the specimen even when adhesion is present. The loading and unloading rates were 1 µm s−1 for all tests. 10 tests were completed at each location. 8 particles were tracked for measurement of ur and uz at Position 1 on both the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS specimens and 6 particles were tracked for Position 2 on both the 10
1 PDMS specimens and 6 particles were tracked for Position 2 on both the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 specimens.
1 specimens.
Misalignment between the indenter and specimen surface was removed prior to testing by adjusting the tip-tilt. The indenter was positioned sufficiently close to the specimen surface to allow interference fringes to form due to the gap between the indenter and the specimen surface. The number and spacing of the fringes that formed were a function of the misalignment between the indenter and surface. The tip-tilt stage was manually adjusted to minimize the misalignment. The alignment was adjusted until the indenter surface was covered by at most one bright and dark fringe. When this was achieved, the angle of misalignment was less than 0.03° given the wavelength of the light source was 470 nm and the a of 248 µm.
4 Analysis
A linear elastic constitutive model based on E and ν was used to characterize the PDMS films. This is a common assumption for Sylgard 184 PDMS as it is a crosslinked silicone where the dominant response is elastic.34 A representative stress–strain curve for PDMS is available in ref. 35. These previous reports indicate that PDMS exhibits minimal viscoelastic dissipation at small strains. Constant displacement rate tensile tests completed on 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS demonstrated that the stress–strain response is nearly linear when strain was less than 40%.35 As the nominal strains in the experiments presented here are less than 10%, neither viscoelastic nor nonlinear elastic effects are expected to contribute significantly to the mechanical response, suggesting that the assumption of linear elasticity was appropriate.
1 PDMS demonstrated that the stress–strain response is nearly linear when strain was less than 40%.35 As the nominal strains in the experiments presented here are less than 10%, neither viscoelastic nor nonlinear elastic effects are expected to contribute significantly to the mechanical response, suggesting that the assumption of linear elasticity was appropriate.
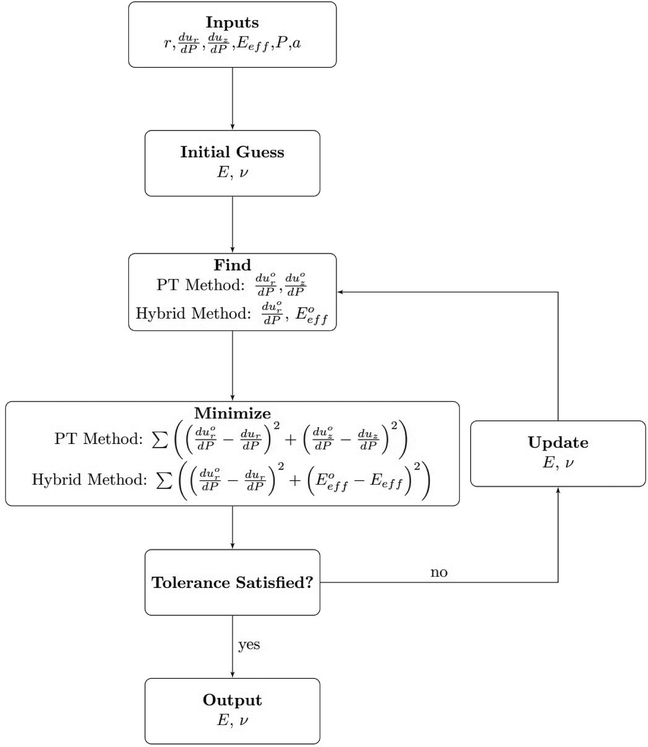
Two numerical algorithms, described in Fig. 6, were developed to extract E and ν from experimentally measured force and displacement data. In each method, E and ν are determined using a nonlinear least squares algorithm, which minimizes the difference between experimentally measured parameters and the equivalent quantities in the FE model. The FE model was identical to the one described above except a was changed to 248 µm and h was 165 µm for the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS specimen and 186 µm for the 20
1 PDMS specimen and 186 µm for the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS specimen to match experiment conditions. E and ν in the FE model were varied by the optimization algorithm. ur and uz were calculated from the FE model at the radial locations of the particles measured from the experiments using linear interpolation between the two nearest surface nodes. ur and uz of all particles tracked in each experiment were used to determine E and ν. In addition to assuming the particles were located along the surface (z = 0), the analysis was also completed for particles 3.15 µm below the surface, corresponding to the z-location of the widest section of the particle as viewed through the microscope. This was accomplished by calculating ur and uz 3.15 µm below the surface at the radial locations of the particles using the FE model. The methods each require P and the radial positions of the particles. To ensure physically realistic results, ν was constrained between 0 and 0.500, and E was constrained to positive values.
1 PDMS specimen to match experiment conditions. E and ν in the FE model were varied by the optimization algorithm. ur and uz were calculated from the FE model at the radial locations of the particles measured from the experiments using linear interpolation between the two nearest surface nodes. ur and uz of all particles tracked in each experiment were used to determine E and ν. In addition to assuming the particles were located along the surface (z = 0), the analysis was also completed for particles 3.15 µm below the surface, corresponding to the z-location of the widest section of the particle as viewed through the microscope. This was accomplished by calculating ur and uz 3.15 µm below the surface at the radial locations of the particles using the FE model. The methods each require P and the radial positions of the particles. To ensure physically realistic results, ν was constrained between 0 and 0.500, and E was constrained to positive values.
The first algorithm, the particle tracking (PT) method, used the derivatives of the radial displacement, ur, and surface deformation, uz, with respect to P. The derivatives were calculated by fitting a line to the measured ur and uz as a function of P and calculating the slope. This is preferable to using ur and uz directly because the slopes of the displacement-force relationships for flat punch indentation of linear elastic materials are independent of the absolute displacements and are not affected by errors in determining the zero displacement. This method also measures the surface deformations directly from the specimen, removing the effects of machine compliance and thermal drift, which can be a source of error in indentation measurements. This analysis assumes that there is no significant compliance in the nanopositioning stage or the specimen mount. The addition of compliance in the indenter apparatus below the specimen (Fig. 4) or compliance due the specimen structure or mounting would lead to errors in zstage, which the particle tracking procedure does not take into account.
If the machine compliance is known, a second method, the hybrid method, can be employed. The hybrid method used dur/dP measured from the particle displacements and Eeff using  where k is the measured stiffness corrected for machine compliance.27 The measured stiffness was calculated by fitting the unloading portion of the force-displacement data from 90% to 10% of the maximum compressive load with a linear relationship and calculating the slope. Following the method proposed by Oliver and Pharr,27 the specimen compliance is the difference between the measured compliance and the machine compliance. The machine compliance of the indenter was measured using the approach described in ref. 31. The mean machine compliance is 202 µm N−1 with a standard deviation of 0.85 µm N−1. After determining Eeff, the hybrid method then uses dur/dP measured from the particle displacements to decouple E and ν from Eeff.
where k is the measured stiffness corrected for machine compliance.27 The measured stiffness was calculated by fitting the unloading portion of the force-displacement data from 90% to 10% of the maximum compressive load with a linear relationship and calculating the slope. Following the method proposed by Oliver and Pharr,27 the specimen compliance is the difference between the measured compliance and the machine compliance. The machine compliance of the indenter was measured using the approach described in ref. 31. The mean machine compliance is 202 µm N−1 with a standard deviation of 0.85 µm N−1. After determining Eeff, the hybrid method then uses dur/dP measured from the particle displacements to decouple E and ν from Eeff.
The measured x- and y-displacements were transformed to cylindrical coordinates to determine ur and uθ. The origin of the coordinate system was determined by fitting a circle with a radius of 248 µm to the portion of the indenter circumference in the field-of-view. The out-of-plane surface deformation, uz, was calculated by finding the difference between zstage, and the z-position of the particles, zparticle. As is common in traditional indentation analysis, only displacement measurements from the unloading portion of the test from 90% to 10% of the maximum compressive load were used to obtain the elastic properties.
The measured out-of-plane displacement must also be corrected for the index of refraction mismatch between air, the substrate, and the film. When the specimen is undeformed (Fig. 7a), the apparent position of the particle relative to the lower surface of the specimen, d1, is constant, and the change in aberration ring radius is due only to rigid body motion of the specimen relative to the focal plane. Treating the PDMS and glass layers as thin flat lenses,36 the relationship between actual and apparent particle position in the z-direction is
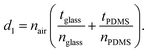 | (1) |
 | (2) |
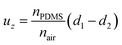 | (3) |
5 Results and discussion
u r (Fig. 8a) and uz (Fig. 8b) measured from a particle located under the indenter (r = 217 µm) and outside of the contact area (r = 518 µm) are shown as a function of P for a typical indentation test on the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS film. As expected, the change in uz is linear with respect to P, and uz inside the contact area is greater than uz outside of the contact area. As predicted by the FE model, ur along the surface is nonzero. Similar to uz, ur is linear with respect to load. At both particle locations, ur was positive, indicating the particles were moving away from the center of the indenter. A small amount of hysteresis was observed in the measured displacements, which may be due to drift in the system during the test.
1 PDMS film. As expected, the change in uz is linear with respect to P, and uz inside the contact area is greater than uz outside of the contact area. As predicted by the FE model, ur along the surface is nonzero. Similar to uz, ur is linear with respect to load. At both particle locations, ur was positive, indicating the particles were moving away from the center of the indenter. A small amount of hysteresis was observed in the measured displacements, which may be due to drift in the system during the test.
 | ||
Fig. 8 (a) ur and (b) uz as a function of P for particles located 217 µm and 518 µm from the center of the indenter for a test on a 165 µm thick 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS film on a glass substrate. 1 PDMS film on a glass substrate. | ||
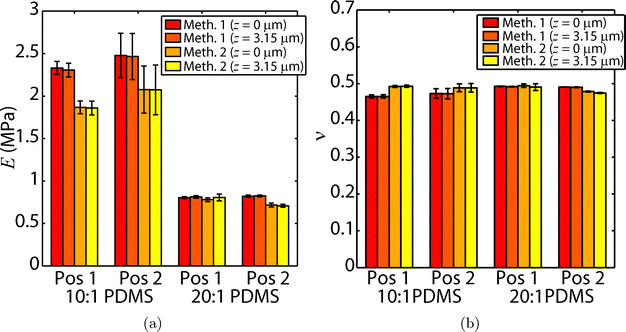
The mean and standard deviation of E and ν obtained from the two optimization algorithms for the perfectly bonded case for two positions on each specimen are shown in Fig. 9 where the particles were assumed to be on the surface and where the z-position of the particles was taken into account. The PT and hybrid methods agree well with each other for both specimens, and the z-position of the particle does not appear to affect the calculated E and ν. For 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, mean E is between 1.8 and 2.5 MPa and mean ν is between 0.46 and 0.5. E calculated by both methods was similar to previously reported results for 10
1 PDMS, mean E is between 1.8 and 2.5 MPa and mean ν is between 0.46 and 0.5. E calculated by both methods was similar to previously reported results for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS. Similarly, for 20
1 PDMS. Similarly, for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, mean E was between 0.71 MPa and 0.83 MPa and mean ν was between 0.47 and 0.49.
1 PDMS, mean E was between 0.71 MPa and 0.83 MPa and mean ν was between 0.47 and 0.49.
Several studies have reported mechanical properties for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 20
1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, which are similar to the results obtained above. Gupta, et al.38 reported E = 1.5 MPa from spherical indentation tests on 10
1 PDMS, which are similar to the results obtained above. Gupta, et al.38 reported E = 1.5 MPa from spherical indentation tests on 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS using the JKR analysis39 to account for adhesion. Kohn and Ebenstein40 reported E = 1.5 MPa (assuming ν = 0.5) from spherical indentation tests on 10
1 PDMS using the JKR analysis39 to account for adhesion. Kohn and Ebenstein40 reported E = 1.5 MPa (assuming ν = 0.5) from spherical indentation tests on 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS again using the JKR analysis. Oak41 reported E = 2.4 MPa for 10
1 PDMS again using the JKR analysis. Oak41 reported E = 2.4 MPa for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS and E = 0.89 MPa for 20
1 PDMS and E = 0.89 MPa for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS using uniaxial compression and E = 1.77 MPa for 10
1 PDMS using uniaxial compression and E = 1.77 MPa for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS and E = 0.59 MPa for 20
1 PDMS and E = 0.59 MPa for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS using spherical indentation experiments, assuming Hertzian contact. In addition, Varner and Cohen34 presented a statistical analysis of PDMS elastic properties measured using multiple test methods and discussed potential sources of variability in values reported in literature, including variations in test method design and curing conditions.
1 PDMS using spherical indentation experiments, assuming Hertzian contact. In addition, Varner and Cohen34 presented a statistical analysis of PDMS elastic properties measured using multiple test methods and discussed potential sources of variability in values reported in literature, including variations in test method design and curing conditions.
The standard deviations of E calculated using each method are smaller for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS compared to those measured for 10
1 PDMS compared to those measured for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS. Because the 10
1 PDMS. Because the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS is stiffer than the 20
1 PDMS is stiffer than the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS, ur and uz measured from the 10
1 PDMS, ur and uz measured from the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS tests are smaller than those measured from the 20
1 PDMS tests are smaller than those measured from the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS specimen. The higher standard deviation observed in the 10
1 PDMS specimen. The higher standard deviation observed in the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS film tests may be due to the smaller measured surface displacements. As the means and standard deviations of E and ν calculated by each method are similar, the method used may be chosen based on the experiment design. The hybrid method is preferable when the machine compliance is known, as it does not require out-of-plane particle tracking. If machine compliance is unknown, the PT method should be used as uz measured using QD is independent of machine compliance.
1 PDMS film tests may be due to the smaller measured surface displacements. As the means and standard deviations of E and ν calculated by each method are similar, the method used may be chosen based on the experiment design. The hybrid method is preferable when the machine compliance is known, as it does not require out-of-plane particle tracking. If machine compliance is unknown, the PT method should be used as uz measured using QD is independent of machine compliance.
To better understand the difference between the frictionless and bonded contact conditions described earlier, dur/dP from the experiments and the FE model were compared for each case where the displacements were assumed to be measured at the specimen surface (z = 0) (Fig. 10). Because E and ν used in the FE model were determined by fitting the experimental results, all of the data would ideally fall on a line with slope of 1. However, in the frictionless case, dur/dP from the FE model and experiments are uncorrelated, suggesting that the assumption of frictionless contact between the indenter and specimen surface does not describe the experiments well. In contrast, dur/dP from the FE model with perfectly bonded contact correlates much better with the experiments. Employing the bonded contact assumption increases dur/dP calculated from the FE model for the particles outside the contact area, bringing the FE model into better agreement with the experiments. While dur/dP calculated from the FE model for particles inside the contact area is always zero due to the assumption of perfect bonding, small radial displacements were measured in the experiments. This may be due to either limited slip at the contact interface or the fact that the center of the particle is located slightly below the surface of the specimen, where the radial displacements are not constrained to be zero.
To investigate the effect of the particles being below the surface further, the analysis described above was repeated by calculating ur and uz 3.15 µm below the specimen surface. This depth was chosen because it corresponds to the z-plane, which passes through the center of the particle and, as such, may more closely represent the displacements measured in the experiment. dur/dP calculated from the FE model for particles located 3.15 µm below the surface is compared to dur/dP from the experiments in Fig. 10. For the frictionless case, the results are very similar to the values calculated for particles located along the specimen surface. Again, this indicates that the frictionless boundary condition is not appropriate for this model. When the contact between the indenter and the specimen is bonded, dur/dP calculated from the FE model for particles inside the contact area and below the surface increases to approximately 17 µm N−1, which shows better agreement with the experimental measurements than when displacements were calculated along the surface. Outside of the contact area, there is very little change between the dur/dP calculated at z = 0 µm and z = 3.15 µm. Despite the better agreement, the mismatch in slope between data points in the contact region and the line with a slope of unity in Fig. 10, suggests there is some limited slip in the contact region that is not described by either the bonded or frictionless model.
dur/dP calculated from the FE model at z = 3.15 µm represents dur/dP calculated from experimental measurements better than assuming the measured displacements are directly along the surface. However, Fig. 9 shows that the difference in E and ν between these two cases is negligible relative to the variation in the calculated values. This suggests that even though accounting for the size of the particle results in better correlation between the experiments and the FE model for the cases examined, there is no apparent advantage to accounting for particle z-position in terms of improving the accuracy of calculated E and ν. In general, the z-location of the particle may be significant and should be accounted for when it is feasible to do so.
There appear to be several advantages to testing soft materials as thin films on substrates when using the QD method to measure surface displacements. The small specimen thickness allows objectives with high numerical aperture to be used, improving the resolution of the measured displacements, leading to lower uncertainty in the calculated E and ν. Because radial displacements are nonzero, the thin film geometry also allows the contact conditions between the indenter and the specimen to be investigated. For example, different slip conditions can be incorporated into the FE model, and displacement data within the contact can be used to quantify the slip criterion.
One potential concern with the indentation technique is that, because the polystyrene particles are stiff relative to the PDMS specimens, the particles may increase the specimen stiffness. Stiff inclusions in an elastic material are known to increase the measured stiffness near the inclusion. In FE simulations of a stiff inclusion near the surface of an elastic halfspace, it was observed that local variations in stress due to the inclusion were limited to distances on the order of the particle diameter from the center of the particle.42 Beyond this distance, the stresses in the inclusion case agreed with the stresses in the inclusion-free case. Increased contact pressure between the indenter and the surface was also observed in the area immediately above the inclusion.42 In the present work, the particles need to be farther than 1 particle diameter away from each other to facilitate the particle tracking algorithm. As such, it appears that the local stress fields due to the inclusions will not interact with one another.
Here, the particles were embedded in the surface of the specimen, which is only applicable to curing materials. The particle tracking technique and the subsequent analysis do not require that the particles be embedded in the surface. For non-curing transparent materials, the particles may be adhered to the specimen surface, rather than embedded in the surface. However, to avoid the particles in the contact area affecting the measurements, the particles should be placed on the surface such that the contact area is free of particles. The analysis described above can then be implemented using surface displacements outside the contact area.
6 Summary and conclusions
An approach for independently measuring E and ν of soft transparent thin films on comparably stiff substrates using instrumented indentation tests combined with optical surface deformation measurements was described and evaluated. In-plane and out-of-plane surface displacements of a thin film on a substrate during a flat punch indentation test were measured using QD. A particle tracking algorithm was developed to track the center and radius of spherical aberration rings. A calibration procedure based on experimental measurements of fluorescent particles embedded near the surface of a PDMS specimen was developed to determine the surface displacements based on the shift of the particle center and change in radius of the particles.Indentation tests on PDMS films on glass substrates with fluorescent particles embedded along the surface were performed to validate the technique. Two FE-based optimization algorithms were developed to extract E and ν from the experimental data. For PDMS films on glass substrates, it was found that perfectly bonded contact between the indenter and specimen better described the results from experiments than frictionless contact. E and ν obtained from the two numerical algorithms were found to be in good agreement, suggesting that the method can be chosen by comparing its strengths and weaknesses relative to the application. The effect of the z-position of the particles was also considered. While the displacements calculated at the widest part of the particle using the FE model described the experimental data better than the surface displacements, the difference between the calculated E and ν from each case was negligible.
The results of these experiments demonstrate that both E and ν can be obtained using particle tracking to measure in-plane displacements along the specimen surface during instrumented indentation tests. In addition, when QD is used to directly measure out-of-plane surface displacements, the z-displacement measured at the indenter during traditional indentation tests is no longer needed. This eliminates errors in the measured displacement due to machine compliance and thermal drift. While the technique discussed in this work was developed for testing soft transparent thin films on stiff substrates, the concept of obtaining both E and ν from in-plane and out-of-plane surface deformation measurements during instrumented indentation tests is applicable to other classes of materials. Furthermore, the QD approach developed in this work may be transferable to other mechanical testing applications in which it is desired to measure 3D surface displacements with a single camera.
Author contributions
Michael J. Wald: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft, writing – review & editing. John M. Considine: conceptualization, funding acquisition, project administration, resources, supervision. Kevin T. Turner: conceptualization, methodology, formal analysis, funding acquisition, investigation, project administration, resources, supervision, visualization, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Data availability
Data associated with this paper is available on ScholarlyCommons, the University of Pennsylvania's open access institutional repository, at https://repository.upenn.edu/handle/20.500.14332/62239.Acknowledgements
This work was supported in part by the United States Postal Service, USDA Forest Service – Forest Products Laboratory, and the National Science Foundation (CMMI-0845294).References
- D. E. Discher, P. Janmey and Y.-L. Wang, Tissue cells feel and respond to the stiffness of their substrate, Science, 2005, 310(5751), 1139–1143 CrossRef CAS PubMed.
- T. A. Ulrich, E. M. de Juan Pardo and S. Kumar, The mechanical rigidity of the extracellular matrix regulates the structure, motility, and proliferation of glioma cells., Cancer Res., 2009, 69, 4167–4174 CrossRef CAS PubMed.
- C. Franck, S. A. Maskarinec, D. A. Tirrell and G. Ravichandran, Three-dimensional traction force microscopy: a new tool for quantifying cell-matrix interactions, PLoS One, 2011, 6(3), e17833 CrossRef CAS PubMed.
- M. J. Wald, J. M. Considine and K. T. Turner, Determining the elastic modulus of compliant thin films supported on substrates from flat punch indentation measurements, Exp. Mech., 2013, 53(6), 931–941 CrossRef.
- U. Chippada, B. Yurke and N. A. Langrana, Indentation of an incompressible elastic film, J. Mater. Res., 2010, 25(3), 545–555 CrossRef CAS.
- W. Gross and H. Kress, Simultaneous measurement of the Young's modulus and the Poisson ratio of thin elastic layers, Soft Matter, 2017, 13(5), 1048–1055 RSC.
- A. Balakrishnan and S. Socrate, Material property differentiation in indentation testing using secondary sensors, Exp. Mech., 2008, 48(4), 549–558 CrossRef.
- Y. Zheng, A. Choi, H. Y. Ling and Y. P. Huang, Simultaneous estimation of Poisson's ratio and Young's modulus using a single indentation: a finite element study, Meas. Sci. Technol., 2009, 20, 045706 CrossRef.
- W. Hayes, L. M. Keer, G. Herrmann and L. Mockros, A mathematical analysis for indentation of articular cartilage, J. Biomech., 1972, 5(5), 541–551 CrossRef CAS PubMed.
- B. Lucas, J. Hay and W. Oliver, Using multidimensional contact mechanics experiments to measure Poisson's ratio, J. Mater. Res., 2004, 19, 58–65 CrossRef CAS.
- M. R. VanLandingham, Review of instrumented indentation, J. Res. Natl. Inst. Stand. Technol., 2003, 108(4), 249–265 CrossRef PubMed.
- A. Fischer-Cripps, Critical review of analysis and interpretation of nanoindentation test data, Surf. Coat. Technol., 2006, 200, 4153–4165 CrossRef CAS.
- R. L. Munisamy, D. A. Hills and D. Nowell, The solution of the contact between a tilted circular rigid punch and an elastic half-space, Wear, 1995, 93–95 CrossRef.
- J. Soons, I. de Baere and J. Dirckx, New double indentation technique for measurement of the elasticity modulus of thin objects, Exp. Mech., 2011, 51(1), 85–95 CrossRef.
- J. D. Kaufman and C. M. Klapperich, Surface detection errors cause overestimation of the modulus in nanoindentation on soft materials, J. Mech. Behav. Biomed. Mater., 2009, 2, 312–317 CrossRef PubMed.
- S. Fulco, S. Wolf, J. E. Jakes, Z. Fakhraai and K. T. Turner, Effect of surface detection error due to elastic-plastic deformation on nanoindentation measurements of elastic modulus and hardness, J. Mater. Res., 2021, 36(11), 2176–2188 CrossRef CAS.
- J. Nohava, N. X. Randall and N. Conté, Novel ultra nanoindentation method with extremely low thermal drift: principle and experimental results, J. Mater. Res., 2009, 24(03), 873–882 CrossRef CAS.
- M. Wu, J. W. Roberts and M. Buckley, Three-dimensional fluorescent particle tracking at micron-scale using a single camera, Exp. Fluids, 2005, 38, 461–465 Search PubMed.
- S. J. Williams, C. Park and S. T. Wereley, Advances and applications on microfluidic velocimetry techniques, Microfluid. Nanofluid., 2010, 8, 709–726 CrossRef.
- D. Semwogerere and E. R. Weeks, Confocal microscopy, Encyclopedia of Biomaterials and Biomedical Engineering, Taylor & Francis, 2005, pp. 1–10 Search PubMed.
- R. Long, M. S. Hall, M. Wu and C.-Y. Hui, Effects of gel thickness on microscopic indentation measurements of gel modulus, Biophys. J., 2011, 101(3), 643–650 CrossRef CAS PubMed.
- M. S. Hall, R. Long, C.-Y. Hui and M. Wu, Mapping three-dimensional stress and strain fields within a soft hydrogel using a fluorescence microscope, Biophys. J., 2012, 102(10), 2241–2250 CrossRef CAS PubMed.
- J. Yoon, S. Cai, Z. Suo and R. C. Hayward, Poroelastic swelling kinetics of thin hydrogel layers: comparison of theory and experiment, Soft Matter, 2010, 6, 6004–6012 RSC.
- S. D. Peterson, H.-S. Chuang and S. T. Wereley, Three-dimensional particle tracking using micro-particle image velocimetry hardware, Meas. Sci. Technol., 2008, 19, 115406 CrossRef.
- Z. Zhang and C.-H. Menq, Three-dimensional particle tracking with subnanometer resolution using off-focus images, Appl. Opt., 2008, 47, 2361 CrossRef PubMed.
- I. N. Sneddon, The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile, Int. J. Eng. Sci., 1965, 3(1), 47–57 CrossRef.
- W. C. Oliver and G. M. Pharr, An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments, J. Mater. Res., 1992, 7(6), 1564–1583 CrossRef CAS.
- F. Yang, Indentation of an incompressible elastic film, Mech. Mater., 1998, 30(4), 275–286 Search PubMed.
- F. Yang, Asymptotic solution to axisymmetric indentation of a compressible elastic thin film, Thin Solid Films, 2006, 515(4), 2274–2283 CrossRef CAS.
- F. M. Borodich and L. M. Keer, Contact problems and depth-sensing nanoindentation for frictionless and frictional boundary conditions, Int. J. Solids Struct., 2004, 41, 2479–2499 Search PubMed.
- M. J. Wald, J. M. Considine and K. T. Turner, Indentation measurements on soft materials using optical surface deformation measurements, Mech. Biol. Syst., 2014, 4, 41–51 Search PubMed.
- J. Crocker and D. G. Grier, Methods of digital video microscopy for colloidal studies, J. Colloid Interface Sci., 1996, 179, 298–310 Search PubMed.
- M. Speidel, A. Jonas and E.-L. Florin, Thee-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of off-focus imaging, Opt. Lett., 2003, 28(2), 69–71 Search PubMed.
- H. Varner and T. Cohen, Explaining the spread in measurement of PDMS elastic properties: influence of test method and curing protocol, Soft Matter, 2024, 20, 9174–9183 RSC.
- I. D. Johnston, D. K. McCluskey, C. K. L. Tan and M. C. Tracey, Mechanical characterization of bulk sylgard 184 for microfluidics and microengineering, J. Micromech. Microeng., 2014, 24, 035017 Search PubMed.
- R. Serway and J. Jewett Jr., Physics for Scientists and Engineers, Brooks Cole, Belmont, CA, 6th edn, 2003 Search PubMed.
- G. M. Whitesides and S. K. Y. Tang, Fluidic Optics, Proc. SPIE, 2006, 6329, 63290A CrossRef.
- S. Gupta, F. Carrillo, C. Li, L. Pruitt and C. M. Puttlitz, Adhesive forces significantly affect elastic modulus determination of soft polymeric materials in nanoindentation, Mater. Lett., 2007, 61, 448–451 CrossRef CAS.
- K. Johnson, K. Kendall and A. Roberts, Surface energy and the contact of elastic solids, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- J. C. Kohn and D. M. Ebenstein, Eliminating adhesion errors in nanoindentation of compliant polymers and hydrogels, J. Mech. Behav. Biomed. Mater., 2013, 20, 316–326 CrossRef CAS PubMed.
- S. Oak, Mechanical Properties of PDMS and the Use of Hybrid Polymer-Grafted Carbon Microspheres as Stimuli-Responsive Lubricating Particles, PhD thesis, Tulane University, 2020 Search PubMed.
- L. Wang, W. Wang, Z. Wang, H. Wang, T. Ma and Y. Hu, Numerical study of contacts between a flat-ended punch and a half-space embedded with inhomogeneities, Sci. China: Phys., Mech. Astron., 2014, 57, 684–697 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |