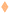Bubble growth in a confined heated polymer: the example of safety glass
C.
Arauz-Moreno
 *ab,
K.
Piroird
b and
E.
Lorenceau
*ab,
K.
Piroird
b and
E.
Lorenceau
 a
a
aUniversité Grenoble Alpes, CNRS, LIPhy, F-38000 Grenoble, France. E-mail: c.arauz_moreno@icloud.com
bSaint-Gobain Research Paris, F-93360 Aubervilliers, France
First published on 8th December 2025
Abstract
Laminated safety glass (LSG) is a composite assembly of glass and polyvinyl butyral (PVB), a viscoelastic polymer. LSG can be found in building facades and in all major forms of transportation. Yet, the assembly suffers from unwanted bubbles which are anathema to one of the most important features of glass: optical transparency. Here, we present an in-depth study of the reasons behind these bubbles, either during high-temperature quality control tests or normal glass operating conditions. We provide a physical model for bubble growth that deals with two gases, thermal effects on gas solubility and diffusivity, and a time–temperature dependent rheology. The model can be extended to n-component bubbles and various materials. By combining experiments and theory, we show that two gases are at play: air trapped in interfacial bubbles during lamination and water initially dissolved in the polymer bulk. Both gases work in tandem to induce bubble growth in finished assemblies of LSG provided that: (i) the original bubble nucleus is large enough and (ii) the polymer relaxes (softens) sufficiently enough, especially at elevated temperatures. The latter constraints are relaxed in a condition we termed anomalous air oversaturation that may even trigger a catastrophic, yet beautiful instability reminiscent of snowflakes or window frost.
1 Introduction
Laminated safety glass (LSG) was invented by French chemist and artist, Edouard Benedictus (1878–1930) in what can only be described as a serendipitous discovery. As the lore suggests, in 1903 Benedictus knocked over a glass flask while on a ladder and much to his surprise, the flask did not break into smithereens after hitting the ground. Upon inspecting what surely was a curious occurrence at the time, he realized that a thin cellulose film held the glass together in place.1–3 Six years later, Benedictus would patent triplex glass: two layers of glass bonded by a celluloid interlayer inspired by the broken flask of years prior. In his 1909 patent (FR405881), Benedictus identified the main advantages of his invention: superior impact resistance in comparison to monolithic glass, and when broken, the glass remains bonded to the interlayer. Despite its humble and lucky beginnings, laminated safety glass, now bonded by polyvinyl butyral (PVB), is currently a staple of modern life, from the world famous pyramid in the Louvre museum to Airbus's cockpit glass, passing by buildings, cars, bridges, balconies, and balustrades.It is not surprising then, that safety glass is the subject of active scientific research in terms of blast, bonding, delamination, and breakage performance,4–9 and that the PVB polymer has been extensively studied in terms of chemical composition, transport properties, deformation mechanisms, and mechanical response to name a few.10–17 Yet, a pressing issue remains largely scientifically unexplored, one the industry recognizes and actively tests against: bubbles. The latter may appear after manufacturing, during quality control tests, or simply over the glass lifetime.
Bubbles can defeat the very purpose of glass which is optical transparency. To this end, Fig. 1 presents cases of safety glass failure by bubbling. The presence of such bubbles leads to entire production batches being scrapped during manufacturing, or worse, recalled from a customer site—a situation that leads to eventual losses, monetary or otherwise, for both suppliers and consumers. This situation comes with environmental implications because safety glass is difficult to recycle, both technically and economically.
The likelihood of bubble formation is tested destructively using a so-called bake test (EN ISO 12543-4) wherein a piece of finished glass is placed inside an oven at 100 °C for 16 hours to induce bubble formation. Presumably, the test indicates whether air—the presupposed culprit behind bubbles—is present in large quantities in the glass assembly.
Yet, the nucleation and growth of bubbles in safety glass remains to a great extent unexplained despite the inherent multi-physics of the problem and the many interesting questions that surround them: how are bubbles nucleated? Is air the real (or only) culprit? What role do the flow properties of the viscoelastic PVB polymer play? Is the bake test an accurate quality control test? Can it be modified or improved? In this paper, we answer many of these questions by combining experiments with theory. In Section 2, we provide a detailed scientific account of the lamination process using our purposefully made laboratory scale protocol. In doing so, we derive observations not readily accessible at the industrial scale in terms of glass optical appearance, mass transfer, adhesion, and polymer rheology. Section 3 is an exemplary toy experiment—first of its kind to the best of our knowledge in the available literature—into the bubbling behaviour of a glass assembly during lamination. In Section 4, we present a physical model for the growth of bubbles in safety glass. The model, while being motivated by the problem at hand, is general enough in its treatment of mass transport, thermal effects, and rheological phenomena and can easily account for n-component bubbles, isothermal/non isothermal conditions, and even different mediums beyond PVB. In the remaining sections, to wit, Sections 5–8 we deal with the subjects of bubble nucleation as well as the role of gases dissolved in the PVB bulk for bubble formation.
2 Scientifically dissecting glass lamination
Laminated safety glass is constituted by two layers of float glass that are bonded together using polyvinyl butyral (PVB), a random chain, amorphous polymer of vinyl acetate, vinyl alcohol, and vinyl butyral that is commonly plasticized with triethylene glycol di(2-ethylhexanoate) to lower the glass transition temperature.18,19 PVB comes in different presentations. For example, Eastman produces rubbery RB41 for building facades, glassy DG41 for balustrades, and tri-layered QS41 for acoustic insulation. Other variations include RB11, an identical blend of RB41 except at half thickness (0.76 mm versus 0.38 mm). In all cases, the PVB polymers come with a given roughness that renders them opaque. The presence of vinyl alcohol groups in the polymer, which can interact with water via hydrogen bonding, renders them highly hygroscopic meaning they readily absorb water from the surrounding atmosphere and must therefore be kept under controlled humidity conditions.11,20–22We have measured the rheological properties of RB41, DG41, and QS41 using shear rheometry and found the blends to be viscoelastic in nature, i.e., they exhibit elastic and viscous responses that are well captured by a Maxwell (shear) relaxation modulus that is time–temperature dependent. In Fig. S1A–C in the SI, we present the time–temperature state diagram for these polymers. In general, they may behave as glassy (low temperature/short timescales), rubbery (mid temperature/medium timescales), and as viscous melts (high temperatures/long timescales). To put the time/temperature scales into perspective, at 25 °C RB41 is rubber-like and would require 109 s (∼32 years) to reach the melt state. In contrast, at the temperature of lamination (e.g., 140 °C), this time is only in the order of minutes!
The lamination process involves three main steps (Fig. 2A–C): stacking, calendering, and autoclaving. There is also the aforementioned quality control step, i.e., the bake test. Each step is scientifically rich enough to warrant its own investigation. To be expeditious, we do not discuss the peculiarities of the industrial process itself (to this end, see Belis et al.23 for an introductory discussion) but rather our own faithful laboratory scale replication. The latter allows us to draw scientific insights not accessible at the industrial scale. In particular, we circle the discussion around the many transformations the polymer/glass assembly undergoes in terms of optical appearance, mass transfer, adhesion, and polymer rheological states—all of which are related to bubble formation.
2.1 Stacking
A PVB sheet of RB41 (roughness of ∼40 µm) is stored under humidity-regulated air inside a climatic chamber to fix the amount of water dissolved in the bulk in a process known as conditioning. The sorption process is self-similar with temperature and thereby simplifies the number of parameters which must be controlled to a single one: the chemical activity a of water vapour in air.11 The standard conditions are a = 0.25 which results in RB41 having ∼0.4% wt of water dissolved in the bulk. Then, a PVB sandwich of glass/PVB/glass is stacked in a clean room. Atmospheric air becomes trapped in the polymer roughness at both polymer/glass interfaces and the sandwich is thus opaque or hazy (Fig. 2D). There is no appreciable adhesion between the glass and the polymer (in the figure, the sample is held in place using tape) and gases can freely flow either in or out of the sandwich via the exposed polymer edges (Fig. 2G). In this regard, the polymer roughness forms a percolating network with the outside environment. The polymer can be considered as very much rubber-like throughout this step. Finally, the stacking step hints at two gases as the possible culprits behind bubble formation: water dissolved in the PVB bulk and air trapped by the polymer surface roughness.2.2 Calendering
The PVB sandwich is slightly heated in a convection oven (e.g., 90 °C for 15 min) and bonded together using a nip-roll press (Linea DH-360, 1.4 m min−1) forming what is called a pre-press. The PVB sandwich turns translucent as air is partially removed. At the same time, adhesion develops, and the glass/polymer cannot be set apart. The edges of the sample become somewhat transparent because of perfect adhesion between the polymer and the glass (Fig. 2E). The assembly is thus sealed and gases may either only enter or leave through the polymer bulk in a process that is bound by mass diffusion (Fig. 2H). The percolating network formed by the random polymer roughness is no longer present and gases are trapped in interfacial bubbles or gas pockets of irregular shape (hereafter, we shall refer to such bubbles as non-spherical bubbles for clarity). Despite the increase in temperature, the polymer remains rubber-like during the calendering step. From this step onwards, the non-spherical bubbles (or any other kind of bubble) form a closed thermodynamic system with the bulk of the PVB polymer, insofar as they are sufficiently away from the edges of the glass sample.2.3 Autoclaving
The pre-press is heated (e.g. 140 °C) while simultaneously being subjected to a hydrostatic load (e.g., 10–14 bar) (Fig. 2C). Gaseous exchanges take place between the non-spherical bubbles and the polymer bulk (see Section 4). A typical autoclave cycle involves a complex schedule of heating and cooling ramps connected by an isothermal segment, hereafter called the hold temperature. The pressure schedule is similarly intricate and may either lag, be in phase, or ahead of the temperature schedule. Post autoclaving, the pre-press is rendered transparent (Fig. 2F) thus yielding a finished sample of laminated safety glass, adhesion is maximized, while the edges remain sealed (Fig. 2I). The polymer, however, experiences a rubbery-to-viscous transition and back. Post autoclaving, the amount of water dissolved in the PVB bulk does not appreciably vary compared to the initial stacking step (see Fig. S3 in the SI). However, extra air is dissolved in the bulk from the non-spherical bubbles (see Section 6).2.4 Bake test
A sample of LSG is heated for 16 hours at 100 °C inside a pre-heated convection oven (Memmert) and is afterwards visually inspected for bubble formation (Fig. 2J). Two types of bubbles are considered (Fig. 2K):• Edge bubbles are found within 15 mm from the edges. These bubbles are associated with mass diffusion and are thus neglected in the test. We can estimate the lengthscale in question as  , where D ∼ 1–10 × 10−10 m2 s−1 is the representative diffusion coefficient and t is the test time.
, where D ∼ 1–10 × 10−10 m2 s−1 is the representative diffusion coefficient and t is the test time.
• Full face bubbles are located deeper than 15 mm inside the glass samples and constitute failure regardless of size and number.
3 Toy experiments
We developed a set of transparent autoclaves that allowed us to visualize and track bubbles in whatever type of glass sample we desired (see Fig. S4 in the SI). The autoclaves are flexible enough to accommodate arbitrary schedules of temperature and pressure. In Fig. 3A, we present a simple, yet powerful toy experiment that elegantly showcases the various physical ingredients behind bubble growth in glass assemblies with PVB. In said figure, a pre-press was subjected to an isobaric heating ramp and the non-spherical bubbles were tracked via the interfacial bubble ratio A/A0 (normalized surface area of non-spherical bubbles in the target area of the sample). Two PVB conditioning levels were probed: standard moist (a = 0.25) and dry PVB (reduced moisture content, a = 0.05). | ||
| Fig. 3 (A) Example of bubble dynamics in a pre-press (RB41) during a toy autoclave schedule which included a heating ramp without overpressure. Circles represent the interfacial bubble ratio A/A0 (bubble area/initial bubble area) inside the target area in the sample. Two PVB humidity conditioning levels were tested, standard (a = 0.25, blue circles) and reduced humidity (a = 0.05, red circles). Green diamonds represent the PVB relaxation modulus using eqn (21) for RB41 at standard humidity conditions only. The inset is the temperature schedule (color-matched to the main figure). See Fig. S4 in the SI for the experimental set-up details. (B) Sketch of gaseous exchanges that take place in a pre-press when heated: water (blue) escapes from the bulk towards the non-spherical bubbles seeking to inflate them, while air (red) does the opposite. Each gas has a distinct heat of solution ΔHs sign which leads them to follow distinct thermodynamic paths with temperature, solubility (H) wise, in the PVB polymer. For completeness, the sketch also depicts the gaseous exchanges that take place between the PVB polymer and the surrounding atmosphere via the exposed edges of the polymer. Air enters while water leaves. | ||
In the pre-press with moist PVB (blue curve), the non-spherical bubbles initially remain stable during the early stages of heating (A/A0 ∼ 1) up to 80–90 °C when explosive growth ensued (A/A0 > 1). We thus rapidly conclude that the natural tendency of a glass assembly at elevated temperatures with standard PVB is to bubble! New bubbles never nucleate, and coalescence is likewise not observed.
The growth of the non-spherical bubbles during the heating ramp betrays the volatile essence of water in PVB. This gas has a negative heat of solution in the polymer (ΔHs,w < 0) and therefore, has a solubility which diminishes when the temperature is increased.11 Accordingly, water tends to escape from the PVB bulk and form bubbles (the reverse evidently holds under a cooling ramp). The more water is initially dissolved in the bulk, the larger the bubbles (not shown).
Repeating the toy experiment with the pre-press using dry PVB (red curve), on the contrary, leads to no bubbling at all. In this case, bubbles shrink rather than grow during the heating ramp as air—the predominant gas in the non-spherical bubble (see Section 4)—becomes more soluble in PVB with temperature (ΔHs,a > 0).24 In other words, air flows from the non-spherical bubbles towards the polymer bulk when the latter is heated.
Therefore, thermodynamically speaking and as sketched in Fig. 3B, water promotes non-spherical bubble growth, while air favors bubble shrinkage in pre-press assemblies during a heating ramp. In other words, the gases compete for the fate of these bubbles. Notice, however, that below a seemingly critical temperature, the competition is rendered moot as the bubbles are stable (A/A0 = cte). As we will show in the next section, this stability is linked to the viscoelastic nature of the polymer—in particular its dramatic relaxation with temperature (see the green curve in Fig. 3B). Only when the PVB polymer softens sufficiently enough can bubbles grow or shrink.
So far, our results indicate a strong link between water and bubble formation in glass assemblies with PVB, especially in a pre-press during autoclaving at elevated temperatures. Thus, is water directly responsible for bubbles in finished samples of LSG? If so, this begs the question, what is the role played by air? We answer these questions in the remaining sections of the paper.
4 Physical description
Below, we propose a physical model for the growth of bubbles in finished assemblies of laminated safety glass with PVB, but which is general enough to cover other time–temperature dependent soft matter materials. The model determines the bubble radius R from a system of coupled linear differential equations that simultaneously address mass transport of multiple gases, thermal effects, and rheological phenomena. We make some simplifying assumptions:(i) There is a pre-existent gas nucleus of radius R0 of a micrometric size (see Section 6).
(ii) Confinement effects are negligible, at least at first order. For simplicity, we assume spherical symmetry throughout.
(iii) The medium is taken as infinite, thus, there is ample gas supply.
(iv) Bubbles are well-separated from one another so that bubble-to-bubble effects are ignored.
(v) The temperature field is homogeneous in time and space.
(vi) For mass transport specifically: (a) There are only two gaseous species of relevance, water and air, each one behaving as ideal gases. Air, being a mixture of several gases, is approximated as nitrogen for simplicity;† (b) Each species has a dissolved concentration profile in the PVB bulk that obeys the diffusion equation separately; (c) The time dynamics are quasi-static; (d) Transport constants, in particular the activation energy for diffusion Ed and the heat of solution ΔHs, are constant with temperature and pressure.
(vii) The deformation (and its rate) is small, i.e., the PVB polymer stays in the range of linear viscoelasticity.
4.1 Mass transport
Broadly, we solved the diffusion equation to obtain the concentration of dissolved gas in the polymer and thence determined the flux of gas at the bubble interface using Fick's law. Expressions for the bubble composition were then obtained from the mol fraction and Dalton's law of partial pressures.The diffusion equation reads
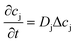 | (1) |
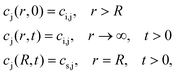 | (2) |
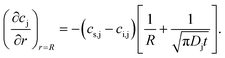 | (3) |
The above is simplified by noting that the rightmost term vanishes with time whenever 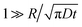 , which is our case. We thus have
, which is our case. We thus have
 | (4) |
| Jj,r=R = −Dj∇cj,r=R. | (5) |
Merging eqn (4) and (5), defining flow into the bubble as positive, and multiplying the result by the bubble's surface area yields
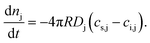 | (6) |
Eqn (6) predicts mass exchanges (or lack thereof) between the hosting medium and the bubble because of oversaturation (cs,j − ci,j < 0), saturation (cs,j − ci,j = 0), and undersaturation (cs,j − ci,j > 0). These conditions are likewise quantified via the oversaturation driver fj = ci,j/cs,j. Accordingly, we have fj > 1 (gas flow into the bubble), fj = 1 (no mass flow) and fj < 1 (flow away from the bubble).
We now write explicit expressions for air and water (vi.a)
 | (7) |
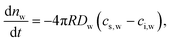 | (8) |
 | (9) |
The bubble composition is obtained from the mol fraction of the gases xj = nj/nB, such that,  . Therefore,
. Therefore,
 | (10) |
 | (11) |
Since we take the gases as ideal (vi.a), Dalton's law links simultaneously the partial pressure of the gases, the mol fractions and the bubble pressure pj = xjPB. Accordingly, for each gas we have
 | (12) |
 | (13) |
Eqn (7)–(13) are general in nature and can be used to solve the mass transport problem for any two-component bubble system. They can also be expanded to n-component bubbles by slightly modifying eqn (11) to resemble eqn (10) for n gases.
4.2 Thermal effects
Changes in temperature modify transport constants as well as material properties in important and non-trivial ways.We suppose diffusivity and solubility are temperature activated processes that follow an Arrhenius behaviour with temperature. In compact form, both transport mechanisms can be expressed as
 | (14) |
The initial gas concentration in the PVB bulk (during conditioning) is set by the partial pressures of water and air in the surrounding atmosphere. As a result,
| ci,w = Hw(Ti)pi,w | (15) |
| ci,a = Ha(Ti)pi,a | (16) |
| pi,w = aPSat(Ti) | (17) |
| pi,a = P0 − aPSat(Ti). | (18) |
The above conditions set the initial composition of the bubbles in the pre-press since chemical equilibrium mandates fj = 1 for the gases inside these bubbles and those in the polymer bulk. We accordingly have xi,a ∼ pi,a/P0 ∼ 0.99 and xi,w ∼ pi,w/P0 ∼ 0.01. During autoclaving, the equilibrium is shifted so that fj ≠ 1 and hence, mass exchanges take place between the non-spherical bubbles in the pre-press and the polymer bulk. For a finished assembly of glass, which is our goal, the initial conditions are slightly shifted (see Section 6). Moreover, for most structural glass applications, chemical equilibrium is broken solely by temperature since pressure can be assumed as constant.
4.3 Rheology
The presence of rheological effects adds an extra stress at the bubble interface and thus affects the overall bubble pressure. Generally speaking, under spherical symmetry and in the limit of small deformation (vii), PB is27,28| PB = P0 − τrr|r=R | (19) |
For PVB, the extra stress is related to the macroscopic strain γrvia the shear relaxation modulus G,
| τrr = 2G(t, T)γr | (20) |
 | (21) |
 | (22) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 (see Table S1 in the SI for the complete set of constants and Fig. S2 for a comparison of the model to experimental data).
16 (see Table S1 in the SI for the complete set of constants and Fig. S2 for a comparison of the model to experimental data).
Finally, the macroscopic strain γr, at an arbitrary radial location r, is obtained from mass continuity by integrating the rate of deformation imposed by a growing bubble in an infinite medium29,30
 | (23) |
Combining eqn (19), (20) and (23) yields,
 | (24) |
 | (25) |
4.4 Bubble radius
The radius differential dR/dt is obtained from the ideal gas law, which for general purposes we write in the differential form | (26) |
The temperature field is typically imposed, ergo the temperature (and its possible variation) in the vicinity of the bubble is a known quantity (v). Combining eqn (25), (26) leads to
 | (27) |
Eqn (27) is very general in its nature. It can be used to model bubble growth (or shrinkage) under isothermal or non-isothermal conditions, can account for multiple gases via the mass transport problem, and can even be used to simulate classical Neo–Hookean solids (under small deformation) if G(t, T) is set as a constant. For a medium with a different rheology, it suffices to determine τrrvia a constitutive equation and replace eqn (27) by eqn (26).
Likewise, eqn (27) already explains, at least qualitatively, some of the bubble observations made in Section 3. At low temperatures, the polymer elasticity is quite high (G ∼ 107 Pa). It must then be the case that under these circumstances, the G(t, T) term in the numerator dominates the dynamics, which results in bubbles being stabilized dR/dt ∼ 0 even under a non-isothermal temperature field. As time progresses and/or the temperature is increased, this term continuously loses strength until it is overcome by the combined effect of thermal dilation dT/dt (which inherently tends to swell the bubble) and mass transport dnB/dt. An upper bound for this condition is P0 ≫ 4/3G, i.e., when the polymer rheology effectively vanishes and no longer affects the bubble pressure. The actual threshold may be lower than this depending on the magnitude of the driver and the temperature.
All things equal, the mass transfer term favors bubble growth, stability, or shrinkage depending on whether the gas is under oversaturation, saturation, or undersaturation conditions. When dealing with multiple gases, the situation is intricate as gases may cooperate or compete against one another for the fate of the bubble. This is indeed the case for non-spherical bubbles in the pre-press. Air favors bubble shrinkage while water promotes bubble growth (Fig. 3B) because these gases have different heat of solution signs in PVB. In a finished sample of LSG, the situation is different, and the gases cooperate to induce bubble growth (see Section 6). Finally, we remark that under isothermal conditions (dT/dt = 0) or after a temperature jump, the absolute value of T plays a role by directly influencing how fast and how large bubbles may become. As we discuss later in the paper, the situation is a bit more involved as there is also a size effect at play.
5 Nucleation
Using our transparent autoclave, we investigated different lamination parameters deemed a priori conducive to bake test failure, such as PVB type and moisture conditioning level as well as autoclave temperature and pressure conditions. The common denominator for bake test failure was often the presence of undissolved gaseous inclusions that served as nucleation sites in the glass assembly. These sites are invisible to the human eye but were relatively large enough to cause a distinction in the images taken by our autoclave set-up (resolution ∼10 µm). For samples that failed the bake test, the autoclave images often appeared grainy or dusty because they were populated by pixel-sized dark dots (Fig. S5A in the SI). The latter can easily pass off as dust-like contamination. After bake testing and in numerous occasions, bubbles grew in many of these pixel-sized dots (see Fig. S5B in the SI).We thus proceed to carefully scan our samples before and after bake testing under the microscope. In many of the aforementioned pixel-sized dots, we often found gas nuclei of different sizes and morphologies. They were always at one of the glass/polymer interfaces but never in the PVB bulk, i.e., nucleation was entirely of the heterogeneous kind. In Fig. 5, we present a small subset of the type of naturally occurring nuclei we observed (row i, Cols. A–F) accompanied by the resulting bubbles that grew after bake testing (row ii, idem. Cols.). Fig. 5A shows a rare nuclei variety, a seemingly spherical nuclei that led to a binary bubble system post bake testing. Fig. 5B illustrates a gas inclusion inside what is apparently a fiber in a situation reminiscent of Champagne (see Liger-Belair et al.31 for a review on the subject), while Fig. 5C is a glass inclusion around a fiber. In Fig. 5D, undissolved non-spherical bubbles grow into large bubbles post bake testing. The bubbles apparently grew with a pinned contact line. See how the original contour of the nuclei is very much noticeable in the final bubble. Fig. 5E is apparently a region of wrinkled or folded PVB matter that trapped gases. Finally, Fig. 5F is an artificially made inclusion. A crenel was etched on the glass surface (towards the center of the image) using a UV laser. During autoclaving, the crenel was partially filled by PVB leaving behind undissolved gases whence a bubble grew during bake testing. The final size of the bubbles was proportional to the original volume of gas in the crenel (not shown).
We close this section by briefly discussing the role played by interlayer rheology. To this end, Fig. 6A–C compare the bubbling behavior of RB41, QS41, and DG41 post bake testing, respectively. While the commonality for failure was again the presence of undissolved gas nuclei, DG41—the stiffer version of the three PVB interlayers—seemed more resilient to test failure as it yielded comparatively smaller bubbles. This is probably a reflection of the high stiffness of this interlayer. On the other hand, RB41 and QS41 behaved roughly the same as demonstrated by their comparatively similar number of bubbles and their size.
 | ||
| Fig. 6 Bake testing results for different PVB interlayers. (A) RB41 (standard). (B) QS41 (acoustic). (C) DG41 (stiff). | ||
6 Describing the bake test
We used the physical description presented in Section 4 to simulate the growth of bubbles during bake testing of finished assemblies of LSG. Specifically, we simultaneously solved the equations for the bubble radius (eqn (27)), mass transport (eqn (7)–(13)), and bubble pressure (eqn (25)). The temperature field was assumed homogeneous throughout and in the form of a step jump from Ti = 20 °C to TBT = 100 °C. Solubility and diffusivity were computed viaeqn (14), and the polymer relaxation viaeqn (21) and (22). In total, our description requires more than 30 different physical constants that were determined by direct experimentation. See the SI for the constant values.Computationally, a constant step size of Δt = 0.1 s was used and the total simulation time was equal to 16 hours. The variables were initialized and the system of equations was solved in a loop using the odeint package in python. To simulate the bake test, two crucial assumptions were made:
6.1 Oversaturation
Post lamination, the amount of water in the PVB bulk remains unchanged (see Fig. S3 in the SI), but extra air is dissolved therein. To determine air oversaturation, we assume next ideal calendering, i.e., air is displaced but not absorbed in the PVB bulk. The edges of the glass assembly are likewise perfectly sealed so the high-pressure air applied during autoclaving cannot oversaturate the PVB bulk (except at the edges which we disregard). Under this framework, the total amount of air , from the pre-press to the finished assembly, remains constant and is equal to
, from the pre-press to the finished assembly, remains constant and is equal to | (28) |
Eqn (28) can be re-written as
 | (29) |
 is an effective solubility constant that takes into account the total number of air moles in the system.
is an effective solubility constant that takes into account the total number of air moles in the system.
6.2 Nucleus composition
There is a nucleus of size R0 of micrometric size, in mechanical equilibrium with the surroundings at atmospheric conditions so that at t = 0, PB = P0 in agreement with eqn (24), and is also in chemical equilibrium with the gases dissolved in the PVB bulk. Therefore, the gaseous composition of this nucleus is the same as the non-spherical bubbles in a pre-press (eqn (17) and (18)), i.e., the initial partial pressure of our bubbles/nuclei remains unchanged after lamination.With these assumptions, the driver for air in our experiments is fa ∼ 1.68–1.85 at room condition. We therefore reach a peculiar conclusion for finished assemblies of LSG: the gas nuclei contained therein are in a metastable state, as air wants to come out of solution from the PVB bulk and hence, grow a bubble. It is only the (high) stiffness of the interlayer which prevents air from doing so under room conditions as already discussed in connection with eqn (27). Note, however, how temperature is a key factor for bubble growth because it simultaneously: (i) accelerates the polymer relaxation, thus progressively easing the constraints which prevent the nuclei from growing in the first place and (ii) shifts the chemical equilibrium of water vapor, which has bubble-forming tendencies to begin with in PVB.
7 When water is partly to blame
We prepared samples of RB41 at standard humidity conditions (a = 0.25) and with a low quantity of initial interfacial bubbles (A/A0 ∼ 0.4). Under these conditions, the instantaneous oversaturation driver for water at 100 °C is roughly fw ∼ 40, meaning that, like its air counterpart, water-driven bubbles are thermodynamically favorable during the bake test. Nevertheless, visible bubbles should only form provided that the original gaseous inclusion or nuclei are sufficiently large, i.e., there is a size effect, which we discuss next.Kloek et al.28 have shown that bulk elasticity can arrest bubble dissolution, with the final bubble size Rf being a function of the initial bubble radius R0. In particular, larger bubbles shrink less compared to smaller ones. Furthermore, provided the elastic shear modulus is sufficiently high, the bubble may remain stable at R0 regardless of initial size, i.e., there is a complex interplay between rheology and R0 which ultimately dictates the final radius of the bubble. Our case is somewhat the reverse: larger values of R0 lead to an equally greater bubble size Rf after bake testing. Our point of departure, however, is not whether bubbles reach a final equilibrium but whether they become observable at all post bake testing. Rheology aside, the final bubble size is also inherently affected by the bubble surface area 4πR2 which governs the mass transfer problem. Evidently, larger bubbles have an equally greater surface area through which gas can diffuse.
We have estimated the critical size that leads to an observable bubble post bake testing by performing a numerical sweep for nuclei sizes ranging between R0 = 10–100 µm. For reference, the resolution of the human eye is around 100 µm (the thickness of a hair strand). We took an arbitrary bubble size of half a millimeter as the threshold for a visible bubble, and thus, bake test failure.
Fig. 7A shows the results of the bake test simulation. Very small nuclei, below 30 µm in size, cannot significantly expand during the bake test and stay below the lower limit of resolution of the human eye. A sample of LSG populated with such nuclei will thus surely always pass the test. Nuclei of intermediate sizes, of around 40–60 µm, can reach sizes between 0.3–0.5 mm and will therefore, depending on the observer, result in possible test failure. Large nuclei (>70 µm), however, grow to sizes between 0.5–0.7 mm and will most definitely result in test failure regardless of the observer.
As qualitative confirmation of the aforementioned results, Fig. 7B presents a picture of one of our many bubbling samples of LSG post bake testing. The final size of the bubbles that grew therein agree with the order of magnitude of the simulation, i.e., ∼1 mm.
To better gauge the efficacy of our model, Fig. 7C compares the predicted final bubble size Rf—as a function of the initial gaseous inclusion size R0—against their experimental counterparts. For the latter, we selected gaseous inclusions having a morphology similar to those portrayed in Fig. 5D, i.e., partially dissolved non-spherical bubbles (Fig. 7D [top row]). We additionally included measurements from artificial inclusions trapped in cylindrical crenels that were etched on the glass surface (Fig. 7D [bottom row]). When determining R0, Rf, two approximations were made.
7.1 2-D approximation
The observed projection of the non-spherical inclusion/bubbles was approximated as an ellipse. We manually determined the semi-major axes a0,f, b0,f, wherein a0,f > b0,f, and the indices 0, f denote, as before, conditions before and after bake testing, respectively. The value of R0,f corresponds to a circle of equivalent area of the measured ellipse in 2-D. We thus have (blue circles in Fig. 7C). The same approximation was used for the artificial inclusions (blue squares in Fig. 7C).
(blue circles in Fig. 7C). The same approximation was used for the artificial inclusions (blue squares in Fig. 7C).
7.2 3-D approximation
We approximate the gaseous inclusions/bubbles as ellipsoid caps with a corresponding additional semi-major axis c0,f. R0,f is then the radius of a spherical bubble in 3-D space of equivalent volume as that of the ellipsoid cap. We thus have . Meanwhile, c0,f was estimated as follows. Post bake testing, the gaseous inclusions/bubbles evolve from being highly ellipsoidal with a0/b0 ≈ 3.1 to becoming circular like since af/bf ≈ 1.3. Because both af,bf ≪ h (PVB half thickness, 380 µm), we can rightly assume that the resulting 2-D symmetry between the semi-major axes af, bf extends to cf as well. Conservatively, we thusly take cf ≈ bf when computing Rf. Prior to bake testing, we find that a0 ≈ 35 µm is in the same order of magnitude as e (PVB roughness, ∼40 µm), whereas b0 is roughly one third of this value. Heuristically, we assumed symmetry with either semi-major axis to provide bounds for R0. The upper bound of the ellipsoid volume—and evidently R0—is set by c0 ≈ a0 (grey circles in Fig. 7C). This bound tacitly implies the polymer roughness was relatively unaffected during autoclaving for the gaseous inclusion in question. Meanwhile, a lower bound for R0 is given by c0 ≈ b0 (red circles in Fig. 7C).
. Meanwhile, c0,f was estimated as follows. Post bake testing, the gaseous inclusions/bubbles evolve from being highly ellipsoidal with a0/b0 ≈ 3.1 to becoming circular like since af/bf ≈ 1.3. Because both af,bf ≪ h (PVB half thickness, 380 µm), we can rightly assume that the resulting 2-D symmetry between the semi-major axes af, bf extends to cf as well. Conservatively, we thusly take cf ≈ bf when computing Rf. Prior to bake testing, we find that a0 ≈ 35 µm is in the same order of magnitude as e (PVB roughness, ∼40 µm), whereas b0 is roughly one third of this value. Heuristically, we assumed symmetry with either semi-major axis to provide bounds for R0. The upper bound of the ellipsoid volume—and evidently R0—is set by c0 ≈ a0 (grey circles in Fig. 7C). This bound tacitly implies the polymer roughness was relatively unaffected during autoclaving for the gaseous inclusion in question. Meanwhile, a lower bound for R0 is given by c0 ≈ b0 (red circles in Fig. 7C).
Overall, as shown in Fig. 7C, the above described approximations for R0, Rf cluster around similar values but most importantly, align closely with the trend set by the bubble model (orange circles in Fig. 7C). In particular, this holds in the region where we expect our model to be most quantitatively valid. This is represented as the shaded region in the figure, which is bounded by a nuclei of size R0 ≈ 42 µm for which the final bubble size is predicted to match the PVB thickness, namely, Rf = h. Beyond this region, we expect confinement effects to play a major role on bubble kinetics, and thus, on the final bubble size. Indeed, for larger nuclei and as demonstrated by the artificial inclusions (blue squares in Fig. 7C), the model overshoots the experimental data. The overall experimental trend, nevertheless, matches the simulated one.
Therefore, we reach a first conclusion regarding bake test failure: even if invisible to the human eye, the presence of large nuclei post lamination in a sample of LSG can result in (partly) water-driven bubble growth (the bubbles in the simulation can reach xw ∼ 0.18). This holds for excellent de-airing and regardless of whether the PVB polymer is meticulously prepared at standard humidity conditions. To reiterate, failure in this first case is driven by a combination of heterogeneous nucleation, critical nuclei size, and water working in tandem with air to form visible bubbles.
8 When air is the main culprit
During lamination, the amount of air dissolved in the PVB bulk can exceed that which is originally present in the interfacial bubbles from the pre-press. We refer to this condition as anomalous air oversaturation. The reasons are manifold and beyond the scope of the present work, but the condition is extremely detrimental—bubble wise—in LSG.We induced anomalous air oversaturation in glass sandwiches (30 × 50 cm) of RB11 (thickness 0.38 mm, a = 0.25) where we prematurely sealed three edges of the sample by heat and pressure. By subsequent calendering along the longest edge (50 cm), we trapped high quantities of excess air in a region equal to 1/5 of the total length. Such samples were autoclaved and the trap region subdivided into three 10 × 10 cm samples for bake testing. The driver in this case is fa ∼ 10 at room conditions.
When performing the same numerical sweep in terms of initial bubble size as in the previous section, we found that bubbles grow irrespective of initial size during the bake test (not shown). The bubbles are also comprised mostly by air (xa ∼ 0.92). For clarity, in Fig. 8A we present only the curve for the smallest nucleus R0 = 10 µm (red line). Compared to the (worse) water-driven case at R0 = 100 µm, bubbles growing under anomalous air conditions can reach large sizes in a short period of time. In the example at hand, the difference in size is a factor of five, and the timescale is in the order of minutes compared to hours. This suggests that bubble size (and onset of visibility) is a proxy indicator for the gas responsible behind bubble growth. Finally, notice that the predicted bubble size for anomalous air oversaturation is much larger than the PVB thickness R/h ∼ 18! At these sizes, our physical description is quantitatively questionable since the assumption of spherical symmetry is violated. Indeed as shown in Fig. 8B, bubbles do not maintain sphericity but rather a beautiful instability, similar to window frost or snowflakes, is triggered instead. Nonetheless, the general truths obtained from the model are unchanged: in anomalous air oversaturation conditions, bubbles can reach large sizes in a short amount of time during bake testing at 100 °C.
Because anomalous air oversaturation can be so catastrophic for LSG, we investigated in Fig. 8A the effect of different temperature levels on bubble growth, seeing that the nucleus size was of less importance. We tested the already discussed temperature of 100 °C, down to 80, 60, 40, and 25 °C all with a timescale of 16 hours. Under room conditions, the nucleus is stable and there is no indication from the figure that significant bubble growth may occur (black line). In this case, the high stiffness of the polymer (Fig. 8C) forcibly stabilizes the nucleus and prevents it from growing as expected from eqn (27). However, the moment the temperature is increased, to say 40 °C (blue line), bubbles can reach a visible size (0.5 mm) in as little as 16 hours. Evidently, and as predicted by eqn (27), the higher the temperature, the bigger the bubble.
Fig. 8D presents the results of a short bake test (4 hours) using our transparent autoclave where indeed, and in qualitative agreement with our model, we observed bubble growth after barely ∼42 min or T ∼ 75 °C which is much sooner than the target temperature of the test (95–100 °C). The bubble initially expands in a circular fashion, until a size of roughly R ∼ 1.9 mm (R/h ∼ 10), after which the instability kicks in. The bubble develops branching arms which is a strong indication that our model, despite being qualitatively adequate, is not quantitatively applicable in this situation. First and foremost, the high level of deformation, even before the instability appears, implies the relaxation modulus cannot be presumed as independent of the applied strain. Regrettably, relaxation data for PVB under large deformation—for elevated temperatures and long timescales—is unavailable in the existent literature; an unfortunate situation that renders our model for bubbles driven by anomalous air oversaturation in LSG as qualitative only.
8.1 On the nature of the instability
Mechanical instabilities in polymers may stem from a number of reasons. Often, they are triggered whenever the rate of deformation is faster than the polymer relaxation time,32 are influenced by the initial size of the nucleus/imperfection,33 may be impacted by the aspect ratio of the polymer sheet,34 or even the presence of neighboring bubbles.35In our case, the instability is seemingly and primarily a mix of confinement and high adhesion effects. As the gas expands, it burrows inside the polymer and triggers the instability because delamination never occurs. Saintyves et al.36 have studied this type of instability—in connection with soft matter materials—where they have indeed identified the drivers behind it: confinement, adhesion, and a critical strain level. Secondarily, the instability is influenced by a property of bubbles in safety glass which we discussed in passing in Section 3. Notice in Fig. 8E how the irregular bubble structures are densely packed, yet they never coalesce because the PVB polymer never delaminates from the glass. Each bubble, despite its inherent anisotropy, maintains a distinct shape that is strongly affected by the presence of neighboring bubbles (see Fig. 8F).
9 Discussion and concluding remarks
Our results indicate that a finished sample of laminated safety glass is in a metastable state from the point of view of bubble formation. The PVB bulk is oversaturated with air post lamination, meaning that bubbles are thermodynamically favorable to being in these assemblies, i.e., their natural tendency is indeed to bubble. It is only the stiff nature of the polymer at room conditions that prevents them from doing so. How long before (and whether) they will bubble at all depends on the nature of the polymer itself (e.g., composition, thickness), the level of air oversaturation, the temperatures faced by the glass assembly, and the presence (or lack thereof) of gaseous nuclei and their size.We discussed two cases for bubble growth during bake testing, when water is partly to blame, and when air is the main culprit. A passing juxtaposition of Fig. 7A and 8A reveals some important distinctions between the two cases. The expected bubble size is markedly different and low-temperature bubbles are more likely in one case than in the other. These bubble features may qualitatively hint at the gas most responsible for bubble formation in industrial settings. In short, large bubbles that appear rapidly, or at cold temperature, are most likely stemming from air-related problems, rather than water-related issues. The current test, in this regard, does not discriminate between these two mechanisms.
On purpose, we did not discuss a third scenario for bubble formation during bake testing: when water is the main culprit. In this situation, the PVB polymer contains a large amount of water dissolved in the bulk compared to standard conditions. The omission of this case responds to a technical reason. It is a relatively simple matter to non-destructively measure the amount of water in the PVB bulk post lamination (see Fig. S3 in the SI), and thus, appraise if water is fully to blame.
Setting aside the above discussion, we have presented a physical description for bubble growth that deals with multiple gases, thermal effects, as well as a complex time–temperature influenced rheology. The description highlights the cross-disciplinary nature of bubble phenomena and can be extended to other polymer systems as well.
Logically, our physical model is directly applicable to Maxwell-type polymers in general, such as molten PDMS or polyisoprene, which display—like PVB—time–temperature dependent vanishing shear relaxations. Viscoelastic solids are equally concerned. The latter are adeptly described via the generalized Maxwell model by the addition of a single spring constant G∞ that reflects the asymptotic, elastic behavior of the polymer. This means that the bubbling behavior of crosslinked polymers, of which ethyl vinyl acetate (EVA) is a great example, can equally be modeled under our framework. Finally, our bubble model is equally applicable to more classical polymers, such as elastomers (e.g., natural rubber) or hydrogels since the latter can be treated as viscoelastic solids with an infinite relaxation time.
Author contributions
CAM, KP, and EL conceived the research project and drafted/edited the research paper. CAM carried out the experimental campaigns, performed the necessary analysis, developed the physical model, and associated python codes. CAM/EL devised the experimental set-up. KP conceived the experimental settings for anomalous air oversaturation. CAM/KP worked jointly in the setup of the simulations.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). All other remaining data is available upon reasonable request from the corresponding author.Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00735f.
Acknowledgements
We gratefully thank Jerome Giraud for helping design and build the experimental autoclave set-up, Lionel Bureau for facilitating the equipment for bake testing, and Bruno Travers for his aid in the instrumentation of temperature sensors. We also extend our deepest gratitude to Vincent Rachet and Nicolas Nadaud for their interest and support during our study, as well as Richard Villey and Anne-Laure Vayssade for fruitful discussions around bubbles in glass.Notes and references
- M. L. F. Nascimento and E. D. Zanotto, World Pat. Inf., 2016, 47, 54–66 CrossRef.
- C. Panati, Panati's extraordinary origins of everyday things, Chartwell Books, 2016 Search PubMed.
- C. Carrot, A. Bendaoud, C. Pillon, O. Olabisi and K. Adewale, Handb. Termoplast., 2016, 2, 89–137 Search PubMed.
- P. Del Linz, Y. Wang, P. A. Hooper, H. Arora, D. Smith, L. Pascoe, D. Cormie, B. R. Blackman and J. P. Dear, Exp. Mech., 2016, 56, 1501–1517 Search PubMed.
- M. A. Samieian, D. Cormie, D. Smith, W. Wholey, B. R. Blackman, J. P. Dear and P. A. Hooper, Eng. Fract. Mech., 2019, 214, 504–519 CrossRef.
- P. Fourton, K. Piroird, M. Ciccotti and E. Barthel, Glass Struct. Eng., 2020, 5, 397–410 Search PubMed.
- X. Chen, M. Schuster and J. Schneider, Compos. Struct., 2022, 280, 114878 CrossRef CAS.
- P. Müller, C. Schuler, J. Grötzner, S. Dix and S. Hiss, Challenging Glass Conference Proceedings, 2024.
- S. Zhou, S. Cattaneo and L. Biolzi, Challenging Glass Conference Proceedings, 2024.
- E. Corroyer, M.-C. Brochier-Salon, D. Chaussy, S. Wery and M. N. Belgacem, Int. J. Polym. Anal. Charact., 2013, 18, 346–357 CrossRef CAS.
- C. Arauz-Moreno, K. Piroird and E. Lorenceau, J. Phys. Chem. B, 2023, 127, 11064–11073 CrossRef CAS PubMed.
- A. Pauli and G. Siebert, Glass Struct. Eng., 2024, 9, 59–73 CrossRef.
- E. Yang, R. Ji, J. Miao, Q. Yan, L. Li, H. Guo and K. Cui, Macromolecules, 2024, 57, 8123–8133 CAS.
- M. López-Aenlle, A. Noriega and F. Pelayo, Composites, Part B, 2019, 169, 9–18 Search PubMed.
- X. Centelles, F. Pelayo, M. J. Lamela-Rey, A. I. Fernández, R. Salgado-Pizarro, J. R. Castro and L. F. Cabeza, Constr. Build. Mater., 2021, 279, 122503 CrossRef CAS.
- C. Arauz Moreno, K. Piroird and E. Lorenceau, Rheol. Acta, 2022, 61, 539–547 CrossRef CAS.
- W. Stevels and P. D'Haene, Challenging Glass Conference Proceedings, 2020.
- P. Elziere, P. Fourton, Q. Demassieux, A. Chenneviere, C. Dalle-Ferrier, C. Creton, M. Ciccotti and E. Barthel, Macromolecules, 2019, 52, 7821–7830 CrossRef CAS.
- W. Stevels, Challenging Glass Conference Proceedings, 2024.
- X. Chen, B. Lin, M. Schuster, S. Chen, B.-X. Xu and J. Schneider, Compos. Struct., 2023, 322, 117381 Search PubMed.
- M. Botz, K. Wilhelm and G. Siebert, Glass Struct. Eng., 2019, 4, 389–402 CrossRef.
- M. Desloir, C. Benoit, A. Bendaoud, P. Alcouffe and C. Carrot, J. Appl. Polym. Sci., 2019, 136, 47230 CrossRef.
- J. Belis, C. Louter, J. H. Nielsen and J. Schneider, Springer handbook of glass, Springer, 2019, pp. 1781–1819 Search PubMed.
- C. Arauz-Moreno, K. Piroird and E. Lorenceau, Phys. Rev. E, 2025, 112, 015424 Search PubMed.
- K. Haraya and S.-T. Hwang, J. Membr. Sci., 1992, 71, 13–27 CrossRef CAS.
- P. S. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505–1509 Search PubMed.
- M. Fyrillas, W. Kloek, T. Van Vliet and J. Mellema, Langmuir, 2000, 16, 1014–1019 CrossRef CAS.
- W. Kloek, T. van Vliet and M. Meinders, J. Colloid Interface Sci., 2001, 237, 158–166 Search PubMed.
- X. Yang and C. C. Church, J. Acoust. Soc. Am., 2005, 118, 3595–3606 CrossRef.
- I. R. Webb, S. J. Payne and C.-C. Coussios, J. Acoust. Soc. Am., 2011, 130, 3458–3466 CrossRef CAS PubMed.
- G. Liger-Belair, G. Polidori and P. Jeandet, Chem. Soc. Rev., 2008, 37, 2490–2511 RSC.
- H. Tabuteau, S. Mora, G. Porte, M. Abkarian and C. Ligoure, Phys. Rev. Lett., 2009, 102, 155501 Search PubMed.
- S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963–3968 Search PubMed.
- J. Guo and K. Ravi-Chandar, Int. J. Fract., 2023, 243, 1–29 CrossRef.
- F. Haudin, X. Noblin, Y. Bouret, M. Argentina and C. Raufaste, Phys. Rev. E, 2016, 94, 023109 Search PubMed.
- B. Saintyves, O. Dauchot and E. Bouchaud, Phys. Rev. Lett., 2013, 111, 047801 Search PubMed.
Footnote |
† Of the multiple gases that constitute atmospheric air, only nitrogen's mass transport properties (e.g., solubility constant, diffusion coefficient) have been characterized for different temperatures and pressures in the PVB polymer.24 Therefore, assumption vi.a is in principle utilitarian but ultimately tenable since air is largely a two-component mixture of N2 and O2. While the PVB polymer has been shown to absorb less nitrogen than oxygen at room conditions under equal pressure (ratio of nitrogen to oxygen equal to  ),25 nitrogen is by far the dominant gas, both in the bubbles and in dissolved form in the PVB bulk, given its prevalence in atmospheric air ),25 nitrogen is by far the dominant gas, both in the bubbles and in dissolved form in the PVB bulk, given its prevalence in atmospheric air  . . |
| This journal is © The Royal Society of Chemistry 2026 |