DOI:
10.1039/D5SM00634A
(Paper)
Soft Matter, 2026,
22, 64-83
Orientational order induced mode switching at coupled interfaces of a nematic–isotropic free bilayer
Received
22nd June 2025
, Accepted 24th October 2025
First published on 3rd November 2025
Abstract
Instabilities at the coupled deformable interfaces of a nematic–isotropic free bilayer can engender rich morphological patterns governed by an intricate interplay of nematic elasticity, surface and interfacial energetics, gravitational forces, and intermolecular forces. This work presents a theoretical investigation of the instability in a bilayer composed of a liquid crystal film resting on a water layer having a free deformable nematic–air surface and a confined nematic–isotropic interface. Utilizing a long-wave hydrodynamic model, the formulation couples the Ericksen–Leslie equations with the Navier–Stokes equations to quantify growth rates of the instability across NLC thickness and director orientations. The formulation examines the competing roles of gravitational, van der Waals, and elastic forces in governing the deformations at the bilayer interfaces. For micro-thick films, density contrast between the layers initiates classical Rayleigh–Taylor instabilities (RTIs), while in nano-thin regimes, disjoining pressure drives mode dynamics. In both scenarios, we identify a pair of primary instability modes—the confined interfacial mode (CIM) and the free surface mode (FSM)—whose relative dominance is dictated by film thickness, anchoring configuration, and the spreading coefficients at the surface or interface. Systematic variation of director orientations and three canonical surface anchoring arrangements reveals critical transitions and instability mode responses, especially under asymmetrical spreading conditions. The results uncover mode switching controlled by NLC orientation and interfacial energetics, offering fundamental insights into the spatiotemporal structuring of layered soft materials. The framework provides an elementary direction for designing reconfigurable morphologies in NLC-based bilayer systems relevant to wetting, templating, and self-patterning applications.
1. Introduction
The interfacial dynamics of unstable thin liquid films have inspired research enthusiasts for ages because of their prominence in a wide range of applications, which include paints,1,2 coatings,2,3 flotation,4 artificial skins,5 mucous linings,6 packaging,7 emulsification,8 and phase transition,9 among many others. It is now well explored that the physics behind the interfacial instability of a thick film is fundamentally different from that of an ultra-thin (<100 nm) film.10 For example, while an ultra-thin liquid film can self-organize an array of correlated holes when the van der Waals interactions overpower the stabilizing surface tension forces,10–12 a relatively thicker film can dewet a surface following the defect-induced heterogeneous nucleation pathway.12,13 In such a scenario, in the late stages of the dewetting process, the competition between the stabilizing and destabilizing components of the surface tension forces triggers Rayleigh–Plateau instability14,15 to facilitate the formation of the droplets. Although the breaking of thin films is an unwanted phenomenon for the paints or coatings, the self-organized dewetted patterns with a large-area ordering16 find important applications in modern display units,17 microreactors,18 optofluidic devices,19 photodetectors,20 photovoltaic cells,21 and soft lithography.22
Interestingly, when another immiscible layer confines a liquid film, the interface may also develop interesting morphologies under varied conditions based on the contrast of body forces – Rayleigh–Taylor instability (RTI),23,24 viscous forces – Saffman–Taylor instability (STI),25 surface tension forces – Marangoni (MI),26,27 or inertial forces – Kelvin–Helmholtz (KHI)28 instability. Importantly, such systems can largely be classified into two types: (i) a confined bilayer – a pair of immiscible fluids with a single confined interface29 and (ii) a free bilayer – a pair of films with confined and free interfaces.30,31 In particular, the dynamics of the free bilayers are far more complex owing to the presence of the twin liquid–liquid and liquid–air interfaces, which help develop fascinating flow and droplet morphologies under varied conditions.32 For example, when the films are thicker and a denser fluid is dispensed on a rarer fluid, the destabilizing gravitational field overpowers the stabilizing surface tension to manifest an RTI.24,33,34 On the other hand, when both the films are ultra-thin, a different type of RTI may be expected wherein the destabilizing van der Waals forces overpower the stabilizing surface tension forces to engender micro- or nanoscale patterns.12,30 Furthermore, the kinetic factors, such as the contrast of the viscous, elastic, or viscoelastic forces across the interface, play key roles in deciding the morphologies of the patterns decorated.31,35 Previous studies suggested that using external fields in such systems can significantly influence the length and time scales of such instabilities.36–39
The spontaneous rupture and pattern formation in thin polymer films over thick liquids have been widely studied experimentally and theoretically over the past few decades. The seminal experiments conducted by Lambooy et al.40 and Sferrazza et al.41 demonstrated dewetting and instability in thin polymer bilayers, revealing how van der Waals and capillary forces govern interfacial modulation and rupture kinetics. More recently, Das et al.42 and Bhandaru and Mukherjee43 have reported ordering transitions and regular pattern formation in polymer bilayers during dewetting, showing that the interplay of viscosity contrast, interfacial tension, and confinement leads to tunable morphologies. These studies collectively underline that when two immiscible polymeric layers are coupled, instabilities arise through competing capillary and intermolecular interactions, resulting in coupled-mode deformations. Of late, investigations have highlighted ordering dynamics in polymer bilayers and composite films.29,44 These works emphasize how hydrodynamic coupling and substrate interactions can dictate the wavelength and symmetry of dewetted patterns, offering parallels to the coupled-interface phenomena explored in the present work.
Importantly, the free surface instabilities of the isotropic viscous, elastic, or viscoelastic films are vastly different from those of the anisotropic liquid crystal (LC) films. The inherent orientational order of LCs quantified by a ‘director’ field45,46 adds an additional handle to tune the length and time scales of such instabilities. Previous studies showed that the primary focus in this regard has been on studying the phase transition of ultrathin LC films47–49 or the contact line instabilities of LC droplets.50,51 The literature indicates that the elastic rigidity of the LCs originating from their director field may help control the deformation dynamics of the interfaces in a free bilayer.45,52 In particular, if a nematic liquid crystal (NLC) film is placed on a liquid layer to form a free bilayer, the orientation of the LC molecules at the boundaries has the capacity to control the dynamics of both the NLC–air and NLC–liquid interfaces to develop interesting flow morphologies.53–55
On the theoretical front, a number of pioneering articles56,57 published previously have explored theoretically the free surface dynamics of the NLC droplets while considering an additional stress term originating from Frank's bulk elasticity. In this regard, different approaches58,59 unveil the influence of the weak to strong elastic effects of the NLC droplets or films alongside considering the effects of anchoring conditions of NLC directors at the boundaries, e.g., homeotropic, planar, and angular.45,46 In this regard, the electrohydrodynamic convection of nematic films has been studied using the Ericksen–Leslie governing equation,60–62 considering the Frank–Oseen elastic energy.63,64 The deformation of the NI interface has also been studied using uniform and non-uniform AC electric fields65 and magnetic fields66 employing long-wave linear stability analysis. Recently, general linear stability analysis (GLSA)67 involving the Ericksen–Leslie governing equations coupled with the anisotropic Maxwell stresses for a free NLC film showed that the air-to-NLC filling ratio between the electrodes, dielectric anisotropy of the film, Frank elasticity, director orientations, Leslie coefficients, and boundary conditions play pivotal roles in selecting instability modes.60,62–64
In view of this background, the instabilities of a free bilayer have been explored, which is composed of an NLC upper layer and a water layer resting on a rigid surface, as schematically shown in Fig. 1. The system is composed of a free NI surface and confined nematic–water (NW) interface, wherein the NLC molecules are capable of anchoring at both these places. For the NLC layer, the Ericksen–Leslie governing equations, coupled with Frank bulk elasticity, have been considered to capture the dynamics, while Navier–Stokes equations have been used to model the water layer. The set of equations with the appropriate boundary conditions are linearized (LWLSA) following the lubrication approximations to estimate these instabilities' time and length scales. A mathematical formulation has been developed in such a manner that the bilayer composed of micro-thick (μm thickness) and nano-thin (≤100 nm) films can be analyzed simultaneously in the asymptotic limits.
 |
| | Fig. 1 Schematic representations of (a) an NLC–water bilayer system bound by the air and (b) director orientation configurations. In the schematic (a) h1(x, t) and h2(x, t) are the local thicknesses with h20 and h10 as the mean thicknesses of NLC and water films, respectively. ρ2 and ρ1 are the densities of NLC and water films, and s stands for the substrate location, respectively. The θ is the angle that the director (n) makes with the positive z-axis direction as displayed on the right side zoomed circle in the schematic (b) and has components nx = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and nz = cos θ and nz = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The schematic (b) shows the different director orientation configuration combinations used in the present theoretical analysis, wherein θ1 and θ2 are the director angles at the NW and NI interfaces, respectively. The designated abbreviations in b(i)–(v) stand for homeotropic–planar (H–P, θ1 = 0, θ2 = π/2), homeotropic–homeotropic (H–H, θ1 = 0, θ2 = 0), planar–homeotropic (P–H, θ1 = π/2, θ2 = 0), planar–planar (P–P, θ1 = π/2, θ2 = π/2), and planar–angular (P–A, θ1 = π/2, θ2 = π/4), respectively. Here, g is the gravity acting in the negative z-direction. θ. The schematic (b) shows the different director orientation configuration combinations used in the present theoretical analysis, wherein θ1 and θ2 are the director angles at the NW and NI interfaces, respectively. The designated abbreviations in b(i)–(v) stand for homeotropic–planar (H–P, θ1 = 0, θ2 = π/2), homeotropic–homeotropic (H–H, θ1 = 0, θ2 = 0), planar–homeotropic (P–H, θ1 = π/2, θ2 = 0), planar–planar (P–P, θ1 = π/2, θ2 = π/2), and planar–angular (P–A, θ1 = π/2, θ2 = π/4), respectively. Here, g is the gravity acting in the negative z-direction. | |
For the micro-thick films, a denser NLC layer on a rarer water film is expected to stimulate RTI due to the density difference, whereas for the nano-thin films, the long-range van der Waals interactions facilitate the instabilities suppressing the classical RTI due to the density difference.68–70 In both situations, the surface and interfacial tensions at the interfaces, the NLC film's nematic elasticity, and the NLC molecules' anchoring at the surface/interfaces may impart a stabilizing influence to the systems. The results reported in this work uncover the possible length and time scales of the interfacial instabilities recently encountered in an NLC–water system.53,71 Furthermore, this work also reports the possibilities in the case of similar systems at the nanoscale.
2. Mathematical problem formulation
Fig. 1 schematically shows a bilayer comprised of water (lower, 1) and NLC (upper, 2) films resting on a solid substrate (s), depicting relative deformation at the respective interfaces. The schematic pictorially shows the typical rod-like NLC molecules oriented inside the NLC film while resting on the water layer. The NLC film with long-range orientational order directors is exposed to the bounding medium – an inviscid gas such as air. The long-range orientational order of NLC molecules is described by a director vector n = (nx, nz). The formulation utilizes a two-dimensional (2D) Cartesian coordinate system with the origin at the solid substrate interface. Here, x and z represent the coordinates parallel and perpendicular to the substrate, respectively, while the variable t denotes time. Boldface variables signify vectors and tensors. The present formulation assumes isothermal and incompressible films for both layers.
A. NLC description
The director field deformation contribution to the free energy, which, in the context of the NLC, is referred to as the Frank–Oseen elastic energy (Ef) as represented in eqn (1), wherein, K1, K2, and K3 represent the elastic splay, twist, and bend constants. The saddle-splay constant (K2 + K4) is later eliminated due to no contribution to governing equations for the case of strong anchoring, as elaborated in the SI. These modifications turn into46| | | Ef = 0.5K1(∇·n)2 + 0.5K2(n·∇ × n)2 + 0.5K3(n × ∇ × n)2 + 0.5(K2 + K4)∇·((n·∇)n − (∇·n)n). | (1) |
The implication of one constant approximation46,58 simplifies the Ef as follows,| | | Ef = 0.5Kf((∇·n)2 + |∇ × n|2). | (2) |
where Kf= K1 = K2 = K3 and K4 = 0 and Kf is the NLC bulk elastic constant.
In order to describe the NLC dynamics, the equation of balance of couple (angular momentum balance) reads as follows, ensuring the director field constraint58
as,
| |  | (4) |
The Lagrange multiplier
λ also confirms the director constraint in the couple balance.
58,72 A unit vector describing the director,
n, in a 2D can be expressed as
n (sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ, cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ), where
θ represents the director angle with positive
z-axis (
Fig. 1(b)) that also satisfies
eqn (3). The other variables in
eqn (4) are – the body force due to any external field (
G), an intrinsic director and body force (
g). In our formulation, there is no external field present that leads to
G = 0, and
g reads as,
The rotation vector
N and the strain tensor
e in
eqn (5) can be expressed as,
N =
ṅ −
ω·
n, where the spin tensor,
ω = 0.5(
∇u −
∇uT) and
e = 0.5(
∇u +
∇uT).
The NLC film's constitutive relation is described using a viscous stress tensor τV as,56,73,74
| | | τV = α1e: nnnn + α2nN + α3nN + α4e + α5nn·e + α6e·nn, | (6) |
where the component
αi (
i = 1–6) represents the Leslie viscosity coefficient that later can be related to the rotational viscosity (
λ1) and irrotational torque coefficient (
λ2)
58,74 as
λ1 =
α3 −
α2,
λ2 =
α6 −
α5 and to each other using the Onsager relation as
α2 +
α3 =
α6 −
α5 respectively. However, they do not necessarily have to be all positive, and 0.5
α4 > 0 when other coefficients are zero resembles a typical Newtonian-isotropic system of common viscosity. Furthermore, the elastic (Ericksen) stress tensor,
τE, is described as,
58| | 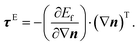 | (7) |
B. Momentum balance equations
The conservation of mass and momentum equations for the lower layer (1) in the vectorial form can be expressed as,| | 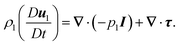 | (9) |
where u(u, w), p1 read as (P1 + ϕ1), ϕ1, ρ1, ∇, I and τ read as (∇u + ∇uT) are the velocity vector, pressure, body force term, water density, gradient operator, identity tensor, and hydrodynamic stress tensor, respectively. Here, D/Dt = ∂/∂t + u·∇ is the total derivative, and t is the time. Similar common notations are used in the following equations unless mentioned.
Similarly, for the upper NLC layer, the mass and momentum equations read as,
| |  | (11) |
where
p2(
P2 +
ϕ2),
ϕ2,
τV, and
τE are pressure, body force potential, viscous, and elastic stress tensors, respectively. The detailed term-by-term simplifications of
eqn (11) are mentioned in the SI and elsewhere.
56,58
C. Boundary conditions
In the bilayer, the lower layer is placed on the rigid and impervious substrate – s and the NLC film rests on top, exposed to the air medium, respectively. The no-slip and impermeability are assumed at the substrate at the location z = 0, which reads as,The system consists of an interface – NW at z = h1(x, t) and a surface NI at z = h2(x, t), respectively. At these locations, the continuity of velocities, normal and tangential stress balances, and kinematic conditions are implemented as boundary conditions. Subscripts h1 and h2 in eqn (16) and (19) denote locations at which u1 and u2 are evaluated. These boundary conditions read as, at z = h1(x, t),| | | n1·T2·n1 − n1·T1·n1 = γ12κ1, | (14) |
| | | n1·T2·t1 − n1·T1·t1 = 0, | (15) |
| | | ∂h1/∂t + (u1)h1∂h1/∂x = (w1)h1, | (16) |
at z = h2(x, t),| | | n2·T0·n2 − n2·T2·n2 = γ2κ2, | (17) |
| | | n1·T0·t1 − n1·T2·t1 = 0, | (18) |
| | | ∂h2/∂t + (u2)h2∂h2/∂x = (w2)h2. | (19) |
Subscripts 0, 1, and 2 denote air, water, and NLC layers. The components hi, γ12, γ2, and κi = ∇·ni (i = 1, 2) represent the respective film thickness, interfacial tension, surface tension, and the respective deforming interface curvature. The notations ∇s (= I − nn), 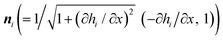 and
and  represent the surface gradient operator, outward surface normal, and tangent vectors. At the NI interface, we assume that there exists no tangential surface tension gradient, which leads to no jump at NI, that is n2·T2·n2 = −γ2κ2 and n1·T2·t1 = 0, since T0 = 0 (eqn (16) and (17)) for the bounding medium (air), making it appropriate for assumed strong anchoring conditions. Essentially, by maintaining the general form of normal and tangential stresses at the interface, the derived equation can examine different body and interface forces arising from specific influences such as gravity and surface tension and including disjoining pressures within the body force potential term. Furthermore, the strong anchoring boundary conditions are executed to express the director field (n) in order to achieve the planar (P) and homeotropic (H) director positions at NW and NI, respectively. In this study, the LC–water interface is modeled with boundary conditions representing two experimentally relevant anchoring types, as mentioned above, which are commonly observed in NLCs like 5CB. The polarity of water aligns the LC's polar cyano (–CN) groups toward the aqueous phase, promoting homeotropic or tilted orientation, while the hydrophobic alkyl chains orient away.71 These molecular interactions form the physical basis for the imposed boundary conditions. The enforcement of these boundary conditions at NW (z = h1(x, t)) and NI (z = h2(x, t)) leads to,
represent the surface gradient operator, outward surface normal, and tangent vectors. At the NI interface, we assume that there exists no tangential surface tension gradient, which leads to no jump at NI, that is n2·T2·n2 = −γ2κ2 and n1·T2·t1 = 0, since T0 = 0 (eqn (16) and (17)) for the bounding medium (air), making it appropriate for assumed strong anchoring conditions. Essentially, by maintaining the general form of normal and tangential stresses at the interface, the derived equation can examine different body and interface forces arising from specific influences such as gravity and surface tension and including disjoining pressures within the body force potential term. Furthermore, the strong anchoring boundary conditions are executed to express the director field (n) in order to achieve the planar (P) and homeotropic (H) director positions at NW and NI, respectively. In this study, the LC–water interface is modeled with boundary conditions representing two experimentally relevant anchoring types, as mentioned above, which are commonly observed in NLCs like 5CB. The polarity of water aligns the LC's polar cyano (–CN) groups toward the aqueous phase, promoting homeotropic or tilted orientation, while the hydrophobic alkyl chains orient away.71 These molecular interactions form the physical basis for the imposed boundary conditions. The enforcement of these boundary conditions at NW (z = h1(x, t)) and NI (z = h2(x, t)) leads to,| | n·z = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1, θ1, | (20) |
| | n·ti = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2. θ2. | (21) |
3. Long-wave hydrodynamics
A. Thin film equation
In this section, we show the equations that describe the temporal evolution of the deforming NW interface and NI-free surface. This is achieved in the framework of the lubrication or long-wave approximation (ε = 2πhi0/λw ≪ 1), considering the general properties of the layers involved. In the framework of lubrication approximation, we determined that the x-direction and time scale as O(1/ε), while the z-direction scales as O(1). This considers the wavelength for the x-directional length scale and the mean film thickness (hi0) for the z-directional length scale. Additionally, the velocities (u, w), total pressure, director orientation (θ),67 and surface or interfacial tension (γ) scale as follows – O(1), O(ε), O(1/ε), O(1), and O(1/ε)3. Utilizing this, we simplify all governing equations and boundary conditions. We conduct an order analysis on each equation, retaining only the leading-order terms and disregarding any higher-order terms. The evolution equation is subsequently derived from these simplified equations. The following equations outline all the reduced governing equations obtained from eqn (8)–(11) and boundary conditions from eqn (12)–(19).| | | ∂/∂x(p2 + 0.5Kf(∂θ/∂z)2) = ∂/∂z(c2∂u2/∂z), | (26) |
| | | ∂/∂z(p2 + 0.5Kf(∂θ/∂z)2) = 0, | (27) |
| | | P1 + ϕ1 − P2 − ϕ2 − Kf(∂θ/∂z)2 = −γ12(∂2h1/∂x2); at (z = h1(x, t)), | (29) |
| | | c2∂u2/∂z = μ1∂u1/∂z; at (z = h1(x, t)), | (30) |
| | | P2 + ϕ2 − p0 + Kf(∂θ/∂z)2 = −γ2(∂2h2/∂x2); at (z = h2(x, t)), | (31) |
| | | ∂u2/∂z = 0; at (z = h2(x, t)), | (32) |
| | | ∂h1/∂t + (u1)h1∂h1/∂x = (w1)h1, | (33) |
| | | ∂h2/∂t + (u2)h2∂h2/∂x = (w2)h2. | (34) |
The term c2 in eqn (26) and (30) is one of the coefficients (the remaining are given in the SI) that belongs to the hydrodynamic stress, which survives after scaling analysis and is expressed as, c2 = 0.5(2α1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + α4 + (α2 + α5)sin2
θ + α4 + (α2 + α5)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + (α6 − α3)cos2
θ + (α6 − α3)cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). Solving the aforementioned governing equations and boundary conditions and substituting the obtained terms in the kinematic condition result in the evolution equations for the respective layers. For the NLC layer, the Leibnitz formula is utilized to transform eqn (19) into a mathematically more convenient form,
θ). Solving the aforementioned governing equations and boundary conditions and substituting the obtained terms in the kinematic condition result in the evolution equations for the respective layers. For the NLC layer, the Leibnitz formula is utilized to transform eqn (19) into a mathematically more convenient form, 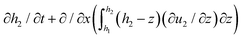 . The resulting evolution equations, detailed below, describe the stability, dynamics, and morphology of both NI and NW.
. The resulting evolution equations, detailed below, describe the stability, dynamics, and morphology of both NI and NW.| |  | (35) |
| |  | (36) |
where,  ;
;  ;
;  ;
;  ; and
; and  . Here, we call P2M = P2 + 0.5Kf(∂θ/∂z)2 as a modified pressure, and the NLC bulk viscosity is defined by μ2 = 0.5α4, where, α4 is the fourth Leslie coefficient.
. Here, we call P2M = P2 + 0.5Kf(∂θ/∂z)2 as a modified pressure, and the NLC bulk viscosity is defined by μ2 = 0.5α4, where, α4 is the fourth Leslie coefficient.
B. Micro-thick and nano-thin cases
(i) Gravity and surface tension.
In the present study, the bilayer comprises an NLC film on the top of a water layer, which introduces the density difference, as NLC is physically a higher-density fluid than water. In order to examine the system dynamics and interfacial stability under this condition, we incorporate the inertial effects in the body force terms appearing in the momentum balances and normal stresses for the individual layers as follows.| | | ϕ1 = ρ1gz and ϕ2 = ρ2gz, | (37) |
where g is the gravitational constant, which is in the negative z direction in the present case. The linear stability analysis is performed after solving momentum balance and normal stress simplification for the interface locations utilizing the normal linear modes (hi = hi0 + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ieωt+ikx), where, hi0, ω, k and
ieωt+ikx), where, hi0, ω, k and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) i are the mean or base thickness, linear growth rate of disturbance, wavenumber, and infinitesimal initial surface perturbation amplitudes. The present longwave formulation utilizes strong anchoring conditions, where surface and interfacial tensions are assumed constant. Therefore, it is essential to understand that constant interfacial tensions correspond to the fixed base-state director angles θ1 and θ2. Moreover, if an explicit γ(θ) was included, the surface tension would vary locally with the perturbation amplitude. The resulting dispersion relation (see Bandyopadhyay et al. (2005) for a detailed derivation of the isotropic bilayer)30 from eqn (33) and (34) is expressed as follows:
i are the mean or base thickness, linear growth rate of disturbance, wavenumber, and infinitesimal initial surface perturbation amplitudes. The present longwave formulation utilizes strong anchoring conditions, where surface and interfacial tensions are assumed constant. Therefore, it is essential to understand that constant interfacial tensions correspond to the fixed base-state director angles θ1 and θ2. Moreover, if an explicit γ(θ) was included, the surface tension would vary locally with the perturbation amplitude. The resulting dispersion relation (see Bandyopadhyay et al. (2005) for a detailed derivation of the isotropic bilayer)30 from eqn (33) and (34) is expressed as follows:| |  | (40) |
with
(ii) Disjoining pressure.
The long-range intermolecular forces can significantly influence the nano-thin film stability by affecting the intermolecular interactions at the interfaces.12,30 These forces are particularly critical in determining the equilibrium configurations and potential dewetting phenomena in thin liquid films. The van der Waals effects are incorporated into the stability analysis (detailed steps in the SI) through an additional pressure term that represents the disjoining pressure following a few previous studies.47,75–78 The effective Hamaker constants (Al) are related to the binary Hamaker constants (Alm) appearing in the ΔGLWE as follows,
| Al = Amm − Alm = −12πd02Slm; Am = All + Asm − Asl − Alm = −12πd02Sslm; |
and
| An = Asm − Alm = −12πd02Sslm + 12πd02Ssl, |
where l, m, and n represent subscripts 1, 2, and 3. The macroscopic equilibrium spreading coefficients utilised in primed coefficients of eqn (46) below, denoted by the respective subscripts where n is a gas medium. The letter ‘a’ is used to represent the bounding medium (air) in Section 4(C) while writing the respective spreading coefficients in place of n just for simplification. Therefore, Slm = γl − γm − γlm,  and d0(∼0.157 nm) is the van der Waals cut-off distance between the two surfaces, determined by incorporating the short-range Born repulsion.30,79 The excess free energy (ΔGLWE) for the present bilayer configuration can be expressed as,47,76,78
and d0(∼0.157 nm) is the van der Waals cut-off distance between the two surfaces, determined by incorporating the short-range Born repulsion.30,79 The excess free energy (ΔGLWE) for the present bilayer configuration can be expressed as,47,76,78| |  | (41) |
The term h3, representing the NLC layer thickness, is the same as h2−h1 and alternatively used in the rest of the manuscript. Thus, the disjoining pressure (Π = −∂/∂h(ΔGLWE)) is negative of the van der Waals conjoining pressure (Φ) and for a particular interface that modifies the pressure distribution within the film and is given by,
Here,  is a constant and obtained from the angular momentum balance equation. The total pressures (P1 = p0 − γ2∂2h2/∂x2 − γ12∂2h1/∂x2 − Π1) and (P2 = p0 − Kf(∂θ/∂z)2 − γ2∂2h2/∂x2 − Π2) at the NW and NI interfaces are double differentiated (details in the SI) with respect to x and then linearized as follows,
is a constant and obtained from the angular momentum balance equation. The total pressures (P1 = p0 − γ2∂2h2/∂x2 − γ12∂2h1/∂x2 − Π1) and (P2 = p0 − Kf(∂θ/∂z)2 − γ2∂2h2/∂x2 − Π2) at the NW and NI interfaces are double differentiated (details in the SI) with respect to x and then linearized as follows,| |  | (42) |
| |  | (43) |
Eqn (35) and (36) can be modified by substituting eqn (42) and (43) and performing linear stability analysis utilizing normal modes, which leads to the following forms,| |  | (46) |
where,
The obtained quadratic equations (eqn (40) and (46)) provide the wavenumber spectrum for disturbances where the real part of ω(Re{ω} > 0) is positive, indicating the condition for instability. We focus on the largest positive root of this equation for a given wavenumber, as it represents the maximum growth rate of the disturbance. In the unstable range of wavenumbers, the most rapidly growing or dominant wavenumber (km) is determined by the condition ∂ω/∂k = 0. This wavenumber corresponds to the dominant wavelength (λm) of the instability, where λm = 2π/km. The associated growth rate, ωm, at km is the highest initial growth rate for small-amplitude perturbations, which defines the characteristic time scale of the instability.
4. Results and discussion
A. Validation
In this section, the formulations for both micro-thick and nano-thin cases are validated in the asymptotic limits with existing analytical solutions, as illustrated in Fig. 2. Following a previous80 formulation, which focuses on the bilayer RTI in isotropic films, the result is reproduced for the dispersion relation as displayed in plot (a) in the creeping flow limit. In order to validate these existing results, the NLC terms are eliminated from the present formulation, and as per their criterion, equal viscosities (μ1 = μ2) are maintained with upper film density (in their case – ρ1) ρ1 = 1100 kg m−3 (NLC – ρ2 in the present case) and interfacial tension γ12 = 0.0036 N m−1 (γ12 = 0.0075 N m−1 in the present case) at the lower layer mean thickness h0 = 0.1 μm (h10 in the present case). Note here that the present formulation is in good agreement with their work. However, the slight deviation in the dispersion curve at higher wavenumbers might be attributed to the fact that the existing work has solved the equations at the interface in the semi-infinite upper film thickness.
 |
| | Fig. 2 Asymptotic validation plots for the present formulation via dispersion relations comparing the linear growth rate (ω, s−1) as a function of wave number (k, m−1). All the solid color hollow circle symbols denote the previous studies, and the solid (cyan) line represents the NLC–water bilayer system of the present work. Plot (a) shows the validation with Stergios and Brian's (1989)80 formulation to compare the bilayer RTI in the limit of isotropic films, wherein ρ1 (upperlayer) > ρ2 and ρ1 is the density of the NLC layer in the present case. Plot (bii) shows the validation result with a single NLC film on the solid substrate studied by Ben and Cumming (2001)56 and validated in the limit of h10 → 0 and using P–H director orientation, as shown in plot (bi). Plot (c) shows the isotropic bilayer validation with Bandyopadhyay et al. (2005)30 in the limit of Kf → 0, θ1 → 0 and θ2 → 0 considering the nano-thin film. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
Plot (bii), on the other hand, is for the case where a previous work56 has dealt with the single layer of NLC on the solid substrate and modeled the system using lubrication approximation. The study has considered two cases – gravity in perpendicular and parallel directions to the film, wherein they found that instability may arise for the former case, but instability always prevails for the latter case. However, in the present work, we find different modes of instability for the case, pointing towards the different NLC behavior when in contact with the liquid substrate instead of the solid counterpart. For this case, we validate our results within the limit of h10 → 0 (water film thickness) for the P–H director orientation, as shown in plot (bi).
In order to validate the nano-thin film bilayer configuration and the characteristic instability emerging from the van der Waals interactions between films, we verify the present formulation with the literature.30 The result in plot (c) shows an agreement in the isotropic limit with case 3 for the surface tension combination γ2 > γ1 > γs. The bilayer instability of NLC film atop a water film is examined through a theoretical framework based on the thickness ranges of the films, as mentioned in the problem formulation section. The forces that drive instabilities are highly sensitive to the thickness of the films, so to achieve a thorough understanding of the instability dynamics, the present study is divided into two sections: micro-thick and nano-thin bilayers. Analyzing these two regimes allows us to capture each case's distinct instability mechanisms accurately.
B. Micro-thick films
For the micro-thick bilayers, the gravitational forces arising from the density difference between the NLC and water layers play a dominant role in destabilizing the system. For example, a higher-density 5-cyano-bisphenyl (5CB) film on a water layer may manifest an RTI. The length and time scales of the instability have been decided by the competition between gravitational forces with the surface and interfacial tensions at the interfaces, along with the elastic rigidity of the NLC film. Thus, the focus of discussion in this section has been on parameters such as the density difference, film thickness, surface and interfacial tensions, and Frank's elasticity of the NLC layer. As mentioned before, the free bilayer system considered here has a pair of coupled deformable interfaces – NI and NW, respectively. Thus, there is a possibility that both interfaces may assume a similar length or time scale when they are fully coupled or may assume different length and time scales if they are not. Previous studies indicate that while the coupled interfaces may deform following a single length and time scale, the decoupled ones may lead to bimodality, wherein the interfaces may deform following different lengths and time scales.12,30 In the latter case, the NI surface is expected to assume a longer wavelength owing to a larger surface tension, whereas the NW interface may assume a shorter one owing to a weaker stabilizing interfacial tension.
In this direction, Fig. 3 shows some interesting results wherein such free bilayers are considered with two different director orientations at the boundaries of the NLC layer, homeotropic–homeotropic (H–H – θ1 = 0, θ2 = 0) and planar–homeotropic (P–H – θ1 = 0, θ2 = π/2), as shown schematically in the first column of the images. The P–P and H–P configurations at the boundaries are not explored because of their remote possibility. Furthermore, angular anchoring is also not considered because such director orientation shows results similar to those of homeotropic anchoring.
 |
| | Fig. 3 The dispersion curves and neutral stability for the NLC–water bilayer configuration under varying layer thickness and director orientations. Schemes (i) and (ii) show NLC director (solid green) orientations under P–H and H–H conditions, respectively. Plots (a) and (c) show the growth rate (ω) versus wavenumber (k) for varying water layer thickness (h10, μm) for the respective director configurations at constant h30 = 10 μm, indicating increased instability at higher thicknesses. Plots (b) and (d) depict the corresponding (to plots (a) and (c)) contour of the critical wavenumber (kc, m−1) on the plane kc–h10 showing the influence of thickness on stability. Plots (e) and (g) show the ω for varying NLC layer thickness (h30, μm) in both configurations at constant h10 = 10 μm, showing a stabilizing effect with increasing thickness. Plots (f) and (h) depict contour plots of kc for varying h30 on the plane kc–h30, highlighting the stabilizing role of the NLC layer in both configurations. Plots (c), (e) and (g) show bimodality, indicating the presence of FSM and CIM instability modes in the bilayer system shown on the respective curves. Arrows (solid color with dash-dotted lines) on the particular curves indicate increasing and/or decreasing trends. Besides contour plots, color bars indicate the respective contour curve values. The neutral stability curves (ω = 0) are represented by the dash-dotted lines (bold black) on the respective contour plots demarcating the region of stability (ω < 0) from the unstable (ω > 0) region. Schemes (j)–(l) illustrate the in-phase (coupled) and out-of-phase (decoupled) deformation modes of a two-layer thin film system supported on a solid substrate, highlighting the mechanistic origin of unimodal and bimodal responses. The other dash-dotted color lines (green) present the respective ω values. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
Table 1 Typical parameter values to perform calculations for bilayer films45,46,53,67
| Parameters |
Units |
Values |
|
α
1
|
Pa s |
0.0065 |
|
α
2
|
Pa s |
−0.007 |
|
α
3
|
Pa s |
−0.001 |
|
α
4
|
Pa s |
0.085 |
|
α
5
|
Pa s |
0.05 |
|
γ
1
|
N m−1 |
0.072 |
|
γ
2
|
N m−1 |
0.033 |
|
γ
s
|
N m−1 |
0.0265 |
|
ρ
1
|
kg m−3 |
1000 |
|
ρ
2
|
kg m−3 |
1020 |
|
K
f
|
pN |
5 |
|
μ
1
|
Pa s |
0.001 |
|
μ
2 = α4/2 |
Pa s |
0.0425 |
|
h
10
|
μm (thick films) or nm (thin films) |
5–100 |
|
h
20
|
μm (thick films) or nm (thin films) |
5–100 |
|
g
|
m s−2 |
9.81 |
Fig. 3(a), (c), (e) and (g) shows the variations in the growth rate (ω) and wavenumber (k) for the P–H and H–H systems. The plot (a) shows that, for the P–H system, both the NI surface and NW interface deform by assuming a single mode with a distinct single maximum, ωm, when the films are of similar thicknesses. The plots also show that, as the lower layer thickness, h10, increases under a thin upper layer, h30 = 30 μm, a reduction in the frictional influence at the bottom water layer rapidly increases ω while the length scale shifts more towards the shorter wavelength regime (larger wavenumber). On the other hand, plot (c) shows that when an H–H configuration is considered, the interfaces may assume a bimodal behavior with a pair of distinct maxima in place. The emergence of bimodality can be elucidated by examining schemes (j)–(l), which reveal that a unimodal response arises when both layers deform cooperatively, i.e., in-phase.81–84 In contrast, when the layers deform out-of-phase,81–84 exhibiting relative displacement or antagonistic curvature, the system transitions to a bimodal configuration. In such a scenario, the NI surface may assume an instability mode with a longer wavelength (smaller wavenumber), and the confined NLC–water interface may assume a shorter wavelength (larger wavenumber) mode. However, the system may eventually assume the length and time scale corresponding to the dominant mode among the two. In order to distinguish the pair of modes in a bimodal behavior, we term them as the free surface (FSM) and confined interface (CIM) modes in this work. The plot (c) also suggests that when the h10 is smaller, the dominant FSM mode of instability stays at the NI surface, showing a larger wavelength (smaller wavenumber). However, with the increase in the h10, a mode switching is observed wherein the CIM becomes the dominant one at the NW interface.
The plots (b) and (d) show the contours of ω > 0 in the k vs. h10 plane wherein we clearly distinguish the zones of CIM and FSM dominance. Unlike in plots (a) and (c), where the gravitational forces drive the instability with the increasing h10, in plot (e), the instability is more influenced by the NLC layer thickness. For example, the plot suggests that when both films are thinner and under the P–H configuration, a bimodal behavior may be observed, with the CIM being the dominant mode. However, as h30 increases, the increasing effect of Frank's elasticity at the confined interface may cause the reduction of ωm. Plot (g) shows a situation wherein an H–H configuration may show the emergence of a dominant FSM mode with increased NLC layer thickness. In this situation, we have employed the term associated with the Ericksen stress as the destabilizing term (Kf(∂θ/∂z)2) in eqn (29) and (31) on the left-hand side, which eventually helps fuel the FSM mode to become the dominant one over the CIM.46,47,58,67,85Fig. 3(b), (d), (f) and (h) shows the situations discussed in their respective dispersion relation plots through contours for ω on the h10–kc and h30–kc planes when h30 and h10 are kept constant in the alternative case. Plots (b) and (d) reveal that the CIM mode can be fueled up merely by switching the director orientation from P–H to H–H and increasing h10. In contrast, both the modes appear with increasing NLC-layer thickness, as shown in the plot (f) for the values ∼h30 > 20 μm. Furthermore, plot (h) shows that changing the boundary conditions from P–H to H–H results in a dominant FSM mode with increasing h30.
Fig. 4 shows that the influence of Kf in P–H and H–H configurations arises from the fundamental differences in the director orientation at the interfaces. The asymmetry in director orientation results in an imbalance in the elastic response at the two interfaces. When perturbations occur, the NLC's ability to resist these disturbances is strongly influenced by Kf,67 mainly because the elastic forces at the planar interface are weaker.
 |
| | Fig. 4 The dispersion curves and neutral stability for the NLC–water bilayer configuration under varying NLC bulk elastic constant (Kf) and density differences (Δρ). Plots (a), (c), (e) and (g) depict ω as a function of k for various Kf and Δρ at P–H and H–H director configurations, respectively, at constant film thicknesses h10 = 20 μm, h30 = 10 μm for Kf and h10 = 10 μm, h30 = 60 μm for Δρ, respectively. Plots (b) and (d) depict corresponding (to plots (a) and (c)) neutral stability curves on the plane (kc–Kf) for P–H and H–H director configurations, respectively. Similarly, plots (f) and (g) depict neutral stability curves (corresponding to plots (e) and (g)) on the plane kc–Δρ for H–P and H–H director configurations, respectively. Arrows (dash-dotted solid color) on the respective curves indicate increasing and/or decreasing trends. Besides contour plots, colour bars indicate individual contour curve values. The neutral stability curves (ω = 0) are represented by the dash-dotted lines (bold black) on the respective contour plots, demarcating the region of stability (ω < 0) from the unstable (ω > 0) region. The other dash-dotted colour lines (green) present the respective ω values. Insets inside plots (e) and (g) are meant to show distinct curves. An inset inside plot (f) shows the zoomed-in section of the plot representing the values marked inside the rectangular box (pink color). Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
As Kf increases, the overall director field elastic energy becomes larger, especially at the planar interface, where the director is more flexible. This additional elastic energy provides a restoring force that suppresses perturbations,67 particularly those with short wavelengths (high k), which are more sensitive to local distortions in the director field. The Kf effectively reduces the ω (plot (a)), especially at higher wavenumbers, by providing more resistance to director distortions. However, the H–H alignment at both interfaces is resistant to deformations; increasing Kf does not significantly alter the stability of the system. The elastic forces are uniformly applied across both interfaces, so even a high Kf value (50 pN) does not introduce any new restoring forces or additional stability, as shown in plot (c). Furthermore, plots (b) and (d) collectively show that irrespective of the Kf magnitude, the system becomes more stable in the H–H director configuration. Nevertheless, an unstable system attempts to nullify the destabilizing effect of increasing Kf indicating its stabilizing role in conjunction with the surface tension. The stabilizing contributions of Kf (the fourth term on the left side) and surface tension (right-hand side term) are also evident in eqn (31). Moreover, we observe that Kf can potentially reduce the CIM arising in addition to the prevailing FSM at higher NLC (h30 ≥ 40 μm) and lower water film (h10 = 10 μm) thicknesses67 in contrast to the results shown in plot (a) for h10 = 20 and h30 = 10 μm.
The stability analysis of the P–H and H–H configurations under varying density differences (Δρ = ρ2–ρ1) reveals interesting insights into the underlying physics governing these systems. In both the P–H and H–H configurations (plots (e) and (g)), we again observe a bimodal behavior with a pair of distinct maxima at the smaller (CIM) and larger (FSM) wavelengths. Interestingly, when the magnitude of Δρ is smaller, the longer wavelength FSM modes show a dominant behavior. However, with the increase in Δρ, mode switching is observed as the dominant mode of instability shifts from the higher to lower wavelength regime when the CIM becomes the dominant one. Furthermore, the neutral stability contour plots (f) and (h) corresponding to plots (e) and (g) reveal that the mode switching can simply be achieved by tuning the Δρ in the case of P–H as well as H–H configurations. Concisely, Fig. 4 summarizes that the elasticity of the NLC film and the density contrast between the NLC and liquid layer can not only play a key role in altering the length scales from larger to smaller wavelengths but also may cause switching of the dominant mode from the free surface to the confined interface.
Fig. 5 and 6 summarize the predictions of the dominant growth rate – ωm and wavelength – λm for the various parametric combinations discussed in Fig. 3 and 4. Plots (a)–(d) depict the variations of ωm and λm, respectively, with h30 for various h10 (10–30 μm for P–H and 10–50 μm for H–H configurations). Similarly, plots (e)–(h) depict the same results with h10 for various h30 (10–20 μm for both P–H and H–H configurations). As discussed previously, the dominant instability mode is indeed a smaller wavelength CIM, wherein λm reduces with the increasing h10 (b) and (d) for both P–H and H–H configurations, whereas the same decreases in the case of increasing h30.
 |
| | Fig. 5 Variation of the maximum growth rate (ωm) and the dominant wavelength (λm) for parametric variations at different director orientation configurations. Schematics (i) and (ii) show director orientation configurations P–H and H–H, respectively. Plots (a)–(d) depict ωm and λm for h10 variations at different constants h30 for P–H and H–H orientations. Similarly, plots (e)–(h) depict ωm and λm for h30 variations at different constants h10 for P–H and H–H orientations. The inset in (ii-g) shows the prominent mode switching starting from h10 = 16 μm and onward. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
 |
| | Fig. 6 Plots (j)–(n) depict ωm and λm for Kf variations at different h30 while maintaining constant h10 = 20 μm for P–H and H–H orientations. Plots (p) and (q) depict ωm and λm for Δρ variations at different h30 while maintaining constant h10 = 10 μm. For Δρ variations, both P–H and H–H orientations show nearly similar trends without significant differences. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
The increased ωm may be attributed to the lower frictional influence of the increase in the film thicknesses. On the other hand, the plots also suggest that the presence of the thinner water layers favors longer wavelengths, while thicker layers produce shorter wavelengths for the CIM. Overall, the plots highlight that there can be a pair of instability modes, FSM and CIM, and the transition of the same depends on both NLC and water layer thicknesses.
Fig. 6 displays the impact of Kf and Δρ on ωm and λm for the P–H and H–H configurations. The plots suggest that ωm decreases and λm increases with the increase in the Kf. The rapid decline in the growth rate with increasing Kf suggests that as the NLC elasticity increases, it resists deformation more effectively, thereby slowing the growth of any perturbations. Thinner NLC films are less affected, implying that thinner films are less sensitive to elastic effects, while thicker films stabilize more as elasticity increases. Interestingly, plot (m) shows a slight crossover at h30 between 10 and 20 μm. This crossover is attributed to the FSM dominance, depicting slightly higher growth rates. Beyond the crossover thickness, the system switches to the CIM, where a thinner water layer stabilizes the interface. Consequently, the growth rate trend reverses, making this configuration a stable one. Furthermore, the plots suggest that the bimodality and mode switching can be fueled by the variation in the Δρ. The ωm increases monotonically with the increase in Δρ for both P–H and H–H configurations with the possibility of transition from the FSM to CIM and switching of the dominant mode from the free surface to the confined interface. In summary, Fig. 3–6 show the key possibilities of different modes of instabilities for the RTI of a free bilayer composed of a nematic and a water film.
C. Nano-thin films
Apart from instigating RTI arising due to the density contrast across a soft interface, the instabilities in the NLC–water free bilayers can also be triggered by employing other body forces. For example, the nano-thin films (<100 nm) can also show the instabilities originating from the van der Waals forces across the films30 because of the insignificance of the gravitational effects in such systems. In the present study, we consider three different varieties of NLC–water free bilayers based on the different spreading coefficients that are most common in the experimental systems – Case (I) S12s > 0 and S21a < 0 when the NLC layer has the highest surface tension (γ2 > γ1 > γs); Case (II) S12s < 0 and S21a > 0 when the water layer has the highest surface tension (γ1 > γ2 > γs); and Case (III) S12s < 0 and S21a < 0 when the substrate has the highest surface tension (γs > γ2 > γ1). Here Slmn (Almn) is the spreading coefficient (effective Hamaker constant) of the layer l sandwiched between the bounding layers m and n, wherein Slmn < 0 and Almn > 0 (Slmn > 0 and Almn < 0) signify an unstable (stable) ‘lth’ layer. The Hamaker constant values used in nano-thin film analysis are calculated from formulas enlisted in Section 3(B-ii).
Case I (S12s > 0 and S21n < 0; γ2 > γ1 > γs): the spreading coefficients chosen in this case indicate that the free bilayer has a stable liquid layer while the NLC layer can be unstable when the van der Waals forces overcome the stabilizing influences arising from the surface/interfacial tensions at the surface/interfaces and the NLC elastic forces.47,76,77Fig. 7 shows some interesting results regarding the P–H configuration. The plots (a) and (b) suggest that when the Kf is vanishingly small, we observe a bimodal behavior for this case, as has been seen previously in the literature for a purely viscous free bilayer.30 Physically, the bimodality indicates the presence of competing instability modes at both the NI surface and NW interface, in which the shorter-wavelength CIM is the dominant one at the thickness combination chosen for the bilayer. However, with the increase in the Kf, as the deformability of the NLC layer reduces, the dominant mode's length scale progressively switches towards the FSM while suppressing the CIM. The phenomenon resembles the mode-switching behavior observed for the micro-thick films. Fig. 7(c) and (d) shows that such mode-switching behaviors, in this case, can also be achieved by changing either h10 or h30, which is signified by the discontinuities in the plots. A thinner upper layer on a thicker lower layer may ensure a smaller wavelength and faster CIM, while a thicker upper layer may assume a larger wavelength FSM.
 |
| | Fig. 7 Dispersion relation results, the maximum growth rate (ωm), and dominant wavelength (λm) for the variation of the NLC bulk elastic constant (Kf) considering Case I (γ2 > γ1 > γs) at the P–H director orientation configuration. In plot(a), the variation of the linear growth rate (ω, s−1) as a function of wave number (k, μm−1) at different Kf values for fixed h10 = h30 = 10 nm upper NLC and solvent film thicknesses. Plot (b) displays the expanded view of the short wavenumber in the dispersion curve for Kf variation. Plots (c) and (d) are for the variation of the ωm and λm with the Kf at h30 = 5–25 nm NLC on h10 = 10 nm solvent film. Similarly, plots (e) and (f) display the variation of ωm and λm with Kf for a h10 = 5–50 nm solvent layer, under a 10 nm thick NLC film. The different symbols in plots (e) and (f) merely depict the distinction between the overlapping trends. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
Fig. 8 highlights the role of the film thickness for a given Kf. Fig. 8(a)–(c) shows that for a thin and fixed h10, at the smaller values of h30 the smaller wavelength CIM is the dominant mode of instability, but with increasing h30, mode switching from the CIM to the FSM takes place with λm shifting towards the longer wavelength regime. On the other hand, Fig. 8(d)–(f) shows another interesting scenario of mixed-mode instability, wherein a thin h30 on a thicker h10 shows a smaller λm, which progressively increases with the increase in h10. Fig. 9 shows the same systems as in Fig. 7 and 8, however, with P–A and P–P configurations at the interfaces, as depicted schematically. A comparison between the results of Fig. 7 and 8 help conclude that P–P, P–H, and P–A configurations essentially show very similar behaviors in terms of mode-switching if other parameters are kept very similar. The figures also suggest that the conditions for mode switching and the associated length (λm) and time scales (ωm) can be altered simply by tuning the director orientation at the boundaries.
 |
| | Fig. 8 Dispersion relation results, the maximum growth rate (ωm), and dominant wavelength (λm) for the variation of the respective layer thicknesses considering Case I (γ2 > γ1 > γs) at the P–H configuration. Plot (a) shows the variation of the linear growth rate (ω, ms−1) as a function of wave number (k, μm−1) at a fixed solvent layer thickness h10 = 10 nm with h30 = 5–15 nm NLC layer thickness. Plots (b) and (c) show the variations of ωm and λm with h30 for a h10 = 10–30 nm thick solvent layer. Plot (d) shows the variation of ω with k for a fixed NLC layer thickness of h30 = 10 nm with h10 = 5–20 nm solvent layer thicknesses. Plots (e) and (f) show the variations of ωm and λm with the h30 = 9–17 nm thick NLC layer. The different symbols in the plot (c) merely depict the distinction between the overlapping trends. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
 |
| | Fig. 9 Dispersion relation results, the maximum growth rate (ωm), and dominant wavelength (λm) for the variation of layer thicknesses considering Case I (γ2 > γ1 > γs.) at P–A (plots (a)–(f)) and P–P (plots (j)–(f)) director configurations, respectively. Plot (a) shows the variation of the ω, ms−1 as a function of k, μm−1 at a fixed lower layer thickness h10 = 10 nm with varying NLC layer thickness in the range h30 = 5–15 nm. Plots (b) and (c) show the variations of ωm and λm with a h30 = 10–30 nm thick solvent layer. Plot (d) shows the variation of ω with k for a h30 = 10 nm fixed upper NLC layer and h10 = 5–20 nm lower layers. Plots (e) and (f) show the variations of ωm and λm with the h10 = 8–22 nm thick upper NLC layer. Plots (g) and (h) show the variations of ωm and λm with h30 = 10–30 nm thick solvent layers. Plots (i) and (j) show the variations of ωm and λm with the h10 = 8–22 nm thick NLC layers. The different symbols in the plot (c) merely depict the distinction between the overlapping trends. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
Interestingly, Fig. 8 and 9 highlight the critical influence of orientational anisotropy in governing the transition from a mixed-mode response to distinct individual mode-switching, observed upon varying the orientational order while keeping all other system parameters fixed.
Case II (S12s < 0 and S21a > 0; γ1 > γ2 > γs): the characteristics of a bilayer system under the spreading conditions γ1 > γ2 > γs, wherein the NLC layer is placed between the water layer and the air, illustrated in Fig. 10. The resulting negative spreading coefficient (S12s < 0) in this case indicates the unstable configuration. When the NLC layer comes into contact with the substrate, it also results in an unstable case – S2sa < 0, that is the reason bimodality appears. However, in the presence of a water layer, the NLC layer shows stable behavior. On the other hand, in the absence of a water layer, NLC may destabilize; as a result, the upper interface may show instability.
 |
| | Fig. 10 Dispersion relation results, the maximum growth rate (ωm), and dominant wavelength (λm) for the variation of layer thicknesses considering Case II (γ1 > γ2 > γs) at P–H and P–A director configurations, respectively. Furthermore, plots (a) and (d) show variations of ω, ms−1 as a function of k, μm−1 for h10 and h30 variations, respectively. Plots (b), (c), (e) and (f) illustrate the variation of ωm and λm for the P–H (i) configuration. Similarly, plots (g)–(k) display the variation of ωm and λm for the P–A (ii) configuration. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
Fig. 10(a)–(k) summarizes the prominent features of Case II when the layer thicknesses are varied at P–H and P–A director orientations. The increasing h10 initially shows a unimodal behavior at small water layer thickness, which is a longer wavelength (shorter wavenumber) FSM. As the h10 increases, the mode switches towards a shorter wavelength (larger wavenumber), that is, the CIM slowly becomes dominant (plot (a)). On the other hand, for thinner NLC layers, the FSM initially shows dominance, driven by van der Waals near the NI surface. However, as the h30 increases, mode-switching is observed, where the CIM begins to dominate due to increased destabilization at the NW interface (plot (d)). Furthermore, ωm and λm indicate that the thicker NLC layers correspond to the instability of the water layer and exclusively depend on the water layer thicknesses, as shown in plots (b), (c), (g) and (h) for both P–H and P–A, respectively. In the case of small h30, ωm (plots (b) and (g)) and λm (plots (c) and (h)) show the mode switching behavior as the unstable water layer largely controls the instability. This instability grows stronger by decreasing h10, as shown in plots (e), (f), (j) and (k). This is attributed to the fact that the increasing h10 results in weaker intermolecular disjoining pressure, and NLC upper layer instability weakens because the NLC layer on a thick water layer configuration is stable.
Case III (S12s < 0 and S21a < 0; γs > γ2 > γ1): this case corresponds to the surface tension ordering γs > γ2 > γ1, wherein both the layers are unstable, closely resembling Case-I, as shown in Fig. 8 and 9. In this scenario, a thin water lower layer shows stable behavior in the absence of the upper NLC layer. However, it is unstable in the presence of a thicker NLC layer as the spreading coefficient becomes negative, S12s < 0. Moreover, if the water layer is absent, the NLC layer is stable but becomes unstable on a thicker lower layer. Given this background, it can be expected that the overall dominating instability mechanism is essentially controlled by the relatively thin NLC upper layer unstable behavior. In contrast, the lower layer is confined between two bounding media, and the water layer instability indeed controls the system for a comparatively thick NLC layer.
In view of this, Fig. 11 summarizes the linear stability analysis for Case III bilayer configuration and surface tension arrangements. The dominant mode of instability is certainly CIM (shorter wave), and the wavelength decreases with either of the layer thickness (h10 or h30) elevation for both P–P and P–A director configurations. However, the present surface tension and layer thickness arrangement depict the presence of bimodality through the occurrence of FSM, which increases with either of the layer thickness, as shown in plots (a) and (d). Moreover, plots (b)–(f) and (g)–(k) depict that ωm and λm gradually become nearly independent of the water layer thickness, h10, in the presence of relatively smaller h30, indicating that the upper NLC thickness of a bulk of water layers largely controls the instability. On the other hand, plots also show that ωm and λm gradually become independent of the h30 when the water layer thickness, h10, is small enough. As a result, the instability in this case is entirely controlled by the lower water layer, which is confined between the top and bottom bulk media. Interestingly, the figure also indicates that the mode switching and associated ωm and λm are the cumulative outcomes of the net influences of film thickness tuning and director arrangements. However, for physically realistic parameter regimes, the long-wavelength (short-wavenumber) maxima remain subdued in magnitude, as can be seen in plots (a) and (d). Consequently, a clear manifestation of mode-switching from FSM to CIM is not observed in ωm and λm plots (b)–(f) and (g)–(k) for the P–P and P–A director configurations. This suppression of distinct mode transitions may be attributed to director anchoring, which reduces the effective elasticity role within the layer.
 |
| | Fig. 11 Dispersion relation results, the maximum growth rate (ωm), and dominant wavelength (λm) for the variation of layer thicknesses considering Case III (γs > γ2 > γ1) for kf = 0.05 pN considering P–P and P–A director configurations, respectively. Plots (a) and (d) show variations of the ω, ms−1 as a function of k, μm−1 for h10 and h30 variations, respectively. Furthermore, plots (b), (c), (e) and (f) illustrate the variation of the ωm and λm for the P–H (i) configuration. Similarly, plots (g)–(k) display the variation of ωm and λm for the P–A (ii) configuration. Unless otherwise stated, the other essential parameters used for the plots are displayed in Table 1. | |
As the dispersion relation intrinsically depends on the density contrast, viscosity, and interfacial tension between the two layers, variations in these parameters can significantly influence the system's stability characteristics if water is replaced with another fluid. For example, (i) a more viscous subphase (e.g., glycerol) would suppress short-wavelength perturbations, favoring long-wave-dominated instability; (ii) a less viscous and less dense subphase (e.g., a light oil) would diminish gravitational effects and enhance capillary and elastic contributions, thereby promoting finite-wave modes; and (iii) modifications in interfacial tension would alter the stabilizing term in the dispersion relation, consequently shifting the growth rate and the wavelength of the most unstable mode. However, the qualitative nature of the instability, particularly the coexistence and possible transition between the CIM and the FSM, is expected to remain robust. This robustness arises from the fundamental competition between viscous–gravitational destabilization and elastic–capillary stabilization that governs the bilayer dynamics. Hence, while quantitative aspects such as growth rates and characteristic wavelengths may vary with the choice of subphase, the essential physical mechanisms delineated in this study would largely persist. Furthermore, the anisotropy in the present system manifests through elastic and viscous stresses (eqn (11)), rather than through solid-like bending rigidity as happens in transversely isotropic elastic films. Thus, no direct quantitative comparison can be drawn between the two systems, although the presence of anisotropy conceptually connects them.
5. Conclusions
We investigate two asymptotic regimes – micro-thick and nano-thin bilayer systems revealing two distinct forms of RTIs – one driven by density differences and the other by intermolecular force contrasts. Mode switching from the free surface – the FSM to the confined interface – the CIM governed by the interplay of elasticity, surface tension combinations, and film thickness is observed. The analysis is performed using linear stability analysis and coupled Ericksen–Leslie and Navier–Stokes equations across different director configurations. In micro-thick films, mode selection is influenced by layer elasticity, density contrast, and thickness, revealing bimodality emergence for out-of-phase deformations and unimodal behavior for in-phase relative deformation. For nano-thin bilayers, three cases are classified based on spreading coefficient magnitudes. These cases, combined with stability analysis, assist in understanding the instability criteria across physical settings and asymptotic film behaviors when regimes where one layer dominates due to vanishing or excessive thickness. Notably, Case I shows the existence of the bimodality even at vanishingly small Kf values, with mode switching emerging as Kf increases due to reduced NLC layer deformability in the P–H configuration. Case II highlights the distinctive mode switching at P–H and P–A, indicating the predominance of layer thickness that can be harnessed to control the instability. Case III underlines the subtle role of spreading asymmetry and director orientation at boundaries to modulate the instability pathways. Comparative analysis of cases I–III demonstrates that the layer thickness, director orientations, and spreading condition serve as effective handles to modulate interfacial coupling and mode switching in bilayer systems. The identified linear modes have far-reaching consequences on the morphological evolution of thin films, representing the main uniqueness of the present investigation. The findings offer a predictive and tunable framework for precise control of the length and time scales of the instability-driven morphologies in layered NLC systems, with broader relevance to soft matter design, microfluidic patterning, and anisotropic functional material engineering involving thin films. However, fully nonlinear simulations of the present system could reveal complex interfacial morphologies arising from the nonlinear coupling of the two modes. A comprehensive nonlinear nemato-hydrodynamic analysis thus represents a promising direction for future investigation.
Author contributions
VBV and DB conceived the project. VBV, NY, and AG have performed derivations. VBV and NY performed all the simulations and analyzed and validated the results. VBV, NY, DB, and SD wrote the manuscript. DB acquired funding, supervised the progress and revised the final draft. TKM supervised the progress.
Conflicts of interest
The authors do not have any conflicts to declare.
Data availability
All the data utilized in this work are incorporated in the main manuscript. The detailed derivations concerning the manuscript are given in the supplementary information (SI). Supplementary information: the detailed derivation steps of longwave linear stability analysis and dispersion relations – Appendix A, B, and C. See DOI: https://doi.org/10.1039/d5sm00634a.
Acknowledgements
We thank the Government of India for providing financial support through MeitY Grant No. 5(1)/2022-NANO and ICMR Grant No. 5/3/8/20/2019-ITR. VBV is incredibly thankful to Dr Siddharth Thakur for engaging in discussions about the experimental relevance of the theoretical NLC bilayer systems.
References
- H. M. van der Kooij and J. Sprakel, Soft Matter, 2015, 11, 6353–6359 RSC.
- J. Marthelot, E. F. Strong, P. M. Reis and P.-T. Brun, Nat. Commun., 2018, 9, 4477 CrossRef CAS.
- S. J. Weinstein and K. J. Ruschak, Annu. Rev. Fluid Mech., 2004, 36, 29–53 CrossRef.
- J. Ralston, S. S. Dukhin and N. A. Mishchuk, Adv. Colloid Interface Sci., 2002, 95, 145–236 CrossRef CAS PubMed.
- C. Jiang, X. Wang, R. Gunawidjaja, Y.-H. Lin, M. K. Gupta, D. L. Kaplan, R. R. Naik and V. V. Tsukruk, Adv. Funct. Mater., 2007, 17, 2229–2237 CrossRef CAS.
- A. Sharma and E. Ruckenstein, J. Colloid Interface Sci., 1986, 113, 456–479 CrossRef CAS.
-
A. Sorrentino, in Nanocoatings and Ultra-Thin Films, ed. A. S. H. Makhlouf and I. Tiginyanu, Woodhead Publishing, 2011, pp. 203–234 Search PubMed.
- P. Tchoukov, F. Yang, Z. Xu, T. Dabros, J. Czarnecki and J. Sjöblom, Langmuir, 2014, 30, 3024–3033 CrossRef CAS PubMed.
- S. R. Nagel, Rev. Mod. Phys., 2017, 89, 025002 CrossRef.
- A. Sharma and R. Khanna, Phys. Rev. Lett., 1998, 81, 3463 CrossRef CAS.
- A. Sharma, Langmuir, 1993, 9, 861–869 CrossRef CAS.
- D. Bandyopadhyay and A. Sharma, J. Chem. Phys., 2006, 125, 054711 CrossRef.
- R. Konnur, K. Kargupta and A. Sharma, Phys. Rev. Lett., 2000, 84, 931 CrossRef CAS.
- C. Zhao, J. E. Sprittles and D. A. Lockerby, J. Fluid Mech., 2019, 861, R3 CrossRef CAS.
- C. Zhao, Y. Zhang and T. Si, J. Fluid Mech., 2023, 954, A46 CrossRef.
- R. Mukherjee and A. Sharma, Soft Matter, 2015, 11, 8717–8740 RSC.
- R. Martinez-Cuenca, G. Saavedra, M. Martinez-Corral and B. Javidi, J. Disp. Technol., 2005, 1, 321–327 CrossRef.
- S. Maity, T. Bhuyan, R. Bhattacharya and D. Bandyopadhyay, ACS Appl. Mater. Interfaces, 2021, 13, 19430–19442 CrossRef CAS.
- X. Fan and I. M. White, Nat. Photonics, 2011, 5 Search PubMed.
- X. Meng, Y. Lu, B. Yang, G. Yi and J. Jia, ACS Appl. Mater. Interfaces, 2010, 2, 3467–3472 CrossRef CAS.
- S. Thakur, S. Rarotra, M. Bhattacharjee, S. Mitra, G. Natu, T. K. Mandal, A. K. Dasmahapatra and D. Bandyopadhyay, Phys. Rev. Appl., 2018, 10, 064012 CrossRef CAS.
- Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 550–575 CrossRef.
- N. Sabet, H. Hassanzadeh, A. De Wit and J. Abedi, Phys. Rev. Lett., 2021, 126, 094501 CrossRef CAS PubMed.
- V. B. Vanarse, S. Thakur, A. Ghosh, P. R. Parmar and D. Bandyopadhyay, Phys. Fluids, 2024, 36, 022115 CrossRef CAS.
- P. Tabeling, G. Zocchi and A. Libchaber, J. Fluid Mech., 1987, 177, 67–82 CrossRef CAS.
- O. K. Matar and S. M. Troian, Chaos, 1999, 9, 141–153 CrossRef CAS.
- S. S. Usgaonkar, C. J. Ellison and S. Kumar, Langmuir, 2021, 37, 6660–6672 CrossRef CAS PubMed.
- D. I. Pullin, J. Fluid Mech., 1982, 119, 507–532 CrossRef.
- N. Bhandaru, A. Das and R. Mukherjee, Nanoscale, 2015, 8, 1073–1087 RSC.
- D. Bandyopadhyay, R. Gulabani and A. Sharma, Ind. Eng. Chem. Res., 2005, 44, 1259–1272 CrossRef CAS.
- D. Bandyopadhyay, A. Sharma and V. Shankar, J. Chem. Phys., 2008, 128, 154909 CrossRef.
- J. Léopoldès and P. Damman, Nat. Mater., 2006, 5, 957–961 CrossRef PubMed.
- A. R. Piriz, J. J. L. Cela, O. D. Cortázar, N. A. Tahir and D. H. H. Hoffmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 056313 CrossRef CAS.
- Y. Chao, L. Zhu and H. Yuan, Phys. Rev. Fluids, 2021, 6, 064001 CrossRef.
- A. Pototsky, M. Bestehorn, D. Merkt and U. Thiele, J. Chem. Phys., 2005, 122, 224711 CrossRef.
- D. Bandyopadhyay, A. Sharma, U. Thiele and D. S. Reddy, Langmuir, 2009, 25, 9108–9118 CrossRef CAS PubMed.
- D. Bandyopadhyay, A. Sharma and V. Shankar, EPL, 2010, 89, 36002 CrossRef.
- D. Bandyopadhyay, P. D. S. Reddy, A. Sharma, S. Joo and S. Qian, Theor. Comput. Fluid Dyn., 2012, 26, 23–28 CrossRef CAS.
- D. Bandyopadhyay, P. D. S. Reddy and A. Sharma, Phys. Fluids, 2012, 24, 074106 CrossRef.
- P. Lambooy, Phys. Rev. Lett., 1996, 76, 1110–1113 CrossRef CAS.
- M. Sferrazza, Phys. Rev. Lett., 1998, 81, 5173–5176 CrossRef CAS.
- A. Das, A. B. Dey, G. Manna, M. K. Sanyal and R. Mukherjee, Macromolecules, 2022, 55, 1657–1668 CrossRef CAS.
- N. Bhandaru and R. Mukherjee, Macromolecules, 2021, 54, 4517–4530 CrossRef CAS.
- S. Roy, D. Biswas, N. Salunke, A. Das, P. Vutukuri, R. Singh and R. Mukherjee, Macromolecules, 2013, 46, 935–948 CrossRef CAS.
-
S. Chandrasekhar, Liquid Crystals, Cambridge University Press, 1992 Search PubMed.
-
P. G. D. Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, Oxford, 1993 Search PubMed.
- F. Vandenbrouck, M. P. Valignat and A. M. Cazabat, Phys. Rev. Lett., 1999, 82, 2693 CrossRef CAS.
- B. Ravi, R. Mukherjee and D. Bandyopadhyay, Soft Matter, 2015, 11, 139–146 RSC.
- S. Žumer and J. W. Doane, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 3373–3386 CrossRef.
- C. Poulard and A. M. Cazabat, Langmuir, 2005, 21, 6270–6276 CrossRef CAS.
- A. D. Rey and E. E. Herrera-Valencia, Soft Matter, 2014, 10, 1611–1620 RSC.
- P. G. D. Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef.
- S. Thakur, A. K. Dasmahapatra and D. Bandyopadhyay, ACS Appl. Mater. Interfaces, 2021, 13, 60697–60712 CrossRef CAS.
- V. B. Vanarse, S. Thakur and D. Bandyopadhyay, Langmuir, 2025, 41, 5933–5946 CrossRef CAS PubMed.
- R. Bolleddu, S. Chakraborty, M. Bhattacharjee, N. Bhandaru, S. Thakur, P. S. Gooh-Pattader, R. Mukherjee and D. Bandyopadhyay, Ind. Eng. Chem. Res., 2020, 59, 1902–1913 CrossRef CAS.
- M. Ben Amar and L. J. Cummings, Phys. Fluids, 2001, 13, 1160–1166 CrossRef CAS.
- L. J. Cummings, Eur. J. Appl. Math., 2004, 15, 651–677 CrossRef.
- T. S. Lin, L. J. Cummings, A. J. Archer, L. Kondic and U. Thiele, Phys. Fluids, 2013, 25, 082102 CrossRef.
- T.-S. Lin, L. Kondic, U. Thiele and L. J. Cummings, J. Fluid Mech., 2013, 729, 214–230 CrossRef CAS.
- J. L. Ericksen, Arch. Ration. Mech. Anal., 1962, 9, 371–378 CrossRef.
- J. L. Ericksen, Trans. Soc. Rheol., 1967, 11, 5–14 Search PubMed.
- F. M. Leslie, Continuum Mech. Thermodyn., 1992 DOI:10.1007/BF01130288.
- C. W. Oseen, Trans. Faraday Soc., 1933, 29, 883–899 RSC.
- F. C. Frank, Discuss. Faraday Soc., 1958 10.1039/DF9582500019.
- H. Yokoyama, S. Kobayashi and H. Kamei, Mol. Cryst. Liq. Cryst., 1985, 129, 109–126 CrossRef CAS.
- V. A. Raghunathan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995 DOI:10.1103/PhysRevE.51.896.
- K. Mondal, A. Ghosh, J. Chaudhuri and D. Bandyopadhyay, J. Fluid Mech., 2018, 834, 464–509 CrossRef CAS.
- D. H. Sharp, Phys. D, 1984 DOI:10.1016/0167-2789(84)90510-4.
- L. Rayleigh, Philos. Mag., 1882, 14, 184–186 Search PubMed.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1950, 201, 192–196 Search PubMed.
- P. Dhara and R. Mukherjee, London, Edinburgh Dublin Philos. Mag. J. Sci., 2020, 124, 1293–1300 CAS.
- M. J. Stephen and J. P. Straley, Rev. Mod. Phys., 1974, 46, 617–704 CrossRef CAS.
- S. J. Tavener, T. Mullin, G. I. Blake and K. A. Cliffe, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 011708 CrossRef.
- L. J. Cummings, T.-S. Lin and L. Kondic, Phys. Fluids, 2011, 23, 043102 CrossRef.
- D. van Effenterre, M. P. Valignat and D. Roux, Europhys. Lett., 2003, 62, 526–532 CrossRef CAS.
- M.-P. Valignat, D. Duca, R. Barberi, A.-M. Cazabat and R. Bartolino, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 301, 151–156 CrossRef CAS.
- M. P. Valignat, S. Villette, J. Li, R. Barberi, R. Bartolino, E. Dubois-Violette and A. M. Cazabat, Phys. Rev. Lett., 1996, 77, 1994–1997 CrossRef CAS PubMed.
- E. Perez, J. E. Proust and L. Ter-Minassian-Saraga, Colloid Polym. Sci., 1978, 256, 784–792 CrossRef CAS.
- C. J. Van Oss, M. K. Chaudhury and R. J. Good, Chem. Rev., 1988, 88, 927–941 CrossRef CAS.
- S. G. Yiantsios and B. G. Higgins, Phys. Fluids, 1989, 1, 1484–1501 CrossRef CAS.
- C. Maldarelli, R. K. Jain, I. B. Ivanov and E. Ruckenstein, J. Colloid Interface Sci., 1980, 78, 118–143 CrossRef CAS.
- K. D. Danov, V. N. Paunov, N. Alleborn, H. Raszillier and F. Durst, Chem. Eng. Sci., 1998, 53, 2809–2822 CrossRef CAS.
- K. D. Danov, V. N. Paunov, S. D. Stoyanov, N. Alleborn, H. Raszillier and F. Durst, Chem. Eng. Sci., 1998, 53, 2823–2837 CrossRef CAS.
- V. N. Paunov, K. D. Danov, N. Alleborn, H. Raszillier and F. Durst, Chem. Eng. Sci., 1998, 53, 2839–2857 CrossRef CAS.
- S. Herminghaus, K. Jacobs, K. Mecke, J. Bischof, A. Fery, M. Ibn-Elhaj and S. Schlagowski, Science, 1998, 282, 916–919 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Neeru
Yadav
a,
Srijita
De
a,
Neeru
Yadav
a,
Srijita
De
 b,
Abir
Ghosh
c,
Tapas Kumar
Mandal
b,
Abir
Ghosh
c,
Tapas Kumar
Mandal
 abd and
Dipankar
Bandyopadhyay
abd and
Dipankar
Bandyopadhyay
 *abd
*abd

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, cos
θ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where θ represents the director angle with positive z-axis (Fig. 1(b)) that also satisfies eqn (3). The other variables in eqn (4) are – the body force due to any external field (G), an intrinsic director and body force (g). In our formulation, there is no external field present that leads to G = 0, and g reads as,
θ), where θ represents the director angle with positive z-axis (Fig. 1(b)) that also satisfies eqn (3). The other variables in eqn (4) are – the body force due to any external field (G), an intrinsic director and body force (g). In our formulation, there is no external field present that leads to G = 0, and g reads as,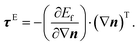
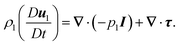

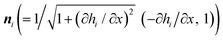 and
and  represent the surface gradient operator, outward surface normal, and tangent vectors. At the NI interface, we assume that there exists no tangential surface tension gradient, which leads to no jump at NI, that is n2·T2·n2 = −γ2κ2 and n1·T2·t1 = 0, since T0 = 0 (eqn (16) and (17)) for the bounding medium (air), making it appropriate for assumed strong anchoring conditions. Essentially, by maintaining the general form of normal and tangential stresses at the interface, the derived equation can examine different body and interface forces arising from specific influences such as gravity and surface tension and including disjoining pressures within the body force potential term. Furthermore, the strong anchoring boundary conditions are executed to express the director field (n) in order to achieve the planar (P) and homeotropic (H) director positions at NW and NI, respectively. In this study, the LC–water interface is modeled with boundary conditions representing two experimentally relevant anchoring types, as mentioned above, which are commonly observed in NLCs like 5CB. The polarity of water aligns the LC's polar cyano (–CN) groups toward the aqueous phase, promoting homeotropic or tilted orientation, while the hydrophobic alkyl chains orient away.71 These molecular interactions form the physical basis for the imposed boundary conditions. The enforcement of these boundary conditions at NW (z = h1(x, t)) and NI (z = h2(x, t)) leads to,
represent the surface gradient operator, outward surface normal, and tangent vectors. At the NI interface, we assume that there exists no tangential surface tension gradient, which leads to no jump at NI, that is n2·T2·n2 = −γ2κ2 and n1·T2·t1 = 0, since T0 = 0 (eqn (16) and (17)) for the bounding medium (air), making it appropriate for assumed strong anchoring conditions. Essentially, by maintaining the general form of normal and tangential stresses at the interface, the derived equation can examine different body and interface forces arising from specific influences such as gravity and surface tension and including disjoining pressures within the body force potential term. Furthermore, the strong anchoring boundary conditions are executed to express the director field (n) in order to achieve the planar (P) and homeotropic (H) director positions at NW and NI, respectively. In this study, the LC–water interface is modeled with boundary conditions representing two experimentally relevant anchoring types, as mentioned above, which are commonly observed in NLCs like 5CB. The polarity of water aligns the LC's polar cyano (–CN) groups toward the aqueous phase, promoting homeotropic or tilted orientation, while the hydrophobic alkyl chains orient away.71 These molecular interactions form the physical basis for the imposed boundary conditions. The enforcement of these boundary conditions at NW (z = h1(x, t)) and NI (z = h2(x, t)) leads to,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1,
θ1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2.
θ2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + α4 + (α2 + α5)sin2
θ + α4 + (α2 + α5)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + (α6 − α3)cos2
θ + (α6 − α3)cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). Solving the aforementioned governing equations and boundary conditions and substituting the obtained terms in the kinematic condition result in the evolution equations for the respective layers. For the NLC layer, the Leibnitz formula is utilized to transform eqn (19) into a mathematically more convenient form,
θ). Solving the aforementioned governing equations and boundary conditions and substituting the obtained terms in the kinematic condition result in the evolution equations for the respective layers. For the NLC layer, the Leibnitz formula is utilized to transform eqn (19) into a mathematically more convenient form, 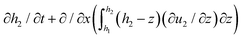 . The resulting evolution equations, detailed below, describe the stability, dynamics, and morphology of both NI and NW.
. The resulting evolution equations, detailed below, describe the stability, dynamics, and morphology of both NI and NW.

 ;
;  ;
;  ;
;  ; and
; and  . Here, we call P2M = P2 + 0.5Kf(∂θ/∂z)2 as a modified pressure, and the NLC bulk viscosity is defined by μ2 = 0.5α4, where, α4 is the fourth Leslie coefficient.
. Here, we call P2M = P2 + 0.5Kf(∂θ/∂z)2 as a modified pressure, and the NLC bulk viscosity is defined by μ2 = 0.5α4, where, α4 is the fourth Leslie coefficient.
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ieωt+ikx), where, hi0, ω, k and
ieωt+ikx), where, hi0, ω, k and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) i are the mean or base thickness, linear growth rate of disturbance, wavenumber, and infinitesimal initial surface perturbation amplitudes. The present longwave formulation utilizes strong anchoring conditions, where surface and interfacial tensions are assumed constant. Therefore, it is essential to understand that constant interfacial tensions correspond to the fixed base-state director angles θ1 and θ2. Moreover, if an explicit γ(θ) was included, the surface tension would vary locally with the perturbation amplitude. The resulting dispersion relation (see Bandyopadhyay et al. (2005) for a detailed derivation of the isotropic bilayer)30 from eqn (33) and (34) is expressed as follows:
i are the mean or base thickness, linear growth rate of disturbance, wavenumber, and infinitesimal initial surface perturbation amplitudes. The present longwave formulation utilizes strong anchoring conditions, where surface and interfacial tensions are assumed constant. Therefore, it is essential to understand that constant interfacial tensions correspond to the fixed base-state director angles θ1 and θ2. Moreover, if an explicit γ(θ) was included, the surface tension would vary locally with the perturbation amplitude. The resulting dispersion relation (see Bandyopadhyay et al. (2005) for a detailed derivation of the isotropic bilayer)30 from eqn (33) and (34) is expressed as follows:![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1ω +
1ω + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2A +
2A + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1B = 0,
1B = 0,![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2ω +
2ω + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2C +
2C + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1D = 0,
1D = 0,
 and d0(∼0.157 nm) is the van der Waals cut-off distance between the two surfaces, determined by incorporating the short-range Born repulsion.30,79 The excess free energy (ΔGLWE) for the present bilayer configuration can be expressed as,47,76,78
and d0(∼0.157 nm) is the van der Waals cut-off distance between the two surfaces, determined by incorporating the short-range Born repulsion.30,79 The excess free energy (ΔGLWE) for the present bilayer configuration can be expressed as,47,76,78
 is a constant and obtained from the angular momentum balance equation. The total pressures (P1 = p0 − γ2∂2h2/∂x2 − γ12∂2h1/∂x2 − Π1) and (P2 = p0 − Kf(∂θ/∂z)2 − γ2∂2h2/∂x2 − Π2) at the NW and NI interfaces are double differentiated (details in the SI) with respect to x and then linearized as follows,
is a constant and obtained from the angular momentum balance equation. The total pressures (P1 = p0 − γ2∂2h2/∂x2 − γ12∂2h1/∂x2 − Π1) and (P2 = p0 − Kf(∂θ/∂z)2 − γ2∂2h2/∂x2 − Π2) at the NW and NI interfaces are double differentiated (details in the SI) with respect to x and then linearized as follows,

![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1ω +
1ω + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2A′ +
2A′ + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1B′ = 0,
1B′ = 0,![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2ω +
2ω + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 2C′ +
2C′ + ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) 1D′ = 0,
1D′ = 0,





















