Open Access Article
Open Access ArticleThermodynamics of microphase separation in a swollen, strain-stiffening polymer network
Carla
Fernández-Rico†
 a,
Robert W.
Style†
a,
Robert W.
Style†
 a,
Stefanie
Heyden
b,
Shichen
Wang
a,
Stefanie
Heyden
b,
Shichen
Wang
 c,
Peter D.
Olmsted
c,
Peter D.
Olmsted
 c and
Eric R.
Dufresne
c and
Eric R.
Dufresne
 *d
*d
aDepartment of Materials, ETH Zürich, 8093 Zurich, Switzerland
bDepartment of Civil, Environmental and Geomatic Engineering, ETH Zürich, 8093 Zurich, Switzerland
cDepartment of Physics, and Institute for Soft Matter Synthesis and Metrology, Georgetown University, Washington, DC 20057, USA
dDepartment of Materials Science and Engineering, Department of Physics, Cornell University, Ithaca, NY 14853, USA. E-mail: erd43@cornell.edu
First published on 16th December 2025
Abstract
Elastic MicroPhase separation (EMPS) provides a simple route to create soft materials with homogeneous microstructures by leveraging the supersaturation of crosslinked polymer networks with liquids. At low supersaturation, network elasticity stabilizes a uniform mixture, but beyond a critical threshold, metastable microphase-separated domains emerge. While previous theories have focused on describing qualitative features about the size and morphology of these domains, they do not make quantitative predictions about EMPS phase diagrams. In this work, we extend Flory–Huggins theory to quantitatively capture EMPS phase diagrams by incorporating strain-stiffening effects. This model requires no fitting parameters and relies solely on independently measured solubility parameters and large-deformation mechanical responses. Our results confirm that strain-stiffening enables metastable microphase separation within the swelling equilibrium state and reveal why the microstructures can range from discrete droplets to bicontinuous networks. This works highlights the critical role of nonlinear elasticity in controlling phase-separated morphologies in polymer gels.
1 Introduction
Phase separation is a ubiquitous process that can be harnessed to create structured materials.1,2 In this process, two or more components demix, typically triggered by changes in temperature, composition, or degree of polymerization.3–5 Demixing creates microstructures with discrete domains or bicontinuous channels. For classical phase-separation processes, like liquid–liquid phase separatation, domains gradually coarsen due to the influence of surface tension.6,7 When this coarsening is arrested (for example by solidification, or going through a glass transition8–10), solid materials with intricate and stable microstructures can be created.11,12 Synthetic examples include metal alloys,13 membranes,14 and cell tissue scaffolds,15,16 while natural examples include structurally-colored materials produced by many different animals,17,18 and phase-separated domains inside cytoplasm and lipid membranes.19–22Recently, elastic microphase separation (EMPS) has emerged as an alternative, convenient route to create phase-separated microstructures that do not coarsen.11,23,24 In essence, EMPS exploits mechanical forces imposed by a polymer network to counteract interfacial tension. In typical EMPS experiments, an elastomer is equilibrated with solvent at high temperatures (see Fig. 1A). Then, cooling triggers phase separation of the solvent within the elastomer. Phase separation occurs rapidly and locally, within a few seconds. Microstructures with either discrete droplets or bicontinuous channels form, depending on the elastomer's degree of swelling and stiffness (see Fig. 1B and C). This process is simple and robust enough to easily produce large pieces of material with precisely controlled microstructures. While these microphase-separated structures are stable to coarsening, they are unstable to the loss of solvent to the surrounding bath on a timescale that is O(10 h).25 The onset of elastic microphase separation is characterized by a novel phase boundary inside the super-saturated regime of the network-solvent swelling equilibrium, as described in ref. 23 and 24.
 | ||
| Fig. 1 Schematic of EMPS. (A) First, an elastomer is swollen in a liquid bath at elevated temperatures. After swelling equilibrium is reached, cooling induces phase separation. Different phase separated morphologies and sizes are obtained as a function of the matrix's composition and stiffness: (B) droplet23 and (C) bicontinuous morphologies.24 | ||
EMPS is closely connected to liquid–liquid phase separation. At the monomer scale, both the elastomer and solvent are liquid-like. Thus, we expect the earliest stages of phase separation to be insensitive to the relatively sparse elastic constraints imposed by the cross-links between the polymer chains. However, at later stages of phase separation, we expect the elasticity of the polymer phase to become important – in a similar fashion to how elasticity controls swelling and volume phase transitions in gels.26–35 Indeed experiments suggest that the elastomer's Young's modulus plays an essential role in defining morphology and thermodynamics.23–25,36 Importantly though, theoretical studies agree that linear elasticity is insufficient to capture key aspects of the experiments. For example, previous works have investigated the role of mesh size,37,38 viscoelasticity,39 damage,40,41 and heterogeneous or non-local elasticity42–46 and non-linear elasticity.37,47,48
Out of all these topics, several recent theoretical studies have emphasized that strain stiffening of the polymer network should be a key feature controlling EMPS. For example, strain-stiffening has been shown to play a role in setting the scale of of microphase-separated structures,48–51 in determining whether separated domains can grow larger than the mesh size of an elastomer,37 and in cavitation: where solvent-filled droplets form in quenched elastomers.52 Finally, Hennessy et al.47 showed that 1D gels with non-linear elasticity have similar phase diagrams to EMPS with two distinct phase boundaries. While all of the above theories qualitatively capture different aspects of EMPS, there have been no quantitative comparisons of theory and experiments.
Here, we explore the impact of strain-stiffening on the phase separation of liquids within elastic matrices by extending Flory–Huggins’ (FH) theory of macromolecular liquid–liquid phase separation, incorporating energy stored in large elastic deformations. We show that strain-stiffening enables metastable microphase separation in a subset of the super-saturated region of the swelling phase diagram – indeed, this type of phase separation does not occur without strain stiffening. Using this model, we can quantitatively predict EMPS phase diagrams from measurements of the (i) stress–strain relationship of the neat elastomer and (ii) solubility of uncrosslinked polymer in the solvent. These predictions are in reasonable agreement with measured phase diagrams of fluorinated oil in a silicone elastomer. Finally, we discuss the role of cavitation instabilities in selecting the microphase-separated morphology.
2 Liquid–liquid phase separation
In order to understand how elasticity affects phase separation, we start by characterizing liquid–liquid phase separation of the elastomer's uncrosslinked polymer precursors in the solvent of interest. Here, this consists of 28 kDa vinyl-terminated PDMS chains in heptafluorobutyl methacrylate (HFBMA, 268.1 Da) (see Fig. 2A). As reported previously,24 we determine the phase diagram of this system by recording the temperature at which phase separation initiates during simultaneous cooling and observation under a light microscope (see Materials & methods). The resulting phase diagram takes the classical LLPS form shown in Fig. 2B (see black circles). Above a critical temperature Tc ≈ 60 °C, the two fluids are always miscible. At lower temperatures, demixing occurs for a range of HFBMA volume fractions, ϕ, in the mixture.LLPS phenomena can be described using Flory–Huggins (FH) theory,53 which expresses the stability of solvent–polymer mixtures based on an expression for the dimensionless Helmholtz free energy per unit volume of a mixture of the form:54
 | (1) |
To convert an expression for free energy, like that above, into a phase diagram, we use the classical approach illustrated in Fig. 2C and D.54Fig. 2C and E show schematic representations of fFH at different temperatures (Fig. 2C and E). Above Tc, fFH(ϕ) is globally convex downward, due to the dominance of the entropic terms (see Fig. 2C). The free energy of the mixture can not be lowered by separating into two phases. Thus, the system remains completely mixed. Below Tc, the enthalpy of mixing becomes more important, and fFH develops concavity (see Fig. 2E). In this case, phase separation can occur because the system's free energy can be reduced by splitting into two different phases. The range of ϕ where phase separation occurs can be found by applying the double-tangent construction (see full derivation in Appendix A), which essentially consists of a tangent line (see yellow line in Fig. 2E) that connects the bottom sides of the two convex regions. This double-tangent line ensures that the chemical potentials of the solvent and the polymer are equal in both phases, fulfilling the condition for phase equilibrium. Furthermore, the points of tangency (yellow crosses in Fig. 2E) then represent the equilibrium composition of the two phases and are known as the binodal points.
The range of ϕ over which the system undergoes phase separation can be further subdivided, based on the curvature of fFH. When ∂2fFH/∂ϕ2 > 0 (outside the blue crosses), the mixture is metastable and phase separation occurs by localized nucleation and growth (see droplet morphologies in Fig. 2D). When ∂2fFH/∂ϕ2 < 0, (between the blue crosses, Fig. 2E), the mixture is unstable, and system separates continuously through spinodal decomposition (see interconnected structures in Fig. 2D).54 By performing this calculation across a range of different temperatures, we construct the binodal and spinodal curves of the phase diagram shown in Fig. 2D.
To fit our LLPS data using Flory–Huggins theory, we need to determine vs/vp and χ(ϕ,T). While vs/vp is easily calculated from molar volumes of the two components (vs/vp = 6.90 × 10−3), we fit the experimental binodal (black circles in Fig. 2A) with χ(ϕ,T)58 using the simplest ϕ-dependent form:59–61
| χ(ϕ,T) = A + B/T + Cϕ. | (2) |
We find best-fit values of A = 0.2108, B = 247.76 K and C = −0.227 (see fitted binodal and spinodal dashed lines in Fig. 2B).
Although it may seem excessive to use three fitting parameters to fit 6 data points, it is not possible to fit the data with less, as each parameter has a separate effect on the phase diagram: A essentially moves the phase diagram up and down, B changes the width of the peak, while C is the only parameter that moves the peak laterally. See the supplement for a description of the fitting process, and a demonstration that the results presented here are insensitive to changes in these fitting parameters and to the specific form chosen for χ.
In Section 3.4, we will use these parameters to predict EMPS phase diagrams. This assumes that χ(ϕ,T) does not change when the silicone chains cross-link into an elastic network.
3 Phase separation in an elastic network
In this section, we briefly review the essential features of phase diagrams in elastic microphase separating systems before extending Flory–Huggins theory to account for large-deformation elasticity of polymer matrices upon swelling and phase separation.Compared to LLPS, crosslinking silicone chains into elastic networks qualitatively changes phase separation of HFBMA in silicone. This is shown in the experimental phase diagrams for polymer networks with shear moduli μ = 485 kPa and 118 kPa shown in Fig. 3A and B respectively. The higher boundary (circles) represents macroscopic swelling equilibrium of the silicone swollen in pure HFMBA (see sketch Fig. 3C(i)). Below this boundary (shallow quench), the system is super-saturated, but no microscopic phase separation is observable (see Fig. 3C(ii)). Instead, the solvent inside the matrix diffuses to the bath until it reaches a new swelling equilibrium (see Fig. 3C(iv)). This deswelling process takes a time τdeswell = O(10 h) for a cm-scale sample. The lower boundary (crosses) marks the onset of microphase separation. When cooled below this line (deep quench), the system undergoes microscopic phase separation as shown in Fig. 3C(iii). This microscopic process occurs within a much shorter time, τμPS = O(1 min), and involves no exchange of material out of the gel. The micro-scale structures are metastable and after a long time, τdeswell, the solvent inside the microstructures diffuses to the bath and reaches a new swelling equilibrium (see dashed arrows). The microphase-separation boundary does not behave like classical spinodal and binodal curves. Like a spinodal, we observe a continuous phase transformation when the boundary is crossed. Like a binodal, phase-separated domains dissolve at the same temperature they form.24
Importantly, the size of the gap between the swelling equilibrium and microphase boundaries depends on the stiffness of the unswollen silicone, with the stiffer silicone having a much larger gap than the softer one.24 The gap, or ‘mechanically-stabilized regime’, vanishes as stiffness decreases, and the two phase boundaries merge into one that approaches the LLPS phase boundary in Fig. 2B.
There are two further key differences between the phase diagram for a solvent in an elastic network and the phase diagram for liquid mixtures. First, there are no phase boundaries at high temperature (above the critical point) in liquid mixtures. However, swollen elastic networks always have at least one phase boundary at any temperature – the swelling equilibrium curve. Second, while phase-separated domains in LLPS always coarsen (due to coalescence and Ostwald ripening),39,44 this coarsening is completely suppressed in the microphase separation in EMPS.23–25
3.1 Thermodynamics of phase separation in an elastic network
To model these phenomena, we update the free-energy density shown in eqn (1) to include the effects of crosslinking of the silicone chains into an elastic network. Crosslinking removes the translational entropy of the polymer (i.e., the second term in eqn (1)) as vp/vs → ∞.‡ We account for elasticity of the polymer network by simply adding an additional elastic free-energy density fel to fFH.26,47,50,62,63 Then, the resulting free-energy density isftot(ϕ,T) = ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + χ(ϕ,T)ϕ(1 − ϕ) + fel(ϕ). ϕ + χ(ϕ,T)ϕ(1 − ϕ) + fel(ϕ). | (3) |
For comparison with data, we will assume that crosslinking does not alter the form of χ(ϕ,T) (eqn (2)). Here, fel is related to the standard strain-energy density, Wel, from elasticity theory, as:
 | (4) |
Here, the factor of kBT/vs non-dimensionalizes Wel, while the factor of (1 − ϕ) converts from a free energy per volume of dry polymer to a free energy per unit volume in the swollen state. In general, Wel is a function of the principal stretches in the polymer network: λ1, λ2, λ3. For many simple polymer networks,64
Wel = ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) el(I1) − αμ el(I1) − αμ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J, J, | (5) |
3.2 Characterizing polymer network elasticity
We obtain expressions for![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) el(I1) for our polymer networks by performing large extension tensile tests on unswollen samples (ϕ = 0, J = 1) of the five different types of silicone elastomers used in our EMPS experiments (see Materials and methods). Example plots of engineering stress, σeng, versus stretch, λ, are shown in Fig. 4 for several different stiffness silicone networks.
el(I1) for our polymer networks by performing large extension tensile tests on unswollen samples (ϕ = 0, J = 1) of the five different types of silicone elastomers used in our EMPS experiments (see Materials and methods). Example plots of engineering stress, σeng, versus stretch, λ, are shown in Fig. 4 for several different stiffness silicone networks.
 | ||
| Fig. 4 Mechanical characterization of the silicone polymer networks prior to swelling with the HFBMA solvent. Examples of engineering stress versus stretch λ for an incompressible uniaxial extension, with neo-Hookean curves fitted up to λ = 2 and then Arruda–Boyce curves fit over the whole range of λ. The inset shows the Arruda–Boyce fit parameters for all the materials used here (see Table 1 in Materials and methods). Error bars show standard deviations of the measured values. | ||
At small stretch (λ ≲ 2), all the polymer networks can be well-described by classical (non strain-stiffening) neo-Hookean solids (see fits as green dashed lines in Fig. 4), with
 | (6) |
![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) el as:67
el as:67 | (7) |
For λ > 2, all our silicone elastomers strain stiffen, diverging from the neo-Hookean model predictions (see fits as green dashed lines in Fig. 4). To capture this behavior, we fit the results with the strain-stiffening Arruda–Boyce model.68 This continuum model is based on the physics of the underlying polymer chains, accounting for the limiting stretch of each chain. The Arruda–Boyce model can be approximated by
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750. Again, μ is the small-strain shear modulus, while λm is the maximum “locking” stretch of individual polymer chains relative to their end-to-end distance in the as-prepared elastomers. The stress–stretch relationship is again found by inserting the strain-energy density into eqn (7). The resulting fits are shown in Fig. 4 as the red dashed lines, showing a good agreement between the data and the model over the whole range of λ. We extract values of μ and λm for five different polymer networks containing different amounts of crosslinker, and obtain values of μ ranging from 10 to ∼490 kPa and λm values ranging from 4 and 3 (see Table 1, Materials and methods), as shown in the inset in Fig. 4. Note that, in uniaxial tension, samples can reach stretches λ > λm. This is counterintuitive, but permitted, as individual chains stretch significantly less than the applied macroscopic stretch λ applied to a sample. E.g., in the Arruda–Boyce model, individual chain stretch during a uniaxial test is
750. Again, μ is the small-strain shear modulus, while λm is the maximum “locking” stretch of individual polymer chains relative to their end-to-end distance in the as-prepared elastomers. The stress–stretch relationship is again found by inserting the strain-energy density into eqn (7). The resulting fits are shown in Fig. 4 as the red dashed lines, showing a good agreement between the data and the model over the whole range of λ. We extract values of μ and λm for five different polymer networks containing different amounts of crosslinker, and obtain values of μ ranging from 10 to ∼490 kPa and λm values ranging from 4 and 3 (see Table 1, Materials and methods), as shown in the inset in Fig. 4. Note that, in uniaxial tension, samples can reach stretches λ > λm. This is counterintuitive, but permitted, as individual chains stretch significantly less than the applied macroscopic stretch λ applied to a sample. E.g., in the Arruda–Boyce model, individual chain stretch during a uniaxial test is  .69 Thus, chain locking (which causes stress divergence) will only occur when this reaches λm. I.e. for a material with λm = 3, the maximum possible uniaxial sample stretch is λ = 5.2.
.69 Thus, chain locking (which causes stress divergence) will only occur when this reaches λm. I.e. for a material with λm = 3, the maximum possible uniaxial sample stretch is λ = 5.2.
| Crosslinker density (mol%) | μ AB (kPa) | λ m (—) |
|---|---|---|
| 12.9 | 485.3 | 3.2 |
| 10.3 | 158.4 | 3.0 |
| 7.4 | 117.7 | 3.2 |
| 6.4 | 29.8 | 2.6 |
| 5.2 | 9.8 | 3.7 |
Note that in previous works23,24 we characterized the same silicone samples using indentation with a flat punch. Here, we characterize the materials using uniaxial tension testing, as this allows us to probe the large-strain material response, and provides more accurate measurements. We also use μ instead of the Young's modulus E (which we reported previously), as this is a more natural parameter for working with swollen materials.70
With the mechanical fits, we now have expressions for fel that we can use in the total free energy (3). This allows us to compare the predicted phase diagrams for the neo-Hookean and Arruda–Boyce models, and examine the role of strain-stiffening in EMPS.
3.3 Phase separation in a neo-Hookean matrix
We first examine the stability of swollen neo-Hookean networks. This is the simplest hyperelastic model, and does not feature any strain stiffening. To do this, we insert eqn (6) into eqn (4) to obtainfnhel = 3![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) [(1 − ϕ)1/3 − (1 − ϕ)], [(1 − ϕ)1/3 − (1 − ϕ)], | (9) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = μ/(2kBT/vs) is the dimensionless, small-strain shear modulus. The form of fnhel(ϕ) is shown in Fig. 5A. Interestingly, it does not monotonically increase as the network swells. This is because the network volume increases faster than the total stored elastic energy in the system. Thus, the elastic energy density (measured with respect to the current state) decreases at high swelling.
= μ/(2kBT/vs) is the dimensionless, small-strain shear modulus. The form of fnhel(ϕ) is shown in Fig. 5A. Interestingly, it does not monotonically increase as the network swells. This is because the network volume increases faster than the total stored elastic energy in the system. Thus, the elastic energy density (measured with respect to the current state) decreases at high swelling.
To calculate the phase diagram for EMPS, where we ignore the slow exchange of solvent with the surroundings, we must include fnhel(ϕ) in the free energy, eqn (3) (see full expression in Appendix B). Then, ftot(ϕ) takes the form shown schematically in Fig. 5C, where the curve is convex for small ϕ, and concave for large ϕ (where elasticity dominates). This concave section indicates the presence of phase separation, but there is no stabilizing convexity at large ϕ, which is needed to perform the double-tangent construction. Hence, thermodynamic phase separation between networks at different levels of swelling (i.e. EMPS) is not possible using neo-Hookean elasticity and the measured χ(ϕ,T).
However, there is a macroscopic swelling equilibrium between pure HFMBA and a swollen network, which occurs at long times. Geometrically, this is found with a single-tangent construction that passes through the point where (ftot = 0, ϕ = 1) (see dotted line in the figure, and derivation in Appendix A). The tangent point (yellow cross) then represents swelling equilibrium in pure solvent, while spinodal decomposition still happens when ∂2ftot/∂ϕ2 < 0 (to the right of the blue cross). The resulting schematic form of the phase diagram is shown in Fig. 5B. Note that the swelling equilibrium curve is essentially the same as the predictions of Flory–Rehner theory.26
Overall, the resulting phase diagram does not fully capture the EMPS behavior seen in Fig. 3. While this model is capable of describing the swelling equilibrium boundary (long-time equilibrium at fixed chemical potential, with solvent exchange between the gel and the surroundings) it cannot predict EMPS (short-time phase separation at fixed volume). Note that the spinodal boundary (see dashed boundary in Fig. 5B) cannot explain the onset of EMPS. If phase separation were to occur at the spinodal, the resulting phase-separated domains would only dissolve when heated up to the separate binodal curve. However, when observing EMPS in experiments, we see the formation and dissolution of microphase separated domains at the same temperature.24
3.4 Phase separation in a strain-stiffening matrix
When we introduce strain-stiffening into the elastic network, we obtain a phase diagram (see Fig. 6) which much more closely resembles the EMPS phase diagram (Fig. 3A and B). Now, we use the Arruda–Boyce strain-energy density, eqn (8) to obtain the elastic free energy-density, fabel(ϕ):71 | (10) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) = μ/(2kBT/vs), as before.
= μ/(2kBT/vs), as before.
The typical form of fabel is shown in Fig. 6A. While the free energy density decreased monotonically in the neo-Hookean case, there is now a divergence in the elastic energy density as the chains reach their locking stretch: 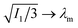 . This occurs when ϕ → (λm3 − 1)/λm3.
. This occurs when ϕ → (λm3 − 1)/λm3.
At high temperature (Fig. 6B), ftot is convex. A single-tangent construction (dashed yellow line) reveals the macroscopic swelling equilibrium of a swollen network with pure solvent (yellow cross). At lower temperatures (Fig. 6D), ftot becomes partially concave. As before, a single-tangent construction yields the macroscopic swelling equilibrium (yellow cross). However, now a double-tangent construction (green dotted line) also reveals the coexistence of two partially-swollen phases (green crosses). These states have a higher energy than the macroscopic swelling equilibrium (the green line is above the yellow line). Thus, the partially-swollen phases are metastable with respect to deswelling to the macroscopic swelling equilibrium.§ However, when the system is thermally quenched, the microphase separation into partially-swollen states is kinetically favored, since it can be achieved through rapid exchange of solvent between microscopic domains on a timescale τμPS ≃ R2/D, where D is a diffusion coefficient and R ≃ µm is the characteristic domain size. To reach the macroscopic swelling equilibrium, solvent must be transported across the whole sample, which takes a time τds ≃ L2/D, where L ≃ mm–cm is the sample size. The ratio of timescales τds/τμPS ∼ 106–108 can be enormous, leading to the persistent EMPS phase. Note that such behavior follows Ostwald's step rule by proceeding through phases with successively lower free energies.72
The form of the phase diagram for a swollen strain-stiffening network is shown schematically in Fig. 6C. It displays the essential features of the data in Fig. 3. In particular, we obtain the two phase boundaries, representing where macroscopic swelling equilibrium (yellow curve) and metastable microphase separation (green curve) occur. Thus, strain-stiffening behavior appears to be a key ingredient in capturing the phase behavior of EMPS.
Using this strain-stiffening model of elasticity, we obtain reasonable agreement between calculated phase diagrams and our experimental data, as shown in Fig. 7. There, we have used χ(ϕ,T) from the fit of LLPS of HFBMA and silicone and μ and λB from the stress–strain curves of neat (ϕ = 0) silicone elastomers. Thus, there are no fitting parameters specific to EMPS (see the full expression for ftot in Appendix B). There is surprisingly good agreement between theory and experiments for both the macroscopic swelling equilibria, and microphase phase separation boundaries (Fig. 7). Deviations between predictions and experiments are largest at high stiffnesses. In that limit, however, the predictions still capture essential trends.
Elasticity has different effects on the two phase boundaries in EMPS. We highlight this by separating the predicted macroscopic swelling equilibrium curves and microphase separation curves into two panels (see Fig. 8A and B – yellow curves show LLPS results). The predicted macroscopic swelling equilibrium is quite strongly affected by increasing network stiffness (Fig. 8A): the stiffer the network, the less it swells, especially at higher temperatures. By contrast, the predicted microphase phase boundary is relatively insensitive to changes in network stiffness (Fig. 8B) – leading to an increasing ‘mechanically-stablized regime’ between the two boundaries as stiffness increases. We note, that there is a small overall movement of this microphase phase boundary to higher temperatures with increasing stiffness.
The elastic properties μ and λm have different effects on phase equilibria. Results for varying μ at fixed λm are shown in Fig. 8C and D, and for varying λm at fixed μ are shown in Fig. 8E and F. The results show that the polymer network's stiffness has a significantly larger impact than λm in the position of the swelling equilibrium curve (see Fig. 8C and E), suggesting that macroscopic swelling equilibrium is relatively insensitive to strain-stiffening. On the other hand, the microphase-separation binodals seem to be similarly sensitive to both stiffness and strain-stiffening with a shift towards higher temperatures and slightly lower solvent-rich composition with increasing μ and λm.
3.5 Structure: channels vs. cavitation
In EMPS experiments, we generally observe the formation of bicontinuous structures at the onset of microphase separation (see Fig. 1B). The domains are swollen polymer networks, with different concentrations of solvent. This bicontinuous structure is stable in stiff networks (μ > 200 kPa). In soft networks, the bicontinous morphology is unstable, and we observe the nucleation and grown of droplets of pure solvent, embedded in swollen networks.24 The composition of the droplets can be quantified with stimulated Raman spectroscopy (SRS), see Fig. 9A, which shows the presence of holes in the silicone network (see right Fig. 9A), filled in with pure HFBMA solvent (see left image Fig. 9A). The latter state can only occur when the phase separation is able to cavitate the silicone networks – i.e. to push open macroscopic, liquid-filled holes in the polymer networks.23,37,40,49,73 Our theoretical model can be further extended to capture the onset of this cavitation behavior.For cavitation to occur, the excess pressure of solvent that fills any microscopic flaws in the material has to reach a critical value Pc ∼ μ (e.g. Pc = 5μ/2 for incompressible neo-Hookean elastomers74). At this point, the liquid can push open the flaws without a further increase in pressure.23 Thus, the criterion for observation of droplets is when the solvent in the EMPS system is in equilibrium with pure solvent in the cavities with an excess pressure, Pc. As shown in Appendix A, this condition can be found graphically with an additional single-tangent construction: cavitation can occur at any concentration, ϕ, when the tangent line to ftot at that concentration (e.g. dashed lines, Fig. 9B) meets the right-hand vertical axis above the point [ϕ = 1, ftot = Pcvs/(kBT)]. This last point represents pure solvent at an excess pressure, Pc. For example, in Fig. 9B, we show the three concentrations where the cavitation condition is exactly met (yellow crosses). In this case, cavitation can only occur in the marked ranges in the figure.
With this, we can predict quite accurately when cavitation occurs. Fig. 9C shows observed microphase separated morphologies in our experimental system. We saturate polymer networks in the HFBMA solvent at 60 °C and cool them down, and observe when phase separation/cavitation occurs. For small amounts of cooling there is no phase separation (see green area Fig. 9C). For intermediate cooling, we observe microphase separation with a bicontinuous morphology (see blue area Fig. 9C). For deep cooling, or the softest materials, the bicontinuous morphology abruptly changes to droplets (see orange area Fig. 9C). We next apply the two tangent constructions (see Fig. 6D and 9B) to predict the phase separation boundary (dotted curve in Fig. 9C) and cavitation threshold (dashed curve in Fig. 9C). For the cavitation boundary, we assume that the cavitation threshold in our swollen strain-stiffening material is the same as for an incompressible neo-Hookean network (Pc = 5μ/2). Even with this drastically simplifying assumption we find a remarkably good quantitative agreement between the observed experimental regimes and the predicted ones.
4 Discussion and conclusions
We have demonstrated good agreement between experimental phase diagrams and a simple extension of Flory–Huggins theory, incorporating non-linear elasticity. We have confirmed that strain-stiffening is an essential ingredient for microphase phase separation in elastic matrices. By integrating this with models for elastic cavitation, we can rationalize the selection of bicontinuous and droplet morphologies.While this model successfully captures the phase diagram, some observations of EMPS remain unexplained. First, microphase separation forms domains with a well-defined length scale that does not coarsen. Our model has no mechanism to select this length scale. Secondly, in experiments, we observe microphase separation to be continuous: there is a vanishingly small contrast between the domains just below the microphase separation phase boundary. However, the current model suggests that microphase phase separation should display a sharp contrast between the domains, having compositions on the two sides of the binodal curve.
These considerations imply that the model is still missing some important physics. For example, while we have assumed isotropic elastic stresses in the network, stresses should be very anisotropic near phase interfaces, and this has been shown to be able to arrest coarsening.49 We have also ignored the effects of the interfacial energy of these phase interfaces (e.g. ref. 48), and the potential breakage of locally stretched polymer strands.73 Further, recent theory has shown that accounting for the mesh-scale heterogeneity of the polymer network via non-local elasticity can qualitatively capture the missing features described above.42,75 In this last case, further work is needed to extend these predictions to three-dimensions and to build a experimental foundation for non-local elasticity in real polymer networks. In particular, a key challenge will be to characterize how the continuum elastic behavior of a polymer network changes at scales approaching the mesh-scale.
Despite its imperfections, our model suggests practical design principles. First, one needs to select a solvent that swells the elastomer enough to feel the non-linearity of the network. Second, in order to acheive bicontinous morphologies, the elastomer needs to be stiff enought to avoid cavitation.
We envision several directions for future work. Most importantly, the physical mechanism underlying length-scale selection remains unresolved. Further, EMPS experiments have been limited to silicone elastomers. It will be fruitful to test these concepts in other polymer networks, like hydrogels. Finally, from a mechanical perspective, we have investigated only one type of strain-stiffening. Strongly-strain stiffening networks, like biopolymers, could show very different behavior.
5 Materials & methods
5.1 Fabrication of polymer matrices
We prepare pure PDMS matrices by mixing PDMS chains (DMS-V31, Gelest, Mw = 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) with a crosslinker (HMS-301, Gelest Mw = 1900 g mol−1) and a platinum-based catalyst (SIP6831.2, Gelest) (see full recipe in ref. 76). We typically prepare two parts: part A which consists of PMDS chains with 0.05 wt% of catalyst and part B which consists of PDMS chains with 10 wt% of crosslinker. The stiffness of the resulting matrix depends on the mass ratio between part A and part B (typically ranging from 3
000 g mol−1) with a crosslinker (HMS-301, Gelest Mw = 1900 g mol−1) and a platinum-based catalyst (SIP6831.2, Gelest) (see full recipe in ref. 76). We typically prepare two parts: part A which consists of PMDS chains with 0.05 wt% of catalyst and part B which consists of PDMS chains with 10 wt% of crosslinker. The stiffness of the resulting matrix depends on the mass ratio between part A and part B (typically ranging from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 9
1 to 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), while keeping the catalyst concentration constant (0.0019% in volume). Once the different parts are thoroughly mixed together, we pour the mixture into a Petri dish, degas it in vacuum, and finally cure it at 60 °C for approximately 6 days. After curing, the resulting PDMS elastomer is carefully removed from the Petri dish and cut into rectangular pieces (∼1 cm × 2 cm × 0.5 cm).
1), while keeping the catalyst concentration constant (0.0019% in volume). Once the different parts are thoroughly mixed together, we pour the mixture into a Petri dish, degas it in vacuum, and finally cure it at 60 °C for approximately 6 days. After curing, the resulting PDMS elastomer is carefully removed from the Petri dish and cut into rectangular pieces (∼1 cm × 2 cm × 0.5 cm).
5.2 EMPS and LLPS experiments
PDMS pieces are transferred into a bath of heptafluorobutyl methacrylate (HFBMA, Apollo scientific, Mw = 268.1) (∼1 mL HFBMA/0.5 g of PDMS), in a 25 mL glass bottle. This bath is then typically incubated at Tswell = 60 °C in a pre-heated oven during 2.5 days. After the elastomer is saturated with the liquid, the sample is then transferred into a preheated heating stage at 60 °C (INSTEC), which is coupled to an optical microscope. We then use custom image analysis routines to carefully detect the emergence of phase separation as a function of temperature. For these experiments, we use a 60× air objective, to avoid temperature variations in the sample.Note that experiments with uncrosslinked PDMS are performed by preparing mixtures of PDMS chains and HFBMA liquid in glass bottles, and then following the same steps described above for determining the phase separation boundaries.
5.3 Swelling equilibrium experiments
To measure the equilibrium concentration of HFBMA in PDMS as a function of the swelling temperature, Tswell, we take 1 × 2 × 0.5 cm3 PDMS samples and record their original weight (mdry). We then incubate the samples into bath of HFBMA liquid (∼1 mL) in a well-sealed glass bottle. The samples are left incubating for 2.5–3 days at the desired swelling temperature. After the incubation, we remove the swollen pieces of PDMS from the bath, gently remove the excess of liquid on its surface, and measure their increase in mass with a microbalance (mswollen). This extra mass corresponds to the liquid that has diffused inside the PDMS. However, we also note that a fraction of uncrosslinked PDMS leaves the PDMS during the incubation period and goes to the bath of HFBMA. To take this mass of uncrosslinked PDMS into account, we let the HFBMA evaporate from the swollen sample for a period of 24 hours. We then weigh the mass of the resulting dry PDMS (mevap). This mass is usually 5–20% lighter than the original dry mass of PDMS depending on the stiffness of the sample and swelling temperature. The mass fraction of liquid inside the matrix is calculated as mliquid = mswollen − mevap/mswollen. The resulting the volume fraction of the liquid, ϕ, is then calculated as: | (11) |
5.4 Uniaxial tensile tests and fitting parameters
To measure the non-linear behavior of the pure, unswollen silicone networks, we prepare cylindrical silicone samples by using Teflon tubes with an internal diameter of 1.5 mm as molds. After pouring the mixture of PDMS chains and crosslinker into the tubes, we transfer them into a 60 °C oven for a week. After fully curing the materials, we carefully peal off the Teflon tubing, and cut the resulting PDMS cylinders into lengths of 5 cm long pieces. We then glue the end of the tubes into rectangular pieces of PDMS of the same stiffness, using a drop of the PDMS mixture as a glue. The rectangular ends enable an easier clamping for the mechanical test. We cure the whole construct over two days at 60 °C.We next perform uniaxial tests on our samples using a tensile testing machine (stable micro systems), where we record the engineering strain–stress curves until failure. All mechanical tests were performed in air, at room temperature, and at elongation speeds of 0.05 mm per second.
Using the Arruda–Boyce model,68 we fit the strain–stress curves for multiple samples with five different crosslinking densities and obtain the fitted values shown in Table 1. Each value reports average results for three replicates – except the samples with 7.4 mol% crosslinker, where two specimens were measured. All values of μ deviated from the mean by less than ∼15%, and values of λm by less than ∼20%.
5.5 Calculating phase diagrams
We use the convex-hull technique described by77 to calculate phase diagrams. In brief, this finds concave sections of a free-energy curve by comparing the curve with its convex hull. Example code is given as a supplement to this paper.Author contributions
Conceptualisation: CF-R, RWS, ERD, formal analysis: CF-R, RWS, SH, SW, PDO, ERD investigation: CF-R, methodology: CF-R, SH, RWS, resources: ERD, software: RWS, SH, supervision: RWS, ERD, validation: SW, PDO, visualisation: CF-R, RWS, writing – original draft: CF-R, RWS, writing – review & editing: CF-R, RWS, PDO, ERD.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00594a.Data for this article, including data for the mechanical characterization and code to generate phase diagrams are available at the Figshare repository at https://doi.org/10.6084/m9.figshare.29153642.
Appendices
Appendix A: conditions for phase equilibrium
In our experiments, phase separation takes place at constant pressure and temperature, and with the total number of solvent and polymer molecules fixed. Thus, phase equilibrium is found by minimizing the Gibbs free energy, G, of the whole sample. Following Doi,54 we can write the Gibbs free energy of a two component, solvent/polymer system as | (12) |
We note that many works assume that phase separation occurs at constant (V,T) instead of constant (P,T). In the former case, it is appropriate to work with the Helmholtz free energy, F, instead of G (e.g. ref. 47 and 48). To avoid confusion, we note that both approaches are equivalent. In particular, because the solvent and polymer do not change volume upon mixing, V is fixed. Hence, G and F only differ by a constant, PV, and minimizing G to determine phase equilibria gives identical results to minimizing F.
To minimize G, we require that the chemical potentials of solvent, μ*, in equilibrated phases are the same. The chemical potential is defined as:
 | (13) |
Minimizing G also requires the exchange chemical potential,  , to be the same in any phases that contain polymer.78
, to be the same in any phases that contain polymer.78 is the energy change caused by adding a solvent molecule, and removing the same volume of polymer from a phase:
is the energy change caused by adding a solvent molecule, and removing the same volume of polymer from a phase:
 | (14) |
 must take the same value in the two phases. Having the same value of
must take the same value in the two phases. Having the same value of  means that the two equilibrium phases (ϕ1, ϕ2) must be at points with the same tangent slope:
means that the two equilibrium phases (ϕ1, ϕ2) must be at points with the same tangent slope:  . Enforcing equivalency of μ* in the two phases then yields that
. Enforcing equivalency of μ* in the two phases then yields that | (15) |
Geometrically, these conditions are then satisfied by the double tangent construction.
 in the two phases. Instead we only require that the chemical potential of pure solvent, at a pressure P: i.e.
in the two phases. Instead we only require that the chemical potential of pure solvent, at a pressure P: i.e.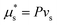 is equal to the chemical potential of the solvent in the swollen polymer network. This gives that
is equal to the chemical potential of the solvent in the swollen polymer network. This gives that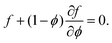 | (16) |
This condition is satisfied by a single-tangent construction with a tangent line that passes through the point (ϕ = 1, f = 0).
Note that, in the literature, equilibrium gel swelling is often calculated by considering equilibrium of a system consisting of just the swollen polymer gel phase. There, the gel is assumed to be in equilibrium with a bath of solvent at fixed chemical potential  (e.g. ref. 63). This approach is entirely consistent with our derivation above. We see this by minimizing the relevant free energy for a gel at constant (P,T,μ*): Ω* = G − μ*Ns. Taking ∂Ω*/∂Ns = 0 and setting μ* = Pvs yields eqn (16).
(e.g. ref. 63). This approach is entirely consistent with our derivation above. We see this by minimizing the relevant free energy for a gel at constant (P,T,μ*): Ω* = G − μ*Ns. Taking ∂Ω*/∂Ns = 0 and setting μ* = Pvs yields eqn (16).
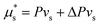 . Thus, the droplet and swollen polymer network are in equilibrium when
. Thus, the droplet and swollen polymer network are in equilibrium when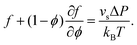 | (17) |
For cavitation to occur, the excess pressure in the droplet must exceed the critical pressure: ΔP > Pc. Thus the cavitation condition is
 | (18) |
This is satisfied when a tangent to the f curve meets the vertical axis at the right side of the phase diagram (ϕ = 1) above the point (ϕ = 1, f = vsPc/kBT).
Appendix B: full expressions for EMPS free energies
The total dimensionless free-energy density in a swollen neo-Hookean gel is | (19) |
The total dimensionless free-energy density in a swollen Arruda–Boyce gel is
 | (20) |
All constants are given in the main text.
Note, that the translational entropy term in Flory–Huggins theory ((νs/νp)(1 − ϕ)log(1 − ϕ)) does not appear in these expressions. This term is generally assumed to disappear in a polymer gel, where νs/νp → ∞. However, the last term in ftot has the same (1 − ϕ)log(1 − ϕ) form, but a different prefactor – now arising from the elastic energy of the gel. The presence of this latter term (if α ≠ 0, despite calculations suggesting that it vanishes66) may partially justify the argument of some previous works that a free energy term that resembles the standard translational entropy term should be maintained in modeling gel behavior.42,48,50
Acknowledgements
We thank Sanat Kumar for useful discussions and Michael Rubinstein for helpful feedback. We thanks Justine Kush and Dorothea Pinotsi from ScopeM for help during the SRS experiments. CF-R acknowledges funding from the ETH Zürich Postdoctoral Fellowship. PDO and SW thank the Ives Foundation and Georgetown University for support.Notes and references
- Z. Xu, W. Wang, Y. Cao and B. Xue, Supramol. Mater., 2023, 100049 Search PubMed.
- Z. Wang, W. Qiu and Q. Zhang, Prog. Polym. Sci., 2024, 101847 CrossRef CAS.
- G. R. Guillen, Y. Pan, M. Li and E. M. V. Hoek, Ind. Eng. Chem. Res., 2011, 50, 3798–3817 CrossRef CAS.
- D. R. Lloyd, S. S. Kim and K. E. Kinzer, J. Membr. Sci., 1991, 64, 1–11 CrossRef CAS.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- J. W. Gibbs, Trans. Conn. Acad. Arts Sci., 1879, 3, 108 Search PubMed.
- R. A. L. Jones, Soft condensed matter, Oxford University Press, 2002, vol. 6 Search PubMed.
- S. Manley, H. Wyss, K. Miyazaki, J. Conrad, V. Trappe, L. Kaufman, D. Reichman and D. Weitz, Phys. Rev. Lett., 2005, 95, 238302 CrossRef CAS PubMed.
- I. Wienk, R. Boom, M. Beerlage, A. Bulte, C. Smolders and H. Strathmann, J. Membr. Sci., 1996, 113, 361–371 CrossRef CAS.
- F. Cardinaux, T. Gibaud, A. Stradner and P. Schurtenberger, Phys. Rev. Lett., 2007, 99, 118301 CrossRef.
- C. Fernández-Rico, T. Sai, A. Sicher, R. W. Style and E. R. Dufresne, JACS Au, 2022, 2, 66–73 CrossRef.
- A. Sicher, R. Ganz, A. Menzel, D. Messmer, G. Panzarasa, M. Feofilova, R. Prum, R. Style, V. Saranathan and R. M. Rossi, et al. , Soft Matter, 2021, 17, 5772 RSC.
- A. J. Ardell, Metall. Trans. A, 1985, 16, 2131–2165 Search PubMed.
- G. R. Guillen, Y. Pan, M. Li and E. M. V. Hoek, Cell, 2011, 175, 3798 Search PubMed.
- O. Y. Dudaryeva, L. Cousin, L. Krajnovic, G. Gröbli, V. Sapkota, L. Ritter, D. Deshmukh, Y. Cui, R. W. Style, R. Levato and C. Labouesse, Adv. Mater., 2024, 37, 2410452 CrossRef.
- A. Puiggalí-Jou, I. B. Hui, C. Fernandez-Rico and M. Zenoby-Wong, Adv. Mater., 2025 DOI:10.1002/adma.202507385.
- S. L. Burg and A. J. Parnell, J. Phys.: Condens. Matter, 2018, 30, 413001 CrossRef.
- E. R. Dufresne, H. Noh, V. Saranathan, S. G. Mochrie, H. Cao and R. O. Prum, Soft Matter, 2009, 5, 1792–1795 Search PubMed.
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732 CrossRef CAS.
- M. Feric, N. Vaidya, T. S. Harmon, D. M. Mitrea, L. Zhu, T. M. Richardson, R. W. Kriwacki, R. V. Pappu and C. P. Brangwynne, Cell, 2016, 165, 1686–1697 CrossRef CAS.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298 Search PubMed.
- E. L. Elson, E. Fried, J. E. Dolbow and G. M. Genin, Annu. Rev. Biophys., 2010, 39, 207–226 CrossRef CAS.
- R. W. Style, T. Sai, N. Fanelli, M. Ijavi, K. Smith-Mannschott, Q. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. X, 2018, 8, 011028 CAS.
- C. Fernández-Rico, S. Schreiber, H. Oudich, C. Lorenz, A. Sicher, T. Sai, V. Bauernfeind, S. Heyden, P. Carrara and L. D. Lorenzis, et al. , Nat. Mater., 2024, 23, 124–130 CrossRef.
- K. A. Rosowski, T. Sai, E. Vidal-Henriquez, D. Zwicker, R. W. Style and E. R. Dufresne, Nat. Phys., 2020, 16, 422–425 Search PubMed.
- P. J. Flory and J. Rehner, J. Chem. Phys., 1943, 11, 521–526 Search PubMed.
- Y.-W. Chang, M. S. Dimitriyev, A. Souslov, S. V. Nikolov, S. M. Marquez, A. Alexeev, P. M. Goldbart and A. Fernández-Nieves, Phys. Rev. E, 2018, 98, 020501 CrossRef.
- M. S. Dimitriyev, Y.-W. Chang, P. M. Goldbart and A. Fernández-Nieves, Nano Futures, 2019, 3, 042001 CrossRef CAS.
- N. Boon and P. Schurtenberger, Phys. Chem. Chem. Phys., 2017, 19, 23740–23746 RSC.
- M. Shibayama and T. Tanaka, Responsive gels: volume transitions I, 1993, pp. 1–62 Search PubMed.
- Y. Li and T. Tanaka, Annu. Rev. Mater. Res., 1992, 22, 243–277 CrossRef CAS.
- A. Onuki, Phase Transition Dynamics, Cambridge University Press, 2002 Search PubMed.
- A. Onuki, in Theory of phase transition in polymer gels, ed. K. Dušek, Springer Berlin Heidelberg, Berlin, Heidelberg, 1993, pp. 63–121 Search PubMed.
- A. Onuki, Phys. Rev. A:At., Mol., Opt. Phys., 1989, 39, 5932–5948 CrossRef CAS PubMed.
- A. Onuki and S. Puri, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, R1331–R1334 CrossRef CAS.
- Y. Shin, Y.-C. Chang, D. S. Lee, J. Berry, D. W. Sanders, P. Ronceray, N. S. Wingreen, M. Haataja and C. P. Brangwynne, Cell, 2018, 175, 1481–1491 CrossRef CAS PubMed.
- P. Ronceray, S. Mao, A. Košmrlj and M. P. Haataja, Europhys. Lett., 2022, 137, 67001 CrossRef CAS.
- J. X. Liu, M. P. Haataja, A. Košmrlj, S. S. Datta, C. B. Arnold and R. D. Priestley, Nat. Commun., 2023, 14, 6085 CrossRef CAS.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207 Search PubMed.
- E. Vidal-Henriquez and D. Zwicker, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102014118 Search PubMed.
- O. W. Paulin, L. C. Morrow, M. G. Hennessy and C. W. MacMinn, J. Mech. Phys. Solids, 2022, 164, 104892 Search PubMed.
- Y. Qiang, C. Luo and D. Zwicker, Phys. Rev. X, 2024, 14, 021009 CAS.
- E. Vidal-Henriquez and D. Zwicker, Soft Matter, 2020, 16, 5898–5905 Search PubMed.
- L. Meng, S. Mao and J. Lin, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2316610121 Search PubMed.
- M. Mannattil, H. Diamant and D. Andelman, Phys. Rev. Lett., 2025, 135, 108101 CrossRef CAS.
- D. Deviri and S. A. Safran, Eur. Phys. J. E:Soft Matter Biol. Phys., 2024, 47, 16 CrossRef CAS PubMed.
- M. G. Hennessy, A. Münch and B. Wagner, Phys. Rev. E, 2020, 101, 032501 CrossRef CAS.
- S. Biswas, B. Mukherjee and B. Chakrabarti, Soft Matter, 2022, 18, 8117–8123 RSC.
- M. Kothari and T. Cohen, J. Mech. Phys. Solids, 2020, 145, 104153 CrossRef.
- X. Wei, J. Zhou, Y. Wang and F. Meng, Phys. Rev. Lett., 2020, 125, 268001 CrossRef CAS PubMed.
- S. Raayai-Ardakani and T. Cohen, Extreme Mech. Lett., 2019, 31, 100536 CrossRef.
- J. Little, A. J. Levine, A. R. Singh and R. Bruinsma, Phys. Rev. E, 2023, 107, 024418 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- M. Doi, Soft matter physics, Oxford University Press, USA, 2013 Search PubMed.
- R. Koningsveld, W. H. Stockmayer and E. Nies, Polymer phase diagrams: a textbook, Oxford University Press, USA, 2001 Search PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell, Ithaca, 1975 Search PubMed.
- P. B. Warren, Phys. Rev. Lett., 1998, 80, 1369 CrossRef CAS.
- B. A. Wolf, Polymer Thermodynamics: Liquid Polymer-Containing Mixtures, 2011, pp. 1–66 Search PubMed.
- S. Hirotsu, J. Chem. Phys., 1991, 94, 3949–3957 CrossRef CAS.
- B. Erman and P. Flory, Macromolecules, 1986, 19, 2342–2353 CrossRef CAS.
- T. A. Orofino and P. Flory, J. Chem. Phys., 1957, 26, 1067–1076 CrossRef.
- G. B. McKenna, K. M. Flynn and Y. Chen, Polymer, 1990, 31, 1937–1945 CrossRef CAS.
- W. Hong, X. Zhao, J. Zhou and Z. Suo, J. Mech. Phys. Solids, 2008, 56, 1779–1793 CrossRef CAS.
- K. Binder and H. Frisch, J. Chem. Phys., 1984, 81, 2126–2136 CrossRef CAS.
- P. J. Flory, Proc. R. Soc. London, Ser. A, 1976, 351, 351–380 CAS.
- S. Panyukov and Y. Rabin, Phys. Rep., 1996, 269, 1–131 CrossRef CAS.
- G. Marckmann and E. Verron, Rubber Chem. Technol., 2006, 79, 835–858 CAS.
- E. M. Arruda and M. C. Boyce, J. Mech. Phys. Solids, 1993, 41, 389–412 CrossRef CAS.
- S. Rickaby and N. Scott, Int. J. Non Linear Mech., 2015, 68, 71–86 CrossRef.
- J. R. Rice and M. P. Cleary, Rev. Geophys., 1976, 14, 227–241 CrossRef.
- D. Okumura and S. A. Chester, Int. J. Mech. Sci., 2018, 144, 531–539 CrossRef.
- W. Ostwald, Z. Phys. Chem., 1897, 22, 289–330 CrossRef CAS.
- J. Y. Kim, Z. Liu, B. M. Weon, T. Cohen, C.-Y. Hui, E. R. Dufresne and R. W. Style, Sci. Adv., 2020, 6, eaaz0418 CrossRef CAS PubMed.
- A. Gent and P. Lindley, Proc. R. Soc. London, Ser. A, 1959, 249, 195–205 Search PubMed.
- H. Oudich, P. Carrara and L. De Lorenzis, J. Mech. Phys. Solids, 2025, 206, 106380 CrossRef.
- R. W. Style, R. Boltyanskiy, B. Allen, K. E. Jensen, H. P. Foote, J. S. Wettlaufer and E. R. Dufresne, Nat. Phys., 2015, 11, 82–87 Search PubMed.
- S. Mao, D. Kuldinow, M. P. Haataja and A. Košmrlj, Soft Matter, 2019, 15, 1297–1311 RSC.
- F. Jülicher and C. A. Weber, Annu. Rev. Condens. Matter Phys., 2024, 15, 237–261 CrossRef.
Footnotes |
| † These authors contributed equally to this work. |
| ‡ Note that some previous works do not remove the translational entropy term, and it qualitatively changes predicted phase behavior.48,50,51 |
| § In principle, it is possible for the partially-swollen phases to have a lower energy than the macroscopic swelling equilibrium, so that a gel would spontaneously phase separate into coexisting swollen phases. However, this only occurs for unusual functional forms of χ(ϕ).59,60 |
| This journal is © The Royal Society of Chemistry 2026 |