Open Access Article
Open Access ArticleCellular mechanosensing on a cell-scale stiffness gradient substrate
Indrajit
Bhattacharjee
a,
Gautam V.
Soni
 b and
Bibhu Ranjan
Sarangi
b and
Bibhu Ranjan
Sarangi
 *ac
*ac
aPhysical and Chemical Biology Laboratory, Dept of Physics, Indian Institute of Technology Palakkad, Palakkad, 678623, Kerala, India. E-mail: 222014001@smail.iitpkd.ac.in
bRaman Research Institute, Bangalore, 560080, India. E-mail: gvsoni@rri.res.in
cDept of Biological Sciences and Engineering, Indian Institute of Technology Palakkad, Palakkad, 678623, Kerala, India. E-mail: bibhu@iitpkd.ac.in
First published on 17th December 2025
Abstract
Cells have the ability to sense and respond to various mechanical cues from their immediate surroundings. One of the manifestations of such a process, which is also known as “mechanosensing”, is directed cell migration. Various biological processes have been shown to be controlled by extracellular matrix (ECM) stiffness. Substrates with a high stiffness gradient have been used as a platform to investigate cellular motion in response to mechanical cues. However, creating a cell scale stiffness gradient in such a cell adhesion friendly substrate still remains elusive. In this study, we present a simple and versatile method for fabricating substrates with a periodically varying stiffness profile at the cellular scale, featuring customizable high stiffness gradients. Fibroblast cells, when presented with such continuous yet anisotropic variation of stiffness, preferentially position their nuclei in stiffer regions of the substrate and align themselves along the direction of the lowest rigidity gradient. Furthermore, when the rigidity of the substrate is sufficiently high, cells exhibit less sensitivity to stiffness gradients, with their elongation and nuclear positioning becoming independent of stiffness variations. Overall, our experimental results reveal new insights into the process of cellular mechanosensing where the cell-scale gradient drives strong positional and orientational order.
1 Introduction
Cells assess the stiffness of their environment by attaching themselves to and exerting force on the surrounding matrix. This mechanosensing influences various cellular processes, including migration, differentiation, proliferation, wound healing, tissue remodeling, and morphogenesis, as well as the progression of disease.1–9 At the level of individual cells, substrate rigidity affects cell morphology, actin cytoskeleton organization, polarization, and movement. As the substrate becomes stiffer, the actomyosin network within the cell becomes more organized, leading to a shift in cell shape from a nearly circular to a more elongated one. Furthermore, the area of cell adhesion expands with increasing substrate rigidity.10–12 When exposed to a stiffness gradient, cells are generally known to migrate towards the stiffer regions of the substrate.13–17 It is also well established that variations in substrate stiffness significantly affect cell orientation and spatial distribution.18–22The investigation of such mechanosensing behaviors often involves a cell adhesion friendly substrate with spatially varying stiffness. Hydrogels are usually used to prepare cell adhesive substrates, as they are easy to functionalize with ECM proteins such as fibronectin. Various methods have been used to produce rigidity gradients in the hydrogel substrate. One of the simple methods is to use the spatial variation of the cross-linker concentration on a length scale through simple diffusion.23 The variation in cross-linker concentration results in varying degrees of polymerization and, hence, varying stiffness. However, the achievable stiffness gradient value with such a method is typically small (0.001–0.01 kPa µm−1). Diffusion, along with controlled photopolymerization, was also used as a tool to create a stiffness gradient on the hydrogel substrate, and a comparatively higher stiffness gradient (0.01–0.04 kPa µm−1) was reported.12,24–26 The use of a moving mask with controlled UV exposure during photopolymerization offers an advanced technique for the fabrication of substrates with a stiffness gradient in the range of 0.067 to 0.2 kPa µm−1.11 By making a junction between two materials in which one is hard and the other is comparable to soft, a step stiffness gradient substrate was developed.27,28 The majority of the procedures mentioned above provide fairly restricted linear stiffness gradient values or step stiffness gradients, and some of them require quite a complex experimental setup. So far, there has been a lack of studies on substrates with a continuous stiffness gradient at the scale of an individual cell. Producing a high stiffness gradient at the cell scale for studying cellular mechanosensing remains a significant challenge.
A relatively recent strategy involves the use of layered substrates in which a soft layer is deposited atop a rigid base. By varying the thickness of the compliant layer over the stiff substrate, stiffness gradients in the range of approximately 0.1–0.25 kPa µm−1 have been demonstrated.29–33 Adhered cells continuously apply forces on their supporting substrate. The way in which the substrate deforms in response is influenced by both its mechanical properties and the amount of force applied. When cells are on a flexible gel that is firmly connected to an infinitely rigid material beneath it, the gel appears to be stiffer. This effect becomes more pronounced as the thickness of the gel approaches the length scale of the deforming region where the deformation occurs.34–36 When the thickness of the compliant layer is small compared to the lateral extent of cellular traction forces, the rigid base restricts vertical and lateral deformation, leading to an effectively stiffer response.35
In this study, we present a novel and accessible method to fabricate cell-adhesion-friendly substrates with exceptionally high stiffness gradients. Our approach is simple, robust, and allows fine tuning of the stiffness gradient at the scale of individual cells. The fabrication relies on using the topography of an underlying glass substrate as a template to generate a controlled stiffness variation within a homogeneous polyacrylamide (PAA) gel layer. This ensures uniform extracellular matrix (ECM) protein attachment while maintaining gradient precision. The method requires only standard laboratory equipment, making it easy to implement. The resulting substrates display steep and tunable stiffness gradients across cellular length scales. Fibroblast cells exposed to an anisotropic stiffness gradient display distinct positional and orientational responses. Our experiments reveal that the nuclei preferentially localize in regions of higher stiffness, while the cells align along the direction of the minimum rigidity gradient. Notably, when the minimum stiffness of the polyacrylamide (PAA) substrate exceeds a threshold value, the cells exhibit diminished responsiveness to the gradient. Overall, we demonstrate a simple yet powerful method for fabricating substrates with tunable, cell-scale stiffness gradients. These substrates offer a versatile platform for probing the physical limits of cellular mechanosensing.
2 Methods
2.1 Substrate fabrication
Our substrate consists of a thin layer of hydrogel deposited on top of an array of glass capillaries of selected diameters assembled on a coverslip. The schematic diagram of the substrate is shown in Fig. 1(a). This substrate preparation process was performed in several steps. The first step involves the preparation of a stiffer bottom substrate, which essentially consists of glass capillaries (Narishige G-1) that were pulled using a micro-pipette puller (Narishige PC-100) to achieve the desired outer diameter. In order to maintain uniformity, we only selected suitable sections of the pulled glass capillaries, verified through the microscope, for further fabrication procedures. The outer diameter of the selected capillaries was 53.9 ± 1.3 µm (see the SI, Fig. S1). In the rest of our discussion, these glass capillaries are referred to as rods, and polyacrylamide gels are referred to as PAA gels. For the assembly of the rods, we first washed the coverslips with 70% ethanol and allowed them to dry at room temperature. After that, the glass rods were aligned on top of the coverslip with the help of very fine tweezers under the microscope. To stabilize the rods on the coverslips, a tiny amount of silicone sealant was used only on the edges as needed.The coverslips (containing rods) were amino-silanated to facilitate the binding of the PAA gel following standard procedures.37 Briefly, the glass coverslips (containing rods) were first washed with 70% ethanol and then heated to 80 °C on a hot plate in the presence of a solution of 0.1 M NaOH. Subsequently, 3-aminopropyltriethoxysilane (APTES, Sigma-Aldrich) was added to the solution and allowed to react for 5 minutes. After the reaction, the coverslips were thoroughly rinsed with deionized water to remove any unreacted agents. The coverslips were then immersed in 0.5% (v/v) glutaraldehyde in phosphate-buffered saline (PBS, Sigma-Aldrich) for 30 minutes to facilitate crosslinking. Finally, the coverslips were allowed to air dry at room temperature. We also prepared Chloro-silanated glass slides to be used to flatten the hydrogel layer without attaching to it. Dichlorodimethylsilane (Sigma, USA) was used as a hydrophobic coating on the glass slides.
To create PAA hydrogel films on top of the glass rods, polymer solutions were prepared using acrylamide monomers (Sigma-Aldrich) and bis-acrylamide (Sigma-Aldrich) in deionized water (DI) in specific ratios to obtain the desired stiffness value. In particular, we used 4%, 10%, and 12% (w/v) acrylamide monomers (Sigma-Aldrich) with 0.1%, 0.1%, and 0.25% bis-acrylamide (Sigma-Aldrich) in deionized (DI) water, respectively, to achieve low (∼3 kPa), medium (∼14 kPa), and high (∼56 kPa) ranges of stiffness (see the SI, Fig. S2).37,38 The mixtures were then degassed under high vacuum for 40 minutes. After degassing, 1 mL of the PAA solution was taken, and 10 µL of 10% (w/v) ammonium persulfate (APS, ICT) along with 1 µL of N,N,N′,N′-tetramethylethylenediamine (TEMED, Sigma-Aldrich) was added. The solution was then vortexed to ensure thorough mixing. After that, 10 µL of mixed solution was quickly pipetted onto the top of the coverslip-containing glass rods, and the chlorosilanated glass slide was placed on top of it. In order to ensure the desired thickness of the hydrogel, it was subjected to a compression of 50 g of weight. The solution was polymerized for one hour. The chlorosilanated glass slide was gently detached, and the substrates were rinsed in a Petri dish and kept in deionized (DI) water for future use. Substrates containing rods with PAA solutions of 4% acrylamide monomers and 0.1% bis-acrylamide, 10% acrylamide monomers and 0.1% bis-acrylamide, and 12% acrylamide monomers and 0.25% bis-acrylamide are hereafter referred to as S-1, S-2, and S-3, respectively.
To verify the thickness of the PAA gel on top of the glass rods, 0.25 µm Tetraspek fluorescent beads (Thermofisher, USA) were embedded in the gel, and cross-sectional images of the substrate (S-1) were taken with a confocal microscope (Olympus flv-3000) using a 10× objective. The minimum gel thickness was found to be on the order of ∼6 µm (Fig. 1c and d). A theoretical estimation of the thickness variation was performed based on the geometry of the arrangements, using the following equation.
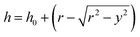 | (1) |
2.2. Characterization of the stiffness gradient
The stiffness of the substrates is characterized by measuring the Young's modulus (E), for which atomic force microscopy (AFM)(Oxford Instruments) was used with a colloidal AFM probe (Novascan). The AFM probe consisted of a polystyrene bead with a diameter of 4.5 µm, attached to silicon nitride cantilevers with a nominal spring constant of ∼44 pN nm−1 that were used to measure the stiffness variation on S-1 substrates, while stiffer cantilevers with a spring constant of ∼400 pN nm−1 were chosen for the S-2 and S-3 substrates to accommodate their higher stiffness variation. The bulk stiffness of the PAA gels of substrates S-1, S-2, and S-3 was measured using the same AFM probes to ensure consistency across the experiments. The spring constant of the cantilever was determined through calibration using the thermal fluctuation method.39 Force–distance (F–d) curves were acquired in a liquid medium on substrates for each combination (n = 3 per condition), covering a scan area of 108 µm × 108 µm across a 28 × 28 grid. Furthermore, additional measurements were conducted to measure the bulk stiffness of the PAA gels corresponding to each substrate's composition (n = 3 per condition), with the same scan area of 108 µm × 108 µm across a 10 × 10 grid (see the SI, Fig. S2).The AFM data analysis was performed using a custom-built Matlab program.40,41 In short, the approach and retract curves were extracted from each raw AFM data set, and the indentation depth (h) was calculated for different applied forces, defined as h = d − D, where d is the sample displacement and D is the deflection of the cantilever. Force (P) vs. indentation depth (h) plots were analyzed using the Oliver–Pharr method for the spherical probe. Briefly, the peak force of the indenter, the peak displacement, and the slope of the unloading curve were used to compute the reduced modulus (Er) using the following equation:
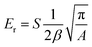 | (2) |
| A = π(2Rhc − hc2) | (3) |
Here, R is the radius of the tip and hc = (hm − hs), where hm is the maximum indentation depth and  , with ε = 0.75 for a spherical indenter, and Pm is the maximum load. Young's modulus E was calculated from the reduced modulus Er using the equation:
, with ε = 0.75 for a spherical indenter, and Pm is the maximum load. Young's modulus E was calculated from the reduced modulus Er using the equation:
| E = Er(1 − σ2) | (4) |
2.3 Substrate functionalization
To facilitate cell adhesion, Sulfo-SANPAH-mediated succinimide crosslinking was used to covalently attach fibronectin to the PAA hydrogels.43 In brief, a solution of 0.2 mg mL−1 Sulfo-SANPAH in HEPES buffer (pH 8.5) was added to the substrate, which was then exposed to UV light for 30 minutes to facilitate the reaction. The substrate was then rinsed with 50 mM HEPES buffer, and the process was repeated to ensure efficient protein binding. Subsequently, 50 µL of Bovine Plasma Fibronectin (0.2 mg mL−1) (Thermo Fisher Scientific) was added to the substrate and incubated for 5 hours to allow sufficient time for fibronectin binding.44 Finally, the substrate was thoroughly rinsed with HEPES to remove excess fibronectin and stored in PBS at 4 °C for further use.2.4 Cell culture and imaging
Fibroblasts (3T3) were maintained in DMEM 10% fetal bovine serum (HIMEDIA) and supplemented with 80 U penicillin, 80 µg streptomycin, and 0.2 µg of Amphotericin B per mL in 37 °C with 5% CO2. For immunostaining, cells were seeded in 35 mm Petri dishes containing the prepared fibronectin-coated substrates. The seeding density was approximately 35 cells per mm2. After 24 h of incubation, the cells were fixed with 4% paraformaldehyde for 30 min at room temperature and washed with 1× PBS (containing 0.05% Tween-20) three times, each for 5 min. The cells were then permeabilized with 0.3% Triton X-100 for 15 min at room temperature and washed with 1× PBS (containing 0.05% Tween-20) three times. For cell nucleus staining, DAPI (Sigma-Aldrich) was used at a concentration of 1 µg mL−1 in 1× PBS for 5 min and then washed three times. For actin staining, we used the ActinRed™ 555 ReadyProbes™ Reagent (Rhodamine phalloidin from Thermo Fisher Scientific) for a 1 hour incubation and washed it three times. In order to avoid aberrations while imaging directly through the rods and to make the high NA objectives usable, custom imaging setups were used for both fixed-cell and live-cell imaging. For fixed cells, the substrates along with the fixed cells were inverted over a mounting solution (Sigma-Aldrich) containing cover glasses with spacers (No 1 coverslip was used as a spacer, providing a thickness ∼ 170 µm). Images were acquired using a confocal microscope with 10× and 20× objectives and suitable combinations of lasers and fluorescence filters. Images from various positions of the substrate were stitched together for further analysis of the entire substrate area.For live cell imaging, CO2 independent media (Thermo Fisher Scientific) have been used. Cells were first seeded with a similar density of approximately 35 mm−2 on the substrate inside a 35 mm petridish. In order to facilitate adhesion to the substrate, the cells were incubated on the substrate for two hours. We used the SiR-Actin Kit (Cytoskeleton, Inc.) and Hoechst (Thermo Fisher Scientific) for actin and nuclei staining, respectively. Live cell images were acquired using a 20× air objective of a confocal system equipped with a live cell imaging setup (Tokai Hit). CO2 independent medium (Thermo Fisher Scientific) was used in the live cell chamber. For live cell imaging of cells on the substrates, the observation area of the glass bottom petridish (ibidi, µ-Dish 35 mm) was modified with spacers made from thin glass pieces (∼ 170 µm) derived from broken No. 1 coverslips. Then, the substrate containing the cells was inverted onto it (Fig. 1e). This setup allowed for the use of high numerical aperture (NA) objectives with the substrates, enabling high-quality live-cell imaging of the actin cytoskeleton. The images were captured at 5-minute intervals for approximately 36 hours.
2.5 Image analysis
The fluorescence images of fixed-cell nuclei and F-actin on various substrates, as well as the frame corresponding to 24 hours post-seeding extracted from the live-cell recordings, were analyzed using open-source ImageJ software (National Institutes of Health, USA). The merged images of the cells on the substrates were aligned horizontally through a rotational transformation to enable the measurement of the orientation angle. The regions (mostly at the edges) where the alignment of the rods was non-uniform were excluded from our analysis to avoid substrate non-uniformity effects. The cropped images of fluorescently labeled nuclei were thresholded and masked using the analyze particles tool for a particular particle size. The image segmentation was performed using the Star Disk segmentation tool plugin in ImageJ.45 Subsequently, using particle analysis tools, all the nuclear positions were extracted. In addition, from the bright field images, the peak position of the rods was extracted. To find the distribution of nuclei on the substrates, we analyzed this data using a custom-built Matlab program. Each nucleus was mapped uniquely to the nearest rod, thus avoiding overcounting. With a bin size of 7 µm, the number of nuclei belonging to each bin was counted and normalized with the total count. The orientational distribution of the cells on the substrates was analyzed by thresholding the cropped fluorescently labeled f-actin images of the cells. Individual cells were manually selected and fitted with an ellipse, and the angle(θ) between the major axis and the horizontal axis was measured.To obtain the orientational information of both cells and nuclei, all positions of all the cells and their corresponding nuclei are extracted. The center of mass (COM) was determined by fitting an ellipse to the thresholded images of both cells and nuclei. Along with that, their orientational angle was determined by measuring the angle between the ellipse major axis and the rod's long direction. The distance between the center of mass (COM) of the cells and the corresponding nuclei was determined using the following equation:
 | (5) |
The distribution of the difference between the orientation angles of the cells and the corresponding orientation angles of their nuclei was plotted. The cell aspect ratio was calculated as the ratio of the major axis to the minor axis of the ellipses fitted to the cells. Additionally, the circularity and aspect ratio of the cell nuclei, as well as the cell spreading area, were quantified with respect to each cell's relative position from the peak of the rods. The comparisons of the cell spreading area were also performed on the soft (∼3 kPa), stiff (∼56 kPa) and gradient substrates (S-1).
Time lapse fluorescence microscopy images of live cells were analyzed using ImageJ software to track individual cells. Initially, the sequential images of the nuclei of the cells were thresholded and masked using the analyze particles tool to remove all other backgrounds. Then the trajectories of individual cell nuclei were tracked through TracKMate software Plugin in ImageJ.46 After the positional data of the nuclei were obtained along with the frames, the peak positions of the rods were taken from the bright-field images. Using a custom-built Matlab program, the speed of the cells in different positions and the location-based dwell time were calculated, considering the distance from the nearest rods. After that, corresponding to these shortest distances, the horizontal component (along the rods) and vertical component (perpendicular to the rods) of the speed of the nuclei were calculated. Then these distances were binned to the 4 µm interval from the peak of the rods, along with the corresponding speed components. To calculate the average migration speed along the horizontal and vertical directions in different locations, the mean of the speed components was taken within each 4 µm bin size. The dwell time based on the location of the cell nuclei was analyzed within individual bins from the time lapse images. The distribution of the speed components within each 7 µm region was also obtained (see the SI, Fig. S5). In total, more than 80 cell tracks were observed across four replicates of S-1 substrates, over an approximate period ranging from 8 h to 37.5 h. All plots were prepared using Matlab.
2.6 Statistical analysis
The AFM data are reported as the mean ± standard deviation (SD), while all other data are expressed as mean ± standard error (SE). All experiments were performed in triplicate unless stated otherwise, and the number of cells included in each measurement is indicated where applicable. The statistical significance was assessed by One-Way ANOVA followed by Tukey's HSD Post hoc Test (pairwise comparisons); for all: *P < 0.05, **P < 0.002, ***P < 0.0002, ****p < 0.000001; ns p > 0.05, not significant.3 Results and discussion
3.1 Topography mediated stiffness variation
Cells have the ability to sense the rigidity of the underlying substrate up to a few microns.34 So, it is crucial to ensure that the thickness of the PAA gel film does not exceed a few micrometers. As described in the previous section, our confocal imaging of the substrate embedded with fluorescent beads allowed us to characterize the thickness of the hydrogel film on top of the rods. The film thickness was found to be ∼6 µm at the peak position of the rods, which is optimal for cells to sense the effects of the underlying hard substrate. The periodicity and continuous variation in the thickness of the PAA films are clearly evident from the height profile observed in the fluorescent images. Furthermore, the thickness variation observed in the fluorescent cross-sectional image closely matched the theoretical height calculations based on the geometry of the film, indicating a smooth and consistent change in height (Fig. 1c and d). The height profile of the PAA films from the fluorescent images showed a maximum thickness of around 32 µm in the middle between the two rods and gradually decreased toward the peak of the rods. AFM topography images of the substrates revealed an approximate height variation of 4 µm over a scan area of 120 µm × 120 µm. It has been previously reported that, in the absence of pronounced valleys or hills, surface topography does not significantly influence the cell migration process, even when the height difference is on the order of several tens of microns.47,48 Therefore, the surface of the substrates was considered homogeneous, with no significant height differences that could affect cell migration. Consequently, any observed differences in cell migration behavior can be attributed predominantly to variations in substrate stiffness rather than to surface topography (see the SI, Fig. S1).To characterize the mechanical properties of the prepared substrates, atomic force microscopy (AFM) was used. Three distinct types of stiffness in PAA gels were polymerized on top of the rods to produce substrates having a tunable range of stiffness gradients. The bulk stiffness of the PAA gels, modulated by varying the acrylamide and bis-acrylamide concentrations, was measured to be around ∼3 kPa (S-1 substrate), ∼14 kPa (S-2 substrate), and ∼56 kPa (S-3 substrate), thereby categorizing the substrates into discrete stiffness regimes: low (S-1), intermediate (S-2), and relatively high (S-3) stiffness conditions. This approach provides controlled, mechanically heterogeneous microenvironments at the single-cell scale. The stiffness map covers a scan area of 108 µm × 108 µm across a 10 × 10 grid of the uniform substrates (see the SI, Fig. S2). Stiffness mapping of the stiffness gradient substrates S-1, S-2, and S-3 indicates that the variation in substrate stiffness correlates with the film thickness of the PAA gel, transitioning from stiffer to softer from the peak of the rods to the midpoint between the two adjacent rods (Fig. 2a–c). The stiffness values at the peak of the rods were found to be 35 ± 2 kPa, 54 ± 8 kPa, and 447 ± 38 kPa for the S-1, S-2, and S-3 substrates, respectively. Moving laterally away from the peaks, the stiffness values gradually decreased on both sides of the peak, reaching a minimum of around 3.0 ± 0.1, 14.0 ± 0.4, and 56 ± 4 kPa at the midpoint between the two rods for the S-1, S-2, and S-3 substrates, respectively (Fig. 2d–f). This minimum value was comparable to the bulk stiffness of the PAA gel of the substrate (see the SI, Fig. S2).37 The maximum stiffness gradient, observed across the region surrounding the peak of the rods, was ∼46 kPa µm−1 for the S-3 substrate. In comparison, the corresponding values for the S-1 and S-2 substrates were found to be ∼4.5 kPa µm−1 and ∼4.4 kPa µm−1, respectively. Notably, this gradient value gradually decreased toward the midpoint between the two rods (Fig. 2g–i). Therefore, from the above observations, it can be concluded that the stiffness of the substrate varies periodically in correlation with the film thickness across the rods. As the thickness of the PAA film decreases, the stiffness increases, and vice versa. Furthermore, by varying the composition of PAA gels with the rods, a wide and tunable range of stiffness gradient substrates was produced. One of the important aspects of our observation is that the substrate stiffness at any position is crucially dependent on the film thickness at that position. Overall, our experimental observation suggests that the film thickness and, hence, the topography of the substrates' underlying rods dictate, the local stiffness value and the associated gradient at that position.
3.2 Positional and orientational distribution
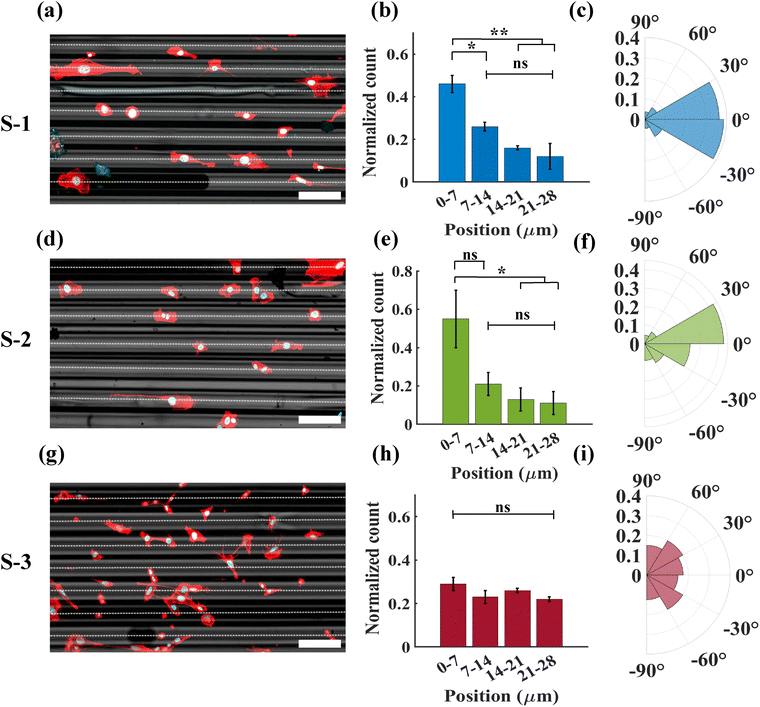
In order to investigate the effect of spatial inhomogeneity of stiffness on cellular position and orientation, we used 3T3 fibroblast cells on substrates with a tunable cell scale stiffness gradient, as mentioned in the methodology. We used the fluorescence microscopy data to quantify the positions and orientations of the cells. Fluorescent images of cell nuclei, captured 24 hours after seeding on the substrate, showed that most of the cell nuclei were concentrated in the region of hydrogel near the peaks of the rods. This region, as mentioned previously, corresponds to the highest stiffness due to the smallest thickness of the PAA film (Fig. 3a and d). From the distribution of cell nuclei in different positions on the substrates S-1 and S-2, it was found that 46 ± 4% and 55 ± 15% of the nuclei were located within ± 7 µm around the peak of the rods, respectively. This distribution rapidly decreased towards the middle region between the two rods. Only 12 ± 6% and 11 ± 6% of the cell nuclei were found in areas farther from the peak, specifically between ± 21 µm to ± 28 µm on the substrates S-1 and S-2, respectively (Fig. 3b and e).Moreover, we investigated the influence of the asymmetric stiffness gradient produced by the substrate on the orientation of the cells. The angular plots present the cell orientational distribution from 0° to ±90°, hence only considering the acute angles. 0° represents the direction along the rods and ±90° represents the angle perpendicular to the orientation of the rods. Approximately 75% and 68% of the cells were found to have an orientation angle of ±30° when they were seeded on substrates S-1 and S-2, respectively, which coincides with the direction of the low rigidity gradient (Fig. 3c and f). In addition, they also elongated themselves in the direction of the minimum rigidity gradient, which is along the rods (Fig. 3a and d).
In order to understand the effect of both local stiffness and the associated stiffness gradient, we prepared a substrate S-3 using rods of the same diameter and, hence, the same topographical features, but with a PAA film that has a high bulk stiffness (∼56 kPa). On this substrate, we observed contrasting behavior regarding both the position and orientation of the cells. The cell nuclei were distributed uniformly throughout the substrate, indicating no preference for specific regions (Fig. 3h). It was evident that cells attempted to position their nuclei on the stiffer parts of the substrate. However, when the stiffness of the PAA gel was sufficiently high, cells no longer showed a preference for positioning their nuclei based on the substrate's effective stiffness. We also observed a nearly uniform orientational distribution on this substrate (Fig. 3i).
From the comparative study mentioned above, it is evident that beyond a certain value of local stiffness, the gradient effects become less prominent. We expect this value of stiffness to depend on the cell type. Fibroblast cells have a typical value of 5 kPa to 17 kPa depending on the part of the cell.49 It has also been predicted that cells adapt to the ECM stiffness by modulating their own stiffness. We believe that beyond a certain threshold stiffness, this mechanism may reach saturation, thereby making the cell insensitive to variations in stiffness.
Furthermore, we analyzed the relative positions and orientations of cell nuclei with reference to the center of mass of the cell (Fig. 4a and b). Most of the cells on this patterned substrate S-1 showed elongated morphology (Fig. 4c). Interestingly, the nucleus position showed a measurable shift from that of the center of mass of the cell (Fig. 4e). This may indicate the existence of a phase lag between the movements of the nucleus and the cell. Previous studies indicate that the nuclei preferentially position themselves at the rear end of the cell during migration.50 Interestingly, we find a strong correlation between the orientations of the nucleus and the cell (Fig. 4d). The shape of the nucleus is adaptive and may result from the ordering of the cytoskeletal network of the cell. The anisotropy of this patterned substrate (S-1) drives the polarity observed in the mechanosensing network inside the cell, which, in turn, drives both cell and nuclear polarity, as observed in our experiments. From the measurements of nuclear circularity, nuclear aspect ratio, and cell spreading as a function of each cell's relative position from the peak of the rods (S-1), these parameters appear uniform. This supports the view that the stiffness-gradient length scale is comparable to the cell dimension, such that each cell simultaneously experiences a continuum of stiffness values across its body. Moreover, comparisons of cell spreading on the soft (∼3 kPa), stiff (∼56 kPa), and gradient (S1) substrates show that the spreading area on the gradient substrate falls between the two extremes, consistent with this interpretation (see the SI, Fig. S3). It is well established that actin organization is sensitive to substrate rigidity, as demonstrated in studies showing rigidity dependent cytoskeletal alignment.2,10 However, on a substrate with an asymmetric rigidity gradient, no global ordering is favoured. Instead, the actin network exhibits locally ordered domains rather than a uniform orientation (see the SI, Fig. S4).
3.3 Role of local stiffness and stiffness gradient in cell migration and location-specific dwell time
Time-lapse images of the fluorescence-labeled cell nuclei and the substrate were recorded for 3T3 fibroblast cells grown on the substrate (S-1) over a period of approximately 36 hours. Using tracking algorithms, as mentioned in the methodology, the position of the cell nuclei was extracted as a function of time (supplementary movie). From the trajectory of the nuclei, it is apparent that the spatial inhomogeneity, both in stiffness and stiffness gradient, influences the migration in a significant way. To quantify this, we analyzed the vertical (perpendicular to the rod) and horizontal (along the rod) migration speeds at different locations, taking the peak of the rods as our reference point for distance.As evident from our experiments, both the horizontal speed (Vx) and the vertical speed (Vy) are influenced not only by the spatial coordinates of the cell on the substrate, but also by the directional stiffness gradient. When cells were positioned in the region of the hydrogel near the peak position of the rod, their motion was nearly one-dimensional along the rod, which is also in the direction of the nearly zero stiffness gradient. The motion was primarily dominated by the horizontal component (large Vx and small Vy) (Fig. 5a). However, the situation is reversed when the cell is positioned far away from the peak of the rod. When the cells were at the peak of the rods, around 60% of the values of the vertical speed were in the range of 0 to 5 µm h−1, and only approximately 8% of the values were higher than 15 µm h−1. However, when the cells were farther from the peak position of the rods, the peak of the distribution of the vertical speed values shifted towards a value higher than 15 µm h−1. For the farthest position of the cells from the peak of the rods, approximately 24% of the vertical speed values were more than 15 µm h−1. In contrast, the distribution of horizontal speed values in different locations showed no significant variation with the relative positions of the cells. Compared to the peak position of the rods, the percentage of horizontal speed values greater than 15 µm h−1 increased from approximately 25% to 28% at the farthest position of the cells (see the SI, Fig. S5). From the plots (Fig. 5b and c), the average vertical speed at different cell locations indicates that when the cells were at the peak of the rods, their average vertical speed was 5.7 ± 0.4 µm h−1. This value gradually increased as the cells moved away, reaching a value of 10.4 ± 0.9 µm h−1 at locations more than 12 µm from the peak of the rods. However, the average horizontal speed of the cells changed from 11.1 ± 0.9 µm h−1 to 12.5 ± 1.4 µm h−1 as their position shifted from the peak of the rods to locations more than 12 µm away. It was observed that when cells were located more than 12 µm from the peak of the pattern, there was no significant change in the average values of their vertical and horizontal speeds.
The migration speed data were further corroborated by the location specific dwell time of the cells. When the cells were situated within a ±4 µm region around the peak of the rods, they spent approximately 8.6 ± 0.5 hours during the 20-hour observation period. This value decreased to 3.8 ± 0.3 hours in the subsequent 4 µm region. However, as the cells shifted away from the peak, a rapid decrease in dwell time was observed. At locations greater than 12 µm from the peak of the rods, the dwell time decreased significantly to around 1.7 ± 0.2 hours (Fig. 5d).
From the experimental observations, it was evident that cells preferentially positioned themselves at the peak of the rods, where they encountered the minimum stiffness gradient and the highest stiffness. This preference suggests that the mechanical properties at the peak provide an optimal environment for cell adhesion and stability. Additionally, when cells moved away from this peak position, they tended to make a “jump” to return to the same peak or to another peak position within the rods. This behavior was associated with a significant increase in their vertical speed, indicating a dynamic response to the mechanical landscape. Furthermore, the analysis of dwell time supported this observation; cells spent significantly more time at the peaks than at locations further away from the peak. The rapid decrease in dwell time as cells moved away from the peak reinforced the idea that the mechanical properties at the peaks were critical for maintaining cellular stability.
4 Conclusion
Cell adhesion friendly substrates with a very high stiffness gradient are extremely useful in the investigation of durotaxis. However, existing methods have been inadequate either in terms of the gradient values they produce or in terms of tunability and robustness. We present a straightforward and reliable approach for fabricating cell-adhesive hydrogel substrates with tunable, cell-scale stiffness gradients by utilizing the topography of an underlying substrate as a template. Fibroblast cells exhibit clear mechanical anisotropy in their response, aligning along the direction of the minimal rigidity gradient and positioning their nuclei toward stiffer regions. The observed threshold in mechanosensitivity suggests saturation of cellular rigidity sensing, which may potentially indicate limits in focal adhesion maturation or cytoskeletal tension. This platform provides a valuable model for dissecting the physical principles underlying mechanotransduction and durotaxis. Overall, this study introduces a versatile platform for investigating cellular responses to mechanical cues across a broad dynamic range. Moreover, this technique offers valuable insights for tissue engineering, wound healing, and regenerative medicine, where the mechanical properties of the extracellular matrix play a decisive role in guiding cell behavior and function.Author contributions
Indrajit Bhattacharjee: writing – preparing the initial draft, writing, review and editing of the original draft, substrate design conceptualization, methodology, all experimental investigations, data analysis, software validation, and conceptualization. Gautam V. Soni: writing – review and editing of the original draft, proposed the analysis for AFM, and validation. Bibhu Ranjan Sarangi: writing – review, editing, and writing the original draft, project design, project administration, proposed the analysis, validation, funding acquisition, and conceptualization.Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are openly available at the following link: https://drive.google.com/drive/folders/178IORLbpJalTnadKETjQNWtOL2nYiDxK? usp = sharingDrive link.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5sm00592b.
Acknowledgements
Confocal microscopy was performed at the central instrumentation facility of the Indian Institute of Technology, Palakkad. For AFM experiments, we acknowledge the support of the Raman Research Institute's AFM facility, as well as assistance from Mr Arkabrata Mishra and Mr Yatheendran. The project was supported by funding from the Indian Institute of Technology (ERG Grant-2023-161-PHY-BRS-ERG-SP).References
- C.-M. Lo, H.-B. Wang, M. Dembo and Y.-L. Wang, Biophys. J., 2000, 79, 144–152 CrossRef CAS PubMed.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS PubMed.
- R. McBeath, D. M. Pirone, C. M. Nelson, K. Bhadriraju and C. S. Chen, Dev. Cell, 2004, 6, 483–495 CrossRef CAS PubMed.
- T. A. Ulrich, E. M. de Juan Pardo and S. Kumar, Cancer Res., 2009, 69, 4167–4174 CrossRef CAS PubMed.
- D. E. Jaalouk and J. Lammerding, Nat. Rev. Mol. Cell Biol., 2009, 10, 63–73 CrossRef CAS PubMed.
- M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo and D. Boettiger, et al. , Cancer Cell, 2005, 8, 241–254 CrossRef CAS PubMed.
- D. E. Discher, P. Janmey and Y.-L. Wang, Science, 2005, 310, 1139–1143 CrossRef PubMed.
- M. A. Wozniak and C. S. Chen, Nat. Rev. Mol. Cell Biol., 2009, 10, 34–43 CrossRef CAS PubMed.
- B. J. Dickson, Science, 2002, 298, 1959–1964 CrossRef CAS PubMed.
- M. Gupta, B. R. Sarangi, J. Deschamps, Y. Nematbakhsh, A. Callan-Jones, F. Margadant, R.-M. Mège, C. T. Lim, R. Voituriez and B. Ladoux, Nat. Commun., 2015, 6, 7525 CrossRef CAS PubMed.
- R. Sunyer, A. J. Jin, R. Nossal and D. L. Sackett, PLoS One, 2012, 7, 1–9 CrossRef PubMed.
- I. Bhattacharjee, S. Sudhiram, M. Nithya, B. Kumar and B. R. Sarangi, Eur. Phys. J.:Spec. Top., 2024, 1–9 Search PubMed.
- P. Roca-Cusachs, R. Sunyer and X. Trepat, Curr. Opin. Cell Biol., 2013, 25, 543–549 CrossRef CAS PubMed.
- B. C. Isenberg, P. A. DiMilla, M. Walker, S. Kim and J. Y. Wong, Biophys. J., 2009, 97, 1313–1322 CrossRef CAS PubMed.
- B. J. DuChez, A. D. Doyle, E. K. Dimitriadis and K. M. Yamada, Biophys. J., 2019, 116, 670–683 CrossRef CAS PubMed.
- T. Kawano and S. Kidoaki, Biomaterials, 2011, 32, 2725–2733 CrossRef CAS PubMed.
- S. V. Plotnikov and C. M. Waterman, Curr. Opin. Cell Biol., 2013, 25, 619–626 CrossRef CAS PubMed.
- Y. S. Choi, L. G. Vincent, A. R. Lee, K. C. Kretchmer, S. Chirasatitsin, M. K. Dobke and A. J. Engler, Biomaterials, 2012, 33, 6943–6951 CrossRef CAS PubMed.
- B. Cortese, G. Gigli and M. Riehle, Adv. Funct. Mater., 2009, 19, 2961–2968 CrossRef CAS.
- J. T. Pham, L. Xue, A. Del Campo and M. Salierno, Acta Biomater., 2016, 38, 106–115 CrossRef CAS PubMed.
- P. Tseng and D. Di Carlo, Adv. Mater., 2013, 26, 1242 CrossRef PubMed.
- A. Khadpekar, N. Dwivedi, P. Tandaiya and A. Majumder, Cell Rep. Phys. Sci., 2025, 6, 102456 CrossRef CAS.
- R. J. Pelham Jr and Y.-L. Wang, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 13661–13665 CrossRef CAS PubMed.
- J. A. Burdick, A. Khademhosseini and R. Langer, Langmuir, 2004, 20, 5153–5156 CrossRef CAS PubMed.
- D. Lee, K. Golden, M. M. Rahman, A. Moran, B. Gonzalez and S. Ryu, Exp. Mech., 2019, 59, 1249–1259 CrossRef CAS.
- Y. Yang, K. Xie and H. Jiang, Biophys. J., 2020, 119, 1427–1438 CrossRef CAS PubMed.
- H. Ebata, K. Moriyama, T. Kuboki and S. Kidoaki, Biomaterials, 2020, 230, 119647 CrossRef CAS PubMed.
- S. Kidoaki and T. Matsuda, J. Biotechnol., 2008, 133, 225–230 CrossRef CAS PubMed.
- D. Joaquin, M. Grigola, G. Kwon, C. Blasius, Y. Han, D. Perlitz, J. Jiang, Y. Ziegler, A. Nardulli and K. J. Hsia, Biotechnol. Bioeng., 2016, 113, 2496–2506 CrossRef CAS PubMed.
- C.-H. R. Kuo, J. Xian, J. D. Brenton, K. Franze and E. Sivaniah, Adv. Mater., 2012, 24, 6059–6064 CrossRef CAS PubMed.
- H. Zhang, F. Lin, J. Huang and C. Xiong, Acta Biomater., 2020, 106, 181–192 CrossRef PubMed.
- H. Zhang, Y. Ma, W. Shu, Y. Wang, C. Cao, W. Wan, N. Shi, Z. Wei, D. Pei and A. Li, et al. , Adv. Funct. Mater., 2024, 34, 2309676 CrossRef CAS.
- Y. Shu, H. N. Chan, D. Guan, H. Wu and L. Ma, Sci. Bull., 2017, 62, 222–228 CrossRef CAS PubMed.
- A. Buxboim, K. Rajagopal, B. Andre’EX and D. E. Discher, J. Phys.: Condens. Matter, 2010, 22, 194116 CrossRef PubMed.
- J. M. Maloney, E. B. Walton, C. M. Bruce and K. J. Van Vliet, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2008, 78, 041923 CrossRef PubMed.
- S. Sen, A. J. Engler and D. E. Discher, Cell. Mol. Bioeng., 2009, 2, 39–48 CrossRef PubMed.
- J. R. Tse and A. J. Engler, Curr. Protoc. Cell Biol., 2010, 47, 10–16 Search PubMed.
- S. Syed, J. Schober, A. Blanco and S. Zustiak, PLoS One, 2017, 12(11), e0187853 CrossRef PubMed.
- H.-J. Butt and M. Jaschke, Nanotechnology, 1995, 6, 1 CrossRef.
- M. D. Norman, S. A. Ferreira, G. M. Jowett, L. Bozec and E. Gentleman, Nat. Protoc., 2021, 16, 2418–2449 CrossRef CAS PubMed.
- Y.-R. Chang, V. K. Raghunathan, S. P. Garland, J. T. Morgan, P. Russell and C. J. Murphy, J. Mech. Behav. Biomed. Mater., 2014, 37, 209–218 CrossRef CAS PubMed.
- A. M. Smith, D. G. Inocencio, B. M. Pardi, A. Gopinath and R. C. Andresen Eguiluz, ACS Appl. Poly. Mater., 2024, 6, 2405–2416 CrossRef CAS PubMed.
- C. E. Kandow, P. C. Georges, P. A. Janmey and K. A. Beningo, Methods Cell Biol., 2007, 83, 29–46 CAS.
- F. J. Byfield, Q. Wen, I. Levental, K. Nordstrom, P. E. Arratia, R. T. Miller and P. A. Janmey, Biophys. J., 2009, 96, 5095–5102 CrossRef CAS PubMed.
- U. Schmidt, M. Weigert, C. Broaddus and G. Myers, Medical Image Computing and Computer-Assisted Intervention-MICCAI 2018: 21st International Conference, Granada, Spain, September 16-20, 2018, Proceedings, Part III 21, 2018, pp. 265–272.
- D. Ershov, M.-S. Phan, J. W. Pylvänäinen, S. U. Rigaud, L. Le Blanc, A. Charles-Orszag, J. R. Conway, R. F. Laine, N. H. Roy and D. Bonazzi, et al. , Nat. Methods, 2022, 19, 829–832 CrossRef CAS PubMed.
- K. Moriyama and S. Kidoaki, Langmuir, 2018, 35, 7478–7486 CrossRef PubMed.
- A. Ueki and S. Kidoaki, Biomaterials, 2015, 41, 45–52 CrossRef CAS PubMed.
- J. Solon, I. Levental, K. Sengupta, P. C. Georges and P. A. Janmey, Biophys. J., 2007, 93, 4453–4461 CrossRef CAS PubMed.
- F. J. Calero-Cuenca, C. S. Janota and E. R. Gomes, Curr. Opin. Cell Biol., 2018, 50, 35–41 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |