Hidden in plain sight: commonly used copper N-heterocyclic carbene catalysts gain stabilization from anagostic Cu⋯H–C interactions

Abstract

The ubiquity in organic chemistry of copper catalysts supported by N-heterocyclic carbene (NHC) ligands is often attributed to the ability of sterically bulky and electronically donating NHCs to stabilize low-coordinate intermediates. Here, we show using meta-analysis of 893 solid-state Cu–NHC structures that nearly all Cu–NHC complexes contain at least one short Cu⋯H–C contact within the range expected for anagostic interactions, implying that Cu⋯H–C stabilization is prevalent in commonly used Cu–NHC catalysts. A quantum crystallography study of one example, I^tBuCuCl (1), provided evidence for four Cu⋯H–C anagostic interactions in the solid state. Based on experimental solid-state NMR spectroscopy and QTAIM analysis of theoretical charge density, evidence for four Cu⋯H–C anagostic interactions was also obtained for the solid-state structure of IPrCuCl (2), a ubiquitous complex in homogeneous Cu catalysis. The effect of these anagostic interactions on the solution-phase chemistry of 1 was probed by comparing catalytic activity of I^tBuCuCl with its deuterated analogue, d₁₈-I^tBuCuCl, revealing a secondary kinetic isotope effect (KIE) of k_H/k_D = 1.09 ± 0.01 for the hydrosilylation of a ketone at 315 K. Since these anagostic interactions were not previously assigned apart from selected supramolecular systems, knowledge of anagostic stabilization of Cu–NHC complexes is expected to guide future catalyst designs.

---

Introduction

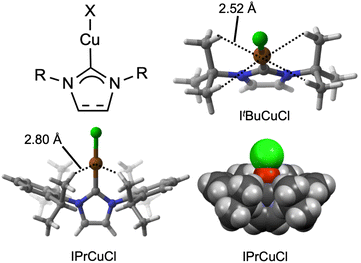
Copper(I) N-heterocyclic carbene (NHC) complexes have become nearly ubiquitous in homogeneous catalysis, promoting organic transformations including conjugate addition, allylic substitution, hydrofunctionalization, transfer hydrogenation, cyclopropanation, aziridination, cross coupling, click chemistry, C–H functionalization, carboxylation, carbonylation, olefination, and fluorination reactions.^1–8 Since the first Cu–NHC complex, [Cu(IMes)₂]OTf (IMes = 1,3-dimesitylimidazol-2-ylidene), was reported in 1993 by Arduengo,⁹ the unique properties of Cu–NHC complexes have often been attributed to their unusually low coordination numbers relative to four-coordinate, 18-electron Cu^I compounds. A meta-analysis of structural data in the Cambridge Structural Database (CSD) by Braunstein in 2019 indicated that ∼40% of the >650 Cu–NHC compounds reported at that time were classified as containing two-coordinate Cu centers, compared to only ∼5% of Cu–PR₃ complexes.¹⁰ This distinction between NHC and PR₃ ligation to Cu^I is usually ascribed to their different steric profiles, with PR₃ ligands giving conical shapes best described by “cone angles”¹¹ and NHC ligands projecting their N-substituents over the metal center in a manner best described by “buried volume” of the metal coordination sphere.^12–14 However, it should be noted that, in other contexts, nominally low-coordinate metal centers have often been documented to engage in agostic M⋯H–C interactions with bulky ligand substituents that serve to bring the metal centers toward coordinative saturation.^15,16 Thus, questions are raised based on the close proximity between the Cu centers and NHC substituents in many reported solid-state structures (Fig. 1): are nominally two-coordinate Cu–NHC complexes really two-coordinate, or do they gain stability from intramolecular Cu⋯H–C interactions? Answering these questions may impact how future Cu–NHC catalysts are designed for emerging catalytic applications.

Fig. 1 Representative solid-state structures of (NHC)CuX complexes, I^tBuCuCl and IPrCuCl (CSD codes RIPWAR and EVICER, respectively), highlighting potential close contacts between the Cu centers and calculated H atom positions of the NHC ligands.

A relevant precedent emerged in a 2021 study by Alabugin and Sollogoub of NHC-capped cyclodextrins metalated by coinage metals.¹⁷ These complexes feature NHC–M–Cl groups (M = Cu^I, Ag^I, Au^I) encapsulated within cyclodextrin cavities and were characterized as featuring “anagostic” M⋯H–C interactions, i.e., 3-center-4-electron bonding dominated by electrostatic forces. Specifically, close contacts between the encapsulated metal centers and the C⁵–H positions of two glucose rings were enforced by the rigid supramolecular scaffold, thus permitting spectroscopic and crystallographic characterization that calibrated extensive density functional theory (DFT) calculations. Inspired by those results, we hypothesized that conventional Cu–NHC complexes likely also feature anagostic Cu⋯H–C interactions that have eluded spectroscopic characterization in the absence of rigid supramolecular architectures exploited by Sollogoub and Alabugin. Here, not only do we present evidence using a combination of CSD meta-analysis, quantum crystallography, solid-state ¹³C NMR spectroscopy, and DFT calculations that solid-state Cu⋯H–C interactions occur in nearly every known Cu–NHC complex, but also that these anagostic interactions are relevant to solution-phase chemistry as evidenced by observation of an N-alkyl kinetic isotope effect (KIE) during hydrosilylation catalysis by I^tBuCuCl (I^tBu = 1,3-di-tert-butyl-imidazole-2-ylidene) and its d₁₈ analogue.

Results and discussion

Meta-analysis of Cu(NHC) structural data

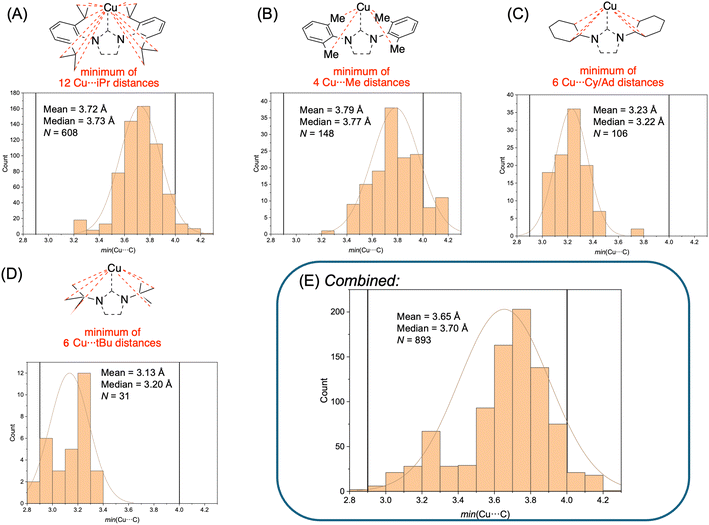
In the study by Alabugin and Sollogoub,¹⁷ the experimentally determined average Cu⋯H distance and Cu⋯H–C angle for the anagostic interactions were ∼2.5 Å and ∼140°, respectively, for their crystallographically characterized α-ICyD^MeCuCl complex. Because H atoms tend to be placed in calculated rather than experimentally determined positions in most crystallographic models, we have chosen to examine Cu⋯C distances rather than Cu⋯H distances when considering literature crystal structures. Computationally, it was determined by Alabugin and Sollogoub that the optimal ranges to maximize anagostic Cu⋯H–C interaction strength are 2.5–2.9 Å and 100–180°. Therefore, based on simple trigonometry (Fig. S1), the optimal anagostic Cu⋯C distance range is 2.9–4.0 Å.

To determine how common it is for Cu(NHC) complexes to have Cu⋯C distances within the 2.9–4.0 Å range, we conducted a meta-analysis of CSD data.¹⁸ For example, a search for Cu(NHC) structures with N-dipp substituents (dipp = 2,6-di-iso-propylphenyl) was conducted to analyze compounds containing the commonly used IPr and SIPr ligands (608 hits; see Díez-González & Nolan¹³ for common NHC abbreviations). For each entry, the minimum value among the 12 unique Cu⋯C_iPr distances was tabulated, and the min(Cu⋯C_iPr) data for all 608 entries are plotted in Fig. 2A. Analogous searches were conducted for N-aryl groups with 2,6-dimethyl substitution (thus including IMes and SIMes among others; Fig. 2B; 148 hits), N-cyclohexyl groups (ICy, SICy, IAd, SIAd; Fig. 2C; 106 hits), and N-tert-butyl groups (I^tBu and SI^tBu; Fig. 2D; 31 hits). It should be noted no other N-substituents were included in this meta-analysis, searching was restricted only to 5-membered NHC ligands, and other carbenes such as cyclic alkyl(amino) carbenes¹⁹ were excluded. Combining these datasets together, a total of 893 entries were included in the meta-analysis of min(Cu⋯C) (Fig. 2E). Separately, and in agreement with the previous meta-analysis by Braunstein,¹⁰ a search of all 5-membered Cu(NHC) structures without restrictions on the identity of the N-substituents indicated that over 40% of the 1391 hits are classified in the CSD as containing two-coordinate Cu centers (Fig. S2).

Fig. 2 Results of CSD meta-analysis for Cu(NHC) structures with (A) 2,6-di-iso-propylphenyl, (B) 2,6-dimethyl, (C) cyclohexyl/adamantyl, and (D) tert-butyl substituents on the N atoms. (E) Results combining datasets (A)–(D). Vertical black lines indicate the 2.9–4.0 Å range in which Cu⋯H–C interactions are expected.

The mean and median min(Cu⋯C) distances in the entire 893-membered dataset are 3.65 and 3.70 Å, respectively. Removing duplicate CSD reference codes for redundant entries arising from repeatedly reported structures gave a smaller the dataset with 558 unique counts, for which the mean and median min(Cu⋯C) distance are 3.70 and 3.72 Å, respectively (Fig. S3). Regardless, all these values are well within the 2.9–4.0 Å range identified by Alabugin and Sollogoub as being optimal for anagostic Cu⋯H–C interactions.¹⁷ Furthermore, when considering the distribution of min(Cu⋯C) distances for the entire dataset (Fig. 2E), it can be concluded that nearly every Cu(NHC) complex reported in the CSD contains at least one anagostic interaction. As such, our hypothesis that commonly used Cu(NHC) catalysts feature anagostic Cu⋯H–C interactions hidden in plain sight is validated by this meta-analysis, which also implies that two-coordinate Cu(NHC) complexes really have effective coordination numbers approaching the value of four expected from valence electron counting considerations. The overall min(Cu⋯C) distribution appears to be bimodal, with peaks at ∼3.25 Å and ∼3.75 Å. This bimodality reflects the fact that Cu(NHC) complexes in this dataset with N-alkyl groups tend to have shorter min(Cu⋯C) distances (e.g., 3.13 Å on average for N-tert-butyl) than those with ortho-substituted N-aryl groups (e.g., 3.72 Å on average for N-dipp). Nonetheless, even when examining each subset of compounds individually (Fig. 2A–D), it is clear that the vast majority of Cu(NHC) entries in the CSD contain at least one anagostic Cu⋯H–C interaction regardless of the N-substituents. In other words, there were no examples of N-substituents in this meta-analysis that showed significant min(Cu⋯C) populations outside the 2.9–4.0 Å range.

Quantum crystallography

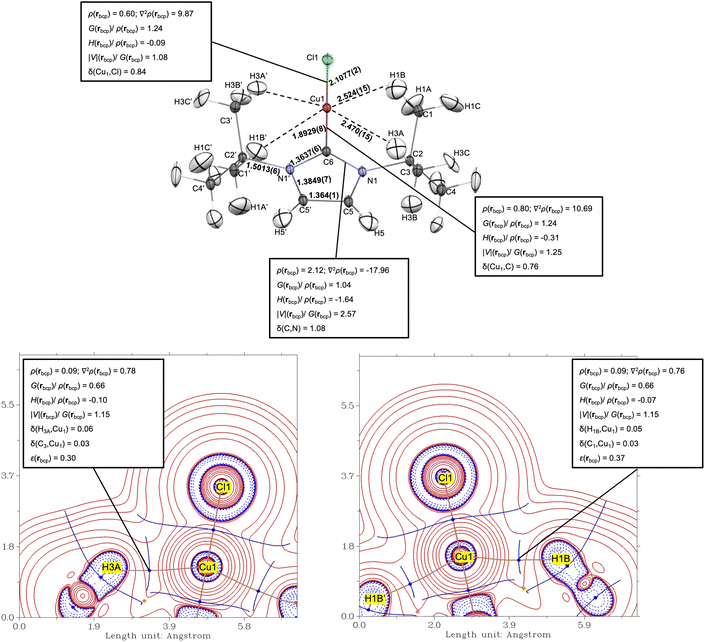
To further probe the possible existence of anagostic interactions in a conventional Cu(NHC) complex, we conducted a quantum crystallography^20,21 analysis of I^tBuCuCl (1) using experimental high-resolution (0.47 Å) charge density data collected at 10 K. The data were processed using Hirshfeld atomic refinement (HAR) and X-ray constrained wave function fitting.²² Consistent with a previous literature report (CSD entry: RIPWAR),²³ the solid-state structure of 1 (Fig. 3) in the C2/c space group features a crystallographic C₂ axis along the C_carbene–Cu–Cl bond, causing only half of the molecule (i.e., a single tert-butyl group) to appear in the asymmetric unit. The Cu(1)⋯C(1) and Cu(1)⋯C(3) distances involving the methyl groups nearest to Cu(1) are 3.3470(6) Å and 3.3085(6) Å, both falling within the optimal anagostic Cu⋯C distance range (2.9–4.0 Å) indicated above. The HAR-treated structure yielded corresponding Cu(1)⋯H(1B) and Cu(1)⋯H(3A) distances of 2.524(15) Å and 2.470(15) Å, along with Cu⋯H–C angles of 130.2(11)° and 132.3(10)°, respectively. The overall experimental Cu⋯H–C geometries in 1 show good agreement with those reported by Alabugin and Sollogoub,¹⁷ implying the presence of anagostic interactions in this complex.

Fig. 3 Crystal structure of I^tBuCuCl (1, top) with topological analysis of principal interactions according to high-resolution X-ray diffraction experimental data. All atoms (including hydrogens) are shown as thermal ellipsoids (50% probability), and distances are given in Å. Contour plots of ∇²ρ(r) for 1 in the plane defined by Cl (1), Cu(1), and H(3A) atoms (bottom left), and in the plane defined by Cl(1), Cu(1), and H(1B) atoms (bottom right). Interbasin paths are colored solid lines; blue dots correspond to position of (3,−1) critical points.

A quantum theory of atoms in molecules (QTAIM)²⁴ analysis of the experimental charge density for 1 was carried out to gain further insight into the nature of the Cu⋯H–C interactions. Consistent with the experimental geometry, bond paths each with a bond critical point (bcp) were located along the Cu(1)⋯H(1B) and Cu(1)⋯H(3A) vectors (Fig. 3). The Laplacian of the electron density [∇²ρ(r)], from the second derivative of charge density [ρ(r)], at a bcp often reports on the nature of a bonding interaction. A value of ∇²ρ(r_bcp) < 0 indicates accumulation of electron density between the atoms, whereas a value of ∇²ρ(r_bcp) > 0 corresponds to electron depletion between the atoms and accumulation at the atomic basins. From the experimental data for 1, the (3,-1) type Cu⋯H bcps were found to have low ρ(r_bcp) (0.09 e Å⁻³ for both) and positive ∇²ρ(r_bcp) (0.78 and 0.76 e Å⁻⁵) values, a topology typically associated with “closed-shell” interactions. However, the energy densities per electron at both bcps, H(r_bcp)/ρ(r_bcp), were found to be small and negative (−0.10 and −0.07), whereas closed-shell interactions are typically associated with positive H(r_bcp) values.²⁵ Further evaluation using the ratio of potential energy density to kinetic energy density at the bcps, |V|(r_bcp)/G(r_bcp),²⁶ yielded the value of 1.15 for both Cu⋯H anagostic interactions, placing them in the transit region (∇²ρ(r_bcp) > 0; H(r_bcp) < 0; and 1 < |V|(r_bcp)/G(r_bcp) < 2) regarded as intermediate between closed-shell and shared-shell bonding character. Nevertheless, it is important to note that such classifications were derived from by meta-analysis of bonding between either two main-group light atoms or two heavy (>three atomic shells²⁵) atoms. In contrast, the Cu⋯H interaction represents a heavy-light atom pair, for which standard topological criteria may not be robust. As previously highlighted in studies of metal–metal bonding,^25,27,28 bonds involving transition metals include simultaneous participation of diffuse ns and contracted (n-1)d orbitals, complicating the qualitative interpretation of bcp indicators that is otherwise standard in QTAIM analysis. For comparison, a Ag(I)-silyl complex with anagostic interactions was reported to have stronger Ag⋯H interactions than the Cu⋯H–C contact in 1, as reflected in its shorter Ag⋯H distance and larger bcp indicators (see SI for detailed comparison).²⁹ Nonetheless, both complexes fall within the “transit region” of M⋯H–C classification.²⁶

To better characterize the nature of the anagostic interaction in 1, we compared its bcp indicators with those of established agostic M⋯H–C motifs, which are described as partially covalent (rather than electrostatic) three-center, two-electron (3c–2e) bonding.³⁰ Unlike anagostic interactions, agostic interactions feature shorter M⋯H distances, smaller M⋯H–C angles, and upfield shifted ¹H NMR resonances,¹⁵ though experimental charge density studies of such interactions in organometallic systems remain scarce despite their long history.^16,31 A representative agostic example, EtTiCl₃(dmpe) (dmpe = 1,2-bis(dimethylphosphino)ethane),³² shows larger bcp indicators and a shorter Ti⋯H_β distance than 1, and the adjacent C_Me–H(3A) bond in 1 shows a larger ρ(r) and more negative ∇²ρ(r) value than C_Et–H_β, reflecting more pronounced orbital involvement and σ_CH → M_d donation in agostic systems³⁰ (see SI for detailed comparison).

To further probe the anagostic interactions, we considered bond ellipticity at the bcps, which reflects the deviation of ρ(r) from axial symmetry along the bond path.³³ In the case of 1, the ε values for Cu(1)⋯H(1B) and Cu(1)⋯H(3A) were found to be 0.37 and 0.30, respectively. These values indicate notable charge asymmetry along the Cu⋯H bond paths, consistent with the DFT-calculated electron delocalization from the Cu toward the methyl hydrogens (Fig. S12). Bond ellipticity has been employed previously in investigations of M⋯H–C agostic interactions^32,34,35 as well as M–H⋯H–C hydrogen bonding.³⁶ Indeed, as Brookhart noted,¹⁵ anagostic interactions are more akin to hydrogen bonds than agostic interactions and are often characterized by downfield ¹H NMR resonances (vide infra). Additionally, it is well known that for hydrogen-bonded systems, ρ(r_bcp) typically falls within the range of 0.002–0.034 a.u. (i.e., 0.0135–0.2362 e Å⁻³), with corresponding ∇²ρ(r_bcp) values of 0.024–0.139 a.u. (i.e., 0.5784–3.3497 e Å⁻⁵).³⁷ In contrast, agostic interactions generally exhibit ρ(r_bcp) and ∇²ρ(r_bcp) values outside these ranges.³⁸ Accordingly, a comparison of our system with experimentally characterized M–H⋯H–X hydrogen bonding is relevant and instructive. For example, a Mn–H⋯H–C interaction in cis-HMn(CO)₄PPh₃ was characterized as a weak, closed-shell hydrogen bond between electrophilic and nucleophilic hydrogens (H⋯H, 2.101(3) Å; Mn–H⋯H, 126.5(1)°).³⁶ In this complex, the Mn–H⋯H–C hydrogen bond descriptors (ρ(r_bcp) = 0.066(5) e Å⁻³, ∇²ρ(r_bcp) = 0.79(3) e Å⁻⁵, and ε = 0.40) are comparable to those for the Cu⋯H–C interaction in 1. Taken together, these electron density topologies support the Cu⋯H–C interactions as being weak and dominated by electrostatic forces, akin to a hydrogen bond.³⁹

Table 1 summarizes the atomic charges calculated from quantum crystallographic data of 1 using various methods. The magnitude of atomic charges follows the trend: Hirshfeld-I (HI)⁴⁰ ≫ charge model 5 (CM5)⁴¹ > atomic dipole moment-corrected Hirshfeld (ADCH)⁴² > Hirshfeld.⁴³ All methods provided chemically reasonable signs, apart from the CM5, which shows an anomaly in assigning the N–C–N fragment on the NHC carbene.⁴⁴ It is well known that NHC ligands are stabilized by aromaticity, and the N–C bonds in complex 1 exhibit significant π-bonding reflected by the Mayer bond order⁴⁵ and Wiberg bond order⁴⁶ values of 1.15 and 1.42, respectively. Moreover, the contour plots of experimental ρ(r) and ∇²ρ(r) (Fig. S27) within the NHC ring revealed a shift of the (3,−1) type bcp toward the nodal surface of carbon, indicating that the carbon in the N–C–N fragment is more electronegative than the adjacent nitrogen atoms. Apparently, in this case, the CM5 method fails to correct for the underestimation of atomic charges in the classic Hirshfeld scheme,⁴⁷ likely due to strong dependence on interatomic distances.⁴⁸

Table 1 Principal atomic charges of 1 calculated by different methods

Atom	Hirshfeld (a.u.)	Hirshfeld-I (a.u.)	ADCH (a.u.)	CM5 (a.u.)
Cu(1)	0.183	0.619	0.131	0.323
Cl(1)	−0.459	−0.653	−0.431	−0.519
N(1)	0.010	0.079	0.043	−0.240
C(5)	−0.021	−0.109	−0.098	−0.006
H(5)	0.051	0.127	0.136	0.124
C(2)	0.088	0.454	0.049	0.106
C(6)	−0.062	−0.314	−0.128	0.023
C(1)	−0.083	−0.504	−0.256	−0.229
H(1C)	0.030	0.126	0.086	0.085
H(1B)	0.029	0.105	0.074	0.082
H(1A)	0.034	0.140	0.123	0.093
C(3)	−0.085	−0.510	−0.255	−0.234
H(3A)	0.026	0.099	0.067	0.081
H(3B)	0.031	0.131	0.094	0.090
H(3C)	0.036	0.141	0.119	0.091
C(4)	−0.081	−0.506	−0.263	−0.226

---

Gratifyingly, all atomic charge distributions consistently showed that the hydrogen atoms closest to the Cu^I carry a lower positive charge (by 0.005–0.052 e⁻ depending on the method) compared both to other hydrogen atoms in the same methyl group and (by 0.013–0.048 e⁻ depending on the method) to other hydrogen atoms on the methyl group not directed at Cu. Notably, the ADCH method provides clearer differentiation among the hydrogen atoms, making it particularly useful for assessing relative trends. Overall, the reduced positive charge on the hydrogen participating in the Cu⋯H–C interactions suggests a partial shift of electron density from the metal toward the hydrogen atoms, consistent with topological analyses presented above.

Theoretical analysis

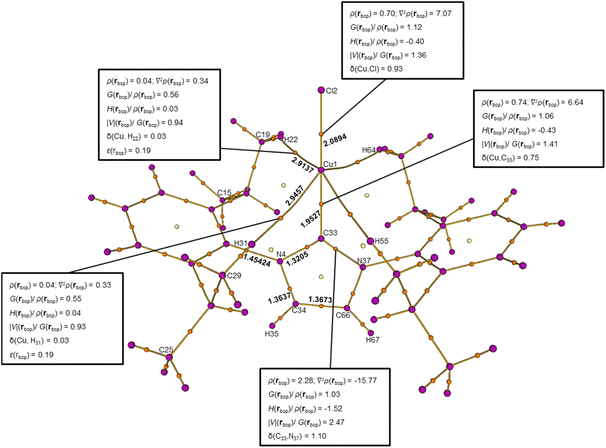
We further performed a QTAIM analysis of charge density for 1 calculated by density functional theory (DFT) using previously published crystallographic coordinates.²³ Topological plots of the theoretical density also indicated Cu⋯H bond paths each with a corresponding bcp (see Fig. S15 and S16). Good agreement in topological features between the experimental and theoretical densities (Fig. 3 and S14) validates the reliability of both the experimental and DFT methods. Collectively, we infer that four Cu⋯H–C anagostic interactions are simultaneously present in the molecule in its crystallographic conformation. When considering the Cu–C_carbene and Cu–Cl interactions, it is evident that the Cu center in 1 is surrounded by 6 bcps in a pseudo-octahedral arrangement. Thus, while the Cu center in 1 has a formal coordination number of 2, the effective coordination number when including non-covalent interactions is 6.

Subsequently, we moved into another common (NHC)CuX complex, IPrCuCl (2). First synthesized by Sadighi and Buchwald,⁴⁹ complex 2 is one of the most commonly-used Cu^I pre-catalysts⁵⁰ and has even been incorporated into undergraduate laboratory courses.⁵¹ The theoretical models of 2 used for this analysis were based on published crystallographic coordinates (CSD entries: EVAHEO and EVICER).^52,53 Notably, the EVICER has two co-crystallized dichloromethane molecules that apparently cause slight tilting of the N-aryl group, whereas EVAHEO contains no co-crystallized solvents in the lattice and shows N-aryl groups nearly orthogonal to the N-heterocyclic ring. For both structures (P2₁/m vs. Pccn, respectively), complex 2 itself retains crystallographic C₂ symmetry (as does complex 1) causing only half the molecule to reside in each asymmetric unit. Topological analysis of electronic density for the EVAHEO structure is included here, and corresponding discussion of the EVICER structure is given in SI.

The EVAHEO structure has two short Cu⋯H distances (Cu⋯H(22) = 2.9137 Å and Cu⋯H(31) = 2.9457 Å), with corresponding Cu⋯C separations of Cu⋯C(19) = 3.8130 Å and Cu⋯C(29) = 3.8668 Å both falling within the 2.9–4.0 Å range. In this case, QTAIM analysis revealed (3,–1) bcps for both Cu⋯H(22) (ρ(r_bcp) = 0.04 e Å⁻³ and ∇²ρ(r_bcp) = 0.34 e Å⁻⁵) and Cu⋯H(31) (ρ(r_bcp) = 0.04 e Å⁻³ and ∇²ρ(r_bcp) = 0.33 e Å⁻⁵) vectors (Fig. S18 and S19). Consequently, four Cu⋯H–C anagostic interactions are simultaneously present in 2, together with Cu–C_carbene and Cu–Cl interactions, placing the Cu center in a pseudo-octahedral arrangement defined by 6 bcps. The bcp indicators associated with the Cu⋯H(22) and Cu⋯H(31) interactions unambiguously point to a closed-shell interaction, as characterized by H(r_bcp) > 0, ∇²ρ(r_bcp) > 0, and |V|(r_bcp)/G(r_bcp) < 1.²⁶ The significantly lower Cu⋯H bond ellipticity determined for 2 (ε(r_bcp) = 0.19 and 0.19) compared to 1 (ε(r_bcp) = 0.53 and 0.41) can be attributed to differences in Cu⋯H–C bond angles (2: 153.26° and 156.98°; 1: 134.67° and 136.09°). Similarly, it has been reported that the geometry of agostic interactions in NHC–Ni(I) complexes is markedly influenced by the steric constraints imposed by the side chain of the NHC.⁵⁴

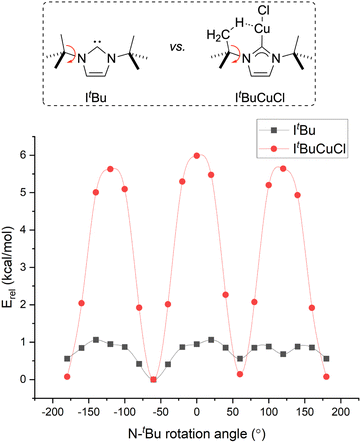
Further evidence for anagostic Cu⋯H–C interactions was obtained from the DFT models. First, the H atoms near the Cu centers (and, thus, engaged in anagostic interactions) in 1 and 2 were calculated to have gas-phase ¹H NMR chemical shifts downfield (by 1.39 and 1.13 ppm, respectively) of analogous H atoms pointed away from Cu (Fig. S9 and S10). This predicted chemical shift effect for 1 and 2 is similar to the experimentally observed downfield (by 1.2 ppm) ¹H NMR resonances for the anagotic C⁵–H positions of α-ICyD^MeCuCl relative to [α-ICyD^Me·H]⁺.¹⁷ Second, for 1, a frontier molecular orbital (HOMO−1) was calculated to have some C–H character (Fig. S12). Third, the barrier for N–C_^tBu rotation was calculated for 1 by systematically varying the dihedral angle between the N–C_carbene plane and one of the C_^tBu–C_Me planes (Fig. S10). The same calculation was carried out for the free I^tBu ligand (Fig. S13). The difference between the two rotational barriers of 4.9 kcal mol⁻¹ (Fig. 5) can be attributed to the energy required to disrupt two anagostic Cu⋯H–C interactions from the lowest-energy configuration, implying that each anagostic interaction contributes 2.5 kcal mol⁻¹ of stabilization. This energy estimation is in line with a recent computational study of Cu⋯H–C anagostic interactions by Hernández Sánchez and Shee.⁵⁵ Since the ground-state structure of 1 features four anagostic interactions, it can be concluded that 1 gains roughly 10 kcal mol⁻¹ of cumulative ground-state stabilization that is typically ignored when designing Cu(NHC) catalysts.

Fig. 4 Molecular graph from a computational model of IPrCuCl (2) (CSD code EVAHEO) with bond lengths and topological analysis of principal interactions displaying (3,−3) type critical points (violet), (3,−1) type bond critical points (orange), and (3,+1) type ring critical points (yellow).

Fig. 5 Computed N-^tBu rotational barriers for I^tBu and I^tBuCuCl.

Solid-state NMR spectroscopy

Given the calculated interaction strength of 2.5 kcal mol⁻¹, it is unlikely that low-temperature NMR experiments would feasibly provide spectroscopic evidence for Cu⋯H–C interactions in solution. Therefore, we sought to further characterize these interactions using solid-state NMR (SSNMR) analysis of 2. Though the resolution of a ¹H Hahn echo spectrum was insufficient to resolve overlapping resonances (Fig. S28), the variety of ¹³C SSNMR spectra revealed desymmetrization due to anagostic interactions compared to the reported solution-phase ¹³C NMR spectra. Because anagostic Cu⋯H–C interactions in 2 involve the carbon atoms on the iso-propyl groups, we focused on the aliphatic region of the ¹³C SSNMR spectra (ca. 20–30 ppm).

In the solution-phase ¹³C{¹H} NMR spectrum of 2, three iso-propyl resonances were observed at δ = 28.8 (methine), 24.9 (methyl), and 23.9 (methyl) ppm.⁵⁶ On the other hand, in the ¹³C cross-polarization magic angle spinning (CPMAS) SSNMR spectrum, six iso-propyl resonances were observed at δ = 28.7, 28.0, 27.6, 26.9, 24.0, and 21.1 ppm (Fig. 6). A ¹³C direct-polarization magic angle spinning (DPMAS) Hahn-echo SSNMR spectrum with a short recycle delay (d₁ = 5 s) attenuated the two downfield resonances substantially, consistent with these two resonances (δ = 28.7 and 28.0 ppm) corresponding to inequivalent methine carbons. The remaining four aliphatic resonances (δ = 27.6, 26.9, 24.0, and 21.1 ppm), are then assigned to inequivalent methyl environments in the solid state. The downfield shift of two methyl resonances (δ = 27.6 and 26.9 ppm) into the methine region is consistent with Cu⋯H–C anagostic bonding, relative to the other two resonances (δ = 24.0 and 21.1 ppm) corresponding to methyl groups oriented away from the Cu center. In short, the methyl groups involved in anagostic interactions are shifted downfield by an average of 4.7 ppm in ¹³C SSNMR. These assignments were further supported by a ¹³C{¹H} HETCOR spectrum (Fig. S32), which confirmed that the anagostic methyl ¹³C resonances have a correlation to ¹H resonances that are, similarly, downfield shifted.

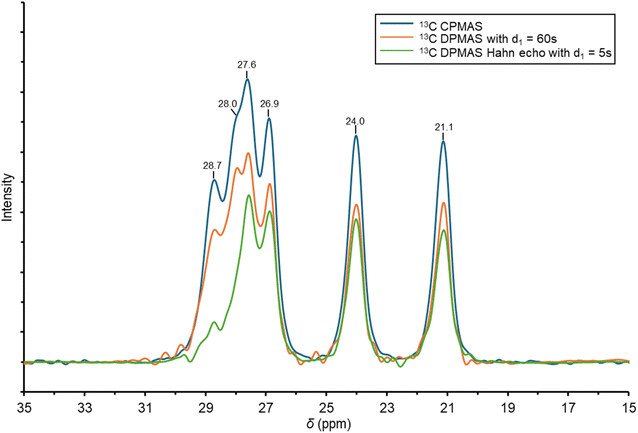Fig. 6 Expansion of the ¹³C CPMAS (in blue), ¹³C DPMAS with d₁ = 60 s (in orange), and ¹³C DPMAS Hahn Echo with d₁ = 5 s (in green) spectra for complex 2.

Simulated ¹³C SSNMR chemical shifts (see SI for details) generated from the solid-state EVAHEO structure using plane-wave DFT calculations⁵⁷ showed excellent agreement with experiment and reproduced the six iso-propyl resonances corresponding to the carbon sites assigned above. Both the experimental and simulated spectra indicate that the methyl groups not involved in anagostic interactions differ markedly from each other compared to the inequivalent but similar shifts for the Cu⋯H–C methyl or methine carbons. This distinction between methyl groups oriented away from the Cu center is attributed to packing-dependent shielding effects. Nonetheless, the simulation further supports the presence of anagostic interactions in the solid state.

Given that the quantum crystallographic study of 1 established the ADCH method as particularly effective in differentiating hydrogen atom charges, this method was also used to analyze 2. Once again, the ADCH calculation⁴² of 2 (Fig. 4 and Table S1) revealed distinct atomic charges for all six aliphatic carbons, with the carbons involved in anagostic interactions carrying less negative charges than those uninvolved (i.e., Cu⋯C(19) = −0.229 a.u. and Cu⋯C(29) = −0.231 a.u. vs. Cu⋯C(15) = −0.352 a.u. and Cu⋯C(25) = −0.246 a.u.), correlating qualitatively with the ¹³C SSNMR chemical shifts. While this trend is consistent with expected changes in shielding based on electron density, it should be regarded as supportive rather than causal, as NMR chemical shifts originate from magnetic shielding tensors rather than atomic charges.

Kinetic isotope effect

The preceding experimental and computational data establish the presence of anagostic interactions for most Cu(NHC) complexes in the solid state. Since most applications of Cu(NHC) complexes are in solution phase, we next sought evidence for anagostic interactions in solution. Thus, we chose to examine whether anagostic interactions influence catalytic reaction rates by comparing the behavior of I^tBuCuCl with its deuterated analogue, d₁₈-I^tBuCuCl (Fig. 7).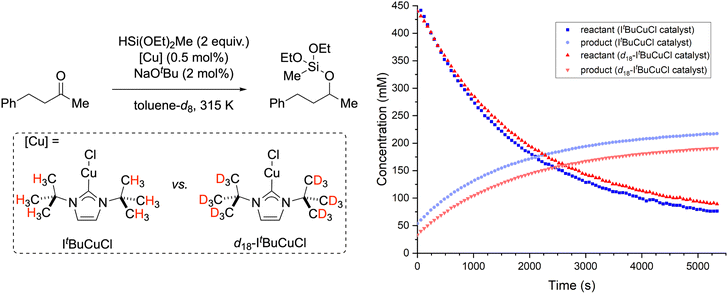

Fig. 7 Determination of a kinetic isotope effect for ketone hydrosilylation catalyzed by I^tBuCuCl vs. d₁₈-I^tBuCuCl. Averaging over multiple runs, it was determined that k_H/k_D = 1.09 ± 0.01.

The probe reaction we chose was hydrosilylation with methyldiethoxysilane of benzylacetone, duplicating catalytic reaction conditions reported by Leyssens that give pseudo-first order kinetics with ketone hydrocupration by (NHC)CuH being turnover limiting.⁵⁸ When comparing rates for reactions catalyzed by I^tBuCuCl vs. d₁₈-I^tBuCuCl, a secondary kinetic isotope effect (KIE) of k_H/k_D = 1.09 ± 0.01 was measured reproducibly. Representative reaction profile data is presented in Fig. 7. The observation of a secondary KIE is consistent with what is often observed for the equilibrium isotope effect (EIE) of M⋯H–C agostic interactions.⁵⁹ Thus, the observed rate constant for the current reaction is likely a composite of two terms, an equilibrium constant (with a secondary EIE) for reversible Cu⋯H–C dissociation and a rate constant (presumably insensitive to the isotopic substitution) for ketone hydrocupration, as summarized in Fig. 8. Although a normal isotope effect was observed under these conditions, the EIE values for agostic interactions are known to be highly temperature sensitive, switching from normal to inverse at critical temperatures specific to the complex under investigation.⁵⁹ Therefore, there are likely to be Cu(NHC)-catalyzed reactions for which inverse isotope effects would be measured at optimized conditions. As such, hypothetical Cu(NHC) compounds lacking anagostic interactions could, in principle, produce faster catalytic rates in some cases. Although this analysis is based on the literature of agostic interactions and other σ-complexes with covalent character, the anagostic interactions in questions exhibit characteristics of (contra-electrostatic) hydrogen bonds as discussed above and described by Alabugin and Sollogoub.¹⁷ In this regard, it is important to note that hydrogen bonds, too, are known to exhibit equilibrium isotope effects of complex origin.^60,61

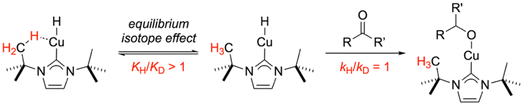Fig. 8 Proposed involvement of an anagostic equilibrium in the turnover-limiting step for the model reaction probed by isotopic substitution.

Conclusions

Although many Cu–NHC catalysts are assigned in the literature as having low coordination numbers and, thus, coordinative unsaturation, the work in this study indicates conclusively that nearly every Cu–NHC complex gains stabilization from at least one – and often multiple – Cu⋯H–C anagostic interactions between the metal center and the NHC N-substituents. In other words, while (NHC)CuX complexes have coordination numbers of 2 in the classical sense, their effective coordination numbers are higher when considering all non-covalent interactions at play. Close examination of such interactions by quantum crystallography, solid-state NMR, and DFT calculations confirmed the presence of Cu⋯H–C anagostic interactions showing characteristics of closed-shell (non-covalent) interactions akin to hydrogen bonds. The influence of the anagostic interactions on solution-phase chemistry was revealed by experimental kinetics measurements comparing I^tBuCuCl and d₁₈-I^tBuCuCl as catalysts for ketone hydrosilylation. Collectively, these observations point to non-covalent interactions between the Cu center and the NHC N-substituents as a previously unaccounted feature when considering Cu(NHC) complexes. These Cu⋯H–C interactions may serve as the basis for catalyst design principles akin to the recent literature of Au catalysis.^62,63

Author contributions

C. Y.: conceptualization, investigation, analysis, writing. T. C.: methodology, investigation. Y.-S. C.: methodology, resources, supervision, funding acquisition. A. L. P.: methodology, investigation. D. M.: methodology, investigation, analysis. N. P. M.: conceptualization, funding acquisition, investigation, analysis, supervision, writing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The supporting data has been provided as part of the supplementary information (SI).

CCDC 2494348 contains the supplementary crystallographic data for this paper.⁶⁴

Supplementary information: supplementary procedures & data, CSD search results, crystallographic data. See DOI: https://doi.org/10.1039/d5sc09643j.

Acknowledgements

Funding was provided by NIH/NIGMS (kinetics, CSD meta-analysis) and NSF (quantum crystallography, theory) under grants R35 GM140850 and CHE-2451851, respectively. Computational resources and services were provided by the Advanced Cyberinfrastructure for Education and Research (ACER) group at UIC. NSF's ChemMatCARS, Sector 15 at the Advanced Photon Source (APS), Argonne National Laboratory (ANL) is supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant numbers CHE-1834750 and CHE-2335833. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. This study made use of the National Magnetic Resonance Facility at Madison, an NIH Biomedical Technology Research Resource Center NIH R24 GM141526. Dr Pinar Alayoglu (UIC) and Jonathan Alvarado (Walter Payton High School) assisted with crystallographic data collection and CSD searching, respectively.

Notes and references

1. F. Lazreg, F. Nahra and C. S. J. Cazin, Coord. Chem. Rev., 2015, 293–294, 48–79.
2. S. Díez-González and S. Nolan, Synlett, 2007, 14, 2158–2167.
3. N. Beig, V. Goyal and R. K. Bansal, Beilstein J. Org. Chem., 2023, 19, 1408–1442.
4. S. Gaillard, C. S. J. Cazin and S. P. Nolan, Acc. Chem. Res., 2012, 45, 778–787.
5. L. J. Cheng and N. P. Mankad, Acc. Chem. Res., 2021, 54, 2261–2274.
6. L. J. Cheng and N. P. Mankad, Chem. Soc. Rev., 2020, 49, 8036–8064.
7. T. Fujihara, K. Semba, J. Terao and Y. Tsuji, Catal. Sci. Technol., 2014, 4, 1611–1699.
8. S. Budagumpi, R. S. Keri, G. Achar and K. N. Brinda, Adv. Synth. Catal., 2020, 362, 970–997.
9. A. J. I. Arduengo, H. V. R. Dias, J. C. Calabrese and F. Davidson, Organometallics, 1993, 12, 3405–3409.
10. A. A. Danopoulos, T. Simler and P. Braunstein, Chem. Rev., 2019, 119, 3730–3961.
11. C. A. Tolman, Chem. Rev., 1977, 77, 313–348.
12. L. Cavallo, A. Correa, C. Costabile and H. Jacobsen, J. Organomet. Chem., 2005, 690, 5407–5413.
13. S. Díez-González and S. P. Nolan, Coord. Chem. Rev., 2007, 251, 874–883.
14. D. E. Ryan, J. T. I. Fuller, E. A. Patrick, J. D. Erickson, A. L. Speelman, T. G. Carroll, G. K. Schenter, B. Ginovska, S. Raugei, R. M. Bullock and B. L. Tran, J. Am. Chem. Soc., 2025, 147, 14280–14298.
15. M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914.
16. M. Brookhart and M. L. H. Green, J. Organomet. Chem., 1983, 250, 395–408.
17. G. dos Passos Gomes, G. Xu, X. Zhu, L. M. Chamoreau, Y. Zhang, O. Bistri-Aslanoff, S. Roland, I. V. Alabugin and M. Sollogoub, Chem.–Eur. J., 2021, 27, 8127–8142.
18. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
19. R. Jazzar, M. Soleilhavoup and G. Bertrand, Chem. Rev., 2020, 120, 4141–4168.
20. A. Genoni, L. Bučinský, N. Claiser, J. Contreras-García, B. Dittrich, P. M. Dominiak, E. Espinosa, C. Gatti, P. Giannozzi, J.-M. Gillet, D. Jayatilaka, P. Macchi, A. Ø. Madsen, L. Massa, C. F. Matta, K. M. Merz Jr, P. N. H. Nakashima, H. Ott, U. Ryde, K. Schwarz, M. Sierka and S. Grabowsky, Chem.–Eur. J., 2018, 24, 10881–10905.
21. T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1628.
22. M. Woińska, D. Jayatilaka, B. Dittrich, R. Flaig, P. Luger, K. Woźniak, P. M. Dominiak and S. Grabowsky, ChemPhysChem, 2017, 18, 3334–3351.
23. L. Kuehn, A. F. Eichhorn, T. B. Marder and U. Radius, J. Organomet. Chem., 2019, 881, 25–33.
24. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990.
25. P. Macchi, D. M. Proserpio and A. Sironi, J. Am. Chem. Soc., 1998, 120, 13429–13435.
26. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
27. P. Macchi and A. Sironi, Coord. Chem. Rev., 2003, 238–239, 383–412.
28. C. Yan, M. R. Radzhabov, T. Chang, Y.-S. Chen and N. P. Mankad, Inorg. Chem., 2025, 64, 4514–4523.
29. E. Hupf, L. A. Malaspina, S. Holsten, F. Kleemiss, A. J. Edwards, J. R. Price, V. Kozich, K. Heyne, S. Mebs, S. Grabowsky and J. Beckmann, Inorg. Chem., 2019, 58, 16372–16378.
30. M. Lein, Coord. Chem. Rev., 2009, 253, 625–634.
31. W. I. Sundquist, D. P. Bancroft and S. J. Lippard, J. Am. Chem. Soc., 1990, 112, 1590–1596.
32. W. Scherer, W. Hieringer, M. Spiegler, P. Sirsch, G. S. McGrady, A. J. Downs, G. S. McGrady, A. Haaland and B. Pedersen, Chem. Commun., 1998, 2471–2472.
33. R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068.
34. W. Scherer, P. Sirsch, D. Shorokhov, M. Tafipolsky, G. S. McGrady and E. Gullo, Chem.–Eur. J., 2003, 9, 6057–6070.
35. M. Padilla, M. Batuecas, P. García-Orduña, I. Fernández and F. J. Fernández-Álvarez, Inorg. Chem., 2025, 64, 255–267.
36. Y. A. Abramov, L. Brammer, W. T. Klooster and R. M. Bullock, Inorg. Chem., 1998, 37, 6317–6328.
37. U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754.
38. P. L. A. Popelier and G. Logothetis, J. Organomet. Chem., 1998, 555, 101–111.
39. T. S. Thakur and G. R. Desiraju, Chem. Commun., 2006, 552–554.
40. P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111.
41. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 527–541.
42. T. Lu and F. Chen, J. Theor. Comput. Chem., 2012, 11, 163–183.
43. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
44. M. Tafipolsky, W. Scherer, K. Öfele, G. Artus, B. Pedersen, W. A. Herrmann and G. S. McGrady, J. Am. Chem. Soc., 2002, 124, 5865–5880.
45. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
46. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
47. E. R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319–330.
48. T. Lu and Q. Chen, Partial Charges in Exploring Chemical Concepts Through Theory and Computation, John Wiley & Sons, Ltd, 2024, vol. 1 pp. 161–188.
49. V. Jurkauskas, J. P. Sadighi and S. L. Buchwald, Org. Lett., 2003, 5, 2417–2420.
50. V. A. Voloshkin, L. P. Zorba and S. P. Nolan, Chem. Sci., 2025, 16, 2062–2082.
51. F. Bru, S. M. P. Vanden Broeck, G. Pisanò, K. De Buysser and C. S. J. Cazin, J. Chem. Educ., 2023, 100, 2359–2366.
52. H. Kaur, F. K. Zinn, E. D. Stevens and S. P. Nolan, Organometallics, 2004, 23, 1157–1160.
53. N. P. Mankad, T. G. Gray, D. S. Laitar and J. P. Sadighi, Organometallics, 2004, 23, 1191–1193.
54. W. He, D. Dawson Beattie, H. Zhou, E. G. Bowes, L. L. Schafer, J. A. Love and P. Kennepohl, Chem. Sci., 2021, 12, 15298–15307.
55. D. Awasthi, M. Friede, M. K. Osei, A. Hansen, R. H. Sánchez and J. Shee, J. Phys. Chem. A, 2025, 129, 7689–7699.
56. W. Zeng, E. Wang, R. Qiu, M. Sohail, S. Wu and F.-X. Chen, J. Organomet. Chem., 2013, 743, 44–48.
57. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys. Condens. Matter, 2009, 21, 395502.
58. T. Vergote, F. Nahra, A. Merschaert, O. Riant, D. Peeters and T. Leyssens, Organometallics, 2014, 33, 1953–1963.
59. G. Parkin, Acc. Chem. Res., 2009, 42, 315–325.
60. P. E. Hansen, in Spectroscopy and Computation of Hydrogen-Bonded Systems, ed. M. J. Wójcik and Y. Ozaki, Wiley, 1st edn, 2023, pp. 173–212.
61. L. Sobczyk, M. Obrzud and A. Filarowski, Molecules, 2013, 18, 4467–4476.
62. H. Darmandeh, J. Löffler, N. V. Tzouras, B. Dereli, T. Scherpf, K. Feichtner, S. Vanden Broeck, K. Van Hecke, M. Saab, C. S. J. Cazin, L. Cavallo, S. P. Nolan and V. H. Gessner, Angew. Chem., Int. Ed., 2021, 60, 21014–21024.
63. A. Sorroche, S. Moreno, M. Elena Olmos, M. Monge and J. M. López-de-Luzuriaga, Angew. Chem., Int. Ed., 2023, 62, e202310314.
64. CCDC 2494348: Experimental Crystal Structure Determination, 2026,  DOI:10.5517/ccdc.csd.cc2pqkvv.

---