Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sensitive detection of spin-electric coupling in a Cr3 antiferromagnetic triangle
Leonardo Tacconi†
 a,
Shubham Bisht†
a,
Shubham Bisht† b,
Alberto Cini†
b,
Alberto Cini† cd,
Mauro Perfetti
cd,
Mauro Perfetti ad,
Tomas Orlando
ad,
Tomas Orlando e,
Maria Fittipaldi
e,
Maria Fittipaldi *cd,
Michael Shatruk
*cd,
Michael Shatruk *b and
Roberta Sessoli
*b and
Roberta Sessoli *ad
*ad
aDipartimento di Chimica “U. Schiff”, Università degli Studi di Firenze, Sesto Fiorentino, Firenze, I-50019, Italy. E-mail: roberta.sessoli@unifi.it
bDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: shatruk@chem.fsu.edu
cDipartimento di Fisica e Astronomia, Università degli Studi di Firenze, Sesto Fiorentino, Firenze, I-50019, Italy. E-mail: maria.fittipaldi@unifi.it
dConsorzio Interuniversitario Nazionale per la Scienza e Tecnologia Dei Materiali, Firenze, I-50121, Italy
eNational High Magnetic Field Laboratory, Tallahassee, FL 32310, USA
First published on 4th December 2025
Abstract
Molecular antiferromagnetic triangles are a convenient platform to study the effect of an electric field on the magnetic exchange interactions. However, such effects are typically hard to detect, especially in systems with weak spin–orbit coupling. In this work, an asymmetric µ3-oxo-centered Cr3 triangle was synthesized and structurally characterized as a non-centrosymmetric molecular crystal suitable for probing Spin Electric Coupling (SEC). A combination of single-crystal magnetometry, cantilever torque magnetometry, and continuous-wave electron paramagnetic resonance (EPR) allowed precise determination of the spin Hamiltonian parameters, including the weak Dzyaloshinskii–Moriya interaction. Electric-field-modulated EPR (EFM-EPR) experiments provided the first direct observation of SEC in a CrIII-based complex, revealing measurable electric-field effects on the single-ion 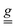 tensor and setting an upper bound for the SEC influence on magnetic exchange interactions. These findings demonstrate the exceptional sensitivity of EFM-EPR spectroscopy for quantifying SEC and highlight the crucial role of molecular symmetry and ligand environment in enabling electric control of spin states, thus advancing the rational design of molecular systems for quantum technologies.
tensor and setting an upper bound for the SEC influence on magnetic exchange interactions. These findings demonstrate the exceptional sensitivity of EFM-EPR spectroscopy for quantifying SEC and highlight the crucial role of molecular symmetry and ligand environment in enabling electric control of spin states, thus advancing the rational design of molecular systems for quantum technologies.
Introduction
Spins in molecules are a potential resource for quantum technologies.1–3 They can act as quantum sensors of magnetic fields or as active units (qubits) in quantum information processing. If properly designed, they can exhibit remarkable quantum coherence and can be integrated into more complex architectures. Individual spin addressability remains critical if probed with magnetic fields. Conversely, electric fields can be confined at the level of a single molecule and have been employed to address molecular spins in nanojunctions4 or under a scanning probe tip.5Electric field control of the magnetization is a widely investigated phenomenon in extended inorganic lattices,6–9 but less explored in molecular materials.10 In the latter, we can distinguish two main research lines, reflecting the different mechanisms that lead to spin-electric coupling (SEC). The first is the electric field control of single-ion magnetic anisotropy, which can be detected as a shift in the resonance field in continuous-wave Electron Paramagnetic Resonance (EPR) or the accumulation of a phase in pulsed EPR experiments.11–16 Additionally, spin transitions can be coherently promoted by the electric field, and the effects are enhanced in piezo-17 and ferroelectric materials.18 Spin–orbit coupling (SOC) plays a crucial role in this context, and several useful correlations with the molecular structure have been recently established.15,19,20 The second line, more relevant here, is the electric field control of systems with active exchange interactions between spins.21–24 Optimizing such an effect could provide a pathway to scalable quantum architectures based on molecular spins, as proposed by Kane for spins in semiconductors.25
A fascinating platform for investigating the effect of an electric field on magnetic exchange is formed by antiferromagnetic triangles of half-integer spins. Spin frustration results in two degenerate doublet ground states in the case of strict three-fold symmetry.26 The degeneracy can be removed by coupling with vibrations, i.e., static or dynamic Jahn–Teller effect,27 by SOC-mediated antisymmetric or Dzyaloshinskii–Moriya (DM) exchange interaction,28 or by an electric field.29,30 EPR experiments with electric field pulses superimposed on the sequence of the electromagnetic radiation pulses have detected SEC effects in the spin echo of FeIII3 (ref. 22) and CuII3 triangles.12 Conversely, no effect was detected for CrIII3 triangles,22 and the absence was attributed to the small single-ion magnetic anisotropy and very weak DM interactions compared to those observed for FeIII3.22
CW-EPR spectroscopy with electric field modulation (EFM-EPR), instead of the conventional magnetic field modulation, constitutes a relatively underutilized yet powerful tool for investigating the SEC phenomenon in single crystals, enabling a detailed analysis of the SEC anisotropy.16,21,23,31,32 In fact, EFM-EPR retains the full spectroscopic potential of EPR by providing informative spectral line shapes at each orientation. However, the detection of the linear effect requires the use of non-centrosymmetric crystals. We stress here that the use of EFM-EPR associated with first-order detection is possible only for samples that lack global inversion symmetry. The currents in the transmission line that charge the capacitor also generate an oscillating magnetic field,24 which, if overlooked, may lead to data being misinterpreted as an EFM-EPR signal from a randomly oriented powder specimen.33
In this study, we demonstrate the exceptional sensitivity of the EFM-EPR technique by investigating SEC in the elusive case of CrIII3, which did not show any effect in pulsed EPR experiments.22 To that end, we have synthesized an asymmetric µ3-oxo-centered triangle where six 4-aminobenzoate bridges connect the CrIII ions. The terminal ligands are two methanol molecules and one 3-trifluoromethylpyridine (Fig. 1). A combination of single-crystal magnetometry (both standard and torque) and EPR experiments provided an accurate quantification of the Spin Hamiltonian parameters, including the very weak DM interaction. Single-crystal CW EPR spectra under electric field modulation were acquired and simulated, providing the first evidence of SEC in a CrIII-based molecular material. Our findings highlight EFM-EPR spectroscopy as a key tool for advancing understanding of SEC mechanisms and for identifying strategies to exploit it for quantum applications based on molecular spins.
Results and discussion
All details on materials and methods are available in the SI.Synthesis
Complex [Cr3(µ3-O)(µ2-4-H3NBzO)6(3-CF3py)(MeOH)2](NO3)7 (1) was synthesized by a reaction between Cr(NO3)3 and 4-aminobenzoic acid (4-H3NBzOH) in MeOH, followed by addition of 3-trifluoromethylpyridine (3-CF3py). Performing the second step at room temperature resulted in a mixture of two types of crystals, corresponding to [Cr3(µ3-O)(µ2-4-H3NBzO)6(MeOH)3](NO3)7 (1′), previously reported by Zaworotko et al.,34 and complex 1, reported here for the first time and formed by replacement of one of the MeOH ligands in 1′ by 3-CF3py. Crystals of 1′ were extremely hygroscopic, while the crystals of 1 appeared more stable when exposed to air. Performing the reaction under reflux forced more complete replacement of the MeOH ligand, leading to the isolation of pure 1 in good yield (60%). Crystallization of 1 was achieved by vapor diffusion of Et2O into the methanolic solution of the complex. The identity of the complex was established by single-crystal X-ray diffraction (see below). The elemental analysis showed that the powder sample absorbed water upon exposure to air, to yield the bulk product as 1·6H2O.The FT-IR spectroscopy revealed a characteristic peak at 630 cm−1, corresponding to an asymmetric vibration of the Cr3O triangle unit,35,36 as well as peaks at 1540 cm−1 and 1398 cm−1 assigned to the asymmetric and symmetric vibrational modes of the carboxylate ligands (Fig. S1). The energy difference of 142 cm−1 between the carboxylate vibrations is smaller than that reported for sodium benzoate (186 cm−1), as expected for the bidentate bridging mode of carboxylates in 1.36,37 TGA analysis showed an initial mass loss of ∼8%, which can be attributed to the loss of a single 3-CF3py ligand or the removal of crystallization solvent. The mass loss reaches 25% at 170 °C, followed by the decomposition of the complex at higher temperatures (Fig. S2).
Crystal structure
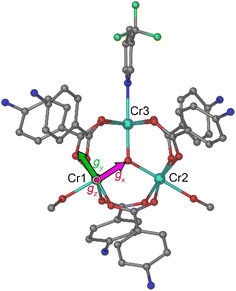
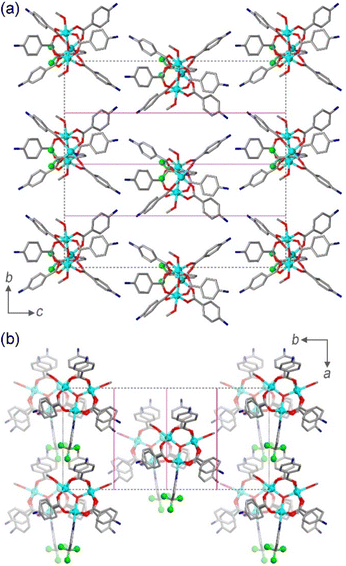
Complex 1 crystallizes in the polar space group Cc, with four formula units per monoclinic cell. The asymmetric unit contains one [Cr3(µ3-O)(µ2-4-NH3BzO)6(3-CF3py)(MeOH)2]7+ cation, seven NO3− anions, and one MeOH solvate molecule. The coordination environment of each CrIII ion is a distorted octahedron (Fig. 1), with the equatorial plane formed by four O atoms of neutral zwitterionic η1:η1-µ2-4-NH3BzO ligands and the axial positions occupied by the µ3-bridging oxide anion in the endo-site and in the exo-site either a MeOHfor Cr(1) and Cr(2) or a 3-CF3py molecule for Cr(3). In contrast to the previously reported structure of 1′, with the high-symmetry space group R3m, the crystal structure of 1 exhibits lower symmetry. The substitution of 3-CF3py for one of the MeOH molecules results in the loss of the 3-fold rotation axis and the mirror plane. The majority of complexes with the Cr3(µ3-O) triangle were reported with equivalent ligands in the axial exo-site,35 while only a few such complexes with different exo-ligands are known.34,38 Our work demonstrates that complex 1 can be formed as a pure compound in good yield by forcing the replacement of one of the MeOH molecules with the stronger pyridine-based ligand.The low symmetry of the molecule leads to different distances between the metal centers. The Cr(1)–Cr(2) distance (3.301(1) Å) between the MeOH-coordinated CrIII ions is longer than the Cr(1)–Cr(3) and Cr(2)–Cr(3) distances to the 3-CF3py-coordinated CrIII ion (3.279(1) Å and 3.289(1) Å, respectively). The lack of equilateral geometry in the central triangle also leads to slightly different Cr–O–Cr angles at the µ3-bridging oxide (Table S2). The Cr–(µ3-O) bonds are 1.908(4) Å, 1.894(4) Å, and 1.896(4) Å for the Cr(1), Cr(2), and Cr(3) sites, respectively, while the Cr–OMeOH bonds, 2.048(4) and 2.078(5) Å, are notably shorter than the Cr–Npyr bond of 2.111(5) Å. The Cr–OBzO distances to the zwitterionic 4-H3NBzO ligands are similar for all three metal sites and vary from 1.927(5) to 2.000(2) Å. An examination of the crystal packing reveals that the two magnetically non-equivalent Cr3 triangles, related by a c-glide mirror plane perpendicular to the b axis, are almost coplanar, with the dihedral angle of 9.64°. The plane of each triangle is tilted by 10.64° relative to the ab lattice plane (Fig. 2a). When the structure is viewed approximately perpendicular to the triangular plane, down the [001] direction, it can be seen that the triangles are oriented in the same direction (Fig. 2b), with the imaginary line that bisects the Cr(1)–Cr(3)–Cr(2) angle passing at ∼19° relative to the a axis.
Magnetic properties
The magnetic properties of oxo-bridged chromium triangles can be derived from the following Hamiltonian for three s = 3/2 spins:
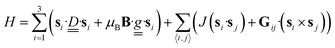 | (1) |
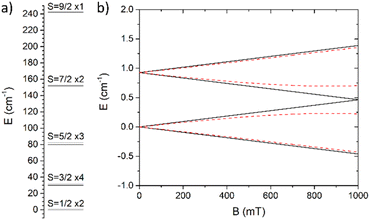
The first term represents the single-ion contribution, including the zero-field splitting (ZFS) and the Zeeman interaction, while the second term accounts for exchange interactions, divided into isotropic (Heisenberg) and antisymmetric (Dzyaloshinskii–Moriya, DM) components. The anisotropic (or symmetric) part of the interactions, due to dipolar coupling, has been neglected for simplicity, as it does not affect the phenomena investigated here (see below). In oxo-bridged CrIII triangles, the Heisenberg term is dominant,39–41 whereas ZFS and DM interactions are small perturbations linked to the spin–orbit coupling (SOC), which is largely quenched in CrIII. In the case of antiferromagnetic (AFM) interactions, a spin-level diagram with high degeneracy is expected, as shown in Fig. 3a.
The single ion ZFS tensor 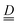 can be estimated from the anisotropy of the
can be estimated from the anisotropy of the 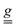 tensor (eqn (2)), where k denotes each of the principal magnetic axes, ge ≈ 2.0023 is the free-electron g factor, and λ = 91 cm−1 is the SOC constant for CrIII:42
tensor (eqn (2)), where k denotes each of the principal magnetic axes, ge ≈ 2.0023 is the free-electron g factor, and λ = 91 cm−1 is the SOC constant for CrIII:42
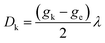 | (2) |
The three orthogonal components of the DM vector G follow general symmetry constraints. In systems possessing a C3 rotation axis, the relation GZ ≫ GX = GY ≃ 0 stands, where the Z molecular magnetic axis is parallel to C3 axis.40
While DC magnetometry on powder samples delivers a good estimation of the magnitude of the Heisenberg interaction,39,43–45 an insight into the anisotropic terms of the Hamiltonian requires single-crystal measurements. The magnetic properties of 1 were investigated by DC magnetometry on both powder (Fig. S3) and single crystal samples (Fig. S4 and S5). The magnetic field applied along two different crystallographic orientations, namely the c* and a axes, allowed probing the magnetic response of the molecules approximately perpendicular and parallel to the Cr3 triangle plane, respectively, as visually represented in Fig. 2.
The experimental χT vs. T curves are shown in Fig. S4. For both orientations, the room temperature value is ≈ 4.33 emu K mol−1, which is significantly smaller than the value expected for three uncoupled CrIII ions (5.625 emu K mol−1) and consistent with strong antiferromagnetic (AFM) exchange interactions. Upon lowering the temperature, the value of χT decreases similarly for both orientations, suggesting that the ZFS and DM interactions must be considered perturbations of the AFM exchange. At 2 K, the experimental χT is 3% higher along the c* axis than along the a axis (0.393 vs. 0.382 emu K mol−1), indicative of a weak easy-axis magnetic anisotropy of the triangle. The field-dependent magnetization isotherms, shown in Fig. S5, reveal similar magnetization values along both directions, again indicating a weak easy-axis anisotropy. The maximum value obtained at 2 K and 5 T in both cases is around 0.95 µB, in agreement with the S = 1/2 ground state of the spin-frustrated triangle.46
Powder DC magnetometry data allowed for the estimation of the average J value, whereas single crystal data revealed a magnetic anisotropy, which is determined by both the asymmetry in the J values and the DM interaction. The best fit of the DC magnetic data (Fig. S3) was obtained considering an isosceles AFM-coupled triangle with J13 = J23 = 20.0(1) cm−1 and J12 = 20.4(2) cm−1, based on the different ligand environment around the CrIII ions (Fig. 1). This results in an energy gap of 30.6 cm−1 between the almost degenerate ground doublets and the first excited state with total spin S = 3/2.
Whilst single-crystal magnetic measurements demonstrate the presence of a certain magnetic anisotropy in the sample, they do not allow for disentangling the contributions from g-anisotropy and DM interaction. One of the primary techniques for accessing such information is cantilever torque magnetometry (CTM).47 It has been intensively used to reveal and understand the magnetic anisotropy in 3d48,49 and 4f50–52 metal complexes, but its application in molecular triangles has been poorly explored,53,54 and DM interactions have not been addressed.
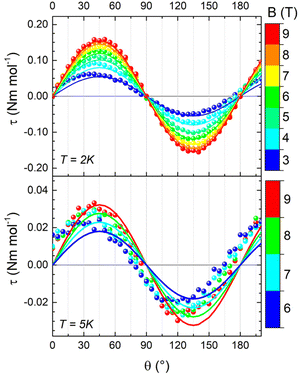
We performed two different rotations of the sample (depicted in Fig. S6) around the a and c* axes, thus probing the triangle plane-to-axis magnetic anisotropy and the in-plane magnetic anisotropy, respectively. The results of the first rotation are shown in Fig. 4. At 2 K and 9 T, the phase of the curve unambiguously confirms the easy-axis anisotropy (i.e. the pseudo-C3 axis of the triangle has a larger magnetization than the plane). However, even in these extreme experimental conditions, the signal intensity is minute, suggesting a weak magnetic anisotropy. Upon increasing the temperature to 5 K, the signal rapidly diminished, hindering the acquisition of additional curves at fields below 6 T or at higher temperatures. Conversely, during the second rotation, the very weak signal could only be detected at 2 K and 9 T (see Fig. S7), thereby impeding further investigations. The lack of 120° periodicity is consistent with our model, which predicts isotropy in the plane, even for non-uniform values of the isotropic exchange constants. The 180° periodicity and the weakness of the signal in this rotation can be attributed to a minor misalignment of the crystal.
To understand the origin of such anisotropy, we simulated the experimental measurements using the Hamiltonian in eqn (1), accounting for the presence of two magnetically inequivalent molecules within the crystal. Axial 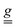 and
and 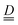 tensors for the single-ion s = 3/2 were assumed with identical orientations. Their unique axis, defined as x, was fixed along the unique axis of the octahedron, which, for 1, corresponds to the Cr–O(µ3) bond. The z magnetic axis was oriented perpendicular to the triangle plane, while y completed the Cartesian tern, as indicated in Fig. 1. Under these conditions, for CrIII ions, the relations gx ≠ gy = gz and, as derived from eqn (2), Dx ≠ Dy = Dz stand. The Euler angles describing the rotation from the molecular to the tensor frames,
tensors for the single-ion s = 3/2 were assumed with identical orientations. Their unique axis, defined as x, was fixed along the unique axis of the octahedron, which, for 1, corresponds to the Cr–O(µ3) bond. The z magnetic axis was oriented perpendicular to the triangle plane, while y completed the Cartesian tern, as indicated in Fig. 1. Under these conditions, for CrIII ions, the relations gx ≠ gy = gz and, as derived from eqn (2), Dx ≠ Dy = Dz stand. The Euler angles describing the rotation from the molecular to the tensor frames, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) M–T, and from crystallographic to molecular frames,
M–T, and from crystallographic to molecular frames, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) C–M, are reported in Tables S2 and S3. A visual representation of the magnetic reference frames in the two inequivalent triangles is depicted in Fig. S8.
C–M, are reported in Tables S2 and S3. A visual representation of the magnetic reference frames in the two inequivalent triangles is depicted in Fig. S8.
In the temperature range of CTM measurements, only the almost degenerate total spin S = 1/2 states are populated. As the ZFS and dipolar interactions exclusively affect excited states with higher spin multiplicity, the torque signal must arise from either the DM interaction and/or the anisotropy of the g factor. Due to the pseudo-trigonal symmetry of the complex, we considered GZ as the dominant parameter and imposed GX = GY = 0. This assumption leads to only two parameters as possible sources of magnetic anisotropy: GZ and the axis-plane anisotropy of the single-ion g factor, indicated as δg = gz,y − gx.
We recall that in the case of the AFM triangles, DM interactions tend to orient the in-plane component of the spins in a toroidal arrangement, whose winding depends on the sign of GZ. This reduces the response to the in-plane magnetic field, i.e., the effective in-plane g is reduced, while the out-of-plane component is practically unaffected. Additionally, the extent of deviation from the equilateral triangle is crucial in the presence of DM interaction, as the effect of DM on lowering the effective g value in the plane of the triangle is strongly reduced as the ratio δJ/GZ increases, i.e., if different J values lift the degeneracy of the two ground-state doublets.
Interestingly, g-anisotropy and DM interactions induce significantly different dependencies of the overall magnetic anisotropy on field and temperature – i.e., practically independent for the former – allowing an accurate disentanglement of the two contributions. Therefore, we attempted two fit procedures, fixing one of the two parameters to zero. The first fit procedure (GZ = 0, δg = 0.012, Fig. S9) did not reproduce the in-field evolution of the signal at 2 K and its thermal evolution, resulting in a significant overestimation of the magnetic anisotropy at 5 K. The second fit procedure (δg = 0, GZ = 0.07 cm−1, Fig. S10) showed better congruence with the in-field and temperature evolutions of the signal, even though the magnetic anisotropy at 5 K remained underestimated. Consequently, both factors were considered, leading to the best parameter combination of δg = 0.0013(3) and GZ = 0.067(3) cm−1. This model accurately reproduces both the thermal and in-field evolutions of the signal, as shown in Fig. 4. The spin state energy ladder and the Zeeman diagrams computed with these parameters are shown in Fig. 3, and simulations of the DC properties are shown in Fig. S11 snd S12. The inclusion of the dipolar term in the interaction has no sizeable effect on the magnetic properties (see Fig. S13).
Electron paramagnetic resonance
EPR spectroscopy is a powerful tool for determining g anisotropy and, in some cases, the DM interaction, even when investigating polycrystalline samples.40,41,55,56 X-band EPR spectra on the powder and single crystal of 1 at 5 K are reported in Fig. 5. The powder spectrum shows an almost single resonance with a linewidth of approximately 50 G and a small splitting, indicating that the parallel and perpendicular g values should be very similar. Moreover, the lineshape is asymmetric, a feature reported also for a similar Cr3 compound.44 The same feature is encountered in the single-crystal spectrum for a//B0, while for c*//B0 the line becomes narrower and more symmetric. The complete angular dependence of the EPR spectra is reported in Fig. S14. The asymmetric shape is quite common in frustrated AFM triangles exhibiting DM interactions, as the distribution of J values strongly impacts the resonance field when the field is in the plane of the triangle.39–41,43,45,55–57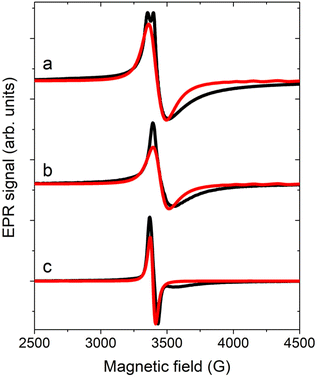 | ||
| Fig. 5 EPR spectra acquired at 5 K (black line) on a powder sample (a) and on the single crystal of 1 with a//B0 (b) and c*//B0 (c). Red lines are the corresponding simulations. | ||
To simulate the spectra, we considered the model employed for CTM simulations with gy,z = 1.976(1) and gx = 1.9740(1), which led to a D = 3/2 Dx = 0.09 cm−1 (see eqn (2)). Concerning the exchange interaction, the isosceles model was considered with J13 = J23 = J = 20 cm−1 and J12 = J + δJ. The DM interaction with GZ = 0.067 cm−1 was also introduced, consistent with the results of the CTM analysis. In contrast to the choice reported in the earlier work,44 where empirical distributions of δJ and/or GZ values were considered to simulate the asymmetric shape, we employed only a Gaussian distribution of δJ values having a center at 1.10(2) cm−1 and σδJ = 1.10(5) cm−1 (see Fig. S15). These values are compatible within errors with those extracted from magnetic measurements. This model enabled us to simulate the EPR spectra measured at 5 K (Fig. 5) and those measured at 15 K, which served as a reference for the EFM-EPR measurements (Fig. 6, top panels), even though the broadening at high fields was not fully reproduced.
EFM-EPR
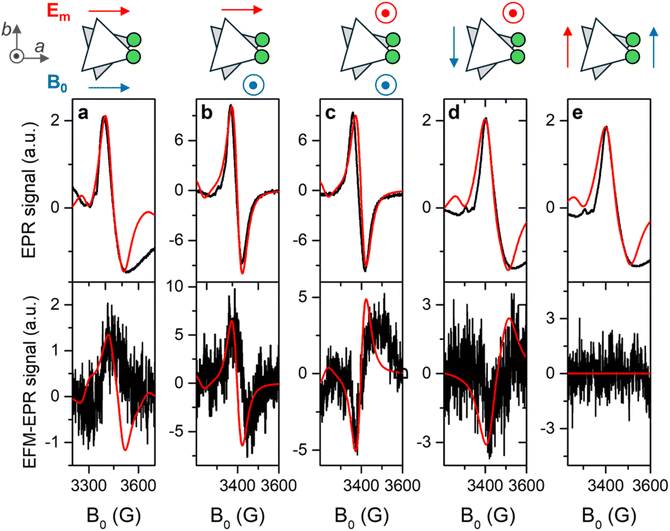
The EFM-EPR technique differs from the standard EPR spectroscopy in the field modulation used to acquire the spectrum. In place of the standard magnetic field modulation, an oscillating electric field E(t) = Emcos(ωt) with Em = 60 kV m−1 and ω = 2π·30 kHz is applied. This was achieved by employing a home-made setup described in SI. By employing phase-sensitive detection, a derivative signal may appear if the electric field shifts the resonance frequency of a quantity that is sufficiently small compared to the peak's intrinsic linewidth. On the other hand, an absorption-like EFM-EPR signal is detected if the oscillating electric field modifies the transition probability.To address the anisotropy of the SEC, the EPR and EFM-EPR spectra were acquired on an oriented single crystal at 15 K for different mutual orientations between the crystal axes, the magnetic field B0, and the electric field Em. In Fig. 6a, the standard EPR spectrum acquired with the a axis parallel to B0 is reported (top panel), together with the corresponding EFM-EPR spectrum acquired with Em parallel to the a axis (bottom panel). The latter has the same phase and center as the EPR spectrum. The phase changes sign if the direction of Em is reversed (Fig. S16), as expected in a noncentrosymmetric crystal. An EFM-EPR signal is also observed rotating the sample holder by 90°, such that the a axis is still along Em, but the c* axis is along B0 (Fig. 6b). Moreover, a EFM-EPR signal is also clearly detected for c*//Em with either c*//B0 (Fig. 6c) or −b//B0 (Fig. 6d). When b//Em the EFM-EPR signal is within the noise level (Fig. 6e), as expected by symmetry reasons (Em perpendicular to the mirror plane).
To understand the origin of the SEC effect and estimate its intensity, a phenomenological model was applied, starting from the one used to simulate the EPR spectra and complementing the Hamiltonian in eqn (1) with terms accounting for the effect of the Em field as a perturbation on either the 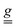 tensor or the exchange interaction J. For simplicity, we have not considered a SEC on the single-ion ZFS, as we have verified that it does not substantially affect the intensity of the EFM-EPR signal.
tensor or the exchange interaction J. For simplicity, we have not considered a SEC on the single-ion ZFS, as we have verified that it does not substantially affect the intensity of the EFM-EPR signal.
The Δg variation for each CrIII center induced by the applied Em results in
| gi(Em//j) = gi + Δgi,j = gi + EjTj,i | (3) |
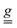 tensor for i = x, y, z, and j varies over the laboratory axes (X, Y, Z) with X//a and Z//c*, while Tj,i is the SE coupling tensor component. The meaning of eqn (3) is that Em may not only produce a perturbation along its direction, but also perpendicular to it. For the sake of simplicity, only the diagonal terms of the SEC are considered, i.e., the electric field does not modify the orientation of the principal axes, a circumstance theoretically verified for a Cu3 triangle.23
tensor for i = x, y, z, and j varies over the laboratory axes (X, Y, Z) with X//a and Z//c*, while Tj,i is the SE coupling tensor component. The meaning of eqn (3) is that Em may not only produce a perturbation along its direction, but also perpendicular to it. For the sake of simplicity, only the diagonal terms of the SEC are considered, i.e., the electric field does not modify the orientation of the principal axes, a circumstance theoretically verified for a Cu3 triangle.23
The effect of SEC on the exchange interaction can be correlated with the change in the electric dipole moment when an electron hops from one site to another, a virtual process responsible for the AFM exchange interaction.58 The perturbation ΔJ on the exchange interaction was introduced as
Jln,E = Jln + (![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ln·Êm)ΔJ ln·Êm)ΔJ
| (4) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ln are the unit vectors of the applied Em and of the electric dipole moment that is associated with the spin flip that transforms the high spin state to a broken symmetry state.24,58 This dipole is assumed to lie in the plane of the triangle and perpendicular to the line connecting the Crl and Crn sites, as theoretically predicted for other molecular triangles29,30 with a deviation smaller than 10°.24 The same value of ΔJ was considered for the three Cr–Cr pairs.
ln are the unit vectors of the applied Em and of the electric dipole moment that is associated with the spin flip that transforms the high spin state to a broken symmetry state.24,58 This dipole is assumed to lie in the plane of the triangle and perpendicular to the line connecting the Crl and Crn sites, as theoretically predicted for other molecular triangles29,30 with a deviation smaller than 10°.24 The same value of ΔJ was considered for the three Cr–Cr pairs.
An electric field effect on DM interaction could also be present. It was proposed59 and recently confirmed by ab initio calculations20 that such an effect takes the form:
| ΔGln,E ∝ (E × rln) | (5) |
To mimic the modulation of Em used in the experiments, the EFM-EPR spectra were simulated as the difference between the absorption spectra acquired with +Em and −Em. This treatment is valid in the approximation that the shift of the resonance field is much smaller than the signal linewidth.11 Since the first publications,21,23 the analysis of experimental data obtained by EFM-EPR on single crystals has reached a more mature stage, particularly in terms of simulation and interpretation of the resulting spectra, including a comprehensive analysis of molecular symmetry, line shape, and intensity.16 This development allows for the determination of the SE coupling tensor component Tj,i = ∂gi/∂Ej, going therefore well above the mere comparison of the intensity of the EFM-EPR and EPR signals for the evaluation of the SEC.
Simulations of the EFM-EPR spectra with the phenomenological model are reported in the bottom panels of Fig. 6. The spectrum acquired with a//B0//Em (panel a) was simulated with Δgx,a = Δgy,a = 1 × 10−6 (Δgi,j = EjTj,i). In this orientation, Em can also influence J and, through the combination with the weak DM interaction, the resonance position. Indeed, the spectrum can be simulated with ΔJ = 2 × 10−6 cm−1 (ΔJ/J ∼ 10−7), and a reasonable simulation is also obtained by including both effects, as reported in Fig. S18. Disentangling the two contributions is a challenging task. However, when Em//c*, i.e., orthogonal to the spin flip-induced dipole moment, only the SEC effect on g survives. For c*//B0//Em (Fig. 6c) a satisfying simulation is obtained considering Δgz,c = 0.8 × 10−6. When c*//Em but −b//B0 Δgx,c = Δgy,c = 0.9 × 10−6 needs to be included to get the correct intensity (Fig. 6d). Additionally, when Em is along a, but the signal is acquired with c*//B0 (Fig. 6b), neither ΔJ nor Δgx,a = Δgy,a = 1 × 10−6 are sufficient to reproduce the intensity of the EFM-EPR spectrum (see Fig. S19). Consequently, a term Δgz,a = 0.9 × 10−6 is introduced, which, however, does not alter the simulation of the spectrum acquired with a//B0//Em. As expected, both simulations, whether Δg or ΔJ is considered, yield zero EFM-EPR spectra for b//Em (Fig. 6d), consistent with the experimental results. Therefore, we determined the first and third rows of the tensor 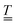 . The second row cannot be experimentally determined (n.d.) because for the given crystal symmetry of 1 the EFM-EPR signal is zero when the electric field is applied along b. The resulting SEC tensor is:
. The second row cannot be experimentally determined (n.d.) because for the given crystal symmetry of 1 the EFM-EPR signal is zero when the electric field is applied along b. The resulting SEC tensor is:
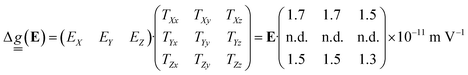 | (6) |
Two possible mechanisms can contribute to SEC on single-ion parameters: (i) atomic displacement under the electric field if the latter couples with a permanent electric dipole moment, (ii) a pure electronic one, which does not require an electric dipole moment, but is usually weaker.15 A SEC effect ΔgE/E of the order of 1–2 × 10−11 m V−1 is observed in Cr3 when the electric field is directed along the a or c* axes. This value is approximately one order of magnitude larger than that determined for a Cu3 triangle in directions lacking a permanent electric dipole, but it is smaller than the value along the Cu3 polar axis.24 Given the low symmetry of the Cr3 system, it is reasonable to observe an almost isotropic and not negligible SEC effect on the 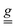 tensor. The inclusion in the phenomenological model of the dipolar interaction between the CrIII pairs does not alter the evaluation of the SEC (see Fig. S20).
tensor. The inclusion in the phenomenological model of the dipolar interaction between the CrIII pairs does not alter the evaluation of the SEC (see Fig. S20).
The upper limit for SEC on J, 3 × 10−11 cm−1 m V−1, is more than two orders of magnitude smaller than that estimated by ab initio calculations and experimentally detected in the Cu3 triangle.24 Also, considering the weaker AFM interaction between CrIII spins, the relative value ΔJE/J remains significantly smaller than in Cu3. This finding can be tentatively assigned to the different bridge of the latter, i.e., the multi-chelating ligand anion of tris(2-hydroxybenzylidene)triaminoguanidine, which was found to contribute significantly to the spin-flip-induced dipole moment.24 Indeed, the relative SEC on J in Cr3 has the same order of magnitude as that computed for a Cu3 system in a polyoxometalate structure.30
Conclusions
In this study, we synthesized an oxo-centered Cr3 frustrated spin triangle crystallizing in a non-centrosymmetric space group. A multi-technique approach was employed to fully characterize its spin Hamiltonian. In particular, the weak anisotropy induced by the presence of antisymmetric exchange was disentangled from the anisotropy of the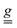 tensor, by means of torque magnetometry in variable magnetic fields and temperatures, providing the essential foundation to investigate spin-electric effects in this system. To this purpose, we employed EPR spectroscopy under a modulated electric field. When properly applied to non-centrosymmetric crystals, EFM-EPR spectroscopy demonstrates exceptional sensitivity to electric-field-induced changes, enabling precise quantification of the effects through spectral simulations. The independent control of the magnetic and electric field orientations within the molecular reference frame further allows assessment of the anisotropy of the spin–electric effect and a microscopic disentanglement of its different contributions.
tensor, by means of torque magnetometry in variable magnetic fields and temperatures, providing the essential foundation to investigate spin-electric effects in this system. To this purpose, we employed EPR spectroscopy under a modulated electric field. When properly applied to non-centrosymmetric crystals, EFM-EPR spectroscopy demonstrates exceptional sensitivity to electric-field-induced changes, enabling precise quantification of the effects through spectral simulations. The independent control of the magnetic and electric field orientations within the molecular reference frame further allows assessment of the anisotropy of the spin–electric effect and a microscopic disentanglement of its different contributions.
In the specific case of Cr3, which had previously shown no sizable spin–electric coupling, we were able to quantify the electric-field effect on the single-ion 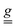 tensor and to estimate an upper limit for the effect on the isotropic exchange interaction. The observation that the SEC on J is significantly smaller than that observed for a Cu3 complex bridged by an organic ligand, yet comparable to that computed for a Cu3 polyoxometallate, highlights the critical role of the bridging ligand in mediating the SEC effect.
tensor and to estimate an upper limit for the effect on the isotropic exchange interaction. The observation that the SEC on J is significantly smaller than that observed for a Cu3 complex bridged by an organic ligand, yet comparable to that computed for a Cu3 polyoxometallate, highlights the critical role of the bridging ligand in mediating the SEC effect.
Overall, these findings demonstrate the power of EFM-EPR spectroscopy as a quantitative probe of SEC in molecular systems. Building on its sensitivity and versatility, a systematic investigation of different bridging ligands, supported by theoretical modeling, could establish design criteria to optimize SEC effects, thereby paving the way for rational engineering of molecular systems with efficient electric control of spin.
Author contributions
RS, MS, and MF conceptualized the idea of this work. BS synthesized and structurally characterized the material under the supervision of MS and TO. LT recorded the EPR spectra and performed the magnetic characterization under the supervision of MP and RS. AC, LT, and MF recorded the EFM-EPR spectra. AC simulated the EPR and EFM-EPR spectra under the supervision of MF. All authors have critically reviewed each aspect of the research and have contributed to the drafting and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
Experimental and simulated magnetic data and spectra will be available from the authors upon request.CCDC 2493370 contains the supplementary crystallographic data for this paper.61
Supplementary information (SI): additional figures; tables reporting crystallographic data (CCDC 2493370), and reference frame rotations; materials and methods. See DOI: https://doi.org/10.1039/d5sc08012f.
Acknowledgements
The work was funded by the Italian MUR through the FIS project ELECOS (FIS00001045), by the European Union (ERC, ELECTRA, 101039890), and by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award no. DESC0019330. The MPMS-3 system used for magnetic measurements was supported by a Major Research Instrumentation grant from the National Science Foundation (NSF DMR-2216125). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement DMR-2128556, and the State of Florida. The X/Q EPR instrument at the NHMFL is supported by the grant NSF/CHE2320338. The support by the Italian MUR through the Dipartimenti di Eccellenza 2023–2027 (DICUS 2.0) (ref. no. B96C1700020008) is also acknowledged. The financial support provided by INFN through the projects NAMASSTE and next-NAMASSTE is acknowledged. The position of A. C. was financed through the project NAMASSTE- UNIFI funded by Banca d’Italia. M. F. is grateful to Giampaolo Tobia for technical assistance.Notes and references
- A. Chiesa, P. Santini, E. Garlatti, F. Luis and S. Carretta, Molecular nanomagnets: a viable path toward quantum information processing?, Rep. Prog. Phys., 2024, 87, 034501 Search PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Exploiting chemistry and molecular systems for quantum information science, Nat. Rev. Chem., 2020, 4, 490–504 Search PubMed.
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352 Search PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Electrically driven nuclear spin resonance in single-molecule magnets, Science, 2014, 344, 1135–1138 Search PubMed.
- D. Xuan, Y. Wang and X. Zhang, Electrically coherent manipulation of individual atomic and molecular spins on surface, Phys. Chem. Chem. Phys., 2025, 27, 5443–5458 Search PubMed.
- M. Mostovoy, Multiferroics: different routes to magnetoelectric coupling, npj Spintronics, 2024, 2, 18 Search PubMed.
- R. Gupta and R. K. Kotnala, A review on current status and mechanisms of room-temperature magnetoelectric coupling in multiferroics for device applications, J. Mater. Sci., 2022, 57, 12710–12737 Search PubMed.
- J. T. Heron, J. L. Bosse, Q. He, Y. Gao, M. Trassin, L. Ye, J. D. Clarkson, C. Wang, J. Liu, S. Salahuddin, D. C. Ralph, D. G. Schlom, J. Íñiguez, B. D. Huey and R. Ramesh, Deterministic switching of ferromagnetism at room temperature using an electric field, Nature, 2014, 516, 370–373 Search PubMed.
- N. A. Spaldin and M. Fiebig, The Renaissance of Magnetoelectric Multiferroics, Science, 2005, 309, 391–392 Search PubMed.
- Y.-F. Zhang, L.-A. Gui, Y. Peng, Z.-B. Hu and Y. Song, Perspective on room temperature and low-field-induced magnetoelectric coupling in molecular complexes, Dalton Trans., 2025, 54, 881–888 Search PubMed.
- W. B. Mims, The linear electric field effect in paramagnetic resonance, Clarendon Press, Oxford, 1976 Search PubMed.
- J. J. Liu, J. Mrozek, W. K. Myers, G. A. Timco, R. E. P. Winpenny, B. Kintzel, W. Plass and A. Ardavan, Electric Field Control of Spins in Molecular Magnets, Phys. Rev. Lett., 2019, 122, 037202 Search PubMed.
- Z. Liu, Y.-X. Wang, Y.-H. Fang, S.-X. Qin, Z.-M. Wang, S.-D. Jiang and S. Gao, Electric field manipulation enhanced by strong spin-orbit coupling: promoting rare-earth ions as qubits, Nat. Sci. Rev., 2020, 7, 1557–1563 Search PubMed.
- J. Liu, J. Mrozek, A. Ullah, Y. Duan, J. J. Baldoví, E. Coronado, A. Gaita-Ariño and A. Ardavan, Quantum coherent spin–electric control in a molecular nanomagnet at clock transitions, Nat. Phys., 2021, 17, 1205–1209 Search PubMed.
- M. V. Vaganov, N. Suaud, F. Lambert, B. Cahier, C. Herrero, R. Guillot, A.-L. Barra, N. Guihéry, T. Mallah, A. Ardavan and J. Liu, Chemical tuning of quantum spin–electric coupling in molecular magnets, Nat. Chem., 2025, 1903–1909 Search PubMed.
- L. Tacconi, A. Cini, A. Raza, L. Tesi, P. Bartolini, A. Taschin, J. van Slageren, M. Briganti, L. Sorace, M. Fittipaldi and M. Perfetti, Spin-Electric Effect on a Chiral Dysprosium Complex, J. Am. Chem. Soc., 2025, 147, 33040–33051 Search PubMed.
- R. E. George, J. P. Edwards and A. Ardavan, Coherent Spin Control by Electrical Manipulation of the Magnetic Anisotropy, Phys. Rev. Lett., 2013, 110, 027601 Search PubMed.
- Y.-C. Liu, J.-X. Chen, J.-F. Bu, P.-X. Fu, Y.-X. Wang, Z. Liu, S. Gao and S.-D. Jiang, Ferroelectricity and Strong Spin–Orbit Coupling to Enhance Molecular Spin-Electric Coupling, J. Am. Chem. Soc., 2025, 147, 10423–10429 Search PubMed.
- W. T. Morrillo, H. I. J. Cumming, A. Mattioni, J. K. Staab and N. F. Chilton, Ab Initio Design of Molecular Qubits with Electric Field Control, J. Am. Chem. Soc., 2024, 146, 25841–25851 Search PubMed.
- B. Pradines, B. Cahier, N. Suaud and N. Guihéry, Impact of the electric field on isotropic and anisotropic spin Hamiltonian parameters, J. Chem. Phys., 2022, 157, 204308 Search PubMed.
- M. Fittipaldi, A. Cini, G. Annino, A. Vindigni, A. Caneschi and R. Sessoli, Electric field modulation of magnetic exchange in molecular helices, Nat. Mater., 2019, 18, 329–334 Search PubMed.
- J. Robert, N. Parizel, P. Turek and A. K. Boudalis, Polyanisotropic Magnetoelectric Coupling in an Electrically Controlled Molecular Spin Qubit, J. Am. Chem. Soc., 2019, 141, 19765–19775 Search PubMed.
- B. Kintzel, M. Fittipaldi, M. Bohme, A. Cini, L. Tesi, A. Buchholz, R. Sessoli and W. Plass, Spin-Electric Coupling in a Cobalt(II)-Based Spin Triangle Revealed by Electric-Field-Modulated Electron Spin Resonance Spectroscopy, Angew. Chem., Int. Ed., 2021, 60, 8832–8838 Search PubMed.
- A. Cini, M. Böhme, B. Kintzel, M. Perfetti, W. Plass, R. Sessoli and M. Fittipaldi, Electric control of magnetic exchange in a molecular spin triangle, Nat. Commun., 2025, 16, 6564 Search PubMed.
- B. E. Kane, A silicon-based nuclear spin quantum computer, Nature, 1998, 393, 133–137 Search PubMed.
- A. K. Boudalis, Half-Integer Spin Triangles: Old Dogs, New Tricks, Chem.–Eur. J., 2021, 27, 7022–7042 Search PubMed.
- A. N. Georgopoulou, I. Margiolaki, V. Psycharis and A. K. Boudalis, Dynamic versus Static Character of the Magnetic Jahn–Teller Effect: Magnetostructural Studies of [Fe3O(O2CPh)6(py)3]ClO4·py, Inorg. Chem., 2017, 56, 762–772 Search PubMed.
- B. S. Tsukerblat, M. I. Belinski and V. E. Fainzil'berg, Antisymmetric exchange, Sov. Sci. Rev., Sect. B, 1987, 9, 339 Search PubMed.
- M. Trif, F. Troiani, D. Stepanenko and D. Loss, Spin-Electric Coupling in Molecular Magnets, Phys. Rev. Lett., 2008, 101, 217201 Search PubMed.
- M. F. Islam, J. F. Nossa, C. M. Canali and M. Pederson, First-principles study of spin-electric coupling in a {Cu_{3}} single molecular magnet, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155446 Search PubMed.
- A. Maisuradze, A. Shengelaya, H. Berger, D. M. Djokić and H. Keller, Magnetoelectric Coupling in Single Crystal Cu2OSeO3 Studied by a Novel Electron Spin Resonance Technique, Phys. Rev. Lett., 2012, 108, 247211 Search PubMed.
- P. Wysling and K. A. Muller, Electric-field-modulated resonance lines of non-Kramers ions, J. Phys. C: Solid State Phys., 1975, 9, 635 Search PubMed.
- J.-M. Song, J.-X. Chen, Y.-S. Zhang, Q.-S. Deng, Y. Xie, S. Gao, Y.-X. Wang, Z. Liu and S.-D. Jiang, Exploring Spin-Electric Coupling in an Electrically-Controlled Rare-Earth Molecular Qubit, Angew. Chem., Int. Ed., 2025, e202513081 Search PubMed.
- A. Schoedel, L. Wojtas, S. P. Kelley, R. D. Rogers, M. Eddaoudi and M. J. Zaworotko, Network Diversity through Decoration of Trigonal-Prismatic Nodes: Two-Step Crystal Engineering of Cationic Metal–Organic Materials, Angew. Chem., Int. Ed., 2011, 50, 11421–11424 Search PubMed.
- D. R. Cannon and R. P. White, Chemical and Physical Properties of Triangular Bridged Complexes, Prog. Inorg. Chem., 1988, 36, 195–298 Search PubMed.
- G. B. Deacon and R. J. Phillips, Relationships between the carbon-oxygen stretching frequencies of carboxylato complexes and the type of carboxylate coordination, Coord. Chem. Rev., 1980, 33, 227–250 Search PubMed.
- A. Harton, M. K. Nagi, M. M. Glass, P. C. Junk, J. L. Atwood and J. B. Vincent, Synthesis and characterization of symmetric and unsymmetric oxo-bridged trinuclear chromium benzoate complexes: Crystal and molecular structure of [Cr3O(O2CPh)6(py)3]ClO4, Inorg. Chim. Acta, 1994, 217, 171–179 Search PubMed.
- V. Corradini, C. Cervetti, A. Ghirri, R. Biagi, U. del Pennino, G. A. Timco, R. E. P. Winpenny and M. Affronte, Oxo-centered carboxylate-bridged trinuclear complexes deposited on Au(111) by a mass-selective electrospray, New J. Chem., 2011, 35, 1683–1689 Search PubMed.
- V. Psycharis, C. P. Raptopoulou, A. K. Boudalis, Y. Sanakis, M. Fardis, G. Diamantopoulos and G. Papavassiliou, Syntheses, Structural, and Physical Studies of Basic CrIII and FeIII Benzilates and Benzoates: Evidence of Antisymmetric Exchange and Distributions of Isotropic and Antisymmetric Exchange Parameters, Eur. J. Inorg. Chem., 2006, 2006, 3710–3723 Search PubMed.
- A. Figuerola, V. Tangoulis, J. Ribas, H. Hartl, I. Brüdgam, M. Maestro and C. Diaz, Synthesis, Crystal Structure, and Magnetic Studies of Oxo-Centered Trinuclear Chromium(III) Complexes: [Cr3(µ3-O)(µ2-PhCOO)6(H2O)3]NO3· 4H2O·2CH3OH, a Case of Spin-Frustrated System, and [Cr3(µ3-O)(µ2-PhCOO)6(µ2-OCH2CH3)2(bpy)2(NCS)3], a New Type of [Cr3O] Core, Inorg. Chem., 2007, 46, 11017–11024 Search PubMed.
- A. K. Boudalis, G. Rogez and P. Turek, Determination of the Distributions of the Spin-Hamiltonian Parameters in Spin Triangles: A Combined Magnetic Susceptometry and Electron Paramagnetic Resonance Spectroscopic Study of the Highly Symmetric [Cr3O(PhCOO)6(py)3](ClO4)·0.5py, Inorg. Chem., 2018, 57, 13259–13269 Search PubMed.
- J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance, John Wiley & Sons Inc, 2006 Search PubMed.
- J. Dong, B. Liu and B. Yang, Synthesis, crystal structure and magnetic properties of trinuclear chromium(III) basic carboxylate assembly: [Cr3O(salH)7(H2O)2] (salH2=salicylic acid), a new member of [Cr3O] family, J. Mol. Struct., 2016, 1116, 311–316 Search PubMed.
- O. Botezat, I. G. Filippova, J. Hauser, K. Krämer, S. Decurtins, S.-X. Liu and S. G. Baca, Synthesis, crystal structure, and properties of a µ3-oxo-trichromium(III) propionate cluster with pyrazole, J. Coord. Chem., 2016, 69, 72–80 Search PubMed.
- A. Vlachos, V. Psycharis, C. P. Raptopoulou, N. Lalioti, Y. Sanakis, G. Diamantopoulos, M. Fardis, M. Karayanni, G. Papavassiliou and A. Terzis, A nearly symmetric trinuclear chromium(III) oxo carboxylate assembly: preparation, molecular and crystal structure, and magnetic properties of [Cr3O(O2CPh)6(MeOH)3](NO3)·2MeOH, Inorg. Chim. Acta, 2004, 357, 3162–3172 Search PubMed.
- O. Kahn, Molecular magnetism, VCH, Weinheim, 1993 Search PubMed.
- M. Perfetti, Cantilever torque magnetometry on coordination compounds: from theory to experiments, Coord. Chem. Rev., 2017, 348, 171–186 Search PubMed.
- V. Thangaraj, D. Sartini, D. Borah, D. Chauhan, V. Sharma, L. Sorace, G. Rajaraman, M. Perfetti and M. Shanmugam, Quantifying Magnetic Anisotropy of Series of Five-Coordinate CoII Ions: Experimental and Theoretical Insights, Adv. Sci., 2025, 12, 2415624 Search PubMed.
- B. Cahier, M. Perfetti, G. Zakhia, D. Naoufal, F. El-Khatib, R. Guillot, E. Riviere, R. Sessoli, A. L. Barra, N. Guihery and T. Mallah, Magnetic Anisotropy in Pentacoordinate Ni-II and Co-II Complexes: Unraveling Electronic and Geometrical Contributions, Chem.–Eur. J., 2017, 23, 3648–3657 Search PubMed.
- M. Briganti, E. Lucaccini, L. Chelazzi, S. Ciattini, L. Sorace, R. Sessoli, F. Totti and M. Perfetti, Magnetic Anisotropy Trends along a Full 4f-Series: The f(n)+7 Effect, J. Am. Chem. Soc., 2021, 143, 8108–8115 Search PubMed.
- L. Tacconi, S. S. Leiszner, M. Briganti, G. Cucinotta, E. Otero, M. Mannini and M. Perfetti, Temperature Induced Reversible Switching of the Magnetic Anisotropy in a Neodymium Complex Adsorbed on Graphite, Small, 2024, 20, 2401627 Search PubMed.
- L. Tacconi, A. S. Manvell, M. Briganti, D. Czernia, H. Weihe, P. Konieczny, J. Bendix and M. Perfetti, Exploiting High Order Magnetic Anisotropy for Advanced Magnetocaloric Refrigerants, Angew. Chem., Int. Ed., 2025, 64, e202417582 Search PubMed.
- M. Gysler, F. El Hallak, L. Ungur, R. Marx, M. Hakl, P. Neugebauer, Y. Rechkemmer, Y. Lan, I. Sheikin, M. Orlita, C. E. Anson, A. K. Powell, R. Sessoli, L. F. Chibotaru and J. van Slageren, Multitechnique investigation of Dy3 - implications for coupled lanthanide clusters, Chem. Sci., 2016, 7, 4347–4354 Search PubMed.
- J. Liu, C. Koo, A. Amjad, P. L. Feng, E. S. Choi, E. del Barco, D. N. Hendrickson and S. Hill, Relieving frustration: The case of antiferromagnetic Mn3 molecular triangles, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094443 Search PubMed.
- A. Ghirri, J. van Tol, I. Vitorica-Yrezabal, G. A. Timco and R. E. P. Winpenny, Effects of the Dzyaloshinskii–Moriya interaction in Cr3 triangular spin clusters detected by specific heat and multi-frequency electron spin resonance, Dalton Trans., 2015, 44, 14027–14033 Search PubMed.
- M. Honda, M. Morita and M. Date, Electron Spin Resonance in Cr-Trimer Complexes, J. Phys. Soc. Jpn., 1992, 61, 3773–3785 Search PubMed.
- H. Nishimura and M. Date, Anomalous g-Value of a Cr-Trimer Complex, Cr-Propionate {Cr3O(C2H5COO)6(H2O)3}NO32H2O, J. Phys. Soc. Jpn., 1985, 54, 395–399 Search PubMed.
- D. I. Khomskii, Spin chirality and nontrivial charge dynamics in frustrated Mott insulators: spontaneous currents and charge redistribution, J. Phys.: Condens. Matter, 2010, 22, 164209 Search PubMed.
- K. Siratori and E. Kita, Magnetoelectric Effect in ZnCr2Se4 with Screw Spin Structure, J. Phys. Soc. Jpn., 1980, 48, 1443–1448 Search PubMed.
- F. Heully-Alary, B. Pradines, N. Suaud and N. Guihéry, Physical origin of the anisotropic exchange tensor close to the first-order spin–orbit coupling regime and impact of the electric field on its magnitude, J. Chem. Phys., 2024, 161, 054310 Search PubMed.
- CCDC 2493370: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2ppk98.
Footnote |
| † These authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2026 |