Natural monosaccharide-based piezoelectric supramolecular materials for energy harvesting and information transmission

Abstract

Biomolecular assemblies with non-centrosymmetric structures exhibit a piezoelectric response that can be applied to bionanotechnology. However, the piezoelectricity of monosaccharide self-assembled materials has not been previously reported. Herein, for the first time, we systematically investigated the piezoelectric properties of fourteen natural monosaccharide-based supramolecular materials, aiming to use them for energy harvesting and information transmission. The supramolecular arrangements and piezoelectricity responses of monosaccharide assemblies are predominantly governed by hydroxyl number and orientation. Density functional theory (DFT) calculations revealed that the maximum piezoelectric coefficients of monosaccharide assemblies ranged from 6 to 13.7 pC/N, in which α-D-Gal assemblies exhibited a higher value. The α-D-Gal assembly-based piezoelectric device generated an open-circuit voltage of 1.08 V under a 55 N mechanical load, enough to power an LED by charging a 0.1 µF capacitor for 1 minute, and produced 32 V across the capacitor after 4 minutes of charging. An α-D-Gal assembly-based composite film was used to generate signals that represented Morse code for information transmission, enabling the conversion of electrical signals into numbers, letters, and words. We report the piezoelectric properties of various monosaccharide self-assemblies and investigate the correlation between supramolecular structure and piezoelectric response, and also provide new ideas for the development of innovative green energy biomaterials and electronic information transmission media.

---

Introduction

Because of their unique electromechanical transduction properties, there has been increased research on piezoelectric materials to determine their optimal applications in biomedical fields and green energy-harvesting technologies.^1–6 When subjected to external mechanical stress, piezoelectric materials efficiently convert mechanical energy into electrical energy through crystalline polarization realignment, and therefore, they are highly attractive as smart functional materials.^7–17

Piezoelectric phenomena are widespread in natural biomaterials and have been extensively studied.^18–25 For example, the piezoelectric effect exists in tissues and organs such as bones,²⁶ skin,²⁷ tendons,²⁰ cornea,¹⁸ and sclera.¹⁹ This effect interacts with bioelectricity,² and an intricate network of electrical phenomena in living organisms is formed. Together, these two entities collaborate in biological processes and exert pivotal effects in multiple aspects, including cell activity and tissue functions such as neural conduction and tissue repair.¹

The research emphasis has progressively transitioned to biomolecular materials (e.g., proteins,^28,29 peptides,^30–32 amino acids,^8,13,33 and vitamins³⁴), with molecular assembly emerging as a particularly promising bottom-up approach for fabricating functional materials.^35–38 A key advantage of molecular assembly lies in its capacity to probe piezoelectric phenomena at the fundamental molecular level, offering deep mechanistic insights for the rational design of high-performance supramolecular materials.³⁹ The change in molecular structure can modulate the supramolecular packing and piezoelectric response of bio- and bio-inspired molecular assemblies. For example, a minimalist collagen-mimicking short peptide (Hyp-Phe-Phe) was designed to demonstrate that optimizing supramolecular polarization through side-chain engineering can significantly enhance the electromechanical response properties of the tripeptide assembly.⁴⁰

Additionally, a supramolecular host–guest ferroelectric crystal exhibits an enhanced piezoelectric coefficient upon H/F substitution, providing compelling evidence that chemical structure modifications can profoundly influence the piezoelectric response of molecular crystals.⁴¹ A side-chain change in acetylated amino acids can alter the supramolecular packing of molecular crystals, thereby regulating their piezoelectric properties.⁴² However, the structure–property relationship in piezoelectric supramolecular materials remains insufficiently understood, which significantly restricts the knowledge of the fundamental origin and the regulatory mechanism of piezoelectricity for material design.

Polysaccharides (e.g., chitin,⁴³ chitosan,⁴⁴ and cellulose⁴⁵) can assemble into piezoelectric biomaterials, offering a sustainable and biocompatible alternative to conventional synthetic piezoelectric materials for flexible electronics and biomedical applications.^46,47 Chitin is composed of repeating β-(1,4)-N-acetylglucosamine units that form a high-strength nanofibrous structure through supramolecular self-assembly, in which the piezoelectricity of assemblies originates from the rearrangement of molecular dipoles caused by an asymmetric hydrogen bond network.⁴⁸ Chitin nanofibers can be successfully fabricated into self-powered sensors capable of sensitively detecting dynamic physiological signals, including human joint movements and pulse waves.⁴⁹

Chitosan, another polysaccharide polymer consisting of 2-amino-2-deoxyglucose repeating units, with numerous polar groups (e.g., amino and hydroxyl groups) on the molecular chain, has demonstrated significant piezoelectric potential. Transparent chitosan films with adjustable crystal orientation and piezoelectric response were developed through a simple solvent-casting technique.⁴⁴

Cellulose relies on the high density of hydroxyl groups in D-Glu units to form a permanent dipole moment, and the ordered hydrogen bond network produces an asymmetric crystal structure, which is a factor influencing the piezoelectric properties of crystalline cellulose. The piezoelectric response of cellulose nanocrystal films has been systematically studied.⁵⁰ The asymmetric network of hydrogen bonds between cellulose nanocrystals effectively promotes the generation of the piezoelectric effect.

Despite these advancements in polysaccharide-based piezoelectric materials, the polycrystalline aggregated state of polysaccharides limits the investigation of structure-piezoelectricity correlation at the molecular level. Monosaccharides are the fundamental building blocks of polysaccharides, and are rich in hydroxyl groups and possess well-defined structures and natural chirality.^44,45 Furthermore, monosaccharides can assemble to form crystal structures that benefit the investigation of the correlation between supramolecular packing and piezoelectricity of the crystals, promoting the design and development of natural sugar-based piezoelectric materials. Yet, the piezoelectric properties of monosaccharide-based assemblies remain unexplored.

Herein, we systematically investigated the piezoelectric response of monosaccharide assemblies for energy harvesting and information transmission, and revealed the relationship between supramolecular structure and piezoelectric properties (Fig. 1). Fourteen monosaccharide crystals were successfully obtained and their crystal structures were characterized using powder X-ray diffraction (PXRD) and single crystal X-ray diffraction (SCXRD). The results showed that a small change in the monosaccharide molecular structure produced a significant impact on the stacking pattern of the monosaccharide crystals.

Fig. 1 Schematic diagram of the piezoelectric property research of natural monosaccharide crystals. (a) The inspiration for this work comes from the piezoelectricity of polysaccharide self-assemblies. (b) Molecular structures of fourteen natural monosaccharides in this work. The molecules with a blue background represent five-carbon aldoses, those with a green background represent six-carbon aldoses, and those with a yellow background represent six-carbon ketoses. (c) Different monosaccharide molecules self-assemble to form four distinct packing modes, and a comparison of the calculated piezoelectric coefficients of different types of monosaccharide crystals. (d) α-D-Gal crystals-based PENG can be used for energy harvesting and α-D-Gal crystals-based flexible film can be used for information transmission.

The monosaccharide crystals exhibited four types of typical characteristic packing modes: parallel stacking, antiparallel stacking, herringbone stacking, and slip stacking. Density functional theory (DFT) calculations indicated that α-D-Gal crystals exhibited a higher maximum piezoelectric coefficient (d₃₆ = 13.7 pC/N) among the fourteen monosaccharide crystals, which was comparable to that of traditional polysaccharide materials (e.g., chitosan, d₃₁ = 10 pC/N⁵¹) and inorganic materials such as zinc oxide (d₃₃ = 9.93 pC/N).⁵²

Furthermore, we developed an α-D-Gal crystal-based piezoelectric nanogenerator (PENG) that can generate a stable electrical output of 1.08 V under a 55 N mechanical force, and it exhibited high mechanical durability over 10 000 press-release cycles. Moreover, this nanogenerator successfully powered a light-emitting diode (LED) by charging a 0.1 µF capacitor for 1 minute and demonstrated capacitor energy storage, reaching 32 V after 4 minutes of charging.

Additionally, we fabricated α-D-Gal crystal-based piezoelectric composite films that can be used to generate international Morse code for information transmission. This work explored the piezoelectric properties of monosaccharide supramolecular assemblies as well as the structure–piezoelectricity relationship, thereby promoting the development of novel natural sugar molecule-based piezoelectric biomaterials.

Results and discussion

Morphology of the monosaccharide self-assemblies

Monosaccharides, as the primary energy source of living organisms, possess characteristics such as readily available raw materials, simple structural units, and biocompatibility. Based on the above characteristics, monosaccharide crystal growth experiments were carried out using the solvent evaporation method. We systematically investigated fourteen monosaccharide molecules and obtained high-quality single crystals for all of them.

It was found that isomers crystallized differently under varying preparation conditions, which may be attributed to the changes in the orientation of hydroxyl groups in their molecular structures. As the solvent molecules slowly evaporated or the solvent temperature decreased, the solution gradually reached the supersaturated state, which eventually led to the crystallization of monosaccharide molecules (Fig. 2(a–i) and S1).

Fig. 2 Microscopy images and PXRD profiles of monosaccharide crystals. (a–i) Microscopy images of (a) α-D-Xyl, (b) β-D-Ara, (c) α-D-Gal, (d) β-D-Psi, (e) α-L-Rha, (f) α-D-Glu, (g) β-L-Ara, (h) α-L-Sor, and (i) α-D-Tag monosaccharide crystals. (j–l) PXRD profiles of (j) α-D-Xyl, (k) β-L-Ara, and (l) β-D-Psi monosaccharide crystals.

Using an inverted microscope, their morphologies were clearly observed, and were classified into three types: long strip-shaped, block-shaped, and irregular-shaped. α-D-Xyl, β-D-Ara, and α-D-Gal self-assembled to form long strip-shaped crystals (Fig. 2(a–c)), whose diameters were approximately 400 µm, 200 µm, and 200 µm, respectively. β-D-Psi, α-L-Rha, and β-D-Fru self-assembled to form block-shaped crystals (Fig. 2(d–e) and S1(a)) with crystal diameters of 800 µm, 250 µm, and 450 µm, respectively. α-D-Glu, β-L-Ara, α-L-Sor, α-D-Tag, α-L-Fuc, β-D-All, β-D-dRib, and α-D-Rib self-assembled in solvents to form irregular-shaped crystals with various morphologies (Fig. 2(f–i) and S1(b–e)). Among them, α-L-Sor exhibited a crystal size of approximately 700 µm, while the others ranged from 20 to 200 µm in size.

These results show that monosaccharide molecules can self-assemble into ordered crystalline materials. Notably, the isomers of pentose and hexose formed different macroscopic crystal morphologies, which may be ascribed to the differences in the orientation of hydroxyl groups in the molecules for the formation of intermolecular hydrogen bonds.

Crystal structures of the monosaccharide self-assemblies

We further analyzed the crystal structure of the monosaccharides using powder X-ray diffraction (PXRD) and single crystal X-ray diffraction (SCXRD) techniques. The PXRD patterns of β-D-Ara,⁵³ α-D-Xyl,⁵⁴ α-D-Rib,⁵⁵ β-L-Ara,⁵⁶ β-D-dRib,⁵⁷ α-D-Glu,⁵⁸ α-D-Gal,⁵⁹ α-L-Sor,⁶⁰ β-D-Psi,⁶¹ β-D-Fru, α-L-Fuc,⁶² α-L-Rha,⁶³ and β-D-All⁶⁴ were characterized. By comparing the PXRD patterns obtained from experiments with the crystal database, we found that the diffraction peaks exhibited high consistency, confirming that the lattice parameters for the obtained crystals were the same as those for the reported crystals (Fig. 2(j–l), S2 and S3). For example, in the PXRD pattern of the long strip-shaped crystal α-D-Xyl (Fig. 2(j)), the irregularly shaped crystal β-L-Ara (Fig. 2(k)), and the block-shaped crystal β-D-Psi (Fig. 2(l)), the main diffraction peaks completely coincided with the simulated diffraction peaks.

The crystal structure of α-D-Tag was determined by SCXRD. The single crystal diffraction data (Table S1) revealed the space group and unit cell parameters of the α-D-Tag crystal. We further analyzed the packing modes formed by monosaccharide molecules (Table S2), and summarized the details of hydrogen bonds in Tables S3–S6.

The spatial packing pattern of the monosaccharide crystals was highly dependent on the directionality and strength of the hydrogen bond network. We systematically analyzed the molecular arrangement patterns of fourteen monosaccharide crystals and found that they can be divided into four typical stacking types: parallel stacking⁶⁵ (α-L-Fuc and α-L-Rha), slip stacking⁴² (α-D-Gal, α-L-Sor, β-D-All, β-D-Psi, β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib), herringbone stacking^66,67 (α-D-Xyl and α-D-Glu), and antiparallel stacking^68,69 (α-D-Rib).

Notably, there are multiple sets of isomers in this study, and they assume different packing modes. For example, α-D-Glu and α-D-Gal are stereoisomers; α-D-Glu forms herringbone packing through hydrogen bond chains along the a-axis and c-axis, while the hydrogen bonds of α-D-Gal extend along the a-, b-, and c-axes, ultimately forming slip packing. α-D-Rib and α-D-Xyl are also stereoisomers. The hydrogen bond network of α-D-Rib forms a layered structure through chains extending parallel to the a-axis and c-axis; hydrogen bonds along the b-axis achieve longitudinal connection, ultimately forming an antiparallel packing structure. In contrast, the hydrogen bonds of α-D-Xyl exist only along the a-axis and b-axis, ultimately forming a herringbone packing structure.

In slip stacking, all monosaccharide crystals were characterized by a helical symmetric molecular arrangement and layered hydrogen bonding. Taking α-L-Sor crystals (P2₁2₁2₁ space group) as an example, the molecules in the unit cell were obtained by 2₁ axis rotation and translation, and were characterized by hydrogen bonding between layers, thereby forming a layered stacking (Fig. S4(a–c)).

We categorized the slipped stacking monosaccharide crystals into two distinct groups based on the differences in the crystal system: orthorhombic type and hexagonal type. Eight monosaccharide crystals were categorized into the orthorhombic crystal system: α-D-Gal, α-L-Sor, β-D-Psi, β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib. Only the β-D-All crystal was classified as belonging to the hexagonal crystal system. The β-D-All crystal (Fig. S4(d–f)) manifests a unique hexagonal layered architecture through directional hydrogen-bonding networks. These networks involve parallel propagation along the a-axis via dual O2–H⋯O2 interactions, lamellar extension along the c-axis through O1–H⋯O4 and O4–H⋯O1 reciprocal bonding, and longitudinal growth along the b-axis mediated by O6–H⋯O6 bonding. This three-dimensional (3D) hydrogen bonding network promoted the formation of hexagonal slipped stacking of β-D-All.

All eight monosaccharide orthorhombic crystals exhibited some identical crystallographic features (e.g., α = β = γ = 90°, Z = 4), and four molecules inside the unit cell were interconnected via 2₁ screw axes. These crystals exhibited layered hydrogen-bonding networks that connected molecules within layers and stabilized the overall structure. In the crystal structure of α-L-Sor, the molecules were interconnected by an extensive hydrogen-bonding network, facilitating a three-dimensional packing arrangement. Along the c-axis, α-L-Sor molecules exhibited continuous parallel extension through intermolecular hydrogen bonds. These hydrogen-bonding interactions resulted in the construction of a 3D network that assumed a slipped stacking pattern.

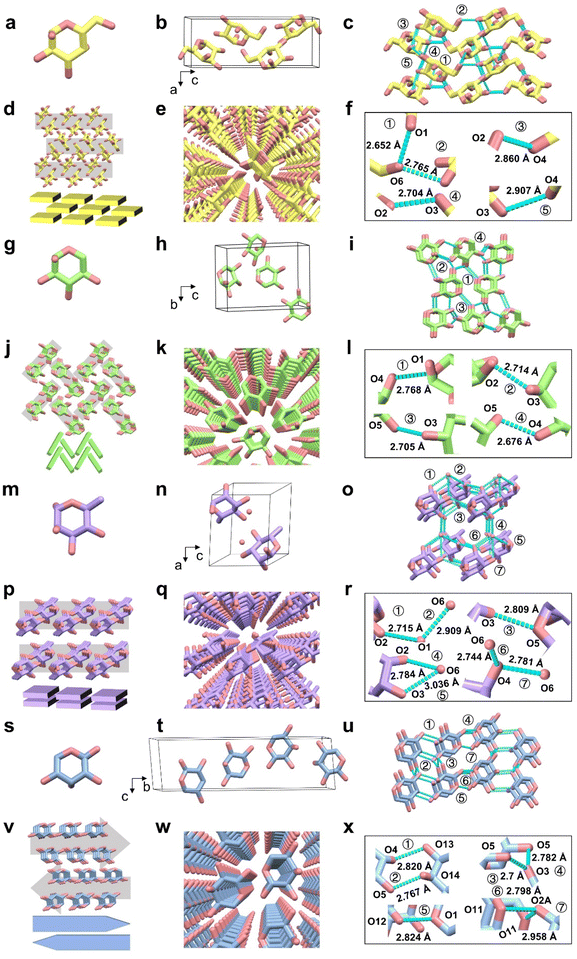
α-D-Gal crystallized in the orthorhombic system with space group P2₁2₁2₁ (Fig. 3(a and b)). Within the 3D framework (Fig. 3(c and f)), α-D-Gal molecules exhibited continuous parallel extension along the a-axis through hydrogen bonds O3–H⋯O4 and O4–H⋯O3, as well as O2–H⋯O3 and O3–H⋯O2. Layer-wise extension along the b-axis was mediated by O4–H⋯O2 and O2–H⋯O4, while longitudinal extension along the c-axis occurred through O2–H⋯O6, O6–H⋯O2, O6–H⋯O1, and O1–H⋯O6. This comprehensive hydrogen-bonding network, featuring relatively short (2.652 Å) and moderate-length (2.907 Å) interactions, formed a slipped stacking architecture (Fig. 3(d and e)).

Fig. 3 Single crystal structures of α-D-Gal, α-D-Xyl, α-L-Rha and α-D-Rib. (a) Asymmetric unit of α-D-Gal. (b) Unit cell of α-D-Gal. (c) Hydrogen bonding network of the α-D-Gal crystal. (d) Slip stacking of the α-D-Gal crystal. (e) 3D framework of the α-D-Gal crystal. (f) Specific hydrogen bonds in α-D-Gal crystals. (g) Asymmetric unit of the α-D-Xyl. (h) Unit cell of α-D-Xyl. (i) Hydrogen bonding network of the α-D-Xyl crystal. (j) Herringbone stacking of α-D-Xyl crystal. (k) 3D framework of α-D-Xyl crystal. (l) Specific hydrogen bonds in α-D-Xyl crystals. (m) Asymmetric unit of α-L-Rha. (n) Unit cell of α-L-Rha. (o) Hydrogen bonding network of the α-L-Rha crystal. (p) Parallel stacking of the α-L-Rha crystal. (q) 3D framework of the α-L-Rha crystal. (r) Specific hydrogen bonds in α-L-Rha crystals. (s) Asymmetric unit of α-D-Rib. (t) Unit cell of α-D-Rib. (u) Hydrogen bonding network of α-D-Rib crystal. (v) Antiparallel stacking of α-L-Rha crystal. (w) 3D framework of α-D-Rib crystal. (x) Specific hydrogen bonds in α-D-Rib crystals. Red represents oxygen atoms, and yellow, green, purple, blue denote carbon atoms for α-D-Gal crystal, α-D-Xyl crystal, α-L-Rha crystal, and α-D-Rib crystal, respectively.

The β-D-Psi, β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib crystals all formed slipped stacking structures through hydrogen bonding networks (Fig. S4 and S5). Their hydrogen bonds directionally extended along their respective crystallographic axes (e.g., in β-D-Psi, connections along the a-, b-, and c-axes are mediated by O1–H⋯O4, O1–H⋯O6, O3–H⋯O5, and O4–H⋯O2, respectively). These interactions collectively sustain layered parallel expansion and longitudinal stability of the crystals. Detailed descriptions of the crystal structures of β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib can be found in the section titled “Crystal structures of the β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib self-assemblies” in the SI.

The α-D-Xyl crystal (P2₁2₁2₁ space group, Z = 4) (Fig. 3(g and h)) and the α-D-Glu crystal (P2₁2₁2₁ space group) are formed by herringbone stacking, and both are characterized by a staggered arrangement via helical symmetry. In the α-D-Xyl crystal structure, O4–H⋯O5 (2.676 Å) hydrogen bond chains extend parallel along the b-axis and are perpendicular to the O5–H⋯O3 (2.705 Å) and O2–H⋯O3 (2.714 Å) hydrogen bond layers along the a-axis, forming a staggered arrangement (Fig. 3(i and l)) and a herringbone stacking architecture (Fig. 3(j and k)). A herringbone structure was formed from the α-D-Glu crystal through the O3–H⋯O2 (2.707 Å) hydrogen bond chains along the a-axis and the O3–H⋯O6 (2.711 Å) and O1–H⋯O5 (2.847 Å) hydrogen bond chains along the c-axis (Fig. S6).

In parallel stacking, two monosaccharide crystals were included (α-L-Fuc, α-L-Rha). The α-L-Fuc crystal adopted an orthorhombic system with space group P2₁2₁2₁ (Z = 4). In the 3D framework of α-L-Fuc, the b-axis parallel extension occurred via hydrogen bonds O1–H⋯O5 (2.756 Å), O2–H⋯O1, and O1–H⋯O2 (2.742 Å); c-axis layer stacking was stabilized by O3–H⋯O2 and O2–H⋯O3 (2.840 Å); and a-axis extension occurred via O4–H⋯O3 and O3–H⋯O4 (2.804 Å). The hydrogen bond network facilitated the formation of parallel stacking (Fig. S7).

In the non-orthorhombic type, α-L-Rha was included (monoclinic system, P2₁ space group) (Fig. 3(m and n)). The α-L-Rha crystal continuously extended in parallel along the c-axis direction through hydrogen bonds O3–H⋯O5 (2.809 Å), was extended layer by layer along the b-axis through hydrogen bonds O6–H⋯O4 (2.781 Å), O4–H⋯O6 (2.781 Å), O2–H⋯O1 (2.715 Å), O1–H⋯O2 (2.715 Å), O1–H⋯O6 (2.909 Å), O6–H⋯O1 (2.909 Å), and through hydrogen bonds O6–H⋯O2 (2.784 Å), O2–H⋯O6 (2.784 Å), O4–H⋯O6 (2.744 Å), O6–H⋯O4 (2.744 Å), O6–H⋯O3 (3.036 Å), and O3–H⋯O6 (3.036 Å) extended longitudinally along the a-axis (Fig. 3(o and r)). Eventually, the α-L-Rha crystal participated in parallel stacking (Fig. 3(p and q)).

In antiparallel stacking, the α-D-Rib crystal (monoclinic system, P2₁ space group, Z = 2) achieved an antiparallel arrangement through a three-dimensional hydrogen bond network (Fig. 3(s and t)). The O5–H⋯O3 (2.700 Å), O15–H⋯O13 (2.682 Å), and O13–H⋯O15 (2.721 Å) hydrogen bonds along the c-axis formed parallel extended chains, and the O11–H⋯O2A (2.798 Å) and O2A–H⋯O11 (2.958 Å) hydrogen bonds along the a-axis formed a layered structure. The O5–H⋯O14 (2.767 Å) hydrogen bonds along the b-axis achieved longitudinal connection (Fig. 3(u and x)), and ultimately underwent antiparallel stacking (Fig. 3(v and w)).

The analysis of the monosaccharide crystal structures revealed that the spatial packing of monosaccharide crystals is dominated by the directionality and strength of hydrogen bond networks. The isomers formed different non-covalent interactions, producing diverse supramolecular packing modes. Fourteen types of monosaccharide crystals fell into four packing categories: parallel, slipped, herringbone, and antiparallel, which showed clear correlations with crystal systems.

Most slipped packing crystals belong to the orthorhombic system, and all form helically symmetric layered structures through dense intralayer hydrogen bonds and interlayer cross-linking. Monosaccharide crystals that undergo herringbone packing belong to the orthorhombic system, forming staggered or parallel arrangements via hydrogen bond chains. This hydrogen bond-mediated structure-packing correlation not only reflects the regulation of intermolecular forces on crystal symmetry but also suggests that packing patterns may affect the functional properties of materials through layered dipole polarization.

The piezoelectric properties of monosaccharide assemblies

The non-centrosymmetric crystalline structure of monosaccharides inherently generates internal polarization, which fundamentally enables their piezoelectric properties. We employed DFT to calculate the piezoelectric coefficients of monosaccharide crystals. The piezoelectric tensor components d_ij (pC/N) were determined through the established electromechanical relationship d_ij = e_ij/C_ij, where e_ij (C m⁻²) represents the anisotropic piezoelectric polarization components, and C_ij (GPa) denotes the corresponding elastic stiffness tensor elements.

Elastic stiffness constant C_ij (Table S8) analysis reveals that all calculated shear elastic constants of the monosaccharide crystals are reduced by two orders of magnitude compared to conventional inorganic piezoelectric materials.⁵² In particular, the α-L-Sor crystal exhibited low shear compliance (C₃₃ = 1.9 GPa), which correlates with its prominent shear-mode piezoelectric activity. In contrast, the C₆₆ of the α-D-Tag crystal is 19.1 GPa, implying stronger shear stiffness.

Moreover, macroscopic mechanical parameters were calculated through the Voigt–Reuss–Hill theoretical model (Table S9). The average Young's modulus, Poisson's ratio, bulk modulus, and shear modulus of the monosaccharide crystals varied from 6.1 to 31.1 GPa, 0.22 to 0.34, 4.4 to 24.7 GPa, and 2.4 to 12.3 GPa, respectively. In addition, we calculated the piezoelectric charge constant e_ij of the monosaccharide crystals (Tables S10–S23). The e₃₆ of the α-D-Gal crystal was 0.195 C m⁻², which is 3 times greater than that of biomolecular crystals, such as proline–phenylalanine–phenylalanine (0.056 C m⁻²).⁴⁰

The piezoelectric strain constant d_ij was derived by dividing the piezoelectric stress constant e_ij by the elastic stiffness constant C_ij (Tables S10–S23). Fig. 4(a) shows that the maximum d_ij values of the monosaccharide crystals ranged from 6.0 to 13.7 pC/N, among which the d_ij value of α-D-Gal crystals with a slip arrangement reached 13.7 pC/N. These results indicated that the piezoelectric strain constants of the monosaccharide molecular crystals were comparable to those of diverse natural biomaterials such as L-valine (1.8 pC/N), chitin (3.98 pC/N), and collagen (12 pC/N) (Fig. 4(b) and Table S7).

Fig. 4 Study on piezoelectric properties of monosaccharide crystals. (a) The piezoelectric strain constants (d_ij) of monosaccharide crystals. (b) Comparison of the piezoelectric coefficient of different inorganic crystals, polymers, biological materials, and monosaccharide crystals. The relevant references were shown in Table S7. (c–e) The angle dependence relations of the Poisson's ratio of (c) α-D-Gal, (d) α-L-Rha, and (e) α-D-Xyl crystals. (f–h) 3D surface plot of computed piezoelectric coefficients (pC/N) of (f) α-D-Gal, (g) α-L-Rha, and (h) α-D-Xyl crystals. (i–k) Dipole moment arrangement model of monosaccharide crystals: (i) α-D-Gal, (j) α-L-Rha, and (k) α-D-Xyl. The green arrow represents the direction of molecular dipole moments.

To assess the anisotropic features of the electromechanical properties of monosaccharide crystals, we further analyzed the anisotropic mechanical and piezoelectric properties of the α-D-Gal, α-L-Rha, and α-D-Xyl crystals. The angular dependence of Poisson's ratio, Young's modulus, and the shear modulus of the α-D-Gal, α-L-Rha, and α-D-Xyl crystals (Fig. 4(c–e), S8 and Table S9) exhibited butterfly-shaped plots, indicating distinct mechanical anisotropy. Moreover, as shown in Fig. 4(c–e), the maximum Poisson's ratio of monosaccharide crystals exhibited significant differences: α-D-Gal – 0.26 (100°/280°), α-L-Rha – 0.29 (122°/303°), α-D-Xyl – 0.33 (77°/257°).

Excellent mechanical anisotropy contributes to the anisotropic piezoelectric response of piezoelectric materials. To characterize the spatial distribution of the piezoelectric coefficients of the monosaccharide crystals, we present the anisotropy of the piezoelectric constants of monosaccharide crystals (Fig. 4(f–h)). The maximum piezoelectric response for the α-D-Gal, α-L-Rha, and α-D-Xyl crystals occurred at the [1, 1, 1], [−1, −1, −1], and [1, −1, −1] directions, respectively. Furthermore, we calculated the dielectric constant (ε_r) (Table S24) and piezoelectric voltage constant (g_ij) (Tables S10–S23) of the monosaccharide crystals.

The calculated dielectric constant (ε_r) of the monosaccharide crystals is approximately 4.00 (Table S24), indicating the intrinsic electronic insulation characteristic of biomolecular solids, which is significantly lower than that of conventional chalcogenide piezoelectrics (ε_r > 200).²⁴ Due to the relationship between dielectric constant ε_r and piezoelectric voltage constant g_ij (g_ij = d_ij/ε_r), this low dielectric constant characteristic generates exceptional voltage sensitivity. Our calculations reveal that the maximum g_ij value of α-D-Gal was 432 mV m N⁻¹, which surpasses that of traditional lead-based ceramics such as BaTiO₃ (g₃₃ = 11.4 mV m N⁻¹).⁷⁰

To elucidate the reason for the difference in piezoelectricity of monosaccharide assemblies, we systematically investigated the molecular and crystal dipole moments of the monosaccharides through DFT calculations (Table S25). The calculated molecular dipole moments spanned a range of 1.8–5.8 Debye (D), with β-D-All exhibiting the largest value of 5.8 D. Our analysis revealed that hydroxyl group count primarily governs molecular dipole moment variations in monosaccharides.

Specifically, compounds with five hydroxyl groups demonstrated higher dipole moments compared to those with fewer hydroxyl groups. This enhanced dipole magnitude originates from the asymmetric spatial distribution of hydroxyl groups, which creates significant intramolecular charge polarization. The analysis of dipole moment orientation patterns (Fig. 4(i–k), S9 and Table S25) revealed distinct polarization mechanisms in crystalline monosaccharides.

The α-D-Gal assemblies exhibited enhanced consistency in molecular dipole moment orientation, resulting in a crystal dipole moment of 7.4 D and superior piezoelectric performance. In comparison, although β-D-All assemblies possess the largest molecular dipole (5.8 D), their piezoelectric coefficient is lower (13.0 pC/N) due to less effective dipole cooperativity within the lattice. By contrast, in crystals such as α-D-Xyl (Fig. 4(k)), α-D-Rib, β-D-dRib, and α-L-Fuc (Fig. S9), significant cancellation between adjacent molecular dipoles results in net crystal moments below 1 Debye, leading to their smaller piezoelectric coefficients (6.0–9.1 pC/N). Notably, α-L-Sor assemblies represent a unique case, in that despite a very low net crystal moment (0.4 Debye), their small elastic tensor (C₃₃ = 1.9 GPa) enhances mechanical compliance under stress, thereby contributing to their appreciable piezoelectric response (d₂₅ = 12.4 pC/N).

Energy-harvesting performance of the α-D-Gal crystal-based piezoelectric nanogenerator

To investigate the piezoelectric response of monosaccharide crystals, a sandwich-structured PENG based on α-D-Gal crystals was constructed. Guided by the DFT predictions, the α-D-Gal crystal, which exhibited the highest maximum piezoelectric coefficient, was selected as the active material for the PENG in energy-harvesting tests. The fabricated α-D-Gal crystal-based PENG featured a typical sandwich structure denoted as the electrode-piezoelectric layer-electrode (Fig. 5(a)).

Fig. 5 Output performance characteristics of the α-D-Gal crystal-based PENG. (a) Schematic structure of the PENG. (b and c) Forward and reverse circuit configurations of the PENG. (d and e) Output voltage of the PENG under forward and reverse connections, respectively. (f) Linear fitting of PENG voltage and current versus applied pressure in forward connection mode. (g and h) Output current of the PENG under forward and reverse connections, respectively. (i) Linear fitting of PENG voltage and current versus applied pressure in reverse connection mode. (j) Continuous output stability of the PENG over 10 000 pressing cycles at 55 N. (k) Magnified view of the region marked in (j). (l) Equivalent circuit diagram for the capacitor charging–discharging test. (m) Photograph of an LED illuminated by the α-D-Gal crystal-based PENG. (n) Charging profiles of five capacitors powered by the α-D-Gal crystal-based PENG.

In this configuration, α-D-Gal crystal powder was evenly dispersed between the electrodes, serving as the core piezoelectric layer. The crystalline powder and electrodes were tightly encapsulated in Kapton tape, forming a physical barrier layer to prevent air gaps during testing. This encapsulation strategy was critical for maintaining the stable output performance of the PENG. The piezoelectric output performance of the α-D-Gal crystal-based PENG was evaluated using a linear motor test platform with forward and reverse connections (Fig. 5(b and c)).

When subjected to a linear gradient pressure ranging from 15 to 55 N, the α-D-Gal crystal-based PENG exhibited a significant coupling effect between the applied pressure and the generated electric signal. Specifically, upon the application of a 15 N mechanical force, the PENG produced an open-circuit voltage of 0.42 V. As the mechanical force increased, the open-circuit voltage also linearly increased. When the mechanical force reached 55 N, the open-circuit voltage reached 1.08 V (Fig. 5(d)). Simultaneously, the short-circuit current synchronously increased from 2.82 nA to 4.36 nA (Fig. 5(g)).

Under the reverse connection, changes in the open-circuit voltage, short-circuit current, and applied mechanical force mirrored those observed in the forward connection. Specifically, as the mechanical force increased from 15 N to 55 N, the output voltage of the α-D-Gal crystal-based PENG changed from −0.67 V to −1.03 V in the opposite direction, and the short-circuit current changed from −3.04 nA to −4.40 nA in the opposite direction (Fig. 5(e and h)).

By analyzing the output characteristics of the α-D-Gal crystal-based PENG in depth, we found that there was an obvious linear relationship between the open-circuit voltage and short-circuit current and the external mechanical force. In the forward connection mode, the slope of the output voltage versus the force curve of the PENG was 0.015, and the corresponding slope of the short-circuit current versus the force curve was 0.040 (Fig. 5(f)). Under a reverse connection, the open-circuit voltage and short-circuit current also maintained linear correlations with applied mechanical force, demonstrating slopes of −0.009 and −0.037, respectively (Fig. 5(i)).

These data indicated that the measured output performance of the reverse connection was similar to that of the forward circuit, which confirmed that the measured electrical signal originated from piezoelectric crystals rather than other mechanisms such as triboelectricity or electrostatic induction. In addition, we tested the stability of the α-D-Gal crystal-based PENG under a constant load of 55 N and a loading period of 3.4 s.

The α-D-Gal crystal-based PENG displayed excellent electromechanical coupling stability. Specifically, after 10 000 press-release cycles, the output performance of the PENG remained consistent with the initial state, and its output voltage stabilized at approximately 1.1 V (Fig. 5(j and k)). This indicated that the prepared PENG can stably function for a long time while maintaining a certain level of output performance. In addition, a sandwich-structured device without α-D-Gal crystals generated negligible voltages and currents under an external force of 55 N compared to that from the device containing α-D-Gal crystals (Fig. S10).

To further explore the practical energy applications of an α-D-Gal crystal-based PENG, we built an electrical energy storage system based on commercial capacitors and demonstrated its potential for harvesting and utilizing mechanical energy in real-world scenarios. The equivalent circuit of the PENG-based self-charging system is shown in Fig. 5(l).

The energy storage process involved a well-defined sequence of steps. First, the bridge rectifier converted the alternating current generated by the PENG under the external force into direct current. Next, the rectified electrical energy was stored in capacitors. Finally, an on–off switch was used to control the series circuit connected to the LED. The entire circuit effectively addressed the challenge of storing alternating current through the rectification unit, enabling the continuous power supply via the capacitor, and ultimately verifying the function of energy storage via the switching circuit.

To demonstrate the functionality of the system, a small motor with a rotation speed of 150 revolutions per minute was used to apply vertical force to the PENG under a mechanical load of 9.8 N. Moreover, we measured the charging performance of the α-D-Gal crystal piezoelectric nanogenerators for capacitors of different models (0.1 µF, 0.47 µF, 1.0 µF, 3.3 µF, and 6.8 µF).

The 0.1 µF capacitor exhibited the fastest charging rate compared to the other capacitors, illuminating five LEDs and reaching 32.0 V within 4 minutes (Fig. 5(m and n)). Notably, when connected to a 0.1 µF capacitor, the α-D-Gal crystal-based PENG was able to light an LED within 1 minute (Fig. S11). These results demonstrated that the α-D-Gal crystal-based PENG exhibited high energy conversion efficiency, highlighting its potential as a micro-green energy device.

Application of α-D-Gal crystal-based film in a Morse code representation system

Morse code, an electronic communication coding system invented in 1837, has maintained its unique application value.⁷¹ Morse code transmits information through different arrangements and combinations of dots (·) and dashes (-), with its principle being similar to the binary logic of modern digital communications. Leveraging the mechanical-to-electrical energy conversion capability of α-D-Gal crystals, we combined Morse code with the electrical signals from α-D-Gal crystal-based piezoelectric devices to explore a novel information transmission method.

The root of this combination lies in the fact that the rapid response characteristic of α-D-Gal crystals ensures the instant conversion of mechanical signals into electrical signals, providing a basis for information encoding. Morse code, with its long-standing history in digital communication, offers a suitable encoding scheme. The combination of the two forms offers a synergistic advantage of ‘efficient conversion + stable encoding’.

To improve the mechanical flexibility of piezoelectric devices and the stability of signals, we constructed a flexible piezoelectric composite film based on the PENG structure. The composite film was designed with a three-part composition: (i) polydimethylsiloxane (PDMS) buffer layers for stress redistribution (top/bottom); (ii) copper foil (intermediate) as the conductive layer, responsible for efficient electrical conduction; and (iii) active piezoelectric layers containing α-D-Gal crystal inclusions within the PDMS (core). This specific composition allowed for maintaining piezoelectric performance, while optimizing flexibility. Based on this design, we present a schematic diagram illustrating the conversion of piezoelectric electrical signals into information carriers (Fig. 6(a)).

Fig. 6 Application of α-D-Gal crystals-based piezoelectric film. (a) In the schematic diagram of piezoelectric composite films and Morse code information transmission. (b) Morse code “0”, “1”, “2”, “3” was generated by piezoelectric composite film. (c) Morse code “A”, “B”, “C”, “D” was generated by piezoelectric composite film. (d) Morse code “SOS”, “Material” were generated by piezoelectric composite film.

To enhance the timeliness and accuracy of information transmission, we aimed to establish an accurate correspondence between the electrical signals generated by the piezoelectric composite film and the basic units of Morse code. Specifically, a single press on the piezoelectric composite film produced a single-peak electrical signal, which was designated to represent the Morse code “·”, while two consecutive presses generated a double-peak electrical signal corresponding to the Morse code “-”. Experimental verification demonstrated that the piezoelectric composite film exhibited excellent stability and sensitivity. It was able to consistently generate standard combinations of dots and dashes based on different pressing patterns.

According to the Morse code rules, the electrical signals generated by these pressing actions successfully enabled the transmission of information corresponding to the numbers “0–9” and the English letters “A–E” (Fig. 6(b, c), S12 and S13). For the transmission of numbers “0–9”, as shown in Fig. 6(b) and S12, each number was encoded with a sequence of five signal peaks. Starting from “0”, the encoding began with five double-peak signals. In successive numbers, the number of double-peak signals decreased by one, while the number of single-peak signals increased. This progression continued until the number “5”, which was represented by five single-peak signals. Then, starting from the number “6”, the number of double-peak signals gradually increased again while the single-peak signals decreased, returning to five double-peak signals for “0”, thus completing a cycle of encoding for the numeric set. The encoding of English letters was achieved through combinations of different dots and dashes (Fig. 6(c) and S13).

Next, we expanded the complexity of information encoding the piezoelectric signals and explored the potential of piezoelectric composite films in complex semantic transmission. The film successfully transmitted the specific information of “SOS” (international distress signal), “CQU”, “Bio”, “Material” and “PENG” through a customized pressing sequence (Fig. 6(d) and S13).

Specifically, we obtained single-peak and double-peak electrical signals by pressing the film, which corresponded to the pulse combinations of “dot-dot-dot, dash-dash-dash, dot-dot-dot”. This combination was accurately recognized as the internationally recognized distress signal “SOS”, demonstrating the versatility and effectiveness of the piezoelectric composite film in facilitating complex information transmission. These results not only validated the feasibility of using the piezoelectric composite films for Morse code-based information transmission but also offered a potential approach for applications requiring rapid and reliable communication in emergency scenarios.

Conclusions

We explored the piezoelectric response of various monosaccharide assemblies for energy harvesting and information transmission. The analysis of the crystal structures showed that the number and orientation of hydroxyl groups on the six-membered ring of monosaccharides can significantly change the supramolecular assembly modes of crystals and affect their piezoelectric responses. The crystal structures of monosaccharides indicated four typical crystal-stacking modes among the different monosaccharide-based assemblies: parallel packing, slip packing, herringbone packing, and antiparallel packing. DFT prediction revealed the higher maximum piezoelectric coefficient of 13.7 pC/N for the α-D-Gal crystal.

The α-D-Gal crystals adopted a slip-stacking mode and formed a highly ordered three-dimensional hydrogen bond network. The anisotropy of the dipole arrangement between molecular layers provided the structural basis for the piezoelectric response. Moreover, the α-D-Gal crystal-based PENG produced a stable open-circuit voltage of 1.08 V under a mechanical force of 55 N. The PENG can charge capacitors with varying capacitances and can be used to fabricate composite film for information transmission.

This work presents a feasible strategy to regulate the piezoelectric response of monosaccharide-based supramolecular assemblies by changing the number and orientation of hydroxyl groups of molecular structures, and to advance the development of high-performance biomolecule-based piezoelectric materials through molecular engineering, aiming at self-powered devices and information transmission technologies.

Author contributions

Siying Chen: conceptualization, methodology, investigation, visualization, writing – original draft, writing – review and editing. Junli Yang: investigation, visualization, writing – original draft, writing – review and editing. Shuaijie Liu: investigation, visualization, writing – original draft, writing – review and editing. Yehong Huo: investigation, writing – review and editing. Xin Cheng: writing – review and editing. Lingling Li: investigation, writing – review and editing. Wei Ji: conceptualization, methodology, supervision, writing – original draft, writing – review and editing. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Data availability

CCDC 2478061 contains the supplementary crystallographic data for this paper.⁷²

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: experimental section, crystal structures of the β-D-Fru, β-D-Ara, β-L-Ara, α-D-Tag, and β-D-dRib self-assemblies, Fig. S1–S13, and Tables S1–S25. See DOI: https://doi.org/10.1039/d5sc07918g.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 52473106), the Fundamental Research Funds for the Central Universities (No. 2024IAIS-QN003 and 2024CDJXY017), and Start-up Funding from Chongqing University. The authors thank Jiaxun Xiao for assistance with the powder X-ray diffraction tests. The authors thank all the members of the laboratories for helpful discussions.

References

1. K. Kapat, Q. T. H. Shubhra, M. Zhou and S. Leeuwenburgh, Adv. Funct. Mater., 2020, 30, 1909045.
2. Q. Q. Xu, X. Y. Gao, S. F. Zhao, Y. N. Liu, D. Zhang, K. C. Zhou, H. Khanbareh, W. S. Chen, Y. Zhang and C. Bowen, Adv. Mater., 2021, 33, 200845.
3. Y. Cheng, J. Xu, L. Li, P. Cai, Y. Li, Q. Jiang, W. Wang, Y. Cao and B. Xue, Adv. Sci., 2023, 10, 2207269.
4. C. Chen, Y. Zhang, Y. Zheng, Y. Zhang, H. Liu, J. Wu, L. Yang and Z. Yang, Adv. Mater., 2025, 37, 2500466.
5. F. Li, B. Wang, X. Gao, D. Damjanovic, L. Q. Chen and S. Zhang, Science, 2025, 389, eadn4926.
6. Y. Cheng, T. Wang, H. Zhu, X. Hu, J. Mi, L. Li, Y. Zhang, J. Yang, L. Dong and Y. Li, Angew. Chem., Int. Ed., 2025, 137, e202500334.
7. F. Yang, J. Li, Y. Long, Z. Y. Zhang, L. F. Wang, J. J. Sui, Y. T. Dong, Y. Z. Wang, R. Taylor, D. L. Ni, W. B. Cai, P. Wang, T. Hacker and X. D. Wang, Science, 2021, 373, 337–342.
8. S. Guerin, A. Stapleton, D. Chovan, R. Mouras, M. Gleeson, C. McKeown, M. R. Noor, C. Silien, F. M. F. Rhen, A. L. Kholkin, N. Liu, T. Soulimane, S. A. M. Tofail and D. Thompson, Nat. Mater., 2018, 17, 180.
9. L. W. Dong, Y. Ke, Y. F. Liao, J. Y. Wang, M. Y. Gao, Y. W. Yang, J. Li and F. Yang, Adv. Funct. Mater., 2024, 34, 2410566.
10. Z. M. Zhang, X. M. Li, Z. H. Peng, X. D. Yan, S. Y. Liu, Y. Hong, Y. Shan, X. T. Xu, L. H. Jin, B. R. Liu, X. Y. Zhang, Y. Chai, S. J. Zhang, A. K. Y. Jen and Z. B. Yang, Nat. Commun., 2023, 14, 4094.
11. T. Li, Y. J. Yuan, L. Gu, J. Li, Y. Shao, S. Yan, Y. H. Zhao, C. Carlos, Y. T. Dong, H. Qian, X. Wang, W. L. Wu, S. V. Wang, Z. K. Wang and X. D. Wang, Sci. Adv., 2024, 10, eadn8706.
12. E. S. Hosseini, L. Manjakkal, D. Shakthivel and R. Dahiya, ACS Appl. Mater. Interfaces, 2020, 12, 9008–9016.
13. J. Li, C. Carlos, H. Zhou, J. J. Sui, Y. K. Wang, Z. Silva-Pedraza, F. Yang, Y. T. Dong, Z. Y. Zhang, T. A. Hacker, B. Liu, Y. C. Mao and X. D. Wang, Nat. Commun., 2023, 14, 6562.
14. S. Chen, P. Zhu, L. Mao, W. Wu, H. Lin, D. Xu, X. Lu and J. Shi, Adv. Mater., 2023, 35, 2208256.
15. F. Dai, Q. Geng, T. Hua, X. Sheng and L. Yin, Soft Sci., 2023, 3, 1.
16. L. Persano, A. Camposeo, F. Matino, R. Wang, T. Natarajan, Q. Li, M. Pan, Y. Su, S. K. Narayan and F. Auricchio, Adv. Mater., 2024, 36, 2405363.
17. Y. Bai, H. Meng, Z. Li and Z. L. Wang, Med Mat, 2024, 1, 40–49.
18. A. C. Jayasuriya, S. Ghosh, J. I. Scheinbeim, V. Lubkin, G. Bennett and P. Kramer, Biosens. Bioelectron., 2003, 18, 381–387.
19. S. Ghosh, B. Z. Mei, V. Lubkin, J. I. Scheinbeim, B. A. Newman, P. Kramer, G. Bennett and N. Feit, J. Biomed. Mater. Res., 1998, 39, 453–457.
20. W. S. Williams and L. Breger, J. Biomech., 1975, 8, 407–413.
21. H. K. Ravi, F. Simona, J. Hulliger and M. Cascella, J. Phys. Chem. B, 2012, 116, 1901–1907.
22. E. Fukada, R. L. Zimmerman and S. Mascarenhas, Biochem. Biophys. Res. Commun., 1975, 62, 415–418.
23. V. V. Lemanov, Ferroelectrics, 2000, 238, 775–782.
24. S. Y. Chen, X. Y. Tong, Y. H. Huo, S. J. Liu, Y. Y. Yin, M. L. Tan, K. Y. Cai and W. Ji, Adv. Mater., 2024, 36, 2406192.
25. Y. Yin, S. Liu, Y. Wang, S. Yang, M. Ding, X. Xu, W. Ji and J. Song, Giant, 2024, 20, 100333.
26. E. Fukada and I. Yasuda, J. Phys. Soc. Jpn., 1957, 12, 1158–1162.
27. H. Athenstaedt, H. Claussen and D. Schaper, Science, 1982, 216, 1018–1020.
28. T. Yucel, P. Cebe and D. L. Kaplan, Adv. Funct. Mater., 2011, 21, 779–785.
29. R. Kumar and S. Bera, Giant, 2024, 17, 100214.
30. H. Yuan, P. Han, K. Tao, S. Liu, E. Gazit and R. Yang, Research, 2019, 9025939.
31. S. Guerin, T. A. M. Syed and D. Thompson, Nanoscale, 2018, 10, 9653–9663.
32. Y. Su, J. Liu, D. Yang, W. Hu, X. Jiang, Z. L. Wang and R. Yang, ACS Mater. Lett., 2023, 5, 2317–2323.
33. T. Hu, J. P. Lee, P. Huang, A. J. Ong, J. Yu, S. Zhu, Y. Jiang, Z. Zhang, M. Reches and P. S. Lee, Adv. Mater., 2025, 37, 2413049.
34. J. Hu, S. J. Liu, Y. H. Huo, B. B. Yang, Y. Y. Yin, M. L. Tan, P. Liu, K. Y. Cai and W. Ji, Adv. Mater., 2025, 37, 2417409.
35. Y. Fu, L. Zhang, X. Yan and K. Liu, Chem. Syst. Chem., 2024, 7, e20240068.
36. R. Fox, J. Klug, D. Thompson and A. Reilly, J. Comput. Chem., 2024, 45, 2465–2475.
37. M. Roemer, X. Chen, Y. Li, L. Wang, X. Yu, P. A. Cazade, C. Nickle, R. Akter, E. Del Barco and D. Thompson, Nanoscale, 2024, 16, 19683–19691.
38. J. Zhang, L. Zhou, X. Jiang, W. Hu and R. Yang, ACS Mater. Lett., 2024, 6, 674–696.
39. X. Su, S. J. Liu, X. W. Gong, X. Y. Tong, L. L. Li, Y. H. Huo, Q. X. Liu, Y. H. Wang, M. L. Tan, Q. Li, S. J. Zhang and W. Ji, J. Am. Chem. Soc., 2025, 147, 16255–16269.
40. S. Bera, S. Guerin, H. Yuan, J. O'Donnell, N. P. Reynolds, O. Maraba, W. Ji, L. J. W. Shimon, P. A. Cazade, S. A. M. Tofail, D. Thompson, R. Yang and E. Gazit, Nat. Commun., 2021, 12, 2634.
41. H. P. Lv, Y. R. Li, X. J. Song, N. Zhang, R. G. Xiong and H. Y. Zhang, J. Am. Chem. Soc., 2023, 145, 3187–3195.
42. Y. H. Wang, S. J. Liu, L. L. Li, H. Li, Y. Y. Yin, S. R. Lazar, S. Guerin, W. E. Ouyang, D. Thompson, R. S. Yang, K. Y. Cai, E. Gazit and W. Ji, J. Am. Chem. Soc., 2023, 145, 15331–15342.
43. N. A. Hoque, P. Thakur, P. Biswas, M. M. Saikh, S. Roy, B. Bagchi, S. Das and P. P. Ray, J. Mater. Chem. A, 2018, 6, 13848–13858.
44. G. de Marzo, V. M. Mastronardi, L. Algieri, F. Vergari, F. Pisano, L. Fachechi, S. Marras, L. Natta, B. Spagnolo, V. Brunetti, F. Rizzi, F. Pisanello and M. De Vittorio, Adv. Electron. Mater., 2023, 9, 2200069.
45. S. Rajala, T. Siponkoski, E. Sarlin, M. Mettänen, M. Vuoriluoto, A. Pammo, J. Juuti, O. J. Rojas, S. Franssila and S. Tuukkanen, ACS Appl. Mater. Interfaces, 2016, 8, 15607–15614.
46. R. X. Wang, J. J. Sui and X. D. Wang, ACS Nano, 2022, 16, 17708–17728.
47. L. Su, Y. L. Feng, K. C. Wei, X. Y. Xu, R. Y. Liu and G. S. Chen, Chem. Rev., 2021, 121, 10950–11029.
48. I. Chae, R. Zu, A. B. Meddeb, Y. Ogawa, Z. Chen, V. Gopalan, Z. Ounaies and S. H. Kim, Biomacromolecules, 2021, 22, 1901–1909.
49. S. K. Ghosh and D. Mandal, Appl. Phys. Lett., 2017, 110, 123701.
50. C. W. Miao, L. Reid and Y. W. Hamad, Appl. Mater. Today, 2021, 24, 101082.
51. A. Amran, F. B. Ahmad, M. H. M. Akmal, A. A. M. Ralib and M. I. Bin Suhaimi, Mater. Today Commun., 2021, 29, 102919.
52. M. H. Zhao, Z. L. Wang and S. X. Mao, Nano Lett., 2004, 4, 587–590.
53. B. Tyson, C. M. Pask, N. George and E. Simone, Cryst. Growth Des., 2022, 13, 1371–1383.
54. Q. Zhou, T. J. Yang, Z. H. Zhong, F. Kausar, Z. Y. Wang, Y. M. Zhang and W. Z. Yuan, Chem. Sci., 2020, 11, 2926–2933.
55. D. Sisak, L. B. McCusker, G. Zandomeneghi, B. H. Meier, D. Bläser, R. Boese, W. B. Schweizer, R. Gilmour and J. D. Dunitz, Angew. Chem., Int. Ed., 2010, 49, 4503–4505.
56. A. Hordvik, Acta Chem. Scand., 1961, 15, 16–30.
57. S. Furberg, Acta Chem. Scand., 1960, 14, 1357–1363.
58. G. M. Brown and H. A. Levy, Science, 1965, 147, 1038–1039.
59. J. Ohanessian and H. Gillierpandraud, Acta Crystallogr., Sect. B, 1976, 32, 2810–2813.
60. S. H. Kim and R. D. Rosenstein, Acta Crystallogr., 1967, 22, 648–656.
61. A. Kwiecien, K. Slepokura and T. Lis, Carbohydr. Res., 2008, 343, 2336–2339.
62. F. Longchambon, J. Ohannessian, D. t. Avenel and A. Neuman, Struct. Sci., 1975, 31, 2623–2627.
63. S. Takagi and G. Jeffrey, Struct. Sci., 1978, 34, 2551–2555.
64. P. A. Bonnet, J. van de Streek, A. V. Trask, W. D. S. Motherwell and W. Jones, Crystengcomm, 2004, 6, 535–539.
65. K. Sata, J. Mizuguchi, Y. Sakai and S. Aramaki, J. Appl. Phys., 2008, 103, 013702.
66. W. Ji, H. Yuan, B. Xue, S. Guerin, H. Li, L. Zhang, Y. Q. Liu, L. J. W. Shimon, M. S. Si, Y. Cao, W. Wang, D. Thompson, K. Y. Cai, R. S. Yang and E. Gazit, Angew. Chem., Int. Ed., 2022, 61, e202201234.
67. J. A. Swift, R. Pal and J. M. McBride, J. Am. Chem. Soc., 1998, 120, 96–104.
68. A. Kálmán, L. Fábián, G. Argay, G. Bernáth and Z. C. Gyarmati, Acta Crystallogr., Sect. B, 2004, 60, 755–762.
69. S. Ganapathy, S. Sengupta, P. K. Wawrzyniak, V. Huber, F. Buda, U. Baumeister, F. Würthner and H. J. M. de Groot, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11472–11477.
70. R. E. Newnham, L. J. Bowen, K. A. Klicker and L. E. Cross, Mater. Eng., 1980, 2, 93–106.
71. N. J. Hu, X. C. Wang, J. Yang, M. Liu, J. W. Chen, X. M. Yu, W. B. Zhu and M. G. Zhang, ACS Appl. Nano Mater., 2023, 6, 19777–19785.
72. CCDC 2478061: Experimental Crystal Structure Determination, 2026,  DOI:10.5517/ccdc.csd.cc2p5mgz.

---

Footnote

† Siying Chen, Junli Yang, and Shuaijie Liu contributed equally to this work.

---