Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New theoretical insights into doping-induced enhancement of ORR activity in molybdenum disulfide: d–p hybridization or the Jahn–Teller effect?
Jia-Cheng
Chen†
a,
Mao-Jun
Pei†
a,
Wen-Bei
Yu
 a,
Xiang
Gao
a,
Qing
Zeng
a,
Jia-Ming
Xu
a,
Wei
Yan
a,
Yao
Liu
*a,
Guo-Qiang
Luo
*b and
Jiujun
Zhang
*a
a,
Xiang
Gao
a,
Qing
Zeng
a,
Jia-Ming
Xu
a,
Wei
Yan
a,
Yao
Liu
*a,
Guo-Qiang
Luo
*b and
Jiujun
Zhang
*a
aCollege of Materials Science & Engineering, Fuzhou University, Fuzhou 350108, China. E-mail: yaoliu@fzu.edu.cn; jiujun.zhang@fzu.edu.cn
bState Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan 430070, China. E-mail: luogq@whut.edu.cn
First published on 2nd January 2026
Abstract
Molybdenum disulfide (MoS2) has emerged as a promising electrocatalyst, garnering considerable attention in recent years. However, the extensive basal-plane sites remain intrinsically inert, thereby limiting the overall catalytic efficiency. Heteroatom doping has been demonstrated as an effective strategy for activating these otherwise inert sites; nevertheless, theoretical investigations remain relatively limited, and the broad diversity of dopants has led to conflicting interpretations of the underlying mechanisms. To elucidate the role of dopants in activating these sites, a total of 64 MoS2-based electrocatalysts incorporating 3d, 4d, and 5d transition metals, along with selected nonmetals, have been systematically investigated. The results reveal two distinct enhancement pathways: (i) d–p hybridization (d1–d3 dopants), which elevates the sulfur p-band center and reduces the oxygen reduction reaction (ORR) overpotential to 0.87 V; and (ii) the Jahn–Teller effect (d7–d9 dopants), which lifts the orbital degeneracy between dxz/dyz and dx2−y2/dxy, thereby inducing lattice distortion. The electron rearrangement at the metal center reduces charge transfer, thereby lowering the electron occupancy of the sulfur atom, upshifting its p-band center, and enhancing ORR performance by decreasing the overpotential to 0.53 V. In summary, these findings provide new theoretical insights into substitutional doping and establish guiding principles for the rational design of efficient MoS2-based ORR electrocatalysts.
1 Introduction
The rapid consumption of fossil fuels to meet the demands of industry development has raised serious concerns regarding resource depletion and environmental degradation, both of which pose a serious threat to the sustainable development of human society.1 To mitigate these challenges, the exploration of clean and renewable energy sources, such as solar, wind, and hydropower, together with advances in energy storage and conversion technologies, constitutes a promising avenue toward sustainable energy development.2,3 For electrical energy storage and conversion, electrochemical technologies, e.g., water electrolysis for hydrogen production and fuel cells for hydrogen-to-electricity conversion, have been widely recognized as efficient and practical solutions. In particular, fuel cells are distinguished by their high energy efficiency and intrinsic environmental advantages, which have attracted considerable attention over the past decades and position them as highly promising candidates for applications in both transportation and distributed power generation.4,5 It is well established that fuel cells operate through two fundamental electrochemical reactions: the hydrogen oxidation reaction (HOR) at the anode and the oxygen reduction reaction (ORR) at the cathode. The ORR, involving multiple intermediate steps in the conversion of O2 to H2O, is widely regarded as one of the most critical catalytic processes.6 Nevertheless, its intrinsically sluggish kinetics, governed by a complex multi-electron transfer pathway, severely hinder overall performance and remain a principal bottleneck to practical implementation.7To date, a diverse array of electrocatalysts have been developed to accelerate the rate of ORR, and many of which have demonstrated notable progress. Among these materials, Pt-based electrocatalysts exhibit outstanding ORR activity and have been successfully commercialized. The prohibitive cost and limited natural abundance of Pt/C electrocatalysts remain formidable obstacles to large-scale deployment, motivating extensive efforts to develop non-precious-metal alternatives.8,9 Recently, two-dimensional (2D) materials have attracted widespread attention owing to their unique structural features and tunable physicochemical properties.10,11 For example, 2D graphene has been extensively utilized as a support for constructing single-atom ORR electrocatalysts, e.g., Fe–N–C, Co–N–C, and Sn–N–C.12–16 Owing to its ultrathin structure, graphene provides shortened charge–transport pathways and excellent electrical conductivity, thereby facilitating electron transfer at metal active sites and enhancing overall catalytic performance. In situ characterization techniques have unequivocally confirmed that electrocatalytic reactions, such as the hydrogen evolution reaction (HER), oxygen reduction reaction (ORR), oxygen evolution reaction (OER), carbon dioxide reduction reaction (CO2RR), and nitrogen reduction reaction (NRR), primarily occur at metal active sites.17–20 Consequently, while M–N–C electrocatalysts can exhibit remarkable catalytic activity, the intrinsic high surface-area advantage of 2D materials remains insufficiently utilized, as the active centers are confined to isolated single atoms.21 In this context, 2D materials containing metal atoms, such as layered-double-hydroxides (LDHs), metal sulfides, and MXenes, have attracted considerable attention as another representative developmental pathway, as they inherently provide a greater number of active sites without the need for additional single-atom incorporation.22–24 Among these, molybdenum disulfide MoS2 has been extensively investigated, primarily due to its availability, chemical stability, and low cost.25 Nevertheless, its catalytic activity is largely confined to edge sites, resulting in a limited number of accessible active centers. By contrast, the metal sites on the basal plane are strongly coordinated and therefore remain largely inert, severely restricting the overall catalytic performance of MoS2.
To address these limitations, extensive efforts have been devoted to modulating the electronic structure and optimizing the surface properties of MoS2 through diverse physical and chemical modifications. Defect engineering, strain modulation, and heteroatom doping have emerged as effective strategies to enhance the intrinsic activity of basal-plane atoms and activate otherwise inert surface regions.26,27 For instance, MoS2 nanosheets enriched with edge defects was fabricated via H2O2 treatment,28 and the optimized electrocatalyst exhibited an onset potential of 0.94 V and a half-wave potential of 0.80 V in 0.1 M KOH. Simultaneously, lanthanide dopants were introduced to modulate the physicochemical properties of MoS2.29 It revealed that lanthanide doping could modulate the ORR activity of MoS2 by altering 4f–5d6s orbital hybridization and Ln–S bonding interactions. In addition, a Co- and Se-codoped MoS2 nanofoam with superior catalytic performance was also constructed.30 The synergistic interaction between Co and Se not only activated the inner Co sites but also stabilized the surface Se sites, thereby achieving a substantial enhancement in the catalytic performance of MoS2. It can be seen that the aforementioned studies clearly demonstrate the critical role of atomic-scale structural regulation in modulating the catalytic behavior of MoS2.
At the current state-of-the-art, MoS2 is predominantly recognized for its excellent performance in the HER, which has directed the majority of research efforts toward this area. By contrast, investigations into its ORR activity remain relatively limited, largely owing to the prevailing assumption that the active sites are Mo atoms, which are typically highly coordinated and therefore less catalytically active. Specifically, the substantial steric hindrance and high coordination stability of Mo atoms on the basal plane render them unsuitable for binding oxygen-containing intermediates, thereby constraining the practical applicability of MoS2 as an ORR electrocatalyst. Fortunately, the recent study has demonstrated that rational heteroatom doping can effectively reconfigure the active sites from Mo to S atoms, thereby enhancing the electrocatalytic ORR activity of MoS2.29 This approach provides a promising strategy for re-engineering MoS2 as an ORR electrocatalyst by fully leveraging its abundant intrinsic active sites. Despite recent advances in experiments, theoretical investigations remain limited, and the wide diversity of dopants has often led to conflicting interpretations of the underlying mechanisms. In particular, the effects of transition metal doping on the ORR mechanism, such as its influence on orbital hybridization, charge transfer, and intermediate adsorption at sulfur sites, have not been systematically explored. This has resulted in a critical gap in understanding the structure–activity relationships that underpin the rational design of high-performance ORR electrocatalysts; hence, further theoretical investigations are both necessary and timely.
Accordingly, a series of MoS2-based electrocatalysts doped with various transition-metal (M@MoS2, M = metal) and non-metal elements (NM–M@MoS2, NM = non-metal) are constructed in this study to systematically investigate how different dopants modulate ORR catalytic performance. Based on the calculated overpotentials and the degree of lattice distortion in M@MoS2 before and after structural relaxation, the doped transition metals can be classified into three categories according to the number of outermost d-orbital electrons, i.e., d1–d3, d4–d6, and d7–d9. The enhanced ORR performance of M@MoS2 is primarily attributed to the upward shift of the sulfur p-band center, which optimizes the adsorption strength of ORR intermediates and lowers the associated reaction energy barriers, thereby improving the overall catalytic activity. However, the underlying mechanisms responsible for this shift vary across the different classes of dopants discussed above. For transition metals in the d1–d3 region, the sulfur p-band center (3p) is modulated by the dopant d-band electrons (3d, 4d, and 5d) through a d–p orbital hybridization effect. In contrast, doping elements with electronic configurations in the d7–d9 range induce significant structural distortion in M@MoS2. Therefore, the upshift of the p-band center is attributed to the Jahn–Teller effect. Under this circumstance, the degeneracy between the dxz/dyz and dx2−y2/dxy orbitals is lifted, leading to a rearrangement of the electronic configuration at the metal center to maintain structural stability. A reduced number of electrons are transferred to the sulfur atom, thereby lowering its electron occupancy and elevating the p-band center, which effectively activates the sulfur active site, as evidenced by a reduced overpotential in the range of 0.53–0.74 V. Building on these findings, five non-metal elements are selected for dual-doping to further improve the catalytic activity, e.g., C–, N–, O–, P–, and Se–M@MoS2. Among them, only the systems incorporating Se as the non-metal dopant displayed outstanding ORR activity, achieving overpotentials in the range of 0.41–0.50 V. In summary, this study presents a comprehensive theoretical framework for synergistically tuning the electronic structure of MoS2-based electrocatalysts through metal and non-metal co-doping, thereby providing new avenues for the rational design of highly selective and efficient ORR electrocatalysts.
2 Computational details
In this study, first-principles calculations were performed within the framework of density functional theory (DFT) using the Vienna Ab initio Simulation Package (VASP).31–33 The exchange–correlation interactions were described using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.34 The ion–electron interactions were conducted using the projector-augmented wave (PAW) approach, with a plane-wave energy cutoff of 450 eV.35,36 The exposed (001) facet of MoS2, which is of greater interest, was therefore selected as the focus of this investigation. A vacuum layer of 15 Å was introduced along the z-direction to effectively eliminate spurious interactions between periodic images. To evaluate the reliability of the computational methodology, comparative calculations were performed using 3 × 3 and 4 × 4 supercells, respectively, i.e., Co@MoS2, Ni@MoS2, and Cu@MoS2. As shown in Fig. S1 of the SI, only minor discrepancies in the overpotentials are observed between these results, i.e., 0.58 V (0.61 V), 0.53 V (0.53 V), and 0.65 V (0.67 V). Therefore, a 3 × 3 supercell was adopted for geometry optimization and static calculations to conserve computational resources.The Brillouin zone was sampled with a 3 × 3 × 1 k-point mesh for geometry optimizations and a 12 × 12 × 1 mesh for electronic structure computations. Notably, all atomic positions were fully relaxed without any spatial constraints. Spin-polarized calculations were employed, and long-range van der Waals interactions were incorporated using the DFT-D3 dispersion correction method within Grimme's scheme to improve computational accuracy.37,38 The convergence thresholds for atomic force and electronic energy were set to 0.01 eV Å−1 and 10−5 eV, respectively, during the structural optimization. Atomic charge analysis was conducted using the atom-in-molecule (AIM) approach as proposed by Bader.39 To enable a more detailed investigation of interatomic bonding interactions, Crystal Orbital Hamilton Population (COHP) analysis was carried out using the LOBSTER 5.0.0 package.40,41Ab initio molecular dynamic (AIMD) simulations were performed in the NVT ensemble at 500 K, with the system temperature controlled by the Nosé–Hoover thermostat.42 A time step of 1 fs was employed, and the simulation was conducted for 10 ps to evaluate the structural and dynamic stability. The VASPKIT code was utilized for post-processing the computational data obtained from VASP.43,44 Migration barriers were determined using the climbing-image nudged elastic band (CI-NEB) method.45 The O2 dissociation barrier was computed by constrained AIMD combined with the slow-growth protocol, employing a collective-variable increment of 4 × 10−4 Å.46,47 In addition, implicit solvent effects were evaluated for pristine MoS2 with VASPsol.48,49 As shown in Fig. S2, the ORR overpotential differs by only 0.09 V between vacuum and implicit solvent conditions, indicating a minimal solvent correction. Accordingly, unless otherwise noted, all remaining calculations were performed under vacuum conditions. The formation energy (Efor) quantifies the thermodynamic cost of incorporating dopants into the host lattices and serves as an indicator of system stability, which can be expressed as
| Efor = Etot − Esub − (EM + ENM) | (1) |
| Udiss = UΘdiss(metal,bulk) − Efor/eNe | (2) |
| O2 + * + H+ + e− → OOH* | (3) |
| OOH* + H+ + e− → O* + H2O(l) | (4) |
| O* + H+ + e− → OH* | (5) |
| OH* + H+ + e− → * + H2O(l) | (6) |
ΔGads = ΔE + ΔZPE − TΔS − neU − kbT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[H+] ln[H+] | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[H+] = −kbT
ln[H+] = −kbT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × pH, which represents the correction to the free energy of H+ due to its concentration, where kb is the Boltzmann constant. Notably, a zero voltage under the acidic condition is adopted in this work, i.e., U = 0 and pH = 0. The overpotential, i.e., η, which stands for the ORR activity can be defined as:
10 × pH, which represents the correction to the free energy of H+ due to its concentration, where kb is the Boltzmann constant. Notably, a zero voltage under the acidic condition is adopted in this work, i.e., U = 0 and pH = 0. The overpotential, i.e., η, which stands for the ORR activity can be defined as:| ΔGmin = min{ΔG1, ΔG2, ΔG3, ΔG4} | (8) |
| η = 1.23 − ΔGmin/e | (9) |
It is evident that a lower overpotential indicates a reduced energy barrier, underscoring the minimization of η as a crucial factor in the design of high-performance electrocatalysts. Based on eqn (8) and (9), it can be inferred that achieving the minimum η necessitates the Gibbs free energy of the four fundamental steps to be identical, specifically 1.23 eV.52
3 Results and discussion
3.1 Structural and thermodynamic stability
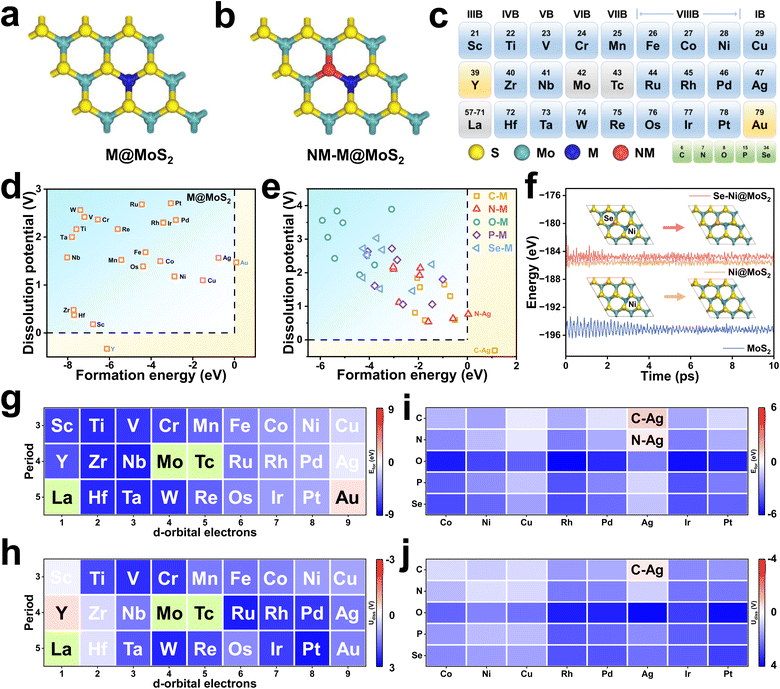
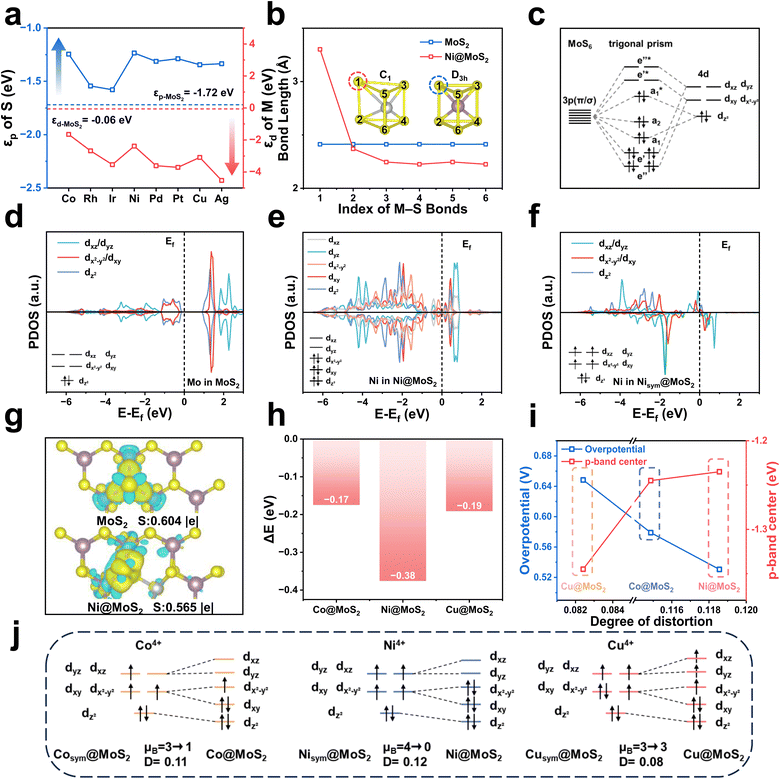
Fig. 1a and b depict schematic illustrations of M@MoS2 and NM–M@MoS2, where “M” and “NM” denote the doped metal and non-metal elements, respectively. To identify the preferred doping site of transition metals on MoS2, the formation energies of four representative configurations are calculated, e.g., Motop, Vstop, Ssub, and Mosub, as shown in Fig. S3. Ni@MoS2 is selected as a representative example, with the corresponding formation energies are 1.21, 1.73, 0.32, and −2.88 eV, respectively. Therefore, Mosub is identified as the most thermodynamically stable doping position, and subsequent investigations will focus on this configuration.29,53Fig. 1c presents a total of 24 dopants for MoS2, spanning the 3d, 4d, and 5d transition metal series, where technetium (Tc) and the lanthanides are excluded due to concerns regarding toxicity and radioactivity. To eliminate the influence of outermost orbitals, i.e., 4s, 5s, and 6s, the transition metals are classified by disregarding two valence electrons. Accordingly, “M” can be classified as d1 to d9, depending on the number of d-orbital electrons in their penultimate or outermost shell.Structural and thermodynamic stability are essential criteria for evaluating the viability of the constructed electrocatalysts, e.g., M@MoS2 and NM–M@MoS2. Consequently, their formation energies and the dissolution potentials are calculated and presented in Fig. 1d and e, respectively, with detailed values provided in Table S1. Fig. 1d and g show that the formation energies for single-atom doping are negative in all cases except Au@MoS2, i.e., Efor = 0.09 eV, indicating that most M@MoS2 structures are thermodynamically stable. In addition, Fig. 1h illustrates that all constructed M@MoS2 systems exhibit positive dissolution potential values, except for Y@MoS2, which presents a dissolution potential of −0.33 eV. Based on the aforementioned results, a total of 22 stable M@MoS2 electrocatalysts are selected for subsequent investigations, excluding Y@MoS2 and Au@MoS2. To quantify the degree of structural distortion, the stability is examined before and after geometry relaxation, with the distortion index (D) defined as follows:
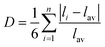 | (10) |
In view of the growing interest in leveraging diatomic synergistic effects to develop high-performance electrocatalysts, a portion of NM–M@MoS2 samples are investigated and the schematics are shown in Fig. S5. As the following results demonstrate that M@MoS2 doped with d7–d9 transition metals can exhibit superior ORR performance, thus are selected as the “M” component in NM–M@MoS2, i.e., M = Co, Ni, Cu, Rh, Pd, Ag, Ir, Pt, and Au. Five non-metal elements (NM = C, N, O, P, and Se) are chosen for co-doping, yielding a total of 40 NM–M@MoS2 electrocatalysts. Fig. S6 depicts the dual-doped configuration exhibit structural distortions comparable to those observed in the single-doped system, i.e., 0.12 (Ni@MoS2) and 0.13 (Se–Ni@MoS2). Consequently, the structural distortion of NM–M@MoS2 is primarily attributed to the transition metal dopants rather than the non-metal dopants. As shown in Fig. 1e, i and j, the calculated formation energies and the dissolution potentials of NM–M@MoS2 are presented. Except for C–Ag@MoS2 and N–Ag@MoS2, which exhibit the formation energies of 1.12 and 0.04 eV, respectively, the remaining 38 configurations demonstrate satisfactory stability and are suitable for analysis. To further assess the kinetic stability, dopant migration barriers at the Mo sites were calculated for Ti@MoS2, Cr@MoS2, and Ni@MoS2. As shown in Fig. S7, the barriers are 11.12, 10.36, and 4.62 eV for Ti, Cr, and Ni, respectively, indicating strong dopant–lattice interactions and thus negligible diffusion. In addition, AIMD simulations were carried out to monitor their structural evolution over time. Fig. 1f shows that the total energies remain stable throughout the 10 ps simulation, and only negligible structural deformation can be observed. Se–Ni@MoS2 and Ni@MoS2 exhibit higher total energies compared to pristine MoS2, i.e., −184.79, −185.54, and −195.16 eV, further indicating that the introduction of dopants disrupts the structure. Such lattice destabilization can reduce reaction barriers and enhance catalytic activity, similar to the effects observed in amorphous structures, thereby highlighting the potential of these doped configurations as efficient ORR electrocatalysts.
3.2 Mechanism of the ORR activity
To further address potential ambiguities in the identification of active sites, ORR free energy profiles were calculated for both edge Mo and edge S sites on the MoS2 (100) surface, as shown in Fig. S11a and c. The results indicate that the ORR overpotential at the edge Mo site is 2.87 V, substantially higher than that at the S site on the (001) surface, i.e., 1.93 V. Fig. S11b and d reveal that the edge Mo site binds ORR intermediates much more strongly than the surface S site; for instance, the adsorption free energy of *OH is approximately 1.94 eV at the S site on the (001) surface but around −2.13 eV on the Mo-edge site. In contrast, the ORR overpotential at the edge S site is only 0.78 V, suggesting that edge S sites are more likely to function as the actual highly active catalytic centers. However, previous studies have demonstrated that MoS2 edges exhibit poor chemical stability and are prone to oxidation and corrosion under electrochemical conditions,58 which undermines the practical viability of edge S sites as stable catalytic centers. Accordingly, S sites on the (001) surface are selected as the active centers for systematic investigation, both to elucidate the impact of electronic-structure modulation and to reflect realistic operational constraints.59,60
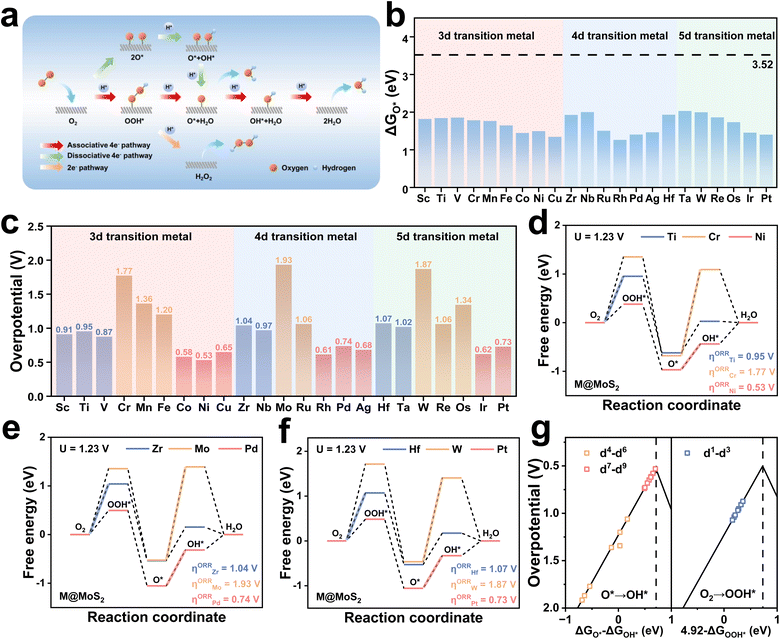
Fig. 2a illustrates three possible pathways may occur during the ORR. According to previous studies,61 the dissociation activation barrier of O2 on MoS2-based electrocatalysts is approximately 1.59 eV, rendering the dissociative pathway kinetically unfavorable. In view of the fact that doping and lattice distortion may significantly influence the O2 dissociation pathway, the energy barrier was further evaluated for a representative system in the d7–d9 region, i.e., Ni@MoS2. Constrained AIMD combined with a slow-growth scheme was employed to probe O2 dissociation, with the O–O bond length serving as the collective variable for direct evaluation of the finite-temperature free-energy barrier (ΔEfree). As shown in Fig. S12, the O2 dissociation barrier on Ni@MoS2 is 0.62 eV, substantially lower than that on pristine MoS2i.e., 3.10 eV, indicating that lattice distortion indeed facilitates O–O bond cleavage. Nevertheless, it is noteworthy that O–O bond cleavage with an activation barrier exceeding 0.6 eV is kinetically hindered at practical electrode potentials.62 Under realistic conditions, Ni@MoS2 is expected to favor the associative pathway as the dominant ORR mechanism rather than the dissociative pathway.
To initiate the ORR process, O2 should first be adsorbed onto the catalyst surface. Fig. S13 presents the calculated adsorption energies of O2 on the surfaces of M@MoS2, which range from −0.28 to −0.06 eV. Experimental evidence suggests that the adsorption of O2 proceeds via a two-step process: an initial reduction of O2 to OOH− in the outer Helmholtz plane, followed by the adsorption of OOH− onto the electrocatalyst surface to form OOH*.63 Although the activation barrier for the O2 → OOH− conversion is relatively low, the ORR is not significantly affected by the weak O2 adsorption energy. After OOH* adsorbs on the surface of M@MoS2, two competing routes may proceed: (i) a four-electron pathway that generates water, i.e., OOH* + H+ + e− → O* + H2O, or (ii) a two-electron pathway that yields hydrogen peroxide, i.e., OOH* + H+ + e− → H2O2. As shown in Fig. S14, it is widely acknowledged that when ΔGO* is below 3.52 eV, the electrocatalyst exhibits strong O* adsorption capability, thereby facilitating the associative four-electron ORR pathway for H2O production.64 On this basis, Fig. 2b presents the Gibbs free energy of O*, showing that all M@MoS2 systems exhibit values below 3.52 eV. Therefore, the associative four-electron pathway is thermodynamically favored and will therefore serve as the primary focus of the main text.
Fig. 2c and e show that the calculated ORR overpotential of MoS2 is 1.93 V, and the potential-determining step (PDS) is the protonation of O* to OH*. Compared with MoS2, transition-metal doping enhances the catalytic activity of M@MoS2 to varying extents, with the overpotentials ranging from 0.53 to 1.87 eV. Moreover, the overpotential initially increases with the rising d-electron count and subsequently decreases, exhibiting a periodic trend across the different main groups. Taking the 3d transition metals as examples, e.g., Sc, Ti, V, Cr, Mn, Fe, Co, Ni, and Cu, the corresponding overpotentials are 0.91, 0.95, 0.87, 1.77, 1.36, 1.20, 0.58, 0.53, and 0.65 V, respectively. Based on these findings, the dopants can be roughly categorized into three categories according to their d-electron count, i.e., d1–d3, d4–d6, and d7–d9. For transition metals with electronic configurations in the d7–d9 range, the corresponding M@MoS2 exhibits superior activity compared to other dopants. The overpotentials follow the order: Ni (0.53 V) < Co (0.58 V) < Rh (0.61 V) < Ir (0.62 V) < Cu (0.65 V) < Ag (0.68 V) < Pt (0.73 V) < Pd (0.74 V). In contrast, doping with transition metals in the d1–d3 range results in moderate enhancement relative to MoS2, with the overpotential remaining around 1 V. The introduction of d4–d6 metals offers limited improvement, as most M@MoS2 exhibit overpotentials exceeding 1.2 V. In addition, Fig. 2c and Table S2 reveal an intriguing phenomenon that doping with Cr (3d4) or W (5d4), metals whose outermost d-orbital electronic configurations closely resemble that of Mo (4d4), yields overpotentials for Cr@MoS2 and W@MoS2 that are comparable to MoS2, with values of 1.77, 1.87, and 1.93 V, respectively. Fig. 2d to f display the free-energy diagrams of representative electrocatalysts from the three activity regions, including Ti (3d2), Cr (3d4), Ni (3d8), Zr (4d2), Mo (4d4), Pd (4d8), Hf (5d2), W (5d4), and Pt (5d8). The overpotential of M@MoS2 initially increases and then decreases, with the corresponding values are 0.95 (Ti), 1.77 (Zr), and 0.53 V (Ni), in the case of 3d transition metal dopants. A similar trend is also observed in the 4d (Zr, Mo, and Pd) and 5d (Hf, W, and Pt) transition metal series, and the free-energy diagrams for the remaining electrocatalysts are provided in Fig. S15.
Fig. 2g illustrates the overpotential volcano plot encompassing all M@MoS2, aiming to identify the factor governing catalytic activity. It is evident that for transition metals with d4–d9 configurations, the PDS corresponds to ΔG3 (O* → OH*), whereas ΔG1 (O2 → OOH*) is identified as the PDS for those in the d1–d3 region. In addition, M@MoS2 doped with d7–d9 metals cluster to the left of the vertex, indicating strong OH* adsorption, whereas those doped with d4–d6 transition metals lie farther from the vertex, suggesting weaker OH* adsorption.65 For M@MoS2 doped with d1–d3 transition metals, moderate OH* adsorption is observed relative to the other two groups, and the PDS is identified as OOH* adsorption. These findings underscore the critical role of OH* adsorption in dictating the catalytic performance of M@MoS2-based electrocatalysts. Accordingly, the subsequent discussion adopts OH* as the primary descriptor, providing a unified framework for interpreting adsorption trends across various metal dopants.
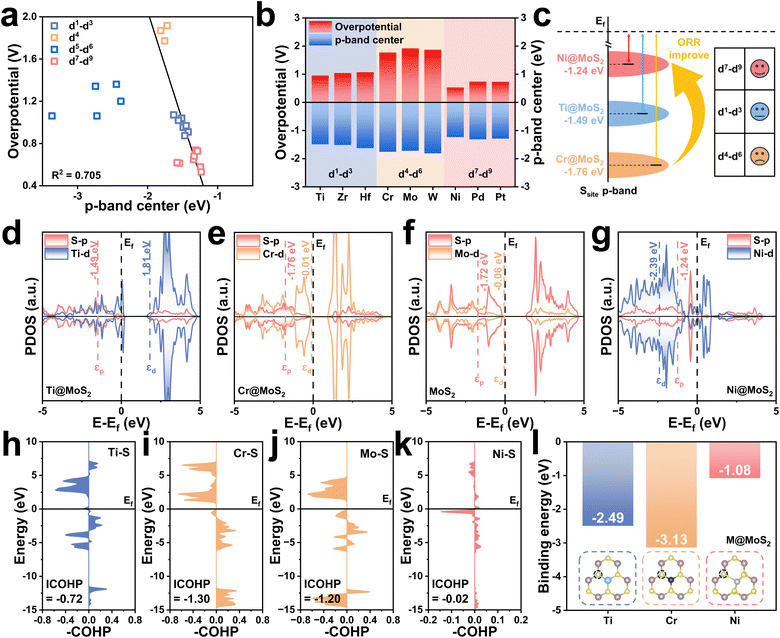
Ti@MoS2, Cr@MoS2, and Ni@MoS2, which belong to the same period and represent the d1–d3, d4–d6, and d7–d9 categories, respectively, are selected for detailed investigation. As shown in Fig. S4, Ti@MoS2 and Cr@MoS2 exhibit no structural distortions upon doping, indicating that the observed activity differences are attributed primarily to variations in εp. To elucidate the influence of electronic configuration on catalytic activity and modulation of the p-band center, Fig. 3d to g present the PDOS of Ti@MoS2, Cr@MoS2, MoS2 and Ni@MoS2. For Ti@MoS2, the p-band center of the active S-atom and the d-band center of the dopant Ti-atom are −1.49 and 1.81 eV, respectively, whereas for Cr@MoS2 these values shift to −1.76 and −0.01 eV. By comparison, pristine MoS2 exhibits corresponding values of −1.72 and −0.06 eV, while in Ni@MoS2, the p- and d-band centers are positioned at −1.24 and −2.39 eV, respectively. Additionally, the PDOS reveals that the overlapping region between Cr and S locates at a lower energy compared to that between Ti and S, indicative of a stronger Cr–S bond. This is corroborated by the ICOHP values for the Ti–S, Cr–S, Mo–S, and Ni–S bonds presented in Fig. 3h–k, e.g., −0.72, −1.30, −1.20, and −0.02. Fig. 3l further shows that the binding energies of the S-atom adjacent to the dopant are −2.49, −3.13, and −1.08 eV, respectively. These findings collectively suggest that d electrons of the M-atom transfer to the neighboring S-atom, thereby modulating its p-band center, which can be referred to as the d–p orbital hybridization effect. Specifically, Cr and Mo possess identical outermost d-orbital electronic configurations, and their corresponding εd values are closely aligned, i.e., −0.01 and −0.06. This suggests that the degree of d–p orbital hybridization, and consequently its effect on the p-band center, should be comparable in Cr@MoS2 and pristine MoS2. Consistent with this expectation, the corresponding values of εp for these two electrocatalysts are nearly identical, i.e., −1.76 and −1.72 eV. Due to the much higher εd of Ti compared with Cr, i.e., 1.81 and −0.01 eV, the εp of the active S atom in Ti@MoS2 shifts upward significantly under strong d–p hybridization. In contrast, Ni@MoS2 doping induces pronounced structural distortion, which weakens the Ni–S bond interaction, i.e., ICOHP = −0.02. Therefore, the upward shift of εp in Ni@MoS2 is more reasonably ascribed to distortion effects rather than d–p hybridization.68
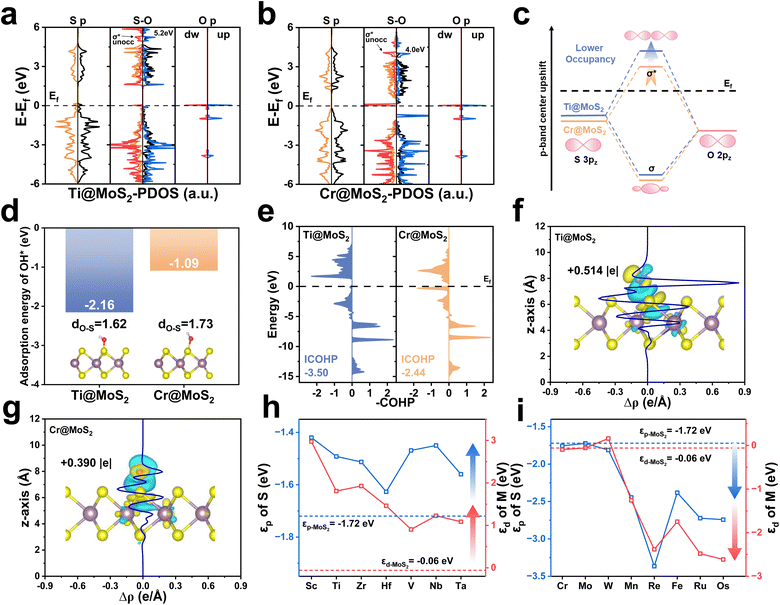
Fig. 4a and b present the PDOS for OH* adsorption on Ti@MoS2 and Cr@MoS2, respectively. The left and right panels display the active S-atom and the O-atom of OH*, respectively, both of which are in their isolated states, and the selected atoms are shown in Fig. S16. It reveals that the O 2p orbitals partially overlaps with the S 3p orbitals, indicating the bonding of S–O. The corresponding PDOS of the two systems during S–O interaction is presented in the center, with spin-up and spin-down states distinguished by different colors. Fig. 4c presents a molecular-orbital schematic illustrating the interaction between O and S atoms upon OH* adsorption, which results in the formation of σ bonding (O 2p–S 3p) and σ* (O 2p–S 3p) antibonding orbitals, respectively. Due to the aforementioned d–p hybridization effect, Ti doping elevates the energy level of the S 3p orbitals, resulting in an upward shift of the p-band center in Ti@MoS2 relative to Cr@MoS2. The resulting σ* antibonding orbital is also elevated, accompanied by a decrease in the occupation of the O–H σ* orbital, forming a more robust S–O bond, which implies an increase in the adsorption of OH*. As shown in Fig. 4d, the adsorption energy of OH* on Ti@MoS2 (−2.16 eV) is substantially more negative than that on Cr@MoS2 (−1.09 eV), indicating stronger adsorption. Correspondingly, the S–O bond lengths are shortened to 1.62 and 1.73 Å, respectively, further indicating that OH* binding on Ti@MoS2 is more thermodynamically favorable. In addition, Fig. 4e demonstrates that the ICOHP value of the S–O bond in Ti@MoS2 is −3.50, lower than the value of −2.44 in Cr@MoS2, validating the aforementioned analysis. As shown in Fig. 4f and g, the Bader charge and the plane-averaged charge density difference reveal the charge transfer characteristics of M@MoS2 toward the adsorbed OH*, providing insights into the charge distribution. Regarding Ti@MoS2, the O-atom of OH* accepts 0.514 |e|, which is significantly higher than 0.390 |e| observed in Cr@MoS2. This enhancement is attributed to the upward shift of the σ* antibonding orbitals associated with OH* adsorption induced by Ti doping, which reduces its electronic occupancy and thereby strengthens the S–O bond.
The preceding discussion demonstrates that the improved ORR performance of M@MoS2, particularly for dopants with d1–d3 configurations, arises from modulation of the p-band center through the d–p hybridization effect, i.e., M (3d, 4d or 5d)–S (3p). Fig. 4h and i summarize the εd values of all d1–d6 dopants and the εp values of their corresponding active sites to illustrate the d–p hybridization effect. It can be seen that the similar trends of the εd and εp curves underscore a clear linear correlation, highlighting the pronounced influence of the d–p hybridization effect. As shown in Fig. 4h, the εd values of these transition metals are higher than that of Mo when the dopants are located in d1–d3, and the resulting d–p hybridization leads to an upward shift in the p-band centers of the active sites upon doping. Fig. 4i depicts that d4–d6 transition metals exhibit the εd values comparable to or even lower than that of Mo. As a result, the d–p hybridization effect yields εp that are also comparable to or lower than that of Mo. Nevertheless, the electrocatalytic activities of Fe@MoS2, Ru@MoS2, and Os@MoS2 are superior to that of MoS2, despite their lower p-band centers. These results appear to contradict the aforementioned conclusion that εp closer to the Fermi level can improve the catalytic activity. This phenomenon is attributable to the structural distortion introduced by d4–d6 dopants in M@MoS2. For transition metals with electronic configurations ranging from d1–d3, the relaxed M@MoS2 structures exhibit no significant structural distortion. Accordingly, the p-band center in these systems is modulated solely by the d–p interaction, accounting for the observed enhancement in catalytic performance. By contrast, with d4–d6 and d7–d9 configurations, both the d–p hybridization effect and the lattice distortion should be considered, as the latter can introduce additional complexity and new mechanism. Hence, the d–p hybridization effect alone cannot explain the behavior across all M@MoS2 cases.
To elucidate this effect, MoS2 and Ni@MoS2 are discussed in Fig. 5b, revealing significant differences in their geometric configurations. All Mo–S bond lengths in MoS2 are approximately 2.4 Å, indicating that Mo atoms are situated in a regular trigonal prismatic coordination environment with D3h symmetry. Consequently, MoS2 exhibits a high degree of d-orbital degeneracy, with notable overlap between the dxz/dyz and dxy/dx2−y2 orbitals,23 as shown in Fig. 5d. With the introduction of Ni-atom, Ni@MoS2 exhibits a distinctly coordination environment with C1 symmetry, with one bond significantly elongated to 3.3 Å and the remaining bonds shortened to 2.2–2.3 Å. Fig. 5e depicts a pronounced splitting of the d orbitals in Ni@MoS2, including dxz, dyz, dxy, dx2−y2, dz2. To further confirm that the orbital splitting arises from lattice distortion rather than differences in the metal center, i.e., Mo and Ni. Nisym@MoS2 with D3h symmetric and no lattice distortion has been constructed as a comparative reference. Fig. 5f shows that, even for the Ni atom, the same orbital degeneracies observed in MoS2 are retained, specifically dxz/dyz and dxy/dx2−y2. These results demonstrate that the disruption of orbital degeneracy is not dependent on the dopant element but is closely associated with the coordination environment. This phenomenon, known as the Jahn–Teller effect, induces orbital energy level splitting and modulates the electronic configuration, thereby playing a critical role in governing ORR performance. Further calculations on MoS2 and Ni@MoS2 are presented to verify the role of the Jahn–Teller effect in modulating the electronic configuration. Fig. S18 illustrates that the ICOHP value of the M–S bond increases from −1.20 to −0.02, indicating a substantial weakening of the bonding interaction due to the Jahn–Teller effect. Additionally, the S-atom receives 0.604 |e| from the metal center, which decreases to 0.565 |e| in Ni@MoS2, indicating reduced electron transfer upon Ni doping, as shown in Fig. 5g. The reduced charge transfer lowers the electron occupancy of the S-atom 3p orbitals, thereby elevating the 3p-band center and strengthening the S–OH* coupling. To validate this conclusion, Fig. S19 shows that the electron transfer from the S-atom to OH* are 0.340 |e| and 0.444 |e| for the Ni-doped and undoped cases, respectively. These results not only demonstrate that the electronic structure of the S-atom is closely associated with the Jahn–Teller effect, but also provide direct evidence of an intrinsic correlation between the p-band center and enhanced adsorption capacity.
To deepen the understanding, a detailed molecular-orbital analysis is subsequently performed to elucidate how the Jahn–Teller effect modulates the electronic configuration of the active center. Fig. 5c depicts the molecular orbitals of the MoS6 cluster, comprising a series of bonding, antibonding, and non-bonding orbitals.69 From the perspective of classical chemistry theory, the valence state of Mo is designated as +4, thus Mo4+ is adopted for the electronic structure analysis. According to the reference, the six S atoms contribute twelve lone pairs that occupy the low-energy bonding orbitals, i.e., e″, e′, and a1, as well as the non-bonding orbital, i.e., a2. The remaining high-energy antibonding orbitals are governed chiefly by the d-electrons of Mo, i.e., d2, with two d electrons occupying the  antibonding orbital.70 The metal center in the cluster will be substituted with various transition metal dopants, e.g., M@MoS2. When the number of d-orbital electrons is low, i.e., d1–d3, fewer electrons occupy the
antibonding orbital.70 The metal center in the cluster will be substituted with various transition metal dopants, e.g., M@MoS2. When the number of d-orbital electrons is low, i.e., d1–d3, fewer electrons occupy the  antibonding orbital, resulting in a relatively stable MS6 cluster that retains the original trigonal prismatic coordination structure. As the d-electron count increases to d5 and d6, electrons begin to occupy the higher-energy e′* antibonding orbitals, destabilizing the system and inducing slight distortions in the coordination environment. With a further increases to d7–d9, electrons may occupy the highest-energy e″* antibonding orbital, rendering in pronounced instability, as shown in Fig. S4. At this stage, the Jahn–Teller effect reduces orbital degeneracy through structural distortion, thereby lowering the total energy and enhancing structural stability. Fig. 5h illustrates that the total energy of Nisym@MoS2 is significantly higher than that of Ni@MoS2, i.e., −190.81 and −191.19 eV, corresponding to a difference of −0.38 eV. To further validate this trend, the energy differences between undistorted and distorted configurations are calculated for Co (Cosym@MoS2/Co@MoS2) and Cu (Cusym@MoS2/Cu@MoS2) transition metal dopants, yielding values of −0.17 and −0.19 eV, respectively. It can be seen that the distorted structures consistently display lower energies, indicating that structural distortion is thermodynamically favorable and contributes to system stabilization. To validate the change in orbital degeneracy, the magnetic moments of Co, Ni, and Cu in Msym@MoS2 are calculated to analyze their electron configurations. As shown in Fig. 5j, µB = 3, 4, and 3 for the corresponding Msym@MoS2 systems, in which the cluster retains a regular trigonal prismatic coordination environment. Moreover, the degenerate orbitals can be clearly observed, i.e., dxz/dyz and dxy/dx2−y2. Under the realistic conditions, accounting for the Jahn–Teller effect, the magnetic moments of M@MoS2 decrease to 1, 0, and 3, respectively. Consequently, the orbital degeneracy is lifted, and the electronic configuration adjusts to preserve structural stability. The relationships among structural distortion, the p-band center, and catalytic performance have been investigated, as shown in Fig. 5i. As structural distortion increases, from Cu@MoS2 to Co@MoS2 and finally to Ni@MoS2, the p-band center of the S-atom progressively shifts upward toward the Fermi level. This modulation enhances the adsorption capacity of the active site for ORR intermediates, thereby effectively promoting catalytic performance.
antibonding orbital, resulting in a relatively stable MS6 cluster that retains the original trigonal prismatic coordination structure. As the d-electron count increases to d5 and d6, electrons begin to occupy the higher-energy e′* antibonding orbitals, destabilizing the system and inducing slight distortions in the coordination environment. With a further increases to d7–d9, electrons may occupy the highest-energy e″* antibonding orbital, rendering in pronounced instability, as shown in Fig. S4. At this stage, the Jahn–Teller effect reduces orbital degeneracy through structural distortion, thereby lowering the total energy and enhancing structural stability. Fig. 5h illustrates that the total energy of Nisym@MoS2 is significantly higher than that of Ni@MoS2, i.e., −190.81 and −191.19 eV, corresponding to a difference of −0.38 eV. To further validate this trend, the energy differences between undistorted and distorted configurations are calculated for Co (Cosym@MoS2/Co@MoS2) and Cu (Cusym@MoS2/Cu@MoS2) transition metal dopants, yielding values of −0.17 and −0.19 eV, respectively. It can be seen that the distorted structures consistently display lower energies, indicating that structural distortion is thermodynamically favorable and contributes to system stabilization. To validate the change in orbital degeneracy, the magnetic moments of Co, Ni, and Cu in Msym@MoS2 are calculated to analyze their electron configurations. As shown in Fig. 5j, µB = 3, 4, and 3 for the corresponding Msym@MoS2 systems, in which the cluster retains a regular trigonal prismatic coordination environment. Moreover, the degenerate orbitals can be clearly observed, i.e., dxz/dyz and dxy/dx2−y2. Under the realistic conditions, accounting for the Jahn–Teller effect, the magnetic moments of M@MoS2 decrease to 1, 0, and 3, respectively. Consequently, the orbital degeneracy is lifted, and the electronic configuration adjusts to preserve structural stability. The relationships among structural distortion, the p-band center, and catalytic performance have been investigated, as shown in Fig. 5i. As structural distortion increases, from Cu@MoS2 to Co@MoS2 and finally to Ni@MoS2, the p-band center of the S-atom progressively shifts upward toward the Fermi level. This modulation enhances the adsorption capacity of the active site for ORR intermediates, thereby effectively promoting catalytic performance.
To verify the generality of conclusions, the analysis was expanded from 3d dopants, e.g., Cu, Co, and Ni, to representative 4d and 5d dopants, e.g., Pd, Rh, Ag, Pt, and Ir. As shown in Fig. S20a and b, increasing lattice distortion leads to a pronounced upward shift of εp, accompanied by a significant decrease in η. This trend is preserved across elements from the 3d, 4d, and 5d series, thereby confirming the generality of the correlation between Jahn–Teller distortion, electronic structure, and catalytic activity. It is worth noting that a few outliers may arise from the omission of explicit relativistic effects (spin–orbit coupling) for the 4d and 5d elements;71,72 however, these deviations do not alter the overall trend or the main conclusions. In addition, the edge S site of the MoS2 (100) surface was carried out for a comparative analysis under an identical computational framework and convergence criteria. Within the edge environment, Fig. S21a and b depict the ORR activity and p-band center after doping. The results show that, for the MoS2 (100) edge systems, the overpotential remains strongly correlated with the p-band center (R2 = 0.89), consistent with the trend established for the (001) surface. The specific values of edge S sites are ηMoS2 = 0.78 V (εp = −1.37 eV), ηNi@MoS2 = 1.04 V (εp = −2.20 eV), and ηTi@MoS2 = 1.60 V (εp = −2.73 eV), respectively. In contrast to the doped systems, the pristine MoS2 edge S site exhibits superior ORR performance, indicating that introducing dopants at the MoS2 (100) edge may suppress rather than enhance the catalytic activity. As shown in Fig. S21c and d, no appreciable d–p hybridization is observed at the edge S sites of Ti@MoS2. Regarding the edge S sites in Ni@MoS2, although a Jahn–Teller distortion occurs, it does not lead to any enhancement in activity. These results demonstrate that the p-band center activity descriptor established for the (001) surface remains valid at the edge; however, the specific promotion mechanisms identified for the (001) surface cannot be directly transferred to the MoS2 (100) edge.
In summary, unlike d1–d3 transition-metal dopants, d7–d9 dopants can trigger the Jahn–Teller effect, thereby inducing structural distortion. Moreover, the Jahn–Teller effect produces synergistic consequences, rearranging the orbital energy levels of the dopants and redistributing charge between M–S, that collectively drive a pronounced upward shift of the p-band center of the active S-atom, thereby enhancing its electronic coupling with and adsorption of ORR intermediates. This mechanism not only reveals the deep physical origin of the improved catalytic performance of Ni@MoS2, but also provides theoretical support for the construction of transition metal regulation strategies. Fig. S22 further presents the PDOS of nine transition-metal dopants, i.e. Sc to Cu. Except for the d4 system, all dopants convert MoS2 from a semiconductor to a metal, imparting pronounced conductivity. This electronic-structure transformation is expected to enhance electron-transfer efficiency during electrocatalysis, thereby promoting the ORR.
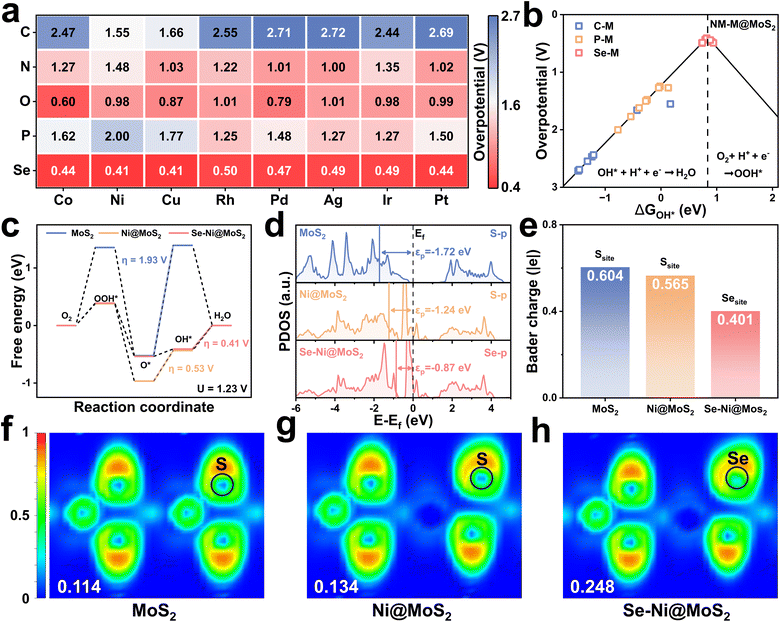
3.3 ORR performance with diatomic doping
As demonstrated in Fig. 2c, M@MoS2 doped with transition metals possessing d7–d9 electronic configurations exhibit superior ORR performance. Consequently, five non-metal elements, i.e., NM = C, N, O, P, and Se, located near sulfur in the periodic table, are selected for diatomic doping with the aim of further enhancing the catalytic activity. Fig. 6a presents the calculated overpotentials of 40 NM–M@MoS2 in the form of a heat map. The results indicate that only dual-doped systems incorporating Se as the non-metal dopant exhibit outstanding ORR catalytic activity. Specifically, the overpotentials are ranked as follows: Se–Ni@MoS2 (0.41 V) = Se–Cu@MoS2 (0.41 V) < Se–Co@MoS2 (0.44 V) = Se–Pt@MoS2 (0.44 V) < Se–Pd@MoS2 (0.47 V) < Se–Ir@MoS2 (0.49 V) = Se–Ag@MoS2 (0.49 V) < Se–Rh@MoS2 (0.50 V). In contrast, NM–M@MoS2 incorporating other non-metal elements, such as C, N, O, and P, exhibit comparatively lower catalytic activity. Among these, C–M@MoS2 exhibits the largest overpotential, i.e., η > 1.6 V, primarily due to its excessively strong adsorption capacity, which signifies substantial reaction barriers during the catalytic process. As shown in Fig. S23, in the case of O–M@MoS2, most O* and OOH* adsorption configurations are unstable, indicating structural instability and disqualifying these systems as viable electrocatalyst candidates.Table S2 indicates that the PDS is primarily ΔG4 for NM–M@MoS2 with C, P, and Se as non-metal dopants. Consequently, Fig. 6b depicts the volcano plot of NM–M@MoS2 (NM = C, P, and Se), elucidating the trends in their catalytic activity. It is evident that the Se–metal dual-doped structures exhibit the highest catalytic performance, with Se–Ni and Se–Cu doped MoS2 achieving overpotentials of 0.41 V, positioning them near the volcano apex. In contrast, the C–metal and P–metal doped systems exhibit significantly higher overpotentials, indicating that their catalytic activities are constrained by the excessively strong adsorption of OH*. Additionally, the volcano plot of the O–metal and N–metal doped electrocatalysts is presented in Fig. S24 due to their distinct PDS. To elucidate the electronic and structural role of Se in nonmetal co-doping, PDOS, ICOHP and charge density difference analyses for the representative Se–Ni@MoS2 and O–Ni@MoS2 were shown in Fig. S25. The p-band center of Se–Ni@MoS2 is εp = −0.87 eV, whereas that of O–Ni@MoS2 is εp = −3.07 eV. A higher εp supports more moderate adsorption of OOH*/OH*, whereas an overly negative εp corresponds to excessively weak adsorption, thereby accounting for the inferior activity of the O co-doped system. The Ni–O bond is markedly stronger than the Ni–Se bond, i.e., ICOHP = −0.49 vs. −0.02, indicating that the stronger Ni–O interaction is accompanied by more substantial electron transfer and occupation rearrangement. In contrast, the weaker Ni–Se interaction preserves a higher p-band center and optimal adsorption strengths, consistent with the lower overpotential of Se–Ni@MoS2. These results indicate that Se co-doping primarily serves to maintain an elevated p-band center and near-optimal adsorption of oxygenated intermediates, whereas O co-doping induces an excessive downward shift of the p-band center that suppresses ORR activity.
To further investigate the impact of diatomic doping on catalytic activity, MoS2, Ni@MoS2, and Se–Ni@MoS2 are selected as representative models for detailed analysis. The corresponding free energy diagrams and the p-band centers are presented in Fig. 6c and d, respectively. The results indicate that dopants induce a progressive upward shift in the p-band center of the catalyst, i.e., εp = −1.72, −1.24, and −0.87 eV, thereby enhancing its catalytic activity as reflected by the corresponding overpotentials of, i.e., η = 1.93, 0.53, and 0.41 V. Fig. 6e and S26 illustrate the calculated Bader charge analysis and the charge density difference, and in pristine MoS2, the Mo atom transfers 0.604 |e| to the adjacent S-atom. For comparison, the Ni-atom transfers 0.565 |e| to the active S-atom in Ni@MoS2, whereas in Se–Ni@MoS2, the electron transfer from Ni to Se decreases to 0.401 |e|. Notably, the reduced electron transfer in Se–Ni@MoS2 relative to Ni@MoS2 leads to an upward shift of the p-band center. As shown in Fig. 6f to h, the electron localization functions (ELF) of the corresponding electrocatalysts are calculated to further validate these findings. The results reveal a progressive increase in ELF values at the active sites upon Ni and Se–Ni doping, rising from 0.114 to 0.134 and 0.248, respectively. This trend indicates enhanced electron localization around the active sites and a corresponding reduction in electron transfer to the surrounding atoms, consistent with the Bader charge analysis.73
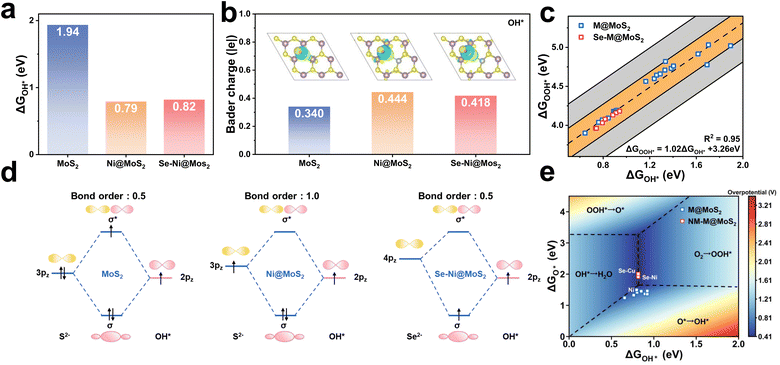
As presented in Fig. 7a, the adsorption energies of OH* and MoS2, Ni@MoS2 and Se–Ni@MoS2 are 1.94, 0.79, and 0.82 eV, respectively. Combined with Fig. 6d, although the p-band center of Se is close to the Fermi level, which enhances the catalytic performance, it also weakens the adsorption of OH*. It is worth noting that these results seem to be contrary to the previous discussion. Therefore, the electronic structures of OH* on the electrocatalysts are further analyzed, and the corresponding charge transfer between the active site and OH* is presented in Fig. 7b. Following Se doping, the adsorption capacity of the active site for OH* decreases, as evidenced by a reduction in the Bader charge from 0.444 |e| to 0.418 |e|. Fig. 7d illustrates the energy level diagram formed by the p orbitals of the active site and the OH* intermediate, e.g., σ (S 3p–2p OH*), σ* (S 3p–2p OH*), σ (Se 4p–2p OH*), σ* (Se 4p–2p OH*). The bond order b is calculated to deepen the understanding and is expressed as follows
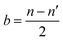 | (11) |
Fig. 7c illustrates the relationship between ΔGOH* and ΔGOOH* of the constructed active centers. Notably, Cr@MoS2 and W@MoS2 are excluded due to their poor adsorption of intermediates. The Gibbs free energies of adsorbed OH* and OOH* follow a linear relationship, expressed as ΔGOOH* = 1.02 ΔGOH* + 3.26 eV, with a coefficient of determination R2 = 0.95, as shown by the black dashed line. In addition, the orange and gray shaded regions represent deviations from the fitted black line, with values of ±0.2 eV and ±0.5 eV, respectively. All active sites are fall within the yellow shaded region, indicating that the derived equation is reasonable and consistent with the catalyst model. Based on the relationship, the Gibbs free energy for ORR can be expressed by eqn (12)–(15):
| ΔG1 = 4.92 − (1.02ΔGOH* + 3.26) | (12) |
| ΔG2 = (1.02ΔGOH* + 3.26) − ΔGO* | (13) |
| ΔG3 = ΔGO* − ΔGOH* | (14) |
| ΔG4 = ΔGOH* | (15) |
Consequently, the ORR performance can be evaluated with two descriptors, i.e., ΔGO* and ΔGOH*. To further screen the potential catalysts in various models, Fig. 7e further presents a two-dimensional volcano plot, which utilizes these independent descriptors. This methodology has been validated in numerous prior studies as effective predictors of the theoretical minimum overpotential for specific electrocatalytic models. As indicated by the black solid lines, the contour plot is divided into four distinct regions, each corresponding to a different PDS in the ORR process, i.e., PDS1, PDS2, PDS3, and PDS4. It reveals that for MoS2 doped with d7–d9 transition metals, the predominant PDS is the ΔG3 step. In contrast, for Se–Ni@MoS2 and Se–Cu@MoS2, the primary PDS shifts to the ΔG4 step. The minimum theoretical overpotential can be derived from the condition ΔG1 = ΔG4 in the 2D volcano plot, which is 0.41 V.52 In conclusion, Se–Ni@MoS2 and Se–Cu@MoS2 exhibit the lowest overpotentials among the investigated systems, highlighting their superior catalytic activity. These findings underscore the significant potential of MoS2 as an ORR electrocatalyst.
4 Conclusions
The incorporation of specific heteroatoms enables precise regulation of the electronic structure and active sites of MoS2, thereby markedly enhancing its ORR catalytic performance. Nevertheless, the broad diversity of dopants has led to conflicting interpretations of the underlying mechanisms, leaving a significant knowledge gap in elucidating the structure–activity relationships that are critical for the rational design of high-performance MoS2-based ORR electrocatalysts. Accordingly, a total of 64 MoS2-based electrocatalysts, comprising transition metals from the 3d, 4d, and 5d series, together with selected non-metal dopants, are systematically examined to elucidate the underlying modulation mechanisms. This theoretical study demonstrates that the doped transition metals are classified into three categories according to their outermost d-electron count based on the calculated overpotentials and lattice distortions, i.e., d1–d3, d4–d6, and d7–d9. In addition, the upward shift of the p-band center constitutes the critical factor underpinning the enhanced ORR electrocatalytic activity of MoS2; however, the underlying causes of this shift vary across different systems. For d1–d3, no structural distortion is observed, and the elevated sulfur p-band center is solely attributed to the d–p hybridization effect induced by metal doping. This upward shift in the p-band center leads to a reduction in ORR overpotential compared to pristine MoS2, with values ranging approximately from 0.87 to 1.07 V. In contrast, d7–d9 dopants induce the Jahn–Teller effect, breaking the orbital degeneracy between dxz/dyz and dx2−y2/dxy, and leading to lattice distortion. The electron rearrangement at the metal center reduces charge transfer, thereby lowering the electron occupancy of the sulfur atom, upshifting its p-band center, and enhancing ORR performance by decreasing the overpotential to 0.53–0.74 V. Building on this, dual doping of NM–M@MoS2 with non-metal atoms is further explored, revealing that the incorporation of Se atoms yields the most significant reduction in overpotential, decreasing that of Se–Ni@MoS2 to 0.41 V. In summary, the enhancement mechanisms of MoS2 through substitutional doping can be broadly categorized into two types: d–p hybridization and the Jahn–Teller effect. These findings provide new theoretical insights for guiding the rational design of highly efficient MoS2-based ORR electrocatalysts. Furthermore, by bridging atomic-scale electronic structure modulation with macroscopic catalytic performance, this work establishes a robust theoretical framework that can guide the experimental synthesis and rational optimization of MoS2-based catalysts for practical deployment in fuel cells and metal-air battery systems.Author contributions
J.-C. Chen and M.-J. Pei performed the calculations and contributed to the manuscript preparation. Y. Liu and G.-Q. Luo were responsible for conceptualization, data curation, formal analysis, methodology, and funding acquisition. J. Zhang contributed to conceptualization, review and editing, and project administration. The other authors provided guidance and advice for this work. All authors have read and approved the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5sc07227a.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 52503286 and No. 22409030), the Natural Science Foundation of Fujian Province, China (No. 2024J01259 and No. 2024J08028), the Pilot Group Program of the Research Fund for International Senior Scientists (No. 22250710676), and the National Key R&D Program of China (No. 2022YFB4004100). The authors also acknowledged the Foundation from Hubei University of Technology (No. 202307A08).Notes and references
- B. Wu, H. Meng, X. Chen, Y. Guo, L. Jiang, X. Shi, J. Zhu, J. Long, W. Gao and F. Zeng, et al. , Angew. Chem., 2025, 137, e202415071 CrossRef.
- S. Huang, F. Lin, S. Wang, X. Zeng, H. Ling, X. Hu, Z. Shen and D. Cao, Adv. Mater., 2024, 36, 2407974 CrossRef CAS.
- Y. Chen, J. Mao, H. Zhou, L. Xing, S. Qiao, J. Yuan, B. Mei, Z. Wei, S. Zhao and Y. Tang, et al. , Adv. Funct. Mater., 2024, 34, 2311664 CrossRef CAS.
- T. Yang, Z. Chen, Y. Yang and S. Zhao, Joule, 2024, 8, 287–290 CrossRef.
- W. Huo, L. Fan, Y. Xu, M. Benbouzid, W. Xu, F. Gao, W. Li, N. Shan, B. Xie and H. Huang, et al. , Energy Environ. Sci., 2025, 18, 631–644 RSC.
- X. Luo, W. Wu, Y. Wang, Y. Li, J. Ye, H. Wang, Q. Jiang, Z. Zhou, Y. C. Li and Y. Wang, et al. , Adv. Funct. Mater., 2023, 33, 2215021 Search PubMed.
- Y. Zhao, D. P. Adiyeri Saseendran, C. Huang, C. A. Triana, W. R. Marks, H. Chen, H. Zhao and G. R. Patzke, Chem. Rev., 2023, 123, 6257–6358 Search PubMed.
- M. Luo and M. T. Koper, Nat. Catal., 2022, 5, 615–623 Search PubMed.
- Y. Yu, J. Zhou and Z. Sun, Adv. Funct. Mater., 2020, 30, 2000570 CrossRef CAS.
- Y. Ying, K. Fan, Z. Lin and H. Huang, Adv. Mater., 2025, 37, 2418757 CrossRef CAS.
- M. Wang, M. Langer, R. Altieri, M. Crisci, S. Osella and T. Gatti, ACS Nano, 2024, 18, 9245–9284 CrossRef CAS PubMed.
- Z. Sun, Y. Zhong, H. Sui, J. Liu, P. Xie, S. Ding and Y. Su, Adv. Funct. Mater., 2024, 34, 2410774 CrossRef CAS.
- J. Zhang, Y. Mou, W. Suo, S. Yang, J. Shen, H. Xu, Z. Zeng, R. Zhang, Z. Liang and Y. Wang, et al. , Adv. Funct. Mater., 2025, 35, 2417621 Search PubMed.
- F. Luo, A. Roy, L. Silvioli, D. A. Cullen, A. Zitolo, M. T. Sougrati, I. C. Oguz, T. Mineva, D. Teschner and S. Wagner, et al. , Nat. Mater., 2020, 19, 1215–1223 Search PubMed.
- Z. Zhang, Y. Zhu, X. Shi, B. Qi, Y. Ding, Y. Du, W. Shi, J. Zhang, J. Liu and Y. Sang, et al. , Adv. Funct. Mater., 2024, 34, 2316448 CrossRef CAS.
- J. Yu, C. Su, L. Shang and T. Zhang, ACS Nano, 2023, 17, 19514–19525 Search PubMed.
- N. Deka, T. E. Jones, L. J. Falling, L.-E. Sandoval-Diaz, T. Lunkenbein, J.-J. Velasco-Velez, T.-S. Chan, C.-H. Chuang, A. Knop-Gericke and R. V. Mom, ACS Catal., 2023, 13, 7488–7498 CrossRef CAS PubMed.
- N. Karmodak and J. K. Nørskov, Angew. Chem., 2023, 135, e202311113 CrossRef.
- R. M. Yoo, D. Yesudoss, D. Johnson and A. Djire, ACS Catal., 2023, 13, 10570–10601 Search PubMed.
- B. B. Sarma, F. Maurer, D. E. Doronkin and J.-D. Grunwaldt, Chem. Rev., 2022, 123, 379–444 CrossRef.
- C. Jia, Q. Sun, R. Liu, G. Mao, T. Maschmeyer, J. J. Gooding, T. Zhang, L. Dai and C. Zhao, Adv. Mater., 2024, 36, 2404659 CrossRef CAS.
- S. Jiang, M. Zhang, C. Xu, G. Liu, K. Zhang, Z. Zhang, H.-Q. Peng, B. Liu and W. Zhang, ACS Nano, 2024, 18, 16413–16449 CrossRef CAS.
- M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275 CrossRef.
- B. R. Anne, J. Kundu, M. K. Kabiraz, J. Kim, D. Cho and S.-I. Choi, Adv. Funct. Mater., 2023, 33, 2306100 CrossRef CAS.
- Y. Jia, Y. Zhang, H. Xu, J. Li, M. Gao and X. Yang, ACS Catal., 2024, 14, 4601–4637 Search PubMed.
- Q. Fu, J. Han, X. Wang, P. Xu, T. Yao, J. Zhong, W. Zhong, S. Liu, T. Gao and Z. Zhang, et al. , Adv. Mater., 2021, 33, 1907818 Search PubMed.
- Y. Xu, R. Ge, J. Yang, J. Li, S. Li, Y. Li, J. Zhang, J. Feng, B. Liu and W. Li, J. Energy Chem., 2022, 74, 45–71 CrossRef CAS.
- H. Huang, X. Feng, C. Du, S. Wu and W. Song, J. Mater. Chem. A, 2015, 3, 16050–16056 Search PubMed.
- Y. Hao, L. Wang and L.-F. Huang, Nat. Commun., 2023, 14, 3256 Search PubMed.
- Z. Zheng, L. Yu, M. Gao, X. Chen, W. Zhou, C. Ma, L. Wu, J. Zhu, X. Meng and J. Hu, et al. , Nat. Commun., 2020, 11, 3315 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 Search PubMed.
- S. Nosé, J. Phys. Chem., 1984, 81, 511–519 Search PubMed.
- L. Zhang, X. Guo, S. Zhang, T. Frauenheim and S. Huang, Adv. Energy Mater., 2024, 14, 2302754 CrossRef CAS.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- T. K. Woo, P. M. Margl, P. E. Blöchl and T. Ziegler, J. Phys. Chem. B, 1997, 101, 7877–7880 CrossRef CAS.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690 CrossRef CAS.
- K. Mathew, V. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721 CrossRef CAS PubMed.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS.
- Z. Xue, X. Zhang, J. Qin and R. Liu, J. Energy Chem., 2021, 55, 437–443 CrossRef CAS.
- J. Deng, H. Li, J. Xiao, Y. Tu, D. Deng, H. Yang, H. Tian, J. Li, P. Ren and X. Bao, Energy Environ. Sci., 2015, 8, 1594–1601 RSC.
- C. Cai, S. Liu, F. Zhao, H. Cai, Z. Song and Q. Liu, J. Mater. Chem. C, 2023, 11, 8462–8469 RSC.
- Y. Cheng, Z. Zhu, W. Mi, Z. Guo and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 100401 CrossRef.
- S. J. Rowley-Neale, J. M. Fearn, D. A. Brownson, G. C. Smith, X. Ji and C. E. Banks, Nanoscale, 2016, 8, 14767–14777 RSC.
- T. Sun, Z. Tang, W. Zang, Z. Li, J. Li, Z. Li, L. Cao, J. S. Dominic Rodriguez, C. O. M. Mariano and H. Xu, et al. , Nat. Nanotechnol., 2023, 18, 763–771 CrossRef CAS PubMed.
- J. Gao, B. Li, J. Tan, P. Chow, T.-M. Lu and N. Koratkar, ACS Nano, 2016, 10, 2628–2635 Search PubMed.
- S. Jayabal, G. Saranya, J. Wu, Y. Liu, D. Geng and X. Meng, J. Mater. Chem. A, 2017, 5, 24540–24563 RSC.
- A. Zhang, Y. Liang, H. Zhang, Z. Geng and J. Zeng, Chem. Soc. Rev., 2021, 50, 9817–9844 RSC.
- S. Kc, R. C. Longo, R. M. Wallace and K. Cho, J. Appl. Phys., 2015, 117, 135301 CrossRef.
- E. Diesen, A. M. Dudzinski, K. Reuter and V. J. Bukas, ACS Catal., 2025, 15, 5403–5411 CrossRef CAS.
- C. H. Choi, H.-K. Lim, M. W. Chung, J. C. Park, H. Shin, H. Kim and S. I. Woo, J. Am. Chem. Soc., 2014, 136, 9070–9077 CrossRef CAS.
- X. Guo, S. Lin, J. Gu, S. Zhang, Z. Chen and S. Huang, ACS Catal., 2019, 9, 11042–11054 CrossRef CAS.
- C. Fang, J. Zhou, L. Zhang, W. Wan, Y. Ding and X. Sun, Nat. Commun., 2023, 14, 4449 CrossRef CAS PubMed.
- Z. Xie, X. Huang, Z. Zhang and H. Xu, Phys. Chem. Chem. Phys., 2021, 23, 15101–15106 RSC.
- S. Jiao, X. Fu and H. Huang, Adv. Funct. Mater., 2022, 32, 2107651 Search PubMed.
- W.-B. Yu, H.-R. Zhang, H.-W. Zhang, Y. Liu, Y. Li and B.-L. Su, Adv. Funct. Mater., 2024, 34, 2410816 CrossRef CAS.
- R. Huisman, R. De Jonge, C. Haas and F. Jellinek, J. Solid State Chem., 1971, 3, 56–66 CrossRef CAS.
- Z. Han, S. Zhao, J. Xiao, X. Zhong, J. Sheng, W. Lv, Q. Zhang, G. Zhou and H.-M. Cheng, Adv. Mater., 2021, 33, 2105947 CrossRef CAS PubMed.
- G. L. Stamokostas and G. A. Fiete, Phys. Rev. B, 2018, 97, 085150 CrossRef CAS.
- A. S. Miñarro and G. Herranz, Phys. Rev. B, 2022, 106, 165108 CrossRef.
- Q. Ye, X. Yi, C.-Z. Wang, T. Zhang, Y. Liu, S. Lin and H. J. Fan, Adv. Funct. Mater., 2024, 34, 2400107 CrossRef CAS.
Footnote |
| † J.-C. Chen and M.-J. Pei contributed equally to this paper. |
| This journal is © The Royal Society of Chemistry 2026 |