Indirect hard modeling of low resolution benchtop NMR data for the kinetic fitting of a complex organic reaction

Abstract

Despite recent significant advances in hardware, software, and data analysis, low resolution benchtop NMR systems are still underutilized for the kinetic investigation of organic reactions. Moreover, their use has typically been restricted to monitoring a limited number of species with well-behaved peaks that were easily integrable. In this work, the chlorination reaction of 4-fluorothiophenol with N-chlorosuccinimide (NCS) was investigated by continuous in-line monitoring of five different reaction species through the utilization of a 43 MHz benchtop NMR instrument. The reaction was carried out under synthetically relevant conditions within different modes of operation, including re-circulating batch and single pass continuous flow modes. Quantitative concentration values could be obtained even when peaks overlapped through the use chemometric modeling, specifically indirect hard modeling (IHM). The reaction profiles were then fitted to obtain kinetic parameter estimates for a six step model structure. This study demonstrates that complex organic reaction kinetics can be explored using a low resolution NMR setup for quantitative monitoring.

---

Introduction

Process analytical technology (PAT) has emerged as a crucial tool to support pharmaceutical development and manufacturing and to enable quality by design (QbD).^1,2 The implementation of PAT is of fundamental importance for obtaining understanding of organic reactions. Regulatory agencies, in particular the US Food and Drug Administration (FDA), are encouraging industrial process chemistry labs to integrate real-time inline and online PAT, as part of pharmaceutical development and manufacturing.³ Inline and online PAT can enable faster and more reliable process optimization and enhanced process control when compared to using offline analysis only.⁴

Ultraviolet-visible (UV-vis), Raman and infrared (IR) spectroscopy, and also chromatographic techniques such as high/ultra performance liquid chromatography (HPLC/UPLC) and gas chromatography (GC) are all widely utilized.^1,2,4 These techniques are applied in high throughput synthesis campaigns,^5,6 for reaction optimization, including techniques such as statistical design of experiments (DoE), dynamic experimentation and automated self-optimization, and for reaction kinetics.^7–10

There has also been a shift in the pharmaceutical industry from traditional batch manufacturing to continuous processing.^11,12 This shift is reflected by a focus in this industry on process intensification, sustainability, product quality, safety, energy usage and cost.¹³ Continuous-flow reactors are often used as an alternative technology when a reaction cannot be operated safely in batch.^14,15 The control of exothermicity is improved due to the enhanced heat and mass transfer properties. Hazardous intermediates can easily be handled because only a small inventory is produced at any one time. Furthermore, flow has been exploited for data-rich experimentation due to the ease associated with the incorporation of PAT inline and online.^16,17 Owing to the characteristics of flow reactors, continuous flow aided kinetic analysis continues to increase in popularity.¹⁸

Blackmond formalized reaction progress kinetic analysis for the definition of rate expressions for catalytic reaction mechanism elucidation in batch under conditions that are synthetically relevant to organic chemists.^19,20 Interestingly, Blackmond strongly encouraged users of the approach to apply in situ techniques, such as IR or calorimetry, for experimental data collection which is subsequently analyzed using computational curve fitting software.

In situ NMR analysis can provide deep mechanistic insight into homogeneous solution phase reactions.²¹ It has been argued that NMR can perform a “detective role” and that it acts as a “magnifying lens” facilitating the visualization of chemical problems in detail to provide solutions.²² The last 10–15 years has seen the release of commercially available benchtop NMR options.²³ Low field benchtop NMR instruments are relatively affordable, easy to use in a plug and play manner, compact and low in maintenance.²⁴ In addition, they operate without the need for deuterated solvents and cryogens. Portable benchtop NMR instruments make NMR spectroscopy more accessible in industrial and academic environments for process monitoring.^23–26 However, these advantages come at a significant downside, as the magnetic field of a permanent magnet is much weaker than that of a superconductor used in high resolution NMR. This aspect culminates not only in lower sensitivity and signal to noise ratio but also in variations in peak splitting and intensity. Low field spectra are far from resembling the spectra generated by their high field counterparts, and quantification by integration is typically only possible in simple cases. In most reported studies, well-resolved peaks are monitored, and a long acquisition time is generally utilized. Thus, interpretation and quantification in complex mixtures can be very difficult. However, much of the structural and quantitative data is still available and can be deconvoluted, when an appropriate chemometric technique is applied.^27,28

Powerful chemometric processing techniques, such as multivariate analysis (MVA), indirect hard modeling (IHM) and artificial neural networks (ANNs), are necessary to obtain quantification in spectra which cannot be easily integrated.^28–33 Interestingly, the application of chemometric techniques for low field NMR spectra has been limited to date, when compared to other commonly employed techniques such as IR spectroscopy.

In 2020, Sagmeister et al. utilized low resolution NMR as an online analysis tool for a complex nitration reaction when paired with an MVA model, for spectrally overlapping compounds.²⁸ MVA is a statistical approach to quantify components by their “fingerprint” signals in a measurement. Typically, an MVA model is built using a training set, consisting of mixtures of the analytes with known concentrations. In this instance, the team applied PLS regression as their MVA approach. Subsequently, the team used data-driven ANNs, as an alternative advanced data processing technique, to predict concentrations for the same nitration reaction.²⁹ However, a limitation of using neural networks is that high volume datasets are required to be trained and tested.

Maiwald et al. have demonstrated a process monitoring strategy of an industrial lithiation and nucleophilic aromatic substitution (S_NAr) flow process by using online low field NMR, quantified with an MVA-PLS model.³⁰ Most noteworthily, in a later report, the same group established IHM for the chemometric analysis of the same reaction.³¹ IHM uses physically motivated spectral models, which are derived from pure component NMR spectra. A key benefit of IHM is that it requires relatively low calibration effort when compared to PLS. We previously utilized IHM for the online analysis of ¹H NMR benchtop spectra for a continuous flow Michael addition reaction forming a desired product and its undesired regioisomer.³² Even with these advanced chemometrics available, the study of complex reactions, featuring multiple species, is mostly conducted with expensive high resolution NMR instruments. Recently, the self-optimization of a [3 + 3] cycloaddition was investigated utilizing the Nelder–Mead algorithm for the fine-tuning of the residence time, stoichiometry, and catalyst loading as input variables.³³ The automated flow system was guided by in-line high-field NMR spectroscopy to explore the reaction system.

Hein and co-workers developed a stopped-flow benchtop NMR method for the collection of continuous flow data.³⁴ The benefit of a stopped flow method is that it overcomes the measurement limitations associated with flow dynamics and changes in flow rate.³⁵ The stopped flow method enabled the monitoring of quantitative reaction trends. Subsequently, the same group compared ¹⁹F NMR reaction profiles acquired using both online continuous-flow and stopped-flow sampling methods.³⁶ The stopped flow sampling method provided improved measurement profiles, but this advantage came at the cost of time and higher material consumption.

The study reported herein aimed to bridge the gap in the utilization of low resolution benchtop NMR instruments to obtain quantitative data to study a complex organic reaction system. We were interested in developing accessible setups, which when combined with NMR enabled online quantitative monitoring. IHM was utilized to obtain quantification of the reaction species. The reaction profiles could then be fitted to obtain kinetic parameter estimates for a multistep model structure.

Results and discussion

Preliminary experiments with GC analysis

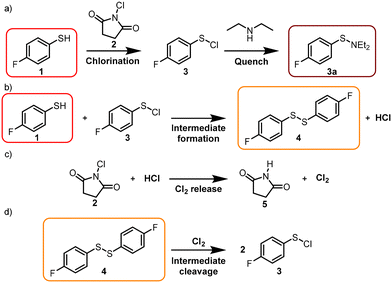
We selected the chlorination of 4-fluorothiophenol (1) using N-chlorosuccinimide (NCS, 2) as a reagent to form 4-fluorobenzenesulfenyl chloride (3) as our model reaction system (Scheme 1a). Previous research has observed unusual sigmoidal behaviour for the product formation in this transformation and related systems.^37–39

Scheme 1 a) Chlorination of 4-fluorothiophenol (1) with NCS (2) to give product 3 and the subsequent diethylamine quenching to give the corresponding sulfenamide 3a. b) After the chlorination, rapid condensation of 3 and 1 leads to bis-(4-fluorophenyl)-disulfide (4) as an intermediate. c) HCl is a by-product of the condensation and reacts with NCS (2) to give succinimide (5) and Cl₂. d) Disulfide 4 is cleaved by Cl₂ leading to sulfenyl chloride 4 as the final product.

Thiol chlorination via NCS (2) is reported to first produce sulfenyl chloride, which then reacts with unreacted thiol to form disulfide 4 (Scheme 1b).³⁷ The addition of diethylamine trapped the sulfenyl chloride product (3), as less reactive sulfenamide (3a). Preliminary reaction profiling was performed to explore the design space by using offline GC-FID/GC-MS analysis. The chlorination of 1 (80 mM) with 2 (200 mM, 2.5 eq) was carried out in 4 mL vials, at 25 °C and using anhydrous ethyl acetate (EtOAc) as a solvent. Aliquots were periodically taken (at time intervals up to 20 min), and the aliquots were quenched with a large excess of diethylamine and by dilution. These samples were subsequently analyzed by GC-FID and the product compositions were compared via GC-FID area%.

Furthermore, disulfide 4 is an intermediate in this reaction and its cleavage, resulting in 3, has been recently reported to occur via Cl₂, which stems from the reaction of NCS (2) and HCl released during the condensation reaction (Schemes 1b–d). We reasoned that owing to the large excess and higher nucleophilicity of diethylamine, the remaining NCS would rapidly form N-chlorodiethylamine and succinimide (5), preventing the release of Cl₂ and therefore the cleavage of 4. The disulfide 4 concentration increased for the initial four minutes, after which it gradually decreased, and 3a was the only observable species by GC-FID. Interestingly, the reaction proceeded at a faster rate in the presence of higher equivalents of NCS or water, with water having the largest influence on the reaction rate. By adding 40 mM water to the previously described conditions, the reaction already showed full conversion after four minutes instead of fourteen minutes (cf. Fig. 1a and b). However, only trace amounts of thiol 1 were observed. Adding diethylamine in the absence of NCS (2), only disulfide 4 was observed (Fig. 1a and b t = 0). This is likely due to diethylamine induced homodimerization of thiol 1, which is reported in the literature.⁴⁰ The reaction is proposed to proceed via deprotonation followed by subsequent oxidation by atmospheric oxygen to form the respective radicals which then dimerize. These experiments not only provided information on the influence of the reaction parameters and the performance over time, but also highlighted potential problems of the GC analysis, such as reactions during analysis, time delay between sampling and analysis and the need for manual intervention. Overall, offline methods may not give a true representation of the reaction behavior and lead to confusion regarding the reaction understanding, thus we explored different options using online NMR.

Fig. 1 Profile of the chlorination of 1 with 2, captured via aliquot quenching with diethylamine. First aliquot (time = 0) taken before addition of 2. Reaction conditions: 1 (80 mM) with 2 (200 mM) in dry EtOAc as a solvent at 25 °C. a) Without addition of water and b) with addition of water (40 mM).

Initial NMR experiments

Initial experiments using the benchtop NMR instrument were performed in a borosilicate glass NMR tube by combining separately pre-prepared solutions of 1 and 2. The chlorination reaction was analyzed using a benchtop low field Magritek, Spinsolve Ultra 43 MHz NMR device. The experiments were performed under ambient conditions as there was no ability to heat or cool within the benchtop NMR instrument. Trifluorotoluene (TFT) was selected as an internal standard (IS), as it showed a well-resolved signal in both the ¹H and ¹⁹F NMR spectra at 7.76 ppm and −63.7 ppm, respectively. For reaction monitoring, the proton spectra were referenced to the methyl peak of EtOAc (2.1 ppm), while the TFT peak (−63.7 ppm) was selected as a reference for the ¹⁹F spectra.

Our initial intention was to monitor the fluorine-containing species by ¹⁹F NMR,⁴¹ since the peaks assigned to the aromatic protons were very broad, between 6.8 and 7.8 ppm, in the low field ¹H NMR spectra. In contrast to the GC analysis, thiol 1 could be monitored. Two of the main benefits of ¹⁹F over ¹H NMR are the absence of solvent signals and the large chemical shift range. To illustrate this, we observed a change in the ¹⁹F chemical shift for 1 (−119.0 ppm), 4 (−115.2 ppm) and 3 (−109.8 ppm), which was sufficient to observe all the different sulfur species with baseline separation. At the same time, the conversion of NCS (2) (3.04 ppm) to succinimide (NHS) (5) (2.80 ppm) could be monitored by ¹H NMR (Fig. 2a). However, we found that precise integration was difficult due to an overlap between the NHS singlet and the carbon satellites of the solvent. This highlights an additional restriction during solvent selection when monitoring reactions with a benchtop NMR instrument in protonated solvents. Besides general solvent considerations, such as solubility and adequate reaction rate to be monitored, the much stronger solvent signals must appear at a different chemical shift from the analytes. Consequently, most aromatic solvents are ruled out as an option for our reaction system, as their peaks would overlap with the already convoluted signals of the analytes. It should be noted that there are techniques for the suppression of solvent signals and ¹³C satellites, making peak overlap and baseline distortion from the solvent signals more manageable. We selected EtOAc as a solvent as it fits the previously described criteria and has relatively green credentials.⁴² We operated with an alternating ¹H/¹⁹F protocol script, so that all five reaction components and the internal standard could be monitored. A pulse angle of 90° was selected and each spectrum was composed of four scans with a 10 s and 15 s delay for the ¹H NMR and ¹⁹F NMR spectrum, respectively. An additional delay of 2 s between scans was implemented, corresponding to a ¹H and ¹⁹F NMR spectrum every 104 seconds. The setup was successfully implemented to investigate different reaction conditions under ambient conditions.

Fig. 2 Representative a) ¹H and b) ¹⁹F NMR spectra as encountered for the reaction of 1 (150 mM) and 2 (150 mM). The ¹H NMR spectrum allowed for monitoring of the transformation of 2 (blue dot, 3.04 ppm) into 5 (green dot, 2.80 ppm), while the dimerization of 1 (red dot, −119.0 ppm) to 4 (orange dot, −115.2 ppm) could be observed in the ¹⁹F spectrum. *Since sulfenyl chloride (3, brown dot, −109.8 ppm) was not observed during NMR analysis until all the thiol (1, red dot, −119.0 ppm) was consumed, its position is indicated in both spectra.

However, on attempting to obtain quantitative reaction profile data, we realized that the noisy baseline within the ¹⁹F NMR spectra made this difficult. Thus, we decided to test whether it would be possible to overcome the problems associated with overlapping peaks of the fluorine-containing compounds in the ¹H NMR spectra. The potential difficulties with this approach were highlighted when comparing the spectra of 4-fluorothiophenol (1) and the corresponding disulfide 4 measured on a 300 MHz NMR instrument and on a 43 MHz benchtop NMR instrument (Fig. 3). While a highly resolved baseline separation was achieved for the high field spectrum, these spectra show complete overlap when the same sample was measured with the benchtop NMR instrument.

Fig. 3 Comparison of the ¹H NMR spectra of bis-(4-fluorophenyl)-disulfide (4, spectra on top) and 4-fluorothiophenol (1, spectra on the bottom) on a high field and low field NMR device.

Indirect hard modeling and reaction profiling

Despite the difficulties, we were interested in exploring the possibility of monitoring all involved species simultaneously in the ¹H NMR spectrum. Moreover, the interval between scans would be shortened, resulting in more data-rich experimentation. However, due to the overlapping peaks, simple peak integration was not feasible. The training of a PLS model can be difficult, especially when spectra with known concentrations of all analytes cannot be recorded for the calibration solutions, due to their reactivity with one another, as was the case for this system. Thus, IHM was selected as the data processing technique of choice. IHM is not a statistical but a physics-based technique that mathematically describes all pure component spectra by a sum of peak shaped Gaussian/Lorentzian curves, allowing the deconvolution of superimposed peaks. This technique appeared to be well-suited for our NMR analysis, as the spectrum of a specific component gives a very characteristic peak shape and splitting. Additionally, since the IHM directly provides peak areas, it uses the benefit of NMR as an absolute measurement technique (peak integration directly relates to the number of protons), requiring no to minimal experimental calibration, only model validation.

Thus, a spectral hard modeling approach to quantification was attempted by building a chemometric model within the PEAXACT 5.3 software (S-PACT). We collected individual pure component spectra for each component, including the solvent and internal standard (seven compounds in total), and created hard models for each of them. Combining these into a mixture model allowed for deconvolution, providing peak areas for each individual component. Fig. 4 depicts the individual hard models of 1, 4 and 3, as well as the resulting mixture model. Quantification of the individual components was performed directly without calibration. To our delight, the five reaction species could thereby be simultaneously monitored and quantified by using low resolution ¹H NMR.

Fig. 4 Depiction of the indirect hard models (IHMs) created for 1, 4 and 3. The bottom image shows the mixture spectrum created by combination of these 3 models as well as the model for TFT (one peak at 7.76 ppm).

To evaluate the performance of the model, two sets of validation experiments were carried out, each consisting of five samples of known concentration. The first series contained NCS (2) and NHS (5) in concentrations between 0 mM and 150 mM. The second validation set was comprised of thiol 1 and disulfide 4 at concentrations of up to 150 mM and 75 mM, respectively. Product 3 could not be added for validation, because it would react with thiol 1. The internal standard (TFT) was present in all samples at a concentration of 100 mM. The values predicted using the chemometric model were in good agreement with the experimental concentrations. Slight overprediction of higher concentrations was observed for disulfide 4 and NHS (5), whose quantification could subsequently be improved by the addition of a correction factor of 0.95. For evaluation of our newly developed chemometric model, we then carried out further reactions in the NMR tube utilizing our newly developed chemometric model to evaluate the obtained spectra. The data obtained were then smoothed using a moving average of three data points, resulting in a reaction profile as depicted in Fig. 5.

Fig. 5 Reaction profile for the chlorination of 1 (150 mM initial concentration) with 2 (120 mM initial concentration). Mass balance for 1, 4 and 3 (light grey), as well as 2 and 5 (grey), which shows that the model slightly overpredicted the mass balance.

These initial results showed consumption of thiol (1) and NCS (2), producing NHS (5) and disulfide (4) at a similar rate. As expected, no sulfenyl chloride (3) and only disulfide (4) was observed until all thiol (1) was consumed, likely due to the rapid condensation of sulfenyl chloride and thiol. This behavior has recently been studied by Lloyd-Jones and co-workers, who proposed that the condensation produces HCl as a by-product, which then in turn increases the reaction rate through the release of Cl₂ from NCS (2). NCS alone is not fully capable of chlorinating bis-(4-fluorophenyl)-disulfide (4) under these conditions, which indicates the involvement of another chlorinating reagent (see the SI).³⁷ Similar behavior has been also proposed for N-bromosuccinimide.³⁸ As Cl₂ is a more reactive chlorination agent than NCS, this chlorination pathway accelerates the product formation and could explain the sigmoidal reaction profile observed. This pathway can be expressed in a five step model structure comprising second order reactions (Fig. 6b), which we then used for the kinetic fitting. Four additional experiments at initial thiol (1) and NCS (2) concentrations between 60 and 150 mM were carried out in NMR tubes and used for fitting of kinetic reaction parameters (all reaction profiles and fits are depicted in the SI). The kinetic fitting was performed in Dynochem (Scale-up Systems, Mettler Toledo), which uses a modified Arrhenius equation for the fitting of the rate constants (T_ref = 25 °C). The simultaneous model fit was in good agreement with the experimental data whose concentrations were closer to the center of the explored space (Fig. 6a) but deviated for all other profiles (Fig. 6c). When the profiles were fitted separately, the models closely matched the experimental data.

Fig. 6 a) Reaction profile (dots) and kinetic fit (lines) of the reaction of 1 (100 mM initial concentration) and 2 (150 mM initial concentration). b) 5 step reaction mechanism used for kinetic fitting of rate constants. c) Comparison of the concentration profiles for the intermediate 4 at three different initial reagent concentrations. The kinetic fit (lines) deviates from the experimental data (dots), as the reaction rate is underpredicted at higher concentrations (purple) and overpredicted at lower concentrations (red), showing the lack of precise control over the reaction setpoint for this mode of operation.

A limitation of the initial experiments performed in an NMR tube under ambient conditions was the lack of heat control within the NMR tube. The ability to heat or cool a sample has only been implemented in very recently developed benchtop NMR instruments and is still difficult to achieve.⁴³ Since this class of reactions is known to be exothermic, we expected the model mismatch to be a result of an increase in reaction temperature, which is more prominent at higher concentrations. Subsequently, calorimetric experiments were carried out, showing an overall reaction enthalpy of −121 ± 6 kJ mol⁻¹, which would give a calculated adiabatic temperature rise of 11 °C. Another challenge associated with using an NMR tube was the inability to determine the exact start time as the reaction mixture was sealed, shaken and then loaded into the NMR device. We anticipated that a recirculating batch system would allow better control. Flow chemistry has frequently been employed to enable the safe processing of exothermic reactions due to improved heat and mass transfer characteristics.³⁹ Thus, we were interested in studying this reaction within different setups that would enable more precise temperature control of the reaction mixture.

Batch re-circulation experiments

To obtain reasonable temperature control over the reaction mixture, while having the ability to study longer reaction times within a single experiment, a batch recirculation setup was assembled. The reaction was carried out in a round bottom flask (25 mL solution reaction volume), placed in a heated water bath. The reactor was connected to the NMR flow cell with PFA tubing and the reaction mixture continuously circulated through the NMR device with a peristaltic pump at a constant flow rate of 2 mL min⁻¹, as depicted in Fig. 7a. This corresponded to an approximate recirculation time of 75 seconds and a total volume of the flow setup of 2.5 mL. On performing the chlorination in this setup, at 25 °C and an initial thiol (1) and NCS (2) concentration of 150 mM each, we observed full consumption of the starting material (1) after 13.5 min. This reaction time was more than twice the observed time compared to running the reaction in the NMR tube, at the same initial concentrations, indicating a more stable temperature profile for the reaction.

Fig. 7 a) Schematic depiction of the recirculation setup. b) Comparison of the experimental data (dots) and fits (lines) of the increase and decrease of disulfide (4) at five different initial reagent concentrations. c) Profile of the reaction of 1 and 2 when performed at 25 °C in recirculation performed for model validation. Experimental data (dots) and model prediction (lines) were in good agreement.

Nine additional reactions, using starting concentrations of 1 and 2 between 60 and 150 mM and at two temperature levels of 25 °C and 35 °C, were carried out. In three of these reactions, 6–15 mM water was added as an additive. The addition of water was observed to strongly increase the rate of the chlorination reaction. This behavior could best be explained through the addition of a sixth reaction equation, assigning water as having a catalytic effect on the release of Cl₂ from NCS (2). The obtained reaction profiles were then used to fit reaction constants and activation energies for the previously described six step mechanism. While showing slight deviations for two of the profiles, the kinetic model was in good agreement with the experimental data. The fit is illustrated in Fig. 7b, which depicts the experimental values and model for the disulfide in five different reaction profiles. The hydrolysis of 2 was also explored as a reasonable two step pathway for the catalytic effect of water, releasing HOCl as a first step, which can then react with HCl to give Cl₂. However, this explanation was discarded, as this model showed a poor fit, overpredicting the formation of 5. Furthermore, the hydrolysis of NCS (2) has been reported to be a slow reaction, which was not in agreement with the fitted rate constant of 5.51 M⁻¹ min⁻¹ predicted by our model.⁴⁴ We also performed a control experiment for the hydrolysis of NCS (2) using 0.2 equiv. of water in EtOAc as a solvent; no formation of NHS (5) was observed after 30 min (see the SI).

Subsequently, we were interested in using our kinetic model to simulate different experimental scenarios in silico for the re-circulating batch. It should be noted that while extrapolation beyond the explored chemical space is generally seen as an advantage of mechanistic over purely statistical models,¹⁸ this is most often only possible for rather simple and well-explored reaction mechanisms. Extrapolation should always be made with caution. When dealing with complicated reactions, it is generally advisable to model within the experimental space of interest and establish a robust model in this region. With the fitted values established, the kinetic model was used to predict the optimal reaction time for achieving maximum intermediate 4 concentration under two different conditions. Given the initial concentrations of 1 and 2 of 150 and 120 mM, respectively, and no water, the simulation was in excellent agreement with the experimental data (Fig. 7c). The model fit predicted the maximum concentration of 4 at 16.5 min with a value of 72.3 mM (the experimentally observed maximum concentration was 80.1 mM also at 16.5 min). For the second case, using equimolar initial concentrations (100 mM) of both thiol 1 and NCS (2) and 0.1 eq of H₂O, the model predicted a maximum concentration of intermediate 4 (46.7 mM) at 9.4 min, which was slightly different to the observed maximum (48.1 mM at 8.7 min).

Given these improvements in parameter control and subsequently the predictive power of the model, we were interested in studying the chlorination reaction in a continuous flow set-up, expecting even better temperature control and a different explorable reaction space.

Flow experiments

We set out to assemble a simple flow setup comprising two syringe pumps for the introduction of substrate 1 and NCS (2) as separate feeds. These feeds were combined in a T-piece and then subsequently reacted in a heated tubular coil (internal volume = 2.5 mL) submerged within a water bath. After the reactor, the mixture flowed through a smaller cooling coil (internal volume = 1 mL) at 0–10 °C to quench the reaction prior to exiting through a back pressure regulator (BPR) (5 bar). Potentially, there could be conversion after the reactor, but at this temperature, it would be negligible, based on the established kinetics (vide infra). The effluent then passed through the NMR flow cell, where it was measured. A schematic depiction is given in Fig. 8a.

Fig. 8 a) Schematic depiction of the assembled continuous flow setup. b) Profile obtained by reaction of 1 and 2 at 80 °C. Experimental data (dots) and kinetic fit (lines) are in good agreement. c) Comparison of the disulfide profile at three different initial reagent concentrations.

Four flow reactions were carried out in dry EtOAc at 50 to 80 °C using equimolar amounts (1 : 1) of thiol 1 and NCS (2) at either 60 or 150 mM. Additionally, three more experiments were conducted at a temperature of 70 °C and 80 °C using a thiol 1 and NCS (2) concentration of 60 mM, using water as an additive to study its effect on the reaction rate. Twelve different residence times, between 1.25 and 6.25 min, were captured for each experiment, through a variation of the total flow rate between 0.4 and 2 mL min⁻¹. This flow rate range is advised for obtaining the best results when performing NMR measurements within the flow cell. However, this does limit the explorable residence times feasible within the single pass flow system when considering the analytics, whereas the re-circulation approach allowed for a wider time profile range to be explored, i.e., longer reaction times.

The first four reaction profiles were then used to fit the previously described six steps, resulting in a new model fit. The model was in excellent agreement with the experimental data for all the conditions explored, showing the precise parameter control within the flow setup, especially for temperature. At 80 °C and a thiol 1/NCS (2) concentration of 60 mM, all of the starting material was consumed and the highest intermediate 4 concentration was measured after 6.5 min. Increasing both concentrations to 150 mM at the same temperature reduced this time to 2.5 min, while more than half of the substrate remained after 6 min when the temperature was lowered to 50 °C, demonstrating the strong temperature dependence of this reaction. The presence of water also played a crucial role in the chlorination reaction rate. At an initial thiol 1 and NCS (2) concentration of 60 mM and 80 °C, the addition of only 0.2 eq of water (11 μL to 100 mL solution) almost doubled the reaction rate, as depicted in Fig. 8c.

The Cl₂ dependent chlorination of 1 and 4 was found to proceed at a moderate speed of 13.2 and 24.7 M⁻¹ min⁻¹ and low activation energies of 13.7 and 7.9 kJ mol⁻¹, respectively. The condensation reaction was found to be very fast at 606 M⁻¹ min⁻¹, and as a result, the kinetic fit correctly predicted the absence of product 3 before almost all the starting material 1 has been consumed. Compared to all other rate constants, the sensitivity of this fit was low, which would be expected due to its very high value, and the reaction was found to show no significant temperature dependency. The initial chlorination reaction and the release of Cl₂ were found to be slow at 0.2 and 0.07 M⁻¹ mol⁻¹, with activation energies of 25.5 and 79.4 kJ mol⁻¹, respectively. The catalytic effect of water increased the rate constant of the Cl₂ release by almost 3 orders of magnitude to 32.2 M⁻² mol⁻¹ with an activation energy of 65 kJ mol⁻¹. The rate constants and activation energies are summarized in Table 1.

Table 1 Fitted rate constants and activation energies for the six step reaction network for the flow experiments (for full details, see SI Table S6). Values stated without deviation were fitted with high uncertainty. Reaction profiles with the corresponding model fit are depicted in Fig. S56–S62. Standard error based on 95% confidence level

Model step	k ± SE [M^−1 min^−1]	Ea ± SE [kJ mol^−1]
a Unit of rate constant for the sixth reaction step: [M^−2 min^−1].b Model fitting showed low temperature sensitivity for the second reaction step.
Thiol + NCS → sulfenyl chloride + NHS	0.24 ± 0.02	25.5 ± 0.4
Thiol + sulfenyl chloride → disulfide + HCl	606	–^b
NCS + Cl2 → Cl2 + NHS	0.07 ± 0.01	79.4 ± 0.3
Thiol + Cl2 → sulfenyl chloride + HCl	13.2 ± 3.7	13.7 ± 0.2
Disulfide + Cl2 → 2 sulfenyl chloride	24.7 ± 3.7	7.9 ± 0.2
NCS + HCl + H2O → Cl2 + NHS + H2O	32.2 ± 1.9^a	65 ± 0.6

---

To our delight, the incorporation of flow chemistry enabled us to study the kinetics of this reaction with temperature control and under synthetically relevant conditions, leading to the development of a kinetic model that was in very good agreement with the experimental data. A wider temperature range was possible to be investigated in flow, including above the boiling point of the solvent.

Conclusions

We reported the ability to capture quantitative concentration profiles for a complex reaction network using a low resolution benchtop NMR instrument. 4-Fluorothiophenol was chlorinated by using N-chlorosuccinimide (NCS) as a reagent at synthetically relevant concentrations using anhydrous ethyl acetate as a solvent. This reaction was particularly challenging to study due to its exothermic nature (ΔH_rxn = −121 kJ mol⁻¹) and unusual sigmoidal product formation. Indirect hard modeling was employed to deconvolute the ¹H NMR spectra of five reaction species, allowing for quantification within a mass balance error of less than 10%. The reaction profile data were then simultaneously fitted to investigate the chemical kinetics. Initially, reaction profiles were obtained using a standard NMR tube at ambient temperature. However, there was limited temperature control with this setup. Thus, we investigated two further modes of operation, recirculating batch and single-pass continuous flow. These both enabled the investigation of the reaction temperature dependence. Overall, the study demonstrated that both low resolution NMR and chemometric modeling can be combined to obtain data for kinetic fitting of a complex reaction system. We hope that this study will increase the utilization of benchtop NMR systems for the study of organic reactions displaying challenging chemical kinetics.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: including experimental details, creation and validation of the chemometric model, calorimetry experiments and all individual reaction profiles that were used for kinetic fitting. See DOI: https://doi.org/10.1039/D5RE00436E.

Acknowledgements

The Research Center Pharmaceutical Engineering (RCPE) is funded within the framework of COMET – Competence Centers for Excellent Technologies by BMK, BMAW, Land Steiermark, and SFG. The COMET program is managed by the FFG. This work was funded through the Austrian Research Promotion Agency (FFG) as part of the “Twin4Pharma” project within the COMET Module program. We would like to thank Scale-up Systems/Mettler Toledo for providing the kinetic software and Charles Gordon for his support.

References

1. L. L. Simon, et al., Org. Process Res. Dev., 2015, 19, 3–62.
2. C. N. Talicska, E. C. O'Connell, H. W. Ward, A. R. Diaz, M. A. Hardink, D. A. Foley, D. Connolly, K. P. Girard and T. Ljubicica, React. Chem. Eng., 2022, 7, 1419–1428.
3. L. Lee, T. F. O'Connor, X. Yang, C. N. Cruz, S. Chatterjee, R. D. Madurawe, C. M. V. Moore, L. X. Yu and J. Woodcock, J. Pharm. Innov., 2015, 10, 191–199.
4. P. Sagmeister, J. D. Williams and C. O. Kappe, Chimia, 2023, 77, 300–306.
5. S. M. Mennen, et al., Org. Process Res. Dev., 2019, 23, 1213–1242.
6. S. W. Krska, D. A. DiRocco, S. D. Dreher and M. Shevlin, Acc. Chem. Res., 2017, 50, 2976–2985.
7. C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126.
8. J. D. Williams, P. Sagmeister and C. O. Kappe, Curr. Opin. Green Sustainable Chem., 2024, 47, 100921.
9. G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish, H. Hao, S. Lo, S. Pablo-García, E. M. Rajaonson, M. Skreta, N. Yoshikawa, S. Corapi, G. D. Akkoc, F. Strieth-Kalthoff, M. Seifrid and A. Aspuru-Guzik, Chem. Rev., 2024, 124, 9633–9732.
10. M. Abolhasani and E. Kumacheva, Nat. Synth., 2023, 2, 483–492.
11. J. C. McWilliams, A. D. Allian, S. M. Opalka, S. A. May, M. Journet and T. M. Braden, Org. Process Res. Dev., 2018, 22, 1143–1166.
12. M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796–11893.
13. J. Krueger, et al., Angew. Chem., Int. Ed., 2025, 64, e202420719.
14. N. Kockmann, P. Thenée, C. Fleischer-Trebes, G. Laudadio and T. Noël, React. Chem. Eng., 2017, 2, 258–280.
15. M. Movsisyan, E. I. P. Delbeke, J. K. E. T. Berton, C. Battilocchio, S. V. Ley and C. V. Stevens, Chem. Soc. Rev., 2016, 45, 4892–4928.
16. M. A. Morin, W. P. Zhang, D. Mallik and M. G. Organ, Angew. Chem., Int. Ed., 2021, 60, 20606–20626.
17. M. Rodriguez-Zubiri and F.-X. Felpin, Org. Process Res. Dev., 2022, 26, 1766–1793.
18. C. J. Taylor, J. A. Manson, G. Clemens, B. A. Taylor, T. W. Chamberlain and A. A. Lapkin, React. Chem. Eng., 2022, 7, 1037–1046.
19. D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320.
20. D. G. Blackmond, J. Am. Chem. Soc., 2015, 137, 10852–10866.
21. Y. Ben-Tal, P. J. Boaler, H. J. A. Dale, R. E. Dooley, N. A. Fohn, Y. Gao, A. García-Domínguez, K. M. Grant, A. M. R. Hall, H. L. D. Hayes, M. M. Kucharski, R. Wei and G. C. Lloyd-Jones, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 129, 28–106.
22. M. V. S. Elipe, Org. Process Res. Dev., 2025, 29, 255–269.
23. H.-Yeon Yu, S. Myoung and S. Ahn, Magnetochemistry, 2021, 7, 121.
24. T. Castaing-Cordier, D. Bouillaud, J. Farjon and P. Giraudeau, Annu. Rep. NMR Spectrosc., 2021, 103, 191–258.
25. P. Giraudeau and F.-X. Felpin, React. Chem. Eng., 2018, 3, 399–413.
26. M. V. Gomez and A. de la Hoz, Beilstein J. Org. Chem., 2017, 13, 285–300.
27. (a) Y. B. Monakhova, U. Holzgrabe and B. W. K. Diehl, J. Pharm. Biomed. Anal., 2018, 147, 580–589; (b) P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., Int. Ed., 2021, 60, 8139–8148.
28. P. Sagmeister, J. Poms, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2020, 5, 677–684.
29. P. Sagmeister, R. Hierzegger, J. D. Williams, C. O. Kappe and S. Kowarik, Digital Discovery, 2022, 1, 405–412.
30. F. Dalitz, M. Cadaj, M. Maiwald and G. Guthausen, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 60, 52–70.
31. S. Kern, K. Meyer, S. Guhl, P. Gräßer, A. Paul, R. King and M. Maiwald, Anal. Bioanal. Chem., 2018, 410, 3349–3360.
32. P. Sagmeister, C. Schiller, P. Weiss, K. Silber, S. Knoll, M. Horn, C. A. Hone, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2023, 8, 2818–2825.
33. N. El Sabbagh, M. Bazzoni, Y. Horbenko, A. Bernard, D. Cortés-Borda, P. Giraudeau, F.-X. Felpin and J.-N. Dumez, React. Chem. Eng., 2024, 9, 2599–2609.
34. T. Maschmeyer, L. P. E. Yunker and J. E. Hein, React. Chem. Eng., 2022, 7, 1061–1072.
35. A. Friebel, T. Specht, E. von Harbou, K. Münnemann and H. Hasse, J. Magn. Reson., 2020, 312, 106683.
36. T. Maschmeyer, D. J. Russell, J. G. Napolitano and J. E. Hein, Magn. Reson. Chem., 2024, 62, 310–322.
37. A. García-Domínguez, N. M. West, R. T. Hembre and G. C. Lloyd-Jones, ACS Catal., 2023, 13, 9487–9494.
38. J. I. Murray, M. V. Silva Elipe, A. Cosbie, K. Baucom, K. Quasdorf and S. Caille, Org. Process Res. Dev., 2020, 24, 1523–1530.
39. D. Polterauer, D. M. Roberge, P. Hanselmann, R. Littich, C. A. Hone and C. O. Kappe, React. Chem. Eng., 2022, 7, 2582–2592.
40. M. S. Abaee, M. M. Mojtahedi and S. Navidipoor, Synth. Commun., 2010, 41, 170–176.
41. N. Sulzer, D. Polterauer, C. A. Hone and C. O. Kappe, Previously we performed a preliminary ¹⁹F NMR experiment that monitored the oxidative chlorination of 1,2-bis(4-fluorophenyl) disulfide to the corresponding sulfonyl chloride derivative using HNO₃/HCl/O₂, ChemSusChem, 2024, 17, e202400292.
42. C. M. Alder, J. D. Hayler, R. K. Henderson, A- M. Redman, L. Shukla, L. E. Shuster and H. F. Sneddon, Green Chem., 2016, 18, 3879–3890.
43. M. Bornemann-Pfeiffer, K. Meyer, J. Lademann, Matthias Kraume and M. Maiwald, Magn. Reson. Chem., 2024, 62, 259–268.
44. A.-R. A. Samarkandy, S. A. Al-Thabaiti and A.-H. A. El-Bellihi, Mater. Sci. Res. India, 2008, 5, 219–226.

---