 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles calculations to investigate structural, electronic, optical, elastic, mechanical and phonon properties of novel Q3GaBr6 (Q = Na and K) for next-generation lead-free solar cells
Rifat Rafiua,
Md. Sakib Hasana,
Md. Azizur Rahman *b,
Imtiaz Ahamed Apon
*b,
Imtiaz Ahamed Apon c,
Karim Kriaad,
Mohamed Benghanem*e,
S. AlFaifyf and
Noureddine Elboughdirig
c,
Karim Kriaad,
Mohamed Benghanem*e,
S. AlFaifyf and
Noureddine Elboughdirig
aDepartment of Material Science and Engineering, Khulna University of Engineering & Technology (KUET), Khulna-9203, Bangladesh
bInnovative Solar and Energy Materials Laboratory (ISEML), Department of Electrical and Electronic Engineering, Begum Rokeya University, Rangpur, 5400, Bangladesh. E-mail: azizurrahmanatik49@gmail.com
cDepartment of Electrical and Electronic Engineering, Bangladesh Army University of Science and Technology (BAUST), Saidpur-5311, Bangladesh
dCollege of Engineering, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh 11432, Saudi Arabia
ePhysics Department, Faculty of Science, Islamic University of Madinah, Madinah 42351, Saudi Arabia. E-mail: mbenghanem@iu.edu.sa
fDepartment of Physics, College of Sciences, King Khalid University, P.O. Box 960, AlQura'a, Abha 61421, Saudi Arabia
gChemical Engineering Department, College of Engineering, University of Ha'il, P.O. Box 2440, 81441 Ha'il, Saudi Arabia
First published on 6th February 2026
Abstract
Lead-free halide perovskites have emerged as promising alternatives to toxic Pb-based photovoltaic absorbers, yet many candidates suffer from poor stability or unfavorable electronic properties. In this work, we present the first comprehensive first-principles and device-level investigation of the novel vacancy-ordered perovskites Q3GaBr6 (Q = Na, K) to evaluate their potential for next-generation optoelectronic and solar-cell applications. Density functional theory (DFT) calculations confirm that both compounds crystallize in a stable cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase with negative formation energies, favorable tolerance factors, and strong Ga–Br bonding within rigid octahedral frameworks. Electronic-structure analysis reveals direct band gaps of 1.445 eV (K3GaBr6) and 1.991 eV (Na3GaBr6), with Br-4p states dominating the valence band and Ga-/Q-site orbitals contributing to the conduction band. Optical studies show high absorption (>104 cm−1 in the visible region), low reflectivity, strong dielectric response, and pronounced UV absorption, indicating suitability for broadband optoelectronics. Mechanical and phonon analyses further confirm mechanical stability, moderate stiffness, and absence of imaginary phonon modes, while AIMD simulations validate excellent thermal robustness at elevated temperatures. Incorporating DFT-extracted parameters into SCAPS-1D device modeling demonstrates promising photovoltaic performance, with efficiency, current density, and fill factor strongly influenced by absorber thickness, defect density, and doping concentration. Under ideal simulated conditions, the device shows a theoretical upper-limit efficiency of 22.21%. The proposed DFT–SCAPS integrated approach provides an efficient and computationally economical route to screen and optimize lead-free perovskite absorbers, significantly reducing experimental trial-and-error while enabling accurate prediction of photovoltaic performance.
m phase with negative formation energies, favorable tolerance factors, and strong Ga–Br bonding within rigid octahedral frameworks. Electronic-structure analysis reveals direct band gaps of 1.445 eV (K3GaBr6) and 1.991 eV (Na3GaBr6), with Br-4p states dominating the valence band and Ga-/Q-site orbitals contributing to the conduction band. Optical studies show high absorption (>104 cm−1 in the visible region), low reflectivity, strong dielectric response, and pronounced UV absorption, indicating suitability for broadband optoelectronics. Mechanical and phonon analyses further confirm mechanical stability, moderate stiffness, and absence of imaginary phonon modes, while AIMD simulations validate excellent thermal robustness at elevated temperatures. Incorporating DFT-extracted parameters into SCAPS-1D device modeling demonstrates promising photovoltaic performance, with efficiency, current density, and fill factor strongly influenced by absorber thickness, defect density, and doping concentration. Under ideal simulated conditions, the device shows a theoretical upper-limit efficiency of 22.21%. The proposed DFT–SCAPS integrated approach provides an efficient and computationally economical route to screen and optimize lead-free perovskite absorbers, significantly reducing experimental trial-and-error while enabling accurate prediction of photovoltaic performance.
1. Introduction
Perovskite solar cells (PSCs) have rapidly emerged as a transformative photovoltaic technology, with power conversion efficiencies (PCEs) rising from 3.8% in 2009 to over 25% for single-junction devices by 2023, while perovskite-silicon tandem cells have reached 29.8%.1 The remarkable progress of halide perovskite-based optoelectronic devices represents a major turning point in materials science, primarily driven by their outstanding structural flexibility and exceptional optoelectronic properties.2–4 Such rapid advancement is attributed to features such as high optical absorption coefficients, direct and tunable band gaps, long carrier lifetimes, and high defect tolerance. In addition to experimental developments, recent comprehensive reviews have highlighted how combined computational approaches—such as density functional theory (DFT), machine learning, and high-throughput screening—are increasingly essential for guiding the discovery and optimization of lead-free perovskite materials with competitive performance metrics.5 However, most high-performing candidates rely on toxic Pb, and additionally, many of these compounds suffer from intrinsic instability when exposed to ambient conditions.6,7 The combined issues of toxicity and instability have created an urgent need to identify Pb-free, stable halide perovskites with competitive optoelectronic behavior.One intuitive approach is to substitute Pb with elements possessing similar electronic configurations, such as tin (Sn2+) and germanium (Ge2+), both of which belong to the same group as Pb.8–10 While these substitutions hold promise, Sn-based perovskites readily oxidize from Sn2+ to Sn4+, producing degradation by-products such as SnI2, which may be nearly as harmful as Pb itself.11 Likewise, Ge-based perovskites suffer from rapid oxidation of Ge2+ to Ge4+ upon exposure to air and moisture, resulting in severe structural and electronic degradation.12 Beyond these divalent cations, Group VA elements such as bismuth (Bi3+) and antimony (Sb3+) have been explored due to their valence electronic configurations (6s26p0 for Bi3+ and 5s25p0 for Sb3+), which resemble that of Pb2+.13 However, their trivalent nature, along with differences in electronegativity and ionic radii, drives a structural shift away from the traditional ABX3 perovskite framework toward more stable, ternary halides of the A3MX6 type structures.14–16 Although these materials offer improved stability and reduced toxicity, they often exhibit less favorable optoelectronic characteristics compared to their Pb-based counterparts. Among these, significant attention has been given to the influence of alkaline metal cations on the electrical conductivity of molten cryolites such as K3AlF6, Rb3AlF6, and Cs3AlF6, where variations in ionic size and bonding environments strongly affect ionic mobility and melt behavior.17 Additionally, polymorphism in A3MF6 compounds (A = Rb, Cs; M = Al, Ga) has been investigated, particularly in crystals grown using mixed-halide fluxes, revealing how subtle chemical substitutions and growth conditions can drive the stabilization of multiple structural phases.14 Furthermore, first-principles DFT studies on K3GaF6 have provided valuable insights into its structural, electronic, and optical characteristics, contributing to a broader understanding of fluoride-based materials and their potential technological relevance.18 Cs3SbX6 (X = F, Cl) was shown to exhibit wide band gaps (up to ∼5.5 eV), stable cubic phases, and negative Gibbs free energies, alongside strong optical absorption and high light yields, suggesting potential in both photovoltaic and scintillation applications.19 Similarly, Rb3SbX6 (X = F, Cl, Br, I) displays a systematic reduction in bandgap from 5.47 eV (F) to 2.85 eV (I), consistent with increasing halide ionic radii, while maintaining excellent thermal stability and ductile mechanical properties.20 Sodium all-solid-state batteries (ASSBs) with superionic solid electrolytes such as Na3MX6 (X = Cl, Br, and I) show strong potential for safe and large-scale energy-storage applications.21 Such computational studies not only validate the structural and thermodynamic feasibility of A3BX6-type compounds but also highlight their potential as environmentally benign, tunable materials for next-generation optoelectronics.
To further enhance photovoltaic performance, researchers have begun to explore rudorffite-type Ag–Bi–I perovskites (Ag3BiI6, Ag2BiI5, AgBiI4) in tandem configurations with silicon. Through SCAPS-1D simulations, the optimization of absorber thickness, carrier transport layers, and defect densities has demonstrated significant efficiency improvements, with simulated tandem efficiencies reaching above 22% for Ag3BiI6/Si, far exceeding the single-junction values of 5 to 10%.22 These findings illustrate the importance of combining first-principles electronic structure modeling with device-level simulations, providing a multi-scale perspective that can guide the practical design of lead-free perovskite solar cells. Stability issues have motivated the development of advanced fabrication methods, such as dynamic casting (DC) combined with ramped annealing (RA), which improves surface coverage, crystallinity, and film density, thereby enhancing device performance. Using this approach, the PCE of inverted planar Ag3BiI6 devices increased from 0.07% to 1.08%, demonstrating the effectiveness of processing optimization for Pb-free rudorffites.23 These considerations highlight the dual challenge of achieving intrinsic material stability alongside effective film and device engineering, both of which are essential for the development of reliable Pb-free photovoltaic absorbers. To date, the vacancy-ordered halide perovskites Q3GaBr6 (Q = Na, K) have not been reported in prior theoretical or experimental studies, motivating their investigation as potential lead-free photovoltaic materials.
In this work, we employ first-principles density functional theory (DFT) to systematically examine the structural, electronic, optical, mechanical, dynamical, and thermodynamic properties of Na3GaBr6 and K3GaBr6. Particular attention is given to evaluating their stability, band structure, and optical absorption characteristics relevant to solar-energy conversion. The DFT-derived material parameters are subsequently incorporated into SCAPS-1D simulations to explore device-level photovoltaic performance. The device results are intended to provide theoretical performance limits rather than realistic device predictions. Key device parameters, including absorber thickness, defect density, and doping concentration, are varied to assess performance trends and identify optimal operating conditions. By combining atomistic insights with device-scale simulations, this study aims to connect intrinsic material properties with photovoltaic behavior. The results are therefore presented as theoretical performance limits intended to guide future experimental exploration of Ga-based vacancy-ordered halide perovskites as promising Pb-free absorber candidates for stable and sustainable solar-cell technologies.
2. Computational method
This section describes the theoretical framework and computational procedures adopted to evaluate the structural, electronic, optical, mechanical, vibrational, and thermodynamic properties of Q3GaBr6 (Q = Na, K). Density Functional Theory (DFT) is employed because of its proven reliability in predicting ground-state properties of crystalline materials, while SCAPS-1D device simulation is used to bridge atomic-scale material properties with macroscopic photovoltaic performance.24,25 The combined approach enables a comprehensive multiscale assessment of these materials for solar-cell applications.26–28 Density Functional Theory (DFT) simulations were undertaken using the CASTEP code within the Materials Studio framework29,30 to systematically evaluate the structural, electronic, optical, mechanical, photonic, thermodynamic, and charge-related properties of Q3GaBr6 (Q = Na, K). The exchange–correlation interactions were described by the Generalized Gradient Approximation based on the Perdew–Burke–Ernzerhof (GGA-PBE) functional,31 mGGA-RSCAN and HSE06 while a plane-wave basis set with a cutoff energy of 600 eV and Norm-Conserving Pseudopotentials (NCPP) was employed for all elements.32 This strategy ensures high computational efficiency by minimizing calculation time while retaining sufficient accuracy for large-scale material screening and device optimization. Brillouin-zone integrations were performed using a 7 × 7 × 7 Monkhorst–Pack k-point mesh for structural optimization and SCF convergence,33 whereas, a denser 12 × 12 × 12 grid was used during non-SCF calculations to obtain high-resolution electronic band structures and projected density of states.34 The total energy convergence criterion was set to 10−8 eV per atom, and structural relaxation proceeded until the Hellmann–Feynman forces fell below 0.01 eV Å−1 and the residual stresses were under 0.02 GPa.35 The optimized structures were employed to determine lattice parameters, bond lengths, formation enthalpy, and unit-cell volume to confirm structural and thermodynamic stability. Subsequent calculations were mainly performed using the GGA-PBE functional because of its computational efficiency and reliable accuracy, while the mGGA-RSCAN functional was used selectively for improved band-gap estimation despite its higher computational cost.36 Electronic band structures and DOS/PDOS were calculated to analyze band gaps and orbital contributions, while Mulliken, Hirshfeld, and Bader analyses were used to examine charge transfer and bonding characteristics. Charge density and charge density difference maps were employed to visualize electron distribution and bonding nature. Optical properties were derived from the complex dielectric function to evaluate absorption, refractive index, conductivity, reflectivity, and energy-loss behavior relevant to optoelectronic applications.37 Mechanical properties were evaluated from elastic constants obtained by the stress–strain method to determine elastic moduli and confirm mechanical stability. Phonon dispersion curves and phonon density of states were calculated to verify dynamic stability and analyze lattice vibrations. Thermodynamic parameters were derived from phonon data using the quasi-harmonic Debye model.Additionally, AIMD simulations were carried out at physically realistic temperatures of 300 K, 400 K, and 500 K to represent ambient and moderately elevated operating conditions relevant for halide perovskite solar-cell applications. The simulations were performed in the NVT ensemble using a Nosé–Hoover thermostat with a time step of 1.0 fs and a total simulation time of 8 to 10 ps, following sufficient equilibration. These temperatures were selected to ensure physically meaningful evaluation of thermal stability and structural robustness.
While DFT provides accurate intrinsic material properties, photovoltaic performance ultimately depends on device-level factors such as charge transport, recombination, and interface effects; therefore, to bridge this gap between atomistic predictions and practical device behavior, SCAPS-1D simulations were incorporated to translate the DFT-derived parameters into realistic solar-cell characteristic. The DFT-derived electronic and optical parameters, including bandgap, electron affinity, dielectric constant, and effective carrier masses, were incorporated into the SCAPS model. A systematic variation of absorber thickness (300 to 2100 nm), shallow acceptor density (1013 to 1020 cm−3), and total defect density (1010 to 1017 cm−3) was performed to identify optimal device configurations. Standard operating conditions were applied, including AM1.5G illumination at 1000 mW cm−2 and a temperature of 300 K, with appropriate series and shunt resistances and interface defect states introduced at ETL/absorber (Q3GaBr6) interfaces. The current density–voltage (J–V) characteristics were simulated to extract key photovoltaic parameters such as power conversion efficiency (PCE), open-circuit voltage (VOC), short-circuit current density (JSC), and fill factor (FF). Additionally, quantum efficiency (QE) spectra were generated to evaluate wavelength-dependent carrier generation, absorption, and collection efficiency. This combined DFT–SCAPS framework offers a comprehensive understanding of the intrinsic material properties and their device-level implications, providing a robust foundation for exploring the optoelectronic, thermal, and photovoltaic potential of Q3GaBr6 (Q = Na and K) structure.
Overall, the computational methodology adopted in this study combines first-principles electronic-structure calculations with device-level modeling to provide a complete and reliable evaluation of Q3GaBr6 (Q = Na, K). This integrated approach ensures that both intrinsic material stability and practical photovoltaic performance are simultaneously addressed, strengthening the predictive power of the present investigation.
3. Findings and discussion
3.1. X-ray diffraction (XRD) analysis
The simulated XRD patterns of Q3GaBr6 (Q = K and Na), obtained using CASTEP, are shown in Fig. 1 and provide essential insight into their structural characteristics. X-ray diffraction operates on the principle of constructive interference of X-rays scattered from periodic atomic planes, governed by Bragg's law nλ = 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, which directly relates peak positions to interplanar spacing and lattice dimensions.38 The diffraction profiles of both compounds exhibit sharp, well-defined peaks indicative of high crystallinity and confirm the formation of the desired cubic structure with Fm
θ, which directly relates peak positions to interplanar spacing and lattice dimensions.38 The diffraction profiles of both compounds exhibit sharp, well-defined peaks indicative of high crystallinity and confirm the formation of the desired cubic structure with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry.
m symmetry.
For Na3GaBr6 (green pattern, bottom), the prominent reflections appear at low angles around 12° to 13°, corresponding to the (100) and (110) planes, followed by intense peaks indexed to the (111), (200), (210), and (211) planes in the 20° to 27° region. Additional characteristic reflections associated with the (220), (221), (310), (311), and (222) planes are observed at higher angles, completing the diffraction fingerprint of the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. For K3GaBr6 (pink pattern, top), the main diffraction peaks are indexed to the (100), (111), (210), (211), (221), (222), and (321) crystallographic planes. Compared with Na3GaBr6, all diffraction peaks of K3GaBr6 are systematically shifted toward lower 2θ values. This shift reflects an expansion of the unit cell, which is consistent with the substitution of the smaller Na+ ion (1.02 Å) by the larger K+ ion (1.38 Å) according to Shannon's ionic radii.39 The incorporation of the larger K+ cation increases the lattice spacing and interplanar distances, resulting in a systematic displacement of the diffraction peaks toward lower angles in K3GaBr6.
m phase. For K3GaBr6 (pink pattern, top), the main diffraction peaks are indexed to the (100), (111), (210), (211), (221), (222), and (321) crystallographic planes. Compared with Na3GaBr6, all diffraction peaks of K3GaBr6 are systematically shifted toward lower 2θ values. This shift reflects an expansion of the unit cell, which is consistent with the substitution of the smaller Na+ ion (1.02 Å) by the larger K+ ion (1.38 Å) according to Shannon's ionic radii.39 The incorporation of the larger K+ cation increases the lattice spacing and interplanar distances, resulting in a systematic displacement of the diffraction peaks toward lower angles in K3GaBr6.
The most intense peaks for both compounds correspond to low-index planes such as (111), (200)/(210), and (221), indicating strong diffraction from densely packed atomic planes. The consistency of the peak positions with the cubic indexing and the absence of any extra reflections confirm that both materials preserve the same cubic structural symmetry while differing only in lattice size.
3.2. Analysis of structural properties
The Q3GaBr6 (Q = Na and K) materials crystallize in the cubic Fm3m (space group 225) structure, which is characteristic of highly symmetric halide frameworks.18 In this configuration, the Q cations occupy the 8c Wyckoff sites at (0.25, 0.25, 0.25), while Ga resides at the 4a position (0, 0, 0), forming the center of the GaBr6 octahedra. The Br anions are distributed over the 24e positions (x, 0, 0) with a refined positional parameter of x = 0.236![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 024, ensuring the correct octahedral coordination around Ga. This atomic arrangement stabilizes the cubic lattice and highlights the structural role of the Q-site cation in dictating the symmetry of Q3GaBr6 compounds. The corresponding crystal structure is shown in Fig. 2.
024, ensuring the correct octahedral coordination around Ga. This atomic arrangement stabilizes the cubic lattice and highlights the structural role of the Q-site cation in dictating the symmetry of Q3GaBr6 compounds. The corresponding crystal structure is shown in Fig. 2.
The structural properties of Q3GaBr6 (Q = Na and K) show a clear dependence on both the Q-site cation size and the choice of exchange–correlation functional. As summarized in Table 1, GGA-PBE predicts a lattice constant of 7.747 Å and a unit-cell volume of 328.804 Å3 for Na3GaBr6, while the incorporation of the larger K+ ion in K3GaBr6 leads to an expanded lattice constant of 8.085 Å and a volume of 373.764 Å3, consistent with the expected ionic-radius-driven lattice expansion. When recalculated using the meta-GGA SCAN functional, both compounds exhibit noticeably reduced lattice volumes (308.729 Å3 for Na3GaBr6 and 355.000 Å3 for K3GaBr6), reflecting the well-known tendency of SCAN to yield more compact and energetically accurate structures due to its improved treatment of intermediate-range exchange–correlation effects.40 In terms of electronic properties the electronic band gaps of several Cs-based halide compounds (Cs3InI6, Cs3InCl6, Cs3InBr6, Cs3TlI6, Cs3TlCl6, and Cs3TlBr6) using both GGA-level and hybrid HSE06 calculations.41 At the GGA level, these materials exhibit moderate band gaps in the range of about 0.93 to 1.60 eV, while the corresponding HSE06 values are significantly higher, lying between ∼1.72 and 2.79 eV. This systematic increase from GGA to HSE06 highlights the well-known underestimation of band gaps by semi local functionals and the improved accuracy obtained from hybrid approaches. In our work, Na3GaBr6 and K3GaBr6 show the same band-gap trend. The GGA-PBE band gaps (1.991 and 1.445 eV) lie in the same range as those of Cs3QR6 (Q = In, Tl, Ga; R = I, Cl, Br). With more advanced functionals, the band gaps increase to 2.602 and 1.985 eV (mGGA-rSCAN) and further to 3.096 and 2.567 eV (HSE06), respectively. This systematic increase from GGA → mGGA → HSE06 is fully consistent with the behavior observed.41 Moreover, while mainly focuses on band-gap values,41 our work extends this analysis by providing a comprehensive set of structural and thermodynamic parameters, including lattice constants, unit-cell volumes, densities, and formation enthalpies. This makes our study completer and more systematic, offering not only electronic properties but also stability and structural validation, thereby strengthening the reliability and applicability of Na3GaBr6 and K3GaBr6 as promising lead-free halide materials.
| Ref. | Compounds | GGA-PBE | mGGA-RSCAN | HSE06 | Formation enthalpy, ΔEf (eV per atom) | |||
|---|---|---|---|---|---|---|---|---|
| Energy band gap, eV | Lattice constant a0 (Å) | Unit cell volume, V (Å3) | Density, g cm−3 | Energy band gap, eV | Energy band gap, eV | |||
| This Work | Na3GaBr6 | 1.991 | 7.747 | 328.804 | 3.121 | 2.602 | 3.096 | −2.9357 |
| K3GaBr6 | 1.445 | 8.085 | 373.764 | 2.960 | 1.985 | 2.567 | −2.9906 | |
| 41 | Cs3InI6 | 1.60 | — | — | — | — | 2.79 | — |
| Cs3InCl6 | 1.45 | — | — | — | — | 2.68 | — | |
| Cs3InBr6 | 1.55 | — | — | — | — | 2.78 | — | |
| Cs3TlI6 | 0.99 | — | — | — | — | 1.73 | — | |
| Cs3TlCl6 | 0.93 | — | — | — | — | 1.72 | — | |
| Cs3TlBr6 | 1.01 | — | — | — | — | 1.78 | — | |
The formation energy (ΔEf) of a compound quantifies its thermodynamic stability with respect to decomposition into its elemental constituents. A negative formation energy indicates that the material is thermodynamically stable, whereas a positive value implies instability.42 For the halide perovskites Q3GaBr6 (Q = Na, K), the formation energy can be evaluated using eqn (1),
| ΔEf = Etot(A3GaBr6) − 3E(A) − E(Ga) − 6E(Br) | (1) |
From a thermodynamic perspective, GGA-PBE-calculated formation enthalpies are markedly negative (−2.9357 eV per atom for Na3GaBr6 and −2.9906 eV per atom for K3GaBr6), confirming their stability and spontaneous formation tendency. The slightly more negative value for K3GaBr6 suggests marginally greater energetic favorability, potentially due to enhanced lattice relaxation enabled by the larger K+ cation. The combined structural compactness, moderate-to-wide band gaps, and high thermodynamic stability indicate that both Na3GaBr6 and K3GaBr6 are promising candidates for optoelectronic and related functional applications.
The Goldschmidt tolerance factor (t) is a classical geometric descriptor widely used to assess the formability and structural stability of perovskite and double-perovskite materials. An ideal cubic perovskite corresponds to t = 1, where the ionic sizes are optimally matched and lattice distortions are minimal. When 0.8 ≤ t ≤ 0.9, the structure is generally stable but often exhibits cooperative tilting of the GaBr6 octahedra, leading to orthorhombic or rhombohedral distortions. For 0.9 ≤ t ≤ 1.0, the perovskite typically maintains a high-symmetry cubic or slightly tetragonal phase with limited octahedral rotations. In contrast, values of t < 0.8 or t > 1.0 tend to destabilize the perovskite framework, promoting non-perovskite or hexagonal phases.43,44
 | (2) |
Using the ionic radii rA, rB, and rX, the calculated tolerance factor increases from 0.918 for Na3GaBr6 to 0.987 for K3GaBr6, reflecting the larger ionic radius of K+, as shown in Table 2. This increase shifts the structure closer to the ideal cubic limit, indicating that K3GaBr6 is likely to be more symmetric and more stable in a cubic phase compared to Na3GaBr3.
The variation of bond length within a compound refers to the differences in distances between atoms of the same bonding type, indicating that not all atoms experience identical local environments. Such variations often arise from lattice distortions, differences in ionic sizes, or symmetry breaking within the crystal structure. This is important in research because bond length variation directly influences a material's structural stability, bonding strength, and electronic properties. Shorter bonds usually indicate stronger interactions, while longer ones suggest weaker bonding or lattice strain. Understanding these variations helps researchers explain and predict changes in mechanical, optical, and electronic behavior, enabling the design of materials with optimized performance for specific applications.
Table 3 presents the bond lengths of Na3GaBr6 and K3GaBr6 compounds, revealing how cation size influences their structural geometry. In both compounds, the Ga–Br bonds are the shortest (≈2.56 to 2.57 Å), indicating strong covalent interactions within the GaBr6 octahedra, while the longer Na–Br and K–Br bonds suggest weaker ionic interactions. When the larger K ion replaces Na, all bond lengths increase slightly, reflecting lattice expansion due to the larger ionic radius of K+. The presence of multiple A–Br and A–Ga distances implies a distorted coordination environment, but the Ga–Br framework remains relatively stable. Overall, the table indicates that cation substitution from Na to K leads to an expanded and slightly distorted lattice without significantly affecting the rigid GaBr6 octahedral structure.
| Compounds | Bonds | Bond length, L (Å) |
|---|---|---|
| Na3GaBr6 | Na (1,2)–Br | 2.911 |
| Na (3)–Br | 3.877 | |
| Ga–Br | 2.566 | |
| Na (1,2)–Ga | 4.744 | |
| Na (3)–Ga | 5.477 | |
| K3GaBr6 | K (1,2)–Br | 3.144 |
| K (3)–Br | 4.052 | |
| Ga–Br | 2.572 | |
| K (1,2)–Ga | 4.951 | |
| K (3)–Ga | 5.717 |
3.3. Electronic properties
After completing the geometric optimization of Q3GaBr6 (Q = Na and K), it is essential to investigate their electronic structure to determine whether these materials exhibit semiconducting behavior and evaluate their potential suitability for photoelectric and optoelectronic applications. The electronic band structure and density of states (DOS) calculations provide fundamental insights into the energy dispersion of electrons, band-gap characteristics, and orbital contributions that govern optical absorption, carrier transport, and radiative efficiency.46 Fig. 3 presents the band structures of Na3GaBr6 and K3GaBr6, obtained using two different exchange–correlation functionals along the high-symmetry paths. In both materials, the conduction band minimum (CBM) and valence band maximum (VBM) occur at the same symmetry point (M), confirming their direct band-gap nature. Such a direct band gap is highly advantageous, as it facilitates stronger optical absorption and efficient radiative recombination, making these compounds promising candidates for optoelectronic and photoelectric applications.47 Using the GGA-PBE functional (Fig. 3(a)), K3GaBr6 exhibits a conduction band minimum (CBM) of 1.445 eV and a valence band maximum (VBM) located at 0 eV, both occurring at the M high-symmetry point, yielding a direct band gap of 1.445 eV. Similarly, Na3GaBr6 shows a direct band gap of 1.991 eV at the same k-point. When the more advanced mGGA-rSCAN functional (Fig. 3(b)) is employed, the calculated band gaps increase to 1.985 eV for K3GaBr6 and 2.602 eV for Na3GaBr6, highlighting the well-known tendency of semi local GGA to underestimate band gaps and the improved accuracy provided by meta-GGA approaches. Furthermore, the hybrid HSE06 functional (Fig. 3(c)) predicts even larger band gaps of 3.096 eV for K3GaBr6 and 2.567 eV for Na3GaBr6, owing to the inclusion of a fraction of exact Hartree–Fock exchange, which significantly improves the description of electronic exchange correlation effects. The HSE06 results are generally considered closer to experimental values and therefore serve as a reliable benchmark for validating the electronic structure obtained from semi local and meta-GGA functionals. | ||
| Fig. 3 The different atomic orbitals to the valence and conduction bands of Q3GaBr6 (where A = Na, K) (a) GGA-PBE, (b) mGGA-RSCAN and (c) HSE06 with electronic band structure. | ||
The systematic increase in band-gap values from GGA-PBE to mGGA-rSCAN and further to HSE06 reflects the intrinsic limitation of semi local exchange–correlation functionals in underestimating band gaps due to the absence of derivative discontinuity in the exchange potential. The consistency of the GGA → mGGA → HSE06 trend observed in this work confirms the robustness of the calculated electronic structure and supports the reliability of the predicted semiconducting behavior of Na3GaBr6 and K3GaBr6.
Although mGGA-rSCAN and HSE06 provide more accurate band-gap estimations, both are computationally more demanding, with HSE06 being particularly expensive in terms of computational resources and time. As a result, these functionals are less practical for extensive calculations of optical, mechanical, and other physical properties on standard personal-computer platforms. In contrast, GGA-PBE offers an optimal balance between computational efficiency and acceptable quantitative accuracy. Therefore, all subsequent calculations in this work were performed using the GGA-PBE functional, while mGGA-rSCAN and HSE06 were employed mainly for band-gap correction and validation purposes.48
3.4. Density of states (DOS)
The DOS describes the number of electronic states available at each energy level in a material. It is obtained by integrating the electronic band structure over the Brillouin zone and indicates how electrons occupy different energy ranges. Peaks in the DOS correspond to energies where many states are concentrated, while low-DOS regions reflect fewer available states.49 The Partial Density of States (PDOS) further resolves these states into contributions from specific atoms or orbitals, helping to identify the origin of the valence and conduction bands, as well as possible hybridization between atomic orbitals. DOS and PDOS together provide essential insight into the electronic structure and bonding characteristics of the material.50In both K3GaBr6 and Na3GaBr6, the valence band region (below the Fermi level, EF) is predominantly governed by the Br-4p orbitals, which exhibit strong hybridization with minor contributions from Ga-4p states.
This confirms that bromine plays the dominant role in defining the bonding characteristics and shaping the valence band maximum.51 The conduction band region (above EF) mainly originates from the Na-3s and K-4s orbitals, along with noticeable hybridization from Br-4s states, indicating that Ga–Br interactions significantly influence the conduction band minimum and consequently determine the bandgap nature. As expected, the alkali cations (Na, K) contribute minimally to the electronic states, functioning primarily as charge-compensating species within the lattice. The corresponding PDOS profiles are illustrated in Fig. 4(a and b). For Na3GaBr6 [Fig. 4(a)], the VBM and CBM peaks appear at 18.08 eV and 13.32 eV, respectively, while for K3GaBr6 [Fig. 4(b)], the VBM and CBM peaks are observed at 23.81 eV and 17.084 eV. In both materials, the TDOS plots show valence- and conduction-band peaks extending slightly into one another, which arises from DFT-related smearing or numerical broadening parameters rather than indicating physical overlap. The calculated bandgap values obtained from the DOS are 1.991 eV for Na3GaBr6 and 1.445 eV for K3GaBr6, consistent with their electronic band structures.
3.5. Optical properties
Optical properties describe how a material interacts with incident light through processes such as absorption, reflection, transmission, refraction, and emission, all of which are fundamentally governed by its electronic structure. Key optical parameters include the absorption coefficient, which quantifies light absorption per unit distance; the refractive index, representing the reduction of light speed within the medium; the dielectric function, describing the material's response to external electromagnetic fields; and the optical conductivity, which characterizes the current generated under optical excitation.52 Understanding these properties is essential for the design and optimization of optoelectronic and photonic devices such as solar cells, photodetectors, LEDs, and optical coatings.53It should be noted that the present optical property calculations are performed within the independent-particle approximation using standard DFT, where excitonic effects arising from electron–hole interactions are not explicitly included. In halide perovskites, excitonic contributions can be significant, particularly near the absorption edge, and may lead to a red shift and enhancement of optical absorption. Therefore, the calculated optical spectra represent the intrinsic interband transition behavior of the materials and may slightly underestimate excitonic features. A more accurate description would require many-body approaches such as the GW approximation combined with the Bethe–Salpeter equation (GW-BSE), which are computationally demanding and beyond the scope of the present work.
| ε(ω) = ε1(ω) + jε2(ω) | (3) |
The real part, ε1(ω) is obtained using the Kramers–Kronig relation:
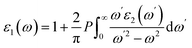 | (4) |
At zero photon energy, the real part ε1(ω) of Na3GaBr6 begins at approximately 3.39 and increases to a maximum value of about 5.02 near 4.8 eV, indicating strong polarization and enhanced photon-matter interaction. Beyond 8.32 eV, ε1(ω) decreases and becomes zero to negative, suggesting the emergence of plasmonic-like or high-reflectivity behavior at higher photon energies. In comparison, K3GaBr6 exhibits a slightly higher static dielectric constant with an initial ε1(0) value of approximately 3.75, and reaches its maximum of about 5.09 around 4.72 eV. With further increase in photon energy, ε1(ω) gradually decreases and crosses zero near 10.27 eV, becoming negative thereafter. Overall, while both compounds demonstrate similar dielectric characteristics, Na3GaBr6 shows the onset of negative dielectric behavior at a lower energy than K3GaBr6, indicating comparatively stronger plasmonic tendencies in the high-energy region. The spectrum also highlights the behavior of the imaginary part ε2(ω), which is critical for understanding the optical absorption properties. The imaginary component is calculated from the momentum-matrix elements between occupied and unoccupied states as,
 | (5) |
The imaginary part of the dielectric function, ε2(ω) starts to rise at photon energies of about 1.59 eV for Na3GaBr6 and 1.06 eV for K3GaBr6, corresponding to the onset of optical absorption in these materials. Within the visible energy range (1.65 to 3.1 eV), both compounds exhibit distinct absorption peaks, with Na3GaBr6 showing a peak value of approximately 0.92 at 2.72 eV and K3GaBr6 exhibiting a peak of about 0.76 at 3.10 eV. As the photon energy further increases into the ultraviolet region, the intensity of ε2(ω) increases significantly, reaching maximum values of about 4.82 at 7.30 eV for Na3GaBr6 and 4.21 at 7.80 eV for K3GaBr6. Although Na3GaBr3 shows stronger optical transitions, the lower absorption onset and extended response toward lower photon energies in K3GaBr6 suggest comparatively better suitability for optoelectronic applications, particularly in devices requiring enhanced low-energy light absorption.
 | (6) |
Fig. 5(b) presents the absorption spectra of Na3GaBr6 and K3GaBr6, illustrating their spectral response and light-harvesting capability over a wide photon-energy range. This optical parameter is crucial for the design of optoelectronic devices such as solar cells, ultraviolet (UV) photodetectors, and photodiodes, where strong and efficient photon absorption is required. In the infrared region (0–1.5 eV), both compounds show negligible absorption, indicating minimal photon interaction due to the absence of available electronic transitions below the band gap. In the visible energy range (1.65 to 3.10), the absorption coefficients exceed 104 cm−1 for both compounds, signifying the onset of strong interband electronic transitions from the valence to the conduction band, which is essential for efficient solar light harvesting.57,58 Specifically, absorption peaks of approximately 0.98 × 104 cm−1 for Na3GaBr6 and 1.12 × 104 cm−1 for K3GaBr6 are observed near 3.10 eV, indicating effective interaction with visible photons and strong electronic transitions. In the ultraviolet region, the absorption intensifies significantly, reaching maximum values of about 1.71 × 105 cm−1 at 7.89 eV for Na3GaBr6 and 1.88 × 105 cm−1 at 10.57 eV for K3GaBr6. This strong UV absorption originates from high-energy electronic transitions involving deeper valence states, highlighting their suitability for UV-sensitive optoelectronic applications. Overall, the absorption behavior directly reflects the electronic band structure of these materials, with K3GaBr6 showing comparatively stronger high-energy absorption.
 | (7) |
In the infrared (IR) region (0–1.65 eV), both compounds exhibit low reflectivity values of about 0.116 for Na3GaBr6 and 0.097 for K3GaBr6 at 1.65 eV, as shown in Fig. 5(d), indicating minimal surface reflection and good optical transparency. As the photon energy enters the visible range (1.65–3.10 eV), a slight increase in reflectivity is observed in Fig. 5(d), with peak values of approximately 0.121 at 2.35 eV for Na3GaBr6 and 0.111 at 2.65 eV for K3GaBr6, where Na3GaBr6 exhibits marginally higher reflectance. In the ultraviolet (UV) region (>3.10 eV), a pronounced rise in reflectivity is also evident in Fig. 5(d), reflecting stronger photon–electron interactions at higher energies. Since the objective of this study is to identify efficient solar-cell absorber materials, the consistently low reflectivity across the visible and near-IR regions shown in Fig. 5(d) indicates enhanced light coupling and reduced optical losses. Consequently, both compounds are promising candidates as absorber layers for photovoltaic devices.
 | (8) |
 | (9) |
As shown in Fig. 5(e), the static refractive index n(0) is 1.84 for Na3GaBr6 and 1.98 for K3GaBr6, indicating moderate optical polarization, with the higher value for K3GaBr6 suggesting stronger electronic polarizability due to its larger cation size. Visible-range peaks appear at 2.44 eV (n(ω) = 1.98) for Na3GaBr6 and 1.77 eV (n(ω) = 2.04) for K3GaBr6, attributed to band-edge electronic transitions. In the UV region (3.2 to 12 eV), n(ω) increases further, reaching maxima of 2.28 and 2.30, respectively, due to strong interband excitations. The extinction coefficient k(ω) remains nearly zero in the IR-visible range, confirming low optical loss and high transparency. Absorption begins at about 1.99 eV for Na3GaBr6 and 1.45 eV for K3GaBr6, consistent with band-gap energies. Strong UV peaks (1.35 at 7.68 eV and 1.25 at 8.34 eV) arise from deeper interband transitions, indicating potential for UV-optoelectronic applications.64
 | (10) |
Fig. 5(f) shows the loss function of Na3GaBr6 and K3GaBr6 over the photon-energy range of 0–12 eV. In the infrared region (0 to 1.65 eV), both materials exhibit negligible optical loss, confirming high transparency and minimal energy dissipation. In the visible region, small maxima appear at 2.50 eV (0.54) for Na3GaBr6 and at 3.21 eV (0.525) for K3GaBr6, though the overall loss remains low, indicating good optical performance in this spectrum.66 As the photon energy enters the ultraviolet region, the loss function increases significantly, indicating the onset of strong electronic excitations. K3GaBr6 reaches a maximum value of 0.72 at 11.9 eV, while Na3GaBr6 exhibits a slightly lower peak of 0.63 near 11.3 eV. These peaks correspond to the plasma resonance frequency, where collective oscillations of conduction electrons strongly interact with incident electromagnetic radiation.59 The earlier and stronger plasmonic response of K3GaBr6 suggests higher electronic polarizability compared with Na3GaBr6.
3.6. Elastic and mechanical properties
| C11 > 0,4C44 > 0, C11 − C12 > 0 and C11 + 2C12 > 0 | (11) |
The mechanical stability of Na3GaBr6 and K3GaBr6 was evaluated using the Born stability criteria for cubic systems. For Na3GaBr6 and K3GaBr6, the calculated elastic constants satisfy all stability conditions: C11 = 13.704 and 26.798 GPa, C11 − C12 = 19.848 and 22.065 GPa, C44 = 2.776 and 0.211 GPa, and C11 + 2C12 = 1.424 and 36.264 GPa, respectively, as shown in Fig. 6(a). The fulfillment of these inequalities (C11 > 0, 4C44 > 0, C11 − C12 > 0 and C11 + 2C12 > 0) confirms that both compounds are mechanically stable. Comparatively, K3GaBr6 exhibits a higher C11 value, indicating stronger resistance to uniaxial compression, whereas the lower C44 value of K3GaBr6 suggests reduced resistance to shear deformation compared with Na3GaBr6. These results indicate that Na3GaBr6 is relatively more resistant to shear stress, while K3GaBr6 demonstrates greater compressive stiffness. Physically, the higher C11 value of K3GaBr6 indicates stronger resistance to uniaxial compression along the principal crystallographic directions. The negative C12 value for Na3GaBr6 suggests an unusual lateral strain response under axial loading, which is often associated with auxetic-like behavior and requires careful interpretation.
In contrast, the positive C12 of K3GaBr6 reflects a more conventional elastic response. Furthermore, the much lower C44 value of K3GaBr6 indicates weaker resistance to shear deformation, implying a comparatively softer lattice under shear stress. Overall, Na3GaBr6 appears more resistant to shear distortion, while K3GaBr6 exhibits greater compressive stiffness.
 | (12) |
 | (13) |
 | (14) |
 | (15) |
 | (16) |
 | (17) |
As shown in Fig. 6(b), the extremely low bulk modulus of Na3GaBr6 (0.471 GPa) reflects its highly compressible lattice and originates from the weak ionic interaction between Na+ and Br− ions, combined with the open framework formed by isolated GaBr6 octahedra. Such a structure can undergo significant volume reduction under small external pressure, which naturally results in a low resistance to hydrostatic compression. In contrast, K3GaBr6 exhibits stronger interatomic cohesion and a more compact framework, leading to a much higher bulk modulus (12.088 GPa).
However, despite its high compressibility, Na3GaBr6 shows a comparatively larger shear modulus (4.767 GPa) than K3GaBr6 (2.443 GPa), indicating better resistance to shape distortion and shear deformation. This contrasting behavior suggests that while Na3GaBr6 is easily compressible under hydrostatic pressure, its lattice maintains appreciable rigidity against shear stresses due to the directional strength of the Ga–Br bonds within the rigid GaBr6 octahedra. Conversely, the more compact structure of K3GaBr6 enhances its resistance to volume compression but reduces its ability to withstand shear deformation. This anisotropic mechanical response highlights the distinct deformation mechanisms operating in the two compounds and underscores the strong influence of lattice topology and bonding nature on their elastic behavior. Likewise, Young's modulus is higher for K3GaBr6 (6.868 GPa) compared with Na3GaBr6 (3.274 GPa), confirming greater stiffness and tensile strength.
The Poisson's ratio (ν) describes the transverse strain response under axial loading and provides insight into the nature of chemical bonding. Typically, values close to 0.25 indicate mixed ionic-covalent bonding. The strongly negative Poisson's ratio in Fig. 6(b) obtained for Na3GaBr6 (ν = −0.438) indicates auxetic behavior, in which the material expands laterally under tensile strain. Such behavior, although uncommon, has been reported in framework-type materials and structures composed of rigid polyhedral units connected through flexible linkages. In Na3GaBr6, the rigid GaBr6 octahedra are interconnected by comparatively weak Na–Br ionic bonds, forming an open structural network that can accommodate transverse expansion through rotation and hinging of the octahedra under applied stress. This structural flexibility provides a plausible microscopic origin for the predicted auxetic response.
 | (18) |
Pugh's ratio (B/G) is widely used to assess ductility, with values greater than 1.75 indicating ductile behavior and lower values signifying brittleness. The calculated B/G ratios are 0.099 for Na3GaBr6 and 4.948 for K3GaBr6, indicating that Na3GaBr6 is strongly brittle, whereas K3GaBr6 shows pronounced ductile character. These results suggest that K3GaBr6 is mechanically more suitable for flexible device fabrication, while Na3GaBr6 may be more prone to mechanical failure under stress.
Mechanical parameters derived from elastic constants provide valuable insight into a material's rigidity, deformation resistance, and structural reliability in device environments. Hardness reflects resistance to permanent deformation, while the machinability index indicates ease of mechanical processing.
 | (19) |
 | (20) |
Table 4 presents the calculated mechanical parameters of Na3GaBr6 and K3GaBr6 materials, Na3GaBr6 exhibits significantly higher hardness (52.495) than K3GaBr6 (13.413), indicating stronger resistance to surface deformation and wear. The machinability index is much lower for Na3GaBr6 (0.17) than for K3GaBr6 (57.289), suggesting that K3GaBr6 is easier to machine and mechanically process.
| Mechanical properties | Na3GaBr6 | K3GaBr6 |
|---|---|---|
| Hardness (H) | 52.495 | 13.413 |
| Machinability index (µM) | 0.17 | 57.289 |
| Elastic Debye temperature | 52.772 | 112.484 |
| Average sound velocity (Vm (m s−1)) | 593.528 | 1212.156 |
| Anisotropy (AU) | 2.225 | 60.279 |
| Zener isotropic factor (A) | 0.28 | 0.0019 |
| Equivalent Zener anisotropy measure (Aeq) | 3.574 | 52.213 |
| Anisotropy in share (AG) | 0.182 | 0.858 |
The elastic Debye temperature is associated with lattice vibration behavior and bond strength, with higher values implying stronger interatomic interactions. The average sound velocity correlates with elastic stiffness and phonon transport. The larger Debye temperature (112.484 K) and sound velocity (1212.156 m s−1) of K3GaBr6 imply stronger bonding and lattice stiffness compared with Na3GaBr6 (52.772 K and 593.528 m s−1).
To assess the directional dependency of mechanical properties in Q3GaBr6 (Q = Na and K) perovskites, various anisotropy factors were calculated, including the universal anisotropy index (Au), Zener anisotropy factor (A), equivalent Zener anisotropy (Aeq), and shear anisotropy index (AG). These parameters reveal the extent to which a material's elastic response varies with direction, and help identify potential weaknesses in structural applications shown in Table 4.
 | (21) |
The Zener isotropic factor A can be defined as,
 | (22) |
For an isotropic material, A = A1 = A2 = A3 = 1, and the variation from unity corresponds to the anisotropy of a material.70
 | (23) |
 | (24) |
 | (25) |
 | (26) |
Anisotropy analysis further shows that K3GaBr6 is highly anisotropic, with a universal anisotropy index AU = 60.279, Zener factor A = 0.0019, and equivalent anisotropy measure Aeq = 52.213, while Na3GaBr6 displays comparatively lower anisotropy (AU = 2.225, A = 0.28, Aeq = 3.574). This indicates that Na3GaBr6 possesses a more uniform mechanical response along different crystallographic directions, whereas K3GaBr6 exhibits strong directional dependence. The lower shear anisotropy index AG of Na3GaBr6 (0.182) compared to K3GaBr6 (0.858) further confirms its superior mechanical isotropy. Consequently, Na3GaBr6 shows higher hardness, stiffness, and directional stability, while K3GaBr6 is comparatively softer, more ductile, and easier to machine but strongly anisotropic.
The auxetic behavior predicted for Na3GaBr6 is consistent with its elastic characteristics and structural flexibility. The finite universal anisotropy index (AU = 2.225) together with the directional variation of Poisson's ratio shown in Fig. 7 reflects the presence of deformation pathways that allow transverse expansion under applied strain. Importantly, the absence of imaginary phonon modes confirms that this response arises from an intrinsically stable lattice, where the rigid GaBr6 octahedra can undergo rotational and hinging motions mediated by weak Na–Br interactions, rather than from any mechanical or dynamical instability.
3.7. Correlation between structural and elastic properties
The elastic behavior of Q3GaBr6 (Q = Na, K) is strongly governed by their underlying structural characteristics. The increase in lattice constant and unit-cell volume from Na3GaBr6 to K3GaBr6, caused by the larger ionic radius of K+, leads to a more expanded crystal framework with longer A–Br and A–Ga bond lengths. This structural expansion reduces resistance to shear deformation, which is reflected in the significantly lower C44 and shear modulus of K3GaBr6 compared to Na3GaBr6, while simultaneously enhancing its resistance to volume compression as indicated by the higher bulk modulus. Furthermore, the tolerance factor increases from 0.918 for Na3GaBr6 to 0.987 for K3GaBr6, shifting the structure closer to an ideal cubic geometry. This improved geometrical stability promotes ductile behavior in K3GaBr6, as confirmed by its large B/G ratio and positive Poisson's ratio. In contrast, the relatively smaller lattice constant and shorter bond lengths in Na3GaBr6 result in stronger directional bonding, higher shear modulus, and greater hardness, but also lead to brittle behavior and negative Poisson's ratio. Therefore, the observed elastic and mechanical responses can be directly correlated with the structural parameters: lattice expansion favors ductility and compressive stiffness, whereas structural compactness enhances shear rigidity and hardness. This strong structure property relationship highlights how Q-site cation substitution serves as an effective strategy to tune the mechanical performance of vacancy-ordered halide perovskites for device applications.3.8. Anisotropy
To better understand the anisotropic mechanical behavior of Q3GaBr6 (Q = Na and K), both 2D and 3D visualizations of directional elastic properties, Young's modulus, shear modulus, and Poisson's ratio, were analyzed.In Fig. 7 reveal how, each property varies with crystallographic direction, offering insights into the degree of anisotropy. Na3GaBr6 shows highly anisotropic behavior, particularly in Young's modulus and Poisson's ratio, with sharp directional variations and pronounced surface lobes. In contrast, K3GaBr6 displays more moderate anisotropy with relatively smoother 3D profiles. The influence of the Q-site cation is evident in shaping the directional stiffness and flexibility of the compounds. Additionally, the symmetry and shape of the 3D surfaces align with the underlying crystal structure, while 2D projections aid in identifying principal directions and extrema. These anisotropic traits are crucial for evaluating the suitability of these materials in directional stress-sensitive device applications.
3.9. Phonon analysis
Phonon stability analysis is employed to evaluate the dynamical stability of crystalline materials by investigating their lattice vibrations, where atoms oscillate around their equilibrium positions and their collective motions are quantized as phonons. These phonons play a fundamental role in governing the thermal, mechanical, and structural properties of solids.71In lattice dynamics, phonon frequencies and vibrational modes are obtained by solving the eigenvalue problem of the dynamical matrix, which is constructed from the second-order derivatives of the total energy with respect to atomic displacements. A material is considered dynamically stable only when all phonon frequencies are real and positive throughout the entire Brillouin zone.72 The presence of imaginary (negative) frequencies signifies lattice instability and indicates the tendency of the system toward structural distortion or a possible phase transition.73 Therefore, the phonon spectrum provides direct evidence of the dynamical stability of a material, where the absence of imaginary modes confirms its structural robustness. Moreover, phonons are responsible for key physical properties such as thermal conductivity, heat capacity, electron phonon coupling, and lattice-mediated phase transitions. The phonon band structures reveal that Q3GaBr6 (Q = Na and K) materials are dynamically stable, as no imaginary (negative) phonon frequencies are detected along any high-symmetry directions (W–L–Γ–X–W–K) in the Brillouin zone, as shown in Fig. 8. This confirms that the optimized crystal structures correspond to local minima on the potential energy surface. The acoustic phonon branches originate from zero frequency at the Γ point, in agreement with the translational invariance of the lattice and the satisfaction of basic mechanical stability conditions. The optical phonon modes extend up to approximately 6 THz, reflecting moderate interatomic force constants in the studied systems. Notably, a large number of phonon branches are concentrated in the frequency range between 1 and 5.5 THz, indicating strong vibrational interactions among the constituent atoms. The absence of soft modes throughout the entire Brillouin zone suggests that no structural phase transition occurs at zero temperature, and the phonon spectra further support the thermodynamic stability of the investigated materials.
3.10. Ab initio molecular dynamics analysis
AIMD analysis serves as a powerful tool to bridge theoretical predictions and experimental conditions, ensuring that newly designed materials are not only stable in theory but also reliable in practical applications. Unlike static DFT calculations, which only provide ground-state properties, AIMD captures the dynamic evolution of a material's structure, energies, and thermodynamic parameters over time. This allows researchers to evaluate the thermal and dynamic stability of compounds, monitor fluctuations in total, kinetic, and potential energies, and track changes in temperature, pressure, and enthalpy, all of which are critical for determining whether a material can maintain structural integrity under realistic operating conditions.Moreover, AIMD can reveal phase stability, anharmonic vibrations, melting behavior, lattice distortions, and resistance to external perturbations, providing insights into material performance beyond equilibrium.
The AIMD simulation results shown in Fig. 9(a–f) demonstrate the thermal and energetic stability of Na3GaBr6 and K3GaBr6 over a 50 ps time scale at 300 K, 400 K, and 500 K. For Na3GaBr6 (Fig. 9(a, c and e)), the total energy remains nearly constant at ∼3600 kcal mol−1 throughout the simulation at all temperatures, showing no systematic drift with time. The kinetic energy fluctuates around ∼2600 kcal mol−1 at 300 K, ∼2700 kcal mol−1 at 400 K, and ∼2850 kcal mol−1 at 500 K, consistent with the expected increase in atomic vibrations with temperature. Meanwhile, the potential energy stabilizes around ∼900–1100 kcal mol−1 with small oscillations, indicating that the crystal framework retains its structural integrity without any bond breaking or structural distortion. Similarly, for K3GaBr6 (Fig. 9(b, d and f)), the total energy remains stable at ∼3400 kcal mol−1 across the entire simulation period. The kinetic energy varies from ∼2500 kcal mol−1 at 300 K to ∼2700 kcal mol−1 at 500 K, while the potential energy fluctuates near ∼850–1000 kcal mol−1. The absence of any abrupt energy variation or drift confirms dynamic stability at elevated temperatures. The slightly lower total and potential energy values of K3GaBr6 compared to Na3GaBr6 suggest comparatively weaker lattice interactions and reduced vibrational stiffness, which is consistent with its softer lattice behavior observed in mechanical analysis. Overall, the steady energy profiles with temperature-dependent kinetic energy increase confirm that both compounds are thermally stable and dynamically robust up to 500 K.
The temperature evolution shown in Fig. 10 further confirms the thermal stability of both compounds during the 50 ps AIMD simulations. For Na3GaBr6 (Fig. 10(a)), the temperature fluctuates around the set values after initial equilibration, with averages of 300 K (ranging 250–350 K), 400 K (ranging 350–450 K), and 500 K (ranging 450–600 K). The oscillations slightly increase with temperature, which is expected due to enhanced atomic vibrations at higher thermal energy. Similarly, in Fig. 10(b), K3GaBr6 maintains stable temperature profiles centered near the target temperatures. At 300 K, the temperature varies within 260–340 K; at 400 K, within 350–460 K; and at 500 K, within 430–650 K. No systematic drift or abnormal thermal spike is observed after the equilibration period, confirming proper thermostat regulation and thermodynamic stability.
 | ||
| Fig. 10 Temperature evolution during AIMD simulations of (a) Na3GaBr6 and (b) K3GaBr6 and at 300 K, 400 K, and 500 K. | ||
A comparison between the two compounds indicates that K3GaBr6 exhibits comparatively smoother and slightly narrower temperature fluctuations than Na3GaBr6, especially at elevated temperatures. This observation is consistent with the energy stability trends in Fig. 9 and suggests that K substitution contributes to improved dynamic and thermal stability of the lattice.
3.11. Experimental feasibility, chemical stability, and synthesis prospects
From an experimental viewpoint, the predicted negative formation energies, favorable tolerance factors (0.918 to 0.987), absence of imaginary phonon modes, and thermal robustness observed from AIMD simulations strongly indicate that Q3GaBr6 (Q = Na, K) compounds are chemically and structurally feasible for synthesis under laboratory conditions. The rigid GaBr6 octahedral framework and strong Ga–Br bonding suggests good resistance against lattice decomposition, while the alkali-metal cations provide ionic stabilization without participating directly in electronic degradation pathways. Similar vacancy-ordered A3BX6 halides such as Cs3InX6, Cs3SbX6, and Ag3BiI6 have already been experimentally synthesized using conventional solution processing, solid-state reactions, and flux growth methods, which indicates that Q3GaBr6 compounds are likely to be experimentally accessible through comparable synthesis routes. Possible fabrication strategies include solution-based crystallization using metal halide precursors, solid-state reactions under controlled atmospheres, and low-temperature melt or flux-assisted growth. However, challenges may arise from moisture sensitivity of bromide compounds and potential phase purity control, which require careful optimization of reaction temperature, stoichiometry, and encapsulation.3.12. Population analysis
To further elucidate the electronic structure and bonding environment in the Q3GaBr6 (Q = Na, K) perovskites, a comprehensive Mulliken and Hirshfeld charge population analysis was carried out (Table 5). The low charge spilling values (0.13% for Na3GaBr6 and 0.10% for K3GaBr6) indicate reliable basis set convergence. In both compounds, the Q-site cations (Na+/K+) show partial charge transfer, with Mulliken charges of +0.50 (Na1,2) and +0.56 (K1,2), suggesting slight covalent interactions with nearby Br atoms, deviating from a purely ionic model. Notably, the third A-site ion in each case (Na3 = +0.19, K3 = −0.10) shows reduced or even reversed charge transfer, likely due to asymmetric local environments or polarization effects.| Compound | Change spilling | Species | Mulliken atomic populations | Mulliken change | Hirshfeld change | ||||
|---|---|---|---|---|---|---|---|---|---|
| s | P | d | f | Total | |||||
| Na3GaBr6 | 0.13% | Na (1) | 2.14 | 6.37 | 0.00 | 0.00 | 8.50 | 0.50 | 0.36 |
| Na (2) | 2.14 | 6.37 | 0.00 | 0.00 | 8.50 | 0.50 | 0.36 | ||
| Na (3) | 2.24 | 6.57 | 0.00 | 0.00 | 8.81 | 0.19 | 0.15 | ||
| Ga | 1.41 | 1.51 | 10.00 | 0.00 | 12.92 | 0.08 | 0.26 | ||
| Br | 1.74 | 5.47 | 0.00 | 0.00 | 7.21 | −0.21 | −0.19 | ||
| K3GaBr6 | 0.10% | K (1) | 2.04 | 6.19 | 0.21 | 0.00 | 8.44 | 0.56 | 0.31 |
| K (2) | 2.04 | 6.19 | 0.21 | 0.00 | 8.44 | 0.56 | 0.31 | ||
| K (3) | 2.11 | 6.43 | 0.56 | 0.00 | 9.10 | −0.10 | 0.17 | ||
| Ga | 1.46 | 1.52 | 10.00 | 0.00 | 12.98 | 0.02 | 0.28 | ||
| Br | 1.75 | 5.42 | 0.00 | 0.00 | 7.18 | −0.18 | −0.18 | ||
Ga atoms in both structures maintain almost neutral Mulliken charges (+0.08 in Na3GaBr6 and +0.02 in K3GaBr6), despite hosting significant d-electron density (∼10 e−), hinting at a delocalized bonding character with Br. The Br atoms, with negative Mulliken charges (−0.21 to −0.18), serve as primary electron acceptors, consistent with their higher electronegativity. Hirshfeld charge trends qualitatively support these observations but show slightly reduced magnitudes due to different partitioning criteria.74,75 The comparative results underscore the influence of ionic radius and electronegativity, Na+ exhibiting stronger localization than K+, and collectively suggest a complex interplay of ionic and covalent character in Ga–Br and A–Br bonds. These charge distributions align well with oxidation state expectations and provide deeper insight into the compounds' electrostatic stability and potential functional behavior.
4. Device performance and photovoltaic parameters
Driven by the favorable optoelectronic and structural properties of Q3GaBr6 (Q = Na, K), including suitable semiconducting behavior, mechanical robustness, strong light absorption, low optical loss, high refractive index, and confirmed thermodynamic and dynamical stability, we designed and simulated a Ni/Q3GaBr6/SnS2/FTO/Al perovskite solar cell using the SCAPS-1D platform. In this architecture, Q3GaBr6 serves as the absorber layer, while SnS2 is employed as the electron transport layer (ETL) due to its inorganic nature, excellent resistance to moisture and heat, low cost, non-toxicity, and ease of fabrication.76Nickel and aluminum are used as the back and front contacts,77 respectively, and fluorine-doped tin oxide (FTO) functions as the transparent conducting electrode.78 The schematic illustration of the device structure is presented in Fig. 11, and the material parameters utilized in the SCAPS-1D simulations are summarized in Table 6.
| Parameters | FTO | SnS2 | K3GaBr6 | Na3GaBr6 |
|---|---|---|---|---|
| Thickness (nm) | 50 | 50 | 800 | 800 |
| Band gap, Eg (eV) | 3.6 | 2.24 | 1.445 | 1.991 |
| Dielectric permittivity, εr | 10 | 10 | 3.7564 | 3.3865 |
| Electron affinity, χ (eV) | 4.5 | 4.24 | 3.655 | 3.109 |
| CB effective density of states, NC (cm−3) | 2 × 1018 | 2.2 × 1018 | 1.08 × 1019 | 1.240 × 1019 |
| VB effective density of states, NV (cm−3) | 1.8 × 1019 | 1.8 × 1019 | 1.476 × 1019 | 2.124 × 1019 |
| Donor density, ND (cm−3) | 1 × 1018 | 1 × 1017 | 0 | 0 |
| Acceptor density, NA (cm−3) | 0 | 0 | 1 × 1017 | 1 × 1017 |
| Electron mobility, µn (cm2 V−1 s −1) | 50 | 50 | 90 | 80 |
| Hole mobility, µh (cm2 V−1 s −1) | 20 | 50 | 38 | 44 |
| Defect density, Nt (cm−3) | 1 ×1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 |
By evaluating parameters such as capture cross-section, defect type, and defect density, one can reveal how easily electrons or holes are trapped, whether the defects act as recombination centers, and how severely they limit the open-circuit voltage (VOC), short circuit current density (JSC), and power conversion efficiency (PCE).79 This analysis provides insights into interface quality, potential recombination losses, and pathways for optimizing material selection or surface passivation, ultimately guiding the design of high-performance solar cells.80
Table 7 summarizes the interfacial defect parameters of the SnS2/Q3GaX6 solar cell systems, with particular emphasis on the SnS2/Na3GaBr6 and SnS2/K3GaBr6 interfaces. In this work, a capture cross-section of 1 × 10−19 cm2 for both electrons and holes and a neutral defect type were considered, following commonly adopted assumptions for well-passivated heterointerfaces in numerical simulations. Similar ranges of capture cross-section (10−18–10−20 cm2) and neutral interface states have been widely reported in previous SCAPS and DFT-assisted device studies of chalcogenide/perovskite and metal-chalcogenide heterojunctions, where minimized trap activity is assumed to represent optimized interface conditions. The interfacial defect density was limited to 1 × 1011 cm−2, which is consistent with previously reported values for high-quality, chemically stable heterointerfaces in simulated perovskite and chalcogenide solar cells. Earlier studies have shown that interface defect densities in the range of 1010–1012 cm−2 correspond to well-passivated junctions with suppressed recombination losses, while higher values (>1013 cm−2) lead to severe carrier recombination and performance degradation.81–83 Therefore, the selected value represents a realistic yet optimistic scenario frequently adopted to model an upper-bound device performance under improved interface quality. These parameter choices indicate that the SnS2/Na3GaBr6 and SnS2/K3GaBr6 heterojunctions can be regarded as relatively clean and stable interfaces with low defect activity. Such conditions are highly favorable for efficient charge carrier transport across the junction and for minimizing non-radiative recombination losses in the simulated solar cells, while remaining consistent with defect density ranges reported in previous theoretical and simulation-based photovoltaic studies.
| Interfaces | Capture cross section: electrons/holes (cm2) | Defect type | Total defect density (cm−2) |
|---|---|---|---|
| SnS2/Na3GaBr6 | 1 × 10−19 | Neutral | 1 × 1011 |
| SnS2/K3GaBr6 | 1 × 10−19 | Neutral | 1 × 1011 |
All simulations were carried out at a temperature of 300 K under an incident light intensity of 1000 W m−2, corresponding to the standard AM 1.5G solar illumination condition. To achieve optimal device performance, a comprehensive parametric optimization was conducted by systematically varying key absorber-layer properties, including the thickness, defect density, shallow acceptor concentration, and operating temperature. These parameters critically influence charge generation, recombination behavior, carrier transport, and overall device efficiency. Optimizing the absorber thickness ensures sufficient photon absorption while minimizing carrier recombination losses. Reducing defect density suppresses non-radiative recombination pathways and enhances carrier lifetime, while tuning the shallow acceptor concentration improves electrical conductivity and charge extraction efficiency. Additionally, the temperature dependence was analyzed to evaluate thermal stability and device reliability under realistic operating conditions. This optimization strategy provides a more reliable assessment of device performance and highlights the potential of the proposed solar cell structure for practical applications.
4.1. Energy band alignment analysis
Fig. 12(a) and (b) illustrate the energy band alignment of the Ni/Q3GaBr6/SnS2/FTO/Al solar cell, showing the variations of the conduction band (EC), valence band (EV), and quasi-Fermi levels for electrons (Fn) and holes (Fp) across the device thickness. For Na3GaBr6 (Fig. 12(a)) exhibits a wider bandgap of 1.991 eV, which may reduce absorption but favor a higher open-circuit voltage. In contrast K3GaBr6 (Fig. 12(b)), the bandgap is 1.445 eV, enabling strong visible-light absorption and efficient electron–hole generation. K3GaBr6 (Fig. 12(b)), the bandgap is 1.445 eV, enabling strong visible-light absorption and efficient electron–hole generation. In both devices, Fn stays close to EC while FP lies near Ev within the absorber, indicating effective charge separation and low bulk recombination. A favorable conduction band offset at the absorber/SnS2 interface facilitates electron transfer into the ETL while suppressing interfacial recombination. Since no hole transport layer is used, holes are collected directly by the Ni back contact, where the valence band alignment suggests near-ohmic behavior and effective electron blocking.On the front side, electrons are transported through SnS2 to the FTO/Al contact with minimal energetic barriers, enabling efficient charge extraction. Overall, the band profiles indicate well-matched energy levels, enhanced carrier selectivity, and reduced recombination losses. K3GaBr6 is more suitable for light harvesting, whereas Na3GaBr6 offers potential for higher voltage output due to its wider bandgap, highlighting the complementary photovoltaic behavior of the two absorber materials.
4.2. Effect of absorber thickness on photovoltaic performance
Fig. 13 illustrates the variation of the photovoltaic performance parameters as a function of absorber layer thickness for the Q3GaBr6-based solar cell devices over a thickness range of 0.3 to 2.1 µm. A clear improvement in PCE, FF, and JSC is observed for both materials as the absorber thickness increases, followed by saturation at higher thickness values.84 For Na3GaBr6, as shown in Fig. 13(a–c), the PCE, FF, and JSC increase significantly from 7.54%, 78.651%, and 10.64 mA cm−2 at 0.3 µm to 9.83%, 78.87%, and 13.64 mA cm−2 at 0.8 µm, respectively, establishing 0.8 µm as the optimum thickness. | ||
| Fig. 13 Variation of (a) PCE, (b) FF, (c) JSC, and (d) VOC with absorber layer thickness for Na3GaBr6 and K3GaBr6-based solar cells. | ||
This improvement occurs because a thicker absorber enhances photon absorption, generating more charge carriers while still allowing efficient carrier collection. Beyond 0.8 µm, the improvement slows, and the values approach saturation at 10.49%, 78.883%, and 14.52 mA cm−2 at 2.1 µm. This behavior indicates that further thickness increase leads to longer carrier transport paths, which enhances recombination probability and reduces the effectiveness of additional light absorption.85 Similarly, for K3GaBr6, the performance metrics increase rapidly from 18.1%, 79.553%, and 23.95 mA cm−2 at 0.3 µm to 22.21%, 79.67%, and 29.04 mA cm−2 at 0.8 µm, confirming 0.8 µm as the optimal absorber thickness. With further increase in thickness, PCE, FF, and JSC exhibit minor enhancement and finally saturate at 23.0%, 79.65%, and 30.14 mA cm−2 at 2.1 µm. As shown in Fig. 13(d), the VOC remains nearly unchanged with increasing thickness, maintaining values of approximately 0.901 V for Na3GaBr6 and 0.951 V for K3GaBr6, which indicates that the absorber thickness has negligible influence on the device VOC. Notably, K3GaBr6 consistently exhibits superior performance across the entire thickness range, delivering more than twice the PCE and nearly double the JSC compared to Na3GaBr6, while the FF values remain comparable (79%), indicating similar resistive losses. Bring it all together, K3GaBr6 emerges as the superior absorber material owing to its higher efficiency, stronger photocurrent, and improved voltage output, while 0.8 µm is identified as the optimum thickness for both absorber layers.
4.3. Effect of total defect density on photovoltaic performance
Fig. 14(a) illustrates the dependence of photovoltaic performance parameters PCE, FF, JSC and VOC on the total defect density (Nt) for Q3GaBr6 -based solar cell devices over a wide defect density range from 1010 to 1017 cm−3. At low and moderate Nt (1010 to 1014 cm−3), both devices exhibit nearly stable photovoltaic behavior. Within this range, the PCE remains almost constant at 9.83% for Na3GaBr6 and 22.21% for K3GaBr6, indicating strong tolerance against bulk defects at low concentrations. Notably, the K3GaBr6-based device consistently delivers superior performance compared to its Na3GaBr6 counterpart. This enhancement is mainly attributed to its significantly higher JSC, measured as 13.643 mA cm−2 for Na3GaBr6 and 29.041 mA cm−2 for K3GaBr6, along with its improved VOC of 0.913 V for Na3GaBr6 and 0.960 V for K3GaBr6, as shown in Fig. 14(a). These findings suggest more favorable charge transport characteristics and reduced recombination losses in the K3GaBr6 absorber layer, leading to improved photovoltaic performance under low-defect conditions. | ||
| Fig. 14 Variation of photovoltaic parameters of Na3GaBr6 and K3GaBr6 as a function of (a) total defect density and (b) shallow acceptor density. | ||
When the Nt exceeds 1014 cm−3, both devices exhibit pronounced performance degradation, with the PCE decreasing to 6.391% for Na3GaBr6 and 14.41% for K3GaBr6 at 1017 cm−3. This decline is driven by the simultaneous reduction in JSC, FF, and VOC due to the formation of deep-level defect states that enhance non-radiative recombination. The FF decreases from stable values of 78.87% (Na3GaBr6) and 79.66% (K3GaBr6) to 69.25% and 68.33%, respectively, while JSC drops to 10.818 mA cm−2 and 23.96 mA cm−2 at 1017 cm−3 due to intensified Shockley–Read–Hall recombination.86 Likewise, VOC declines to 0.853 V for Na3GaBr6 and 0.879 V for K3GaBr6, reflecting the increased recombination current at high defect densities.
In addition to defect-induced limitations, the lower efficiency of Na3GaBr6 is fundamentally constrained by the Shockley–Queisser limit associated with its wider bandgap, which restricts photon absorption and current generation even under ideal conditions.87 Consequently, both intrinsic thermodynamic losses and enhanced defect sensitivity contribute to the inferior performance of Na3GaBr6 compared to K3GaBr6. K3GaBr6, by contrast, exhibits superior defect tolerance and operates closer to its theoretical efficiency limit, highlighting its greater potential for high-performance photovoltaic applications.
4.4. Effect of shallow acceptor density
Fig. 14(b) illustrates the variation of photovoltaic parameters as a function of shallow acceptor density (NA) for Q3GaBr6 absorbers over the range of 1013 to 1020 cm−3. Increasing the shallow acceptor density enhances p-type conductivity by raising the hole concentration, which directly influences the absorber's built-in electric field, carrier transport properties, and recombination dynamics.88 At the initial doping level of 1013 cm−3, the PCE values are 9.07% for Na3GaBr6 and 20.45% for K3GaBr6. With the moderate NA of 1017 cm−3, both materials exhibit notable improvement, achieving PCEs of 9.83% and 22.21%, which marks the most balanced operating point before the onset of diminishing returns at higher doping levels. At extreme doping (1020 cm−3), a further rise in PCE is observed, reaching 11.20% and 24.69%, though such high concentrations may not be practically favorable. A similar trend is observed for FF and VOC: from initial (1013 cm−3) values of 74.33% and 0.895 V for Na3GaBr6 and 74.88% and 0.941 V for K3GaBr6, both parameters increase at the moderate NA = 1017 cm−3 to 78.87% and 0.913 V for Na3GaBr6, and 79.66% and 0.96 V for K3GaBr6, reflecting enhanced carrier extraction and reduced recombination. At 1020 cm−3, FF rises further to above 86.25% and 86.05 for both materials, while VOC increases only modestly. Throughout the entire NA ranges, JSC remains nearly constant 13.64 mA cm−2 for Na3GaBr6 and 29.04 mA cm−2 for K3GaBr6 indicating that acceptor density has little effect on optical absorption or carrier generation.4.5. Effect of temperature variation
The influence of temperature on the device performance of Na3GaBr6- and K3GaBr6-based solar cells is governed by several intrinsic physical mechanisms, including bandgap shrinkage, enhanced carrier-phonon scattering, increased intrinsic carrier concentration, and temperature-activated recombination. As the operating temperature rises, lattice vibrations intensify, leading to reduced carrier mobility and a higher probability of recombination through both radiative and non-radiative pathways. Additionally, temperature-induced bandgap narrowing decreases VOC due to its inverse dependence on the saturation current density. These combined effects result in the systematic degradation of photovoltaic performance at elevated temperatures.In Fig. 15(a), this behavior is reflected in the temperature-dependent variation of PCE. At 280 K, the devices show efficiencies of 9.99% and 22.48% for Na3GaBr6 and K3GaBr6, respectively. When the temperature is increased to 300 K, the PCE slightly decreases to 9.83% and 22.21%, indicating the onset of thermally enhanced recombination and minor mobility loss. A further increase to 390 K causes more pronounced degradation, with PCE dropping to 9.07% for Na3GaBr6 and 20.85% for K3GaBr6. At 480 K, this trend continues, and the efficiencies fall to 8.30% and 18.23%, respectively.
 | ||
| Fig. 15 Temperature-dependent photovoltaic parameters ((a) PCE, (b) FF, (c) JSC, (d) VOC) of Na3GaBr6 and K3GaBr6-based solar cells (280 to 480 K). | ||
These reductions are consistent with theoretical expectations, as higher temperatures accelerate recombination and weaken the built-in potential essential for efficient carrier extraction. A similar temperature dependence is observed in Fig. 15(b) and (d) for FF and VOC. At 280 K, Na3GaBr6 exhibits an FF of 79.91% and VOC of 0.92 V, while K3GaBr6 shows 80.61% and 0.96 V. Increasing the temperature to 300 K slightly reduces the FF to 78.87% and 79.67%, but VOC remains nearly unchanged at 0.91 V and 0.92 V due to the relatively small bandgap shift in this temperature window. However, at 480 K, the combined effects of increased recombination and reduced carrier mobility significantly degrade both parameters, with FF and VOC decreasing to 70.06% and 0.87 V for Na3GaBr6 and 77.34% and 0.81 V for K3GaBr6. In contrast, Fig. 15(c) shows that JSC remains effectively constant over the entire temperature range, with values of 13.64 mA cm−2 for Na3GaBr6 and 29.04 mA cm−2 for K3GaBr6. This nearly unchanged behavior indicates that the optical absorption coefficient and photogenerated carrier density are minimally affected by temperature. Since JSC primarily depends on photon flux and absorption rather than on carrier recombination mechanisms, its stability is consistent with theoretical predictions. Overall, the combined theoretical framework and simulation results clearly demonstrate that while temperature variations significantly influence VOC, FF, and PCE due to enhanced recombination and reduced mobility, JSC remains unaffected. Despite the observed degradation at high temperatures, the Q3GaBr6 absorbers retain a reasonably stable performance profile, confirming their potential suitability for environments with moderate thermal fluctuations.
4.6. JV and QE
The J–V characteristics presented in Fig. 16(a) clearly distinguish the photovoltaic behavior of the Na3GaBr6- and K3GaBr6-based solar cells, with the K3GaBr6 device demonstrating markedly superior performance. The higher VOC of 0.960 V, enhanced JSC of 29.04 mA cm−2, and elevated PCE of 22.21% obtained for K3GaBr6 indicate more efficient charge generation and reduced recombination losses within the absorber layer. In contrast, the Na3GaBr6 device exhibits comparatively lower VOC of 0.913 V and JSC of 13.643 mA cm−2, resulting in a reduced PCE of 9.82%, primarily due to its limited current-producing capability.These differences are strongly supported by the quantum efficiency spectra shown in Fig. 16(b), where K3GaBr6 maintains a high QE exceeding 90% over a broad wavelength range and extends its spectral response up to approximately 900 nm. Conversely, Na3GaBr6 displays a significantly narrower absorption window, with QE rapidly declining beyond 600 nm, consistent with its larger effective bandgap and weaker long-wavelength absorption. The combined J–V and QE analyses confirm that K3GaBr6 possesses superior optoelectronic properties such as improved light-harvesting ability, longer carrier diffusion lengths, and reduced recombination which collectively contribute to its enhanced solar cell performance compared with Na3GaBr6.
4.7. Overall device performance
Under the optimized device conditions comprising an absorber thickness of 0.8 µm, shallow acceptor density of 1017 cm−3, total defect density of 1014 cm−3, an operating temperature of 300 K, and an interface defect density of 1011 cm−2 the Q3GaBr6 (Q = Na, K) double perovskite absorbers exhibit distinct photovoltaic performances. In Fig. 17, a clear comparison between Na3GaBr6 and K3GaBr6 shows that the K-based material significantly surpasses its Na counterpart. The Na3GaBr6 device achieves a PCE of 9.83%, with a JSC of 13.643 mA cm−2, VOC of 0.913 V, and FF of 78.87%. | ||
| Fig. 17 Comparative photovoltaic performance parameters PCE, JSC, VOC, and FF of optimized Na3GaBr6 and K3GaBr6 perovskite structures. | ||
Under the same idealized simulation conditions, K3GaBr6 delivers markedly enhanced performance, reaching a PCE of 22.21%, with a much higher JSC of 29.041 mA cm−2, VOC of 0.960 V, and a FF of 79.67%. This improvement can be attributed to enhanced photon absorption, more favorable charge transport, and reduced recombination losses predicted for the K-based compound. It is important to emphasize that these results represent theoretical upper-limit device performances obtained from SCAPS-1D simulations under optimized and ideal assumptions. Therefore, they should not be interpreted as realistic experimental efficiencies but rather as an indication of the intrinsic photovoltaic potential of these materials. To the best of our knowledge, prior studies have not reported photovoltaic performance simulations for A3BX6-type materials, and this work provides initial simulation-based insight into their possible device behavior and efficiency limits.
5. Potential applications of Q3GaBr6 (Q = Na, K)
Based on the comprehensive first-principles and device-level investigations, the vacancy-ordered halide perovskites Q3GaBr6 (Q = Na, K) exhibit a unique combination of suitable band gaps, strong optical absorption in the visible and ultraviolet regions, good mechanical stability, and excellent thermal and dynamical robustness. These characteristics make them promising candidates for several optoelectronic and energy-related applications. The direct band gaps of 1.445 to 1.991 eV (GGA-PBE) and their corrected values from mGGA-rSCAN and HSE06 place Q3GaBr6 within the optimal range for photovoltaic absorbers, enabling efficient sunlight harvesting and charge-carrier generation. Their high absorption coefficients (>104 cm−1 in the visible region) and low reflectivity further enhance their suitability as absorber layers in lead-free perovskite solar cells. Moreover, the strong ultraviolet absorption and pronounced dielectric response suggest potential applications in UV photodetectors, optical sensors, and radiation-detection devices. The moderate refractive index and low optical losses in the visible region also indicate possible use in transparent optoelectronic coatings and antireflection layers. From a mechanical and thermal standpoint, the dynamical stability confirmed by phonon dispersion and the excellent thermal robustness observed in AIMD simulations imply that these materials can withstand realistic device-operating conditions, making them viable for long-term practical deployment. In particular, the ductile nature and higher mechanical flexibility of K3GaBr6 make it especially attractive for thin-film and flexible optoelectronic devices. Finally, the successful integration of DFT-derived parameters into SCAPS-1D simulations demonstrates that Q3GaBr6 compounds are not only theoretically stable but also technologically relevant, bridging the gap between material discovery and device engineering. Therefore, Na3GaBr6 and especially K3GaBr6 emerge as promising lead-free absorber materials for next-generation solar cells, UV photodetectors, and other sustainable optoelectronic applications.6. Limitation
This study is subject to several theoretical limitations arising from both the DFT calculations and the device-level simulations. From the DFT perspective, the calculated electronic and optical properties do not explicitly account for excitonic effects, which can be significant in halide perovskites and may influence light absorption and carrier dynamics. Although advanced functionals (HSE06 and mGGA-RSCAN) were employed to improve band gap accuracy, inherent approximations of DFT still remain. From the device simulation perspective, the SCAPS-1D results were obtained under idealized assumptions. Key parameters such as defect density, carrier mobility, and recombination velocities were either optimized within the simulator or assumed within reasonable ranges due to the absence of experimental data for these materials. Therefore, the predicted photovoltaic efficiencies should be regarded as theoretical upper-limit estimates rather than realistic device performance. In practical implementations, material imperfections, interface losses, and additional physical effects not considered here may lead to reduced efficiencies.7. Conclusion
This work establishes an efficient multiscale framework by coupling first-principles calculations with SCAPS-1D device modeling, enabling a direct and systematic link between intrinsic material properties and photovoltaic performance. Such an integrated strategy minimizes computational overhead and experimental uncertainty, providing a practical pathway for the rapid identification and optimization of promising lead-free absorber materials. Moreover, we report the first complete theoretical and device-level assessment of the vacancy-ordered halide perovskites Q3GaBr6 (Q = Na, K) for photovoltaic and optoelectronic applications. The DFT results verify that Na3GaBr6 and K3GaBr6 adopt a cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure with thermodynamically stable configurations, supported by negative formation energies, suitable tolerance factors, and structurally rigid GaBr6 octahedra. These characteristics confirm their structural robustness and highlight their potential as stable, environmentally benign alternatives to conventional Pb-based perovskite absorbers. Their direct band gaps, strong dielectric response, and high absorption coefficients (>104 cm−1 in the visible range) highlight their potential as efficient light-harvesting materials. Mechanical and phonon analyses, along with AIMD simulations, further demonstrate that both compounds possess excellent thermodynamic and dynamical stability in different temperature, with K3GaBr6 exhibiting slightly enhanced structural robustness and ductility compared to Na3GaBr6. Device-level simulations using SCAPS-1D, incorporating DFT-derived parameters, reveal that absorber thickness, defect concentration, and acceptor density significantly influence photovoltaic performance. Both materials show promising behavior under optimized conditions, indicating their viability as Pb-free absorber layers. At the optimized absorber thickness of 0.8 µm, the Na3GaBr6-based device achieves a PCE of 9.83%, whereas the K3GaBr6-based device reaches a significantly higher theoretical upper-limit PCE of 22.21%, owing to its superior JSC (29.04 mA cm−2) and VOC (0.96 V).
m structure with thermodynamically stable configurations, supported by negative formation energies, suitable tolerance factors, and structurally rigid GaBr6 octahedra. These characteristics confirm their structural robustness and highlight their potential as stable, environmentally benign alternatives to conventional Pb-based perovskite absorbers. Their direct band gaps, strong dielectric response, and high absorption coefficients (>104 cm−1 in the visible range) highlight their potential as efficient light-harvesting materials. Mechanical and phonon analyses, along with AIMD simulations, further demonstrate that both compounds possess excellent thermodynamic and dynamical stability in different temperature, with K3GaBr6 exhibiting slightly enhanced structural robustness and ductility compared to Na3GaBr6. Device-level simulations using SCAPS-1D, incorporating DFT-derived parameters, reveal that absorber thickness, defect concentration, and acceptor density significantly influence photovoltaic performance. Both materials show promising behavior under optimized conditions, indicating their viability as Pb-free absorber layers. At the optimized absorber thickness of 0.8 µm, the Na3GaBr6-based device achieves a PCE of 9.83%, whereas the K3GaBr6-based device reaches a significantly higher theoretical upper-limit PCE of 22.21%, owing to its superior JSC (29.04 mA cm−2) and VOC (0.96 V).
Ethical statement
The manuscript's authors agree that there is no research involving human participants, human data or tissue, or animal subjects.Author contributions
Rifat Rafiu, Md. Sakib Hasan: methodology, validation, software, conceptualization, investigation, formal analysis, data curation, visualization, writing – original draft, and review and editing. Md. Azizur Rahman, Imtiaz Ahamed Apon, Karim Kriaa, Mohamed Benghanem, S. AlFaify, Noureddine Elboughdiri: investigation, validation, software, formal analysis, data curation, writing – original draft, and review and editing.Conflicts of interest
The authors have no conflicts of interest.Data availability
Data will be made available on reasonable request.Acknowledgements
The researchers wish to extend their sincere gratitude to the Deanship of Scientific Research at the Islamic University of Madinah (KSA) for the support provided to the Post-Publishing Program.References
- P. Chen, Y. Xiao, S. Li, X. Jia, D. Luo, W. Zhang, H. J. Snaith, Q. Gong and R. Zhu, The Promise and Challenges of Inverted Perovskite Solar Cells, Chem. Rev., 2024, 124, 10623–10700, DOI:10.1021/acs.chemrev.4c00073.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051, DOI:10.1021/ja809598r.
- M. A. Green, E. D. Dunlop, M. Yoshita, N. Kopidakis, K. Bothe, G. Siefer, D. Hinken, M. Rauer, J. Hohl-Ebinger and X. Hao, Solar cell efficiency tables (Version 64), Prog. Photovoltaics, 2024, 32, 425–441, DOI:10.1002/pip.3831.
- Y. Fu, H. Zhu, J. Chen, M. P. Hautzinger, X.-Y. Zhu and S. Jin, Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties, Nat. Rev. Mater., 2019, 4, 169–188, DOI:10.1038/s41578-019-0080-9.
- S. K. Fatima, R. H. Alzard, R. Amna, M. H. Alzard, K. Zheng and M. Abdellah, Lead-free perovskites for next-generation applications: a comprehensive computational and data-driven review, Adv. Mater., 2025, 6, 7634–7661, 10.1039/D5MA00681C.
- A. Mahmood, Z. Bai, T. Wang, Y. Lei, S. Wang, B. Sun, H. Khan, K. Khan, K. Sun and G. Wang, Enabling high-performance multivalent metal-ion batteries: current advances and future prospects, Chem. Soc. Rev., 2025, 54, 2369–2435, 10.1039/D4CS00929K.
- S. T. Thornton, G. Abdelmageed, R. F. Kahwagi and G. I. Koleilat, Progress towards l ead-free , efficient, and stable perovskite solar cells, J. Chem. Technol. Biotechnol., 2022, 97, 810–829, DOI:10.1002/jctb.6830.
- S. Chatterjee and A. J. Pal, Influence of metal substitution on hybrid halide perovskites: towards lead-free perovskite solar cells, J. Mater. Chem. A, 2018, 6, 3793–3823, 10.1039/C7TA09943F.
- S. Ghosh, H. Shankar and P. Kar, Recent developments of lead-free halide double perovskites: a new superstar in the optoelectronic field, Adv. Mater., 2022, 3, 3742–3765, 10.1039/D2MA00071G.
- T. Miyasaka, A. Kulkarni, G. M. Kim, S. Öz and A. K. Jena, Perovskite Solar Cells: Can We Go Organic-Free, Lead-Free, and Dopant-Free?, Adv. Energy Mater., 2020, 10, 1902500, DOI:10.1002/aenm.201902500.
- F. Giustino and H. J. Snaith, Toward Lead-Free Perovskite Solar Cells, ACS Energy Lett., 2016, 1, 1233–1240, DOI:10.1021/acsenergylett.6b00499.
- C. C. Stoumpos, L. Frazer, D. J. Clark, Y. S. Kim, S. H. Rhim, A. J. Freeman, J. B. Ketterson, J. I. Jang and M. G. Kanatzidis, Hybrid Germanium Iodide Perovskite Semiconductors: Active Lone Pairs, Structural Distortions, Direct and Indirect Energy Gaps, and Strong Nonlinear Optical Properties, J. Am. Chem. Soc., 2015, 137, 6804–6819, DOI:10.1021/jacs.5b01025.
- G. K. Grandhi, L. Krishnan Jagadamma, V. Sugathan, B. Al-Anesi, D. Manna and P. Vivo, Lead-free perovskite-inspired semiconductors for indoor light-harvesting – the present and the future, Chem. Commun., 2023, 59, 8616–8625, 10.1039/D3CC01881D.
- G. Morrison, L. W. Masachchi, H. B. Tisdale, T. Chang, V. G. Jones, K. P. Zamorano, L. S. Breton, M. D. Smith, Y.-S. Chen and H.-C. zur Loye, Polymorphism in A3MF6 (A = Rb, Cs; M = Al, Ga) grown using mixed halide fluxes, Dalton Trans., 2023, 52, 8425–8433, 10.1039/D3DT00352C.
- A. Rakhmatullin, G. King, M. S. Molokeev, I. B. Polovov, K. V. Maksimtsev, E. Suard, R. Bakirov, F. Šimko, C. Bessada and M. Allix, Crystal Structures of Three Polymorphs of Cs3ScF6 by Means of Solid-State NMR, X-Ray, and Neutron Diffraction, Cryst. Growth Des., 2025, 25, 1217–1223, DOI:10.1021/acs.cgd.4c01598.
- F. Benachenhou, G. Mairesse, G. Nowogrocki and D. Thomas, Structural studies of Cs-K-Bi mixed chlorides relation to the crystal structures of A2BMX6, A3MX6, and A2MX6, J. Solid State Chem., 1986, 65, 13–26, DOI:10.1016/0022-4596(86)90085-X.
- F. Šimko, J. Priščák, E. Kubiňáková and M. Korenko, Effect of the Alkaline Metal Cations on the Electrical Conductivity of the Molten Cryolites (K3AlF6, Rb3AlF6, and Cs3AlF6), J. Chem. Eng. Data, 2020, 65, 2642–2648, DOI:10.1021/acs.jced.0c00023.
- A. Albaghdadi, A. Bakhshayeshi, R. Taghavimendi and L. Motevalizadeh, First principles calculations of structural, electronic, and optical properties of K3GaF6 structure using density functional theory approach, Eur. Phys. J. B, 2025, 98, 166, DOI:10.1140/epjb/s10051-025-01014-0.
- M. Y. Khan, M. A. Jehangir, N. Israr, U. Younis, J. Khan, M. Khan, A. Khan and A. A. Souwaileh, First-principles study of Cs3SbX6 (X = F, Cl) for scintillation and optoelectronic applications, Phys. B, 2025, 417150, DOI:10.1016/j.physb.2025.417150.
- M. A. Jehangir, M. Y. Khan, M. Noman, I. E. Lee, Q. Wali, T. Usman, Y. Mu and A. A. Souwaileh, First-principles investigation of lead-free Rb3 SbX6 (X = F, Cl, Br, I) mixed-halide double perovskites promising for photovoltaics and scintillation, RSC Adv., 2025, 15, 33708–33725, 10.1039/D5RA04902D.
- S. Yu, K. Kim, B. C. Wood, H.-G. Jung and K. Y. Chung, Structural design strategies for superionic sodium halide solid electrolytes, J. Mater. Chem. A, 2022, 10, 24301–24309, 10.1039/D2TA05158C.
- Md. A. U. Islam, O. Das, D. B. Khadka, S. Kato and T. Soga, Tandem Solar Cell Approach: Unveiling the Potential of Rudorffite/Silicon Combinations for Providing the Best Solar Cell Performance, Phys. Status Solidi A, 2025, 222, 2500011, DOI:10.1002/pssa.202500011.
- Y. Seo, S. R. Ha, S. Yoon, S. M. Jeong, H. Choi and D.-W. Kang, Dynamic casting in combination with ramped annealing process for implementation of inverted planar Ag3BiI6 rudorffite solar cells, J. Power Sources, 2020, 453, 227903, DOI:10.1016/j.jpowsour.2020.227903.
- B. L. Farah, K. Radja, A. Ibrahim, K. Khadra, A. Mohammed and Y. Al-Douri, RbNbX3 (X = cl, Br, I) lead-free halide perovskites: A DFT study of structural, elastic, electronic, and thermoelectric properties for energy applications, Chem. Phys., 2025, 598, 112843, DOI:10.1016/j.chemphys.2025.112843.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, Y.-G. Choe, W. Hao and S. Li, First-Principles Study on Structural, Electronic, and Optical Properties of Inorganic Ge-Based Halide Perovskites, Inorg. Chem., 2019, 58, 4134–4140, DOI:10.1021/acs.inorgchem.8b03095.
- S. S. Essaoud, M. Radjai, A. Bouhemadou, M. E. Ketfi, D. Allali, R. Khenata and Y. Al-Douri, Rhombohedral Ba2NbBO6 (B = As, Sb, and Bi) Double Perovskites' Elastic, Thermodynamic, and Directional Thermoelectric Properties, J. Supercond. Novel Magn., 2025, 38, 142, DOI:10.1007/s10948-025-06981-0.
- H. Allaf, D. Allali, M. Radjai, A. Bouhemadou, S. Saad Essaoud, A. Bedjaoui, S. Bin-Omran, R. Khenata, Y. Al-Douri and S. Chaba Mouna, Electronic and optical characteristics of CaLiX3 (X = Cl, Br, I) perovskite compounds using the Tran–Blaha modified Becke–Johnson potential, Phys. Scr., 2024, 99, 085935, DOI:10.1088/1402-4896/ad5d29.
- T. Nouri, F. Khelfaoui, K. Amara, F. Belkharroubi, Y. Al-Douri, A. Abu Odeh and R. A. Al-Samarai, A first-principles investigation of structural, mechanical, electronic and magnetic properties of CsMgO3 perovskite, Chem. Phys., 2024, 586, 112391, DOI:10.1016/j.chemphys.2024.112391.
- D. Bagayoko, Understanding density functional theory (DFT) and completing it in practice, AIP Adv., 2014, 4, 127104, DOI:10.1063/1.4903408.
- S. Chen, T. Bimenyimana and M. Guli, First-principles study on the electronic properties of perovskites MASnaPb(1 − a)XbY(3 − b) (X, Y = Cl, Br, I), Results Phys., 2019, 14, 102408, DOI:10.1016/j.rinp.2019.102408.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- E. L. Shirley, D. C. Allan, R. M. Martin and J. D. Joannopoulos, Extended norm-conserving pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3652–3660, DOI:10.1103/PhysRevB.40.3652.
- K. Choudhary and F. Tavazza, Convergence and machine learning predictions of Monkhorst-Pack k-points and plane-wave cut-off in high-throughput DFT calculations, Comput. Mater. Sci., 2019, 161, 300–308, DOI:10.1016/j.commatsci.2019.02.006.
- M. Wang, K. Tanaka, S. Sakai, Z. Wang, K. Deng, Y. Lyu, C. Li, D. Tian, S. Shen, N. Ogawa, N. Kanazawa, P. Yu, R. Arita and F. Kagawa, Emergent zero-field anomalous Hall effect in a reconstructed rutile antiferromagnetic metal, Nat. Commun., 2023, 14, 8240, DOI:10.1038/s41467-023-43962-0.
- X. Li, L. Sun, P. Guo, P. Ke and A. Wang, Structure and residual stress evolution of Ti/Al, Cr/Al or W/Al co-doped amorphous carbon nanocomposite films: Insights from ab initio calculations, Mater. Des., 2016, 89, 1123–1129, DOI:10.1016/j.matdes.2015.10.106.
- J. Doumont, F. Tran and P. Blaha, Implementation of self-consistent MGGA functionals in augmented plane wave based methods, Phys. Rev. B, 2022, 105, 195138, DOI:10.1103/PhysRevB.105.195138.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71, DOI:10.1016/j.cpc.2006.03.007.
- N. H. Perry, S. R. Bishop and H. L. Tuller, Tailoring chemical expansion by controlling charge localization: in situ X-ray diffraction and dilatometric study of (La,Sr)(Ga,Ni)O3−δ perovskite, J. Mater. Chem. A, 2014, 2, 18906–18916, 10.1039/C4TA02972K.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A, 1976, 32, 751–767, DOI:10.1107/S0567739476001551.
- S. Yu, K. Kim, B. C. Wood, H.-G. Jung and K. Y. Chung, Structural design strategies for superionic sodium halide solid electrolytes, J. Mater. Chem. A, 2022, 10, 24301–24309, 10.1039/D2TA05158C.
- M. J. Islam and R. Amin, DFT-based numerical study of Cs3 QR6 (Q = In, Tl, Ga; R = I, Cl, Br) compounds for opto-solar applications, Mater. Res. Express, 2026, 13, 015902, DOI:10.1088/2053-1591/ae2f2a.
- X. Yang, Y. Han, P. Xu and F. Liu, Thermodynamic stability descriptor of A2BX6-type perovskite materials, Mater. Chem. Phys., 2025, 333, 130324, DOI:10.1016/j.matchemphys.2024.130324.
- V. M. Goldschmidt, Crystal structure and chemical constitution, Trans. Faraday Soc., 1929, 25, 253, 10.1039/tf9292500253.
- S. C. Tidrow, Mapping Comparison of Goldschmidt's Tolerance Factor with Perovskite Structural Conditions, Ferroelectrics, 2014, 470, 13–27, DOI:10.1080/00150193.2014.922372.
- R. Rafiu, K. Kriaa, Md. S. H. Saikot, Md. A. Rahman, I. A. Apon, N. Sfina, M. T. Khan, N. Elboughdiri, S. AlFaify and I. A. Talukder, Comprehensive first-principles analysis and device simulations of vacancy-ordered D2CeX6 double perovskites for high-efficiency lead-free solar cells, RSC Adv., 2025, 15, 44711–44748, 10.1039/D5RA07162C.
- M. Benaadad, A. Nafidi, S. Melkoud, I. Mahraj and M. Salmi, Investigation of structural, optoelectronic and thermoelectric properties of GaCuX2 (X = S, Se and Te) chalcopyrites semiconductors using the accurate mBJ approach, Phys. B, 2022, 642, 414118, DOI:10.1016/j.physb.2022.414118.
- Y. Saeed, B. Amin, H. Khalil, F. Rehman, H. Ali, M. I. Khan, A. Mahmood and M. Shafiq, Cs2NaGaBr6: a new lead-free and direct band gap halide double perovskite, RSC Adv., 2020, 10, 17444–17451, 10.1039/D0RA01764G.
- N. Younes, B. Abdennour and R. E. Ouardi, Study of Mechanical, Electronic and Optical Characteristics for AuBiF3 Material, Islamic University Journal of Applied Sciences, 2025, 113–122 Search PubMed.
- Md. S. H. Saikot, R. Rafiu, I. A. Apon, A. El-Rayyes, Md. A. Rahman, M. Shkir, Z. Ahmad and R. Marnadu, First-principles investigation of structural, electronic, optical, mechanical, and phonon properties of Pb- and Sn-based cubic oxide perovskites for optoelectronic applications, RSC Adv., 2025, 15, 39071–39091, 10.1039/D5RA06065F.
- Md. S. Hasan Saikot, R. Rafiu, Md. A. Rahman, I. A. Apon, A. El-Rayyes, M. T. Khan, Z. Ahmad and M. Shkir, First-principles design and photovoltaic evaluation of alkali-based M3 ClO anti-perovskites for high-efficiency lead-free solar cells, New J. Chem., 2025, 49, 16340–16369, 10.1039/D5NJ03069B.
- P. Ranjan, P. Kumar, T. Chakraborty, M. Sharma and S. Sharma, A study of structure and electronic properties of chalcopyrites semiconductor invoking Density Functional Theory, Mater. Chem. Phys., 2020, 241, 122346, DOI:10.1016/j.matchemphys.2019.122346.
- I. A. Apon, Md. R. Hasan, R. Rafiu, R. Kawsar, Md. S. Hasan Saikot, Md. A. Hossain, Md. A. Rahman, K. Kriaa, N. Elboughdiri, Q. Mohsen, M. T. Khan and A. A. Alshihri, Unveiling the Electronic, Optical, and Mechanical Properties of Lithium-Based Perovskites for Next-Generation Solar Cells, J. Inorg. Organomet. Polym., 2025 DOI:10.1007/s10904-025-03957-4.
- I. A. Apon, K. Kriaa, Md. A. Rahman, Md. Alamgir Hossain, C. Maatki, A. A. Assadi and N. Elboughdiri, Rb2 BX6 double perovskites: unlocking 22% efficiency through structural, electronic, mechanical, and optical insights, RSC Adv., 2025, 15, 40209–40230, 10.1039/D5RA03981A.
- B. C. Biswas, A. I. Shimul, M. Shkir, F. S. Khan, M. Benghanem, R. Marnadu and M. A. Rahman, A computational and machine learning-driven investigation of Ca3BiBr3 perovskite solar cells: Fine-tuning the hole transport layer for enhanced performance, Polyhedron, 2026, 284, 117871, DOI:10.1016/j.poly.2025.117871.
- M. A. Rahman, R. Rafiu, I. A. Apon, M. S. H. Saikot, I. A. Ovi, N. Elboughdiri, M. Benghanem, S. AlFaify, I. M. Ashraf and H. Albalawi, Pressure-tunable optoelectronic and photovoltaic properties of lead-free ZnAgF3 and ZnAg(F0.5Cl0.5)3 Perovskites: A first-principles and device-level study, Mater. Chem. Phys., 2026, 349, 131777, DOI:10.1016/j.matchemphys.2025.131777.
- J. H. Simmons and K. S. Potter, Optical Materials, Academic Press, San Diego, 2000 Search PubMed.
- P. G. Gonzales-Ormeño, M. A. Mendoza and C. G. Schön, Thermodynamic and optoelectronic properties of GaAs(1−x)Mx (M = Fe,Cu) ternary compounds via first principles, Mater. Today Commun., 2022, 31, 103200, DOI:10.1016/j.mtcomm.2022.103200.
- Y. Selmani, H. Labrim and L. Bahmad, Structural, optoelectronic and thermoelectric properties of the new perovskites LiMCl3 (M = Pb or Sn): a DFT study, Opt. Quant. Electron., 2024, 56, 1416, DOI:10.1007/s11082-024-07319-1.
- R. Rafiu, Md. S. Hasan Saikot, I. A. Apon, I. Boukhris, A. El-Rayyes, M. T. Khan, Q. Mohsen and Md. A. Rahman, Comprehensive DFT and SCAPS - 1D Study of Structural, Electronic, Optical, Mechanical, Phonon, Thermoelectric, and Photovoltaic Properties of Lead-Free Z3 BrO (Z = K, Rb, Cs, and Fr) Anti-Perovskites, J. Comput. Chem., 2025, 46, e70221, DOI:10.1002/jcc.70221.
- G. O. Igomah, F. A. Nelson, F. F. Sead, M. Runde, I. Hossain and A. A. Ayi, Insight into the effect of Mg-substitution on the electronic, optoelectronic, and hydrogen storage density of NbH2 fluorite structured: a DFT study, RSC Adv., 2025, 15, 27113–27127, 10.1039/D5RA03949E.
- R. Rafiu, Md. S. Hasan Saikot, A. El-Rayyes, I. A. Apon, M. Shkir, M. T. Khan, M. A. Sayed and Md. A. Rahman, Exploring A2CeCl6 (A = K, Rb, Cs, Fr) lead-free double perovskites via first-principles and device simulation for photovoltaic applications, J. Phys. Chem. Solids, 2026, 208, 113126, DOI:10.1016/j.jpcs.2025.113126.
- J.-L. Meyzonnette, J. Mangin and M. Cathelinaud, Refractive Index of Optical Materials, in Springer Handbook of Glass, J. D. Musgraves, J. Hu and L. Calvez, Springer International Publishing, Cham, 2019, pp. 997–1045, DOI:10.1007/978-3-319-93728-1_29.
- V. Milman, K. Refson, S. J. Clark, C. J. Pickard, J. R. Yates, S.-P. Gao, P. J. Hasnip, M. I. J. Probert, A. Perlov and M. D. Segall, Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation, J. Mol. Struct., 2010, 954, 22–35, DOI:10.1016/j.theochem.2009.12.040.
- A. Lipson, S. G. Lipson and H. Lipson, Optical Physics, Cambridge University Press, Cambridge ; New York, 4th edn, 2011 Search PubMed.
- S. V. Boriskina, T. A. Cooper, L. Zeng, G. Ni, J. K. Tong, Y. Tsurimaki, Y. Huang, L. Meroueh, G. Mahan and G. Chen, Losses in plasmonics: from mitigating energy dissipation to embracing loss-enabled functionalities, Adv. Opt. Photon, 2017, 9, 775, DOI:10.1364/AOP.9.000775.
- T. Hao, Y. Liu, J. Tang, Q. Cen, W. Li, N. Zhu, Y. Dai, J. Capmany, J. Yao and M. Li, Recent advances in optoelectronic oscillators, J. Mol. Struct., 2020, 2, 1, DOI:10.1117/1.AP.2.4.044001.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press New, York, NY, 1996, DOI:10.1093/oso/9780192670083.001.0001.
- A. M. Oni, A. S. M. Mohsin, Md. M. Rahman and M. B. Hossain Bhuian, A comprehensive evaluation of solar cell technologies, associated loss mechanisms, and efficiency enhancement strategies for photovoltaic cells, Energy Rep., 2024, 11, 3345–3366, DOI:10.1016/j.egyr.2024.03.007.
- Md. R. Hasan, I. A. Apon, Md. M. Islam, A. U. Azad, Md. Solayman and Md. S. Haque, Pressure-induced multi-functional property analysis of lead-free tin based halide perovskites ASnCl3 (A = Ga, In, Tl) for advanced optoelectronic applications, Mater. Adv., 2025, 6(5), 1794–1821, 10.1039/D5MA00039D.
- M. Born, On the stability of crystal lattices. I, Math. Proc. Camb. Phil. Soc., 1940, 36, 160–172, DOI:10.1017/S0305004100017138.
- Md. S. H. Saikot, R. Rafiu, I. A. Apon, A. El-Rayyes, Md. A. Rahman, M. Shkir, Z. Ahmad and R. Marnadu, First-principles investigation of structural, electronic, optical, mechanical, and phonon properties of Pb- and Sn-based cubic oxide perovskites for optoelectronic applications, RSC Adv., 2025, 15, 39071–39091, 10.1039/D5RA06065F.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5, DOI:10.1016/j.scriptamat.2015.07.021.
- I. A. Apon, Md. A. Hossain, R. Rafiu, Md. S. Hasan Saikot, Md. A. Rahman, J. R. Rajabathar, I. Boukhris, H. Albalawi, K. Kriaa and N. Elboughdiri, Comprehensive analysis of novel In2GeX6 (X = Cl, Br) double perovskites: Structural, electronic, optical, mechanical, phonon, population analyses and solar cell performance via DFT and SCAPS-1D, Phys. B, 2025, 717, 417836, DOI:10.1016/j.physb.2025.417836.
- R. S. Mulliken, Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833–1840, DOI:10.1063/1.1740588.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, Critical analysis and extension of the Hirshfeld atoms in molecules, J. Chem. Phys., 2007, 126, 144111, DOI:10.1063/1.2715563.
- M. Li, S. Guo, X. Zhao, S. Quan, X. Wang, M. Wu, R. Liu and D. Weller, Modeling and Simulation of MAPbI3-Based Solar Cells with SnS2 as the Electron Transport Layer (ETL) and MoS2 as the Hole Transport Layer (HTL), ACS Appl. Electron. Mater., 2024, 6, 5997–6004, DOI:10.1021/acsaelm.4c00936.
- M. Rauer, A. Mondon, C. Schmiga, J. Bartsch, M. Glatthaar and S. W. Glunz, Nickel-plated Front Contacts for Front and Rear Emitter Silicon Solar Cells, Energy Procedia, 2013, 38, 449–458, DOI:10.1016/j.egypro.2013.07.303.
- A. Muthukumar, G. Rey, G. Giusti, V. Consonni, E. Appert, H. Roussel, A. Dakshnamoorthy and D. Bellet, Fluorine doped tin oxide (FTO) thin film as transparent conductive oxide (TCO) for photovoltaic applications, AIP Conf. Proc., 2013, 1512, 710–711, DOI:10.1063/1.4791235.
- A. O. M. Alzahrani, High-efficiency, lead-free FA0.8MA0.2SnI3 perovskite solar cell with passivated interfaces and tuned energy alignment: A wxAMPS simulation study, Results Eng., 2025, 28, 108123, DOI:10.1016/j.rineng.2025.108123.
- N. Yadav and A. Khare, Resolving interfacial challenges in perovskite solar cells: From defect control to energy band optimization, Surf. Interfaces, 2025, 56, 105593, DOI:10.1016/j.surfin.2024.105593.
- S. Srivastava, S. Singh and V. K. Singh, Bulk and interface defects analysis of n-CdS/p-Si heterojunction solar cell, Opt. Mater., 2021, 111, 110687, DOI:10.1016/j.optmat.2020.110687.
- A. S. Chouhan, N. P. Jasti and S. Avasthi, Effect of interface defect density on performance of perovskite solar cell: Correlation of simulation and experiment, Mater. Lett., 2018, 221, 150–153, DOI:10.1016/j.matlet.2018.03.095.
- T. K. Tulka, N. Alam, M. Akhtaruzzaman, K. Sobayel and M. M. Hossain, Optimization of a high-performance lead-free cesium-based inorganic perovskite solar cell through numerical approach, Heliyon, 2022, 8(11), e11719, DOI:10.1016/j.heliyon.2022.e11719.
- A. Mortadi, E. El Hafidi, H. Nasrellah, M. Monkade and R. El Moznine, Analysis and optimization of lead-free perovskite solar cells: investigating performance and electrical characteristics, Mater. Renew. Sustain. Energy, 2024, 13, 219–232, DOI:10.1007/s40243-024-00260-z.
- R. Kundu, Numerical Optimization of La0.5Ce0.5Fe0.9Zn0.1O3-Based Perovskite Solar Cell Using NiO as Hole Transport Layer and TiO2 as Electron Transport Layer for Enhanced Photovoltaic Performance, Adv. Theory Simul., 2026, 9(2), e01186, DOI:10.1002/adts.202501186.
- F. Olivier, A. Daami, C. Licitra and F. Templier, Shockley-Read-Hall and Auger non-radiative recombination in GaN based LEDs: A size effect study, Appl. Phys. Lett., 2017, 111, 022104, DOI:10.1063/1.4993741.
- S. Rühle, Tabulated values of the Shockley–Queisser limit for single junction solar cells, Sol. Energy, 2016, 130, 139–147, DOI:10.1016/j.solener.2016.02.015.
- T. S. Sherkar, C. Momblona, L. Gil-Escrig, J. Ávila, M. Sessolo, H. J. Bolink and L. J. A. Koster, Recombination in Perovskite Solar Cells: Significance of Grain Boundaries, Interface Traps, and Defect Ions, ACS Energy Lett., 2017, 2, 1214–1222, DOI:10.1021/acsenergylett.7b00236.
| This journal is © The Royal Society of Chemistry 2026 |











