DOI:
10.1039/D5RA09092J
(Paper)
RSC Adv., 2026,
16, 8401-8418
First-principles insights into half-metallic ferromagnetism, lattice dynamics, and thermoelectric performance of MgX2Se4 (X=Ti, Mn) spinel chalcogenides
Received
25th November 2025
, Accepted 2nd February 2026
First published on 11th February 2026
Abstract
Half-metallic ferromagnets are central to spintronic and energy-conversion technologies due to their high spin polarization and multifunctional transport behavior. In this study, a first-principles investigation based on density functional theory within the GGA framework employing the modified Becke–Johnson potential is carried out to examine the structural, electronic, magnetic, optical and thermoelectric properties of the spinel chalcogenides MgTi2Se4 and MgMn2Se4. Total-energy calculations identify the ferromagnetic configuration as the ground state for both compounds. The negative formation enthalpies and phonon dispersion spectra free of imaginary frequencies confirm their thermodynamic and dynamical stability. Electronic band-structure analysis reveals half-metallicity arising from strong hybridization between transition-metal-d and Se-p orbitals, which is characterized by metallic behavior in the spin-up channel and a semiconducting gap in the spin-down channel. This electronic structure yields integer magnetic moments of 4 µB per formula unit for MgTi2Se4 and 16 µB per formula unit for MgMn2Se4 and is consistent with half-metallic ferromagnetism. The calculated elastic constants satisfy the Born stability criteria, confirming mechanical stability. The materials exhibit intrinsic ductility and pronounced elastic anisotropy. High elastic moduli, sound velocities and Debye temperatures further indicate enhanced lattice rigidity and high thermal stability. Optical properties derived from the complex dielectric function reveal large static dielectric constants. Strong interband transitions lead to intense ultraviolet absorption and high optical conductivity. These features indicate efficient electron–photon coupling. Spin-resolved transport analysis reveals pronounced Seebeck asymmetry, confirming dominant majority-spin carrier transport. The combined effects of finite Seebeck coefficients, relatively high electrical conductivity and suppressed lattice thermal conductivity lead to enhanced thermoelectric performance under n-type doping, with the dimensionless figure of merit reaching ZT ≈ 0.9 for MgTi2Se4 and ZT ≈ 0.99 for MgMn2Se4 at room temperature. These results establish MgTi2Se4 and MgMn2Se4 as promising multifunctional materials for spintronic, spin-caloritronic, and energy-harvesting applications.
1 Introduction
The search for multifunctional materials capable of addressing both energy and technological demands has intensified due to the growing global emphasis on sustainable energy solutions and advanced electronic systems.1 Simultaneously, the advancement of spin-based electronics relies critically on achieving high spin polarization in solid-state materials.2,3 Moreover, increasing environmental and economic concerns necessitate the development of non-toxic, earth-abundant, and cost-effective materials to ensure ecological safety and large-scale applicability.4–6 Among the diverse material classes explored, spinel-type chalcogenides have attracted significant attention owing to their excellent mechanical robustness, tunable electronic characteristics, and high structural flexibility.7–10 In particular, thiospinels with the general chemical formula AB2X4 (where A is a divalent cation, B is a transition or rare-earth metal, and X = S or Se) typically crystallize in a cubic spinel structure and exhibit a wide range of functional properties, including magnetic ordering, metal–insulator transitions, superconductivity, structural phase transitions, and notable thermoelectric responses.11–14 Recent first-principles investigations on chalcogenide spinel systems such as CdTi2X4 (X = S, Se), MgSm2(S/Se)4, and rare-earth-based CdGd2(S/Se)4 have reported ferromagnetic semiconducting and half-metallic behaviour, along with promising transport and thermoelectric characteristics, underscoring the multifunctional nature of these materials.15–17 The magnetic behaviour in these systems primarily originates from strong hybridization between chalcogen p orbitals and transition-metal or rare-earth d/f orbitals, which plays a key role in stabilizing spin-polarized electronic states.18–20 A particularly attractive feature of several spinel chalcogenides is half-metallic ferromagnetism (HMF),21 characterized by 100% spin polarization at the Fermi level, with metallic conductivity in one spin channel and semiconducting or insulating behaviour in the other. This property is highly desirable for spintronic applications such as spin injection, spin filtering, and polarized current transport in semiconductor-based devices.22,23 Beyond magnetism, spinel chalcogenides have also emerged as promising candidates for thermoelectric energy conversion. The efficiency of thermoelectric materials is quantified by the dimensionless figure of merit zT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, and κ represents the total thermal conductivity.24–26 Enhancing zT typically involves band-gap engineering and phonon-scattering mechanisms to suppress lattice thermal conductivity. Several transition-metal-based thiospinels, including HgY2(S/Se)4, ZnMn2(S/Se/Te)4, Mg(Lu/La)2Z4 (Z = S, Se), SrX2S4 (X = Mn, Fe, Co), as well as MgNi2S4 and MgNi2Se4, have been recently identified as promising candidates for thermoelectric and spintronic applications.27–30 Furthermore, intriguing magnetic and electronic phenomena have been reported in spinel systems containing transition metals such as Ti, V, Cr, and Mn, as well as doped Sr–S-based compounds.31 Despite these advances, magnesium-based thiospinels remain comparatively underexplored, despite their appealing advantages of low toxicity, elemental abundance, and lightweight nature. Motivated by these considerations, the present work employs density functional theory (DFT) to conduct a comprehensive first-principles investigation of MgTi2Se4 and MgMn2Se4 thiospinels. The electronic band structures are analyzed using the modified Becke–Johnson (mBJ) potential, known for its reliable prediction of band gaps and exchange splitting in correlated systems. Additionally, thermoelectric properties are evaluated within the Boltzmann transport framework under the constant relaxation time approximation to capture carrier-dependent transport behaviour. The results demonstrate that both MgTi2Se4 and MgMn2Se4 exhibit a favorable combination of strong spin polarization, half-metallic ferromagnetism, and promising thermoelectric performance, highlighting their potential for future spintronic and energy-conversion technologies and motivating further experimental exploration.
2 Computational details
Density functional theory (DFT) provides a robust and widely adopted framework for exploring the intrinsic properties of materials across diverse applications. In this study, the electronic and magnetic properties of Mg(Ti/Mn)2Se4 spinel compounds were investigated using the WIEN2k code, employing the full-potential linearized augmented plane wave (FP-LAPW) method.32 Structural optimization and total-energy calculations were performed for both ferromagnetic (FM) and non-magnetic (NM) configurations within the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional.33 While PBE reliably predicts equilibrium lattice parameters and relative energy trends, it is known to underestimate band gaps and related electronic properties. Although GGA + U was employed to account for on-site Coulomb interactions it induces only minute changes in the band gap. To overcome this limitation and obtain a more accurate description of the electronic structure, the Tran–Blaha modified Becke–Johnson (TB-mBJ) potential was employed.34 The TB-mBJ potential serves as a computationally efficient alternative to more demanding approaches such as PBE + U and hybrid functionals (e.g., HSE06), offering improved accuracy in predicting band gaps and density of states. Given the relatively moderate electronic correlations among the Ti/Mn-3d, Mg, and Se states in the present compounds, the TB-mBJ scheme was deemed appropriate, providing reliable results at a substantially reduced computational cost. In the FP-LAPW formalism, the crystal was partitioned into muffin-tin spheres and an interstitial region; the wavefunctions were expanded in spherical harmonics within the muffin-tin spheres and in plane waves in the interstitial space. Brillouin-zone integration was carried out using a 12 × 12 × 12 Monkhorst–Pack k-point mesh. The plane-wave cutoff was set to Kmax × RMT = 8.0, with a maximum angular momentum 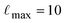 , and total-energy convergence was achieved within 0.1 mRy. The thermoelectric properties of Mg(Ti/Mn)2Se4 were evaluated using the BoltzTrap code, which is based on semi-classical Boltzmann transport theory.35 Temperature-dependent transport coefficients, including the Seebeck coefficient and electrical conductivity, were calculated within the constant relaxation time approximation using well-established transport equations reported in the literature.36 These parameters provide critical insight into the thermoelectric performance and potential applicability of the studied materials.
, and total-energy convergence was achieved within 0.1 mRy. The thermoelectric properties of Mg(Ti/Mn)2Se4 were evaluated using the BoltzTrap code, which is based on semi-classical Boltzmann transport theory.35 Temperature-dependent transport coefficients, including the Seebeck coefficient and electrical conductivity, were calculated within the constant relaxation time approximation using well-established transport equations reported in the literature.36 These parameters provide critical insight into the thermoelectric performance and potential applicability of the studied materials.| |
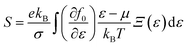 | (1) |
| |
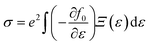 | (2) |
| |
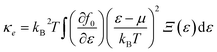 | (3) |
Here, Ξ(ε) is a transport distribution function specified by 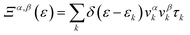 .where vαkrepresent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100
.where vαkrepresent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-k points.
000-k points.
3 Results and discussion
3.1 Structural properties
The spinel-type compounds MgX2Se4 (X = Ti, Mn), crystallizes in the cubic spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227). There are eight magnesium, sixteen transition metal (Ti/Mn) and thirty-two selenium atoms in each unit cell. In this structure, the tetrahedral 8a Wyckoff positions (0.125, 0.125, 0.125) are occupied by Mg atoms and the octahedral 16d sites (0.5, 0.5, 0.5) are occupied by Ti and Mn atoms. To preserve the cubic symmetry of the structure the Se atoms occupy the 32e Wyckoff positions with fractional coordinates typically optimized around (0.25 0.25 0.25).37 The optimized crystal structure is shown in Fig. 1(a). To determine the equilibrium structural parameters, total energy versus volume (E–V) curves were generated using the generalized gradient approximation (GGA) as proposed by Perdew–Burke–Ernzerhof (PBE). These data were fitted using the Murnaghan equation of state38 as:
m (No. 227). There are eight magnesium, sixteen transition metal (Ti/Mn) and thirty-two selenium atoms in each unit cell. In this structure, the tetrahedral 8a Wyckoff positions (0.125, 0.125, 0.125) are occupied by Mg atoms and the octahedral 16d sites (0.5, 0.5, 0.5) are occupied by Ti and Mn atoms. To preserve the cubic symmetry of the structure the Se atoms occupy the 32e Wyckoff positions with fractional coordinates typically optimized around (0.25 0.25 0.25).37 The optimized crystal structure is shown in Fig. 1(a). To determine the equilibrium structural parameters, total energy versus volume (E–V) curves were generated using the generalized gradient approximation (GGA) as proposed by Perdew–Burke–Ernzerhof (PBE). These data were fitted using the Murnaghan equation of state38 as: 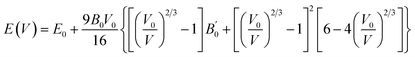 where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus and
where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus and 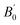 is its pressure derivative which enables the extraction of key parameters such as the equilibrium volume, bulk modulus, and its pressure derivative. By connecting these physical quantities to the total energy E(V) at a specific volume V, this equation offers a solid understanding of the structural behaviour of the compounds under various volumes. The total energies of the ferromagnetic (FM) and non-magnetic (NM) configurations were compared to assess the magnetic stability of both compounds. The FM phase is energetically more stable as confirmed by the positive energy differences (ΔE = ENM–EFM) suggesting that MgTi2Se4 and MgMn2Se4 possess ferromagnetic ground states. The E–V curves of the FM configurations shown in Fig. 1(b). Exhibit well-defined minima confirming thermodynamic equilibrium and proper structural optimization. Thermodynamic stability was further assessed through the enthalpy of formation (ΔHf) calculated using
is its pressure derivative which enables the extraction of key parameters such as the equilibrium volume, bulk modulus, and its pressure derivative. By connecting these physical quantities to the total energy E(V) at a specific volume V, this equation offers a solid understanding of the structural behaviour of the compounds under various volumes. The total energies of the ferromagnetic (FM) and non-magnetic (NM) configurations were compared to assess the magnetic stability of both compounds. The FM phase is energetically more stable as confirmed by the positive energy differences (ΔE = ENM–EFM) suggesting that MgTi2Se4 and MgMn2Se4 possess ferromagnetic ground states. The E–V curves of the FM configurations shown in Fig. 1(b). Exhibit well-defined minima confirming thermodynamic equilibrium and proper structural optimization. Thermodynamic stability was further assessed through the enthalpy of formation (ΔHf) calculated using 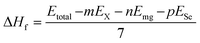 where Etotal is the total energy of the spinel and EX, EMg and ESe are the elemental reference energies for Ti/Mn, Mg, and Se, respectively. The calculated formation enthalpies are −0.820 eV for MgTi2Se4 and −0.579 eV for MgMn2Se4 both negative values confirming the thermodynamic viability of the compounds. To evaluate structural compatibility within the spinel framework, the tolerance factor (τ) was computed using the formula:
where Etotal is the total energy of the spinel and EX, EMg and ESe are the elemental reference energies for Ti/Mn, Mg, and Se, respectively. The calculated formation enthalpies are −0.820 eV for MgTi2Se4 and −0.579 eV for MgMn2Se4 both negative values confirming the thermodynamic viability of the compounds. To evaluate structural compatibility within the spinel framework, the tolerance factor (τ) was computed using the formula: 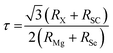 are the ionic radii of Ti/Mn, Mg, and Se, respectively. For MgTi2Se4 and MgMn2Se4, the estimated τ values were 0.92 and 0.94. These values suggest a structurally stable cubic configuration because they are close to unity. The structural and thermodynamic robustness of MgX2Se4 (X = Ti, Mn) spinels is supported by the near-unity tolerance factor and negative enthalpy of formation. Table 1 reports the calculated values, which are in good agreement with previous theoretical DFT studies.39 They are therefore excellent options for use in optoelectronic and thermoelectric technologies. Their potential for magnetic and multifunctional device applications is further enhanced by the observed FM ground state. The computed values from our first-principles simulations are shown in Table 1.
are the ionic radii of Ti/Mn, Mg, and Se, respectively. For MgTi2Se4 and MgMn2Se4, the estimated τ values were 0.92 and 0.94. These values suggest a structurally stable cubic configuration because they are close to unity. The structural and thermodynamic robustness of MgX2Se4 (X = Ti, Mn) spinels is supported by the near-unity tolerance factor and negative enthalpy of formation. Table 1 reports the calculated values, which are in good agreement with previous theoretical DFT studies.39 They are therefore excellent options for use in optoelectronic and thermoelectric technologies. Their potential for magnetic and multifunctional device applications is further enhanced by the observed FM ground state. The computed values from our first-principles simulations are shown in Table 1.
 |
| | Fig. 1 (a) Crystal structure of the material in the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase and (b) optimized total energy as a function of volume. m phase and (b) optimized total energy as a function of volume. | |
Table 1 Lattice parameter (Å), bulk modulus (GPa), energies differences (eV), enthalpy of formation eV per atom, spin-down gap (↓Eg (eV)), half-metallic gap, ghm (eV) and spin splitting gap along with tolerance factor are calculated for spinels MgTi2Se4 and MgMn2Se4
| Parameters |
Present |
Work |
Reported |
Work39 |
| MgTi2Se4 |
MgMn2Se4 |
MgTi2S4 |
MgMn2S4 |
| a0 |
10.87 |
10.89 |
10.19 |
10.17 |
| B0 |
66.96 |
55.91 |
83.17 |
86.25 |
| ΔE1 |
1.33 |
0.097 |
— |
— |
| ΔHf |
−0.820 |
−0.579 |
−1.22 |
−0.98 |
| ↓Eg |
1.29 |
1.86 |
1.65 |
2.00 |
| ghm |
0.29 |
1.1 |
0.15 |
0.75 |
| Δspin |
2 |
1.4 |
— |
— |
| τ |
0.92 |
0.94 |
— |
— |
3.2 Electronic structure
A material's electronic configuration governs its physical behavior and determines its suitability for a wide range of technological applications. Among electronic parameters the band gap plays a central role as a key tuning factor for optimizing performance in advanced technologies such as spintronics optoelectronics and non-volatile memory devices. In this work the electronic band structures of MgTi2Se4 and MgMn2Se4 were calculated using three exchange–correlation approaches namely the generalized gradient approximation GGA + U and the modified Becke–Johnson potential combined with GGA mBJ–GGA. Although the GGA + U method accounts for on-site coulomb interactions it produces only marginal changes in the band gap. Consequently, the final electronic structure analysis is primarily based on the more reliable mBJ–GGA results. A systematic comparison between GGA and mBJ–GGA shows that both approaches predict qualitatively similar electronic features. However, mBJ–GGA yields significantly larger and more realistic band gap values. This improvement highlights the superior capability of the mBJ–GGA functional in describing exchange–correlation effects in transition-metal-based spinel chalcogenides where conventional GGA typically underestimates band gaps due to its limited treatment of localized d-electron interactions. All atomic orbital contributions are included in the band structure calculations providing a comprehensive description of the electronic environment and enabling an accurate assessment of the optoelectronic and spintronic potential of these materials. Both MgTi2Se4 and MgMn2Se4 exhibit half-metallic ferromagnetism as shown in Fig. 2 with pronounced spin asymmetry in their band structures. The spin-down minority channel shows semiconducting behavior with the Fermi level located within a clear energy gap whereas the spin-up majority channel exhibits metallic behavior with the Fermi level crossing the valence band. This spin-dependent band distribution confirms 100% spin polarization at the Fermi level which is a defining feature of half-metallicity and is crucial for efficient spin injection and filtering in spintronic devices. Using both functionals the band gap (Eg) defined as the energy difference between the valence band maximum and the conduction band minimum was calculated and is presented in Table 1. The mBJ–GGA results closely match previous theoretical reports39 confirming the reliability of this approach for spinel-type materials. Spin-dependent features are further emphasized through a detailed analysis of the band dispersion. Charge transport benefits from the more dispersive bands in the spin-up channel, which reflects a lower effective mass and higher carrier mobility. In contrast the flatter bands observed in the spin-down channel indicate higher effective masses which are favorable for spin-selective transport mechanisms but result in reduced charge carrier mobility.40 Strong exchange interactions essential for stabilizing ferromagnetic ordering give rise to the direct band gap observed in the spin-down channel near the Fermi level. The spin-splitting energy gap defined as the energy difference between the Fermi level and the valence band maximum or conduction band minimum in each spin channel was calculated and is listed in Table 1. Furthermore, the degree of spin polarization (P) at the Fermi level was determined using the expression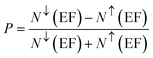 ×100 where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A result of P = 100%confirms complete spin polarization, a hallmark of half-metallicity.41 The energy difference between the highest occupied and lowest unoccupied states in the spin-down channel, known as the half-metallic gap (Ehmg), was also calculated. Because it controls the stability and robustness of the half-metallic state, this parameter is especially important for spin-filtering and tunnelling magnetoresistance (TMR) applications. These compounds' half-metallic ferromagnetic nature is further supported by the presence of a finite Ehmg, highlighting their potential as next-generation magneto-optoelectronic materials, magnetic sensors, and spintronic switches.
×100 where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A result of P = 100%confirms complete spin polarization, a hallmark of half-metallicity.41 The energy difference between the highest occupied and lowest unoccupied states in the spin-down channel, known as the half-metallic gap (Ehmg), was also calculated. Because it controls the stability and robustness of the half-metallic state, this parameter is especially important for spin-filtering and tunnelling magnetoresistance (TMR) applications. These compounds' half-metallic ferromagnetic nature is further supported by the presence of a finite Ehmg, highlighting their potential as next-generation magneto-optoelectronic materials, magnetic sensors, and spintronic switches.
 |
| | Fig. 2 Plot of electronic band structure for MgX2Se4 in spin-up and spin-down channels using the GGA + mBJ potential approximation (X = Ti/Mn). | |
3.2.1 Density of states analysis. To gain a detailed understanding of the electronic structure and orbital hybridization mechanisms in MgTi2Se4 and MgMn2Se4, the total density of states (TDOS) and partial density of states (PDOS) were systematically analyzed. These analyses provide clear insight into the orbital-resolved contributions to the electronic structure and elucidate the distribution of electronic states over different energy ranges. The calculated TDOS and PDOS spectra, presented in Fig. 3, are in good agreement with the corresponding band structures and validate the reliability of the electronic structure calculations. For MgTi2Se4, the metallic nature in the spin-up channel originates from strong hybridization between Ti-3d and Se-3p orbitals within the energy window of approximately −2 eV to +2 eV around the Fermi level. In contrast, the spin-down channel exhibits semiconducting behavior, with predominantly localized states distributed between −4.3 eV and −2.5 eV, leading to a clear spin-dependent electronic structure. In MgMn2Se4, the PDOS reveals pronounced spin asymmetry, where spin-up states are mainly located between −4.2 eV and −2.2 eV, while spin-down sub-bands extend from −4.1 eV to −2.1 eV. These features indicate that the Mn-3d and Se-4p orbitals play a dominant role in governing both the electronic and magnetic properties of the compound. Moreover, the clear exchange splitting evidenced by the energy separation between spin-up and spin-down states confirms the energetic stability of the ferromagnetic ground state in both materials. The coexistence of complete spin polarization, visible-range band gaps in the spin-down channel, and strong exchange interactions establishes MgTi2Se4 and MgMn2Se4 as promising candidates for next-generation spintronic, optoelectronic, and magneto-transport applications.
 |
| | Fig. 3 Plot of total density (TDOS) of states and partial density of states in spin up and spin down channels for MgX2Se4 (X = Ti/Mn). | |
3.3 Magnetic behaviour
The ferromagnetic nature of MgTi2Se4 and MgMn2Se4 spinels was established through spin-polarized DFT-based volume optimization, confirming that both compounds energetically favor a ferromagnetic (FM) ground state. These materials crystallize in the cubic spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, where Mg occupies tetrahedral (A) sites and the transition metals Ti or Mn reside at octahedral (B) sites, each coordinated by six Se atoms. In MgTi2Se4, although Ti4+ (3d0) is formally expected to be nonmagnetic, a finite local magnetic moment of ∼0.88762 µB per Ti atom is obtained. Such induced magnetism in nominally d0 cations has been widely reported and is commonly attributed to strong p–d hybridization between the transition-metal d states and ligand p orbitals, leading to partial occupation and spin polarization of the d states rather than purely ionic Ti4+ behavior.42–45 Under octahedral coordination, the Ti-3d orbitals split into lower-energy t2g and higher-energy eg states due to crystal-field effects. Spin-resolved partial density of states (PDOS) analysis reveals an exchange splitting of the Ti-t2g states near the Fermi level, confirming that the induced moment originates from hybridization-driven charge transfer from Se-4p states into Ti-3d orbitals. Similar hybridization-induced d0 magnetism has been previously reported in Ti-based oxides and chalcogenides, where ligand-to-metal charge transfer and covalent bonding give rise to finite magnetic moments on otherwise nonmagnetic cations.42–44 The reduction of the Ti moment from the ideal 1 µB further reflects the itinerant nature of the spin density, which is redistributed into ligand and interstitial regions. This interpretation is supported by the substantial interstitial magnetic moment (0.53244 µB) and the negative spin polarization of Se atoms (−0.01283 µB each), a hallmark of p–d hybridization-mediated magnetism.45 The atomic contributions of Mg (0.00988 µB), Ti (0.88762 µB), Se (−0.01283 µB), and the interstitial region (0.53244 µB) yield a total magnetic moment of approximately 4.0004 µB per conventional unit cell, consistent with the integer moment expected for half-metallic ferromagnets. This internal consistency between integer magnetization and spin-polarized electronic structure further validates the half-metallicity of MgTi2Se4. The ferromagnetic exchange interaction in this compound is therefore mediated by hybridization-induced spin polarization and itinerant exchange mechanisms rather than purely localized moments. In contrast, MgMn2Se4 exhibits strong localized ferromagnetism. Mn2+ ions (3d5) adopt a high-spin configuration in an octahedral crystal field, resulting in a large local magnetic moment. The calculated Mn moment of 4.20762 µB is slightly reduced from the ideal 5 µB due to p–d hybridization with Se-4p states, as evidenced by the negative Se polarization (−0.13507 µB) and a modest interstitial contribution (0.21045 µB). The resulting total magnetic moment of approximately 16.0005 µB per unit cell confirms robust ferromagnetic ordering and supports a superexchange-driven Mn–Se–Mn interaction pathway. While MgMn2Se4 is dominated by localized magnetic moments and strong exchange coupling, the larger interstitial contribution in MgTi2Se4 indicates more delocalized spin density and weaker, itinerant magnetic interactions.43 The computed atomic and interstitial magnetic moments for both compounds are summarized in Table 2. These findings not only substantiate the intrinsic ferromagnetism of both materials but also highlight their strong potential for spintronic applications requiring high spin polarization and stable magnetic ordering.
m, where Mg occupies tetrahedral (A) sites and the transition metals Ti or Mn reside at octahedral (B) sites, each coordinated by six Se atoms. In MgTi2Se4, although Ti4+ (3d0) is formally expected to be nonmagnetic, a finite local magnetic moment of ∼0.88762 µB per Ti atom is obtained. Such induced magnetism in nominally d0 cations has been widely reported and is commonly attributed to strong p–d hybridization between the transition-metal d states and ligand p orbitals, leading to partial occupation and spin polarization of the d states rather than purely ionic Ti4+ behavior.42–45 Under octahedral coordination, the Ti-3d orbitals split into lower-energy t2g and higher-energy eg states due to crystal-field effects. Spin-resolved partial density of states (PDOS) analysis reveals an exchange splitting of the Ti-t2g states near the Fermi level, confirming that the induced moment originates from hybridization-driven charge transfer from Se-4p states into Ti-3d orbitals. Similar hybridization-induced d0 magnetism has been previously reported in Ti-based oxides and chalcogenides, where ligand-to-metal charge transfer and covalent bonding give rise to finite magnetic moments on otherwise nonmagnetic cations.42–44 The reduction of the Ti moment from the ideal 1 µB further reflects the itinerant nature of the spin density, which is redistributed into ligand and interstitial regions. This interpretation is supported by the substantial interstitial magnetic moment (0.53244 µB) and the negative spin polarization of Se atoms (−0.01283 µB each), a hallmark of p–d hybridization-mediated magnetism.45 The atomic contributions of Mg (0.00988 µB), Ti (0.88762 µB), Se (−0.01283 µB), and the interstitial region (0.53244 µB) yield a total magnetic moment of approximately 4.0004 µB per conventional unit cell, consistent with the integer moment expected for half-metallic ferromagnets. This internal consistency between integer magnetization and spin-polarized electronic structure further validates the half-metallicity of MgTi2Se4. The ferromagnetic exchange interaction in this compound is therefore mediated by hybridization-induced spin polarization and itinerant exchange mechanisms rather than purely localized moments. In contrast, MgMn2Se4 exhibits strong localized ferromagnetism. Mn2+ ions (3d5) adopt a high-spin configuration in an octahedral crystal field, resulting in a large local magnetic moment. The calculated Mn moment of 4.20762 µB is slightly reduced from the ideal 5 µB due to p–d hybridization with Se-4p states, as evidenced by the negative Se polarization (−0.13507 µB) and a modest interstitial contribution (0.21045 µB). The resulting total magnetic moment of approximately 16.0005 µB per unit cell confirms robust ferromagnetic ordering and supports a superexchange-driven Mn–Se–Mn interaction pathway. While MgMn2Se4 is dominated by localized magnetic moments and strong exchange coupling, the larger interstitial contribution in MgTi2Se4 indicates more delocalized spin density and weaker, itinerant magnetic interactions.43 The computed atomic and interstitial magnetic moments for both compounds are summarized in Table 2. These findings not only substantiate the intrinsic ferromagnetism of both materials but also highlight their strong potential for spintronic applications requiring high spin polarization and stable magnetic ordering.
Table 2 The total and partial spin magnetic moments for MgX2Se4 (X = Ti/Mn) Spinels
| Compound |
Total (µB) |
Int (µB) |
Mg (µB) |
Ti/Mn (µB) |
Se(µB) |
| MgTi2S4 |
4.00004 |
0.53244 |
0.00988 |
0.88762 |
−0.1283 |
| MgMn2Se4 |
16.00044 |
0.21045 |
0.02003 |
4.20762 |
−0.1309 |
3.4 Elastic properties
The elastic and mechanical properties of the cubic MgX2Se4 (X = Ti, Mn) spinel chalcogenides were systematically examined using the second-order elastic constants C11, C12, and C44, as reported in Table 2. In cubic crystals the mechanical stability is governed by the Born stability criteria which require C11 > 0, C44 > 0, C11–C12 > 0, C11 + 2C12 > 0, and C11 > B > C12.46 The calculated elastic constants for MgTi2Se4 and MgMn2Se4 satisfy all these conditions confirming their mechanical stability in the cubic phase with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The relatively larger values of C11 compared to C12 further indicate strong resistance to uniaxial deformation, while the finite values of C44 confirm stability against shear strain. To obtain macroscopic mechanical parameters the elastic constants were converted into bulk shear and Young's moduli using the Voigt–Reuss–Hill approximation which provides reliable estimates for polycrystalline materials.47–49 The Voigt bulk modulus is defined as BV = (C11 + 2C12)/3 and for cubic symmetry BV = BR where BR denotes the Reuss bulk modulus. The shear modulus bounds were evaluated using GV = (C11–C12 + 3C44)/5 and GR = 5(C11–C12)C44/[4C44 + 3(C11–C12)] with the effective shear modulus given by G = (GV + GR)/2. The resulting bulk moduli of 66.96 GPa for MgTi2Se4 and 55.07 GPa for MgMn2Se4 indicate moderate resistance to uniform compression. In contrast the lower shear moduli of 36.31 GPa and 27.19 GPa respectively indicate that these compounds are more compliant under shear deformation than under volumetric compression. The Young's modulus was calculated using E = 9BG/(3B + G) and attains values of 92.48 GPa for MgTi2Se4 and 69.65 GPa for MgMn2Se4, reflecting the comparatively higher stiffness of the Ti-containing compound. The observed trend E > B > G highlights the high stiffness combined with enhanced shear flexibility in these spinel structures. The ductile or brittle nature of the compounds was evaluated using multiple mechanical indicators. According to Pugh's criterion, materials with a ratio B/G > 1.75are classified as ductile.50 The calculated ratios of 1.87 for MgTi2Se4 and 1.95 for MgMn2Se4 clearly place both compounds in the ductile regime. This conclusion is further supported by Poisson's ratio, determined from ν = (3B–E)/(6B), which exceeds the critical value of 0.26 associated with ductile and metallic bonding characteristics.51 Additionally, the positive Cauchy pressure, defined as C12–C44, yields values of 3.7 GPa and 2.5 GPa for MgTi2Se4 and MgMn2Se4, respectively, signifying the dominance of non-directional bonding and further confirming their ductile behaviour. Elastic anisotropy, which plays a crucial role in determining crack propagation, mechanical reliability, and direction-dependent response, was analyzed using both the Zener anisotropy factor and the universal anisotropy index. The Zener factor, defined as A = 2C44/(C11–C12), deviates significantly from unity, with values of 0.48 for MgTi2Se4 and 0.37 for MgMn2Se4, indicating pronounced elastic anisotropy. To provide a more comprehensive measure, the universal anisotropy index was calculated using AU = 5(GV/GR − 1), yielding values of 0.67 and 1.30 for MgTi2Se4 and MgMn2Se4, respectively. The larger AU value for MgMn2Se4 suggests stronger anisotropic elastic behaviour, particularly in shear-dominated deformation modes. Further insight into the microscopic deformation mechanism was obtained from the Kleinman parameter ξ, which describes the relative ease of bond stretching versus bond bending during elastic deformation. The calculated values of 0.37 for MgTi2Se4 and 0.33 for MgMn2Se4 indicate a balanced contribution of bond-angle bending and bond-length stretching, implying moderate resistance to angular distortions. In addition, the evaluated sound velocities, Debye temperatures, and thermophysical parameters reveal that MgTi2Se4 exhibits higher lattice stiffness and thermal robustness compared to MgMn2Se4, consistent with its larger elastic moduli. We created 3D contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (v) using the Elate visualization tool to obtain a more thorough grasp of the elastic and anisotropic properties of the compounds under study. These plots illustrate how these properties vary with crystallographic direction and are displayed in Fig. 4 and 5 for MgX2Se4 (X = Ti/Mn), respectively. The findings unequivocally demonstrate that all elastic parameters, except for linear compressibility, exhibit a significant deviation from a spherical shape, highlighting their anisotropic behaviour. Furthermore, the direction-dependent mechanical response of these spinel structures is confirmed by the anisotropy's uniform distribution across various directions. Table 3 displays the calculated values. Overall, the detailed elastic analysis demonstrates that MgX2Se4 (X = Ti, Mn) compounds are mechanically stable, elastically anisotropic, and intrinsically ductile. The combination of moderate stiffness, enhanced shear compliance, and pronounced elastic anisotropy makes these materials promising candidates for technological applications where mechanical reliability, flexibility, and anisotropic response are desirable
m. The relatively larger values of C11 compared to C12 further indicate strong resistance to uniaxial deformation, while the finite values of C44 confirm stability against shear strain. To obtain macroscopic mechanical parameters the elastic constants were converted into bulk shear and Young's moduli using the Voigt–Reuss–Hill approximation which provides reliable estimates for polycrystalline materials.47–49 The Voigt bulk modulus is defined as BV = (C11 + 2C12)/3 and for cubic symmetry BV = BR where BR denotes the Reuss bulk modulus. The shear modulus bounds were evaluated using GV = (C11–C12 + 3C44)/5 and GR = 5(C11–C12)C44/[4C44 + 3(C11–C12)] with the effective shear modulus given by G = (GV + GR)/2. The resulting bulk moduli of 66.96 GPa for MgTi2Se4 and 55.07 GPa for MgMn2Se4 indicate moderate resistance to uniform compression. In contrast the lower shear moduli of 36.31 GPa and 27.19 GPa respectively indicate that these compounds are more compliant under shear deformation than under volumetric compression. The Young's modulus was calculated using E = 9BG/(3B + G) and attains values of 92.48 GPa for MgTi2Se4 and 69.65 GPa for MgMn2Se4, reflecting the comparatively higher stiffness of the Ti-containing compound. The observed trend E > B > G highlights the high stiffness combined with enhanced shear flexibility in these spinel structures. The ductile or brittle nature of the compounds was evaluated using multiple mechanical indicators. According to Pugh's criterion, materials with a ratio B/G > 1.75are classified as ductile.50 The calculated ratios of 1.87 for MgTi2Se4 and 1.95 for MgMn2Se4 clearly place both compounds in the ductile regime. This conclusion is further supported by Poisson's ratio, determined from ν = (3B–E)/(6B), which exceeds the critical value of 0.26 associated with ductile and metallic bonding characteristics.51 Additionally, the positive Cauchy pressure, defined as C12–C44, yields values of 3.7 GPa and 2.5 GPa for MgTi2Se4 and MgMn2Se4, respectively, signifying the dominance of non-directional bonding and further confirming their ductile behaviour. Elastic anisotropy, which plays a crucial role in determining crack propagation, mechanical reliability, and direction-dependent response, was analyzed using both the Zener anisotropy factor and the universal anisotropy index. The Zener factor, defined as A = 2C44/(C11–C12), deviates significantly from unity, with values of 0.48 for MgTi2Se4 and 0.37 for MgMn2Se4, indicating pronounced elastic anisotropy. To provide a more comprehensive measure, the universal anisotropy index was calculated using AU = 5(GV/GR − 1), yielding values of 0.67 and 1.30 for MgTi2Se4 and MgMn2Se4, respectively. The larger AU value for MgMn2Se4 suggests stronger anisotropic elastic behaviour, particularly in shear-dominated deformation modes. Further insight into the microscopic deformation mechanism was obtained from the Kleinman parameter ξ, which describes the relative ease of bond stretching versus bond bending during elastic deformation. The calculated values of 0.37 for MgTi2Se4 and 0.33 for MgMn2Se4 indicate a balanced contribution of bond-angle bending and bond-length stretching, implying moderate resistance to angular distortions. In addition, the evaluated sound velocities, Debye temperatures, and thermophysical parameters reveal that MgTi2Se4 exhibits higher lattice stiffness and thermal robustness compared to MgMn2Se4, consistent with its larger elastic moduli. We created 3D contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (v) using the Elate visualization tool to obtain a more thorough grasp of the elastic and anisotropic properties of the compounds under study. These plots illustrate how these properties vary with crystallographic direction and are displayed in Fig. 4 and 5 for MgX2Se4 (X = Ti/Mn), respectively. The findings unequivocally demonstrate that all elastic parameters, except for linear compressibility, exhibit a significant deviation from a spherical shape, highlighting their anisotropic behaviour. Furthermore, the direction-dependent mechanical response of these spinel structures is confirmed by the anisotropy's uniform distribution across various directions. Table 3 displays the calculated values. Overall, the detailed elastic analysis demonstrates that MgX2Se4 (X = Ti, Mn) compounds are mechanically stable, elastically anisotropic, and intrinsically ductile. The combination of moderate stiffness, enhanced shear compliance, and pronounced elastic anisotropy makes these materials promising candidates for technological applications where mechanical reliability, flexibility, and anisotropic response are desirable
 |
| | Fig. 4 (a–d) Directional dependence of (a) Young's modulus (Y), (b) linear compressibility (β), (c) shear modulus (G), and (d) Poisson's ratio (v) for MgTi2Se4 compound. | |
 |
| | Fig. 5 (a–d) Directional dependence of (a) Young's modulus (Y), (b) linear compressibility (β), (c) shear modulus (G), and (d) Poisson's ratio (v) for MgMn2Se4 compound. | |
Table 3 Elastic, mechanical, and thermophysical properties of MgTi2Se4 and MgMn2Se4
| Property |
Symbol |
Unit |
MgTi2Se4 |
MgMn2Se4 |
| Elastic constant |
C11 |
GPa |
142.6 |
118 |
| Elastic constant |
C12 |
GPa |
30.7 |
20.5 |
| Elastic constant |
C44 |
GPa |
27 |
18 |
| Bulk modulus |
B |
GPa |
66.96 |
55.07 |
| Density |
ρ |
g cm−3 |
1.82 |
2.56 |
| Cauchy pressure |
Cp |
GPa |
3.7 |
2.5 |
| Shear modulus (VRH) |
G |
GPa |
36.31 |
27.19 |
| Young's modulus |
E |
GPa |
92.48 |
69.65 |
| Pugh's ratio |
B/G |
— |
1.87 |
1.95 |
| Poisson's ratio |
ν |
— |
0.273 |
0.281 |
| Gruneisen parameter |
G |
— |
1.616 |
1.660 |
| Linear compressibility |
B |
Pa−1 |
0.0049 |
0.0059 |
| Elastic anisotropy factor |
A |
— |
0.48 |
0.37 |
| Universal anisotropy factor |
AU |
— |
0.67 |
1.30 |
| Kleinman parameter |
Ξ |
— |
0.37 |
0.33 |
| Transverse sound velocity |
vt |
km s−1 |
4.47 |
3.26 |
| Longitudinal sound velocity |
vl |
km s−1 |
8.00 |
5.90 |
| Average sound velocity |
vm |
km s−1 |
4.97 |
3.63 |
| Debye temperature |
ΘD |
K |
414 |
339 |
| Melting temperature* |
Tm |
K |
1396 |
1250 |
| Minimum thermal conductivity* |
Kmin |
W m−1 K−1 |
0.47 |
0.43 |
| Hardness* |
Ha |
GPa |
13.36 |
10.81 |
3.5 Optical properties
Light is a plentiful, sustainable, and clean energy source with immense potential for next-generation optoelectronic technologies. In recent years, significant attention has been directed toward the development of high-performance materials capable of efficiently harvesting and converting light into electrical energy. The interaction of materials with electromagnetic radiation is primarily governed by electronic transitions induced by photon excitation, which can be classified as intra-band and inter-band transitions. Inter-band transitions, arising from the excitation of electrons from the valence band to the conduction band, play a dominant role in semiconductors and insulators, whereas intra-band transitions occur within the same electronic band and are typically prevalent in metallic systems. Consequently, optical absorption, emission, and the overall photo response of materials are largely dictated by inter-band transitions.52 The optical properties of MgTi2Se4 and MgMn2Se4 were systematically investigated using the complex dielectric function including both the real ε1(ω) and imaginary ε2(ω) components, along with related optical parameters such as absorption coefficient, reflectivity, refractive index, and optical conductivity over the photon energy range of 0–14 eV. The imaginary part ε2(ω) represents photon absorption associated with electronic transitions, while the real part ε1(ω) describes the dispersive behavior and the degree of polarization induced by an external electric field. The calculated dielectric functions of MgTi2Se4 and MgMn2Se4 are shown in (Fig. 6a and b), respectively. For MgTi2Se4 (Fig. 6(a)), the static dielectric constant ε1(0) is approximately 10, and ε1(ω) decreases with increasing photon energy, becoming negative in the energy range of about 3.5–6 eV, indicating plasmonic-like behavior. The ε2(ω) spectrum exhibits pronounced absorption peaks around 1.5, 3.5, 5, 7, and 10 eV, originating from allowed inter-band electronic transitions. In the case of MgMn2Se4 (Fig. 6b), the static dielectric constant ε1(0) attains a higher value of approximately 35–40, signifying strong low-energy electronic polarization. With increasing photon energy, ε1(ω) rapidly decreases and shows negative values up to nearly 1.5 eV, followed by weak negative regions at higher energies around 12–14 eV, associated with plasmonic-type excitations. The ε2(ω) spectrum displays dominant peaks at approximately 0.5, 2, 4, and 6 eV, corresponding to inter-band transitions, while both ε1(ω) and ε2(ω) gradually diminish at higher photon energies, indicating reduced optical response. These trends are further supported by the optical conductivity spectra shown in (Fig. 6(c). Both compounds exhibit very low optical conductivity below 2 eV, consistent with their optical band gaps. The conductivity increases sharply in the energy range of 2–10 eV and reaches maximum values around 8–10 eV with peak conductivities of approximately 7000 Ω−1 cm−1 for MgTi2Se4 and 6500 Ω−1 cm−1 for MgMn2Se4, indicating efficient photon-induced charge carrier excitation and strong electron–photon coupling. The absorption coefficient spectra (Fig. 7(d) reveal low absorption in the visible and infrared regions below 3 eV, suggesting optical transparency, followed by strong absorption maxima of about 2.0–2.2 × 106 cm−1 in the 12–14 eV range, attributed to high-energy inter-band transitions. MgTi2Se4 exhibits marginally higher absorption intensity, reflecting stronger transition probabilities. The refractive index n(ω), derived from ε1(ω) and ε2(ω) and presented in (Fig. 6(e), shows high static values of approximately 8–9 at zero photon energy, indicating strong light–matter interaction and high optical density. In the ultraviolet region, n(ω) decreases steadily and stabilizes between 2 and 3, reflecting weak dispersion. The extinction coefficient k(ω), shown in (Fig. 6(f), varies from 1.0 to 2.7 in the energy range of 5–14 eV, confirming the presence of multiple inter-band transitions and complex energy-loss mechanisms Overall, MgTi2Se4 and MgMn2Se4 exhibit robust optical responses spanning the visible to ultraviolet regions. Their large static dielectric constants pronounced ε2(ω) peaks, high optical conductivity, and substantial absorption coefficients demonstrate strong electron–photon interactions and high polarizability. The tunability of optical properties through B-site substitution (Ti ↔ Mn) highlights compositional engineering in spinel chalcogenides as an effective strategy for tailoring materials for advanced optoelectronic, ultraviolet photodetector, solar energy harvesting, and photocatalytic applications. The key optical parameters are summarized in Table 4.
 |
| | Fig. 6 (a) Represents the real part ε1(ω) and imaginary part ε2(ω) of dielectric constant of MgTi2Se4 and (b) represents real part ε1(ω) and imaginary part ε2(ω) of dielectric constant of MgMn2Se4 (c) represents optical conductivity, (d) represents absorption coefficient (e) represents reflective index and (f) excitation coefficient under GGA-mBJ potential approximation. | |
 |
| | Fig. 7 (a–d) Temperature dependence of (a) the Seebeck coefficient, (b) electrical conductivity (c) total thermal conductivity, and (d) lattice thermal conductivity in the temperature range of 100–800 K. | |
Table 4 Key optical properties of MgTi2Se4 and MgMn2Se4 from first-principles calculations
| Optical parameter |
MgTi2Se4 |
MgMn2Se4 |
| Static dielectric constant ε1(0) |
∼10–11 |
∼35–40 |
| Dielectric constant at UV (>5 eV) |
∼4–7 |
∼3–6 |
| Imaginary dielectric peak (energy) |
∼4.0–4.3 eV |
∼3.5–3.9 eV |
| Imaginary dielectric peak (height) ε2 |
∼9–10 |
∼28–30 |
| Optical conductivity peak (energy) |
∼7000 Ω−1 cm−1 |
∼6500 Ω−1 cm−1 |
| Absorption coefficient (at 14 eV) |
∼2.2 × 106 cm−1 |
∼2.0 × 106 cm−1 |
| Static refractive index n0 |
∼8.5 |
∼2.8 |
| Refractive index in UV (5–14 eV) |
∼2.0–3.0 |
∼1.8–2.8 |
| Energy range of main optical transitions |
∼3–10 eV |
∼2.5–9 eV |
| Extinction coefficient at ∼0.5 eV |
∼4.0 |
∼0.9 |
| Extinction coefficient (5–14 eV) |
1.0 to 2.7 |
1.0 to 2.7 |
| Transparency region (low loss) |
<2 eV |
<2 eV |
3.6 Transport properties
The thermoelectric effect arises when a temperature gradient is applied across a material resulting in the generation of an electric voltage or current. This effect constitutes the fundamental operating principle of thermoelectric devices which are widely employed in temperature control solid-state refrigeration and waste heat recovery for power generation. The performance or efficiency of a thermoelectric material is commonly characterized by the dimensionless figure of merit (zT), expressed as:53 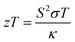 , where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (including both electronic and lattice contributions), and T is the absolute temperature. To achieve a high zT value, a material must possess a large Seebeck coefficient and high electrical conductivity, while simultaneously maintaining low thermal conductivity. The electron relaxation time (τ) is the average time between consecutive charge carrier scattering events and is a crucial factor affecting these transport characteristics. The constant relaxation time approximation (CRTA) assumes that the relaxation time varies slowly with energy over a range comparable to the thermal energy (kBT) and is therefore frequently used in practice. The power factor per unit time (S2σ/τ), electrical conductivity per unit time (σ/τ) and electronic thermal conductivity per unit time (κe/τ) are examples of transport coefficients that can be easily expressed in terms of τ under this assumption. Owing to computational limitations, the relaxation time (τ) in this study was assumed to be constant and typically of the order of 10−15 seconds, which is consistent with values for semiconducting thermoelectric materials that have been previously reported. As is common in DFT-based thermoelectric studies of related systems a carrier concentration of 1 × 1020 cm−3 was chosen. Boltzmann transport theory under the rigid band approximation (RBA) and the constant relaxation time approximation (CRTA) as implemented in the BoltzTraP code35 was used to evaluate these interdependent transport parameters. Since these compounds are expected to be ferromagnetic the two-current model was also used to investigate how magnetism affects thermoelectric behaviour.54 This model separates the transport properties into spin-up (↑) and spin-down (↓) channels, which is essential for capturing spin-dependent scattering and mobility effects that arise due to interactions between conduction electrons and localized magnetic moments. Consequently, the transport quantities become spin-resolved (S↑, S↓, σ↑, σ↓, κe↑, κe↓), and the total values are computed as σ = σ↑ + σ↓, κe = κe↑ + κe↓, and
, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (including both electronic and lattice contributions), and T is the absolute temperature. To achieve a high zT value, a material must possess a large Seebeck coefficient and high electrical conductivity, while simultaneously maintaining low thermal conductivity. The electron relaxation time (τ) is the average time between consecutive charge carrier scattering events and is a crucial factor affecting these transport characteristics. The constant relaxation time approximation (CRTA) assumes that the relaxation time varies slowly with energy over a range comparable to the thermal energy (kBT) and is therefore frequently used in practice. The power factor per unit time (S2σ/τ), electrical conductivity per unit time (σ/τ) and electronic thermal conductivity per unit time (κe/τ) are examples of transport coefficients that can be easily expressed in terms of τ under this assumption. Owing to computational limitations, the relaxation time (τ) in this study was assumed to be constant and typically of the order of 10−15 seconds, which is consistent with values for semiconducting thermoelectric materials that have been previously reported. As is common in DFT-based thermoelectric studies of related systems a carrier concentration of 1 × 1020 cm−3 was chosen. Boltzmann transport theory under the rigid band approximation (RBA) and the constant relaxation time approximation (CRTA) as implemented in the BoltzTraP code35 was used to evaluate these interdependent transport parameters. Since these compounds are expected to be ferromagnetic the two-current model was also used to investigate how magnetism affects thermoelectric behaviour.54 This model separates the transport properties into spin-up (↑) and spin-down (↓) channels, which is essential for capturing spin-dependent scattering and mobility effects that arise due to interactions between conduction electrons and localized magnetic moments. Consequently, the transport quantities become spin-resolved (S↑, S↓, σ↑, σ↓, κe↑, κe↓), and the total values are computed as σ = σ↑ + σ↓, κe = κe↑ + κe↓, and 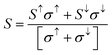 . These spin-resolved calculations allow for a more precise understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. For possible thermoelectric and spintronic applications, the thermal stability and performance of MgTi2Se4 and MgMn2Se4 spinels are clarified by a detailed analysis of the variation of thermoelectric coefficients over the 100–800 K temperature range in the section that follows.
. These spin-resolved calculations allow for a more precise understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. For possible thermoelectric and spintronic applications, the thermal stability and performance of MgTi2Se4 and MgMn2Se4 spinels are clarified by a detailed analysis of the variation of thermoelectric coefficients over the 100–800 K temperature range in the section that follows.
3.6.1 Seebeck coefficient. On applying a temperature gradient (ΔT) across a thermoelectric material, an induced voltage (ΔV) is generated and their ratio defines the Seebeck coefficient (S) according to ΔV = SΔT. The magnitude and sign of S are governed by several factors, including operating temperature, carrier concentration, and dominant scattering mechanisms.55 As illustrated in Fig. 7(a), both MgTi2Se4 and MgMn2Se4 exhibit pronounced spin-dependent thermoelectric behavior over the investigated temperature range of 100–800 K. For MgTi2Se4 Fig. 7(a), the spin-up channel shows a positive Seebeck coefficient, increasing monotonically from approximately 5 µV K−1 at 100 K to about 32 µV K−1 at 800 K. In contrast, the spin-down channel exhibits a negative Seebeck coefficient with a much larger magnitude, decreasing from roughly −2000 µV K−1 at 100 K to about −400 µV K−1 at 800 K. The opposite signs and distinctly different temperature dependences of the two spin channels confirm the half-metallic ferromagnetic nature of MgTi2Se4, indicating hole-dominated transport in the spin-up channel and electron-dominated transport in the spin-down channel. A similar spin-resolved trend is observed for MgMn2Se4, also shown in Fig. 7(a). The spin-up Seebeck coefficient remains positive and increases steadily from around 15 µV K−1 at 100 K to approximately 105 µV K−1 at 800 K, suggesting enhanced thermally activated carrier transport with increasing temperature. Meanwhile, the spin-down channel displays a negative Seebeck coefficient, whose magnitude decreases from nearly −3000 µV K−1 at 100 K to about −500 µV K−1 at 800 K, reflecting a metallic-like transport character at elevated temperatures.
3.6.2 Electrical conductivity (σ). Fig. 7(b) presents the temperature dependence of the electrical conductivity per unit relaxation time (σ/τ), calculated using the BoltzTraP code within the constant relaxation time approximation (RTA). This method allows the evaluation of electronic transport properties without explicitly determining the relaxation time τ and is widely used for comparative thermoelectric studies.56 Both MgTi2Se4 and MgMn2Se4 exhibit pronounced spin-dependent transport behavior over the temperature range of 100–800 K. For MgTi2Se4, the spin-up channel shows a monotonic decrease in σ/τ with increasing temperature, decreasing from approximately 4.5 × 1019 Ω−1 m−1 s−1 at 100 K to about 3.4 × 1019 Ω−1 m−1 s−1 at 800 K, indicating metallic-like conduction dominated by majority-spin carriers. In contrast, the spin-down conductivity remains nearly zero at low temperatures and begins to increase noticeably above ∼400 K, reaching around 0.06 × 1019 Ω−1 m−1 s−1 at 800 K. This behavior reflects the half-metallic nature of MgTi2Se4, where electrical transport is primarily governed by the spin-up channel, while minority-spin carriers are thermally activated at elevated temperatures. A similar trend is observed for MgMn2Se4. The spin-up σ/τ gradually decreases from approximately 7.7 × 1019 Ω−1 m−1 s−1 at 100 K to nearly 7.1 × 1019 Ω−1 m−1 s−1 at 800 K, confirming dominant metallic transport in the majority-spin channel. Meanwhile, the spin-down conductivity remains negligible up to about 450 K, after which it increases rapidly, reaching approximately 0.025 × 1019 Ω−1 m−1 s−1 at 800 K. The delayed yet sharp rise in the minority-spin contribution indicates thermally activated spin-down carriers at higher temperatures.
3.6.3 Thermal conductivity. One of the most important parameters governing thermoelectric efficiency is the thermal conductivity (κ), which quantifies a material's ability to transport heat through both charge carriers and lattice vibrations. In crystalline solids, the total thermal conductivity (κtotal) is composed of the electronic contribution (κe) and the lattice contribution (κl), arising from phonon-mediated heat transport. In the present work, the electronic thermal conductivity per unit relaxation time (κe/τ) was evaluated using the BoltzTraP code within the constant relaxation time approximation, while the lattice thermal conductivity (κl) was analyzed separately using slacks model57,58 as shown in Fig. 7(d). The temperature dependence of κe/τ for MgTi2Se4 and MgMn2Se4 is presented in Fig. 7(c). For MgTi2Se4, the spin-up channel exhibits a steady increase in κe/τ from approximately 1.0 W m−1 K−1 s−1 at 100 K to nearly 11.0 W m−1 K−1 s−1 at 800 K, indicating enhanced heat transport by majority-spin carriers at elevated temperatures. In contrast, the spin-down contribution remains very small at low temperatures and rises gradually beyond ∼400 K, reaching about 0.6 W m−1 K−1 s−1 at 800 K, confirming its comparatively weaker role in thermal transport. A similar trend is observed for MgMn2Se4, where the spin-up κe/τ increases from roughly 2.0 W m−1 K−1 s−1 at 100 K to around 12.0 W m−1 K−1 s−1 at 800 K, while the spin-down channel increases modestly to approximately 0.55 W m−1 K−1 s−1 at the highest temperature. These results indicate that electronic heat transport in both compounds is dominated by the spin-up channel, consistent with their half-metallic ferromagnetic character. The lattice thermal conductivity κl, shown in Fig. 7(d), displays a strong temperature-dependent decrease for both compounds, characteristic of enhanced phonon–phonon scattering at elevated temperatures. For MgTi2Se4, κl decreases rapidly from about 1.6 W m−1 K−1 at 150 K to approximately 0.2 W m−1 K−1 near 800 K. Similarly, MgMn2Se4 exhibits a reduction in κl from around 1.7 W m−1 K−1 at 150 K to nearly 0.25 W m−1 K−1 at 800 K. The low magnitude of κl at high temperatures is favorable for thermoelectric applications, as it suppresses parasitic heat flow and helps maintain a large temperature gradient.
3.6.4 Figure of merit (zT). One of the standard parameters used to assess the thermoelectric efficiency of a material is the dimensionless figure of merit (ZT), which describes the effectiveness of converting thermal energy into electrical power. It is defined as:53  where S denotes the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ = κe + κl represents the total thermal conductivity, including electronic and lattice contributions. Efficient thermoelectric performance requires a suitable compromise between a high Seebeck coefficient, sufficient electrical conductivity, and low thermal conductivity. Fig. 8 present the calculated variation of ZT as a function of chemical potential (µ–EF) for MgTi2Se4 and MgMn2Se4 at temperatures of 300, 600, and 800 K. Since zT incorporates the combined effects of charge transport and heat conduction, it provides a comprehensive measure of thermoelectric performance. For both compounds, the zT profiles are strongly asymmetric with respect to the chemical potential. In the negative chemical potential region (µ–EF < 0), corresponding to p-type doping, zT values remain very small over the entire investigated range and do not exhibit any pronounced maxima. In contrast, the positive chemical potential region shows well-defined zT peaks, indicating that thermoelectric performance is dominated by n-type charge carriers. For MgMn2Se4 at 300 K, the main ZT maximum is in the range µ–EF ≈ 1.0–1.3 eV, with peak values approaching unity (0.99). As the temperature increases to 600 K and 800 K, the position of the maximum remains nearly unchanged, while the zT peak becomes slightly broader, suggesting an expanded chemical potential window for favorable n-type transport. A comparable trend is observed for MgTi2Se4. At room temperature, the zT curve exhibits a dominant n-type peak in the vicinity of µ–EF ≈ −1.0 to 1 eV, with maximum zT values slightly below unity (0.9). With increasing temperature, the peak height shows only a modest change, whereas the width of the zT peak increases gradually, indicating enhanced thermoelectric response over a wider doping range. Throughout the studied temperature range, zT values on the p-type side remain negligible in comparison to those on the n-type side. The concentration of the zT maxima near the conduction-band edge indicates that moderate n-type doping is required to achieve an optimal balance between the Seebeck coefficient and electrical conductivity. Away from this region, zT decreases rapidly due to the combined effects of reduced Seebeck coefficient and increased electronic thermal conductivity. The slight broadening of the ZT peaks with temperature can be attributed to thermal smearing of the electronic states and the temperature dependence of the transport coefficients. Overall, the consistently higher ZT values obtained under n-type conditions, particularly at elevated temperatures, indicate that MgTi2Se4 and MgMn2Se4 are more suitable for n-type thermoelectric applications than for p-type operation.
where S denotes the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ = κe + κl represents the total thermal conductivity, including electronic and lattice contributions. Efficient thermoelectric performance requires a suitable compromise between a high Seebeck coefficient, sufficient electrical conductivity, and low thermal conductivity. Fig. 8 present the calculated variation of ZT as a function of chemical potential (µ–EF) for MgTi2Se4 and MgMn2Se4 at temperatures of 300, 600, and 800 K. Since zT incorporates the combined effects of charge transport and heat conduction, it provides a comprehensive measure of thermoelectric performance. For both compounds, the zT profiles are strongly asymmetric with respect to the chemical potential. In the negative chemical potential region (µ–EF < 0), corresponding to p-type doping, zT values remain very small over the entire investigated range and do not exhibit any pronounced maxima. In contrast, the positive chemical potential region shows well-defined zT peaks, indicating that thermoelectric performance is dominated by n-type charge carriers. For MgMn2Se4 at 300 K, the main ZT maximum is in the range µ–EF ≈ 1.0–1.3 eV, with peak values approaching unity (0.99). As the temperature increases to 600 K and 800 K, the position of the maximum remains nearly unchanged, while the zT peak becomes slightly broader, suggesting an expanded chemical potential window for favorable n-type transport. A comparable trend is observed for MgTi2Se4. At room temperature, the zT curve exhibits a dominant n-type peak in the vicinity of µ–EF ≈ −1.0 to 1 eV, with maximum zT values slightly below unity (0.9). With increasing temperature, the peak height shows only a modest change, whereas the width of the zT peak increases gradually, indicating enhanced thermoelectric response over a wider doping range. Throughout the studied temperature range, zT values on the p-type side remain negligible in comparison to those on the n-type side. The concentration of the zT maxima near the conduction-band edge indicates that moderate n-type doping is required to achieve an optimal balance between the Seebeck coefficient and electrical conductivity. Away from this region, zT decreases rapidly due to the combined effects of reduced Seebeck coefficient and increased electronic thermal conductivity. The slight broadening of the ZT peaks with temperature can be attributed to thermal smearing of the electronic states and the temperature dependence of the transport coefficients. Overall, the consistently higher ZT values obtained under n-type conditions, particularly at elevated temperatures, indicate that MgTi2Se4 and MgMn2Se4 are more suitable for n-type thermoelectric applications than for p-type operation.
 |
| | Fig. 8 Variation of the dimensionless thermoelectric figure of merit (ZT) as a function of chemical potential at different temperatures. | |
3.7 Phonon dynamics
The vibrational and dynamical stability of the spinel compounds MgTi2Se4 and MgMn2Se4 was systematically examined by calculating their phonon dispersion relations within the framework of density functional perturbation theory (DFPT), as implemented in the Quantum ESPRESSO package.59 To accurately capture long-range interatomic interactions and lattice dynamics the interatomic force constants (IFCs) were computed using a 2 × 2 × 2 supercell combined with a 3 × 3 × 3 q-point mesh in the Brillouin zone. The exchange–correlation effects were treated within the generalized gradient approximation (GGA) which provides a reliable description of lattice vibrations and bonding characteristics in transition-metal chalcogenides. The primitive unit cell of MgX2Se4 (X = Ti, Mn) contains seven atoms giving rise to 21 phonon branches including three acoustic and eighteen optical modes, as depicted in Fig. 9. Group-theoretical analysis of the zone-center (Γ-point) vibrations based on the cubic spinel structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, No. 227) yields the irreducible representation Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g. Several modes, namely Eu, Tg, Tu, and Eg, are degenerate due to the high cubic symmetry. In terms of optical activity, A1g, Eg, and T2g modes are Raman-active while T1u modes are infrared-active. The remaining A2u, Eu, and T2u modes are optically silent. Although Raman and infrared measurements are not reported here the vibrational mode assignment is rigorously determined from group-theoretical symmetry considerations. The calculated phonon dispersion curves for both compounds show a complete absence of imaginary (negative) frequencies throughout the Brillouin zone confirming their dynamical stability at 300 K. Combined with their negative formation enthalpies this result establishes that MgTi2Se4 and MgMn2Se4 are stable both thermodynamically and against lattice instabilities. A detailed inspection of the phonon spectra provides microscopic insight into the lattice dynamics. In MgTi2Se4 the low-frequency region up to ∼150 cm−1 is dominated by acoustic modes mainly arising from translational vibrations of Mg atoms reflecting their relatively weak bonding environment. The intermediate frequency ranges from ∼180 to 290 cm−1 is primarily governed by vibrational modes of Ti atoms indicating strong coupling between Ti and the surrounding Se framework. The high-frequency optical modes spanning ∼360–440 cm−1 are mainly due to Ti–Se stretching vibrations reflecting enhanced bond stiffness and increased covalent character within the Ti–Se network. In contrast, for MgMn2Se4 the acoustic branches extend up to ∼90 cm−1 and are dominated by Mg-related translational motions. The intermediate frequency ranges from ∼130 to 200 cm−1 is mainly associated with Mn-centered vibrations, while the high-frequency optical modes between ∼240 and 320 cm−1 originate primarily from Mn–Se stretching vibrations. The comparatively lower maximum phonon frequencies in MgMn2Se4 reflect the larger atomic mass of Mn and relatively weaker Mn–Se bonding compared to the Ti–Se bonds in MgTi2Se4. These high-frequency optical phonons play a crucial role in determining electron–phonon coupling, charge-carrier scattering, and thermal transport properties. In both compounds, the separation between acoustic and optical branches and the relatively low dispersion of optical modes are expected to contribute to suppressed lattice thermal conductivity, which is highly desirable for thermoelectric applications.60 Moreover, the coexistence of light Mg-dominated acoustic modes and stiffer transition-metal–Se optical modes promote enhanced phonon scattering, thereby reducing heat transport without significantly compromising electronic conductivity. Overall, the phonon dispersion analysis not only confirms the dynamical stability of MgTi2Se4 and MgMn2Se4 but also provides valuable insight into the interplay between atomic mass, bonding strength, and lattice vibrations. These characteristics are directly linked to their favorable thermal and electronic transport behavior, reinforcing their potential as promising candidates for spin-dependent thermoelectric and multifunctional device applications.
m, No. 227) yields the irreducible representation Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g. Several modes, namely Eu, Tg, Tu, and Eg, are degenerate due to the high cubic symmetry. In terms of optical activity, A1g, Eg, and T2g modes are Raman-active while T1u modes are infrared-active. The remaining A2u, Eu, and T2u modes are optically silent. Although Raman and infrared measurements are not reported here the vibrational mode assignment is rigorously determined from group-theoretical symmetry considerations. The calculated phonon dispersion curves for both compounds show a complete absence of imaginary (negative) frequencies throughout the Brillouin zone confirming their dynamical stability at 300 K. Combined with their negative formation enthalpies this result establishes that MgTi2Se4 and MgMn2Se4 are stable both thermodynamically and against lattice instabilities. A detailed inspection of the phonon spectra provides microscopic insight into the lattice dynamics. In MgTi2Se4 the low-frequency region up to ∼150 cm−1 is dominated by acoustic modes mainly arising from translational vibrations of Mg atoms reflecting their relatively weak bonding environment. The intermediate frequency ranges from ∼180 to 290 cm−1 is primarily governed by vibrational modes of Ti atoms indicating strong coupling between Ti and the surrounding Se framework. The high-frequency optical modes spanning ∼360–440 cm−1 are mainly due to Ti–Se stretching vibrations reflecting enhanced bond stiffness and increased covalent character within the Ti–Se network. In contrast, for MgMn2Se4 the acoustic branches extend up to ∼90 cm−1 and are dominated by Mg-related translational motions. The intermediate frequency ranges from ∼130 to 200 cm−1 is mainly associated with Mn-centered vibrations, while the high-frequency optical modes between ∼240 and 320 cm−1 originate primarily from Mn–Se stretching vibrations. The comparatively lower maximum phonon frequencies in MgMn2Se4 reflect the larger atomic mass of Mn and relatively weaker Mn–Se bonding compared to the Ti–Se bonds in MgTi2Se4. These high-frequency optical phonons play a crucial role in determining electron–phonon coupling, charge-carrier scattering, and thermal transport properties. In both compounds, the separation between acoustic and optical branches and the relatively low dispersion of optical modes are expected to contribute to suppressed lattice thermal conductivity, which is highly desirable for thermoelectric applications.60 Moreover, the coexistence of light Mg-dominated acoustic modes and stiffer transition-metal–Se optical modes promote enhanced phonon scattering, thereby reducing heat transport without significantly compromising electronic conductivity. Overall, the phonon dispersion analysis not only confirms the dynamical stability of MgTi2Se4 and MgMn2Se4 but also provides valuable insight into the interplay between atomic mass, bonding strength, and lattice vibrations. These characteristics are directly linked to their favorable thermal and electronic transport behavior, reinforcing their potential as promising candidates for spin-dependent thermoelectric and multifunctional device applications.
 |
| | Fig. 9 Phonons dispersion plots of MgX2Se4(X = Ti/Mn). | |
3.8 Electron density
In this work, we investigate charge sharing and bonding interactions among the constituent atoms by analysing the electron density distributions of magnesium-based transition-metal chalcogenides, namely MgTi2Se4 and MgMn2Se4, along the (001) crystallographic plane, as shown in Fig. 10. Covalent bonding interactions are indicated by the distinct overlapping charge regions between Ti/Mn and Se, as well as between Mg and Se, that are visible in the electron density maps. These maps clarify the bonding type and general structural stability of these spinel compounds by offering important insights into the dynamics of charge transfer between the cations (Mg and Ti/Mn) and the anion (Se). We computed the differences in electronegativity between the cations and anions to further evaluate the bonding properties. For Ti–Se and Mn–Se, the differences are 0.66 and 0.69, respectively, whereas for Mg–Se, the value is 1.24. These values validate the primarily covalent bonding character with slight ionic polarization because they fall below the critical threshold of 2.0. This suggests that the bonds in MgTi2Se4 and MgMn2Se4 are mixed ionic–covalent, with the covalent component greatly enhancing the materials' stability and electronic properties and the ionic contribution resulting from the metal–chalcogen separation.
 |
| | Fig. 10 Plot of electron density plots of (001) plane for MgTi/Mn2Se4. | |
4 Conclusion
This study presents a systematic first-principles investigation of the spinel chalcogenides MgTi2Se4 and MgMn2Se4 using density functional theory. Both compounds exhibit thermodynamic, dynamic, and mechanical stability. The ferromagnetic phase is energetically favored. The electronic structure reveals half-metallic behaviour with 100% spin polarization at the Fermi level, arising from strong hybridization between transition-metal-d and Se-p orbitals. This half-metallicity is accompanied by integer total magnetic moments of 4 µB per formula unit for MgTi2Se4 and 16 µB per formula unit for MgMn2Se4, confirming their half-metallic ferromagnetic nature. Elastic constant analysis demonstrates that both materials satisfy the Born stability criteria. They exhibit intrinsic ductility and pronounced elastic anisotropy. Enhanced lattice rigidity is further evidenced by high elastic moduli and Debye temperatures. Optical property analysis indicates strong electron–photon coupling. This behavior is characterized by large static dielectric constants, intense interband transitions, and efficient ultraviolet absorption with high optical conductivity. Spin-resolved thermoelectric transport calculations reveal favorable Seebeck coefficients, suppressed lattice thermal conductivity, and dominant majority-spin carrier transport. As a result, the dimensionless thermoelectric figure of merit reaches ZT ≈ 0.9 for MgTi2Se4 and ZT ≈ 0.99 for MgMn2Se4 near room temperature under n-type doping. The coexistence of half-metallicity, robust mechanical stability, strong optical response, and high thermoelectric efficiency establishes MgTi2Se4 and MgMn2Se4 as promising multifunctional materials. These features make them suitable for spintronic, spin-caloritronic, and energy-harvesting application
Conflicts of interest
The authors declare no competing interests.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- T. Naito, Functional Materials: Advances and Applications in Energy Storage and Conversion, Jenny Stanford Publishing, 1st edn, 2018 Search PubMed
 .
. - A. Hirohata, K. Yamada, Y. Nakatani, I. L. Prejbeanu, B. Dieny, P. Pirro and B. Hillebrands, Review on spintronics: principles and device applications, J. Magn. Magn. Mater., 2020, 509, 166711 CrossRef CAS
 .
. - W. Zeng, L. Shu, Q. Li, S. Chen, F. Wang and X. M. Tao, Fiber-based wearable electronics: a review of materials, fabrication, devices, and applications, Adv. Mater., 2014, 26, 5310–5336 CrossRef CAS PubMed
 .
. - F. Ozel, et al., A general review on the thiospinels and their energy applications, Mater. Today Energy, 2021, 21, 100822 CrossRef CAS
 .
. - R. M. Fleming, F. J. DiSalvo, R. J. Cava and J. V. Waszczak, Observation of charge-density waves in the cubic spinel structure CuV2S4, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 2850–2853 CrossRef CAS
 .
. - F. K. Lotgering and R. P. Van Stapele, Magnetic properties and electrical conduction of copper-containing sulfo- and selenospinels, J. Appl. Phys., 1968, 39, 417–423 CrossRef CAS
 .
. - N. H. Van Maaren, G. M. Schaeffer and F. K. Lotgering, Superconductivity in sulpho- and selenospinels, Phys. Lett. A, 1967, 25, 238–239 CrossRef
 .
. - F. Majid, M. T. Naisr, E. Algrafy, M. Sajjad, N. A. Noor, A. Mahmood and S. M. Ramay, Optical and magnetic properties of thiospinels for multifunctional applications, J. Mater. Res. Technol., 2020, 9, 6135–6142 Search PubMed
 .
. - N. Imanishi, K. Inoue, Y. Takeda and O. Yamamoto, Thiospinels as cathode for lithium secondary battery, J. Power Sources, 1993, 44, 619–625 CrossRef CAS
 .
. - S. A. Abbas, I. Mahmood, M. Sajjad, N. A. Noor, Q. Mahmood, M. A. Naeem, A. Mahmood and S. M. Ramay, Spinel-type Na2MoO4 and Na2WO4 as promising optoelectronic materials: first-principles DFT calculations, Chem. Phys., 2020, 538, 110902 CrossRef CAS
 .
. - G. J. Snyder, T. Caillat and J. P. Fleurial, Thermoelectric properties of chalcogenides with the spinel structure, Mater. Res. Innov., 2001, 5, 67–73 CrossRef CAS
 .
. - K. Hashikuni, K. Suekuni, H. Usui, M. Ohta, K. Kuroki and T. Takabatake, High power factor in thiospinels Cu2TrTi3S8 (Tr = Mn, Fe, Co, Ni) arising from TiS6 octahedron network, Appl. Phys. Lett., 2016, 109, 182110 CrossRef
 .
. - M. Yousaf, S. A. Dalhatu, G. Murtaza, R. Khenata, M. Sajjad, A. Musa, H. A. R. Aliabad and M. A. Saeed, Optoelectronic properties of XIn2S4 (X = Cd, Mg) thiospinels through highly accurate all-electron FP-LAPW method, J. Alloys Compd., 2015, 625, 182–187 CrossRef CAS
 .
. - O. Volnianska and P. Bogusławski, Magnetic and structural properties of IIA–V nitrides, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224418 CrossRef
 .
. - G. M. Mustafa, A. Ayaz, N. A. Noor, S. Mumtaz, A. Laref and A. Ibrahim, Theoretical investigation of semiconducting CdTi2X4 (X = S, Se) ferromagnetic spinels as multifunctional energy materials, Results Eng., 2025, 107311 CrossRef CAS
 .
. - H. A. Alburaih, N. A. Noor, M. Bououdina, H. Ullah, A. Laref and R. Sharma, First-principles study of Mg-based rare-earth spinels MgSm2Y4 (Y = S, Se) for spintronic and thermoelectric devices, Mater. Chem. Phys., 2024, 313, 128756 CrossRef CAS
 .
. - G. M. Mustafa, B. Younas, S. Saba, N. A. Noor, Y. Saeed, S. Mumtaz and M. K. Al-Sadoon, Half-metallic ferromagnetic and transport behavior of rare-earth-based CdGd2(S/Se)4 spinels, Mater. Today Commun., 2024, 40, 109567 CrossRef CAS
 .
. - Q. Mahmood, M. Hassan, G. Murtaza, M. Sajjad, A. Laref and B. Haq, Theoretical investigation of electronic, magnetic, and thermoelectric behavior of LiZ2O4 (Z = Mn, Fe, Co, Ni), J. Supercond. Novel Magn., 2019, 32, 1231–1239 Search PubMed
 .
. - T. H. Flemban, V. Singaravelu, A. A. S. Devi and I. S. Roqan, Homogeneous vertical ZnO nanorod arrays with high conductivity on an in situ Gd nanolayer, RSC Adv., 2015, 5, 94670–94678 Search PubMed
 .
. - R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50, 2024 Search PubMed
 .
. - J. M. D. Coey and M. Venkatesan, Half-metallic ferromagnetism: example of CrO2, J. Appl. Phys., 2002, 91, 8345 Search PubMed
 .
. - M. Horne, P. Strange, W. M. Temmerman, Z. Szotek, A. Svane and H. Winter, Electronic structure of europium chalcogenides and pnictides, J. Phys.: Condens. Matter, 2004, 16, 5061 Search PubMed
 .
. - Y. Lang, L. Pan, C. Chen and Y. Wang, Thermoelectric properties of thiospinel-type CuCo2S4, J. Electron. Mater., 2019, 48, 4179–4187 Search PubMed
 .
. - W. Tahir, G. M. Mustafa, N. A. Noor, S. M. Alay-e-Abbas, Q. Mahmood and A. Laref, Analysis of optoelectronic and transport properties of magnesium-based MgSc2X4 (X = S, Se) spinels, Ceram. Int., 2020, 46, 26637–26645 CrossRef CAS
 .
. - G. M. Mustafa, S. Saba, N. A. Noor, A. Laref, M. Abd El-Rahman, Z. Farooq, R. B. Behram and Z. Ullah, First-principles calculations to investigate HgY2(S/Se)4 spinel chalcogenides, J. Mater. Res. Technol., 2023, 22, 97–106 Search PubMed
 .
. - N. A. Noor, M. Rashid, G. M. Mustafa, A. Mahmood, W. Al-Masry and S. M. Ramay, Zinc-based chalcogenides ZnMn2X4 (X = S, Se, Te) as promising spintronic materials, J. Alloys Compd., 2021, 856, 157198 Search PubMed
 .
. - G. M. Mustafa, N. A. Noor, M. W. Iqbal, M. Sajjad, M. A. Naeem, Q. Mahmood, H. M. Shaikh, A. Mahmood and W. Al-Masry, Optoelectronic and transport properties of MgLu2Z4 (Z = S, Se) spinels, Mater. Sci. Semicond. Process., 2021, 121, 105452 CrossRef CAS
 .
. - G. M. Mustafa, T. Zelai, S. Bouzgarrou, M. H. Alhossainy, Q. Mahmood, A. Mera, H. H. Hegazy, S. Alharthi and M. A. Amin, First-principles study of magnesium-based MgLa2(S/Se)4 chalcogenides, Appl. Phys. A, 2022, 128, 38 CrossRef CAS
 .
. - A. Ramzan, M. Y. Sofi, M. Ishfaq-ul-Islam, M. S. Khan and M. A. Khan, Half-metallic ferromagnetism and thermoelectric-efficient behavior in MgNi2X4 (X = S, Se) spinels, RSC Adv., 2025, 15, 24002–24018 RSC
 .
. - S. A. Rouf, H. Albalawi, T. Zelai and O. Hakami, Half-metallic ferromagnetism and thermoelectric effect in SrX2S4 (X = Mn, Fe, Co), J. Phys. Chem. Solids, 2023, 182, 111601 CrossRef CAS
 .
. - Q. Mahmood, G. Nazir, J. Alzahrani and N. A. Kattan, Room temperature ferromagnetism and thermoelectric behavior of calcium-based spinel chalcogenides CaZ2S4 (Z = Ti, V, Cr, Fe), J. Phys. Chem. Solids, 2022, 167, 110742 Search PubMed
 .
. - P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowski, F. Tran and L. D. Marks, WIEN2k: an Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Technische Universität Wien, 2019 Search PubMed
 .
. - J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
 .
. - D. Koller, F. Tran and P. Blaha, Improving the modified Becke–Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155109 CrossRef
 .
. - G. K. H. Madsen and D. J. Singh, BoltzTraP: a code for calculating band-structure-dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS
 .
. - M. Y. Sofi, M. S. Khan and M. A. Khan, Semiconducting ferromagnetism and thermoelectric performance of Rb2GeMI6 (M = V, Ni, Mn), Mater. Adv, 2025, 6, 2071–2089 RSC
 .
. - A. Ramzan, M. Y. Sofi, M. S. Khan, J. Ali and M. A. Khan, First-principles investigation of MgAl2X4 (X = S, Se) spinels, Eur. Phys. J. B, 2025, 98, 102 Search PubMed
 .
. - F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS PubMed
 .
. - M. Khalid, M. W. Iqbal, M. Asghar, N. A. Noor, G. M. Mustafa and S. M. Ramay, Exchange mechanism and transport characteristics of Mg-based spinel chalcogenides, Eur. Phys. J. Plus, 2022, 137, 1 Search PubMed
 .
. - Z. Szotek, W. M. Temmerman, A. Svane, L. Petit, P. Strange, G. M. Stocks, D. Kodderitzsch, W. Hergert and H. Winter, Electronic structure of half-metallic ferromagnets and spinel ferromagnetic insulators, J. Phys.: Condens. Matter, 2004, 16, S5587–S5600 Search PubMed
 .
. - A. Mahmood, S. M. Ramay, W. Al-Masry, C. W. Dunnill and N. Y. Al-Garadi, First-principles computations of ferromagnetic HgCr2Z4 (Z = S, Se) spinels, J. Mater. Res. Technol., 2020, 9, 16159–16166 CrossRef CAS
 .
. - G. M. Mustafa, A. Ayaz, N. A. Noor, S. Mumtaz, A. Laref and A. Ibrahim, Semiconducting CdTi2X4 (X = S, Se) ferromagnetic spinels, Results Eng., 2025, 107311 Search PubMed
 .
. - R. Trivedi and B. Chakroborty, Design of room-temperature d0 ferromagnetism for spintronics applications, in Fundamentals of Low Dimensional Magnets, CRC Press, 2022, pp. 161–182 Search PubMed
 .
. - H. Yilin, W. Yang, L. Tingzhou, Y. Tie and W. Xiaotian, Electronic, magnetic, half-metallic, and mechanical properties of equiatomic quaternary Heusler compound YRhTiGe, Materials, 2018, 11, 797 Search PubMed
 .
. - H. Peng, H. J. Xiang, S.-H. Wei, S.-S. Li, J.-B. Xia and J. Li, Origin and enhancement of hole-induced ferromagnetism in first-row d0 semiconductors, Phys. Rev. Lett., 2009, 102, 017201 CrossRef PubMed
 .
. - M. Born, On the stability of crystal lattices, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160 Search PubMed
 .
. - W. Voigt, Textbook of Crystal Physics, G. B, Teubner, 1928 Search PubMed
 .
. - A. Reuss, Calculation of the flow limit of mixed crystals, Z. Angew. Math. Mech., 1929, 9, 49–58 Search PubMed
 .
. - R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc. A, 1952, 65, 349 Search PubMed
 .
. - S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed
 .
. - S. A. Raza, G. M. Mustafa, M. A. Ameer, N. A. Noor, Z. Farooq, S. Mumtaz and I. M. Moussa, Investigation of MnSc2X4 (X = S, Se) spinels, RSC Adv., 2025, 15, 9662–9675 Search PubMed
 .
. - T. Alshahrani, G. M. Mustafa, T. H. Flemban, H. Althib, S. Al-Qaisi, N. A. Kattan and Q. Mahmood, Optoelectronic and transport properties of ZnY2X4 (X = S, Se) spinels, ECS J. Solid State Sci. Technol., 2020, 9, 105001 CrossRef CAS
 .
. - M. Y. Sofi, M. S. Khan and M. A. Khan, Eco-friendly lead-free halide double perovskites A2CuMCl6 (A = K, Rb; M = Sb, Bi), J. Mater.
Chem. C, 2024, 12, 16045–16058 Search PubMed
 .
. - M. Y. Sofi, M. S. Khan and M. A. Khan, Harnessing half-metallicity and thermoelectric insights in Cs2AgMBr6 (M = V, Mn, Ni), Mater. Sci. Semicond. Process., 2025, 186, 109023 Search PubMed
 .
. - Q. Mahmood, G. M. Mustafa, B. Younas, S. Bouzgarrou, A. I. Aljameel, M. H. Mashniwi, M. Y. Almashnowi and N. Sfina, Structural, magnetic, and thermoelectric properties of CdCe2X4 (X = S, Se, Te) spinels, J. Phys. Chem. Solids, 2025, 197, 112433 Search PubMed
 .
. - M. Furqan, G. M. Mustafa, H. D. Alkhaldi, F. Alhajri, G. I. Ameereh, M. Al-Anazy, A. El-Rayyes and Q. Mahmood, Electronic, magnetic, and thermoelectric aspects of SrCe2Z4 (Z = Te, Se, S), RSC Adv., 2025, 15, 37288–37298 Search PubMed
 .
. - G. A. Slack, Non-metallic crystals with high thermal conductivity, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS
 .
. - M. Y. Sofi, M. S. Khan, J. Ali and M. A. Khan, Role of 3d electrons in ferromagnetism and spin-dependent transport in K2GeNiX6 (X = Br, I), J. Phys. Chem. Solids, 2024, 192, 112022 Search PubMed
 .
. - P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 Search PubMed
 .
. - M. Y. Sofi, M. S. Khan and M. A. Khan, Control of spin on ferromagnetism and thermoelectric properties of K2GeMnX6 (X = Cl, Br, I), Mater. Adv., 2024, 5, 4913–4931 Search PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
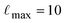 , and total-energy convergence was achieved within 0.1 mRy. The thermoelectric properties of Mg(Ti/Mn)2Se4 were evaluated using the BoltzTrap code, which is based on semi-classical Boltzmann transport theory.35 Temperature-dependent transport coefficients, including the Seebeck coefficient and electrical conductivity, were calculated within the constant relaxation time approximation using well-established transport equations reported in the literature.36 These parameters provide critical insight into the thermoelectric performance and potential applicability of the studied materials.
, and total-energy convergence was achieved within 0.1 mRy. The thermoelectric properties of Mg(Ti/Mn)2Se4 were evaluated using the BoltzTrap code, which is based on semi-classical Boltzmann transport theory.35 Temperature-dependent transport coefficients, including the Seebeck coefficient and electrical conductivity, were calculated within the constant relaxation time approximation using well-established transport equations reported in the literature.36 These parameters provide critical insight into the thermoelectric performance and potential applicability of the studied materials.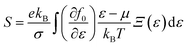
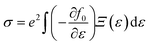
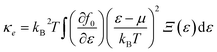
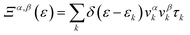 .where vαkrepresent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100
.where vαkrepresent αth component of the group velocity with wave vector k. For improved output, the k-mesh was expanded to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-k points.
000-k points.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 227). There are eight magnesium, sixteen transition metal (Ti/Mn) and thirty-two selenium atoms in each unit cell. In this structure, the tetrahedral 8a Wyckoff positions (0.125, 0.125, 0.125) are occupied by Mg atoms and the octahedral 16d sites (0.5, 0.5, 0.5) are occupied by Ti and Mn atoms. To preserve the cubic symmetry of the structure the Se atoms occupy the 32e Wyckoff positions with fractional coordinates typically optimized around (0.25 0.25 0.25).37 The optimized crystal structure is shown in Fig. 1(a). To determine the equilibrium structural parameters, total energy versus volume (E–V) curves were generated using the generalized gradient approximation (GGA) as proposed by Perdew–Burke–Ernzerhof (PBE). These data were fitted using the Murnaghan equation of state38 as:
m (No. 227). There are eight magnesium, sixteen transition metal (Ti/Mn) and thirty-two selenium atoms in each unit cell. In this structure, the tetrahedral 8a Wyckoff positions (0.125, 0.125, 0.125) are occupied by Mg atoms and the octahedral 16d sites (0.5, 0.5, 0.5) are occupied by Ti and Mn atoms. To preserve the cubic symmetry of the structure the Se atoms occupy the 32e Wyckoff positions with fractional coordinates typically optimized around (0.25 0.25 0.25).37 The optimized crystal structure is shown in Fig. 1(a). To determine the equilibrium structural parameters, total energy versus volume (E–V) curves were generated using the generalized gradient approximation (GGA) as proposed by Perdew–Burke–Ernzerhof (PBE). These data were fitted using the Murnaghan equation of state38 as: 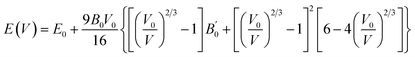 where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus and
where E(V) is the total energy at volume V, E0 is the equilibrium total energy, V0 is the equilibrium volume, B0 is the bulk modulus and 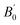 is its pressure derivative which enables the extraction of key parameters such as the equilibrium volume, bulk modulus, and its pressure derivative. By connecting these physical quantities to the total energy E(V) at a specific volume V, this equation offers a solid understanding of the structural behaviour of the compounds under various volumes. The total energies of the ferromagnetic (FM) and non-magnetic (NM) configurations were compared to assess the magnetic stability of both compounds. The FM phase is energetically more stable as confirmed by the positive energy differences (ΔE = ENM–EFM) suggesting that MgTi2Se4 and MgMn2Se4 possess ferromagnetic ground states. The E–V curves of the FM configurations shown in Fig. 1(b). Exhibit well-defined minima confirming thermodynamic equilibrium and proper structural optimization. Thermodynamic stability was further assessed through the enthalpy of formation (ΔHf) calculated using
is its pressure derivative which enables the extraction of key parameters such as the equilibrium volume, bulk modulus, and its pressure derivative. By connecting these physical quantities to the total energy E(V) at a specific volume V, this equation offers a solid understanding of the structural behaviour of the compounds under various volumes. The total energies of the ferromagnetic (FM) and non-magnetic (NM) configurations were compared to assess the magnetic stability of both compounds. The FM phase is energetically more stable as confirmed by the positive energy differences (ΔE = ENM–EFM) suggesting that MgTi2Se4 and MgMn2Se4 possess ferromagnetic ground states. The E–V curves of the FM configurations shown in Fig. 1(b). Exhibit well-defined minima confirming thermodynamic equilibrium and proper structural optimization. Thermodynamic stability was further assessed through the enthalpy of formation (ΔHf) calculated using 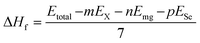 where Etotal is the total energy of the spinel and EX, EMg and ESe are the elemental reference energies for Ti/Mn, Mg, and Se, respectively. The calculated formation enthalpies are −0.820 eV for MgTi2Se4 and −0.579 eV for MgMn2Se4 both negative values confirming the thermodynamic viability of the compounds. To evaluate structural compatibility within the spinel framework, the tolerance factor (τ) was computed using the formula:
where Etotal is the total energy of the spinel and EX, EMg and ESe are the elemental reference energies for Ti/Mn, Mg, and Se, respectively. The calculated formation enthalpies are −0.820 eV for MgTi2Se4 and −0.579 eV for MgMn2Se4 both negative values confirming the thermodynamic viability of the compounds. To evaluate structural compatibility within the spinel framework, the tolerance factor (τ) was computed using the formula: 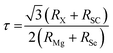 are the ionic radii of Ti/Mn, Mg, and Se, respectively. For MgTi2Se4 and MgMn2Se4, the estimated τ values were 0.92 and 0.94. These values suggest a structurally stable cubic configuration because they are close to unity. The structural and thermodynamic robustness of MgX2Se4 (X = Ti, Mn) spinels is supported by the near-unity tolerance factor and negative enthalpy of formation. Table 1 reports the calculated values, which are in good agreement with previous theoretical DFT studies.39 They are therefore excellent options for use in optoelectronic and thermoelectric technologies. Their potential for magnetic and multifunctional device applications is further enhanced by the observed FM ground state. The computed values from our first-principles simulations are shown in Table 1.
are the ionic radii of Ti/Mn, Mg, and Se, respectively. For MgTi2Se4 and MgMn2Se4, the estimated τ values were 0.92 and 0.94. These values suggest a structurally stable cubic configuration because they are close to unity. The structural and thermodynamic robustness of MgX2Se4 (X = Ti, Mn) spinels is supported by the near-unity tolerance factor and negative enthalpy of formation. Table 1 reports the calculated values, which are in good agreement with previous theoretical DFT studies.39 They are therefore excellent options for use in optoelectronic and thermoelectric technologies. Their potential for magnetic and multifunctional device applications is further enhanced by the observed FM ground state. The computed values from our first-principles simulations are shown in Table 1.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase and (b) optimized total energy as a function of volume.
m phase and (b) optimized total energy as a function of volume.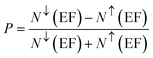 ×100 where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A result of P = 100%confirms complete spin polarization, a hallmark of half-metallicity.41 The energy difference between the highest occupied and lowest unoccupied states in the spin-down channel, known as the half-metallic gap (Ehmg), was also calculated. Because it controls the stability and robustness of the half-metallic state, this parameter is especially important for spin-filtering and tunnelling magnetoresistance (TMR) applications. These compounds' half-metallic ferromagnetic nature is further supported by the presence of a finite Ehmg, highlighting their potential as next-generation magneto-optoelectronic materials, magnetic sensors, and spintronic switches.
×100 where N↑(EF) and N↓(EF) represent the density of states (DOS) at the Fermi level for spin-up and spin-down channels, respectively. A result of P = 100%confirms complete spin polarization, a hallmark of half-metallicity.41 The energy difference between the highest occupied and lowest unoccupied states in the spin-down channel, known as the half-metallic gap (Ehmg), was also calculated. Because it controls the stability and robustness of the half-metallic state, this parameter is especially important for spin-filtering and tunnelling magnetoresistance (TMR) applications. These compounds' half-metallic ferromagnetic nature is further supported by the presence of a finite Ehmg, highlighting their potential as next-generation magneto-optoelectronic materials, magnetic sensors, and spintronic switches.

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, where Mg occupies tetrahedral (A) sites and the transition metals Ti or Mn reside at octahedral (B) sites, each coordinated by six Se atoms. In MgTi2Se4, although Ti4+ (3d0) is formally expected to be nonmagnetic, a finite local magnetic moment of ∼0.88762 µB per Ti atom is obtained. Such induced magnetism in nominally d0 cations has been widely reported and is commonly attributed to strong p–d hybridization between the transition-metal d states and ligand p orbitals, leading to partial occupation and spin polarization of the d states rather than purely ionic Ti4+ behavior.42–45 Under octahedral coordination, the Ti-3d orbitals split into lower-energy t2g and higher-energy eg states due to crystal-field effects. Spin-resolved partial density of states (PDOS) analysis reveals an exchange splitting of the Ti-t2g states near the Fermi level, confirming that the induced moment originates from hybridization-driven charge transfer from Se-4p states into Ti-3d orbitals. Similar hybridization-induced d0 magnetism has been previously reported in Ti-based oxides and chalcogenides, where ligand-to-metal charge transfer and covalent bonding give rise to finite magnetic moments on otherwise nonmagnetic cations.42–44 The reduction of the Ti moment from the ideal 1 µB further reflects the itinerant nature of the spin density, which is redistributed into ligand and interstitial regions. This interpretation is supported by the substantial interstitial magnetic moment (0.53244 µB) and the negative spin polarization of Se atoms (−0.01283 µB each), a hallmark of p–d hybridization-mediated magnetism.45 The atomic contributions of Mg (0.00988 µB), Ti (0.88762 µB), Se (−0.01283 µB), and the interstitial region (0.53244 µB) yield a total magnetic moment of approximately 4.0004 µB per conventional unit cell, consistent with the integer moment expected for half-metallic ferromagnets. This internal consistency between integer magnetization and spin-polarized electronic structure further validates the half-metallicity of MgTi2Se4. The ferromagnetic exchange interaction in this compound is therefore mediated by hybridization-induced spin polarization and itinerant exchange mechanisms rather than purely localized moments. In contrast, MgMn2Se4 exhibits strong localized ferromagnetism. Mn2+ ions (3d5) adopt a high-spin configuration in an octahedral crystal field, resulting in a large local magnetic moment. The calculated Mn moment of 4.20762 µB is slightly reduced from the ideal 5 µB due to p–d hybridization with Se-4p states, as evidenced by the negative Se polarization (−0.13507 µB) and a modest interstitial contribution (0.21045 µB). The resulting total magnetic moment of approximately 16.0005 µB per unit cell confirms robust ferromagnetic ordering and supports a superexchange-driven Mn–Se–Mn interaction pathway. While MgMn2Se4 is dominated by localized magnetic moments and strong exchange coupling, the larger interstitial contribution in MgTi2Se4 indicates more delocalized spin density and weaker, itinerant magnetic interactions.43 The computed atomic and interstitial magnetic moments for both compounds are summarized in Table 2. These findings not only substantiate the intrinsic ferromagnetism of both materials but also highlight their strong potential for spintronic applications requiring high spin polarization and stable magnetic ordering.
m, where Mg occupies tetrahedral (A) sites and the transition metals Ti or Mn reside at octahedral (B) sites, each coordinated by six Se atoms. In MgTi2Se4, although Ti4+ (3d0) is formally expected to be nonmagnetic, a finite local magnetic moment of ∼0.88762 µB per Ti atom is obtained. Such induced magnetism in nominally d0 cations has been widely reported and is commonly attributed to strong p–d hybridization between the transition-metal d states and ligand p orbitals, leading to partial occupation and spin polarization of the d states rather than purely ionic Ti4+ behavior.42–45 Under octahedral coordination, the Ti-3d orbitals split into lower-energy t2g and higher-energy eg states due to crystal-field effects. Spin-resolved partial density of states (PDOS) analysis reveals an exchange splitting of the Ti-t2g states near the Fermi level, confirming that the induced moment originates from hybridization-driven charge transfer from Se-4p states into Ti-3d orbitals. Similar hybridization-induced d0 magnetism has been previously reported in Ti-based oxides and chalcogenides, where ligand-to-metal charge transfer and covalent bonding give rise to finite magnetic moments on otherwise nonmagnetic cations.42–44 The reduction of the Ti moment from the ideal 1 µB further reflects the itinerant nature of the spin density, which is redistributed into ligand and interstitial regions. This interpretation is supported by the substantial interstitial magnetic moment (0.53244 µB) and the negative spin polarization of Se atoms (−0.01283 µB each), a hallmark of p–d hybridization-mediated magnetism.45 The atomic contributions of Mg (0.00988 µB), Ti (0.88762 µB), Se (−0.01283 µB), and the interstitial region (0.53244 µB) yield a total magnetic moment of approximately 4.0004 µB per conventional unit cell, consistent with the integer moment expected for half-metallic ferromagnets. This internal consistency between integer magnetization and spin-polarized electronic structure further validates the half-metallicity of MgTi2Se4. The ferromagnetic exchange interaction in this compound is therefore mediated by hybridization-induced spin polarization and itinerant exchange mechanisms rather than purely localized moments. In contrast, MgMn2Se4 exhibits strong localized ferromagnetism. Mn2+ ions (3d5) adopt a high-spin configuration in an octahedral crystal field, resulting in a large local magnetic moment. The calculated Mn moment of 4.20762 µB is slightly reduced from the ideal 5 µB due to p–d hybridization with Se-4p states, as evidenced by the negative Se polarization (−0.13507 µB) and a modest interstitial contribution (0.21045 µB). The resulting total magnetic moment of approximately 16.0005 µB per unit cell confirms robust ferromagnetic ordering and supports a superexchange-driven Mn–Se–Mn interaction pathway. While MgMn2Se4 is dominated by localized magnetic moments and strong exchange coupling, the larger interstitial contribution in MgTi2Se4 indicates more delocalized spin density and weaker, itinerant magnetic interactions.43 The computed atomic and interstitial magnetic moments for both compounds are summarized in Table 2. These findings not only substantiate the intrinsic ferromagnetism of both materials but also highlight their strong potential for spintronic applications requiring high spin polarization and stable magnetic ordering.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The relatively larger values of C11 compared to C12 further indicate strong resistance to uniaxial deformation, while the finite values of C44 confirm stability against shear strain. To obtain macroscopic mechanical parameters the elastic constants were converted into bulk shear and Young's moduli using the Voigt–Reuss–Hill approximation which provides reliable estimates for polycrystalline materials.47–49 The Voigt bulk modulus is defined as BV = (C11 + 2C12)/3 and for cubic symmetry BV = BR where BR denotes the Reuss bulk modulus. The shear modulus bounds were evaluated using GV = (C11–C12 + 3C44)/5 and GR = 5(C11–C12)C44/[4C44 + 3(C11–C12)] with the effective shear modulus given by G = (GV + GR)/2. The resulting bulk moduli of 66.96 GPa for MgTi2Se4 and 55.07 GPa for MgMn2Se4 indicate moderate resistance to uniform compression. In contrast the lower shear moduli of 36.31 GPa and 27.19 GPa respectively indicate that these compounds are more compliant under shear deformation than under volumetric compression. The Young's modulus was calculated using E = 9BG/(3B + G) and attains values of 92.48 GPa for MgTi2Se4 and 69.65 GPa for MgMn2Se4, reflecting the comparatively higher stiffness of the Ti-containing compound. The observed trend E > B > G highlights the high stiffness combined with enhanced shear flexibility in these spinel structures. The ductile or brittle nature of the compounds was evaluated using multiple mechanical indicators. According to Pugh's criterion, materials with a ratio B/G > 1.75are classified as ductile.50 The calculated ratios of 1.87 for MgTi2Se4 and 1.95 for MgMn2Se4 clearly place both compounds in the ductile regime. This conclusion is further supported by Poisson's ratio, determined from ν = (3B–E)/(6B), which exceeds the critical value of 0.26 associated with ductile and metallic bonding characteristics.51 Additionally, the positive Cauchy pressure, defined as C12–C44, yields values of 3.7 GPa and 2.5 GPa for MgTi2Se4 and MgMn2Se4, respectively, signifying the dominance of non-directional bonding and further confirming their ductile behaviour. Elastic anisotropy, which plays a crucial role in determining crack propagation, mechanical reliability, and direction-dependent response, was analyzed using both the Zener anisotropy factor and the universal anisotropy index. The Zener factor, defined as A = 2C44/(C11–C12), deviates significantly from unity, with values of 0.48 for MgTi2Se4 and 0.37 for MgMn2Se4, indicating pronounced elastic anisotropy. To provide a more comprehensive measure, the universal anisotropy index was calculated using AU = 5(GV/GR − 1), yielding values of 0.67 and 1.30 for MgTi2Se4 and MgMn2Se4, respectively. The larger AU value for MgMn2Se4 suggests stronger anisotropic elastic behaviour, particularly in shear-dominated deformation modes. Further insight into the microscopic deformation mechanism was obtained from the Kleinman parameter ξ, which describes the relative ease of bond stretching versus bond bending during elastic deformation. The calculated values of 0.37 for MgTi2Se4 and 0.33 for MgMn2Se4 indicate a balanced contribution of bond-angle bending and bond-length stretching, implying moderate resistance to angular distortions. In addition, the evaluated sound velocities, Debye temperatures, and thermophysical parameters reveal that MgTi2Se4 exhibits higher lattice stiffness and thermal robustness compared to MgMn2Se4, consistent with its larger elastic moduli. We created 3D contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (v) using the Elate visualization tool to obtain a more thorough grasp of the elastic and anisotropic properties of the compounds under study. These plots illustrate how these properties vary with crystallographic direction and are displayed in Fig. 4 and 5 for MgX2Se4 (X = Ti/Mn), respectively. The findings unequivocally demonstrate that all elastic parameters, except for linear compressibility, exhibit a significant deviation from a spherical shape, highlighting their anisotropic behaviour. Furthermore, the direction-dependent mechanical response of these spinel structures is confirmed by the anisotropy's uniform distribution across various directions. Table 3 displays the calculated values. Overall, the detailed elastic analysis demonstrates that MgX2Se4 (X = Ti, Mn) compounds are mechanically stable, elastically anisotropic, and intrinsically ductile. The combination of moderate stiffness, enhanced shear compliance, and pronounced elastic anisotropy makes these materials promising candidates for technological applications where mechanical reliability, flexibility, and anisotropic response are desirable
m. The relatively larger values of C11 compared to C12 further indicate strong resistance to uniaxial deformation, while the finite values of C44 confirm stability against shear strain. To obtain macroscopic mechanical parameters the elastic constants were converted into bulk shear and Young's moduli using the Voigt–Reuss–Hill approximation which provides reliable estimates for polycrystalline materials.47–49 The Voigt bulk modulus is defined as BV = (C11 + 2C12)/3 and for cubic symmetry BV = BR where BR denotes the Reuss bulk modulus. The shear modulus bounds were evaluated using GV = (C11–C12 + 3C44)/5 and GR = 5(C11–C12)C44/[4C44 + 3(C11–C12)] with the effective shear modulus given by G = (GV + GR)/2. The resulting bulk moduli of 66.96 GPa for MgTi2Se4 and 55.07 GPa for MgMn2Se4 indicate moderate resistance to uniform compression. In contrast the lower shear moduli of 36.31 GPa and 27.19 GPa respectively indicate that these compounds are more compliant under shear deformation than under volumetric compression. The Young's modulus was calculated using E = 9BG/(3B + G) and attains values of 92.48 GPa for MgTi2Se4 and 69.65 GPa for MgMn2Se4, reflecting the comparatively higher stiffness of the Ti-containing compound. The observed trend E > B > G highlights the high stiffness combined with enhanced shear flexibility in these spinel structures. The ductile or brittle nature of the compounds was evaluated using multiple mechanical indicators. According to Pugh's criterion, materials with a ratio B/G > 1.75are classified as ductile.50 The calculated ratios of 1.87 for MgTi2Se4 and 1.95 for MgMn2Se4 clearly place both compounds in the ductile regime. This conclusion is further supported by Poisson's ratio, determined from ν = (3B–E)/(6B), which exceeds the critical value of 0.26 associated with ductile and metallic bonding characteristics.51 Additionally, the positive Cauchy pressure, defined as C12–C44, yields values of 3.7 GPa and 2.5 GPa for MgTi2Se4 and MgMn2Se4, respectively, signifying the dominance of non-directional bonding and further confirming their ductile behaviour. Elastic anisotropy, which plays a crucial role in determining crack propagation, mechanical reliability, and direction-dependent response, was analyzed using both the Zener anisotropy factor and the universal anisotropy index. The Zener factor, defined as A = 2C44/(C11–C12), deviates significantly from unity, with values of 0.48 for MgTi2Se4 and 0.37 for MgMn2Se4, indicating pronounced elastic anisotropy. To provide a more comprehensive measure, the universal anisotropy index was calculated using AU = 5(GV/GR − 1), yielding values of 0.67 and 1.30 for MgTi2Se4 and MgMn2Se4, respectively. The larger AU value for MgMn2Se4 suggests stronger anisotropic elastic behaviour, particularly in shear-dominated deformation modes. Further insight into the microscopic deformation mechanism was obtained from the Kleinman parameter ξ, which describes the relative ease of bond stretching versus bond bending during elastic deformation. The calculated values of 0.37 for MgTi2Se4 and 0.33 for MgMn2Se4 indicate a balanced contribution of bond-angle bending and bond-length stretching, implying moderate resistance to angular distortions. In addition, the evaluated sound velocities, Debye temperatures, and thermophysical parameters reveal that MgTi2Se4 exhibits higher lattice stiffness and thermal robustness compared to MgMn2Se4, consistent with its larger elastic moduli. We created 3D contour plots for Young's modulus (Y), linear compressibility (β), shear modulus (G), and Poisson's ratio (v) using the Elate visualization tool to obtain a more thorough grasp of the elastic and anisotropic properties of the compounds under study. These plots illustrate how these properties vary with crystallographic direction and are displayed in Fig. 4 and 5 for MgX2Se4 (X = Ti/Mn), respectively. The findings unequivocally demonstrate that all elastic parameters, except for linear compressibility, exhibit a significant deviation from a spherical shape, highlighting their anisotropic behaviour. Furthermore, the direction-dependent mechanical response of these spinel structures is confirmed by the anisotropy's uniform distribution across various directions. Table 3 displays the calculated values. Overall, the detailed elastic analysis demonstrates that MgX2Se4 (X = Ti, Mn) compounds are mechanically stable, elastically anisotropic, and intrinsically ductile. The combination of moderate stiffness, enhanced shear compliance, and pronounced elastic anisotropy makes these materials promising candidates for technological applications where mechanical reliability, flexibility, and anisotropic response are desirable


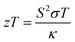 , where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (including both electronic and lattice contributions), and T is the absolute temperature. To achieve a high zT value, a material must possess a large Seebeck coefficient and high electrical conductivity, while simultaneously maintaining low thermal conductivity. The electron relaxation time (τ) is the average time between consecutive charge carrier scattering events and is a crucial factor affecting these transport characteristics. The constant relaxation time approximation (CRTA) assumes that the relaxation time varies slowly with energy over a range comparable to the thermal energy (kBT) and is therefore frequently used in practice. The power factor per unit time (S2σ/τ), electrical conductivity per unit time (σ/τ) and electronic thermal conductivity per unit time (κe/τ) are examples of transport coefficients that can be easily expressed in terms of τ under this assumption. Owing to computational limitations, the relaxation time (τ) in this study was assumed to be constant and typically of the order of 10−15 seconds, which is consistent with values for semiconducting thermoelectric materials that have been previously reported. As is common in DFT-based thermoelectric studies of related systems a carrier concentration of 1 × 1020 cm−3 was chosen. Boltzmann transport theory under the rigid band approximation (RBA) and the constant relaxation time approximation (CRTA) as implemented in the BoltzTraP code35 was used to evaluate these interdependent transport parameters. Since these compounds are expected to be ferromagnetic the two-current model was also used to investigate how magnetism affects thermoelectric behaviour.54 This model separates the transport properties into spin-up (↑) and spin-down (↓) channels, which is essential for capturing spin-dependent scattering and mobility effects that arise due to interactions between conduction electrons and localized magnetic moments. Consequently, the transport quantities become spin-resolved (S↑, S↓, σ↑, σ↓, κe↑, κe↓), and the total values are computed as σ = σ↑ + σ↓, κe = κe↑ + κe↓, and
, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity (including both electronic and lattice contributions), and T is the absolute temperature. To achieve a high zT value, a material must possess a large Seebeck coefficient and high electrical conductivity, while simultaneously maintaining low thermal conductivity. The electron relaxation time (τ) is the average time between consecutive charge carrier scattering events and is a crucial factor affecting these transport characteristics. The constant relaxation time approximation (CRTA) assumes that the relaxation time varies slowly with energy over a range comparable to the thermal energy (kBT) and is therefore frequently used in practice. The power factor per unit time (S2σ/τ), electrical conductivity per unit time (σ/τ) and electronic thermal conductivity per unit time (κe/τ) are examples of transport coefficients that can be easily expressed in terms of τ under this assumption. Owing to computational limitations, the relaxation time (τ) in this study was assumed to be constant and typically of the order of 10−15 seconds, which is consistent with values for semiconducting thermoelectric materials that have been previously reported. As is common in DFT-based thermoelectric studies of related systems a carrier concentration of 1 × 1020 cm−3 was chosen. Boltzmann transport theory under the rigid band approximation (RBA) and the constant relaxation time approximation (CRTA) as implemented in the BoltzTraP code35 was used to evaluate these interdependent transport parameters. Since these compounds are expected to be ferromagnetic the two-current model was also used to investigate how magnetism affects thermoelectric behaviour.54 This model separates the transport properties into spin-up (↑) and spin-down (↓) channels, which is essential for capturing spin-dependent scattering and mobility effects that arise due to interactions between conduction electrons and localized magnetic moments. Consequently, the transport quantities become spin-resolved (S↑, S↓, σ↑, σ↓, κe↑, κe↓), and the total values are computed as σ = σ↑ + σ↓, κe = κe↑ + κe↓, and 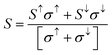 . These spin-resolved calculations allow for a more precise understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. For possible thermoelectric and spintronic applications, the thermal stability and performance of MgTi2Se4 and MgMn2Se4 spinels are clarified by a detailed analysis of the variation of thermoelectric coefficients over the 100–800 K temperature range in the section that follows.
. These spin-resolved calculations allow for a more precise understanding of the interplay between magnetism and thermoelectricity in ferromagnetic materials. For possible thermoelectric and spintronic applications, the thermal stability and performance of MgTi2Se4 and MgMn2Se4 spinels are clarified by a detailed analysis of the variation of thermoelectric coefficients over the 100–800 K temperature range in the section that follows.
 where S denotes the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ = κe + κl represents the total thermal conductivity, including electronic and lattice contributions. Efficient thermoelectric performance requires a suitable compromise between a high Seebeck coefficient, sufficient electrical conductivity, and low thermal conductivity. Fig. 8 present the calculated variation of ZT as a function of chemical potential (µ–EF) for MgTi2Se4 and MgMn2Se4 at temperatures of 300, 600, and 800 K. Since zT incorporates the combined effects of charge transport and heat conduction, it provides a comprehensive measure of thermoelectric performance. For both compounds, the zT profiles are strongly asymmetric with respect to the chemical potential. In the negative chemical potential region (µ–EF < 0), corresponding to p-type doping, zT values remain very small over the entire investigated range and do not exhibit any pronounced maxima. In contrast, the positive chemical potential region shows well-defined zT peaks, indicating that thermoelectric performance is dominated by n-type charge carriers. For MgMn2Se4 at 300 K, the main ZT maximum is in the range µ–EF ≈ 1.0–1.3 eV, with peak values approaching unity (0.99). As the temperature increases to 600 K and 800 K, the position of the maximum remains nearly unchanged, while the zT peak becomes slightly broader, suggesting an expanded chemical potential window for favorable n-type transport. A comparable trend is observed for MgTi2Se4. At room temperature, the zT curve exhibits a dominant n-type peak in the vicinity of µ–EF ≈ −1.0 to 1 eV, with maximum zT values slightly below unity (0.9). With increasing temperature, the peak height shows only a modest change, whereas the width of the zT peak increases gradually, indicating enhanced thermoelectric response over a wider doping range. Throughout the studied temperature range, zT values on the p-type side remain negligible in comparison to those on the n-type side. The concentration of the zT maxima near the conduction-band edge indicates that moderate n-type doping is required to achieve an optimal balance between the Seebeck coefficient and electrical conductivity. Away from this region, zT decreases rapidly due to the combined effects of reduced Seebeck coefficient and increased electronic thermal conductivity. The slight broadening of the ZT peaks with temperature can be attributed to thermal smearing of the electronic states and the temperature dependence of the transport coefficients. Overall, the consistently higher ZT values obtained under n-type conditions, particularly at elevated temperatures, indicate that MgTi2Se4 and MgMn2Se4 are more suitable for n-type thermoelectric applications than for p-type operation.
where S denotes the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and κ = κe + κl represents the total thermal conductivity, including electronic and lattice contributions. Efficient thermoelectric performance requires a suitable compromise between a high Seebeck coefficient, sufficient electrical conductivity, and low thermal conductivity. Fig. 8 present the calculated variation of ZT as a function of chemical potential (µ–EF) for MgTi2Se4 and MgMn2Se4 at temperatures of 300, 600, and 800 K. Since zT incorporates the combined effects of charge transport and heat conduction, it provides a comprehensive measure of thermoelectric performance. For both compounds, the zT profiles are strongly asymmetric with respect to the chemical potential. In the negative chemical potential region (µ–EF < 0), corresponding to p-type doping, zT values remain very small over the entire investigated range and do not exhibit any pronounced maxima. In contrast, the positive chemical potential region shows well-defined zT peaks, indicating that thermoelectric performance is dominated by n-type charge carriers. For MgMn2Se4 at 300 K, the main ZT maximum is in the range µ–EF ≈ 1.0–1.3 eV, with peak values approaching unity (0.99). As the temperature increases to 600 K and 800 K, the position of the maximum remains nearly unchanged, while the zT peak becomes slightly broader, suggesting an expanded chemical potential window for favorable n-type transport. A comparable trend is observed for MgTi2Se4. At room temperature, the zT curve exhibits a dominant n-type peak in the vicinity of µ–EF ≈ −1.0 to 1 eV, with maximum zT values slightly below unity (0.9). With increasing temperature, the peak height shows only a modest change, whereas the width of the zT peak increases gradually, indicating enhanced thermoelectric response over a wider doping range. Throughout the studied temperature range, zT values on the p-type side remain negligible in comparison to those on the n-type side. The concentration of the zT maxima near the conduction-band edge indicates that moderate n-type doping is required to achieve an optimal balance between the Seebeck coefficient and electrical conductivity. Away from this region, zT decreases rapidly due to the combined effects of reduced Seebeck coefficient and increased electronic thermal conductivity. The slight broadening of the ZT peaks with temperature can be attributed to thermal smearing of the electronic states and the temperature dependence of the transport coefficients. Overall, the consistently higher ZT values obtained under n-type conditions, particularly at elevated temperatures, indicate that MgTi2Se4 and MgMn2Se4 are more suitable for n-type thermoelectric applications than for p-type operation.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, No. 227) yields the irreducible representation Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g. Several modes, namely Eu, Tg, Tu, and Eg, are degenerate due to the high cubic symmetry. In terms of optical activity, A1g, Eg, and T2g modes are Raman-active while T1u modes are infrared-active. The remaining A2u, Eu, and T2u modes are optically silent. Although Raman and infrared measurements are not reported here the vibrational mode assignment is rigorously determined from group-theoretical symmetry considerations. The calculated phonon dispersion curves for both compounds show a complete absence of imaginary (negative) frequencies throughout the Brillouin zone confirming their dynamical stability at 300 K. Combined with their negative formation enthalpies this result establishes that MgTi2Se4 and MgMn2Se4 are stable both thermodynamically and against lattice instabilities. A detailed inspection of the phonon spectra provides microscopic insight into the lattice dynamics. In MgTi2Se4 the low-frequency region up to ∼150 cm−1 is dominated by acoustic modes mainly arising from translational vibrations of Mg atoms reflecting their relatively weak bonding environment. The intermediate frequency ranges from ∼180 to 290 cm−1 is primarily governed by vibrational modes of Ti atoms indicating strong coupling between Ti and the surrounding Se framework. The high-frequency optical modes spanning ∼360–440 cm−1 are mainly due to Ti–Se stretching vibrations reflecting enhanced bond stiffness and increased covalent character within the Ti–Se network. In contrast, for MgMn2Se4 the acoustic branches extend up to ∼90 cm−1 and are dominated by Mg-related translational motions. The intermediate frequency ranges from ∼130 to 200 cm−1 is mainly associated with Mn-centered vibrations, while the high-frequency optical modes between ∼240 and 320 cm−1 originate primarily from Mn–Se stretching vibrations. The comparatively lower maximum phonon frequencies in MgMn2Se4 reflect the larger atomic mass of Mn and relatively weaker Mn–Se bonding compared to the Ti–Se bonds in MgTi2Se4. These high-frequency optical phonons play a crucial role in determining electron–phonon coupling, charge-carrier scattering, and thermal transport properties. In both compounds, the separation between acoustic and optical branches and the relatively low dispersion of optical modes are expected to contribute to suppressed lattice thermal conductivity, which is highly desirable for thermoelectric applications.60 Moreover, the coexistence of light Mg-dominated acoustic modes and stiffer transition-metal–Se optical modes promote enhanced phonon scattering, thereby reducing heat transport without significantly compromising electronic conductivity. Overall, the phonon dispersion analysis not only confirms the dynamical stability of MgTi2Se4 and MgMn2Se4 but also provides valuable insight into the interplay between atomic mass, bonding strength, and lattice vibrations. These characteristics are directly linked to their favorable thermal and electronic transport behavior, reinforcing their potential as promising candidates for spin-dependent thermoelectric and multifunctional device applications.
m, No. 227) yields the irreducible representation Γ = 7Eu + 3A2u + 5Tg + 3Tu + 2Eg + A1g. Several modes, namely Eu, Tg, Tu, and Eg, are degenerate due to the high cubic symmetry. In terms of optical activity, A1g, Eg, and T2g modes are Raman-active while T1u modes are infrared-active. The remaining A2u, Eu, and T2u modes are optically silent. Although Raman and infrared measurements are not reported here the vibrational mode assignment is rigorously determined from group-theoretical symmetry considerations. The calculated phonon dispersion curves for both compounds show a complete absence of imaginary (negative) frequencies throughout the Brillouin zone confirming their dynamical stability at 300 K. Combined with their negative formation enthalpies this result establishes that MgTi2Se4 and MgMn2Se4 are stable both thermodynamically and against lattice instabilities. A detailed inspection of the phonon spectra provides microscopic insight into the lattice dynamics. In MgTi2Se4 the low-frequency region up to ∼150 cm−1 is dominated by acoustic modes mainly arising from translational vibrations of Mg atoms reflecting their relatively weak bonding environment. The intermediate frequency ranges from ∼180 to 290 cm−1 is primarily governed by vibrational modes of Ti atoms indicating strong coupling between Ti and the surrounding Se framework. The high-frequency optical modes spanning ∼360–440 cm−1 are mainly due to Ti–Se stretching vibrations reflecting enhanced bond stiffness and increased covalent character within the Ti–Se network. In contrast, for MgMn2Se4 the acoustic branches extend up to ∼90 cm−1 and are dominated by Mg-related translational motions. The intermediate frequency ranges from ∼130 to 200 cm−1 is mainly associated with Mn-centered vibrations, while the high-frequency optical modes between ∼240 and 320 cm−1 originate primarily from Mn–Se stretching vibrations. The comparatively lower maximum phonon frequencies in MgMn2Se4 reflect the larger atomic mass of Mn and relatively weaker Mn–Se bonding compared to the Ti–Se bonds in MgTi2Se4. These high-frequency optical phonons play a crucial role in determining electron–phonon coupling, charge-carrier scattering, and thermal transport properties. In both compounds, the separation between acoustic and optical branches and the relatively low dispersion of optical modes are expected to contribute to suppressed lattice thermal conductivity, which is highly desirable for thermoelectric applications.60 Moreover, the coexistence of light Mg-dominated acoustic modes and stiffer transition-metal–Se optical modes promote enhanced phonon scattering, thereby reducing heat transport without significantly compromising electronic conductivity. Overall, the phonon dispersion analysis not only confirms the dynamical stability of MgTi2Se4 and MgMn2Se4 but also provides valuable insight into the interplay between atomic mass, bonding strength, and lattice vibrations. These characteristics are directly linked to their favorable thermal and electronic transport behavior, reinforcing their potential as promising candidates for spin-dependent thermoelectric and multifunctional device applications.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.






