 Open Access Article
Open Access ArticleEnhancing gas sensing and optoelectronic properties of rutile TiO2 via transition metal doping: a DFT + U study
Lemma Tirfie Zegbrealab,
Newayemedhin Aberra a,
David E. Motaung
a,
David E. Motaung c,
S. Z. Wertad and
Fekadu Gashaw Hone
c,
S. Z. Wertad and
Fekadu Gashaw Hone *a
*a
aDepartment of Physics, Addis Ababa University, P. O. Box: 1176, Addis Ababa, Ethiopia. E-mail: fekadu.gashaw@aau.edu.et
bDepartment of Physics, Kotebe University of Education, P. O. Box: 31248, Addis Ababa, Ethiopia
cDepartment of Physics, University of the Free State, P. O. Box 339, Bloemfontein ZA9300, South Africa
dDepartment of Physics, Dire Dawa University, P. O. Box 1362, Dire Dawa, Ethiopia
First published on 15th January 2026
Abstract
This research employs DFT + U calculations to investigate the impact of doping with Co, Ni, Cu, and Zn on the structural, electronic, optical, and gas sensing characteristics of rutile TiO2. The doping process results in lattice expansion, with optimized lattice constants increasing from 4.630 Å (a) and 2.980 Å (c) in pure TiO2 to as much as 4.681 Å and 3.143 Å in Zn-doped systems. This expansion is explained by the variation in atomic radii between Ti and the doped atoms. A reduction in the bandgap is noted across all doped systems (pure: 3.04 eV; Co: 2.51 eV; Cu: 2.63 eV; Ni: 2.66 eV; Zn: 2.56 eV), which enhances the absorption of visible light and promotes p-type conductivity. The analysis of the PDOS indicates significant hybridization among the Ti-3d, O-2p, and dopant 3d orbitals, as well as magnetic properties in the Co, Ni, and Cu-doped systems. The optical properties, including the dielectric function and absorption spectra, further indicate a redshift in all transition metal (TM) doped systems. The gas sensing evaluation shows enhanced detection of CO and NO, with Zn-doping achieving superior selectivity for CO with an adsorption energy of −0.949 eV, while Ni-doping demonstrates a strong affinity for both CO (−0.726 eV) and NO (−0.639 eV), making it suitable for multi-gas detection. Doped rutile TiO2 systems exhibit enhanced sensitivity, stability, and reusability, positioning them as promising candidates for optoelectronic and gas sensing applications.
1. Introduction
The increasing global crisis of air pollution, primarily caused by emissions from industrial and urban sources, has heightened the need for efficient, selective, and cost-effective gas sensors capable of identifying dangerous pollutants such as carbon monoxide (CO) and nitric oxide (NO).1–3 Among the various semiconductor metal oxides, rutile TiO2 stands out as a potential chemiresistive sensing material owing to its remarkable chemical stability, non-toxic nature, adjustable surface chemistry, affordability, widespread availability, high-temperature resilience, and ability to withstand harsh environmental conditions.4 Nevertheless, its practical use is significantly restricted by a large band gap (∼3.0 eV), which constrains the generation of charge carriers, as well as by its limited intrinsic selectivity and low response/recovery kinetics.5Doping with transition metals (TMs) is a well-established approach to modify the electronic structure of rutile TiO2.6,7 Groundbreaking theoretical research conducted by Saini et al. indicated that 3d TM dopants (ranging from Sc to Zn) generate impurity states, which narrow the band gap and may lead to p-type conductivity, particularly with Co, Ni, and Cu.8 Nevertheless, studies that depend on standard DFT utilizing GGA functionals are inadequate in accurately representing the strongly correlated 3d electrons, resulting in an inaccurate representation of electronic structures.9 To obtain a physically precise depiction of localized d-states and electronic properties in TMOs, the DFT + U method is crucial for correcting the self-interaction error that is characteristic of traditional DFT.10,11 Samat et al. significantly illustrated the importance of this approach for TiO2, demonstrating that DFT + U produces optical properties that are more consistent with experimental findings.12 Recent studies indicate an increasing focus on correlating these essential electronic alterations with effective gas sensing capabilities. For example, Z. Yan et al. integrated experimental methods with DFT to demonstrate that Co-doping improves the NO2 sensing characteristics of TiO2 nanotubes, thereby establishing a direct link between a particular dopant and enhanced sensor performance.13 Similarly, Abd-Elkader et al. performed a DFT analysis of TiO2 quantum dots for different gases, evaluating recovery times to determine reusability, which is a vital aspect of practical sensor development.14 Research is often confined to individual dopants or low-dimensional materials, and theoretical analyses frequently employ insufficient functionals or concentrate on a limited range of properties. As a result, a considerable knowledge gap persists: there is currently no systematic and unified computational investigation that thoroughly compares the series of essential transition metal dopants (Co, Ni, Cu, and Zn) within a consistent rutile TiO2 framework utilizing a robust DFT + U methodology. To address this gap, the present study adopts a robust DFT + U methodology utilizing the Quantum ESPRESSO package to conduct a unified and predictive analysis of Co-, Ni-, Cu-, and Zn-doped rutile TiO2. By transcending the limitations of previous fragmented studies, it systematically correlates the electronic structure, including band-gap modulation and density of states, with the resultant optical property and gas-sensing behavior towards CO and NO. The sensing potential is quantitatively assessed through adsorption energy, structural stability, recovery time, and reusability across varying temperatures. This integrated framework establishes clear structure property relationships and provides a predictive design principle for the development of high-performance transition metal doped rutile TiO2 materials for optoelectronic and chemiresistive gas-sensing applications.
2. Computational details
The results found in this paper are investigated on transition metal-doped rutile TiO2 is studied with supercell approach using the Quantum Espresso package code on the density functional theory (DFT). First, the unit cell of rutile-TiO2 contains two Ti atoms and four oxygen atoms along with the cell parameters a = b = 4.599 Å, c = 2.959 Å, α = β = γ = 90° tetragonal structure used. The rutile TiO2 crystal with 2 × 2 × 2 supercell model is taken into consideration for the study of the pure TiO2 and transition metal doping effect. The obtained results and calculations are simulated under the plane wave ultra-soft and norm-conserving pseudopotentials.15 Our pseudopotentials for the pure and dopants has Ti, O, Co, Ni, Cu and Zn are 3d2 4s2, 2s2 2p4, 3d8 4s1, 3d9 4s1, 3d10 4s1 and 3d10 4s2, respectively were considered. The exchange–correlation functional is treated using generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE).16 For kinetic energy cutoff, 80 Ry, which has been obtained from the convergence calculation seen in Fig. S1(a), and for charge density cutoff 640 Ry were used throughout the study. The special points sampling integration in the Brillouin zone were employed using the Monkhorst–Pack method with 6 × 6 × 5 special k-points mesh in all self-consistent field calculations, which was obtained from the convergence calculations shown in Fig. S1(b), has been used. In our simulations, the total energy and force convergence was set at 10−6 eV and 10−3 eV Å−1, respectively. For band structure calculations the high symmetry k-point was used for the convenient purpose. To achieve high-resolution dispersion curves, the path was sampled along the Γ–X–M–Γ–Z–R–A path, utilizing a density of 20 k-points per segment to accurately capture the electronic transitions. For total and projected density of states calculations, the high dense k-points 18 × 18 × 15 was used in order to investigate more around the Brillion zone. The standard GGA underestimates the energy bandgap of transition metal oxides.17,18 Due to this limitation, the Hubbard correction (U), which introduces a correction for the self-interaction of the Ti localized d orbital, is used. In this study, on-site Hubbard corrections were implemented within the DFT + U framework to accurately capture the localized characteristics of transition-metal 3d electrons. The U values were determined based on well-established literature benchmarks instead of being fitted to specific systems. For Ti-3d states, a U value of 7.5 eV was utilized, which is commonly cited as effectively reproducing the experimental band gap and electronic structure of rutile TiO2.15,19 For the dopant 3d states, U values of 4.0 eV (Co), 5.0 eV (Ni), 5.0 eV (Cu), and 4.0 eV (Zn) were chosen in line with previous computational investigations of transition-metal-doped TiO2 and related oxides.20–24 These values ensure a physically reasonable localization of the dopant 3d electrons and support the experimentally relevant +2 oxidation states of the impurities. All U parameters were kept fixed throughout all calculations to ensure a consistent and transferable theoretical framework for evaluating the impacts of various dopants. The crystal geometry was fully optimized by using relax and variable cell relaxation calculation, and to find the ground state energy, we have used the Broyden Fletcher Goldfarb Shanno (BFGS) minimization method. For crystal structure visualization, modeling, and designing we have used XCrySDen, BURAI and VESTA software.3. Results and discussions
3.1 Structural optimization
A rutile TiO2 has a tetragonal crystal structure with a basis in which the two Ti are positioned at (0, 0, 0) and (1/2, 1/2, 1/2), and the four oxygen atoms are at position ±(u, u, 0, 1/2 + u, 1/2 − u, 1/2) with u = 0.233 (ref. 25) and is categorized in a space group of group p42/mnm number 136. The unit cell of rutile TiO2 is characterized by lattice constants a = b and c which were determined to be a = b = 4.59 Å, c = 2.96 Å, while α = β = γ = 90°, sourced from the materials project as illustrated in Fig. S2(a).16 Structural optimization results obtained in this work yield that the lattice constants, a = b and c at the minimum energy to be 4.630 Å and 2.980 Å, respectively, as depicted in Fig. 1(a) and (b). These lattice constants were used for creating a 2 × 2 × 2 supercell consisting of 48 atoms of Ti16O32 as shown in Fig. S2(b). | ||
| Fig. 1 The graph depicting total energy (Ry) against lattice parameter (Ȧ): (a) lattice constants a = b and (b) lattice constant c. | ||
Following the structural optimization of pure rutile TiO2, the structure of transition-metal doped TiO2 was optimized utilizing the same ultra-soft pseudopotentials, with their lattice parameters detailed in Table 1. These parameters were observed to increase compared to the corresponding values of the pure structure. Notably, the calculated lattice parameters closely align with both experimental and theoretically established values.16,26,27 This phenomenon is attributed to the substitution of Ti4+ (0.605 Å) with transition metals possessing larger ionic radii, such as Co2+ (0.745 Å), Ni2+ (0.690 Å), Cu2+ (0.730 Å), and Zn2+ (0.740 Å), which consequently results in an increase in the unit cell volume, as illustrated in Table 1. Furthermore, a structural distortion in the doped TiO2 was observed, evidenced by the increases in bond lengths and angles, namely α, β, and γ. This led to a localized lattice expansion, resulting in octahedral distortion.28
| Materials | Lattice parameters | Bond length (Å) | Bond angle (°) | ||
|---|---|---|---|---|---|
| a = b | c | V (Å)3 | |||
| Pure rutile TiO2 | 4.63 | 2.98 | 63.88 | Ti–O = 2.01 | O–Ti–O = 90.00 |
| Ti–O = 1.95 | |||||
| Co-doped TiO2 | 4.68 | 3.09 | 67.68 | Co–O = 2.08 | O–Co–O = 91.20 |
| Co–O = 2.00 | |||||
| Cu-doped TiO2 | 4.66 | 3.13 | 67.97 | Cu–O = 2.1 | O–Cu–O = 92.50 |
| Cu–O = 1.99 | |||||
| Ni-doped TiO2 | 4.67 | 3.10 | 67.74 | Ni–O = 2.04 | O–Ni–O = 91.00 |
| Ni–O = 1.98 | |||||
| Zn-doped TiO2 | 4.68 | 3.14 | 68.87 | Zn–O = 2.09 | O–Zn–O = 91.40 |
| Zn–O = 2.00 | |||||
3.2 Electronic structure
The band gap of pure rutile TiO2 was determined to be 1.77 eV through uncorrected GGA calculations, which aligns with theoretical predictions16 illustrated in Fig. 2(a). However, this value was significantly lower than the experimentally measured value due to the GGA functionals underestimation of Ti 3d states. Hence, a Hubbard U correction (DFT + U) was applied, resulting in a band gap of 3.02 eV for pure rutile TiO2, as depicted in Fig. 2(b), which is an excellent agreement with the experimentally determined value.19 Additionally, the electronic structure of rutile TiO2 calculated using DFT + U indicated that the CBM and the VBM are located at the same k-point (Γ point), thereby confirming its direct band gap semiconductor property, while its the Fermi level was observed to be nearer to the VBM, further indicating that the material is a p-type semiconductor.18
The electronic structure of the TM-doped materials illustrated in Fig. 2(c–f) also demonstrated that the direct band gap characteristic is maintained. These band structures correspond to a 6.25% doping concentration, modeled by a single substitution in a 2 × 2 × 2 supercell. The apparent dispersion of the dopant-induced states (spaghetti-like bands) arises from the artificial periodicity of the supercell. In practical scenarios involving disordered doping, these impurity levels would be essentially k-independent, appearing as flat bands or discrete energy levels. Nevertheless, the supercell approach provides a consistent theoretical baseline for analyzing the electronic transitions introduced by the dopant at this concentration.8
The CBM (VBM) for Co, Cu, Ni, and Zn-doped TiO2 were determined to be 2.53 (0.02) eV, 2.89 (0.26) eV, 2.05 (−0.61) eV, and 2.94 (0.38) eV, respectively, with corresponding band gaps of 2.51 eV, 2.63 eV, 2.66 eV, and 2.56 eV respectively. It is clear that the band gap of pure rutile TiO2 can be significantly reduced through doping, which is expected to enhance the electrical conductivity of the doped materials, thereby improving their gas-sensing capabilities. The observed decrease in bandgap can be attributed to the expansion of the unit cell when the larger atomic radii TM substitute Ti4+ as discussed above. It was noted that the Fermi level of the doped samples is lowered towards the VBs and resides within defect-induced valence states, thereby confirming their p-type semiconducting nature. Moreover, the observed bandgap reduction and the type of conductivity across all dopants underscores a promising strategy to push the absorbance of the pure TiO2 to the visible, enabling enhanced performance in visible-light-driven applications such as optoelectronics and gas sensing, as supported by both experimental and theoretical findings.8,19,29,30
 | ||
| Fig. 3 The total and partial density of states GGA + U for (a) pure rutile TiO2, (b) Co-doped rutile TiO2, (c) Cu-doped rutile TiO2, (d) Ni-doped rutile TiO2, and (e) Zn-doped rutile TiO2. | ||
Following doping, the Fermi level of the TM-doped TiO2 shifted further into the VB accompanied by the dopant-derived states near the band edges, which effectively narrowed the bandgap to a range of 2.66–2.51 eV, as illustrated in Fig. 3(c)–(e), while maintaining the p-type conductivity of the pure TiO2. This modification will enhance the absorption of visible light. Moreover, in the case of the introduction of dopants similar to pure rutile TiO2, the VB is predominantly formed from contributions of the O 2p orbitals, while the CB is primarily influenced by the Ti 3d orbitals, nevertheless, the 3d orbitals of the dopants introduce supplementary states near the band edges, which significantly alter the electronic and magnetic characteristics.
Among the four dopants, Co, Ni, and Cu-doped TiO2 demonstrate spin asymmetry in the PDOS, indicating the introduction of magnetic behavior, whereas Zn-doped TiO2 maintains spin symmetry and is non-magnetic. The magnetic property that was introduced by the three dopant is due to their unpaired d electron that is responsible for creating local magnetic moment as can be seen in their electronic configurations as Co2+ (3d7), Ni2+ (3d8), and Cu2+ (3d9) while the full d orbital in Zn2+ (3d10) led to spin pairing that will cancel out the magnetic moment in the Zn doped rutile TiO2. The effective +2 oxidation state of the transition-metal dopants was determined by Bader charge analysis, which quantified net charge transfer consistent with divalent cations, and is further supported by the calculated local magnetic moments matching the expected high-spin TM2+ configurations.31,32 Charge compensation during the aliovalent substitution of Ti4+ by TM2+ is achieved through the generation of holes in the valence band, leading to a downward shift of the Fermi level into the valence states and confirming the observed p-type semiconducting behavior upon doping.33,34 From a chemical perspective, the incorporation of transition-metal dopants generates localized TM-3d states that engage with lattice O-2p orbitals. This hybridization alters the density of states close to the band edges, resulting in available electronic states that improve the surface's chemical reactivity, thereby establishing a basis for effective adsorption and redox processes.
The results of the PDOS analysis indicate that Co 3d states are located close to the CBM, thereby introducing shallow donor levels. In contrast, Ni and Cu 3d states are predominantly found near the VBM, creating acceptor-like states that improve hole conductivity. Conversely, Zn 3d orbitals are situated deep within the valence band, contributing minimally to the states near the Fermi level. These differences illustrate the gradual filling of the 3d orbitals from Co to Zn, which influences both the hybridization strength with Ti 3d and O 2p orbitals and the positioning of states induced by dopants. In particular, for the Ni-doped system, the PDOS indicates robust hybridization between Ni-3d states and lattice O-2p orbitals, leading to an elevated density of electronic states near the Fermi level. This electronic characteristic offers accessible pathways for bidirectional charge transfer with adsorbed molecules and signifies a crucial chemical aspect underlying the dual affinity of Ni-doped TiO2 for both CO and NO gases. In summary, in addition to the electronic and magnetic alterations, the PDOS exhibits characteristics that are significantly useful to gas sensing such as (i) the presence of dopant-induced shallow states near to the Fermi level facilitates enhanced charge transfer between the surface and the adsorbed gas molecules, thereby increasing sensitivity, (ii) magnetic dopants such as Co, Ni, and Cu create active sites that interact with paramagnetic gases like NO, which in turn influences the energetics of adsorption and the behavior of the response, and (iii) an elevated PDOS near the band edges leads to an increase in carrier density beneficial for gas sensing through reduction/oxidation.
3.3 Optical properties
In this section, we examine the optical characteristics of pure rutile TiO2 and the impact of TM doping at a fixed concentration of 6.25% (one Ti atom replaced per 2 × 2 × 2 supercell containing 16 Ti sites). To explore these optical properties, we have computed the dielectric function, which consists of three components: εxx(E), εyy(E), and εzz(E). For all optical calculations, we averaged these three components. Given that our calculations incorporate spin-polarized data, we combined the spectra for both spin-up and spin-down states for pure and TM-doped rutile TiO2, resulting in a single optical plot for each system.35The available optical transition states in both pure and TM-doped TiO2 were determined by analyzing their joint density of states (JDOS) across an energy spectrum of 0–15 eV, as illustrated in Fig. 4. This is mathematically represented as ℏω = ∑_(k,n,m)δ(Em, k − En, k − ℏω) × f(En, k) × [1 − f(Em, k)], where ℏω is photon energy, En, k represents the nth energy band at the k-point K, while f(E) and δ are Fermi-Dirac and Dirac delta functions, respectively. The JDOS curves calculated for the materials under investigation indicate an increase in transition states with doping, ranked in the following order: Co > Cu > Zn > Ni in comparison to the pristine state. These optical properties are specific to the studied doping concentration and may vary with different dopant densities.
 | ||
| Fig. 4 Joint density of states (JDOS) versus photon energy for pure rutile TiO2 and for rutile TiO2 doped with Co, Ni, Cu, or Zn at a concentration of 6.25%. | ||
The optical properties, namely refractive index, absorption and reflectivity, of the materials at the studied doping concentration are further determined after calculating their real (ε1) and imaginary dielectric (ε2) spectra's given in Fig. S3(a) and (b). The spectra distinctly demonstrate that dopants significantly influence the polarizability at this concentration, suggesting their additional role in the gas sensing mechanism when incorporated into gas sensors. It is crucial to note that the optical properties presented in this study pertain specifically to the modeled doping concentration of 6.25%. Although qualitative trends across various dopants may remain consistent, the quantitative metrics, including the refractive index and dielectric constant, are anticipated to fluctuate with variations in dopant density. This fluctuation is attributed to alterations in the collective electron response and the onset of dopant–dopant interactions. The real (n) and imaginary (k) parts of the refractive index (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (ω) = n(ω) + ik(ω)) for the studied materials were derived using eqn (1) and (2);19,36
(ω) = n(ω) + ik(ω)) for the studied materials were derived using eqn (1) and (2);19,36
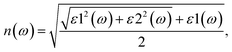 | (1) |
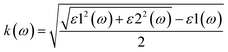 | (2) |
The refractive index spectra of the materials show a high refractive index within the visible spectrum, as illustrated in Fig. 5(a). Additionally, it is observed that doping at 6.25% has a negligible effect on the refractive index spectra, particularly in the energy range below 4 eV, with the exception of Zn-doped TiO2, which is attributed to its lower real dielectric function in that region. Moreover, the extinction coefficient spectra demonstrate that Cu-doped TiO2 exhibits the highest extinction at low energy levels, whereas Ni-doped TiO2 presents the lowest values at this specific doping level. In contrast, the pure material shows an onset around 3 eV, thereby confirming the effective influence of the dopants in our model on the shifting of their band gap, as depicted in Fig. 5(b).
 | ||
| Fig. 5 (a) Refractive index and (b) extinction coefficient as a function of photon energy for pure and 6.25% TM-doped rutile TiO2. | ||
Following to this, the absorption coefficient spectra were computed utilizing eqn (3):
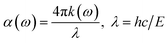 | (3) |
The results further confirmed that with doping at the modeled concentration, a red-shift of the absorption onset of TiO2, originally at 3 eV, thereby reducing the band gap of the studied TM-doped systems as illustrated in Fig. 6(a). This reduction in the band gap enhances the efficiency of electron injection and withdrawal in the gas sensing mechanism when employing this material, as the majority of gases possess oxidation/reduction energy levels within this region. Finally, the reflectivity spectra of the materials are determined using eqn (4).
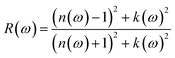 | (4) |
 | ||
| Fig. 6 (a) The absorption coefficient (α (cm−1)), (b) the reflectivity as a function of photon energy for pure and 6.25% TM-doped rutile TiO2. | ||
In the visible region, all the materials have highest reflectivity below 2 eV consistent with their much lower absorption coefficients in the region. Furthermore, as illustrated in Fig. 6(b), both Ni-doped and pure TiO2 demonstrate the lowest reflectivity under 2 eV. Evidently, higher energy photons are reflected by the pure and studied TM-doped TiO2 which confirms their excellent UV-screen property.
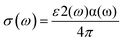 | (5) |
The optical conductivity spectra of pure TiO2 reveal two prominent peaks, with the most pronounced peak occurring at approximately 8 eV, indicating substantial interband transitions from the O 2p valence band to the Ti 3d conduction band. At a concentration of 6.25%, the introduction of Co, Ni, Cu, and Zn dopants modifies the optical conductivity, especially in the visible region, and results in a reduction of the bandgap compared to pure rutile TiO2. This reduction enhances optical conductivity at lower energy levels. A recognized limitation for gas sensing under visible light is that the relatively low conductivity of TiO2 below 3 eV suggests limited photon-induced carrier generation in the visible spectrum, despite this confirming the material's significant optical activity in the UV region.40 This increased conductivity observed in the doped materials at this concentration may be attributed to the presence of structural defects. Generally, all studied systems exhibit a decline in optical conductivity as the photon energy rises. Recent experimental and theoretical investigations support these findings, which also validate the trends observed in other optical parameters such as extinction and absorption coefficients.
3.4 Gas sensing analysis
To elucidate the essential sensing mechanisms, this section presents a comprehensive analysis of gas sensing capabilities of pure and TM-doped rutile TiO2 for the detection of CO and NO (see Fig. 8). Special emphasis is placed on adsorption energy, stability, recovery dynamics, reusability, and sensing mechanisms. To simulate the gas-sensing interface, periodic slab models of the rutile TiO2 (110) surface were employed, representing the most thermodynamically stable and experimentally relevant facet for gas–surface interactions.37–40 The models were constructed as a 2 × 2 supercell with cell parameters of 9.26 Å × 9.26 Å in the xy-plane and 25.96 Å along the z-direction. This configuration corresponds to a slab thickness of approximately 5.96 Å (containing 4 atomic layers of TiO2) with a vacuum region of 20.0 Å along the surface normal to eliminate spurious interactions between periodic images.41The surface was modeled with the stoichiometric, oxygen-bridged termination that exposes characteristic rows of five-fold coordinated titanium (Ti5C) atoms and two-fold coordinated bridging oxygen atoms. This termination represents the standard rutile TiO2 (110) surface that has been extensively characterized in both experimental and theoretical studies.37 During structural optimization, all atoms in the system (surface, dopant, and adsorbates) were allowed to relax fully without constraints, with the in-plane lattice parameters fixed to the optimized bulk values. The choice of full relaxation was made to accurately capture the structural reorganization induced by doping and gas adsorption, particularly important for transition metal dopants that may induce significant local distortions.
The adsorption of CO and NO was systematically investigated by exploring multiple adsorption configurations at the exposed Ti5C sites, which have been established as the primary active centers for gas interaction on TiO2 (110).42 For each Ti5C site, we tested: (i) atop adsorption with the molecule perpendicular to the surface (CO: C-down and O-down; NO: N-down and O-down); (ii) tilted configurations with angles ranging from 90° to 180° relative to the surface normal; and (iii) bridge configurations between Ti5C and neighboring oxygen sites. We have examined various sites to identify distinct initial geometries per gas molecule per doped system were optimized to ensure convergence to the global minimum energy configuration. This systematic approach ensured comprehensive sampling of the conformational space while maintaining consistency with established adsorption geometries reported in the literature.14
| Eads = Ematerial+gas − Ematerial − Egas | (6) |
| System | Eads (eV) of CO | Eads (eV) of NO | τ (s) of CO | τ (s) of NO |
|---|---|---|---|---|
| Pure TiO2 | −0.620 | −0.186 | 2.60 × 10−2 | 1.33 × 10−9 |
| Co-doped TiO2 | −0.898 | −0.396 | 1.22 × 103 | 4.49 × 10−6 |
| Ni-doped TiO2 | −0.726 | −0.639 | 1.57 × 100 | 5.43 × 10−2 |
| Cu-doped TiO2 | −0.914 | −0.381 | 2.26 × 103 | 2.51 × 10−6 |
| Zn-doped TiO2 | −0.949 | −0.559 | 8.76 × 103 | 2.46 × 10−3 |
The Eads of CO and NO on pure rutile TiO2 were determined to be −0.620 eV and −0.186 eV, respectively, demonstrating the material's higher sensitivity to CO in comparison to NO. Moreover, the Eads values confirm that the adsorption of CO occurs via a chemisorption mechanism, as the energy values range from −0.5182 to −9.9497 eV.14,45 In contrast, NO undergoes a physisorption process, with its adsorption energy falling between −0.1036 eV and −0.3109 eV.14,45 Upon doping, the Eads of gases on TM doped rutile TiO2 increases, leading to a more stable interaction between the gas and the surface. This stability is beneficial for both the durability and responsiveness of sensors. For CO, the Eads was observed to increase in the following order: Zn–TiO2 > Cu–TiO2 > Co–TiO2 > Ni–TiO2 > TiO2 while for NO, the order is Ni–TiO2 > Zn–TiO2 > Co–TiO2 > Cu–TiO2 > TiO2. A detailed examination of the Eads values for the gases adsorbed on the TM doped rutile TiO2 indicates that the adsorption process for both CO and NO transitions to chemisorption following doping, with NO specifically changing from physisorption to chemisorption after the doping process. Additionally, it can be seen that the Eads values of all the materials for CO is much higher than for NO except for Ni-doped TiO2 where the values were found to be closer confirming that all the pure and TM-doped TiO2 with the exception of Ni-doped TiO2 has lower selectivity while the Ni-doped TiO2 can be used to sense multiple gases confirming its higher selectivity. The dual affinity exhibited by Ni-doped TiO2 towards CO and NO can be explained by the electronic alterations caused by the incorporation of Ni. The PDOS analysis of the clean surfaces (Fig. 3) indicates that Ni introduces additional states close to the Fermi level and modifies the electronic structure of the neighboring five-fold coordinated Ti (Ti5C) sites through mechanisms of orbital hybridization and charge transfer. This redistribution of electronic density enhances the chemical reactivity of Ti5C sites for the adsorption of both CO and NO. In the case of CO, the increased electron density at Ti5C sites promotes σ donation from the CO 5σ orbital to the surface, as well as π back-donation from surface states into the CO 2π* orbital. Conversely, for NO, this same electronic enhancement facilitates stronger π back-donation into the half-filled NO π* orbital, which accounts for its relatively higher adsorption energy. This general electronic activation mechanism, wherein Ni modifies the characteristics of neighboring Ti5C sites instead of functioning as a direct adsorption center, elucidates the observed dual affinity and differentiates Ni from other dopants that tend to induce more gas-specific effects.
Moreover, comparing the Eads values of CO to NO to both pure and TM-doped materials, it can be concluded that the materials are more sensitive to the reducing CO gas compared to the oxidizing gas NO indicating a better charge transfer with CO. As calculated in Section 3.4, all the materials were found to be p-type which is expected to have a tendency of electron withdrawing favoring electron transfer from the reducing gas (CO) more favorable and hence higher adsorption energy than the oxidizing gas (NO). This enhanced electron-withdrawing capability is further justified by the p-type nature of the aliovalent TM2+ dopants, which creates a more reactive surface for redox-based chemisorption. The electronic states induced by the dopant enhance the binding affinity of gas molecules on the TiO2 surface. This is evident in the increased adsorption energies relative to the pristine surface, signifying a shift towards chemisorption and suggesting that the dopant sites act as active centers that promote interactions between molecules and the surface.
A similar result was also reported by Amogh A. Sambare et al. (2023), who studied CO gas adsorption on transition metal (Co, Cr, Cu, Mn, Mo, and Nb)-doped BiFeO3 using DFT + U + V calculations.46 Furthermore, doping was confirming from the TDOS and electronic structure in Fig. 3 showed an increased hole conductivity that was confirmed by the down ward shift of the Fermi level towards the VB which consequently can improve the materials electron withdrawing property that led to a stronger chemisorption of even the reducing gas upon doping. Hence, it can be concluded TM-doping can effectively enhance the gas sensing performance of rutile TiO2 in addition to increasing its selectivity towards reducing and oxidizing gases such as CO and NO.
τ = ν−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Eads/kBT) exp(Eads/kBT)
| (7) |
The recovery times for the gases examined, including CO and NO, calculated at room temperature, are presented in Table 2. The results show that pure rutile TiO2 demonstrates fast recovery times for both CO (26.00 ms) and NO (1.33 ns) at room temperature. This implies weak interactions and remarkable reusability, although it may exhibit limited sensitivity, especially for NO.51 In contrast, the recovery times for CO when doped with Co, Cu, and Zn in rutile TiO2 are significantly longer, measuring 1220 s, 2260 s, and 8760 s, respectively. This indicates enhanced adsorption and potentially greater sensitivity, albeit with diminished reusability. The doped systems show a relatively rapid recovery time for NO, with recovery durations of 4.49 µs for Co-doped rutile, 2.51 µs for Cu-doped rutile, and 2.46 ms for Zn-doped rutile. This suggests improved interaction compared to pure rutile TiO2, while still allowing for a fast reset. The optimal performance is exhibited by Ni-doped rutile TiO2, which demonstrates moderate recovery times for CO and NO gases, specifically 1.57 seconds and 54.3 milliseconds, respectively. This suggests enhanced gas interaction with commendable recovery times, positioning it as the most suitable choice for practical gas sensing applications where both sensitivity and reusability are essential. In conclusion, the adsorption energy governs the balance between recovery time and reusability.14 Doped rutile TiO2 systems are better suited for practical gas sensing applications where stability and long-term efficacy are essential, as they offer enhanced sensitivity and improved reusability, despite necessitating longer recovery periods.
3.5 Gas sensing mechanism
Gas sensing mechanism of the materials under this study work on the principle of electron transfer between the gasses and pure and TM-doped rutile TiO2 which directly affects its resistivity according to the empirical relation; R ∝ exp (qVs/kBT).49–51 When the TiO2 sensor is exposed to clean air at its operating temperature, atmospheric oxygen (O2 (gas)) acts as an electron acceptor. O2 adsorbs onto the surface and extracts mobile electrons from the semiconductor conduction band, forming negatively charged chemisorbed oxygen ions, such as the O2− (ads) ion at low temperatures as follows:| O2 (g) → O2 (ads) |
| O2 (ads) + e− → O2− (ads) (T < 100 °C) |
Once the adsorbed oxygen ion (O2ads−) is formed by withdrawing electron from the semiconductor, the baseline resistance (Rair) increases if the materials is an n-type semiconductor as TiO2 following the increase in the depletion region. To determine the adsorption mechanism of on the pure TiO2, looking into the processes by their adsorption energy given in Table 2, the chemisorption process of CO is by reaction of the gas on adsorbed oxygen as follows:52
| 2CO (gas) + O2− (ads) → 2CO2 (gas) + 2e− | (8) |
This reaction converts the oxygen ion into CO2 gas and, most critically, releases the previously trapped electron back into the TiO2 conduction band (see eqn (8)). The potential barrier (eVs) lowers significantly, facilitating the flow of electrons across the grain boundaries. This results an increase conductivity and a corresponding decrease in electrical resistance (Rgas < Rair), for n-type sensors exposed to reducing gases.
In contrast, when NO an oxidizing gas (electron acceptor) is introduced; it weakly adsorbs onto the TiO2 surface and extracts additional electrons from the conduction band as shown below:
| NO (gas) + e− → NO− (ads) |
This process the conduction band is forced to bend further upwards, widening the distance between the conduction band edge and the Fermi energy line. The potential barrier (eVs) increases, further restricting electron transport across the semiconductor material. This effect leads to a decrease in conductivity and a measurable increase in electrical resistance (Rgas > Rair) for n-type sensors exposed to oxidizing gases. Upon doping, a similar mechanism to that of pure TiO2 is anticipated for CO sensing, stronger as confirmed by the higher Eads owing to the increased conductivity. However, the NO sensing mechanism shifts to chemisorption where a definite reaction between the gas. In this context, the TM doping results in the surface functioning as a catalytically active interface, where the dopant centers facilitate electron exchange and redox interactions with the adsorbed gas molecules. In the case of Ni-doped TiO2, the PDOS analysis reveals that Ni-3d orbitals are capable of donating electrons to CO antibonding orbitals while simultaneously accepting electrons from the lone pairs of NO, thereby elucidating the observed dual affinity and selective adsorption. These interactions mediated by the dopants effectively modulate the surface charge and carrier concentration, thereby enhancing the gas-sensing response. The gas sensing mechanism of CO, NO on pure TiO2 is summarized in a sketch given in Fig. 9.
4. Conclusion
This research illustrates that the doping of transition metals (Co, Ni, Cu, and Zn) significantly improves the structural, electronic, optical, and gas sensing characteristics of rutile TiO2, as evidenced by DFT + U calculations pertaining to optoelectronics and gas sensing. Our findings indicate that all dopants cause considerable structural distortion and lattice expansion, which correlates with their atomic radii, thereby triggering a series of advantageous electronic effects. Each doped system displays diminished bandgaps, reaching as low as 2.51 eV for Co, which facilitates visible-light activity and p-type conductivity. The analysis of the projected density of states (PDOS) reveals substantial orbital hybridization and introduces magnetic properties in the Co-, Ni-, and Cu-doped systems. Optical assessments indicate a redshift in absorption, signifying enhanced light harvesting capabilities. The gas sensing performance of doped TiO2 is markedly improved, with Zn-doped TiO2 demonstrating the most substantial CO adsorption (–0.949 eV) and Ni-doped TiO2 showing the highest sensitivity to NO (–0.639 eV). Additionally, the doped systems exhibit superior recovery dynamics and reusability at elevated temperatures. These results position doped rutile TiO2 as a promising multifunctional material for advanced optoelectronic devices and high-performance gas sensors. Future investigations should focus on exploring the effects of dopant concentration and co-doping strategies to further enhance selectivity and operational stability.Conflicts of interest
This work is original and has not been published nor is it currently under consideration for publication elsewhere. Moreover, we declared that there is no conflict of interest.Data availability
The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.Supplementary information (SI): figures related to the computational details, structural analysis, and optical properties discussed in the main manuscript. See DOI: https://doi.org/10.1039/d5ra08889e.
Acknowledgements
Prof. Fekadu Gashaw acknowledges the financial support of Addis Ababa University through the Thematic Research Grant (ORA/013/18/25).References
- B. Zong, S. Wu, Y. Yang, Q. Li, T. Tao and S. Mao, Smart gas sensors: recent developments and future prospective, Nano-Micro Lett., 2025, 17, 54 Search PubMed.
- S. Panda, S. Mehlawat, N. Dhariwal, A. Kumar and A. Sanger, Comprehensive review on gas sensors: Unveiling recent developments and addressing challenges, Mater. Sci. Eng., B, 2024, 308, 117616 Search PubMed.
- X. Liu, T. Ma, N. Pinna and J. Zhang, Two-dimensional nanostructured materials for gas sensing, Adv. Funct. Mater., 2017, 27, 1702168 CrossRef.
- J. Bai and B. Zhou, Titanium dioxide nanomaterials for sensor applications, Chem. Rev., 2014, 114, 10131–10176 CrossRef CAS PubMed.
- D. Degler, U. Weimar and N. Barsan, Current understanding of the fundamental mechanisms of doped and loaded semiconducting metal-oxide-based gas sensing materials, ACS Sens., 2019, 4, 2228–2249 CrossRef CAS PubMed.
- J. Zhao, H. Wang, Y. Cai, J. Zhao, Z. Gao and Y.-Y. Song, The challenges and opportunities for TiO2 nanostructures in gas sensing, ACS Sens., 2024, 9, 1644–1655 CrossRef CAS.
- S. M. Al-Jawad, M. Rasheed and Z. Y. Abbas, Effect of doping on the structural, optical and electrical properties of TiO2 thin films for gas sensor, J. Opt., 2024, 1–22 Search PubMed.
- M. Saini, M. Kumar and T. Som, ab initio study of 3d transition metal-doping effects in rutile-TiO2: Role of bandgap tunability in conductivity behaviour, Appl. Surf. Sci., 2017, 418, 302–307 CrossRef CAS.
- I. Østrøm, M. A. Hossain, P. A. Burr, J. N. Hart and B. Hoex, Designing 3d metal oxides: selecting optimal density functionals for strongly correlated materials, Phys. Chem. Chem. Phys., 2022, 24, 14119–14139 RSC.
- A. Bajaj and H. J. Kulik, Molecular DFT+ U: a transferable, low-cost approach to eliminate delocalization error, J. Phys. Chem. Lett., 2021, 12, 3633–3640 CrossRef CAS.
- S. A. Tolba, K. M. Gameel, B. A. Ali, H. A. Almossalami, and N. K. Allam, The DFT+ U: Approaches, accuracy, and applications, in Density Functional Calculations-Recent Progresses of Theory and Application, IntechOpen, 2018 Search PubMed.
- M. Samat, A. Ali, M. Taib, O. Hassan and M. Yahya, Hubbard U calculations on optical properties of 3d transition metal oxide TiO2, Results Phys., 2016, 6, 891–896 Search PubMed.
- Z. Yan, Y. Zhang, W. Kang, N. Deng, Y. Pan, W. Sun, J. Ni and X. Kang, TiO2 gas sensors combining experimental and DFT calculations: a review, Nanomaterials, 2022, 12, 3611 CrossRef CAS.
- O. H. Abd-Elkader, M. A. Sakr, M. A. Saad, H. Abdelsalam and Q. Zhang, Electronic and gas sensing properties of ultrathin TiO2 quantum dots: A first-principles study, Results Phys., 2023, 52, 106804 CrossRef.
- F. T. Geldasa and F. B. Dejene, Exploration of vanadium and rhenium co-doped TiO2 for enhanced photocatalytic performance via first principle density functional theory investigation, Phys. Scr., 2025, 100, 085924 CrossRef CAS.
- F. T. Geldasa and F. B. Dejene, Effects of S Doping and Oxygen Vacancy on the Physical Properties of Rutile TiO2 for Photocatalysis Applications Based on Density Functional Theory Study, Materials, 2025, 18, 1688 CrossRef CAS PubMed.
- S. M. Rasul, D. R. Saber and S. B. Aziz, Role of Titanium replacement with Pd atom on band gap reduction in the anatase Titanium Dioxide: First-Principles calculation approach, Results Phys., 2022, 38, 105688 CrossRef.
- F. T. Geldasa, M. A. Kebede, F. G. Hone and E. T. Jira, Influence of non-metals doping on the structural, electronic, optical, and photocatalytic properties of rutile TiO2 based on density functional theory computations, Comput. Condens. Matter, 2024, 41, e00970 CrossRef.
- F. T. Geldasa, F. B. Dejene, M. A. Kebede, F. G. Hone and E. T. Jira, Density functional theory study of Chlorine, Fluorine, Nitrogen, and Sulfur doped rutile TiO2 for photocatalytic application, Sci. Rep., 2025, 15, 3390 CrossRef CAS PubMed.
- M. Capdevila-Cortada, Z. Łodziana, and N. López, in Performance of DFT + U Approaches in the Study of Catalytic Materials, ACS Publications, 2016, pp. 8370–8379 Search PubMed.
- S. K. Iyemperumal and N. A. Deskins, Activation of CO 2 by supported Cu clusters, Phys. Chem. Chem. Phys., 2017, 19, 28788–28807 RSC.
- M. M. Hasan, A. Kabir and M. Kamruzzaman, The structural, elastic, electronic, magnetic and optical properties of SrNiO3 perovskite: A DFT and DFT+ U study, Results Phys., 2022, 41, 105920 CrossRef.
- V. Christhunathan, P. Farràs and M. Tong, First-principles study of electronic properties of Zn and La doped and co-doped anatase TiO2, AIP Adv., 2023, 13, 125013 CrossRef CAS.
- K. Ohno, R. Sahara, T. Nanri and Y. Kawazoe, Optical properties of rutile TiO2 with Zr, Mo, Zn, Cd impurities, Comput. Condens. Matter, 2024, 41, e00977 CrossRef.
- N. Gonzalez Szwacki, P. Fabrykiewicz, I. Sosnowska, F. o. Fauth, E. Suard and R. Przeniosło, Orthorhombic symmetry and anisotropic properties of rutile TiO2, J. Phys. Chem. C, 2023, 127, 19240–19249 CrossRef CAS.
- H. Chen, X. Li, R. Wan, S. Kao-Walter, Y. Lei and C. Leng, A DFT study on modification mechanism of (N, S) interstitial co-doped rutile TiO2, Chem. Phys. Lett., 2018, 695, 8–18 CrossRef CAS.
- P. Santos-Aguilar, J. Bernal-Ramírez, E. Vazquez-Garza, L. Y. Vélez-Escamilla, O. Lozano, G. d. J. Garcia-Rivas and F. F. Contreras-Torres, Synthesis and characterization of rutile TiO2 nanoparticles for the toxicological effect on the H9c2 cell line from rats, ACS Omega, 2023, 8, 19024–19036 Search PubMed.
- S. Sahoo, G. Ghorai, K. Ghosh, B. Das, M. K. Sikdar and P. K. Sahoo, Anharmonicity of optical phonon modes in copper doped rutile TiO2 nanorod composed microflowers, AIP Adv., 2021, 11, 105013 Search PubMed.
- H. Heffner, R. Faccio and I. López-Corral, C–doped TiO2 (B): a density functional theory characterization, Appl. Surf. Sci., 2021, 551, 149479 CrossRef CAS.
- F. Amano, A. Yamamoto and J. Kumagai, Highly Active Rutile TiO2 for Photocatalysis under Violet Light Irradiation at 405 Nm, Catalysts, 2022, 12(10), 1079 CrossRef CAS.
- W. C. P. Wanniarachchi, T. Arunasalam, P. Ravirajan, D. Velauthapillai and P. Vajeeston, Hybrid functional study on electronic and optical properties of the dopants in anatase TiO2, ACS Omega, 2023, 8, 42275–42289 CrossRef CAS.
- Z. Zhang, Q. Hou, M. Qi and S. Sha, First principles of Fe/Co/Ni doping and the coexistence of O vacancy in the magnetic and optical properties of rutile TiO2 (110) surface, Phys. Scr., 2022, 97, 045815 CrossRef CAS.
- A. Iwaszuk and M. Nolan, Charge compensation in trivalent cation doped bulk rutileTiO2, J. Phys.: Condens. Matter, 2011, 23, 334207 CrossRef.
- Y. Matsumoto, M. Katayama, T. Abe, T. Ohsawa, I. Ohkubo, H. Kumigashira, M. Oshima and H. Koinuma, Chemical trend of Fermi-level shift in transition metal-doped TiO2 films, J. Ceram. Soc. Jpn., 2010, 118, 993–996 CrossRef CAS.
- F. T. Geldasa, M. A. Kebede, M. W. Shura and F. G. Hone, Different metal dopants effects on the structural, electronic, and optical properties of β-PbO: a density functional theory study, Eur. Phys. J. Plus, 2023, 138, 165 CrossRef CAS.
- F. T. Geldasa, The structural, electronic, and optical properties of metals doped litharge PbO: A density functional theory study, Eur. Phys. J. B, 2024, 97, 78 CrossRef CAS.
- C. Tesvara, C. Walenta and P. Sautet, Oxidative decomposition of dimethyl methylphosphonate on rutile TiO 2 (110): the role of oxygen vacancies, Phys. Chem. Chem. Phys., 2022, 24, 23402–23419 RSC.
- H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Optimisation of accurate rutile TiO2 (110),(100),(101) and (001) surface models from periodic DFT calculations, Theor. Chem. Acc., 2007, 117, 565–574 Search PubMed.
- T. Zheng, C. Wu, M. Chen, Y. Zhang and P. T. Cummings, A DFT study of water adsorption on rutile TiO2 (110) surface: The effects of surface steps, J. Chem. Phys., 2016, 145, 044702 CrossRef PubMed.
- R. Panta and V. Ruangpornvisuti, Unusual adsorption behavior of hydrogen molecules on Zr–doped perfect and oxygen–vacancy defective rutile TiO2 (110) surfaces: Periodic DFT study, Int. J. Hydrogen Energy, 2019, 44, 32101–32111 CrossRef CAS.
- T. T. Thoa, T. T. Nguyen, H. Van Hung and N. T. M. Hue, Slab models of rutile TiO2 (110) surface: DFT and DFT+ U calculations, Vietnam J. Chem., 2023, 61, 563–570 CrossRef CAS.
- J. P. P. Ramalho, F. Illas and J. R. Gomes, Adsorption of CO on the rutile TiO 2 (110) surface: a dispersion-corrected density functional theory study, Phys. Chem. Chem. Phys., 2017, 19, 2487–2494 RSC.
- M. I. Khan, M. Hassan, A. Majid, M. Shakil and M. Rafique, DFT perspective of gas sensing properties of Fe-decorated monolayer antimonene, Appl. Surf. Sci., 2023, 616, 156520 Search PubMed.
- Y. Yu and C. Dai, DFT study of gas adsorption and sensing based on noble metal (Ag, Au and Pt) functionalized boron selenide nanosheets, Phys. E, 2021, 125, 114409 CrossRef CAS.
- Y. Qu, L. Qin, M. Guo, X. Liu and Y. Yang, Multilayered molecularly imprinted composite membrane based on porous carbon nanospheres/pDA cooperative structure for selective adsorption and separation of phenol, Sep. Purif. Technol., 2022, 280, 119915 CrossRef CAS.
- A. A. Sambare, R. Pawar and M. Shirsat, A DFT investigation on transition metal (Co, Cr, Cu, Mn, Mo and Nb)-doped bismuth ferrite oxide (BiFeO3) for CO gas adsorption, Theor. Chem. Acc., 2023, 142, 61 Search PubMed.
- M. I. Khan, M. I. Akber, M. Gul, T. Iqbal, S. S. Alarfaji and A. Mahmood, Exploring the sensing potential of Fe-decorated h-BN toward harmful gases: a DFT study, RSC Adv., 2024, 14, 7040–7051 RSC.
- V. Parey, B. M. Abraham, N. K. Gaur and R. Thapa, First-principles study of two-dimensional B-doped carbon nanostructures for toxic phosgene gas detection, ACS Appl. Nano Mater., 2022, 5, 12737–12745 CrossRef CAS.
- H. Ji, W. Zeng and Y. Li, Gas sensing mechanisms of metal oxide semiconductors: a focus review, Nanoscale, 2019, 11, 22664–22684 RSC.
- K. L. Morulane, Z. P. Tshabalala, H. C. Swart and D. E. Motaung, Assembly of np In2O3-Co3O4 heterostructures and their surface and structural analyses towards trace level detection of acetone, Appl. Surf. Sci., 2024, 671, 160714 CrossRef CAS.
- K. L. Morulane, H. C. Swart and D. E. Motaung, A review on topical advancement and challenges of indium oxide based gas sensors: Future outlooks, J. Environ. Chem. Eng., 2024, 12, 112144 Search PubMed.
- A. Pathania, N. Dhanda, R. Verma, A.-C. A. Sun, P. Thakur and A. Thakur, Metal oxide chemoresistive gas sensing mechanism, parameters, and applications, ECS Sens. Plus, 2024, 3, 013401 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |




