Fragment to framework: automatic fragmentation of covalent organic frameworks into building blocks for band gap analysis

Abstract

Understanding structure–property relationships in ordered functional materials is essential for their rational design and optimisation. Fragment-based approaches relating materials’ properties to those of their building blocks (fragments) are intuitive to chemistry and have been successfully applied in the design of metal–organic frameworks (MOFs). However, covalent organic frameworks (COFs) are resistant to such in silico fragmentation due to their covalent bonds and ambiguous definitions of nodes and linkers. Here we introduce a new algorithm, deCOFpose, designed to systematically fragment COFs into building blocks according to chemically intuitive rules, enabling fragment-based structure–property analysis, and exemplify the latter for COF band gaps. Our results reveal that the electronic features (e.g., energies of the frontier molecular orbitals) of the building blocks alone are insufficient to fully represent these materials, and the inclusion of their topological characteristics is required to engineer bespoke COFs with desired band structures.

---

Introduction

Reticular chemistry establishes a direct link between small-molecule building blocks (nodes and linkers) and extended ordered materials such as metal–organic and covalent organic frameworks (MOFs and COFs, respectively).¹ This fragment-based rationale not only enables one to construct extensive virtual databases in silico,^2–8 but also provides insight into how the material's properties emerge from those of the building blocks. For example, tuning the functionalisation of the secondary building units afforded band gap engineering in MOFs.^9,10 By decomposing experimentally characterised MOFs into their building blocks, analysing their influence on the material's properties, reconstructing new MOFs from selected fragments, and predicting their properties with machine learning, new frameworks with improved stability,¹¹ thermal conductivity,¹² and gas adsorption capacity¹³ were realised. For MOFs, identification of the metal-containing nodes and organic linkers is straightforward. However, adapting similar fragmentation techniques to COFs, composed exclusively from organic building blocks connected by covalent bonds, represents a challenge. For instance, the same building block – benzene – can be considered a node in one framework, and a linker in another (Fig. 1).

Fig. 1 Exemplary COFs with a benzene building block (shown with balls and sticks) serving as node in COF-16 Ź⁴ and as linker in CTF-1.¹⁵.

Despite this complexity, fragment-based simulation and screening approaches have been exemplified for COFs in several recent studies. Using bespoke building-block-specific forcefields, a so-called ReDD-COFFEE database was constructed and screened to identify promising materials for vehicular methane storage⁶ and carbon capture.¹⁶ Electric quadrupole building blocks have been utilised to engineer the electrostatic potential inside COF pores, crucial for such practical applications as gas storage, sensing, and catalysis.¹⁷ Finally, for five COFs with distinct topologies, Troisi and colleagues demonstrated that conduction and valence bands, key to their optical, electronic, and catalytic properties, could be expressed as a linear combination of the frontier molecular orbitals (MOs) localised on the individual molecular building blocks.¹⁸

To transition from such insightful yet case-by-case analysis to high-throughput screening and, ultimately, targeted inverse design of COFs, an automated fragmentation tool is necessary. In this work, we present deCOFpose – an algorithm which automatically fragments COFs into their building blocks based on predefined rules and prepares these fragments for subsequent computational analysis. We apply deCOFpose to the CoRE-COFs database¹⁹ of experimental structures and probe the relationship between the energies of fragments’ frontier molecular orbitals and the band gaps of the frameworks for hundreds of systems.

Methodology

deCOFpose algorithm

The algorithm consists of five steps, illustrated in Fig. 2 and discussed in detail below.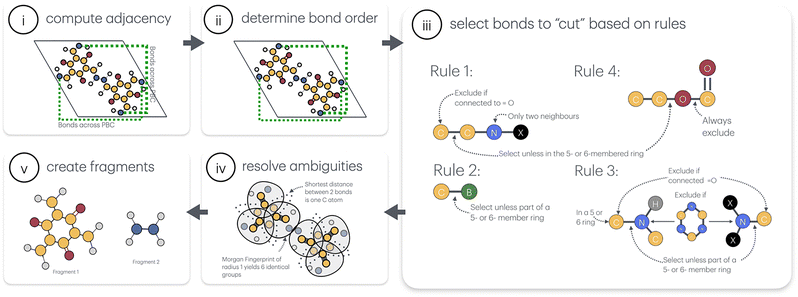

Fig. 2 Schematic illustration of the steps involved in applying the deCOFpose algorithm to a framework material.

(i) Conversion of a periodic framework structure into a finite molecular structure. COF structures, including those in the CoRE-COF database, are typically deposited in the Crystallographic information file (CIF) format, which readily conveys their periodic nature but is not easily processable for fragmentation. Therefore, starting with a CIF, a 3 × 3 × 3 supercell is generated for the periodic structure, and a central unit cell within this supercell is identified and isolated. Next, atoms are mapped back from the supercell to their original positions in the central unit cell. Bonds connecting atoms across periodic boundary conditions (PBCs) are mapped according to their corresponding central unit cell atoms.

(ii) Bond order determination is necessary since the fragmentation rules rely on this information. Bond orders are determined based on the type, valency, and connectivity of the atoms, as well as aromaticity (defined as iterating double bonds within a ring). Importantly, bond order information is retained for bonds crossing the arbitrary cell boundaries. Steps (i) and (ii) are implemented in an algorithm called cif2mol (consistent with the xyz2mol notation)²⁰ and integrated into deCOFpose. cif2mol transforms CIF-formatted periodic structures into molecular structures with bond-type information using RDKit²¹ and ASE²² libraries. At this stage, periodic SMILES strings and Morgan fingerprints are generated, providing a representation of the molecular structure that can be used in subsequent analysis.

(iii) Selection of the bonds to “cut”. Covalent organic frameworks generally feature appreciable electron delocalisation (conjugation) over large portions of their structure, responsible for their unique electronic properties (see Fig. S1, S2 and the accompanying discussion in the SI). However, this same feature greatly complicates the selection of bonds to break when determining the COF fragments. Lacking occupation- or orbital-based guidelines applicable to a variety of COFs, we started instead with a retrosynthetic perspective.^17–19 Specifically, to capture the synthetic diversity of COFs in a systematic and computationally tractable manner, we categorised the linkage types found in COFs into four distinct decomposition families, each representing a class of chemically analogous transformations^23,24 and underlying a specific “cutting” rule (Fig. 3). In defining these “cutting” rules, we aimed to:

Fig. 3 Retrosynthetic origins of the “cutting” rules.

• Capture the chemical diversity of COFs;

• Ensure, as much as possible, the continuity of the electronic structure (e.g., avoiding cutting through π-conjugation, double and triple bonds, or cyclic moieties);

• Generate fragments that are common, i.e., found in as many COFs as possible, to enable direct comparison and fast pre-screening.

As a result, in deCOFpose, the bonds selected to be “cut” are:

(1) Carbon–carbon bonds adjacent to a doubly-substituted nitrogen, i.e., C₂–C₁–N–X, except for carbonyl, i.e., O=C₂–C₁–N–X, and bonds that are components of 5- or 6-membered rings.

(2) Boron–carbon bonds B–C, except when they are components of 5- or 6-membered rings.

(3) Nitrogen–carbon bonds involving triply-substituted nitrogen, e.g., C–NR₁R₂, except for carbonyl, i.e., O=C–NR₁R₂, and bonds that are components of 5- or 6-membered rings.

In the case of a secondary nitrogen atom, the C–N bond is only selected for “cutting” if the carbon atom is part of a 5- or a 6-membered ring, while the nitrogen is not in the ring.

(4) Oxygen–carbon bonds C–O except when they are components of 5- or 6-membered rings. In a C₁–O–C₂=O motif, the C₁–O single bond is selected for “cutting”.

(iv) Resolving ambiguities and “cutting” bonds. In cases where applying the aforementioned rules leads to conflicting choice of the bond(s) to be “cut”, the following additional criteria are imposed:

• Grouping bonds: bonds are grouped by similarity based on the applied selection rule and the nearby atomic environment (quantified via the Morgan fingerprint surrounding the bond). Groups are sorted first by size (largest first) and then by lexicographical order of fingerprint values. This ensures that bonds with similar chemical environments are treated similarly.

• Graph representation: a graph is created where nodes represent candidate bonds to be “cut” and edges represent the shortest bond-atomic paths between them. An adjacency matrix is constructed to capture the bond connectivity.

• Finding symmetrical routes: the algorithm searches for symmetrical triangles in the graph (indicating three preselected bonds with similar paths). If found, these triangles are selected for “cutting”. If no symmetrical triangles are found, the algorithm selects all routes with the same minimum number of atoms.

(v) Fragment creation. Once the selected bonds are “cut”, hydrogen atoms are added to obtain neutral closed-shell molecular fragments. deCOFpose generates both the individual nodes and linkers and their combinations termed “node + linker”. Identified individual building blocks are not assigned as “node” and “linker”, to account for situations like the benzene example discussed above; instead, in our analysis we simply denote them as a “smaller” and a “larger” fragment.

Computations

Periodic computations of the band gaps were performed at the PBE0-D3/pob_TZVP_rev2 level of theory in Crystal17.²⁵ All fragment geometry optimisations and computations of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies were conducted at the PBE0-D3/dev2-TZVP level in ORCA 5.0.4.^26,27

Data analysis

For each COF, volume, density, and accessible surface area were taken from the CoRE_COF database. Principal component analysis (PCA) was performed in Python to further analyse the dataset using the unit cell volume, density, and accessible surface area, as well as computed HOMO–LUMO gaps of the building blocks and of the “node + linker” constructs. The data was normalised before PCA.

Results and discussion

Fragmentation of the COFs from CoRE-COF

Out of the 591 COFs in the CoRE-COF database, 47 were excluded due to the presence of metal atoms, which greatly influence the band gaps.²⁸ For 121 COFs, conversion into molecular structures failed, primarily due to incorrect structural information in the database. A total of 422 COFs were successfully decomposed into building blocks. We visualised the chemical space of these COFs using the “cutting” rules as a similarity measure (Fig. 4). Prevalence of the “cuts” according to rule 1 reflects the predominance of imine-linked COFs in the database. Analysing the generated fragments, we identified another subset of frameworks containing incorrect structural information, which were also removed. The final dataset for subsequent fragment-based analysis includes 316 COFs. Detailed discussion of these data cleaning procedures is provided in the SI.

Fig. 4 Chemical space of studied COFs. Each framework is represented by a circle with a corresponding number referring to its position in the CoRE-COF database. Points are coloured by the rule used to separate them. Two points are connected by a grey line if they share a building block. For selected clusters, the most common building block is shown in an inset.

Framework band gap vs. fragment HOMO–LUMO gap

The investigated COFs display a wide range of band gaps, from as low as 0.02 eV (COF no. 15 in the CoRE-COF database) to as high as 4.80 eV (COF no. 44), with an average band gap of 2.37 eV. Most systems behave as semiconductors, although several have near-insulating behaviour. Most of the computed band gaps are indirect, with only a few COFs exhibiting direct band gaps. The HOMO–LUMO gaps of the individual nodes and linkers range from 0.63 eV to 9.06 eV, with an average of 5.18 eV, while for their combinations – the “node + linker” fragments – these values range from 0.79 eV to 6.02 eV, with an average of 3.95 eV.

In an effort to track the emergence of the electronic structures of the frameworks, we analysed the relationships between their band gaps and the HOMO–LUMO gaps of their building blocks (where HOMO and LUMO used to compute the gap always refer to the same species, i.e., either the node, the linker, or the “node + linker” fragment). Considering the individual nodes or linkers, we found virtually no correlation between these parameters (see Fig. S4 in the SI). Similarly, the coefficient of determination (R²) for the relationship between the computed band gaps of the frameworks and the HOMO–LUMO gaps of the “node + linker” fragments is only 0.22. This observation is unsurprising considering that (i) in creating the fragments, by necessity we occasionally “cut” through π-conjugated moieties, thus disrupting the electron delocalisation, and (ii) molecular orbitals of the fragments cannot, by definition, capture the complex nature of the periodic electronic structure featuring band dispersion, etc.

We also do not observe a particularly strong distinction in the band gaps between two- and three-dimensional COFs (Fig. 5, top). It is worth noting that the CoRE-COF database contains a limited number of 3D COFs, and even fewer of them were successfully deCOFposed. However, certain patterns in the data arise when we consider the topologies of the frameworks (Fig. 5, bottom). The two prevalent topologies are the hcb (honeycomb) network, in which each node is connected to three linkers at 120° angles, and the sql (square lattice) network, where one node connects with four linkers at 90° angles. Interestingly, COFs with an hcb topology tend to exhibit higher HOMO–LUMO gaps relative to those with an sql topology, despite the fact that hcb systems are flatter and thus afford better electron delocalisation (conjugation) throughout the framework. This emphasises the subtle interplay between the topology and the chemistry of the building blocks in defining the electronic properties of the resulting frameworks. The high structural diversity observed across network topologies indicates that even identical building blocks can yield distinct properties depending on their connectivity²⁹ – a facet that is neglected in our fragmentation approach. Furthermore, the interlayer stacking arrangements recorded in the commonly used databases of both experimental and hypothetical 2D-COFs are frequently oversimplified, idealised, or even incorrect,³⁰ additionally obfuscating the structure–property analysis.

Fig. 5 Plots of computed “node + linker” HOMO–LUMO gaps vs. COFs band gaps, coloured by their dimensionality (top) and topology (bottom). Dashed black line represents the x = y relationship.

Composition-based subsets

The lack of pronounced correlation between the electronic structure properties of molecular fragments and frameworks does not imply that the building blocks have no bearing on these properties. This notion is supported not only by the topology-based analysis above, but also by the relationships that emerge once the entire dataset is split into subsets based on the type and number of heteroatoms in a COF (Fig. 6, see also Fig. S5 in the SI). Within these relatively homogeneous subsets, there is a stronger correlation between the “node + linker” HOMO–LUMO gaps and the COF band gaps.

Fig. 6 Correlation analysis within the heteroatom-based subsets of the investigated COFs composed of the “node + linker” fragments containing (from left to right) three boron atoms, six nitrogen atoms, and four oxygen atoms.

Principal component analysis

To account for the entangled influences of the framework topology, elemental composition, and the electronic structure of the building blocks, we performed PCA of the computed building blocks using simple physical descriptors of the fragments and the frameworks. The two principal components, PC1 and PC2, explain 39% and 25% of the data variance, respectively. In the two-dimensional space of these PCs, computed band gaps follow a clear pattern: higher band gaps are generally found in the top left corner, and lower band gaps in the bottom right (Fig. 7, left). Tendentially, PC1 correlates inversely with the HOMO–LUMO gaps, whereas PC2 correlates positively with the volume and internal pore surface (Fig. 7, right; see also Fig. S6 in SI, for a detailed breakdown of the contributions to each principal component). Thus, low PC1 (higher HOMO–LUMO gaps of the fragments) and high PC2 (high volume and surface area of the frameworks) are associated with higher COF band gaps, and vice versa.

Fig. 7 Principal component analysis of the computed COF band gaps. Left: chemical space of investigated COFs with its dimensionality reduced to the first two principal components. The datapoints are coloured by the values of the computed band gaps. Right: Illustrative composition of the two principal components with the highest data variance.

Conclusions

In this work, we demonstrate that a fragment-based approach only partially captures the complex electronic structure of the covalent organic frameworks. Observed weak correlations between the HOMO–LUMO gaps of the building blocks (fragments) and the COF band gaps can be attributed to the high extent of electron delocalisation throughout the framework which were disrupted upon fragmentation. Improved correlations emerge only in the curated subsets of COFs with similar heteroatom profiles in their building blocks, e.g., those containing exactly three boron atoms. Admittedly, our investigation is limited to the CoRE-COF database, dominated by the imine-based linkers. This suggests that holistic representation of the band structures of the covalent organic frameworks, realised experimentally so far, requires combining electronic structure features of the fragments with the topological characteristics of the frameworks. Specifically, our analysis demonstrates that COFs with, e.g., lower band gaps can be engineered from building blocks with low HOMO–LUMO gaps arranged into compact networks. These findings highlight a crucial distinction between COFs, composed entirely of robust covalent bonds imparting high thermal stability, and MOFs, which feature dynamic metal-linker bonds³¹ and are well-represented with fragment-based techniques.^11–13

Properties other than band gaps, relying on more localised phenomena, are likely to display a more direct emergence from the features of the building blocks. These potentially include the host–guest interactions (as shown in our previous work),³² acid/base character, and local reactivity. Our new fragmentation algorithm, deCOFpose, not only enables this analysis for COFs, but can be easily modified to accommodate alternative “cutting” rules and describe many other types of ordered functional materials.

Author contributions

ME: conceptualisation, methodology, supervision, writing – original draft. RF: investigation, methodology, software, formal analysis, writing – review & editing. AC: investigation, methodology, formal analysis. CM, FFG, SB: investigation, formal analysis. GG: conceptualisation, funding acquisition, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

Full set of computed data and exemplary input and output files are freely available from Zenodo via https://doi.org/10.5281/zenodo.14855145. The deCOFpose algorithm is freely available from GitHub via https://github.com/grynova-ccc/deCOFpose.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5qm00727e.

Acknowledgements

The authors acknowledge support from the Klaus Tschira Foundation (SIMPLAIX Project 6), funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 101042290 PATTERNCHEM), the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster), and the University of Birmingham's BlueBEAR HPC service, which provides a High Performance Computing service to the University's research community (see http://www.birmingham.ac.uk/bear for more details). The authors acknowledge helpful discussions with Stiv Llenga and thank Dr John Lindner for proofreading this manuscript.

References

1. O. Yaghi, M. O'Keeffe, N. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Reticular Synthesis and the Design of New Materials, Nature, 2003, 423, 705–714,  DOI:10.1038/nature01650.
2. C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-Scale Screening of Hypothetical Metal-Organic Frameworks, Nat. Chem., 2012, 4, 83–89,  DOI:10.1038/nchem.1192.
3. P. G. Boyd and T. K. Woo, A Generalized Method for Constructing Hypothetical Nanoporous Materials of Any Net Topology from Graph Theory, CrystEngComm, 2016, 18, 3777–3792,  10.1039/C6CE00407E.
4. S. Majumdar, S. M. Moosavi, K. M. Jablonka, D. Ongari and B. Smit, Diversifying Databases of Metal Organic Frameworks for High-Throughput Computational Screening, ACS Appl. Mater. Interfaces, 2021, 13, 61004–61014,  DOI:10.1021/acsami.1c16220.
5. S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, Computational Screening of Trillions of Metal-Organic Frameworks for High-Performance Methane Storage, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654,  DOI:10.1021/acsami.1c02471.
6. J. S. De Vos, S. Borgmans, P. Van Der Voort, S. M. J. Rogge and V. Van Speybroeck, ReDD-COFFEE: a Ready-To-Use Database of Covalent Organic Framework Structures and Accurate Force Fields to Enable High-Throughput Screenings, J. Mater. Chem. A, 2023, 11, 7468–7487,  10.1039/D3TA00470H.
7. R. Mercado, R. S. Fu, A. V. Yakutovich, L. Talirz, M. Haranczyk and B. Smit, In Silico Design of 2D and 3D Covalent Organic Frameworks for Methane Storage Applications, Chem. Mater., 2018, 30, 5069–5086,  DOI:10.1021/acs.chemmater.8b01425.
8. Y. Lan, X. Han, M. Tong, H. Huang, Q. Yang, D. Liu, X. Zhao and C. Zhong, Materials Genomics Methods for High-Throughput Construction of COFs and Targeted Synthesis, Nat. Commun., 2018, 9, 5274,  DOI:10.1038/s41467-018-07720-x.
9. H. Q. Pham, T. Mai, N.-N. Pham-Tran, Y. Kawazoe, H. Mizuseki and D. Nguyen-Manh, Engineering of Band Gap in Metal–Organic Frameworks by Functionalizing Organic Linker: A Systematic Density Functional Theory Investigation, J. Phys. Chem. C, 2014, 118, 4567–4577,  DOI:10.1021/jp405997r.
10. K. I. Williamson, D. J. C. Herr and Y. Mo, Toward Tuning the Bandgap in Meta-Substituted Fe-MOFs, Mater. Adv., 2024, 5, 6842–6852,  10.1039/D4MA00512K.
11. A. Nandy, C. Duan and H. J. Kulik, Using Machine Learning and Data Mining to Leverage Community Knowledge for the Engineering of Stable Metal–Organic Frameworks, J. Am. Chem. Soc., 2021, 143, 17535–17547,  DOI:10.1021/jacs.1c07217.
12. Y. Lin, R. Cheng, T. Liang, W. Wu, S. Li and W. Li, Understanding the Influence of Secondary Building Units on the Thermal Conductivity of Metal–Organic Frameworks via High-Throughput Computational Screening, Phys. Chem. Chem. Phys., 2023, 25, 32407–32415,  10.1039/D3CP04640K.
13. Z. Wang, Y. Zhou, T. Zhou and K. Sundmacher, Identification of Optimal Metal-Organic Frameworks by Machine Learning: Structure Decomposition, Feature Integration, and Predictive Modelling, Comput. Chem. Eng., 2022, 160, 107739,  DOI:10.1016/j.compchemeng.2022.107739.
14. R. W. Tilford, S. J. Mugavero, P. J. Pellechia and J. J. Lavigne, Tailoring Microporosity in Covalent Organic Frameworks, Adv. Mater., 2008, 20, 2741–2746,  DOI:10.1002/adma.200800030.
15. P. Kuhn, M. Antonietti and A. Thomas, Porous, Covalent Triazine-Based Frameworks Prepared by Ionothermal Synthesis, Angew. Chem., Int. Ed., 2008, 47, 3450–3453,  DOI:10.1002/anie.200705710.
16. J. S. De Vos, S. Ravichandran, S. Borgmans, L. Vanduyfhuys, P. Van Der Voort, S. M. J. Rogge and V. Van Speybroeck, High-Throughput Screening of Covalent Organic Frameworks for Carbon Capture Using Machine Learning, Chem. Mater., 2024, 36, 4315–4330,  DOI:10.1021/acs.chemmater.3c03230.
17. E. A. Bittner, K. Merkel and F. Ortmann, Engineering the Electrostatic Potential in a COF's Pore by Selecting Quadrupolar Building Blocks and Linkages, npj 2D Mater. Appl., 2024, 8, 58,  DOI:10.1038/s41699-024-00496-3.
18. C. Ding, X. Xie, L. Chen and A. Troisi, Intuitive and Efficient Approach to Determine the Band Structure of Covalent Organic Frameworks from Their Chemical Constituents, J. Chem. Theory Comput., 2024, 20, 1252–1262,  DOI:10.1021/acs.jctc.3c01302.
19. M. Tong, Y. Lan, Q. Yang and C. Zhong, Exploring the Structure-Property Relationships of Covalent Organic Frameworks for Noble Gas Separations, Chem. Eng. Sci., 2017, 168, 456–464,  DOI:10.1016/j.ces.2017.05.004.
20. Y. Kim and W. Y. Kim, Universal Structure Conversion Method for Organic Molecules: From Atomic Connectivity to Three-Dimensional Geometry, Bull. Korean Chem. Soc., 2015, 36, 1769–1777,  DOI:10.1002/bkcs.10334.
21. RDKit: Open-source cheminformatics. https://www.rdkit.org.
22. K. W. Jacobsen, et al., The Atomic Simulation Environment—A Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29, 273002,  DOI:10.1088/1361-648X/aa680e.
23. N. Huang, P. Wang and D. Jiang, Covalent Organic Frameworks: A Materials Platform for Structural and Functional Designs, Nat. Rev. Mater., 2016, 1, 16068,  DOI:10.1038/natrevmats.2016.68.
24. K. T. Tan, et al., Covalent Organic Frameworks, Nat. Rev. Methods Primers, 2023, 3, 1,  DOI:10.1038/s43586-022-00181-z.
25. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-Mechanical Condensed Matter Simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360,  DOI:10.1002/wcms.1360.
26. F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78,  DOI:10.1002/wcms.81.
27. F. Neese, Software Update: the ORCA Program System – Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606,  DOI:10.1002/wcms.1606.
28. M. Ernst, J. Hutter and S. Battaglia, Extensive Band Gap Tunability in Covalent Organic Frameworks via Metal Intercalation and High Pressure, J. Phys. Chem. Lett., 2025, 16, 7398–7405,  DOI:10.1021/acs.jpclett.5c01216.
29. S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J. L. Bredas, Electronic Structure of Two-Dimensional π-Conjugated Covalent Organic Frameworks, Chem. Mater., 2019, 31, 3051–3065,  DOI:10.1021/acs.chemmater.8b04986.
30. A. M. Pütz, M. W. Terban, S. Bette, F. Haase, R. E. Dinnebier and B. V. Lotsch, Total Scattering Reveals the Hidden Stacking Disorder in a 2D Covalent Organic Framework, Chem. Sci., 2020, 11, 12647–12654,  10.1039/D0SC03048A.
31. E. S. Grape, A. M. Davenport and C. K. Brozek, Dynamic Metal-Linker Bonds in Metal–Organic Frameworks, Dalton Trans., 2024, 53, 1935–1941,  10.1039/D3DT04164F.
32. M. Ernst and G. Gryn’ova, Strength and Nature of Host-Guest Interactions in Metal-Organic Frameworks from a Quantum-Chemical Perspective, ChemPlusChem, 2022, 23, e202200098,  DOI:10.1002/cphc.202200098.

---