Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phosphorus chirality assignment and solution dynamics of lanthanide(III) complexes of a monomethylphosphinate analogue of H4dota: a multinuclear NMR and DFT study
Adam
Svítok
 a,
Carlos
Platas-Iglesias
a,
Carlos
Platas-Iglesias
 b,
Jan
Kotek
b,
Jan
Kotek
 a and
Petr
Hermann
a and
Petr
Hermann
 *a
*a
aDepartment of Inorganic Chemistry, Faculty of Science, Charles University, Hlavova 2030, 12843 Prague 2, Czech Republic. E-mail: petrh@natur.cuni.cz; Tel: +420-22195-1263
bUniversidade da Coruña, Centro Interdisciplinar de Química e Bioloxía (CICA) and Departamento de Química, Facultade de Ciencias, 15071, A Coruña, Galicia, Spain
First published on 6th November 2025
Abstract
Analogues of H4dota form kinetically inert and thermodynamically stable complexes with lanthanide(III) ions and they are used in many applications in biology and medicine, mostly as imaging or therapeutic agents. Many properties of the complexes depend on their solution isomerism and dynamics which, however, have not been so thoroughly studied for ligands with phosphinate-containing pendant arms. In particular, the absolute chirality of the phosphorus atom in the diastereoisomers detected in solution by NMR has not been assigned until now, and coordinated-noncoordinated oxygen atom exchange, a process analogous to the “phosphonate rotation” in phosphonate-containing derivatives, was not studied. Here, a model H4dota analogue with one methylphosphinate group was prepared, and its LnIII complexes were studied by multinuclear (1H, 13C, 17O, 31P) NMR and DFT calculations in solution and by X-ray diffraction in the solid state. Chiral pentavalent tetrahedral phosphorus atoms are present in a number of phosphorus acid derivatives. Here, we present the first method to determine the absolute P-chirality in solution using the paramagnetic relaxation enhancement (PRE) of 13C NMR signals of the YbIII complex. The method allowed the assignment of two major diastereoisomers of the complexes as R-Λλλλλ/S-Δδδδδ (v-TSA, vertical twisted-square antiprism) and R-Λδδδδ/S-Δλλλλ (v-SA, vertical square antiprism). The assignment agrees with the solid-state structure and DFT calculations. This method enables absolute P-chirality determination in LnIII complexes of various phosphorus acid H4dota analogues in solution and can be also applied to other rigid systems. The “phosphinate rotation” process was observed by 17O/1H–1H EXSY NMR only for large LnIII ions and only in the TSA isomers. Its mechanism is analogous to that of the “phosphonate rotation” investigated recently on complexes of the mono(phosphonate monoester) H4dota analogue, but the “phosphinate rotation” is more sterically demanding in complexes of smaller lanthanide(III) ions due to the higher bulkiness of the methyl group compared with the oxygen in the ester derivatives.
Introduction
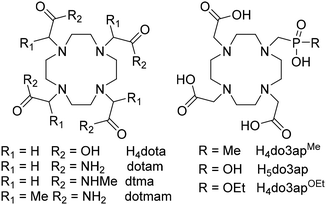
Lanthanide(III) complexes of macrocyclic ligands derived from H4dota (1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid, Fig. 1) are usually kinetically inert and thermodynamically stable. These properties efficiently decrease their in vivo toxicity, leading to many biological/medicinal applications. Thus, they are used as gadolinium(III)-based MRI contrast agents (MRI CA's),1–6 carriers of metal radioisotopes for imaging and therapy,5,7–9 fluorescence probes,5,6,10–12 or as protein paramagnetic tags.13–15 Over the years, investigations of various properties of LnIII complexes of this type of ligands have led to a better understanding of the chemistry and physics behind these applications.The properties of these complexes, important for the applications mentioned above, depend on their solution isomerism. In the complexes, the LnIII ions are sandwiched between the N4-plane formed by the cyclen nitrogen atoms and the O4-plane defined by the oxygen atoms of the coordinating pendant arms.16,17 This coordination leads to two diastereoisomers differing in the conformations of the macrocycle and pendant five-membered chelate rings. Thus, a combination of two possible macrocycle chelate ring configurations, δδδδ and λλλλ, and two possible pendant arms orientations, Δ and Λ, gives two diastereoisomers traditionally labelled as twisted-square antiprism (TSA) and square antiprism (SA). Each diastereoisomer consists of an enantiomeric pair (Δδδδδ/Λλλλλ for TSA and Λδδδδ/Δλλλλ for SA). In addition, an apically coordinated water molecule may be present above the O4-plane, leading to the coordination number nine (CN 9) for large LnIII ions. If the complexes are non-aquated (i.e., having CN 8), the isomers are labelled as TSA′ and SA′, respectively. The abundance of the isomers in solution depends on LnIII size and ligand structure.16,17 The TSA arrangement is preferred by large LnIII ions and bulky H4dota derivatives as the ligand cavity in the TSA isomer is larger and more flexible than that of the SA isomer. In solution, the TSA/SA isomers are in a mutual dynamic exchange proceeding on a millisecond time scale.16,18 The TSA/SA diastereoisomers interchange by inverting the macrocycle chelate ring conformations or by re-orienting the pendant arms. A combination of both movements forms the other enantiomer of the diastereoisomer. Another dynamic process, an exchange between coordinated and non-coordinated carboxylate oxygen atoms of H4dota, was observed by 17O NMR, and it also happens on a millisecond time scale.19–22 This “carboxylate rotation” exchanges the oxygen atoms without the SA/TSA interchange.
Carboxylate group(s) in H4dota may be replaced with acidic moieties derived from phosphoric, phosphonic or phosphinic acid groups. Gradual substitution of carboxylates with bulkier phosphorus acid groups increases the TSA abundance in solution,23–28 and LnIII complexes of tetraphosphorus acid H4dota analogues occur only as the TSA isomers over the whole lanthanide series.29–32 If an oxygen atom of a tetrahedral phosphinate or phosphonate monoester groups is coordinated to a metal ion, the phosphorus atom become chiral (R/S), leading to more diastereoisomers due to the combination of three chirality elements. Thus, LnIII complexes of H4dota analogues with only one phosphinic acid/phosphonic monoester group have a maximum of four diastereoisomers (i.e. four enantiomeric pairs), R/S-SA and R/S-TSA. A full set of diastereoisomers is observed in complexes of H4dota derivatives with phosphonate monoesters (having the P–OR bond) or phosphinates containing P–H/P-aryl bonds.33–36 For compounds with P-alkyl bonds, one phosphorus atom configuration is highly preferred which lowers the number of the observed diastereoisomers; a single diastereoisomer is detected for complexes of tetraphosphinate H4dota analogues.31,32,35,36 Commonly, all isomers interchange but this isomerism in complexes of the phosphorus acid derivatives has not been studied in detail. Recently, we have studied these exchange processes on LnIII complexes of monophosphorus acid analogues of H4dota, H5do3ap and H4do3apOEt (Fig. 1), by multinuclear NMR spectroscopy and DFT calculations.37,38 In the complexes of H5do3ap, the pendant arm rotation (i.e., the Λ/Δ exchange) was found to be faster than the macrocycle chelate ring inversion (i.e., the λλλλ/δδδδ exchange), and the pendant arm movement was suggested to involve a transient bidentate κ2-O,O′-PO2 coordination of the phosphonate group.38 This coordination mode was later confirmed in a transition state for the mutual exchange of coordinated/uncoordinated oxygen atoms of the chiral phosphonate monoester group (“phosphonate rotation”) of H4do3apOEt by multinuclear (1H, 17O and 31P) NMR investigations and DFT calculations.37 However, the absolute R/S configuration of the phosphorus atom in individual diastereoisomers could not be determined.
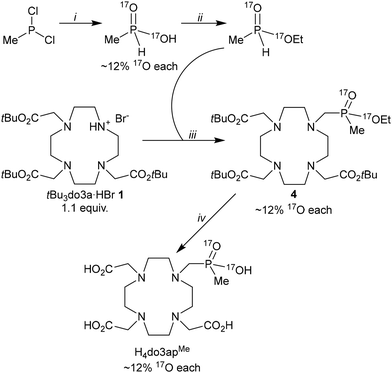
As mentioned above, one P-configuration is preferred in the complexes of phosphinate H4dota analogues with P-alkyl substituents.25,27,31,32,35,36 However, there has been no method suggested for determination of the absolute P-configuration of the diastereoisomer until now. Moreover, labelling the phosphinate group with 17O in a monophosphinate H4dota derivative offers a possibility to investigate the dynamics of the complexes analogously to the mono(phosphonate monoester) ligand.
Different pentavalent phosphorus acid derivatives (phosphoric acid esters, sulfur or nitrogen derivatives etc.) can also contain a chiral tetrahedral phosphorus atom. These compounds are inherently chiral or become chiral after their coordination to a metal ion (e.g. in an enzyme active site) if they contain the (>PO2)− fragment. They are present in nature and their biological behaviour (e.g. ester hydrolysis) often depends on the phosphorus atom chirality.39–42 However, a direct experimental determination of their absolute P-configuration in solution is problematic.
In this work, we present a new method for the determination of the absolute configuration of the coordinated phosphorus atom in compounds with a tetrahedral phosphoryl group. Thus, we prepared the 17O-labelled mono(methylphosphinic acid) derivative H4do3apMe (Fig. 1) and its LnIII complexes, and we investigated the complexes by multinuclear NMR and DFT calculations. Activation parameters for the coordinated/non-coordinated oxygen atoms exchange of the (>PO2)− group, “phosphinate rotation”, were determined for the H4do3apMe complexes and compared with those of the “phosphonate rotation” in the H4do3apOEt complexes. Identifying the preferential orientation of the phosphorus atom substituent(s) in the complexes can be useful to fine tuning the physico-chemical properties of the macrocyclic complexes. Furthermore, the (κ2-PO2)− coordination mode of the tetrahedral oxophosphorus groups, involved in the isomer interconversion, has been only sparingly experimentally or theoretically investigated.43–46 Thus, the data presented here also contribute to a fundamental understanding of the coordination behaviour of the tetrahedral phosphorus acid anions.
For clarity reasons, in the following text and in the SI, the coordinated water molecule is omitted in all formulae, labels and pictures, and the complexes are denoted with general formulae [Ln(ligand)]n−.
Results and discussion
Synthesis of ligands and complexes
The non-labelled ligand H4do3apMe was prepared by a phospha–Mannich reaction of a macrocyclic precursor, tBu3do3a·HBr, with isopropyl methyl-H-phosphinate in anhydrous pyridine, catalysed by one equivalent of HBr. This procedure avoids the use of oxidation-prone free methyl-H-phosphinic acid in the Moedritzer–Irani variant47 of the phospha–Mannich reaction in aqueous HCl. Next, the esters were hydrolysed to afford H4do3apMe in an overall 73% isolated yield (based on tBu3do3a·HBr). It should be mentioned that the use of methyl or ethyl esters of methyl-H-phosphinic acid in the reaction led to significantly lower yields due to the competing reductive N-methylation of tBu3do3a (coupled with the P–H bond oxidation) and phosphinic ester hydrolysis (see also below). The 17O-enriched H4do3apMe was prepared (Scheme 1) by a multi-step synthesis incorporating 17O in the first step, as the phosphinate group cannot be enriched by heating with H217O in acidic solutions, unlike the carboxylate group.48 Methyl-dichlorophosphine was hydrolysed by 17O-enriched water (approx. 12% 17O) to get the 17O-enriched methyl-H-phosphinic acid. To preserve the 17O isotope in the structure, the acid was esterified by an alkylation with (Et3O)BF4 in the presence of 2,6-lutidine as a weak base to prevent an alkylation of the phosphorus atom.49 The 17O-enriched ethyl methyl-H-phosphinate reacted with the macrocyclic precursor, tBu3do3a·HBr, similarly to the non-labelled compound. Finally, the phosphorus ester groups were removed by TMS-Br, preserving the 17O-labelling,50 and the tBu groups were cleaved by anhydrous TFA. The overall isolated yield of the 17O-labelled H4do3apMe was 17% (four steps; based on MePCl2). The low yield can be attributed to the low stability of the required 17O-labelled ethyl H-phosphinate precursor, which is caused mainly by oxidation of the P–H bond (connected with reductive N-methylation of tBu3do3a) and decomposition (ester hydrolysis) of the labelled ethyl methyl-H-phosphinate (see above). Lanthanide(III) complexes of H4do3apMe (both labelled and non-labelled) were prepared by reacting LnCl3 with a slight ligand excess in aqueous solutions to ensure that free LnIII ions were fully complexed in the final mixture. Solid-state structures of the unlabelled H4do3apMe ligand and the [Yb(do3apMe)]− complex were determined by X-ray diffraction and are discussed in SI and below (Fig. 5 and S1, S2).Phosphorus atom absolute configuration and diastereoisomer assignment
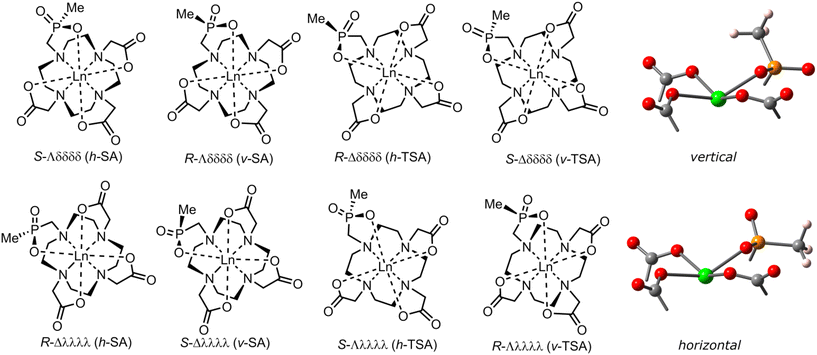
The [Ln(do3apMe)]− complexes form up to four diastereoisomers, each consisting of an enantiomeric pair, by a combination of the macrocycle chelate ring conformations δδδδ/λλλλ, the pendant arms orientations Δ/Λ (leading to the SA or TSA arrangements), and R/S configurations on the phosphorus atom of coordinated phosphinic group (Fig. 2). Here for the first time, it was possible to assign the absolute orientation of the phosphorus atom substituents and to distinguish the phosphorus-based isomers. In the following text, we will use abbreviations “v-TSA/v-SA” and “h-TSA/h-SA” where “v” and “h” denote “vertical” and “horizontal” positions of the P-substituents, respectively. In the “vertical” isomer, the phosphorus substituent is directed approximately perpendicularly to the O4 plane of the complex. In the “horizontal” isomer, the phosphorus substituent lies approximately horizontally to the O4 plane of the complex. Here, all four diastereoisomers could be detected by NMR but signals of two minor diastereoisomers were often unidentifiable due to a low signal intensity as a result of the low abundance of the isomers (Fig. S4–S9).In previous works on LnIII complexes of cyclen–phosphinate derivatives,25,27,31,32,35,36,51,52 their TSA/SA geometry in solution was easily assigned by their 1H NMR spectra. However, it was impossible to determine the orientation of the phosphorus atom substituent (i.e., the R/S configuration). For a better interpretation of experimental and computational data here (see below), it is advantageous to assign the R/S configuration on the phosphorus atom in each diastereoisomer of the [Ln(do3apMe)]− complexes. Thus, we analysed the lanthanide-induced paramagnetic relaxation enhancement (PRE) effect on the 13C NMR signals to determine experimentally the P-substituent orientation in the different diastereoisomers. For the experiment, the [Yb(do3apMe)]− complex was selected due to the abundance of only one major diastereoisomer (either h-TSA′, or v-TSA′), its slow dynamics and the knowledge of its solid-state structure (see below). Theoretically, complexes of any paramagnetic LnIII might be used but those with a larger PRE are preferred. Here, the YbIII complex was selected due to the difficulty of assigning NMR signals in complexes of LnIII ions with larger PRE (for details, see Experimental part).
Structures of the diastereoisomers were calculated by DFT and are shown in Fig. 3. The distances between the methyl carbon atom and the YbIII ion, determined by the DFT calculations, differ significantly between the h-TSA′ and v-TSA′ diastereoisomers (4.75 vs. 4.40 Å, respectively) and, thus, can be used to unambiguously assign the diastereoisomers. The distances determined from the 13C NMR relaxation times (Table S3), by DFT calculations and by X-ray diffraction are given in Table 1. The 13C PRE method was first tested by determination of the distances between YbIII ion and the easily assignable (Fig. S10 and the accompanying text) carboxylate 13C atoms. The distances found in the solid state, determined by DFT calculations and by the PRE method, are all in good agreement. Then, the same comparison was done for the P-bound methyl carbon atom; its 13C NMR signal was assigned by a selective 1H decoupling (Fig. S11). The experimental H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb distance determined by 13C PRE is close to that found/calculated for the R-Λλλλλ/S-Δδδδδ, vertical-TSA (v-TSA), diastereoisomer (Fig. 3).
⋯Yb distance determined by 13C PRE is close to that found/calculated for the R-Λλλλλ/S-Δδδδδ, vertical-TSA (v-TSA), diastereoisomer (Fig. 3).
 | ||
| Fig. 3 The DFT-calculated structures of the v-TSA′ (A) and h-TSA′ (B) diastereoisomers of [Yb(do3apMe)]−; colour code: carbon – grey, hydrogen – white, nitrogen – blue, oxygen – red, phosphorus – orange and ytterbium – green. Hydrogen atoms, except those at the methyl group, are omitted for clarity. Visualised in VESTA software.53 | ||
| Isomer/method | Distances, Å | |||
|---|---|---|---|---|
| d 1(OC⋯Yb) | d 2(OC⋯Yb) | d 3(OC⋯Yb) | r(H3C⋯Yb) | |
| R-Λλλλλ/S-Δδδδδ v-TSA′ (X-ray) | 3.17 | 3.13 | 3.09 | 4.31 |
| R-Λλλλλ/S-Δδδδδ v-TSA′ (DFT) | 3.15 | 3.14 | 3.13 | 4.40 |
| S-Λλλλλ/R-Δδδδδ h-TSA′ (DFT) | 3.15 | 3.14 | 3.13 | 4.73 |
| PRE | 3.1 | 3.0 | 3.0 | 4.2 |
Previously, this method was used to determine the Tb/Dy/Ho⋯H distances in H4dota complexes.54 A similar method has been also used to determine the Ln⋯X distances. The Tb/Nd/Sm⋯H distances were determined in complexes of various ligands by comparing the paramagnetic relaxation times of different 1H atoms55–57 (see below) and Tb/Dy/Ho/Er/Tm/Yb⋯F/P distances were determined from paramagnetic T1,M relaxation times determined at multiple magnetic fields.58,59 Moreover, Gd⋯Y/C distances were obtained using only the T1,M of 89Y shortened by GdIII, which is possible due to the magnetic properties of the GdIII ion.60
The PRE method has some advantages and limitations. It might be generally applied to determine Ln⋯X distances in compounds where “X” is a non-quadrupolar NMR-active nucleus and various paramagnetic lanthanide(III) ions can be used. The complex or system should be (semi)rigid on NMR time scale. In chemistry of macrocyclic complexes, the method may be used to define diastereoisomers, to assign NMR signals or to determine the solution structure. In biochemistry, it could be used if the compound of interest is locked (e.g. inside a peptide) and the paramagnetic probe is bound at such a distance that PRE of the “X” nucleus is measurable. The main advantage of using lanthanide-induced relaxation is its independence on the position/orientation of the magnetic axis of the complex, unlike lanthanide-induced shifts (LIS).61
The method utilizing the difference between relaxation rates R2 and R1, presented here, could be used for these purposes with the advantage of not requiring multiple magnetic fields, the knowledge of some Ln⋯X distance or a large distance from the LnIII ion in the case of GdIII. However, it requires determination of the T2 relaxation time and the rotational correlation time τR. Nowadays, the method may be used in the rapidly growing field of 19F MRI, where the Ln⋯19F distance is one of the most important parameters of potential contrast agents. Due to the long T1 relaxation times of 19F, paramagnetic relaxation enhancement of 19F is advantageous and complexes of various LnIII are studied for this purpose. Both T1 and T2 of 19F MRI in these contrast agents strongly depend on the Ln⋯19F distance which affects the 19F MRI signal intensity and contrast.
The H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb distance can also be determined from the ratio of paramagnetically enhanced R1M relaxation rates of the carbonyl and methyl carbon atoms (Table S3). Average values of d(H3
⋯Yb distance can also be determined from the ratio of paramagnetically enhanced R1M relaxation rates of the carbonyl and methyl carbon atoms (Table S3). Average values of d(H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb) = 4.40 and 4.45 Å were determined at 0 °C and 5 °C, respectively, assigning the shorter distances to the faster relaxation rates. These values agree well with the H3
⋯Yb) = 4.40 and 4.45 Å were determined at 0 °C and 5 °C, respectively, assigning the shorter distances to the faster relaxation rates. These values agree well with the H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb distance in the vertical R-Λλλλλ/S-Δδδδδ (v-TSA) diastereoisomer (Table 1).
⋯Yb distance in the vertical R-Λλλλλ/S-Δδδδδ (v-TSA) diastereoisomer (Table 1).
The R-Λλλλλ/S-Δδδδδ (v-TSA) isomer is also energetically favoured by DFT calculations, being ∼4 kJ mol−1 lower in energy at 25 °C (Table S4) over the entire LnIII series. Based on 1H and 31P NMR spectra (Fig. S4–S6), the major diastereoisomers have the same phosphorus configuration for all [Ln(do3apMe)]− complexes. The h/v-SA diastereoisomers were assigned based on 1H–1H EXSY of the EuIII complex which distinguishes macrocycle inversion from pendant arms re-orientation. The major v-TSA diastereoisomer interchanges with the major SA diastereoisomer by macrocycle inversion (see Fig. 6 below). Thus, the major SA diastereoisomer must be the vertical-SA (v-SA). Based on DFT, the v-SA is also the energetically favoured SA diastereoisomer for all complexes (Table S4).
By comparing the relative 1H chemical shifts with those of the [Ln(do3apOEt)]− complexes studied previously (Fig. 4),37 the major SA diastereoisomer is the same, vertical-SA (v-SA), as for the title phosphinate complexes but the major TSA diastereoisomer is the other one: horizontal-TSA (h-TSA). This correlates with 1H–1H EXSY data, which showed that the major TSA and SA diastereoisomers of the H4do3apOEt complexes interchange by pendant arms re-orientation,37 unlike the major diastereoisomers of [Ln(do3apMe)]−. Thus, if the major SA isomer of [Ln(do3apOEt)]− is the v-SA, the major TSA diastereoisomer of [Ln(do3apOEt)]− must be the h-TSA.37
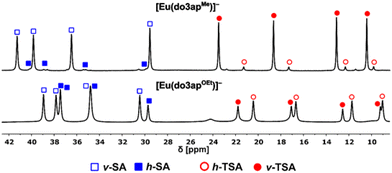 | ||
| Fig. 4 A comparison of 1H NMR spectra of the axial protons of [Eu(do3apMe)]− (top) and [Eu(do3apOEt)]− (bottom, data from ref. 37) complexes at 5 °C and ν(1H) = 600 MHz. | ||
For the [Ln(do3apMe)]− complexes, abundances of the SA/TSA diastereoisomers were determined from relative intensities (as the sum of the v-SA + h-SA and v-TSA/v-TSA′ + h-TSA/h-TSA′ signal integrals, respectively) of their 1H and 31P NMR signals at 5 °C (Fig. S13). The abundances depend on the LnIII size similarly to complexes of other H4dota derivatives – SA abundance increases with decreasing LnIII size to DyIII and then decreases after this LnIII ion. The trend originates from a smaller ligand cavity of the SA isomers vs. TSA isomers and from an even smaller ligand cavity of the TSA′ isomers, better accommodating the smallest LnIII ions.24,62 Energies determined by DFT also follow this trend (Table S4). Analogously to the [Ln(do3apOEt)]− complexes, the abundances of the TSA diastereoisomers increase with a higher temperature but ratios of the vertical/horizontal diastereoisomers remain nearly constant for all v/h-TSA, v/h-SA and v/h-TSA′ pairs at all measured temperatures (Fig. S13 and Table S5). Moreover, the relative ratios of vertical/horizontal diastereoisomers are independent of LnIII ions, and they are approximately 96%, 90% and 95% for v-SA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h-SA, v-TSA
h-SA, v-TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h-TSA and v-TSA′
h-TSA and v-TSA′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h-TSA′ ratios, respectively (Table S6). Based on DFT, these ratios slightly vary, but the calculated energy differences are negligible, especially when compared with calculated differences in the TSA/SA ratio (Fig. S4). For the [Ln(do3apOEt)]− complexes, these ratios are also independent of LnIII and temperature but the mixtures contain only approximately 65% of the major diastereoisomer (v-SA, h-TSA or h-TSA′) for all of v-SA
h-TSA′ ratios, respectively (Table S6). Based on DFT, these ratios slightly vary, but the calculated energy differences are negligible, especially when compared with calculated differences in the TSA/SA ratio (Fig. S4). For the [Ln(do3apOEt)]− complexes, these ratios are also independent of LnIII and temperature but the mixtures contain only approximately 65% of the major diastereoisomer (v-SA, h-TSA or h-TSA′) for all of v-SA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h-SA, h-TSA
h-SA, h-TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v-TSA and h-TSA′
v-TSA and h-TSA′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v-TSA′ ratios.37 Accordingly, energy differences of diastereoisomers in these pairs calculated by DFT are minimal for [Ln(do3apOEt)]− and do not even allow for predicting the more stable phosphorus configuration (Fig. S4). Thus, the character and abundance of major diastereoisomeric species in solution differ for various phosphorus substituents. This agrees with previous studies of solutions of complexes of tetraphosphorus H4dota derivatives (see below).
v-TSA′ ratios.37 Accordingly, energy differences of diastereoisomers in these pairs calculated by DFT are minimal for [Ln(do3apOEt)]− and do not even allow for predicting the more stable phosphorus configuration (Fig. S4). Thus, the character and abundance of major diastereoisomeric species in solution differ for various phosphorus substituents. This agrees with previous studies of solutions of complexes of tetraphosphorus H4dota derivatives (see below).
To gain more insight on the influence which the nature of P-substituent has on the relative energy of the isomers, we carried out additional DFT calculations on [Eu(do3apR)]− complexes, where R = H (the smallest substituent, a full isomer set is generally observed in solution) or the unknown analogue with R = tBu (a bulky substituent; a preference for the vertical isomer is expected). The relative energies of the isomers in this series of phosphorylated derivatives (R = H, OEt, Me and tBu) were subsequently compared. If the P-bound atom/group is small (R = H or OEt), the energy differences between the vertical and horizontal isomers are small (∼1 kJ mol−1), with the lowest-energy isomers being the horizontal ones. For bulkier groups (R = Me or tBu), the differences were more significant (∼3–8 kJ mol−1) and these differences were more pronounced for the bulky tBu group. The vertical isomers were strongly preferred for the latter complexes, indicating that steric requirements probably impose the isomer preferences.
Solid-state structures
The solid-state structures of the [Yb(do3apMe)]− and [Yb(do3apOEt)]− complexes (Fig. 5) were studied to determine the phosphorus atom configuration and compare the structures with the solution data (Fig. S3 and Table S1). The solid-state structure of [Li(H2O)3][Yb(do3apMe)]·H2O contains two complex enantiomers R-Λλλλλ and S-Δδδδδ corresponding with the v-TSA′ isomer while the [Li(H2O)3][Yb(do3apOEt)]·H2O structure contains the two enantiomers S-Λλλλλ and R-Δδδδδ corresponding with the h-TSA′ isomer, analogously to the h-TSA′ isomers of the [Ho/Er(do3apOEt)]− anions found in the solid state previously.37 The trans-O-Yb-O opening angles of 119.7° and 130.1° for [Yb(do3apMe)]−, and of 121.5° and 129.4° for [Yb(do3apOEt)]− are lower than the limiting value of ∼135° for the TSA isomers to accommodate a coordinated water molecule.24,63,64 Thus, the structures are better labelled as v/h-TSA′, which is further supported by the twist angles between the O4 and N4 planes of 26.2–27.4° and 27.6–28.9° for [Yb(do3apMe/OEt)]−, respectively.24,63,64 The v-TSA′ and h-TSA′ diastereoisomers found for the [Yb(do3apMe/OEt)]− complexes, respectively, correspond to the major diastereoisomers observed in solutions of these complexes (see above) and with the major diastereoisomers predicted by DFT (Table S4).The solid-state structures of complexes of H4dota derivatives with one (4-nitro-benzyl)- or (dibenzylamino)methyl-phosphinate pendant arm also contain only the v-TSA isomer.27,64,65 In solution, LnIII complexes of these and all other monophosphinic acid H4dota analogues (DO3APR ligands) have only one major TSA diastereoisomer (>95%), similarly to the title [Ln(do3apMe)]− complex.25,27,60,66 Complexes of tetra(alkylphosphinic acid) H4dota analogues (DOTPR ligands, R = Me, Et, Bn, CH2OH etc.) were found in the solid state also exclusively as the v-TSA isomers31,32 and only one major TSA diastereoisomer was observed for their complexes in solution.31,32,35,36,51,67 On the other hand, complexes of ligands with phenyl–phosphinate, H-phosphinate or phosphonate monoester pendants contain the h-TSA species33,35,37,68 or a mixture of v-TSA and h-TSA isomers35 in their solid-state structures. Similarly to the [Ln(do3apOEt)]− complexes,26,37 solutions of complexes of these ligands always contain a mixture of all possible diastereoisomers, i.e., four h/v-SA and h/v-TSA isomers. For complexes of these tetraphosphorus acid derivatives, mixtures of diastereoisomers have been observed (up to eight isomers; they are only present as TSA species).33–36
Comparison of the solid-state structures with the solution isomer speciation allows a general assessment of about the influence of the P-substituents in phosphorus acid pendant arms of polyaza-macrocyclic ligands on the stereochemistry of their complexes. Preferential orientation of the phosphorus atom substituents and, thus, abundances of diastereoisomers of the complexes depend on the substituents, and two types of substituents can be distinguished. (i) Phosphinate groups with P-alkyl substituents form predominantly complexes with the “vertical” orientation of the substituent(s) in both TSA/SA species. This leads to two major diastereoisomers (in sum >95%), v-TSA and v-SA, for the LnIII complexes of DO3APR derivatives and to one major (>90%) v-TSA diastereoisomer for complexes of DOTPR derivatives, as all phosphorus atoms have the same configuration. (ii) Phosphonate monoester groups, or phosphinates substituted with a phenyl group or with a P–H bond (R = OR′, aryl, H) form complexes which are present in solution as a mixture of (all) possible diastereoisomers. Complexes of these DO3APR derivatives exhibit two major diastereoisomers (approx. 60–70%) in solution. The relatively low excess of the major isomers agrees well with DFT calculations (Table S4) as relative energy differences between all isomeric complexes of H4do3apOEt are smaller than relative energy differences between isomers of H4do3apMe complexes. Based on the data above and those in the literature, we can state that major isomers of complexes of these DO3APR derivatives should have the h-TSA and v-SA arrangements. For complexes of DOTPR ligands with these P-substituents (forming only the TSA isomers), up to all eight possible phosphorus-based diastereoisomers have been observed in solution. In both categories, preference for the phosphorus atom configuration does not depend on the size of LnIII ions (see also above).
The configuration on the coordinated phosphorus acid groups induced by the character of the P-substituents can also be extended to complexes of other trivalent metal ions with tris-phosphorus acid analogues of H3nota; these hexacoordinated complexes exhibit stereochemistry analogous to the SA/TSA isomerism of H4dota complexes and contain chiral phosphorus atoms. In the solid state, they have an SA-like combination of ring- and pendant arm-based chiralities (Δλλλ/Λδδδ). The solid-state structures of FeIII, CoIII, GaIII and InIII complexes with tris(phenyl-phosphinic acid) analogue of H3nota have three vertical P-substituents, in agreement with the preferences given above for the SA isomers.69 Similarly, the GaIII complex of the ligand with R = CH2CH2CO2H has three vertical P-substituents in the solid state.70 However, in solution, gallium(III) complexes of tris(R-phosphinic acid) H3nota analogues with R = CH2CH2CO2H or CH2OH are present as one major (>90%) isomer but the complex of the ligand with R = H has at least four diastereoisomers.70,71 Thus, phosphorus stereochemistry in complexes of macrocyclic ligands controlled by the P-substituents seems to be a general phenomenon and might be used for a prediction of the phosphorus-based stereochemistry in systems where a detailed analysis suggested here cannot be carried out.
Dynamic processes
Dynamic processes were investigated on the [Eu(do3apMe)]− complex whose EXSY spectra are measurable and evaluable due to the relatively low PRE of the EuIII ion. Signals of the axial (ax) protons (for their definition, see SI in ref. 37) were assigned by analogy with the [Eu(dota)]− and [Eu(do3ap)]2− complexes.38,72 Signals of the equatorial (eq) protons were assigned by 2D 1H–1H EXSY (Fig. S15) and 1H–1H COSY (Fig. S16) experiments. In the 2D 1H–1H EXSY spectrum, cross-peaks relating the axial and equatorial protons of v-TSA/v-SA and h-TSA/h-SA pairs confirm the interchange by the macrocycle inversion. Cross-peaks of both axial or both equatorial protons of h-TSA/h-SA and v-TSA/v-SA pairs confirm exchange by the pendant arms re-orientation. Moreover, detected cross-peaks of h-TSA/v-TSA exchange correspond to a phosphinate rotation. Similarly to the phosphonate rotation in the [Eu(do3apOEt)]− complex,37 a phosphinate rotation interconverting h-SA/v-SA was not detected, as seen from the absence of cross-peaks of the axial h-SA/v-SA protons (Fig. 6).Next, rates of the dynamic processes were determined using 2D 31P–31P EXSY spectra (Fig. S17) as the signals of the isomers overlap in 2D 1H–1H EXSY spectra. The 1D 1H EXSY spectra applied for this purpose previously37,38 could not be used here due to the low signal intensities of the minor diastereoisomers. The rate constants for all processes were calculated from integral intensities of the cross- and diagonal peaks as averages at multiple mixing times (Table S7), and their values were checked by comparison of values of equilibrium constants calculated from these rate constants and from the 31P signal intensities (Table S8). To compare rates of the processes, values weighted by the isomer abundances were used (Table 2).
| Exchanging isomers | Processa | Rate constant k [s−1] for the [Eu(L)] complexes of the ligands | ||||||
|---|---|---|---|---|---|---|---|---|
| do3apMe | do3apOEt | Hdo3ap/do3apb | dota | dotamc | dtmac | dotmamc | ||
| a Process abbreviations: cycle = macrocycle inversion, arms = pendant arms re-orientation and phos = phosphinate/phosphonate rotation. b Data for monoprotonated (L = Hdo3ap) and deprotonated (L = do3ap, as dianion) complexes. c Rate constants were calculated from the published activation parameters. d Only one SA and one TSA isomer are present in these complexes containing non-chiral/no phosphorus atom. e The process is very slow. f Not applicable to this systems. | ||||||||
| h-TSA/h-SA | Cycle | 17.1 | 11.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
21.2/17.8d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 38 |
17.8d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 38 |
—e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
23d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
41d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
| v-TSA/v-SA | Cycle | 13.3 | 10.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
|||||
| h-TSA/v-SA | Arms | 1.73 | 32.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
24/83.3d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 38 |
9.1d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 38 |
592d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 75 |
172d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
—e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
| v-TSA/h-SA | Arms | 7.41 | 11.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
|||||
| h-TSA/v-TSA | Phos | 2.54 | 6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
—f | —f | —f | —f | —f |
The rate of macrocycle inversion for the [Eu(do3apMe)]− complex is approximately the same as for the EuIII complexes of other H4dota derivatives, consistent with the fact that macrocycle inversion is generally independent of the pendant arms substitution.73,74 However, the pendant arms re-orientation is slower than the macrocycle inversion in the [Eu(do3apMe)]− complex while it is faster in the complexes of derivatives with phosphonate groups or carboxamide pendant arms.37,38,75,76 Rate of pendant arms re-orientation is generally very sensitive to the pendant arms substitution, being the fastest for complexes with carboxamide pendant arms like DOTAM and slowed down with an increase in pendant arms bulkiness. Substitution on α-carbon atoms of pendant arm acetates completely halts the process. The pendant arms re-orientation rate in the [Eu(do3apMe)]− anion is the slowest among the complexes with non-α-substituted acetates which is likely caused by the steric requirements of the tetrahedral methyl group (if compared with an oxygen atom, e.g., in the phosphonate monoesters) and/or by different electronic effects of the electron-donating methyl group if compared with electron-withdrawing OH/OEt groups. This effect is likely similar to the decrease of pendant arms re-orientation rate by substituting the amine on carboxamide pendant arms, as seen by the drastic difference in the process rates between DOTAM and DTMA.75,76
Phosphinate rotation
The 1H–1H EXSY confirmed the phosphinate rotation interchanging v-TSA and h-TSA. Previously, two possible mechanisms not involving a decoordination of the phosphorus acid group were proposed:37 (i) Phosphorus group rotation changing only the phosphorus atom configuration, i.e., v-TSA/h-TSA or v-SA/h-SA interchange, and (ii) a simultaneous phosphorus group rotation and pendant arms re-orientation, i.e., h-TSA/h-SA or v-TSA/v-SA interchange. Based on the presence of cross-peaks between the v-TSA/h-TSA axial protons and the lack of the h-TSA/h-SA or v-TSA/v-SA axial protons cross-peaks in the 1H–1H EXSY spectrum of the EuIII complex (Fig. 4), the mechanism of phosphinate rotation is the same as that of phosphonate rotation, i.e., proceeding through a simple rotation of the phosphinate group changing the phosphorus atom configuration but preserving the pendant arms orientation.Furthermore, this mechanism was confirmed combining DFT calculations and variable-temperature (VT) 17O NMR (Table S4, Fig. S18 and S19). In principle, up to eight signals are observable by 17O NMR for the title complexes (signals of the coordinated and non-coordinated oxygen atoms of four diastereoisomers) but signals of different diastereoisomers are often indistinguishable due to mutual overlap. At low temperatures, signals of coordinated and non-coordinated oxygen atoms were well separated for all paramagnetic complexes. Signals of non-coordinated oxygen atoms, but not those of coordinated oxygen atoms, could be detected even for the GdIII complex, analogously to the GdIII complexes of H4dota and H4do3apOEt.22,37 Usually, NMR signals are undetectable for GdIII complexes due to the fast relaxation, with 17O NMR signals of non-coordinated oxygen atoms being the notable exception.22,37 With temperature increase, signals of coordinated oxygen atoms of different diastereoisomers coalesce first, and the same applies to signals of non-coordinated oxygens of different diastereoisomers. Then, the coordinated and non-coordinated phosphinate oxygen atoms, each represented by a coalesced signal consisting of up to four signals of different diastereoisomers, interchange with an increase in signal linewidths. These processes are detectable for complexes of LnIII ions larger than GdIII. Thus, the variable-temperature (VT) 17O NMR spectra were evaluated as an interchange between two equally populated sites, as the oxygen atoms of the same type (coordinated or non-coordinated) but originating from different diastereoisomers of the studied LnIII (La–Sm) complexes coalesce at a lower temperature than the lowest experimental temperature. The determined rate constants (Table S9) were used to calculate activation parameters with the Eyring equation (Table 3, Table S10 and Fig. S20). The 298ΔG‡ values for the phosphinate rotation have the same magnitude as that for the phosphonate rotation,37 pendant arms re-orientation and the macrocycle inversion38,74–83 in LnIII complexes of H4dota and its amide or phosphonate derivatives but they are much lower than those for the carboxylate rotation (Table S11).19,21 Activation energies increase with decreasing LnIII ion size, and the trend is similar for the phosphonate, phosphinate and carboxylate rotations (Fig. 7).19,21,37
 | ||
| Fig. 7 Activation free energies 298ΔG determined by VT 17O NMR or DFT for phosphinate/phosphonate rotation in the [Ln(do3apMe/OEt)]− complexes and for carboxylate rotation in [Ln(dota)]−. Data for the complexes of H4dota and H4do3apOEt were taken from literature.19,21,37 Lines are included only as guides for the eyes. | ||
| LnIII | [Ln(do3apMe)]−a | [Ln(do3apOEt)]−b | ||||
|---|---|---|---|---|---|---|
| 298ΔG‡ [kJ mol−1] | 298ΔG‡calc (TSA) [kJ mol−1] | k obs (5 °C) [s−1] | 298ΔG‡calc (SA)c [kJ mol−1] | 298ΔG‡ [kJ mol−1] | 298 G ‡calc [kJ mol−1] | |
| a This work. b Values from the literature (ref. 37). c Values for hypothetical h-SA/v-SA exchange. d It could not be determined due to the influence of TSA/SA exchange processes. e Value from 2D 31P–31P EXSY. f Exchange was not detected experimentally. g Value for hypothetical h-TSA′/v-TSA′ exchange. h Not calculated. | ||||||
| La | 57.7 | 28.8 | 2.52 × 105 | 37.8 | 51.8 | 52/36.0a |
| Ce | 50.9 | 31.9 | 1.60 × 103 | 41.2 | 52.9 | 55.6 |
| Pr | 54.3 | 37.4 | 3.68 × 102 | 45.6 | 55.7 | 58 |
| Nd | 56 | 42.7 | 1.77 × 102 | 49.7 | 57.1 | 61.2 |
| Sm | 63.5 | 49.6 | 6.89 | 58.3 | 64 | 69 |
| Eu | —d | 52.9 | 2.54e | 62.7 | 61 | 71.5/59.7a |
| Yb | —f | 107.8 (TSA′)g | —f | — | —f | —h |
Here, the activation energies of pendant arms re-orientation and the macrocycle inversion in complexes of large LnIII ions follow the same trend as in complexes of H4dota-like ligands, and are similar to those for the phosphinate rotation in the H4do3apMe complexes (Table S11).74,81 These trends are usually caused by an increase in charge density for the smaller LnIII ions but are much more profound for the phosphinate, phosphonate and carboxylate rotations due to steric effects. The LnIII ions are localised progressively deeper in the ligand cavity with the decreasing ion size,24,64 making their transition states with the κ2-PO2/κ2-CO2 bidentate binding progressively less favourable. While the phosphonate rotation was detected in [Ln(do3apOEt)]− complexes for La–Tb, the phosphinate rotation was observed in [Ln(do3apMe)]− complexes only for La–Eu (Table 3). The phosphinate rotation is also slower in the [Eu(do3apMe)]− complex than in the [Eu(do3apOEt)]− anion based on 1H–1H EXSY data (Table 2). This is likely due to the same steric effect as the decrease in the rate of pendant arms re-orientation if comparing re-orientation in the [Eu(do3apOEt)]− complex and that in other EuIII complexes (see above). The comparison also indicates that the P-methyl group with a “branched” –CH3 group is bulkier than the phosphonate group(s) where the first phosphorus-bound atom is a “non-branched” oxygen atom. However, the activation free energies of both rotations are nearly the same in complexes of LaIII–SmIII ions. Thus, the steric effect of the phosphorus substituent seems to affect the processes only if the LnIII ion is localised deeper in the ligand cavity.
The phosphinate rotation was confirmed by DFT calculations. Relative energies of all diastereoisomers of complexes of large LnIII ions and of the YbIII ion, energies of the corresponding transition states for the exchanges between h-SA/v-SA and h-TSA/v-TSA were calculated (Table S4). The calculated activation Gibbs energies for the v-TSA/h-TSA exchange are shown in Fig. 7 and Table 3, and they agree with the trend in experimental values determined from VT 17O NMR, but are somewhat lower. This is likely due to the difficulties of modelling solvent effects by DFT using polarized continuum models. In particular, our calculations appear to over-stabilize the transition state responsible for the v-TSA/h-TSA exchange, which displays a bidentate κ2-PO2 coordination. This group is probably forming rather strong hydrogen bonds with water molecules in solution. These directional interactions are not well described by PCM,84 resulting in an overestimation of the interaction between the metal ion and the bidentate κ2-PO2 group. These limitations of PCM were evidenced previously while investigating the rotation of acetate groups in DOTA derivatives.19
The theoretical activation energies for the v-SA/h-SA exchange are higher than those for the v-TSA/h-TSA exchange for all LnIII ions. This, together with the absence of cross-peaks corresponding to this exchange in 1H-1H EXSY spectrum of the EuIII complex, shows that the v-SA and h-SA isomers do not interconvert by phosphinate rotation. The same behaviour was observed for the phosphonate rotation in the [Ln(do3apOEt)]− complexes.37 Based on the experimental data, the phosphinate rotation was also not detected for the “anhydrous” v-TSA′/h-TSA′ isomers, in line with the very large theoretical value of 298G‡calc = 107.8 kJ mol−1 calculated for this process. Thus, the phosphinate rotation was confirmed only in the TSA diastereoisomers of the [Ln(do3apMe)]− complexes for Ln = La–Eu. The phosphinate rotation proceeds by a mechanism analogous to that of the phosphonate rotation, and both exchange processes have similar rates.
In the complexes investigated here, all isomers are in a dynamic equilibrium and pure isomers cannot be present in solution. Thus, properties of an individual isomer cannot be directly determined. However, even a small abundance of one isomer can influence the macroscopic properties of such complexes in solution. A classical example of this behaviour is the different water exchange dynamics of the SA and TSA isomers of DOTA derivatives which influences their properties as MRI CA's.16,75,76 For the vertical/horizontal isomers, the structures of the first coordination sphere are very similar each other, according to the X-ray data, but differences in the second hydration sphere may be expected. This is relevant for the design of MRI CAs. Thus, we performed DFT calculations with one coordinated and four second-sphere water molecules for all four isomers of the [Gd(H2O)(do3apMe)]− complex. The calculations showed (Fig. S21) that the second-sphere water molecules are more ordered in both horizontal isomers. The GdIII coordinated water distance, Gd–Ow, is similar in both SA isomers (2.583 and 2.617 Å for v-SA and h-SA, respectively) but significantly different in the TSA isomers (2.718 and 2.629 Å for v-TSA and h-TSA, respectively). Thus, the v-TSA isomer might exchange the coordinated water molecule significantly faster than the other isomers. On the other hand, the more ordered second-sphere hydration in the horizontal isomers might influence the bulk water relaxation or fluorescence quenching more than that in vertical isomers. To test these hypotheses, complexes with a defined configurationally stable arrangement on phosphorus atom(s) have to be prepared. This can be, in principle, achieved with optically active phosphine oxide pendant arm(s), or perhaps by locking a given configuration of the complex by ligand C-functionalization.85
Conclusions
In this work, we introduced a new method for the determination of the absolute configuration on a chiral tetrahedral phosphorus atom in solution. The method is suitable for rigid systems and a paramagnetic metal has to be used as probe/label. A combination of DFT calculations and 13C PRE allows identification of the location of the substituents on the phosphorus atom. Here, the defined spatial arrangement was assured by a coordination of the phosphorus group to a metal ion. In general, the method can be used for other (semi)rigid complexes/systems where the Ln⋯X distances in solution are fixed and the necessary NMR data can be obtained in a presence of the paramagnetic probe located at a close distance to alter the relaxation times of the measured nucleus. In principle, the method might be used in systems with any paramagnetic LnIII ion as a probe and for atoms of any non-quadrupolar NMR-active nuclei.The lanthanide(III) complexes of the title ligand, H4do3apMe, can be present as four diastereoisomers. All expected diastereoisomers v-TSA, h-TSA, v-SA and h-SA were identified, but with a low abundance of the minor diastereoisomers, h-TSA and h-SA. The method presented here enables us to assign the observed NMR signals to the vertical/horizontal diastereoisomers for complexes of this type for the first time. Thus, they were experimentally attributed by determining the distances between the YbIII ion and the P-bound methyl 13C atoms in the [Yb(do3apMe)]− complex from NMR data. These distances were compared with those obtained by DFT calculations and X-ray diffraction data. Through comparison with previously published data, the orientation of a phosphorus substituent in complexes of other phosphorus acid H4dota analogues was also assigned.
Isomerism and dynamics of LnIII complexes of H4do3apMe, were investigated by multinuclear NMR and DFT calculations. The diastereoisomers are in mutual exchange, observable by NMR. The interchange of the diastereoisomers was confirmed by 1H–1H EXSY experiments and proceeds by the expected processes, i.e., pendant arms re-orientation, macrocycle inversion and phosphinate rotation. The phosphinate rotation is fully analogous to the recently reported phosphonate rotation, but it was confirmed for a phosphinate group for the first time here. The phosphinate and phosphonate rotations proceed by analogous mechanisms through an intermediate with bidentate κ2-PO2 coordination. Based on VT NMR and DFT calculations, the phosphinate rotation occurs only in complexes of large LnIII ions (LaIII–EuIII) and only in diastereoisomers with TSA geometry, analogously to the monophosphonate complexes. The data point to somewhat higher bulkiness of the P–CH3 moiety compared with a phosphonate monoester fragment, P–O–R. Thus, on the basis of our data, a prediction on isomer preferences in complexes of macrocyclic ligands is now possible. For instance, in complexes of phosphinate H4dota derivatives, the very bulky phosphorus substituent should induce an exclusive preference for the vertical isomers.
These findings contribute to further elucidation of the solution isomerism/dynamics of LnIII complexes of phosphorus acid derivatives of H4dota, which will help in the design of new complexes for specific applications. The position of the phosphorus substituent subtly alters the arrangement of the ligand in the complexes, which could be employed in the design of LnIII complexes with tailored properties.
The scope of “a phosphorus group rotation” was confirmed to be wider than just in phosphonate complexes and seems to be a general feature, expected to take place even in coordinated phosphates in biochemistry. Thus, the methods presented here may be applied to areas across the chemistry of phosphorus acid derivatives.
Experimental
The general experimental methods, synthesis of the unlabelled H4do3apMe, the 17O-labelled ethyl methylphosphinate and the H4do3apMe complexes, and experimental information for the X-ray crystal structure determination are in the Experimental Details section of the SI. The NMR spectra of all complexes were measured in D2O at pD ∼6.5 adjusted by diluted LiOD/D2O or DCl/D2O solutions at 14.1 T (i.e. at 600 MHz for 1H).Synthesis of 17O-labelled H4do3apMe
The 17O-labelled (approx. 12% enrichment on each phosphinate oxygen atom) title ligand was prepared following Scheme 1 from the tBu3do3a·HBr and 17O-labelled ethyl methyl-H-phosphinate which was prepared from methyl-dichlorophosphine and 17O-enriched water (see SI).Compound 4
The tBu3do3a·HBr 1 (4.87 g, 8.2 mmol) was dissolved in anhydrous pyridine (40 ml). The freshly prepared solution of ethyl methyl-H-phosphinate (7.3 mmol) in CH2Cl2 (20 ml) and paraformaldehyde (0.90 g, 30 mmol) were added to this mixture. The mixture was stirred at 40 °C for 36 h. The volatiles were evaporated from the reaction mixture in vacuo. The residue was partially dissolved in CH2Cl2 (100 ml) and washed with 20% (w/w) aq. K2CO3 (100 ml) and water (100 ml). The organic phase was dried with Na2SO4, the drying agent was filtered off on a glass frit and washed with CH2Cl2 (approx. 50 ml). After evaporation of volatiles from the filtrate at reduced pressure, the mixture of compound 4 (approx. 50 molar%), tBu3do3a and a by-product, N-methylated tBu3do3a, was obtained. This mixture was used in the subsequent reaction without further purification. 31P NMR (162 MHz, CDCl3) δ: 52.5–52.9 (m). 17O NMR (54 MHz, CDCl3) δ: 97 (bs, 1O, CH2P(O)(CH3)![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) Et), 101 (bs, 1O, CH2P(
Et), 101 (bs, 1O, CH2P(![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) )(CH3)(OEt)). MS (ESI+): m/z = 635.7 [M(16O) + H]+, 636.5 [M(17O) + H]+. TLC (EtOH–conc. aq. NH3 20
)(CH3)(OEt)). MS (ESI+): m/z = 635.7 [M(16O) + H]+, 636.5 [M(17O) + H]+. TLC (EtOH–conc. aq. NH3 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1): Rf = 0.7.
1): Rf = 0.7.
17O-labelled H4do3apMe
The mixture containing compound 4 from the previous step was dissolved in anhydrous CHCl3 (∼200 ml), and excess TMSBr (12 ml, 91 mmol) was slowly added. The mixture was stirred at room temperature in the dark for 72 h, and volatiles were evaporated in vacuo. The residue was dissolved in CH3OH (∼200 ml), the solution was stirred for 1 h, and volatiles were evaporated in vacuo. The residue was dissolved in a CH2Cl2−TFA mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 200 ml) and the solution was stirred at room temperature for 2 d. Volatiles were evaporated at reduced pressure, and the residual TFA was co-evaporated with CH3OH (50 ml) in vacuo. The residue was dissolved in a minimal amount of water, and the solution was passed through an Amberlite CG50 weak cation exchange resin (H+-cycle, 6 × 4 cm, the resin was washed with approx. 400 ml of water). Volatiles from the eluate were evaporated in vacuo, the residue was re-dissolved in a minimal amount of water, and further purified on a Dowex-50 W×4 strong cation-exchange resin (H+-cycle, 5 × 40 cm). The resin was washed with water until the eluate pH was neutral. The product was eluted with 10% aq. pyridine (approx. 400 ml). Volatiles were evaporated at reduced pressure. The residue was dissolved in a minimal amount of water and further purified by chromatography on Amberlite CG50 weak cation exchanger (H+-cycle, 5 × 40 cm, elution by water). Volatiles were evaporated from the combined product-containing fractions. The residue was dissolved in MeOH (approx. 10 ml) with a few drops of water, and the product was precipitated by a slow addition of EtOH (approx. 30 ml) followed by a slow addition of Et2O (approx. 30 ml). The precipitate was filtered on a fine glass frit, washed with Et2O (3 × 30 ml) and dried in an oven (90 °C, 15 min). The product was isolated as a white powder comprised of the zwitter-ionic (17O)H4do3apMe·2H2O (0.7 g, 17% based on Me-PCl2, ∼12% 17O at each oxygen atom of the phosphinate group). 17O NMR (54 MHz, D2O/CsOD, 85 °C, pD ≈ 14) δ: 121 (d, 1JOP 109 Hz). MS (ESI+): m/z 439.3 [M(16O) + H]+, 440.4 [M(17O) + H]+, 461.3 [M(16O) + Na]+, 462.3 [M(17O) + Na]+. The 1H, 13C and 31P NMR spectra and TLC data are the same as those of the non-labelled H4do3apMe (see SI).
1, 200 ml) and the solution was stirred at room temperature for 2 d. Volatiles were evaporated at reduced pressure, and the residual TFA was co-evaporated with CH3OH (50 ml) in vacuo. The residue was dissolved in a minimal amount of water, and the solution was passed through an Amberlite CG50 weak cation exchange resin (H+-cycle, 6 × 4 cm, the resin was washed with approx. 400 ml of water). Volatiles from the eluate were evaporated in vacuo, the residue was re-dissolved in a minimal amount of water, and further purified on a Dowex-50 W×4 strong cation-exchange resin (H+-cycle, 5 × 40 cm). The resin was washed with water until the eluate pH was neutral. The product was eluted with 10% aq. pyridine (approx. 400 ml). Volatiles were evaporated at reduced pressure. The residue was dissolved in a minimal amount of water and further purified by chromatography on Amberlite CG50 weak cation exchanger (H+-cycle, 5 × 40 cm, elution by water). Volatiles were evaporated from the combined product-containing fractions. The residue was dissolved in MeOH (approx. 10 ml) with a few drops of water, and the product was precipitated by a slow addition of EtOH (approx. 30 ml) followed by a slow addition of Et2O (approx. 30 ml). The precipitate was filtered on a fine glass frit, washed with Et2O (3 × 30 ml) and dried in an oven (90 °C, 15 min). The product was isolated as a white powder comprised of the zwitter-ionic (17O)H4do3apMe·2H2O (0.7 g, 17% based on Me-PCl2, ∼12% 17O at each oxygen atom of the phosphinate group). 17O NMR (54 MHz, D2O/CsOD, 85 °C, pD ≈ 14) δ: 121 (d, 1JOP 109 Hz). MS (ESI+): m/z 439.3 [M(16O) + H]+, 440.4 [M(17O) + H]+, 461.3 [M(16O) + Na]+, 462.3 [M(17O) + Na]+. The 1H, 13C and 31P NMR spectra and TLC data are the same as those of the non-labelled H4do3apMe (see SI).
Determination of 13C NMR relaxation times
The 13C T1,2 NMR relaxation times of the paramagnetic [Yb(do3apMe)]− complex were determined at 5 °C (see SI), where dynamic processes are slow and have negligible effects on the relaxation rates. Paramagnetic T1,M and T2,M were calculated from these values by subtracting the T1 and T2 values for the analogous signals in the diamagnetic [Lu(do3apMe)]− complex determined by the same methods. Differences in paramagnetic relaxation times were used to determine the Yb–13C distances in the complex. First, value of the rotational correlation time τR was determined from 13C T1 values and NOE factors of the CH2 signals of a diamagnetic complex; the same approximation was successfully used for complexes of H4dota before.86 The NOE factor was determined by comparing the signal intensities in two 13C NMR experiments, one with and one without 1H NOE, measured by the standard pulse-acquire sequence with relaxation delay of d1 ∼ 10T1. Then, the τR was approximated by eqn (1) and (2) where R1 is the 13C longitudinal relaxation rate, RDD1 is the dipolar 13C longitudinal relaxation rate, NOE is the NOE enhancement factor, rCH is the CH2 carbon–proton distance taken as 1.09 Å based on the DFT-optimized structure, NH is the number of hydrogen atoms bonded to the carbon atom, γH = 2.675 × 108/γC = 6.728 × 108 rad s−1 T−1 are the 1H and 13C magnetogyric ratios, respectively, and ħ = 1.0546 × 10−34 J s is the reduced Planck constant.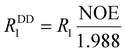 | (1) |
 | (2) |
In this way, the value of rotational correlation time, τR ∼ 138 ps, was determined from 13C NMR relaxation times of the pendant arm and macrocycle CH2 groups of the diamagnetic [Lu(do3apMe)]− complex (Table S2). This rotational correlation time was used to determine Yb–C distance using YbIII as a paramagnetic probe. Paramagnetic enhancements of longitudinal T1,M and transverse T2,M relaxation times of NMR signals of nuclei in LnIII complexes consist of contact Ti,c, dipolar Ti,p and Curie Ti,χ (i = 1,2) contributions.61 The contact contribution, Ti,c, is usually negligible for Ln ≠ Gd and for nuclei not directly bound to the LnIII ion. The dipolar and Curie contributions, Ti,p and Ti,χ, were separated as dipolar relaxation times T1,p and T2,p are very similar for Ln ≠ Gd. Thus, the Curie contribution of the YbIII complex atoms not directly bound to YbIII could be separated from the difference between T1,M and T2,M.54 This difference depends only on the distance of the nucleus from the YbIII ion and on the rotational correlation time τR of the complex. Thus, 13C NMR PRE of the P-methyl group could be used for the phosphorus atom configuration assignment. The 13C NMR relaxation times used for the determination of Yb–C distances in the [Yb(do3apMe)]− complex were determined at 5 °C where dynamic processes are slow and have negligible effects on the NMR relaxation times. The Yb–C distances r were then computed from the difference of the paramagnetic T1,M and T2,M relaxation times of the particular 13C nuclei as defined by eqn (3).61
 | (3) |
Here, (μ0/4π) = 10−7 N A−2 is the magnetic permeability of vacuum, γC is the 13C magnetogyric ratio (see above), μeff = 4.173 × 10−23 J T−1 is the effective magnetic moment of YbIII, H0 [in T] is the external magnetic field strength, k = 1.381 × 10−23 J K−1 is the Boltzmann constant, T is the thermodynamic temperature, ωC is the Larmor frequency of 13C and τR is the rotational correlation time of the complex.
To determine the H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb distance, the ratio of paramagnetically enhanced R1M relaxation rates of the carbonyl and methyl carbon atoms at 0 and 5 °C can also be used. Here, the Yb⋯13C distance is the only parameter that changes values of R1M for different 13C sites. Then, the H3
⋯Yb distance, the ratio of paramagnetically enhanced R1M relaxation rates of the carbonyl and methyl carbon atoms at 0 and 5 °C can also be used. Here, the Yb⋯13C distance is the only parameter that changes values of R1M for different 13C sites. Then, the H3![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ⋯Yb distance can be calculated according to eqn (4)61 where dX are distances of the nuclei and R1M,X are the corresponding transverse relaxation rates.
⋯Yb distance can be calculated according to eqn (4)61 where dX are distances of the nuclei and R1M,X are the corresponding transverse relaxation rates.
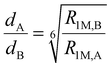 | (4) |
Quantitative EXSY spectra
The 2D 31P EXSY was used to determine the rate constants of dynamic processes. Integral intensities of all 31P EXSY signals were determined by signal deconvolution in Topspin© after phase and baseline corrections. Rate constants and relaxation times of signals were calculated at each mixing time τm in Matlab© by the eqn (5)87,88 describing a dependence between rate constants and integral intensities of the signals. Here, R is a 4 × 4 matrix containing the rate constants of all dynamic processes and R1 relaxation rates of signals of all four diastereoisomers, and A is a 4 × 4 matrix containing integral intensities of signals divided by initial integral intensities I0 (for definition of R and A, see SI).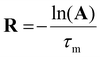 | (5) |
Initial integral intensities I0 were interpolated from the 31P EXSY spectra measured at short mixing times (τm = 0.001, 0.01 and 0.1 s). After the calculation, outliers (defined as three scaled median absolute deviations from the median) were removed from the calculated parameters, and the rate constants and relaxation times were calculated as the mean of the remaining values.
DFT calculations
All calculations in this work were performed in ORCA 6.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 89 using DFT with the wB97X functional and Grimme's D4 dispersion correction.90–92 All calculations were performed with a large integration grid (DEFGRID3),93 a tight SCF energy convergence threshold and RIJCOSX approximation.94–96 Geometry optimizations for all diastereoisomers and transition states of the [Ln(do3apMe/OEt/H/tBu)]− complexes were performed employing the large core effective core potentials of the Stuttgart type for all LnIII,97 ECP(46 + n)MWB which include 46 + 4fn electrons in the core, with the corresponding (6s6p5d)/[4s4p4d] + 2s1p1d basis sets for the valence space. For all remaining atoms, the def2tzvp basis set was used.98,99 For transition states, the Hessian was calculated before the geometric optimisation and then after each five steps. For complexes of large LnIII (La–Eu), models with one coordinated water molecule were used. For complexes of smaller YbIII, no explicit water molecule was used. Bulk solvent effects of water were accounted for by the conductor-like polarisation continuum model.100 To study the second coordination sphere in GdIII complexes, models with one coordinated and four more explicit water molecules were used. All optimised structures were tested by the frequency analysis at the same computational level. Relative free energies (zero-point energies and thermal terms at 25 °C) were also obtained by frequency analysis.
89 using DFT with the wB97X functional and Grimme's D4 dispersion correction.90–92 All calculations were performed with a large integration grid (DEFGRID3),93 a tight SCF energy convergence threshold and RIJCOSX approximation.94–96 Geometry optimizations for all diastereoisomers and transition states of the [Ln(do3apMe/OEt/H/tBu)]− complexes were performed employing the large core effective core potentials of the Stuttgart type for all LnIII,97 ECP(46 + n)MWB which include 46 + 4fn electrons in the core, with the corresponding (6s6p5d)/[4s4p4d] + 2s1p1d basis sets for the valence space. For all remaining atoms, the def2tzvp basis set was used.98,99 For transition states, the Hessian was calculated before the geometric optimisation and then after each five steps. For complexes of large LnIII (La–Eu), models with one coordinated water molecule were used. For complexes of smaller YbIII, no explicit water molecule was used. Bulk solvent effects of water were accounted for by the conductor-like polarisation continuum model.100 To study the second coordination sphere in GdIII complexes, models with one coordinated and four more explicit water molecules were used. All optimised structures were tested by the frequency analysis at the same computational level. Relative free energies (zero-point energies and thermal terms at 25 °C) were also obtained by frequency analysis.
Variable-temperature NMR
The VT NMR data were processed in Mestrenova© where phase and baseline were corrected. Diastereoisomer ratios were determined from the signals integrated or deconvoluted to a Lorentzian–Gaussian shape (for overlapping signals). Kinetic parameters of the oxygen atom exchange were determined from these pre-processed spectra in Asymexfit101 as the best fit to the analytical solution of Bloch-McConnel equations, analogously to the approach used previously for the phosphonate rotation37 (for details, see SI). Activation parameters, ΔH‡, ΔS‡ and ΔG‡, of the phosphinate rotation were determined by fitting the temperature dependence of the rate constants to the Eyring law, eqn (6) and (7). Here, kB, h and R are the Boltzmann, Planck and universal gas constant, respectively. The ΔH‡ and ΔS‡ were considered temperature-independent.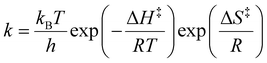 | (6) |
| ΔG‡ = ΔH‡ − TΔS‡ | (7) |
Author contributions
A. S. – syntheses of ligands and complexes, NMR measurements, DFT calculations, study concept; J. K. – X-ray data fitting, C. P. I. – DFT calculations, supervision of DFT calculations; P. H. – study concept and money acquisition. All authors participated in the manuscript writing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: details on synthesis of ligands and complexes; X-ray experimental data and extended discussion of solid-state structures; 1H, 17O and 31P NMR spectra of LnIII complexes; NMR relaxation rate of selected nuclei in complexes; various 2D NMR spectra of complexes; DFT-calculated energies and structures of complexes; abundances of isomeric species for complexes of different LnIII ions; 17O VT-NMR spectra; experimental values of rate constants and activation parameters; definition of matrixes and equations used for calculations. See DOI: https://doi.org/10.1039/d5qi01885d.CCDC 2470192–2470194 contain the supplementary crystallographic data for this paper.102a–c
Acknowledgements
We thank Dr I. Císařová for X-ray data collection and Dr Z. Tošner for help with NMR measurements. The work was supported by GACR (22-34083S) and the Grant Agency of Charles University (no. 68122 to A. S.). Computational resources were provided by CESGA – Centro de Supercomputación de Galicia (C. P. I. and A. S.) and the e-INFRA CZ project (ID: 90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic.References
- J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI contrast agents: Current challenges and new frontiers, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS.
- H. Li and T. J. Meade, Molecular magnetic resonance imaging with Gd(III)-based contrast agents: Challenges and key advances, J. Am. Chem. Soc., 2019, 141, 17025–17041 CrossRef CAS.
- P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Gadolinium(III) chelates as MRI contrast agents: structure, dynamics, and applications, Chem. Rev., 1999, 99, 2293–2352 CrossRef CAS.
- P. Hermann, J. Kotek, V. Kubíček and I. Lukeš, Gadolinium(III) complexes as MRI contrast agents: Ligand design and properties of the complexes, Dalton Trans., 2008, 3027–3047 RSC.
- R. E. Mewis and S. J. Archibald, Biomedical applications of macrocyclic ligand complexes, Coord. Chem. Rev., 2010, 254, 1686–1712 CrossRef CAS.
- M. C. Heffern, L. M. Matosziuk and T. J. Meade, Lanthanide probes for bioresponsive imaging, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed.
- C. S. Cutler, H. M. Hennkens, N. Sisay, S. Huclier-Markai and S. S. Jurisson, Radiometals for combined imaging and therapy, Chem. Rev., 2013, 113, 858–883 CrossRef CAS PubMed.
- E. W. Price and C. Orvig, Matching chelators to radiometals for radiopharmaceuticals, Chem. Soc. Rev., 2014, 43, 260–290 RSC.
- T. I. Kostelnik and C. Orvig, Radioactive main group and rare earth metals for imaging and therapy, Chem. Rev., 2019, 119, 902–956 CrossRef CAS.
- E. Mathieu, A. Sipos, E. Demeyere, D. Phipps, D. Sakaveli and K. E. Borbas, Lanthanide-based tools for the investigation of cellular environments, Chem. Commun., 2018, 54, 10021–10035 RSC.
- U. Cho and J. K. Chen, Lanthanide-based optical probes of biological systems, Cell Chem. Biol., 2020, 27, 921–936 CrossRef CAS.
- D. Parker, J. D. Fradgley and K. L. Wong, The design of responsive luminescent lanthanide probes and sensors, Chem. Soc. Rev., 2021, 50, 8193–8213 RSC.
- E. Ravera, L. Gigli, L. Fiorucci, C. Luchinat and G. Parigi, The evolution of paramagnetic NMR as a tool in structural biology, Phys. Chem. Chem. Phys., 2022, 24, 17397–17416 RSC.
- Q. Miao, C. Nitsche, H. Orton, M. Overhand, G. Otting and M. Ubbink, Paramagnetic chemical probes for studying biological macromolecules, Chem. Rev., 2022, 122, 9571–9642 CrossRef CAS PubMed.
- D. Joss and D. Häussinger, Design and applications of lanthanide chelating tags for pseudocontact shift NMR spectroscopy with biomacromolecules, Prog. NMR Spectrosc., 2019, 114–115, 284–312 CrossRef.
- J. A. Peters, K. Djanashvili, C. F. G. C. Geraldes and C. Platas-iglesias, Structure, dynamics, and computational studies of lanthanide-based contrast agents, in The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, Wiley, Chichester, 2nd edn, 2013, pp. 209–276 Search PubMed.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. G. C. Geraldes, D. Pubanz and A. E. Merbach, Conformational and coordination equilibria on DOTA Complexes of lanthanide metal ions in aqueous solution studied by 1H-NMR spectroscopy, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- C. Platas-Iglesias, The solution structure and dynamics of MRI probes based on lanthanide(III) DOTA as investigated by DFT and NMR spectroscopy, Eur. J. Inorg. Chem., 2012, 2023–2033 CrossRef CAS.
- F. Mayer, C. Platas-Iglesias, L. Helm, J. A. Peters and K. Djanashvili, 17O NMR and density functional theory study of the dynamics of the carboxylate groups in DOTA complexes of lanthanides in aqueous solution, Inorg. Chem., 2012, 51, 170–178 CrossRef CAS.
- L. Fusaro and M. Luhmer, 17O NMR study of diamagnetic and paramagnetic lanthanide(III)-DOTA complexes in aqueous solution, Inorg. Chem., 2014, 53, 8717–8722 CrossRef CAS PubMed.
- L. Fusaro and M. Luhmer, An oxygen-17 dynamic NMR study of the Pr-DOTA complex, Dalton Trans., 2014, 43, 967–972 RSC.
- L. Fusaro, G. Casella and A. Bagno, Direct detection of 17O in [Gd(DOTA)]− by NMR spectroscopy, Chem. – Eur. J., 2015, 21, 1955–1960 CrossRef CAS.
- J. Rudovský, P. Cígler, J. Kotek, P. Hermann, P. Vojtíšek, I. Lukeš, J. A. Peters, L. Vander Elst and R. N. Muller, Lanthanide(III) complexes of a mono(methylphosphonate) analogue of H4dota: The influence of protonation of the phosphonate moiety on the TSAP/SAP isomer ratio and the water exchange rate, Chem. – Eur. J., 2005, 11, 2373–2384 CrossRef.
- P. Vojtíšek, P. Cígler, J. Kotek, J. Rudovský, P. Hermann and I. Lukeš, Crystal structures of lanthanide(III) complexes with cyclen derivative bearing three acetate and one methylphosphonate pendants, Inorg. Chem., 2005, 44, 5591–5599 CrossRef.
- J. Rudovský, J. Kotek, P. Hermann, I. Lukeš, V. Mainero and S. Aime, Synthesis of a bifunctional monophosphinic acid DOTA analogue ligand and its lanthanide(III) complexes. A gadolinium(III) complex endowed with an optimal water exchange rate for MRI applications, Org. Biomol. Chem., 2005, 3, 112–117 RSC.
- P. Lebdušková, P. Hermann, L. Helm, É. Tóth, J. Kotek, K. Binnemans, J. Rudovský, I. Lukeš and A. E. Merbach, Gadolinium(III) complexes of mono- and diethyl esters of monophosphonic acid analogue of DOTA as potential MRI contrast agents: Solution structures and relaxometric studies, Dalton Trans., 2007, 493–501 RSC.
- P. Urbanovský, J. Kotek, F. Carniato, M. Botta and P. Hermann, Lanthanide complexes of DO3A-(dibenzylamino)methylphosphinate: Effect of protonation of the dibenzylamino group on the water-exchange rate and the binding of human serum albumin, Inorg. Chem., 2019, 58, 5196–5210 CrossRef PubMed.
- M. Purgel, Z. Baranyai, A. de Blas, T. Rodríguez-Blas, I. Bányai, C. Platas-Iglesias and I. Tóth, An NMR and DFT investigation on the conformational properties of lanthanide(III) 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate analogues containing methylenephosphonate pendant arms, Inorg. Chem., 2010, 49, 4370–4382 CrossRef CAS PubMed.
- C. F. G. C. Geraldes, A. D. Sherry and G. E. Kiefer, The solution structure of Ln(DOTP)5− complexes. A comparison of lanthanide-induced paramagnetic shifts with the MMX energy-minimized structure, J. Magn. Reson., 1992, 97, 290–304 CAS.
- F. Avecilla, J. A. Peters and C. F. G. C. Geraldes, Crystal structure of a sodium salt of [Gd(DOTP)]5−: Implications for Its second-sphere relaxivity and the 23Na NMR hyperfine shift effects of [Tm(DOTP)]5−, Eur. J. Inorg. Chem., 2003, 4179–4186 CrossRef CAS.
- S. Aime, A. S. Batsanov, M. Botta, J. A. K. Howard, D. Parker, K. Senanayake and G. Williams, Solution and solid-state characterization of highly rigid, eight-coordinate lanthanide(III) complexes of a macrocyclic tetrabenzylphosphinate, Inorg. Chem., 1994, 33, 4696–4706 CrossRef CAS.
- S. Aime, A. S. Batsanov, M. Botta, R. S. Dickins, S. Faulkner, C. E. Foster, A. Harrison, J. a. K. Howard, J. M. Moloney, T. J. Norman, D. Parker and J. A. G. Williams, Nuclear magnetic resonance, luminescence and structural studies of lanthanide complexes with octadentate macrocyclic ligands bearing benzylphosphinate groups, J. Chem. Soc., Dalton Trans., 1997, 3623–3636 RSC.
- J. Rohovec, P. Vojtíšek, P. Hermann, J. Mosinger, Z. Žák and I. Lukeš, Synthesis, crystal structures and NMR and luminescence spectra of lanthanide complexes of 1,4,7,10-tetraazacyclododecane with N-methylene(phenyl)phosphinic acid pendant arms, J. Chem. Soc., Dalton Trans., 1999, 3585–3592 RSC.
- W. D. Kim, G. E. Kiefer, J. Huskens and A. D. Sherry, NMR studies of the lanthanide(III) complexes of 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrakis[methanephospho-nic acid mono(2,2′,2′-trifluoroethyl) ester], Inorg. Chem., 2002, 36, 4128–4134 CrossRef.
- Z. Kotková, G. A. Pereira, K. Djanashvili, J. Kotek, J. Rudovský, P. Hermann, L. Vander Elst, R. N. Muller, C. F. G. C. Geraldes, I. Lukeš and J. A. Peters, Lanthanide(III) complexes of phosphorus acid analogues of H4DOTA as model compounds for the evaluation of the second-sphere hydration, Eur. J. Inorg. Chem., 2009, 119–136 CrossRef.
- G. A. Pereira, L. Ball, A. D. Sherry, J. A. Peters and C. F. G. C. Geraldes, NMR characterization of lanthanide(3+) complexes of tetraazatetrakisphosphinato and tetraazatetrakis phosphonato ligands, Helv. Chim. Acta, 2009, 92, 2532–2551 CrossRef CAS.
- A. Svítok, J. Blahut, P. Urbanovský and P. Hermann, Dynamics of coordinated phosphonate group directly observed by 17O–NMR in lanthanide(III) complexes of a mono(ethyl phosphonate) DOTA analogue, Chem. – Eur. J., 2024, 30, e202400970 CrossRef.
- J. Blahut, P. Hermann, Z. Tošner and C. Platas-Iglesias, A combined NMR and DFT study of conformational dynamics in lanthanide complexes of macrocyclic DOTA-like ligands, Phys. Chem. Chem. Phys., 2017, 19, 26662–26671 RSC.
- S. C. L. Kamerlin, P. K. Sharma, R. B. Prasad and A. Warshel, Why nature really chose phosphate, Q. Rev. Biophys., 2013, 46, 1–132 CrossRef CAS.
- J.-B. Wang, J. Y. Lv, S. K. Bankar, S.-S. Fang and M. Shang, Stereoselective synthesis of P-stereogenic nucleotide prodrugs and oligonucleotides, Chem. Soc. Rev., 2025, 54, 9370–9406 RSC.
- C. Nowlan, Y. Li, J. C. Hermann, T. Evans, J. Carpenter, E. Ghanem, B. K. Shoichet and F. M. Raushel, Resolution of chiral phosphate, phosphonate, and phosphinate esters by an enantioselective enzyme library, J. Am. Chem. Soc., 2006, 128, 15892–15902 CrossRef CAS PubMed.
- P.-C. Tsai, Y. Fan, J. Kim, L. Yang, S. C. Almo, Y. Q. Gao and F. M. Raushel, Structural determinants for the stereoselective hydrolysis of chiral substrates by phosphotriesterase, Biochemistry, 2010, 49, 7988–7997 CrossRef CAS.
- C. Boehme and G. Wipff, The energetic and structural effects of steric crowding in phosphate and dithiophosphinate complexes of lanthanide cations M3+: A computational study, Chem. – Eur. J., 2001, 7, 1398–1407 CrossRef CAS.
- E. Mayaan, K. Range and D. M. York, Structure and binding of Mg(II) ions and di-metal bridge complexes with biological phosphates and phosphoranes, J. Biol. Inorg. Chem., 2004, 9, 807–817 CrossRef CAS PubMed.
- E. L. Christian, V. E. Anderson, P. R. Carey and M. E. Harris, A quantitative Raman spectroscopic signal for metal-phosphodiester interactions in solution, Biochemistry, 2010, 49, 2869–2879 CrossRef CAS PubMed.
- A. S. Petrov, J. Funseth-Smotzer and G. R. Pack, Computational study of dimethyl phosphate anion and its complexes with water, magnesium, and calcium, Int. J. Quantum Chem., 2005, 102, 645–655 CrossRef CAS.
- K. Moedritzer and R. R. Irani, Aminomethylphosphonic acids, Mannich-type reactions with orthophosphorous acid, J. Org. Chem., 1966, 31, 1603–1607 CrossRef CAS.
- V. Theodorou, K. Skobridis, D. Alivertis and I. P. Gerothanassis, Synthetic methodologies in organic chemistry involving incorporation of [17O] and [18O] isotopes, J. Labelled Compnd. Radiopharm., 2014, 57, 481–508 CrossRef CAS PubMed.
- J. Zhang, E. Lambert, Z. F. Xu, J. Brioche, P. Remy and S. R. Piettre, From oxygen to sulfur and back: Difluoro-H-phosphinothioates as a turning point in the preparation of difluorinated phosphinates: Application to the synthesis of modified dinucleotides, J. Org. Chem., 2019, 84, 5245–5260 CrossRef CAS PubMed.
- K. M. Błazewska, McKenna reaction - Which oxygen attacks bromotrimethylsilane?, J. Org. Chem., 2014, 79, 408–412 CrossRef.
- S. Aime, M. Botta, D. Parker and J. A. G. Williams, Nuclear magnetic resonance studies of neutral lanthanide(III) complexes with tetraaza-macrocyclic ligands containing three phosphinate and one carboxamide co-ordinating arms, J. Chem. Soc., Dalton Trans., 1995, 2259–2266 RSC.
- S. Aime, M. Botta, R. S. Dickins, C. L. Maupin, D. Parker, J. P. Riehl and J. A. G. Williams, Synthesis, NMR, relaxometry and circularly polarised luminescence studies of macrocyclic monoamide-tris(phosphinate) complexes bearing a remote chiral centre, J. Chem. Soc., Dalton Trans., 1998, 881–892 RSC.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- S. Aime, L. Barbero, M. Botta and G. Ermondi, Determination of metal-proton distances and electronic relaxation times in lanthanide complexes by nuclear magnetic resonance spectroscopy, J. Chem. Soc., Dalton Trans., 1992, 225–228 RSC.
- M. D. C. Fernández-Fernández, R. Bastida, A. Macías, P. Pérez-Lourido, C. Platas-Iglesias and L. Valencia, Lanthanide(III) complexes with a tetrapyridine pendant-armed macrocyclic ligand: 1H NMR structural determination in solution, X-ray diffraction, and density-functional theory calculations, Inorg. Chem., 2006, 45, 4484–4496 CrossRef.
- S. Koeller, G. Bernardinelli, B. Bocquet and C. Piguet, A novel extended covalent tripod for assembling nine-coordinate lanthanide(III) podates: A delicate balance between flexibility and rigidity, Chem. – Eur. J., 2003, 9, 1062–1074 CrossRef CAS.
- L. Brachais and M. Visseaux, NMR T1-relaxation measurements on paramagnetic organolanthanides: An alternative tool for structure determination in solution, Eur. J. Inorg. Chem., 2005, 2486–2492 CrossRef CAS.
- J. W. Walton, R. Carr, N. H. Evans, A. M. Funk, A. M. Kenwright, D. Parker, D. S. Yufit, M. Botta, S. D. Pinto and K. L. Wong, Isostructural series of nine-coordinate chiral lanthanide complexes based on triazacyclononane, Inorg. Chem., 2012, 51, 8042–8056 CrossRef CAS PubMed.
- K. H. Chalmers, E. De Luca, N. H. M. Hogg, A. M. Kenwright, I. Kuprov, D. Parker, M. Botta, J. I. Wilson and A. M. Blamire, Design principles and theory of paramagnetic fluorine-labelled lanthanide complexes as probes for 19F magnetic resonance: A proof-of-concept study, Chem. – Eur. J., 2010, 16, 134–148 CrossRef CAS PubMed.
- J. Rudovský, M. Botta, P. Hermann, A. Koridze and S. Aime, Relaxometric and solution NMR structural studies on ditopic lanthanide(III) complexes of a phosphinate analogue of DOTA with a fast rate of water exchange, Dalton Trans., 2006, 2323–2333 RSC.
- J. A. Peters, J. Huskens and D. J. Raber, Lanthanide induced shifts and relaxation rate enhancements, Prog. NMR Spectrosc., 1996, 28, 283–350 CrossRef CAS.
- J. A. Peters, K. Djanashvili, C. F. G. C. Geraldes and C. Platas-Iglesias, The chemical consequences of the gradual decrease of the ionic radius along the Ln-series, Coord. Chem. Rev., 2020, 406, 213146 CrossRef CAS.
- I. Lukeš, J. Kotek, P. Vojtíšek and P. Hermann, Complexes of tetraazacycles bearing methylphosphinic/phosphonic acid pendant arms with copper(II), zinc(II) and lanthanides(III). A comparison with their acetic acid analogues, Coord. Chem. Rev., 2001, 216–217, 287–312 CrossRef.
- P. Urbanovský, J. Kotek, I. Císařová and P. Hermann, The solid-state structures and ligand cavity evaluation of lanthanide(III) complexes of a DOTA analogue with a (dibenzylamino)methylphosphinate pendant arm, Dalton Trans., 2020, 49, 1555–1569 RSC.
- J. Kotek, J. Rudovský, P. Hermann and I. Lukeš, Three in one: TSA, TSA′, and SA units in one crystal structure of a yttrium(III) complex with a monophosphinated H4dota analogue, Inorg. Chem., 2006, 45, 3097–3102 CrossRef CAS.
- T. Vitha, V. Kubíček, J. Kotek, P. Hermann, L. Vander Elst, R. N. Muller, I. Luke and J. A. Peters, Gd(III) complex of a monophosphinate-bis(phosphonate) DOTA analogue with a high relaxivity; Lanthanide(III) complexes for imaging and radiotherapy of calcified tissues, Dalton Trans., 2009, 3204–3214 RSC.
- K. P. Pulukkody, T. J. Norman, D. Parker, L. Royle and C. J. Broan, Synthesis of charged and uncharged complexes of gadolinium and yttrium with cyclic polyazaphosphinic acid ligands for in vivo applications, J. Chem. Soc., Perkin Trans. 2, 1993, 605–620 RSC.
- S. Procházková, V. Kubíček, J. Kotek, A. Vágner, J. Notni and P. Hermann, Lanthanide(III) complexes of monophosphinate/monophosphonate DOTA-analogues: Effects of the substituents on the formation rate and radiolabelling yield, Dalton Trans., 2018, 47, 13006–13015 RSC.
- E. Cole, R. C. B. Copley, J. A. K. Howard, D. Parker, G. Ferguson, J. F. Gallagher, B. Kaitner, A. Harrison and L. Royle, 1,4,7-Triazacyclononane-1,4,7-triyl-trimethylene-tris(phenylphosphinate) enforces octahedral geometry: Crystal and solution structures of its metal complexes and comparative biodistribution studies of radiolabelled indium and gallium complexes, J. Chem. Soc., Dalton Trans., 1994, 1619–1629 RSC.
- J. Notni, P. Hermann, J. Havlíčková, J. Kotek, V. Kubíček, J. Plutnar, N. Loktionova, P. J. Riss, F. Rösch and I. Lukeš, A triazacyclononane-based bifunctional phosphinate ligand for the preparation of multimeric 68Ga tracers for positron emission tomography, Chem. – Eur. J., 2010, 16, 7174–7185 CrossRef CAS.
- J. Šimeček, M. Schulz, J. Notni, J. Plutnar, V. Kubíček, J. Havlíčková and P. Hermann, Complexation of metal ions with TRAP (1,4,7-triazacyclononane phosphinic acid) ligands and 1,4,7-triazacyclononane-1,4,7-triacetic acid: Phosphinate-containing ligands as unique chelators for trivalent gallium, Inorg. Chem., 2012, 51, 577–590 CrossRef.
- S. Hoeft and K. Roth, Struktur und dynamik von lanthanoid–tetraazacyclododecantetraacetat–(DOTA–) komplexen in lösung, Chem. Ber., 1993, 126, 869–873 CrossRef CAS.
- D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. K. Howard, Being excited by lanthanide coordination complexes : Aqua species, chirality, excited-state chemistry, and exchange dynamics, Chem. Rev., 2010, 102, 1977–2010 Search PubMed.
- E. N. Zapolotsky, Y. Qu and S. P. Babailov, Lanthanide complexes with polyaminopolycarboxylates as prospective NMR/MRI diagnostic probes: peculiarities of molecular structure, dynamics and paramagnetic properties, J. Inclusion Phenom. Macrocyclic Chem., 2022, 102, 1–33 CrossRef CAS.
- F. A. Dunand, S. Aime and A. E. Merbach, First 17O NMR observation of coordinated water on both isomers of [Eu(DOTAM)(H2O)]3+: A direct access to water exchange and its role in the isomerization, J. Am. Chem. Soc., 2000, 122, 1506–1512 CrossRef CAS.
- F. A. Dunand, R. S. Dickins, D. Parker and A. E. Merbach, Towards rational design of fast water-exchanging Gd(dota-like) contrast agents? Importance of the M/m ratio, Chem. – Eur. J., 2001, 7, 5160–5167 CrossRef CAS.
- J. F. Desreux, Nuclear magnetic resonance spectroscopy of lanthanide complexes with a tetraacetic tetraaza macrocycle, Unusual conformation properties, Inorg. Chem., 1980, 19, 1319–1324 CrossRef CAS.
- S. P. Babailov, E. N. Zapolotsky, A. I. Kruppa, P. A. Stabnikov, I. A. Godovikov, E. v. Bocharov and E. S. Fomin, Two types of conformational dynamics and thermo-sensor properties of praseodymium-DOTA by 1H/13C NMR, Inorg. Chim. Acta, 2019, 486, 340–344 CrossRef CAS.
- Q. Miao, R. Dekkers, K. B. S. S. Gupta, M. Overhand, R. Dasgupta and M. Ubbink, Rigidified and hydrophilic DOTA-like lanthanoid ligands: Design, synthesis, and dynamic properties, Inorg. Chem., 2023, 62, 3776–3787 CrossRef CAS.
- S. P. Babailov, P. v. Dubovskii and E. N. Zapolotsky, Paramagnetic lanthanides as magnetic resonance thermo-sensors and probes of molecular dynamics: Holmium-DOTA complex, Polyhedron, 2014, 79, 277–283 CrossRef CAS.
- S. P. Babailov and E. N. Zapolotsky, Tm-DOTA as responsive relaxation and shift probe for NMR local temperature monitoring at high magnetic fields, Inorg. Chim. Acta, 2021, 517, 120153 CrossRef CAS.
- V. Jacques and J. F. Desreux, Quantitative two-dimensional EXSY spectroscopy and dynamic behavior of a paramagnetic lanthanide macrocyclic chelate: YbDOTA (DOTA = 1,4,7,10-tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetic acid), Inorg. Chem., 1994, 33, 4048–4053 CrossRef CAS.
- S. Aime, A. Barge, M. Botta, M. Fasano, J. D. Ayala and G. Bombieri, Crystal structure and solution dynamics of the lutetium(III) chelate of DOTA, Inorg. Chim. Acta, 1996, 246, 423–429 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard III, Calculation of solvation free energies of charged solutes using mixed cluster/continuum models, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- J. Zhang, L. Dai, L. He, A. Bhattarai, C.-M. Chan, W. C.-S. Tai, V. Vardhanabhuti and G.-L. Law, Design and synthesis of chiral DOTA-based MRI contrast agents with remarkable relaxivities, Commun. Chem., 2023, 6, 251 CrossRef CAS.
- S. Aime, M. Botta and G. Ermondi, An NMR relaxation study of aqueous solutions of Gd(III) chelates, J. Magn. Reson., 1991, 92, 572–580 CAS.
- C. L. Perrin and T. J. Dwyer, Application of two-dimensional NMR to kinetics of chemical exchange, Chem. Rev., 1990, 90, 935–967 CrossRef CAS.
- Z. Zolnai, N. Juranić, D. Vikić-Topić and S. Macura, Quantitative determination of magnetization exchange rate constants from a series of two-dimensional exchange NMR spectra, J. Chem. Inf. Comput. Model., 2000, 40, 611–621 CAS.
- F. Neese, Software update: The ORCA program system – Version 6.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70019 Search PubMed.
- E. Caldeweyher, J. M. Mewes, S. Ehlert and S. Grimme, Extension and evaluation of the D4 London-dispersion model for periodic systems, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A generally applicable atomic-charge dependent London dispersion correction, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- F. Neese, The SHARK integral generation and digestion system, J. Comput. Chem., 2023, 44, 381–396 CrossRef CAS.
- F. Neese, An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- D. Bykov, T. Petrenko, R. Izsák, S. Kossmann, U. Becker, E. Valeev and F. Neese, Efficient implementation of the analytic second derivatives of Hartree–Fock and hybrid DFT energies: a detailed analysis of different approximations, Mol. Phys., 2015, 113, 1961–1977 CrossRef CAS.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Energy-adjusted pseudopotentials for the rare earth elements, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- G. L. Stoychev, A. A. Auer and F. Neese, Automatic generation of auxiliary basis sets, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS.
- M. Garcia-Ratés and F. Neese, Efficient implementation of the analytical second derivatives of Hartree–Fock and hybrid DFT energies within the framework of the conductor-like polarizable continuum model, J. Comput. Chem., 2019, 40, 1816–1828 CrossRef.
- V. Římal, H. Štěpánková and J. Štěpánek, Analysis of NMR spectra in case of temperature-dependent chemical exchange between two unequally populated sites, Concepts Magn. Reson., Part A, 2011, 38A, 117–127 CrossRef.
- (a) CCDC 2470192: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nxfmn; (b) CCDC 2470193: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nxfnp; (c) CCDC 2470194: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2nxfpq.
| This journal is © the Partner Organisations 2026 |