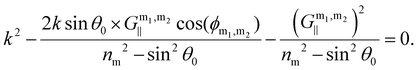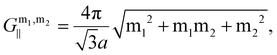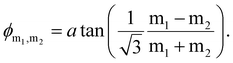Emission enhancement of colloidal quantum dots confined in double disc nano-antennas with controlled opening

Abstract

Plasmonic nanocavities, formed by closely spaced metal nanostructures, can generate electromagnetic hotspots with significantly enhanced electromagnetic fields. Here, we introduce a strategy to form accessible hotspot regions within plasmonic double disc nanoantennas, which we use to enhance the luminescence properties of colloidal quantum dots. The nanoantennas, formed by two gold discs separated by a silica spacer, are fabricated via colloidal lithography. A controlled wet-chemical etching step partly removes the spacer, thereby exposing the cavity gap, which enables colloidal quantum dot deposition. Finite-difference time domain (FDTD) simulations are used to study the plasmonic properties of this structure and their influence on the quantum dot emission profile. These simulations show that the gap opening leads to distinct plasmonic properties capable of enhancing the quantum yield via coupling to the excitation (633 nm) and emission (900 nm) wavelengths of the QDs. Experimentally, QDs interfaced with the exposed gap by capillary forces exhibit up to a tenfold increase in photoluminescence compared to a continuous gold film and a 3.5-fold enhancement over nanoantennas with a closed gap. These findings highlight the potential of precise structural control in plasmonic devices to enhance and control emission properties of colloidal light sources.

---

Introduction

Plasmonic nanocavities are formed in small gaps when two metal nanostructures are brought in close proximity.^1,2 As the localized surface plasmon resonances of both particles hybridize,³ the small mode volume of the nanocavity gives rise to a hotspot with strongly enhanced electric field.⁴ The high E-field density in such hotspot regions enhances light matter interactions,^5–7 paving the way for applications in different areas, such as sensing,⁸ biomedicine,^9,10 energy harvesting,^11–13 or catalysis.^14,15 A particular consequence of the confined E-field is the enhancement of luminescence of a quantum emitter, such as a fluorescent dye or a semiconductor quantum dot (QD) placed within the cavity, by the modification of the excitation rates and the quantum yield.¹⁶

This emission enhancement strongly depends on the position of the emitter within the cavity.^6,17 Quenching of emission is observed if the emitter is very close to the metal surface (<5 nm), while enhancement occurs at slightly larger distances within a range of 5 nm to 20 nm.^18,19 Consequently, in order to exploit plasmon-enhanced light emission, both structural and optical properties of the two components need to be carefully aligned. First, the emitter position within the cavity needs to be precisely controlled to avoid quenching, yet provide high E-field enhancement.²⁰ Second, the excitation of the emitter needs to be spectrally matched with the absorption of the plasmonic mode to harvest excitation enhancement.¹⁹ Finally, when the emission wavelength of the emitter coincides with the prevailing scattering resonance of the cavity, the emission properties can be altered, e.g. to provide directionality in the far-field.^16,21,22

The typical target wavelength of plasmon-enhanced luminescence is in the visible range,^23,24 which is of interest for designing efficient light sources. Recently, emission enhancement in the IR region has been demonstrated for biomedical applications, to enhance sensing capabilities²⁵ or to design optical devices at telecommunication wavelengths. While fundamental research has often focused on the emission properties of organic dyes as model systems,^26,27 colloidal QDs provide attractive properties as light sources.^28–30 QDs exhibit nanoscale dimensions, allowing integration into small cavities, yet are colloidal particles, and can thus be deposited, adsorbed, and self-assembled with high controllability.^31,32 In addition, QDs show robust, non-bleachable emission with high photoluminescence quantum yields (PLQY) and tunable emission properties in the visible and NIR region. QDs emitting in the visible range are typically based on cadmium selenium (CdSe), while NIR emitters often employ lead chalcogenide such as lead sulfide (PbS) and lead selenide (PbSe).^33–35

To enhance QD emission properties, the task is to identify suitable plasmonic structures. Complex gold nanostructures, including nanowires,³⁶ nanocages,³⁷ nanostars,³⁸ or faceted nanoparticles,²⁰ provide tunable optical resonance.³³ However, these individual plasmonic components are challenged by losses that can compromise their quality factor (Q-factor). The assembly of individual plasmonic building blocks into dimer,³⁹ oligomer,⁴⁰ or a nanoparticle-on-mirror (NPoM)^41,42 configurations lead to hybridized resonances with enhanced electromagnetic near-fields localized in the cavities separating the plasmonic elements.^43,44 Such defined assemblies can be achieved by DNA origami,^21,27,45 template-assisted-self-assembly,^46,47 electrophoretic deposition,⁴⁸ or sequential capillary deposition.⁴⁹ These techniques offer deterministic control over the number and positioning of building blocks, whether they are plasmonic elements or QDs.⁵⁰ Arraying such materials in a defined fashion further offers the possibility to employ Fano resonances,^51,52 and surface lattice resonances (SLR)^53–56 to control spectral position and increase Q-factors.

Double disc nanoantennas, consisting of two metal nano-discs separated by a thin dielectric spacer are comparably simple cavity structures. Such structures can be conveniently prepared by colloidal lithography with well-defined sizes of the discs and adjustable dielectric spacer.⁵⁷ These structures are also known as metal–insulator–metal architectures,⁵⁸ in-tandem pair,⁵⁹ or nanosandwiches.⁵⁷ The coupling of plasmonic modes of single discs results in hybrid modes that can be characterized by strong field enhancement within the dielectric gap.⁵⁹ The spectral properties of these hybridized plasmonic modes can be tuned by manipulating parameters such as disc size,⁶⁰ material composition,^57,59,60 and spacing.⁶¹ In a modified version, single discs can be positioned on a continuous metal film to form patch antennas.^62–64

The challenge to use such patch or double disc architectures for QD emission enhancement is the inaccessibility of the cavity to the colloidal QDs, which can therefore not be interfaced directly with the hot spot region of high E-fields located within the dielectric spacing layer.²³ One potential solution is to integrate a colloidal QD layer directly as the spacer material during fabrication.⁶ However, the emission properties of the integrated QD layer can be compromised by the fabrication process of double disc antenna architectures, which involve nanolithographic processes such as reactive ion etching.⁶⁵

Here, we propose a conceptually different strategy for the integration of QDs within the plasmon nanocavity formed by a double disc nanoantenna. By decoupling the integration of the QDs into the nanocavity from the fabrication process, we ensure that their emission properties remain intact. First, we use colloidal lithography to fabricate an array of double disc nanoantenna structures consisting of two gold discs separated by a silicon dioxide spacer. We then partially expose the cavity by selectively removing the silicon dioxide spacer via a wet-chemical etching process. Importantly, as the etching proceeds from the outside towards the center of the spacer layer, we can control the region of exposed gap via the etching time and etchant concentration. Finally, we take advantage of capillary forces, which drive particulate materials into small gaps, wedges and other surface features⁶⁶ to position QDs into the opened cavity. We first explore the plasmonic properties of the double disc nanoantenna, in particular as a function of gap exposed, combining experiments and electromagnetic simulations based on the finite-difference time domain (FDTD) method to understand the resultant optical properties. Building on the understanding of these plasmonic modes, we then investigate the emission properties of a layer of colloidal QDs interfaced with the double disc nanoantenna. Our results indicate that the opening of the cavity by etching is central to observe emission enhancement.

Results and discussion

We use colloidal lithography^67–69 to fabricate arrays of double disc nanoantennas in a simple and parallelized way. Fig. 1A schematically illustrates the fabrication process. First, thin films of gold (30 nm thick), silicon dioxide (25 nm thick), and gold (30 nm thick) are deposited on a glass substrate by thermal evaporation. A colloidal monolayer of polystyrene particles with a diameter of around 330 nm preassembled at the air/water interface⁶⁶ is transferred onto the substrate. We then reduce the size of the polystyrene particles using isotropic oxygen plasma to prepare a non-close packed arrangement.⁷⁰ Next, we use a directed reactive ion etching normal to the surface to remove any material not shielded by the particles. Upon removal of the colloidal mask by adhesive tape, an array of double disc nanoantenna structure results. Fig. 1B shows a representative top-view scanning electron microscopy (SEM) image of the fabricated structures array, highlighting the regularity of the individual structures.

Fig. 1 Fabrication of double disc nanoantennas via colloidal lithography. (A) Schematic illustration of the fabrication process. (i & ii) Thin films of gold, SiO₂, and gold are deposited on a substrate. (iii) A colloidal monolayer is deposited onto the substrate and (iv) reduced in size by oxygen plasma. (v) A directed argon-ion etch removes all material not shielded by the templating particles. (vi) An array of double disc nanoantenna finally results after removal of the particles. (B) Top-view scanning electron microscope (SEM) image showing the double disc array.

We now subject the double disc nanoantenna to a basic-pH environment using NaOH solutions with different concentrations to etch the SiO₂ spacer layer separating the two gold nano-discs as schematically illustrated in Fig. 2A. The tilted SEM images of double disc nanoantenna arrays—both without etching and after immersion in 0.4 M or 2 M NaOH solutions for 10 minutes—reveal the morphological changes induced from these etching processes as shown in Fig. 2C. The increased removal of the SiO₂ layer is evident by the visible contour of both discs in the etched samples. In the case of a 4 M NaOH treatment, the SiO₂ layer was completely dissolved, resulting in the removal of the top disc. Only few, separated discs reminiscent of the second disc remained on a single nano-disc array in this case (Fig. S1). Note that due to the fabrication process, the upper gold disc is slightly smaller than the lower gold disc in all our nanoantenna structures. We assess the plasmonic properties of these double disc nanoantenna arrays by measuring absorbance (defined as −log(T), where T is the transmittance) spectra under linearly polarized light for normal incidence (Fig. 2B). When the dielectric SiO₂ layer is etched, the low energy peak undergoes a noticeable blue shift, which is attributed to a reduction in the effective refractive index as the dielectric layer is removed.

Fig. 2 Plasmonic properties of double disc nanoantenna with different degree of cavity opening: (A) illustration of both non-etched and consecutively etched double disc structures with different NaOH concentrations. (B) Experimental (continuous lines) and simulated (dashed lines) absorbance spectra at 0° angle of incidence for three different etching conditions. (C) Side view SEM images highlight the structural transformation and clearly show the opening of a gap in the dielectric SiO₂ layer. Scale bar is 400 nm. (D) Experimental and (E) simulated absorbance spectra for the no-etch (solid lines) and 2 M etch (dashed lines) double disc nanoantenna array under TM excitation with varying angles of incidence.

To estimate the diameter of the remaining SiO₂ layer separating the two gold nano-discs, and the corresponding size of the exposed region (difference in the radius of the SiO₂ spacer before and after etching) in the double disc nanoantenna structures after the etching process, we perform numerical calculations of the extinction spectra at normal incidence where we fix the diameters of the gold discs from SEM images (see Fig. 2C), and considered infinite hexagonal array of double disc nanoantenna over a glass substrate. We estimate the size of the SiO₂ diameter by fitting the theoretical and experimental spectra. The optimization of this diameter ensures that the peak positions in the simulated absorbance spectra closely match those observed in the experimental absorbance measurements (see Fig. 2B; dashed lines). Through this process, we found that the best fit for all three cases was achieved when the metal–insulator–metal thicknesses were set to 20 nm (gold)–35 nm (SiO₂)–20 nm (gold). From the shift of peak positions, we estimate a ∼7% etching of the SiO₂ disc for the 0.4 M NaOH treatment, and a ∼13% etching for the 2 M NaOH treatment. These etch rates correspond to a reduction in SiO₂ disc radius hence a cavity gap opening of ∼20 nm (0.4 M) and ∼40 nm (2 M). To get further insights into the effect of the etching of the gap, as well as into the optical interaction of the double disc surfaces in the nanoantenna array, we measured the absorbance of etched and non-etched structures at incident angles from 0° to 60° using a UV-Vis-NIR spectrometer with a quasi-collimated 2 × 2 mm beam. The sample was mounted on a rotating stage for angle variation. For these angle-dependent measurements, we define TM polarization as the case where the magnetic field is transverse to the plane of incidence. In Fig. 2D and E we show measured and simulated absorbance spectra where one can observe that the absorption peaks of the etched structures at long wavelength are systematically blue-shifted with respect to the non-etched ones. The agreement between experimental and simulated spectra suggests that the experimental etching steps produces well-defined structures with predictable plasmonic properties.

With increasing angle of incidence (AOI), a progressively complex structure of peaks is revealed at shorter wavelengths, with emergence of peak splitting, and disappearance of other peaks. This behavior is connected with the type of plasmonic modes excited at different incident angles, which calls for further analysis of such underlying modes.

To understand the plasmonic properties of the etched double disc nanoantenna arrays under off-normal illumination it is necessary to perform the numerical analysis of the spectra directly from absorption, (1 − R − T, where R is the reflectance and T the transmittance), rather than from the peaks in the absorbance spectra (Fig. 2B, D and E), given by −log(T), which do not allow for unambiguous identification of plasmonic modes with generality, due to the mixing of modes building up some absorbance peaks, as well as to distortions induced by the logarithmic representation of this magnitude. This is indeed a situation often found in absorption spectroscopy, and at times neglected, that we emphasize in the following.

To carry out a proper analysis of the plasmonic modes in our structures, we perform numerical calculations of the absorption spectra of the same structures as in Fig. 2, using the FDTD method implemented in LUMERICAL. Fig. 3A illustrates the geometry and dimensions of the double disc nanoantennas used in the simulations. The absorption spectra in Fig. 3B compare the optical response of the nanoantenna array for different AOIs ranging from 0° to 60°, considering two different loss conditions in the plasmonic material: realistic metallic losses (solid lines) and reduced metallic losses (dashed lines). The latter is implemented because under regular losses (taken the permittivity from Johnson and Christy⁷¹), the plasmonic resonances appear broadened and difficult to resolve, particularly at higher frequencies, due to intrinsic dampening in gold. This broadening results in overlapping modes, making individual plasmonic resonances harder to identify. To address this problem, we performed simulations with the imaginary part of gold's permittivity reduced by a factor of 10, effectively lowering absorption losses and sharpening the spectral features. Indeed, the low loss simulations in Fig. 3B reveals distinct resonance peaks, allowing for clearer mode identification. The resonance positions with increasing AOI remain nearly fixed, indicating strong localization at each double-disc unit and a weak effect of the grating. This behavior is characteristic of localized plasmons, where the individual nanoantenna units dominate the optical response, with the periodic array (grating) having minimal influence on the resonance positions. Although a grating mode is not clearly observable in the spectra, calculations for the hexagonal array confirm the presence of a grating mode (−1, 0) in the 650–750 nm region. This suggests that while the grating effect is weak, it is not entirely absent. Instead of shifting resonance positions, we observe a redistribution of spectral intensities: some modes at higher frequencies decrease in intensity, suggesting a reduced excitation efficiency, while some intermediate modes become more pronounced due to the modified coupling with the illumination. This behavior results from the interplay between the incident wavevector and the symmetries inherent to each mode, which produces a complex balance of activation and deactivation of modes all over the spectrum. Increasing AOI produces more effective coupling of certain symmetries and reduced coupling in others.

Fig. 3 Simulated near electric field and absorption spectra of etched double disc nanoantenna array: (A) schematic illustration of the geometry of the simulated 2 M NaOH etched double disc nanoantenna array. (B) Simulated absorption spectra of the etched nanoantenna array at different AOIs for regular losses (solid lines) and reduced losses (dashed lines). (C) Electric field enhancement (|E(r)/E₀|) distributions in the etched double disc nanoantenna on a glass substrate for reduced-loss simulations. Side profiles and top-view perspectives are displayed for six wavelengths that correspond to distinct peaks in the spectra and that we associate with the modes denoted as S₁₁, S₂₁, S₀₁, S*₃₁, S*₁₂ and S*₀₂ (also labeled in B), all observed at an AOI of 60°. The low-loss spectrum shows a small peak around 1040 nm that indicates the presence of an additional mode, but this peak is not observable in the simulation with realistic losses and should thus not affect the experimental results.

To provide further insights into the properties and symmetries of these plasmonic resonances, we first discuss the modes supported by a cylindrical cavity of radius R, focusing on the spatial field distribution in the middle plane of the gap (Fig. 3C). To a first approximation, this cavity supports S_mn modes corresponding to z-component of the electric fields in this plane E_m,n(r,φ) ∼ J_m(a_mnr/R)cos(mφ), which are solutions of Helmholtz equation in cylindrical coordinates.^72,73 In this expression J_m is the Bessel function of m-th order describing the radial oscillation of the field, and cos(mφ) governs its azimuthal distribution. The a_mn values correspond to the n-th roots of the derivative of the Bessel function of m-th order, i.e., , so that the fields are stronger at the patch edges (taken in our system as the edge of the upper metallic disc), which is consistent with the relatively strong fields in this region in the simulations discussed below. Within this terminology, n is the number of radial nodes along the radial direction (from r = 0 to R) and m denotes the number of azimuthal nodes along a semicircle (from azimuthal angle φ = 0 to π). The top panels in Fig. 3C display the simulated electric field enhancement (|E(r)/E₀|, where E(r) is the total electric field at position r and E₀ is the incident electric field) distributions at the wavelength of the spectral peaks that we associate with the excitation of the S₁₁, S₂₁ and S₀₁ modes. For the analysis of this figure, the simulations are always performed at AOI = 60° in a situation of reduced absorption losses. The side view of the electric field distributions, shown in a vertical cross section through the center of the double disc nanoantennas, highlights the strong field enhancement in the gap between the two gold discs. This enhancement arises from the interaction of charges excited at the inner surfaces of the gold discs, which are separated by the dielectric spacer. Meanwhile, the top view of the electric field distributions, shown in the plane parallel to the gold discs at the center of the SiO₂ gap, reveals the confinement of the fields within the dielectric spacer.

The dipolar mode, S₁₁, is characterized by one radial node and one circular node, with a simple charge distribution featuring two opposing lobes (Fig. 3C, see SI Fig. S2). As expected for a dipolar mode, the intensity of this mode decreases with increasing AOI, consistent with a cos²(θ) dependence. This trend arises from the reduced coupling between the incident electric field and the dipole moment at larger angles. Meanwhile, the resonance wavelength of the mode remains nearly constant across all AOIs, indicating that the spectral position of the mode is robust against angular variations. This behavior highlights the strong localization of the mode within the double disc structure, which minimizes the influence of the incident angle on the resonance condition. The quadrupolar mode, S₂₁, exhibits one radial node, and two circular nodes (from φ = 0 to π), resulting in four charge lobes, and its intensity gradually increases in the spectra at higher AOIs due to stronger coupling efficiency with the incoming light. The S₀₁ mode, a breathing mode, is characterized by one radial node and no circular node, resulting in a rotationally symmetric charge distribution. However, its angular dependence is difficult to observe due to overlap with other modes and the grating mode discussed earlier.

At higher energies, the modes present more complex field distributions, as shown in the bottom panels of Fig. 3C for the spectral peaks attributed to the S*₃₁, S*₁₂, and S*₀₂ modes. These modes exhibit weaker field enhancement, which, together with the presence of many other modes, makes it difficult to assign clear nodal patterns and distinguish them from those of neighboring modes. This complexity justifies the use of the asterisk (*) to indicate that these modes are only tentatively identified, because they are not as well-defined as their lower-energy counterparts. The mode labeled S*₀₂ is particularly difficult to identify, and the field distribution associated with mode S*₃₁ presents a strong contribution from the spectrally-near S₀₁ mode, which explains why the underlying field distribution E_m,n is not directly apparent in the plotted fields without further analysis (SI Fig. S3). Importantly, several modes such as S₁₁, S₂₁, and S*₃₁ show pronounced field enhancements in the outer region of the gap between the metal discs, a region that has become accessible by the etching step. This emphasizes the potential of such etched double-disc nanoantennas for applications in surface-enhanced spectroscopy and photoluminescence enhancement.

From our analysis of the optical properties of the double disc nanoantenna array, we now identify suitable resonances to exploit QD emission enhancement. To achieve this, we focus on the simulated electromagnetic near field distributions and resonance peaks of the sample with the largest gap opening (2 M etch) described in Fig. 3. The high energy absorption peak at ∼680 nm for 60° AOI (Fig. 3B) originates from the spectral overlap of several high-order modes, with main contributions from the S₀₁ and S*₃₁ modes. Other modes (e.g., S*₁₂, S*₀₂, which are more pronounced only under low-loss conditions) can also contribute to the absorption at the 633 nm illumination wavelength. However, their contribution to the electric field enhancement in the gap at this wavelength is found to be weak (Fig. 4A). This peak at ∼680 nm is spectrally close to a 633 nm laser, which we can use experimentally to excite the QDs, thereby leveraging excitation enhancement via these modes. In the same sample, the S₂₁ mode is excited at 852 nm as shown in Fig. 3B. We therefore select PbS QDs with an emission peak at 900 nm and a FWHM of ∼130 nm (SI Fig. S4), as these commercially-sourced QDs exhibit the closest spectral proximity to this mode, potentially enabling emission enhancement via the quantum yield enhancement (discussed below). Note that an emission enhancement via the S₁₁ mode at 1145 nm could be highly beneficial for increasing the excitation enhancement factor due to the large near-field intensity at the accessible position within the opened gap (Fig. 3C). However, in our experiments we failed to identify QDs with a suitable absorption profile and emission stability at this wavelength.

Fig. 4 Simulated emission enhancement of a dipole emitter with the etched double disc nanoantenna structure (40 nm gap opening): (A) electric field enhancement (|E/E₀|) spectra at the QE position within the gap region of the etched double disc nanoantenna for varying AOIs. (B) Simulated Purcell factor (Γ_T/Γ₀), radiative (Γ_R/Γ₀) and non-radiative (Γ_NR/Γ₀) decay rates enhancement of a dipole source placed in the gap region, illustrating how the nanoantenna modifies the emitter's spontaneous emission properties. (C) Excitation enhancement factor (|K|² = |E/E₀|²) calculated at λ_exc = 633 nm for different AOIs, providing insight into how efficiently the structure enhances the illumination of the emitter. (D) Effective quantum yield (η) spectrum of the dipole source within the gap region, highlighting the quantum yield at λ_em = 900 nm.

Having established the plasmonic mode characterization for the double disc nanoantennas with an accessible cavity (2 M NaOH etch, 40 nm gap opening) and identified the required QD excitation and emission wavelengths to suitably take advantage of their plasmonic properties, we next simulate the emission properties of a QD in the double disc nanoantenna structure (Fig. 4A), by considering a point dipole emitter excited at the laser wavelength, located at the center of the edge of the dielectric disc filling the gap, where the E-field peaks in the S* high frequency mode region. The position of the dipole in the vertical direction is chosen to be at equal distance from both the top and the bottom gold surface. We set the intrinsic quantum yield (QY), denoted as η₀, to 0.45 as specified by the supplier of the chosen QDs (SI Fig. S4). To assess the impact of the etched double disc nanoantenna on the photoluminescence properties of a dipole emitter, we analyze its field enhancement, decay rates, excitation efficiency, and quantum yield under different illumination conditions. Fig. 4A presents the simulated electric field enhancement (|E(r_QD)/E₀|) spectra within the gap region at the emitter's position (r_QD), showing how the local field intensity varies with AOI from 0° to 60°. The strongest enhancement occurs at specific resonant wavelengths, revealing very effective excitation conditions for embedded emitters. Fig. 4B illustrates the total decay rate and the corresponding radiative and non-radiative decay rates enhancement of a dipole placed in the nanoantenna gap, demonstrating how the confined plasmonic environment modifies the emitter's emission rate. The radiative decay rate increases significantly for certain resonances, indicating enhanced light extraction efficiency. The excitation enhancement factor, defined as |K|² = |E/E₀|², shown in Fig. 4C, is calculated at the excitation wavelength λ_exc = 633 nm, and exhibits strong AOI dependence with maximum enhancement of up to a factor of 22 at an AOI of 30° (see Table 1). Finally, Fig. 4D presents the quantum yield (η) spectrum of the emitter in the presence of the nanoantenna, where the emission at λ_em = 900 nm is highlighted with a quantum yield of 0.56, showing how the nanoantenna increases the intrinsic radiative yield with a quantum yield enhancement of η/η₀ = 1.24, by balancing radiative enhancement and non-radiative losses. Note that these values arise from the simplified model that uses a point dipole instead of a QD with finite dimensions that can sit closer to the metal surface compared to the point dipole emitter. Table 1 shows the emission enhancement determined from the multiplication of the excitation enhancement and quantum yield enhancement, obtained under these conditions (λ_exc = 633 nm and λ_em = 900 nm). A maximum enhancement by a factor of 27 is obtained at AOI = 30°.

Table 1 Simulated excitation enhancement, quantum yield and emission enhancement for 2 M NaOH etched nanoantennas at various AOIs

AOI (°)	Excitation enhancement (|K|^2) at λexc = 633 nm	Quantum yield enhancement (η/η0) at λem = 900 nm	Emission enhancement (|K|^2 × η/η0)
0	4.7	1.24	5.9
10	8.3		10.3
20	13.6		16.9
30	21.6		26.9
40	21.4		26.63
50	18.3		22.8
60	14.6		18.2

---

To further underline the importance of the accessible gap in the etched double disc nanoantennas, we also simulated two different scenarios: the dipole emitter placed on top of a continuous gold film with a distance of 10 nm, and the dipole emitter placed in the gap of a less etched sample (20 nm gap opening, 0.4 M NaOH treatment, see Fig. 2C). As shown in SI Fig. S5, in both cases, the quantum yield at 900 nm and emission enhancement were lower compared to the double disc with an accessible gap.

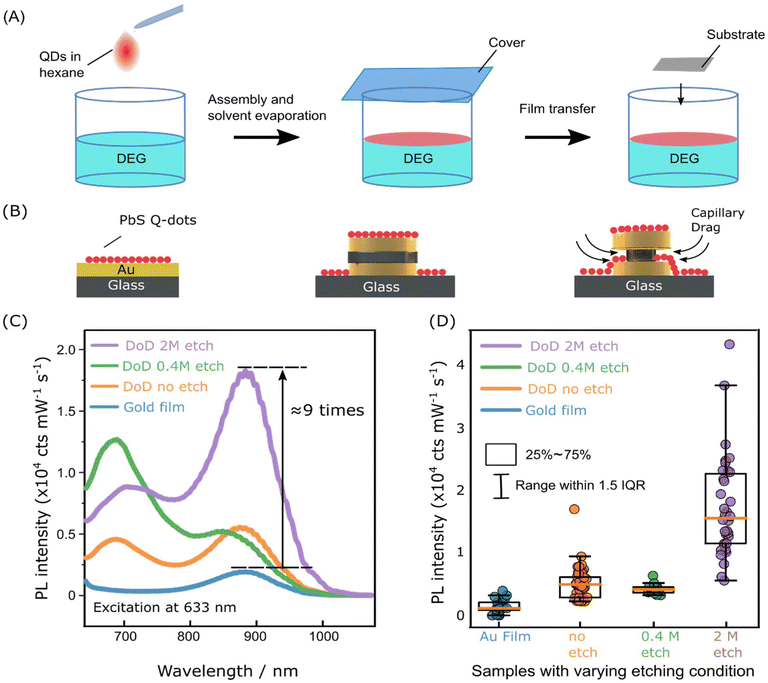
Having explored the potential for emission enhancement through electromagnetic simulations, we now experimentally incorporate QDs into the double disc nanoantenna array with a controlled gap opening. Specifically, we first pre-assemble a colloidal monolayer of PbS QDs with the absorption and emission properties discussed above (633 nm, 900 nm)—at the air/diethylene glycol interface, as illustrated in Fig. 5A.⁷⁴ We then deposit this monolayer onto substrates containing the fabricated nanostructure arrays, as schematically shown in Fig. 5B. This monolayer-based deposition strategy ensures that QDs are distributed uniformly across the entire nanostructure—including both the top surfaces and the gap regions—allowing a direct comparison of the emission properties between different samples: As the total QD coverage remains comparable between all samples (Fig. S6), differences in light emission properties must arise from the structure of the plasmonic nanoantennae, in particular the open gaps in the etched samples.

Fig. 5 PL measurements for different cavity openings: (A) illustration of the deposition of a monolayer of PbS colloidal quantum dots onto the patterned substrate. (B) Illustration of the different QD/nanoantenna samples investigated for photoluminescence enhancement. (C) PL intensity spectra for all different samples. (D) Statistical evaluation of the PL intensity recorded at 900 nm on ∼30 different spots for all samples.

We compare four distinct samples as shown in Fig. 5B: a 30 nm thick continuous gold film as reference, a double disc array without etching step to open the dielectric gap, and two etched double disc arrays, one 0.4 M NaOH etch with small gap opening, and another one 2 M etch with larger cavity opening.

Importantly, when a thin liquid film dries on a structured surface, capillary forces drag the meniscus into small structural features, because of the decreased vapor pressure in these regions.⁷⁵ This effect, commonly used in everyday life to stabilize sand grains in sand castles, serves as an efficient tool to drag the QDs into the small gap opening with enhanced electromagnetic near fields. We uniformly excite all structures using a 633 nm laser, focused by an objective lens (numerical aperture ∼0.9) with a collection angle of ∼60°, consistent with the simulation parameters. The spot size was thus maintained at ∼1 µm. Fig. 5C shows the photoluminescence (PL) intensity as a function of emission wavelength for all the samples. Several features can be identified. First, the broad mode around 700 nm in the PL spectra can be attributed to the nanoantenna structure itself. This effect is more pronounced when using a high-NA objective and is not visible in Fig. 2D, where a loosely focused beam was used (2 mm × 2 mm spot, divergence ≈ 0.57°). Because the Rayleigh anomaly for our 390 nm hexagonal lattice lies below 510 nm, we do not expect any influence of lattice or diffraction-related resonances in the region around 700 nm. To explicitly verify that this feature is not due to QDs, we performed control measurements on bare double-disc nanoantennas. The reflection spectra (SI Fig. S7) clearly show a mode at 700 nm, confirming that the enhanced inelastic scattering arises from the nanoantenna itself. These results directly address the origin of the PL feature and clarify that it is intrinsic to the plasmonic system. Second, at an emission wavelength of 900 nm, which is the maxima for bare QDs (SI Fig. S8), an increase in PL for all QD-coated double disc nanoantennas compared to the continuous gold film reference is observed. The PL intensity is highest for the sample with the large gap opening (2 M etch), which shows an increase of ∼9 times compared to the QDs deposited on the gold film.

For the sample with QDs on the continuous gold film, the QD emission is partially quenched compared to a similar film on a glass substrate (SI Fig. S8). In the case of the double disc nanoantennas with completely closed gap, the capacities for excitation enhancement of the QDs are limited because the region of near field enhancement within the gap is not accessible. Hence, any further increase in emission compared to the gold film can only be provided by a quantum yield enhancement. For the 0.4 M NaOH etch case, the PL intensity increases to a factor of ∼2 compared to the plain gold film (Fig. 5C). Here, the calculated quantum yield enhancement at the gap remains at 1, meaning no enhancement or reduction of the quantum yield is expected (Fig. S5B). The observed emission enhancement is therefore solely attributed to excitation enhancement due to the gap opening, with a calculated excitation enhancement factor of |K|² = 10.2 for AOI = 60° at the excitation wavelength of 633 nm. The sample with the largest gap opening (2 M NaOH etch) exhibits the highest QD PL intensity (Fig. 3C). This higher excitation enhancement is attributed to the increased accessibility of QDs to the high near-field regions within the gap, where the electromagnetic field is most strongly concentrated with a calculated excitation enhancement factor of |K|² = 16.91 weighted average at an AOI range of 0° to 60° and an excitation wavelength of 633 nm. Additionally, the simulated quantum yield enhancement at 900 nm increases to 1.24, compared to ∼1 in the 0.4 M NaOH etch case (Fig. S5B). The experimental results align reasonably well with simulations, supporting the conclusion that increasing the gap opening allows QDs to access regions of high near-field enhancement, leading to enhanced emission. Additionally, the PL enhancement in our system could, in principle, be influenced by possible energy transfer between adjacent QDs through the Förster Resonance Energy Transfer (FRET) mechanism. However, for identical or nearly identical QDs, such homo-FRET typically leads to photoluminescence quenching rather than enhancement,⁷⁶ as energy is funneled to non-emissive or lower-energy QDs (concentration quenching). Therefore, the observed PL enhancement in our case is likely not due to FRET effects.

We further statistically evaluate the emission properties by measuring PL intensities at 900 nm across 30 different spots on the surface for all samples (Fig. 5D). Fig. 5D shows the data of the interquartile range with a black rectangle, encompassing the 25% to 75% range of the PL intensity dataset. The orange line represents the median value. Note that the spread in the data can arise from the small area probed in the microscopic measurements, where each spot size only contains a limited number of individual double discs. For the reference gold film, the median PL intensity is approximately 1567 counts per mW per s, while for the double disc nanoantennas with larger gap opening, it reaches ∼16 228 counts per mW per s, resulting in a ∼10 times PL enhancement.

In conclusion, we prepared double disc nanoantennas by colloidal lithography as a cost-effective and parallel fabrication tool. We controllably open the dielectric gap separating the two gold discs by a selective wet-chemical etching step of the silica spacer. This enables us to access electromagnetic hotspots in the gap between the discs. We first establish the optical properties of the double disc nanoantenna as a function of the gap opening. We then numerically investigate how the emission profile of a dipole emitter placed within the hotspot regions of the opened gap is influenced by the plasmonic modes of the double disc nanoantenna. These simulations identify suitable modes that provide near-field enhancements within the accessible dielectric gap and thus produce an enhancement of emitted light intensity. We take advantage of capillary forces to deposit colloidal QDs within the opened gap of the double disc nanoantenna, and confirm experimentally our theoretical predictions. We demonstrate that the accessibility of the gap provides an experimental ∼10-fold enhancement of the QD photoluminescence compared to the gold film and a ∼3.5-fold enhancement compared to conventional double disc nanoantenna without gap opening prepared under identical conditions and comparable number of QDs deposited onto the antenna structure. Further improvements could be achieved by selectively directing quantum dots toward the hotspot regions through controlled particle–surface interactions or tailored surface chemistries⁷⁷ and could enhance material efficiency and emission performance in future implementations.

Experimental and methods

Sample fabrication

In order to produce double disc nanoantenna structure firstly a 30 nm of gold (HMW Hauner, 99.99%, <3 mm granulate) layer was evaporated followed by a reactive evaporation of 25 nm silicon monoxide (Sigma-Aldrich, powder 325 mesh) and finally again a 30 nm gold thin film was deposited using a custom build thermal evaporator (Torr International Inc, TH3-KW) on a cleaned microscope glass slide (Menzel). Further polystyrene beads were synthesized using a surfactant-free emulsion polymerization and a colloidal monolayer of 330 nm in diameter polystyrene nanoparticles were first assembled at the air/water interface and subsequently transferred on to the thin film deposited glass substrate.

PbS monolayer preparation

PbS quantum dot (QD) solutions (λ_abs = 800 nm, DQD = ∼2.9 nm) are purchased from Quantum Solutions with a concentration of 10 mg ml⁻¹ and intrinsic quantum yield of 0.45 in solution. The QD solution is diluted by 20 times and spread (100 μL) on a diethylene glycol (DEG) surface in a clean Petri dish. The Petri dish is covered with a lid for 10 min to slow down the evaporation of hexane that enables an assembly of close-packed monolayer QDs on the surface. After that, the lid is opened for 5 min to ensure the complete evaporation of hexane. The monolayer QD film is transferred by gently touching the film with a substrate and lifting up. The substrate is rinsed with ethanol to remove the extra DEG and dried with nitrogen.

Photoluminescence measurements

Photoluminescence (PL) spectroscopy is performed using a home-built automated confocal microscopy system. A dark-field objective (Olympus ×100, NA 0.9) focuses a 633 nm excitation laser onto the sample while collecting the emission signal over the same angular range (maximum collection angle: ∼64°). The PL signal is dispersed by a Triax spectrometer equipped with an Andor CCD detector, using a 150 g mm⁻¹ grating. To ensure statistically robust comparison of signal enhancement, measurements are taken at 30 randomly selected locations per sample.

Surface and optical characterization

SEM images were captured using a GeminiSEM 500 (Zeiss, Germany) operating at an accelerating voltage of 2 kV. UV-Vis-NIR spectra were taken using a conventional spectrometer (Lambda 950, PerkinElmer) where sample rotation was performed using a rotating stage mount.

FDTD simulation

The absorbance spectra of the double discs structures were computed using the finite-difference time-domain (FDTD) method.⁷⁸ The electrodynamical model involved sandwiched gold–silica–gold nano-disc (double disc nanoantenna structures) positioned within the lattice sites of a hexagonal array unit cell. These sandwiched structures were supported on a glass substrate, precisely placed within a cubic-space simulation domain. The simulation domain was bounded in the x and y directions by Bloch periodic boundaries to reproduce an infinite array and in the z direction by perfect matched layers (PML) consisting of 60 layers. To induce excitation, TM polarized light was utilized within the wavelength range spanning from 400 nm to 1500 nm. A two-dimensional transmission monitor was situated beneath the array on the substrate, measuring the electromagnetic power transmitted through the array, and a similar monitor above the system to measure the reflected power by the system. Calculation of absorbance was executed via the well-established Beer–Lambert law, expressed as A = −log(T), where A represent absorbance and T transmittance, and the absorption was calculated by 1 − R − T where R represents the reflectance. E-Field maps encompassing the xz cross-section (side view), along with charge density distribution within the double disc structures, were determined using E-field monitors. The latter calculation employed the relationship ρ = ε₀∇·E, wherein ρ and ε₀ represent the charge density and the dielectric constant, respectively. For the purpose of computing the quantum yield, η = Γ_rad/Γ₀/(Γ_tot/Γ₀ + k_nr/Γ₀), of a quantum emitter situated within a double disc nanoantenna structure, the emitter was modeled as an electric dipole source oriented perpendicular to the metal discs (Z-direction)⁷⁹ emitting light at a wavelength within the 400 nm to 1200 nm range. Here, k_nr represents the intrinsic non-radiative decay rate of the quantum emitter which is related to the intrinsic quantum yield through η₀ = Γ₀/(Γ₀ + k_nr). Subsequently, the emitted power from the dipole source in isolation (P_0,dip), in conjunction with its corresponding value within the double disc nanoantenna structure (P_dip), and the power radiated into the far field of the dipole-double disc nanoantenna system (P_out), were determined. To accomplish this, 3D transmission monitor was positioned around the dipole source to capture P_0,dip in the absence of the nanoantenna, while in another configuration a 3D transmission monitor was positioned around the dipole source in the presence of the nanoantenna to capture P_dip and another 3D transmission monitor encompassed both the dipole source and the nanoantenna to monitor P_out. As per the methodology outlined in Kaminski et al.,⁸⁰ the normalized total and radiative decay rates were computed as Γ_tot/Γ₀ = P_dip/P_0,dip and Γ_rad/Γ₀ = P_out/P_0,dip, respectively. PML boundary conditions were used for the simulation domain.

Throughout all simulations, the refractive index for gold material was taken from Johnson and Christy,⁷¹ except for those with reduced losses in which the imaginary part was divided by 10, while that for SiO₂ was extracted from ref. 81. To simplify the background medium, a vacuum condition (n_m = 1) was adopted. Additionally, the Courant number was maintained below 0.9 by adjusting spatial and temporal resolutions to ensure numerical convergence.

The diffraction modes of the hexagonal array were computed based on the following equation from Brakstad et al.:⁸²

In this equation, k represents the light wavevector in free space, θ₀ signifies the AOI of the incoming light, and 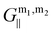and ϕ_m1,m2 are defined for the hexagonal array as follows:

Here, m₁ and m₂ denote the diffraction modes, and a represents the lattice parameter.

Author contributions

V. G. and J. L. M. P. contributed equally to this work. N. V., J. A., and J. J. B. conceived the idea and supervised the project. V. G. and E. S. A. G. fabricated the etched double disc nanoantenna array and performed optical measurements. S. H. incorporated QDs and carried out PL enhancement measurements. J. L. M. P., M. Z. H., R. E., N. Z., and J. A. performed the FDTD simulation-based study and analyzed the optical modes and Purcell enhancement inside the cavity. All authors reviewed and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are publicly available via zenodo under the following https://doi.org/10.5281/zenodo.15591604.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5nr03524d.

Acknowledgements

This project received funding from the European Union's Horizon 2020 Research and Innovation Programme under grant agreement no. 861950, project POSEIDON. J. L. M.-P. acknowledges the financial support received from the IKUR Strategy under the collaboration agreement between the Ikerbasque Foundation and Materials Physics Center on behalf of the Department of Science, Universities and Innovation of the Basque Government. M. Z.-H., R. E, N. Z. and J. A. acknowledge grant PID2022-139579NB-I00 funded by MICIU/AEI/10.13039/501100011033 and by ERDF, EU, as well as financial support from the Department of Science, Universities and Innovation of the Basque Government through project no. IT 1526-22 and from the Department of Economy of the Basque Government through project 4usmart Elkartek. N. V. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project-ID 416229255 – SFB 1411. J. L. M.-P., M. Z.-H., R. E., N. Z. and J. A. acknowledge the technical and human support provided by the DIPC Supercomputing Center, where the simulations were performed.

References

1. E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419.
2. W. Zhu, R. Esteban, A. G. Borisov, J. J. Baumberg, P. Nordlander, H. J. Lezec, J. Aizpurua and K. B. Crozier, Nat. Commun., 2016, 7, 11495.
3. P. Nordlander, C. Oubre, E. Prodan, K. Li and M. I. Stockman, Nano Lett., 2004, 4, 899.
4. F. Le, D. W. Brandl, Y. A. Urzhumov, H. Wang, J. Kundu, N. J. Halas, J. Aizpurua and P. Nordlander, ACS Nano, 2008, 2, 707.
5. H. Yu, Y. Peng, Y. Yang and Z. Y. Li, npj Comput. Mater., 2019, 5, 1.
6. J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen and D. R. Smith, Nat. Mater., 2019, 18, 668.
7. N. A. Güsken, M. Fu, M. Zapf, M. P. Nielsen, P. Dichtl, R. Röder, A. S. Clark, S. A. Maier, C. Ronning and R. F. Oulton, Nat. Commun., 2023, 14, 1.
8. B. Sepúlveda, P. C. Angelomé, L. M. Lechuga and L. M. Liz-Marzán, Nano Today, 2009, 4, 244.
9. A. G. Brolo, Nat. Photonics, 2012, 6, 709.
10. L. Rodríguez-Lorenzo, R. De La Rica, R. A. Álvarez-Puebla, L. M. Liz-Marzán and M. M. Stevens, Nat. Mater., 2012, 11, 604.
11. V. Gupta, S. Sarkar, O. Aftenieva, T. Tsuda, L. Kumar, D. Schletz, J. Schultz, A. Kiriy, A. Fery, N. Vogel and T. A. F. König, Adv. Funct. Mater., 2021, 31, 2105054.
12. L. Wen, Z. Sun, Q. Zheng, X. Nan, Z. Lou, Z. Liu, D. R. S. Cumming, B. Li and Q. Chen, Light: Sci. Appl., 2023, 12, 76.
13. X. Shi, K. Ueno, T. Oshikiri, Q. Sun, K. Sasaki and H. Misawa, Nat. Nanotechnol., 2018, 13, 953.
14. C. T. Dinh, T. Burdyny, G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. Pelayo García de Arquer, A. Kiani, J. P. Edwards, P. De Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783.
15. E. Cortés, L. V. Besteiro, A. Alabastri, A. Baldi, G. Tagliabue, A. Demetriadou and P. Narang, ACS Nano, 2020, 14, 16202.
16. J. L. Montaño-Priede, M. Zapata-Herrera, R. Esteban, N. Zabala and J. Aizpurua, Nanophotonics, 2024, 13, 4771.
17. F. Benz, M. K. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. De Nijs, R. Esteban, J. Aizpurua and J. J. Baumberg, Science, 2016, 354, 726.
18. S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 17402.
19. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 3.
20. S. Hu, E. Elliott, A. Sánchez-Iglesias, J. Huang, C. Guo, Y. Hou, M. Kamp, E. S. A. Goerlitzer, K. Bedingfield, B. de Nijs, J. Peng, A. Demetriadou, L. M. Liz-Marzán and J. J. Baumberg, Adv. Sci., 2023, 10, 1.
21. C. Vietz, I. Kaminska, M. Sanz Paz, P. Tinnefeld and G. P. Acuna, ACS Nano, 2017, 11, 4969.
22. T. H. Taminiau, F. D. Stefani, F. B. Segerink and N. F. Van Hulst, Nat. Photonics, 2008, 2, 234.
23. A. R. Dhawan, C. Belacel, J. U. Esparza-Villa, M. Nasilowski, Z. Wang, C. Schwob, J. P. Hugonin, L. Coolen, B. Dubertret, P. Senellart and A. Maître, Light: Sci. Appl., 2020, 9, 33.
24. A. Singh, P. M. de Roque, G. Calbris, J. T. Hugall and N. F. van Hulst, Nano Lett., 2018, 18, 2538.
25. H. Altug, S.-H. Oh, S. A. Maier and J. Homola, Nat. Nanotechnol., 2022, 17, 5.
26. A. Kinkhabwala, Z. Yu, S. Fan, Y. Avlasevich, K. Müllen and W. E. Moerner, Nat. Photonics, 2009, 3, 654.
27. K. Trofymchuk, K. Kołątaj, V. Glembockyte, F. Zhu, G. P. Acuna, T. Liedl and P. Tinnefeld, ACS Nano, 2023, 17, 1327–1334.
28. C. B. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706.
29. A. L. Efros and L. E. Brus, ACS Nano, 2021, 15, 6192.
30. G. L. Whitworth, C. Roda, M. Dalmases, N. Taghipour, M. Dosil, K. Nikolaidou, H. Dehghanpour and G. Konstantatos, Adv. Mater., 2025, 37, 2410207.
31. W. Xie, R. Gomes, T. Aubert, S. Bisschop, Y. Zhu, Z. Hens, E. Brainis and D. Van Thourhout, Nano Lett., 2015, 15, 7481.
32. M. Barelli, C. Vidal, S. Fiorito, A. Myslovska, D. Cielecki, V. Aglieri, I. Moreels, R. Sapienza and F. Di Stasio, ACS Photonics, 2023, 10, 1662.
33. A. P. Litvin, A. A. Babaev, A. Dubavik, S. A. Cherevkov, P. S. Parfenov, E. V. Ushakova, M. A. Baranov, O. V. Andreeva, F. Purcell-Milton, Y. Gun'ko, A. V. Fedorov and A. V. Baranov, Adv. Opt. Mater., 2018, 6, 1.
34. R. Saran and R. J. Curry, Nat. Photonics, 2016, 10, 81.
35. F. C. J. M. Van Veggel, Chem. Mater., 2014, 26, 111.
36. M. Mayer, L. Scarabelli, K. March, T. Altantzis, M. Tebbe, M. Kociak, S. Bals, F. J. García de Abajo, A. Fery and L. M. Liz-Marzán, Nano Lett., 2015, 15, 5427.
37. K. H. Song, C. Kim, C. M. Cobley, Y. Xia and L. V. Wang, Nano Lett., 2009, 9, 183.
38. F. Hao, C. L. Nehl, J. H. Hafner and P. Nordlander, Nano Lett., 2007, 7, 729.
39. L. Gunnarsson, T. Rindzevicius, J. Prikulis, B. Kasemo, M. Käll, S. Zou and G. C. Schatz, J. Phys. Chem. B, 2005, 109, 1079.
40. D. Dregely, M. Hentschel and H. Giessen, ACS Nano, 2011, 5, 8202.
41. S. Hu, J. Huang, R. Arul, A. Sánchez-Iglesias, Y. Xiong, L. M. Liz-Marzán and J. J. Baumberg, Nat. Commun., 2024, 15, 6835.
42. R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Nature, 2016, 535, 127.
43. Y. Huang, L. Ma, M. Hou, J. Li, Z. Xie and Z. Zhang, Sci. Rep., 2016, 6, 30011.
44. J. H. Yoon, F. Selbach, L. Langolf and S. Schlücker, Small, 2018, 14, 1702754.
45. S. Verlekar, M. Sanz-Paz, M. Zapata-Herrera, M. Pilo-Pais, K. Kołątaj, R. Esteban, J. Aizpurua, G. P. Acuna and C. Galland, ACS Nano, 2025, 19, 3172.
46. V. Gupta, P. T. Probst, F. R. Goßler, A. M. Steiner, J. Schubert, Y. Brasse, T. A. F. König and A. Fery, ACS Appl. Mater. Interfaces, 2019, 11, 28189.
47. T. Kraus, L. Malaquin, H. Schmid, W. Riess, N. D. Spencer and H. Wolf, Nat. Nanotechnol., 2007, 2, 570.
48. H. Zhang, J. Cadusch, C. Kinnear, T. James, A. Roberts and P. Mulvaney, ACS Nano, 2018, 12, 7529.
49. S. Ni, L. Isa and H. Wolf, Soft Matter, 2018, 14, 2978.
50. O. Aftenieva, J. Brunner, M. Adnan, S. Sarkar, A. Fery, Y. Vaynzof and T. A. F. König, ACS Nano, 2023, 17, 2399.
51. R. Verre, Z. J. Yang, T. Shegai and M. Käll, Nano Lett., 2015, 15, 1952.
52. B. Luk'Yanchuk, N. I. Zheludev, S. A. Maier, N. J. Halas, P. Nordlander, H. Giessen and C. T. Chong, Nat. Mater., 2010, 9, 707.
53. V. G. Kravets, A. V. Kabashin, W. L. Barnes and A. N. Grigorenko, Chem. Rev., 2018, 118, 5912.
54. B. Auguié and W. L. Barnes, Phys. Rev. Lett., 2008, 101, 143902.
55. V. Gupta, O. Aftenieva, P. T. Probst, S. Sarkar, A. M. Steiner, N. Vogel, A. Fery and T. A. F. König, Adv. Photonics Res., 2022, 3, 2200152.
56. M. Kularia, O. Aftenieva, S. Sarkar, A. M. Steiner, V. Gupta, A. Fery, J. Joseph, M. A. Schmidt and T. A. F. König, J. Polym. Sci., 2023, 61, 1893.
57. A. Dmitriev, T. Pakizeh, M. Käll and D. S. Sutherland, Small, 2007, 3, 294.
58. G. Schaffernak, M. K. Krug, M. Belitsch, M. Gašparić, H. Ditlbacher, U. Hohenester, J. R. Krenn and A. Hohenau, ACS Photonics, 2018, 5, 4823.
59. Y. Ekinci, A. Christ, M. Agio, O. J. F. Martin, H. H. Solak and J. F. Löffler, Opt. Express, 2008, 16, 13287.
60. A. B. Yankovich, R. Verre, E. Olsén, A. E. O. Persson, V. Trinh, G. Dovner, M. Käll and E. Olsson, ACS Nano, 2017, 11, 4265.
61. K. H. Su, Q. H. Wei and X. Zhang, Appl. Phys. Lett., 2006, 88, 63118.
62. C. Belacel, B. Habert, F. Bigourdan, F. Marquier, J.-P. Hugonin, S. Michaelis de Vasconcellos, X. Lafosse, L. Coolen, C. Schwob, C. Javaux, B. Dubertret, J.-J. Greffet, P. Senellart and A. Maitre, Nano Lett., 2013, 13, 1516.
63. R. Esteban, T. V. Teperik and J. J. Greffet, Phys. Rev. Lett., 2010, 104, 1.
64. C. Zhang, J. P. Hugonin, J. J. Greffet and C. Sauvan, ACS Photonics, 2019, 6, 2788.
65. A. R. Dhawan, M. Nasilowski, Z. Wang, B. Dubertret and A. Maître, Adv. Mater., 2022, 34, 2108120.
66. S. Ni, H. Wolf and L. Isa, Langmuir, 2018, 34, 7.
67. T. Qiu, E. M. Akinoglu, B. Luo, M. Konarova, J.-H. Yun, I. R. Gentle and L. Wang, Adv. Mater., 2022, 34, 2103842.
68. N. Vogel, C. K. Weiss and K. Landfester, Soft Matter, 2012, 8, 4044.
69. A. Al-Hamadani, V. Gupta, J. L. Montaño-Priede, R. Thomas, A. Muravitskaya, L. Markey, C. Roux-Byl, T. Pons, M. Zapata-Herrera, N. Zabala, J.-C. Weeber, S. Suckow, N. Vogel, J.-S. G. Bouillard and A. M. Adawi, ACS Appl. Nano Mater., 2025, 8, 19474.
70. F.-P. Schmidt, H. Ditlbacher, U. Hohenester, A. Hohenau, F. Hofer and J. R. Krenn, Nano Lett., 2012, 12, 5780.
71. P. B. Johnson and R. W. Christy, Phys. Rev. B, 1972, 6, 4370.
72. J. D. Jackson, Classical electrodynamics, John Wiley & Sons, 1998.
73. F. Minkowski, F. Wang, A. Chakrabarty and Q.-H. Wei, Appl. Phys. Lett., 2014, 104, 021111.
74. A. Dong, J. Chen, P. M. Vora, J. M. Kikkawa and C. B. Murray, Nature, 2010, 466, 474.
75. N. Vogel, M. Retsch, C.-A. Fustin, A. del Campo and U. Jonas, Chem. Rev., 2015, 115, 6265.
76. M. Chern, R. Toufanian and A. M. Dennis, Analyst, 2020, 145, 5754.
77. E. S. A. Goerlitzer, L. E. Speichermann, T. A. Mirza, R. Mohammadi and N. Vogel, Nanoscale Adv., 2020, 2, 394.
78. “Lumerical Inc.”.
79. L. A. Blanco and F. J. García de Abajo, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 205414.
80. F. Kaminski, V. Sandoghdar and M. Agio, J. Comput. Theor. Nanosci., 2007, 4, 635–643.
81. E. D. Palik, Handbook of Optical Constants of Solids, Academic Press, Boston, 1985.
82. T. Brakstad, M. Kildemo, Z. Ghadyani and I. Simonsen, Opt. Express, 2015, 23, 22800.

---