Structure and mechanical properties of grain boundaries in molybdenum disulfide (MoS₂)

Abstract

Molybdenum disulfide (MoS₂) is a two-dimensional material widely used as a lubricant in many applications involving mechanical loading under a wide range of operating temperatures. Since many synthesis and processing techniques yield MoS₂ in its polycrystalline form, establishing grain boundary (GB) structure–property relations is key to designing MoS₂ microstructures with tailored properties. Here, we employ classical, reactive atomistic simulations to investigate the structure and mechanical behavior of a wide range of GBs in MoS₂ as a function of temperature. Using a bicrystal MoS₂ geometry, we characterize the atomic structure and calculate the energy of several low-angle GBs. Then, we simulate the tensile deformation behavior of MoS₂ bicrystals at several temperatures. Our results reveal that at temperatures above 100 K, the deformation of MoS₂ bicrystals is characterized by the nucleation of shear bands from GBs that grow, with subsequent loading, into the MoS₂ crystals. At low temperatures, the tensile deformation is characterized by the nucleation and propagation of deformation fronts, resulting in altered bond angles and bond lengths. Quantitative analysis reveals a decrease in the ultimate tensile stress and ultimate failure strain of MoS₂ bicrystals with the increase in temperature. Furthermore, our simulations of the mechanical behavior of metastable GBs reveal that the strength and ductility decrease with the increase in energy of these boundary structures. In broad terms, our work provides future avenues to employ GB engineering as a strategy to tailor the properties of MoS₂ microstructures.

---

Introduction

Molybdenum disulfide (MoS₂), a two-dimensional (2D) transition-metal dichalcogenide, exhibits a compelling combination of engineering and functional properties. MoS₂ layers have been found to possess high in-plane stiffness of ∼200 GPa,^1,2 an ultimate tensile strain of ∼0.3,³ and even exhibit self-healing behavior after mechanical damage.⁴ Its layered structure, characterized by weak van der Waals interactions between sheets, gives rise to exceptionally low friction coefficients and outstanding tribological performance.^5–7 Furthermore, monolayer MoS₂ exhibits a direct band gap of ∼1.8 eV,⁸ which can be tuned via strain⁹ or polymorphic phase transitions,^10–12 enabling tunable functionality through heterostructure engineering. These unique properties make MoS₂ a highly versatile material platform with applications spanning solid lubrication,⁶ electronics,¹³ photovoltaics,¹⁴ transistors,¹⁵ and catalysis.¹⁶

To enable the use of MoS₂ in the above-mentioned applications, scalable processing routes, such as chemical vapor deposition,^17,18 have been employed to synthesize large-area polycrystalline MoS₂.^19–24 These 2D sheets are composed of differently oriented crystalline grains that are joined at grain boundaries (GBs). In these materials, GBs often exhibit arrangements of atomic rings, or ring motifs, and can include combinations of four-, five-, six-, seven-, and eight-membered rings. These motifs have been observed and characterized in both experimental and computational studies.^21,25,26 Several studies revealed that GBs and their atomic structures play a critical role in determining the properties and functionalities of polycrystalline MoS₂. For example, experimental studies showed that GBs can lead to significant variations in the band gap,^27,28 and that electrical conduction can be modulated by engineering the GB structure and its alignment with the conducting channel.^22,29,30 Computational and experimental studies demonstrated that the thermal conductivity across GBs is highly sensitive to their atomic structure.^31–35 Moreover, recent studies revealed that GBs can impart new functional capabilities to MoS₂. Shen et al.³⁶ exploited GBs as sub-nanometer pores, enabling selective water transport and ion rejection without the need for artificial pore drilling. Zhao et al.³⁷ demonstrated that GBs can activate the otherwise inert basal plane of monolayer MoS₂, facilitating CO₂ reduction through localized electronic modification. Yan et al.³⁸ showed that metal atoms can penetrate along GBs in multilayer MoS₂, forming conductive filaments that govern resistive switching in memristive devices.

Beyond its functional properties, many applications of MoS₂ rely on its mechanical and tribological behavior. For example, in flexible electronics such as foldable displays, stretchable sensors, and wearable biomedical devices, MoS₂ must withstand repeated bending and stretching without failure.³⁹ In applications involving nano-electro-mechanical systems, its atomic-scale thickness and high Young's modulus permit robust, low-mass resonators and switches.⁴⁰ MoS₂ is also widely used as a solid lubricant in spacecraft mechanisms, where components experience large temperature changes.⁴¹ Because friction and wear vary strongly with temperature, the low-temperature mechanical behavior of MoS₂ has attracted substantial interest. Experiments on MoS₂ films tested between 298 K and 473 K revealed lower wear but higher friction coefficients at lower temperatures.⁴² Similarly, a different study at temperatures below 250 K also reported an increase in the friction coefficient of MoS₂ as the temperature decreases.⁴³ At even lower temperatures, ∼4 K in liquid helium, tribological tests on MoS₂/Cr coatings revealed that the friction coefficient of MoS₂ remained low, yet the wear life decreased dramatically.⁴⁴

These application-driven demands have motivated prior studies aimed at understanding the mechanical behavior of MoS₂. For example, atomistic simulations revealed an inverse Hall-Petch behavior in which the mechanical strength of polycrystalline MoS₂ sheets decreases with decreasing grain size.⁴⁵ This trend was corroborated by Sabbaghi et al.,⁴⁶ who observed a similar grain-size dependence on fracture strength. MoS₂ bicrystal sheets with GB misorientations of 30° and 45° were found to have lower mechanical strength than single crystal sheets.⁴⁷ Wang et al.⁴⁸ reported that GBs composed of eight-membered ring motifs exhibit higher fracture resistance than boundaries with four-membered rings. In a study exploring the strain dependence of the optical properties of polycrystalline MoS₂, complete strain transfer across GBs was observed when MoS₂ sheets were loaded in tension.⁴⁹ Another study revealed reduction of stresses at GBs due to the accumulation of nanopores.⁵⁰

While the above-mentioned investigations highlight the key role that GBs play in controlling the properties of MoS₂, absent from such investigations is a detailed exploration of the geometry and atomic structure of GBs and their impact on the mechanical properties of MoS₂ sheets as a function of temperature. Furthermore, the impact of metastable GB structures on the mechanical properties of MoS₂ remains unexplored. Recent advances in materials synthesis and processing techniques have enabled the fabrication of far-from-equilibrium materials nanostructures, including non-equilibrium GB structures.^51,52 Indeed, recent studies explored the impact of GB metastability on boundary and bulk properties in metallic systems.^53–57 Here we use classical, reactive atomistic simulations to investigate the atomic structures and energies of GBs in MoS₂ as a function of boundary geometry, and to examine the temperature dependence of the deformation behavior of MoS₂. We further identify multiple metastable GB configurations, quantify their boundary energies, and explore their impact on the mechanical properties of monolayer MoS₂. We construct a series of 2D bicrystal MoS₂ sheets with various GB misorientations. For each GB geometry, we report several GB atomic structures and their resultant boundary energies. Then we investigate the tensile deformation behavior of MoS₂ bicrystals as a function of GB geometry at temperatures in the range 5 K to 300 K. By correlating the mechanical response with the GB atomic structure, our work provides avenues for employing GB engineering to tailor the mechanical properties of polycrystalline MoS₂ sheets.

Methods

We leverage classical atomistic simulations employing Molecular Statics (MS) and Molecular Dynamics (MD) to examine the impact of GB structure and geometry on the mechanical behavior of MoS₂ sheets at various temperatures. All atomistic simulations reported in this work were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)⁵⁸ and visualizations of atomistic structures were generated using OVITO.⁵⁹

A series of monolayer MoS₂ sheets with symmetric GBs were generated using a recently developed ReaxFF^60,61 bond order potential, fit to an extensive set of density functional theory (DFT) calculations with the aim of accurately describing the thermodynamic and physical properties of MoS₂ sheets and point defect energies. This ReaxFF potential has previously been used to explore the mechanical properties of MoS₂.^47,62–67 For example, Shi et al.⁶⁸ employed this ReaxFF potential to investigate the deformation and tribological response of monolayer MoS₂ over a broad temperature range spanning 1–600 K. We consider ten GB misorientations in MoS₂ bicrystals that were generated using the γ-surface method.⁶⁹ For each MoS₂ bicrystal, a fully periodic system was created from two MoS₂ half-crystals, each of which was rotated from the original armchair configurations such that the resulting GB (line) between the half-crystals had the prescribed misorientation angle θ and the corresponding Σ value, where 1/Σ represents the fraction of lattice points that are in coincidence,⁷⁰ see Fig. S1 for representative dichromatic patterns of the Σ37 and Σ19 GBs. Fig. 1(a) shows a schematic of our monolayer MoS₂ bicrystal geometry, where the GB plane normal aligns with the global x-axis and L_x, L_y, and L_z are the dimensions describing the size of the atomistic simulation box. Once generated, a sequence of relatively small displacements of 0.2 Å along the y-direction [see Fig. 1(a)] between the two MoS₂ half-crystal sheets was used in conjunction with conjugate gradient energy minimizations to identify low-energy GB configurations. The MoS₂ bicrystal sheets were allowed to expand or contract along the x-direction perpendicular to the GB plane. Following an initial 0 K energy minimization, with a force tolerance of 1 × 10⁻⁸ (kcal mol⁻¹) Å⁻¹ and relative energy tolerance of 1 × 10⁻⁸, the MoS₂ bicrystals were annealed at 10 K for 5 ps in the NPT ensemble with a Berendsen barostat⁷¹ to maintain zero pressure, then brought back to 0 K and their energy minimized while allowing the simulation box to expand or contract to maintain zero pressure. For each GB geometry, a stoichiometric bounding box that encompasses the GB at the center of the MoS₂ sheet and extends into the monolayer was selected and used to calculate the GB energy γ_gb as

Fig. 1 Grain boundaries in MoS₂. (a) A schematic of the monolayer MoS₂ bicrystal geometry employed in this work, where L_x, L_y, and L_z are the dimensions describing the size of the simulation box. (b) The GB energy as a function of misorientation angle using the γ-surface method. Red stars correspond to the 5|7 ring structures and cyan circles represent all other structures. (c) Atomic structures of three GBs with misorientation angles of 1.3°, 5.1°, and 13.2°. Increasing the misorientation angle corresponds to a decrease in the spacing between the 5|7 ring structures.

Here, E_tot is the total energy of all MoS₂ unit cells in the bounding box, E_unit is the energy of one unit of MoS₂, N_tot is the number of MoS₂ unit cells in the bounding box, and L_y is the relaxed sheet width.

Following the construction of the MoS₂ bicrystals, we performed MD simulations of uniaxial tension along the x-axis of each sample at temperatures in the range 5 K to 300 K, while keeping the pressure in the transverse y-direction at zero to allow for lateral expansion/shrinkage. We defined upper and lower atomic slabs [refer to Fig. 1(a)] of width ∼2 nm in which the z-component of the velocities and forces of all atoms were set to zero. The MoS₂ bicrystals were brought to the desired temperature and annealed for 50 ps using the NPT ensemble with a Berendsen barostat to maintain zero pressure components along the x and y directions. After annealing, the x- and z-components of the velocities and forces of all atoms in the lower slab were set to zero. Uniaxial tension was applied by moving all fixed atoms of the upper slab along the x-direction with a constant velocity ranging from 0.04–0.4 Å ps⁻¹ resulting in strain rates in the range 10⁸–10⁹ s⁻¹. In all cases the lower slab remained fixed in both the x and z directions. The nominal strain along the x-direction of the sample was calculated as ε = ΔL_x/L_x(0), where L_x(0) is the initial length. To obtain tensile stress–strain diagrams, the per-atom virial stress⁷² was summed over all dynamic atoms in the sheet (i.e., excluding the upper and lower atomic slabs) and normalized by the volume of the sheet assuming a thickness of 6.1 Å.⁶⁰ We also used the per-atom shear strain⁷³ implemented in Ovito as 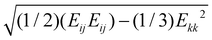, where E_ij are the Green-Lagrange strains and Einstein summation convention is invoked.

Here, we emphasize the computational scope of our study. We employ atomistic simulations to investigate ten distinct GB misorientations, along with their associated metastable configurations identified via the γ-surface method. Subsequently, the mechanical response of these GB structures is examined across a temperature range of 5–300 K. To account for sample-to-sample variations, multiple independent runs are performed for each simulation exploring the mechanical behavior of MoS₂. The total number of simulations of GB systems performed in this work is ≈1000, and the number of atoms in each GB system is in the range of 14 000 to 37 000 atoms.

Results and discussion

Atomic structure and energy of GBs in MoS₂

We start by investigating the atomic structure and energy of GBs in MoS₂. Fig. 1(b) shows a plot of the GB energy as a function of misorientation angle θ, where for each angle θ the energies of all structures resulting from the γ-surface search are shown in cyan circles. The energies of GBs with 5|7 structural motifs are identified with red stars. Such motifs are commonly observed in experimental studies of MoS₂ GBs.^21,74–76 Several key observations emerge from Fig. 1(b). First, for a given misorientation angle, there is considerable variation in GB energies for the structures generated using the γ-surface search. Second, in the low-angle regime, GBs with the 5|7 structural motifs are the lowest energy boundaries based on the γ-surface method and all others are metastable structures. Third, the number density of these 5|7 motifs (i.e., number per unit length of GB) increases with the misorientation angle θ. Fig. 1(c) shows representative GBs with misorientation angles θ = 1.3°, 5.1° and 13.2°, which reveal an increase in the density of 5|7 motifs with the misorientation angle. A study combining DFT and microscopy on low-angle (3–4°) MoS₂ GBs revealed 5|7 ring motifs⁷⁴ in agreement with the structures we obtained for the Σ271 and Σ127 GBs, see Fig. 1(b) and (c). Another DFT study by Gao et al.⁷⁷ identified 5|7 ring motifs for the GB with a misorientation angle of 12.5°. The interested reader is referred to Fig. S2 for close-up views of the atomic structures of all GB misorientations explored in this work. In the Read-Shockley dislocation model of low-angle GBs, the dislocation spacing within the dislocation array that makes up the GB decreases with increasing misorientation angle,⁷⁸ and this is clearly visible in Fig. 1(c) for 5|7 motifs. For a validation of this particular motif, we performed DFT-based, see SI for details, structural optimization of the 5|7 motif for the Σ19 GB. Fig. S6 in the SI shows the agreement between DFT and ReaxFF structures for this particular boundary. Fourth, Fig. 1(b) shows that at misorientation angles θ ≳ 7°, GB structures with energy lower than those with 5|7 motifs emerge. For example, for the GB with θ = 13.2° Fig. 2 shows several atomic structures of this GB generated using the γ-surface method, where the insets provide schematics of the rings that define the boundary motifs. Fig. 2(a) shows the boundary with 4|4 structural motifs which has the lowest energy of γ_gb = 2.4 eV nm⁻¹. Fig. 2(b) and (c) shows metastable structures, where the GB with 5|7 motifs and energy of γ_gb = 3.2 eV nm⁻¹ is shown in Fig. 2(b) and the one with a more complex 5|8|4|7 motif and boundary energy of γ_gb = 7.8 eV nm⁻¹ is shown in Fig. 2(c). Here, we note that for all GBs generated in this work the MoS₂ bicrystals were annealed at 10 K for 5 ps to ensure local structural relaxations and help avoid the generation of unstable GBs. The results depicted in Fig. 1(b) and 2 reveal a plethora of MoS₂ GB structures with large variations in energy even for the same GB geometry (i.e., misorientation angle and plane normal).

Fig. 2 Metastable grain boundaries in MoS₂. For the Σ19 GB with a misorientation angle of 13.2°: (a) the lowest energy GB structure with 4|4 motifs and energy γ_gb = 2.4 eV nm⁻¹, (b) GB structure with 5|7 motifs and energy γ_gb = 3.2 eV nm⁻¹, and (c) GB structure with 5|8|4|7 motifs and a boundary energy of γ_gb = 7.8 eV nm⁻¹. The insets show schematics of polygons to reveal the GB ring structures.

Role of GBs in the mechanical behavior of MoS₂

We now direct our attention to the impact of GB structure and geometry on the mechanical behavior of MoS₂ bicrystals at 300 K. For all boundary misorientations explored in this work, we simulated the tensile deformation behavior using GBs with 5|7 structural motifs (i.e., structures highlighted by the red stars in Fig. 1(b)). The rationale for choosing boundaries with 5|7 motifs is that these structures are commonly observed experimentally.^21,74,75 To account for sample-to-sample variations, five independent simulations were performed for each GB misorientation. Fig. 3(a) shows stress–strain curves averaged over five simulations as a function of misorientation angle. Beyond the elastic regime, the MoS₂ bicrystals show nonlinear behavior before failure at an applied strain >15%. It is also interesting to note that while we simulated bicrystals with different GB misorientations the sheets exhibit a similar stress–strain response, mainly due to the fact that all these boundaries have the same 5|7 structural motifs albeit with different spacing, see Fig. 1(c) for examples of boundaries with misorientation angles of 1.3°, 5.1°, and 13.2°.

Fig. 3 Mechanical behavior of MoS₂ bicrystals. (a) Stress–strain curves as a function of GB misorientation angle using boundaries with 5|7 ring structures. Solid lines in black represent curves averaged over five independent runs and the shaded regions represent bounds of these runs. (b) For GBs with misorientation angles of 1.3° and 13.2°, atomic structures depicting the spacing of the 5|7 ring structures and per-atom shear strains at an applied tensile strain of 6.8%. (c) A close-up view of the shear band in the region, along with the outline of the 5|7 motif, enclosed in black dashed lines in (b) showing the S–S bond length L_S–S in the initial and deformed states. In panel (c), sulfur (molybdenum) atoms are shown in blue square (red circle) markers.

To reveal the deformation behavior at the atomic scale, Fig. 3(b) shows the atomic structure and per-atom shear strain for GBs with misorientation angles of 1.3° (Σ1951) and 13.2° (Σ19) at an applied tensile strain of ε = 6.8%. For the GB with a misorientation angle of 1.3°, thin regions with highly localized shear strains (i.e., shear bands) initiating from the GB can be clearly seen. Such shear bands have been observed in experimental and computational studies.^47,79 However, for the GB with θ = 13.2° the deformation is accommodated along the entire GB region, mainly due to the closely-spaced 5|7 structural motifs, and no shear bands nucleate at ε = 6.8%.

To better understand the atomic configuration of these shear bands that initiate from the GBs, Fig. 3(c) shows a close-up view of a shear band in the region enclosed in black dashed lines in Fig. 3(b). The side-view direction, along the yellow arrow in Fig. 3(c), reveals the S–S bond length L_S–S. In the initial state, L_S–S for the pristine MoS₂ 2H phase given by the ReaxFF bond order potential is ∼3.19 Å.⁶⁰ At an applied strain ε = 6.8%, L_S–S along the shear band decreases to ∼1.9 Å. Fig. 3(c) shows that at the atomic scale these shear bands are characterized by the collapse of the S–S bond length as a result of the applied strain.

The γ-surface method employed in this work reveals several GB structures [see Fig. 1(b)], however, the impact of these boundary structures on the deformation behavior of MoS₂ is not well understood. To demonstrate the impact of such metastable boundary structures, we select the GB with a misorientation angle of 13.2° and employ three distinct boundary structures; specifically those with 4|4, 5|7, and 5|8|4|7 motifs. These structures are shown in Fig. 4(a) noting that the GB with 4|4 motifs has the lowest energy as predicted by the γ-surface method, whereas those with 5|7 and 5|8|4|7 motifs are metastable structures. Fig. 4(b) shows close-up views depicting these boundaries at a tensile strain of ε = 8.8% with atoms colored according to the per-atom shear strain. For the GB with 4|4 motifs, the deformation is mediated along the GB without the formation of shear bands at this applied strain. However, for the GBs with 5|7 and 5|8|4|7 motifs Fig. 4(b) show the nucleation of shear bands from the boundaries and subsequent growth into the bulk MoS₂ sheet. The results depicted in Fig. 4(b) suggest that the mechanical behavior of MoS₂ can be controlled by the direct manipulation of the local GB structure—a GB engineering approach that can be achieved using strategies such as doping and the use of strain gradients.

Fig. 4 The role of GB metastability in the mechanical behavior of MoS₂. For the Σ19 GB with a misorientation angle of 13.2°: (a) atomic configurations depicting 4|4 (top), 5|7 (middle), and 5|8|4|7 (bottom) ring structures with their motifs outlined. (b) Snapshots at an applied tensile strain of 8.8% and T = 300 K, with atoms colored according to the per-atom shear strain. (c) A plot of ultimate tensile stress and ultimate failure strain as a function of the boundary energy of these metastable structures at 10 K (blue) and 300 K (red). The error bars represent one standard deviation using five simulations for each GB structure.

To quantify the results depicted in Fig. 4(b), we calculated the ultimate tensile stress and ultimate failure strain corresponding to the peak point in stress–strain curves. Fig. 4(c) shows plots of the ultimate tensile stress and ultimate failure strain as a function of boundary energy and temperature for the GB with a misorientation angle of 13.2° with the 4|4, 5|7, and 5|8|4|7 motifs. The error bars represent one standard deviation from the average of five tensile simulations. It can be clearly seen that for this specific GB the lowest energy structure (i.e., one with 4|4 motifs) has the largest ultimate tensile stress and ultimate failure strain values, whereas the highest energy structure, one with 5|8|4|7 motifs, shows lower values. This trend is observed even as the temperature is lowered to 10 K as represented by the blue data points in Fig. 4(c). The results shown in Fig. 4 demonstrate that the GB atomic structure plays an important role in the strength and ductility of MoS₂ sheets. Although the mechanical response is explicitly shown for a representative 13.2° tilt boundary, similar structural motifs (e.g., 5–7 and 4–4) have been observed in lower-Σ boundaries, suggesting that the impact of GB metastability on ductility shown in Fig. 4 reflects a broader structural trend rather than a single misorientation effect. It would be interesting, in future work, to systematically investigate the influence of metastable boundary structures across a broad spectrum of GB misorientations on the mechanical strength and ductility of MoS₂ monolayers.

Temperature effects on the deformation behavior of MoS₂

The results presented thus far describe the deformation behavior of GBs at room temperature T = 300 K. However, MoS₂ is widely used as a solid lubricant in devices that require structural durability under a wide range of operating temperatures.^41,80 Here, we investigate the role of GBs in the deformation pathways of MoS₂ bicrystals as a function of temperature. As an example, in Fig. 5 we show results for a MoS₂ bicrystal with a Σ19 GB (misorientation angle θ = 13.2°) at temperatures ranging from 5 K to 300 K using a constant strain rate of 1 × 10⁹ s⁻¹.

Fig. 5 The impact of temperature on the deformation behavior of MoS₂ bicrystals. For the Σ19 GB with a misorientation angle of 13.2°: (a) snapshots at applied tensile strains of 12% and 16% and temperatures of 5 K, 200 K, and 300 K to demonstrate shear bands and deformation fronts. Atoms are colored according to the per-atom shear strain. (b) A plot of the ultimate tensile stress and ultimate failure strain as a function of temperature. The error bars represent one standard deviation using five tensile deformation simulations for each temperature.

Fig. 5(a) shows snapshots of MoS₂ bicrystals deformed at applied strains ε = 12% and 16% with atoms color-coded according to the per-atom shear strain. The deformation behavior at temperatures of 5 K is shown in the top row, 200 K in the middle row, and 300 K in the bottom row of Fig. 5(a). At low temperatures (i.e., 5 K) the deformation of the MoS₂ bicrystal is homogeneous in the initial stage [see top panels of Fig. 5(a)], then a deformation front initiates at the GB and propagates in one of the MoS₂ half crystals leaving in its wake regions with high shear strains. As will be discussed later in Fig. 6, the region in the wake of this deformation front is characterized by a collapse of the S–Mo–S bond angle and a stretching of the Mo–S bond. The initiation and propagation of such deformation fronts is consistently observed at temperatures up to ∼100 K. In contrast, at higher temperatures (i.e., 300 K) the deformation follows the previously described mechanism characterized by the nucleation of shear bands from the GB, see bottom panels of Fig. 5(a). At intermediate temperatures as in the case of 200 K, the middle panels in Fig. 5(a) reveal that the deformation of the MoS₂ bicrystal exhibits a mixed character of both deformation fronts and shear bands, where the propagating shear bands interact with the deformation fronts. Here, we note that this temperature dependence of the deformation behavior is observed over a wide range of strain rates, the reader is referred to Fig. S3 for results demonstrating the deformation behavior at strain rates in the range of 10⁶ to 10¹⁰ s⁻¹.

Fig. 6 Atomistic insights into the deformation of MoS₂. For the Σ19 GB deformed to 20% tensile strain at a temperature of 5 K: (a) an atomistic close-up view of the deformation front, with atoms color-coded by their local shear strain. The front delineates regions characterized by low (Region I) and high (Region II) shear strain. (b) MoS₂ unit cells in regions I and II with Mo–S bonds colored by length. Histograms of the (c) Mo–S bond lengths L_Mo–S and (d) S–Mo–S bond angles θ_S–Mo–S in regions I and II, with the equilibrium bond length/angle indicated by the black dashed lines.⁶⁰

From the stress–strain curves at various temperatures (see Fig. S4) we show in Fig. 5(b) the ultimate tensile stress and ultimate failure strain values as a function of temperature for the MoS₂ bicrystal with a GB misorientation angle of 13.2°. At low temperatures, where the deformation fronts dominate mechanical behavior, Fig. 5(b) shows large values of ultimate tensile stress and ultimate failure strain of the MoS₂ bicrystal. Fig. 5(b) also reveals a rapid decrease in ultimate tensile stress (i.e. mechanical strength) and ultimate failure strain (i.e. ductility) as the temperature increases above ∼100 K. In the temperature range of ∼100–200 K, the deformation of the MoS₂ bicrystal involves both deformation fronts and shear bands, while the behavior is shear band-dominated at higher temperatures. The reader is referred to Fig. S5 for similar results for MoS₂ bicrystals with GB misorientations of 1.3° and 5.1°. The transition observed near 100 K signifies a shift between two primary deformation mechanisms—shear-band nucleation and front-propagated bond collapse. Although the present study identifies this transition through direct atomistic observations, a quantitative assessment of the corresponding activation energies requires explicit sampling of the relevant transition pathways. Such an analysis is beyond the scope of the current study, but constitutes an important avenue for future investigation to establish a quantitative connection between the observed mechanistic transition and its underlying energy barriers. The increase in ultimate tensile stress and failure strain at lower temperatures has been reported in single crystal MoS₂ sheets in prior computational studies.^80–82 Furthermore, recent experimental investigations reported reduced hardness in sputtered MoS₂ films at 123 K compared to room temperature.⁸³ Similarly, self-lubricating CoCrNi–Al₂O₃–Ni/MoS₂ composite films have been shown to exhibit lower friction coefficients and reduced wear at cryogenic temperatures.⁸⁴ These studies suggest that the temperature-dependent mechanical response of MoS₂ bicrystals can directly influence the tribological performance of components and devices operating across a wide range of temperatures.

To provide atomistic insights into the deformation fronts observed at low temperatures, we examine a representative case of a MoS₂ bicrystal with a Σ19 GB (θ = 13.2°) deformed to 20% at 5 K. A region of the bicrystal encompassing the deformation front is shown in Fig. 6(a), with atoms colored according to the per-atom shear strain. We identify two distinct regions, labeled Region I and Region II, that are separated by the planar deformation front and accommodate different amounts of shear strain. Region I corresponds to the original structure of MoS₂, but now the whole bicrystal is under a 20% applied tensile strain, while Region II is swept by the deformation front. We record the bond lengths and angles and Fig. 6(b) show representative MoS₂ units from Regions I and II, where we label the relevant Mo–S bond length L_Mo–S and out-of-plane S–Mo–S bond angle θ_S–Mo–S.⁸⁵Fig. 6(c) shows histograms of the Mo–S bond length for Region I, L^I_Mo–S, and Region II, L^II_Mo–S. Under no externally applied strains, the Mo–S bond length L_Mo–S for the 2H phase is 2.43 Å⁶⁰ and Fig. 6(c) shows that the Mo–S bond length in Region I is peaked at ∼2.5 Å. As mentioned above, Region I corresponds to the original MoS₂ atomic structure, but now under a 20% externally applied tensile strain leading to an increase in Mo–S bond length. In Region II, which was swept by the deformation front, the distribution of Mo–S bond lengths L^II_Mo–S has four peaks (i.e., L^II₁, L^II₂, L^II₃, and L^II₄) indicating atomic-level heterogeneity in the accommodation of applied strains. A close examination of Fig. 6(b) and (c) suggests that the multimodal nature of the distribution of Mo–S bond lengths L^II_Mo–S in Region II arises from the orientation of Mo–S bonds with respect to the tensile loading direction. Bonds with some degree of alignment with the loading direction such as L^II₂, L^II₃, and L^II₄ in Fig. 6(b) increase in length with applied loading, whereas bonds labeled L^II₁ in Fig. 6(b) are nearly perpendicular to the loading direction and decrease in length under applied tensile strain.

The distributions of the S–Mo–S angles θ_S–Mo–S in Regions I and II are shown in Fig. 6(d). Under no externally applied strains, the equilibrium S–Mo–S angle θ_S–Mo–S for the 2H phase is 81.8°.⁶⁰ In Region I, corresponding to the original MoS₂ 2H structure but now at a 20% externally applied strain, the angle distribution has a single peak at ∼79°, below the equilibrium angle. Tensile loading leads to a reduction of the S–S distance through the thickness of the MoS₂ layer and a decrease in the S–Mo–S bond angle θ_S–Mo–S. In Region II, which is swept by the deformation front, the distribution of the S–Mo–S bond angles θ_S–Mo–S is bimodal with one peak θ^II₁ ∼ 72° and a second peak θ^II₂ centered approximately at the same mean angle as that in Region I. A close examination of Fig. 6(b) and (d) reveals that in Region II the first peak θ^II₁ in the bond angle histogram corresponds to S–Mo–S angles on planes parallel to the tensile loading direction, while the second peak θ^II₂ corresponds to angles on planes that are perpendicular to the loading direction. As a result of their aligned orientation with the loading direction, the S–Mo–S bond angles θ^II₁ decrease from their equilibrium values under applied tensile strains. Together, panels (b) through (d) of Fig. 6 reveal an atomic-level heterogeneity, in which the low temperature deformation of monolayer MoS₂ bicrystals is characterized by deformation fronts leading to multimodal distributions of bond lengths and angles. This is in contrast to the cases at 300 K where inelastic deformation is driven by localized shear bands that nucleate from GBs and propagate through the MoS₂ sheet.

The results shown in Fig. 5 and 6 highlight the role of GBs in accommodating externally applied strains and reveal temperature-sensitive mechanical strength and ductility of MoS₂. Fig. 3 shows that GBs serve as nucleation sites of shear bands, that at the atomic scale are regions characterized by reduced S–S bond length compared to pristine MoS₂. Also, GBs in general do not always attain their ground-state structures due to several factors, including geometric constraints imposed on the GB network in polycrystalline MoS₂ or the use of advanced, yet far-from-equilibrium processing routes to fabricate MoS₂. Fig. 4 demonstrates the impact of GB metastability on the mechanical behavior of MoS₂, where the strength is found to decrease with increasing the energy of boundary structures, at least for the GB with a misorientation angle of 13.2°.

Conclusions

In this work, we employed classical reactive atomistic simulations to investigate the atomic structure and mechanical response of a wide range of GBs in monolayer MoS₂, including the role of temperature in governing deformation mechanisms. We employed the MoS₂ bicrystal geometry, which allowed for the generation and exploration of GB geometries with various misorientation angles in a systematic manner. The focus on mechanical behavior is motivated by the widespread use of MoS₂ as a solid lubricant in applications where materials are subjected to high contact stresses under a wide range of operating temperatures.

Using the γ-surface method, we generated atomic structures and computed energies of several low-angle, symmetric GBs. For example, for the GB with a misorientation angle of 13.2°, we identified several metastable structures and examined their tensile deformation behavior, revealing that mechanical strength and ductility decrease with increasing boundary energy. At temperatures above 200 K, simulation results of all GB geometries explored in this work revealed that the tensile deformation behavior is dominated by the nucleation of localized shear bands at GBs, that then propagate with subsequent loading into the MoS₂ crystals. At lower temperatures, however, the deformation behavior is characterized by the nucleation and growth of deformation fronts, leaving in its wake regions with high atomic shear strain. Our results revealed that the ultimate tensile stress and ultimate failure strain of MoS₂ bicrystals decrease with increasing temperature. Simulation results highlighted the critical role that GBs play in controlling the mechanical performance of MoS₂ over a wide range of operating temperatures. In broad terms, insights gained from our work provide future avenues to explore GB engineering as a near-atomic scale strategy to design MoS₂-based materials with tailored mechanical properties. For example, approaches such as selective doping may be used to alter the structure of GBs and stabilize specific GB configurations, thereby tailoring the mechanical properties of MoS₂. Synthesis and processing routes employing strain gradients, for example, may also be used to fabricate polycrystalline MoS₂ with controlled density of GB misorientations, thus providing a pathway to control the macroscopic properties of MoS₂ sheets.

Author contributions

R. Moore: writing – review & editing, writing – original draft, visualization, methodology, investigation, formal analysis, data curation. N. Bobbitt: methodology, writing – review & editing, visualization. I. Winter: methodology, writing – review & editing, investigation. J. Curry: writing – review & editing, funding acquisition, conceptualization. L. Levandosky: formal analysis, visualization, data curation, writing – review & editing. S. Renaud: formal analysis, visualization, data curation, writing – review & editing. M. Chandross: conceptualization, funding acquisition, methodology, project administration, writing – review & editing, writing – original draft. F. Abdeljawad: conceptualization, funding acquisition, methodology, project administration, supervision, writing – review & editing, writing – original draft, resources.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data for the atomistic grain boundary structures (with 5|7 motifs) supporting this article have been included as part of the supplementary information (SI). Supplementary information: additional figures and data. See DOI: https://doi.org/10.1039/d5nr03362d.

Acknowledgements

R. M. and F. A. acknowledge support from Sandia National Laboratories through the Advanced Simulation and Computing program. F. A. and R. M. acknowledge the generous allotment of compute time on the Lehigh University Hawk cluster. This article has been authored by an employee of National Technology & Engineering Solutions of Sandia, LLC under Contract No. DE-NA0003525 with the U.S. Department of Energy (DOE). The employee owns all right, title and interest in and to the article and is solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.

References

1. S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709.
2. A. Castellanos-Gomez, M. Poot, G. A. Steele, H. S. J. van der Zant, N. Agraït and G. Rubio-Bollinger, Adv. Mater., 2012, 24, 772–775.
3. Q. Peng and S. De, Phys. Chem. Chem. Phys., 2013, 15, 19427–19437.
4. G. Casillas, U. Santiago, H. Barrón, D. Alducin, A. Ponce and M. José-Yacamán, J. Phys. Chem. C, 2015, 119, 710–715.
5. H. Song, B. Wang, Q. Zhou, J. Xiao and X. Jia, Appl. Surf. Sci., 2017, 419, 24–34.
6. M. R. Vazirisereshk, A. Martini, D. A. Strubbe and M. Z. Baykara, Lubricants, 2019, 7, 57.
7. N. S. Bobbitt, J. F. Curry, T. F. Babuska and M. Chandross, RSC Adv., 2024, 14, 4717–4729.
8. R. Ganatra and Q. Zhang, ACS Nano, 2014, 8, 4074–4099.
9. T. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235407.
10. D. Gupta, V. Chauhan and R. Kumar, Inorg. Chem. Commun., 2020, 121, 108200.
11. J. S. Kim, J. Kim, J. Zhao, S. Kim, J. H. Lee, Y. Jin, H. Choi, B. H. Moon, J. J. Bae and Y. H. Lee, et al. , ACS Nano, 2016, 10, 7500–7506.
12. G. Eda, T. Fujita, H. Yamaguchi, D. Voiry, M. Chen and M. Chhowalla, ACS Nano, 2012, 6, 7311–7317.
13. M. Arfaoui and S. Jaziri, J. Phys. Commun., 2022, 6, 115004.
14. E. Singh, K. S. Kim, G. Y. Yeom and H. S. Nalwa, ACS Appl. Mater. Interfaces, 2017, 9, 3223–3245.
15. A. Nourbakhsh, A. Zubair, R. N. Sajjad, A. T. KG, W. Chen, S. Fang, X. Ling, J. Kong, M. S. Dresselhaus and E. Kaxiras, et al. , Nano Lett., 2016, 16, 7798–7806.
16. J. Xu, G. Shao, X. Tang, F. Lv, H. Xiang, C. Jing, S. Liu, S. Dai, Y. Li and J. Luo, et al. , Nat. Commun., 2022, 13, 2193.
17. J. Sun, X. Li, W. Guo, M. Zhao, X. Fan, Y. Dong, C. Xu, J. Deng and Y. Fu, Crystals, 2017, 7, 198.
18. T. Wang, J. Guo, Y. Zhang, W. Yang, X. Feng, J. Li and P. Yang, Cryst. Growth Des., 2024, 24, 2755–2763.
19. Y. Yao, K. Ao, P. Lv and Q. Wei, Nanomaterials, 2019, 9, 844.
20. I. S. Kim, V. K. Sangwan, D. Jariwala, J. D. Wood, S. Park, K.-S. Chen, F. Shi, F. Ruiz-Zepeda, A. Ponce and M. Jose-Yacaman, et al. , ACS Nano, 2014, 8, 10551–10558.
21. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. M. Ajayan, B. I. Yakobson and J.-C. Idrobo, Nano Lett., 2013, 13, 2615–2622.
22. A. M. Van Der Zande, P. Y. Huang, D. A. Chenet, T. C. Berkelbach, Y. You, G.-H. Lee, T. F. Heinz, D. R. Reichman, D. A. Muller and J. C. Hone, Nat. Mater., 2013, 12, 554–561.
23. L. Yang, J. Liu, Y. Lin, K. Xu, X. Cao, Z. Zhang and J. Wu, Chem. Mater., 2021, 33, 8758–8767.
24. J. Hong, Z. Hu, M. Probert, K. Li, D. Lv, X. Yang, L. Gu, N. Mao, Q. Feng and L. Xie, et al. , Nat. Commun., 2015, 6, 6293.
25. S. Najmaei, Z. Liu, W. Zhou, X. Zou, G. Shi, S. Lei, B. I. Yakobson, J.-C. Idrobo, P. M. Ajayan and J. Lou, Nat. Mater., 2013, 12, 754–759.
26. S. Najmaei, J. Yuan, J. Zhang, P. Ajayan and J. Lou, Acc. Chem. Res., 2015, 48, 31–40.
27. Y. L. Huang, Y. Chen, W. Zhang, S. Y. Quek, C.-H. Chen, L.-J. Li, W.-T. Hsu, W.-H. Chang, Y. J. Zheng and W. Chen, et al. , Nat. Commun., 2015, 6, 6298.
28. D. Wang, H. Yu, L. Tao, W. Xiao, P. Fan, T. Zhang, M. Liao, W. Guo, D. Shi and S. Du, et al. , Nano Res., 2018, 11, 6102–6109.
29. S. Najmaei, M. Amani, M. L. Chin, Z. Liu, A. G. Birdwell, T. P. O'Regan, P. M. Ajayan, M. Dubey and J. Lou, ACS Nano, 2014, 8, 7930–7937.
30. P. Man, D. Srolovitz, J. Zhao and T. H. Ly, Acc. Chem. Res., 2021, 54, 4191–4202.
31. C. Lin, X. Chen and X. Zou, ACS Appl. Mater. Interfaces, 2019, 11, 25547–25555.
32. K. Xu, T. Liang, Z. Zhang, X. Cao, M. Han, N. Wei and J. Wu, Nanoscale, 2022, 14, 1241–1249.
33. B. Mortazavi, R. Quey, A. Ostadhossein, A. Villani, N. Moulin, A. C. van Duin and T. Rabczuk, Appl. Mater. Today, 2017, 7, 67–76.
34. M. Sledzinska, R. Quey, B. Mortazavi, B. Graczykowski, M. Placidi, D. S. Reig, D. Navarro-Urrios, F. Alzina, L. Colombo and S. Roche, et al. , ACS Appl. Mater. Interfaces, 2017, 9, 37905–37911.
35. J. Liu, M. Fang, E.-H. Yang and X. Zhang, Sci. Rep., 2025, 15, 1976.
36. J. Shen, A. Aljarb, Y. Cai, X. Liu, J. Min, Y. Wang, Q. Wang, C. Zhang, C. Chen and M. Hakami, et al. , Science, 2025, 387, 776–782.
37. Y. Zhao, Y. Chen, P. Ou and J. Song, ACS Catal., 2023, 13, 12941–12951.
38. H. Yan, P. Zhuang, B. Li, T. Ye, C. Zhou, Y. Chen, T. Li, W. Cai, D. Yu and J. Liu, et al. , Adv. Electron. Mater., 2025, 11, 2400264.
39. E. Singh, P. Singh, K. S. Kim, G. Y. Yeom and H. S. Nalwa, ACS Appl. Mater. Interfaces, 2019, 11, 11061–11105.
40. S. Manzeli, D. Dumcenco, G. M. Marega and A. Kis, Nat. Commun., 2019, 10, 4831.
41. E. Roberts, Thin Solid Films, 1989, 181, 461–473.
42. M. A. Hamilton, L. A. Alvarez, N. A. Mauntler, N. Argibay, R. Colbert, D. L. Burris, C. Muratore, A. A. Voevodin, S. S. Perry and W. G. Sawyer, Tribol. Lett., 2008, 32, 91–98.
43. A. Banerji, S. Bhowmick and A. Alpas, Surf. Coat. Technol., 2017, 314, 2–12.
44. T. Gradt and T. Schneider, Lubricants, 2016, 4, 32.
45. J. Wu, P. Cao, Z. Zhang, F. Ning, S.-s. Zheng, J. He and Z. Zhang, Nano Lett., 2018, 18, 1543–1552.
46. S. Sabbaghi, E. Hosseinian and V. Bazargan, ACS Appl. Mater. Interfaces, 2024, 16, 22676–22688.
47. Z. Islam and A. Haque, J. Phys. Chem. Solids, 2021, 148, 109669.
48. W. Wang, H. Zhao, H. Liu, L. Wang and Y. Li, J. Phys. Chem. C, 2022, 126, 17692–17698.
49. I. Niehues, A. Blob, T. Stiehm, R. Schmidt, V. Jadriško, B. Radatović, D. Čapeta, M. Kralj, S. M. de Vasconcellos and R. Bratschitsch, 2D Mater., 2018, 5, 031003.
50. K. Elibol, T. Susi, O. Maria, B. C. Bayer, T. J. Pennycook, N. McEvoy, G. S. Duesberg, J. C. Meyer and J. Kotakoski, et al. , Nanoscale, 2017, 9, 1591–1598.
51. B. Straumal, O. Kogtenkova, F. Muktepavela, K. Kolesnikova, M. Bulatov, P. Straumal and B. Baretzky, Mater. Lett., 2015, 159, 432–435.
52. T. Meiners, T. Frolov, R. E. Rudd, G. Dehm and C. H. Liebscher, Nature, 2020, 579, 375–378.
53. J. Han, V. Vitek and D. J. Srolovitz, Acta Mater., 2016, 104, 259–273.
54. V. Vitek, A. Sutton, G. J. Wang and D. Schwartz, Scr. Metall., 1983, 17, 183–189.
55. T. Frolov, W. Setyawan, R. J. Kurtz, J. Marian, A. R. Oganov, R. E. Rudd and Q. Zhu, Nanoscale, 2018, 10, 8253–8268.
56. T. Frolov, Q. Zhu, T. Oppelstrup, J. Marian and R. E. Rudd, Acta Mater., 2018, 159, 123–134.
57. Q. Xia, D. Hua, Y. Shi, Q. Zhou, B. Zhu, X. Yu, H. Wang and W. Liu, Int. J. Plast., 2025, 104451.
58. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
59. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012.
60. A. Ostadhossein, A. Rahnamoun, Y. Wang, P. Zhao, S. Zhang, V. H. Crespi and A. C. Van Duin, J. Phys. Chem. Lett., 2017, 8, 631–640.
61. B. Mortazavi, A. Ostadhossein, T. Rabczuk and A. C. Van Duin, Phys. Chem. Chem. Phys., 2016, 18, 23695–23701.
62. M. H. Rahman, E. H. Chowdhury and S. Hong, Surf. Interfaces, 2021, 26, 101371.
63. W. Xu and W. K. Kim, Comput. Mater. Sci., 2024, 231, 112559.
64. V. E. Claerbout, T. Polcar and P. Nicolini, Comput. Mater. Sci., 2019, 163, 17–23.
65. E. Serpini, A. Rota, S. Valeri, E. Ukraintsev, B. Rezek, T. Polcar and P. Nicolini, Tribol. Int., 2019, 136, 67–74.
66. P. J. Peña-Obeso, R. Huirache-Acuña, F. I. Ramirez-Zavaleta and J. L. Rivera, Membranes, 2022, 12, 818.
67. S. Zhu and H. T. Johnson, Nanoscale, 2018, 10, 20689–20701.
68. Y. Shi, Z. Cai, J. Pu, L. Wang and Q. Xue, Ceram. Int., 2019, 45, 2258–2265.
69. Y. Mishin and D. Farkas, Philos. Mag. A, 1998, 78, 29–56.
70. V. Randle, The measurement of grain boundary geometry, CRC Press, 2017.
71. H. J. Berendsen, J. v. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
72. D. M. Heyes, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 755.
73. F. Shimizu, S. Ogata and J. Li, Mater. Trans., 2007, 48, 2923–2927.
74. T. H. Ly, D. J. Perello, J. Zhao, Q. Deng, H. Kim, G. H. Han, S. H. Chae, H. Y. Jeong and Y. H. Lee, Nat. Commun., 2016, 7, 10426.
75. S. Lan, F. Zheng, C. Ding, Y. Hong, B. Wang, C. Li, S. Li, H. Yang, Z. Hu and B. Pan, et al. , Nano Lett., 2024, 24, 15388–15395.
76. M.-Y. Choi, C.-W. Choi, D.-Y. Kim, M.-H. Jo, Y.-S. Kim, S.-Y. Choi and C.-J. Kim, Nano Lett., 2023, 23, 4516–4523.
77. N. Gao, Y. Guo, S. Zhou, Y. Bai and J. Zhao, J. Phys. Chem. C, 2017, 121, 12261–12269.
78. W. T. Read and W. Shockley, Phys. Rev., 1950, 78, 275.
79. S. Wang, Z. Qin, G. S. Jung, F. J. Martin-Martinez, K. Zhang, M. J. Buehler and J. H. Warner, ACS Nano, 2016, 10, 9831–9839.
80. J. Zhao, L. Kou, J.-W. Jiang and T. Rabczuk, Nanotechnology, 2014, 25, 295701–295701.
81. V. Pham and T. Fang, Thermal and mechanical characterization of nanoporous two-dimensional MoS₂ membranes, Sci. Rep., 2022, 12, 7777.
82. A. Faiyad, F. H. Bhuiyan, A. Vellore, D. A. Johnson, A. Kennett and A. Martini, Friction, 2025, 13, 9441020.
83. H. Hu, Y. He, Q. Wang and L. Tao, Tribol. Int., 2023, 189, 108967.
84. Y. Wang, Z. Jiao, Y. Shi, Q. Zhou, Q. Jia, M. Xie, Y. Ren, H. Teng and H. Wang, Surf. Coat. Technol., 2025, 500, 131906.
85. S. Chu, C. Park and G. Shen, Phys. Rev. B, 2016, 94, 020101.

---