Revisiting ion transport through micropores: significant and non-negligible surface transport
Wenchang Zhang†
a,
Ao Zhang†b,
Wenzhe Zhoua,
Yu Jia,
Zhiping Xu b and
Pengzhan Sun
b and
Pengzhan Sun
 *a
*a
aInstitute of Applied Physics and Materials Engineering, University of Macau, Macau SAR 999078, P. R. China. E-mail: pengzhansun@um.edu.mo
bApplied Mechanics Laboratory, Department of Engineering Mechanics and Center for Nano and Micro Mechanics, Tsinghua University, Beijing 100084, P. R. China
First published on 24th December 2025
Abstract
From a theoretical perspective, ion transport through micrometer or nanometer-sized pores under a cross-pore electric field can be described well by the Hall equation, involving only the bulk conductivity, if the solution is not too dilute. For dilute solutions, it is predicted that the surface conduction will become important, especially in nanopores. Nonetheless, this remains unsupported by experiments, especially for micropores, where the experimentally observed ion conductance is intuitively thought to be dominated by bulk conduction. Herein, our electrical measurements of ion transport through silicon nitride pores having diameters ranging from sub-µm up to a few µm show that the surface conduction can be significant and non-negligible in such large pore systems, especially at solution concentrations lower than 1 mM. In the latter case, the observed surface conductivity of the order of 1 nS can dominate over the bulk contribution, yielding a Dukhin length comparable to or even larger than the pore size and a Dukhin number up to 10. The surface conduction can be further enhanced by covering the silicon nitride surface with two-dimensional (2D) crystals such as graphene, graphene oxide, or monolayer titania sheets. The resulting surface conductivity is seen to increase upon increasing the solution concentration and can be increased by up to one or two orders of magnitude. Our observations provide insights into ion transport in micropore systems and suggest the possibility of exploiting surface conduction in such large pores for new technologies that were previously believed to apply only to nanopores.
New conceptsIon transport through nanofluidic systems, for example, pores of only a few nanometers in size, is important from a fundamental perspective owing to many unconventional phenomena observed in experiments, and for new technologies such as sieving, sensing, energy harvesting, and neuromorphic computing. One of the key factors underlying this importance is surface conduction. In nanopores, both experiments and theory have shown that this surface effect is pronounced. However, in larger and micrometer-sized pores, one generally believes that bulk conduction through the pore interior should dominate, whereas surface conduction is insignificant and can be neglected. This paper presents measurements for the transport of ions through pores made in silicon nitride membranes and shows that surface conduction can be significant and non-negligible even in micropores. The surface conductivity is of the order of 1 nS, independent of solution concentrations, and can dominate over the bulk contribution in dilute solutions with concentrations lower than 1 mM. The dominance of surface conduction is also evident from the extracted Dukhin numbers, which characterize the relative importance of the surface and bulk contributions and can be up to 10. Notably, the surface conductivity can be further enhanced by over two orders of magnitude through surface modification, for example, coating the bare silicon nitride surfaces with two-dimensional (2D) crystals, such as graphene or graphene oxide. In this context, the observed ion transport in the micropores can be primarily attributed to surface conduction, whereas the bulk contribution can be neglected. These findings provide insights into ion transport through confinement systems and emphasize the importance of surface conduction not only in well-documented nanopores but also in micropores. The results also suggest the possibility of replacing the core of nanofluidic systems, that is, nm-size pores, with µm-size ones for new technologies, and therefore circumventing many issues intrinsic to nanopores, some of which are challenge of fabrication and scale up, susceptibility to contamination and clogging during operation in electrolytes. |
Introduction
Ion transport in nanofluidic systems, for example, nanopores and nanochannels, has attracted intense research interest owing to many unconventional phenomena arising from the comparable sizes of the permeating species and the channels, and potential applications from biosensors to sieving membranes and from blue energy harvesting to neuromorphic computing.1–6 An important property rooted in these novel transport phenomena and technologies is the strong surface interactions, resulting in pronounced surface conduction. When the pore size is comparable with the Debye length λD, most of the pore volume is occupied by an electric double layer. Accordingly, the electrostatic interactions between the permeating ions and the surface charges on the pore walls exclude co-ions and enrich counter-ions, leading to pore conductance independent of the bulk concentration and deviating from the bulk conduction, i.e. conductance does not scale linearly with bulk concentration.2,7–9 However, the challenges associated with fabricating nm-sized pores and channels impede the advancement of nanofluidic research into new technologies. Also, these nanofluidic systems are prone to various problems during measurements in electrolytes, such as pore clogging, improper wetting, or contamination.10–12 The difficulties often lead to large device-to-device variations and insufficient stability during long-term operation. The challenges could, in principle, be mitigated by using pores much larger than a few nm, for example, of a few µm. However, although the relative importance of surface and bulk conductivities can be predicted in theory,9 this remains to be supported by experiments, especially in pores up to a few µm in size and/or having different surface properties.From a theoretical standpoint, the bulk contribution comes from the permeating ions inside the bulk space of a channel, whereas the surface contribution is due to excess counter-ions in the vicinity of the channel's surface, screening its residual charges, resulting in the formation of an electric double layer (EDL).2 Its thickness is characterized by the Debye length λD ∝ C−1/2, where C is the concentration of the bulk solution. At room temperature and for a univalent electrolyte such as KCl, λD falls into the nanometer regime for C ≤ 0.1 M.2 In this context, for channels having radii r comparable to or smaller than λD, the formed EDLs are expected to overlap inside the channels, resulting in the enrichment of counter-ions and depletion of co-ions (i.e. ion selectivity).13,14 Accordingly, the measured G as a function of C typically displays two characteristic segments. In the high-C regime with λD notably smaller than r, G scales linearly as a function of C. In the lower C regime, where λD becomes comparable to or larger than r, G is independent of C because the concentration of (counter-)ions inside the channel is determined by the surface charge density.2,7 The described G(C) dependence is measured for nanochannels such as carbon and boron nitride nanotubes,15–17 and for nanopores such as those made in thin silicon nitride (SiNx) and two-dimensional (2D) membranes including graphene and molybdenum disulfide (MoS2).5,14
Furthermore, in nanochannels with length L much longer than r, the entrance effect (characterized by the access resistance Ra) can be safely neglected, and G is primarily determined by a combination of bulk and surface transport. However, this is not true in nanopores, where L is comparable to or smaller than r. In such cases, the entrance effect can no longer be neglected, and ion transport in nanopores is significantly more complex than in nanochannels.9 To account for Ra, Hall18 constructed a theoretical model by simplifying the pore system as two hemispheres that are connected by a cylinder. Both the hemispheres and the cylinder had the same diameter D as the studied pore and the cylinder's length L was also the same as that of the pore. Assuming bulk conductivity kb throughout the pore system, the model describes G as:
 | (1) |
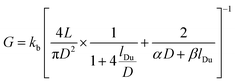 | (2) |
Herein, we performed careful electrical measurements for the transport of ions through SiNx pores up to a few µm in size (Fig. 1). We found that in such large pores, ks of the order of 1 nS was determined, which was independent of C. The surface contribution could even dominate over the bulk at C < 1 mM, and the resulting Du could reach up to 10. In contrast, ks increased with C if the outer SiNx surfaces became more hydrophilic, for example, by coating them with graphene, graphene oxide (GO) or monolayers of titania, and ks could be further increased by one or two orders of magnitude at C = 1 mM.
Results
Device fabrication and electrical measurements
The studied pores were drilled using the focused ion beam (FIB) technique in freestanding SiNx membranes that were embedded in silicon wafers. Fabrication of the latter structure has been well-documented previously,20,21 and is detailed in the SI (Device fabrication). The length (L) of the pores was either 500 nm or 300 nm, and their diameter (D) was 0.2–5 µm (Fig. 1b). Fig. 1d shows a representative micrograph for one of the fabricated pores with sharp edges and µm-scale D. Such devices were used to separate two liquid cells (Fig. 1a) containing either HCl or KCl solutions of C = 10−2–102 mM and the ion current I was measured using a pair of Ag/AgCl electrodes under an applied bias V (Fig. 1c, for details see the SI, device fabrication). For comparison, deionized water was also measured.We typically applied the limit V ≤ 0.1 V for linear I–V responses (Fig. 2a and b) and accordingly, the total ion conductance through the studied pore was calculated as G = I/V. The resulting G for both HCl and KCl solutions at different C and using SiNx pores of different D are summarized in Fig. 2c and d. They show that higher G was generally observed in pores having larger D and at higher C, in agreement with predictions from both eqn (1) and (2). Pores of both L = 500 nm and 300 nm yielded practically the same G for the same D and C within our experimental accuracy (Fig. S8). For the same D and C (≥1 mM), the observed G values in HCl solutions were systematically higher than those in KCl. This can be attributed to the higher mobility of H+ than that of K+ in bulk solutions.22,23 In particular, we found that the observed G for both HCl and KCl solutions scaled linearly as a function of C until C was decreased down to 1–0.1 mM, after which the evolution of G gradually deviated from the linear trend. The linear dependence of G in the high-C regime is consistent with expectations from eqn (1) and (2), showing the dominance of bulk conduction. However, the saturated G observed at lower C is intuitively surprising for such µm-size pores notably larger than λD. This could be attributed to the deviation of the bulk conductivity kb from the linear trend at lower C because the measurements were carried out under an ambient atmosphere, and CO2 could dissolve in the tested solutions, resulting in the presence of excess ions (e.g. protons, as evidenced by pH ≈ 6 for deionized water). Alternatively, the observed saturation in G could be explained by non-negligible surface conduction. Indeed, the Dukhin length lDu in eqn (2) that includes contributions from the surface conduction can be further extended and estimated (assuming the Poisson−Boltzmann estimate for ks) as:2
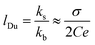 | (3) |
To distinguish which of the two possibilities described above was the real origin, we performed two additional experiments. First, we directly measured the bulk conductivities kb using a conductivity meter for the tested solutions of C = 10−2–102 mM (Fig. 5a) and found that for both KCl and HCl, kb depended linearly on C. This is in stark contrast to the observed saturation in G at C < 1 mM and therefore rules out possible changes in kb as the primary reason. Second, we deliberately covered a 2-µm pore's outer space (except the pore's top) with either graphene (made by chemical vapour deposition, CVD),24,25 GO (made by the modified Hummers’ method)26,27 or monolayers of titania28–30 (made by chemical exfoliation, for all details see the SI, device fabrication) and repeated the measurements using HCl and KCl solutions with C = 10−1–10−5 M (Fig. 4). Compared with the bare SiNx devices, all 2D crystal-covered devices yielded systematically higher G in the low-C regime (10−3–10−5 M). In a separate experiment, we sought to measure the wettability of these four samples’ surfaces. To prepare surfaces with sufficiently large areas for contact angle measurements, in addition to the bare SiNx substrate, we transferred a piece of graphene film (about 5 mm × 5 mm) over a SiNx wafer using the standard technique for van der Waals assembly,31,32 and deposited monolayers of GO and titania nanosheets, to form large-area and dense membranes by the well-established Langmuir–Blodgett assembly technique33,34 (for detailed characterizations see Fig. S2b). The contact angles of water on these four samples turned out to be about 74° (bare SiNx), 40° (graphene-covered SiNx), 32° (GO-covered SiNx), and 42° (titania-covered SiNx). The results suggest that the observed higher G for 2D crystal-covered devices should be strongly correlated with their more hydrophilic surfaces that adsorbed more water together with dissolved ions and therefore, contributed to the enhanced G. These measurements unambiguously corroborate the importance of surface conduction in the tested µm-size pores.
Surface conduction
To gain more quantitative information on the surface contribution to the overall G, instead of plotting G as a function of C as in Fig. 2c and d, we next plot them as a function of D (Fig. 3). Linear dependences were observed for both HCl and KCl solutions at all C, which, according to eqn (1) and (2), indicate the dominance of access resistance Ra over that associated with ion transport inside the pore. The linear G(D) is consistent with our measurements using pores having different L, showing essentially the same G independently of L (Fig. S8), and also with our theoretical analysis (Fig. S3–S5, for details see the SI). In the latter case, finite element analysis was employed to solve the Poisson–Nernst–Planck (PNP) equations for ion transport using the same setup as in the experiments. We mapped the spatial distribution of current streamlines and found that a substantial proportion of current was contributed by ions flowing across the pore edges, while the rest was directly through the bulk cylindrical region right above the pore. This distribution became more pronounced in smaller pores (Fig. S3 and S4). To be more quantitative, we defined the current across the side walls of the cylinder above the pore as the edge current Iedge and compared it with the total current Itotal at different pore radii r (0.2–2 µm), solution concentrations C (0.01–100 mM) and surface charge densities σ (0.01 and 0.02 C m−2) (Fig. S5). We found that both Iedge and Itotal scale linearly as a function of r, in agreement with our experiments (Fig. 3). Nonetheless, the calculations failed to capture any surface effects because Iedge amounts to 78–84% of Itotal under all the conditions considered and regardless of variations in C and σ. Furthermore, we note that the results were insensitive to the size of solution reservoirs used (SI, Fig. S6). In addition, whether or not the Stokes equation was coupled with PNP equations during our finite element simulations, no noticeable impact was seen in the resulting Iedge and Itotal (SI, Fig. S7). This suggests that the effect of electroosmosis is insignificant. | ||
| Fig. 3 Pore size dependence of the ion conductance. (a) HCl and (b) KCl solutions, respectively, at different C (color coded). The symbols show experimental data averaged over 3 independent I–V measurements using bare SiNx pores of different D. The error bars on the grey symbols show the same as in Fig. 2c and d. The solid lines show the best linear fits (same color-coding as the symbols). | ||
In a different context, the observed linear G(D) in experiments (Fig. 3) indicates that the first term in the square brackets of eqn (2) can be neglected and is reduced to:
| G = kbD + ks | (4) |
 | (5) |
Fitting the data in Fig. 3 using eqn (4) yields both kb and ks, as plotted in Fig. 5. The fitted kb agrees quite well with those directly measured for bulk solutions, suggesting that despite the simplified form of eqn (4), it could provide a reasonably good description of our experimental data. With this in mind and because we were interested in the contribution of surface conduction that causes the deviation of the linear dependence of G at C lower than 1 mM (Fig. 2c and d), we extracted ks from the linear fittings for the lower-C regime and plotted it in Fig. 5b. For both HCl and KCl solutions, the extracted ks at C ≤ 1 mM was of the order of 1 nS for SiNx devices and independent of the solutions’ C. The extracted Du from eqn (5) exhibited an increasing trend with decreasing C from 1 mM and could be up to ∼10 at extremely low C down to that of deionized water (∼10−3 mM). This shows that in µm-size SiNx pores that are far larger than the Debye length λD, surface conduction is important and non-negligible, especially in dilute solutions, and even dominates over the bulk conduction. In contrast, devices with their outer surfaces covered by graphene, GO and titania yielded a different ks(C) trend (Fig. 5b). For all three 2D crystal coated devices, ks increased with C for both HCl and KCl solutions (Fig. 5b). Notably, the maximum ks values observed at C = 1 mM were 1–2 orders of magnitude higher than that of the bare SiNx device (Fig. 5b). This emphasizes engineering the surface properties outside the pore as an effective strategy for enhancing the surface conduction.
 | ||
| Fig. 5 Bulk and surface conductivities. (a) Comparison of the fitted kb using eqn (4) with those directly measured for the bulk solutions of HCl and KCl (color coded), at different C. Shown also are the fitted and measured kb values for deionized water (coded in grey). For both HCl and KCl solutions, the fitted and measured kb values display a linear trend as a function of C from 100 mM down to 0.01 mM (shaded in green). (b) Extracted ks (from eqn (4), shaded in green) and Du (from eqn (5), shaded in purple) for bare SiNx pores in HCl and KCl (color coded) as a function of C. The data for deionized water is shown coded in grey. Shown also are ks values for devices with surfaces covered by graphene (circular symbols), GO (square symbols) and monolayers of titania nanosheets (diamond symbols) in KCl and HCl solutions (hollow points represent HCl solution, solid points represent KCl solution) for different C (shaded in yellow). | ||
Discussion
Comparisons of the devices coated by graphene, GO and titania on their outer surfaces with respect to bare SiNx pores allow us to discuss the possible mechanism for the observed enhanced surface conduction. We first rule out surface charges as the possible origin because of the following two facts: (1) the impact of surface charges on the observed G should be stronger with increasing λD, that is, decreasing C, whereas the observed ks(C) in Fig. 5b always exhibits an inverse trend; (2) the chosen 2D crystals have rather different surface charge densities, with CVD-graphene being much less defective than GO (due to severe oxidation) and titania (due to the presence of high-density Ti vacancies),35,36 whereas ks(C) displays the same trend for both (Fig. 5b). We next rule out electroosmosis as the possible origin. This effect involves the movement of bulk flows driven by the movement of ions in the EDL and is expected to be stronger with increasing λD and decreasing C, which is opposite to our observed ks(C) trend (Fig. 5b). Our finite element simulations with the Stokes equation coupled with PNP equations also suggest that the electroosmosis effect is insignificant. Conversely, we note that the observed ks(C) trend is consistent with the evolution of surface hydrophilicity, showing that compared with bare SiNx surfaces, those covered by graphene, GO or titania become more hydrophilic. We believe the enhanced hydrophilicity underlies the observed enhanced surface conduction, which requires further exploration.From an application perspective, our results have implications for nanopore technologies. In nanopore systems, the pore dimension is comparable to λD and therefore, most of the pore volume is occupied by the EDL, leading to strong interactions between the permeating species and the pore surface. However, key challenges associated with fabricating and measuring such tiny pores remain, for example, large device-to-device variations, clogging and contamination in electrolytes. From a technological standpoint, these challenges could, in principle, be overcome by using µm-size pores instead, which are easier to fabricate and more stable during measurements in electrolytes than nm-size pores. Our measurements provide fundamental support for that. Results show that surface conduction can be important and non-negligible in dilute solutions for µm-size SiNx pores and more importantly, engineering the surface properties could further enhance the surface conduction. The suggested surface modification strategy can be extended to other hydrophilic coatings and beyond the 2D ones discussed here. Our work provides insights into ion transport through solid-state pores and is potentially important for nanofluidic technologies where surface conduction is important.
Conflicts of interest
The authors declare no conflicts of interest.Data availability
All data supporting the findings in this paper are included in the main text and supplementary information (SI). They can be accessed from the plots in the figures. Supplementary information includes experimental section and additional characterization data, such as optical microscope, as well as finite element analysis. See DOI: https://doi.org/10.1039/d5nh00582e.Acknowledgements
This work is supported by the Natural Science Foundation of China (52322319), the Science and Technology Development Fund, Macao SAR (0063/2023/RIA1, 0107/2024/AMJ), UM research grant (MYRG-GRG2025-00006-IAPME, MYRG-CRG2024-00012-IAPME, MYRG-GRG2024-00064-IAPME).References
- T. Emmerich, N. Ronceray, K. V. Agrawal, S. Garaj, M. Kumar, A. Noy and A. Radenovic, Nat. Rev. Methods Primers, 2024, 4, 69 CrossRef CAS.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
- R. B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 Search PubMed.
- A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 0091 CrossRef CAS.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200 CrossRef CAS PubMed.
- P. Robin, T. Emmerich, A. Ismail, A. Niguès, Y. You, G.-H. Nam, A. Keerthi, A. Siria, A. K. Geim, B. Radha and L. Bocquet, Science, 2023, 379, 161–167 CrossRef CAS PubMed.
- D. Stein, M. Kruithof and C. Dekker, Phys. Rev. Lett., 2004, 93, 035901 CrossRef PubMed.
- R. B. Schoch, H. van Lintel and P. Renaud, Phys. Fluids, 2005, 17, 100604 CrossRef.
- C. Lee, L. Joly, A. Siria, A.-L. Biance, R. Fulcrand and L. Bocquet, Nano Lett., 2012, 12, 4037–4044 CrossRef CAS PubMed.
- P. Abgrall and N. T. Nguyen, Anal. Chem., 2008, 80, 2326–2341 CrossRef CAS PubMed.
- J. Li, D. Stein and C. McMullan, Nature, 2001, 412, 166–169 CrossRef CAS PubMed.
- A. Bhardwaj, M. V. Surmani Martins, Y. You, R. Sajja, M. Rimmer, S. Goutham, R. Qi, S. Abbas Dar, B. Radha and A. Keerthi, Nat. Protoc., 2024, 19, 240–280 CrossRef CAS PubMed.
- A. R. Poggioli, A. Siria and L. Bocquet, J. Phys. Chem. B, 2019, 123, 1171–1185 CrossRef CAS PubMed.
- R. C. Rollings, A. T. Kuan and J. A. Golovchenko, Nat. Commun., 2016, 7, 11408 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- G. Cui, Z. Xu, H. Li, S. Zhang, L. Xu, A. Siria and M. Ma, Nat. Commun., 2023, 14, 2295 CrossRef CAS PubMed.
- A. Siria, P. Poncharal, A.-L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef CAS PubMed.
- J. E. Hall, J. Gen. Physiol., 1975, 66, 531–532 CrossRef CAS PubMed.
- S. W. Kowalczyk, A. Y. Grosberg, Y. Rabin and C. Dekker, Nanotechnology, 2011, 22, 315101 CrossRef PubMed.
- S. Hu, M. Lozada-Hidalgo, F. C. Wang, A. Mishchenko, F. Schedin, R. R. Nair, E. W. Hill, D. W. Boukhvalov, M. I. Katsnelson, R. A. W. Dryfe, I. V. Grigorieva, H. A. Wu and A. K. Geim, Nature, 2014, 516, 227–230 CrossRef CAS PubMed.
- M. Lozada-Hidalgo, S. Hu, O. Marshall, A. Mishchenko, A. N. Grigorenko, R. A. W. Dryfe, B. Radha, I. V. Grigorieva and A. K. Geim, Science, 2016, 351, 68–70 CrossRef CAS PubMed.
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS.
- R. A. Robinson and R. H. Stokes, Electrolyte Solutions, Butterworth, London, 2nd edn, 1970 Search PubMed.
- A. Reina, X. Jia, J. Ho, D. Nezich, H. Son, V. Bulovic, M. S. Dresselhaus and J. Kong, Nano Lett., 2009, 9, 30–35 CrossRef CAS PubMed.
- A. Reina, S. Thiele, X. Jia, S. Bhaviripudi, M. S. Dresselhaus, J. A. Schaefer and J. Kong, Nano Res., 2009, 2, 509–516 CrossRef CAS.
- S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- P. Sun, M. Zhu, K. Wang, M. Zhong, J. Wei, D. Wu, Z. Xu and H. Zhu, ACS Nano, 2013, 7, 428–437 CrossRef CAS PubMed.
- T. Sasaki, M. Watanabe, H. Hashizume, H. Yamada and H. Nakazawa, J. Am. Chem. Soc., 1996, 118, 8329–8335 CrossRef CAS.
- T. Sasaki, Y. Ebina, Y. Kitami, M. Watanabe and T. Oikawa, J. Phys. Chem. B, 2001, 105, 6116–6121 CrossRef CAS.
- T. Tanaka, Y. Ebina, K. Takada, K. Kurashima and T. Sasaki, Chem. Mater., 2003, 15, 3564–3568 CrossRef CAS.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- L. Wang, I. Meric, P. Y. Huang, Q. Gao, Y. Gao, H. Tran, T. Taniguchi, K. Watanabe, L. M. Campos, D. A. Muller, J. Guo, P. Kim, J. Hone, K. L. Shepard and C. R. Dean, Science, 2013, 342, 614–617 CrossRef CAS PubMed.
- A. Ulman, An Introduction to Ultrathin Organic Films: From Langmuir–Blodgett to Self–Assembly, Academic Press, 2013 Search PubMed.
- K. Matsuba, C. Wang, K. Saruwatari, Y. Uesusuki, K. Akatsuka, M. Osada, Y. Ebina, R. Ma and T. Sasaki, Sci. Adv., 2017, 3, e1700414 CrossRef PubMed.
- Y. Ji, G.-P. Hao, Y.-T. Tan, W. Xiong, Y. Liu, W. Zhou, D.-M. Tang, R. Ma, S. Yuan, T. Sasaki, M. Lozada-Hidalgo, A. K. Geim and P. Sun, Nat. Commun., 2024, 15, 10546 CrossRef CAS PubMed.
- M. Ohwada, K. Kimoto, T. Mizoguchi, Y. Ebina and T. Sasaki, Sci. Rep., 2013, 3, 2801 CrossRef PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |




