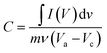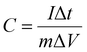Sodium cholate orchestrated synthesis of silver deposited camphorsulphonic acid doped rodlike polypyrrole architecture for asymmetric supercapacitor applications

Abstract

An asymmetric supercapacitor (ASC) was developed using camphorsulphonic acid (CSA)-doped polypyrrole (PPY) nanorods as the positive electrode and activated carbon as the negative electrode. The CSA doping and rod-like morphology enhanced the conductivity and electrochemical activity of PPY. Density functional theory (DFT) analysis revealed that CSA significantly lowers the HOMO–LUMO energy gaps of pyrrole oligomers, particularly with increasing chain length, indicating improved electronic properties favorable for charge storage. Electrochemical testing showed that the pristine CSA-doped PPY electrode exhibited a moderate specific capacitance of 180 F g⁻¹ at 2 mV s⁻¹, which decreased at higher scan rates. However, after silver nanoparticle deposition on the PPY surface, it displayed a highly reversible and rectangular-type cyclic voltammetry (CV) profile, indicating ideal capacitive behavior, with a specific capacity of 527.28 F g⁻¹ at a scan rate of 2 mV s⁻¹. This enhancement was attributed to the strong interaction between silver and the CSA-doped PPY nanorods, which synergistically improved the capacitive performance. The energy density value obtained from the Ragone plot was 12.57 Wh kg⁻¹. These findings demonstrated the potential of metal-doped conductive polymers for high-performance supercapacitor applications. For real-time evaluation, cyclic voltammetry (CV) and galvanostatic charge–discharge (GCD) tests were performed on the assembled asymmetric supercapacitor (ASC). The ASC employed an Ag-deposited, CSA-doped polypyrrole (PPY) positive electrode and a biowaste-derived activated porous carbon negative electrode. The device delivered a specific capacitance of 208.88 F g⁻¹ at 2 mA cm⁻², with corresponding gravimetric energy and power densities of 41.78 Wh kg⁻¹ and 886.89 W kg⁻¹, respectively.

---

1. Introduction

Numerous critical issues, including environmental pollution, unrestricted utilization of fossil fuels, and the rapid expansion of the global economy, have sparked significant interest in diverse energy storage and delivery systems, along with high-performance power sources. The escalating global energy demand, coupled with the rise of intermittent renewables, has thrust energy storage into the forefront. Consequently, there is a burgeoning demand for cost-effective yet enhanced electrochemical energy storage devices featuring high-performance electrode materials.¹ Consequently, there has been a surge of efforts in the fabrication of this class of materials. Supercapacitors represent one such pioneering device developed to meet the demands of both capacitors and batteries. Low-voltage devices generated revenue worth $115 million for the global supercapacitor market in 1999, while the worldwide battery industry reached $50 billion in revenue by 2010.² Among the different types of energy storage devices, batteries and supercapacitors constitute the two primary electrochemical energy storage technologies.³ Batteries exhibit several intrinsic limitations, including resistive losses arising from inefficient ion and electron transport mechanisms. Furthermore, under high-power operating conditions, excessive heat generation and dendritic growth may occur, adversely affecting battery performance and safety.⁴ Another important class of electrochemical energy storage materials is supercapacitors, which offer high power density and long cycle life, making them a promising alternative or complementary technology to conventional batteries. In recent times, the industry has witnessed the introduction of high-performance double-layered supercapacitors utilizing activated carbon. Supercapacitors are classified based on their constituent electrode materials into symmetric and asymmetric configurations. Based on their charge storage mechanisms, supercapacitors can be broadly classified into electric double-layer capacitors (EDLCs), pseudocapacitors, and asymmetric supercapacitors (ASCs). Symmetric supercapacitors, which utilize the same active material for both electrodes, inherently exhibit low energy density and a narrow potential window, limiting their overall performance.⁵ Asymmetric supercapacitors effectively overcome this limitation due to their wide potential window and enhanced energy density. Asymmetric supercapacitors (ASCs) coupled by two distinct electrode materials furnish a particular benefit of wide operational voltage window, which remarkably improves the energy density compared with symmetric supercapacitors.⁶ Various types of electrode materials have been reported.^7–9 Recently, high-performance double-layered supercapacitors based on activated carbon have been introduced in the industry.¹⁰ Although carbon-based supercapacitors offer large power capacities owing to facile ion sorption and desorption, they suffer from the disadvantage of low specific energy.¹¹ To counter this problem, highly conductive polymers like polypyrrole (PPY), polyaniline (PANI), and polythiophene (PTH) were used instead of carbonaceous materials to prepare the supercapacitors.^12,13 Conducting polymers are intriguing because they are cost-effective and possess high charge density compared to their expensive metal oxide counterparts.¹⁴ Conducting polymers enhance the device's charge retention properties by a redox mechanism to retain charge in the bulk site of the material, thus augmenting the stored energy and minimizing self-discharge. A relatively low rate of charge–discharge, which implies a low power, is observed owing to the sluggish mobility of ions in the bulk electrode. Despite this shortcoming, it is a well-agreed opinion that conducting polymers are preferable candidates over inorganic battery electrode materials in truncating the aperture between double-layer supercapacitors and batteries, courtesy of better kinetics.¹⁵ Polypyrrole is arguably the best-conducting polymer candidate due to a greater extent of flexibility in electrochemical processing.¹⁶ Polypyrrole possesses a high capacitance per unit volume (400–500 F cm⁻³) owing to its higher density.¹⁷ A better electrochemical performance can be achieved by fabricating nanostructures because materials at the nanometre scale can offer a huge contact surface area, thus augmenting the charge–discharge rate.¹⁸ In contrast to their bulk forms, conducting polymers with nanostructured morphology manifest many advantages like modified mechanical features for the accommodation of strain, a large surface area, and a shortened route for mass/ion/charge transport, along with additional features like flexibility and a mixed conductive mechanism, which specifically offer an avenue for the reduction of interfacial impedance at the electrode–electrolyte junction.¹⁹ Fabricating 1D nanostructures (such as nanotubes and nanorods) and 3D micro-/nanostructures has posed significant challenges. Synthesis pathways using hard and soft template assisted methodologies are the most common strategies for fabricating 1D polypyrrole nanomaterials.²⁰ Anodic aluminum oxide (A.A.O.), track-etched polycarbonate membranes, and inorganic V₂O₅ nanofibers are used in the case of a hard template approach with the aid of electrochemical polymerization and chemical oxidation polymerization.²¹ However, the hard template approach is hindered by the difficulty in removing the template, which can impact the structure of the conducting polymer or cause distortion of the nanostructures. On the other hand, the soft template strategy relies on the use of structure-guiding molecules such as surfactants, liquid guiding phases, and organic dopant anions.²² Furthermore, the characteristics of the surfactant, chain length, polymerization temperature, and surfactant concentration all play crucial roles in controlling the size and morphology of nanostructures. These factors essentially drive the development of various structural morphologies of polymers, such as fibrous, tubular, spherical, and rod shapes.²³ For the sake of achieving a nicely arranged PPY nanostructure, Han et al.²⁴ comprehensively scrutinized the consequences of concentrations of the surfactant [cetyltrimethylammonium bromide (CTAB)] as well as the monomer, reaction temperature, various oxidants, etc. in the aqueous polymerization of pyrrole. D. P. Dubal et al.²⁵ reported a facile reactive template route for the development of PPY nanostructures possessing three different morphologies i.e., nanofibers, nanotubes, and urchins. These distinctive morphologies of PPY lead to better interfacial/chemical distribution, fast ion and electron transfer by enhancing the electroactive surface area. The PPY nanofibers exhibit the maximum specific capacitance of 604 F g⁻¹ at a current density of 1.81 A g⁻¹ as a supercapacitor electrode.

Gan et al.²⁶ fabricated silver nanoparticle-/nanocluster-decorated polypyrrole (Ag@PPY) nanocomposites. The resulting hybrid Ag@PPY nanocomposites exhibited an enhanced specific capacitance of 414 F g⁻¹, compared to 273 F g⁻¹ for the pure PPY electrode. Fine-sized Ag nanoparticles (2–4 nm) were uniformly dispersed within the PPY matrix, enhancing electron hopping and increasing the capacitance of PPY. Medium-sized Ag nanoparticles (55–100 nm) adhered to the PPy surface, serving as spacers that mitigated PPY restacking. This hierarchical morphology shortened electron transport pathways, thereby improving the cycling stability and specific capacitance of the Ag@PPY nanocomposites. A thin-film electrode composed of ceramic oxide and yttrium aluminum garnet (YAG:Al₅Y₃O₁₂) integrated with polypyrrole (PPY) was developed by Ehsani et al.²⁷ The novel film electrode was fabricated using pulse electrochemical deposition technology and exhibited a significantly enhanced specific capacitance of 254.0 F g⁻¹, compared to 109.0 F g⁻¹ for a pure PPY electrode. The authors also highlighted the superior stability of these thin-film electrodes in aqueous electrolytes relative to conventional ruthenium-based perovskite electrodes. We synthesized sodium cholate assisted polypyrrole nanorods doped with camphorsulphonic acid (CSA) (PPY) and investigated their performance for energy storage applications. Herein, sodium cholate with its ability to form micelles is used as a soft template to control the morphology and structure during the synthesis of PPY.²⁸ In addition, CSA as a dopant can enhance the electrical conductivity through effective synergetic interaction, improve solubility and lead to more uniform granular nanostructured morphology.²⁹

2. Materials and methods

The pyrrole monomer (purchased from Sigma-Aldrich Inc.) was distilled under a vacuum atmosphere, purged with nitrogen, followed by wrapping with aluminium foil to avert any photolytic consequence and put in a refrigerator at 4 °C. Camphorsulphonic acid was procured from Sigma-Aldrich. Ammonium persulphate was supplied by Merck India Ltd. Triple distilled water was employed for the whole experimental work wherever required. Ammonium persulfate (APS) and silver nitrate were acquired from Merck India Ltd. Sodium cholate was procured from Sisco Research Laboratories Pvt. Ltd (SRL), located in Mumbai, India.

2.1. Synthesis of camphorsulphonic acid doped PPY nanorods

For the synthesis of sodium cholate assisted camphorsulphonic acid doped rod-like polypyrrole (PPY), first, a requisite amount of camphor-sulphonic acid was added to ice cold triple distilled water followed by dispersion of sodium cholate. The pyrrole monomer was then introduced into the dispersion under stirring conditions. Subsequently, incorporation of ammonium persulphate solution as an oxidant was executed under stirring conditions. The pyrrole monomer to ammonium persulphate molar ratio was maintained at 1 : 2. As polymerization commenced, the color of the mass turned black. The polymerization reaction was carried out at 0–4 °C for 5 hours. At the end of the polymerization reaction, the black solid mass was filtered and washed with acidic water followed by washing with acetone. Finally, the washed black solid polymer (black powder) was dried and kept in a vacuum desiccator for further characterization.

2.2. Characterization

Fourier transform infrared (FTIR) spectroscopic scanning of PPY–Ag nanocomposite powder samples with KBr (in pellet form) was accomplished using a FTIR spectrophotometer (model: PerkinElmer Spectrum Two) in the wave number range of 400–4000 cm⁻¹.

For the investigation of interfacial interaction between the PPY matrix and Ag nanoparticles, the X-ray photoelectron spectroscopy (XPS) analysis was executed using a Thermo-VG Scientific ESCALAB 250 microprobe equipped with an Al Kα monochromatic source (1486.6 eV photons) operated at 14 kV and 20 mA.

The Ag percentage dispersed within the PPY matrix was investigated by inductively coupled plasma optical emission spectrometry (ICP-OES) using an Optima 2100DV ICP optical emission spectrometer, PerkinElmer, USA. For ICP-OES analysis, the dispersion of samples was prepared by adding the powder sample of about 1 mg in 20 mL concentrated nitric acid and then diluting with water to 100 mL.

For scrutiny of the surface morphology, scanning electron microscopy (SEM) analysis of the PPY–silver nanocomposite samples was performed using a scanning electron microscope (model: ZEISS EVO 18). The nanocomposite samples, mounted on a specimen stub, were sputter coated with Pt prior to scanning under the microscope.

The bulk architecture of PPY–Ag nanocomposite samples was also investigated using a transmission electron microscope (model: JEOL-JEM-2100). For transmission electron microscopy (TEM) analysis the PPY–Ag nanocomposite sample was dispersed in distilled water with the help of a probe sonicator for the purpose of drop casting on a carbon coated copper grid followed by air drying.

To detect the structural composition, Raman spectral analysis was performed.

The analysis of electrochemical and other capacitive characteristics was executed by employing cyclic voltammetry (CV) (C–H 660 instrument). In order to accomplish the fabrication of electrodes for CV investigation, 5 mg carbon black and a same amount of PVDF (polyvinylidene fluoride) were mixed with 40 mg of each of the samples and adequate amount of NMP (N-methyl-2-pyrrolidone) was added to the mixture. This blend was kept under stirring until it became homogeneous and produced a uniform gel for the fabrication of the electrode. A 1 × 1 cm² nickel foam was cut and washed with absolute ethanol (99.9%) several times to ensure that it is devoid of impurities and thus to facilitate the fastening of the synthesised gel to the foam wall. The amount of gel applied on the foam wall was 8 mg. Furthermore, the nickel foam was cut into 1 × 3 cm² size rectangles and cleaned thoroughly. The asymmetric solid-state device performance study was performed to apprehend energy storage in real-time analysis. However, the asymmetric supercapacitor was also investigated in the non-aqueous ionic liquid for solid gel formation. In this case, polyvinyl alcohol (PVA) dissolved in DMSO solvent and EMIM-BF4 was used as an ionic electrolyte. Initially, the solvent DMSO and the ionic electrolyte liquid were mixed in a 80 : 20 weight percentage ratio, then 2.0 g PVA was poured, and the whole mixture was placed under vigorous stirring at 95 °C for 1.5 h. Furthermore, the as-formed gel type slurry was cast in a Teflon Petri dish and cooled down. After being cooled to RT, the obtained electrolyte gel was subjected to a freezing/thawing cycle (12 h freezing at −10 °C followed by thawing at RT).

The electrodes fabricated with samples set-1 to set-3 were allowed to dry at room temperature for 24 hours. 1 M aqueous Na₂SO₄ (pH ∼ 7) was chosen as the primary reagent for electrolyte medium, which was introduced in a three-electrode glass cell setup for CV measurement. Here, nickel foams coated with the prefabricated sample gels acted as a working electrode (WE), a platinum wire as a counter electrode (CE), and Ag/AgCl as the reference electrode (RE).

Moreover, the asymmetric supercapacitor is assembled and investigated for the greater electrochemical energy response. In this asymmetric supercapacitor system, the PPY–Ag nanocomposite acted as a cathode material, and the lignocellulose derived activated porous carbon work as a anode material.

2.2.1. DFT calculations. All calculations were performed with Gaussian 16.³⁰ Density functional theory (DFT) can handle long π-conjugated systems without spin contamination in unrestricted open-shell formalism. Hence, we used the B3LYP^31,32 hybrid functional in combination with the 6-31G(d,p) basis set for our target species.³³ Polypyrroles (PPY) of varying lengths were modeled as nPy oligomers (where n = 6, 9, and 12), and their structures were optimized. Beyond n = 9, the electronic structure properties were observed to be length independent, inferring that the 9Py oligomer can sufficiently represent the polymer. Hereafter, 9Py was used for doping with camphorsulfonic acid (CSA). Geometries of the neutral 9Py, dopant, and dopant–9Py complexes were optimized at the B3LYP/def2TZVP³⁴ level of theory. No imaginary frequency was obtained in the frequency calculation, which confirms the successful geometry optimization. While comparing two basis sets 6-31G(d,p) and def2TZVP, the results did not differ. Hence, the rest of the electronic-structure calculations were carried out with B3LYP/6-31G(d,p). From DFT results, we determined the highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), ionization potential (IP), and electron affinity (EA). For excited absorption spectra, we used the time-dependent DFT (TD-DFT) method. Furthermore, the binding energy of the 9Py–CSA complex was computed. All calculations were performed in the gas phase. GaussView was used for visualization.³⁵

3. Results and discussion

3.1. Preparation of PPY nanorods

PPY was synthesized in an aqueous camphorsulfonic acid medium using ammonium persulfate as the oxidant, with the assistance of sodium cholate as a surfactant acting as a soft template. Sodium cholate manifests self-assembled rodlike micellar aggregates in aqueous dispersion^20,36,37 and assists the encapsulation of the hydrophobic pyrrole monomer favouring its oxidative polymerization by ammonium persulphate.³⁸ The camphorsulfonic acid doping was achieved during the polymerization of pyrrole within camphorsulphonic acid medium. To get rid of excess ammonium persulphate and sodium cholate from the black polymer composite, it was properly washed with acidified water (% camphorsulphonic acid), which also ensured proper doping, followed by drying and storage in a vacuum desiccator.^39–41

3.2. Preparation of silver deposited rodlike PPY

Silver deposited rodlike PPY was synthesized in an aqueous acidic media in the presence of ammonium persulphate as an oxidant and under the guidance of sodium cholate acting as a soft template. For in situ deposition of silver nanoparticles on camphorsulphonic acid doped PPY nanorods, a requisite quantity of AgNO₃ solution was added with PPY dispersion before oxidant addition. For the investigation of the influence of silver content on the PPY nanocomposites, pyrrole was polymerized by using ammonium persulphate as the oxidant in the presence of varying concentration of silver nitrate. In order to get rodlike nanostructures of the polymer, sodium cholate surfactant was utilized as a soft template. Sodium cholate manifests self-assembled rodlike micellar aggregates in aqueous dispersion and assists the encapsulation of the hydrophobic pyrrole monomer, favouring its oxidative polymerization by ammonium persulphate. In the course of polymerization reactions of the pyrrole monomer, silver nitrate got reduced to metallic silver and deposited on the CSA doped PPY nanorod surface. The concentration of silver nitrate was changed (Table 1 and Scheme 1).

Table 1 Formulations used for camphorsulphonic acid doped PPY–Ag nanocomposite synthesis

Sample designation	PY (mL)	Components			Volume of 0.01 M silver nitrate solution (mL)	Volume of 0.116 M APS
		Sodium cholate dispersion
		Sodium cholate (g)	Water (mL)	CSA (g)
Set-1	0.20	0.344	35	0.060	0	15
Set-2	0.20	0.344	21	0.060	14	15
Set-3	0.20	0.344	19	0.060	16	15

---

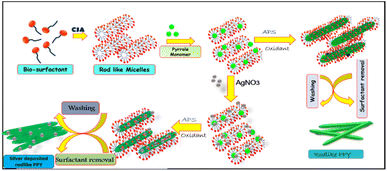Scheme 1 Schematic presentation of synthesis of camphor sulphonic acid doped PPY and silver deposited PPY.

3.3. SEM analysis

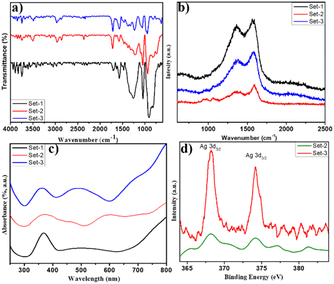
SEM analysis was performed to scrutinize the morphology of the CSA doped PPY nanostructures. Fig. 1a presents the SEM images of PPY nanorods under different magnifications. The average diameter of the synthesized PPY exhibits an average diameter around 134 nm to 157 nm. SEM images of the surface morphology of the as-developed CSA doped PPY–Ag nanocomposite are depicted in Fig. 1b. Ag nanoparticles were explored to stick in situ to the surface of PPY nanorods, most likely owing to redox interactions between pyrrole, APS, and AgNO₃.

Fig. 1 (a) SEM images of CSA doped PPY nanorods with different magnifications. (b) SEM images of silver deposited (various concentrations) CSA doped PPY nanorods.

3.4. TEM analysis

The samples of the PPY–Ag nanocomposite were also subjected to TEM examination in order to evaluate the bulk shape. Fig. S1 displays a TEM image of a rod-like PPY–Ag nanocomposite. TEM images of depicted portion of the sample indicate that the diameter of the PPY nanorod is ∼48–114 nm, and the diameter of the deposited AgNPs, seen as dark spots, is ∼3.50–3.9 nm.

3.5. Spectroscopic analysis

3.5.1. FTIR spectroscopy. FTIR analysis was executed to scrutinize the information regarding the chemical structure of camphorsulphonic acid doped sodium cholate soft template guided PPY nanorods in the 600 to 4000 cm⁻¹ wave number range. From Fig. 2a, it has been discerned that the distinctive peaks around 1570 cm⁻¹ and 1463 cm⁻¹ correspond to the symmetrical (C=C) and antisymmetrical (C=N) stretching vibrations, respectively.⁴² The peaks around 1060 cm⁻¹ and 1364 cm⁻¹ are ascribed to the vibrations resulting from C–H displacement and bending, respectively. The peak around 942 cm⁻¹ results from PPY doping. The peak around 1235 cm⁻¹ is associated with vibrations caused by C–N displacement. The C–H wagging occurs around the peak at 816 cm⁻¹. However, the distinctive peak at 1710 cm⁻¹ (C=O) is attributed to CSA doping in PPY.⁴³ The band appearing at 1318 cm⁻¹ results from antisymmetric stretching vibration. Two weak bands attributable to methylene group stretching vibrations are observed at 2971 and 2864 cm⁻¹. The bands at around 3494 cm⁻¹ can be ascribed to C–H and N–H stretching vibrations. The vibration bands appearing at 752 cm⁻¹ and 636 cm⁻¹ ascribe to the C–S and S–O stretching vibration, respectively, indicating the doping of CSA into the PPY nanorod chains.⁴⁴

Fig. 2 (a) FTIR spectra of PPY nanostructures, (b) Raman spectra of PPY nanostructures, (c) UV-vis spectra of PPY nanostructures, and (d) XPS spectra of PPY nanostructures.

3.5.2. Raman spectroscopy. Raman spectroscopy is a crucial approach to achieve structure related details regarding polymers. In a majority of instances, Raman scattering is very proficient to detect the degree of crystallinity in a sample. Generally, a crystalline material exhibits a very sharp, intense Raman peak, whereas an amorphous material reveals broader Raman peaks with less intensity. Raman analysis of PPY–CSA nanorods and silver doping (with varying concentration) exhibited various Raman bands between 600 cm⁻¹ and 2000 cm⁻¹. The most intense and sharp peak exhibited in Fig. 2b is the one at about 1587 cm⁻¹, which can be imputed to C–C and C=C ring stretching and N–H in-plane bending vibration.⁴⁵ The peak at approximately 1070 cm⁻¹ corresponds to C=C ring stretching and C–H in-plane bending vibration. The sharp peak at 1363 cm⁻¹ arises from C–H and N–H in-plane bending vibrations. The peaks at 936 cm⁻¹ and 975 cm⁻¹ correspond to C–C ring deformation.⁴⁶ The intensity and sharpness of the peaks were found to decrease by incorporation of silver nanoparticles, indicating the slight decrease in the crystallinity of the CSA doped PPY nanorods upon further doping with silver nanoparticles. An intense G-band at 1587 cm⁻¹ appeared in the Raman spectra of silver deposited PPY nanorods and a varying relative intensity D band appeared at 1363 cm⁻¹. A clear decrease in ID/IG was observed with increasing silver deposition, indicating the improvement in the conjugation through PPY chain, extension of molecular delocalization through chains and the decrease in imperfection level of subsequent doping in PPY.⁴⁷

3.5.3. UV-vis spectroscopy. The UV-vis absorption spectra of CSA doped PPY and silver deposited CSA doped PPY are illustrated in Fig. 2c. The UV-vis spectra depicted two absorption peaks at 370 nm and 478 nm along with a free tail located above 680 nm in the NIR region. The source of various absorption bands can be elucidated as follows: the neutral PPY is an insulator with an electronic band that is distinguished by a 3.2 eV band gap.^48,49 As a consequence of doping of PPY with CSA, the electrons from the PPY backbone chains are eliminated, which causes the introduction of polaronic states within the neutral band gap. An occupied bonding polaron level (BPL) and an empty anti-bonding polaron level (APL) are two localized electronic bands that are introduced into the energy gap by the production of polarons. A stable bipolaron is created when the two polarons amalgamate together. Contrary to the polaron states, the bipolaron bonding state is empty as the bonding bipolaron level (BBL) and antibonding bipolaron level (ABL) approach each other. As a result, the interband π–π* transition, whose intensity is correlated with the PPY content, corresponds to the absorption band at 376 nm. The band at approximately 478 nm is attributed to the transition from the valence band to the antibonding polaron or bipolaron state, as a result of polaron absorption. The broad tail absorption band at 680 nm, which is mostly caused by bipolaron absorption, corresponds to the transition from the valence band to the antibonding polaron or bipolaron state.^44,50,51

3.5.4. XPS study. The XPS spectra (Fig. 2d) reveal Ag 3d doublet peaks at binding energies of 368.2 eV and 374.2 eV, which correlate with photoelectrons released from the two spin states of the 3d core level. The spin energy separation between those two peaks was calculated as 6.0 eV corresponding to the spin–orbit coupling of Ag 3d_5/2 and Ag 3d_3/2 levels.^52,53 Comparing with the values of pure silver, deposition of metallic silver (0) on the PPY nanorods was confirmed by XPS analysis.⁵⁴

3.6. DFT calculations

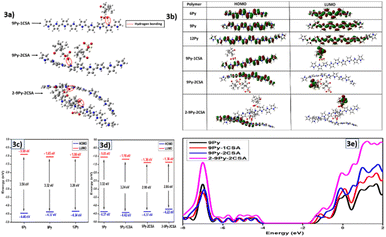
The DFT investigation was conducted on a range of pyrrole oligomers nPy (n = 6, 9, and 12), where “n” stands for the no. of monomer (py) units present in an oligomer. For all oligomers, the B3LYP/def2tzvp-level optimized structures and geometrical parameters are shown in Fig. S2 and Table S1. While comparing the bond distances (of ring and bridging atoms) and C–N–C angles across all oligomers, no change of structural parameters was observed after n = 9. While all C–C (1.42 Å) and N–C (1.38 Å) bond distances of ring atoms and C–C (1.45 Å) bridging distances remained the same, the C–N–C angle changed from the initial value of 110.8° for n = 6 to 110.64° for n = 9 where it converged. Therefore, a minimum of 9 pyrrole units are essential to best represent the polymer. CSA-doped polymers, i-9Py–jCSA (i, j = 1 and 2), were studied employing B3LYP/6-31G(d,p).

Fig. 3a displays energy-minimized structures of three doped compositions of the polymer, namely 9Py–1CSA, 9Py–2CSA, and 2-9Py–2CSA. As a result of strong interaction with the dopant, the polymer chain curves from being linear is evidenced by a decrease of the C–N–C angle from 110.64° (free polymer) to 110.24° (doped polymer). As is obvious, DFT provides insights into an N–H (Py)⋯O (CSA)-type of H-bond interaction between the polymer and the dopant.

Fig. 3 (a) The optimized structures of 9Py–1CSA, 9Py–2CSA, and 2-9Py–2CSA. (b) HOMO–LUMO structures of 6Py, 9Py, 12Py, 9Py–1CSA, 9Py–2CSA, and 2-9Py–2CSA. (c)–(e) The HOMO–LUMO energy level diagrams of (c) undoped oligomers nPy (n = 6, 9, and 12) and (d) doped 9Py–1CSA, 9Py–2CSA, and 2-9Py–2CSA, including 9Py. (e) The density of states plots of 9Py, 9Py–1CSA, 9Py–2CSA, and 2-9Py–2CSA.

Various doping scenarios were explored by doping two CSA (i.e., 9Py–2CSA) or one CSA and two polymer chains. Because of the bulkiness, the two CSA dopants cannot come close to each other to form H-bonds with two neighboring N–H sites. Overall, with dopants, the ring C–C bond increases and the [double bond splayed right]C–N–C angle decreases to a certain extent in the polymer.

3.6.1. Infrared (IR) spectra. DFT computations yield simulated IR spectra on the selected best representable form of polymer, i.e., 9Py and its two doped composites. Fig. S3a and b display the scaled IR spectra and absorption spectra of the selected systems, respectively. While comparing the important bands of simulated spectra with those of experiments, an excellent agreement between theory (using a uniform scaling factor) and experimental data was obtained using B3LYP.

The functional group region of the simulated scaled IR spectra exhibits two noticeable peaks for 9Py: 3677 cm⁻¹ for N–H stretching and 3245 cm⁻¹ for C–H stretching. Besides, there appear a few distinguishable bands (fingerprint regions) of the polymer backbone for conjugation, including 1560 cm⁻¹ (N–H wagging), 1255 cm⁻¹ (N–C stretching), 1347 cm⁻¹ (C–H wagging), and 1086 cm⁻¹ (C–H wagging). Differences between experimental and simulated frequencies primarily arise from comparing the condensed phase (experimental) and gas phase (simulation) spectral data.

Doped and undoped states can be characterized by the presence of additional spectral peaks in the former. Compared to undoped 9Py, 9Py–nCSA has three extra peaks in the functional group region (Fig. S3a): 3440 cm⁻¹ instead of 3245 cm⁻¹ (N–H stretching), 3160 cm⁻¹ (O–H stretching), and 3108 cm⁻¹ (C–H stretching of –CH₃ in CSA). A new peak for the C=O stretching also appears at 1822 cm⁻¹ in the presence of CSA.

3.6.2. UV-visible spectroscopic study. In Fig, S3b, the UV-vis spectra of PPY show three distinct peaks at 278 nm (π–π*), 332 nm (midgap transition), and 426 nm (valence to conduction band transition) corresponding to the maximum intensity.⁵⁵ Doping causes slight blue-shifting, e.g., the peaks at λ_max (426 → 422 nm) and the midgap transition (332 → 327 nm). Furthermore, in the presence of CSA, the π–π * transition peak at 278 nm vanishes. The simulated UV-vis spectral data accord well with the experiment. With a decreasing band gap, conduction and delocalization are slightly enhanced in 9Py–CSA compared to 9Py. The blue shifts in 9Py–CSA are attributed to distortion in the regular pyrrole rings, resulting in a decrease in interband transition.

3.6.3. HOMO–LUMO energy and band gap. Fig. 3b depicts the HOMOs and LUMOs of 6Py, 9Py, 12Py, 9Py–CSA, 9Py–2CSA, and 2-9Py–2CSA and the corresponding energies in Table S2 obtained from the B3LYP/6-31G(d,p) level of calculations.

In nPy and CSA-doped 9Py, the HOMO electron density is delocalized on the polymer backbone, sprawling on all carbons, hydrogens, and nitrogens. On the other hand, the LUMO is confined in the polymeric framework since only the core backbone atoms contribute to it. A comparison of HOMO–LUMO energies (Fig. 3b) of 6Py, 9Py, and 12Py reveals that the band gap shifts significantly from 6Py to 9Py but barely differs between 9Py and 12Py. Considering less computational overhead and convergence of properties, a PPY polymeric chain of length n = 9 is thus suitable for investigation.

Concerning doped configurations shown in Fig. 3c, the HOMO is 100% located on 9Py, whereas the LUMO is 100% situated on the CSA dopant. This implies the feasibility of charge transfer from the polymer to the dopant, i.e., between the HOMO and the LUMO. Furthermore, CSA doping results in the lowering of the band gap of the polymer by lowering both the HOMO and LUMO energy levels. When the amount of dopant CSA or polymer 9Py increases, Fig. 3d shows that the band gap steadily decreases. Moving from 9Py–1CSA to 2-9Py–2CSA, the HOMO energy increases from −4.42 to −4.22 eV, and the LUMO energy decreases from −1.18 to −1.36 eV, reducing the HOMO–LUMO gap from 3.24 to 2.86 eV. Arguably, when infinite amounts of pyrrole polymer and dopant CSA are present, the band gap will dramatically reduce, which could be in the interest of electrochemical device research.

To further confirm the change of electronic properties and band gaps, we plotted the total density of states (DOS) for 9Py, 9Py–CSA, 9Py–2CSA, and 2-9Py–2CSA (Fig. 3e). The figure shows that the total DOS comprises a lower energy valence band (VB) and a higher energy conduction band (CB). The separation between the VB and the CB gives an estimate of the band gap. The VB position remains unaltered in the presence of the CSA dopant, although the CB shifts closer to it (see the black and red curves), decreasing the band gap. As the number of dopant molecules increases, the CB shift is more. With increased polymer (9Py) molecules, the VB energy also increases, predominantly decreasing the band gap (magenta curve). Clearly, the study highlights that PPY may behave as a semiconductor in the presence of a CSA dopant due to the gradual decrease of the band gap.

3.6.4. Ionization potential (IP) and electron affinity (EA). The IP and EA are two important electrochemical parameters. Koopman's theorem help estimate the IP and EA by taking the negative of the HOMO and LUMO energies from DFT, respectively.⁵⁶ With the conventional exchange-correlation functional, these are typically underestimated compared to experimental values. However, hybrid functionals such as B3LYP, which partially considers the effects of self-interaction, produce a better result. Table S2 provides the IP and EA values computed with the B3LYP functional.

3.6.5. Binding energy. To quantify the interaction between the polymer and the dopant, we also estimated the binding energy (E_bind) of a 9Py–CSA complex as follows:

E_bind = E(9Py–CSA) − [E(9Py) + E(CSA)],

where E(9Py–CSA) is the energy of the 9Py–CSA complex, while E(9Py) and E(CSA) are energies corresponding to 9Py and CSA dopant, respectively. We obtained −41.67 kcal mol⁻¹ binding energy between 9Py and CSA, indicating a strong interaction between the two for a large magnitude.

So, the overall theoretical (DFT) analysis closely supports and complements the experimental findings. Geometry optimization reveals that a 9-unit pyrrole chain (9Py) effectively represents the polymer structure, consistent with the stable backbone confirmed by FTIR. The simulated IR and UV-vis spectra of CSA-doped PPY reproduce experimental spectral shifts, including the appearance of new functional group vibrations and blue-shifted absorption peaks, validating dopant incorporation and structural distortion. The HOMO–LUMO analysis show charge transfer from the polymer to the dopant and a progressive band gap reduction with increasing CSA, which correlates with the improved conductivity and capacitive behavior observed in CV profiles. The density of states (DOS) plots confirm the narrowing of the band gap, supporting the semiconductor-like behavior of doped PPY. Additionally, the high binding energy between CSA and PPY underscores the strong dopant–polymer interaction, explaining the enhanced electrochemical stability and performance. Overall, DFT provides a molecular-level explanation for the experimentally observed spectral features and improved supercapacitor characteristics.

3.7. Electro-chemical analysis

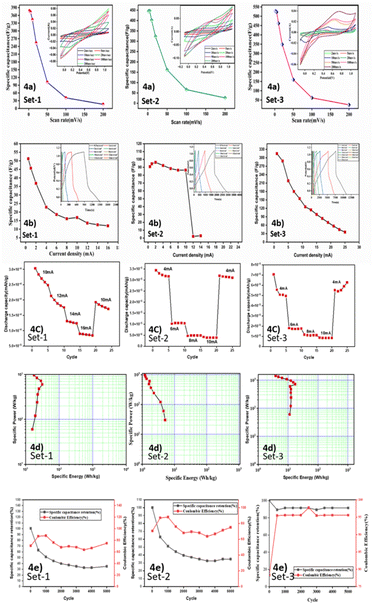
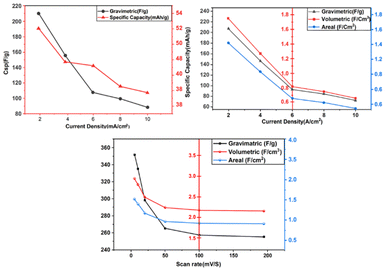
The final thrust of this work was analysis of the charge storage phenomena related to energy storage. Cyclic voltammetry studies with an archetypical three electrode system were employed to examine the performance of rodlike PPY doped with CSA and silver deposited rodlike PPY doped with CSA. The attained current voltage profile due to the redox reaction of the improved electrode is demonstrated in Fig. 4a. The electrochemical redox switching of the PPY units through protonation/deprotonation by the CSA dopant was found to be responsible for improved electrochemical activity. The modification of the electrode because of PPY and the redox couple exhibits the current–voltage characteristics, as shown in Fig. 4a. The outcome of the scan rate variation on CV data was investigated. The scan rate was varied in the range of 2–200 mV s⁻¹ in the potential window maintained in between −0.1 V to 1.1 V. The redox reaction in CSA doped PPY was monitored in the entirety of CV analysis, where prominent presence for the anodic and the other for the cathodic reaction were observed. It is noteworthy to mention that the oxidation peak shifted a bit to the positive value, whereas the reduction peak shifted slightly to the negative values on increasing the scan rate. The appearance of unsymmetrical redox peaks denotes the pseudocapacitive nature of the material due to predominate surface redox reactions.⁵⁷ The specific capacitance value of 180 F g⁻¹ at 2 mV s⁻¹ sharply decreased with increasing scan rate and reached an almost minimum constant value of 40 F g⁻¹ from 25 mV s⁻¹ onwards. After silver deposition in rodlike PPY doped with CSA, the nature of the rectangular type CV curve was altered, and improved results were obtained due to excellent capacitance behavior. The pure electrostatic reversible storage of charges happened through combining ion adsorption/desorption and surface redox reactions.⁵⁸ The synergistic effect of Ag nanoparticles having strong interaction with the rodlike CSA doped PPY was considered to govern the storage behaviour indicated by distinction of the area within the rectangular type CV curve.⁵⁹ Here, the counter-ion of CSA dopant oxidized the PPY backbone to create positive charge carriers such as polarons (radical ions) and bipolarons (dications). In addition, the deposited silver nanoparticles provided effective conduction pathways in homogeneous dispersion by preventing the agglomeration of PPY chains.

Fig. 4 (a) Cyclic voltammetry analysis and specific capacity of camphorsulphonic acid doped PPY and camphorsulphonic acid doped silver deposited PPY. (b) Galvanostatic charge–discharge analysis of camphorsulphonic acid doped PPY and camphorsulphonic acid doped silver deposited PPY. (c) Discharge capacity of PPY nanostructures. (d) Ragone plot of camphorsulphonic acid doped PPY and camphorsulphonic acid doped silver deposited PPY. (e) Long cycle stability response.

The specific capacity values could be measured based on the C–V results as shown below:

Here, C denotes the specific capacity (C g⁻¹), I is the current density, which is dependent on the potential, and ν and m denote the scan rate and the active mass, respectively. The difference between V_a and V_c is indicative of the potential range between −0.1 V and 1.1 V.

The specific capacitance of the electrode is directly proportional to charge accumulation and the respective redox reaction occurred that is traced by the area of CV curves. By altering the scan rate, the ion interaction with the nanoparticle decorated polymer is varied, and the respective capacitance value is also differed. At low scan rates, the faradaic process plays the dominant role, while with increasing scan rate the capacitive process becomes more prominent gradually. As the faradaic process is largely controlled by adsorption and diffusion processes, the reduction of diffusion at a higher scan rate (due to rapid movement of ions) has a negative impact on the faradaic current leading to a decrement in faradaic process contribution in the total current. Still, at high scan rates, the faradaic process persists (low value compared to the capacitive process) due to near surface adsorption by the electrode material, which also synchronized with the surface controlled capacitive process. Fig. 4a depicts that a maximum specific capacity of 527.28 F g⁻¹ is achieved for set-3 at a scan rate of 2 mV s⁻¹. This is probably due to the maximum amount of silver deposition on the polymer matrix, which is evidenced in ICP-OES measurement. The incorporation of silver nanoparticles helps to increment the ion transportation as well as enhance material conductivity. Energy storage capability of a device is extensively influenced by galvanostatic charge–discharge (GCD). The GCD curve is plotted in Fig. 4b, showing a nearly triangular shape, which is an indication of the presence of pseudocapacitive response with an ohmic polarization plateau. The corresponding charge and discharge times at 1 mA cm⁻² (lowest current) scan rate are tabulated in Table S3.

The specific capacitance from the charge–discharge plot is determined as follows:

In the above equation, C stands for the specific capacitance, I denotes the constant discharge current density, m is the active mass, the discharge period is denoted by Δt, and ΔV is the potential difference for that particular discharge period.

The coulombic efficiency(η) was determined using the following formula,

η = discharge capacitance/charging capacitance

Specific energy and power were calculated by the galvanometric study using the following two equations:⁴³

U (Wh kg⁻¹) = [C × V²]/[2 × 3.6]

P (W kg⁻¹) = specific energy × 3600/t

Here, C denotes the specific capacitance calculated from before. V is the potential range and t is the time taken for that voltage to discharge.

The charge storage mechanism of composite electrodes was investigated, and the impedance analysis was also conducted (Fig. S4) by assessing the impedance spectroscopy of the prepared composites in the range of 0.1 Hz to 100 Hz. This study offers detailed information regarding the ionic transfer and the charge transfer properties, as illustrated by the Nyquist plot. The information regarding the ohmic property of the electrode can be derived from the real part of the Nyquist plot, whereas the complex or the imaginary part is suggestive of the capacitive response tendency. The equivalent series resistance (ESR) value can be computed from the intercept value on the real axis at a higher frequency. Experimental results suggest that the resistance of the fabricated electrode is low. The mechanism of electron shuttling between the electrode and the electrolyte is denoted by the arc of the semi-circular part of the high frequency region. The diameter of the arc denotes the charge transfer resistance value. The resistance at the electrode–electrolyte interface from the analysis is presented in Table S3. The lower value of the resistance is indicative of the high ionic conductivity and diffusivity within the interface. Congruently, the slope of the Nyquist plot becomes steeper in the lower frequency zone towards the imaginary impedance Y-axis, specifying the capacitive type of nature of the electrode ideally and lower Warburg diffusion coefficient. Practically, the ions in the electrolyte solution must move through several layers of the electrochemical system one at a time. The migration of ions also consists of the electrolyte resistance factor in the electrolyte solution. Furthermore, the electrode surface layer is roofed up by the interpolated particles, which ascend the capacitance and contribute to the diffusion impedance for the gradient of concentration at the surface. The contribution of the inherent resistance of electrode material, in conjunction with the bulk resistance of the electrolyte and the resistance at the electrolyte–electrode interface, is represented as equivalent series resistance. In the mid-frequency region of the impedance spectra, the charge transfer resistance is depicted alongside the capacitance of the double layer. At the contact between the surface layer and the intercalated particles, the double layer's capacitance is generated. It influences additional electrolyte ion diffusion in the solid electrode and engenders a different diffusion impedance. However, the intercalated capacitance is produced for the electrolyte ion accretion and intercalated materials. It should be noted that the Warburg constant also denotes the value of the ion diffusion constant appropriate for increased ion transport. It is settled that the ion diffusion coefficient in the electrolyte is less reversible. The R_ct values obtained from Nyquist plots are given in Table S3.

The R_ct value of rodlike PPY doped with CSA decreased from the initial value of 1.6 ohm with increasing silver deposition in rodlike PPY doped with CSA and reached a minimum value of 0.9 ohm for set 3. In general, the increasing percentage of silver loading should simply improve the conducting nature, i.e., decrease the R_ct value of the composite for the conduction through the added conductive silver filler. Alternately, the charge transfer through the composite layer is also governed by the interfacial doping interaction of silver nanoparticles with the PPY matrix. The synergistic doping effect of Ag nanoparticles with the rodlike CSA doped PPY is considered to observe a minimum R_ct value for set 3.

A critical criterion for the next generation of supercapacitors is long cycle life, and as a consequence researchers are searching for new materials. The electrode materials of a supercapacitor must exhibit excellent cycle stability and durability. This is particularly crucial for conducting polymers, as the insertion and removal of counter-ions during the oxidation and reduction processes often induce volume changes. These volume fluctuations can lead to a deterioration in cycling stability. To ensure optimal performance, supercapacitors require electrode materials that can maintain their specific capacitance throughout the charge–discharge cycles. The capacity retention variation as a function of cycle number is shown in Fig. 4c. Fig. 4d presents the Ragone plot from which the energy density value obtained at 12.57 Wh kg⁻¹. The retention of discharge capacitance and coulombic efficiency at varying current was analyzed up to 5000k cycles, and the entire analysis is depicted in Fig. 4e. The plot shows the legibility of the material. The stability of supercapacitors during the charge and discharge operation was demonstrated by the cycle life of the electrodes [value of col% and ret%].

The variation of peak current as a function of scan rate square root is shown in Fig. 5. Moreover, the power law⁶⁰ was utilized to emphasize the peak current dual contribution as follows:

I_p = aV^b

Here, I_p, V, and a and b denote the peak current (A), scan rate (V s⁻¹), and variable parameters, respectively. The slope and intercept of the linear plot of log(I_p) vs. log(V) in Fig. 5 were used to calculate b and a values. The value of b typically exemplifies the working electrode's electrochemical storage mechanism type. For an ideal capacitive process, the b value should be 1, even though b = 0.5 signifies the faradaic process of total diffusion controlled. Because supercapacitor charging–discharging are facilitated by reversible action, the anodic oxidation peak is denoted as I_p, and a consistent linear plot of log(I_p) vs. log v is demonstrated in Fig. 5. The b value calculated for the CSA doped silver deposited PPY in 1 M Na₂SO₄ was 0.49233 within 0.5 and 1, which asserted the process of mixed charge storage.

Fig. 5 Electrokinetic study of different composites.

3.8. Asymmetric device performance

For further real-time investigation, cyclic voltammetry and galvanostatic charge–discharge tests of the assembled asymmetric supercapacitors (ASC) were performed. The Ag deposited CSA doped PPY electrode was used as the positive electrode and the biowaste derived activated porous carbon electrode was used as the negative electrode in the assembled ASC, where PVA–DMSO–EMIM-BF4 served as the ionic liquid polymer electrolyte gel, which are illustrated in Fig. 6, and inspected under diverse electrochemical parameters. The working potential window was 0 to 2.5 V for the whole asymmetric supercapacitor. The asymmetric device's cyclic voltammetry response is shown in Fig. 6a in the form of a rectangle with redox peaks. The response curve delineated as redox peaks is attributed to pseudo-capacitance behaviour. According to previous analysis, the activated porous carbon reveals an EDLC response and the oxides exhibit pseudo-capacitive redox peaks. The whole cyclic voltammetry measurement of this ASC device displays the pseudocapacitance of the manufactured PPY–Ag electrode and the cumulative response of the EDLC of the as-made APC electrode. The CV evaluation was done by varying the scan rate from 5 mV s⁻¹ to 200 mV s⁻¹ maintaining the voltage within the range of 0–2.5 V. The charge–discharge patterns of the ASC device are illustrated by Fig. 6b. The discharge profiles captured from the ASC device exhibited a linear decline alongside a notable phase-changing plateau, highlighting the combined influence of pseudocapacitance and EDLC. The ASC device was charged with a current ranging from 2 to 10 mA cm⁻² up to 2.5 V and then discharged. A minimal ohmic decrease was noticed for the internal resistance of the ASC device, primarily during high current density discharge times. The specific capacitance assessments were performed by taking the discharge time into account. This analysis identified the maximal specific capacitance of this device as 352.324 F g⁻¹, which is relatively greater at a scan rate of 2 mV s.

Fig. 6 Electrochemical analysis of the assembled asymmetric device. (a) Cyclic voltammetry analysis of different scan rate; (b) galvanostatic charge discharge of the device on different current density; (c) Nyquist analysis of the device and whole plot in inset; (d) corresponding Ragone plot of the device to comprehend its specific energy and power.

In addition, the specific capacitance value was 208.88 F g⁻¹ at 2 mA cm⁻². Fig. 6b depicts the specific capacitance data of the ASC device. A few formulations, which are depicted in the SI, were used to calculate the specific capacitances. The analysis of impedance spectra was done in the frequency range of 0.01 Hz to 100 kHz for a comprehensive investigation of the ASC's electrochemical properties. In the low-frequency region, the response exhibited a constant increase along the impedance plot's imaginary axis. As shown in Fig. 6c, the primary circle may represent the counter electrode and electrolyte's interkinetic advantages. The succeeding circular region diameter aids in determining the resistance to faradaic charge transfer (R_ct) at larger frequencies. The x-axis's principal cutoff represents the relationship between the resistance of the electrode. The low-frequency diffusion of ions from the electrolyte is responsible for the linear Warburg impedance diagrams in the linear zone. However, when the Warburg impedance value is lower, the conductivity and ion diffusion resistance are increased. Fig. 6d depicts the comparable data after 10 000 long cycles along with the ASC in magnification. The morphological uniqueness of the porous floral fragments substantiates the device's dependable electrochemical storage performance. The active surface area corresponds to the notable interaction between the electrolyte and active materials, which demonstrates effective ion diffusion. Comparatively greater specific capacitance is exhibited by active materials with lower working electrode mass loadings, and it is optimized by incorporating the charge balance law. From the charge–discharge profile, the specific energy and power of the as-prepared solid-state asymmetric device were analyzed. The gravimetric specific energy and power were 41.78 Wh kg⁻¹ and 886.89 W kg⁻¹, respectively. The as-optimized EMIM-BF4, PVA–DMSO-based electrolyte gel exhibited a relatively wide potential window and good conductivity at high temperatures, making them a promising contender for electrolytes in supercapacitors. The reduction in activation energy E_a may be attributed to the surface charge generated on the electrode material, which reduces the attractive attraction between BF4⁻ and its counterion EMIM⁺. When the working voltage exceeded 2.0 V, the anodic and cathodic currents increased for the electro-oxidation of BF4 and fluorocarbons and the electro-reduction of imidazolium cations. The Ragone plot is depicted in Fig. 6d, which can be used to illustrate the perception of trade-offs in the realm of energy devices. Charge–discharge analysis, impedance spectroscopy, and cyclic voltammetry validated the superior electrochemical accomplishment of our ASC device. This investigation demonstrated that our ASC device is capable of powering multiple commercial electronic devices. If this is manufactured and precisely integrated on a large scale, it possesses a premier approach for platforms of intelligent next-generation energy storage. This investigation can be enlightened by the unique assembly of an electrochemical capacitor. The design and formulation of electrodes, the chemistry of the electrode surface, the electrolyte, and electrochemical investigations all have a significant impact on capacitance. Compared to the two-electrode system, the capacitance value of the three-electrode cell is significantly greater. In addition, despite the similarity of the electrochemical processes, there are some variables, such as alterations in mass loading, binder quantity, electrode thickness, and current collector types, that have a significant impact on the capacitance value. At modest scan rates, the mechanism for storing charge is closely tracked by diffusion and adsorption. At an elevated scan rate for rapid ion transport, the reduction in ion diffusion has a negative effect on the current, resulting in a decline in the entire current in the contribution process. At high scan rates, the charge storage activities are maintained by the close-by adsorption of electrode material to the surface. This aligns with the surface-controlled methods. In the initial phase, the greater rate capability is demonstrated by a higher capacitance and boosted current density. However, the fast movement of ions decreases the capacitance, which hinders the interaction between ions and the material electrode. Variable current densities were used to evaluate the specific power and energy of the cathode materials. The investigation of impedance spectrum, cyclic voltammetry, and charge–discharge profiles has validated the enhanced electrochemical presentation of the ASC device of PPY–Ag–APCs. This evidence supports the applicability of the ASC device in actual commercial setups. This device can represent a sample design and has potential state-of-the-art applications for energy storage systems if fabricated with care and assembled on a large scale (Fig. 7).

Fig. 7 Obtained specific capacitance data.

4. Conclusion

In a nutshell, a soft template assisted aqueous dispersion polymerization technique was employed for the synthesis of camphorsulphonic acid doped rodlike conducting polypyrrole. Silver nanoparticles were also deposited at various concentrations on the rodlike polypyrrole. FTIR and Raman analyses of the PPY samples were done to scrutinize the information regarding the chemical structure. The XPS study of the sample affirmed the metallic silver deposition on the surface of rodlike PPY. The appearance of unsymmetrical redox peaks in the CV pattern of rodlike PPY doped with CSA indicated the pseudocapacitive nature of the resistive behaviour material due to predominating surface redox reactions. A very low specific capacitance value of 180 F g⁻¹ was obtained at 2 mV s⁻¹ which sharply decreased with increasing scan rate and reached an almost minimum constant value of 40 F g⁻¹ from 25 mV s⁻¹ onwards. After silver deposition in rodlike PPY doped with CSA, a perfect reversible rectangular type CV curve was achieved due to excellent capacitive behaviour. The energy density value obtained from the Ragone plot was 12.57 Wh kg⁻¹. The synergistic effect of Ag nanoparticles having strong interaction with the rodlike CSA doped PPY was considered to dominate the capacitive behaviour, which was indicated by increasing the area within the rectangular type CV curve. Real-time performance was evaluated by cyclic voltammetry (CV) and galvanostatic charge–discharge (GCD) measurements on the assembled asymmetric supercapacitor (ASC). The ASC employed an Ag-deposited, camphorsulfonic acid (CSA)-doped polypyrrole (PPY) positive electrode paired with a biowaste-derived activated porous carbon negative electrode. The device exhibited a specific capacitance of 208.88 F g⁻¹ at 2 mA cm⁻² and gravimetric energy and power densities of 41.78 Wh kg⁻¹ and 886.89 W kg⁻¹, respectively.

Author contributions

Arpita Adhikari – conceptualization, methodology, writing of the original draft, supervision. Monojit Mondal – did the experiments for the electrochemical part. Dipankar Singha – did the theoretical part and writing. Malay Kumar Rana – review and writing of the theoretical part. Souvik Das – data curation. Samparka Sanyal – data curation. Pradip Kar – investigation, data curation, editing. Tarun Kanti Bhattacharyya – supervision. Basudev Lahiri – supervision.

Conflicts of interest

The authors declare no competing financial interest.

Data availability

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5na00792e.

References

1. X. W. D. Lou, L. A. Archer and Z. Yang, Hollow Micro-/Nanostructures: Synthesis and Applications, Adv. Mater., 2008, 20(21), 3987–4019,  DOI:10.1002/adma.200800854.
2. M. Mastragostino, C. Arbizzani and F. Soavi, Polymer-Based Supercapacitors, J. Power Sources, 2001, 97–98, 812–815,  DOI:10.1016/S0378-7753(01)00613-9.
3. J. R. Miller and P. Simon, Electrochemical Capacitors for Energy Management, Science, 2008, 321, 651–652,  DOI:10.1126/science.1158736.
4. L. Hu and K. Xu, Nonflammable Electrolyte Enhances Battery Safety, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3205–3206,  DOI:10.1073/pnas.1401033111.
5. N. Wu, X. Bai, D. Pan, B. Dong, R. Wei, N. Naik, R. R. Patil and Z. Guo, Recent Advances of Asymmetric Supercapacitors, Adv. Mater. Interfaces, 2021, 8(1), 2001710,  DOI:10.1002/admi.202001710.
6. N. Choudhary, C. Li, J. Moore, N. Nagaiah, L. Zhai, Y. Jung and J. Thomas, Asymmetric Supercapacitor Electrodes and Devices, Adv. Mater., 2017, 29(21), 1605336,  DOI:10.1002/adma.201605336.
7. S. Jha, Y. Qin, Y. Chen, Z. Song, L. Miao, Y. Lv, L. Gan and M. Liu, Hydrogen-bond-guided micellar self-assembly-directed carbon superstructures for high-energy and ultralong-life zinc-ion hybrid capacitors, J. Mater. Chem. A, 2025, 13, 15101–15110,  10.1039/D5TA00357A.
8. T. Shi, Z. Song, Y. Lv, D. Zhu, L. Miao, L. Gan and M. Liu, Hierarchical porous carbon guided by constructing organic-inorganic interpenetrating polymer networks to facilitate performance of zinc hybrid supercapacitors, Chin. Chem. Lett., 2025, 36(1), 109559,  DOI:10.1016/j.cclet.2024.109559 , ISSN 1001-8417..
9. Y. Qin, C. Hu, Q. Huang, Y. Lv, Z. Song, L. Gan and M. Liu, Hydrogen-Bonded Interfacial Super-Assembly of Spherical Carbon Superstructures for High-Performance Zinc Hybrid Capacitors, Nano-Micro Lett., 2026, 18, 38,  DOI:10.1007/s40820-025-01883-1.
10. J. P. C. Trigueiro, R. S. Borges, R. L. Lavall, H. D. R. Calado and G. G. Silva, Polymeric Nanomaterials as Electrolyte and Electrodes in Supercapacitors, Nano Res., 2009, 2(9), 733–739,  DOI:10.1007/s12274-009-9080-1.
11. A. G. Olabi, Q. Abbas, M. A. Abdelkareem, A. H. Alami, M. Mirzaeian and E. T. Sayed, Carbon-Based Materials for Supercapacitors: Recent Progress, Challenges and Barriers, Batteries, 2023, 9, 19,  DOI:10.3390/batteries9010019.
12. J. Jang, Conducting Polymer Nanomaterials and Their Applications, 2006, pp. 189–260,  DOI:10.1007/12_075.
13. E. Frackowiak, V. Khomenko, K. Jurewicz, K. Lota and F. Béguin, Supercapacitors Based on Conducting Polymers/Nanotubes Composites, J. Power Sources, 2006, 153(2), 413–418,  DOI:10.1016/j.jpowsour.2005.05.030.
14. A. Rudge, I. Raistrick, S. Gottesfeld and J. P. Ferraris, A Study of the Electrochemical Properties of Conducting Polymers for Application in Electrochemical Capacitors, Electrochim. Acta, 1994, 39(2), 273–287,  DOI:10.1016/0013-4686(94)80063-4.
15. A. D. Pasquier, A. Laforgue, P. Simon, G. G. Amatucci and J.-F. Fauvarque, A Nonaqueous Asymmetric Hybrid Li₄Ti₅O₁₂/Poly(Fluorophenylthiophene) Energy Storage Device, J. Electrochem. Soc., 2002, 149(3), A302,  DOI:10.1149/1.1446081.
16. M. Hughes, G. Z. Chen, M. S. P. Shaffer, D. J. Fray and A. H. Windle, Controlling the Nanostructure of Electrochemically Grown Nanoporous Composites of Carbon Nanotubes and Conducting Polymers, Compos. Sci. Technol., 2004, 64(15), 2325–2331,  DOI:10.1016/j.compscitech.2004.01.026.
17. J. Keskinen, S. Tuurala, M. Sjödin, K. Kiri, L. Nyholm, T. Flyktman, M. Strømme and M. Smolander, Asymmetric and symmetric supercapacitors based on polypyrrole and activated carbon electrodes, Synth. Met., 2015, 203, 192–199,  DOI:10.1016/j.synthmet.2015.02.034 , ISSN 0379-6779..
18. Y. Huang, H. Li, Z. Wang, M. Zhu, Z. Pei, Q. Xue, Y. Huang and C. Zhi, Nanostructured Polypyrrole as a Flexible Electrode Material of Supercapacitor, Nano Energy, 2016, 22, 422–438,  DOI:10.1016/j.nanoen.2016.02.047.
19. P. Novák, K. Müller, K. S. V. Santhanam and O. Haas, Electrochemically Active Polymers for Rechargeable Batteries, Chem. Rev., 1997, 97(1), 207–282,  DOI:10.1021/cr941181o.
20. A. Adhikari, S. De, A. Halder, S. Pattanayak, K. Dutta, D. Mondal, D. Rana, R. Ghosh, N. K. Bera, S. Chattopadhyay, M. Chakraborty, D. Ghoshal and D. Chattopadhyay, Biosurfactant Tailored Synthesis of Porous Polypyrrole Nanostructures: A Facile Approach towards CO₂ Adsorption and Dopamine Sensing, Synth. Met., 2018, 245, 209–222,  DOI:10.1016/j.synthmet.2018.09.005.
21. A. Adhikari, P. Tiwary, D. Rana, A. Halder, J. Nath, A. Basu, D. Ghoshal, P. Kar, A. K. Chakraborty and D. Chattopadhyay, Na-Cholate Micelle Mediated Synthesis of Polypyrrole Nanoribbons for Ethanol Sensing, J. Environ. Chem. Eng., 2020, 8(5), 104249,  DOI:10.1016/j.jece.2020.104249.
22. A. Adhikari, J. Nath, D. Rana, S. De, M. Chakraborty, P. Kar, A. K. Chakraborty and D. Chattopadhyay, Electrochemical Sensing of Serotonin by Silver Decorated Polypyrrole Nanoribbon Based Electrode Synthesized by Sodium Cholate as Soft Template, Mater. Today Commun., 2022, 31, 103361,  DOI:10.1016/j.mtcomm.2022.103361.
23. H. D. Tran, D. Li and R. B. Kaner, One-Dimensional Conducting Polymer Nanostructures: Bulk Synthesis and Applications, Adv. Mater., 2009, 21(14–15), 1487–1499,  DOI:10.1002/adma.200802289.
24. Y. Han, X. Qing, S. Ye and Y. Lu, Conducting Polypyrrole with Nanoscale Hierarchical Structure, Synth. Met., 2010, 160(11–12), 1159–1166,  DOI:10.1016/j.synthmet.2010.03.002.
25. D. P. Dubal, Z. Caban-Huertas, R. Holze and P. Gomez-Romero, Growth of Polypyrrole Nanostructures through Reactive Templates for Energy Storage Applications, Electrochim. Acta, 2016, 191, 346–354,  DOI:10.1016/j.electacta.2016.01.078.
26. J. K. Gan, Y. S. Lim, N. M. Huang and H. N. Lim, Hybrid silver nanoparticle/nanocluster-decorated polypyrrole for high-performance supercapacitors, RSC Adv., 2015, 5, 75442–75450,  10.1039/C5RA14941J.
27. H. M. Shiri, A. Ehsani and J. S. Shayeh, Synthesis and highly efficient supercapacitor behavior of a novel poly pyrrole/ceramic oxide nanocomposite film, RSC Adv., 2015, 5, 91062–91068,  10.1039/C5RA19863A.
28. J. Jung Hwa, H. Kobayashi, J. C. K. van Bommel, S. Shinkai and T. Shimizu, Chem. Mater., 2002, 14(4), 1445–1447,  DOI:10.1021/cm011625e.
29. S. T. Navale, A. T. Mane, A. A. Ghanwat, A. R. Mulik and V. B. Patil, Camphor sulfonic acid (CSA) doped polypyrrole (PPy) films: measurement of microstructural and optoelectronic properties, Measurement, 2014, 50, 363–369,  DOI:10.1016/j.measurement.2014.01.012 , ISSN 0263-2241..
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji and X. Li, Gaussian 16; Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
31. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789,  DOI:10.1103/PhysRevB.37.785.
32. A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652,  DOI:10.1063/1.464913.
33. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions, J. Chem. Phys., 1980, 72(1), 650–654,  DOI:10.1063/1.438955.
34. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297,  10.1039/b508541a.
35. T. A. K. Roy Dennington and M. M. John, GaussView; Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016.
36. J. Santhanalakshmi, L. G. Shantha, V. K. Aswal and P. S. Goyal, Small-angle neutron scattering study of sodium cholate and sodium deoxycholate interacting micelles in aqueous medium, Proc. - Indian Acad. Sci., Chem. Sci., 2001, 113(1), 55–62,  DOI:10.1007/BF02708552.
37. L. Hao, R. H. Lu, D. G. Leaist and P. R. Poulin, Aggregation number of aqueous sodium cholate micelles from mutual diffusion measurements, J. Solution Chem., 1997, 26(2), 113–125,  DOI:10.1021/la802000x.
38. N. Maráková, P. Humpolíček, V. Kašpárková, Z. Capáková, L. Martinková, P. Bober, M. Trchová and J. Stejskal, Antimicrobial Activity and Cytotoxicity of Cotton Fabric Coated with Conducting Polymers, Polyaniline or Polypyrrole, and with Deposited Silver Nanoparticles, Appl. Surf. Sci., 2017, 396, 169–176,  DOI:10.1016/j.apsusc.2016.11.024.
39. O. Amiri, M. Salavati-Niasari, S. Bagheri and A. T. Yousefi, Enhanced DSSCs Efficiency via Cooperate Co-Absorbance (CdS QDs) and Plasmonic Core-Shell Nanoparticle (Ag@PVP), Sci. Rep., 2016, 6(1), 25227,  DOI:10.1038/srep25227.
40. O. Amiri, M. Salavati-Niasari and M. Farangi, Enhancement of Dye-Sensitized Solar Cells Performance by Core Shell Ag@organic (Organic=2-Nitroaniline, PVA, 4-Choloroaniline and PVP): Effects of Shell Type on Photocurrent, Electrochim. Acta, 2015, 153, 90–96,  DOI:10.1016/j.electacta.2014.11.195.
41. O. Amiri, M. Salavati-Niasari, M. Farangi, M. Mazaheri and S. Bagheri, Stable plasmonic-improved dye sensitized solar cells by silver nanoparticles between titanium dioxide layers, Electrochim. Acta, 2015, 152, 101–107,  DOI:10.1016/j.electacta.2014.11.105.
42. A. Adhikari, S. De, D. Rana, J. Nath, D. Ghosh, K. Dutta, S. Chakraborty, S. Chattopadhyay, M. Chakraborty and D. Chattopadhyay, Selective Sensing of Dopamine by Sodium Cholate Tailored Polypyrrole-Silver Nanocomposite, Synth. Met., 2020, 260, 116296,  DOI:10.1016/j.synthmet.2020.116296.
43. S. L. Patil, M. A. Chougule, S. G. Pawar, S. Sen and V. B. Patil, Effect of Camphor Sulfonic Acid Doping on Structural, Morphological, Optical and Electrical Transport Properties on Polyaniline-ZnO Nanocomposites, Soft Nanosci. Lett., 2012, 02(03), 46–53,  DOI:10.4236/snl.2012.23009.
44. J. Hazarika and A. Kumar, Structural and Optical Properties of Self-Assembled Polypyrrole Nanotubes, J. Polym. Res., 2016, 23(5), 95,  DOI:10.1007/s10965-016-0989-2.
45. P. P. Jeeju, S. J. Varma, P. A. Francis Xavier, A. M. Sajimol and S. Jayalekshmi, Novel polypyrrole films with excellent crystallinity and good thermal stability, Mater. Chem. Phys., 2012, 134(2–3), 803–808,  DOI:10.1016/j.matchemphys.2012.03.072.
46. Q. Wang, Y. Deng, J. Chen, L. Lu, Y. Ma and L. Zang, Electrochemical preparation of polypyrrole-Ag nanoparticles composite film and its resistive switching properties, J. Alloys Compd., 2022, 927, 167117,  DOI:10.1016/j.jallcom.2022.167117.
47. J. John and S. Jayalekshmi, Polypyrrole with appreciable solubility, crystalline order and electrical conductivity synthesized using various dopants appropriate for device applications, Polym. Bull., 2023, 80, 6099–6116,  DOI:10.1007/s00289-022-04354-4.
48. R. Cabala, J. Skarda and K. Potje-Kamloth, Spectroscopic investigation thermal treatment of doped polypyrrole, Phys. Chem. Chem. Phys., 2002, 2, 3283–3291,  10.1039/b002622k.
49. R. Yang, W. H. Smyrl, D. F. Evans and W. A. Hendrickson, Evolution of polypyrrole band structure: a scanning tunneling spectroscopy study, J. Phys. Chem., 1992, 96(3), 1428–1430.
50. J. Zang, C. M. Li, S. J. Bao, X. Cui, Q. Bao and C. Q. Sun, Template-free electrochemical synthesis of superhydrophilic polypyrrole nanofiber network, Macromolecules, 2008, 41(19), 7053–7057.
51. D. Y. Kim, J. Y. Lee, D. K. Moon and C. Y. Kim, Stability of reduced polypyrrole, Synth. Met., 1995, 69(1–3), 471–474.
52. A. Adhikari, P. Kar, D. Rana, S. De, J. Nath, K. Dutta and D. Chattopadhyay, Synthesis of Sodium Cholate Mediated Rod-like Polypyrrole-Silver Nanocomposite for Selective Sensing of Acetone Vapor, Nano-Struct. Nano-Objects, 2020, 21, 100419,  DOI:10.1016/j.nanoso.2019.100419.
53. J. K. Gan, Y. S. Lim, N. M. Huang and H. N. Lim, Hybrid Silver Nanoparticle/Nanocluster-Decorated Polypyrrole for High-Performance Supercapacitors, RSC Adv., 2015, 5(92), 75442–75450,  10.1039/C5RA14941J.
54. M. H. Ullah, I. Kim and C.-S. Ha, In-Situ Preparation of Binary-Phase Silver Nanoparticles at a High Ag⁺ Concentration, J. Nanosci. Nanotechnol., 2006, 6(3), 777–782,  DOI:10.1166/jnn.2006.082.
55. S. Okur and U. Salzner, Theoretical Modeling of the Doping Process in Polypyrrole by Calculating UV/Vis Absorption Spectra of Neutral and Charged Oligomers, J. Phys. Chem. A, 2008, 112(46), 11842–11853,  DOI:10.1021/jp8063257.
56. U. Salzner and R. Baer, Koopmans' springs to life, J. Chem. Phys., 2009, 131, 231101,  DOI:10.1063/1.3269030.
57. C. J. Raj, M. Rajesh, R. Manikandan, S. Park, J. H. Park, K. H. Yu and B. C. Kim, Electrochemical Impedance Spectroscopic Studies on Aging-Dependent Electrochemical Degradation of p-Toluene Sulfonic Acid-Doped Polypyrrole Thin Film, Ionics, 2018, 24(8), 2335–2342,  DOI:10.1007/s11581-017-2382-5.
58. A. Aphale, K. Maisuria, M. K. Mahapatra, A. Santiago, P. Singh and P. Patra, Hybrid Electrodes by In-Situ Integration of Graphene and Carbon-Nanotubes in Polypyrrole for Supercapacitors, Sci. Rep., 2015, 5(1), 14445,  DOI:10.1038/srep14445.
59. J. Zhao, J. Wu, B. Li, W. Du, Q. Huang, M. Zheng, H. Xue and H. Pang, Facile Synthesis of Polypyrrole Nanowires for High-Performance Supercapacitor Electrode Materials, Prog. Nat. Sci.: Mater. Int., 2016, 26(3), 237–242,  DOI:10.1016/j.pnsc.2016.05.015.
60. P. Vishnuprakash, C. Nithya and M. Premalatha, Exploration of V₂O₅ nanorod@rGO heterostructure as potential cathode material for potassium-ion batteries, Electrochim. Acta, 2019, 309, 234,  DOI:10.1016/j.electacta.2019.04.092.

---