Open Access Article
Open Access ArticleEnhancement of deep ultraviolet chiral molecular sensing performance by collective lattice resonances of diamond nanostructure arrays
Shengsui
Cai†
,
Jing
Wang†
*,
Wenxuan
Liu
,
Zhaolong
Cao
,
Huanjun
Chen
 ,
Lei
Shao
,
Lei
Shao
 * and
Shaozhi
Deng
* and
Shaozhi
Deng
State Key Laboratory of Optoelectronic Materials and Technologies, Guangdong Provincial Key Laboratory of Display Materials and Technologies, School of Electronics and Information Technology, Sun Yat-Sen University, Guangzhou, 510275, China. E-mail: shaolei5@mail.sysu.edu.cn; wangj968@mail.sysu.edu.cn
First published on 21st November 2025
Abstract
Detecting the circular dichroism (CD) spectra of chiral molecules in the deep ultraviolet (DUV) region is of significant research importance in the biomedical field, as it can reflect not only enantiomer concentration but also molecular structural information. Although low-loss dielectric materials in the ultraviolet region can avoid the photothermal effects of traditional plasmonic materials, their poor electromagnetic field localization limits their application in molecular signal enhancement. Here, we designed a diamond nanostructure array. By exciting the collective lattice resonance (CLR) modes with non-local field distribution characteristics and introducing the coupling between the electric and magnetic CLRs, the optical chirality enhancement in the gap region between the diamond nanostructures is increased to a maximum of more than 150, with an average of over 52 at DUV wavelengths. Such characteristics allow the largely enhanced spatial superposition between the superchiral near field and the target chiral analytes. Moreover, simulation results demonstrate a 22-fold enhancement in the DUV CD signals of chiral molecules, with the enhanced CD intensity exhibiting a linear dependence on molecular concentration. Our results could be potentially used for ultrasensitive detection of chiral biomolecules, which is of interest in biopharmaceutical research applications such as rapid detection of chiral drug molecules at ultra-low concentrations.
Introduction
Chirality describes the geometric properties where an object cannot be superimposed onto its mirror image by rotation or translation. This concept is pivotal across numerous scientific disciplines and holds vital importance in biology and chemistry: the fundamental biomolecules of life (such as L-amino acids and right-handed DNA) are predominantly chiral. Taking proteins as an example, the precise folding of their tertiary structures strictly depends on sequences composed of L-configured amino acids. This perpetuation of chirality underpins the functionality of biomolecules. Consequently, the enantiomer-specific interaction between chiral pharmaceuticals and biomolecules can elicit profoundly different biological effects. A classic case is thalidomide—the (R)-enantiomer alleviates morning sickness, while the metabolites of the (S)-enantiomer cause severe fetal deformities.1The properties of chiral compounds are dictated by their stereochemistry, making the distinction between enantiomers indispensable in both research and application. Among existing detection techniques, CD spectroscopy characterizes chirality by measuring the differential absorption of left-handed (LCP) and right-handed (RCP) circularly polarized light.2 Most organic molecules absorb light in the ultraviolet (UV) region due to their electronic transitions, and the absorption bands correspond to specific functional groups. Therefore, CD spectroscopy in the deep-ultraviolet (DUV) region with the wavelength λ < 300 nm can simultaneously resolve molecular secondary structure3 and solution purity,4 offering inherent advantages for trace sample detection. However, the intrinsic chiroptical signal of molecules is exceptionally weak because of the size mismatch between molecules and the wavelength of light, with the difference in absorption between RCP and LCP around 10−3 to 10−6 times lower than the absolute absorption.5,6 Besides, conventional optical systems exhibit lower transmittance in the DUV band, and photodetectors show poorer response sensitivity in this spectral region. These factors combine to drastically reduce the signal-to-noise ratio during detection, severely hindering the realization of high-sensitivity chiral detection at low concentrations.
Enhancing the CD signal of chiral molecules is therefore paramount. In recent years, novel nanophotonic materials have emerged that can support superchiral near fields to boost the chiral interaction between light and matter. They can provide large optical chirality density, C, thereby enabling significant enhancement of molecular CD signals.7,8C is defined as follows:
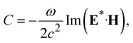 | (1) |
Plasmonic nanostructures can provide strong local field enhancement and have been demonstrated to amplify CD signals of large molecules in the visible–near-infrared range.11–18 However, it should be noted that in most studies within this spectral band, the resonance wavelengths of plasmonic nanostructures do not cover the absorption features of chiral molecules in the UV region.19–23 Consequently, their CD enhancement mechanism primarily originates from plasmon-induced CD responses rather than the intrinsic signals of biological chiral molecules that reflect the molecular secondary structures. Furthermore, except for a few metals such as aluminum,24 most plasmonic materials exhibit high ohmic losses at the absorption peaks of small chiral molecules at DUV wavelengths, limiting their applicability in biosensing.
In contrast to plasmonic metallic materials, high-refractive-index dielectric nanostructures (e.g., silicon nitride, diamond, and silicon) simultaneously support both electric and magnetic Mie resonance modes.9,10,25–28 Through the involvement of mechanisms such as intermodal coupling or excitation of dark modes, these structures can achieve high optical chirality enhancement with uniform handedness within their internal regions.10,27,28 Diamond, in particular, stands out as a highly promising material. The growth and etching techniques of diamond film have achieved great advances recently.29 The extremely low optical loss of diamond in the DUV regime makes it exceptionally suitable for molecular sensing in such a spectral range.30 Introducing asymmetry into diamond cylindrical arrays has been numerically shown to enable optical chirality enhancement factors up to 1100 in the deep ultraviolet.9 This ultrahigh optical chirality significantly enhances the structure's efficacy for enantiomer examination. However, strong optical chirality enhancement supported by diamond and other high-index dielectric nanostructures is predominantly confined in their internal volumes. This restricts the effectiveness of superchiral nearfield in regions outside the nanostructures where molecules interact, which is crucial for sensing applications. Additionally, practical implementation requires careful consideration of micro/nanofabrication feasibility and experimental constraints to ensure the designed structures are viable for real-world use.
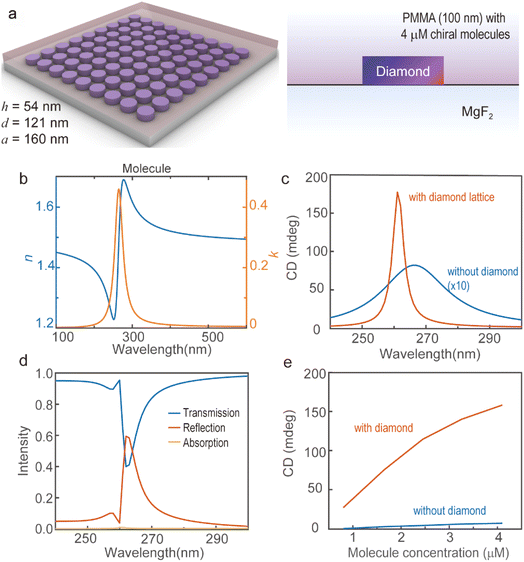
Herein, we designed a single-period square lattice array of diamond nanodisks that will not bring about significant challenges in nanofabrication. By spectrally overlapping two distinct collective lattice resonance (CLR) modes to maximize their coupling through tuning the structure's geometric parameters, we demonstrated numerically significant optical chirality enhancement in the external proximity of the diamond nanostructures at DUV wavelengths. The in-plane nonlocal nature of concentrated electromagnetic fields of CLR modes modulates the concentration of the local density of optical chirality, shifting its spatial distribution with large C enhancement from the interior of the nanostructures to the interstitial spaces between them. The C enhancement in the in-plane non-structural region of the diamond nanodisk lattice reaches a maximum of over 150, with an average of over 52 at the CLR resonance wavelength, which we can readily tune through structural parameter adjustment. We further performed simulations to calculate the performance improvement of the diamond nanodisk array brought into the practical CD measurements. Our results show that a 100-nm-thick chiral molecule film coated on a square lattice array (lattice constant = 160 nm) of diamond nanodisks (diameter = 121 nm, height = 52 nm) exhibited 22 times stronger CD peak signals than the control film without any nanostructures in the DUV region. Thus, our diamond nanostructure array architecture delivers much stronger and more accessible optical chirality enhancement, making it highly suitable for real-world sensing scenarios. These findings hold significant potential for detecting biomolecular chirality, with critical implications for applications such as drug development.
Results and discussion
To quantitatively evaluate the impact of CLRs within diamond nanostructure lattice arrays and reveal their underlying mechanism in improving the chiroptical nearfield surrounding the nanostructure, we first selected diamond nanospheres and their lattice arrays as simple model systems. We conducted finite element method-based numerical simulations on a diamond nanosphere with a diameter of d = 120 nm and an infinitely periodic square lattice array of it (Fig. 1a and b), using the general-purpose commercial software COMSOL (see Methods in the SI). The refractive index of the surrounding medium was set at nbg = 1.46 to mimic the effect of commonly employed substrates and solutions in experiments, as we will present in this work. The refractive index and extinction coefficient of diamond were extracted from ref. 30. The lattice constant of the periodic array was set at a = 154 nm. The array exhibits C4 rotational symmetry, ensuring isotropic optical responses. Circularly polarized light was incident along the z-axis (Fig. 1a).Comparative studies revealed significant differences between the isolated diamond nanosphere and its periodic arrays. The simulation-calculated scattering cross-section spectrum of the isolated diamond nanosphere agrees perfectly with that predicted from Mie theory. We further utilized Mie theory to analyse the contributions from different multipolar resonance modes to the scattering of the isolated nanosphere (Fig. 1a). The mode analysis shows that the broad strongest scattering peak centred at 236 nm results from the excitation of multiple resonance modes including electric dipole resonance (EDR), magnetic dipole resonance (MDR), magnetic quadrupole resonance (MQR), and magnetic octupole resonance (MOR). The MQR mode plays the most important role. In contrast, the scattering peak centred at 305 nm is dominated by the EDR and MDR modes. The scattering peak centred at 202 nm results from the excitation of MDR, MQR, MOR, electric quadrupole resonance (EQR), and electric octupole resonance (EOR), with the MOR dominating. We then constructed an infinitely sized square lattice array of the diamond nanosphere with the same size. The transmission spectrum of the array displayed an asymmetric line shape (Fig. 1b). A Rayleigh Anomaly (RA) at 225 nm (λRA = a·nbg) suppresses higher-order Mie resonances,31,32 leading to the disappearance of the original resonance near 236 nm. CLR modes emerged in the proximity of the RA. The narrow-linewidth (∼3 nm) transmission dip at 264 nm corresponds to the electric dipole CLR (ED-CLR), while the transmission dip at 282 nm corresponds to the magnetic dipole CLR (MD-CLR) (Fig. 1b), similar to the result reported for periodic Si nanosphere arrays.33 The excitation of the CLR modes results in a much more remarkably enhanced electric field (Fig. 1c and d) because of their higher quality factor. The CLR resonances also exhibit an in-plane non-local nature, with their enhanced electromagnetic field extended to non-structural interstitial spaces between the unit nanospheres.
We then studied the optical chirality enhancement (C/|CCPL|) properties of both the isolated diamond nanosphere and its lattice array. We first calculated the average value of C/|CCPL| of the non-structural region over an area of a × a in the horizontal central plane of the nanostructures as a function of wavelength (Fig. 1e and f). The diamond nanosphere was placed in the centre of the square. The spectra of averaged C/|CCPL| display distinct peaks, with wavelengths differing from those of the corresponding scattering spectra. For the isolated diamond nanosphere, the averaged C/|CCPL| reaches its peaks at 204, 250, and 343 nm (Fig. 1e), where the EQR and MOR, EDR and MDR or MQR, and EDR and MDR share the same contribution to scattering, respectively. Similarly, for the diamond nanosphere array, the averaged C/|CCPL| reaches its peak at 266 nm, which is remarkably close to the transmission peak in between the ED-CLR and MD-CLR modes (Fig. 2f). A sign reversal in C/|CCPL| was observed because of the abrupt phase shifts between narrow ED-CLR and MD-CLR at varying wavelengths. Both results imply the importance of interaction between electric and magnetic resonances in generating superchiral near fields. The spectral overlapping between the electric and magnetic optical modes greatly affects the density of the optical chirality. Our results clearly revealed that the excitation of CLRs enables a large enhancement of the optical chirality, with the largest averaged C/|CCPL| at non-structural area increasing from 2.2 to 8. We further plot the spatial distributions of C/|CCPL| at the wavelengths where it reaches its maximum, i.e. 343 nm for the isolated nanosphere and 266 nm for its lattice (Fig. 1g and h). In both cases, the strong optical chirality results from the coupling between electric and magnetic dipolar resonances, which are EDR–MDR coupling for the isolated nanosphere and (ED-CLR)–(MD-CLR) coupling for the nanosphere lattice. The EDR–MDR coupling is weak for an isolated nanosphere, with the superchiral near field primarily confined to the central region inside the nanosphere (Fig. 1e–g). In contrast, (ED-CLR)–(MD-CLR) coupling is much stronger, and the resulting superchiral near field maintains a large concentration in the non-structural area in between the spheres (Fig. 1f–h). Such characteristics are critical for enhancing chiral optical signals in practical applications.
We have not achieved a perfect spectral overlap between the ED-CLR and MD-CLR modes in the nanosphere lattice. Due to the inherent symmetry of the dielectric nanospheres and the resulting poor tunability in their resonance frequencies, it is extremely challenging to tune the geometric parameters of the nanosphere lattice to precisely adjust the ED-CLR and MD-CLR resonances at the same wavelength. The spectral separation of the ED-CLR and MD-CLR modes in symmetric arrays (the lattice constants along x and y direction ax = ay) of nanospheres can be resolved via asymmetric designs (e.g., ax ≠ ay), as one recent experimental work demonstrates in a Si nanosphere lattice.34 However, the fabrication of diamond nanospheres with uniform sizes remains challenging. In contrast, nanodisks offer superior manufacturability, and their Mie resonances can be tuned via both the size and the diameter-to-height aspect ratio.10 We therefore replaced the repeating units in the aforementioned periodic array with diamond nanodisks (Fig. 2a), in order to design a diamond nanostructure lattice that balances high optical chirality enhancement, structural fabrication feasibility, and application viability. To systematically investigate the relationship between CLRs and optical chirality enhancement, we conducted parametric studies by varying the array period a from 150 to 170 nm (Fig. 2b and S1) while keeping the disk diameter d and height h fixed at d = 121 nm and h = 51 nm, respectively. Similar to the periodic diamond nanosphere arrays, we observed the RA at 220–250 nm (λRA = a·nbg) suppressing higher-order Mie resonances of individual nanodisks (Fig. S1). We also observed the excitation of ED-CLR and MD-CLR modes, which account for the dips in the transmission spectra of the diamond nanodisk array (Fig. 2b–d and S1). By varying the lattice constants along the x and y directions, ax and ay, independently, the two CLRs exhibit distinct periodic dependence (Fig. S2).32,35 Under the excitation of linearly polarized light with the polarization direction along the x axis, the ED-CLR redshifts while the MD-CLR rarely shifts as ax increases. In contrast, the MD-CLR redshifts while the ED-CLR rarely shifts as ay increases. A pronounced transmission peak was observed between the ED-CLR and MD-CLR in the transmission spectra. This peak can approach its highest intensity as the ED-CLR and MD-CLR are well aligned at ax = ay, suggesting that such a peak arises from the destructive interference between the ED-CLR and MD-CLR modes and can suppress backscattering under Kerker-like conditions (Fig. S2).32,33,36 In addition, by varying the lattice constant a = ax = ay, we found that the intensity of the peak generated from (ED-CLR)–(MD-CLR) coupling can reach unity at their resonance wavelength.
The in-plane non-local resonance nature of CLR modes enables the distribution of strongly enhanced superchiral near fields beyond the physical boundaries of the diamond nanodisks. The perfect alignment between the ED-CLR and MD-CLR ensures the extremely large local optical chirality in the interstitial spaces between nanodisks. For instance, C/|CCPL| exceeds 150-fold within the gaps at a = 158 nm, with its average value in the in-plane non-structural region reaching 52 at the resonance wavelength (λ = 262 nm), both of which are much larger than that of the isolated diamond nanodisk control structure (Fig. 2e and f). The value of C/|CCPL| can reach up to 300 inside the nanodisk. As predicted, illumination with the opposite handedness of CPL yields results with equal magnitudes but opposite sign (Fig. 2e). The high density of optical chirality in the gap region is highly advantageous for low-concentration chiral molecule detection. We would like to highlight that our symmetric structure enhances the local optical chirality density of the non-structural region by aligning the ED-CLR and MD-CLR modes of the lattice through structure design. It is different from the reported strategy of introducing additional geometrical anisotropy of the diamond nanostructure metasurface.9 Moreover, the resonance wavelengths of the CLRs are primarily governed by the periodicity. In principle, the resonance modes can be tuned to any specific wavelengths as long as the material's refractive index permits. Furthermore, this array allows independent modulation of ED-CLR and MD-CLR modes by adjusting ax and ay separately, making it highly suitable for designs aiming to maximize C at specific wavelength through ED/MD mode engineering. The enhanced chiral field extends beyond the physical boundaries of the nanostructures, creating more accessible regions for enhancing chiral light–matter interaction. Moreover, the CLR resonance wavelengths can also be tuned by adjusting the nanodisk diameter d (Fig. S3). As the diameter d increases from 50 to 150 nm, the CLR modes exhibit continuous red shifts as well as a reduction in quality factor. We also found that the spatial distribution of the superchiral near field can be regulated by the nanodisk diameter d and the lattice constant a. One can therefore achieve stronger and more extended superchiral near fields by properly designing the structure. In our design, the structural parameters (d ∼ 120 nm, h ∼ 50 nm, a ∼ 160 nm) will not raise significant challenges for the nanofabrication, making the single-period diamond nanodisk array highly suitable as an enhancing substrate platform for the detection of the CD signals of chiral molecules.
To advance toward practical device implementation, we replaced the idealized uniform background with a more realistic material system with an organic molecule, poly(methyl methacrylate) (PMMA), as the surrounding medium and MgF2 as the substrate (Fig. 3a and b). We chose the PMMA/MgF2 system because its refractive index profiles closely approximate the homogeneous background conditions in our initial calculations, and the experimental feasibility can be maintained, since MgF2 has a refractive index close to commonly used organic molecules and exhibits excellent DUV transparency with a negligible extinction coefficient.37 In our simulation, we modelled PMMA's optical properties with a Lorentzian resonance by considering its ultraviolet absorption (see Methods in the SI).38 We also provided the complex refractive indices of diamond that we extracted from ref. 25 and employed in our simulation in Fig. 3b for comparison. The primary absorption band of PMMA falls near 320 nm (Fig. 3b), far away from the DUV wavelength range of interest in our study (240–300 nm). This ensures minimal absorption-induced side effects during spectral analysis. Prior studies indicated that the refractive index mismatch suppresses long-range interparticle interactions, consequently inhibiting lattice resonances under normal incidence.39,40 Introducing the PMMA/MgF2 system inevitably disrupts the perfect index-matching conditions of our initial design, inducing a slight spectral shift in the CLR modes. In actual fabrication processes, etching-based control over nanostructure height (depth) provides more direct parametric tunability than lithographic regulation of periodicity and diameter in 2D patterning. We therefore systematically adjusted the nanodisk height within the unit cell to parametrically investigate CLR modes and optical chirality enhancement. We set the lattice constant and the disk diameter of the nanodisk array at a = 160 nm and d = 121 nm, while varying the disk height h between 50 and 60 nm in our simulation (Fig. 3c and d). The calculated performance of the CLRs slightly degrades, as reflected by the less distinct peak and dip features in the transmission spectra (Fig. 3c). Despite this, we can still achieve an alignment between the ED-CLR and the MD-CLR. The largest value of the average C/|CCPL| outside the nanodisk over an area of a × a in the horizontal central plane of the nanostructures only exhibits a slight decrease from 52 to 47 after taking the real experimental conditions into account (Fig. 3d and e), validating the effectiveness of our structure design.
 | ||
| Fig. 3 Superchiral near field enabled by collective lattice resonances in a diamond nanodisk array in an environment mimicking the experimental conditions. (a) Schematics of a square array of diamond nanodisks supported on a MgF2 substrate and coated with PMMA. (b) Dependence of the refractive index and extinction coefficient dispersion curves of MgF2, PMMA, and diamond. The data of MgF2 and diamond were extracted from ref. 32 and 25 respectively. The data of PMMA were obtained from a Lorentzian resonance model by considering the PMMA's absorption at around 320 nm. (c) Transmission spectra of square diamond nanodisk arrays with the lattice constant and the disk diameter fixed at a = 160 nm and d = 121 nm. The disk height h varied between 50 and 60 nm. (d) Averaged C enhancement spectra of the nanodisk arrays with different h. The averaged C enhancements were calculated by averaging the value of C/|CCPL| outside the nanodisk over an area of a × a in the horizontal central plane of the nanostructures. (e) Spatial distributions of C/|CCPL| of a diamond nanodisk in a periodic array with h = 52 nm at λ = 261 nm under RCP excitation. | ||
Our preceding investigations have demonstrated the exceptional DUV optical chirality enhancement capabilities in the non-structural area of periodic diamond nanoarrays. Next, we incorporated chiral molecules into our simulation by blending them with PMMA. We modelled the chiral molecule–PMMA mixture with a 100-nm-thick film to mimic the spin-coating deposited thin layer of chiral molecule samples in sensing experiments (Fig. 4a).41 To include the chiral optical response of chiral molecules, constitutive equations in the simulation were modified by adding the chiral elements:42,43
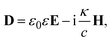 | (2) |
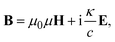 | (3) |
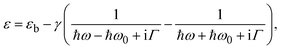 | (4) |
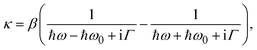 | (5) |
| ε = (n + ik)2, | (6) |
| µ = 1, | (7) |
We then calculated the optical properties of the chiral molecule–PMMA film deposited on MgF2 with and without diamond nanostructures under the illumination of CPL with different handedness. We obtained the CD signal by calculating the degree of ellipticity:
 | (8) |
CD =−tan−1[tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h(k0w h(k0w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Im{κ})], Im{κ})], | (9) |
To further illustrate a clear picture of the distribution of the local optical chirality around the diamond nanostructure in the three-dimensional space and therefore understand the interaction between local superchiral near field and the chiral matter in a more straightforward way, we extracted the value of each local C/|CCPL| in the space (Fig. 5a–c), where a 100 nm-thick PMMA film embedded with chiral molecules coats the diamond nanostructure. Both the contours of C/|CCPL| in the central vertical cross section and the horizontal cross sections at different heights z of the sample were provided at λ = 260 nm (Fig. 5b and c). Our results clearly revealed that excitation of coupled CLRs of the nanodisk array not only largely increases the superchiral near fields in the in-plane non-structural area, but it also increases the superchiral near fields in the space above the array. The averaged in-plane non-structural C/|CCPL| reaches as high as 25 even at the site 20 nm above the nanodisk array, i.e. z = 74 nm (Fig. 5d). Such 3D non-local distribution of strongly enhanced superchiral nearfield is critical for enabling effective interaction between the chiral near field and target chiral molecules. Comparative analysis between periodic arrays and single particle structures, performed after coating with the PMMA–molecule composite solution, revealed distinctly different enhancement characteristics. Compared with the periodic arrays, the isolated diamond nanodisk only produces weak, broadband enhancement outside the nanostructure. This striking difference originates from the coupling between the high-quality-factor CLRs in periodic arrays, which generates sharp, narrowband C enhancement peaks compared to the weak, broadband response of isolated particles.
Conclusions
In summary, through structural design, we have increased the maximum optical chirality enhancement factor C/|CCPL| in the gap region of the diamond array to 150, and the average value of C/|CCPL| in the in-plane non-structural region can reach above 52. The chiral optical enhancement outside the dielectric nanostructure results from the coupling between electric and magnetic CLRs in the diamond lattice. The excitation of CLRs leads to a non-local field enhancement, which enables a greater number of chiral molecules to interact effectively with superchiral regions possessing largely enhanced optical chirality density, giving rise to significantly enhanced chiral optical response of the target chiral molecules. By changing the periodic parameters, the nanostructure array can achieve non-local chiral optical enhancement at specific wavelengths. Our design, based on the excitation of the ED-CLR and MD-CLR modes in the periodic array and boosting their coupling through structure parameter tuning, effectively extends the local superchiral nearfields of the low-loss dielectric structure at DUV wavelengths—fields that are usually confined inside the material—to the area outside the structure. Compared with other diamond nanostructure-based strategies employing periodic structures or asymmetric lattices,9 our design enables the generation of non-structural superchiral near fields with improved optical chirality enhancement of up to 150, without introducing any structural complexity. Such performance improvement is achieved through the mechanism of bringing effective coupling between ED-CLR and MD-CLR modes. Furthermore, considering the actual application scenarios and the requirements of refractive index matching to excite CLRs, we selected PMMA and MgF2 as the ‘solvent’ for chiral molecules and the substrate supporting diamond nanostructures. Our calculation shows that the diamond nanodisk array can amplify the CD signal of a commonly used chiral molecule, sulfated cyclodextrin, in the DUV region by a factor of 22. The peak intensity of the enhanced CD shows a proportional dependence on the concentration of chiral molecules. To summarize, our results provide a powerful solution enabling much stronger and more accessible optical chirality enhancement for chiral sensing. The structural parameters suggested by our calculation will not raise significant challenges in nanofabrication, making the proposed single-period diamond nanostructure array highly suitable as an enhancing substrate for detecting CD signals of chiral molecules. Our results should work for any refractive index-matched surrounding medium (solvents) and substrates, which allows the selection of a suitable solvent to expand our proposed chiral sensing strategy for diverse analytes. In real experiments, one should note that the chiral optical response of the molecules may be influenced by factors other than the designed optical enhancement. For example, the solvent polarity strongly determines the chiral optical signals of the chiral molecules, because it significantly alters the microenvironment of the embedded chiral molecules.48 Chiral molecules embedded in PMMA with moderate polarity and dissolved in solvents with high polarity such as water and dimethyl sulfoxide (DMSO) may exhibit original CD signals with varying intensity, peak position, and line shape. As a result, one should pay attention to the specific chemical environment when making comparisons. Moreover, diamond film's inherent absorption becomes remarkable at wavelengths below 230 nm and would degrade the performance of chiral sensing, constraining the extension of our strategy to shorter wavelengths. Nonetheless, we believe that by carefully designing the experiments, our results could boost the development of DUV nanophotonic technologies for real-world chiral sensing scenarios that are critical in applications such as biomolecular chirality analysis, enantiomer examinations, and drug development.Author contributions
Shengsui Cai: simulation, data curation, and writing–original draft. Jing Wang: conceptualization, formal analysis, data curation, and writing–review & editing. Wenxuan Liu: writing – review & editing. Zhaolong Cao: conceptualization. Huanjun Chen: conceptualization. Lei Shao: conceptualization, resources, supervision, and writing–review & editing. Shaozhi Deng: conceptualization, resources, and writing–review.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5na00768b.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 2024YFA1209003, 62375290, 12088101, 62411560271), the Pearl River Talent Recruitment Program (Grant No. 2019QN01C216), and the Science and Technology Planning Project of Guangdong Province (2023B1212060025). The authors thank Prof. Zhiqin Chu from the University of Hong Kong for valuable discussions.Notes and references
- J. A. Schellman, Chem. Rev., 1975, 75, 323–331 CrossRef CAS
.
-
L. D. Barron, in Molecular Light Scattering and Optical Activity, Cambridge University Press, 2004, pp. 123–169 Search PubMed
.
- O. O. Oshokoya, C. A. Roach and R. D. JiJi, Anal. Methods, 2014, 6, 1691–1699 RSC
.
- X. Lu, J. Tang, X. Dang, X. Jing, K. Xu, H. Li and B. Liang, RSC Adv., 2017, 7, 13552–13560 RSC
.
-
S. R. Martin and M. J. Schilstra, in Biophysical Tools for Biologists, Volume One: In Vitro Techniques, Academic Press, 2008, vol. 84, pp. 263–293 Search PubMed
.
-
Circular Dichroism and the Conformational Analysis of Biomolecules, ed. G. D. Fasman, Springer US, Boston, MA, 1996 Search PubMed
.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed
.
- Y. Tang and A. E. Cohen, Science, 2011, 332, 333–336 CrossRef CAS PubMed
.
- J. Hu, M. Lawrence and J. A. Dionne, ACS Photonics, 2020, 7, 36–42 CrossRef CAS
.
- M. L. Solomon, J. Hu, M. Lawrence, A. García-Etxarri and J. A. Dionne, ACS Photonics, 2019, 6, 43–49 CrossRef CAS
.
-
M. Schäferling, in Chiral Nanophotonics: Chiral Optical Properties of Plasmonic Systems, Springer International Publishing, Cham, 2017, pp. 5–42 Search PubMed
.
- M. Hentschel, M. Schäferling, X. Duan, H. Giessen and N. Liu, Sci. Adv., 2017, 3, e1602735 CrossRef PubMed
.
- M. J. Urban, C. Shen, X.-T. Kong, C. Zhu, A. O. Govorov, Q. Wang, M. Hentschel and N. Liu, Annu. Rev. Phys. Chem., 2019, 70, 275–299 CrossRef CAS
.
- T. Cao, Y. Li, X. Zhang and Y. Zou, Photon. Res., 2017, 5, 441–449 CrossRef CAS
.
- T. Cao, Y. Li, C.-W. Wei and Y. Qiu, Opt. Express, 2017, 25, 9911–9925 CrossRef CAS
.
- L. Mao, K. Liu, S. Zhang and T. Cao, ACS Photonics, 2019, 7, 375 CrossRef
.
- T. Cao, L. Mao, H. Fan, M. Lian, J. Jia, Y. Su and H. Ren, Adv. Opt. Mater., 2023, 11, 2202239 CrossRef CAS
.
- M. Cen, J. Wang, J. Liu, H. He, K. Li, W. Cai, T. Cao and Y. J. Liu, Adv. Mater., 2023, 34, 2270263 CrossRef
.
- M. Schäferling, D. Dregely, M. Hentschel and H. Giessen, Phys. Rev. X, 2012, 2, 031010 Search PubMed
.
- M. Schäferling, X. Yin, N. Engheta and H. Giessen, ACS Photonics, 2014, 1, 530–537 CrossRef
.
- E. Hendry, R. V. Mikhaylovskiy, L. D. Barron, M. Kadodwala and T. J. Davis, Nano Lett., 2012, 12, 3640–3644 CrossRef CAS PubMed
.
- T. J. Davis and E. Hendry, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085405 CrossRef
.
- S. Lee, S. Yoo and Q. H. Park, ACS Photonics, 2017, 4, 2047–2052 CrossRef CAS
.
- L. V. Besteiro, H. Zhang, J. Plain, G. Markovich, Z. Wang and A. O. Govorov, Adv. Opt. Mater., 2017, 5, 1700069 CrossRef
.
- W. Zhang, T. Wu, R. Wang and X. Zhang, Nanoscale, 2017, 9, 5701–5707 RSC
.
- C. S. Ho, A. Garcia-Etxarri, Y. Zhao and J. Dionne, ACS Photonics, 2017, 4, 197–203 CrossRef CAS
.
- O. Yavas, M. Svedendahl and R. Quidant, ACS Nano, 2019, 13, 4582–4588 CrossRef CAS PubMed
.
- J. García-Guirado, M. Svedendahl, J. Puigdollers and R. Quidant, Nano Lett., 2020, 20, 585–591 CrossRef
.
- J. Jing, F. Sun, Z. Wang, L. Ma, Y. Luo, Z. Du, T. Zhang, Y. Wang, F. Xu, T. Zhang, C. Chen, X. Ma, Y. He, Y. Zhu, H. Sun, X. Wang, Y. Zhou, J. K. H. Tsoi, J. Wrachtrup, N. Wong, C. Li, D. K. Ki, Q. Wang, K. H. Li, Y. Lin and Z. Chu, Nature, 2024, 636, 627–634 CrossRef CAS PubMed
.
- H. R. Phillip and E. A. Taft, Phys. Rev., 1964, 136, A1445–A1448 CrossRef
.
- J. H. Yang, V. E. Babicheva, M. W. Yu, T. C. Lu, T. R. Lin and K. P. Chen, ACS Nano, 2020, 14, 5678–5685 CrossRef CAS PubMed
.
- V. E. Babicheva and A. B. Evlyukhin, J. Appl. Phys., 2021, 129, 040902 CrossRef CAS
.
- V. E. Babicheva and A. B. Evlyukhin, Laser Photonics Rev., 2017, 11, 1700132 CrossRef
.
- Y. Hu, P. T. Probst, M. K. Habil, H. Sugimoto and M. Fujii, Adv. Opt. Mater., 2025, 01013 CrossRef CAS
.
- S. S. Wang and R. Magnusson, Appl. Opt., 1993, 32, 2606 CrossRef CAS PubMed
.
- G. W. Castellanos, P. Bai and J. Gómez Rivas, J. Appl. Phys., 2019, 125, 213105 CrossRef
.
- H. H. Li, J. Phys. Chem. Ref. Data, 1980, 9, 161–290 CrossRef CAS
.
- I. A. Aljarrah, A. A. Bani-Salameh, A. A. Ahmad, Q. M. Al-Bataineh, A. M. Alsaad, M.-A. H. Al-Akhras and A. Telfah, Polym. Bull., 2023, 80, 7533–7543 CrossRef CAS
.
- B. Auguié, X. M. Bendaña, W. L. Barnes and F. J. García De Abajo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155447 CrossRef
.
- A. G. Nikitin, T. Nguyen and H. Dallaporta, Appl. Phys. Lett., 2013, 102, 221116 CrossRef
.
- E. S. A. Goerlitzer, M. Zapata-Herrera, E. Ponomareva, D. Feller, A. Garcia-Etxarri, M. Karg, J. Aizpurua and N. Vogel, ACS Photonics, 2023, 10, 1821–1831 CrossRef CAS PubMed
.
- M. L. Nesterov, X. Yin, M. Schäferling, H. Giessen and T. Weiss, ACS Photonics, 2016, 3, 578–583 CrossRef CAS
.
- N. Engheta and P. Pelet, Opt. Lett., 1989, 14, 593 CrossRef CAS PubMed
.
- F. Zsila, Biochem. Biophys. Res. Commun., 2015, 460, 863–867 CrossRef CAS PubMed
.
- V. V. Klimov, I. V. Zabkov, A. A. Pavlov and D. V. Guzatov, Opt. Express, 2014, 22, 18564 CrossRef CAS PubMed
.
- A. O. Govorov and Z. Fan, ChemPhysChem, 2012, 13, 2551–2560 CrossRef CAS PubMed
.
- E. Mohammadi, K. L. Tsakmakidis, A. N. Askarpour, P. Dehkhoda, A. Tavakoli and H. Altug, ACS Photonics, 2018, 5, 2669–2675 CrossRef CAS
.
- E. Yashima, N. Ousaka, D. Taura, K. Shimomura, T. Ikai and K. Maeda, Chem. Rev., 2016, 116, 13752–13990 CrossRef CAS PubMed
.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |