Open Access Article
Open Access ArticleBroadband light absorption in cadmium telluride thin-film solar cells via composite light trapping techniques
Asif Al
Suny
 ,
Tazrian
Noor
,
Tazrian
Noor
 ,
Md. Hasibul
Hossain
,
Md. Hasibul
Hossain
 ,
A. F. M. Afnan Uzzaman
Sheikh
,
A. F. M. Afnan Uzzaman
Sheikh
 and
Mustafa Habib
Chowdhury
and
Mustafa Habib
Chowdhury
 *
*
Department of Electrical and Electronic Engineering, Independent University, Bangladesh, Plot 16, Block B, Aftabuddin Ahmed Road, Bashundhara Residential Area, Dhaka 1229, Bangladesh. E-mail: mchowdhury@iub.edu.bd
First published on 9th December 2025
Abstract
Composite light-trapping structures offer a promising approach to achieving broadband absorption and high efficiency in thin-film solar cells (TFSCs) in order to accelerate sustainable energy solutions. As the leading material in thin-film solar technology, cadmium telluride (CdTe) faces challenges from surface reflective losses across the solar spectrum and weak absorption in the near-infrared (NIR) range. This computational study addresses these limitations by employing a dual light trapping technique: the top surfaces of both the cadmium sulfide (CdS) and CdTe layers are tapered as nanocones (NCs), while germanium (Ge) spherical nanoparticles (NPs) are embedded within the CdTe absorber layer to enhance broadband absorption. Numerical simulations using Finite-Difference Time-Domain (FDTD) and other methods are used to optimize the parameters and configurations of both nanostructures, aiming to achieve peak optoelectronic performance. The results show that a short-circuit current density (Jsc) of 35.38 mA cm−2 and a power conversion efficiency (PCE) of 27.76% can be achieved with optimal nanocone (NC) texturing and spherical Ge NP configurations, an approximately 45% and 81% increase in Jsc and PCE, respectively. To understand the enhancement mechanisms, the study includes analyses using diffraction grating theory and Mie theory. Fabricability of these structures is also evaluated. Furthermore, an additional study on the effects of incident angle variation and polarization change demonstrates that the optimal structure is robust under practical conditions, maintaining consistent performance.
1 Introduction
Sustainable energy development is one of the major aspects of achieving sustainability, which focuses on generating clean energy without emitting greenhouse gases. Solar cells play a vital role in achieving sustainability goals and will continue to do so in the upcoming decades.1 Solar cells convert earth-abundant solar energy into the most useful form of energy, electrical energy. Presently, fossil fuels dominate global electricity generation, yet renewable energy sources are rapidly closing the gap.2 Although less than 5% of the present global electricity generation contribution comes from solar photovoltaics, and this falls short of other forms of renewable sources like wind and hydropower, solar cells are expected to soon overtake the latter two and contribute to 16% by the year 2030.2 By that time, the total solar manufacturing capacity is expected to exceed 1200 GW, i.e., almost double the present capacity.3 Thin-film solar cells (TFSCs) are more sustainable compared to the market-dominant crystalline silicon-based solar cells, since they require less material (being almost 100 times thinner), leave reduced carbon footprint, and have a lower fabrication cost.4 Cadmium Telluride (CdTe) TFSCs dominate the commercial thin-film production and are expected to have a market worth of 27.11 billion dollars by 2030.5 Being a direct bandgap material and having an optimal bandgap of 1.45 eV, CdTe-based TFSCs have the potential to achieve the maximum power conversion efficiency (PCE) possible by the Shockley–Queisser limit.6 Its high absorption coefficient allows it to absorb almost all the photons of the solar AM 1.5G spectrum, having only a 2000 nm thick absorber layer.7 Even at this thickness, the CdTe/CdS II–VI TFSCs are quite flexible, making them a potential choice to be integrated into portable electronic devices, windows, roofs, facades, electric cars, or even large-scale commercial purposes.7 From sustainability prospect, the production of CdTe emits 6 times lower carbon dioxide than silicon (Si) with high-throughput manufacturing methods.8 Furthermore, once it reaches the end of its lifetime, 90% of CdTe modules can be recycled.8 CdTe TFSCs have the potential to be thin, flexible, yet efficient enough to integrate into miniaturized electronic devices. However, their performance is hindered by high surface reflection across all wavelengths and poor light absorption in the near-infrared (NIR) region. Addressing these limitations is essential to fully realize their inherent potential.Light trapping offers a viable solution to this limitation, and previous studies have demonstrated the potential to do so. For example, Çetinkaya et al. have shown a functional design of CdTe solar cells with a 1D photonic crystal, which improved fill factor and efficiency by 15.91% and 21.10% respectively.7 On the other hand, Jain et al. used only a 100 nm thick CdTe solar cell active layer, yet achieved a short-circuit current density (Jsc) of 29.26 mA cm−2 with aluminium (Al) nanoparticle and Al back reflector.9 Nanograting, nanoparticles, and single-layer surface textures have also been investigated and showed promising results in enhancing the efficiency of CdTe solar cells.10–12 However, any light trapping technique with a certain configuration can only provide performance elevation across a limited wavelength range. Broadband absorption, i.e., absorption over a broad wavelength range, can only be achieved by employing composite light trapping techniques. Such composite light trapping works in turns to a specific wavelength to achieve broadband absorption.
Additionally, previous studies have shown that by utilizing composite light trapping techniques, absorption over a broad wavelength can be significantly increased while achieving unique properties, such as insensitivity to polarization and incident angle change, homogenization of optical fields, etc.13,14 In a theoretical study, Li et al. have shown that composite light trapping consisting of SiO2 nanospheres on the front surface and silver (Ag) hemispheres on the rear surface can achieve absorption enhancement in both short and long wavelengths with only a 100 nm thick a-Si absorber layer.15 In another study, Pritom et al. have proposed a parabolic surface texture with gold (Au) NPs on top which can provide broadband absorption between the wavelength range of 300 nm to 1600 nm.16 Furthermore, a similar parabolic texture with embedded dielectric NPs can offer a 52.3% absorption gain compared to the baseline structure.17 On the other hand, Yin et al. were able to maintain high absorption efficiency over an incident angle variation of 0° to 60° by combining semicircular dielectric grooves at the front and trapezoidal metal reflector at the back of a 100 nm thick a-Si TFSCs.18 All the mentioned works are mainly based on either a-Si or perovskite solar cells. However, in terms of CdTe TFSCs, such composite light trapping methods are still unexplored despite the potential to significantly improve absorption and other performance parameters.
In this aspect, this paper presents a composite light trapping technique that consists of a nanocone (NC) shaped surface texture of both the CdS–CdTe surface layers and embedding germanium (Ge) spherical NP into the CdTe absorber layer. The idea is to suppress surface reflection over all the wavelengths, especially in the CdTe absorption window (400 nm to 800 nm), in order to maximize the Jsc. Additionally, the embedded Ge NP would facilitate necessary light trapping to increase absorption for the rest of the wavelengths (800 nm to 1100 nm). Compared to other texture shapes, cone-shaped texture has more desirable performance in suppressing surface reflection for a broad wavelength range and also shows insensitivity to incident and polarization angle variation.19,20 Prashant et al. recently demonstrated that NC structured gallium arsenide (GaAs) solar cells have achieved an average absorption of 94%, outperforming their counterpart nanowire-shaped solar cells, which show an average absorption of 80.8% with an angle of incidence between 0 and 70°. Additionally, NC texture can also function as a diffraction grating to trap light into diffraction modes to achieve enhanced light absorption.21 To realize the highest diffraction efficiency, careful optimization of the base diameter and height is important.21 Nevertheless, Ge NP is considered to be an environment-friendly green material due to its non-toxic nature.22 As found in the literature, high-index semiconductor NPs can open doors to achieve super-absorbing, highly efficient solar cells with unique properties of broadband absorption, insensitivity to polarized, oblique-angled light, and different environmental conditions.23,24 Semiconductor NPs with a high dielectric constant are superior to metallic NPs in terms of ultra-low light-to-heat conversion and simultaneous electric and magnetic resonance excitation.25 At high temperatures, noble metal NPs suffer poor thermal and chemical stability.26,27 On the contrary, semiconductor NPs are less prone to the deterioration of absorption and scattering efficiency at high temperatures.28 While it is true that degradation of Ge NPs through oxidation is a problem, the proposed structure is immune to this problem as Ge NPs are embedded into the CdTe absorber layer. This isolates the Ge NPs from the ambient oxygen to form GeOx.29 Furthermore, it has been observed that thermal stability of Ge NPs is greater when their shape is sphere-like, in contrast to cubes and tetrahedrons.30 In addition to that, Ge nanostructures have been known to hold structural integrity for temperatures as high as 500 °C, which is significantly above the typical operating temperature of solar cells.31 Hence, these attributes ensure the longevity of Ge NPs to be used in solar cells. Ge being a semi-metal NP can be considered a viable alternative to plasmonic metal NP due to its high refractive index.25,32,33 Even compared to its similar semiconductor NP counterparts, such as Si and titanium dioxide (TiO2), Ge NPs possess a higher refractive index, essential to create refractive index contrast (Δn) with the substrate material (CdTe). The large refractive index contrast promotes a powerful Mie scattering in the forward direction34 and is supported by the simulation shown in Fig. S4. Additionally, Fig. S5 shows the optimal Ge NPs scatter light more significantly compared to optimal Si and TiO2 NPs in the wavelength range of 800 to 1100 nm, where CdTe's absorption is poor. Along with a high refractive index, Ge possesses some interesting properties such as high charge carrier mobilities (µe = 3900 cm2 V−1 s−1, µh = 1900 cm2 V−1 s−1) and narrow bandgap (0.67 eV at 300 K).35 Ge is among a few materials whose Re[∈] is greater than 20, which exceeds that of Silicon's (Re[∈] = 11.70).36 Such a high positive permittivity value allows Ge to meet the Mie resonance condition in the subwavelength regime and can have comparable strength to the plasmon resonance of metallic NPs.32 To harness the light scattering capacity of Ge NP to the fullest and utilize it to increase CdTe TFSCs efficiency, optimization of its size and placement is essential.
2 Methodology
2.1 Simulation setup
Fig. 1(a) shows a 3D view of the proposed NC texture and embedded spherical Ge NP in a 3 × 3 array. Using the commercially available Ansys Lumerical software package FDTD and CHARGE suite, simulations have been carried out to find the optimal configuration for NC texture and embedded spherical Ge NP that results in maximum absorption and optimal performance. Overall, the simulations can be divided into two parts – optical simulations and electrical simulations. Using discrete spatial and temporal grid cells (Yee cells), the FDTD solver solves Maxwell's equations to calculate the charge carrier generation, absorption, reflection, transmission, and electric fields.37 For optical simulations, wavelength-dependent material data for cadmium sulfide (CdS), CdTe, Ge, and Ag are all taken from established sources36,38,39 and shown in Fig. S1. Afterwards, the carrier generation data from FDTD are imported into the CHARGE solver to calculate electrical parameters, i.e., short-circuit current density (Jsc), open-circuit voltage (Voc), fill factor, and power conversion efficiency (PCE) by solving Poisson's and drift-diffusion equations. | ||
| Fig. 1 (a) 3D schematic view of the optimal structure (with NC texture & Ge NP), (b) FDTD simulation setup for optical analysis, (c) CHARGE simulation setup for electrical analysis. | ||
Fig. 1(b) illustrates the detailed FDTD simulation setup for 3D optical simulation. Coming from the top: glass (SiO2), CdS, CdTe, and Ag are all stacked together to form the whole structure illuminated by a plane wave source of AM 1.5G solar irradiance (1000 W m−2) along the z-axis. The source wavelength range has been taken from 400 nm to 1100 nm. Considering the two-dimensional symmetry of both the NC texture and spherical Ge NP, antisymmetric and symmetric boundary conditions are imposed in the x and y direction, respectively, to infinitely mirror the unit cell. The unit cell consists of only one pair of CdS–CdTe NC-shaped textures and a single Ge NP. On the contrary, to mimic the real surrounding environment, perfectly matched layer (PML) boundary conditions are applied in both of the z directions, where any light that either passes through the solar cell or is reflected from the solar cell will be absorbed by the PML layers. Here the CdS window layer and CdTe absorber layer thickness of the baseline structure (without texture) are taken at 100 nm and 1500 nm, respectively.40 The 100 nm CdS is ideal for avoiding lattice mismatch and defects at the interface.41 The performance parameters of the baseline structure (without any textures or nanoparticles) are relatively close and consistent with those previously reported in experimental42,43 and simulation studies.40,41 However, it is worth mentioning that in this study, the thickness of the CdTe layer is reduced to 1500 nm, considering its potential application in portable devices as mentioned previously in the introduction. The 1500 nm thick CdTe layer is sufficient to achieve high efficiency in TFSCs.40 The subsequent 100 nm Ag metal contact is working here as a back reflector at the bottom. Two frequency domain power monitors are used to record the amount of reflected and transmitted light, one placed above the CdS layer (R monitor that measures the power of the reflected light) and the other below the Ag back contact (T monitor that measures the power of the transmitted light). The simulation will shut off when the total energy of the simulation volume reaches 10−5 of the incident maximum energy. The polarization angle and the incident angle of the incoming light are both kept at 0° during simulations of every study in this work, except for the polarization angle and incident angle variation studies. To calculate the electric field distribution of the absorber layer, another frequency domain power monitor was placed along the z-axis (not shown in the figure). There are a total of four parameters that are being optimized in this study. NC-shaped texture's base diameter, dcone and height, hcone were optimized first. It is worth mentioning that no space was considered between the two successive NCs, meaning the period of NC is the same as its base diameter. Later upon obtaining the optimal texture structure, Ge NP diameter, dGe, and position, i.e., depth from the top surface of the flat CdS layer, zGe were optimized.
All the optical simulations in Ansys Lumerical FDTD were conducted using conformal mesh technology to achieve better accuracy at the NC's and NP's curvature.44 To further validate convergence and reproducibility, a uniform mesh was used for mesh sizes of 7, 8, 9, and 10 nm, respectively. The results show less than 1% changes in Jsc and absorption for the varied uniform mesh sizes when compared with the default conformal mesh, as shown in Fig. S2. The time step in Ansys Lumerical FDTD is automatically calculated from the simulation mesh size based on the Courant stability criterion.45 To confirm that time step variation has no effect on optical results, dt stability factor (factor of theoretical maximum time step) has been varied from the default 0.99 to 0.95 down to 0.70 with a 0.05 step size. As shown in Fig. S3, similar to mesh convergence, the changes in Jsc and absorption are less than 1%, ensuring numerical stability and convergence. Both the test on the mesh and time step convergence suggest that the results are independent of the spatial grid and time step resolutions.
Fig. 1(c) illustrates the CHARGE simulation setup for 2D electrical simulation. Although the optical simulations were conducted for only a single period, the generation data was then averaged and unfolded for multiple periods for the electrical simulations. To successfully collect the charge carriers, an emitter, and a base metal contact were placed at the top and bottom, respectively. No generation data were considered under the top emitter metal contact to account for the shadowing effect. The p-type CdTe layer and n-type CdS layer were uniformly doped at a concentration of 2 × 1014 cm−3 and 1.1 × 1018 cm−3, respectively.46 Finally, to obtain the P–V and J–V characteristics curve of the solar cells, a voltage sweep from 0 V to 1.2 V with a 0.05 V step size was considered to run the simulation. Fill factor and PCE were also calculated from the P–V and J–V curves. The CHARGE parameters for the electrical simulations are tabulated in Table S1. Lumerical scripting language and Python were used to extract, analyze, and plot the data collected from the optical and electrical simulations.
2.2 Numerical analysis
The finite-difference time-domain (FDTD) method, used to perform the optical simulations of the design, solves Maxwell's equations without approximating any physical components. The generation rate, absorption plot, and electric field plot are generated using FDTD method, as described in the later parts of this study.Depending on its property, a material can transmit, reflect, and absorb a certain percentage of photons that strike it. In the context of a solar cell, it is desirable for the substrate to absorb as much of the incident light as possible, so that more of the photons are used to generate electron–hole pairs for current generation. Thus, the relative absorption is an important factor for the solar cell light absorbing material. The absorption is calculated using the following formula,47
| A(λ) = 1 − R(λ) − T(λ) | (1) |
The optical power absorption per unit volume (Pabs) is calculated as follows,48
| Pabs(r,ω) = −0.5|E(r,ω)|2Im[ε(r,ω)] | (2) |
 | (3) |
The generation rate is exported in CHARGE to calculate the electrical parameters, such as Jsc, Voc, PCE, and fill factor. The quantum efficiency of a solar cell is the ratio of the power of the light absorbed by solar cell (Pabs(λ)) to the power of the light incident (Pin(λ)) on it, as given in the equation below ,49
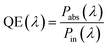 | (4) |
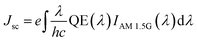 | (5) |
V oc is the output voltage of a solar cell under open-circuit condition, i.e., when the current through the solar cell is 0 A. Thus, it is also the maximum cell voltage when no photocurrent is generated due to the dark current and photocurrent generated being equal. It is calculated using the formula,48
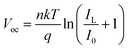 | (6) |
Fill factor (FF) is ratio of the maximum possible power output (Pmax) of a solar cell to the product of its respective Jsc and Voc. It is also an indication of the quality of the solar cell, since a larger fill factor indicates a more optimal performance of the solar cell. It is calculated using the formula,48
 | (7) |
PCE is the key parameter determining how much of the incident power on the solar cell is converted to useful electrical energy, and it is dependent on the other important electrical parameters – Jsc, Voc, and fill factor – as shown below ,48
 | (8) |
3 Results and discussions
3.1 Nanocone texture optimization
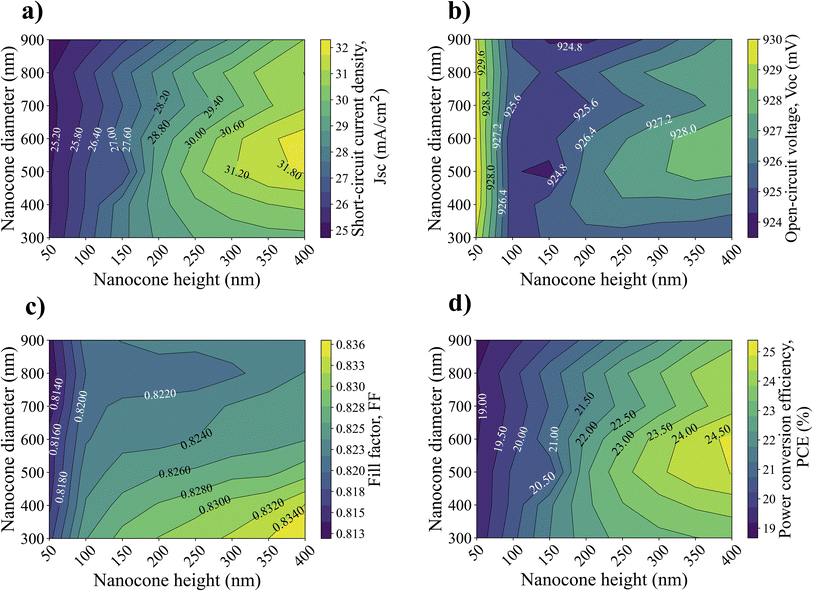
This section systematically optimizes the morphology of the CdS–CdTe NC texture and embedded spherical Ge NP, followed by their underlying enhancement mechanism. It has been shown through grating analysis and Mie analysis that texture and NP are desirable options for achieving broadband light absorption. This section extends further to compare the opto-electronic performance parameters of bare CdTe TFSCs, NC textured CdTe and NC textured CdTe with embedded Ge NPs, respectively. The final subsection includes polarization and angle of incidence analyses of the optimal structure.The initial target of this study is to achieve an optimal texture configuration for which the reflection is minimal, and the absorption is maximum for the NC textured CdTe TFSCs. To achieve this, NC shaped texture of both CdS–CdTe layers has been optimized by varying the cone height and diameter at the same time. Electrical performance parameters like Jsc, Voc, fill factor, and PCE are all taken into consideration to achieve the optimal morphology for the NC texture.
Fig. 2 shows the performance variation of Jsc, Voc, fill factor, and PCE when the NC height and diameter are varied. The cone height was varied from 50 nm to 400 nm with an increment of 50 nm, whereas the base diameter was varied from 300 nm to 900 nm with a 100 nm increment. It is worth mentioning that both parameters were varied at the same time to find the optimal point in the two-dimensional solution space. By changing the structural parameters of NC texture, Jsc can be significantly improved compared to bare CdTe TFSCs.51 From Fig. 2(a), one can easily infer that, for a fixed base diameter, Jsc tends to increase with the increase of cone height. An increase in height also means an increase in aspect ratio, which can be defined as a ratio of height to base diameter. The highest Jsc of 32.09 mA cm−2 (see Table S2) was achieved for a cone base diameter and height of 600 nm and 400 nm, respectively, making the aspect ratio equal to 0.67. Such aspect ratio is found to be a factor in achieving the maximum Jsc for other solar cells with similar types of top surface texturing.37 Compared to bare CdTe TFSCs, this is a 31.93% enhancement (Jsc for bare CdTe is 24.33 mA cm−2). The reason for this increase can be attributed to the increase in diffused transmission of light. That is to say, with the increase in height, surface texture contributes to the increase of light transmission and reduces reflective losses.52 Unlike Jsc, the Voc change in Fig. 2(b) is somewhat different. The highest achievable Voc was 930.4 mV for an NC base diameter and height of 500 nm and 50 nm. Compared to bare CdTe TFSCs (Voc = 978 mV), this is only 5.04% lower. Clearly, surface recombination plays a crucial role when determining the Voc since any textured surface will eventually increase the surface coverage and so can also be expected to increase surface recombination rates. Fig. 2(c) shows the maximum fill factor of 0.8355 was achieved for the highest aspect ratio point, where the base diameter of the cone is minimum (300 nm) and height is maximum (400 nm). Adding texture has significantly improved the quality of the solar cell with respect to base CdTe TFSCs (fill factor for bare is 0.6455) and can be credited to the improved carrier collection. Finally, the PCE of the solar cell with the variation of NC height and base diameter is found to follow the same trend as Jsc because the change in Jsc is significant and contributes more to determining the PCE compared to the other two parameters i.e. Voc and fill factor. The highest PCE of 24.62% was achieved for NC base diameter and height of 600 nm and 400 nm, respectively, a 60.28% increase compared to the bare CdTe TFSC (see Table S2).
Fig. 3(a) depicts the reflectance spectra for bare CdTe TFSCs and CdTe TFSCs modified with the optimal NC structure obtained in the previous section. Reflection from the top surface of the solar cell mainly occurs due to the refractive index mismatch of two different layers.53 It can be realized from Fig. 3(a) that optimal NC texture can suppress reflection from the top surface over almost all the wavelengths from 400 nm to 1100 nm. This is due to the fact that an optimally textured top surface works as an effective medium of graded refractive index as the cross-section starts from zero (at the apex of NC) and reaches the maximum (at the base of NC) as the light goes to the substrate. This allows index matching between glass and CdS–CdTe layers and thus reduces reflection from the top surface.37 Additionally, NC texture breaks the incoming wavefront's uniformity and focuses it into a specific direction to be absorbed.54 Out of all the wavelengths, between 400 nm and 800 nm (absorption window of CdTe), the average reflection came down to almost zero, owing to the pitch or base diameter of the optimal NC. As discussed in the previous theoretical studies, in terms of the light trapping prospect of the texture structure, the base diameter or pitch has to be close to the targeted wavelength.55,56 Since surface texture is suitable for applications in the visible wavelength range, a 600 nm base diameter of NC is optimal and aligns with the target wavelength (midpoint of visible wavelengths). Fig. 3(b) portrays the side-by-side average reflection and absorption for the bare CdTe TFSCs and CdTe TFSCs modified with optimal NC texture. Flat-surfaced bare CdTe TFSCs absorb almost 64% of incoming photons, whereas the remaining 36% are lost as reflective losses. Optimal NC texture, on the other hand, brings down the reflective losses to only 14%, allowing 86% of the photons to be absorbed by the absorber layer. Optimal NC texture scatters incoming transmitted light in different oblique angles, causing them to travel longer than they would have if the surface were flat57 as visually illustrated in Fig. 4(a). Even if the incident light gets reflected by one cone surface, it might reflect the light to the second cone surface for it to be transmitted into the absorber layer, resulting in more absorption as shown in Fig. 4(b). Moreover, this scattered light, then again, might be scattered back into the absorber layer by the back reflector and front texture. This multiple internal reflection largely increases the optical path length and so the absorption.37 In addition to texture, NP later contributes to scattering light in the forward and other directions within the absorbing substrate as illustrated in Fig. 4(c) to aid unabsorbed photons in being absorbed. Further analysis in support of these mechanisms is discussed in the later sections.
 | ||
| Fig. 3 (a) Reflection spectra, (b) average reflection–absorption for bare CdTe TFSCs and NC textured CdTe over the wavelength range of 400 nm to 1100 nm. | ||
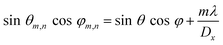 | (9) |
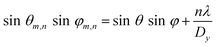 | (10) |
 | (11) |
Far-field effect originating from a diffraction grating can enhance light absorption by increasing the path length and focusing light into specific diffraction modes.54 To visually understand each supported diffraction order, a far-field semi-sphere is often used to locate all the orders along with their angular location and strength. Fig. 5(c–h) depicts the polar and azimuth angular location of all supported orders for the optimal NC texture grating with a color bar to indicate their strength. To be specific, while Fig. 5(c)–(e) shows all the transmitted orders at wavelengths of 450, 750, and 1050 nm, respectively, Fig. 5(f)–(h) shows all the reflected orders for the same wavelengths. As seen in Fig. 5(b), the number of supported transmitted orders is significantly higher than the supported reflected orders, indicating the optimal NC texture can reduce the reflective losses and simultaneously contribute to coupling light into the absorber layer through the far-field effect. The number of supported orders seems to be going down with the increase in wavelength meaning the NC texture has more desirable properties in the shorter wavelength region compared to longer wavelengths. Also, the transmitted orders are found to be focused at the center of the hemisphere at 450 nm wavelength and expanding at the later two wavelengths, meaning the path length increases at longer wavelengths and thus improves photon capture probability.
3.2 Embedded Ge nanoparticle optimization
In this part, the focus is to optimize the spherical Ge NP size, i.e., diameter and its position. It is important to highlight that the NP optimization was done on the previous optimized texture structure where both the CdS–CdTe surface layers were textured as NCs with a base diameter and height of 600 nm and 400 nm, respectively. Since the Ge NP has been embedded into the CdTe absorber layer, its position is defined as the depth (ZGe) from the top CdS flat surface. Both the Ge NP's diameter and depth have been varied at the same time and Jsc, Voc, fill factor, and PCE are all taken into consideration to achieve the optimal position and size for Ge NP.Fig. 6 illustrates the performance variation of Jsc, Voc, fill factor, and PCE when the Ge NP diameter and position are varied. The NP diameter was varied from 50 nm to 300 nm with an increment of 50 nm, whereas the position was varied from 500 nm to 1200 nm from the top of the CdS surface with 100 nm increments. It is noteworthy to mention that the increase in position means the NP is embedded deeper into the CdTe absorber layer. Here, Fig. 6(a), (b) and (d) reveal a similar pattern where better Jsc, Voc, and PCE results were achieved when the Ge NP size was bigger compared to the smaller ones. In those cases, the NP position matters less than the NP size. The reason can be attributed to the fact that the Ge nanosphere shows size-dependent light scattering properties spanning the whole visible to NIR region and the scattering intensity increases with the increase in size.25 However, in the case of the fill factor, the trend is slightly different, and one may conclude that the NP position is prominent in terms of change compared to the NP size. Yet, all the performance parameters, including the fill factor, demonstrate the highest value for the NP's diameter and depth of 300 nm and 500 nm, respectively. The highest Jsc, Voc, fill factor, and PCE was found to be 35.38 mA cm−2, 933.2 mV, 0.8406, and 27.76%, respectively (see Table S3). When compared with the only optimal NC textured structure, this optimized Ge NP with NC texture adds more than 20% PCE enhancement, while the performance of the rest of the parameters were also elevated, as shown in Table 1. This supports the fact that composite light trapping can provide a means to achieve highly efficient CdTe TFSCs.
| Configuration | J sc (mA cm−2) | V oc (mV) | Fill factor | PCE (%) |
|---|---|---|---|---|
| Bare CdTe TFSCs | 24.33 | 978 | 0.6455 | 15.36 |
| NC textured CdTe | 32.09 | 928.7 | 0.8259 | 24.62 |
| NC textured CdTe with embedded Ge NP | 35.38 | 933.2 | 0.8406 | 27.76 |
The proposed design concept, i.e., NC-shaped texturing of the top surface and embedding Ge NP in the absorber layer, is translatable to other TFSC platforms. However, the choice of NP material, its placement, and size should be tailored according to the solar cell's absorbing material, as light scattering is highly sensitive to these parameters. Additionally, NC's morphology also plays a vital role in suppressing surface reflection; thus, optimization will be necessary when integrating it into other thin-film solar cell technologies.
 | (12) |
| Cabs = kIm[αsph.] | (13) |
 | (14) |
To normalize against the geometrical cross sections, the following formulas are used,64
 | (15) |
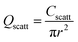 | (16) |
Fig. S4(a and b) presents the normalized scattering and absorption cross sections, respectively, for Ge NPs with diameters between 50 nm and 300 nm, with an increment of 50 nm. It is evident from these two figures that, except for the 50 nm diameter Ge NP, normalized scattering cross sections are higher compared to the absorption cross sections. To effectively measure this parameter, the scattering to absorption cross-section ratio was plotted in Fig. S4(c). Here, it is clear that as the size increases, Ge NP tend to scatter more light than it absorbs, which is consistent with the previously reported literature.25,32,63 The highest scattering to absorption cross-section ratio was achieved for the 300 nm diameter Ge NP, which is close to 4 at above λ = 1000 nm. Furthermore, in contrast to smaller Ge NP, as the diameter of the Ge NP increases, red shifting is observed in the scattering cross sections. Finally, Fig. S4(d) depicts the absorption, scattering, and extinction cross sections (sum of the absorption and scattering cross sections) for 300 nm diameter Ge NP.
In the context of this work, these results justify why 300 nm sized Ge NP and 500 nm NP position resulted in the highest Jsc, Voc, fill factor, and PCE. As 300 nm Ge NP scatters more light compared to the other NP sizes, it increases the possibility of low-frequency photons being absorbed by the CdTe absorber layer since most of the photons of NIR range light remain unabsorbed.64 This might be due to the fact that embedded NPs in the absorber layer redistributes the optical field to result in a homogenization of the optical field (HOF).13 This can significantly increase the carrier generation at longer wavelengths. Furthermore, the placement of the NPs is immensely important considering their light-scattering properties and the direction in which they scatter light. For example, if the NP is scattering light in the downward direction and placed at the bottom of the absorber layer, it would not effectively contribute to absorption enhancement, since scattered light does not have enough absorber material to be coupled with. Thus, when the optimal Ge NP is placed at 500 nm depth i.e. closer to the top surface, its forward scattered light can pass through a sufficiently large portion of CdTe absorber material, giving a chance to generate more charge carriers.
Apart from quantitatively measuring the scattered light through scattering and absorption cross-sections, a far-field scattering plot is also important, considering it can provide fundamental insight into the direction of the scattered light. Ge being a high-indexed semiconductor NP can trap light via far-field light coupling of scattered light and nearfield coupling of localized light.24 To calculate far-field scattering, a 300 nm diameter Ge NP was illuminated with a TFSF source as shown in Fig. 7(a) and the direction of incident light is from the positive towards the negative z-direction. Fig. 7(b) defines the angle in each plane with respect to the x, y, and z axes. Fig. 7(c–f) presents far-field scattered light in the x–y plane, Fig. 7(g–j) for the y–z plane, and Fig. 7(k–n) for the x–z plane along with a color bar representing the intensity of light. All these far-field angular distributions are plotted against four different wavelengths of 500, 900, 1000, and 1100 nm marked at the top of each column in Fig. 7 grid. The far-field radiation pattern at a wavelength of 500 nm provides the baseline pattern, where the contribution of Ge NPs is minimal compared to the near-infrared (NIR) wavelengths of 900, 1000, and 1100 nm, where the Ge NPs significantly contribute to light absorption. From Fig. 7(g–n), one can deduce that the angular far-field distribution of the y–z and the x–z plane shows the scattered light is only focused in the z-direction (at 270°), meaning almost all the light is scattered in the forward direction and there is very little (if any) backward reflection of the incident light from the Ge NPs. On the other hand, Fig. 7(c–f) shows an alternating dipole resonance between the direction of electric and magnetic fields with the change in wavelengths for the x–y plane. Subwavelength Ge NP can demonstrate both electric and magnetic dipole resonance as described in previous literature.65 The direction of both electric and magnetic dipole lobes is transverse to the direction of incident light. However, the light intensity of this dipole response (10−15 order) is comparatively less than the forward scattered light (10−13 order) in the direction of incident light in the y–z and x–z plane. In the y–z and the x–z plane, it can be seen that with the increase of incident light wavelength, the light scatters forward (at 270°) at a wider angle. This eventually increases the optical path length with the help of the metal back reflector leading to enhanced absorption.54 This further validates why the absorption of CdTe TFSCs is significantly enhanced in the wavelength range of 800 nm to 1100 nm, as shown in the absorption plots in the later sub-sections.
3.3 Comparative analysis of bare CdTe TFSCs, nanocone textured CdTe, and nanocone textured CdTe with Ge NP
 | (17) |
Fig. 8(b) reveals that the highest enhancement has taken place in the long wavelength range due to the weak absorption of CdTe TFSCs at this range. Compared to only NC texture configuration, CdTe with optimal NC texture with Ge NP can provide higher enhancement in this wavelength region. The inset figure in Fig. 8(b) shows the enhancement factor in the short wavelength region. The reason the enhancement factor tends to remain between 1.1 to 1.3 is that the absorption of bare CdTe TFSCs is already high in this region. Similar to average absorption, Jsc contribution over certain wavelength ranges is plotted in Fig. S6(a–c). For λ = 400–800 nm, Jsc elevates from 18.77 mA cm−2 to 22.78 mA cm−2 in a similar manner of average absorption for NC texture with and without Ge NP as seen in Fig. S6(a). However, NC texture increases Jsc to almost double (6.63 mA cm−2) and embedded Ge NP with NC texture to more than three times (11.65 mA cm−2) compared to bare CdTe TFSCs (3.45 mA cm−2) when λ = 800–1100 nm, as shown in Fig. S6(b).
For the planar CdTe TFSCs, the Fabry–Perot resonance mode constructed from the constructive and destructive interference of incoming and reflected lights can be seen in Fig. 9(a–d).23 Additionally, the thickness and width of this Fabry–Perot resonance mode can be seen increasing with the increase in wavelength. As for optimal NC texture, having a constant periodicity allows it to work as a diffraction grating.66 Broadband absorption through NC texture can be achieved in two ways.20 The texture layer significantly suppresses the reflective losses at shorter wavelengths and focuses light into the absorber layer as seen in Fig. 9(e–f). On the other hand, at longer wavelengths, CdTe is less absorptive, and therefore incident light can not be absorbed in a single path length, i.e., path taken by light to travel without being reflected. With the help of the back reflector, the diffraction distribution pattern arises as seen in Fig. 9(g and h), increasing the optical path length to several folds.67 For both the NC texture and Ge NP configuration, the electric field distribution plot (Fig. 9(i and j)) is somewhat similar to the only NC texture configuration at 545 and 785 nm owing to the fact that Ge NP contributes less to the light coupling due to its low scattering cross-section at these wavelengths, as described in the previous section. However, at long wavelengths i.e. 935 nm and 1035 nm, Ge NP can be found to increase light coupling through its strong forward scattering mechanism and near field effect demonstrated in Fig. 9(k and l) and also in the 3D field distribution of Fig. 9(o and p). Being a radiative process, Far-field scattering transfers energy through the emission and propagation of photons.68 On the other hand, non-radiative near-field enhancement can substantially amplify incoming light intensity by concentrating light into a small volume.69 Several hotspots are visible at 1035 nm (Fig. 9(l)), suggesting the strong light coupling in the presence of Ge NP can contribute to the electron–hole pair generations and thus increase the overall PCE.70 Clearly, optimal NC texture and Ge NP configuration together provide an improved method to utilize light to increase carrier generation at both short and long wavelengths compared to the other two configurations.
| Solar cell structure | Light trapping technique | J sc (mA cm−2) | V oc (V) | Fill factor | PCE (%) | References |
|---|---|---|---|---|---|---|
| SiO2/Si(DBR)/ZnTe/CdTe/CdS/ZnO/FTO/glass | SiO2/Si (DBR) | 10.98 | 1.201 | 0.82 | 10.39 | 71 |
| FTO/SnO2/CdS/CdTe/MoO3/(MgF2/MoO3)4 | 1D-PC | 17.23 | 0.960 | 0.63 | 10.47 | 7 |
| ITO/CdS/CdTe/Ag | Micro-texturing | 24.29 | 0.798 | 0.57 | 10.98 | 72 |
| Au/ZnO/CdS/CdTe/Au | ZnO nanopillar | 16.90 | 1.008 | 0.75 | 12.60 | 73 |
| Ag/CdS/CdTe/Al(coating)/glass(grating)/Ag | Nano-grating | 30.52 | 1.020 | 0.75 | 23.48 | 10 |
| ZnS/CdTe/BSF/DBR | Si/Al2O3 DBR | 25.04 | 1.065 | 0.88 | 23.94 | 74 |
| ITO/CdS/CdTe/Au/Ni | NW SC & ITO FS | 41.56 | 0.871 | 0.73 | 26.45 | 75 |
| Glass/Ag/CdS/CdTe/Ge/Ag | NC texture & Ge NP | 35.38 | 0.933 | 0.84 | 27.76 | This work |
It is worth noting that the optimal structure proposed in this study incorporates various recombination mechanisms, including Shockley–Read–Hall, radiative, and auger recombination, as outlined in Table S4. Additionally, when the series resistance (Rs = 1.5 ohm cm−2)76 of the emitter was added into the structure, the fill factor and PCE are found to drop from 0.8406 to 0.7890 and 27.76% to 26.19%, respectively. The remaining Jsc (35.38 mA cm−2) and Voc (0.9381 V) values remain fairly similar to the optimal parameter values. Another type of loss considered in the proposed structure is parasitic absorption by the CdS window layer. As shown in Fig. S7, it absorbs around 9% of the total incoming light, especially in the wavelength region below 525 nm. Future studies may focus on achieving improved surface and interface quality, as well as the use of alternative materials for the window layer and the metal contact, which can be expected to further increase the Jsc and PCE of the proposed solar cells.
3.4 Polarization & incident angle variation analysis
Although all the simulations conducted in this study are for TM polarized light in normal incident angle, the actual sunlight is unpolarized light and follows an oblique solar path. This is even more true if the solar cell is being used in a country located far from the equator, where the incident angle is further sloped. Therefore, incident and polarization variation studies are critical to gain a better understanding of the phenomenon of light interaction with the NC structures and embedded Ge NPs in the CdTe TFSC. Fig. 11(a) shows the polarization angle variation from 0° to 90° as a function of incident light wavelengths for the CdTe solar cells with optimal NC texture and embedded Ge NP. It is essential to note that 0° corresponds to the TM polarized light whereas 90° refers to TE polarized light. Additionally, the absorption remained the same for all polarized angles since both the NC texture and Ge spherical NP have x–y axial symmetry. This means the optimal structure obtained in this study can keep a consistent performance for any polarized light. Next, the incident angle has been varied from 0° to 70° as a function of incident light wavelengths for the same optimal structure. The results shown in Fig. 11(b) are consistent with the previously reported study, where the nanotextured front surfaces have shown almost no significant efficiency degradation of the solar cell over an incident angle of 0° to 70°.66,77 However, it can be observed that the absorption at longer wavelengths is more pronounced, which can be attributed to the optical path length change resulting from the increase in incident angle. Despite this, the average absorption is maintained well above 85% over all the angle variations, as shown in Fig. S8. The optimal NC texture plays an important role in this aspect, providing enhanced absorption over a broad wavelength range and large incident angle variation.78 This further supports the robustness of the optimal structure obtained in this study and its insensitivity against polarization and incident angle of the incoming solar radiation. | ||
| Fig. 11 Absorption as a function of (a) polarization angle, (b) incident angle for optimal NC textured CdTe with embedded Ge NP. | ||
3.5 Proposed fabrication technique
Over the years, the fabrication process of CdTe TFSCs have been streamlined industrially.6 While optimizing the proposed structure in this study, one of the goals was its ease of fabrication by implementing additional steps to existing processes. Hence, additional methods for the NC structure and embedding of Ge NP have to be adopted to fabricate the proposed structure shown in Fig. 1. The suggested fabrication process is summarized in Fig. 12. CdTe TFSCs are generally fabricated in a top-down approach, i.e., CdS (window layer) is deposited on a substrate, then CdTe (absorber layer), and then the back contact.6,79 Similarly, top-down approach was taken by Tavakoli et al., where layers of a perovskite solar cell were deposited on a plastic textured with hexagonally ordered inverted NC structure, essentially, the plastic substrate acted as the mold for the NC texture formation.80 This approach can be adopted to potentially fabricate the NC textures in the proposed structure. Industrially, soda lime glass is used as a substrate for CdTe TFSC production due to its minimal parasitic light absorption and cost effectiveness.6Ding et al. devised a method to imprint high resolution images based on inverted nanopyramid textures on Si wafers and also claimed the method can be applied to produce nanowires and nanoholes.81 This method can potentially be adopted to imprint square arrays of inverted NCs by preparing the computer-aided design (CAD) file containing the NC pattern to produce the SiO2 hard mask directly on a soda lime substrate using laser ablation. Soft mask is not a reliable approach for this task, as it has been previously reported that the desired features cannot be attained while etching nanopatterns on silicon. This is because the soft mask has weak resistivity to the caustic etchants.82 Soft masks also lead to undercut, leading to further disfiguration of desired nanopatterns.82 Subsequently, the NCs can be produced using wet etching solution comprising potassium hydroxide (KOH), ethanol, and deionized water. Additionally, potassium hydroxide was used by Sakai et al. as an etchant to produce microstructures on soda lime.83 So, this method of NC texturing may be potentially used on soda lime substrate as well. To deposit the CdS and CdTe layers, chemical bath deposition (CBD) and closed space sublimation (CSS) can be used, respectively.6 Ruiz-Ortega et al. fabricated CdS ultrathin films with thickness ranging from 27 nm to 48 nm using CSS, hence, the CdS window layer thickness of 100 nm for the proposed configuration is potentially achievable.84
For the next part, the deposition of CdTe layer has to be done in two steps for enabling the placement of a Ge NP array. This could be thought of as a layer-by-layer approach where CdTe filled up to a thickness, then fabrication and placement of Ge NP, then again deposition of CdTe as depicted in Fig. 12(d–g). This approach was taken for embedding Ag NPs in amorphous Si by Santbergen et al. and also an almost similar approach can be seen for embedding SiO2 NPs in organic solar cells, where a mixture of PEDOT:PSS and SiO2 NPs was spin coated onto a substrate and then P3HT:PC61BM was deposited on top.85,86 Henceforth, CdTe can potentially be deposited using CSS by maintaining substrate temperature at 500 °C up to a thickness of 400 nm so that Ge NP can be placed.6 Bollani et al. reported a procedure to embed ordered arrays of gallium (Ga) NPs on the surface of Si substrate, where pit arrays acting as place holders were patterned on to the Si using electron beam lithography (EBL), and the Ga NPs were grown using molecular beam epitaxy (MBE) in the ordered pits.87 Although Ju et al. reported a less intensive and less expensive method, i.e., colloidal synthesis, the desired size and perfect array cannot be achieved through this method.88 This method could potentially be expanded to CdTe, where the pit arrays could be textured onto CdTe using EBL and the Ge NPs could be produced using molecular beam epitaxy following the methodology of Aouassa et al., where they deposited Mn-doped Ge NPs on to SiO2 thin-films for solar cell applications.89
Once Ge NPs are implanted, CdTe deposition can be continued for another 800 nm to attain a final thickness of 1500 nm of the absorber layer. Moving forward, the structure is to be annealed in the presence of chlorine (Cl) atmosphere, also known as Cl treatment or activation treatment, where Cl is supplied by cadmium chloride (CdCl2), or alternatively magnesium chloride (MgCl2), which is non-toxic and cheaper.6,79 This ensures the recrystallization of the CdTe removing lattice defects from the CdS/CdTe heterojunction interface and reduce lattice mismatch.6 This step can be followed by a chemical treatment of the CdTe surface using Br2-methanol or a mixture of HNO3/HPO3 acids to create a Te-rich layer. This step has the potential to facilitate alignment between the valence band of CdTe and the work function of the metal contact.6 Lastly, the Ag back contact can be deposited using magnetron sputtering following the methodology proposed by Eze et al.90
Conclusions
In conclusion, the results presented in this computational study reveal that a composite light-trapping technique combining NC-shaped surface texturing and embedded Ge NPs can significantly enhance light absorption in CdTe TFSCs, achieving 95% absorption compared to 64% in CdTe TFSCs without any light-trapping approach. The NC texture, optimized with a 600 nm base diameter and a 400 nm height, effectively reduces surface reflection across the incident light spectrum. Additionally, it acts as a diffraction grating, directing light into the absorber layer to increase carrier generation by extending optical path lengths. Embedding 300 nm Ge NPs at a depth of 500 nm from the top surface helps address the weak absorption of CdTe at near-infrared wavelengths. Scattering cross-sections calculated using Mie theory reveal that, upon light incidence, the Ge NPs exhibit strong forward-scattering behavior, coupling scattered light deeper into the CdTe absorber and enhancing current density. The optimal NC texture with Ge NPs yields the highest simulated values for short-circuit current density (Jsc) at 35.38 mA cm−2, open-circuit voltage (Voc) at 933.2 mV, fill factor at 0.8406, and power conversion efficiency (PCE) at 27.76%. Furthermore, additional analyses indicate that the performance of this structure is stable under varying polarization angles (0° to 90°) and incident angles (0° to 70°) of the incident solar radiation, demonstrating its robustness for practical applications. This resilience can potentially make the optimized CdTe TFSCs viable for integration into miniaturized electronic devices. Although the optimal solar cell structure has not been fabricated in this computational study, a fabrication process has been proposed based on the established fabrication-related literature. Future work will focus on actual device fabrication to establish performance benchmarks, aiming for a cost-effective approach without compromising efficiency.Author contributions
Asif Al Suny: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, validation, visualization, writing – original draft, writing – review & editing. Tazrian Noor: formal analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. Md. Hasibul Hossain: data curation, formal analysis, investigation, methodology, writing – original draft, writing – review & editing. A. F. M. Afnan Uzzaman Sheikh: data curation, visualization, writing – review & editing. Mustafa Habib Chowdhury: formal analysis, funding acquisition, project administration, resources, supervision, validation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
Data generated for this article are available at https://doi.org/10.5281/zenodo.14993647.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5na00325c.
Acknowledgements
The authors would like to acknowledge Independent University, Bangladesh (IUB) for funding this research (VC's Research Fund 2024; Research Project Number: VCRF-SETS:24-020) and providing other logistical support.References
- A. O. Maka and J. M. Alabid, Clean Energy, 2022, 6, 476–483 CrossRef.
- https://www.iea.org/reports/renewables-2024/executive-summary .
- https://www.iea.org/reports/world-energy-outlook-2023/executive-summary .
- G. Regmi and V. Subramaniam, Sustainable Material Solutions for Solar Energy Technologies, Elsevier, 2021, pp. 131–173 Search PubMed.
- G. Hashmi, M. S. Hossain and M. H. Imtiaz, J. Theor. Appl. Phys., 2023, 17, 172328–172329 Search PubMed.
- A. Bosio, S. Pasini and N. Romeo, Coatings, 2020, 10, 344 CrossRef CAS.
- Ç. Çetinkaya, E. Çokduygulular, B. Kınacı, F. Güzelçimen, Y. Özen, N. A. Sönmez and S. Özçelik, Sci. Rep., 2022, 12, 11245 CrossRef PubMed.
- https://www.energy.gov/eere/solar/cadmium-telluride .
- S. K. Jain, V. Janyani and N. D. Gupta, Opt. Quantum Electron., 2023, 55, 665 CrossRef CAS.
- R. B. Sultan, A. A. Suny, M. H. Hossain, T. Noor and M. H. Chowdhury, Heliyon, 2024, 10, e38775 CrossRef CAS PubMed.
- A. Al Suny, R. B. Sultan, S. Tohfa, A. J. Haque and M. H. Chowdhury, 2023 International Conference on Electrical, Computer and Communication Engineering (ECCE), 2023, pp. 1–6 Search PubMed.
- A. A. Suny, S. Tohfa, R. B. Sultan, M. H. Hossain, T. Noor and M. H. Chowdhury, 2023 5th International Conference on Sustainable Technologies for Industry 5.0 (STI), 2023, pp. 1–6 Search PubMed.
- Y. Hou, J. Zhang, X. Zheng, Y. Lu, A. Pogrebnyakov, H. Wu, J. Yoon, D. Yang, L. Zheng and V. Gopalan, et al. , ACS Energy Lett., 2022, 7, 1657–1671 CrossRef CAS.
- B. E. Abu-Elmaaty, T. Ismail, A. H. Sabeeh and I. H. Khawaji, Appl. Opt., 2024, 63, 3885–3891 CrossRef CAS PubMed.
- H. Li, Y. Hu, Y. Yang and Y. Zhu, Sol. Energy Mater. Sol. Cells, 2020, 211, 110529 CrossRef CAS.
- Y. A. Pritom, D. K. Sikder, S. Zaman and M. Hossain, Nanoscale Adv., 2023, 5, 4986–4995 RSC.
- J. R. Nagel and M. A. Scarpulla, Appl. Phys. Lett., 2013, 102, 151111 CrossRef.
- Y. Yin, Z. Yu, Y. Liu, H. Ye, W. Zhang, Q. Cui, X. Yu, P. Wang and Y. Zhang, Opt. Commun., 2014, 333, 213–218 CrossRef CAS.
- Y. Wang, B. Shao, Z. Zhang, L. Zhuge, X. Wu and R. Zhang, Opt. Commun., 2014, 316, 37–41 CrossRef CAS.
- J. Zhu, Z. Yu, S. Fan and Y. Cui, Mater. Sci. Eng., R, 2010, 70, 330–340 CrossRef.
- D. Prashant, S. K. Agnihotri, S. Bhattarai, R. Pandey, J. Madan, M. K. Hossain and D. P. Samajdar, ACS Appl. Electron. Mater., 2023, 5, 4885–4898 CrossRef CAS.
- S. Vadavalli, S. Valligatla, B. Neelamraju, M. H. Dar, A. Chiasera, M. Ferrari and N. R. Desai, Front. Phys., 2014, 2, 57 Search PubMed.
- M. L. Brongersma, Y. Cui and S. Fan, Nat. Mater., 2014, 13, 451–460 CrossRef CAS PubMed.
- C. Zhang, Z. Li, X. Deng, B. Yan, Z. Wang, X. Chen, Z. Sun and S. Huang, Sol. Energy, 2019, 188, 839–848 CrossRef CAS.
- C. Ma, J. Yan, Y. Huang and G. Yang, Adv. Opt. Mater., 2017, 5, 1700761 CrossRef.
- G. V. Naik, V. M. Shalaev and A. Boltasseva, Adv. Mater., 2013, 25, 3264–3294 CrossRef CAS PubMed.
- A. Boltasseva and H. A. Atwater, Science, 2011, 331, 290–291 CrossRef CAS PubMed.
- V. Thakore, J. Tang, K. Conley, T. Ala-Nissila and M. Karttunen, Adv. Theory Simul., 2019, 2, 1800100 CrossRef.
- P. Mahale, P. Moradifar, H. Y. Cheng, N. N. Nova, A. J. Grede, B. Lee, L. R. De Jesús, M. Wetherington, N. C. Giebink and J. V. Badding, et al. , ACS Nano, 2020, 14, 12810–12818 CrossRef CAS PubMed.
- B. Bonham and G. Guisbiers, Nanotechnology, 2017, 28, 245702 CrossRef PubMed.
- A. Garcia-Gil, S. Biswas and J. D. Holmes, Nanomaterials, 2021, 11, 2002 CrossRef CAS PubMed.
- S. Ishii, K. Chen, H. Okuyama and T. Nagao, Adv. Opt. Mater., 2017, 5, 1600902 CrossRef.
- S. Luo, S. Wang, Y. Zhu, E. Zhu and Z. Li, Opt. Commun., 2022, 507, 127606 CrossRef CAS.
- Á. Barreda, P. Albella, F. Moreno and F. González, Molecules, 2021, 26, 4421 CrossRef PubMed.
- D. Carolan, Prog. Mater. Sci., 2017, 90, 128–158 CrossRef CAS.
- E. Palik, Handbook of Optical Constants of Solids, Elsevier Science, 1998 Search PubMed.
- X. Chen, Q. Liu, W. Liu, X. Mao, B. Wei, C. Ji, G. Yang, Y. Bao, F. Yang and X. Wang, Appl. Opt., 2023, 62, 7111–7118 CrossRef CAS.
- R. Treharne, A. Seymour-Pierce, K. Durose, K. Hutchings, S. Roncallo and D. Lane, J. Phys.: Conf. Ser., 2011, 012038 CrossRef.
- H.-J. Hagemann, W. Gudat and C. Kunz, J. Opt. Soc. Am., 1975, 65, 742–744 CrossRef CAS.
- H. A. Al-shamiri, M. O. Sid-Ahmed and F. A. Hezam, J. Photonic Mater. Technol., 2016, 2, 14–19 CrossRef.
- L. Nykyruy, R. Yavorskyi, Z. Zapukhlyak, G. Wisz and P. Potera, Opt. Mater., 2019, 92, 319–329 CrossRef CAS.
- T. Baines, G. Zoppi, L. Bowen, T. P. Shalvey, S. Mariotti, K. Durose and J. D. Major, Sol. Energy Mater. Sol. Cells, 2018, 180, 196–204 CrossRef CAS.
- N. R. Paudel, C. R. Grice, C. Xiao and Y. Yan, J. Mater. Sci.: Mater. Electron., 2015, 26, 4708–4715 CrossRef CAS.
- https://optics.ansys.com/hc/en-us/articles/360034382614-Selecting-the-best-mesh-refinement-option-in-the-FDTD-simulation-object .
- https://optics.ansys.com/hc/en-us/articles/11277217507603-Troubleshooting-diverging-simulations-in-FDTD .
- H. Fardi and F. Buny, Int. J. Photoenergy, 2013, 2013, 576952 CrossRef.
- R. Levinson, P. Berdahl and H. Akbari, Sol. Energy Mater. Sol. Cells, 2005, 89, 319–349 CrossRef CAS.
- J. Su, H. Yang, Y. Xu, Y. Tang, Z. Yi, F. Zheng, F. Zhao, L. Liu, P. Wu and H. Li, Coatings, 2021, 11, 748 CrossRef CAS.
- https://optics.ansys.com/hc/en-us/articles/360042165634-Solar-cell-methodology .
- https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html .
- H. Liu, Y. Du, X. Yin, M. Bai and W. Liu, J. Nanomater., 2022, 2022, 8139174 CrossRef.
- S. Ahn, H. Park, J. Cho, C. Park, J. Park, H. Lee, K. Hong, S. Bong and J. Yi, Optik, 2021, 229, 166304 CrossRef CAS.
- K. X. Wang, Z. Yu, V. Liu, Y. Cui and S. Fan, Nano Lett., 2012, 12, 1616–1619 CrossRef CAS PubMed.
- M. M. Olaimat, L. Yousefi and O. M. Ramahi, J. Opt. Soc. Am. B, 2021, 38, 638–651 CrossRef.
- Z. Yu, A. Raman and S. Fan, Opt. Express, 2010, 18, A366–A380 CrossRef CAS PubMed.
- Z. Yu, A. Raman and S. Fan, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17491–17496 CrossRef CAS PubMed.
- Y. Shi, X. Wang, W. Liu, T. Yang, J. Ma and F. Yang, Opt. Express, 2014, 22, 20473–20480 CrossRef PubMed.
- S. Mokkapati and K. R. Catchpole, J. Appl. Phys., 2012, 112, 101101 CrossRef.
- P. Sheng, A. Bloch and R. Stepleman, Appl. Phys. Lett., 1983, 43, 579–581 CrossRef CAS.
- Q. Zhang, D. Liu, J. Su, S. Zhou, Y. Kong, H. Luo, L. Gao, Y. Xiong and W. Duan, Results Phys, 2023, 45, 106238 CrossRef.
- M. Elimelech, J. Gregory, X. Jia and R. Williams, Particle Deposition I& Aggregation, Butterworth-Heinemann, Woburn, 1995, pp. 263–289 Search PubMed.
- F. Ruffino, Micromachines, 2021, 12, 1050 CrossRef PubMed.
- P. K. Das and A. Dhawan, RSC Adv., 2023, 13, 26780–26792 RSC.
- B. Shi, W. Wang, X. Yu, L. Yang and Y. Xu, Opt. Eng., 2017, 56, 057105 CrossRef.
- R. Gómez-Medina, B. García-Cámara, I. Suárez-Lacalle, F. González, F. Moreno, M. Nieto-Vesperinas and J. J. Sáenz, J. Nanophotonics, 2011, 5, 053512 CrossRef.
- X. Shen, Z. Wang, P. Wangyang and H. Zhou, Opt. Commun., 2023, 545, 129624 CrossRef CAS.
- A. H. K. Mahmoud, M. Hussein, M. F. O. Hameed, M. Abdel-Aziz, H. Hosny and S. Obayya, J. Opt. Soc. Am. B, 2019, 36, 357–365 CrossRef CAS.
- P. Yu, Y. Yao, J. Wu, X. Niu, A. L. Rogach and Z. Wang, Sci. Rep., 2017, 7, 7696 CrossRef PubMed.
- S. B. Ivriq, M. H. Mohammadi and R. S. Davidsen, Sci. Rep., 2025, 15, 1478 CrossRef CAS PubMed.
- M. Eskandari and A. Habibzadeh-Sharif, Photon. Nanostruct: Fundam. Appl., 2024, 58, 101229 CrossRef.
- Y. Özen, Appl. Phys. A:Mater. Sci. Process., 2020, 126, 632 CrossRef.
- L. Vandana, G. Ahmad and S. Mallik, Mater. Today: Proc., 2024 DOI:10.1016/j.matpr.2024.06.016.
- D. Kumar and S. K. Ramasesha, et al. , IEEE Trans. Electron Devices, 2021, 68, 4504–4508 CAS.
- S. A. A. Kazmi, A. D. Khan, A. D. Khan, A. Rauf, W. Farooq, M. Noman and H. Ali, Appl. Phys. A:Mater. Sci. Process., 2020, 126, 1–8 CrossRef.
- M. Ferdoushi, S. Wahid and M. K. Alam, RSC Adv., 2022, 12, 19359–19374 RSC.
- A. M. Bothwell, J. A. Drayton and J. R. Sites, IEEE J. Photovoltaics, 2019, 10, 259–266 Search PubMed.
- J. Zhu, C.-M. Hsu, Z. Yu, S. Fan and Y. Cui, Nano Lett., 2010, 10, 1979–1984 CrossRef CAS PubMed.
- J. Zhu, Z. Yu, G. F. Burkhard, C.-M. Hsu, S. T. Connor, Y. Xu, Q. Wang, M. McGehee, S. Fan and Y. Cui, Nano Lett., 2009, 9, 279–282 CrossRef CAS.
- M. Barbato, E. Artegiani, M. Bertoncello, M. Meneghini, N. Trivellin, E. Mantoan, A. Romeo, G. Mura, L. Ortolani and E. Zanoni, et al. , J. Phys. D: Appl. Phys., 2021, 54, 333002 CrossRef CAS.
- M. M. Tavakoli, Q. Lin, S.-F. Leung, G. C. Lui, H. Lu, L. Li, B. Xiang and Z. Fan, Nanoscale, 2016, 8, 4276–4283 RSC.
- K. Ding, M. Zhang, J. Mao, P. Xiao, X. Zhang, D. Wu, X. Zhang and J. Jie, Mater. Today Energy, 2020, 18, 100493 CrossRef CAS.
- S. Choi and S. J. Hong, Trans. Electr. Electron. Mater., 2015, 16, 312–316 CrossRef.
- D. Sakai, K. Harada, D. Barada and T. Fukuda, Jpn. J. Appl. Phys., 2013, 52, 036701 CrossRef.
- R. C. Ruiz-Ortega, L. A. Esquivel-Mendez, M. A. Gonzalez-Trujillo, C. Hernandez-Vasquez, Y. Matsumoto and M. d. L. Albor-Aguilera, ACS Omega, 2023, 8, 31725–31737 CrossRef CAS PubMed.
- R. Santbergen, R. Liang and M. Zeman, 2010 35th IEEE Photovoltaic Specialists Conference, 2010, pp. 000748–000753 Search PubMed.
- P. Shao, X. Chen, X. Guo, W. Zhang, F. Chang, Q. Liu, Q. Chen, J. Li, Y. Li and D. He, Org. Electron., 2017, 50, 77–81 CrossRef CAS.
- M. Bollani, S. Bietti, C. Frigeri, D. Chrastina, K. Reyes, P. Smereka, J. Millunchick, G. Vanacore, M. Burghammer and A. Tagliaferri, et al. , Nanotechnology, 2014, 25, 205301 CrossRef CAS PubMed.
- Z. Ju, X. Qi, R. Sfadia, M. Wang, E. Tseng, E. C. Panchul, S. A. Carter and S. M. Kauzlarich, ACS Mater. Au, 2022, 2, 330–342 CrossRef CAS PubMed.
- M. Aouassa, M. Bouabdellaoui, M. Yahyaoui, T. Kallel, T. Ettaghzouti, S. A. Algarni and I. O. Althobaiti, ACS Appl. Electron. Mater., 2023, 5, 2696–2703 CrossRef CAS.
- M. C. Eze, G. Ugwuanyi, M. Li, H. U. Eze, G. M. Rodriguez, A. Evans, V. G. Rocha, Z. Li and G. Min, Sol. Energy Mater. Sol. Cells, 2021, 230, 111185 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |