Unveiling the sensing mechanism at the molecular level: a DFT study on the disaggregation of perylene diimide radical anion pimers
Hanlin
Gan
 ab,
Haiquan
Zhang
ab,
Haiquan
Zhang
 *ac,
Yuguang
Ma
*ac,
Yuguang
Ma
 ab and
Qinglin
Jiang
ab and
Qinglin
Jiang
 *ab
*ab
aState Key Laboratory of Luminescent Materials and Devices, Institute of Polymer Optoelectronic Materials and Devices, South China University of Technology, Guangzhou 510640, P. R. China. E-mail: jiangql@scut.edu.cn
bGuangdong Basic Research Center of Excellence for Energy and Information Polymer Materials, Guangdong Provincial Key Laboratory of Luminescence from Molecular Aggregates, South China University of Technology, Guangzhou 510640, P. R. China
cState Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, P. R. China. E-mail: hqzhang@ysu.edu.cn
First published on 25th October 2025
Abstract
The radical anion of amide-functionalized perylene diimide (TFPDIOH˙−) aggregates into a pimer that is stabilized through pancake bonding. In the presence of primary amines, this pimer can undergo disaggregation, offering potential for responsive organic sensors. In this study, density functional theory calculations were employed to elucidate the sensing mechanism, which can be represented as follows: 1/2[TFPDIOH]22− + nBuNH2 → [nBuNH2·TFPDIOH]˙−. Computational results reveal that steric hindrance from the bulky substituents on the amide positions weakens π-stacking interactions, thereby allowing strong hydrogen bonding to induce pimer disaggregation. The phenolic hydroxyl group on the substituent forms a low-barrier hydrogen bond (LBHB) with nBuNH2, which is characterized by a short N⋯O distance, high ρBCP, 3c–4e bonding pattern, and nearly barrierless proton transfer. The electron-withdrawing fluorine atoms on the substituent enhance hydroxyl acidity, further stabilizing LBHB formation. These findings reveal the LBHB-driven disaggregation mechanism and demonstrate that the rational combination of pancake bonding and LBHB interactions offers a novel strategy for developing π-radical-based organic sensors with enhanced sensitivity.
New conceptsBased on the interplay between low-barrier hydrogen bonds (LBHBs) and pancake bonding, this study introduces a molecular design strategy to create highly selective stimuli-responsive organic sensors. While LBHBs have been extensively studied in biological systems for enzymatic catalysis, their rational incorporation into artificial supramolecular architectures for sensor applications represents an unexplored frontier. By strategically incorporating electron-withdrawing fluorinated substituents to enhance hydroxyl acidity while using steric bulk to weaken π-stacking interactions, a novel framework for developing π-radical-based sensors is established. Through a comprehensive density functional theory study, we demonstrate that the formation of a thermodynamically favorable LBHB between a phenolic hydroxyl group and a primary amine provides the dominant driving force to overcome the robust pancake bonding that stabilizes perylene diimide radical anion pimers. This LBHB-driven disaggregation can directly translate into macroscopic property changes. More importantly, the concept extends beyond perylene diimide systems, offering a generalizable design principle for next-generation organic sensors and smart materials. |
1 Introduction
Molecular recognition represents one of the most fundamental challenges in chemistry and materials science. The high selectivity of recognition processes is achieved via the combination of non-covalent interactions, such as hydrogen bonding and π–π stacking, which are crucial for engineering highly specific binding sites.1,2 Among these, low-barrier hydrogen bonds (LBHBs) stand out as a particularly intriguing class, characterized by unusually short donor–acceptor distances (2.3–2.5 Å), significant covalent character, and nearly symmetric potential energy surfaces for proton transfer.3 While extensively studied in biological systems,4–6 the rational design and systematic exploitation of LBHBs in artificial molecular recognition systems represents a promising yet insufficiently explored area. Concurrently, the controlled assembly and disassembly of supramolecular architectures has become a cornerstone strategy for developing smart materials. A major challenge in developing selective stimuli-responsive materials is that traditional methods lack molecular-level specificity. This calls for a new design system where a specific molecular recognition event, such as the formation of an LBHB, can effectively compete with strong intermolecular assembly interactions like π–π stacking, thus enabling stimuli-induced disassembly.Perylene diimide (PDI) derivatives exemplify this challenge and have attracted significant research interest from both academia and industry due to their exciting performance.7–9 Under appropriate conditions, PDI molecules can be reduced to form various anionic species, including radical anions (PDI˙−) and dianions (PDI2−). These reduced PDI species tend to form aggregates through π–π stacking interactions, which exhibit distinctive spectroscopic,10,11 electronic,12 and ferromagnetic13,14 properties that are markedly different from those of their neutral counterparts. Specifically, PDI˙− monomers are capable of forming pimers through pancake bonding interactions, where two radical species antiferromagnetically couple through direct overlap of the singly occupied molecular orbitals.15 The unique spectroscopic and electronic properties of these pimers are also notably distinct from those of their monomers.
The controllable formation and disaggregation of such pimers enable the development of stimuli-responsive materials, where additive binding directly modulates the aggregation state and consequently leads to dramatic changes in optical absorption spectra and electronic conductivity. Recently, Sun and coworkers16 experimentally demonstrated that the radical anion pimer of a certain PDI (TFPDIOH) can be disaggregated using n-butylamine (nBuNH2) as an additive, where the amide positions of PDI were functionalized with tetrafluorophenol (R1) and tetrafluorophenylethyl ether (R2) groups. The skeletal formula of TFPDIOH is shown in Fig. 1. The addition of nBuNH2 resulted in the emergence of a new absorption peak at approximately 800 nm in the UV-Vis spectra and enhanced conductivity according to the I–V curves of thin film devices, making it a potential organic sensor toward primary amines. The incorporation of electron-withdrawing fluorinated substituents in these systems suggests that the enhanced acidity of hydrogen bond donors may play a crucial role, potentially creating conditions that are favorable for LBHB formation. Understanding the microscopic sensing mechanism is essential not only for optimizing current systems but also for establishing broader design principles that could guide the development of next-generation molecular sensors and responsive materials.
 | ||
| Fig. 1 The UKS spin density distribution (isovalue = 0.002 a.u.) and MK atomic charges of the hydrogen bond acceptor atoms of TFPDIOH˙−. | ||
Inspired by this experimental work, comprehensive density functional theory (DFT) calculations are performed to investigate the disaggregation mechanism of TFPDIOH˙− pimers induced by nBuNH2. Notably, these calculations highlight the critical role of LBHBs in driving this disaggregation process. Our computational results reveal that the steric hindrance from R1 and R2 groups results in weakened pancake bonding in the pimers, while the phenolic hydroxyl group on R1 forms strong LBHBs with nBuNH2, leading to pimer disaggregation. Through systematic theoretical investigations, this work demonstrates that the combination of LBHBs and pancake bonding holds promise as a design strategy for distinctive organic sensors.
2 Computational details
Conformational searches were conducted using the GFN-xTB17 and DFT methods to identify the most stable conformations of the complexes. The computational protocol consisted of the following steps: (1) molecular dynamics (MD) simulations at the GFN2-xTB theoretical level18 were performed at 400 K for 200 ps to sample the conformational space randomly. A spherical logfermi potential was employed during MD simulations. (2) All conformations obtained from the MD trajectories were initially optimized at the GFN2-xTB level. (3) The isostat tool in the Molclus program was used to remove duplicates, with energy and structural similarity thresholds set to 0.5 kcal mol−1 and 0.25 Å, respectively, yielding a set of nonredundant conformations. (4) The remaining structures were further optimized at the same theoretical level by incorporating the ALPB solvation model19 (solvent = DMF), followed by an additional filtering step to ensure uniqueness and structural diversity. The six lowest-energy conformers were selected for subsequent high-level calculations. (5) Geometry optimization and vibrational frequency calculations were performed at the M05-2X/6-31G(d,p) level of theory20–23 using the Gaussian 16 program.24 The selection of the M05-2X functional is based on its proven capability in describing π-radical pimers; previous studies25 have indicated that the M06-2X and B3LYP functionals fail to obtain the broken-symmetry singlet ground state of the pancake bonding dimer. Furthermore, based on prior benchmark research,26 the M05-2X functional has been shown to successfully capture the necessary broken-symmetry singlet state and provide a good description of the stacked structure. Single-point energy calculations of the optimized structures were carried out utilizing the B2GP-PLYP-D4 functional27–29 and the def2-TZVP basis set30 to refine the electronic energy Eelec in the ORCA 5.0.3 program.31–34 MP2 steps included in the double-hybrid functional were accelerated using the resolution of the identity (RI) approximation and the default frozen core settings. The RIJCOSX and RI-C approximations35 were employed in conjunction with def2/J and def2-TZVP/C auxiliary basis sets,36,37 respectively. The gCP method38 was employed to eliminate the influence of basis-set superposition error (BSSE) on the computational results. Approximate solvent effects were taken into consideration based on the SMD solvation model39 with DMF as the solvent throughout all DFT calculations. All wavefunction analyses were performed using Multiwfn 3.8(dev).40,41The solution-phase Gibbs free energy Gsoln is determined by42
| Gsoln = Eelec + GQRRHOcorr + ΔG298.15Kconc, | (1) |
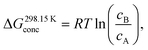 | (2) |
3 Results and discussion
Experimental investigations conducted by Gabba's group revealed that the electron-withdrawing effect of the naphthalimide (NDI) moiety enhances the acidity of solvent molecules interacting with the NDI in alkaline solution.45 This enhanced acidity facilitates deprotonation of these solvent molecules by basic species (F−, CO32−, organic bases, etc.). Subsequently, the deprotonated solvent species can then reduce NDIs to their corresponding radical anion states. While this thermal reduction process is complex and its reaction mechanism remains debated,46,47 the formation of NDI radical anions is demonstrated through both UV-Vis spectroscopy and electron paramagnetic resonance. Similarly, owing to the structural similarity between PDI and NDI, deprotonated solvent species are likewise capable of reducing PDI derivatives to their corresponding radical anion states under the same conditions.16,48,49 The spin density distribution and Merz–Kollman (MK) atomic charges50 of the hydrogen bond acceptor atoms of TFPDIOH˙− are shown in Fig. 1.While the formation of PDI radical anions is observed, an essential aspect for modeling their subsequent dimerization and disaggregation lies in understanding the influence of the counterions, specifically K+. Previous studies established that K+ is fully solvated in DMF,51 with molecular dynamics simulations52 further suggesting that six DMF molecules occupy the first solvation shell of K+. Given this established understanding of K+ solvation, it is necessary to investigate the tendency for TFPDIOH˙− to directly interact with K+ within its first solvation shell. To this end, we initially computed the ΔGsoln associated with the replacement of two DMF molecules in the first solvation shell of K+ by TFPDIOH˙−. The computational results are shown in Fig. 2. The involved structure of (DMF)4 was constructed based on the work by Malloum et al.53 The calculated ΔGsoln for the ligand exchange reaction was +9.5 kcal mol−1, indicating that the process was thermodynamically unfavorable. Therefore, to simplify the computational model, the counterions were omitted in the subsequent calculations, and solvent effects were approximated using the implicit solvation model.
3.1 Formation of TFPDIOH˙− pimers
The TFPDIOH˙− monomers combined to yield low-spin pimers (PB), where their spins were aligned anti-parallel. Therefore, six lowest-energy pimers were optimized following the conformational search procedure, and the ΔGsoln for the dimerization process was computed. Notably, the standard concentration for the pimer was set to half that of the monomer. The computational results indicated that the unrestricted Kohn–Sham (UKS) wave function solutions for all pimers exhibit a minor degree of spin contamination. Details regarding their optimized geometries are summarized in Fig. 3, and the definitions of the structural indicators are provided in the SI (Fig. S1). Among the various stacking configurations, the stacking mode observed in PB1 (ΔGsoln = −5.2 kcal mol−1) was the most stable on the low-spin potential energy surface (PES). Notably, the UKS method may overestimate the stability of open-shell singlet states.54In the TFPDIOH˙− monomer, the dihedral angles between R1, R2 and the PDI moiety were 66.7° and 66.5°, respectively. Due to the steric effect between these bulky substituents, the formation of low-spin pimers by TFPDIOH˙− precluded parallel stacking along the molecular long axis. Instead, the two monomers adopted a twisted π–π stacking (34.1°) to prevent close contacts between the bulky substituents. In contrast, the hydrogen atoms at the amide positions of PDI˙− monomers resulted in minimal steric hindrance. Consequently, the PDI˙− monomers tended to stack in a parallel fashion along the molecular long axis during dimerization.15 The interplanar distance in PB1 (R = 3.582 Å) was longer than twice the vdW radius of carbon atoms (3.40 Å), which would weaken the through-space electronic coupling between monomers. At the M05-2X/6-31G(d,p) and B2GP-PLYP-D4-gCP/def2-TZVP theoretical levels, the exchange coupling in PB1 consistently exhibited moderate antiferromagnetic coupling characteristics, with values of −146.3 cm−1 and −104.6 cm−1, respectively, based on Yamaguchi's approximate spin projection.55,56 As evident from the spin density distribution of PB1 (Fig. S2), regions with opposite spin density signs were delocalized across the two radical moieties, and the isosurface lobes were nearly identical. This indicated a broken-symmetry open-shell singlet state. Given the moderate spin coupling between TFPDIOH˙− units in the low-spin pimers, the disaggregation of these pimers could be induced by strong hydrogen bonding interactions formed between the monomers and the additives.
3.2 Conventional hydrogen bonding: insufficient for pimer disaggregation
Given that most hydrogen bonds are predominantly driven by electrostatic interactions,57 the MK charges of TFPDIOH˙− were used to identify the most probable hydrogen bond acceptor sites with nBuNH2 (Fig. 1). The calculations revealed that oxygen atoms on the PDI moiety exhibited more negative MK charges, suggesting that the formation of hydrogen bond complexes (HBs) with nBuNH2 at these sites would likely be thermodynamically favorable. Appropriate initial structures were generated after the conformational searches, leading to six lowest-energy HB structures where TFPDIOH˙− acted as the hydrogen bond acceptor. The optimized geometries and ΔGsoln for HB formation are summarized in Fig. 4. The electronic structures of these HBs exhibited little spin polarization. Among these, HB1 was the lowest-energy hydrogen bond complex formed with TFPDIOH˙− acting as the hydrogen bond acceptor. The bond critical point (BCP) is the local minimum in the electron density along the bond path where the density gradient is zero, and the resulting electron density value (ρBCP) provides a direct measure of the strength of the hydrogen bond.57 Wavefunction analysis revealed that the hydrogen bond in HB1 had a ρBCP value of 0.0116, indicating a weak hydrogen bond. The ρBCP for the hydrogen bond in HB2 is 0.0113, which was very similar to that of HB1, and their H⋯O distances were also close. This suggested that the differences between R1 and R2 had little impact on the strength of the hydrogen bonds formed at the oxygen sites of the PDI moiety. The ρBCP values for the hydrogen bonds in the remaining HB were 0.0137, 0.0136, 0.0146, and 0.0145, respectively. Evidently, based on their ρBCP and H⋯O distances, these hydrogen bonds were stronger than those in HB1 and HB2. However, the enhanced CH–π interactions between nBuNH2 and the PDI moiety in HB1 and HB2 compensated for the weaker hydrogen bond strength, ultimately resulting in HB1 being the lowest-energy HB among them. Nevertheless, the formation of HB1 was thermodynamically unfavorable (ΔGsoln = +5.8 kcal mol−1), indicating that the strength of the [nBuHNH⋯O] hydrogen bond was insufficient to induce disaggregation of the pimers. Consideration of other forms of hydrogen bonding was therefore needed.TFPDIOH˙− featured a hydroxyl group that could act as a hydrogen bond donor. However, the hydrogen atom already formed an intramolecular hydrogen bond with the fluorine atom in R1. Therefore, understanding the strength of this intramolecular [F⋯HO] hydrogen bond was crucial before considering the formation of HBs containing [nBuH2N⋯HO] hydrogen bonds. The torsional PES of the hydroxyl group in perfluorophenol, which was constructed at the B3LYP/6-311++G(d,p) theoretical level,58 indicated that the torsional barrier of the hydroxyl group was 3.0 kcal mol−1. This suggested a weak [F⋯HO] hydrogen bond strength. We constructed the hydroxyl torsional PES of TFPDIOH˙− at the UM05-2X/6-31G(d,p) theoretical level, and the computational results are presented in Fig. 5. The results indicated that the torsional barrier of the hydroxyl group was 3.5 kcal mol−1, which was close to previously reported values. This further confirmed that the intramolecular [F⋯HO] hydrogen bond in TFPDIOH˙− was weak, and its barrier would be overcome at room temperature.
3.3 LBHB-driven disaggregation
In the experimental study by Sun and coworkers,16 two PDI radical pimers were synthesized. However, it was observed that only the pimer derived from TFPDIOH˙− disaggregated into the corresponding hydrogen-bonded complexes upon the addition of a primary amine in DMF or DMSO. This observation suggests that the formation of these complexes may be related to the phenolic hydroxyl group, prompting us to investigate its role in the disaggregation process. Similarly, following a conformational search procedure, six lowest-energy HB structures with TFPDIOH˙− acting as the hydrogen bond donor were obtained. Fig. 6 illustrates the optimized geometries and the corresponding ΔGsoln values for HB formation. The results indicated that the ΔGsoln for HB7 was −1.5 kcal mol−1, suggesting a higher thermodynamic feasibility compared to HB1. In contrast to the ρBCP of the hydrogen bond in HB1, the ρBCP of the [nBuH2N⋯HO] in HB7 was 0.0960. This value classified it as a strong hydrogen bond,57 exhibiting substantially greater strength when the hydroxyl group on R1 formed a hydrogen bond with nBuNH2. The ρBCP range for hydrogen bonds in the remaining HBs shown in the figure was 0.0931–0.0957. Based on ΔGsoln and wavefunction analysis, the proportion of nBuNH2 binding to the hydroxyl group on R1 was larger compared to binding at four oxygen sites on the PDI moiety.To investigate the influence of fluorine substitution on HB7 formation, we compared the ΔGsoln and ρBCP values of HB7 and HB7-H, where HB7-H was obtained by replacing all fluorine atoms on the R1 group with hydrogen atoms and subsequently optimizing its structure. It was shown that after hydrogen substitution, ΔGsoln changed to +1.7 kcal mol−1, and ρBCP decreased to 0.0654, indicating a significant weakening of the hydrogen bond. This was primarily due to the electron-withdrawing effect of fluorine, which enhanced the acidity of the phenolic hydroxyl group. It can be observed from the difference in pKa between phenol and pentafluorophenol that, in aqueous solution, the experimental pKa of the former is 9.98,59 while that of the latter is 5.41.60 Due to the lack of experimental pKa for nBuNH3+ and TFPDIOH˙−, to approximately determine their pKa, we calculated ΔGsoln for their respective proton transfer to DMF. The calculation results showed that the ΔGsoln value for the proton transfer from TFPDIOH˙− to DMF was +24.4 kcal mol−1, while that from nBuNH3+ was +22.2 kcal mol−1. This indicates that their acidity is similar in DMF solution, and similar acidity is one of the characteristics of LBHB formation.61
To gain a deeper understanding of the differences in hydrogen bond strength among HB1, HB7-H, and HB7, GKS-EDA calculations were performed on these hydrogen bond complexes incorporating an implicit solvent model.62–65 The results are shown in Fig. 7. Here, the ΔGTOT term can be decomposed into five terms:
| ΔGTOT = ΔGele + ΔGexrep + ΔGpol + ΔGcorr + ΔGdesol, | (3) |
The distance between the N atom of nBuNH2 and the O atom of TFPDIOH˙− in HB7 was 2.549 Å. This distance was shorter than that of a typical hydrogen bond (∼2.70 Å) and was close to the N⋯O distance (∼2.55 Å) in a typical LBHB system. To fully demonstrate that an LBHB was formed between TFPDIOH˙− and nBuNH2 in HB7, we calculated the proton transfer transition state and the relative electronic energy along the intrinsic reaction coordinate,66,67 as shown in Fig. 8(a). The asymmetric characteristics of the hydrogen bond implied that its PES curve was double-welled. The electronic energy barrier at the UM05-2X/6-31G(d,p) level was approximately 0.5 kcal mol−1, suggesting that the PES for the proton transfer process was very flat. After considering zero-point energy correction, the proton transfer barrier disappeared. It could be inferred that the proton tunneling effects caused this process to become a barrierless reaction, which was consistent with theoretical calculations for the two typical LBHB systems: [HCOO−⋯HOCHO] and [CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHO−⋯HOCH
CHO−⋯HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2].68,69 The HB generated after proton transfer from TFPDIOH˙− to nBuNH2 was labeled as HB13, which is shown in Fig. 8(b). After applying the single-point energy correction at the UB2GP-PLYP-D4-gCP/def2-TZVP level, its ΔGsoln was found to be −2.4 kcal mol−1. The N⋯O distance in HB13 was 2.500 Å, which was shorter than that in HB7. The ρBCP value for the hydrogen bond in HB13 was determined to be 0.1208. For a detailed analysis of the electron delocalization of the LBHBs formed in HB7 and HB13, adaptive natural density partitioning (AdNDP) analysis70 on the wavefunctions of these two systems was performed. The results are shown in Fig. 9. Obviously, the [nBuH2N⋯HO] hydrogen bond in HB7 would be described by two asymmetric three-center–two-electron (3c–2e) bonds with occupation numbers of nearly 2.00|e|, corresponding to a σ-bonding orbital and a non-bonding orbital. This finding was consistent with the AdNDP analysis of the [F⋯HF]− system,71 suggesting the presence of a certain degree of covalent bond character. After proton transfer to form HB13, the three-center–four-electron (3c–4e) bond, representing a stabilizing, multi-atom interaction in LBHB systems, became slightly polarized due to the lengthening of the O–H distance. The above results indicated that the [nBuH2N⋯HO] hydrogen bond in HB7 and HB13 could be described based on the 3c–4e model, which, as a result, allowed them to be classified as LBHBs.
CH2].68,69 The HB generated after proton transfer from TFPDIOH˙− to nBuNH2 was labeled as HB13, which is shown in Fig. 8(b). After applying the single-point energy correction at the UB2GP-PLYP-D4-gCP/def2-TZVP level, its ΔGsoln was found to be −2.4 kcal mol−1. The N⋯O distance in HB13 was 2.500 Å, which was shorter than that in HB7. The ρBCP value for the hydrogen bond in HB13 was determined to be 0.1208. For a detailed analysis of the electron delocalization of the LBHBs formed in HB7 and HB13, adaptive natural density partitioning (AdNDP) analysis70 on the wavefunctions of these two systems was performed. The results are shown in Fig. 9. Obviously, the [nBuH2N⋯HO] hydrogen bond in HB7 would be described by two asymmetric three-center–two-electron (3c–2e) bonds with occupation numbers of nearly 2.00|e|, corresponding to a σ-bonding orbital and a non-bonding orbital. This finding was consistent with the AdNDP analysis of the [F⋯HF]− system,71 suggesting the presence of a certain degree of covalent bond character. After proton transfer to form HB13, the three-center–four-electron (3c–4e) bond, representing a stabilizing, multi-atom interaction in LBHB systems, became slightly polarized due to the lengthening of the O–H distance. The above results indicated that the [nBuH2N⋯HO] hydrogen bond in HB7 and HB13 could be described based on the 3c–4e model, which, as a result, allowed them to be classified as LBHBs.
 | ||
| Fig. 8 (a) Intrinsic reaction coordinate and electronic energy relative to HB7 at the UM05-2X/6-31G(d,p) level. (b) Geometry characteristics, 〈Ŝ2〉, and ΔGsoln of HB13. | ||
The above theoretical results suggested that the proton transfer from TFPDIOH˙− to nBuNH2 to form HB13 may compete with the dimerization of TFPDIOH˙− to form PB1 as the concentration of nBuNH2 increases. This competition allows the added nBuNH2 to induce the disaggregation of PB1, which was consistent with the experimental observations of Sun et al.16Fig. 10 shows the ΔGsoln values for the disaggregation reaction at different stoichiometric equivalents of nBuNH2. Therefore, the disaggregation induced by the addition of nBuNH2 was sufficient to cause the material to produce different responses to stimuli such as light and electricity, and the combination of pancake bonding and low-barrier hydrogen bond holds promise as a novel design strategy for organic sensors.
To demonstrate the feasibility of the design strategy, the ΔGsoln for the pimer formed by the electrically neutral TFPDIOH was calculated (Fig. S3). The result (−10.3 kcal mol−1) clearly showed that LBHB formation could not compete with the highly stable neutral aggregate. This comparative analysis clearly showed the necessity of TFPDIOH reduction to the radical anion state for disaggregation to occur. Additional calculations for LBHB complex formation between TFPDIOH˙− and two additional representative amines, MeNH2 and N-methylbutylamine, were included. The calculated ΔGsoln with MeNH2 was −3.0 kcal mol−1, and that with N-methylbutylamine was −3.8 kcal mol−1 (Fig. S4). These computational results were comparable to that of nBuNH2, strengthening the generality of LBHB-driven disaggregation. To broaden the applicability of the design principle beyond the specific PDI system, the calculations on two other π-radical dimer systems were performed (Fig. S5): (1) the TFNDIOH˙−, where the π-skeleton of TFPDIOH was replaced by a naphthalenediimide (NDI) core, and (2) a system based on 2,5,8-tri-tert-butylphenalenyl,72 in which one tert-butyl group was replaced by the R1 substituent (PLY). Our calculations suggested that the SOMO–SOMO orbital overlap in the TFNDIOH˙− and PLY radical pimers was smaller than that of TFPDIOH˙−. This reduced orbital overlap yielded less thermodynamically favorable pimer formation, consequently making LBHB-driven disaggregation more facile in these two systems. Therefore, it can be inferred that the proposed molecular design strategy is likely applicable to other π-radical pimers where the SOMO orbital overlap is smaller than that of TFPDIOH˙−.
4 Conclusions
This comprehensive DFT study reveals the disaggregation mechanism of the TFPDIOH˙− pimer through LBHB formation with nBuNH2. Our computational results demonstrate that the hydrogen bonds between nBuNH2 and PDI oxygen atoms are thermodynamically unfavorable (ΔGsoln = +5.8 kcal mol−1), while the formation of LBHB involving the phenolic hydroxyl group is favorable (ΔGsoln = −2.4 kcal mol−1), providing the driving force for pimer disaggregation. Wavefunction analysis confirms the LBHB nature through high electron density at bond critical points (ρBCP = 0.1208), short N⋯O distances (2.500 Å), and distinctive 3c–4e bonding patterns revealed by AdNDP analysis. The nearly barrierless proton transfer (∼0.5 kcal mol−1) and the crucial role of fluorine substitution in enhancing hydroxyl acidity further support the LBHB mechanism. This work establishes LBHB-driven disaggregation as a robust strategy for developing stimuli-responsive supramolecular materials. The theoretical framework, which is predicated on the design principles of optimal pKa matching and steric modulation of π-stacking, is not limited to PDI systems but also applicable to other π-conjugated architectures.Author contributions
Hanlin Gan: conceptualization, DFT calculations, validation, visualization, and manuscript writing; Haiquan Zhang: conceptualization, supervision, project administration, funding acquisition, and manuscript writing; Yuguang Ma: conceptualization, supervision, project administration, funding acquisition, and manuscript writing; Qinglin Jiang: conceptualization, supervision, project administration, funding acquisition, and manuscript writing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: definition of the structural indicators for pimers; spin density of PB1; supporting data for the design strategy; and U-DFT optimized structural coordinates. See DOI: https://doi.org/10.1039/d5mh01664a.Additional relevant data are available from the authors upon reasonable request.
Acknowledgements
We gratefully appreciate the financial support from the Natural Science Foundation of China (52203221 and 92463310), the National Key Research and Development Program of China (2020YFA0714604), the Guangdong Provincial Key Laboratory of Luminescence from Molecular Aggregates (2023B1212060003), the Guangdong Provincial Quantum Science Strategic Initiative (GDZX2301002), the Science and Technology Projects in Guangzhou (2024A04J2529), the Young Talent Support Project of Guangzhou Association for Science and Technology (QT2024-001), the Fundamental Research Funds of State Key Laboratory of Luminescent Materials and Devices (No. Skllmd-2023-03 and Skllmd-2024-23), and the Open Research Fund of Songshan Lake Materials Laboratory (2023SLABFK05).Notes and references
- J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319 CrossRef.
- X. Yang, Z. Ullah, J. F. Stoddart and C. T. Yavuz, Chem. Rev., 2023, 123, 4602–4634 CrossRef CAS.
- L. J. Karas, C.-H. Wu, R. Das and J. I.-C. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1477 CAS.
- J. A. Gerlt and P. G. Gassman, Biochemistry, 1993, 32, 11943–11952 CrossRef CAS PubMed.
- S. Dai, L.-M. Funk, F. R. von Pappenheim, V. Sautner, M. Paulikat, B. Schröder, J. Uranga, R. A. Mata and K. Tittmann, Nature, 2019, 573, 609–613 CrossRef CAS.
- V. Borshchevskiy, K. Kovalev, E. Round, R. Efremov, R. Astashkin, G. Bourenkov, D. Bratanov, T. Balandin, I. Chizhov and C. Baeken, et al. , Nat. Struct. Mol. Biol., 2022, 29, 440–450 CrossRef CAS.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052 Search PubMed.
- D. Powell and L. Whittaker-Brooks, Mater. Horiz., 2022, 9, 2026–2052 RSC.
- L. Montesino, M. López-Valdeolivas, J. I. Martnez and C. Sánchez-Somolinos, Mater. Horiz., 2025, 12, 5149–5161 RSC.
- R. O. Marcon and S. Brochsztain, J. Phys. Chem. A, 2009, 113, 1747–1752 CrossRef CAS PubMed.
- Y. Jia, Q. Jiang, B. Wang, J. Yang, J. Zhang and Y. Ma, Chem. Res. Chin. Univ., 2023, 39, 187–191 Search PubMed.
- Y. Jia, Q. Jiang, H. Gan, B. Wang, X. He, J. Zhou, Z. Ma, J. Zhang and Y. Ma, Natl. Sci. Rev., 2024, 11, nwae087 CrossRef CAS PubMed.
- Q. Jiang, J. Zhang, Z. Mao, Y. Yao, D. Zhao, Y. Jia, D. Hu and Y. Ma, Adv. Mater., 2022, 34, 2108103 CrossRef CAS.
- J. Yang, H. Gan, X. He, Y. Zhu, S. Tong, W. Cui, J. Zhang, Q. Jiang and Y. Ma, Interdiscip. Mater., 2025, 4, 576–584 CAS.
- H. Gan, Q. Jiang and Y. Ma, Phys. Chem. Chem. Phys., 2023, 25, 30005–30013 RSC.
- M. Sun, W. Fan, X. Liu, G. Yin, W. Hou, L. Liu, P. Lu, C. Fan and H. Zhang, Dyes Pigm., 2022, 197, 109847 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Z. Tang, Z. Jiang, H. Chen, P. Su and W. Wu, J. Chem. Phys., 2019, 151, 244106 CrossRef.
- Z. Mou, Y.-H. Tian and M. Kertesz, Phys. Chem. Chem. Phys., 2017, 19, 24761–24768 RSC.
- A. Karton, A. Tarnopolsky, J.-F. Lamére, G. C. Schatz and J. M. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu, J. Chem. Phys., 2024, 161, 082503 CrossRef CAS.
- J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442–13444 CrossRef CAS PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- T. Lu and Q. Chen, Comput. Theor. Chem., 2021, 1200, 113249 CrossRef CAS.
- G. Bélanger-Chabot, A. Ali and F. P. Gabba, Angew. Chem., Int. Ed., 2017, 56, 9958–9961 CrossRef PubMed.
- S. Saha, Acc. Chem. Res., 2018, 51, 2225–2236 CrossRef CAS PubMed.
- T. L. D. Tam and J. W. Xu, Chem. Commun., 2019, 55, 6225–6228 RSC.
- V. Sharma, U. Puthumana, P. Karak and A. L. Koner, J. Org. Chem., 2018, 83, 11458–11462 CrossRef CAS PubMed.
- M. Sun, H. Liu, G. Yin, W. Hou, L. Liu, X. Liu, C. Fan and H. Zhang, Dyes Pigm., 2023, 209, 110934 CrossRef CAS.
- B. H. Besler, K. M. Merz Jr and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- D. A. Owensby, A. Parker and J. W. Diggle, J. Am. Chem. Soc., 1974, 96, 2682–2688 CrossRef CAS.
- Y. P. Pukhovskii, D. Sakharov and L. Safonova, J. Struct. Chem., 2002, 43, 284–292 CrossRef CAS.
- A. Malloum and J. Conradie, Mol. Phys., 2022, 120, e2118188 CrossRef.
- Y. Kitagawa, T. Saito, Y. Nakanishi, Y. Kataoka, T. Matsui, T. Kawakami, M. Okumura and K. Yamaguchi, J. Phys. Chem. A, 2009, 113, 15041–15046 CrossRef CAS PubMed.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. Houk, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS.
- K. Yamaguchi, M. Okumura, K. Takada and S. Yamanaka, Int. J. Quantum Chem., 1993, 48, 501–515 CrossRef.
- S. Emamian, T. Lu, H. Kruse and H. Emamian, J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed.
- P. V. R. Rao, K. Srishailam, L. Ravindranath, B. V. Reddy and G. R. Rao, J. Mol. Struct., 2019, 1180, 665–675 CrossRef CAS.
- K. C. Gross and P. G. Seybold, Int. J. Quantum Chem., 2001, 85, 569–579 CrossRef CAS.
- K. Kipper, K. Herodes and I. Leito, J. Chromatogr. A, 2011, 1218, 8175–8180 CrossRef CAS PubMed.
- G. A. Kumar and M. A. McAllister, J. Am. Chem. Soc., 1998, 120, 3159–3165 CrossRef CAS.
- P. Su, Z. Jiang, Z. Chen and W. Wu, J. Phys. Chem. A, 2014, 118, 2531–2542 CrossRef CAS PubMed.
- P. Su, Z. Tang and W. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460 CAS.
- Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu, W. Wu and P. Su, J. Comput. Chem., 2021, 42, 2341–2351 CrossRef CAS PubMed.
- G. M. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina and E. Guidez, et al. , J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- Y. Pan and M. A. McAllister, J. Am. Chem. Soc., 1997, 119, 7561–7566 CrossRef CAS.
- Y. Pan and M. A. McAllister, J. Org. Chem., 1997, 62, 8171–8176 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- W. Feng, D. Li and L. Cheng, J. Chem. Phys., 2022, 157, 094302 CrossRef CAS PubMed.
- S. Suzuki, Y. Morita, K. Fukui, K. Sato, D. Shiomi, T. Takui and K. Nakasuji, J. Am. Chem. Soc., 2006, 128, 2530–2531 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |








