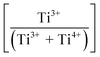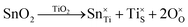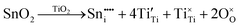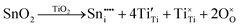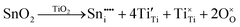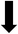Effects of Sn⁴⁺ solid solubility mechanisms on the electromechanical and energy storage performance of (Ba_0.85Ca_0.15)(Ti_0.92Zr_0.08)O₃

Abstract

The electromechanical properties of piezoelectric materials are influenced significantly by the defect chemistry, which is determined by the solid-solubility and charge-compensation mechanisms. In the present work, the effects of Sn⁴⁺ doping of lead-free (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) ceramics on these parameters and the resultant electromechanical properties and energy-storage efficiencies are reported. The complex nature of the solid solubility mechanisms as a function of dopant content is elucidated through comprehensive analyses of the structures, microstructures, and surface chemistry. The corresponding charge compensation mechanisms are determined by correlating these characterization data with corresponding defect equilibria, which then provide the basis for the interpretation of the mechanisms governing the electromechanical properties and energy-storage efficiencies. The combined data for the surface Ti oxidation state (XPS) and bulk unit cell volumes (XRD) for the three observed polymorphs (orthorhombic Pmm2, tetragonal P4mm, and cubic Pm3̄m) reveal interstitial solid solubility at low (0.00 ≤ x ≤ 0.04) and high (0.08 ≤ x ≤ 0.10) Sn⁴⁺ doping levels, with intermediate (0.04 < x < 0.08) Sn⁴⁺ doping levels exhibiting mixed interstitial-substitutional solid solubility. The trends in the electromechanical properties correlate directly with the solid solubility mechanisms, with two resultant inflections at x = 0.04 (maximal defect concentration) and x = 0.08 (minimal defect concentration). These mechanisms significantly influence the electromechanical properties, where maxima occur for polarization at x = 0.04, bipolar strain at x = 0.08, and energy storage efficiency at x = 0.10. The latter is notable because this parameter reaches >95% across the wide temperature range of 25°–130 °C.

---

New concepts

It is universal to assume that BaTiO₃ doping is substitutional. The present work documents data for five different and consistent analytical methods that show unambiguously that the solid solubility mechanism initially is interstitial. With increasing doping, the solubility limit is reached, initiating substitutional solid solubility. With yet more doping and the achievement of saturation solubility, the associated lattice distortion allows interstitial solid solubility to be reactivated. Differences: this assumption is a convenience that has become a universally accepted simplification. This work demonstrates across multiple platforms that this can be incorrect. This work also demonstrates that a single solid solubility mechanism is another potentially incorrect assumption. These observations build on a growing body of work that confirms that mixed solid solubility and changing solid solubility mechanisms occur commonly in other materials. This work is the first to show that this applies to BaTiO₃-based materials. Insights: this work has ramifications for the functional materials industries because doping of these invariably is done using stoichiometric compensation, where dopant levels are decreased according to the dopant addition amount. When this assumption is incorrect, the result involves unrecognised metal vacancies, which inevitably have an effect on the functional properties.

1. Introduction

Defects play a significant role in the response mechanisms of electroceramics, influencing the motion of domain walls,^1–3 creating defect dipoles that interact with the spontaneous polarization,^4–6 and lead to conductivity mechanisms.^7–9 Understanding and controlling defects is essential for tailoring the properties and optimizing their performance in various applications, including sensors, actuators, and data- and energy-storage devices. The solid solubility mechanisms can often be elucidated through consideration of the defect equilibria in conjunction with supporting experimental data.^10–15 Defect equilibria in electroceramics are expressed in terms of Kröger–Vink notation,^10–16 which defines the defect chemistry. However, when Kröger–Vink notation¹⁶ was developed, there were limited means of examining variable cation valences, so this formalism does not provide a discrete notation to illustrate redox effects.^10–15 Furthermore, while many oxides contain intrinsic vacancies and interstitials, doping and impurities lead to the formation of extrinsic vacancies; substitutionals; interstitials; and Frenkel, Schottky, and antisite pairs. The expression of the associated defect equilibria is contingent upon knowledge of the solid solubility mechanism, which is rarely the case. This differentiation is then critical to the assessment of the different charge compensation mechanisms such that both mass and charge balances are maintained.

Lead-based Pb(Zr_1−xTi_x)O₃ (PZT) ceramics are used extensively for energy harvesting and storage applications as they exhibit higher power densities, faster charging/discharging, and superior performance compared to those of Li-ion batteries, electrochemical capacitors, and fuel cells. Moreover, the outstanding piezoelectric and ferroelectric performances extend these ceramics’ significance to electrocaloric and electromechanical applications.^17–28 Further enhancement of these properties was found in other related materials, including Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ (PMN-PT) and Pb(Zn_1/3Nb_2/3)O₃–PbTiO₃ (PZN-PT) solid solutions.^26–29 However, concerns about the toxicity of Pb and its impact on human health and the environment have restricted their applicability,^37–40 thus directing research toward alternative lead-free materials.

Pure BaTiO₃ is one of the potential lead-free candidates and it is well known to exhibit a high dielectric constant.⁴¹ However, owing to its low dielectric breakdown strength (∼1.2 kV⁴²), low discharge energy density (370 mJ cm⁻³ (ref. 43)), and minimal energy storage efficiency (40.3%⁴³), its applicability for high-energy-density materials is limited.^44–46 A typical strategy to improve these performance parameters is doping the A-, B-, or both A- and B-sites of cubic BaTiO₃;^47–56 these sites are structured around an AO₁₂ cuboctahedron and a BO₆ octahedron. In this context, simultaneous A- and B-site doped lead-free (Ba,Ca)(Ti,Zr,Sn)O₃ (BCTZS) is one of the most promising candidates and consequently has generated considerable interest based on demonstrated technical progress in the electromechanical and energy storage sectors over the last decade^57–81 (Table S1). To date, there have been just over twenty studies on BCTZS.^{57–70,72,75–81} There are also several other works on BCTZS that report the use of dopants Pb²⁺,⁷² Sr²⁺,^71,73 and Bi³⁺.⁷⁴ Of these, ten are limited to reports of the structural evolution and electrical properties (2008–2023^{59,60,64,65,70,75,77–80}), five focus on the electrocaloric effect (2015,⁶⁹ 2016,⁵⁸ 2019,^62,76 and 2020⁷³), three focus on the energy-harvesting performance (2020,⁸¹ 2022,⁶¹ and 2023⁶⁶), and three focus on the energy storage efficiency (2022^63,67 and 2023⁸²). These also include six studies that examine the effects of varying the Ti⁴⁺/Sn⁴⁺ ratio.^{58,61,64,65,80,81} These studies reveal some ambiguity about the maximal Sn⁴⁺ solubility, where two of the studies reported it to be <6.0 mol%^61,64 while the other four^58,65,80,81 reported solid solubility up to 6.0–8.0 mol%.

Unfortunately, all twenty-one sets of publications assumed that substitutional solid solubility would occur. Furthermore, none of these studies investigated the solid solubilities, charge compensation mechanisms, or the associated defect chemistry and the resultant effects on the material properties, energy storage capacity, or electromechanical performance. Such an approach is critical because, if the interpretation of the solid solubility and/or charge compensation mechanism is incorrect, then this impacts on the accuracy of the resultant defect equilibria, thereby affecting appropriate assessment of the bases for the energy storage and electromechanical properties.

In contrast, the approach for halide perovskites is different. These perovskites are less stable than oxide perovskites owing to the larger anions, greater polarizability, less rigid BX₆ octahedra, and greater extent of ionic bonding.^83–90 Furthermore, the smaller and more covalent-bonding oxygen ion results in converse characteristics, thereby resulting in smaller interstices and more constrained structures.⁹¹

Consequently, both substitutional^92–102 and interstitial solid solubilities^99,103–112 have been reported for halide perovskites. There does not appear to be any example of experimental validation for the substitutional solid solubility. However, lattice parameter measurements from X-ray diffraction (XRD) were used to support the conclusion of interstitial solid solubility in at least eleven publications.^99,103–112 This one experimental technique was used to support their claim. The possibility of interstitial solid solubility in oxide perovskites is rarely considered; when such consideration is given, it appears to have been limited to only two comparative computational studies of substitutional vs. interstitial solid solubility.^113,114 In both of these studies, the simulations indicated that the former is favoured over the latter for oxide perovskites.

More generally, there are numerous experimental studies in which the solid solubility mechanism has been considered:

• Pb-based: Pb(Zr_1−xTi_x)O₃ (PZT),^{17,19,20,26–28} Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ (PMN-PT),^29–32 and Pb(Zn_1/3Nb_2/3)O₃–PbTiO₃ (PZN-PT)^33–36

• Pb-free: BaTiO₃-based (BTO),^115–120 (Ba_1−xCa_x)(Ti_1−yZr_y)O₃-based (BCTZ),^121–156 (Ba_1−xCa_x)(Ti_1−ySn_y)O₃-based (BCTS),^{52,54,56,157–162} (Ba_1−xCa_x)(Ti_1−y−zZr_ySn_z)O₃-based (BCTZS),^{57,58,66,69,71,75–77,79,80,163} K_0.5Na_0.5NbO₃-based (KNN),^164–177 Bi_0.5Na_0.5TiO₃-based (BNT),^178–182 KNbO₃-based (KN),^183–187 and BiFeO₃-based (BFO).^188–190

In all cases, substitutional solid solubility was assumed but without any experimental evidence to support this conclusion. Although a few computational modelling studies suggest that what appears to be a universal assumption is justified, there remains an apparent absence of experimental validation. Consequently, the present work aims to probe this issue using a case study involving a specific system that is processed under specific conditions. The present work appears to be the first experimental investigation to provide evidence for the solid solubility mechanism, whether substitutional, interstitial, or mixed. The implications of this uncertainty highlight the potential to generate defect equilibria considerably different from those that result from the assumption of substitutional solid solubility.

The present work demonstrates the solid solubility mechanisms, charge compensation mechanisms, and corresponding defect chemistries involved in Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10). This phase was selected as a representative example of similar lead-free phases. Although preliminary stoichiometry compensation for the assumed substitution of Sn⁴⁺ for Ti⁴⁺ invariably is done on the basis of the assumption of substitutional solid solubility,^{57,58,66,69,71,75–77,79,80,163} the present work reveals that, for the specific experimental conditions used, this may not be a correct assumption. This contradiction has significant ramifications for the resultant defect equilibria.

The resultant solid solubility mechanisms in the present work are supported by five distinctly different sets of data, which are unambiguous in demonstrating both interstitial and mixed solid solubilities, where the former is dominant. These outcomes required the implementation of new concepts for Kröger–Vink redox charge compensation formalism,^10–15 which have been made possible by the advent of new room-temperature characterization techniques. The capacity to examine resultant valences through X-ray photoelectron spectroscopy (XPS) allows assessment of the types of defects while photoluminescence (PL) spectroscopy allows assessment of their relative amounts. These data can be confirmed by complementary lattice parameter measurements by XRD and even true density. Combining these experimental data with defect equilibria offers the potential to elucidate the solid solubility mechanism without resorting to analytical techniques such as neutron diffraction (ND), X-ray absorption spectroscopy (XAS), small-angle X-ray scattering (SAXS), and solid-state nuclear magnetic resonance (NMR). Hence, the present work elucidates the roles of the solid solubility mechanisms, resultant charge compensation mechanisms, and underpinning defect equilibria in the modulation of the energy storage efficiency and electromechanical properties.

2. Experimental procedure

2.1. Materials synthesis

The conventional solid-state sintering technique was adopted for the synthesis of Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10). BaCO₃, CaCO₃, TiO₂, ZrO₂, and SnO₂ (Sigma Aldrich, ACS reagent, purity ≥99.00 wt%) were used as initial raw materials. Stoichiometric compensation for the Sn⁴⁺ content was used on the basis of the preliminary assumption of substitutional solid solubility and neutral charge compensation. The powder was initially oven-dried at 100 °C for 24 h (heating rate: 300 °C h⁻¹) to remove moisture. The appropriate proportions of the starting materials were measured using a digital balance (0.0001 g precision) and transferred to a high-density polyethylene (HDPE) ball mill (75 mm H × 65 mm Ø). The mill was filled to 2/3 volume with yttria-stabilized zirconia balls of 10 mm and 5 mm Ø, 60/40 wt% ratio, ∼60 g of powder was added, and ethanol was added until it reached the height of the balls (∼220 mL). Rotary ball milling was carried out at 265 rpm for 24 h. After milling, the slurry was transferred to a Pyrex beaker and dried in an oven at 100 °C for 24 h (heating rate: 300 °C h⁻¹). The dried powders were deagglomerated by gentle hand-crushing using an agate mortar and pestle. The free-flowing powders were transferred into a Pt crucible for calcination at 1300 °C for 2 h (100 °C h⁻¹ heating rate; natural cooling) in a muffle furnace (LABEC, Model CEMMS, Australia; 200 mm W × 400 mm L × 160 mm H, heating element MoSi₂).

After calcination, the reagglomerated powders again were deagglomerated by gentle hand-crushing using an agate mortar and pestle, after which they were ball milled for 96 h, dried, and deagglomerated as described above. The samples (pellets) were formed by uniaxial vacuum pressing (rotary vacuum pump) the powders in a hardened tool steel die (∼110 MPa pressure, ∼1 min holding time, ∼13 mm Ø, ∼2 mm thickness).

Five samples of identical composition were sandwiched in an alumina crucible (∼20 mm ID, 25 H), in which powder identical to that of the samples was used for embedding; each pellet was isolated by a layer of powder of ∼3 mm thickness (the diametral clearance to the crucible wall was ∼4 mm). These procedures were followed in order to reduce/eliminate volatilization and contamination during the sintering conditions. The pellets were sintered at 1500 °C for 12 h (100 °C h⁻¹ heating rate; natural cooling) using the muffle furnace as described above. Any powder adhered to the pellets (∼10 mm diameter) could be removed easily by hand rubbing.

2.2. Characterization and testing

Before characterization, both planar surfaces of the pellets were wet-polished sequentially with SiC papers of varying grit sizes (800 (22.5 μm), 1200 (14.0 μm), and 2500 (7.8 μm)) at 200 rpm. The final thickness of the pellets was held at ∼1.5 mm, which was the thickness after reduction from the original ∼2.0 mm; thus, the analyses were for the bulk. After polishing, the pellets were cleaned in an ultrasonic bath using laboratory detergent and water, dried using heated flowing air for ∼1 min, and then air dried for 48 h. The pellets then were annealed at 200 °C for 24 h (heating rate of 300 °C h⁻¹) in order to remove residual stress from polishing.

Room temperature X-ray diffraction (XRD; PANalytical Empyrean II, Netherlands; 40 kV, 40 mA, CoKα radiation (0.1789 nm), 20–120° 2θ, 0.026° 2θ step size, 200 steps per s, 0.033° s⁻¹ scan speed) was conducted on the pellets to determine the mineralogies. Si powder was used as an in situ standard (BDH Laboratory Chemicals, −325 mesh, 99% trace metals basis). Each pellet was inserted in a recessed sample holder and levelled to the plane of the sample holder surface. A small amount (∼0.01 g) of Si then was used to decorate the surface, leaving only a sparsely covered surface deposit of Si. The patterns were analyzed by Data Viewer PANalytical software and the peak positions then were normalized. Pawley fitting¹⁹¹ (HighScore Plus PANalytical software) was carried out in order to obtain qualitative and quantitative data for the phases present.

Although Rietveld refinement¹⁹² typically is applied for profile fitting for X-ray refinement, it requires a well-defined crystal structure, often including the assumption of specific lattice occupancy involving typically substitutional solid solubility. However, this assumption is commonly problematic in cases in which the solid solubility mechanism is unknown or there are mixed solid solubilities. This assumption may also be incorrect when multiple polymorphs are present, which introduces the potential for varying interstitial site filling. Since the present work reveals mixed Sn⁴⁺ solid solubilities and up to three simultaneously present polymorphs, Pawley fitting^191,193 was used because it does not require detailed crystal structure parameters while providing approximate lattice parameters and peak profiles. Pawley fitting¹⁹¹ is an iterative technique that requires knowledge of the space group and the initial selection of unit cell parameters. The latter are refined progressively until the selected unit cell parameters match those following the fitting. This method effectively mitigates the potential for error when the preceding assumptions are relevant. However, it has the disadvantage that the deconvolutions of multiple peaks are less reliable than those of Rietveld refinement. Hence, while less precise than Rietveld refinement, it does not require the assumptions of crystal structure or lattice occupancy. In light of the comparative strengths and weaknesses of both approaches, the validity of the fitting can be assessed in light of non-XRD complementary data. Consequently, it has been utilized in recent work owing to this advantage.^194–202

Surface chemical analyses were carried out using X-ray photoelectron spectroscopy (XPS; ESCALAB 250Xi spectrometer, Thermo Fisher Scientific, UK; monochromatic AlKα (1486.68 eV) soft X-ray source; 13.80 kV, 8.7 mA, 500 μm spot size). Although XPS is a surface analysis technique, the data are for the bulk since the surface examined was one quarter into the depth of the pellet.

The true density was determined by He pycnometry (AccuPyc II 1340; Micromeritics, Germany; line pressure >1.3 MPa, triple purge fill pressure 0.134 MPa, triple fill pressure 0.070 MPa, equilibration rate 0.035 kPa min⁻¹).

Microstructural analyses were carried out using field emission scanning electron microscopy (FESEM; FEI Nova NanoSEM 450, USA; 30 kV, secondary electron (SE) mode, 3.5 spot size (30 μm aperture diameter, 140 pA)) on the unpolished and unetched surfaces. The electrical conductivity of each sample was increased using a sputter coater to deposit a ∼10 nm coating of Pt (Leica EM ACE600, Leica Mikrosysteme GmbH, Austria; Ar gas). The average grain sizes were determined by ImageJ software using twenty-five measurements over an area of ∼400 μm × ∼300 μm; corresponding histograms and frequency curves were also generated.

Field emission scanning electron microscopy (FESEM; FEI Nova NanoSEM 230, USA; 30 kV, secondary electron (SE) mode, 3.5 spot size (30 μm aperture diameter, 140 pA)) was used for regular elemental mapping, while a silicon drift detector (SDD) energy dispersive spectroscopy (EDS) detector (SDD-EDS; Bruker Xflash 6|30, Germany; 30 keV) was used to confirm the elemental distributions of the unpolished surfaces. A thin carbon coating (∼15 nm) was sputtered using a turbo-pumped carbon coater (DCT; NSC DCT, Iran, 13 kV) prior to EDS.

For electrical measurement, wet-polished samples were deposited with a ∼60 nm coating of Pt using a sputter coater (Leica EM ACE600, Leica Mikrosysteme GmbH, Austria; Ar gas), after which the samples were subjected to piezoelectric measurements (TF Analyzer 2000 System; aixACCT Systems, Germany; 1 Hz, 1 mA, 0.5–4.0 kV mm⁻¹, 25°–140 °C, 5 °C intervals) in a silicone-oil bath. Temperature-dependent dielectric and ferroelectric measurements were also obtained using the same TF Analyzer 2000 system (2.5 kV mm⁻¹).

3. Results and discussion

3.1. Context

In the present work, the presence of multiple polymorphs and solid solubility mechanisms as well as the uncertainties of lattice occupancy of the dominant interstitial solid solubility mechanism requires the application of Pawley fitting rather than Rietveld refinement, the latter of which requires accurate structural data. The previous discussion concerning the pros and cons of Rietveld refinement and Pawley fitting indicate that the uncertainties associated with the latter are such that the XRD refinement should be confirmed by non-XRD complementary data. To this end, the XRD data are interpreted in terms of four non-XRD parameters. That is, XPS data are correlated with the effects of the three polymorphs detected by XRD. PL data then are correlated with the XPS data, following correlations between true density and bipolar strain data obtained with XPS and PL data. These correlations support the conclusion of the validity of the Pawley fitting for XRD refinement in the present work.

3.2. XRD analysis

The structural features of Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) were determined using XRD (Fig. 1(a)). No additional peaks associated with secondary phases were detected, indicating the complete dissolution of the solutes (Ca²⁺, Zr⁴⁺, Sn⁴⁺). Semiquantitative analyses of the XRD data by Pawley fitting¹⁹¹ (Fig. 1(b)) confirm the presence of mixed polymorphs (orthorhombic Pmm2 and tetragonal P4mm) for all of the compositions. The corresponding XRD refinement parameters (R factors, goodness of fit (GoF)) are provided in Table S2. Furthermore, the changes in the trend of the lattice parameters (Fig. S1(a) and (b)), c/a ratio (Fig. S1(c)), and unit cell volumes (Fig. S1(d)) reveal a significant transition from a dominant Pmm2 (O) to a dominant P4mm (T) polymorph at x = 0.04 (first inflection). The pressure–temperature unary phase diagrams^203–205 (Fig. S2) show that this orthorhombic → tetragonal phase transformation is stress-induced. At the highest Sn⁴⁺ doping level (x = 0.10), the formation of cubic Pm3̄m (C) along with the other two polymorphs (Pmm2 and P4mm) suggests the presence of a triple point (TP) at room-temperature (RT). The data for the c/a ratio at x = 0.04 and x = 0.08 are attributed to the achievement of saturation solid solubility, which will be discussed subsequently.

Fig. 1 (a) XRD patterns for cubic (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) (Si peaks deleted), (b) magnified range (51.5–54.5° 2θ) for (200) peaks, (c) laser Raman microspectra (Raman) for (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃: x = 0.00–0.10 and (d) representative deconvoluted Raman data (x = 0.04; linearized background).

3.3. Raman analysis

Fig. 1(c) shows the Raman data for Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) obtained at RT. The deconvoluted spectra (Fig. 1(d)) identify the characteristic vibrational modes,^206–214 which again confirm the presence of mixed polymorphs (Pmm2 and P4mm) for all samples (Table S3). However, cubic Pm3̄m at the highest Sn⁴⁺ doping level was not detected by this method due to peak overlap from the Pmm2 and P4mm polymorphs. Furthermore, the discrete Raman modes reveal the presence of several defects, viz., v-LVM (caused by interstitial solutes and or vacancies), s-LVM (caused by B-site substitution), and DARS (disorder-activated Raman scattering caused by structural distortion) at all Sn⁴⁺ doping levels.^{211,215–217} These data indicate the presence of mixed substitutional and interstitial solid solubility. Mixed polymorphs are known to enhance the ferroelectric and electromechanical properties,^{45,46,218–226} accelerate the charge and discharge rate,^{57,61,62,72,74,77,80} and improve thermal stability, resulting in materials with exceptional energy storage performance.

3.4. SEM and EDS analyses

Fig. 2 shows the field emission scanning electron microscopy (FESEM) images of the samples, which reveal highly dense microstructures for all compositions. Although the planar nature of many of the grain boundaries suggests microstructural stability, concentric growth artifacts remain visible. The corresponding energy dispersive spectrometry (EDS) elemental mappings (shown in insets) confirm the chemical homogeneity. Furthermore, the grain size distribution curves obtained using ImageJ software (Fig. S3) reveal that the average grain sizes vary in the range of ∼27–40 μm.

Fig. 2 FESEM images of surfaces of unpolished and unetched (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃: (a) x = 0.00, (b) x = 0.02, (c) x = 0.04, (d) x = 0.06, (e) x = 0.08, and (f) x = 0.10.

3.5. XPS analysis

Fig. 3(a) shows the X-ray photoelectron spectroscopy (XPS) survey spectra for the samples. Since the XPS O 1s peak spectra reflect the Ti–O terminating lattice bonding,²²⁷ the subsurface cationic states can be identified. This approach is important because the surface metal species can be present in the form of undissolved, precipitated, and/or segregated solutes. The deconvoluted O 1s peaks shown in Fig. 3(b) correspond to lattice oxygen (Ti⁴⁺–O bond), the oxygen associated with an adjacent oxygen vacancy (Ti³⁺–O bond), and the oxygen in chemisorbed water (H₂O/–OH bond). The effects of the oxygen bonding with Ba²⁺, Ca²⁺, Sn⁴⁺, and Zr⁴⁺ would be minimal because Ba²⁺, Ca²⁺, and Zr⁴⁺ have stable valences and Ca²⁺, Zr⁴⁺, and Sn⁴⁺ are present in low concentrations.

Fig. 3 (a) XPS survey spectra; (b) deconvoluted XPS spectra for O 1s, showing Ti⁴⁺–O, Ti³⁺–O, and Ti–OH bonds; (c) variations in based on O 1s spectra (for subsurface) and unit cell volumes (for bulk orthorhombic Pmm2 and tetragonal P4mm) for (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10).

The multiple Ti valence states evident in the O 1s XPS data are reflected in the normalized plot for 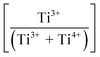as a function of the Sn⁴⁺ doping level (Fig. 3(c)). The corresponding variations in unit cell volumes for Pmm2, and P4mm also are given. The correlation in trends between the subsurface (XPS) and bulk (XRD) data confirms the existence of three, sequential, solubility-driven, redox mechanisms. Furthermore, these data trends in redox confirm the occupancy of Sn⁴⁺, which is isovalent with Ti⁴⁺, in both substitutional and interstitial sites, thus reflecting mixed solid solubility. More broadly, initial dopant incorporation (Mechanism I: 0.00 < x ≤ 0.02) favors Ti⁴⁺ → Ti³⁺ reduction and associated interstitial solid solubility (ISS) in both Pmm2 and P4mm, as shown by the identical trends in unit cell volumes. Subsequent dopant incorporation (mechanism I: 0.02 < x ≤ 0.04) reveals a continued 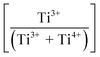increase while the unit cell volumes follow opposite trends. The converse trend is interpreted in terms of the expansion of Pmm2 (from Ti⁴⁺ → Ti³⁺ reduction and continued interstitial solid solubility) and the forced contraction of adjacent P4mm (despite the continued interstitial solid solubility). At higher Sn⁴⁺ concentrations (mechanism II: 0.04 < x ≤ 0.08), the reverse Ti³⁺ → Ti⁴⁺ oxidation occurs. The trends in unit cell volumes for both polymorphs further suggest that the solid solubility mechanism for Pmm2 is consistently interstitial (from the linear baseline trend except at x = 0.04) while that for P4mm (from the staggered baseline) is subject to alteration. That is, these trends are interpreted in terms of the achievement of saturation interstitial solid solubility in P4mm and the onset of substitutional solid solubility (SSS). Hence, the absence of any charge compensation effect from the substitution of Sn⁴⁺ and Ti⁴⁺ effectively reduces the 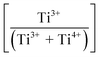, which is equivalent to oxidation. Finally, at the highest Sn⁴⁺ doping levels (mechanism III: 0.08 < x ≤ 0.10), the 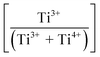trend is reversed again, resulting in the onset of reduction (Ti⁴⁺ → Ti³⁺) owing to reintroduction of interstitial solid solubility in P4mm. This is interpreted in terms of the achievement of saturation substitutional solid solubility at x = 0.08, which distorted the lattice sufficiently to allow additional interstitial solid solubility. Since the linearity of the baseline in the XRD data for Pmm2 do not suggest the achievement of saturation solid solubility, then this polymorph plays no role in the generation of Pm3̄m at x = 0.10. Furthermore, the pressure–temperature unary phase diagrams^203–205 and experimental observations^228–231 show that the polymorphic phase transformation to Pm3̄m is stress-induced. Hence, it is concluded that the second inflection in the redox data (x = 0.08) reflects the generation of Pm3̄m, which is formed directly by stress-induced polymorphic phase transformation from P4mm. The possible defect equilibria related to (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) are given in Table S4. Table 1 summarizes the relevant defect equilibria according to the XPS data and the preceding considerations. In all three cases, the observation of (1) dissolution of Sn⁴⁺ and (2) Ti⁴⁺ → Ti³⁺ reduction forces the charge-compensation mechanism to be redox-ionic^10–15 except for the single case of substitutional solid solubility and neutral charge compensation.

Table 1 Kröger–Vink notation^10–16 for relevant defect equilibria involving Sn⁴⁺

Crystal symmetry	Mechanism I: 0.00 < x ≤ 0.04 (interstitial)	Mechanism II: 0.04 < x ≤ 0.08 (substitutional + interstitial)	Mechanism III: 0.08 < x ≤ 0.10 (interstitial)
T (P4mm)
O (Pmm2)

---

3.6. PL analysis

In order to elucidate the effects of the solid solubility mechanisms on the defect chemistry, reflectance-induced photoluminescence (PL) analyses were carried out. The PL spectra peak intensities are inversely proportional to the rates of recombination, thus revealing electron–hole annihilation.²³² More importantly, the PL spectra identify the presence of point defects by generating energy transitions between the ground and excited states.²³³ These transitions are associated with luminescence centers in the form of color centers (also known as F centers). Fig. 4(a) shows the PL spectra for Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10), which are correlated with ionic and electronic effects. The published four assignments (1–4)^232,234 as defined in Table 2(a) are associated solely with intrinsic effects. The energies generating the relative intensities are ranked on the basis of thermodynamic reasoning. That is, the two electronic defect transitions (assignments 1 and 2) require greater energies to occur as they involve the destabilization of intrinsic oxygen vacancies . Conversely, although the other two intrinsic defect transitions (assignments 3 and 4) are ionic and hence suggest the energies from bond breaking, the charge-compensating Ti⁴⁺ → Ti³⁺ reduction potential is approximately nil.²³⁵ This suggests readily occurring transitions that initiate F⁺ (assignment 3) and F⁰ (assignment 4) color-center formation. The transition of lowest energy is assignment 5, which is proposed in the present work on the basis of the filling of an intrinsic oxygen vacancy , which generally is considered to occur very readily.^236,237

Fig. 4 (a) Photoluminescence spectra, (b) variation in inverse 570 nm intensity, true density and as a function of Sn⁴⁺ doping level, (c) unipolar polarization curves (vertically offset) measured at 2.0 kV mm⁻¹, and (d) variation in coercive field, E_C as a function of Sn⁴⁺ doping level for (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10).

Table 2 Possible (a) intrinsic and (b) extrinsic defects and related transitions inferred from PL data

(a)	Assignment	Charge compensation	Defects and transitions	Decreasing enthalpy	Ref.
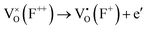
Intrinsic	1	Electronic			232 and 234
	2				232 and 234
	3	Ionic			234
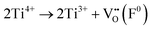
	4				234
	5				Present work

---

(b)	Assignment	Charge compensation	Combined effects	Decreasing enthalpy	Ref.
Extrinsic (SSS)	5	Neutral			Present work
Extrinsic (ISS)	4 + 5	Redox

---

Table 2(b) shows the combined effects of the extrinsic dopant (Sn⁴⁺) and its solid solubility mechanisms in relation to assignments 4 and 5. The column ‘Combined effects’ incorporates the nature of the Sn⁴⁺ solid solubility (substitutional or interstitial) with the single (assignment 5) or double (assignments 4 and 5) defect outcomes ( and/or 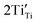). Fig. 4(b) shows that the inverse PL density at 570 nm for assignment 4 (Ti⁴⁺ → Ti³⁺ reduction, 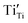) as a function of Sn⁴⁺ doping reaches a maximum at x = 0.04 (interstitial solid solubility) and a minimum at x = 0.08 (substitutional solid solubility). Accordingly, Table 2(b) suggests that the maximum at x = 0.04 is associated with interstitial solid solubility and hence dominated by Ti⁴⁺ → Ti³⁺ reduction over oxygen vacancy annihilation (assignment 5, ). In contrast, the minimum at x = 0.08 is associated with substitutional solid solubility and hence dominated by oxygen vacancy annihilation.

Since lower peak intensities and defect concentrations are inversely proportional, the inverse PL intensity at 570 nm contrasted with the 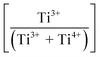and true density as a function of Sn⁴⁺-doping level are shown in Fig. 4(b). These data reveal the maximal defect concentration (i.e., lowest stability) for x = 0.04, which results from the saturated interstitial solid solubility in P4mm. As discussed earlier, at this stage, substitutional solid solubility commences in P4mm, while interstitial solid solubility continues in Pmm2. At this point, the defect concentrations shift toward minima. These data reveal a critical observation for the present work that is at x = 0.04, the maximum defect concentration is dominated by the redox mechanism rather than oxygen vacancy annihilation. While at x = 0.08, oxygen vacancy annihilation dominates, thus stabilizing the lattice to a maximum at x = 0.08 (i.e., highest stability). Since interstitial solid solubility continues in Pmm2, then this continued increase in defect concentration of 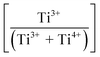must be dominated by the intrinsic annihilation. The reverse trend at x = 0.10 is caused by the recurrence of interstitial solid solubility and increasing 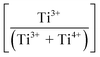but also possibly the structural stress caused by the P4mm → Pm3̄m phase transformation.

Fig. 4(b) integrates PL, XPS, and true density data, all of which provide quantitative estimates of defect concentrations. These data also highlight the risks of assuming substitutional solid solubility because this incorrect assumption results in the introduction of metal vacancies, which are integrated indirectly in the PL data. These particular defects thus are not considered part of the relevant defect equilibria because they do not require charge compensation as they are created by Ti deficiency. In this sense, these defects can be considered to be intrinsic defects, as in intrinsic oxygen vacancies in many oxides. This leads to a second oversight shown by the XPS data, which reveal the importance of redox charge compensation and the formation of Ti³⁺ defects through Ti⁴⁺ → Ti³⁺ reduction. The presence of point defects in the form of substitutional extrinsic dopants (weight gain or loss), interstitial extrinsic dopants (weight gain), and vacancies (weight loss) can be reflected through true density measurements, a technique that has been used previously.^238,239 The similarities in trends between these three disparate techniques demonstrate that interstitial Sn⁴⁺ initiates redox charge compensation, where increasing x and the resultant irregular solid-solution mechanisms are reflected in corresponding changes in the 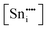, , 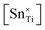, and . However, while the trends in the XRD data (Fig. S1) generally support these data, the correspondence is not perfect owing to the competing trends in lattice constants, c/a ratios, and unit cell volumes of the two polymorphs.

3.7. Ferroelectric property analysis

In addition to consideration of the effects of the chemical, physical, and structural characteristics, the electromechanical properties of Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) were also examined. The RT unipolar polarization curves with no prepoling history (Fig. 4(c)) were used to calculate the coercive field (E_C), which is shown as a function of [Sn⁴⁺] in Fig. 4(d). Relative to undoped (Ba_0.85Ca_0.15)(Ti_0.92Zr_0.08)O₃, the addition of Sn⁴⁺ lowers the E_C, making the materials ferroelectrically soft. The change is greatest for x = 0.02, indicating that only a small amount of Sn⁴⁺ is capable of reducing the energy barrier for domain switching. The negative slopes for interstitial Sn⁴⁺ compared to the nil slope of the substitutional Sn⁴⁺ indicates that the mechanism of solid solubility plays a key role in facilitating domain switching. Furthermore, the gradual approach of the E_C toward 0 suggests the potential for complete elimination of the energy barrier to domain switching.

The E_C data for the doped samples are interpreted in terms of the PL data (Fig. 4(a) and (b)), which reveal the pervasive effect of intrinsic oxygen vacancies and associated color centers. Since oxygen vacancy annihilation (assignment 5) has the lowest energy requirement and so would be expected to occur readily, then this provides the driving force for the trend observed in Fig. 4(d). This is consistent with the effect of oxygen vacancies, which hinder domain wall motion through pinning effects.^240–242 Thus, the gradual annihilation of intrinsic oxygen vacancies would cause a similar trend in increasing the soft ferroelectricity with increasing [Sn⁴⁺]. However, the monotonic trend in Fig. 4(d) in the E_C does not mirror the multiple trends in Fig. 4(b). This is because Fig. 4(b) shows the effect of assignment 4 only (Ti reduction) and Fig. 4(d) shows the effect of assignment 5 only (oxygen vacancy annihilation). This differentiation thus allows decoupling of the data for the two solid solubility mechanisms. Such flexibility offers advantages over the more conventional approach for (Ba,Ca)(Ti,Sn,Zr)O₃^{60,62,63,67,75} that assumed B-site substitutional solid solubility (and hence neutral charge compensation) and unexplained charge compensation by oxygen vacancy formation. The alternative of A-site substitutional solid solubility would result in oxygen vacancy annihilation.

Fig. 5(a) shows the RT bipolar ferroelectric hysteresis (P–E) loops measured at 4.0 kV mm⁻¹. All of the compositions exhibit well-shaped symmetric hysteresis loops with clear saturation, again confirming their conventional ferroelectric nature. However, with increasing Sn⁴⁺ doping level, the P–E loops become narrower, suggesting that Sn⁴⁺ reduces the maximal polarization (P_max) as well as the remanent polarization (P_r), ultimately eliminating the P_r at x = 0.10. These trends clearly demonstrate that the addition of Sn⁴⁺ lowers the energy of the domain wall movement, thus facilitating the domain switching.^243–245

Fig. 5 (a) Bipolar polarization curves (vertically offset) measured at 4.0 kV mm⁻¹, (b) variation in P_max as a function of temperature, (c) bipolar strain curves as a function of electric field and (d) variation in bipolar strain (%) as a function of composition for Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10).

The temperature-dependent bipolar hysteresis curves measured at 2.5 kV mm⁻¹ in the range 25°–140 °C also are provided in Fig. S4. These data were used to determine P_max (Fig. 5(b)) and P_r (Fig. S5). These data are consistent with the observation concerning Fig. 4(c), thus indicating that [Sn⁴⁺] effectively disrupts the long-range order, creating short-range polar regions that lower the energy required for domain wall movement, which is a requirement for high-performance energy storage materials. Furthermore, the variations in P_r with increasing temperature (Fig. S5) are consistent with a shift in polymorphic phase transformation temperatures at different Sn⁴⁺ doping levels. These data also reveal that the addition of Sn⁴⁺ lowers the tetragonal → cubic transformation temperature (Curie temperature, T_C), ultimately reaching RT at x = 0.10.

3.8. Electromechanical property analysis

The unary phase diagrams for BaTiO₃ (Fig. S2) show the influence of stress (and resultant strain) on the phase transformations of this material. The bipolar strain curves as a function of electric field are shown in Fig. 5(c), which reveals the change in shape of the strain curves with increasing Sn⁴⁺ content. These data confirm the gradual reduction in spontaneous strain. Fig. 5(d) shows the variations in the values of positive (S_pos) and negative (S_neg) strains as a function of Sn⁴⁺ doping level, where the two inflections at x = 0.04 and x = 0.08 reflect relatively high respective net strain (ΔS) values of 0.125% and 0.144%.

These data are also interpreted in terms of the PL data (Fig. 4(a) and (b)), which suggests that the gradual reduction in S_neg with increasing Sn⁴⁺ content is associated with the process of oxygen vacancy annihilation. In contrast, the S_pos data show a decreasing trend but accompanied by small increases in strain at x = 0.04 and x = 0.08. Since the PL data for defect concentration (Fig. 4(b)) show a maximum at x = 0.04, then the correlation between the first inflection and the associated stress-induced orthorhombic → tetragonal phase transformation is clear. However, the second inflection at x = 0.08, which reveals minimal defect concentration, exhibits the highest strain in the doped samples. This is interpreted in terms of the transmission of stress and resultant strain, where strain is facilitated by stress transmission through a “perfect” lattice, in contrast with decreased strain from a more compliant lattice distorted by intrinsic 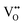. As discussed, at x = 0.08, minimal defect concentration through maximal oxygen vacancy annihilation is expected, which decreases the compliance and so stiffens the lattice, thereby increasing the strain. The significant reduction in strain at x = 0.10 is attributed to the introduction of large-scale microstructural defects in the cubic (Pm3̄m) grains, thus resulting in considerable microstructural disturbance and resultant compliance.

3.9. Dielectric property analysis

Fig. 6(a) shows the variation in maximal dielectric constant (ε_max) as a function of electric field. These data reveal that the optimal samples exhibit ε_max, values in the range 12 000–15 000 (RT, 4.0 kV mm⁻¹, 0.5 kHz) for x = 0.06–0.10. These data show an apparent inconsistency for x = 0.06 and 0.08. The transition from the higher value at x = 0.06 to the lower value at x = 0.08 would result from the transition from minimal to maximal substitutional solid solubility, this component of which effectively would not contribute to the dielectric polarization. This range in maximal dielectric constant may be contrasted with those for (Ba_0.90Ca_0.10)(Ti_0.75Zr_0.25)O₃ (bulk material) of 1992 (RT, 2.0 kV mm⁻¹, 10.0 kHz)²⁴⁶ and for (Ba_0.85Ca_0.15)(Ti_0.90Zr_0.10)O₃ (thin film) of 1600 (RT 100.0 kV mm⁻¹, 10.0 kHz).²⁴⁷ Furthermore, the low slopes of the plots in Fig. 6(a) indicate relatively stable dielectric constants for the range of fields examined (≤4.0 kV mm⁻¹). Thus, these materials are potential candidates for energy storage since they exhibit very high dielectric constants.

Fig. 6 Variation in (a) maximal dielectric constant (ε_max) as a function of electric field, (b) charge and discharge energy densities with Sn⁴⁺ doping level, and energy storage efficiency (η) as a function of (c) electric field and (d) temperature for Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10).

3.10. Energy storage efficiency analysis

Fig. 6(b) shows the variation in charge (W_tot) and discharge energy densities (W_rec + W_loss) measured at room temperature as a function of Sn⁴⁺ doping level. These data reveal that the incorporation of Sn⁴⁺ is beneficial in reducing the loss energy densities (W_loss). The recoverable energy densities (W_rec) increase with increasing Sn⁴⁺ doping level up to x = 0.10, at which point the W_rec approaches W_tot, thus showing that the loss associated with the discharge energy density is negligible at x = 0.10.

The data in Fig. 5(a) and Fig. S4 were used to calculate the energy storage efficiencies, which are shown in Fig. 6(c) and (d). The electric-field-induced energy storage efficiency (η) data in Fig. 6(c) suggest four performance regions (x = 0.00, 0.02–0.04, 0.06–0.08, and 0.10). These data are consistent with the bipolar strain data, which reflect the solid solubility mechanisms.

In the parent BaTiO₃ structure, the two types of interstices are in twofold (unit cell edge) and threefold (tetrahedral void base) coordinations. With interstitial solid solubility, the introduction of the electronegative effect of the irregularly localized Sn⁴⁺ solutes would disrupt the long-range dipole order and generate short-range order. Such disruption is associated solely with relaxor ferroelectrics, which display a rapid response to applied electric fields and hence increased η. Since Sn⁴⁺-doped Ba(Ti_1−xSn_x)O₃ (0.10 ≤ x ≤ 0.27) exhibits relaxor characteristics,²⁴⁸ then it is probable that, Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10) would exhibit relaxor behavior at x > 0.10.

The electric-field-induced temperature-dependent permittivity curves are given in Fig. S6, which suggests shifts in the polymorphic phase transformation temperatures toward RT with increasing Sn⁴⁺ doping level. These data explain the presence of Pm3̄m at x = 0.10, as detected by room-temperature XRD (Fig. 1(b)).

Since thermal stability is an important aspect for practical applications of energy storage materials, then the energy storage efficiencies are shown in Fig. 6(d). These data were generated from the corresponding (20°–140 °C) bipolar hysteresis curves (Fig. S4). The trends in the data, which generally approach constancy, indicate the potential for both high and constant energy-storage efficiencies. This is particularly the case for x = 0.10, where η is >95% for RT to 130 °C.

Fig. 7(a) and (b) show plots of the energy-storage efficiencies (η) vs. recoverable energy densities (W_rec) reported during the period 2013–2024 for BaTiO₃-based materials,^{50,63,67,68,122,249–273} including the relatively few studies of Sn⁴⁺-doped (Ba_0.85Ca_0.15)(Ti,Sn,Zr)O₃ (2022^63,67 and 2023⁸²). The data shown in Fig. 7(a) and (b) are tabulated in Table S5. These data reveal that the majority (∼61%) of these studies involved the application of low electric fields (≤2.5 kV mm⁻¹) and low temperatures (≤100 °C). Of these thirty publications, only two provided data for η for the simultaneous conditions of high electric field (>2.5 kV mm⁻¹) and high temperature (>100 °C).^68,273 This is a critical distinction since both of these parameters influence the η significantly.

Fig. 7 Comparison plots for data reported during 2013–2024 for BaTiO₃-based systems (a) ≤2.5 kV mm⁻¹ (present work: green- and red-shaded regions), and (b) >2.5 kV mm⁻¹ (present work: with given x values).

Fig. 7(a) also reveals that nearly all of the previously reported BaTiO₃-based studies exhibit comparatively low W_rec (grey-shaded region, <100 mJ cm⁻³). Conversely, the present study reports a linear trend with significantly higher values of η at RT and low electric fields. At higher temperatures and low electric field, the materials exhibit a linear trend in η for the materials that outperforms all reported equivalent data. Fig. 7(b) summarizes similar recent reports of energy storage performance in terms of η but at high electric fields. These data reveal that the highest Sn⁴⁺ doping level (x = 0.10), which is from the present work, exhibits an η value (>95%) that is the highest recorded for BaTiO₃-based materials.

4. Conclusions

The present work highlights the significance of the basic science of piezoelectric ceramics using a lead-free analogue of BaTiO₃-based materials, specifically Sn⁴⁺-doped (Ba_0.85Ca_0.15)([Ti_0.92−xSn_x]Zr_0.08)O₃ (x = 0.00–0.10). The effects of the solid solubility mechanism, charge-compensation process, and defect equilibria on the structural, chemical, electromechanical, and energy-storage properties were examined using a comprehensive suite of analytical techniques. Although such systems are considered universally to exhibit substitutional solid solubility, the present work demonstrates that, for this specific set of compositions and processing procedures, identification of the actual solid solubility mechanism, resultant charge compensation, and associated defect chemistry are essential in order to interpret materials properties and performance. The XRD and Raman data reveal the existence of mixed polymorphs (x = 0.00–0.08: Pmm2 + P4mm; x = 0.10: Pmm2 + P4mm + Pm3̄m). The XPS data confirm three, sequential, solubility-driven, redox mechanisms. The two inflections observed at x = 0.04 and x = 0.08 are stress-induced and attributed to the achievement of saturation solid solubility in P4mm. More broadly, x = 0.04 reveals saturation for interstitial solid solubility and x = 0.08 indicates saturation for substitutional solid solubility. The observation from the inverse PL data of the maximal defect concentration (i.e., lowest stability) at x = 0.04 reflects the dominance of redox-charge compensation. In contrast, the minimal defect concentration (i.e., highest stability) at x = 0.08 reflects the role of interstitial Sn⁴⁺ in annihilating intrinsic oxygen vacancies, thus stabilizing the structure. The expected higher stability at x = 0.10 was not observed owing to the introduction of a third phase Pm3̄m.

The polarization data indicate a decrease in the oxygen-vacancy-induced pinning effect with increasing Sn⁴⁺ doping level. The bipolar strain data reveal high net strain (ΔS) values at x = 0.04 and x = 0.08 owing to changes in the solid solubility mechanism. These data reveal the great potential for x = 0.10 in energy storage, where an efficiency of >95% was achieved over the temperature range 25°–130 °C. This is the highest energy storage efficiency reported to date for the system (Ba,Ca)(Ti,Zr,Sn)O₃. The other Sn⁴⁺-doped compositions from the present work also exhibit notably high energy-storage efficiencies up to 130 °C, thus making these materials suitable for high-temperature energy-storage applications.

This synthesis of experimentation and mechanistic interpretation in the present work provides a basis for the engineering of piezoelectric materials with improved electromechanical properties and energy-storage performance. This approach can inform the strategic selection of dopants of specific characteristics that result in the establishment of different solid solubility mechanisms, corresponding charge-compensation processes, and associated defect equilibria, all of which play a pervasive role in the resultant properties.

More broadly, the present work applies a case study to test the apparent paradigm of the general assumption of substitutional solid solubility in the case of doping studies. This common practice for oxide perovskites and for many other materials, if not justified, has ramifications for the defect equilibria and associated performance of functional materials owing to the practice of stoichiometry compensation during fabrication. That is, the outcome can be unsuspected cation vacancies (ionic charge compensation), electron or hole generation (electronic charge compensation), or cation reduction (redox charge compensation). The present work shows that this assumption may not be justified. Thus, if there is one case of interstitial and/or mixed solid solubilities, there may be others.

The present work also introduces the possibility of determining the solid-solubility mechanism without resorting to the application of analytical techniques such as neutron diffraction (ND), X-ray absorption spectroscopy (XAS), small-angle X-ray scattering (SAXS), and/or solid-state nuclear magnetic resonance (NMR). The present work reveals that assessment of the defect equilibria through the use of common experimental techniques is a powerful yet simple method that can lead to the determination of the solid solubility mechanism. These methods, used singly or combined, include X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), photoluminescence (PL) by laser Raman microspectroscopy, and/or true density by He pycnometry.

Conflicts of interest

There are no conflicts to declare.

Data availability

Any further data that support the findings of this study are available on request from the corresponding author.

The supporting data are provided in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5mh01632k.

Acknowledgements

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. The authors acknowledge financial support from the Australian Government Research Training Program (RTP) and the subsidized analytical facilities provided by the Mark Wainwright Analytical Centre, UNSW. The authors also wish to acknowledge the significant assistance with the acquisition of the electromechanical measurements by Mr Bill Joe, Senior Technical Officer, School of Materials Science and Engineering, UNSW Sydney.

References

1. R. Bulanadi, K. Cordero-Edwards, P. Tückmantel, S. Saremi, G. Morpurgo, Q. Zhang, L. W. Martin, V. Nagarajan and P. Paruch, Phys. Rev. Lett., 2024, 133, 106801.
2. Y. X. Liu, H. C. Thong, Y. Y. S. Cheng, J. W. Li and K. Wang, J. Appl. Phys., 2021, 129, 024102.
3. D. Schrade, R. Mueller, D. Gross, T. Utschig, V. Y. Shur and D. C. Lupascu, Mech. Mater., 2007, 39, 161–174.
4. K. Klyukin and V. Alexandrov, Phys. Rev. B, 2017, 95, 035301.
5. P. Gao, C. T. Nelson, J. R. Jokisaari, S. H. Baek, C. W. Bark, Y. Zhang, E. Wang, D. G. Schlom, C. B. Eom and X. Pan, Nat. Commun., 2011, 2, 591.
6. W. Wang, D. Zheng, M. Hu, S. Saeed, H. Liu, Y. Kong, L. Zhang and J. Xu, Materials, 2019, 12, 100.
7. Z. Xu, Y. X. Liu, M. Azadeh, H. C. Thong, Y. Jiang, F. Z. Yao, Z. X. Yue, Z. T. Zhang, Z. L. Tang, J. F. Li, H. Wang, T. Frömling and K. Wang, Angew. Chem., Int. Ed., 2023, 62, e202216776.
8. W. Liu, F. Li, M. Long, J. Zhai, C. Wang and L. Shan, J. Eur. Ceram. Soc., 2022, 42, 6295–6300.
9. X. Wu, L. Liu, X. Li, X. Zhao, D. Lin, H. Luo and Y. Huang, Mater. Chem. Phys., 2012, 132, 87–90.
10. H. Arandiyan, S. S. Mofarah, C. C. Sorrell, E. Doustkhah, B. Sajjadi, D. Hao, Y. Wang, H. Sun, B. J. Ni, M. Rezaei, Z. Shao and T. Maschmeyer, Chem. Soc. Rev., 2021, 50, 10116–10211.
11. A. Chen, W. F. Chen, T. Majidi, B. Pudadera, A. Atanacio, M. Manohar, L. R. Sheppard, R. Liu, C. C. Sorrell and P. Koshy, Int. J. Hydrogen Energy, 2021, 46, 12961–12980.
12. W. F. Chen, H. Chen, P. Koshy, A. Nakaruk and C. C. Sorrell, Mater. Chem. Phys., 2018, 205, 334–346.
13. W. F. Chen, P. Koshy, Y. Huang, E. Adabifiroozjaei, Y. Yao and C. C. Sorrell, Int. J. Hydrogen Energy, 2016, 41, 19025–19056.
14. W. F. Chen, H. Chen, G. Bahmanrokh, P. Koshy, A. Nakaruk and C. C. Sorrell, Int. J. Hydrogen Energy, 2020, 45, 24558–24566.
15. X. Zhang, W. F. Chen, G. Bahmanrokh, V. Kumar, N. Ho, P. Koshy and C. C. Sorrell, Nano-Struct. Nano-Objects, 2020, 24, 100557.
16. F. A. Kröger and H. J. Vink, Solid State Phys., 1956, 3, 307–435.
17. A. Alasmari, P. Thakur, R. Sharma, T. B. Drye and S. R. Saha, Jpn. J. Appl. Phys., 1995, 34, 5683–5688.
18. D.-C. Kong, Q.-Y. Zhu, D.-H. Guan, X.-X. Wang, Y.-L. Liu, H.-F. Wang and J.-J. Xu, Angew. Chem., Int. Ed., 2024, 64, e202418174.
19. M. Arora, S. Kaur, S. Kumar, K. M. Batoo, S. Hussain, A. Sharma, V. Arora, I. Sharma, M. Singh and A. Singh, Ceram. Int., 2024, 50, 10117–10130.
20. F. Craciun, F. Cordero, M. Cernea, V. Fruth, I. Atkinson, N. Stanica, B. S. Vasile, R. Trusca, A. Iuga, P. Galizia and C. Galassi, Ceram. Int., 2019, 45, 9390–9396.
21. M. K. Bhattarai, S. Shweta, S. Choudhary, H. M. Meyer, B. P. Thapaliya, B. R. Weiner, R. S. Katiyar and G. Morell, ACS Omega, 2024, 9, 19219–19226.
22. A. Joshi, S. Bandyopadhyay, A. Gupta, R. K. Srivastava and B. Nandan, J. Alloys Compd., 2023, 948, 169769.
23. M. T. Demirkan and M. Dogrusoz, Discov. Electrochem., 2025, 2, 1–12.
24. Y. Zhang, M. Xie, J. Roscow, Y. Bao, K. Zhou, D. Zhang and C. R. Bowen, J. Mater. Chem. A, 2017, 5, 6569–6580.
25. D. Fu, S. Sogen and H. Suzuki, ACS Appl. Electron. Mater., 2024, 6, 6384–6390.
26. P. Liu, M. Y. Li, Q. Zhang, W. Li, Y. Zhang, M. Shen, S. Qiu, G. Zhang and S. Jiang, J. Eur. Ceram. Soc., 2018, 38, 5396–5401.
27. S. H. Park, S. Ural, C. W. Ahn, S. Nahm and K. Uchino, Jpn. J. Appl. Phys., Part 1 Regul. Pap. Short Notes Rev. Pap., 2006, 45, 2667–2673.
28. S. K. Pradhan, S. N. Das, S. Bhuyan and R. N. P. Choudhary, Mater. Today Proc., 2019, 41, 312–315.
29. K. Ran Han, J. Wung Jeong, C. S. Kim and Y. S. Kwon, Mater. Lett., 2006, 60, 3596–3600.
30. S. Kwon, E. M. Sabolsky and G. L. Messing, J. Am. Ceram. Soc., 2001, 84, 648–650.
31. M. Algueró, C. Alemany, L. Pardo and M. Pham-Thi, J. Am. Ceram. Soc., 2005, 88, 2780–2787.
32. J.-H. Chen and Y.-C. Liou, Ceram. Int., 2004, 30, 157–162.
33. J.-S. Park, J.-K. Lee, H.-M. Park and K. S. Hong, J. Am. Ceram. Soc., 2007, 90, 3512–3516.
34. H. Li, W. Liao, B. Sun, Y. Lu, X. He, Z. Xu, C. Huang, Z. Sun and T. Li, Ceram. Int., 2023, 49, 8325–8330.
35. D. Kobor, L. Lebrun, G. Sébald and D. Guyomar, J. Cryst. Growth, 2005, 275, 580–588.
36. B. Fang, R. Sun, Y. Shan, K. Tezuka and H. Imoto, J. Phys. Chem. Solids, 2009, 70, 893–899.
37. T. R. Shrout and S. J. Zhang, J. Electroceram., 2007, 19, 113–126.
38. C. C. Tsai, W. H. Chao, S. Y. Chu, C. S. Hong, C. M. Weng and H. H. Su, AIP Adv., 2016, 6, 125024.
39. G. Shirane and A. T. Tokyo, J. Phys. Soc. Jpn., 1952, 7, 5–11.
40. E. Sawaguchi, J. Phys. Soc. Jpn., 1953, 8, 615–629.
41. N. H. Yusoff, R. A. M. Osman, M. S. Idris, K. N. D. K. Muhsen and N. I. M. Nor, AIP Conf. Proc., 2020, 2203, 020038.
42. P. Gwizd, D. Sitko, I. Jankowska-sumara, D. Sitko, I. Jankowska-Sumara and M. Krupska-Klimczak, Phase Trans., 2021, 94, 192–198.
43. Y. Zhang, M. Cao, Z. Yao, Z. Wang, Z. Song and A. Ullah, Mater. Res. Bull., 2015, 67, 70–76.
44. T. Zhang, W. Li, W. Cao, Y. Hou, Y. Yu and W. Fei, Appl. Phys. Lett., 2016, 108, 162902.
45. G. Sebald, L. Seveyrat, D. Guyomar, L. Lebrun, B. Guiffard and S. Pruvost, J. Appl. Phys., 2006, 100, 124112.
46. J. Hagberg, A. Uusimäki and H. Jantunen, Appl. Phys. Lett., 2008, 92, 132909.
47. Y. Zhang, J. Glaum, C. Groh, M. C. Ehmke, J. E. Blendell, K. J. Bowman and M. J. Hoffman, J. Am. Ceram. Soc., 2014, 97, 2885–2891.
48. V. Bijalwan, P. Tofel, J. Erhart and K. Maca, Ceram. Int., 2019, 45, 317–326.
49. S. Mahajan, O. P. Thakur, D. K. Bhattacharya and K. Sreenivas, Mater. Chem. Phys., 2008, 112, 858–862.
50. D. Zhan, Q. Xu, D. P. Huang, H. X. Liu, W. Chen and F. Zhang, J. Phys. Chem. Solids, 2018, 114, 220–227.
51. A. D. Loreto, A. Frattini and M. G. Stachiotti, Mater. Lett., 2017, 191, 69–72.
52. W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Eur. Ceram. Soc., 2012, 32, 517–520.
53. Chitra, R. Laishram, S. Rajput and K. C. Singh, J. Alloys Compd., 2020, 812, 152128.
54. M. Chen, Z. Xu, R. Chu, Y. Liu, L. Shao, W. Li, S. Gong and G. Li, Mater. Lett., 2013, 97, 86–89.
55. L. Qifeng, M. Jingjun, M. Sharma and R. Vaish, J. Am. Ceram. Soc., 2019, 102, 5807–5817.
56. L. F. Zhu, B. P. Zhang, X. K. Zhao, L. Zhao, P. F. Zhou and J. F. Li, J. Am. Ceram. Soc., 2013, 96, 241–245.
57. Z. Liu, R. Yuan, D. Xue, W. Cao and T. Lookman, Acta Mater., 2018, 157, 155–164.
58. S. Patel, P. Sharma and R. Vaish, Phase Transitions, 2016, 89, 1062–1073.
59. S. Venkateshwarlu, L. K. Venkataraman, V. Segouin, F. P. Marlton, H. C. Hin, D. Chernyshov, Y. Ren, M. R. V. Jørgensen, S. Nayak, J. Rödel, L. Daniel and A. Pramanick, Commun. Phys., 2020, 3, 1–14.
60. X. Wang and J. Liu, J. Ceram. Soc. Jpn., 2020, 128, 1013–1017.
61. S. Merselmiz, Z. Hanani, U. Prah, D. Mezzane, L. Hajji, Z. Abkhar, M. Spreitzer, D. Vengust, H. Uršič, D. Fabijan, A. G. Razumnaya, O. Shapovalova, I. A. Luk’yanchuk and Z. Kutnjak, Phys. Chem. Chem. Phys., 2022, 24, 6026–6036.
62. S. Belkhadir, A. Neqali, M. Amjoud, D. Mezzane, A. Alimoussa, E. Choukri, Y. Gagou, I. Raevski, M. El Marssi, I. A. Luk’yanchuk, B. Rožič and Z. Kutnjak, J. Mater. Sci.: Mater. Electron., 2019, 30, 14099–14111.
63. S. Belkhadir, S. Khardazi, D. Mezzane, M. Amjoud, O. Shapovalova, V. Laguta, I. Raevski, K. Pushkarova, I. Lukyanchuk and M. El Marssi, Mater. Today Proc., 2022, 51, 2005–2014.
64. S. Khobragade, J. K. Devanuri and S. Patel, Phase Transitions, 2019, 92, 960–973.
65. B. G. Baraskar, P. S. Kadhane, T. C. Darvade, A. R. James and R. C. Kambale, Ferroelectr. Their Appl., IntechOpen, London, 2018, pp. 113–132.
66. K. N. D. K. Muhsen, R. A. M. Osman, M. S. Idris, N. I. M. Nadzri and M. H. H. Jumali, Ceram. Int., 2021, 47, 13107–13117.
67. Y. You and X. Guo, J. Alloys Compd., 2022, 918, 165557.
68. S. Khardazi, H. Zaitouni, A. Neqali, S. Lyubchyk, D. Mezzane, M. Amjoud, E. Choukri and Z. Kutnjak, J. Phys. Chem. Solids, 2023, 177, 111302.
69. H. Kaddoussi, A. Lahmar, Y. Gagou, J. L. Dellis, H. Khemakhem and M. El Marssi, Ceram. Int., 2015, 41, 15103–15110.
70. A. Pramanick, L. Daniel, S. Venkateshwarlu, V. Segouin and Y. Ren, J. Eur. Ceram. Soc., 2023, 43, 3236–3249.
71. X. Liu, Z. Chen, B. Fang, J. Ding, X. Zhao, H. Xu and H. Luo, J. Alloys Compd., 2015, 640, 128–133.
72. X. Wang, J. Liu, P. Liang and Z. Yang, J. Electron. Mater., 2018, 47, 6121–6127.
73. S. Patel and M. Kumar, EPJ Appl. Phys., 2020, 91, 20905.
74. S. Zhou, Q. Liu, P. Xu, L. Yao and E. Cai, Ferroelectrics, 2017, 510, 27–33.
75. K. N. D. K. Muhsen, R. A. M. Osman, M. S. Idris, M. H. H. Jumali and N. H. B. Jamil, J. Mater. Sci.: Mater. Electron., 2019, 30, 20654–20664.
76. P. Suresh, P. Mathiyalagan and K. S. Srikanth, Trans. Nonferrous Met. Soc. China, 2019, 29, 791–798.
77. H. Wang and J. Wu, J. Alloys Compd., 2014, 615, 969–974.
78. M. S. Yoon and S. C. Ur, Ceram. Int., 2008, 34, 1941–1948.
79. E. Cai, Q. Liu, F. Zeng, Y. Wang and A. Xue, Ceram. Int., 2018, 44, 788–798.
80. J. Wu, A. Habibul, X. Cheng, X. Wang and B. Zhang, Mater. Res. Bull., 2013, 48, 4411–4414.
81. S. Khobragade and S. Patel, J. Electron. Mater., 2020, 49, 1194–1203.
82. S. Khardazi, H. Zaitouni, A. Neqali, S. Lyubchyk, D. Mezzane, M. Amjoud, E. Choukri and Z. Kutnjak, J. Phys. Chem. Solids, 2023, 177, 111302.
83. R. Li, Y. Luo, L. Yao, L. Tian, Z. Sun, R. Wang and J. Xue, Appl. Phys. Lett., 2025, 126, 140501.
84. M. P. Hautzinger, W. Mihalyi-Koch and S. Jin, Chem. Mater., 2024, 36, 10408–10420.
85. S. Jin, ACS Energy Lett., 2021, 6, 3386–3389.
86. Z. Guo, J. Wang and W. J. Yin, Energy Environ. Sci., 2022, 15, 660–671.
87. A. C. Ferreira, A. Létoublon, S. Paofai, S. Raymond, C. Ecolivet, B. Rufflé, S. Cordier, C. Katan, M. I. Saidaminov, A. A. Zhumekenov, O. M. Bakr, J. Even and P. Bourges, Phys. Rev. Lett., 2018, 121, 085502.
88. M. Gao, Y. Zhang, Z. Lin, J. Jin, M. C. Folgueras and P. Yang, Matter, 2021, 4, 3874–3896.
89. M. Wuttig, C. F. Schön, M. Schumacher, J. Robertson, P. Golub, E. Bousquet, C. Gatti and J. Y. Raty, Adv. Funct. Mater., 2021, 32, 2110166.
90. X. Liang, J. Klarbring, W. J. Baldwin, Z. Li, G. Csányi and A. Walsh, J. Phys. Chem. C, 2023, 127, 19141–19151.
91. M. A. Peña and J. L. G. Fierro, Chem. Rev., 2001, 101, 1981–2018.
92. M. I. Khan, S. Hussain, M. Atif, J. E. Leal-Perez, B. A. García-Grajeda and J. M. Mendivil-Escalante, Results Chem., 2025, 13, 101974.
93. F. Zheng, W. Chen, T. Bu, K. P. Ghiggino, F. Huang, Y. Cheng, P. Tapping, T. W. Kee, B. Jia and X. Wen, Adv. Energy Mater., 2019, 9, 1901016.
94. T. Cai, J. Wang, W. Li, K. Hills-Kimball, H. Yang, Y. Nagaoka, Y. Yuan, R. Zia and O. Chen, Adv. Sci., 2020, 7, 2001317.
95. X. Wang, Q. Shen, Y. Chen, N. Ali, Z. Ren, G. Bi and H. Wu, J. Alloys Compd., 2022, 895, 162610.
96. S. Tian, X. Zhou, C. Bi, X. Sun, M. Zhang, S. Yang and J. Tian, Adv. Opt. Mater., 2022, 10, 2200751.
97. Z. Zhang, J. Shang, H. Ge, Y. Zhang, Q. Chen, L. Zhou, W. Zhu, D. Chen, H. Xi, J. Zhang, C. Zhang and Y. Hao, Mater. Today Phys., 2023, 37, 101187.
98. A. P. Litvin, I. V. Margaryan, W. Yin, X. Zhang, W. Zheng and A. L. Rogach, Adv. Opt. Mater., 2024, 12, 2301001.
99. J. Gong, M. Yang, D. Rebollar, J. Rucinski, Z. Liveris, K. Zhu and T. Xu, Adv. Mater., 2018, 30, 1800973.
100. G. C. Adhikari, S. Thapa, H. Zhu and P. Zhu, Adv. Opt. Mater., 2019, 7, 1900916.
101. S. Li, Z. Shi, F. Zhang, L. Wang, Z. Ma, D. Yang, Z. Yao, D. Wu, T. T. Xu, Y. Tian, Y. Zhang, C. Shan and X. J. Li, Chem. Mater., 2019, 31, 3917–3928.
102. A. Shapiro, M. W. Heindl, F. Horani, M. H. Dahan, J. Tang, Y. Amouyal and E. Lifshitz, J. Phys. Chem. C, 2019, 123, 24979–24987.
103. N. Phung, R. Félix, D. Meggiolaro, A. Al-Ashouri, G. Sousa, E. Silva, C. Hartmann, J. Hidalgo, H. Köbler, E. Mosconi, B. Lai, R. Gunder, M. Li, K. L. Wang, Z. K. Wang, K. Nie, E. Handick, R. G. Wilks, J. A. Marquez, B. Rech, T. Unold, J. P. Correa-Baena, S. Albrecht, F. De Angelis, M. Bär and A. Abate, J. Am. Chem. Soc., 2020, 142, 2364–2374.
104. W. Wei, J. Gebhardt, D. F. Urban and C. Elsässer, Phys. Rev. B, 2024, 109, 144104.
105. D. Bai, J. Zhang, Z. Jin, H. Bian, K. Wang, H. Wang, L. Liang, Q. Wang and S. F. Liu, ACS Energy Lett., 2018, 3, 970–978.
106. J. Cao, S. X. Tao, P. A. Bobbert, C. P. Wong and N. Zhao, Adv. Mater., 2018, 30, 1707350.
107. F. Zhang, X. Sun, H. Xie, X. Cai, B. Zheng, H. Yu, E. Liu, X. Hao and M. Zhang, Chem. Mater., 2022, 34, 1010–1019.
108. P. Zhao, W. Yin, M. Kim, M. Han, Y. J. Song, T. K. Ahn and H. S. Jung, J. Mater. Chem. A, 2017, 5, 7905–7911.
109. C. Zhou, T. Zhang, C. Zhang, X. Liu, J. Wang, J. Lin and X. Chen, Adv. Sci., 2022, 9, 2103491.
110. Z. Fang, H. He, L. Gan, J. Li and Z. Ye, Adv. Sci., 2018, 5, 1800736.
111. Z. Guo, S. Zhao, A. Liu, Y. Kamata, S. Teo, S. Yang, Z. Xu, S. Hayase and T. Ma, ACS Appl. Mater. Interfaces, 2019, 11, 19994–20003.
112. H. Sun, J. Zhang, X. Gan, L. Yu, H. Yuan, M. Shang, C. Lu, D. Hou, Z. Hu, Y. Zhu and L. Han, Adv. Energy Mater., 2019, 9, 1900896.
113. A. Boonchun, M. F. Smith, B. Cherdhirunkorn and S. Limpijumnong, J. Appl. Phys., 2007, 101, 043521.
114. J. E. Jaffe, R. M. Van Ginhoven and W. Jiang, Comput. Mater. Sci., 2012, 53, 153–157.
115. A. Moutaouaffiq, M. Belhajji, A. Didi Seddik, A. Tahiri, E. Ali, L. Hajji, A. Rjeb, P. Paramasivam, S. S. M. Ghoneim and A. B. A. Sharaf, Results Eng., 2025, 25, 104466.
116. D. He, Z. Wang, S. Ma, L. Yang, L. Tong, X. Zhou and T. Fan, J. Eur. Ceram. Soc., 2024, 44, 3824–3832.
117. P. J. Jumana, T. Karthik and V. Kumar, J. Alloys Compd., 2025, 1014, 178642.
118. V. S. Vinita, S. S. J. Dhas, S. Suresh, S. C. Jeyakumar, S. Srinivasan and C. S. Biju, J. Magn. Magn. Mater., 2023, 565, 170251.
119. G. Y. Lee, G.-G. Lee, Y. S. Lim and S.-H. Yoon, Ceram. Int., 2025, 51, 11627–11633.
120. N. Tanwar, S. Upadhyay, R. Priya, S. Pundir, P. Sharma and O. P. Pandey, J. Solid State Chem., 2023, 317, 123674.
121. X. Chen, X. Ruan, K. Zhao, X. He, J. Zeng, Y. Li, L. Zheng, C. H. Park and G. Li, J. Alloys Compd., 2015, 632, 103–109.
122. K. Xu, P. Yang, W. Peng and L. Li, J. Alloys Compd., 2020, 829, 154516.
123. S. Saparjya, T. Badapanda, S. Behera, B. Behera and P. R. Das, Phase Transitions, 2020, 93, 245–262.
124. J. Gao, Q. Li, H. Liu, J. Shim, Q. Yan, Y. Zhang and X. Chu, Ceram. Int., 2015, 41, 2497–2501.
125. W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Am. Ceram. Soc., 2011, 94, 3181–3183.
126. W. Li, Z. Xu, R. Chu, P. Fu and P. An, Ceram. Int., 2012, 38, 4353–4355.
127. W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Alloys Compd., 2014, 583, 305–308.
128. Q. Li, Q. Zhang, W. Cai, C. Zhou, R. Gao, G. Chen, X. Deng, Z. Wang and C. Fu, Mater. Chem. Phys., 2020, 252, 123242.
129. F. Guo, W. Cai, R. Gao, C. Fu, G. Chen, X. Deng, Z. Wang and Q. Zhang, J. Electron. Mater., 2019, 48, 3239–3247.
130. Y. Yang, J. Guo, W. Ma, H. Zhao, M. Ma, J. Wu and M. Chi, J. Mater. Sci.: Mater. Electron., 2019, 30, 2854–2863.
131. P. Parjansri, U. Intatha and S. Eitssayeam, Mater. Res. Bull., 2015, 65, 61–67.
132. D. Zhang, Y. Zhang and S. Yang, J. Mater. Sci.: Mater. Electron., 2015, 26, 909–915.
133. R. Verma, A. Chauhan, K. M. Batoo, R. Kumar, M. Hadi and E. H. Raslan, Ceram. Int., 2021, 47, 15442–15457.
134. X. Xia, X. Jiang, C. Chen, X. Jiang, N. Tu and Y. Chen, Front. Mater. Sci., 2016, 10, 203–210.
135. P. Parjansri and S. Eitssayeam, Ferroelectrics, 2018, 534, 63–70.
136. M. Gao, W. Ge, X. Li, H. Yuan, C. Liu, H. Zhao, Y. Ma and Y. Chang, Phys. Status Solidi A, 2020, 217, 12000253.
137. Y. Tian, S. Li, Y. Gong, Y. Yu, Y. Tang, P. Liu and Q. Jing, Mater. Chem. Phys., 2018, 204, 163–170.
138. Y. Zhang, H. Deng, S. Si, T. Wang, D. Zheng, P. Yang and J. Chu, J. Am. Ceram. Soc., 2020, 103, 2491–2498.
139. Y. Zhang, H. Sun and W. Chen, J. Electron. Mater., 2016, 45, 5006–5016.
140. Z. Zhao, X. Li, H. Ji, Y. Dai and T. Li, J. Alloys Compd., 2015, 637, 291–296.
141. S. H. Shin, J. D. Han and J. Yoo, Mater. Lett., 2015, 154, 120–123.
142. U. Intatha, P. Parjansri, K. Pengpat, G. Rujijanagul, T. Tunkasiri and S. Eitssayeam, Integr. Ferroelectr., 2012, 139, 83–91.
143. J. Ma, X. Liu and W. Li, J. Alloys Compd., 2013, 581, 642–645.
144. W. Li, J. Hao, W. Bai, Z. Xu, R. Chu and J. Zhai, J. Alloys Compd., 2012, 531, 46–49.
145. W. Liu and S. Li, IEEE Trans. Dielectr. Electr. Insul., 2015, 22, 734–738.
146. F. Zeng, Q. Liu, S. Peng, Y. Wang, E. Cai, A. Xue and S. Zhou, Ceram. Int., 2019, 45, 1416–1419.
147. J. Ma, X. Liu, M. Jiang, H. Yang, G. Chen, X. Liu, L. Qin and C. Luo, J. Mater. Sci.: Mater. Electron., 2014, 25, 992–996.
148. R. Hayati, M. A. Bahrevar, T. Ebadzadeh, V. Rojas, N. Novak and J. Koruza, J. Eur. Ceram. Soc., 2016, 36, 3391–3400.
149. Y. Tian, L. Wei, X. Chao, Z. Liu and Z. Yang, J. Am. Ceram. Soc., 2013, 96, 496–502.
150. S. Patel, A. Chauhan and R. Vaish, Appl. Mater. Today, 2015, 1, 37–44.
151. J. Shi, X. Lu, J. Shao, B. Fang, S. Zhang, Q. Du, J. Ding, X. Zhao and H. Luo, Ferroelectrics, 2017, 507, 186–197.
152. R. Hayati, M. A. Bahrevar, Y. Ganjkhanlou, V. Rojas and J. Koruza, J. Adv. Ceram., 2019, 8, 186–195.
153. C. Han, J. Wu, C. Pu, S. Qiao, B. Wu, J. Zhu and D. Xiao, Ceram. Int., 2012, 38, 6359–6363.
154. P. Yong, D. Shihua, S. Tianxiu, Z. Qian and Z. Zuowei, Ferroelectrics, 2014, 463, 83–89.
155. Q. Li, W. Ma, J. Ma, X. Meng and B. Niu, Mater. Technol., 2016, 31, 18–23.
156. Y. Tian, S. Li, S. Sun, Y. Gong, T. Li, Y. Yu and Q. Jing, J. Electron. Mater., 2018, 47, 684–691.
157. D. Xue, Y. Zhou, H. Bao, J. Gao, C. Zhou and X. Ren, Appl. Phys. Lett., 2011, 99, 122901.
158. M. Chen, Z. Xu, R. Chu, H. Qiu, M. Li, Y. Liu, L. Shao, S. Ma, W. Ji, W. Li, S. Gong and G. Li, Phys. B: Condens. Matter, 2014, 433, 43–47.
159. W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Eur. Ceram. Soc., 2012, 32, 517–520.
160. D. Lin, K. W. Kwok and H. L. W. Chan, Ceram. Int., 2014, 40, 6841–6846.
161. L. Zhao, B.-P. Zhang, P.-F. Zhou, L.-F. Zhu and N. Wang, Ceram. Int., 2016, 42, 1086–1093.
162. Z.-H. Chen, Z.-W. Li, J.-N. Ding, T.-X. Zhao, J.-H. Qiu, K.-Q. Zhu, J.-J. Xu and B. Zhang, J. Electron. Mater., 2018, 47, 3409–3413.
163. J. Gao, D. Xue, W. Liu, C. Zhou and X. Ren, Actuators, 2017, 6, 1–20.
164. W. Shin, S. Kim, E. Kim, D. Kim, S. U. Oh, J. A. Lee, Y. W. Heo, J. H. Lee and S. Nahm, J. Korean Ceram. Soc., 2024, 61, 316–326.
165. X. Zhang, Y. Zhang, Q. Yin, H. Zhang, F. Lin, K. Hu, F. Si, Z. Du, C. Chen, Y. Peng and F. Shi, J. Electron. Mater., 2025, 54, 3260–3268.
166. T. Wang, M. Jiang, L. Li, S. Cheng, H. Lu, P. Ren, Y. Zhao and G. Rao, J. Alloys Compd., 2023, 935, 168126.
167. H. Zubairi, F. Hussain, S. Sheikh, A. A. Shaikh, D. Wang and I. M. Reaney, Mater. Sci. Eng., B, 2023, 296, 116632.
168. C. Liu, Z. Dai, Y. Zheng, X. Li, M. N. Rafiq, S. Tsukada, Y. Cong, T. Karaki and S. Zhou, J. Power Sources, 2025, 640, 236759.
169. Y. Xu, M. Jiang, Y. Zeng, Y. Ouyang, S. Cao, J. Song and G. Rao, Mater. Today Commun., 2025, 42, 111472.
170. X. Gao, H. Sun, H. Hao, C. Wang, Q. Shen and L. Zhang, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2023, 38, 261–266.
171. C. Kaushiga, S. Sakhuja, R. Devasaia, J. Kaarthik, G. Sradha, S. G. Reddy and V. Annapureddy, Appl. Phys. A: Mater. Sci. Process., 2025, 131, 1–13.
172. W. Wu, D. Xiao, J. Wu, W. Liang, J. Li and J. Zhu, J. Alloys Compd., 2011, 509, L 284–L 288.
173. X. Jiang, Y. Chen, J. Wang, N. Tu and C. Chen, Ferroelectrics, 2010, 401, 72–78.
174. W. Liang, Z. Wang, D. Xiao, J. Wu, W. Wu, T. Huang and J. Zhu, Integr. Ferroelectr., 2012, 139, 63–74.
175. A. Kan, R. Onishi, S. Ohashi and H. Ogawa, J. Mater. Chem. C, 2022, 10, 6444–6455.
176. S. Sahoo, D. K. Pradhan, S. Kumari, A. Sahu, K. S. Samantaray, C. Singh, A. Mishra, M. M. Rahaman, A. Kumar, R. Thomas, P. D. Rack and D. K. Pradhan, J. Appl. Phys., 2024, 135, 244101.
177. M. Dubernet, M. J. Pitcher, M. Zaghrioui, M. Bah, J. Bustillo, F. Giovannelli and I. Monot-Laffez, J. Eur. Ceram. Soc., 2022, 42, 2188–2194.
178. J. Suchanicz, M. Wąs, M. Nowakowska-Malczyk, P. Jelen, K. Konieczny, P. Czaja, K. Kluczewska-Chmielarz, D. Sitko, T. V. Kruzina and M. Sokolowski, Phase Transitions, 2020, 93, 877–882.
179. F. M. Volpi, T. J. Castro, A. Franco, S. O. Lira, P. C. Morais and S. W. da Silva, J. Alloys Compd., 2024, 1005, 175963.
180. M. Aggarwal, R. Goel, G. Sharma, A. K. Singh, S. Dhiman and S. Kumar, Mater. Chem. Phys., 2023, 310, 128503.
181. N. Rhimi, N. Dhahri, J. Laifi, F. Bourguiba, N. Abdelmoula, J. Dhahri, C. Castro and J. Juraszek, J. Mol. Struct., 2023, 1294, 136319.
182. S. Lenka, T. Badapanda, P. Nayak, S. Sarangi, S. Anwar and S. N. Tripathy, J. Mol. Struct., 2023, 1274, 134413.
183. L. Dong, D. S. Stone and R. S. Lakes, J. Appl. Phys., 2011, 109, 063531.
184. J. A. Astudillo, S. A. Dionizio, J. L. Izquierdo, O. Morán, J. Heiras and G. Bolaños, AIP Adv., 2018, 8, 055817.
185. P. Naik, S. K. Patri and J. Nanda, J. Alloys Compd., 2025, 1010, 177601.
186. Y. Wang, L. Wang, Y. Zhao and D. Yan, Ceram. Int., 2016, 42, 17911–17915.
187. S. Raja, R. Ramesh Babu, K. Ramamurthi and K. Sethuraman, Mater. Chem. Phys., 2018, 213, 130–139.
188. X. Wang, C. Wang, X. Yao, Y. Zhou, N. Liang, Q. Jin, K. Chen, M. He, E. Guo, C. Ge, G. Yang and K. Jin, ACS Appl. Electron. Mater., 2023, 5, 1234–1242.
189. L. Liao, Q. Yang, C. Cai, Y. Zhou, H. Sun, X. Huang, P. Chen, J. Wang, X. Li, X. Tian, S. Meng, X. Bai and L. Wang, Acta Mater., 2024, 273, 119986.
190. S. S. Brahma, J. Nanda, B. Munisha, S. Parida and S. R. Mohapatra, J. Magn. Magn. Mater., 2023, 587, 171268.
191. G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361.
192. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
193. N. V. Y. Scarlett and I. C. Madsen, Powder Diffr., 2006, 21, 278–284.
194. E. Vega, M. Mollar and B. Marí, Energy Technol., 2020, 8, 1900743.
195. L. Atourki, E. Vega, M. Mollar, B. Marí, H. Kirou, K. Bouabid and A. Ihlal, J. Alloys Compd., 2017, 702, 404–409.
196. T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641.
197. S. Waitschat, M. T. Wharmby and N. Stock, Dalton Trans., 2015, 44, 11235–11240.
198. B. K. Heep, K. S. Weldert, Y. Krysiak, T. W. Day, W. G. Zeier, U. Kolb, G. J. Snyder and W. Tremel, Chem. Mater., 2017, 29, 4833–4839.
199. J. Euvrard, X. Wang, T. Li, Y. Yan and D. B. Mitzi, J. Mater. Chem. A, 2020, 8, 4049–4054.
200. S. Pang, Y. Zhou, Z. Wang, M. Yang, A. R. Krause, Z. Zhou, K. Zhu, N. P. Padture and G. Cui, J. Am. Chem. Soc., 2016, 138, 750–753.
201. S. A. Dalrymple and G. K. H. Shimizu, J. Am. Chem. Soc., 2007, 129, 12114–12116.
202. Y. X. Ma, Z. J. Li, L. Wei, S. Y. Ding, Y. B. Zhang and W. Wang, J. Am. Chem. Soc., 2017, 139, 4995–4998.
203. S. A. Hayward and E. K. H. Salje, J. Phys.: Condens. Matter, 2002, 14, L599–L604.
204. J. Íñiguez and D. Vanderbilt, Phys. Rev. Lett., 2002, 89, 115503.
205. T. Ishidate, S. Abe, H. Takahashi and N. Môri, Phys. Rev. Lett., 1997, 78, 2397–2400.
206. V. Bijalwan, P. Tofel and V. Holcman, J. Asian Ceram. Soc., 2018, 6, 384–393.
207. S. M. Mane, P. M. Tirmali, S. L. Kadam, D. J. Salunkhe, C. B. Kolekar and S. B. Kulkarni, Adv. Appl. Ceram., 2017, 116, 325–332.
208. M. B. Abdessalem, A. Aydi and N. Abdelmoula, J. Alloys Compd., 2019, 774, 685–693.
209. V. S. Puli, D. K. Pradhan, W. Pérez and R. S. Katiyar, J. Phys. Chem. Solids, 2013, 74, 466–475.
210. V. Buscaglia, S. Tripathi, V. Petkov, M. Dapiaggi, M. Deluca, A. Gajović and Y. Ren, J. Phys.: Condens. Matter, 2014, 26, 065901.
211. V. K. Veerapandiyan, S. Khosravi H, G. Canu, A. Feteira, V. Buscaglia, K. Reichmann and M. Deluca, J. Eur. Ceram. Soc., 2020, 40, 4684–4688.
212. S. Adireddy, C. Lin, B. Cao, W. Zhou and G. Caruntu, Chem. Mater., 2010, 22, 1946–1948.
213. J. Pokorńy, U. M. Pasha, L. Ben, O. P. Thakur, D. C. Sinclair and I. M. Reaney, J. Appl. Phys., 2011, 109, 114110.
214. S. Fuentes, F. Céspedes, P. Muñoz, E. Chávez and L. Padilla-Campos, J. Chil. Chem. Soc., 2013, 58, 2077–2081.
215. A. Slodczyk and P. Colomban, Materials, 2010, 3, 5007–5028.
216. D. Schütz, M. Deluca, W. Krauss, A. Feteira, T. Jackson and K. Reichmann, Adv. Funct. Mater., 2012, 22, 2285–2294.
217. H. Harima, J. Phys.: Condens. Matter, 2002, 14, R967–R993.
218. L. Mañosa, A. Planes and M. Acet, J. Mater. Chem. A, 2013, 1, 4925–4936.
219. J. Peräntie, J. Hagberg, A. Uusimäki and H. Jantunen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134119.
220. E. H. Birks, Phys. Status Solidi A, 1986, 94, 523–527.
221. B. Rožič, B. Malič, H. Uršič, J. Holc, M. Kosec, Z. Kutnjak, B. Malič, H. Uršič, J. Holc, M. Kosec and Z. Kutnjak, Ferroelectrics, 2011, 421, 103–107.
222. D. Q. Xiao, Y. C. Wang, R. L. Zhang, S. Q. Peng, J. G. Zhu and B. Yang, Mater. Chem. Phys., 1998, 57, 182–185.
223. J. Peräntie, H. N. Tailor, J. Hagberg, H. Jantunen and Z.-G. Ye, J. Appl. Phys., 2013, 114, 174105.
224. A. S. Mischenko, Q. Zhang, R. W. Whatmore, J. F. Scott and N. D. Mathur, Appl. Phys. Lett., 2006, 89, 242912.
225. M. Valant, Prog. Mater. Sci., 2012, 57, 980–1009.
226. S. G. Lu and Q. Zhang, Adv. Mater., 2009, 21, 1983–1987.
227. Y. Jiang, C. Y. Toe, S. S. Mofarah, C. Cazorla, S. L. Y. Chang, Y. Yin, Q. Zhang, S. Lim, Y. Yao, R. Tian, Y. Wang, T. Zaman, H. Arandiyan, G. G. Andersson, J. Scott, P. Koshy, D. Wang and C. C. Sorrell, ACS Sustainable Chem. Eng., 2023, 11, 3370–3389.
228. G. Schmidt, H. Arndt, G. Borchhardt, J. von Cieminski, T. Petzsche, K. Borman, A. Sternberg, A. Zirnite and V. A. Isupov, Phys. Status Solidi A, 1981, 63, 501–510.
229. B. A. Tuttle, P. Yang, J. H. Gieske, J. A. Voigt, T. W. Scofield, D. H. Zeuch and W. R. Olson, J. Am. Ceram. Soc., 2001, 84, 1260–1264.
230. F. Chen, Y. H. Li, G. Y. Gao, F. Z. Yao, K. Wang, J. F. Li, X. L. Li, X. Y. Gao and W. Wu, J. Am. Ceram. Soc., 2015, 98, 1372–1376.
231. L. M. Riemer, K. V. Lalitha, X. Jiang, N. Liu, C. Dietz, R. W. Stark, P. B. Groszewicz, G. Buntkowsky, J. Chen, S. T. Zhang, J. Rödel and J. Koruza, Acta Mater., 2017, 136, 271–280.
232. X. Zheng, S. S. Mofarah, C. Cazorla, R. Daiyan, A. A. Esmailpour, J. Scott, Y. Yao, S. Lim, V. Wong, E. Y. Chen, H. Arandiyan, P. Koshy and C. C. Sorrell, Adv. Funct. Mater., 2021, 31, 2103171.
233. J. Wang, E. Gürdal, A. Horneber, S. Dickreuter, S. Kostcheev, A. J. Meixner, M. Fleischer, P. M. Adam and D. Zhang, Nanoscale, 2018, 10, 8240–8245.
234. Y. Jiang, C. Y. Toe, S. S. Mofarah, C. Cazorla, S. L. Y. Chang, Y. Yin, Q. Zhang, S. Lim, Y. Yao, R. Tian, Y. Wang, T. Zaman, H. Arandiyan, G. G. Andersson, J. Scott, P. Koshy, D. Wang and C. C. Sorrell, ACS Sustainable Chem. Eng., 2023, 11, 3370–3389.
235. W. M. Haynes, CRC Handbook of Chemistry and Physics, Taylor & Francis Inc, Boca Raton, 2014, p. 2704.
236. J. He, B. Baldassarri and C. Wolverton, Phys. Rev. B, 2023, 108, 104103.
237. Y. Kumagai, N. Tsunoda, A. Takahashi and F. Oba, Phys. Rev. Mater., 2021, 5, 123803.
238. M. E. Straumanis and S. Zyszczynski, J. Appl. Crystallogr., 1970, 3, 1–6.
239. M. E. Straumanis, T. Ejima and W. J. James, Acta Crystallogr., 1961, 14, 493–497.
240. J. E. Garcia, V. Gomis, R. Perez, A. Albareda and J. A. Eiras, Appl. Phys. Lett., 2007, 91, 042902.
241. W. L. Warren, G. E. Pike, K. Vanheusden, D. Dimos, B. A. Tuttle and J. Robertson, J. Appl. Phys., 1996, 79, 9250–9257.
242. S. Takahash, Ferroelectrics, 1982, 41, 143–156.
243. R. Yimnirun, R. Wongmaneerung, S. Wongsaenmai, A. Ngamjarurojana, S. Ananta and Y. Laosiritaworn, Appl. Phys. Lett., 2007, 90, 112906.
244. R. Yimnirun, S. Wongsaenmai, R. Wongmaneerung, N. Wongdamnern, A. Ngamjarurojana, S. Ananta and Y. Laosiritaworn, Phys. Scr., 2007, 184, 184–189.
245. B. Wen, Y. Zhang, X. Liu, L. Ma and X. Wang, J. Mater. Sci., 2012, 47, 4299–4304.
246. X.-G. Tang and H. L. Chan, J. Appl. Phys., 2020, 97, 034109.
247. S. R. Reddy, V. Venkata, B. Prasad, S. Bysakh, V. Shanker, N. Hebalkar and S. K. Roy, J. Mater. Chem. C, 2019, 7, 7073–7082.
248. M. A. Ansari and K. Sreenivas, Ceram. Int., 2019, 45, 20738–20749.
249. Y. Lin, D. Li, M. Zhang, S. Zhan, Y. Yang, H. Yang and Q. Yuan, ACS Appl. Mater. Interfaces, 2019, 11, 36824–36830.
250. V. S. Puli, D. K. Pradhan, D. B. Chrisey, M. Tomozawa, G. L. Sharma, J. F. Scott and R. S. Katiyar, J. Mater. Sci., 2013, 48, 2151–2157.
251. X. Chen, X. Chao and Z. Yang, Mater. Res. Bull., 2019, 111, 259–266.
252. Z. Hanani, S. Merselmiz, M. Amjoud, D. Mezzane, M. Lahcini, J. Ghanbaja, M. Spreitzer, D. Vengust, M. E. Marssi, I. A. Luk’yanchuk, Z. Kutnjak, B. Rožič and M. Gouné, J. Mater., 2022, 8, 873–881.
253. A. B. Swain, V. Subramanian and P. Murugavel, Ceram. Int., 2018, 44, 6861–6865.
254. R. L. Nayak, Y. Zhang, S. S. Dash and M. P. K. Sahoo, Ceram. Int., 2022, 48, 10803–10816.
255. A. Lakouader, H. Mezzourh, D. Mezzane, M. Amjoud, L. Hajji, E. H. Choukri, I. A. Luk’yanchuk, Z. Kutnjak and M. E. Marssi, J. Mater. Sci.: Mater. Electron., 2022, 33, 14381–14396.
256. P. Vineetha, R. Jose, A. Vijay, P. S. Charan and K. V. Saravanan, Mater. Res. Express, 2022, 9, 066303.
257. S. T. Dang, L. L. Xue, L. F. He, Y. C. Shi, H. N. Li, Y. C. Hu, J. Shang, S. Q. Yin and X. W. Wang, J. Mater. Sci.: Mater. Electron., 2022, 33, 26100–26112.
258. A. R. Jayakrishnan, K. V. Alex, A. Thomas, J. P. B. Silva, K. Kamakshi, N. Dabra, K. C. Sekhar, J. Agostinho Moreira and M. J. M. Gomes, Ceram. Int., 2019, 45, 5808–5818.
259. F. C. Su, X. B. Guo, X. L. Lu, Z. Su, W. H. Qiu, X. G. Tang, S. F. Li and W. H. Li, Phys. B: Condens. Matter, 2023, 651, 414597.
260. T. Badapanda, S. Chaterjee, A. Mishra, R. Ranjan and S. Anwar, Phys. B: Condens. Matter, 2017, 521, 264–269.
261. W. Cai, Q. Zhang, C. Zhou, R. Gao, S. Zhang, Z. Li, R. Xu, G. Chen, X. Deng, Z. Wang and C. Fu, J. Mater. Sci.: Mater. Electron., 2020, 31, 9167–9175.
262. V. S. Puli, D. K. Pradhan, I. Coondoo, N. Panwar, S. Adireddy, S. Luo, R. S. Katiyar and D. B. Chrisey, J. Phys. D: Appl. Phys., 2019, 52, 255304.
263. D. Zhan, Q. Xu, D. P. Huang, H. X. Liu, W. Chen and F. Zhang, J. Alloys Compd., 2016, 682, 594–600.
264. A. Dahri, Y. Gagou, N. Abdelmoula, H. Khemakhem and M. E. Marssi, Ceram. Int., 2022, 48, 3157–3171.
265. X. Wang, S. Chen, Y. Liang, B. Zhang, X. Shi, R. Zhang, Y. Shi, Z. Ren, R. Liu, Y. Hu, J. Shang and S. Yin, Eur. Phys. J.: Appl. Phys., 2022, 97, 1–12.
266. E. V. Ramana, N. M. Ferreira, A. Mahajan, D. M. Tobaldi, I. Bdikin, B. Rožič, Z. Kutnjak and M. A. Valente, J. Eur. Ceram. Soc., 2021, 41, 6424–6440.
267. Q. Zhang, B. Chen, D. Wu, Z. Peng, X. Qiao, X. Chao and Z. Yang, Ceram. Int., 2020, 46, 28285–28291.
268. X. W. Wang, B. H. Zhang, Y. Y. Li, Y. C. Shi, L. Y. Sun, G. Feng, C. L. Li, Y. F. Liang, Y. P. Zheng, S. Y. Shang, J. Shang, Y. C. Hu and S. Q. Yin, J. Mater. Sci.: Mater. Electron., 2020, 31, 4732–4742.
269. S. Merselmiz, Z. Hanani, D. Mezzane, M. Spreitzer, A. Bradeško, D. Fabijan, D. Vengust, M. B. Amjoud, L. Hajji, Z. Abkhar, A. G. Razumnaya, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, Ceram. Int., 2020, 46, 23867–23876.
270. H. Mezzourh, S. Belkhadir, D. Mezzane, M. Amjoud, E. Choukri, A. Lahmar, Y. Gagou, Z. Kutnjak and M. E. Marssi, Phys. B: Condens. Matter, 2021, 603, 412760.
271. S. Merselmiz, Z. Hanani, D. Mezzane, A. G. Razumnaya, M. Amjoud, L. Hajji, S. Terenchuk, B. Rožič, I. A. Luk’yanchuk and Z. Kutnjak, RSC Adv., 2021, 11, 9459–9468.
272. Z. Hanani, D. Mezzane, M. Amjoud, A. G. Razumnaya, S. Fourcade, Y. Gagou, K. Hoummada, M. E. Marssi and M. Gouné, J. Mater. Sci.: Mater. Electron., 2019, 30, 6430–6438.
273. Z. Hanani, S. Merselmiz, D. Mezzane, M. Amjoud, A. Bradeško, B. Rožič, M. Lahcini, M. E. Marssi, A. V. Ragulya, I. A. Luk’Yanchuk, Z. Kutnjak and M. Gouné, RSC Adv., 2020, 10, 30746–30755.

---