Hierarchical morphology and interfacial dynamics in silane-free rubber nanocomposites: a SAXS-guided approach toward sustainable high-performance tire materials
Cheng-Ti
Hu
 a,
Heng-Yi
Lin
a,
Po-Hsun
Chiu
a,
Heng-Yi
Lin
a,
Po-Hsun
Chiu
 a,
Heng-Yan
Dai
a,
Lucy
Liberman
c,
Jhih-Min
Lin
d,
U-Ser
Jeng
a,
Heng-Yan
Dai
a,
Lucy
Liberman
c,
Jhih-Min
Lin
d,
U-Ser
Jeng
 d,
Cheng-Si
Tsao
*bd,
Chih-Chen
Hsieh
*a and
Chi-An
Dai
d,
Cheng-Si
Tsao
*bd,
Chih-Chen
Hsieh
*a and
Chi-An
Dai
 *a
*a
aDepartment of Chemical Engineering, National Taiwan University, Taipei 10617, Taiwan. E-mail: ccjhsieh@ntu.edu.tw; polymer@ntu.edu.tw
bDepartment of Materials Science and Engineering, National Taiwan University, Taipei 10617, Taiwan. E-mail: tsaochengsi@gmail.com
cDepartment of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 3200003, Israel
dNational Synchrotron Radiation Research Center, Hsinchu 30076, Taiwan
First published on 1st October 2025
Abstract
Developing sustainable, high-performance elastomers for tire applications has become a growing priority for the chemical industry, driven by environmental mandates and the functional demands of modern transportation. In response, additive engineering is increasingly employed to replace conventional silane coupling agents (SCAs), which raise environmental concerns and constrain optimization of the rolling resistance (RR)–wet grip (WG) trade-off. A central challenge in this domain lies in elucidating how interfacial modifiers reconfigure filler architecture and influence macroscopic properties. In this study, we introduce a novel small angle X-ray scattering (SAXS)-guided analytical framework that integrates a mass-fractal model with a gel-like network model to resolve the hierarchical three-tiered structure of poly(ethylene glycol) (PEG)-modified, silica-filled tire compounds. This hybrid model enables the quantitative extraction of cluster radius and—critically—the contribution of occluded rubber domains, a morphological feature often suggested visually but seldom structurally characterized. In contrast to a widely used SCA, which enhances filler dispersion via covalent silica–rubber linkages, PEG induces greater filler aggregation and occluded rubber formation through hydrogen bonding, while simultaneously promoting interfacial slippage under dynamic strain. These coexisting mesoscale features—quantified via SAXS and directly linked to dynamic mechanical properties—result in a 40% reduction in RR, a 14% enhancement in WG, and 81% higher stiffness relative to the SCA-modified system. This mechanistic breakthrough diverges from conventional dispersion-centric frameworks and establishes PEG as a viable SCA-free alternative. More broadly, this work demonstrates a transferable, structure-informed strategy for the design of next-generation high-performance, environmentally friendly rubber nanocomposites.
New conceptsThis work introduces a SAXS-guided hybrid framework that, for the first time, quantitatively resolves occluded rubber domains in filler-reinforced elastomers. Unlike conventional SAXS approaches that focus solely on filler hierarchy and dispersion, our approach integrates a mass-fractal structural model with a gel-like network function to simultaneously extract aggregate organization and trapped rubber content. This previously unquantified occluded rubber phase emerges as a critical morphological parameter that governs viscoelastic performance but has remained structurally elusive. Leveraging this framework, we demonstrate that poly(ethylene glycol) (PEG)—a physically adsorbed, silane-free interfacial modifier—induces both hierarchical filler aggregation and dynamic interfacial slippage through hydrogen bonding. These dual mechanisms—structural entrapment and interfacial mobility—cooperatively reshape the filler–rubber network. As a result, PEG-modified systems achieve a combination of 40% reduction in rolling resistance, 14% enhancement in wet grip, and 81% higher stiffness compared to TESPT-based composites. This study establishes occluded rubber as a tunable structural parameter directly linked to viscoelastic performance, and highlights multiscale interfacial control as a new strategy for elastomer design. The framework offers practical guidance for developing silane-free, high-performance tire materials. |
1. Introduction
In recent years, the development of automobiles has increasingly prioritized energy efficiency to support environmentally friendly operation without compromising vehicle stability or performance. Among various approaches, the enhancement of rubber tread materials—especially for the development of “green tires”—has gained significant attention in the chemical industry, particularly in light of the rapid expansion of the electric vehicle (EV) market.1–3 Within tire design, critical performance metrics such as rolling resistance (RR), wet grip (WG), and abrasion loss—collectively referred to as the “magic triangle”—serve as key benchmarks for optimizing tread compound formulations.4–6 These properties are largely influenced by the reinforcing fillers, typically silica or carbon black, which form hierarchical morphologies.7,8 Accordingly, fine-tuning both filler-filler and filler-matrix interactions is essential for achieving a balanced performance profile. A widely adopted strategy to enhance filler dispersion involves the use of silane coupling agents (SCAs), which form covalent bonds with polar filler surfaces while introducing functional groups compatible with the rubber matrix.9–11 However, the use of SCAs presents several challenges. Their processing can result in the release of volatile organic compounds (VOCs), raising environmental concerns.12–14 Moreover, their bifunctional nature often results in excessive filler–filler interactions and localized agglomeration, which prevent further reduction of RR and enhancement of WG.15,16 Additionally, while enhanced dispersion can soften the composite and reduce energy loss, it may also impair handling performance—an increasingly critical issue for EVs, which require greater load-bearing capacity and tighter performance margins due to their heavy battery systems.17 These trade-offs underscore the need for alternative materials and strategies that minimize VOC emissions while enhancing mechanical performance to meet evolving mobility demands.In response to these challenges, recent research has shifted toward modified SCAs and non-SCA alternatives for filler-reinforced rubber composites.18–20 Among the candidates under investigation, polyether glycol moieties have emerged as particularly promising due to their ease of synthesis, structural tunability, and broad molecular weight range. Their dynamic adsorption to polar filler surfaces via ether linkages allows for adjustable surface coverage and interaction strength, facilitating more efficient and scalable processing.21,22 For instance, Trinh et al. and Baeza et al. explored polypropylene glycol (PPG) as an interfacial modifier in styrene butadiene rubber (SBR)/silica systems, demonstrating that PPG preserved isostructural stability before and after vulcanization and acted as a lubricant under large strains.21,23 Similarly, Xu et al. examined polyethylene glycol (PEG 400) in conjunction with an organosilane TESPD (bis(triethoxysilylpropyl) disulfide) that is commonly used as an interfacial modifier in silica/SBR composites, finding that optimal PEG concentrations improved silica dispersion and enhanced “magic triangle” performance, while excessive amounts disrupted the filler network and diminished mechanical properties.24 Hussain et al. also investigated PEG-1000 alongside TESPT (bis(triethoxysilylpropyl) tetrasulfide) in silica/SBR composites, revealing that PEG improved dispersion and reduced the Payne effect, though optimal results required the synergy of both modifiers.25 More recently, Li et al. evaluated PEGs of varying molecular weights in TESPT-modified natural rubber systems, and demonstrated that higher molecular weight PEGs enhanced dispersion and mechanical properties while maintaining low RR. Despite these advancements, most studies have focused on partial SCA replacement, leaving full substitution strategies largely unexplored. Furthermore, a detailed quantitative understanding of how morphological modulations correlate with mechanical performance remains limited.
As highlighted, a central challenge in designing high-performance filler-reinforced nanocomposites lies in managing the trade-offs among key mechanical properties, which are governed by the hierarchical dispersion and structuring of fillers within the rubber matrix.26–29 According to prior studies, this multi-length scale hierarchical structure comprises (I) primary particles (basic units), (II) fractal clusters of aggregates formed from primary particles and bound by cured rubber, and (III) larger fractal agglomerates forming interconnected networks.29–32 Techniques such as small-angle X-ray scattering (SAXS) and complementary real-space imaging are commonly used to characterize these structures.33–35 Two SAXS-analysis models are frequently employed: the Beaucage model and the mass-fractal model. The Beaucage model assumes additive scattering contributions across hierarchical levels by generalizing the different scales of Guinier and power-law regions.27,30,36–38 This approach is limited to form-factor modeling and is weak in describing the interaction between filler particles.33 In contrast, the mass-fractal model includes structure factors to account for both intra- and inter-cluster interactions.31 Despite these advances, most SAXS analyses focus exclusively on the scattering from hierarchical filler aggregations and neglect the contribution of occluded rubber—rubber domains physically entrapped within filler clusters. These regions effectively increase the filler's volume fraction and significantly alter the composite's dynamic response. In particular, occluded rubber modulates local mobility and hysteresis, thereby playing a crucial role in shaping the viscoelastic behavior relevant to rolling resistance and wet grip. Yet, quantitative treatment of occluded rubber remains largely absent in existing SAXS models. Thus, advancing SAXS frameworks to simultaneously resolve filler hierarchy and occluded rubber is critical for establishing more robust and predictive structure–property correlations in elastomeric nanocomposites.39–42
In this study, we introduce a novel SAXS-guided structural framework to analyze the hierarchical architecture of silica-reinforced rubber nanocomposites, focusing on polyethylene glycol (PEG 2000) as a silane-free, eco-friendly interfacial modifier. This framework integrates a mass-fractal model to characterize hierarchical filler aggregation and a gel-like network model (squared Lorentzian or Debye–Bueche function) to resolve the mesoscale mesh network formed by occluded rubber. For the first time in this context, this hybrid SAXS model enables the quantitative extraction of occluded rubber domains—a morphologically elusive but mechanically significant phase—thereby providing a new axis for interpreting structure–property relationships in filler-based elastomers. The extracted parameters were validated using transmission electron microscopy (TEM) and atomic force microscopy (AFM), confirming the multiscale filler architecture observed via SAXS. Unlike TESPT, which covalently bridges silica and rubber and thereby suppresses occluded rubber formation, PEG interacts through physical adsorption, promoting filler aggregation and trapping more rubber within the filler network. This leads to an increase in occluded rubber domains, while simultaneously allowing interfacial slippage under dynamic deformation due to the flexible PEG-mediated interfaces. Despite the greater filler connectivity, PEG-modified systems retained better strain accommodation and maintained higher stiffness compared to TESPT-based counterparts. This duality—structural entrapment of occluded rubber coupled with dynamic interfacial modulation—emerged as the mechanistic basis for overcoming the classical trade-off between wet grip (WG) and rolling resistance (RR). By explicitly resolving occluded rubber contributions and correlating them with viscoelastic metrics such as E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at different temperatures, this SAXS-informed framework clarifies how PEG facilitates simultaneous reductions in RR (up to 40%) and enhancements in WG (up to 14%), while achieving 81% higher stiffness relative to TESPT systems. This study not only validates PEG as a high-performance, environmentally friendly SCA alternative, but also establishes a transferable model for rational additive design in next-generation sustainable tire technologies.
δ at different temperatures, this SAXS-informed framework clarifies how PEG facilitates simultaneous reductions in RR (up to 40%) and enhancements in WG (up to 14%), while achieving 81% higher stiffness relative to TESPT systems. This study not only validates PEG as a high-performance, environmentally friendly SCA alternative, but also establishes a transferable model for rational additive design in next-generation sustainable tire technologies.
2. Experimental section
2.1. Materials
Solution-styrene butadiene rubber (sSBR; TUFDENETM 680) and butadiene rubber (BR; TAIPOL 0150) were used as the primary elastomeric components, procured from Asahi Kasei Corporation and Taiwan Synthetic Rubber Corporation (TSRC), respectively. The SBR consisted of 34 wt% bound styrene and 58 mol% vinyl content in the butadiene units, and was pre-compounded with 37.5 parts per hundred rubber (phr) of treated distillates aromatic extract (TDAE). The BR exhibited a cis-1,4 content exceeding 99.3%. Precipitated silica nanoparticles (ULTRASIL® 7100 GR; BET surface area: 170 m2 g−1) were supplied by Evonik. Additional compounding ingredients included zinc oxide and stearic acid (vulcanization promoters), 2, 2′-dithiobis(benzothiazole) (curing accelerator), TDAE oil (lubricant), sulfur (vulcanizing agent), and bis[3-(triethoxysilyl)propyl] tetrasulfide (TESPT; silane coupling agent), all provided by Oriental Silicas Corporation of Taiwan. Polyethylene glycol (PEG; Mw ≈ 2000), used as an alternative interfacial modifier, was purchased from Sigma-Aldrich.2.2. Preparation of the silica-reinforced rubber nanocomposites
Silica-filled rubber composites were prepared following the formulations listed in Table 1 using a laboratory-scale internal mixer (chamber volume: ∼0.25 L). The concentration of TESPT used as an interfacial modifier in the sample (S1) was set at 6.4 phr, in line with standard tire tread formulations.43,44 The compounding was conducted in two stages: (1) master batch (MB) and (2) final mixing (F). In the MB stage, the objective was to achieve uniform silica incorporation and facilitate silanization reaction. The chamber temperature was set to 70 °C, with a rotor speed of 30 rpm. Initially, the rubber matrix was introduced, followed by TDAE, ZnO, stearic acid, half of the silica, and half of the interfacial modifier (TESPT or PEG) at 1 minute. At 4 minutes, the remaining silica and silane or PEG were added. To enhance silane-silica interactions, the temperature was elevated to 120 °C at 5 minutes. The total mixing duration for the MB stage was 40 minutes. In the F stage, the MB compound was blended with sulfur and curing accelerators at 60 °C and 30 rpm for 10 minutes. The resulting compound was passed six times through a two-roll mill to ensure homogeneity. The final sheets (∼1.3 mm thick) were molded and subsequently vulcanized in a hot press at 180 °C for 30 minutes to complete cross-linking.| Ingredients (phra) | P1 | P2 | P3 | P4 | S1 |
|---|---|---|---|---|---|
a Parts per hundred rubber.
b The original SBR contains 37.5 phr of TDAE; therefore, the total rubber content used for fabricating the composites is: 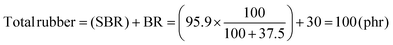 . .
|
|||||
| SBRb/BR | 95.9/30 | 95.9/30 | 95.9/30 | 95.9/30 | 95.9/30 |
| Silica | 80 | 80 | 80 | 80 | 80 |
| PEG2000/TESPT | 0/0 | 3/0 | 6.4/0 | 11/0 | 0/6.4 |
| TDAE | 14.1 | 14.1 | 14.1 | 14.1 | 14.1 |
| Stearic acid | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| ZnO | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| 2,2′-dithiobis(benzothiazole) (MBTS) | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| Sulfur | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 |
2.3. ATR-FTIR measurements
ATR-FTIR analysis was conducted to examine the influence of additive type and dosage on the surface modification of silica fillers in the vulcanized composites. Spectra were recorded using a PerkinElmer Spectrum 100 Plus spectrometer equipped with a PIKE MIRacle™ ATR accessory. Data were collected in the range of 4000–650 cm−1 with a resolution of 1 cm−1, and each spectrum represented the average of 16 consecutive scans.2.4. Small-angle X-ray scattering (SAXS) measurements
SAXS experiments were carried out at the coherent X-ray scattering beamline 25A1 and the BioSAXS beamline 13A of the Taiwan Photon Source (TPS), National Synchrotron Radiation Research Center (NSRRC), Hsinchu, Taiwan.45–48 Monochromatic X-ray beams were used at both beamlines. Two-dimensional scattering patterns were recorded using EIGER X 16M and EIGER X 9M detectors at beamlines 25A1 and 13A, respectively. The raw images were azimuthally averaged to yield one-dimensional scattering profiles. The scattering vector Q was defined as Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)/λ, where λ is the X-ray wavelength and θ is the scattering angle. The measured Q-range spanned approximately 0.0008 to 0.08 Å−1.
sin(θ/2)/λ, where λ is the X-ray wavelength and θ is the scattering angle. The measured Q-range spanned approximately 0.0008 to 0.08 Å−1.
2.5. Transmission electron microscopy (TEM)
TEM was used to visualize the hierarchical filler structure and dispersion within the rubber matrix. Imaging was performed using a Hitachi H-7650 TEM operated at 75 kV at the Technology Commons, National Taiwan University. Rubber specimens were cryo-sectioned with a glass knife into rough slices (1.5, 0.5, and 0.1 μm) using liquid nitrogen. Ultrathin sections (0.1 μm) were then prepared with a DiATOME diamond knife on a Leica EM UC6 ultramicrotome. Final sections were mounted on gold-coated carbon grids for observation at 100k× and 200k× magnification under ambient conditions.2.6. Atomic force microscopy (AFM)
AFM analysis was performed using an Asylum Research Cypher S system (Oxford Instruments) in bimodal tapping mode, operating at dual resonance frequencies of 300 kHz and 1.6 MHz under ambient conditions. A silicon cantilever (OMCL-AC160TS, Olympus) with an aluminum reflex coating and a sharpened tetrahedral tip geometry was used, with a nominal spring constant of 8.4–57 N m−1. The inverse optical lever sensitivity was calibrated to 40 nm V−1, and the free-air amplitude was set to 800 mV. Two types of images were collected: phase-contrast images acquired over 5 × 5 μm2 and 1 × 1 μm2 scan areas, and modulus mapping conducted on 1 × 1 μm2 regions. All scans were performed at a scan speed of 1 Hz with 1024 samples per line. Phase images reflect phase angle variations within a 60° range, and a consistent greyscale was applied across all images for direct comparison. For modulus mapping, the Hertzian contact model was applied to convert force–indentation responses into spatially resolved modulus distributions. Sample preparation followed the same procedure as in the TEM experiments, but AFM measurements were conducted on the exposed cross-sectional surface of the bulk composites.2.7. Payne effects
The Payne effect was evaluated to examine the strain-dependent nonlinear viscoelastic behavior of the rubber composites. Measurements were carried out using a TA Q800 dynamic mechanical analyzer to assess changes in the storage modulus (G′) in response to varying dynamic strain, providing insight into the interactions between the rubber matrix and the filler network. The experiment was conducted in tensile strain sweep mode at a frequency of 1 Hz and a temperature of 30 °C, with strain levels ranging from 0.01% to 110%. Test specimens were precisely prepared with dimensions of 2.3 mm in width, 1.3 mm in thickness, and a gauge length of 5 mm.2.8. Dynamic mechanical properties
The thermomechanical properties of the vulcanized rubber samples were evaluated using a HITACHI DMA 7100 dynamic mechanical analyzer in sinusoidal tension mode. A temperature sweep was performed from –80 °C to 85 °C at a heating rate of 2 °C min−1. The oscillation frequency was set to 10 Hz, and the deformation strain was maintained at 0.3%. Specimens were precisely prepared with dimensions of 1.3 mm in thickness, 2.3 mm in width, and a gauge length of 10 mm. The storage modulus (E′), loss modulus (E′′), and their ratio (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = E′′/E′) were analyzed as functions of temperature to investigate structure–property relationships relevant to dynamic road performance. To simulate real-world conditions, the time–temperature superposition (TTS) method was applied to correlate the experimental data.49 The tan
δ = E′′/E′) were analyzed as functions of temperature to investigate structure–property relationships relevant to dynamic road performance. To simulate real-world conditions, the time–temperature superposition (TTS) method was applied to correlate the experimental data.49 The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ amplitude at 0 °C, averaged over the –5 °C to 5 °C range, was used as an indicator of wet grip (WG), while the tan
δ amplitude at 0 °C, averaged over the –5 °C to 5 °C range, was used as an indicator of wet grip (WG), while the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ amplitude at 60 °C, averaged from 55 °C to 65 °C, was used to assess rolling resistance (RR). Additionally, the average storage modulus (E′) within the 55 °C to 65 °C range was used as a measure of stiffness (S).
δ amplitude at 60 °C, averaged from 55 °C to 65 °C, was used to assess rolling resistance (RR). Additionally, the average storage modulus (E′) within the 55 °C to 65 °C range was used as a measure of stiffness (S).
3. Results and discussion
3.1. ATR-FTIR analysis of interfacial modification in filler-rubber composites
To begin with, surface modification by TESPT and PEG was verified through ATR-FTIR analysis of the vulcanized samples (Fig. S1). Fig. S1(a) presents the full spectra (4000–650 cm−1). The organic phase was identified by characteristic absorptions, including C–H stretching (∼2920, 2850 cm−1), CH2/CH3 deformation (∼1450 cm−1), and H–O–H bending (∼1630 cm−1), while the silica phase was distinguished by Si–OH stretching (∼960 cm−1), Si–O–Si stretching (∼810 cm−1), and the strong band of asymmetric Si–O–Si stretching (∼1100 cm−1).50–53 In addition, the broad absorption between 3000 and 3700 cm−1 corresponded to O–H stretching. Compared with the unmodified sample (P1), all modified samples exhibited lower H–OH peak intensity at 1630 cm−1, indicating reduced moisture due to coverage of the silica surface. To further confirm the effectiveness of PEG and TESPT modification—particularly the dependence on PEG dosage—the broad O–H stretching band was enlarged and compared across different additive concentrations, as shown in Fig. S1(b). The results revealed that, relative to the unmodified sample (P1), the intensity of the O–H band decreased progressively with increasing PEG dosage in P2 (3 phr), P3 (6.4 phr), and P4 (11 phr), accompanied by redshifts of the peak position. Auxiliary dashed lines were added in Fig. S1(b) to facilitate direct comparison of the peak shifts across different samples. These observations confirmed that PEG interacted with surface silanol groups through hydrogen bonding, with the effect strengthening as PEG dosage increased. Similarly, the TESPT-modified sample (S1) exhibited reduced O–H band intensity, also confirming successful modification of the filler–rubber interface.3.2. SAXS analysis of hierarchical structures in silica-rubber composites
Small-angle X-ray scattering (SAXS) is a powerful technique for the quantitative characterization of morphology and multi-length-scale nanostructures in hierarchical systems, such as silica-reinforced rubbers30–32 and gels.54–56 As such, SAXS data offer critical insights into the relationship between processing parameters, structural organization, and mechanical properties. Previous studies on similar nanocomposite systems30,31 have identified distinct hierarchical structural levels associated with self-organized fillers or nanoparticles embedded within the rubber matrix: (1) primary particle of silica or carbon fillers; (2) aggregates of primary particles, which may fuse into dimers or trimers during the compounding process; (3) cluster consisting of primary particles and aggregates interconnected by the cured rubber network; (4) fractal agglomerates, comprising mass-fractal aggregates or networks of clusters dispersed throughout the rubber matrix. In the present study, the hierarchical structure, as characterized by SAXS profiles, can be described in three levels: (I) primary particles exhibiting polydispersity, which includes small aggregates such as dimer or trimer; (II) fractal clusters formed by mass-fractal aggregates or networks of primary particles interconnected through the cured rubber; and (III) fractal agglomerates consisting of mass-fractal aggregate or networks of the fractal clusters. A representative SAXS profile is shown in Fig. 1(a). The high-Q region (0.025–0.08 Å−1) corresponds to SAXS intensity contributions from primary particles (level-I). The radius of these primary particles can be estimated at approximately ∼90 Å using the relation Rp = π/Qp, where Qp ≈ 0.035 Å−1 represents the Guinier shoulder position for primary particles. The SAXS intensity primarily arising from fractal clusters (level-II) is observed within the Q-range of 0.003–0.025 Å−1. A profile shoulder at Qc ≈ 0.004 Å−1 corresponds to a cluster radius (Rc) of approximately 800 Å. Furthermore, power-law scattering behavior in the Q-region of 0.0065–0.025 Å−1 (i.e., I(Q) ∝ Q−α, 1 ≤ α ≤ 3) confirms the presence of mass-fractal aggregation or a dense network composed of primary particles (level-I) within the cluster. At lower Q values (Q ≤ 0.0028 Å−1), power-law scattering arises from mass-fractal aggregation or a network of clusters (level-II). This power-law SAXS analysis enables the extraction of morphological information. However, the profile shoulder corresponding to the global size of the agglomerate (level III) lies beyond the low-Q measurement limit.According to the literature,30,31,54,57 the SAXS profile of the silica-reinforced rubber system, primarily influenced by primary particles and their aggregation into clusters, Ic&p(Q), can be described in the present study using the mass fractal model of polydisperse spheres, as outlined in previous works.58–61 The model can be expressed as follows:
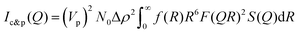 | (1) |
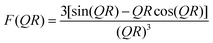 | (2) |
The profile shoulder of the form factor (at ∼0.035 Å−1) corresponds to the inverse of the size of the primary particles. The clusters, which are formed by mass-fractal aggregation or self-organization of primary particles, are described using a structure factor based on the fractal model, which accounts for the interaction between primary particles due to mass-fractal aggregation within a cluster. The mass fractal structure factor can be expressed as:58,62,63
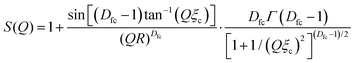 | (3) |
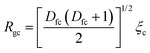 | (4) |
For the level-III structure of the agglomerate, it is assumed that the agglomerate is composed of clusters as a fundamental building unit for the agglomerate. The internal structure of the agglomerate consists of mass-fractal aggregation of clusters, as indicated by the power-law scattering observed in the Q-region of 0.0008∼0.0025 Å−1 in Fig. 1(a). Therefore, the SAXS profile contributed by the agglomerates, Iagg(Q), can be described using the model defined by eqn (1) to (3), along with two new fitting parameters, the primary-cluster radius, Rca, and fractal dimension of agglomerate, Dfa. These two fitting parameters replace R in eqn (1) and (2) and Dfc in eqn (3), respectively. The full SAXS profile can then be modelled by the sum of Ic&p(Q) and Iagg(Q). Notably, it can be expected that Rca could be close to the Rgc because the shoulder positions of fractal cluster and primary-cluster radius are located in the same Q-region. The relationship Rca ≈ Rgc ensures the continuity of boundary conditions between the two equations (Ic&p(Q) and Iagg(Q)). As a result, the hierarchical structure, constructed through multi-length-scale or multi-level aggregation of silica particles can be determined.59 The SAXS profiles can be accurately fitted by the sum of the two models for level I primary particles, level II clusters, and level III agglomerates. An illustration is shown in Fig. S2.
Currently, the hierarchical structure of self-organized silica particles presents a significant challenge in explaining the comprehensive and trade-off mechanical properties of tires. In this study, we aimed to propose a novel structural model for SAXS analysis that successfully and comprehensively correlated with the various trade-off properties exhibited by the filler-rubber composites with interfacial modifier, such as wet grip (WG), rolling resistance (RR) and stiffness, and predictions derived from dynamic mechanical analysis measurements. This new structural model, proposed for the first time, not only included the fractal network/clusters (level-I and level-II) but also considered the structure of occluded rubber, corresponding to the locally defined level-III scale. This model offers a deeper understanding of the correlation among processing, structure and properties. The proposed model retains the fractal model of clusters formed by the aggregation of primary silica particles in the middle- and high-Q regions of the SAXS profile. Additionally, a model commonly used to describe the fractal-like hydrogel networks or meshworks63–65 with hierarchical architecture is applied here to fit the low-Q SAXS profile, which corresponds to the fractal-based agglomerates (level-III structure). This model incorporates the concept of the mesh size in a fractal network or meshwork, which can be described by Debye–Bueche equation (chemical or static aggregation) and is characterized by the static correlation length.55,56,64–66 The SAXS intensity in the low-Q region can thus be modelled by a hydrogel network with a large-scale mesh size as follows:
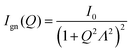 | (5) |
| I(Q) = Ign(Q) + Ic&p(Q) | (6) |
Fig. 2 presents the SAXS profiles of various tire tread samples, aimed at elucidating the hierarchical structures of silica particles, occluded rubber, and their interactions as influenced by different additives. Fig. 2(a) compares the profiles of sample P1—which contains neither TESPT nor PEG and therefore represents a bare interface between the rubber matrix and the silica surface, serving as a reference—with sample S1, which is modified with TESPT, a commonly used silane coupling additive in the tire industry known for its effectiveness. Fig. 2(b) displays the SAXS profiles of the unmodified sample P1 alongside samples P2–P4, which incorporate increasing concentrations of the PEG additive. The SAXS profiles revealed additive-induced evolution of hierarchical structural features: the high-Q region corresponded to the dimensions of primary silica particles, the mid-Q region reflected the size of silica clusters, and the low-Q region indicated the presence of a hydrogel-like network, characterized by a mesh size associated with occluded rubber domains.
The SAXS profiles in the high-Q region showed considerable overlap across all samples, indicating negligible differences in the size of silica primary particles, regardless of additive incorporation. A shoulder feature at Qc ≈ 0.004 Å−1, corresponding to the cluster radius, shifted toward higher Q-values—reflecting reduced cluster size—as the formulation progressed from the unmodified reference sample (P1) to the TESPT-modified sample (S1), as depicted in Fig. 2(a). Conversely, the incorporation of PEG caused this shoulder to shift toward lower Q-values, with a further downshift observed as PEG concentration increases, suggesting progressive cluster growth, as shown in Fig. 2(b). These trends in cluster size reduction with TESPT and growth with PEG addition were further supported by TEM and AFM observations, discussed in later sections.
To quantitatively interpret the SAXS data, all scattering profiles were analyzed using a combined fractal polysphere and gel network model (see eqn (6)), with the corresponding fitting parameters summarized in Table 2. As demonstrated in Fig. 2(c and d) and Fig. S3–S5, this hybrid modeling approach successfully captured the experimental SAXS curves. The radii of gyration extracted from the model were 39 nm for S1 and 46, 53, 57, and 66 nm for samples P1 through P4, respectively—indicating a systematic increase in cluster size with PEG content and a reduction with TESPT modification. Similarly, the static correlation length, representing the mesh size of the gel-like network associated with occluded rubber, increased from 138 nm (S1) to 146, 163, 187, and 206 nm (P1–P4, respectively).
| P1 | P2 | P3 | P4 | S1 | |
|---|---|---|---|---|---|
| a The static correlation length Λ, extracted by Debye–Bueche fitting of the low-q region, was used as a structural proxy for the average size of occluded rubber domains. | |||||
| Static correlation lengthaΛ (Å) | 1467 | 1632 | 1872 | 2058 | 1384 |
| Primary particle radius R (Å) | 66 | 65 | 70 | 71 | 63 |
| Particle polydispersity | 0.254 | 0.213 | 0.213 | 0.211 | 0.258 |
| Fractal dimension Dfc | 2.69 | 2.74 | 2.67 | 2.67 | 2.64 |
| Cluster correlation length ξc (Å) | 205 | 237 | 257 | 297 | 181 |
| Cluster radius of gyration Rgc (Å) | 458 | 535 | 568 | 657 | 396 |
These results underscored the contrasting interaction mechanisms of TESPT and PEG with silica surfaces. TESPT promoted dispersion by forming covalent bonds with surface silanol groups via its ethoxysilyl moieties while simultaneously crosslinking with the rubber matrix through sulfur linkages, thereby inhibiting silica aggregation. In contrast, PEG, composed of repeating ethylene oxide units, interacted with the silica surface primarily through hydrogen bonding between its alkoxy groups and surface silanol groups, which promoted aggregation. This enhanced aggregation led to increased occlusion of rubber within the silica network, forming larger domains. These distinct morphological evolutions directly influenced mechanical performance, as discussed in subsequent sections.
3.3. Morphological analysis of filler-reinforced rubber composites: transmission electron microscopy (TEM)
To further investigate the influence of PEG 2000 on the hierarchical structure of tire tread composites, and to elucidate the relationships among morphology, processing, and the resulting performance trade-offs, transmission electron microscopy (TEM) was employed to complement and validate the findings from the SAXS analysis. In the TEM micrographs, the bright regions correspond to the rubber matrix, while the dark contrast delineates silica-related structures. The discernible structural units are fractal clusters (Level II), which appear as polydisperse, rounded-to-branched aggregates formed from associations of primary particles (Level I). These clusters interconnect to form a continuous gel-like network (Level III). Within this network, localized rubber domains—indicated with blue arrows—are referred to as occluded rubber, whose characteristic dimension corresponds to the static correlation length (Λ) obtained from the SAXS gel-network model. These features define the hierarchical organization of silica and rubber, consistent with the scheme illustrated in Fig. 1(b).TEM observations revealed that sample S1 (Fig. 3(a) and (b)), modified with TESPT, exhibited smaller and more uniformly dispersed silica clusters, resulting in a relatively homogeneous morphology with less pronounced contrast between the silica (dark) and rubber (light) phases. In contrast, the unmodified sample P1 (Fig. 3(c) and (d)) displayed larger, localized silica clusters together with clearly separated silica-rich and rubber-rich domains. The clustering was most pronounced in sample P4 (Fig. 3(e) and (f)), which incorporated the highest PEG content.
The formation of larger clusters in PEG-modified samples, as opposed to the well-dispersed morphology in TESPT-modified counterparts, was attributed to hydrogen bonding between silanol groups on the silica surface and the ethylene oxide (EO) segments of PEG chains. The extended PEG chains promoted the aggregation of surrounding silica particles, leading to the observed cluster enlargement. These morphological features were consistent with the average cluster sizes and polydispersity obtained from SAXS modeling.
To further substantiate this correspondence, quantitative analysis of TEM images was performed using ImageJ software, with the statistical histograms provided in Fig. S6 and the extracted values summarized in Table S1. The cluster size and occluded-rubber mesh sizes obtained from TEM showed close numerical agreement with the fitting parameters derived from SAXS, thereby reinforcing the consistency between direct imaging and scattering-based modeling. This quantitative match further validated the interpretation that PEG promoted silica aggregation and enlarged occluded-rubber domains, whereas TESPT suppressed aggregation and reduced the corresponding domain size.
3.4. Atomic force microscopy (AFM) measurements
To investigate and compare the effects of PEG on the distribution and hierarchical structure of silica particles, Fig. 4 presents fine-cut sectional micrographs of the rubber–filler composites obtained via atomic force microscopy (AFM). Fig. 4(a) shows sample S1 (containing TESPT), Fig. 4(b) depicts sample P1 (without additives), Fig. 4(c) illustrates sample P3 (with 6.4 phr PEG), and Fig. 4(d) presents sample P4 (with the highest PEG content, 11 phr). All micrographs were acquired via phase imaging, where the phase contrast reflects local material stiffness variations: higher phase angles (appearing as light yellow to deep orange regions) correspond to the softer rubber matrix, whereas lower phase angles (appearing as dark regions) are primarily attributed to stiffer silica aggregates. The darker silica regions were dispersed throughout the matrix and interconnected into a gel-like meshwork, within which the rubber was confined in the inter-cluster mesh spaces defined as occluded rubber. This enables clear visualization of filler dispersion and interfacial morphology.These AFM images also demonstrated that different additives had distinct effects on silica dispersion within the rubber matrix. As shown in Fig. 4(a), sample S1 (containing TESPT) resulted in finer and smaller silica clusters, which appeared uniformly dispersed throughout the matrix. The particle domains were subtle and intricately distributed, blending more smoothly with the matrix, giving the overall structure a refined appearance. In contrast, in sample P1, which lacked additives (Fig. 4(b)), silica particles aggregated into larger, more distinct clusters, forming scattered black regions and resulting in a coarser, more heterogeneous morphology compared to Fig. 4(a). In sample P3 (Fig. 4(c)), with a moderate amount of PEG, the silica clusters became even larger and more clearly delineated, with more defined boundaries and increased spacing between them. This made the dark-phase domains appear more isolated and accentuated the contrast between the filler and the surrounding matrix. This behavior became even more pronounced in sample P4 (Fig. 4(d)), which contained the highest PEG content. The particle phase formed densely packed aggregates with strong contrast and reduced spacing, creating a tightly clustered appearance across the image. Moreover, the mesh sizes of the rubber–filler networks also followed the sequence S1 < P1 < P3 < P4, aligning with previous SAXS and TEM results, further confirming the structural adaptation driven by PEG. These morphological differences originated from distinct interfacial interactions at organic–inorganic boundaries. In TESPT-modified samples, silane moieties chemically bonded with both silica particles and the rubber phase, effectively dispersing silica and preventing large-scale aggregation through silanol interactions, as observed in S1 compared to P1. In contrast, PEG-modified samples P3 and P4 via EO-mediated physical adsorption at organic–inorganic interphases. With multiple EO segments in a single PEG molecule, this adsorption promoted silica clustering, forming larger aggregates. The progressive increase in PEG content led to increasingly separated and extensive silica domains from P1 to P3 to P4, accompanied by a stepwise enlargement of the mesh regions between clusters. These structural variations further influenced mesh size, with progressively larger aggregates in PEG-modified samples (P3 and P4) entrapping more occluded rubber, whereas improved silica dispersion in S1 reduced occluded rubber content. Given the critical role of filler dispersion and interfacial interactions in rubber composite mechanics, these morphological variations directly influenced the reinforcement–flexibility trade-off, a key factor in tire tread optimization. To establish a direct structure–property correlation, further mechanical investigations were conducted to link these morphological features to composite performance, as discussed in the following sections.
3.5. Payne effects
A key objective in incorporating interfacial modifiers into filler-reinforced rubber composites is to refine interphase interactions, improve filler–matrix compatibility, and achieve enhanced control over both morphology and mechanical properties. In poorly dispersed systems, physical incompatibility between hydrophilic silica and the hydrophobic rubber matrix often results in the formation of occluded or “dead” rubber—rubber domains entrapped within filler clusters. This phenomenon, structurally resolved via the present SAXS framework and corroborated by TEM and AFM analyses, not only increases the effective filler volume fraction but also constrains chain mobility and impairs elasticity under dynamic deformation.68,69 To assess these interfacial effects, dynamic strain sweep measurements were conducted, as presented in Fig. 5. Fig. 5(a) shows the storage modulus (G′) as a function of strain amplitude, while Fig. 5(b) displays the modulus reduction (ΔG′) for each sample, calculated as the difference between the storage modulus at low strain (0.01%) and that at high strains (>50%): | (7) |
This parameter characterizes the breakdown of the filler network under deformation, commonly referred to as the Payne effect, and serves as a quantitative measure of filler–filler interactions.69–71 As shown in Fig. 5(a), the TESPT-modified sample (S1) exhibited the most significant reduction in initial plateau modulus, followed by PEG-modified samples (P2–P4), with increasing PEG concentration leading to further reductions. In contrast, the unmodified sample P1 showed the highest initial G′, indicative of a highly aggregated, rigid filler network. At higher strain amplitudes, all modified samples converged to similar final G′ values, whereas P1 exhibited greater structural instability and a pronounced modulus drop at 60% strain. This trend was further confirmed in Fig. 5(b), where ΔG′ values progressively decreased from 30.4 MPa in P1 to 13.3 MPa in P4, with S1 exhibiting the lowest ΔG′ at 10.9 MPa.
These results underscored the critical role of interfacial modifiers in regulating filler–filler interaction, which directly influenced the dynamic mechanical behavior of the composites. Sample S1, containing TESPT, achieved the lowest initial G′ and ΔG′, consistent with effective mitigation of filler aggregation via covalent bonding between the silane agent and both silica surfaces and rubber chains. Similarly, PEG-modified samples also demonstrated a reduced modulus compared to the unmodified P1, with ΔG′ values decreasing from 18.1 MPa (P2) to 13.5 MPa (P3) and 13.3 MPa (P4), reflecting progressive structural modification with increasing PEG content.
At first glance, the reduction in G′ with PEG addition appeared contradictory to SAXS and microscopy results, which showed that PEG promoted filler aggregation and increased occluded rubber domains—both typically associated with stiffening. However, this discrepancy stemmed from the fundamentally different interaction mechanisms of the modifiers. Unlike TESPT, which formed covalent bonds to enhance compatibility, PEG interacted with silica via physical adsorption through hydrogen bonding between its ethylene oxide (EO) segments and surface silanol groups. While this promoted the formation of larger silica clusters and increased the occluded rubber fraction, the resulting domains were embedded within PEG-mediated interfacial regions governed by hydrogen bonding. These hydrogen-bonded zones were less constrained and more deformable compared to the rigidly confined rubber seen in poorly dispersed systems, resulting in lower initial G′ values as PEG concentration increased.
As strain increased, these interfacial regions accommodated progressive network rearrangement through interparticle mobility. Notably, SAXS analysis revealed a progressive increase in the size of occluded rubber domains with higher PEG content, consistent with enhanced filler entrapment. Yet rather than reinforcing the matrix, these occluded zones functioned as compliant, friction-reducing interlayers that promoted filler reorganization. Consequently, although PEG induced greater filler aggregation, the final G′ values across PEG- and TESPT-modified systems converged. This indicated that PEG-modified networks, despite their more extensively aggregated and rubber-occluded structures, maintained greater deformability under strain—reflecting a reconfigurable architecture enabled by dynamic interfacial modulation.
To further clarify these interfacial characteristics, AFM nanomechanical mapping was conducted on representative samples within a more focused 1 × 1 μm2 area: S1 (TESPT, 6.4 phr), P1 (unmodified), and P4 (PEG, 11 phr), as shown in Fig. 6(d–f). For reference, the corresponding phase-contrast images are presented in Fig. 6(a–c), which corroborate the larger-area observations in Fig. 4: S1 contained finer and more separated particle domains, P1 showed moderate aggregation with larger clusters, and P4 exhibited the largest aggregates. The modulus maps (Fig. 6(d–f)) provide direct insight into the interfacial environments. In these maps, the modulus of the composite materials is color-coded according to relative stiffness, as indicated in the scale bar: purple–blue denotes rigid, high-modulus silica-rich domains; green corresponds to the elastic bulk rubber matrix; cyan highlights interfacial rims that are slightly stiffer than the matrix due to partial chain confinement; and yellow–red indicates softer, more compliant regions of less-constrained rubber. Distinct contrasts were evident among the samples. In S1, the purple silica-rich domains appeared relatively dispersed and were mostly encircled by narrow cyan rims. Yellow–red soft regions were also present but occurred only as isolated patches or short streaks, occasionally near particle edges but rarely forming continuous compliant paths. This indicated that compliant zones were limited, while the predominant interphase remained thin yet rigid, formed via covalent bridges. Such a configuration suppressed the formation of continuous filler networks, even though the interphase itself was locally stiff. In contrast, P1 displayed broad and interconnected purple silica regions, surrounded by extensive continuous blue–cyan zones with sharp transitions into the green rubber matrix. These rigid networks reflected strong filler–filler contacts and immobilized rubber domains, providing limited interfacial modulation and enhancing network integrity. By comparison, P4 exhibited the most pronounced aggregation in the phase-contrast images, characterized by the largest silica clusters. However, in the modulus maps, these clusters did not form the extensive rigid purple–blue networks observed in P1; instead, they were frequently surrounded and segmented by widespread yellow–red compliant layers along their boundaries, often merging into broad soft corridors that disrupted silica connectivity. Unlike the thin but rigid cyan rims in S1 or the broad immobilized blue–cyan networks in P1, these PEG-induced soft interphases provided deformable hydrogen-bonded layers that facilitated interparticle slippage and structural reorganization under strain. Taken together, the AFM observations correlated well with the Payne effect: in S1, thin rigid interphases combined with improved dispersion weakened filler networking, producing the lowest ΔG′; in P1, strong filler aggregation and extensive immobilized contacts established a rigid, continuous network, resulting in the highest ΔG′; and in P4, although clustering was more pronounced, the presence of compliant interfacial layers enabled network sliding and rearrangement, thereby reducing ΔG′ compared to P1.
Fig. 7 provides a schematic representation of these mechanisms. At low strain, TESPT (S1) promoted uniform dispersion and minimized interparticle interactions, resulting in the lowest initial G′. In contrast, PEG-modified composites (P2–P4) exhibited larger filler clusters due to hydrogen-bonding-induced flocculation. However, the physical nature of these aggregates enabled interfacial sliding, which reduced the initial G′ compared to the unmodified P1. This effect became more pronounced with increasing PEG content, as the higher degree of PEG adsorption contributed to the formation of more compliant filler–matrix interfaces that facilitated slippage. This slippage was further facilitated by the presence of larger occluded rubber domains, which, as suggested by SAXS results, served as deformable zones that helped decouple adjacent filler clusters under strain. At higher strains, the dynamic reorganization of PEG-mediated clusters disrupted the filler network, resulting in a final modulus comparable to that of TESPT-modified systems.
This behavior demonstrates the dual functionality of PEG: while it initially promotes filler clustering and enhances structural integrity, it also facilitates interfacial slippage, allowing for mechanical adaptability under strain. This sliding mechanism provides a more balanced reinforcement strategy than traditional silane coupling agents. TESPT promotes silica dispersion, with a potential trade-off in network stiffness in applications sensitive to mechanical deformation. In contrast, PEG-modified systems offer a tunable balance between stiffness and flexibility by enhancing filler connectivity while enabling structural rearrangement under stress.
These findings suggest that PEG-based interfacial engineering provides a versatile approach to optimizing the reinforcement–flexibility trade-off in dynamic applications such as tire treads. This mechanistic insight paves the way for tailoring composite formulations to meet diverse performance demands, bridging the gap between high stiffness and desirable energy dissipation properties.
3.6. DMA analysis for tread composites
To accurately simulate real-world operational conditions for tire tread applications, it was essential to investigate the viscoelastic behavior of the composites under dynamic loading. Accordingly, dynamic mechanical analysis (DMA) was employed to characterize key parameters—storage modulus (E′), loss modulus (E′′), and loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = E′′/E′)—as functions of temperature. Fig. 8 illustrates the temperature-dependent tan
δ = E′′/E′)—as functions of temperature. Fig. 8 illustrates the temperature-dependent tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles, highlighting the influence of various interfacial modifiers. Specifically, Fig. 8(a) compares the effects of TESPT (S1), while Fig. 8(b) presents the impact of PEG (P2–P4), both relative to the unmodified reference sample (P1). In these profiles, the peak temperature corresponded to the glass transition temperature (Tg), providing insight into molecular mobility within the composites. Additionally, tan
δ profiles, highlighting the influence of various interfacial modifiers. Specifically, Fig. 8(a) compares the effects of TESPT (S1), while Fig. 8(b) presents the impact of PEG (P2–P4), both relative to the unmodified reference sample (P1). In these profiles, the peak temperature corresponded to the glass transition temperature (Tg), providing insight into molecular mobility within the composites. Additionally, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values at 0 °C and 60 °C were marked in orange and green, respectively, serving as indicators of wet grip (WG) and rolling resistance (RR), which are discussed in subsequent sections.
δ values at 0 °C and 60 °C were marked in orange and green, respectively, serving as indicators of wet grip (WG) and rolling resistance (RR), which are discussed in subsequent sections.
The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ results revealed that Tg was significantly influenced by the choice of interfacial modifier. For the TESPT-modified sample, Tg decreased from −4.0 °C in the unmodified reference sample (P1) to −9.9 °C, indicating enhanced chain mobility. In contrast, PEG-modified samples exhibited a progressive increase in Tg, with values of −1.4 °C, 0 °C, and 0.1 °C for P2, P3, and P4, respectively. Moreover, all modified samples displayed higher tan
δ results revealed that Tg was significantly influenced by the choice of interfacial modifier. For the TESPT-modified sample, Tg decreased from −4.0 °C in the unmodified reference sample (P1) to −9.9 °C, indicating enhanced chain mobility. In contrast, PEG-modified samples exhibited a progressive increase in Tg, with values of −1.4 °C, 0 °C, and 0.1 °C for P2, P3, and P4, respectively. Moreover, all modified samples displayed higher tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ intensities, indicative of enhanced molecular relaxation at the transition. From a molecular standpoint, the glass transition represents the transformation of polymer chains from a rigid to a mobile state upon thermal activation. In highly filled systems, portions of the polymer may be immobilized within occluded (or “dead”) rubber regions, trapped between filler aggregates. These confined domains demand greater thermal energy to initiate segmental motion, resulting in elevated Tg values. Consequently, the extent of occluded rubber can be correlated with the observed Tg shifts.
δ intensities, indicative of enhanced molecular relaxation at the transition. From a molecular standpoint, the glass transition represents the transformation of polymer chains from a rigid to a mobile state upon thermal activation. In highly filled systems, portions of the polymer may be immobilized within occluded (or “dead”) rubber regions, trapped between filler aggregates. These confined domains demand greater thermal energy to initiate segmental motion, resulting in elevated Tg values. Consequently, the extent of occluded rubber can be correlated with the observed Tg shifts.
In the case of the TESPT-modified composite (S1), chemical bonding between TESPT and silica significantly reduced the formation of occluded rubber, leading to a higher fraction of mobile polymer chains and a lower Tg compared to the unmodified sample (P1). This enhanced chain mobility facilitated more efficient segmental motion near Tg, contributing to the higher tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak observed in S1. Furthermore, the incorporation of TESPT resulted in a narrower transition region. As shown in Table 3, the full width at half maximum (FWHM) of the tan
δ peak observed in S1. Furthermore, the incorporation of TESPT resulted in a narrower transition region. As shown in Table 3, the full width at half maximum (FWHM) of the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak for S1 was 39.2 °C, significantly narrower than the 47.8 °C observed for P1. This narrowing implies a more well-defined glass transition, likely arising from improved filler dispersion and a reduction in localized chain immobilization. A more uniformly distributed filler network minimizes spatial constraints, promoting a sharper transition from the glassy to the rubbery state.
δ peak for S1 was 39.2 °C, significantly narrower than the 47.8 °C observed for P1. This narrowing implies a more well-defined glass transition, likely arising from improved filler dispersion and a reduction in localized chain immobilization. A more uniformly distributed filler network minimizes spatial constraints, promoting a sharper transition from the glassy to the rubbery state.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ profiles and viscoelastic properties of the studied samples
δ profiles and viscoelastic properties of the studied samples
| P1 | P2 | P3 | P4 | S1 | |
|---|---|---|---|---|---|
a The full width at half maximum (ΔTFWHM) was defined as the temperature range at which the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curve intersects the value calculated as (tan δ curve intersects the value calculated as (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δmax - tan δmax - tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δbaseline)/2. δbaseline)/2.
|
|||||
| ΔTFWHMa (°C) | 47.8 | 45.3 | 37.1 | 33.2 | 39.2 |
| E′ (0 °C) (MPa) | 180.6 | 181.5 | 136.8 | 111.8 | 53.6 |
| E′′ (0 °C) (MPa) | 64.8 | 82.9 | 76.3 | 68.9 | 26.5 |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (0 °C) δ (0 °C) |
0.36 | 0.46 | 0.56 | 0.61 | 0.49 |
| E′ (60 °C) (MPa) | 29.3 | 27.2 | 21.6 | 16.8 | 11.9 |
| E′′(60 °C) (MPa) | 3.4 | 2.2 | 1.7 | 1.2 | 1.5 |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (60 °C) δ (60 °C) |
0.11 | 0.081 | 0.078 | 0.07 | 0.13 |
In contrast, PEG modification led to a systematic increase in Tg with increasing PEG content, consistent with enhanced filler-filler interactions. This behavior was attributed to PEG's physical adsorption onto silica surfaces via hydrogen bonding, promoting filler flocculation and restricting polymer chain mobility. Unlike TESPT, which chemically anchors to the filler and improves dispersion, PEG's physical interaction results in filler aggregation. This aggregation impedes segmental dynamics, thereby elevating Tg. Despite the reduced chain mobility implied by the Tg increase, PEG's interfacial sliding mechanism facilitated partial release of occluded rubber, enhancing energy dissipation during the transition. This was reflected in the progressively higher tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak intensities observed with increasing PEG concentration. Furthermore, PEG incorporation significantly influenced the breadth of the glass transition, as reflected in the FWHM values. Specifically, the FWHM decreased from 47.8 °C in P1 to 45.3 °C, 37.1 °C, and 33.2 °C in P2, P3, and P4, respectively. This trend underscored PEG's dual role in simultaneously restricting and redistributing polymer mobility. Initially, PEG-induced flocculation increased network rigidity by generating occluded rubber. However, at higher concentrations, PEG promoted interfacial slippage and dynamic rearrangement of filler particles, thereby reducing heterogeneity in the polymer–filler network. This redistribution of occluded rubber facilitated more synchronized molecular motion and a more localized energy dissipation process, ultimately resulting in a narrower FWHM. Therefore, as PEG content increased, the accompanying growth in occluded rubber domains—as captured by the SAXS-derived correlation lengths—provided more thermally responsive confined regions that gradually released constrained chains during the glass transition, enhancing damping behavior while sharpening the transition. Despite the initial constraints imposed by occluded regions, this behavior reflects an increasingly stable viscoelastic response, which is advantageous for practical performance.
δ peak intensities observed with increasing PEG concentration. Furthermore, PEG incorporation significantly influenced the breadth of the glass transition, as reflected in the FWHM values. Specifically, the FWHM decreased from 47.8 °C in P1 to 45.3 °C, 37.1 °C, and 33.2 °C in P2, P3, and P4, respectively. This trend underscored PEG's dual role in simultaneously restricting and redistributing polymer mobility. Initially, PEG-induced flocculation increased network rigidity by generating occluded rubber. However, at higher concentrations, PEG promoted interfacial slippage and dynamic rearrangement of filler particles, thereby reducing heterogeneity in the polymer–filler network. This redistribution of occluded rubber facilitated more synchronized molecular motion and a more localized energy dissipation process, ultimately resulting in a narrower FWHM. Therefore, as PEG content increased, the accompanying growth in occluded rubber domains—as captured by the SAXS-derived correlation lengths—provided more thermally responsive confined regions that gradually released constrained chains during the glass transition, enhancing damping behavior while sharpening the transition. Despite the initial constraints imposed by occluded regions, this behavior reflects an increasingly stable viscoelastic response, which is advantageous for practical performance.
Optimally, tire tread composites should exhibit high damping capability at low temperatures (enhancing wet grip) and low energy dissipation at higher temperatures (reducing rolling resistance). These performance characteristics, reflected in the temperature-dependent tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ behavior, will be further explored in the subsequent section.
δ behavior, will be further explored in the subsequent section.
3.7. Viscoelastic contributions to wet grip and rolling resistance
Under typical driving conditions, vehicle tires are subjected to cyclic bulk deformations at frequencies around 10 Hz. These deformations result in hysteresis losses, which elevate the tire temperature to approximately 60 °C. At this temperature, the loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) serves as a critical parameter for evaluating rolling resistance (RR), and lower tan
δ) serves as a critical parameter for evaluating rolling resistance (RR), and lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values are desirable to minimize energy dissipation. Conversely, strain frequencies in the range of 104 and 107 Hz—corresponding to microscale interactions with road surface microtexture—are especially relevant for traction under wet conditions. Through time–temperature superposition, such high-frequency deformations are equivalent to dynamic loading at 0 °C and 10 Hz, making tan
δ values are desirable to minimize energy dissipation. Conversely, strain frequencies in the range of 104 and 107 Hz—corresponding to microscale interactions with road surface microtexture—are especially relevant for traction under wet conditions. Through time–temperature superposition, such high-frequency deformations are equivalent to dynamic loading at 0 °C and 10 Hz, making tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 0 °C an important predictor of wet grip (WG) performance, where higher values are favorable.72–76 This inherent trade-off between reducing RR and enhancing WG remains one of the central challenges in tread compound design. Fig. 8 illustrates the damping behavior of the studied composites, emphasizing the tan
δ at 0 °C an important predictor of wet grip (WG) performance, where higher values are favorable.72–76 This inherent trade-off between reducing RR and enhancing WG remains one of the central challenges in tread compound design. Fig. 8 illustrates the damping behavior of the studied composites, emphasizing the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values at the two critical temperatures: 0 °C and 60 °C. To further elucidate the mechanisms governing these tan
δ values at the two critical temperatures: 0 °C and 60 °C. To further elucidate the mechanisms governing these tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ variations, the storage modulus (E′), loss modulus (E′′), and corresponding tan
δ variations, the storage modulus (E′), loss modulus (E′′), and corresponding tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values at both temperatures are summarized in Fig. 9 and Table 3. Fig. 9(a) presents data at 0 °C, reflecting WG-related characteristics, while Fig. 9(b) presents the results at 60 °C, indicative of RR performance.
δ values at both temperatures are summarized in Fig. 9 and Table 3. Fig. 9(a) presents data at 0 °C, reflecting WG-related characteristics, while Fig. 9(b) presents the results at 60 °C, indicative of RR performance.
With regard to WG, Fig. 9(a) showed that all additive-modified composites exhibited increased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 0 °C compared to the unmodified composite (P1), confirming the beneficial role of additives in enhancing low-temperature traction. However, the underlying mechanisms varied depending on the additive. In the TESPT-modified composite (S1), both E′ and E′′ were reduced relative to P1, leading to a net increase in tan
δ at 0 °C compared to the unmodified composite (P1), confirming the beneficial role of additives in enhancing low-temperature traction. However, the underlying mechanisms varied depending on the additive. In the TESPT-modified composite (S1), both E′ and E′′ were reduced relative to P1, leading to a net increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. This behavior suggested that TESPT primarily improved WG by softening the rubber matrix and reducing E′, thereby enabling greater deformation under applied stress. The significant decrease in Tg (∼6 °C lower than P1) also facilitated increased molecular mobility at 0 °C, diminishing the elastic response and further lowering E′. Altogether, the resulting increase in tan
δ. This behavior suggested that TESPT primarily improved WG by softening the rubber matrix and reducing E′, thereby enabling greater deformation under applied stress. The significant decrease in Tg (∼6 °C lower than P1) also facilitated increased molecular mobility at 0 °C, diminishing the elastic response and further lowering E′. Altogether, the resulting increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ reflected a more compliant material that could dissipate energy more effectively, enhancing WG performance.
δ reflected a more compliant material that could dissipate energy more effectively, enhancing WG performance.
With increasing PEG concentration, the storage modulus (E') progressively decreased, while the loss modulus (E′′) remained higher than that of P1 across all PEG-modified samples—peaking at P2 and gradually decreasing at P3 and P4. Although these composites remained E′-dominated, the origins of stiffness reduction differed markedly from those in TESPT-based systems. Specifically, PEG promoted filler aggregation through hydrogen bonding, which enhanced filler–filler contacts and led to the formation of more extensive occluded rubber domains. These domains, formed via physically adsorbed PEG layers, remained deformable, enabling interfacial sliding under mechanical strain and contributing to reduced E′. The increasing PEG content also shifted Tg closer to the 0 °C testing point (–1.4 °C, 0 °C, and 0.1 °C for P2, P3, and P4, respectively). At this temperature, elevated chain mobility amplified interfacial sliding and allowed for the release of a larger fraction of occluded rubber, whose abundance increased with PEG loading. This augmented release contributed to further network softening and enhanced energy dissipation, as reflected in the elevated tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values.
δ values.
The observed trends in E′′ also supported this interpretation. The initial increase in E′′ (relative to P1) was attributed to enhanced energy dissipation via interfacial sliding. However, with higher PEG content, the progressive coverage of the silica surface reduced direct filler-filler contact, leading to diminished frictional losses and a gradual decrease in E′′. Despite this, E′′ remained above the P1 baseline, indicating that filler mobility and partial rubber release continued to contribute to energy dissipation. Collectively, these effects—including the reduction in E′ due to sliding, moderate variations in E′′, and the shift in Tg—accounted for the improved WG performance observed in PEG-containing systems.
With respect to RR, the results in Fig. 9(b) showed a contrasting trend between TESPT- and PEG-modified composites. The TESPT-modified sample (S1) exhibited increased tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 60 °C relative to P1, implying higher RR. In contrast, PEG-modified samples (P2–P4) displayed a gradual decrease in tan δ with increasing PEG content, indicating reduced RR. These opposing trends could be explained by the distinct viscoelastic responses driven by differences in E′ and E′′ at elevated temperatures. At 60 °C—where RR is assessed—previously discussed mechanisms such as occluded rubber dynamics remain influential, but additional phenomena must also be considered. Prior studies have shown that thin (∼1 nm) layers of rubber adsorbed at the filler interface can form confined glassy regions or “glassy bridges” between adjacent filler particles. These rigid domains can persist up to Tg + 150 °C,77–80 well beyond the 60 °C operating condition, and thus significantly impact the composite's dynamic mechanical response.
δ at 60 °C relative to P1, implying higher RR. In contrast, PEG-modified samples (P2–P4) displayed a gradual decrease in tan δ with increasing PEG content, indicating reduced RR. These opposing trends could be explained by the distinct viscoelastic responses driven by differences in E′ and E′′ at elevated temperatures. At 60 °C—where RR is assessed—previously discussed mechanisms such as occluded rubber dynamics remain influential, but additional phenomena must also be considered. Prior studies have shown that thin (∼1 nm) layers of rubber adsorbed at the filler interface can form confined glassy regions or “glassy bridges” between adjacent filler particles. These rigid domains can persist up to Tg + 150 °C,77–80 well beyond the 60 °C operating condition, and thus significantly impact the composite's dynamic mechanical response.
In S1, both E′ and E′′ were lower than those in P1. The reduction in E′ resulted from improved filler dispersion and decreased occluded rubber content due to TESPT's chemical bonding with silica. However, despite the improved dispersion, TESPT also anchored some interfacial rubber domains, preserving localized confinement. This partial retention of glassy rubber, consistent with the thin but rigid interfacial rims observed in AFM modulus map (Fig. 6(d)), limited the extent of E′′ reduction. Consequently, the imbalance—substantial stiffness reduction with limited hysteresis suppression—led to an increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 60 °C, indicating increased RR.
δ at 60 °C, indicating increased RR.
Conversely, in PEG-modified composites (P2–P4), similar reduction trends in E′ and E′′ were observed, but the overall effect was a reduction in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with increasing PEG concentration. This suggests that the damping mechanism was governed primarily by E′′. At 60 °C, the dominant influence of PEG was its ability to disrupt the formation of rigid glassy rubber bridges by adsorbing at the filler interface, giving rise to more compliant interfacial regions. Alongside this, the increase in PEG content also promoted the formation of occluded rubber domains through enhanced filler aggregation. However, these domains—formed via physically bound PEG layers—remained deformable at this temperature and allowed for interfacial mobility rather than energy dissipation. Unlike glassy bridges that persist near Tg and contribute to frictional losses, the PEG-associated regions accommodated strain with reduced hysteresis. As a result, E′′ steadily decreased with increasing PEG, while E′ also declined due to enhanced filler rearrangement. Together, these effects yielded a consistent reduction in tan
δ with increasing PEG concentration. This suggests that the damping mechanism was governed primarily by E′′. At 60 °C, the dominant influence of PEG was its ability to disrupt the formation of rigid glassy rubber bridges by adsorbing at the filler interface, giving rise to more compliant interfacial regions. Alongside this, the increase in PEG content also promoted the formation of occluded rubber domains through enhanced filler aggregation. However, these domains—formed via physically bound PEG layers—remained deformable at this temperature and allowed for interfacial mobility rather than energy dissipation. Unlike glassy bridges that persist near Tg and contribute to frictional losses, the PEG-associated regions accommodated strain with reduced hysteresis. As a result, E′′ steadily decreased with increasing PEG, while E′ also declined due to enhanced filler rearrangement. Together, these effects yielded a consistent reduction in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, leading to lower RR and thus improved energy-saving performance.
δ, leading to lower RR and thus improved energy-saving performance.
In summary, while TESPT enhanced WG by increasing molecular mobility and reducing matrix stiffness, it did so at the cost of increased RR due to persistent interfacial constraints. In contrast, PEG enhanced WG and reduced RR through a dynamic interplay of filler network reorganization, interfacial sliding, and suppression of glassy rubber bridges. This synergy enabled a more favorable viscoelastic response across temperature ranges, effectively overcoming the WG–RR trade-off observed in TESPT-based systems.
3.8. Evaluation of PEG as an interfacial Modifier in the Modified Performance Triangle
In this section, the overall effectiveness of polyethylene glycol (PEG) as an interfacial modifier is assessed. Traditionally, tire performance is optimized by balancing rolling resistance (RR), wet grip (WG), and abrasion loss, collectively visualized in the well-known “magic triangle”. However, in response to the evolving demands of modern mobility—particularly those associated with electric vehicles (EVs), which require improved load-bearing capacity and handling—a revised framework is proposed. In this study, abrasion loss is replaced by tread stiffness (S), which more accurately reflects the structural performance requirements of EV tires. Accordingly, Fig. 10 presents a modified magic triangle plot, with the TESPT-modified sample (S1) used as a reference to highlight performance enhancements enabled by PEG. For comparative purposes, all performance indices in S1 were normalized to 100. These indices were derived using Equations (S1–S3) and are summarized in Table S2, with detailed calculations provided in the SI.As previously discussed, PEG and TESPT influence WG, RR, and stiffness through distinctly different filler–polymer interaction mechanisms. Each parameter plays a critical role in determining overall tire performance, and achieving the optimal balance among them remains a central challenge in tread compound design.
Wet grip (WG) performance was evaluated using tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 0 °C as the primary viscoelastic indicator. Compared to TESPT-modified S1, PEG incorporation resulted in tan
δ at 0 °C as the primary viscoelastic indicator. Compared to TESPT-modified S1, PEG incorporation resulted in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ changes of −7%, +14%, and +24% for samples P2 (3 phr), P3 (6.4 phr), and P4 (11 phr), respectively. These improvements were attributed to two concurrent effects induced by PEG incorporation: an increase in tan
δ changes of −7%, +14%, and +24% for samples P2 (3 phr), P3 (6.4 phr), and P4 (11 phr), respectively. These improvements were attributed to two concurrent effects induced by PEG incorporation: an increase in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ intensity with peak temperatures lying closer to 0 °C, and the enhanced formation of occluded rubber domains. The former enhanced viscoelastic dissipation at the testing condition, where segmental relaxations are particularly active. Meanwhile, the latter provided additional interfacial dissipation under dynamic strain, as more extensive occluded rubber domains—formed via physically adsorbed PEG layers—enabled greater interfacial sliding without acting as rigid load-bearing zones. This combined effect resulted in a steady decline in E′ and moderate elevation of E′′, reflecting a matrix that was softer yet more capable of dissipating energy. As a result, even low PEG concentrations (e.g., P2) yielded WG performance approaching that of TESPT-modified S1, while higher PEG loadings led to further enhancements.
δ intensity with peak temperatures lying closer to 0 °C, and the enhanced formation of occluded rubber domains. The former enhanced viscoelastic dissipation at the testing condition, where segmental relaxations are particularly active. Meanwhile, the latter provided additional interfacial dissipation under dynamic strain, as more extensive occluded rubber domains—formed via physically adsorbed PEG layers—enabled greater interfacial sliding without acting as rigid load-bearing zones. This combined effect resulted in a steady decline in E′ and moderate elevation of E′′, reflecting a matrix that was softer yet more capable of dissipating energy. As a result, even low PEG concentrations (e.g., P2) yielded WG performance approaching that of TESPT-modified S1, while higher PEG loadings led to further enhancements.
In contrast, RR—quantified by tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at 60 °C—showed substantial reductions with PEG incorporation: by 37%, 40%, and 47% for P2, P3, and P4, respectively. At this temperature, RR is primarily influenced by the presence of confined glassy bridges—immobilized rubber domains between adjacent filler particles—that restrict chain motion and promote hysteresis loss. While TESPT enhanced filler dispersion and reduced both E′ and E′′, its chemical anchoring preserved certain rigid interfacial regions, limiting the extent of hysteresis suppression. PEG, by contrast, physically adsorbed onto silica surfaces and modified the interfacial architecture in two key ways: it disrupted the continuity of glassy bridges and introduced more deformable occluded rubber domains that remained flexible at 60 °C. These domains, formed through PEG-mediated filler aggregation, accommodated strain and facilitated local interfacial mobility. As a result, E′′ steadily decreased with increasing PEG due to reduced energy dissipation at rigid interfaces, while E′ also declined owing to network reorganization. The extent of these effects scaled with PEG content, ultimately producing smoother stress transfer, less frictional loss, and a significant reduction in RR, corresponding to improved energy-saving performance.
δ at 60 °C—showed substantial reductions with PEG incorporation: by 37%, 40%, and 47% for P2, P3, and P4, respectively. At this temperature, RR is primarily influenced by the presence of confined glassy bridges—immobilized rubber domains between adjacent filler particles—that restrict chain motion and promote hysteresis loss. While TESPT enhanced filler dispersion and reduced both E′ and E′′, its chemical anchoring preserved certain rigid interfacial regions, limiting the extent of hysteresis suppression. PEG, by contrast, physically adsorbed onto silica surfaces and modified the interfacial architecture in two key ways: it disrupted the continuity of glassy bridges and introduced more deformable occluded rubber domains that remained flexible at 60 °C. These domains, formed through PEG-mediated filler aggregation, accommodated strain and facilitated local interfacial mobility. As a result, E′′ steadily decreased with increasing PEG due to reduced energy dissipation at rigid interfaces, while E′ also declined owing to network reorganization. The extent of these effects scaled with PEG content, ultimately producing smoother stress transfer, less frictional loss, and a significant reduction in RR, corresponding to improved energy-saving performance.
Stiffness (S) also emerged as a critical performance parameter in this revised framework. While the suppression of filler–filler interactions typically leads to reduced RR—by lowering hysteresis losses at high temperatures—and enhanced WG—by increasing damping at low temperatures—stiffness must be carefully regulated to ensure durability, steering and handling precision, and load-bearing capacity. Excessive stiffness enhances tread strength and abrasion resistance but can lead to increased road noise and reduced ride comfort; conversely, insufficient stiffness compromises structural integrity under dynamic loading. Compared to S1, PEG-modified samples demonstrated increased stiffness by 128%, 81%, and 41% for P2, P3, and P4, respectively. Unlike conventional dispersants that simply weaken filler networks, PEG exerted a dual-phase effect: it promoted filler flocculation, thereby increasing occluded rubber and structural rigidity, while simultaneously enabling interfacial sliding to counterbalance excess stiffness under stress. This dynamic regulation enabled PEG to maintain an optimal stiffness range that supports effective load transfer, abrasion resistance, and balanced handling.
In summary, while TESPT enhances WG through improved dispersion and matrix softening, it also results in higher RR and lower stiffness. In contrast, PEG offers a more balanced approach, leveraging its dual-functionality to simultaneously reduce RR, improve WG, and fine-tune stiffness. This synergistic effect is particularly evident at optimal PEG concentrations, with P3 and P4 demonstrating the most favorable trade-offs among RR, WG, and stiffness. These findings highlight PEG's strong potential as an effective interfacial modifier for next-generation, high-performance tire compounds—especially in EV-oriented applications where balanced mechanical and energy-efficient properties are essential.
4. Conclusion
In this study, we developed a SAXS-guided hybrid modeling strategy that, for the first time in this context, integrates mass-fractal and Debye–Bueche gel-like models to resolve the hierarchical filler architecture in silica-reinforced rubber nanocomposites. A key innovation of this framework is the explicit incorporation of occluded rubber domains—a structurally significant phase—which can be quantitatively extracted and correlated with bulk viscoelastic performance. In particular, occluded rubber serves as a morphological readout of filler network evolution: it increases systematically with PEG content, reflecting enhanced filler aggregation as well as the development of deformable, slippage-prone interfaces under dynamic strain. This framework was used to evaluate poly(ethylene glycol) (PEG) as a sustainable, silane-free interfacial modifier, with TESPT-based systems as benchmarks. While TESPT promotes dispersion and suppresses occluded rubber through covalent coupling, PEG enhances aggregation and occluded rubber formation via hydrogen bonding. Despite this, PEG-modified systems achieved enhanced WG and reduced RR, while retaining 81% higher stiffness. This mechanistic profile diverges from conventional dispersion-centric frameworks by demonstrating that a reconfigurable filler network, enabled by reversible interfacial interactions and tracked via occluded rubber modelling, can drive more enhanced performance. More broadly, this work establishes a transferable, structure-informed strategy for designing high-performance, sustainable rubber nanocomposites.Author contributions
C.-T. H., H.-Y. L.: data curation; analysis; visualization; and draft preparation. P.-H. C., H.-Y. D.: data curation; validation and visualization. J.-M. L., U.-S. J.: data curation. L. L., C.-S. T.: conceptualization, data curation and writing—review and editing. C.-C. H., C.-A. D.: conceptualization; funding, project administration and writing—review and editing.Conflicts of interest
The authors declare no conflict of interest.Data availability
All data supporting this study are presented in the manuscript and the supplementary information (SI). The SI contains tables summarizing filler cluster size, occluded-rubber mesh size, and performance indices, as well as figures including FTIR spectra, SAXS analyses, and TEM statistical results. See DOI: https://doi.org/10.1039/d5mh01389e.Raw data underlying the figures are available from the corresponding author upon reasonable request.
Acknowledgements
The authors gratefully acknowledge the financial support from the National Science and Technology Council of Taiwan (NSTC 110-2221-E-002-005-MY3; 112-2222-E-218-002). They also thank the National Synchrotron Radiation Research Center (NSRRC), Taiwan, for providing beamtime and technical assistance at beamlines TPS 25A1, TPS 13A, and TLS 23A1, and Mr Yu-Ting Yen for conducting the AFM measurements and data analysis.References
- S. Luo, K. Dong, S. Wang and A. He, Compos. Sci. Technol., 2024, 258, 110899 CrossRef CAS.
- P. Weng, Z. Tang and B. Guo, Polymer, 2020, 190, 122244 CrossRef.
- J. Thomas and R. Patil, Environ. Sci. Technol., 2023, 57, 2209–2216 CrossRef CAS PubMed.
- J. T. Byers, Rubber Chem. Technol., 2002, 75, 527–548 CAS.
- S. Sattayanurak, K. Sahakaro, W. Kaewsakul, W. K. Dierkes, L. A. E. M. Reuvekamp, A. Blume and J. W. M. Noordermeer, Polym. Test., 2020, 81, 106173 CrossRef CAS.
- J. Neethirajan, A. R. Parathodika, G.-H. Hu and K. Naskar, Funct. Compos. Mater., 2022, 3, 7 CrossRef CAS.
- A. Mazumder, J. Chanda, S. Bhattacharyya, S. Dasgupta, R. Mukhopadhyay and A. K. Bhowmick, J. Appl. Polym. Sci., 2021, 138, 51236 CrossRef CAS.
- Q. Zhao, F. Niu, J. Liu and H. Yin, Polymers, 2024, 16, 1899 CrossRef CAS PubMed.
- G.-Y. Um, T. Kwon, S. H. Lee, S. H. Kim, M. Y. Kim, S. Choi, S. Yu and J. H. Lee, Funct. Compos. Struct., 2024, 6, 015006 CrossRef CAS.
- D. Wang, F. Ren, C. Zhu, J. Feng, Q. Cheng, S. Chen, G. Shen and F. Wang, Rubber Chem. Technol., 2018, 92, 310–325 Search PubMed.
- S. M. Hosseini, H. Najjarzadeh, M. Razzaghi-Kashani and A. Baniasad, Rubber Chem. Technol., 2023, 96, 383–399 CAS.
- J. Hui, L. Liu, Z. Yu, Q. Wu and L. Zhang, Polym. Compos., 2023, 44, 6957–6968 CrossRef CAS.
- S. Li, X. Zhai, Z. Chen, D. Han, X. Ye and L. Zhang, Compos. Commun., 2024, 46, 101836 CrossRef.
- X. Zhai, Y. Chen, D. Han, J. Zheng, X. Wu, Z. Wang, X. Li, X. Ye and L. Zhang, Appl. Surf. Sci., 2021, 558, 149819 CrossRef CAS.
- C. Lin, Jr., W. L. Hergenrother and A. S. Hilton, Rubber Chem. Technol., 2002, 75, 215–245 Search PubMed.
- K. Lim, Y. A. Kim, M. S. Ryu, J. Jung, D. Kim, Z. Li, J. H. Park and J. Bang, ACS Appl. Polym. Mater., 2025, 7, 2731–2742 CrossRef CAS.
- P. Sekar, EngD Thesis, University of Twente, 2020 Search PubMed.
- C. Liu, M. Guo, X. Zhai, X. Ye and L. Zhang, Polymers, 2020, 12, 1257 CrossRef CAS PubMed.
- S. Yu, Z. Tang, S. Wu and B. Guo, Compos. Sci. Technol., 2022, 227, 109624 CrossRef CAS.
- X. Zhai, D. Han, G. Zhang, X. Chen, X. Wu, X. Li, J. Zheng, X. Ye and L. Zhang, Compos. Sci. Technol., 2022, 223, 109413 CrossRef CAS.
- G. P. Baeza, F. Dalmas, F. Dutertre and J.-C. Majesté, Soft Matter, 2020, 16, 3180–3186 RSC.
- Z. Li, Y. Gong, H. Li, M. Jiang and L. Dong, Adv. Funct. Mater., 2024, 34, 2309157 CrossRef CAS.
- G. H. Trinh, M. Desloir, F. Dutertre, J.-C. Majesté, F. Dalmas and G. P. Baeza, Soft Matter, 2019, 15, 3122–3132 RSC.
- M. Xu, H. Xue, W. Y. Tin, H. Wang, Z. Yong and Q. Wang, Polymers, 2021, 13, 788 CrossRef CAS PubMed.
- S. Hussain, Z. Zhao, Y. Song and C. Zhang, J. Appl. Polym. Sci., 2023, 140, e54401 CrossRef CAS.
- L.-Z. Huang, K. Song, C.-W. Yang, J.-J. Han, T.-T. Yang, J.-Z. Xu, G.-A. Sun, Z.-M. Li and D. Liu, Polymer, 2023, 274, 125926 CrossRef CAS.
- A. Botti, W. Pyckhout-Hintzen, D. Richter, V. Urban, E. Straube and J. Kohlbrecher, Polymer, 2003, 44, 7505–7512 CrossRef CAS.
- J.-J. Han, C.-S. Wei, A. Lu, K. Song, Q. Zhang, G.-A. Sun, J.-Z. Xu, Z.-M. Li and D. Liu, Polymer, 2024, 301, 127044 CrossRef CAS.
- Y. Wang, M. Sun, H. Zhang, Y. Lu, W. You, F. Bian and W. Yu, Macromolecules, 2023, 56, 934–946 CrossRef CAS.
- T. Koga, T. Hashimoto, M. Takenaka, K. Aizawa, N. Amino, M. Nakamura, D. Yamaguchi and S. Koizumi, Macromolecules, 2008, 41, 453–464 CrossRef CAS.
- D. Yamaguchi, T. Yuasa, T. Sone, T. Tominaga, Y. Noda, S. Koizumi and T. Hashimoto, Macromolecules, 2017, 50, 7739–7759 CrossRef CAS.
- K. Rishi, G. Beaucage, V. Kuppa, A. Mulderig, V. Narayanan, A. McGlasson, M. Rackaitis and J. Ilavsky, Macromolecules, 2018, 51, 7893–7904 CrossRef CAS.
- A. Bouty, L. Petitjean, C. Degrandcourt, J. Gummel, P. Kwaśniewski, F. Meneau, F. Boué, M. Couty and J. Jestin, Macromolecules, 2014, 47, 5365–5378 CrossRef CAS.
- D. Liu, J. Chen, L. Song, A. Lu, Y. Wang and G. Sun, Polymer, 2017, 120, 155–163 CrossRef CAS.
- N. Gundlach and R. Hentschke, Polymers, 2018, 10, 446 CrossRef PubMed.
- I. Yakovlev, M. Sztucki, F. Fleck, H. A. Karimi-Varzaneh, J. Lacayo-Pineda, C. Vatterott and U. Giese, J. Appl. Polym. Sci., 2025, 142, e56403 CrossRef CAS.
- G. Beaucage, H. K. Kammler and S. E. Pratsinis, J. Appl. Crystallogr., 2004, 37, 523–535 CrossRef CAS.
- G. J. Schneider, W. Hengl, K. Brandt, R. Schuster and D. Göritz, Soft Mater., 2019, 17, 215–227 CrossRef CAS.
- B. Omnès, S. Thuillier, P. Pilvin, Y. Grohens and S. Gillet, Composites, Part A, 2008, 39, 1141–1149 CrossRef.
- B. Ahn, D. Kim, K. Kim, I. J. Kim, H. J. Kim, C. H. Kang, J.-Y. Lee and W. Kim, Compos. Interfaces, 2019, 26, 585–596 CrossRef CAS.
- P. Thaptong, P. Jittham and P. Sae-oui, J. Appl. Polym. Sci., 2021, 138, 50855 CrossRef CAS.
- M. Barghamadi, M. Karrabi, M. H. R. Ghoreishy and G. Naderi, J. Appl. Polym. Sci., 2023, 140, e53863 CrossRef CAS.
- D. Wang, S. Chen, L. Chen, B. Chen, F. Ren, C. Zhu and J. Feng, J. Appl. Polym. Sci., 2019, 136, 47918 CrossRef.
- H. Zhang, S. Zheng, L. Zheng and M.-J. Wang, Polym. Eng. Sci., 2021, 61, 1368–1378 CrossRef CAS.
- O. Shih, K.-F. Liao, Y.-Q. Yeh, C.-J. Su, C.-A. Wang, J.-W. Chang, W.-R. Wu, C.-C. Liang, C.-Y. Lin, T.-H. Lee, C.-H. Chang, L.-C. Chiang, C.-F. Chang, D.-G. Liu, M.-H. Lee, C.-Y. Liu, T.-W. Hsu, B. Mansel, M.-C. Ho, C.-Y. Shu, F. Lee, E. Yen, T.-C. Lin and U. Jeng, J. Appl. Crystallogr., 2022, 55, 340–352 CrossRef CAS PubMed.
- U.-S. Jeng, C. H. Su, C.-J. Su, K.-F. Liao, W.-T. Chuang, Y.-H. Lai, J.-W. Chang, Y.-J. Chen, Y.-S. Huang, M.-T. Lee, K.-L. Yu, J.-M. Lin, D.-G. Liu, C.-F. Chang, C.-Y. Liu, C.-H. Chang and K. S. Liang, J. Appl. Crystallogr., 2010, 43, 110–121 CrossRef CAS.
- Y.-S. Sun, Y.-Q. Jian, S.-T. Yang, H.-F. Wang, B. A. Junisu, C.-Y. Chen and J.-M. Lin, Langmuir, 2024, 40, 7680–7691 CrossRef CAS PubMed.
- S. Nagarajan, W.-T. Chuang, J.-M. Lin, C.-Y. Chen and E. M. Woo, Mater. Today Chem., 2024, 41, 102312 CrossRef CAS.
- M.-J. Wang, Rubber Chem. Technol., 1998, 71, 520–589 CAS.
- Q. A'Yuni, A. Rahmayanti, H. Hartati, P. Purkan, R. Subagyo, N. Rohmah, L. R. Itsnaini and M. A. Fitri, RSC Adv., 2023, 13, 2692–2699 RSC.
- F. Apriyani, S. R. Sari, H. T. B. M. Petrus, M. Angelina, R. V. Manurung, N. L. W. Septiani, B. Yuliarto and S. N. A. Jenie, Nanoscale, 2025, 17, 5438–5446 RSC.
- R. Z. Douaihy, L. Lakiss, M. El-Roz, Y. Levaque, A. Vimont and P. Bazin, Phys. Chem. Chem. Phys., 2023, 25, 11555–11565 RSC.
- Z. Varga, J. Mihály, S. Berényi and A. Bóta, Eur. Polym. J., 2013, 49, 2415–2421 CrossRef CAS.
- P. Malo de Molina, S. Lad and M. E. Helgeson, Macromolecules, 2015, 48, 5402–5411 CrossRef CAS.
- T.-Y. Yu, Y.-H. Tseng, C.-C. Wang, T.-H. Lin, M.-C. Wu, C.-S. Tsao and W.-F. Su, Macromol. Mater. Eng., 2022, 307, 2100871 CrossRef CAS.
- D. C. Schoenmakers, A. E. Rowan and P. H. J. Kouwer, Nat. Commun., 2018, 9, 2172 CrossRef PubMed.
- M. E. Helgeson, Y. Gao, S. E. Moran, J. Lee, M. Godfrin, A. Tripathi, A. Bose and P. S. Doyle, Soft Matter, 2014, 10, 3122–3133 RSC.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- S. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- G. V. Schulz, Z. Phys. Chem., 1935, 30B, 379–398 CrossRef.
- M. Kotlarchyk and S. H. Chen, J. Chem. Phys., 1983, 79, 2461–2469 CrossRef CAS.
- H.-C. Liao, C.-S. Tsao, Y.-T. Shao, S.-Y. Chang, Y.-C. Huang, C.-M. Chuang, T.-H. Lin, C.-Y. Chen, C.-J. Su, U. S. Jeng, Y.-F. Chen and W.-F. Su, Energy Environ. Sci., 2013, 6, 1938–1948 RSC.
- Y.-C. Huang, C.-S. Tsao, T.-Y. Huang, H.-C. Cha, D. Patra, C.-J. Su, U. S. Jeng, K.-C. Ho, K.-H. Wei and C.-W. Chu, J. Phys. Chem. C, 2015, 119, 16507–16517 CrossRef CAS.
- V. S. Raghuwanshi and G. Garnier, Adv. Colloid Interface Sci., 2019, 274, 102044 CrossRef CAS PubMed.
- M. Shibayama, Polym. J., 2011, 43, 18–34 CrossRef CAS.
- Y. Shinohara, K. Kayashima, Y. Okumura, C. Zhao, K. Ito and Y. Amemiya, Macromolecules, 2006, 39, 7386–7391 CrossRef CAS.
- T. Kakara, A. Izumi, Y. Shudo, A. Shundo and K. Tanaka, Polym. J., 2024, 57, 341–342 Search PubMed.
- P. Sotta, P.-A. Albouy, M. Abou Taha, D. R. Long, P. Grau, C. Fayolle and A. Papon, Macromolecules, 2017, 50, 6314–6322 CrossRef CAS.
- J. Fröhlich, W. Niedermeier and H. D. Luginsland, Composites, Part A, 2005, 36, 449–460 CrossRef.
- M. Viktorova, R. Hentschke, F. Fleck, F. Taherian and H. A. Karimi-Varzaneh, Comput. Mater. Sci., 2023, 223, 112144 CrossRef CAS.
- J. Sun, Y. Song, Q. Zheng, H. Tan, J. Yu and H. Li, J. Polym. Sci. B: Polym. Phys., 2007, 45, 2594–2602 CrossRef CAS.
- V. Bijina, P. J. Jandas, J. Jose, N. Muhammed Ajnas, K. P. Abhitha and H. John, J. Appl. Polym. Sci., 2023, 140, e53508 CrossRef CAS.
- V. D. A. Veiga, T. M. Rossignol, J. d S. Crespo and L. N. Carli, J. Appl. Polym. Sci., 2017, 134, 45334 CrossRef.
- Y. Li, B. Han, S. Wen, Y. Lu, H. Yang, L. Zhang and L. Liu, Composites, Part A, 2014, 62, 52–59 CrossRef CAS.
- H. Takino, R. Nakayama, Y. Yamada, S. Kohjiya and T. Matsuo, Rubber Chem. Technol., 1997, 70, 584–594 CAS.
- N. Vleugels, W. Pille-Wolf, W. K. Dierkes and J. W. M. Noordermeer, Rubber Chem. Technol., 2015, 88, 65–79 CAS.
- A. P. Meera, S. Said, Y. Grohens and S. Thomas, J. Phys. Chem. C, 2009, 113, 17997–18002 CrossRef CAS.
- J. Berriot, H. Montes, F. Lequeux, D. Long and P. Sotta, Europhys. Lett., 2003, 64, 50–56 CrossRef CAS.
- S. Merabia, P. Sotta and D. R. Long, Macromolecules, 2008, 41, 8252–8266 CrossRef CAS.
- S.-S. Choi and E. Ko, Polym. Test., 2014, 40, 170–177 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |










