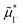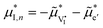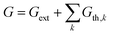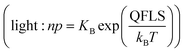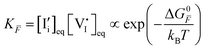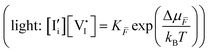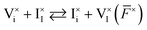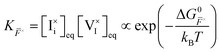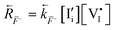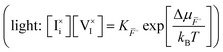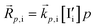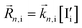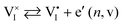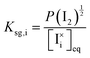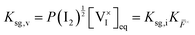Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect chemistry of mixed ionic–electronic conductors under light: halide perovskites as a master example
Davide
Moia†
 * and
Joachim
Maier
* and
Joachim
Maier

Max Planck Institute for Solid State Research, Heisenbergstraße 1, 70569 Stuttgart, Germany. E-mail: moia.davide@gmail.com
First published on 7th November 2025
Abstract
Shining light on a mixed ionic–electronic conductor induces variations in both its electronic and ionic behaviors. While optoelectronic processes in semiconductors with negligible ionic conductivities are well understood, the role of mobile ions in photoactive mixed conductors, such as hybrid halide perovskites, is largely unexplored. Here, we propose a model addressing this problem, combining optoelectronics and optoionics. Using methylammonium lead iodide (MAPI) as a model material, we discuss the expected influence of optical bias on the charge carrier chemistry of mixed conductors under steady-state conditions. We show that changes in the concentration of ionic defects under light with respect to the dark case are a direct consequence of their coupling to electrons and holes through the component chemical potential (iodine in the case of MAPI) and the electroneutrality condition. Based on the trend in the quasi-Fermi level splitting in the mixed conductor, we emphasize implications of controlling point defect chemistry for the function and performance optimization of solar energy conversion devices, including those based on halide perovskites. Lastly, we show that, in the presence of multiple redox reactions mediating the ionic and electronic quasi-equilibrium, either positive or negative changes in the ionic defect pair chemical potential can be obtained. These findings indicate the intriguing possibility to increase or reduce ionic defect concentrations in mixed conductors through exposure to light.
New conceptsWe present a model describing the defect chemistry of mixed conductors under light. The evaluation of the electronic and ionic charge carrier quasi-equilibrium upon illumination reveals light-induced ionic phenomena resulting from the interaction of such charge carriers with each other as well as with the gas phase. Using representative input parameters for iodide perovskites, we identify and explore the key kinetic parameters that control the mixed conductor's electronic and ionic response under light, emphasizing the importance of understanding defect chemical effects in the optimization of solar cells. We demonstrate that light-induced enhancement and reduction in ionic defect concentrations in these materials are a natural consequence of the electroneutrality condition and the coupling between ionic and electronic charge carriers through the component chemical potential. The prediction that light can induce changes in stoichiometry and/or overall enhancement or reduction in ionic defect concentrations has direct consequences for any photoelectrochemical device using mixed conductors that include redox-active ionic defects, such as perovskite solar cells. More broadly, this work points to new avenues in the development of photodriven stoichiometry control in mixed conductors as well as in the design of materials and devices where defect concentrations can be either enhanced or reduced by light. |
Introduction
Understanding the effect of illumination on the properties of mixed ionic–electronic conductors represents a basic yet largely unanswered question in the field of materials science. Addressing this question has fundamental implications not only for existing photoelectrochemical devices, including solar cells and other energy conversion and storage systems, but also for the development of novel devices in the fields of catalysis, computing and beyond.The description of a photoelectrochemical system can be greatly simplified, if the condition of local equilibrium applies during its operation. It is then straightforward to define the thermodynamic state at each position in the device through parameters including the (electro)chemical potential for all charged and neutral species, stoichiometry, defect formation energies to name a few. The quantification of such parameters is still possible locally, when a chemical or electrochemical bias applied across the system induces gradients in the electrochemical potentials of electrons and ions (e.g. batteries or fuel cells under operation).1
In many cases of interest, the applied bias leads to deviation from local equilibrium. This is the case for semiconductors used in solar cells, where light absorption leads to local non-equilibrium between the electronic charges populating different energy bands.2,3 Local non-equilibrium can also arise in the dark, when a voltage bias is applied to such devices, due to injection selectivity of the contacts. A similar condition may, in principle, be obtained for different ionic defects, if the relevant sublattices are not at equilibrium with each other. The discussion of these situations can be addressed using quasi-equilibrium arguments, where different defects related to a specific component (e.g. conduction band electrons, e′, and valence band holes, h˙, related to electrons e−) are described by separate occupation statistical functions and separate quasi-electrochemical potentials. This treatment is applicable if equilibration within each charge carrier population occurs at a much faster rate than any of the reactions in which such carriers are involved.
In general, given a material component or defect j, its quasi-electrochemical potential can be expressed in the form:
 | (1) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) j,eq and δ
j,eq and δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) j, respectively.
j, respectively.
While these are not simple energies, the quasi-electrochemical potentials of electronic charges are often discussed in terms of quasi-Fermi energies for electrons, EFn, and for holes, EFp, each referring to separate Fermi–Dirac statistics.4,5 The resulting quasi-Fermi level splitting QFLS = EFn − EFp can then be expressed as the combined electron–hole chemical potential change according to
QFLS = δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e′ + δ e′ + δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h˙, h˙, | (2) |
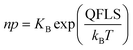 | (3) |
In a mixed ionic–electronic conductor, where electronic and ionic charges are mobile, the equilibrium situation is defined by a more complex set of equations. These are derived from the mass-action laws involving ionic and electronic defects, coupled through the chemical potential (partial pressure) of components associated with the relevant mobile ions.6–8 Under bias, the coupling between electrons and ions in these materials means that the ionic situation can vary too, even when a purely optoelectronic excitation is considered.
Hybrid halide perovskites are a relevant example to this question. These materials are used as active layers for high performance optoelectronic devices while also showing significant ionic conduction even at room temperature.9,10 In methylammonium lead iodide (MAPbI3 or MAPI), a reference compound for hybrid perovskite photovoltaics, migration of iodide defects (specifically vacancies) enables access to its defect chemical behavior by varying the iodine partial pressure in the system (P(I2)).3,11,12 While the characterization of MAPI under equilibrium conditions is becoming established, the study of its properties under light has resulted in numerous peculiar observations including anomalies in mass transport, phase stabilities and mechanical properties. Many of them have been interpreted in terms of coupled ionic–electronic effects and are still matter of debate.13–18
Other “unusual” photoelectrochemical effects in various mixed conductors have also been interpreted based on interactions between photogenerated electronic carriers and ionic defects (photoionic or optoionic effects).14,19–22 The study of light effects in strontium titanate (STO)19 highlighted the enhanced kinetics of oxygen incorporation in the material by (above bandgap) illumination, explained by the electronic contribution to the exchange reaction. While these investigations showed the effect of light on the surface kinetics, later reports discussed stoichiometric changes in conductivity on illumination for MAPI or STO.14,22–24 Light effects have also been reported as far as the grain boundary resistance (for Gd-doped ceria) is concerned.21
All these reports point towards fundamental interactions between electronic and ionic charges, which, upon a drastic increase of electronic charge carrier concentration under light, inevitably modify the ionic equilibrium too. While these studies have suggested models that could explain the experimental results, systematically treating the quasi-equilibrium behavior of mixed conductors under light bias means entering largely unknown territory.
Fig. 1 displays the research question of this study (top schematics): Given a mixed conductor (e.g. MAPI) and the point defect model describing its equilibrium situation (e.g. P(I2) dependence of defect concentrations, cf. dashed lines in Fig. 3), how to describe the situation under light? This question is addressed at the bottom of Fig. 1 based on the generalized energy level representation, which considers the standard partial (free) energy levels and electrochemical potentials associated with the electronic and the ionic (here iodide only, for simplicity) defects.7 In the diagram, the position of the electrochemical potentials ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) I− and
I− and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− relative to the standard potentials (
e− relative to the standard potentials (![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) 0) determines the concentrations of iodide vacancies and interstitials,
0) determines the concentrations of iodide vacancies and interstitials, 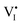 and
and  , and electrons and holes, e′ and h˙, respectively.
, and electrons and holes, e′ and h˙, respectively.
The chemical potential of iodine in MAPI corresponds to μI,MAPI = ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) I− −
I− − ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− and, at equilibrium, it is equal to the given chemical potential of iodine in the gas phase,
e− and, at equilibrium, it is equal to the given chemical potential of iodine in the gas phase, 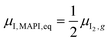 . Taking the former relationship for granted also for the nonequilibrium situation implies that changes in the electrochemical potential of electronic charges due to an applied bias result in changes in the iodine and/or iodide (electro)chemical potential in the material. The situation is complicated by the fact that electrons and holes are now not in equilibrium, as indicated by the two quasi-electrochemical potentials
. Taking the former relationship for granted also for the nonequilibrium situation implies that changes in the electrochemical potential of electronic charges due to an applied bias result in changes in the iodine and/or iodide (electro)chemical potential in the material. The situation is complicated by the fact that electrons and holes are now not in equilibrium, as indicated by the two quasi-electrochemical potentials  and
and 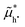 . Furthermore, ionic defect concentrations may also vary under bias. Therefore, the straightforward definition of μI,MAPI used above is no longer applicable (Fig. 1b).
. Furthermore, ionic defect concentrations may also vary under bias. Therefore, the straightforward definition of μI,MAPI used above is no longer applicable (Fig. 1b).
One way to describe this situation involves the definition of iodine quasi-chemical potentials, such as  and
and 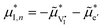 (assuming
(assuming  ), which would be identical at equilibrium but different otherwise (see also discussion by Kim et al.14 and Viernstein et al.23 for halide and oxide perovskites, respectively). Their relationship with the chemical potential of iodine in the gas phase is then kinetically determined. Further complexity is introduced by the influence of mobile ionic defects on the optoelectronic quasi-equilibrium (e.g. the electron–hole recombination rate).25–29 A model to evaluate such interplays and to predict the electronic and ionic charge carrier concentrations as a function of the component partial pressures (e.g. P(I2) in MAPI) in a mixed conductor is currently missing.30
), which would be identical at equilibrium but different otherwise (see also discussion by Kim et al.14 and Viernstein et al.23 for halide and oxide perovskites, respectively). Their relationship with the chemical potential of iodine in the gas phase is then kinetically determined. Further complexity is introduced by the influence of mobile ionic defects on the optoelectronic quasi-equilibrium (e.g. the electron–hole recombination rate).25–29 A model to evaluate such interplays and to predict the electronic and ionic charge carrier concentrations as a function of the component partial pressures (e.g. P(I2) in MAPI) in a mixed conductor is currently missing.30
Here, we address the problem shown in Fig. 1 by coupling the defect chemical relationships describing ionic and electronic disorder in a mixed ionic–electronic conductor and the component quasi-equilibrium with the gas phase, with the equations associated with the generation and recombination of electronic charge carriers. We present results obtained using MAPI as a model system and illustrate the expected trend in defect concentrations under illumination. In the framework of quasi-equilibrium considerations, we discuss implications of these results for the study of photoactive mixed conductors and their use in photoelectrochemical devices for energy conversion. By exploring the effect of relevant kinetic and thermodynamic parameters on the material's defect chemistry under light, special emphasis is given to the predicted possibility to control (increase but also decrease) ionic defect concentration using light.
The model
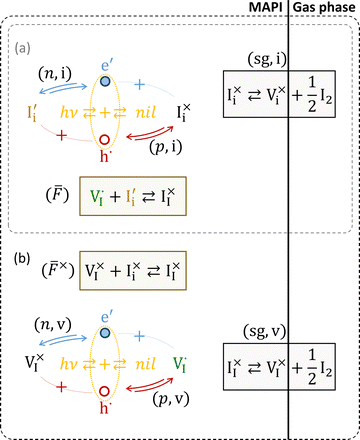
The model presented in this study accounts for internal defect reactions occurring in a mixed ionic–electronic conductor exposed to light and for the exchange quasi-equilibria with the gas phase. The model represents the simplest possible problem that allows for a complete evaluation of the charge carrier chemistry in mixed conductors under light resulting from all the relevant and interacting ionic and electronic processes. For a discussion of the defect chemistry of mixed conductors under equilibrium conditions, we refer the reader to previous studies.7,8 Below, we describe the model in detail (see also schematic representations of the model in Fig. 2 and in Section 1 of the SI).We refer to a pore-free thin film of MAPI exposed to a set illumination condition and to a fixed iodine partial pressure, P(I2), at room temperature. The results and trends presented in the next section are relevant not only to halide perovskites but also to any photo-active mixed conductor, provided that the appropriate variations in chemical and physical properties are accounted for. We assume the film to be thin enough, so that, when exposed to light, the photogeneration rate can be assumed constant throughout the film volume. We also focus on a reaction-limited model, where transport is fast enough, resulting in homogeneous concentration profiles in the film for all mobile defects. Because of the complexity of including all possible defects in MAPI and the reactions involving them, we limit our analysis to the study of iodine and iodide defects, interstitial and vacancies. Regarding the solid–gas exchange of iodine, we focus on processes that involve neutral iodine defects only 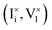 , while other reactions may also contribute to the real system.
, while other reactions may also contribute to the real system.
The relevant reactions are described in Table 1 and schematically represented in Fig. 2. For reaction r, the expressions for the rate of forward and backward reactions used in the kinetic model, ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) r and
r and  , are defined based on rate constants
, are defined based on rate constants  and the concentration of the relevant reactants. We indicate the mass-action constant Kr, defined based on the equilibrium concentrations of the relevant defects
and the concentration of the relevant reactants. We indicate the mass-action constant Kr, defined based on the equilibrium concentrations of the relevant defects  .23 On a first order approximation, and based on the quasi-equilibrium framework, we can assume that the value of the rate constants for the forward and the backward reactions are the same under bias and under dark conditions. All relevant input parameters are shown in Section 1 of the SI.
.23 On a first order approximation, and based on the quasi-equilibrium framework, we can assume that the value of the rate constants for the forward and the backward reactions are the same under bias and under dark conditions. All relevant input parameters are shown in Section 1 of the SI.
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = anti-Frenkel ionic defects,
= anti-Frenkel ionic defects, ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) × = neutral anti-Frenkel ionic defects, sg = solid–gas exchange, n = electrons, p = holes, v = vacancies, i = interstitials). [] indicates defect concentrations. Eg, ΔG0
× = neutral anti-Frenkel ionic defects, sg = solid–gas exchange, n = electrons, p = holes, v = vacancies, i = interstitials). [] indicates defect concentrations. Eg, ΔG0![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) and
and  are the standard free enthalpy of reactions (B), (
are the standard free enthalpy of reactions (B), (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) and (
) and (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×)
×)
Electronic properties
The electronic generation–recombination reaction involves multiple pathways31 which can be described by means of net recombination terms Uk = Rk − Gth,k, where Rk and Gth,k are the recombination and thermal generation rates associated with process k. The following expressions describe the radiative (k = rad), Shockley–Read–Hall (k = SRH) and the Auger (k = Aug) processes:| Urad = krad(np − ni2) | (4) |
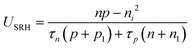 | (5) |
| UAug = γn(n2p − neq2peq) + γp(np2 − neqpeq2) | (6) |
Ionic properties
For the ionic situation, we concentrate on anti-Frenkel disorder32–34 involving iodide vacancies and iodide interstitials (see also energy diagrams in Fig. 1). Being aware of the fact that Schottky disorder (iodine vacancies and methylammonium vacancies and
and  ) is most likely the dominant ionic disorder in MAPI,8,34 we assume anti-Frenkel disorder to be dominant for the purpose of referring to a simple and straightforward model. The general conclusions of this study can be applied to the Schottky disorder case too.
) is most likely the dominant ionic disorder in MAPI,8,34 we assume anti-Frenkel disorder to be dominant for the purpose of referring to a simple and straightforward model. The general conclusions of this study can be applied to the Schottky disorder case too.
Although the ionic defect concentrations are not directly influenced by illumination, the coupling via defect chemical reactions leads to a situation of quasi-equilibrium for the ionic situation, too. In this case, a quasi-electrochemical potential can be assigned to each ionic defect. Besides the mass-action constant associated with the anti-Frenkel disorder reaction at equilibrium, K![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) , we define a chemical potential of the anti-Frenkel ionic defects Δμ
, we define a chemical potential of the anti-Frenkel ionic defects Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) to describe the nonequilibrium case, in analogy with QFLS for the electronic charges:
to describe the nonequilibrium case, in analogy with QFLS for the electronic charges:
 | (7) |
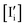 and
and  , while maintaining
, while maintaining 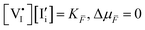 and
and 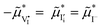 . Other situations where the ionic disorder is taken out-of-equilibrium (Δμ
. Other situations where the ionic disorder is taken out-of-equilibrium (Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≠ 0) are explored in section (b).
≠ 0) are explored in section (b).
Finally, based on reaction (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) shown in Table 1, we introduce the net-recombination term U
) shown in Table 1, we introduce the net-recombination term U![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) for anti-Frenkel defect pairs. Assuming U
for anti-Frenkel defect pairs. Assuming U![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) to follow a bimolecular process, we write
to follow a bimolecular process, we write
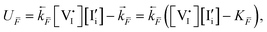 | (8) |
 and
and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) are the rate constants for the recombination and thermal generation of anti-Frenkel defect pairs. The term
are the rate constants for the recombination and thermal generation of anti-Frenkel defect pairs. The term  can be related to the Onsager radius r
can be related to the Onsager radius r![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) describing the recombination of (oppositely) charged defects as follows:
describing the recombination of (oppositely) charged defects as follows: | (9) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) is the sum of the diffusion coefficients of the two defects participating in the recombination process.35,36
is the sum of the diffusion coefficients of the two defects participating in the recombination process.35,36
The analogous treatment of the neutral iodine defects is included in Table 1 together with the definition of parameters  ,
,  . The net-recombination
. The net-recombination  can be defined similarly to eqn (8) (including
can be defined similarly to eqn (8) (including 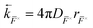 ). In this work, we consider the solid–gas iodine exchange reaction as the only channel through which neutral iodine defects interact. This implies a net-recombination term of neutral defects:
). In this work, we consider the solid–gas iodine exchange reaction as the only channel through which neutral iodine defects interact. This implies a net-recombination term of neutral defects:
 | (10) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×) in Table 1, also shown in Fig. 2b) would be necessary when looking at other situations (e.g. encapsulated samples).
×) in Table 1, also shown in Fig. 2b) would be necessary when looking at other situations (e.g. encapsulated samples).
Iodine exchange and redox reactions
Redox activity of at least one of the charged ionic defects is necessary to mediate the component exchange reaction (more on this in Section 2 of the SI). At equilibrium, the following reaction can be used to describe the iodine exchange between MAPI and the gas phase. | (11) |
 or
or  . Iodine in the gas phase is then either released from MAPI or incorporated in the structure via interaction with such neutral defects (Table 1 and Fig. 2). In the main text of this study, the neutral defects are assumed to be at equilibrium with each other and with the gas phase.
. Iodine in the gas phase is then either released from MAPI or incorporated in the structure via interaction with such neutral defects (Table 1 and Fig. 2). In the main text of this study, the neutral defects are assumed to be at equilibrium with each other and with the gas phase.
A key aspect in the discussion of how the redox reactions influence the defect concentration profiles concerns which of the reactions mediated by electrons or holes is dominant. To parameterize such aspects, we introduce the parameters ΓI,i = ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) p,i/
p,i/![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) n,i and ΓI,v =
n,i and ΓI,v = ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) p,v/
p,v/![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) n,v for reactions involving interstitials and vacancies, respectively, to express the extent to which each reaction is more favorable when mediated by conduction band electrons or by valence band holes. The ΓI,i and ΓI,v parameters are evaluated in the equilibrium case and under the intrinsic composition condition, i.e. neq = peq = ni and
n,v for reactions involving interstitials and vacancies, respectively, to express the extent to which each reaction is more favorable when mediated by conduction band electrons or by valence band holes. The ΓI,i and ΓI,v parameters are evaluated in the equilibrium case and under the intrinsic composition condition, i.e. neq = peq = ni and  , occurring for P(I2) = P(I2)i. Note that, at equilibrium, the ΓI,i and ΓI,v ratios are the same also when considering the backward reaction (i.e.
, occurring for P(I2) = P(I2)i. Note that, at equilibrium, the ΓI,i and ΓI,v ratios are the same also when considering the backward reaction (i.e.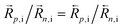 ).
).
The trapping and release of electronic charge carriers from iodide defects can be treated using the Shockley–Read–Hall framework, as discussed above for USRH mediated by an immobile trap (see Section 2 of the SI). This also leads to an additional contribution to net recombination of electronic charge carriers UI (e.g. the combination of 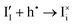 and
and 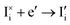 corresponds to the recombination process h˙ + e′ → nil; the same would follow if we consider the reactions involving vacancy defects).
corresponds to the recombination process h˙ + e′ → nil; the same would follow if we consider the reactions involving vacancy defects).
We can express the steady-state net recombination contribution due to all the redox reactions involving iodine defects as follows:
 | (12) |
Steady-state solution
The equations resulting from the model described above are shown in Table 2. They reflect the fact that, at steady-state, no net mass-exchange occurs, the net recombination of electronic charges compensates for the external generation term, and the net recombination of ionic defects due to redox reactions is equal and opposite to their net recombination due to the anti-Frenkel reaction. By also considering the condition of electroneutrality, a system of six equations is obtained.The analytical treatment becomes involved, requiring Brouwer approximations and additional simplification of the recombination terms to extract simple expressions for the P(I2) dependence of the charge carrier concentrations. We present numerical solutions to the problem obtained by solving the equations in Table 2 using the MATLAB function ‘fsolve’ (software version R2019a).
Results and discussion
Single redox-active mobile ionic defect: ionic disorder at equilibrium
We start by considering scenario (a) in Fig. 2, where electronic charge carriers interact only with the interstitial defects , while the rate constants associated with the
, while the rate constants associated with the  reactions are negligibly small. Fig. 3a shows the ionic and electronic defect concentrations as a function of P(I2) for the equilibrium (dashed lines) and the situation under light (solid lines). We consider the (symmetrical) case of ΓI,i = 1 (comparable rates for the redox reactions mediated by electrons or holes at P(I2)i), and a constant optical excitation of ∼10−3 suns equivalent. As expected, the electronic charge concentration is always larger under illumination than at equilibrium. Such an increase is accompanied by a narrowing of the intrinsic region which is the P(I2) range where ionic defects are larger in concentrations than electronic defects.
reactions are negligibly small. Fig. 3a shows the ionic and electronic defect concentrations as a function of P(I2) for the equilibrium (dashed lines) and the situation under light (solid lines). We consider the (symmetrical) case of ΓI,i = 1 (comparable rates for the redox reactions mediated by electrons or holes at P(I2)i), and a constant optical excitation of ∼10−3 suns equivalent. As expected, the electronic charge concentration is always larger under illumination than at equilibrium. Such an increase is accompanied by a narrowing of the intrinsic region which is the P(I2) range where ionic defects are larger in concentrations than electronic defects.
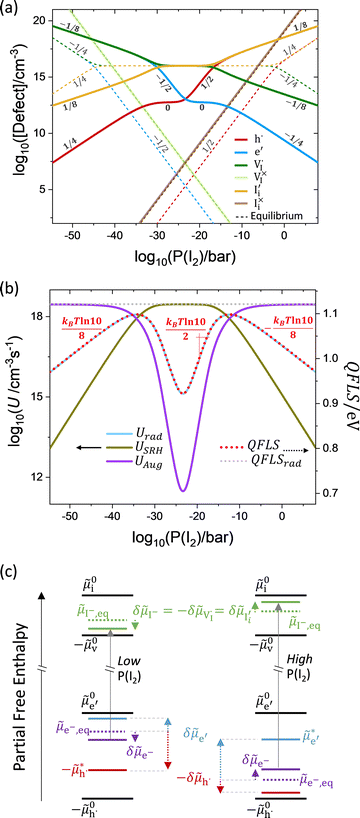 | ||
| Fig. 3 Light-induced stoichiometry change in a mixed conductor with a single redox-active ionic defect. (a) Iodine partial pressure (P(I2)) dependence of the steady-state electronic and ionic defect concentrations in MAPI at equilibrium and under light (∼10−3 suns) plotted in a Kröger–Vink diagram (the numbers close to the data refer to the corresponding slopes). The calculation refers to assuming the redox reaction occurring with iodine interstitials only, and ΓI,i = 1. (b) Net recombination contributions and quasi-Fermi level splitting. (c) Schematic energy diagram emphasizing the change in the position of the electrochemical potentials with respect to the electronic and ionic standard potentials, going from equilibrium (dashed lines) to the situation under light (solid lines), and for cases of low and high P(I2).8 | ||
The concentration of iodide defects is perturbed under light too, as shown by the trend of  and
and  deviating from the equilibrium profile, especially at low or high P(I2). Based on electroneutrality, a significant increase in
deviating from the equilibrium profile, especially at low or high P(I2). Based on electroneutrality, a significant increase in  with respect to equilibrium at low P(I2) compensates for the large concentration of electrons obtained under light (see also
with respect to equilibrium at low P(I2) compensates for the large concentration of electrons obtained under light (see also  and hole concentration at high P(I2)). Interestingly, the profiles of
and hole concentration at high P(I2)). Interestingly, the profiles of  and
and  still obey the anti-Frenkel equilibrium even under light, that is while their individual values are different from the equilibrium case, their product still corresponds to K
still obey the anti-Frenkel equilibrium even under light, that is while their individual values are different from the equilibrium case, their product still corresponds to K![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) . The concentrations of the neutral ionic defects
. The concentrations of the neutral ionic defects  and
and 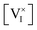 vary with P(I2) according to the mass-action laws for the solid–gas exchange reactions (sg,i and sg,v in Table 1), whether the system is at equilibrium or under light (their profiles are omitted in all figures below).
vary with P(I2) according to the mass-action laws for the solid–gas exchange reactions (sg,i and sg,v in Table 1), whether the system is at equilibrium or under light (their profiles are omitted in all figures below).
The data illustrate that, depending on P(I2), illumination induces a net iodine uptake from or release to the gas phase compared to the equilibrium condition. This results in a steady-state stoichiometry (δ* in MAPbI3+δ*,  ) that differs from the equilibrium stoichiometry (δeq in MAPbI3+δeq). Importantly, we are ignoring any formation of higher order defects due to photogenerated electronic charges,14 meaning that changes in ionic defect concentrations are expected under bias regardless of such events occurring. Note that such stoichiometry changes may correspond to compositions outside of the material's stability region, an aspect that is not included here.14
) that differs from the equilibrium stoichiometry (δeq in MAPbI3+δeq). Importantly, we are ignoring any formation of higher order defects due to photogenerated electronic charges,14 meaning that changes in ionic defect concentrations are expected under bias regardless of such events occurring. Note that such stoichiometry changes may correspond to compositions outside of the material's stability region, an aspect that is not included here.14
We conclude that, if only one ionic defect is involved in redox reactions (here interstitials 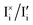 , but similar results would be obtained for vacancies), the application of a light bias to the mixed conductor effects the following:
, but similar results would be obtained for vacancies), the application of a light bias to the mixed conductor effects the following:
– The concentration of the neutral iodine defects 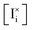 and
and  are exclusively determined and fixed by the value of P(I2), i.e. light-independent, based on the mass-action constants Ksg,i and Ksg,v in Table 1.
are exclusively determined and fixed by the value of P(I2), i.e. light-independent, based on the mass-action constants Ksg,i and Ksg,v in Table 1.
– The rate equations involving reactions (n,i) and (p,i), and the generation and recombination of electronic charge carriers determine the values of n, p and 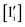 .
.
– The value of  is fixed based solely on the value of
is fixed based solely on the value of  according to the anti-Frenkel disorder reaction, which may shift but remains in equilibrium (Δμ
according to the anti-Frenkel disorder reaction, which may shift but remains in equilibrium (Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = 0). This means that light can induce a change in stoichiometry in the mixed conductor with respect to the equilibrium condition.
= 0). This means that light can induce a change in stoichiometry in the mixed conductor with respect to the equilibrium condition.
Essentially, to obtain the data in Fig. 3, only eqn (1)–(3) in Table 2 need to be solved in combination with the mass-action laws for reactions (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ), (sg,i) and (sg,v). For all calculations in this section, we can obtain exact solutions to the problem by referring to the assumption that neutral defects remain in equilibrium with the gas phase, a condition that we refer to below as “sg-eq”.
), (sg,i) and (sg,v). For all calculations in this section, we can obtain exact solutions to the problem by referring to the assumption that neutral defects remain in equilibrium with the gas phase, a condition that we refer to below as “sg-eq”.
In Fig. 3b, we display the resulting graphs of QFLS as a function of P(I2) (red dotted line), as well as of the rates of recombination associated with the different mechanisms considered here. We find that USRH dominates for P(I2) ≈ P(I2)i, while UAug is dominant in the N and P regions (very high or very low P(I2)). The QFLS is always lower than for the radiative limit (QFLSrad) and it approaches such limit for two narrow ranges of P(I2). The position of the QFLS maxima corresponds to the situations where the contribution of Rrad to the total recombination is fractionally largest, and where RSRH = RAug. Note that the latter condition is not general, but it is based on the input parameters used here (τn = τp, n1 = p1 and γn = γp). The local minimum observed for n = p is consistent with the Shockley–Read–Hall theory of recombination (in the case of τn = τp and for a mid-gap trap level). The slope of the QFLS vs. log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(I2) can be evaluated as the sum of the slopes associated with electrons and holes in the Kröger–Vink diagram times a kBT
P(I2) can be evaluated as the sum of the slopes associated with electrons and holes in the Kröger–Vink diagram times a kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[10] factor. The data in Fig. 3b highlight that the QFLS obtained for a mixed conducting film (here MAPI) depends non-monotonically on the component partial pressure (here P(I2)). Because QFLS is a proxy for the maximum open circuit potential which can be achieved once the material is embedded in a complete solar cell, this analysis emphasizes the importance of the component partial pressure for controlling the performance of optoelectronic devices based on mixed conductors.41
ln[10] factor. The data in Fig. 3b highlight that the QFLS obtained for a mixed conducting film (here MAPI) depends non-monotonically on the component partial pressure (here P(I2)). Because QFLS is a proxy for the maximum open circuit potential which can be achieved once the material is embedded in a complete solar cell, this analysis emphasizes the importance of the component partial pressure for controlling the performance of optoelectronic devices based on mixed conductors.41
In Fig. 3c, we illustrate schematically the corresponding changes in electrochemical potentials for all defects where changes in both the ionic and electronic situations under bias (solid lines) are compared with the equilibrium solution (dashed lines). Consistently with the data in Fig. 3a,  (Δμ
(Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = 0) at any P(I2), with
= 0) at any P(I2), with  in the intrinsic region under light. Because the steady-state condition
in the intrinsic region under light. Because the steady-state condition  is valid both at equilibrium and under bias, based on
is valid both at equilibrium and under bias, based on 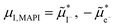 , it follows that δ
, it follows that δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) I− = δ
I− = δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e− at any given P(I2). In Section 3 of the SI, we provide more details on the analysis of this quasi-equilibrium as well as the asymptotic trends for very low and very high P(I2).
e− at any given P(I2). In Section 3 of the SI, we provide more details on the analysis of this quasi-equilibrium as well as the asymptotic trends for very low and very high P(I2).
The data in Fig. 3 refer to the case of Γp,i = 10−2 (low hole trapping rate by  ). Combined with a balanced interaction of interstitials with electrons and holes (ΓI,i = 1), this corresponds to a negligible contribution of recombination due to redox reactions with iodide interstitials UI compared to other recombination pathways for the selected light intensity. In Fig. 4, we display the calculated defect concentrations and QFLS using the same input parameters as in Fig. 3, but with varying rates of hole trapping at iodine interstitials, parameterized through Γp,i. Simultaneous relative variations in electron trapping at iodide interstitials are ensured by selecting ΓI,i = 1 in all cases. Fig. 4a indicates that, for large values of Γp,i, all defect concentrations are varied significantly from the situation shown in Fig. 3 in the high P(I2) region. The resulting QFLS (Fig. 4b) shows a significant drop in such region, which is ascribed to a dominant electron–hole recombination contribution mediated by the forward reactions associated with (n,i) and (p,i). Such contribution is compared with the total net recombination deriving from all the other mechanisms considered (inset of Fig. 4b).
). Combined with a balanced interaction of interstitials with electrons and holes (ΓI,i = 1), this corresponds to a negligible contribution of recombination due to redox reactions with iodide interstitials UI compared to other recombination pathways for the selected light intensity. In Fig. 4, we display the calculated defect concentrations and QFLS using the same input parameters as in Fig. 3, but with varying rates of hole trapping at iodine interstitials, parameterized through Γp,i. Simultaneous relative variations in electron trapping at iodide interstitials are ensured by selecting ΓI,i = 1 in all cases. Fig. 4a indicates that, for large values of Γp,i, all defect concentrations are varied significantly from the situation shown in Fig. 3 in the high P(I2) region. The resulting QFLS (Fig. 4b) shows a significant drop in such region, which is ascribed to a dominant electron–hole recombination contribution mediated by the forward reactions associated with (n,i) and (p,i). Such contribution is compared with the total net recombination deriving from all the other mechanisms considered (inset of Fig. 4b).
We note that the Shockley–Read–Hall rate for recombination mediated by immobile traps is established based on the parameters n1, p1, which depend on the energetic position of the trap, and τn, τp, which depend on the (fixed) concentration and the capture coefficient of the trap. While the recombination due to redox reactions involving  follows a similar principle, the concentration of such recombination centers is determined by the overall evaluation of the charge carrier quasi-equilibrium. In Fig. 4, UI is dominant at high P(I2), due to the increase in
follows a similar principle, the concentration of such recombination centers is determined by the overall evaluation of the charge carrier quasi-equilibrium. In Fig. 4, UI is dominant at high P(I2), due to the increase in 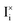 and
and  defect concentrations. The dominant recombination mechanism for different P(I2) values is shown schematically in Fig. 4c (referring to the Γp,i = 106 case). The
defect concentrations. The dominant recombination mechanism for different P(I2) values is shown schematically in Fig. 4c (referring to the Γp,i = 106 case). The  energy level is included within the energy bandgap.
energy level is included within the energy bandgap.
Fig. 5a shows the influence of ΓI,i on the defect quasi-equilibrium. As the reaction (sg,i) is at equilibrium in this scenario, ΓI,i is a measure of the degree to which the “hole channel” vs. the “electron channel” control the iodine incorporation/excorporation at equilibrium (see Table 1 and Fig. 2). Changing ΓI,i does not vary the equilibrium defect concentrations (dashed lines in the Kröger–Vink diagrams) as these depend only on the mass-action constants. On the other hand, the position of the intrinsic region under light shifts on the P(I2) axis when varying ΓI,i, while always remaining within the boundaries of the intrinsic region defined by the equilibrium case (n ≥ neq and p ≥ peq). The iodine partial pressure  at which n = p and
at which n = p and  =
= 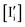 refers to the intrinsic condition under light. While
refers to the intrinsic condition under light. While  is essentially the same as P(I2)i for the example in Fig. 3 (ΓI,i = 1 and low Γp,i), Fig. 5a shows that, in general,
is essentially the same as P(I2)i for the example in Fig. 3 (ΓI,i = 1 and low Γp,i), Fig. 5a shows that, in general,  .
.
Fig. 5b highlights the shrinking of the intrinsic region with increasing light intensity (the same input parameters as for Fig. 3 are used). The trends in QFLS resulting from varying ΓI,i or light intensity are shown in Fig. 5c, emphasizing that the P(I2) values corresponding to local QFLS maxima are dependent on such parameters. The situation is further complicated if larger values of Γp,i are considered (in Fig. 5, Γp,i = 10−2). Fig. 5d displays the light intensity dependence of QFLS evaluated at different values of P(I2) for ΓI,i = 1. The data once again illustrate the influence of P(I2) on the dominant recombination mechanism, as also highlighted by the trends in local ideality factor (defined here as  , see inset).
, see inset).
To conclude this section, we discuss a simple example to understand possible implications of the model under realistic experimental conditions. Let us consider a MAPI film equilibrated at P(I2)i. We hypothesize that only interstitials are redox active and that ΓI,i ≫ 1 (e.g. see Fig. 5a for the case of ΓI,i = 103, colored lines). The interstitial redox reaction mediated by holes essentially dominates in a wide range of P(I2), where the definition of the (pseudo)mass action constant Kp,i (see Table 1) can be extended to the situation under light. We can then write for the iodine quasi-chemical potential associated with holes  , also implying δ
, also implying δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) I− = −δ
I− = −δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) p. The latter relationship means that, upon the increase of the hole concentration in the mixed conductor (assuming
p. The latter relationship means that, upon the increase of the hole concentration in the mixed conductor (assuming  and
and  ) due to illumination, a fractionally equivalent increase in
) due to illumination, a fractionally equivalent increase in  and decrease in
and decrease in is expected (light-induced shift in stoichiometry and excorporation of iodine14). Importantly, when considering the condition of electroneutrality in the bulk of the material, we find that there is a limit to the increase in
is expected (light-induced shift in stoichiometry and excorporation of iodine14). Importantly, when considering the condition of electroneutrality in the bulk of the material, we find that there is a limit to the increase in  to as far as the combination of its charge compensating defects, that is
to as far as the combination of its charge compensating defects, that is  .
.
We also note that, for the same mixed conductor equilibrated at high P(I2), illumination can lead to a shift in stoichiometry of opposite sign (incorporation of iodine, decrease in 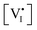 and increase in
and increase in  ) due to the condition of electroneutrality
) due to the condition of electroneutrality  . The effect naturally fades towards a zero change in ionic defect concentrations under light only for the asymptotic case of ΓI,i → ∞, for which δ
. The effect naturally fades towards a zero change in ionic defect concentrations under light only for the asymptotic case of ΓI,i → ∞, for which δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) I− = −δ
I− = −δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) p is valid at any P(I2) (see also Scheme S1 in the SI).
p is valid at any P(I2) (see also Scheme S1 in the SI).
Multiple redox-active mobile ionic defects: ionic disorder out of equilibrium
We now consider situation (b) in the model shown in Fig. 2, whereby both interstitial and vacancy defects interact with electronic charge carriers via redox reactions. For now, we shall continue to assume the “sg-eq” condition. Such a situation may be relevant only to very small particles of the mixed conductor (although see discussion below).Fig. S2 shows that if both interstitials and vacancies show similar coupling to electrons and to holes (ΓI,i = ΓI,v) and the recombination mediated by the mobile ions is negligible (low Γp,i and Γn,v), essentially unchanged trends are found compared with the results obtained using a single redox-active ion (Fig. 3 and 5). If either of these conditions are not met, different trends from the single redox active mobile defect case are obtained (see Fig. S3 for ΓI,i ≠ ΓI,v and low Γp,i, Γn,v, and Fig. S4 for the case of high Γp,i, Γn,v and ΓI,i = ΓI,v). Despite such deviations, equilibrium in the ionic disorder is maintained under light, although shifted with respect to the dark equilibrium case (i.e. light induces stoichiometry changes in the mixed conductor).
We now discuss the implications of both above conditions not being met. Fig. 6 explores the effect of the parameters ΓI,i and ΓI,v, which define to what extent the  and the
and the  quasi-equilibria are established by reactions with holes (ΓI ≫ 1) or electrons (ΓI ≪ 1). The data are obtained considering a value of Γp,i = Γn,v as large as 1011.
quasi-equilibria are established by reactions with holes (ΓI ≫ 1) or electrons (ΓI ≪ 1). The data are obtained considering a value of Γp,i = Γn,v as large as 1011.
Fig. 6a is the reference situation where the redox reactions involving interstitials and the ones involving vacancies are driven by electrons and holes to a similar extent (ΓI,i = ΓI,v), as discussed above for Fig. S4. As ΓI,i = ΓI,v = 1 (and Γp,i = Γn,v), the defect diagram preserves “symmetry” about the pressure value P(I2)i. The ionic defect profiles under light largely follow the same trends in the equilibrium and in the light biased cases. This contrasts with the results in Fig. 3, where significant changes in ionic defect concentrations are encountered especially in the high and low P(I2) ranges. Due to the large values of the redox reactions’ rate constants (related to Γp,i and Γn,v), the iodide vacancy reduction reaction (n,v) at low P(I2) and the iodide interstitial oxidation (p,i) at high P(I2) are essentially operating at equilibrium. Along with the sg-eq condition, this ensures minimal deviations from the equilibrium trends of the relevant defects in these two pressure ranges. The same occurs also for intermediate values of P(I2), due to the symmetrical interaction of the electronic carriers with the ionic defects.
Fig. 6b and c consider situations where the relevance of electrons and holes in the determination of the redox reaction quasi-equilibrium, as expressed by the parameters ΓI,i and ΓI,v, is not the same for interstitials and vacancies (ΓI,i ≠ ΓI,v). The data show a striking increase or decrease (Fig. 6b and c, respectively) in the concentration of both iodide vacancies and iodide interstitials under light with respect to equilibrium. Such observation implies that, for a mixed conductor with more than one type of redox-active ionic species, light can be used to increase or reduce the concentration of such ionic defects.
Such effect requires a deviation from the anti-Frenkel equilibrium due to illumination, which can be explained as follows. Increase in n tends to increase 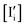 but decrease
but decrease 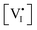 , while an increase in p has the opposite effect (see Table 1). Since
, while an increase in p has the opposite effect (see Table 1). Since  and
and 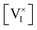 are fixed at any given P(I2), changes in the value of
are fixed at any given P(I2), changes in the value of  and
and  depend on the rates of the reactions that “connect” each of them to either electrons or holes. Such connection is parameterized through ΓI,i and ΓI,v.
depend on the rates of the reactions that “connect” each of them to either electrons or holes. Such connection is parameterized through ΓI,i and ΓI,v.
For example, let us consider a MAPI film equilibrated at P(I2)i and assume that holes dominate the redox chemistry of interstitials while electrons dominate the redox reactions involving vacancies (ΓI,i ≫ 1 and ΓI,v ≪ 1). As the equilibria expressed by the (pseudo)mass action constant Kp,i and Kn,v would tend to remain valid under light too (see Table 1 and Scheme S1 in the SI), their expression points to the reduction in both  and
and  at a fixed P(I2) (and therefore fixed
at a fixed P(I2) (and therefore fixed 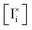 and
and  based on sg-eq).
based on sg-eq).
Analytically, it is useful to define the parameter
 | (13) |
If only one redox active defect is considered, Xvi = 0 by definition, at steady-state. If instead both interstitials and vacancies are redox active, as shown in Fig. 6, such condition is no longer necessarily true. Specifically, if Xvi = 0, the rate of electron trapping by each of the iodide vacancies or iodine interstitials is counter-balanced by an equal rate of hole trapping interacting with the same type of defect (this is the case when ΓI,i = ΓI,v). That means that no reaction between ionic defects is required to mediate the recombination (or thermal generation process).
If instead Xvi ≠ 0, the fraction of the total electron–hole net recombination which is mediated by separate (de-)trapping of electronic charges by the two ionic defects also requires reaction between such ionic defects. Specifically, in the steady-state, such an electron–hole recombination process involves the recombination of the two ionic defects with the trapped carriers and the generation of the two original defects before trapping (similar argument applies to electron–hole thermal generation). The effective ionic defect generation term for charged anti-Frenkel pairs (G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) and neutral anti-Frenkel pairs (G
) and neutral anti-Frenkel pairs (G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×) are defined and, in the steady-state, they relate to each other and to the Xvi term as follows:
×) are defined and, in the steady-state, they relate to each other and to the Xvi term as follows:
G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = −G = −G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) × = Xvi × = Xvi | (14) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) > 0 (analogously to the effect of a positive Gext on the electronic charge carrier concentrations) but also decrease the concentration of ionic defects via a G
> 0 (analogously to the effect of a positive Gext on the electronic charge carrier concentrations) but also decrease the concentration of ionic defects via a G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) < 0. Based on eqn (10), (13) and (14), we find that the rate eqn (3)–(6) in Table 2 related to the ionic defects represent different extended forms of the equations G
< 0. Based on eqn (10), (13) and (14), we find that the rate eqn (3)–(6) in Table 2 related to the ionic defects represent different extended forms of the equations G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = U
= U![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) and G
and G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) × = U
× = U![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×, respectively.
×, respectively.
Based on this interpretation, the trends in Fig. 6 can be explained. By considering the parameter hion = log10(ΓI,v/ΓI,i), we found that situations where G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) = 0, G
= 0, G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) > 0 or G
> 0 or G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) < 0 refer to hion = 0, hion > 0 and hion < 0, respectively (see Fig. 6a–c, and analytical treatment in Section 2 of the SI relating ΓI,v, ΓI,i and hion to SRH trapping parameters associated with the mobile ions).
< 0 refer to hion = 0, hion > 0 and hion < 0, respectively (see Fig. 6a–c, and analytical treatment in Section 2 of the SI relating ΓI,v, ΓI,i and hion to SRH trapping parameters associated with the mobile ions).
We note that a similar change in concentration compared with the equilibrium case affects both ionic defects in the intrinsic regions of Fig. 6b and c. The resulting change in stoichiometry between the dark and the light-bias cases is therefore less significant here than for the situation displayed in the N and P regions of Fig. 3a. The latter largely reflects the discussion of previous studies on light-effects in halide and oxide perovskites (see introduction). On the other hand, obtaining simultaneous increase or decrease in the concentration of both ionic defects involved in the dominant ionic disorder reaction through light may open new opportunities in material science and beyond (see also next section).
Importantly, the data in Fig. 6 are obtained by considering the sg-eq condition, which is not necessarily valid for the multiple redox-active ionic defect case (Fig. 2b). This means that the concentration profiles for the neutral defects are assumed to be unperturbed under light compared with the equilibrium situation (see Fig. 3a), and that only the concentration of the anti-Frenkel pairs is subject to variations, which depend on the value of ΓI,i, ΓI,v and Γp,i, Γn,v. When solving the full kinetic model which includes a finite rate for the solid–gas exchange reactions (sg-eq condition no longer valid), we found that both the charged and the neutral ionic defect concentrations are perturbed by light. The effect described above, with either an increase or a decrease of both  and
and  , still occurs but to a lesser extent (see Section 5 of the SI).
, still occurs but to a lesser extent (see Section 5 of the SI).
Here, we discuss solutions under the sg-eq condition further, as these describe the upper limit to the anti-Frenkel nonequilibrium induced by illumination of the mixed-conductor. In Fig. 7a, the Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) and the QFLS profiles corresponding to the data in Fig. 6 are illustrated. The conditions that lead to an enhancement in the ionic concentrations also lead to a drop in QFLS, while an increase in QFLS is observed when redox reactions reduce the mobile ion concentrations. This can be explained since UI scales with the concentration of mobile ions that can mediate recombination. In Fig. 7b, the electronic generation rate as well as the anti-Frenkel pair effective generation rate are shown. Consistent with the definition of the effective ionic defect generation rate, |G
and the QFLS profiles corresponding to the data in Fig. 6 are illustrated. The conditions that lead to an enhancement in the ionic concentrations also lead to a drop in QFLS, while an increase in QFLS is observed when redox reactions reduce the mobile ion concentrations. This can be explained since UI scales with the concentration of mobile ions that can mediate recombination. In Fig. 7b, the electronic generation rate as well as the anti-Frenkel pair effective generation rate are shown. Consistent with the definition of the effective ionic defect generation rate, |G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) | ≤ Gext. Fig. 7c shows a schematic including the extended energy level diagram summarizing these findings. In the SI, we show other examples where the condition ΓI,i ≠ ΓI,v (hion ≠ 0) results in Δμ
| ≤ Gext. Fig. 7c shows a schematic including the extended energy level diagram summarizing these findings. In the SI, we show other examples where the condition ΓI,i ≠ ΓI,v (hion ≠ 0) results in Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≠ 0, including the case where the same electronic charge carrier dominates redox reactions with both interstitials and vacancies (see Fig. S6).
≠ 0, including the case where the same electronic charge carrier dominates redox reactions with both interstitials and vacancies (see Fig. S6).
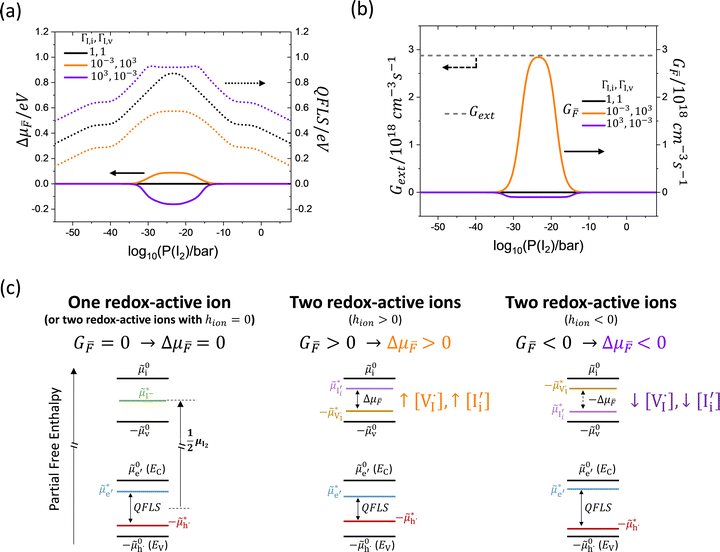 | ||
Fig. 7 Introducing the ionic defect pair chemical potential in analogy to the electronic chemical potential to describe quasi-equilibrium in the mixed conductor under illumination. The consequences of including two redox-active mobile ionic defects in the defect chemical quasi-equilibrium of a mixed conductor exposed to light, assuming equilibrium of the neutral defects ( and and 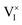 ) with the gas phase (sg-eq) are displayed referring to (a) the ionic (Δμ ) with the gas phase (sg-eq) are displayed referring to (a) the ionic (Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) and the electronic (QFLS) chemical potentials. (b) Electronic generation rate Gext used in the calculations (10−3 suns equivalents) and resulting effective anti-Frenkel ionic generation rate G ) and the electronic (QFLS) chemical potentials. (b) Electronic generation rate Gext used in the calculations (10−3 suns equivalents) and resulting effective anti-Frenkel ionic generation rate G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) for the three situations considered in (a) and in Fig. 6. (c) Generalized energy level diagram corresponding to the (left) unchanged, (center) increased and (right) decreased charged ionic defect concentration upon illumination. for the three situations considered in (a) and in Fig. 6. (c) Generalized energy level diagram corresponding to the (left) unchanged, (center) increased and (right) decreased charged ionic defect concentration upon illumination. | ||
Fig. 8 illustrates the dependence of the ionic defect concentration enhancement or depression on the parameters ΓI,i, ΓI,v, and Γp,i, Γn,v, based on the trends in Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) . While the sign as well as the magnitude of Δμ
. While the sign as well as the magnitude of Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) depend on hion, the data show that obtaining perceptible deviations from the anti-Frenkel equilibrium requires a sufficiently large value of both Γp,i and Γn,v. This is because the extent of the non-equilibrium in the anti-Frenkel disorder (magnitude of Δμ
depend on hion, the data show that obtaining perceptible deviations from the anti-Frenkel equilibrium requires a sufficiently large value of both Γp,i and Γn,v. This is because the extent of the non-equilibrium in the anti-Frenkel disorder (magnitude of Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) correlates with the fraction of the overall electron–hole recombination rate that is due to mobile-ion mediated reactions (dictated by Γp,i, Γn,v as well as by ΓI,i, ΓI,v). Fig. 8a shows that, as the concentration of ionic defects increases for very large values of hion and Γp,i = Γn,v = 1011, Δμ
) correlates with the fraction of the overall electron–hole recombination rate that is due to mobile-ion mediated reactions (dictated by Γp,i, Γn,v as well as by ΓI,i, ΓI,v). Fig. 8a shows that, as the concentration of ionic defects increases for very large values of hion and Γp,i = Γn,v = 1011, Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ≈ QFLS (see also pseudo-mass action laws in Table 1 and Scheme S1 in the SI).
≈ QFLS (see also pseudo-mass action laws in Table 1 and Scheme S1 in the SI).
 | ||
Fig. 8 Dependence of the ionic (Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ) and electronic (QFLS) change in chemical potential on the ΓI,i, ΓI,v, and Γp,i, Γn,v parameters, as a function of P(I2). Trends for (a) increasing hion > 0 (Γp,i = Γn,v = 1011), (b) increasing Γp,i = Γn,v (ΓI,i = 10−3, ΓI,v = 103), (c) decreasing hion < 0 (Γp,i = Γn,v = 1011), and (d) increasing Γp,i = Γn,v (ΓI,i = 103, ΓI,v = 10−3). All remaining parameters are the same as the ones used in Fig. 3. ) and electronic (QFLS) change in chemical potential on the ΓI,i, ΓI,v, and Γp,i, Γn,v parameters, as a function of P(I2). Trends for (a) increasing hion > 0 (Γp,i = Γn,v = 1011), (b) increasing Γp,i = Γn,v (ΓI,i = 10−3, ΓI,v = 103), (c) decreasing hion < 0 (Γp,i = Γn,v = 1011), and (d) increasing Γp,i = Γn,v (ΓI,i = 103, ΓI,v = 10−3). All remaining parameters are the same as the ones used in Fig. 3. 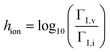 . . | ||
Fig. 8b and d highlight that, for increasing Γp,i and Γn,v, the QFLS decreases less substantially if hion < 0 than if hion > 0. This is due to the depression, rather than enhancement, in  and
and  , which mediate recombination. In other words, light can induce enhancement or reduction in the concentration of recombination-active ionic defects. In either case, it significantly influences not only the ionic but also the electronic quasi-equilibrium. Section 7 of the SI shows similar calculations performed without the SRH recombination mediated by immobile defects to highlight the effect of minimizing the recombination due to anti-Frenkel pairs (for hion < 0) on the QFLS. We emphasize that such situations cannot improve the value of QFLS beyond the limit where the anti-Frenkel defects are not recombination active (see Fig. S7 and S8).
, which mediate recombination. In other words, light can induce enhancement or reduction in the concentration of recombination-active ionic defects. In either case, it significantly influences not only the ionic but also the electronic quasi-equilibrium. Section 7 of the SI shows similar calculations performed without the SRH recombination mediated by immobile defects to highlight the effect of minimizing the recombination due to anti-Frenkel pairs (for hion < 0) on the QFLS. We emphasize that such situations cannot improve the value of QFLS beyond the limit where the anti-Frenkel defects are not recombination active (see Fig. S7 and S8).
Summary and outlook
In summary, the analysis presented in this work:– provides a framework for the study of redox reactions, electron–hole recombination and solid–gas component exchange reactions when photoactive mixed conducting materials are illuminated
– outlines guidelines for material design where ionic defect concentrations (trap densities) can be increased and, strikingly, also decreased by light
– proposes a rationale for the development of photoelectrochemical systems that allow for stoichiometry control using optical stimuli
– emphasizes the importance of understanding electronic and ionic kinetic properties, especially in the context of solar energy conversion devices based on mixed conductors where mobile ions provide a significant contribution to the total electron–hole recombination rate.
– has direct implications to the field of halide perovskites, as well as to any situation where a mixed conducting system is exposed to light (or voltage) bias
This study presents the fundamental effect that light has on the steady-state ionic and electronic bulk properties of mixed conductors. The model can be extended to include transport and interfacial effects, and it can be integrated in physical models of complete mixed conducting devices for the study of their steady-state as well as transient response when exposed to light and/or voltage bias.20,29,42–46
In view of a more complete analysis in one dimension, where the continuity equations referring to mobile defects also include transport terms, we anticipate that:
– The assumption of uniform optoelectronic excitation within the mixed conductor used here would hold only for films that are significantly thinner than the absorption length of the material for the specific excitation wavelength used.
– For thick films, nonequilibrium due to illumination may extend over longer distances than the absorption length in the case of compounds that show long electronic diffusion lengths (as is the case for halide perovskites47). At locations that are sufficiently far from the illuminated surface (distance » diffusion and absorption lengths), the equilibrium defect concentrations at the specific component partial pressure used are maintained (note that diffusion and absorption lengths may depend on the component partial pressure).
– Accounting for ionic defects forming specifically at the surface (and at interfaces) may be critical to accurately describe solid–gas (solid–solid, solid–liquid) exchange as well as interfacial space charge effects. Additional terms associated with surface electronic recombination mediated by such defects can be a dominant loss mechanism in mixed conductors with long bulk charge carrier lifetimes.
– Finite rates of ionic transport and stoichiometric polarization within macroscopic systems, as well as slow solid–gas component exchange reactions may all play a role, depending on the operating conditions, as the rate determining step to reaching quasi-equilibrium. These factors influence the extent of the position-dependent nonequilibrium obtained for the steady-state situation, for which this model represents an upper limit (see Section 5 of the SI in the context of solid–gas exchange kinetics).
– At steady-state under illumination, no net mass transport within the sample and no net mass exchange at the solid–gas phase are expected. For cases where the ionic disorder reaction shifts but remains at equilibrium under light (e.g. case (a) in Fig. 2, one redox active defect), any gradient in chemical potential of the ionic defects across the film's depth must be counterbalanced by an electrostatic potential term (space charge). This ensures a constant  and zero current for each of the ionic defects at all positions. On the other hand, nonequilibrium in the ionic disorder reactions (e.g. case (b) in Fig. 2, two redox active defects) may be reflected in nonzero steady-state transport terms for ionic defects within the sample. Equal and opposite ionic current terms for iodide vacancies and interstitials result in net zero mass transport, similarly to the nonzero steady-state electron and hole current expected in such systems.
and zero current for each of the ionic defects at all positions. On the other hand, nonequilibrium in the ionic disorder reactions (e.g. case (b) in Fig. 2, two redox active defects) may be reflected in nonzero steady-state transport terms for ionic defects within the sample. Equal and opposite ionic current terms for iodide vacancies and interstitials result in net zero mass transport, similarly to the nonzero steady-state electron and hole current expected in such systems.
Additional extensions considering the full ionic defect chemical treatment in terms of ion type and range of accessible oxidation states,34,40 as well as further pathways to ionic defect formation and association could be subject of future work. The current model also represents a starting point for the investigation of photo-induced phase-instability and degradation effects, important questions for the application of halide perovskites.14,37,48,49
Finally, we comment on possible experiments that could test and validate the effects predicted by the model in sections a and b of the Results and discussion.
(a) Previous observations of light-induced ionic responses in MAPI and STO are consistent with the general framework discussed in section a, concerning light-induced component exchange (iodine and oxygen, respectively) and stoichiometry changes in the mixed conductor.14,19,22–24,50,51 The study of similar light effects in other mixed conductors, where interactions between ionic defects and electronic charges can be controlled, should be the subject of future studies. Importantly, estimating changes in mobile ionic defect concentrations from electrochemical measurements of partial conductivities using the analysis typically applied to systems at equilibrium may not always be possible, due to additional coupling between the ionic and electronic response (e.g. ionic-to-electronic current amplification15,46,52,53). The use of multiple independent techniques that can also quantify component incorporation/excorporation can provide more direct evidence for such effects,14 provided that the experimental method's sensitivity and the material's phase stability allow for reliable analysis.
(b) The enhancement/reduction of both ionic defects’ concentration in a mixed conductor exposed to light has, to our knowledge, not been discussed before. Modulation of transport and lifetime of electronic charge carriers upon photo-induced decrease or increase in the concentration of both ionic defects is one of the exciting perspectives for such a prediction. Probing such changes in combination with a negligible variation in stoichiometry may provide compelling, yet indirect, evidence of the effect. Direct quantification of ionic defect concentrations could be achieved via spectroscopic techniques or from the analysis of structural measurements on specifically designed materials providing clear probes for such quantities. Finally, the design of photoelectrochemical devices including electrodes with opposite selectivity to the two ionic defects would allow the measurement of photoinduced ionic currents and electrochemical potentials, in analogy to the measurement of a traditional solar cell (see also demonstrations of water based protonic solar cells54,55). Such approach represents both a promising strategy to investigate light-induced ionic effects in mixed conductors as well as an exciting direction in the development of novel systems for energy conversion and storage, sensing, and computing applications.
Conclusions
We present a model that describes the effect of light on the ionic and electronic properties of a mixed ionic–electronic conductor. Using a simplified description of the halide perovskite methylammonium lead iodide (MAPI) as a model system, we obtain and explore trends that are relevant to any photoactive mixed conductor under fixed component partial pressure. We focus on the rate equations describing defect reactions and neglect defect transport to the solid–gas interface. By coupling the ionic (anti-Frenkel) disorder reaction, the iodine redox reactions and exchange with the gas phase with the electronic (photo-)generation and recombination, we predict the trends of ionic and electronic defect concentrations as a function of the component partial pressure (for MAPI this refers to iodine). We discuss the material's thermodynamic and kinetic parameters that control the steady-state solution to such problem, with a particular focus on the relative contribution of the two electronic charge carriers to the redox and solid–gas exchange reactions. Knowledge of such aspects allows one to determine the steady-state quasi-Fermi level splitting in the material, with relevance to the optimization of solar cells. Light induces changes in stoichiometry (the equilibrium in the ionic disorder reaction is maintained and only shifted) if a single ionic defect is redox-active, regardless of the solid–gas exchange kinetics. As a result, illumination can lead to significant changes in the concentration of mobile ionic defects compared with the dark case. Including redox reactions for multiple ionic defects (for example iodide vacancies and interstitials in MAPI) opens the possibility of taking the ionic disorder reaction out-of-equilibrium. This points to the intriguing opportunity of designing systems where defect concentrations are increased or decreased by light (“light-driven ionic defect generation or recombination”). Such scenarios are described by introducing an ionic defect pair chemical potential and an effective ionic defect generation rate, both of which can be positive (in analogy to their electronic counter parts) but also negative, depending on the ionic–electronic interactions.Conflicts of interest
There are no conflicts to declare.List of symbols
| Symbol | Meaning, units |
e′, h˙,  | Point defect notation for electrons, holes, iodide interstitials, iodide vacancies, iodine interstitials, iodine vacancies, — |
n, p, 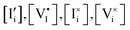 | Concentration of electrons, holes, iodide interstitials, iodide vacancies, iodine interstitials, iodine vacancies, cm−3 |
| I2,g | Iodine molecule in the gas phase, — |
| P(I2)(P(I2)i) | Iodine partial pressure (at the intrinsic condition), bar |
μ
j
(![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) j) j = n, p,… j) j = n, p,… | Equilibrium (electro)chemical potential of species j, eV |
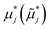
| Nonequilibrium (electro)chemical potential of species j, eV |
δμj(δ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) j) j) | Deviation from equilibrium in the (electro)chemical potential of species j, eV |

| Forward and backward rates for reaction r (see Table 2), cm−3 s−1 |
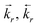
| Forward and backward rate constants for reaction r (see Table 2), s−1, cm−3 s−1, cm−6 s−1… depending on r |
| K r | Mass action constant of reaction r (see Table 2), Depends on r |
| R | Electron–hole recombination rate, cm−3 s−1 |
| G ext | Electron–hole generation rate due to external illumination, cm−3 s−1 |
| U k k = rad, SRH, Aug, I | Electron–hole net recombination due to the process k (radiative, Shockley-Read-Hall, Auger, iodine defect mediated), cm−3 s−1 |
| Γ p,i | Normalized equilibrium hole trapping rate by  at P(I2)i, — at P(I2)i, — |
| Γ n,v | Normalized equilibrium electron trapping rate by 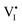 at P(I2)i, — at P(I2)i, — |
| Γ I,i | Ratio between the rate of  oxidation by holes and the rate of electron release from oxidation by holes and the rate of electron release from  at equilibrium and at P(I2)i, — at equilibrium and at P(I2)i, — |
| Γ I,v | Ratio between the rate of  oxidation by holes and the rate of electron release from oxidation by holes and the rate of electron release from  at equilibrium and at P(I2)i, — at equilibrium and at P(I2)i, — |
| h ion | log10(ΓI,v/ΓI,i), — |
G
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) (G
(G![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×) ×) | Effective generation rate of (neutral) anti-Frenkel defects, cm−3 s−1 |
| X vi | Absolute value of electron–hole net recombination involving generation/recombination of a vacancy–interstitial pair, cm−3 s−1 |
U
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) (U
(U![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) ×) ×) | Net recombination of (neutral) anti-Frenkel defects, cm−3 s−1 |
| QFLS | Quasi-Fermi level splitting (i.e. electron–hole chemical potential), eV |
Δμ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) | Anti-Frenkel ionic defect pair chemical potential, eV |
Data availability
The data in this work are available at https://doi.org/10.5281/zenodo.16928557. The codes used to generate the data are available at https://github.com/d-moia/MIEC_light.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5mh01231g.
Acknowledgements
The authors are grateful to Rotraut Merkle for reading and providing useful feedback on this manuscript. D. M. acknowledges financial support from the Alexander von Humboldt Foundation. Open Access funding provided by the Max Planck Society.References
- J. Maier, Physical Chemistry of Ionic Materials, Wiley-VCH Verlag GmbH & Co. KGaA, 2nd edn, 2023 Search PubMed.
- S. M. Sze and K. N. Kwok, Physics of Semiconductor Devices Physics of Semiconductor Devices, John Wiley & Sons, Inc., Hoboken, New Jersey, 1995, vol. 10 Search PubMed.
- P. Y. Yu and M. Cadorna, Fundamentals of Seminconductors, Springer, 4th edn, 2008 Search PubMed.
- J. Nelson, The Physics of Solar Cells, Imperial College Press, 2003 Search PubMed.
- P. Würfel, Physics of Solar Cells: From Basic Principles to Advanced Concepts, 2nd edn, Wiley-VCH Verlag GmbH & Co. KGaA, 2005 Search PubMed.
- F. A. Kroeger, Chemistry of Imperfect Crystals, North-Holland, Amsterdam, 1964 Search PubMed.
- J. Maier, Angew. Chem., Int. Ed. Engl., 1993, 32, 313–335 CrossRef.
- D. Moia and J. Maier, Mater. Horiz., 2023, 10, 1641–1650 RSC.
- T. Y. Yang, G. Gregori, N. Pellet, M. Grätzel and J. Maier, Angew. Chem., Int. Ed., 2015, 54, 7905–7910 CrossRef CAS PubMed.
- C. Eames, J. M. Frost, P. R. F. Barnes, B. C. O’Regan, A. Walsh and M. S. Islam, Nat. Commun., 2015, 6, 2–9 Search PubMed.
- A. Senocrate, I. Moudrakovski, G. Y. Kim, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Angew. Chem., Int. Ed., 2017, 56, 7755–7759 CrossRef CAS PubMed.
- N. Leupold, A. L. Seibel, R. Moos and F. Panzer, Eur. J. Inorg. Chem., 2021, 2882–2889 CrossRef CAS.
- E. Ghahremanirad, S. Olyaee and J. Bisquert, J. Phys. Chem. Lett., 2017, 1402–1406 CrossRef CAS.
- G. Y. Kim, A. Senocrate, T. Yang, G. Gregori, M. Grätzel and J. Maier, Nat. Mater., 2018, 17, 445–450 CrossRef CAS PubMed.
- D. Moia, I. Gelmetti, M. Stringer, O. Game, D. Lidzey, E. Palomares, P. Calado, J. Nelson, W. Fisher and P. R. F. Barnes, Energy Environ. Sci., 2019, 12, 1296–1308 RSC.
- D. A. Egger, A. Bera, D. Cahen, G. Hodes, T. Kirchartz, L. Kronik, R. Lovrincic, A. M. Rappe, D. R. Reichman and O. Yaffe, Adv. Mater., 2018, 30, 1–11 CrossRef PubMed.
- Y. Zhou, L. You, S. Wang, Z. Ku, H. Fan, D. Schmidt, A. Rusydi, L. Chang, L. Wang, P. Ren, L. Chen, G. Yuan, L. Chen and J. Wang, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- Y. Rakita, I. Lubomirsky and D. Cahen, Mater. Horiz., 2019, 6, 1297–1305 RSC.
- R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2002, 4, 4140–4148 RSC.
- A. Senocrate, E. Kotomin and J. Maier, Helv. Chim. Acta, 2020, 103, 1–8 CrossRef.
- T. Defferriere, D. Klotz, J. C. Gonzalez-Rosillo, J. L. M. Rupp and H. L. Tuller, Nat. Mater., 2022, 21, 438–444 CrossRef CAS PubMed.
- G. Walch, B. Rotter, G. C. Brunauer, E. Esmaeili, A. K. Opitz, M. Kubicek, J. Summhammer, K. Ponweiser and J. Fleig, J. Mater. Chem. A, 2017, 5, 1637–1649 RSC.
- A. Viernstein, M. Kubicek, M. Morgenbesser, T. M. Huber, E. Ellmeyer, M. Siebenhofer, C. A. F. Vaz and J. Fleig, Solid State Ionics, 2022, 383, 115992 CrossRef CAS.
- M. Morgenbesser, A. Schmid, A. Viernstein, J. De Dios Sirvent, F. Chiabrera, N. Bodenmüller, S. Taibl, M. Kubicek, F. Baiutti, A. Tarancon and J. Fleig, Solid State Ionics, 2021, 368, 115700 CrossRef CAS.
- D. Meggiolaro, S. G. Motti, E. Mosconi, A. J. Barker, J. Ball, C. Andrea Riccardo Perini, F. Deschler, A. Petrozza and F. De Angelis, Energy Environ. Sci., 2018, 11, 702–713 RSC.
- J. S. Park, J. Calbo, Y. K. Jung, L. D. Whalley and A. Walsh, ACS Energy Lett., 2019, 4, 1321–1327 CrossRef CAS.
- C. J. Tong, L. Li, L. M. Liu and O. V. Prezhdo, J. Am. Chem. Soc., 2020, 142, 3060–3068 CrossRef CAS.
- X. Zhang, M. E. Turiansky, J. X. Shen and C. G. Van De Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 140101 CrossRef CAS.
- S. Bitton and N. Tessler, Energy Environ. Sci., 2023, 16, 2621–2628 RSC.
- D. Moia and J. Maier, ACS Energy Lett., 2021, 6, 1566–1576 CrossRef CAS.
- T. Kirchartz, J. A. Márquez, M. Stolterfoht and T. Unold, Adv. Energy Mater., 2020, 10, 1904134 CrossRef CAS.
- D. Barboni and R. A. De Souza, Energy Environ. Sci., 2018, 11, 3266–3274 RSC.
- S. T. Birkhold, J. T. Precht, R. Giridharagopal, G. E. Eperon, L. Schmidt-mende and D. S. Ginger, J. Phys. Chem. C, 2018, 122, 12633–12639 CrossRef CAS.
- A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S. H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794 CrossRef CAS PubMed.
- M. Von Smoluchowski, Z. Phys. Chem., 1917, 92, 129–168 CAS.
- E. Kotomin and V. Kuzovkov, Rep. Prog. Phys., 1992, 55, 2079–2188 CrossRef CAS.
- J. Hu, Z. Xu, T. L. Murrey, I. Pelczer, A. Kahn, J. Schwartz and B. P. Rand, Adv. Mater., 2023, 35, 2303373 CrossRef CAS.
- X. Zhang, M. E. Turiansky, J.-X. Shen and C. G. Van De Walle, Phys. Rev. B, 2020, 101, 140101 CrossRef CAS.
- Y. Zhou, I. Poli, D. Meggiolaro, F. De Angelis and A. Petrozza, Nat. Rev. Mater., 2021, 6, 986–1002 CrossRef.
- Z. Xu, R. A. Kerner, L. Kronik and B. P. Rand, ACS Energy Lett., 2024, 9, 4645–4654 CrossRef CAS.
- A. Zohar, I. Levine, S. Gupta, O. Davidson, D. Azulay and O. Millo, ACS Energy Lett., 2017, 2, 2408–2414 CrossRef CAS.
- M. T. Neukom, A. Schiller, S. Züfle, E. Knapp, J. Ávila, D. Pérez-del-Rey, C. Dreessen, K. P. S. Zanoni, M. Sessolo, H. J. Bolink and B. Ruhstaller, ACS Appl. Mater. Interfaces, 2019, 11, 23320–23328 CrossRef CAS PubMed.
- W. Clarke, L. J. Bennett, Y. Grudeva, J. M. Foster, G. Richardson and N. E. Courtier, J. Comput. Electron., 2023, 22, 364–382 CAS.
- P. Calado, I. Gelmetti, B. Hilton, M. Azzouzi, J. Nelson and P. R. F. Barnes, J. Comput. Electron., 2022, 21, 960–991 CrossRef CAS.
- J. Bisquert, Adv. Energy Mater., 2024, 2400442, 1–35 Search PubMed.
- D. Moia, Phys. Rev. Appl., 2025, 23, 014055 CrossRef CAS.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS.
- M. C. Brennan, S. Draguta, P. V. Kamat and M. Kuno, ACS Energy Lett., 2018, 3, 204–213 CrossRef CAS.
- Y.-R. Wang, G. Yeong Kim, E. Kotomin, D. Moia and J. Maier, J. Phys. Energy, 2022, 4, 011001 CrossRef CAS.
- A. Schiller, S. Jenatsch, B. Blülle, M. A. Torre Cachafeiro, F. Ebadi, N. Kabir, M. Othman, C. M. Wolff, A. Hessler-Wyser, C. Ballif, W. Tress and B. Ruhstaller, J. Phys. Chem. Lett., 2024, 15, 11252–11258 CrossRef CAS PubMed.
- G. Y. Kim, A. Senocrate, Y. Wang, D. Moia and J. Maier, Angew. Chem., Int. Ed., 2021, 60, 820–826 CrossRef CAS.
- A. Pockett, G. E. Eperon, N. Sakai, H. J. Snaith, L. M. Peter and P. J. Cameron, Phys. Chem. Chem. Phys., 2017, 19, 5959–5970 RSC.
- D. A. Jacobs, H. Shen, F. Pfeffer, J. Peng, T. P. White, F. J. Beck and K. R. Catchpole, J. Appl. Phys., 2018, 124, 225702 CrossRef.
- W. White, C. D. Sanborn, R. S. Reiter, D. M. Fabian and S. Ardo, J. Am. Chem. Soc., 2017, 139, 11726–11733 CrossRef CAS.
- L. Schulte, W. White, L. A. Renna and S. Ardo, Joule, 2021, 5, 2380–2394 CrossRef CAS.
Footnote |
| † Current address: Fluxim AG, Katharina-Sulzer-Platz 2, 8400 Winterthur, Switzerland. |
| This journal is © The Royal Society of Chemistry 2026 |