Molecular insights into CO₂-to-bicarbonate transformation in functionalized anion exchange ionomers for electrochemical separations

Abstract

Bipolar membrane (BPM) electrochemical processes are a promising platform for carbon dioxide (CO₂) separations, but the molecular level thermodynamic and kinetic understanding of CO₂-to-bicarbonate (HCO₃⁻) transformation remain poorly understood. This study employs a multiscale computational approach to systematically explore the adsorption and reactive transformation of CO₂ in five anion exchange ionomer systems. Classical molecular dynamics (MD) simulation results demonstrate that polymers with imidazolium groups significantly reduce CO₂ diffusion and enhance (OH⁻)–CO₂ interactions due to stronger electrostatic and π-interactions. Compared to the commonly used quaternary ammonium ionomers, imidazolium-functionalized ionomers show improved CO₂ proximity and interaction strength. Ab initio MD and density functional theory (DFT) calculations reveal that the benzyl-substituted imidazolium (IM-Ben) substantially reduces the energy barrier for HCO₃⁻ formation (∼72 meV lower) compared to the alkyl-substituted IM-nBu, while also mitigating imidazolium deprotonation under moderate hydration conditions. Transition state analysis shows IM-Ben forms more extensive hydrogen-bonding networks, which stabilize the transition state structure and contribute to a lower energy barrier for bicarbonate formation. These findings highlight the advantage of the adjacent benzyl moiety in enabling efficient CO₂-to-bicarbonate transformation via hydrated hydroxide ion counterions, offering mechanistic insights and clear molecular design principles for optimizing anion exchange ionomers at bipolar membrane interfaces for electrochemical CO₂ separation applications.

---

New concepts

This work presents a multiscale computational approach to uncover how polymer chemistry and hydration structure govern the molecular transformation of CO₂ to bicarbonate (HCO₃⁻) in anion exchange ionomers - key materials in electrochemical CO₂ separation technologies. Using classical MD, ab initio MD, and DFT-based transition state calculations, we reveal how imidazolium-based functional groups promote closer CO₂ association and stabilize reaction intermediates via directional hydrogen bonding leading to lower energy barriers in converting CO₂ and hydroxide to HCO₃⁻. A key conceptual advance is the identification of competing reaction pathways - bicarbonate formation versus imidazolium deprotonation and how solvation and ionomer architecture influence the preferred route. These insights clarify structure–function relationships critical for designing membranes or porous conductors that not only transport but also activate CO₂. This work moves beyond static models of CO₂ binding by elucidating reactive pathways at the molecular level, offering design principles for next-generation materials that integrate ion conduction with selective CO₂ transformation.

1. Introduction

There has been significant interest in turning carbon dioxide (CO₂) into value-added chemicals; however, the chemical transformation processes require concentrated CO₂ feed streams. Hence, concentrating CO₂ from air, oceans, or point sources is required prior to performing reaction processes (e.g., dry reforming or electrolysis). Among various concentrated CO₂ separation approaches, such as adsorption on packed beds and absorption with amines, electrochemical CO₂ separation systems have garnered substantial interest in recent years because they do not generate organic waste, operate at low temperature, and use modular units.^1–4 Bipolar membranes (BPMs), composed of anion exchange layers (AELs) and cation exchange layers (CELs), have emerged as a promising platform for electrochemical CO₂ separations due to their ability for in situ pH adjustment – which exploits CO₂–acid–base equilibria for CO₂ extraction from dilute streams and subsequent concentration.^5–9

The in situ pH adjustment efficacy in BPM electrochemical processes largely depends on the BPM design, such as the anion and cation exchange ionomer chemistry, layer thickness, water dissociation and proton–hydroxide ion recombination catalyst, and the quality of the bipolar junction interface. Recent studies have shown that functional groups within ionomers influence membrane hydration, ion selectivity and ionic conductivity, all of which affect BPM polarization as well as membrane and electrode performance (when used as a binder) in electrochemical processes.^10–13

The most conventional method for electrochemical CO₂ separation and concentration is BPM electrodialysis. However, membrane materials for BPM electrodialysis may not significantly impact cell polarization and energy efficiency when one of the process streams (i.e., the diluate process stream) has a low concentration of ionic species (e.g., carbonate species from the interaction of CO₂ and hydroxide ions). The diluate chamber ohmic resistances can be ameliorated by utilizing a closely related process called electrodeionization. This process features a porous ionic conductor in the diluate chamber to augment the ionic conductivity and to curtail ohmic resistances. Lin and co-workers have used resin wafer BPM electrodeionization for electrochemical CO₂ separation and concentration.¹⁴ Recently, Arges and co-workers have also developed BPM capacitive deionization for pH-assisted selective ion separations.^15–17 Like electrodialysis, the ohmic resistances in the process fluid channel (i.e., spacer channel) of membrane capacitive deionization can also be quite large at low dissolved salt concentrations.¹⁸ Arges and co-workers reduced the ohmic resistances in membrane capacitive deionization systems by using ionomer coated nylon meshes (i.e., a type of porous ionic conductor).^19–21

Most electrochemical CO₂ separation process employ energy intensive faradaic reactions that often use platinum group metals in the electrode layers. Additionally, many of these systems operate with liquid process streams, which can limit CO₂ separation efficiency due to the inherently low solubility of CO₂ in aqueous solutions. The BPM capacitive deionization process proposed in Fig. 1 is being developed for electrochemical CO₂ separations. This process uses a humidified gas stream containing CO₂. This process utilizes a humidified gas stream containing CO₂ and avoids both faradaic reactions and the use of platinum group metals, enabling a more energy-efficient and material-sustainable pathway for CO₂ handling and potential downstream utilization. To realize this process, it is important to design appropriate ionomers in the porous ionic conductor in the spacer channel and for the anion exchange layer in the BPM. Arges and Lin and co-workers have shown that imidazolium ionomers, processed into anion exchange membranes and resin wafers, are effective for selective removal of lactate and p-coumarate (organic acid anions with carbonyl groups) from process streams.^22,23 Their work, and others,^24,25 showed that imidazolium-based functional groups are effective for electrochemical CO₂ separations due to their intrinsic affinity toward CO₂ molecules – which is attributed largely to the planar aromatic structure that facilitates favorable electrostatic and π–π interactions with CO₂. Despite these promising characteristics, detailed mechanistic insights into HCO₃⁻ formation from CO₂–hydroxide counterions in close vicinity to a tethered cation, as well as competing chemical pathways, remain insufficiently understood at the molecular level.

Fig. 1 Bipolar membrane (BPM) capacitive deionization setup with ionomer coated nylon mesh in the spacer compartment (i.e., where the humidified CO₂ fluid flows). (a) Charge mode where water dissociation occurs in the BPM to generate hydroxide ions in the spacer compartment to convert CO₂ (from a dilute stream) to carbonate species. The carbonate species migrate towards the positive electrode and adsorb in the electrochemical double layer of the positive electrode. (b) Discharge mode where the polarity of the cell is flipped and the carbonate species are moved back to the spacer compartment, and the BPM operates in forward bias mode. This leads to a hydroxide ion sink in the spacer channel acidifying the compartment causing the carbonate species to revert to CO₂. The CO₂ generated in discharge mode is concentrated via recirculation during the discharge step only.

To address the said challenges in streamlining materials development for electrochemical CO₂ separations, advanced computational methods, including molecular dynamics (MD) simulations and density functional theory (DFT) calculations, are considered because they offer valuable molecular scale insights that can a priori elucidate the interactions and reaction energetics underlying the chemical transformation of CO₂ in ionomers. Previous computational studies have explored polymer–CO₂ interactions, identifying factors such as backbone chemistry and ionomer functionalization as critical parameters influencing CO₂ diffusivity and interaction strength.^12,26,27 For instance, quaternary benzyl ammonium polysulfone (QAPSf) and quaternary benzyl imidazolium polysulfone (QIPSf) have demonstrated distinct differences in ion selectivity and CO₂ affinity, underscoring the importance of structural features such as backbone rigidity and functional-group positioning (vide infra, structures of the ionomers are schematically shown in Fig. 2).^22,24 Motivated by these findings, we investigate five distinct anion exchange ionomer systems to systematically evaluate the impact of backbone architecture (polysulfone) with cations at the benzyl position vs. poly(m-terphenyl phenylene) with cations at the end of an n-hexyl side chain and functional group chemistry (quaternary ammonium (trimethyl ammonium and n-methyl pyrrolidinium) vs. imidazolium) on CO₂ separation performance and HCO₃⁻ formation efficiency. By integrating classic MD simulations and accurate DFT and AIMD calculations, this work reveals critical molecular-scale phenomena—including CO₂ diffusion, spatial organization, hydration effects, and competing reaction pathways—thus providing a detailed molecular understanding of CO₂ separation and HCO₃⁻ formation in anion exchange ionomers – which can comprise the anion exchange layer of the BPM as well as the porous ionic conductor in Fig. 1. The outcomes from this computational investigation not only clarify fundamental reaction mechanisms but also guides the rational design for next-generation ionomers in electrochemical CO₂ separation processes.

Fig. 2 (a) Chemical structures of the five polymer systems investigated in this study: quaternary trimethylammonium m-terphenyl trifluoromethyl (QTMTTf), quaternary ammonium m-terphenyl trifluoromethyl (QATTf), quaternary imidazolium m-terphenyl trifluoromethyl (QITTf), quaternary benzyl imidazolium polysulfone (QIPSf), and quaternary benzyl ammonium polysulfone (QAPSf). Corresponding subsystem models (TM-nBu, AM-nBu, IM-nBu, IM-Ben, and AM-Ben), used for simulations and analyses (AIMD and DFT), are also depicted. (b) Initial conformation of the QIPSf 20 mer (20 repeat units) used in the simulations. (c) Mean square displacement (MSD) of CO₂ in five polymer membrane systems calculated from classical MD simulations. (d) CO₂ diffusion coefficients (nm² ps⁻¹) (blue bars) and OH⁻ : CO₂ contact ratios (%) (red line) calculated from the same simulations. Error bars represent standard deviations for diffusion coefficients.

2. Computational approach

2.1. Polymer models and computational methods overview

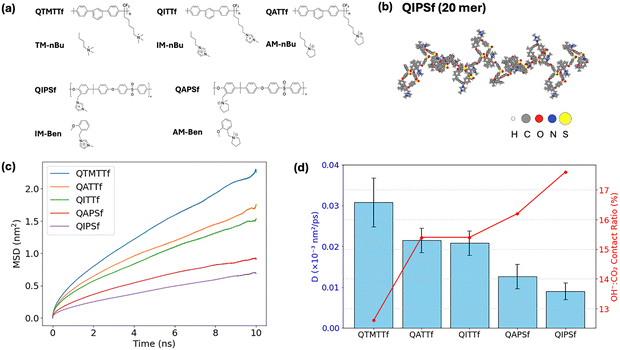
In this study, we first investigated five distinct polymer systems using classical MD simulations. These polymer systems were selected because they contain common cationic functional groups (e.g., quaternary ammonium groups and imidazolium groups) and backbone chemistries that have been successful in making free standing anion exchange membranes and ionomer coated nylon meshes.^19–22 Additionally, these systems can be systematically altered to study how structural variations influence interactions with target species such as OH⁻ and CO₂. Previously, two of the five polymer systems studied, quaternary benzyl ammonium polysulfone (QAPSf) and quaternary benzyl imidazolium polysulfone (QIPSf), were systematically compared when for transferring lactate and p-coumarate anions in electrodialysis and electrodeionization.^22,23 To further explore this phenomenon, we introduced three additional polymer structures: quaternary ammonium m-terphenyl trifluoromethyl (QATTf), quaternary trimethyl ammonium m-terphenyl trifluoromethyl (QTMTTf), and quaternary imidazolium m-terphenyl trifluoromethyl (QITTf), which feature systematic variations in their tethered cation groups and polymer backbone chemistry.

To elucidate deeper structural interactions and energetic characteristics, AIMD simulations and static DFT calculations were further performed on representative subsystems extracted from the polymer systems. These subsystems were specifically chosen to encompass critical interactions between the functional groups and a representative segment of the polymer backbone. This multi-scale modeling approach enabled accurate characterization of key chemical and physical interactions within the polymeric environment. Detailed chemical structures of the complete polymer systems used in the MD simulations and their corresponding subsystem models are presented in Fig. 2(a). The geometries of all models are presented in Fig. S1 and S2.

2.2. Classical MD simulations

Classical MD simulations were performed using GROMACS version 2024²⁸ and the OPLS-AA forcefield²⁹ for the polymer systems, as it has been extensively validated for reproducing structural and thermodynamic properties of polymers in condensed phases.^30–34 Beyond polymers, OPLS-AA has been successfully applied to model imidazolium or ammonium-based systems in their interactions with small molecules. For instance, Shi et al.³⁵ utilized OPLS-AA force field to model ammonia absorption in ionic liquid, demonstrating that the force field captures strong hydrogen bonding interactions between the NH₃ and the imidazolium cation and reproduces experimental adsorption enthalpies. Verma et al.³⁶ applied OPLS-AA to simulate the ionic conductivity of mixed imidazolium-based ionic liquids, reporting good agreement with experimental measurements and confirming the robustness of the force field in describing cation–anion and ion–neutral interactions. More recently, Yang et al.³⁷ employed OPLS-AA (with minor reparameterization) in a hybrid GCMC/MD framework to model CO₂ adsorption in porous organic cages, successfully reproducing multistep adsorption profiles and gas–cage interaction energies consistent with DFT benchmarks. Truszkowska et al.³⁸ used OPLS-AA to simulate plating behavior in ion-exchange membranes, a system chemically and structurally similar to ours, further validating its applicability to polymer–electrolyte environments. Given these precedents, the OPLS-AA force field was selected to describe the polymer components in our systems. For other species, we adopted the rigid three-site CO₂ model developed by Duan et al.³⁹ and the OH⁻ model by Moultos et al.⁴⁰ as well as the TIP3P water model.⁴¹ Previous comparative studies have shown that the Duan's CO₂ model provides reliable predictions of bulk and interfacial properties.^42–45 In particular, it has been shown to reproduce key experimental observables, such as CO₂–CO₂ association, diffusion and plasticization properties,⁴⁶ with fidelity sufficient for the scale and focus of the present work. Likewise, the Moultos's OH⁻ model has been used in studies of ion diffusion and interfacial behavior in aqueous or ionomeric systems,^47,48 where it reproduces experimental trends with good fidelity. Together, these validated models provide a consistent and reliable framework for simulating the coupled polymer–ion interactions investigated in this work. Initial atomic charges for the polymer were determined using DFT-based natural bond orbital (NBO) analyses. To achieve balanced interactions with the hydroxide ion and to ensure accurate predictions of hydration structure, ion transfer behavior and adsorption energies, the polymer partial charges were uniformly scaled by a factor of 0.75, consistent with previous literature recommendations.^49–52

Five distinct monomer polymer repeat units were initially optimized at the B3LYP/6-31g(d) level of theory before being assembled into polymer chains for subsequent simulations, each single chain consists of 20 repeat units, using the mbuild software package from the Molecular Simulation Design Framework (MoSDef).⁵³ The total number of atoms per polymer chain was maintained between approximately 1200 and 1500, to maintain a balance between chemical fidelity and computational efficiency. A representative initial structure of a single polymer chain is shown in Fig. 2(b), while the complete set of initial polymer structures is provided in Fig. S1.

To simulate conditions representative of anion exchange ionomer environments and ensure statistically meaningful sampling, fifty of these single polymer chains were randomly packed into a 50 nm × 50 nm × 20 nm simulation box. This initial box size was selected to accommodate all chains with sufficient spacing to prevent atomic overlap during packing. It serves as a starting configuration that allows for effective rearrangement and densification during the subsequent compression and relaxation process. Following equilibration, the system compresses into a thinner and denser configuration, maintaining an appropriate environment for polymer–solvent–ion interactions, while providing enough area and volume to enable multiple CO₂ and OH⁻ encounters.

To maintain charge neutrality and support realistic hydration conditions, 1000 OH⁻ ions and 5000 water molecules were added to the system, resulting in a hydration number (λ) of 5 (i.e., five water molecules per OH⁻). This hydration level is adopted in the literature to emulate moderate hydration conditions within anion exchange membranes and was selected based on the works by Luo et al.,⁵⁴ which demonstrated that λ in the range of 3–7 is a representative and stable hydration state for evaluating ion transport and membrane morphology under confinement.

To obtain polymer membranes with realistic experimental densities and structures, we employed a multi-step compression and relaxation procedure adapted from Larsen et al.,⁵⁵ which is a refined technique previously developed by Hofmann and Karayiannis et al.^52,56 Specifically, the polymer–water–hydroxide system underwent a carefully structured, 21-step thermal cycling protocol. Each thermal cycle consisted of one NPT (constant number, N, pressure, P, temperature, T) compression step at a low temperature, followed by two NVT (constant number, N, volume, V, temperature, T) equilibration steps, first at a high temperature and then at a lower temperature. A detailed description of this compression and relaxation procedure is provided in Table S1. Recent studies by Risko et al.³⁰ have demonstrated that this methodology reliably yields condensed polymer structures and densities consistent with experimental observations. After the 21-steps compression and relaxation process, 500 carbon dioxide molecules were randomly inserted into the simulation box, and an initial energy minimization was performed to obtain the ground-state structure. The Nose–Hoover thermostat^57,58 was used to stabilize the system temperature at 300 K with a time constant of 1 ps and the Parrinello–Rahman barostat^59,60 was used to maintain the pressure at 1 bar with a time constant of 10 ps. Three-dimensional periodic boundary condition (PBC) was applied, and a spherical cut-off of 1.2 nm was used for all van der Waals (vdW) interactions. The particle-mesh Ewald (PME)⁶¹ with 1.2 nm cutoff for long-range electrostatic interactions were used throughout the simulations. Each system was simulated for 20 ns under the NPT conditions, with the final 10 ns used for analysis with MDAnalysis package.^62,63 The diffusion coefficients were extracted by fitting the mean-squared displacement within the 12–18 ns window using GROMACS tools.

An in-house Python script was utilized to extract smaller sub-systems from the final MD simulation trajectories; a sample script is included in the SI. Each extracted sub-system contains the polymer functional group, a portion of the polymer backbone, a OH⁻ ion with its surrounding water solvation shell, and a CO₂ molecule located within 5 Å of this solvation shell. The total atom in each sub-systems was in the range of 35 to 45 atoms after removing the additional fragments. These sub-systems served as the basis for subsequent AIMD and DFT simulations to provide deeper insights into the structural and energetic characteristics associated with HCO₃⁻ formation.

2.3. Ab initio molecular dynamics (AIMD) simulations

In this study, we conducted AIMD simulations using the CP2K/Quickstep software⁶⁴ on the sub-systems (see scheme in Fig. S2 to view the subsystems) of the polymer model. The total energy calculations and molecular dynamics were carried out using the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional,⁶⁵ supplemented with Grimme's D3 method (DFT-D3).⁶⁶ The atoms were represented using norm-conserving Goedecker, Teter, and Hutter (GTH) pseudopotentials,⁶⁷ coupled with the PBE pseudopotentials.⁶⁸ The electronic wave functions were described using a double ζ valence polarized basis set optimized for molecular systems, as well as the GTH pseudopotentials (DZVP-GTH). The finest level of the multi-grid employed a planewave cutoff (CUTOFF) set to 500 Ry, while the relaxation cutoff (REL_CUTOFF) was set at 60 Ry.

For the AIMD simulations, the initial extracted sub-systems were positioned at the center of a 2 nm × 2 nm × 2 nm simulation box. A temperature of 300 K was maintained for a duration of 80 ps simulation with a time step of 1 fs. The NVT was adopted, utilizing the Nose–Hoover thermostat.⁶⁹ Thermal energies and trajectories were recorded every 1 fs. An example of the input file used for the AIMD simulation is included in the SI. The MDAnalysis package^62,63 was used to analyze the AIMD trajectories and to calculate the atomic distance and radial distribution functions.

2.4. Density functional theory (DFT)

The DFT cluster calculations were carried out using the Gaussian 16 software package.⁷⁰ Potential energy surface (PES) scans were performed at the B3LYP/6-31+G(d,p) level of theory, offering a balance between computational efficiency and reasonable accuracy for exploring reaction coordinates. Multiple solvation states of OH⁻ (varying the number of water molecules in the solvation shell) in the presence of polymer functional groups were optimized to explore the influence of hydration environment on the reaction pathway.

The transition-state (TS) geometries were identified using the quadratic synchronous transit (QST3) method at the ωB97xD/def2-SVP level of theory.⁷¹ Sub-system structures extracted from classical MD simulations served as initial geometries for the reactant states. The TS and final product geometries were obtained by strategically repositioning one water molecule from the solvation shell to the vicinity of CO₂. To accurately capture dispersion interactions, reactant, product, and TS structures were subsequently optimized at the ωB97xD/def2-SVP level of theory. Single-point calculations using the ωB97xD/def2-TZVP level of theory were then conducted to refine the energetic profiles and improve the accuracy of calculated reaction energies. Additionally, frequency analyses performed at the ωB97xD/def2-SVP level confirmed the nature of each stationary point, where TS structures exhibited one imaginary frequency aligned with the reaction coordinate. All TS calculations incorporated the Polarizable Continuum Model (PCM) with a dielectric constant (ε) of 78.3 to correspond to the aqueous conditions.

3. Results and discussions

To generate realistic bulk polymer structures suitable for molecular simulations, we applied the 21-step multi-cycle compression and relaxation protocol across five different maximum pressure values (P_max = 10 000 to 50 000 bar) for each polymer system. This approach, adapted from the work of Larsen⁵⁵ and Risko et al.,³⁰ enables densification of initially low-density polymer configurations while allowing structural relaxation at intermediate and low temperatures. For each pressure condition, five independent simulations were conducted to assess reproducibility and statistical consistency of the final densities.

Based on the analysis of the resulting equilibrium densities, a P_max value of 40 000 bar was selected for all subsequent MD and DFT studies. This choice ensures that the polymer matrices used in downstream simulations are representative of equilibrated bulk systems with consistent densities, while avoiding the added computational cost associated with higher compression pressures. Additional discussion of the density trends and statistical variation across pressure conditions is provided in Fig. S3.

3.1. Diffusion and mobility of CO₂

The computed mean square displacement (MSD) of CO₂ and diffusion coefficients shown in Fig. 2 indicate that CO₂ mobility is strongly correlated with polymer chemistry and the strength of interactions at the polymer's functional groups (quaternary ammonium and imidazolium cations). The simulations indicate that the QIPSf polymer exhibits the highest OH⁻ : CO₂ close-contact ratio (17.6%), notably surpassing the ratios (12–16%) observed in other polymer systems. This elevated ratio suggests that QIPSf provides more robust and effective interaction sites to stabilize CO₂, significantly enhancing its local concentration and immobilization within the polymer matrix. Although HCO₃⁻ formation was not directly modeled, the proximity and strong association between CO₂ and OH⁻ ions observed in QIPSf highlight its potential for facilitating HCO₃⁻ formation relative to other polymers in this study.

To further evaluate the robustness of these observations, we conducted additional simulations in which all atomic charges were uniformly scaled by factors of 0.6, 0.7, 0.8, and 1.0, in addition to the default value of 0.75. The results, presented in Fig. S11, show that while the absolute values of the CO₂ diffusion coefficients decrease with increasing charge magnitude, as expected due to stronger electrostatic interactions, the qualitative trends among polymers remain consistent. Notably, QIPSf consistently exhibits the lowest CO₂ diffusion coefficient across all scaling factors, confirming that its strong interaction with CO₂ is not an artifact of the chosen scaling scheme but rather an intrinsic feature of its chemistry. This reinforces our conclusion that QIPSf provides the most effective environment for stabilizing CO₂ and potentially promoting HCO₃⁻ formation.

QAPSf and QIPSf, which feature a quaternary benzyl polysulfone backbone, exhibit notably lower diffusion coefficients (0.009–0.0126 × 10⁻³ nm² ps⁻¹) than their counterparts (QTMTTf, QATTf and QITTf) containing m-terphenyl units and alkyl chains (0.0208–0.0308 × 10⁻³ nm² ps⁻¹). Additionally, polymer containing the imidazolium functional group displayed the lowest CO₂ diffusion coefficient within each backbone category. The detailed diffusion coefficient value and OH⁻ : CO₂ contact ratio are included in the Table S2. A plausible explanation for this is that the quaternary benzyl polysulfone (PSf) backbone provides enhanced noncovalent interactions—such as π–π stacking or electrostatic forces—between CO₂ and the polymer matrix. These interactions may increase the likelihood of CO₂ being transiently associated with the polymer environment, thereby reducing its effective diffusion. Furthermore, the presence of imidazolium-based functionality (particularly in QIPSf and QITTf) further augments these interactions, as imidazolium's planar ring can engage in robust π-character and electrostatic interactions with CO₂. By contrast, QTMTTf, QATTf and QITTf with their phenyl and alkyl chain structures, appear to offer relatively less affinity towards CO₂, leading to higher MSD values and faster diffusion (Fig. 2(c)). These results underscore how minor structural modifications – such as switching from m-terphenyl plus alkyl groups to a quaternary benzyl polysulfone backbone – significantly influence the polymer's ability to stabilize CO₂ and promote its transformation into carbonate species.

From a practical perspective, lower CO₂ diffusivity may be advantageous if it aligns with longer residence times that enhance the conversion of CO₂ to carbonate species; however, it also raises considerations regarding gas treatment throughput. Overall, QIPSf was identified as a promising ionomer material for use in the BPM electrochemical separation unit because its polymer backbone and tethered imidazolium group work cooperatively to effectively coordinate with CO₂ and potentially promote subsequent carbonate formation reactions.

3.2. The radial distribution functions (RDF) analysis

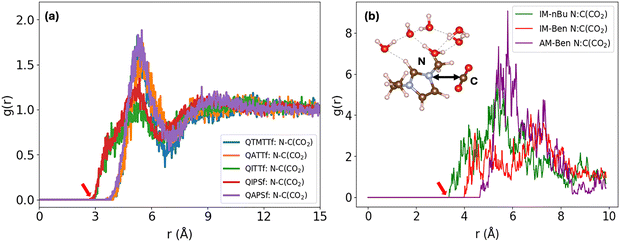
Fig. 3 displays the RDFs between the nitrogen atom in the polymer functional group and the carbon atom of CO₂ (N–C(CO₂)) from classical MD (panel a) and AIMD simulations (panel b). The corresponding RDFs between the nitrogen atom and the oxygen atom of hydroxide (N–O(OH⁻)) are presented in Fig. S4. These RDFs provide a statistical description of how CO₂ and hydroxide ions are spatially distributed around the functional groups in different polymer environments, offering insight into local interaction strength and potential reactivity.

Fig. 3 Radial distribution functions (RDFs) illustrating the spatial distribution of CO₂ relative to the nitrogen centers in polymer systems from (a) classical MD and (b) AIMD simulations. Panel (a) shows N–C(CO₂) RDFs for five polymers, comparing imidazolium- and ammonium-containing systems. Panel (b) presents AIMD-derived RDFs for representative subsystems: imidazolium-based (IM-Ben, IM-nBu) and ammonium-based (AM-Ben). Red arrows highlight the earlier rising peaks observed in the imidazolium systems, indicating closer CO₂ association. The inset in panel (b) depicts the N–C vector used in the RDF calculations and the representative molecular configuration from AIMD trajectories.

In Fig. 3(a), the RDFs from classical MD simulations show that QIPSf and QITTf, both of which incorporate imidazolium-based cations, exhibit earlier rising peaks (indicated by the red arrows) beginning around 3.5–4.0 Å, compared to the ammonium-based systems (QAPSF, QATTf, and QTMTTf), whose RDFs rise later and peak at slightly longer distances (∼5.3 Å). This early rise in RDFs for imidazolium systems reflects closer and more immediate N–C(CO₂) contacts, suggesting a stronger electrostatic and directional interaction between CO₂ and the imidazolium ring. Similar behaviors are also observed in the AIMD-derived RDFs for selected subsystems as shown in Fig. 3(b). Both IM-Ben and IM-nBu show sharp increases at shorter distances compared to AM-Ben, the ammonium containing subsystems. These results further support the idea that the planar aromatic structure of imidazolium enhances CO₂ localization near the cation, likely through π–quadrupole and electrostatic interactions. In contrast, ammonium-based cations tend to stabilize CO₂ at slightly greater distances, consistent with their more spherical and less delocalized charge distribution. The consistency between AIMD and classical MD RDFs further validates the reliability of the simulations performed and supports the choice of the OPLS-AA force field, as discussed in the computational approach section.

The RDF data indicate that imidazolium-functionalized polymers provide a structural advantage in bringing CO₂ into closer proximity to the nitrogen site, a feature that could lower the entropic cost of reactant alignment and enhance the likelihood of CO₂ activation or conversion in HCO₃⁻ transformation reactions.

3.3. Electronic structure and redox stability

The highest occupied molecular orbital (HOMO) energies of the monomers show a clear backbone-dependent trend. The polysulfone-based monomers (QIPSf and QAPSf) exhibit deeper HOMO levels (more negative energies) compared to the m-terphenyl-trifluoromethyl–based monomers (QTMTTf, QITTf, QATTf). A deeper HOMO generally indicates a lower propensity for oxidation, suggesting improved redox stability under electrochemical operation. Among all species, QIPSf shows the largest HOMO–LUMO gap, which implies a more rigid electronic structure and potentially greater intrinsic stability. While the adsorption of CO₂ is primarily influenced by the functional group chemistry at the cationic sites, these frontier orbital characteristics provide additional insight into the stability differences observed between backbone types. Note that a detailed analysis of the orbital energies of monomers is provided in (Fig. S8).

3.4. Bicarbonate formation energy and transition state

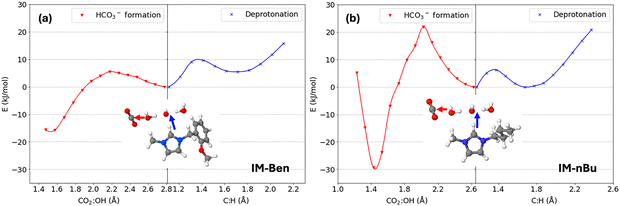
To gain deeper insight into how imidazolium influences HCO₃⁻ formation, we extracted representative configurations from the classical MD simulations and performed a series of DFT calculations at the ωB97xD/def2svp level of theory, followed by single-point energy corrections at ωB97xD/def2tzvp level of theory. Each subsystem consists of a fragment of the polymer chain (AM-Ben, IM-Ben, or IM-nBu), and four explicit water molecules that form the localized solvation shell around OH⁻ and a CO₂ molecule.

Using DFT, we mapped out the relative energy levels where one solvation–shell water molecule reorients to facilitate CO₂ conversion into HCO₃⁻. The results (Fig. 4(a)) indicate that IM-Ben exhibits a substantially lower reaction barrier (∼252 meV) compared to both IM-nBu (∼324 meV) and AM-Ben (∼875 meV). This finding suggests that the aromatic benzyl substitution on the imidazolium ring stabilizes the transition state more effectively, thus promoting a more favorable pathway to HCO₃⁻ formation.

Fig. 4 (a) Relative energies for bicarbonate (HCO₃⁻) formation from CO₂ and OH⁻ across three polymeric model subsystems (IM-Ben, IM-nBu, and AM-Ben, see Fig. 2). The energy profiles represent initial states (IS), transition states (TS), and final states (FS), computed at the ωB97xD/def2-TZVP//ωB97xD/def2-SVP level of theory with PCM solvation (ε = 78.3). (b) Corresponding optimized geometries highlighting hydrogen-bonding interactions (depicted as dashed lines) during the reaction pathway. Energy values (in meV) are relative to the respective IS. Notably, IM-Ben exhibits more extensive hydrogen bonding in the TS structure compared to IM-nBu and AM-Ben (6 vs. 5 interactions), correlating with a lower activation energy barrier and enhanced stabilization during CO₂-to-bicarbonate conversion.

The smaller TS energy barrier (0.25 eV) in IM-Ben indicates a readily accessible route for proton transfer and CO₂ incorporation into the HCO₃⁻ moiety. Such enhanced reactivity may arise from a synergistic interplay between the ring's π-conjugation and the relatively open environment offered by the benzyl group, allowing optimal hydrogen-bonding networks among OH⁻, water molecules, and CO₂. The representative configurations of these subsystems showing the hydrogen-bonding networks in each reaction state are included in Fig. 4(b).

To account for entropic contributions at room temperature (298 K), we also computed Gibbs free energy (ΔG) profiles for the bicarbonate formation reaction (Fig. S9). The inclusion of entropy slightly shifts the energy barriers compared to the enthalpy-only results, but the overall trends remain consistent. Specifically, IM-Ben maintains the lowest barrier (0.15 eV) compared to IM-nBu (0.40 eV) and AM-Ben (0.93 eV). The final states remain exergonic for IM-Ben (−0.56 eV) and IM-nBu (−0.57 eV), while AM-Ben shows a less favorable stabilization (−0.35 eV). To further examine this mechanistic assignment, we analyzed electron-density/ESP maps and NBO charges for representative subsystems (Fig. S10 and Table S3). These results provide direct electronic-level evidence for transition-state stabilization in IM-Ben. Specifically, for the IM-Ben subsystem, the CO₂ carbon becomes more positive at the TS (e.g., IM-Ben: +1.05 → +1.08 e), while the OH⁻ oxygen becomes less negative (−1.24 e→ −1.07 e), consistent with nucleophilic attack and C–O bond formation. Moreover, the O atom from H₂O (that eventually bonds to CO₂) transiently becomes more negative (IM-Ben: −1.03 e → −1.16 e), reflecting strengthening of the H-bonding network at the TS. Simultaneously, the imidazolium unit in IM-Ben exhibits a transient reduction in net positive charge (IS → TS → FS: +0.67 → +0.66 → +0.68 e), reflecting enhanced charge accommodation relative to IM-nBu and AM-Ben analogues. The ESP maps (Fig. S10) further highlight polarization of the benzyl-imidazolium π system, which delocalizes the positive potential and buffers developing charge separation. Together, these data reinforce that the benzyl-substituted imidazolium lowers the CO₂-to-bicarbonate reaction barrier not only through hydrogen-bonding network strengthening but also through π-driven electronic stabilization of the transition state, providing a more favorable kinetic and thermodynamic pathway.

3.5. Influence of hydration environment and reaction pathway

Another critical phenomenon identified in our simulations is the deprotonation of the imidazolium. This behavior, previously reported in literatures,^72,73 is further supported by our AIMD results, which show elongation of the imidazolium C–H bond accompanied by proton transfer to the neighboring hydroxide ion, resulting in the formation of water (Fig. S5). The C–H group between the two nitrogen atoms in the imidazolium ring can be extracted from nearby OH⁻ to produce water rather than the OH⁻ reacting with CO₂ to form HCO₃⁻. To systematically investigate this, we examined multiple hydration environments with varying numbers of water molecules in the OH⁻ solvation shell and calculated potential energy surfaces (PES) for the deprotonation reaction by progressively extending the imidazolium's C–H bond. We focused on two representative subsystems: IM-Ben and IM-nBu because they both have the imidazolium functional group and offer the high favorable formation energy of HCO₃⁻ in each polymer backbone category. The computed relative energy profiles are shown in Fig. 5 and the complete molecular conformations of the multiple solvation models used in these calculations are included in Fig. S6 and S7.

Fig. 5 Potential energy surfaces (PES) of imidazolium deprotonation as a function of the C–H bond length in IM-Ben (benzyl-substituted imidazolium, red) and IM-nBu (alkyl-substituted imidazolium, blue) under varying hydration levels: (a) OH⁻ : H₂O = 1 : 1, (b) OH⁻ : H₂O = 1 : 2, (c) OH⁻ : H₂O = 1 : 3, and (d) OH⁻ : H₂O = 1 : 4, calculated at the B3LYP/6-31+g(d, p) level of theory. Insets in panel (a) illustrate representative unprotonated and protonated conformations of IM-nBu along the deprotonation pathway. Atom color scheme: red = oxygen, gray = carbon, blue = nitrogen, white = hydrogen.

At low hydration (1 : 1 ratio of OH⁻ : H₂O), both IM-Ben and IM-nBu display favorable deprotonation energies of −30.5 and −39.7 kJ mol⁻¹, respectively, indicating that the imidazolium C−H bond is readily cleaved in strongly alkaline or underhydrated conditions. When the water content doubles (1 : 2 ratio), IM-Ben becomes slightly unfavorable for deprotonation (+0.5 kJ mol⁻¹), whereas IM-nBu remains favorable (−5.0 kJ mol⁻¹). The disparity grows with increased hydration: at 1 : 3 ratio, IM-Ben requires +22.0 kJ mol⁻¹vs. +10.9 kJ mol⁻¹ for IM-nBu, and at 1 : 4 ratio, the deprotonation energy barrier climbs further, reaching +34.2 kJ mol⁻¹ for IM-Ben and +22.7 kJ mol⁻¹ for IM-nBu. Consequently, IM-Ben is substantially more resistant to proton loss at moderate to high hydration.

These findings underscore the delicate balance between polymer structure, local pH, and the availability of water molecules in the membrane's solvation shell. Under intensely alkaline or poorly hydrated conditions (1 : 1 or 1 : 2), both imidazolium systems are at risk of deprotonation, which would compromise HCO₃⁻ formation by consuming OH⁻ in water-producing side reactions. By contrast, increased hydration (≥1 : 3) stabilizes the imidazolium ring, thus preserving available OH⁻ for efficient CO₂ conversion to HCO₃⁻. The marked contrast between IM-Ben and IM-nBu at these ratios suggests that benzyl substitution confers greater structural resilience against deprotonation, favoring the formation of HCO₃⁻ intermediates.

In practical terms, these energy profiles emphasize that controlling membrane hydration (or effectively moderating pH) is critical for sustaining imidazolium functionality. Excessively high pH and elevated temperatures (i.e., >40 °C) can accelerate ring deprotonation and reduce the efficiency of CO₂ conversion to bicarbonate and carbonate species, while more moderate alkalinity provides an optimal operating window for robust CO₂ uptake and HCO₃⁻ generation. Mitigating C–H deprotonation in the imidazolium cation can be achieved by adding an ‘R’ group to the C₂ between the nitrogen atoms (e.g., 1,2-dimethyl imidazolium⁷⁴ or trimethoxyphenyl⁷⁵). In concentrated alkaline environments, some researchers have a methyl on all the carbon atoms in the imidazolium ring.⁷⁶ Overall, these insights will be useful in down selecting anion exchange ionomers for the ionomer coated porous fabric in the spacer channel and the anion exchange membrane layer in the bipolar membrane because judicious selection of the material is vital for CO₂ conversion effectiveness.

Distinctly different energetic preferences for HCO₃⁻ formation versus imidazolium deprotonation in IM-Ben and IM-nBu systems were observed, particularly at moderate hydration levels (OH⁻ : H₂O = 1 : 2). To elucidate this behavior, we calculated the PES for both reaction pathways in each subsystem. To compare the imidazolium deprotonation energy with the HCO₃⁻ formation, we used a subsystem that contains two water molecules in the OH⁻ solvation shell, as well as a CO₂ in the outer shell as shown in the insert of Fig. 6. Each geometry was optimized at B3LYP/6-31+g(d,p) level of theory for the PES calculations.

Fig. 6 Comparative potential energy surfaces (PES) illustrating competing reaction pathways in benzyl-substituted ((a) IM-Ben) and alkyl-substituted ((b) IM-nBu) imidazolium systems at 1 : 2 OH⁻ : H₂O ratio, calculated at the B3LYP/6-31+g(d,p) level of theory. The red curves represent the PES as a function of CO₂–OH⁻ distance, indicating HCO₃⁻ formation, while the blue curves represent the PES as a function of the imidazolium C–H bond distance, indicating imidazolium deprotonation. The inserts represent the optimized subsystem as the initial state. The red and blue arrows indicating two competing reaction pathways for HCO₃⁻ formation and IM deprotonation. IM-Ben favors HCO₃⁻ formation energetically, indicated by a lower reaction barrier, whereas IM-nBu preferentially undergoes imidazolium deprotonation under similar hydration conditions.

Our calculations reveal that IM-Ben exhibits a higher energy barrier for imidazolium deprotonation (approximately 10 kJ mol⁻¹), whereas HCO₃⁻ formation remains significantly more energetically favorable with a barrier of 6 kJ mol⁻¹. Conversely, in IM-nBu, the deprotonation pathway has a low reaction barrier of 6 kJ mol⁻¹ and a slightly favorable deprotonated state (−0.3 kJ mol⁻¹), while a high barrier for the HCO₃⁻ formation (23 kJ mol⁻¹), resulting in a competitive reaction route for proton transfer to OH⁻ to produce water and thereby diminishes the availability of OH⁻ for HCO₃⁻ generation.

The underlying structural differences between IM-Ben and IM-nBu were identified to have a profound impact on OH⁻ and CO₂ conversion to HCO₃⁻. The benzyl substitution in IM-Ben provides enhanced electronic and steric stabilization of the imidazolium ring, reducing its susceptibility to proton loss. This stabilization encourages CO₂ to preferentially engage in HCO₃⁻ formation rather than promoting proton transfer to OH⁻. In contrast, the alkyl substituent in IM-nBu lacks this stabilizing effect, rendering the system more prone to undesirable proton loss. Furthermore, IM-Ben is more effective for HCO₃⁻ formation under moderately alkaline conditions because the local solvation environment adequately stabilizes OH⁻ without inducing excessive ring deprotonation. In summary, the results underscore the importance of polymer structure and hydration control in anion exchange ionomer design, suggesting that benzyl-substituted imidazolium systems could deliver enhanced stability and superior CO₂ conversion performance compared to their alkyl-substituted counterparts.

4. Conclusion

In this study, we systematically investigated the structural and energetic factors governing CO₂ adsorption, diffusion, and HCO₃⁻ formation in five anion exchange ionomer materials using an integrated multiscale computational approach. These ionomer materials are used in porous conductors and bipolar membranes for electrochemical separation units for CO₂. Classical MD simulations demonstrated that the anion exchange ionomers featuring quaternary benzyl polysulfone backbones, particularly those with imidazolium functional groups (QIPSf), exhibit significantly reduced CO₂ diffusion and stronger CO₂ : OH⁻ interactions compared to quaternary m-terphenyl trifluoromethyl systems. The enhanced interaction in imidazolium-based systems was confirmed by radial distribution function analyses, which indicated closer spatial proximity of CO₂ and OH⁻ to the aromatic nitrogen centers.

AIMD and DFT calculations further validated these findings, highlighting the benzyl-substituted imidazolium (IM-Ben) as particularly effective in stabilizing the transition state and thus significantly lowering the energy barrier (by approximately 72 meV relative to alkyl-substituted IM-nBu) for HCO₃⁻ formation. Additionally, systematic exploration of hydration conditions revealed that benzyl-substituted imidazolium groups provide superior resistance against undesirable deprotonation at moderate to high hydration levels, preserving the availability of OH⁻ ions for effective CO₂ conversion to HCO₃⁻.

The competing reaction pathways, illustrated by the PES analysis, underscore the advantages of IM-Ben systems over IM-nBu, as the former preferentially favor HCO₃⁻ formation over imidazolium deprotonation under realistic operating conditions. Collectively, these computational insights indicate that carefully engineered polymer structures, particularly benzyl-substituted imidazolium-functionalized membranes, hold considerable promise for improving the efficiency and stability of bipolar membranes in electrochemical CO₂ separation and HCO₃⁻ formation applications. Future experimental validation guided by these computational predictions could further refine polymer design criteria and optimize operational parameters for enhanced CO₂ separations technologies.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting the findings of this study, including molecular geometries, transition-state structures, input file for simulations and relevant scripts have been included in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5mh01229e.

Additional input files, output files, and scripts can be made available on reasonable request to the corresponding author.

Acknowledgements

This material is based upon work supported by Laboratory Directed Research and Development (LDRD) funding from Argonne National Laboratory, provided by the Director, Office of Science, of the U.S. Department of Energy. S. L. and R. S. A. gratefully acknowledge the computing resources provided on Bebop and Improv, the high-performance computing clusters operated by the Laboratory Computing Resource Center (LCRC) at Argonne National Laboratory.

References

1. M. S. Sajna, S. Zavahir, A. Popelka, P. Kasak, A. Al-Sharshani, U. Onwusogh, M. Wang, H. Park and D. S. Han, Electrochemical system design for CO₂ conversion: A comprehensive review, J. Environ. Chem. Eng., 2023, 11(5), 110467,  DOI:10.1016/j.jece.2023.110467.
2. K. Zhang, D. Guo, X. Wang, Y. Qin, L. Hu, Y. Zhang, R. Zou and S. Gao, Sustainable CO₂ management through integrated CO₂ capture and conversion, J. CO2 Util., 2023, 72, 102493,  DOI:10.1016/j.jcou.2023.102493.
3. B. Kumar, B. Muchharla, M. Dikshit, S. Dongare, K. Kumar, B. Gurkan and J. M. Spurgeon, Electrochemical CO₂ Conversion Commercialization Pathways: A Concise Review on Experimental Frontiers and Technoeconomic Analysis, Environ. Sci. Technol. Lett., 2024, 11(11), 1161–1174,  DOI:10.1021/acs.estlett.4c00564.
4. X.-M. Hu, H.-Q. Liang, A. Rosas-Hernández and K. Daasbjerg, Electrochemical valorization of captured CO₂: recent advances and future perspectives, Chem. Soc. Rev., 2025, 54(3), 1216–1250,  10.1039/D4CS00480A.
5. V. J. Frilette, Preparation and Characterization of Bipolar Ion Exchange Membranes, J. Phys. Chem., 1956, 60(4), 435–439,  DOI:10.1021/j150538a013.
6. M. A. Blommaert, D. Aili, R. A. Tufa, Q. Li, W. A. Smith and D. A. Vermaas, Insights and Challenges for Applying Bipolar Membranes in Advanced Electrochemical Energy Systems, ACS Energy Lett., 2021, 6(7), 2539–2548,  DOI:10.1021/acsenergylett.1c00618.
7. Z. Yan and T. E. Mallouk, Bipolar Membranes for Ion Management in (Photo)Electrochemical Energy Conversion, Acc. Mater. Res., 2021, 2(12), 1156–1166,  DOI:10.1021/accountsmr.1c00113.
8. F. Habibzadeh, P. Mardle, N. Zhao, H. D. Riley, D. A. Salvatore, C. P. Berlinguette, S. Holdcroft and Z. Shi, Ion Exchange Membranes in Electrochemical CO₂ Reduction Processes, Electrochem. Energy Rev., 2023, 6(1), 26,  DOI:10.1007/s41918-023-00183-9.
9. K. Khoiruddin, I. G. Wenten and U. W. R. Siagian, Advancements in Bipolar Membrane Electrodialysis Techniques for Carbon Capture, Langmuir, 2024, 40(18), 9362–9384,  DOI:10.1021/acs.langmuir.3c03873.
10. S. Garg, C. A. Giron Rodriguez, T. E. Rufford, J. R. Varcoe and B. Seger, How membrane characteristics influence the performance of CO₂ and CO electrolysis, Energy Environ. Sci., 2022, 15(11), 4440–4469,  10.1039/D2EE01818G.
11. E. Hong, Z. Yang, H. Zeng, L. Gao and C. Yang, Recent Development and Challenges of Bipolar Membranes for High Performance Water Electrolysis, ACS Mater. Lett., 2024, 6(5), 1623–1648,  DOI:10.1021/acsmaterialslett.3c01227.
12. A. Badreldin and Y. Li, A critical appraisal of advances in integrated CO(2) capture and electrochemical conversion, Chem. Sci., 2025, 16(6), 2483–2513,  10.1039/d4sc06642a.
13. S. Han, S. Sasmal, M. Shen, Y. Wu, O. T. Vulpin, S. Hou, S. Kim, J. Y. Lee, J. Yoon and S. W. Boettcher, Advancing SnO₂-Based Water Dissociation Catalysis in Bipolar-Membrane Water Electrolyzers, ACS Energy Lett., 2025, 1633–1641,  DOI:10.1021/acsenergylett.5c00309.
14. S. Datta, M. P. Henry, Y. J. Lin, A. T. Fracaro, C. S. Millard, S. W. Snyder, R. L. Stiles, J. Shah, J. Yuan and L. Wesoloski, et al., Electrochemical CO₂ Capture Using Resin-Wafer Electrodeionization, Ind. Eng. Chem. Res., 2013, 52(43), 15177–15186.
15. T. Kulkarni, A. M. I. Al Dhamen, D. Bhattacharya and C. G. Arges, Bipolar Membrane Capacitive Deionization for pH-Assisted Ionic Separations, ACS ES&T Eng., 2023, 3(12), 2171–2182,  DOI:10.1021/acsestengg.3c00041.
16. T. Kulkarni, A. M. I. Al Dhamen, X. Zhang, C.-W. Chiu, H. Zhang, F. Shi, R. Kumar and C. G. Arges, Bipolar Membrane Capacitive Deionization for the Selective Capture of Lithium Ions from Brines and Conversion to Lithium Hydroxide, J. Electrochem. Soc., 2024, 171(10), 103502,  DOI:10.1149/1945-7111/ad7a25.
17. B. Yang, X. Zhang, B. Shrimant, T. Kulkarni, R. Kumar and C. G. Arges, Selective phosphate removal with manganese oxide composite anion exchange membranes in membrane capacitive deionization, Chem. Eng. J., 2024, 495, 153468,  DOI:10.1016/j.cej.2024.153468.
18. V. M. Palakkal, J. E. Rubio, Y. J. Lin and C. G. Arges, Low-Resistant Ion-Exchange Membranes for Energy Efficient Membrane Capacitive Deionization, ACS Sustainable Chem. Eng., 2018, 6(11), 13778–13786.
19. V. M. Palakkal, M. L. Jordan, D. Bhattacharya, Y. J. Lin and C. G. Arges, Addressing Spacer Channel Resistances in MCDI Using Porous and Pliable Ionic Conductors, J. Electrochem. Soc., 2021, 168(3), 033503.
20. B. Shrimant, T. Kulkarni, M. Hasan, C. Arnold, N. Khan, A. N. Mondal and C. G. Arges, Desalting Plasma Protein Solutions by Membrane Capacitive Deionization, ACS Appl. Mater. Interfaces, 2024, 16(9), 11206–11216,  DOI:10.1021/acsami.3c16691.
21. M. Hasan, B. Shrimant, C. B. Waters, C. A. Gorski and C. G. Arges, Reducing Ohmic Resistances in Membrane Capacitive Deionization Using Micropatterned Ion-Exchange Membranes, Ionomer Infiltrated Electrodes, and Ionomer-Coated Nylon Meshes, Small Struct., 2024, 5(9), 2400090,  DOI:10.1002/sstr.202400090 (accessed 2024/12/21).
22. M. L. Jordan, T. Kulkarni, D. I. Senadheera, R. Kumar, Y. J. Lin and C. G. Arges, Imidazolium-Type Anion Exchange Membranes for Improved Organic Acid Transport and Permselectivity in Electrodialysis, J. Electrochem. Soc., 2022, 169(4), 043511.
23. M. L. Jordan, G. Kokoszka, H. K. Gallage Dona, D. I. Senadheera, R. Kumar, Y. J. Lin and C. G. Arges, Integrated Ion-Exchange Membrane Resin Wafer Assemblies for Aromatic Organic Acid Separations Using Electrodeionization, ACS Sustainable Chem. Eng., 2023, 11(3), 945–956,  DOI:10.1021/acssuschemeng.2c05255.
24. G. P. S. Lau, M. Schreier, D. Vasilyev, R. Scopelliti, M. Grätzel and P. J. Dyson, New Insights Into the Role of Imidazolium-Based Promoters for the Electroreduction of CO₂ on a Silver Electrode, J. Am. Chem. Soc., 2016, 138(25), 7820–7823,  DOI:10.1021/jacs.6b03366.
25. S. S. Daud, M. A. Norrdin, J. Jaafar and R. Sudirman, The effect of material on bipolar membrane fuel cell performance: A review, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 736(3), 032003,  DOI:10.1088/1757-899X/736/3/032003.
26. T. E. Gartner III and A. Jayaraman, Modeling and Simulations of Polymers: A Roadmap, Macromolecules, 2019, 52(3), 755–786,  DOI:10.1021/acs.macromol.8b01836.
27. H. Lei, X. Yang, Z. Chen, D. Rawach, L. Du, Z. Liang, D.-S. Li, G. Zhang, A. C. Tavares and S. Sun, Multiscale Understanding of Anion Exchange Membrane Fuel Cells: Mechanisms, Electrocatalysts, Polymers, and Cell Management, Adv. Mater., 2025, 37(8), 2410106,  DOI:10.1002/adma.202410106.
28. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: A message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91(1), 43–56,  DOI:10.1016/0010-4655(95)00042-E.
29. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236,  DOI:10.1021/ja9621760.
30. C. P. Callaway, J. H. Bombile, W. Mask, S. M. Ryno and C. Risko, Thermomechanical enhancement of DPP-4T through purposeful π-conjugation disruption, J. Polym. Sci., 2022, 60(3), 559–568,  DOI:10.1002/pol.20210494.
31. I. Yungerman, I. Starodumov, A. Fulati, K. Uto, M. Ebara and Y. Moskovitz, Full-Atomistic Optimized Potentials for Liquid Simulations and Polymer Consistent Force Field Models for Biocompatible Shape-Memory Poly(ε-caprolactone, J. Phys. Chem. B, 2022, 126(21), 3961–3972,  DOI:10.1021/acs.jpcb.2c01973.
32. E. Venezia, F. Auriemma, O. R. de Ballestreros, G. Guerra, G. Milano and A. Correa, All-Atom Molecular Dynamics Simulations of Poly(2,6-dimethyl-1,4-phenylene) Oxide: Validation of OPLS-AA Force Field for Conformational Behaviour in Vacuum and in Carbon Tetrachloride, Macromol. Chem. Phys., 2023, 224(21), 2300120,  DOI:10.1002/macp.202300120.
33. I. Yungerman, I. Starodumov, A. Fulati, K. Uto, M. Ebara and Y. Moskovitz, Full-Atomistic Optimized Potentials for Liquid Simulations and Polymer Consistent Force Field Models for Biocompatible Shape-Memory Poly(ε-caprolactone), J. Phys. Chem. B, 2022, 126(21), 3961–3972,  DOI:10.1021/acs.jpcb.2c01973.
34. T. Saito, M. Kubo, T. Tsukada, E. Shoji, G. Kikugawa, D. Surblys and M. Kubo, Molecular dynamics simulations for interfacial structure and affinity between carboxylic acid-modified Al₂O₃ and polymer melts, J. Chem. Phys., 2023, 159, 164708,  DOI:10.1063/5.0169721.
35. W. Shi and E. J. Maginn, Molecular simulation of ammonia absorption in the ionic liquid 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([emim][Tf2N]), AIChE J., 2009, 55(9), 2414–2421,  DOI:10.1002/aic.11910.
36. A. K. Verma, A. S. Thorat and J. K. Shah, Predicting Ionic Conductivity of Imidazolium-Based Ionic Liquid Mixtures Using Quantum-Mechanically Derived Partial Charges in the Condensed Phase, J. Phys. Chem. B, 2025, 129(9), 2546–2559,  DOI:10.1021/acs.jpcb.4c08275.
37. L. Yang, H. Zheng, W. Mei, Z. Wang, Z. Zhang and K. Yu, Molecular Dynamics Simulation of CO₂ Uptake in NKPOC-1: Understanding the Temperature-Dependent Multistep Adsorption in Soft Porous Molecular Crystal, J. Phys. Chem. C, 2024, 128(26), 10997–11005,  DOI:10.1021/acs.jpcc.4c02133.
38. A. Truszkowska, A. Boldini and M. Porfiri, Plating of Ion-Exchange Membranes: A Molecular Dynamics Study, Adv. Theory Simul., 2022, 5(12), 2200523,  DOI:10.1002/adts.202200523.
39. Z. Zhang and Z. Duan, An optimized molecular potential for carbon dioxide, J. Chem. Phys., 2005, 122(21), 214507,  DOI:10.1063/1.1924700.
40. P. Habibi, A. Rahbari, S. Blazquez, C. Vega, P. Dey, T. J. H. Vlugt and O. A. Moultos, A New Force Field for OH⁻ for Computing Thermodynamic and Transport Properties of H₂ and O₂ in Aqueous NaOH and KOH Solutions, J. Phys. Chem. B, 2022, 126(45), 9376–9387,  DOI:10.1021/acs.jpcb.2c06381.
41. P. Mark and L. Nilsson, Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K, J. Phys. Chem. A, 2001, 105(43), 9954–9960,  DOI:10.1021/jp003020w.
42. C. G. Aimoli, E. J. Maginn and C. R. A. Abreu, Transport properties of carbon dioxide and methane from molecular dynamics simulations, J. Chem. Phys., 2014, 141, 134101,  DOI:10.1063/1.4896538.
43. J. Du, A. Zhou, Y. Zhong and S.-L. Shen, Molecular simulation on CO2 adsorption heterogeneity in montmorillonite nanopores with different surface charges in presence of water, Chem. Eng. J., 2024, 482, 148958,  DOI:10.1016/j.cej.2024.148958.
44. T. Merker, J. Vrabec and H. Hasse, Comment on “An optimized potential for carbon dioxide” [J. Chem. Phys. 122, 214507 (2005)], J. Chem. Phys., 2008, 129, 087101,  DOI:10.1063/1.2965899.
45. H. Yu, D. Wang, Y. Li, G. Chen and X. Ma, Explainable molecular simulation and machine learning for carbon dioxide adsorption on magnesium oxide, Fuel, 2024, 357, 129725,  DOI:10.1016/j.fuel.2023.129725.
46. S. Neyertz, D. Brown, S. Pandiyan and N. F. A. van der Vegt, Carbon Dioxide Diffusion and Plasticization in Fluorinated Polyimides, Macromolecules, 2010, 43(18), 7813–7827,  DOI:10.1021/ma1010205.
47. L. Ni and J. Yu, NaOH as an Aqueous Electrolyte to Improve the Performance of Electric Double-Layer Capacitors—A Molecular Dynamics Study, Nanomaterials, 2025, 15(9), 649.
48. F. V. Olowookere and C. H. Turner, An integrated off-lattice kinetic Monte Carlo (KMC)-molecular dynamics (MD) framework for modeling polyvinyl chloride dehydrochlorination, Chem. Eng. Sci., 2025, 302, 120928,  DOI:10.1016/j.ces.2024.120928.
49. V. Chaban, Polarizability versus mobility: atomistic force field for ionic liquids, Phys. Chem. Chem. Phys., 2011, 13(35), 16055–16062,  10.1039/C1CP21379B.
50. D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, B. Roux and C. Schröder, Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields, Chem. Rev., 2019, 119(13), 7940–7995,  DOI:10.1021/acs.chemrev.8b00763.
51. F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, Force Fields for Studying the Structure and Dynamics of Ionic Liquids: A Critical Review of Recent Developments, ChemPhysChem, 2012, 13(7), 1625–1637,  DOI:10.1002/cphc.201100997.
52. J. Schmidt, C. Krekeler, F. Dommert, Y. Zhao, R. Berger, L. D. Site and C. Holm, Ionic Charge Reduction and Atomic Partial Charges from First-Principles Calculations of 1,3-Dimethylimidazolium Chloride, J. Phys. Chem. B, 2010, 114(18), 6150–6155,  DOI:10.1021/jp910771q.
53. C. Klein; J. Sallai; T. J. Jones; C. R. Iacovella; C. McCabe and P. T. Cummings, A Hierarchical, Component Based Approach to Screening Properties of Soft Matter, in Foundations of Molecular Modeling and Simulation: Select Papers from FOMMS 2015, ed. R. Q. Snurr, C. S. Adjiman and D. A. Kofke, Springer, Singapore, 2016, pp. 79–92.
54. X. Luo, D. I. Kushner, J. Li, E. J. Park, Y. S. Kim and A. Kusoglu, Anion Exchange Ionomers: Impact of Chemistry on Thin-Film Properties, Adv. Funct. Mater., 2021, 31(20), 2008778,  DOI:10.1002/adfm.202008778.
55. G. S. Larsen, P. Lin, K. E. Hart and C. M. Colina, Molecular Simulations of PIM-1-like Polymers of Intrinsic Microporosity, Macromolecules, 2011, 44(17), 6944–6951,  DOI:10.1021/ma200345v.
56. N. C. Karayiannis, V. G. Mavrantzas and D. N. Theodorou, Detailed Atomistic Simulation of the Segmental Dynamics and Barrier Properties of Amorphous Poly(ethylene terephthalate) and Poly(ethylene isophthalate), Macromolecules, 2004, 37(8), 2978–2995,  DOI:10.1021/ma0352577.
57. S. Nosé, A molecular dynamics method for simulations in the canonical ensemble, Mol. Phys., 1984, 52(2), 255–268,  DOI:10.1080/00268978400101201.
58. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695–1697,  DOI:10.1103/PhysRevA.31.1695.
59. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190,  DOI:10.1063/1.328693.
60. S. Nosé and M. L. Klein, Constant pressure molecular dynamics for molecular systems, Mol. Phys., 1983, 50(5), 1055–1076,  DOI:10.1080/00268978300102851.
61. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98(12), 10089–10092,  DOI:10.1063/1.464397.
62. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: A toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32(10), 2319–2327,  DOI:10.1002/jcc.21787.
63. R. J. Gowers, M. Linke, J. Barnoud, T. Reddy, M. Melo, S. L. Seyler, J. Domański, D. L. Dotson, S. Buchoux, I. Kenney and O. Beckstein, MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, 2016.
64. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al., CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103,  DOI:10.1063/5.0007045.
65. M. Ernzerhof and G. E. Scuseria, Assessment of the Perdew–Burke–Ernzerhof exchange-correlation functional, J. Chem. Phys., 1999, 110(11), 5029–5036,  DOI:10.1063/1.478401.
66. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104,  DOI:10.1063/1.3382344.
67. S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703–1710,  DOI:10.1103/PhysRevB.54.1703.
68. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
69. D. J. Evans and B. L. Holian, The Nose–Hoover thermostat, J. Chem. Phys., 1985, 83(8), 4069–4074,  DOI:10.1063/1.449071.
70. Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
71. C. Peng and H. Bernhard Schlegel, Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States, Isr. J. Chem., 1993, 33(4), 449–454,  DOI:10.1002/ijch.199300051.
72. C. G. Arges and V. Ramani, Investigation of Cation Degradation in Anion Exchange Membranes Using Multi-Dimensional NMR Spectroscopy, J. Electrochem. Soc., 2013, 160(9), F1006,  DOI:10.1149/2.056309jes.
73. Y. Ye and Y. A. Elabd, Relative Chemical Stability of Imidazolium-Based Alkaline Anion Exchange Polymerized Ionic Liquids, Macromolecules, 2011, 44(21), 8494–8503,  DOI:10.1021/ma201864u.
74. C. G. Arges and L. Zhang, Anion Exchange Membranes' Evolution toward High Hydroxide Ion Conductivity and Alkaline Resiliency, ACS Appl. Energy Mater., 2018, 1(7), 2991–3012.
75. J. Wang, S. Gu, R. B. Kaspar, B. Zhang and Y. Yan, Stabilizing the imidazolium cation in hydroxide-exchange membranes for fuel cells, ChemSusChem, 2013, 6(11), 2079–2082,  DOI:10.1002/cssc.201300285.
76. J. J. Kaczur, H. Yang, Z. Liu, S. D. Sajjad and R. I. Masel, Carbon Dioxide and Water Electrolysis Using New Alkaline Stable Anion Membranes, Front. Chem., 2018, 6, 263,  DOI:10.3389/fchem.2018.00263.

---