A deep learning model for inferring the reverse intersystem crossing rate of TADF organic light-emitting diodes, overcoming the uncertainty of recombination dynamics
Junseop
Lim
 a,
Seungwon
Han
a,
Jae-Min
Kim
a,
Seungwon
Han
a,
Jae-Min
Kim
 *b and
Jun Yeob
Lee
*b and
Jun Yeob
Lee
 *ac
*ac
aSchool of Chemical Engineering, Sungkyunkwan University 2066, Seobu-ro, Jangan-gu, Suwon-si, Gyeonggi-do 16419, Republic of Korea. E-mail: leej17@skku.edu
bDepartment of Advanced Materials Engineering, Chung-Ang University 4726, Seodong-daero, Daedeok-myeon, Anseong-si, Gyeonggi-do 17546, Republic of Korea. E-mail: jmkim52@cau.ac.kr
cSKKU Institute of Energy Science and Technology, Sungkyunkwan University 2066, Seobu-ro, Jangan-gu, Suwon, Gyeonggi 16419, Republic of Korea
First published on 12th September 2025
Abstract
Polaron recombination and reverse intersystem crossing (RISC) are crucial processes related to the performance of thermally activated delayed fluorescence (TADF) organic light-emitting diodes (OLEDs). In this study, we developed a tandem deep neural network (DNN) model to predict the RISC rate from the transient electroluminescence behavior of TADF OLEDs via step-by-step analysis of both recombination and exciton dynamics. Based on the recombination rate results of the first tandem model, we designed an algorithm in which the second model was automatically selected from among the pretrained candidate models to infer the RISC rate. With comprehensive optimization, a tandem DNN model with a determination coefficient value of 0.985 was realized, overcoming the uncertainty of polaron recombination dynamics. The practical application of the developed model was demonstrated by fabricating a state-of-the-art TADF OLED.
New conceptsThis study introduces a novel tandem deep neural network framework that decouples and sequentially analyzes polaron recombination and exciton dynamics in thermally activated delayed fluorescence organic light-emitting diodes. By linking two specialized models—one for recombination rate prediction and another for reverse intersystem crossing rate estimation—the approach enables highly accurate inference of exciton behavior from transient electroluminescence data. The model architecture addresses the inherent uncertainty in polaron dynamics and offers a practical tool for optimizing thermally activated delayed fluorescence device performance through data-driven analysis. |
1. Introduction
Thermally activated delayed fluorescence (TADF) materials have been investigated as hosts,1–3 sensitizers,4–6 and emitters7–9 because of the effective conversion of nonradiative triplet excitons into radiative singlet excitons through the reverse intersystem crossing (RISC) process. Accelerating the RISC process is a key approach for suppressing molecular quenching such as triplet–triplet annihilation (TTA)10,11 and triplet–polaron annihilation (TPA),12,13 leading to improved device efficiency and operational lifetime. Since their first report in 2016,14 multiresonance TADF materials15–17 have demonstrated remarkable efficiency with narrow spectra compared with previous TADF materials that contain electron-donating and electron-accepting fragments.18–20 However, slow RISC rates cause severe efficiency rolloff21–23 in devices because long-living triplets are pertinent to TTA and TPA processes. Therefore, increasing the RISC rate is considered a design factor for efficient TADF materials by reducing the triplet density during operation.In addition to the RISC process related to exciton dynamics, the polaron recombination process has been investigated to improve device performance.24–26 Among the factors involved in electroluminescence (EL) processes, such as charge injection,27–29 charge transport,30–32 and charge trapping,33–35 the recombination rate is significant in determining the polaron and exciton densities in the emitting layer (EML) and the driving voltage corresponding to the specific luminance. In 2023, N. C. Giebink et al. reported that a large Langevin coefficient for polaron recombination can reduce device overpotential, which means increased voltage to achieve the same luminance as inorganic light-emitting diodes.36 Consequently, evaluating the RISC and recombination rate coefficients is important for understanding device performance.
The RISC rate can be determined by measuring the photoluminescence quantum yield (PLQY) and transient photoluminescence (trPL), followed by the introduction of an analytical solution37,38 or a numerical method39,40 on the trPL profile. Using the obtained RISC rate coefficient, along with other monomolecular rate coefficients, the recombination rate coefficient can be evaluated using the transient EL (trEL) profile by applying time-dependent exciton decay equations.41,42 Although monomolecular rate coefficients are determined by trPL analysis in advance, the risk of multiple solutions still exists because of the number of fitting variables. Given that conventional analysis protocols have the advantage of being based on rigorous theories, performing material and device measurements cannot be a viable option in the industry considering the number of candidate materials and the research and development (R&D) cycle period in product development.
As a method to overcome these challenges, deep learning (DL) has been introduced to directly obtain physical factors.43 J.-M. Kim et al. reported a DL model to extract the polaron recombination rate coefficient in exciplex host systems using trEL profiles as input data.44 Recently, J. Lim et al. inferred triplet harvesting factors such as the TTA ratio and the TTA rate coefficient in blue TTA OLEDs and achieved an outstanding determination coefficient (R2) value of 0.999.45 These studies suggested that the DL approach in the assessment of physical factors can reduce resource consumption because it requires only trEL profiles and solves the multiple-solution problem through the correlation between physical factors and trEL profiles.
In this study, we established a tandem deep neural network (DNN) model to predict the RISC rate coefficient by logically connecting the polaron recombination analysis model and the exciton kinetics analysis model. Among the implemented models (models #1–30), the recombination rate model exhibited an R2 value of 0.979 in predicting the recombination rate coefficient, and the RISC rate model exhibited an R2 value of 0.985 in predicting the RISC rate coefficient. By applying the tandem DNN model to a TADF OLED doped with 20 wt% 2,3,4,5,6-penta(9H-carbazol-9-yl)benzonitrile (5CzBN),46 we successfully predicted recombination and RISC rate coefficients of 7.28 × 10−11 s−1 cm3 and 3.19 × 105 s−1, which are comparable to the experimental values of 7.27 × 10−11 s−1 cm3 and 3.01 × 105 s−1, respectively.
2. Results and discussion
The comprehensive behavior of polarons and excitons in the EML, which employs a TADF material as the emitter, is described in Fig. 1(a). Positive and negative polarons are injected from the respective electrodes, followed by polaron recombination or accumulation between the EML and polaron blocking layer. These recombination and accumulation processes are determined by electrochemical properties such as mobility and the recombination rate. The recombination process is insufficiently rapid in organic semiconductors; thus, it causes a bottleneck during the exciton radiation sequence. The recombination rate influences polarons, exciton densities, apparent exciton decay time, and bimolecular interactions. Because the exciton density changes due to this influence, it is appropriate to analyze the polaron and exciton dynamics using trEL profiles. Through numerical analysis of the exciton decay equations, the trEL profiles of TADF OLEDs can be theoretically described. The implemented time-dependent exciton decay equations11 are as follows: | (1) |
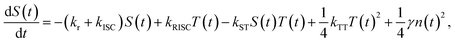 | (2) |
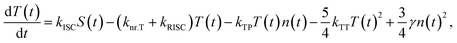 | (3) |
Based on eqn (1)–(3), we simulated the trEL profiles of the TADF OLEDs by varying the recombination rate coefficient (γ) from 1 × 10−13 to 1 × 10−9 s−1 cm3 while keeping the other rate coefficients (kr, knr.T, kISC, kRISC, kTT, kTP, and kST) constant, as shown in Fig. 1(b). The current density was set to 10 mA cm−2. The rate coefficients are summarized in Table S1. The simulated trEL profiles changed depending on the γ values. The results indicate that the recombination rate coefficient significantly affects the apparent decay lifetime and the trEL profile shape, consistent with the significant contribution of the recombination process to exciton decay.
Although the recombination rate coefficient has a dominant impact on the trEL profile shape, other physical factors also contribute to the trEL profile.48 DL can understand the relationship between each parameter and apparent trEL profiles. In this context, we developed DL models to predict kinetic parameters from trEL profiles as input data.
The workflow for developing the DNN model is described in Fig. 1(c). TrEL profiles were generated randomly using eqn (1)–(3) from 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 combinations of rate coefficients in defined boundaries (Table S2) and used as the input data after the featurization process. In the featurization process, the number of data points was adjusted (data compression), followed by logarithm and differentiation.45 The featurized trEL profiles were normalized and used as the input data up to a time range of 10 μs. The DNN models based on multilayer perceptrons predict the rate coefficients (kr, knr.T, kISC, kRISC, kTT, kTP, kST, and γ) of TADF OLEDs as a single task. The input data were training, validation, and test sets at a ratio of 80
000 combinations of rate coefficients in defined boundaries (Table S2) and used as the input data after the featurization process. In the featurization process, the number of data points was adjusted (data compression), followed by logarithm and differentiation.45 The featurized trEL profiles were normalized and used as the input data up to a time range of 10 μs. The DNN models based on multilayer perceptrons predict the rate coefficients (kr, knr.T, kISC, kRISC, kTT, kTP, kST, and γ) of TADF OLEDs as a single task. The input data were training, validation, and test sets at a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.
10.
First, we evaluated the model for predicting the recombination rate coefficient according to the number of data points in the featurized trEL data. For the evaluation, a basic neural network model was implemented. The basic model was constructed with two layers, and each layer had 100/100 nodes and a dropout rate of 0.100/0.100. The learning rate of the basic model was set to 5.00 × 10−5. The evaluated R2 values for the recombination rate coefficient depending on the number of data points on the test dataset are presented in Fig. 2(a) and summarized in Table S3. For the basic model, the R2 values increased as the number of data points increased from 5 to 70 and then decreased. The highest R2 value of the basic model was 0.967, obtained with 70 data points. Therefore, the number of input data points was fixed at 70. After hyperparameter optimization of the basic model using the Optuna module,49 an R2 value of 0.976 was obtained. The optimized DNN model for predicting the recombination rate coefficient was labeled model #1-Recom (Table S5). The hyperparameters of the recombination rate model are summarized in Table S4. The distribution plot between the actual and predicted values of the recombination rate model is shown in Fig. 2(b). The predictability of the recombination rate coefficient validated the importance of the recombination process in EL decay.
The other models for predicting the remaining rate coefficients were trained using the same protocol. These models were labeled according to the predicted rate coefficients (e.g., the DNN model for predicting kr: model #1-Rad). In addition, the model numbers were categorized (models #1–30) based on the boundaries of the rate coefficients (Table S5). For readability, we used functional descriptions such as “the recombination rate model” rather than numerical labels like “model #1-RISC” when referring to models in the main text. The R2 values for the rate coefficients of model #1 are shown in Fig. 2(c). The R2 values for the rate coefficients of all DNN models were consistent on the test set. Except for γ, the predictability of kRISC was highest, with an R2 value of 0.775. Considering that the RISC process primarily determines the delayed exciton decay time in the microsecond range, the high R2 value for kRISC can be rationalized. The low R2 value of 0.119 for the triplet nonradiative rate coefficient (knr.T) was due to its small contribution to the trEL profile because knr.T exhibited a slower rate (102–105 s−1) than the other rate coefficients. The R2 values for the bimolecular rate coefficients kTT and kTP were 0.625 and 0.639, respectively. However, the singlet–triplet bimolecular rate coefficient (kST) exhibited the least R2 value (0.00908). This can be caused by rapid singlet radiative decay, leading to insignificant interactions between singlets and triplets during EL decay. The performance results of model #1 are presented in Fig. S1 and summarized in Table S6.
The predictability of kRISC was evaluated as an R2 value of 0.775; however, this result indicates insufficient performance for practical applications. By examining the distribution plot of kRISC for the RISC rate model (Fig. S1(c)), we found that the low-value region of the rate coefficient (102–105 s−1) was not well predicted. We speculate that the small dominance of triplet excitons on the delayed component due to the inefficient RISC process leads to a weak relationship between the coefficient and the decay curve. At present, TADF materials that exhibit fast RISC processes have been developed and commercialized.50 Considering the practicality of the DNN model for predicting kRISC in the case of commercial TADF materials, the model was rebuilt by dividing the kRISC range of the dataset into 102–105 s−1 (model #2) and 105–107 s−1 (model #3) while maintaining the ranges of the other rate coefficients. The two models were trained and evaluated for the recombination and RISC rate coefficients, as shown in Fig. 3. The recombination rate models #2 and #3 exhibited comparable performance for γ prediction, with R2 values of 0.975 and 0.979, respectively. In contrast, only RISC rate model #3 exhibited improved performance for kRISC prediction (R2: 0.908) compared with RISC rate model #2 (R2: 0.779). These results suggest that the high kRISC values affected the trEL profile shape and that this strong relationship improved the performance of the DNN model. The prediction of kTT and kTP using models #2 and #3 is illustrated in Fig. S2. In contrast to the kRISC prediction result, the predictability of kTT and kTP was evaluated as R2 values less than 0.7 for the two models. The performance results of DNN models #2 and #3 are summarized in Table S7.
To improve the predictability of kRISC, one way is to narrow or fix the boundary of the recombination rate coefficient based on previous work.45 However, analyzing the recombination rate coefficient requires an additional R&D process, which is not appropriate for screening many candidate materials. Therefore, for practical applications, another strategy was introduced to handle the uncertainty of the recombination rate coefficient. We constructed equivalent models #(4–30) that predict γ in a narrow recombination rate coefficient range that was uniformly divided from 1 × 10−13 to 1 × 10−10 s−1 cm3 while maintaining the other rate coefficient boundaries. The boundary information of models #(4–30) is summarized in Table S8. By combining the recombination rate model with RISC rate models, a tandem model architecture was established to predict γ and kRISC consecutively, as described in Fig. 4. In the first step, the recombination rate model predicted the γ value using the trEL profiles of the TADF OLEDs. In the second step, a predictive DNN model, e.g., RISC rate models, was automatically selected among models #(4–30)-RISC according to the value of γ. In the final step, the kRISC value was predicted by employing the selected RISC rate model using the trEL profiles of the TADF OLEDs. In this method, it is important to accurately predict the recombination rate coefficient in the first step because the predictive DNN model for kRISC is selected based on the predicted γ value. The recombination rate model exhibits a high R2 value of 0.979 for predicting γ (Fig. 3(c)); thus, this approach can simultaneously overcome the uncertainty problem of γ and improve the predictability of kRISC.
The performance of models #(1–30) is illustrated in Fig. 5(a). The recombination rate coefficient was predicted using recombination rate models, and the RISC, TTA, and TPA rate coefficients were predicted using models #(1–30). For all models, the predictability of γ exhibited R2 values above 0.975, indicating superior performance independent of the kRISC range. The R2 values for kRISC tended to increase from model #1 to model #30. From RISC rate model #6 onward, the predictability of kRISC was notable, exhibiting R2 values above 0.950, as indicated by the red line in Fig. 5(a). The R2 values for the kRISC of RISC rate models are summarized in Table S9. The highest R2 for kRISC prediction (0.985) was obtained using RISC rate model #28 (range of γ: 7 × 10−11–8 × 10−11 s−1 cm3), which yielded the distribution plot shown in Fig. 5(b). Given that the R2 value for the kRISC of RISC rate model #1 was 0.775, the approach for generating the input dataset within the separate recombination rate coefficient ranges was effective.
In addition, the bimolecular interactions of TTA and TPA were predicted using models #(4–30). The R2 values of the DNN models are presented in Fig. 5(a) and summarized in Tables S10 and S11. Although the overall R2 values for kTT and kTP prediction were less than 0.9, the predictability changed according to the DNN models. The R2 values for kTT (0.518) and kTP (0.613) of model #3 for TTA and TPA were lower than those of model #1 (0.625 for kTT and 0.639 for kTP) and model #2 (0.622 for kTT and 0.635 for kTP). The results can be understood by the increase in the kRISC range of model #3, leading to a reduction in the triplet density that participated in TTA and TPA. The triplet density rate  was dependent on both the rate coefficient and density; thus, the effect of the TTA and TPA rate coefficients decreased under low-density conditions even with the same coefficient value. TTA rate model #4, which exhibited the smallest recombination rate coefficient range, estimated an R2 value of 0.411 for kTT. The predictability increased with γ boundaries, and TTA rate model #30, which exhibited the largest range, estimated an R2 value of 0.856. In contrast, the R2 value for kTP was predicted as 0.831 using TPA rate model #4, and the value decreased to 0.695 for TPA rate model #30. These opposite predictability trends for the two factors can be explained by the different behaviors of the polaron and triplet densities within γ ranges. As the γ boundary increases, the enhanced recombination consumes transported polarons and effectively generates triplet excitons. In model #4, the relatively slow recombination process increased the polaron density in the EML, thereby increasing the possibility of TPA even when the kTP value remained constant. Consequently, TPA exerted a greater influence than TTA on the emissive process, and TPA also affected the trEL profiles. In contrast, in model #30, the TTA process primarily influenced the emissive process compared to the TPA process because of fast polaron consumption. This increased the R2 value for kTT prediction of TTA rate model #30 compared to TTA rate model #4. Fig. 5(c) compares R2 values for kRISC, kTT, and kTP obtained using models #4 and #30 for RISC, TTA, and TPA.
was dependent on both the rate coefficient and density; thus, the effect of the TTA and TPA rate coefficients decreased under low-density conditions even with the same coefficient value. TTA rate model #4, which exhibited the smallest recombination rate coefficient range, estimated an R2 value of 0.411 for kTT. The predictability increased with γ boundaries, and TTA rate model #30, which exhibited the largest range, estimated an R2 value of 0.856. In contrast, the R2 value for kTP was predicted as 0.831 using TPA rate model #4, and the value decreased to 0.695 for TPA rate model #30. These opposite predictability trends for the two factors can be explained by the different behaviors of the polaron and triplet densities within γ ranges. As the γ boundary increases, the enhanced recombination consumes transported polarons and effectively generates triplet excitons. In model #4, the relatively slow recombination process increased the polaron density in the EML, thereby increasing the possibility of TPA even when the kTP value remained constant. Consequently, TPA exerted a greater influence than TTA on the emissive process, and TPA also affected the trEL profiles. In contrast, in model #30, the TTA process primarily influenced the emissive process compared to the TPA process because of fast polaron consumption. This increased the R2 value for kTT prediction of TTA rate model #30 compared to TTA rate model #4. Fig. 5(c) compares R2 values for kRISC, kTT, and kTP obtained using models #4 and #30 for RISC, TTA, and TPA.
To validate the application of the tandem DNN model, a TADF OLED was fabricated. 5CzBN was used as the TADF emitter. 3,3′-Di(9H-carbazol-9-yl)-1,1′-biphenyl (mCBP) and 9-(3′-(9H-carbazol-9-yl)-5-cyano-[1,1′-biphenyl]-3-yl)-9H-carbazole-3-carbonitrile (CNmCBP-CN) were used as the mixed co-hosts (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 wt%). The doping concentration of 5CzBN was 20 wt%. Detailed information is provided in the Experimental section. The molecular and device structures, along with the energy diagram, are shown in Fig. S3. The device characteristics of the TADF OLED are illustrated in Fig. 6 and summarized in Table 1. The turn-on voltage, which represents the voltage at a luminance of 1 cd m−2, was measured as 2.6 V, and the driving voltage was 4.9 V at 1000 cd m−2. The maximum current efficiency, power efficiency, and external quantum efficiency were 50.6 cd A−1, 53.0 lm W−1, and 22.5%, respectively. The trEL was measured at a current density of 10 mA cm−2 for the application of the tandem DNN model. The pulse width was 250 μs, followed by voltage-off for 250 μs. To validate the predictability of the tandem DNN model, conventional RISC analysis with numerical fitting was performed. To reduce the multiple-solution problem during numerical fitting, the monomolecular rate coefficients (kr, knr.T, kISC, and kRISC) were determined via trPL analysis51 (a detailed explanation is presented in the SI). The results of the trPL analysis are presented in Fig. S4 and summarized in Table S12. The numerical fitting of the trEL profile was performed using the monomolecular rate coefficients, as shown in Fig. 6(d). The numerical simulation results are summarized in Table 2.
50 wt%). The doping concentration of 5CzBN was 20 wt%. Detailed information is provided in the Experimental section. The molecular and device structures, along with the energy diagram, are shown in Fig. S3. The device characteristics of the TADF OLED are illustrated in Fig. 6 and summarized in Table 1. The turn-on voltage, which represents the voltage at a luminance of 1 cd m−2, was measured as 2.6 V, and the driving voltage was 4.9 V at 1000 cd m−2. The maximum current efficiency, power efficiency, and external quantum efficiency were 50.6 cd A−1, 53.0 lm W−1, and 22.5%, respectively. The trEL was measured at a current density of 10 mA cm−2 for the application of the tandem DNN model. The pulse width was 250 μs, followed by voltage-off for 250 μs. To validate the predictability of the tandem DNN model, conventional RISC analysis with numerical fitting was performed. To reduce the multiple-solution problem during numerical fitting, the monomolecular rate coefficients (kr, knr.T, kISC, and kRISC) were determined via trPL analysis51 (a detailed explanation is presented in the SI). The results of the trPL analysis are presented in Fig. S4 and summarized in Table S12. The numerical fitting of the trEL profile was performed using the monomolecular rate coefficients, as shown in Fig. 6(d). The numerical simulation results are summarized in Table 2.
| V on /Vb (V) | J (mA cm−2) | CEmaxc/CEb (cd A−1) | PEmaxc/PEb (lm W−1) | EQEmaxc/EQEb (%) | CIEbd (x, y) | |
|---|---|---|---|---|---|---|
| a Turn-on voltage measured at 1 cd m−2. b Measured property at 1000 cd m−2. c Maximum value. d Commission Internationale de l’Eclairage coordinates. | ||||||
| 20 wt% 5CzBN OLED | 2.6/4.9 | 2.8 | 50.6/37.0 | 53.0/23.9 | 22.5/16.8 | (0.175, 0.359) |
| k r (s−1) (×107) | k nr.T (s−1) (×102) | k ISC (s−1) (×107) | k RISC (s−1) (×105) | k TT (s−1 cm3) (×10−13) | k TP (s−1 cm3) (×10−12) | k ST (s−1 cm3) (×10−15) | γ (s−1 cm3) (×10−11) |
R
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
|
|---|---|---|---|---|---|---|---|---|---|
| a Coefficient determined between the trEL experimental profile and fitting results. | |||||||||
| 20 wt% 5CzBN OLED | 1.14 | 5.77 | 6.00 | 3.01 | 5.62 | 4.21 | 8.94 | 7.27 | 0.999 |
The trEL profile of the TADF device was used as the input data for the tandem DNN model to infer the recombination and RISC rate coefficients. Fig. 7 compares the experimental and predicted values. For the recombination rate model, which is the first model to predict the γ value for the tandem DNN model, γ was predicted as 7.28 × 10−11 s−1 cm3. The value is approximately equal to the experimental value (7.27 × 10−11 s−1 cm3). Considering the inferred γ value, RISC rate model #28 was automatically selected from among the prebuilt models. Finally, model #28 predicted the kRISC value as 3.19 × 105 s−1, which was close to the experimental kRISC value (3.01 × 105 s−1). To validate the universality of the model developed in this study, we additionally fabricated 10 wt% 4CzTPN films and OLED devices and applied them to the deep learning model (Fig. S6, S7 and Tables S14–S17).
In this study, 27 models for predicting kRISC were prebuilt using uniformly divided γ boundaries. Although the boundary was narrowed, the prediction accuracy would be lower than that of a model trained on the dataset with a fixed γ value. To investigate the accuracy loss problem, we implemented a new model named model #31, which originated from data with a fixed γ value of 7.27 × 10−11 s−1 cm3 while using the same values of the other coefficient boundaries as those for model #3. The performance of model #31 is illustrated in Fig. S5 and summarized in Table S13. Model #31 exhibited an R2 value of 0.984 for kRISC prediction, which was comparable to the R2 value of 0.985 for model #28. The prediction results of the tandem DNN model and model #31 are summarized in Table 3. Model #31 predicted kRISC as 3.05 × 105 s−1, which is closer to the experimental value (3.01 × 105 s−1) than that predicted using model #28 (3.19 × 105 s−1). Based on these results, the accuracy loss problem can be solved by increasing the number of models (narrowing γ boundary) according to the required model performance.
Our approach that integrates physical modeling and DL can solve the problems associated with the development of practical and superior models. First, during dataset construction, conventional data are collected from actual measurement data and their labels. However, various measurement data are not available in OLED research. Even in the industry, human and equipment errors contribute to the noise factor despite the availability of large-scale data. In addition, the data labels corresponding to the kinetic parameters cannot be obtained. The use of physical modeling to generate data can be an effective strategy to solve data scale, quality, and variety problems simultaneously.
Second, determining the RISC rate from device behavior is a better method than analyzing thin film behavior. In the actual development of OLED panels, device fabrication is the primary process by which candidate materials are tested; however, thin film fabrication requires additional resources and requirements. Direct extraction of physical factors from devices using our strategy accelerates materials and device characterization. In addition, the exciton dynamics of TADF materials is dependent on the surrounding medium and device architecture; thus, the analysis environment of the RISC rate from trEL is closer to the operation state than thin film analysis.
Finally, physical insights are provided by this study. The performance of the tandem model indicates that the recombination and RISC rate coefficients significantly influence the apparent luminance decay. The results of the DNN model indicate that both parameters have equivalent importance. These findings would not be possible with a case study of conventional modeling because the case space of exciton dynamics is too extensive for exploration. Based on these insights, both host and emitter materials should be designed to enhance the recombination and RISC rate coefficients to suppress excitonic quenching, thereby improving device efficiency and lifetime.
3. Conclusions
We developed a tandem DNN model to predict the RISC rate coefficient from the trEL profiles of TADF OLEDs. To address the uncertainty of the recombination rate coefficient, multiple candidate DNN models that predict the kRISC value were developed by dividing the dataset boundary of the recombination rate coefficient. The tandem model predicted γ and kRISC with high R2 values of 0.979 (recombination rate model) and 0.985 (RISC rate model), respectively. In the application of the tandem model, the experimental trEL profile of the TADF OLED was used as the input data. Consequently, the tandem model exhibited impressive prediction accuracy for γ and kRISC compared with the experimental data. We expect that the results of this study will provide an approach to develop DL models with both high accuracy and practicality for the prediction of physical factors related to the polaron and exciton dynamics of TADF OLEDs.4. Experimental section
Device fabrication
A TADF OLED doped with 20 wt% 5CzBN was manufactured via thermal vacuum evaporation under a vacuum of approximately 5 × 10−7 Torr, followed by encapsulation using a glass lid and epoxy resin in a glove box filled with nitrogen gas. The 50-nm anode was composed of indium tin oxide. The 40-nm hole injection layer was composed of N1,N1′-(biphenyl-4,4′-diyl)-bis(N1-phenyl-N4,N4-di-m-tolylbenzene-1,4-diamine) (DNTPD). The 10-nm hole transport layer was composed of N-([1,1′-biphenyl]-4-yl)-9,9-dimethyl-N-(4-(9-phenyl-9H-carbazol-3-yl)phenyl)-9H-fluoren-2-amine (BCFN). The 10-nm electron blocking layer was composed of mCBP. The 30-nm EML was composed of mCBP and CNmCBP-CN mixed hosts with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio. The 5-nm hole blocking layer was composed of 2,8-bis(4,6-diphenyl-1,3,5-triazin-2-yl)dibenzo-[b,d]furan (DBFTrz). The 20-nm electron transport layer was composed of 2-[4-(9,10-di-naphthalen-2-yl-anthracen-2-yl)-phenyl]-1-phenyl-1H-benzoimidazole (ZADN). The 1.5-nm electron injection layer was composed of lithium fluoride. The 200-nm cathode was composed of aluminum.
1 weight ratio. The 5-nm hole blocking layer was composed of 2,8-bis(4,6-diphenyl-1,3,5-triazin-2-yl)dibenzo-[b,d]furan (DBFTrz). The 20-nm electron transport layer was composed of 2-[4-(9,10-di-naphthalen-2-yl-anthracen-2-yl)-phenyl]-1-phenyl-1H-benzoimidazole (ZADN). The 1.5-nm electron injection layer was composed of lithium fluoride. The 200-nm cathode was composed of aluminum.
Measurement equipment
The PLQY was measured using a Quantaurus-QY (HAMAMATSU C11367) after excitation using light-emitting diode lasers in an integrating sphere. A Quantaurus-Tau (Hamamatsu C11347) was used to measure the trPL properties. A CS 2000 spectroradiometer (Konica Minolta, Inc.) and a Keithley 2400 source meter were used to measure device performance. An oscilloscope (Yokogawa DL9140) and a function generator (Keysight 33622A) connected to a photomultiplier tube (HAMAMATSU G1760001) and a current amplifier (DHPCA-100) were used to measure the trEL profiles.Conflicts of interest
J.-M. K., J. L., and J. Y. L. have submitted a patent application for this work.Data availability
The data supporting this article have been included as part of the SI. See DOI: https://doi.org/10.1039/d5mh01156f.Acknowledgements
This work was supported by the Technology Innovation Program (2410011328) through the Korea Planning and Evaluation Institute of Industrial Technology (KEIT) funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea). J. Y. Lee acknowledges support from MOTIE (RS-2024-00418086, HRD Program for Industrial Innovation).References
- Y. S. Park, S. Lee, K. H. Kim, S. Y. Kim, J. H. Lee and J. J. Kim, Adv. Funct. Mater., 2013, 23, 4914 CrossRef CAS.
- M. Sarma and K.-T. Wong, ACS Appl. Mater. Interfaces, 2018, 10, 19279 CrossRef CAS.
- D. Liu, G. X. Yang, Z. Chen, W. Xie, D. Li, W. Li, J. Lin, X. Nie, Z. Li and B. Liang, Adv. Mater., 2024, 36, 2403584 CrossRef CAS PubMed.
- H. Nakanotani, T. Higuchi, T. Furukawa, K. Masui, K. Morimoto, M. Numata, H. Tanaka, Y. Sagara, T. Yasuda and C. Adachi, Nat. Commun., 2014, 5, 4016 CrossRef CAS PubMed.
- S. O. Jeon, K. H. Lee, J. S. Kim, S.-G. Ihn, Y. S. Chung, J. W. Kim, H. Lee, S. Kim, H. Choi and J. Y. Lee, Nat. Photonics, 2021, 15, 208 CrossRef CAS.
- K. Stavrou, L. G. Franca, A. Danos and A. P. Monkman, Nat. Photonics, 2024, 18, 554 CrossRef CAS.
- Y. X. Hu, J. Miao, T. Hua, Z. Huang, Y. Qi, Y. Zou, Y. Qiu, H. Xia, H. Liu and X. Cao, Nat. Photonics, 2022, 16, 803 CrossRef CAS.
- H. L. Lee, S. O. Jeon, I. Kim, S. C. Kim, J. Lim, J. Kim, S. Park, J. Chwae, W. J. Son and H. Choi, Adv. Mater., 2022, 34, 2202464 CrossRef CAS.
- Y. Fu, H. Liu, B. Z. Tang and Z. Zhao, Nat. Commun., 2023, 14, 2019 CrossRef CAS.
- P. L. dos Santos, F. B. Dias and A. P. Monkman, J. Phys. Chem. C, 2016, 120, 18259 CrossRef CAS.
- J. Grüne, N. Bunzmann, M. Meinecke, V. Dyakonov and A. Sperlich, J. Phys. Chem. C, 2020, 124, 25667 CrossRef.
- J. H. Kang, G. W. Baek, J. Y. Lee, J. Kwak and J.-H. Park, J. Inf. Disp., 2024, 25, 219 CrossRef CAS.
- M. Hasan, S. Saggar, A. Shukla, F. Bencheikh, J. Sobus, S. K. McGregor, C. Adachi, S.-C. Lo and E. B. Namdas, Nat. Commun., 2022, 13, 254 CrossRef CAS.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777 CrossRef CAS PubMed.
- Y. Kondo, K. Yoshiura, S. Kitera, H. Nishi, S. Oda, H. Gotoh, Y. Sasada, M. Yanai and T. Hatakeyama, Nat. Photonics, 2019, 13, 678 CrossRef CAS.
- K. R. Naveen, J. H. Oh, H. S. Lee and J. H. Kwon, Angew. Chem., 2023, 135, e202306768 CrossRef.
- R. W. Weerasinghe, S. Madayanad Suresh, D. Hall, T. Matulaitis, A. M. Slawin, S. Warriner, Y. T. Lee, C. Y. Chan, Y. Tsuchiya, E. Zysman-Colman and A. Boron, Adv. Mater., 2024, 36, 2402289 CrossRef CAS.
- R. K. Konidena, J. Lim and J. Y. Lee, Chem. Eng. J., 2021, 416, 129097 CrossRef CAS.
- H. J. Jang, J. Y. Lee, G. W. Baek, J. Kwak and J.-H. Park, J. Inf. Disp., 2022, 23, 1 CrossRef.
- H. Wang, J. X. Chen, Y. Z. Shi, X. Zhang, L. Zhou, X. Y. Hao, J. Yu, K. Wang and X. H. Zhang, Adv. Mater., 2024, 36, 2307725 CrossRef CAS.
- X. Wu, J. W. Huang, B. K. Su, S. Wang, L. Yuan, W. Q. Zheng, H. Zhang, Y. X. Zheng, W. Zhu and P. T. Chou, Adv. Mater., 2022, 34, 2105080 CrossRef CAS.
- S. Wu, L. Zhang, J. Wang, A. Kumar Gupta, I. D. Samuel and E. Zysman-Colman, Angew. Chem., 2023, 135, e202305182 CrossRef.
- J. Moon, S. Han and J. Y. Lee, Adv. Opt. Mater., 2025, 13, 2402214 CrossRef CAS.
- C. H. Lee, J. H. Lee, K. H. Kim and J. J. Kim, Adv. Funct. Mater., 2018, 28, 1800001 CrossRef.
- A. Odinokov, A. Osipov, J. Oh, Y. K. Moon, S. G. Ihn, H. Lee, I. Kim, W. J. Son, S. Kim and D. Kravchuk, Adv. Theory Simul., 2020, 3, 2000028 CrossRef CAS.
- K. H. Lee, S. O. Jeon, Y. S. Chung, J. M. Kim and J. Y. Lee, Adv. Opt. Mater., 2023, 11, 2201687 CrossRef CAS.
- S. Kato, J. Am. Chem. Soc., 2005, 127, 11538 CrossRef CAS.
- J.-H. Kim, R. E. Triambulo and J.-W. Park, J. Appl. Phys., 2017, 121, 10 Search PubMed.
- X. Zhao, X. Tang, H. Zhu, C. Ma, Y. Wang, S. Ye, L. Tu and Z. Xiong, ACS Appl. Electron. Mater., 2021, 3, 3034 CrossRef CAS.
- P. Chulkin, O. Vybornyi, M. Lapkowski, P. Skabara and P. Data, J. Mater. Chem. C, 2018, 6, 1008 RSC.
- P. Li and Z.-H. Lu, Small Sci., 2021, 1, 2000015 CrossRef CAS.
- J. Lim, K. H. Lee, J. M. Kim and J. Y. Lee, Adv. Opt. Mater., 2022, 10, 2201575 CrossRef CAS.
- F. Nüesch, D. Berner, E. Tutiš, M. Schaer, C. Ma, X. Wang, B. Zhang and L. Zuppiroli, Adv. Funct. Mater., 2005, 15, 323 CrossRef.
- K. H. Lee, J. M. Kim and J. Y. Lee, Adv. Opt. Mater., 2024, 12, 2301358 CrossRef CAS.
- E. Stanzani, S. Sem, S. Züfle, B. Ruhstaller and S. Jenatsch, Org. Electron., 2025, 139, 107204 CrossRef CAS.
- N. C. Giebink and S. R. Forrest, Phys. Rev. Lett., 2023, 130, 267002 CrossRef CAS PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234 CrossRef CAS.
- N. Li, Z. Chen, C. Zhou, F. Ni, Z. Huang, X. Cao and C. Yang, Adv. Mater., 2023, 35, 2300510 CrossRef CAS.
- N. Haase, A. Danos, C. Pflumm, A. Morherr, P. Stachelek, A. Mekic, W. Brütting and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 29173 CrossRef CAS.
- O. Sachnik, X. Zhou, J. Nikan, B. van der Zee, Y. G. Li, P. W. M. Blom and G. Wetzelaer, Adv. Opt. Mater., 2024, 12, 9 Search PubMed.
- J. M. Kim, K. H. Lee and J. Y. Lee, Adv. Opt. Mater., 2022, 10, 3 Search PubMed.
- B. J. Park, K. J. Kim and T. Kim, ACS Appl. Electron. Mater., 2024, 6, 5190 CrossRef CAS.
- J. M. Kim, J. Lim and J. Y. Lee, Mater. Horiz., 2022, 9, 2551 RSC.
- J. M. Kim, K. H. Lee and J. Y. Lee, Adv. Mater., 2023, 35, 14 Search PubMed.
- J. Lim, J. M. Kim and J. Y. Lee, Adv. Mater., 2024, 36, 28 Search PubMed.
- Y. J. Cho, S. K. Jeon and J. Y. Lee, Adv. Opt. Mater., 2016, 4, 688 CrossRef CAS.
- C. Deibel, A. Wagenpfahl and V. Dyakonov, Phys. Rev. B:Condens. Matter Mater. Phys., 2009, 80, 7 CrossRef.
- H. Zhao, J. Kim, K. Ding, M. Jung, Y. Li, H. Ade, J. Y. Lee and S. R. Forrest, Adv. Mater., 2023, 35, 2210794 CrossRef CAS PubMed.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, in Proc. 25th ACM SIGKDD Int. Conf. Know. Discovery Data Mini, Association for Computing Machinery, New York, NY, USA 2019, pp. 2623.
- Kyulux, https://www.kyulux.com/, accessed April 03, 2025.
- H. S. Kim, S. H. Lee, S. Yoo and C. Adachi, Nat. Commun., 2024, 15, 1 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |







