 Open Access Article
Open Access ArticleDesign of simple interactions to assemble complex crystals from binary mixtures of colloidal particles
Beth Hsiao-Yen Wei†
 a,
C. Levi Petix†
a,
C. Levi Petix† b,
Qizan Chen
b,
Qizan Chen a,
Michael P. Howard
a,
Michael P. Howard *b and
Jeetain Mittal
*b and
Jeetain Mittal *acd
*acd
aArtie McFerrin Department of Chemical Engineering, Texas A&M University, College Station, USA. E-mail: jeetain@tamu.edu
bDepartment of Chemical Engineering, Auburn University, Auburn, AL 36849, USA. E-mail: mphoward@auburn.edu
cDepartment of Chemistry, Texas A&M University, College Station, USA
dInterdisciplinary Graduate Program in Genetics and Genomics, Texas A&M University, College Station, USA
First published on 22nd December 2025
Abstract
Computational methods for designing interactions between colloidal particles that induce self-assembly have received much attention for their promise to discover tailored materials. However, it often remains a challenge to translate computationally designed interactions to experiments because they may have features that are too complex, or even infeasible, to physically realize. Toward bridging this gap, we leverage relative-entropy minimization to design pair potentials for binary mixtures of colloidal particles that assemble crystal superlattices. We reduce the dimensionality and extent of the interaction design space by enforcing constraints on the form and parametrization of the pair potentials that are physically motivated by DNA-functionalized nanoparticles. We show that several two- and three-dimensional lattices, including honeycomb and cubic diamond, can be assembled using simple interactions despite their complex structures. We also find that the initial conditions used for the designed parameters as well as the assembly protocol play important roles in determining the outcome and success of the assembly process.
Design, System, ApplicationWe present a constrained inverse design strategy that uses relative-entropy minimization to discover simple, experimentally relevant pair potentials for binary colloidal mixtures. By imposing physically motivated constraints inspired by DNA-functionalized nanoparticles, the design space is reduced to parameters directly linked to experimentally tunable variables, enabling the assembly of complex two- and three-dimensional superlattices, including honeycomb and cubic diamond. The system studied, binary colloidal particles with tunable attractions and repulsions, is broadly important for engineering materials with tailored optical, photonic, and catalytic properties. By focusing on experimentally realizable interaction forms rather than highly flexible spline potentials, we show that even low-coordination lattices can be assembled robustly while maintaining a clear path toward physical implementation. This work bridges the gap between computational inverse design and experimental colloidal self-assembly, providing a practical framework to design and realize functional materials with complex architectures. |
I. Introduction
The self-assembly of colloidal particles into crystal superlattices has important applications in the fabrication of optical,1 catalytic2 and plasmonic materials.3 Particle properties such as shape,4 patchiness,5,6 size,7 charge8,9 and surface functionalization10 can be engineered to control the structure of the superlattice and its corresponding properties.11,12 Characterizing the different superlattices that are produced from such a vast design space using traditional “forward” experimentation can be expensive and slow, motivating the use of “inverse” methods that efficiently identify particles that yield desired structures. Inverse-design methods for self-assembly typically consist of a loss function that measures how different the produced structure is from the desired one and an optimization strategy that minimizes the loss function with respect to the particle properties that can be varied.13 These methods include both approaches physically grounded in statistical mechanics,14–17 such as free-energy landscape engineering,18,19 relative-entropy minimization,20–26 and digital alchemy,27,28 as well as data-driven strategies that exploit machine learning.29–32While inverse design has had considerable computational success13,33 in identifying interactions for specific target structures—avoiding exhaustive parameter sweeps34,35 that identify all structures in a space and become prohibitive in high-dimensional space—translation to experiment remains far more limited.36–39 One major challenge is that pairwise potential energy functions, representing the effective interaction between two particles, are typically designed computationally, but creating particles that will produce these interactions can be difficult if the pair potentials do not have physically interpretable parameters. Pair potentials having no experimental realization may even be designed if physical requirements are not enforced in the optimization. For example, relative-entropy minimization has been successfully applied many times to design pair potentials represented using Akima splines.20–23,26,40 Splines have great flexibility in the functions they can represent and so are useful for finding a feasible design, but this flexibility may produce features such as high-frequency oscillations or plateaus that do not readily map to a known particle surface chemistry. Spline potentials can be constrained20 or filtered40 to remove some of these features, but the resulting interactions are still typically challenging to realize. Beyond spline representations, functional forms with many adjustable parameters can also yield interactions that are hard to realize experimentally.41,42 Using multiple types of particles has also been proposed as a strategy to simplify interaction complexity at the expense of compositional complexity;43 however, spline potentials designed for binary mixtures of particles using relative-entropy minimization were not necessarily simpler than those designed for equivalent one-component assemblies.23
We postulate that this challenge is not caused by a nonexistence of experimentally producible designs. The loss function guiding the design may have local minima and/or regions with low curvature near a global minimum, suggesting that other, simpler interactions may produce acceptable or near-optimal structures. Indeed, forward modeling has shown that colloidal particles interacting through simple, often experimentally-motivated, pair potentials can assemble a variety of structures.44–46 However, assembly of open lattices with such potentials remains difficult; cubic diamond has remained particularly challenging despite great interest because of its desirable for photonics properties.47,48 Additionally, these simple interactions may not be selected by inverse methods if they are less optimal than other, more complex interactions that are admissible. Inverse-design methods can be forced to consider only these simpler interactions by designing physically motivated pair potentials with parameters that are directly related to experimentally controllable variables.49–51 The tradeoff is that it may now be more difficult, or even impossible, to produce the desired structure than with a spline potential because the particle interactions are more constrained.
At the same time, DNA-functionalized particles (DFPs) are known to be a versatile material platform of particular interest for colloidal self-assembly. Simple pair potentials,52–54 including Fermi–Jagla55,56 and Lennard-Jones-nm57 potentials, have been developed to capture the effective interactions between DFPs, such as hybridization-driven attraction and repulsion due to chain overlaps, and have been experimentally validated.58–63 While experimental self-assembly of single-component crystals has mostly been limited to simple close-packed structures,62,64,65 binary mixtures of DFPs offer a richer design space because stoichiometry and differences in particle interactions can be exploited to stabilize structures that would be inaccessible with only a single type of DFP.62,66
In this work, we use relative-entropy minimization to optimize pair potentials for binary mixtures of colloidal particles under physical constraints that reflect known features of DFP interactions, namely tunable repulsion ranges and attraction strengths, as well as symmetries of the superlattice. Our goal is to show that simple interactions can be designed to assemble complex crystal superlattices for binary particle mixtures, even though they should not form with only one particle type. We target four lattices of varying complexity: square and honeycomb in two dimensions as well as body-centered cubic (BCC) and cubic diamond in three dimensions. We demonstrate that all these superlattices can be successfully designed for using a bulk isochoric temperature cycling protocol; however, we find that only some designs subsequently reliably self-assemble under bulk isothermal compression. We show that one reason for this behavior may be sensitivity to the initial choice of parameters for optimization, consistent with our postulation about the viability of multiple designs. We additionally probe how our designed interactions perform under dilute conditions typically used in experiments, highlighting the important role of protocol in both the design and assembly processes.
II. Model and methods
We employed the perturbed Lennard-Jones pair potential67,68 as a simple model that captures the essential physics of DFP interactions, namely tunable repulsion and attraction; alternative models for DFPs could be used within the same framework if desired. Specifically, the pair potential uij between two particles of types i and j was
 | (1) |
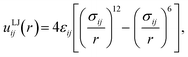 | (2) |
Our target crystal superlattices (Table S1) are formed from binary mixtures containing particles of types A and B, so in principle, 9 parameters are needed to specify the potential energy function corresponding to eqn (1). However, we were able to reduce the dimensionality and size of this design space using physical insights, which is an advantage of performing inverse design using a physically motivated pair potential. Specifically, we assumed that all particles had the same repulsion strength, coming primarily from the core nanoparticle and grafted DNA chains, at the design temperature, so εAA = εAB = εBB = ε, where ε can be considered the unit of energy. Further, the symmetry of the 4 lattices we designed (Fig. 1, Table S1) implies that σAA = σBB and λAA = λBB. Hence, only σAA, σAB, λAA, and λAB needed to be treated as independent parameters. In preliminary tests, we found σij to be numerically challenging to optimize concurrently with λij because eqn (1) is a highly nonlinear function of σij. We accordingly considered 4 parameters θ = (σ6AA, σ6AB, λAA, λAB) for optimization. Based on forward modeling and experiments,57,69,70 we constrained this parameter space to be consistent with 0.5σ ≤ σij ≤ 2σ and 0 ≤ λij ≤ 1, where σ is the unit of length.
 | ||
| Fig. 1 Designed pair potentials and representative snapshots for each crystal (top row) along with g(ij) measured between like (middle row, filled line) and unlike (bottom row, filled line) particles, compared to the target g(ij)0 (dashed line). The four crystal structures are: (a)–(c) square, (d)–(f) honeycomb, (g)–(i) BCC, and (j)–(l) cubic diamond. Snapshots of the target structures (inset) were rendered using VMD (version 1.9.4).77 | ||
To design the parameters θ that self-assembled a specific lattice, we minimized the relative entropy,22,71,72
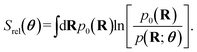 | (3) |
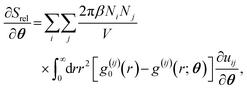 | (4) |
To evaluate g(ij)0, initial configurations that contained at least 1000 total particles were generated at a number density and stoichiometry consistent with the target structure (Table S1). Each particle was tethered to a lattice site by a harmonic potential ϕ(r) = kr2/2, where r is the distance of the center of the particle from the lattice site and k is a spring constant. A target ensemble of particle configurations was then simulated by drawing an independent random displacement for each particle from a Gaussian distribution with zero mean and variance (βk)−1. We chose a spring constant k = 1000ε/σ2, which we found to produce well-defined but numerically integrable peaks in g(ij)0, and used 1000 configurations to compute g(ij)0 up to a distance of 5σ with a bin spacing of 0.05σ.
Relative-entropy minimization was carried out with relentless73 (version 0.1.1 with operations modified to support volume resizing) using HOOMD-blue75 (version 2.9.7). Langevin dynamics simulations were performed to evaluate g(ij) in eqn (4). The simulation timestep was 0.001τ and the particle friction factor was 0.1m/τ, where m is the mass of a particle (taken to be the same for both types) and 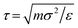 is the unit of time. The particles were initialized in the target structure, then equilibrated for 3 × 104τ at temperature T = 3ε/kB to attempt to melt the crystal. We found this initialization protocol to be necessary because it was often not possible to place the particles in randomized or fluid-like configurations without overlap for suboptimal values of σij. The temperature was then slowly quenched from 3ε/kB to 1ε/kB over 2 × 104τ at a constant rate. The radial distribution function g(ij) was finally sampled every 10τ during a 104τ production period with the same maximum distance and bin spacing as was used for g(ij)0. The parameters θ were then adjusted to attempt to minimize Srel using gradient descent with a step size chosen for each parameter such that the change in σ6ij was approximately 0.25σ6 and the change in λij was approximately 0.05 for the first iteration. We initialized σ6ij to be consistent with the position of the first peak in g(ij)0 based on physical knowledge that it relates to the size of the particle and DNA corona, while λAA and λAB were initialized to 0 and 1, respectively, based on previous work.43,57 The optimization was considered converged when the absolute values of all components of the gradient were less than 0.01 in their respective units or further progress could not be made due to the box constraints on the parameters.
is the unit of time. The particles were initialized in the target structure, then equilibrated for 3 × 104τ at temperature T = 3ε/kB to attempt to melt the crystal. We found this initialization protocol to be necessary because it was often not possible to place the particles in randomized or fluid-like configurations without overlap for suboptimal values of σij. The temperature was then slowly quenched from 3ε/kB to 1ε/kB over 2 × 104τ at a constant rate. The radial distribution function g(ij) was finally sampled every 10τ during a 104τ production period with the same maximum distance and bin spacing as was used for g(ij)0. The parameters θ were then adjusted to attempt to minimize Srel using gradient descent with a step size chosen for each parameter such that the change in σ6ij was approximately 0.25σ6 and the change in λij was approximately 0.05 for the first iteration. We initialized σ6ij to be consistent with the position of the first peak in g(ij)0 based on physical knowledge that it relates to the size of the particle and DNA corona, while λAA and λAB were initialized to 0 and 1, respectively, based on previous work.43,57 The optimization was considered converged when the absolute values of all components of the gradient were less than 0.01 in their respective units or further progress could not be made due to the box constraints on the parameters.
III. Results and discussion
A. Initial design
We carried out our inverse-design procedure starting with the square lattice in two-dimensions (Fig. 1a–c). The procedure quickly converged, finding an interaction between like particles that was purely repulsive and an interaction between unlike particles that was attractive; λAA and λAB remained at their initial values of 0 and 1, respectively, throughout the optimization (Fig. S1). We found that σAA also remained close to its initial value at the first peak in g(AA)0, but σAB somewhat decreased from its initial value at the first peak in g(AB)0. The range of the like-particle repulsions was longer than that of the unlike-particle attractions, which is characteristic of binary DFPs.69,76 Purely repulsive Akima-spline potentials have been designed to self-assemble the square lattice using both one and two types of particles.22,23 Those potentials both have complex features, such as shoulders and plateaus, that our constrained design does not.Encouraged by this success, we proceeded to design the remaining lattices that we anticipated to be more challenging than square: honeycomb (Fig. 1d–f) is a low-coordinated two-dimensional lattice, BCC (Fig. 1g–i) is a three-dimensional lattice, and cubic diamond (Fig. 1j–l) is a low-coordinated three-dimensional lattice. As for the square lattice, σAA typically remained close to its initial value, set by the first peak in g(AA)0, but σAB tended to decrease for all three structures (Fig. S1). For honeycomb, λAB departed from its initial value but quickly returned; the same happened with λAA for BCC. Hence, the interactions for both honeycomb and BCC were purely repulsive between like particles and a Lennard-Jones attraction between unlike particles. Interestingly, the cubic diamond was found to have a nonzero λAA when the optimization converged, corresponding to a weak attraction between like particles in addition to a Lennard-Jones attraction between unlike particles. Such attraction can be achieved by mixing two different DNA strands on each particle78,79 or via linker-mediated binding.79
Overall, our designed interactions are consistent with a pattern observed in a forward modeling study of DFPs:57 the denser crystals (square and BCC) were assembled by competing repulsive and attractive interactions that were closer in range than those of the less dense crystals (honeycomb and cubic diamond). For the less dense crystals, such long-ranged repulsions between like particles can be attained in experiments by shifting the location of the complementary “sticky” DNA sequence from the tail to the middle of the molecule to enhance shell overlap.57 The difference in ranges can be approximately quantified through σAB/σAA, which was about 1.5 (square) and 1.2 (BCC) for the more dense crystal structures and about 1.9 for the less dense crystals (Table S2). This finding is analogous to previous studies that demonstrated the influence of interaction ranges on DFP self-assembly, for instance, different DNA-linker to particle size ratios producing different structures.62,80,81
We further note that it appeared that some of the interaction parameters would slowly evolve with more iterations of gradient descent, particularly for challenging designs like cubic diamond (Fig. S7); however, the optimization stopped because the convergence criteria were satisfied. To investigate whether continued optimization would improve the design, we performed additional iterations with an order of magnitude stricter tolerance. As expected, the parameters continued to evolve but eventually converged (Fig. S2). Counterintuitively, these converged variables performed worse during isothermal compression (see section III.B), producing more polymorphic crystals with greater variability between independent simulations compared to the original convergence criterion (Fig. S3). This behavior reflects our operational definition of convergence, under which the parameters are considered converged even though small changes may continue with further iterations. The target g(ij) were also well-matched at both convergence thresholds, supporting the notion that multiple acceptable designs exist within a relatively shallow region of the relative entropy function landscape and that some designs may be more robust under different assembly protocols depending on the specific numerical details of the optimization procedure. The design that is found depends on the optimization method, convergence criteria, and initial guess. We will discuss some of these considerations later.
B. Validation of design
Inverse design using the relative entropy is sensitive to the simulation protocol because eqn (4) assumes thermodynamic equilibrium, but equilibrium may not be achieved in a self-assembly simulation for a variety of reasons. For example, a crystal may not nucleate and grow if the simulation time is too short, or there may be crystal defects that cannot anneal. For our simulation protocol, we found that none of the initially crystalline particle configurations were actually able to melt during isochoric temperature cycling despite heating to T = 3ε/kB. Lack of melting may indicate thermodynamic stability of the crystal due to a good initial guess of parameters, but it is also possible the crystal is only metastable or the particles are kinetically trapped. Alternative protocols such as designing under isobaric conditions could help circumvent these issues, but can be numerically challenging.82We hence simulated another assembly protocol based on isothermal compression to validate the interactions we designed using isochoric temperature cycling. We placed the same number of particles quasi-randomly in a simulation box whose edge lengths were three times longer than that of the target, then compressed the box isothermally at T = 1ε/kB to its target size by reducing the edge lengths at a constant rate over a period of 5 × 104τ. The particles in the expanded box were gas-like, so they were required to assemble in the validation simulations even if the crystal did not melt in the design simulations (Fig. 2). We then simulated a production period of 104τ, sampling particle configurations every 102τ for structural analysis. We repeated this procedure 5 times starting from different initial configurations to probe variability.
 | ||
| Fig. 2 Snapshots from the first validation (isothermal compression) simulation using the potential designed during isochoric temperature cycling for square, honeycomb, BCC and, cubic diamond. | ||
We are using binary mixtures to assemble the targeted superlattices because the simple interactions we considered are not expected to form them with one particle type; however, from a practical perspective, we may not require perfect compositional order in the final assembled structure. For example, two types of DFPs may have the same nanoparticle core and differ only in their DNA functionalization, making them essentially interchangeable in the lattice for properties that depend only on the arrangement of cores. Hence, we employed two different structural metrics that were agnostic to composition to assess if the designed interactions assembled the target structure. The first was based on the radial distribution function g ignoring particle type, which we calculated from the recorded particle configurations up to distance R = 5σ using bin width 0.05σ. We then evaluated the mean squared error (MSE) in g relative to the type-agnostic radial distribution function g0 for the target,
 | (5) |
We found that square, honeycomb, and BCC all reliably self-assembled in our validation simulations, with at least 80% of particles being classified as belonging to the target lattice on average (Fig. 3). The MSE in g was consistently larger in the validation simulations than in the design simulations. There was also significant variability in g MSE, but not as much in the fraction of particles classified as being in the correct lattice (Fig. S5). In contrast, there was essentially no variability in either quantity between 3 independent simulations performed using the design protocol, with essentially all particles being classified as the target structure. To better understand the assemblies formed using the validation protocol, we inspected the type-agnostic g for the different crystals (Fig. S4). We found that although their peaks were typically correctly located, they often had different heights and widths, particularly at longer distances. This behavior is consistent with the presence of defects disrupting long-ranged ordering, which were also visually apparent in particle configurations colored by the structural classifier (Fig. 2).
Cubic diamond, on the other hand, had a large increase in g MSE and decrease in fraction of particles classified (only about 27%) in the validation simulations. There was also significant variability between the 5 independent simulations. The radial distribution functions all showed a lack of long-ranged order, but some also had a few additional small peaks at shorter separation distances that were not present in the target (Fig. S4d). The structural classification method we used for cubic diamond identified a significant fraction of particles as being hexagonal diamond, a competing polymorph, in some simulations (Fig. S6). Despite their substantial structural differences—75% of rings are boat-like in hexagonal diamond rather than chair-like in cubic diamond—cubic and hexagonal diamond have similar free energies86,87 and subtly different radial distribution functions, making it difficult to select for only one. Overall, our results indicate substantial polymorphism in the diamond structures produced under bulk isothermal compression that was absent under isochoric temperature cycling, likely due to lack of melting. We confirmed that this polymorphism tended to set in early during compression (Fig. 4a) and persist.
 | ||
| Fig. 4 Representative particle snapshots and fractions of particles classified as cubic or hexagonal diamond as a function of (a) number density ρ during bulk isothermal compression and (b) temperature T during isochoric cooling of an initially dilute suspension. In (b), the grey line is the largest cluster size, indicating that essentially all particles have incorporated into the final crystallite. The inset particle snapshots show the transition from an amorphous cluster to a crystallite with diamond structure. Snapshots here, in Fig. 5, and in the supplementary information were rendered using OVITO (version 3.12.0).83 | ||
We were curious whether less polymorphism and/or more consistent crystallization might be achievable for cubic diamond by assembling under conditions that more easily allowed for particle rearrangement. In experiments, self-assembly often occurs from a dilute suspension through a gas–solid-like phase transition.88 Drawing inspiration from this procedure, we initialized simulations in the large simulation box used to start the bulk isothermal compression; however, we now isochorically cooled from T = 1ε/kB to 0.01ε/kB at a constant rate over a period of 105τ. This slow cooling should drive the particles to self-assemble finite-size crystallites. Indeed, we found that a single crystallite formed at around T = 0.18ε/kB by a previously identified two-step mechanism,57 in which the particles first aggregated into an amorphous cluster then crystallized (Fig. 4b). Like the bulk compression simulations, the final crystallite contained both cubic and hexagonal diamond structures; however, unlike the bulk compression simulations (Fig. S6), there was significantly less variability in the fraction of each structure between independent simulations (Fig. S12). The similar free energies of cubic and hexagonal diamond make it challenging to thermodynamically favor one over the other.57 We suspect that our isothermal compression protocol inhibited particles' ability to rearrange after nucleation as they continued to densify, leading to more variability than under dilute assembly conditions.
C. Alternative designs
To investigate whether acceptable alternatives to the interactions designed in section IIIA may exist, we repeated our inverse-design procedure for the honeycomb lattice with different initial guesses for λAA and λAB. We started each of these parameters from either 0 or 1, and we considered all four possible resulting combinations (Fig. S7). We found that the designed interaction between unlike particles was insensitive to the initial value of either λAA or λAB and was always attractive, but the designed interaction between like particles was dictated by the initial value of λAA. Specifically, the designed interaction between like particles was repulsive if λAA = 0 initially and attractive if λAA = 1 initially. During the design process, λAB stabilized quickly but λAA evolved slowly (Fig. S7b and d), suggesting the possibility of convergence of λAA across a broad range of values depending on the criteria specified. We will compare the two designs that both initially had λAB = 1 and either λAA = 0 (repulsive like interactions, designated −+) or λAA = 1 (attractive like interactions, designated ++).The −+ design produced crystals of similar quality as the ++ design under bulk isothermal compression (Fig. 5a and b). The −+ design had a slightly larger deviation from the target g, but there was less variability between independent simulations (Fig. 5a and S8). Both designs had nearly all particles classified as being in the target structure (Fig. 5b). However, there were significant differences in assembly from a dilute suspension (Fig. S9). The −+ design required significantly colder temperature to assemble than the ++ design (Fig. 5c and d). Assembly occurred in two steps for the −+ design, with string-like structures forming before honeycomb, whereas honeycomb directly nucleated for the ++ design. The assembled structures for the −+ design also tended to be less compact than for the ++ design (Fig. S9). The structural classifier identified more particles as being honeycomb for the ++ design than for the −+ design; however, this may be partially due to the larger number of interfacial particles in the −+ assembly that are more challenging to classify.
The string-like structures for the −+ design may be a kinetic effect because the particle dynamics slow considerably as T decreases and assemblies form. To probe this possibility, we ran an additional dilute isochoric simulation where the particles were initialized in the crystallite assembled by the ++ design, and the temperature was held constant at T = 0.0755ε/kB. This temperature is near the nominal melting point for the −+ design estimated from a trace of the potential energy during cooling. We ran a long simulation (duration 105τ), but the honeycomb crystallite remained stable and strings did not form. We then ran similar simulations at 0.1 ≤ kBT/ε ≤ 0.5 at increments of 0.1 (Fig. S13). We found for the −+ potential that strings started to detach from the crystallite surface at T = 0.1ε/kB, and the crystal completely melted at higher temperatures. We performed the same test using the ++ potential and found that it stabilized the crystallite up to at least T = 0.3ε/kB. At T = 0.4ε/kB, there was a coexistence between the crystal and a dilute phase, before complete melting at T = 0.5ε/kB. This behavior is consistent with the crystallization curves observed in cooling simulations (Fig. 5d).
It has been shown that pair potentials designed for two-dimensional structures can also stabilize their three-dimensional analogs, e.g., a potential designed to self-assemble a square lattice in two dimensions may also self-assemble a simple cubic lattice in three dimensions.89 We accordingly tested the ability of both our −+ and ++ designs for honeycomb, performed in two dimensions, to form diamond from a dilute suspension in three dimensions. Consistent with our results in two dimensions, we found that the two designs formed distinct structures in three dimensions. In particular, a multilayered graphene-like structure that was not stacked in the manner of graphite was assembled by the −+ design (Fig. S10), while the ++ design assembled mostly cubic and hexagonal diamond as well as their closest neighbors (Fig. S11). Interestingly for the −+ design, the particles first formed strings, as in two dimensions (Fig. 5c), before the final structure. We suspect that this structure may also be a kinetic effect for similar reasons as in two dimensions. Overall, the difference in transferability to three dimensions demonstrates another practical difference between the two designs, even though both were considered converged and behaved similarly in bulk simulations.
IV. Conclusions
We have applied relative-entropy minimization to design isotropic pair potentials for binary mixtures of colloidal particles that self-assemble square and honeycomb superlattices in two dimensions as well as BCC and cubic diamond superlattices in three dimensions. By imposing a functional form on the pair potential that is physically motivated by interactions between DFPs, we restrict the design space in a way that forces simpler interactions to be designed and may enhance experimental realizability. Our results show that these simple potentials can still drive assembly of complex lattices, e.g., with low coordination. The approach presented is general and extends naturally to additional target structures with different particle size ratios and stoichiometries beyond those demonstrated here.A key observation from this work is that multiple viable designs may be identified depending on the initial parameter guess, but these designs may have rather different behavior under other assembly conditions. We demonstrated this sensitivity by testing several initial values of λij in the two-dimensional honeycomb lattice, which showed distinct assembly behavior during validation despite similar performance in the design protocol. While the present study focuses on stoichiometrically balanced binary mixtures, exploring compositional complexity may offer additional routes to stabilize or tune targeted structures.90 Nevertheless, especially complex lattices may require additional design elements beyond composition and isotropic interactions; directional (e.g., patchy) interactions represent one promising approach that can be systematically parameterized and connected to experiments.91–93 To enhance robustness and practical translation, it may then be important to consider the assembly protocol that will be used in experiments when configuring the computational design protocol. For example, dilute simulations of finite-size crystallites might be used for design rather than simulations of bulk crystals. Moreover, while our design strategy assumes equilibrium thermodynamics, designing for non-equilibrium assembly or processing conditions may also be fruitful.94,95
Author contributions
BHW and CLP contributed equally to protocol development, data analysis, visualization, and writing the initial draft of the manuscript. QC assisted with data analysis and visualization. BHW conducted simulations. CLP and MPH developed the software used. MPH and JM conceptualized the project, supervised the work, and provided critical feedback throughout. All authors contributed to discussions and editing of the final manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The software used to perform the inverse design can be found at https://github.com/mphowardlab/relentless. The parameters of the designed potentials are available as supplementary information (SI). The other data that supports the findings of this study are available from the authors upon reasonable request.Supplementary information is available. See DOI: https://doi.org/10.1039/d5me00129c.
Acknowledgements
Research was sponsored by the Army Research Office and was accomplished under Grant Number W911NF-24-1-0245 (to JM). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. CLP was supported by a fellowship from The Molecular Sciences Software Institute under National Science Foundation Award No. CHE-2136142. We gratefully acknowledge the computational resources provided by the Texas A&M High Performance Research Computing (HPRC) to complete this work.References
- M. A. Boles, M. Engel and D. V. Talapin, Self-assembly of colloidal nanocrystals: From intricate structures to functional materials, Chem. Rev., 2016, 116, 11220–11289 CrossRef.
- Y. Kang, X. Ye, J. Chen, Y. Cai, R. E. Diaz, R. R. Adzic, E. A. Stach and C. B. Murray, Design of Pt–Pd binary superlattices exploiting shape effects and synergistic effects for oxygen reduction reactions, J. Am. Chem. Soc., 2013, 135, 42–45 CrossRef.
- D. J. Park, C. Zhang, J. C. Ku, Y. Zhou, G. C. Schatz and C. A. Mirkin, Plasmonic photonic crystals realized through DNA-programmable assembly, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 977–981 CrossRef.
- S. Lee and S. C. Glotzer, Entropically engineered formation of fivefold and icosahedral twinned clusters of colloidal shapes, Nat. Commun., 2022, 13, 7362 Search PubMed.
- S. C. Glotzer and M. J. Solomon, Anisotropy of building blocks and their assembly into complex structures, Nat. Mater., 2007, 6, 557–562 Search PubMed.
- W. Li, H. Palis, R. Mérindol, J. Majimel, S. Ravaine and E. Duguet, Colloidal molecules and patchy particles: complementary concepts, synthesis and self-assembly, Chem. Soc. Rev., 2020, 49, 1955–1976 RSC.
- T. I. Li, R. Sknepnek, R. J. Macfarlane, C. A. Mirkin and M. Olvera de la Cruz, Modeling the crystallization of spherical nucleic acid nanoparticle conjugates with molecular dynamics simulations, Nano Lett., 2012, 12, 2509–2514 CrossRef.
- A.-P. Hynninen, M. E. Leunissen, A. van Blaaderen and M. Dijkstra, Cuau structure in the restricted primitive model and oppositely charged colloids, Phys. Rev. Lett., 2006, 96, 018303 CrossRef.
- M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Ionic colloidal crystals of oppositely charged particles, Nature, 2005, 437, 235–240 CrossRef.
- A. Dong, X. Ye, J. Chen, Y. Kang, T. Gordon, J. M. Kikkawa and C. B. Murray, A generalized ligand-exchange strategy enabling sequential surface functionalization of colloidal nanocrystals, J. Am. Chem. Soc., 2011, 133, 998–1006 CrossRef.
- S. Wang, S. S. Park, C. T. Buru, H. Lin, P.-C. Chen, E. W. Roth, O. K. Farha and C. A. Mirkin, Colloidal crystal engineering with metal–organic framework nanoparticles and DNA, Nat. Commun., 2020, 11, 2495 CrossRef PubMed.
- G. Posnjak, X. Yin, P. Butler, O. Bienek, M. Dass, S. Lee, I. D. Sharp and T. Liedl, Diamond-lattice photonic crystals assembled from dna origami, Science, 2024, 384, 781–785 CrossRef.
- Z. M. Sherman, M. P. Howard, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Inverse methods for design of soft materials, J. Chem. Phys., 2020, 152, 140902 CrossRef.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Optimized interactions for targeted self-assembly: Application to a honeycomb lattice, Phys. Rev. Lett., 2005, 95, 228301 CrossRef.
- E. Marcotte, F. H. Stillinger and S. Torquato, Optimized monotonic convex pair potentials stabilize low-coordinated crystals, Soft Matter, 2011, 7, 2332–2335 RSC.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Synthetic diamond and wurtzite structures self-assemble with isotropic pair interactions, Phys. Rev. E, 2007, 75, 031403 CrossRef.
- E. Marcotte, F. H. Stillinger and S. Torquato, Communication: Designed diamond ground state via optimized isotropic monotonic pair potentials, J. Chem. Phys., 2013, 138, 061101 Search PubMed.
- A. W. Long and A. L. Ferguson, Rational design of patchy colloids via landscape engineering, Mol. Syst. Des. Eng., 2018, 3, 49–65 RSC.
- Y. Ma and A. L. Ferguson, Inverse design of self-assembling colloidal crystals with omnidirectional photonic bandgaps, Soft Matter, 2019, 15, 8808–8826 Search PubMed.
- B. A. Lindquist, R. B. Jadrich, W. D. Piñeros and T. M. Truskett, Inverse design of self-assembling Frank-Kasper phases and insights into emergent quasicrystals, J. Phys. Chem., 2018, 122, 5547–5556 CrossRef.
- R. B. Jadrich, B. A. Lindquist and T. M. Truskett, Probabilistic inverse design for selfassembling materials, J. Chem. Phys., 2017, 146, 184103 CrossRef.
- B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Communication: Inverse design for self-assembly via on-the-fly optimization, J. Chem. Phys., 2016, 145, 111101 CrossRef.
- W. D. Piñeros, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Inverse design of multicomponent assemblies, J. Chem. Phys., 2018, 148, 104509 Search PubMed.
- R. B. Jadrich, J. A. Bollinger, B. A. Lindquist and T. M. Truskett, Equilibrium cluster fluids: pair interactions via inverse design, Soft Matter, 2015, 11, 9342–9354 RSC.
- B. A. Lindquist, S. Dutta, R. B. Jadrich, D. J. Milliron and T. M. Truskett, Interactions and design rules for assembly of porous colloidal mesophases, Soft Matter, 2017, 13, 1335–1343 RSC.
- D. Banerjee, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Assembly of particle strings via isotropic potentials, J. Chem. Phys., 2019, 150, 124903 CrossRef.
- G. van Anders, D. Klotsa, A. S. Karas, P. M. Dodd and S. C. Glotzer, Digital alchemy for materials design: Colloids and beyond, ACS Nano, 2015, 9, 9542–9553 CrossRef.
- L. Y. Rivera-Rivera, T. C. Moore and S. C. Glotzer, Inverse design of triblock Janus spheres for self-assembly of complex structures in the crystallization slot via digital alchemy, Soft Matter, 2023, 19, 2726–2736 RSC.
- B. Kim, S. Lee and J. Kim, Inverse design of porous materials using artificial neural networks, Sci. Adv., 2020, 6, eaax9324 Search PubMed.
- G. M. Coli, E. Boattini, L. Filion and M. Dijkstra, Inverse design of soft materials via a deep learning-based evolutionary strategy, Sci. Adv., 2022, 8, eabj6731 CrossRef.
- R. Kumar, G. M. Coli, M. Dijkstra and S. Sastry, Inverse design of charged colloidal particle interactions for self assembly into specified crystal structures, J. Chem. Phys., 2019, 151, 084109 Search PubMed.
- C. Wang, A. Pérez de Alba Ortíz and M. Dijkstra, Inverse design method with enhanced sampling for complex open crystals: Application to novel zeolite self-assembly, ACS Nano, 2025, 19, 17423–17437 CrossRef PubMed.
- M. Dijkstra and E. Luijten, From predictive modelling to machine learning and reverse engineering of colloidal self-assembly, Nat. Mater., 2021, 20, 762–773 CrossRef PubMed.
- J. Dshemuchadse, P. F. Damasceno, C. L. Phillips, M. Engel and S. C. Glotzer, Moving beyond the constraints of chemistry via crystal structure discovery with isotropic multiwell pair potentials, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024034118 CrossRef.
- R. A. LaCour, C. S. Adorf, J. Dshemuchadse and S. C. Glotzer, Influence of softness on the stability of binary colloidal crystals, ACS Nano, 2019, 13, 13829–13842 CrossRef PubMed.
- B. Srinivasan, T. Vo, Y. Zhang, O. Gang, S. Kumar and V. Venkatasubramanian, Designing DNA-grafted particles that self-assemble into desired crystalline structures using the genetic algorithm, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18431–18435 CrossRef PubMed.
- H. Liu, M. Matthies, J. Russo, L. Rovigatti, R. P. Narayanan, T. Diep, D. McKeen, O. Gang, N. Stephanopoulos, F. Sciortino, H. Yan, P. Romano and F. Šulc, Inverse design of a pyrochlore lattice of dna origami through model-driven experiments, Science, 2024, 384, 776–781 CrossRef PubMed.
- Y. Geng, G. van Anders, P. M. Dodd, J. Dshemuchadse and S. C. Glotzer, Engineering entropy for the inverse design of colloidal crystals from hard shapes, Sci. Adv., 2019, 5, eaaw0514 CrossRef PubMed.
- C. X. Du, G. van Anders, J. Dshemuchadse, P. M. Dodd and S. C. Glotzer, Inverse design of compression-induced solid – solid transitions in colloids, Mol. Simul., 2020, 46, 1037–1044 CrossRef.
- C. S. Adorf, J. Antonaglia, J. Dshemuchadse and S. C. Glotzer, Inverse design of simple pair potentials for the self-assembly of complex structures, J. Chem. Phys., 2018, 149, 204102 Search PubMed.
- H. Pan and J. Dshemuchadse, Targeted discovery of low-coordinated crystal structures via tunable particle interactions, ACS Nano, 2023, 17, 7157–7169 Search PubMed.
- P. Zhou and S. C. Glotzer, Inverse design of isotropic pair potentials using digital alchemy with a generalized fourier potential, Eur. Phys. J. B, 2021, 94, 243 CrossRef.
- N. A. Mahynski, E. Pretti, V. K. Shen and J. Mittal, Using symmetry to elucidate the importance of stoichiometry in colloidal crystal assembly, Nat. Commun., 2019, 10, 2028 CrossRef PubMed.
- A. Kumar and V. Molinero, Self-assembly of mesophases from nanoparticles, J. Phys. Chem. Lett., 2017, 8, 5053–5058 CrossRef PubMed.
- E. C. Oǧuz, A. Mijailović and M. Schmiedeberg, Self-assembly of complex structures in colloid-polymer mixtures, Phys. Rev. E, 2018, 98, 052601 CrossRef.
- A. Travesset, Binary nanoparticle superlattices of soft-particle systems, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9563–9567 CrossRef.
- E. Yablonovitch, Photonic band-gap structures, J. Opt. Soc. Am. B, 1993, 10, 283–295 CrossRef.
- A. Moroz, Three-dimensional complete photonic-band-gap structures in the visible, Phys. Rev. Lett., 1999, 83, 5274–5277 CrossRef.
- E. A. Bedolla-Montiel, J. T. Lange, A. Pérez de Alba Ortíz and M. Dijkstra, Inverse design of crystals and quasicrystals in a non-additive binary mixture of hard disks, J. Chem. Phys., 2024, 160, 244902 CrossRef CAS PubMed.
- B. A. Lindquist, Inverse design of equilibrium cluster fluids applied to a physically informed model, J. Chem. Phys., 2021, 154, 174907 CrossRef PubMed.
- N. A. Mahynski, R. Mao, E. Pretti, V. K. Shen and J. Mittal, Grand canonical inverse design of multicomponent colloidal crystals, Soft Matter, 2020, 16, 3187–3194 RSC.
- B. D. Rabideau and R. T. Bonnecaze, A computational study of the hydrodynamically assisted organization of DNA-functionalized colloids in 2d, Langmuir, 2007, 23, 10000–10007 CrossRef PubMed.
- E. Auyeung, T. I. N. G. Li, A. J. Senesi, A. L. Schmucker, B. C. Pals, M. O. de la Cruz and C. A. Mirkin, DNA-mediated nanoparticle crystallization into wulff polyhedra, Nature, 2014, 505, 73–77 CrossRef PubMed.
- A. V. Tkachenko, Morphological diversity of DNA-colloidal self-assembly, Phys. Rev. Lett., 2002, 89, 148303 CrossRef.
- M. Song, Y. Ding, H. Zerze, M. A. Snyder and J. Mittal, Binary superlattice design by controlling DNA-mediated interactions, Langmuir, 2018, 34, 991–998 CrossRef.
- E. Pretti, H. Zerze, M. Song, Y. Ding, N. A. Mahynski, H. W. Hatch, V. K. Shen and J. Mittal, Assembly of three-dimensional binary superlattices from multi-flavored particles, Soft Matter, 2018, 14, 6303–6312 RSC.
- R. Mao, B. Minevich, D. McKeen, Q. Chen, F. Lu, O. Gang and J. Mittal, Regulating phase behavior of nanoparticle assemblies through engineering of DNA-mediated isotropic interactions, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2302037120 CrossRef PubMed.
- M. M. Maye, D. Nykypanchuk, D. van der Lelie and O. Gang, DNA-regulated micro- and nanoparticle assembly, Small, 2007, 3, 1678–1682 CrossRef PubMed.
- W. B. Rogers and V. N. Manoharan, Programming colloidal phase transitions with DNA strand displacement, Science, 2015, 347, 639–642 CrossRef PubMed.
- C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607–609 CrossRef PubMed.
- E. W. Gehrels, W. B. Rogers and V. N. Manoharan, Using dna strand displacement to control interactions in DNA-grafted colloids, Soft Matter, 2018, 14, 969–984 RSC.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Nanoparticle superlattice engineering with DNA, Science, 2011, 334, 204–208 CrossRef.
- M. Dwivedi, S. L. Singh, A. S. Bharadwaj, V. Kishore and A. V. Singh, Self-assembly of DNA-grafted colloids: A review of challenges, Micromachines, 2022, 13, 1102 CrossRef PubMed.
- R. J. Macfarlane, B. Lee, H. D. Hill, A. J. Senesi, S. Seifert and C. A. Mirkin, Assembly and organization processes in DNA-directed colloidal crystallization, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10493–10498 Search PubMed.
- R. V. Thaner, Y. Kim, T. I. N. G. Li, R. J. Macfarlane, S. T. Nguyen, M. Olvera de la Cruz and C. A. Mirkin, Entropy-driven crystallization behavior in DNA-mediated nanoparticle assembly, Nano Lett., 2015, 15, 5545–5551 CrossRef.
- Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Crystallization of DNA-coated colloids, Nat. Commun., 2015, 6, 7253 CrossRef PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, Role of repulsive forces in determining the equilibrium structure of simple liquids, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef.
- H. S. Ashbaugh and H. W. Hatch, Natively unfolded protein stability as a coil-to-globule transition in charge/hydropathy space, J. Am. Chem. Soc., 2008, 130, 9536–9542 CrossRef PubMed.
- Y. Ding and J. Mittal, Insights into DNA-mediated interparticle interactions from a coarsegrained model, J. Chem. Phys., 2014, 141, 184901 CrossRef PubMed.
- H. Seyforth, S. Chatterjee, T. E. Videbak, M. Mondal, W. M. Jacobs and W. B. Rogers, The underappreciated role of nonspecific interactions in the crystallization of DNA-coated colloids, Soft Matter, 2025, 21, 2654–2663 RSC.
- M. S. Shell, The relative entropy is fundamental to multiscale and inverse thermodynamic problems, J. Chem. Phys., 2008, 129, 144108 Search PubMed.
- M. S. Shell, Advances in Chemical Physics, John Wiley & Sons, Inc, 2016, pp. 395–441 Search PubMed.
- A. N. Sreenivasan, C. L. Petix, Z. M. Sherman and M. P. Howard, Relentless: Transparent, reproducible molecular dynamics simulations for optimization, J. Chem. Phys., 2024, 161, 212502 CrossRef.
- C. L. Petix, M. Fakhraei, C. A. Kieslich and M. P. Howard, Surrogate modeling of the relative entropy for inverse design using smolyak sparse grids, J. Chem. Theory Comput., 2024, 20, 1538–1546 CrossRef PubMed.
- J. A. Anderson, J. Glaser and S. C. Glotzer, Hoomd-blue: A python package for highperformance molecular dynamics and hard particle monte carlo simulations, Comput. Mater. Sci., 2020, 173, 109363 CrossRef.
- W. B. Rogers and J. C. Crocker, Direct measurements of DNA-mediated colloidal interactions and their quantitative modeling, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15687–15692 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, Vmd: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 Search PubMed.
- M. T. Casey, R. T. Scarlett, W. Benjamin Rogers, I. Jenkins, T. Sinno and J. C. Crocker, Driving diffusionless transformations in colloidal crystals using DNA handshaking, Nat. Commun., 2012, 3, 1209 CrossRef.
- J. Lowensohn, A. Hensley, M. Perlow-Zelman and W. B. Rogers, Self-assembly and crystallization of DNA-coated colloids via linker-encoded interactions, Langmuir, 2020, 36, 7100–7108 CrossRef PubMed.
- H. Xiong, D. van der Lelie and O. Gang, Phase behavior of nanoparticles assembled by DNA linkers, Phys. Rev. Lett., 2009, 102, 015504 CrossRef PubMed.
- R. J. Macfarlane, M. R. Jones, A. J. Senesi, K. L. Young, B. Lee, J. Wu and C. A. Mirkin, Establishing the design rules for DNA-mediated programmable colloidal crystallization, Angew. Chem., Int. Ed., 2010, 49, 4589–4592 CrossRef.
- B. A. Lindquist, R. B. Jadrich, M. P. Howard and T. M. Truskett, The role of pressure in inverse design for assembly, J. Chem. Phys., 2019, 151, 104104 CrossRef PubMed.
- A. Stukowski, Structure identification methods for atomistic simulations of crystalline materials, Modell. Simul. Mater. Sci. Eng., 2012, 20, 045021 CrossRef.
- P. M. Larsen, S. Schmidt and J. Schiotz, Robust structural identification via polyhedral template matching, Modell. Simul. Mater. Sci. Eng., 2016, 24, 055007 CrossRef.
- E. Maras, O. Trushin, A. Stukowski, T. Ala-Nissila and H. Jónsson, Global transition path search for dislocation formation in ge on si(001), Comput. Phys. Commun., 2016, 205, 13–21 CrossRef.
- Y. Ma, J. C. Aulicino and A. L. Ferguson, Inverse design of self-assembling diamond photonic lattices from anisotropic colloidal clusters, J. Phys. Chem. B, 2021, 125, 2398–2410 CrossRef.
- F. Romano and F. Sciortino, Patterning symmetry in the rational design of colloidal crystals, Nat. Commun., 2012, 3, 975 CrossRef PubMed.
- A. Hensley, W. M. Jacobs and W. B. Rogers, Self-assembly of photonic crystals by controlling the nucleation and growth of DNA-coated colloids, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2114050118 CrossRef.
- A. Jain, J. R. Errington and T. M. Truskett, Dimensionality and design of isotropic interactions that stabilize honeycomb, square, simple cubic, and diamond lattices, Phys. Rev. X, 2014, 4, 031049 Search PubMed.
- N. A. Mahynski, R. Mao, E. Pretti, V. K. Shen and J. Mittal, Grand canonical inverse design of multicomponent colloidal crystals, Soft Matter, 2020, 16, 3187–3194 RSC.
- D. Chen, G. Zhang and S. Torquato, Inverse design of colloidal crystals via optimized patchy interactions, J. Phys. Chem. B, 2018, 122, 8462–8468 CrossRef PubMed.
- E. M. King, C. X. Du, Q.-Z. Zhu, S. S. Schoenholz and M. P. Brenner, Programming patchy particles for materials assembly design, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2311891121 CrossRef.
- H. Liu, M. Matthies, J. Russo, L. Rovigatti, R. P. Narayanan, T. Diep, D. McKeen, O. Gang, N. Stephanopoulos, F. Sciortino, H. Yan, F. Romano and P. Šulc, Inverse design of a pyrochlore lattice of DNA origami through model-driven experiments, Science, 2024, 384, 776–781 CrossRef.
- A. Trubiano and M. Holmes-Cerfon, Thermodynamic stability versus kinetic accessibility: Pareto fronts for programmable self-assembly, Soft Matter, 2021, 17, 6797–6807 RSC.
- S. Chatterjee and W. M. Jacobs, Multiobjective optimization for targeted self-assembly among competing polymorphs, Phys. Rev. X, 2024, 15, 011075 Search PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2026 |


