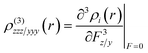Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Functionalization tuning of the nonlinear optical response of perylene diimide derivativatives
George
Skentzos
a,
Efrosyni
Pramatioti
a,
Nathalie
Zink-Lorre
 c,
Ana María
Gutiérrez-Vílchez
c,
Ana María
Gutiérrez-Vílchez
 c,
Eleni
Nikoli
c,
Eleni
Nikoli
 d,
Ruben
Canton-Vitoria
d,
Aggelos
Avramopoulos
d,
Ruben
Canton-Vitoria
d,
Aggelos
Avramopoulos
 *e,
Nikos
Tagmatarchis
*e,
Nikos
Tagmatarchis
 *d,
Fernando
Fernández-Lázaro
*d,
Fernando
Fernández-Lázaro
 *c and
Stelios
Couris
*c and
Stelios
Couris
 *ab
*ab
aDepartment of Physics, University of Patras, 26504 Patras, Greece. E-mail: couris@upatras.gr
bInstitute of Chemical Engineering Sciences (ICE-HT), Foundation for Research and Technology-Hellas (FORTH), Patras, 26504 Patras, Greece. E-mail: couris@iceht.forth.gr
cÁrea de Química Orgánica, Instituto de Bioingeniería, Universidad Miguel Hernández de Elche, Avda. de la Universidad s/n, Elche 03202, Spain. E-mail: fdofdez@umh.es
dTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, 48 Vassileos Constantinou Avenue, Athens 11635, Greece. E-mail: tagmatar@eie.gr
eLaboratory of Condensed Matter Physics, Department of Physics, University of Thessaly, 3rd Old National Road Lamia-Athens, Lamia 35131, Greece. E-mail: aavramopoulos@uth.gr
First published on 16th December 2025
Abstract
The synthesis and characterization of perylene diimide (PDI) derivatives functionalized by electron donating groups at their bay and imide positions have been reported. Five different PDI derivatives were synthesized and their linear optical and third-order non-linear optical (NLO) properties were studied. The NLO measurements of the synthesized PDI derivatives were conducted under nanosecond (ns) and femtosecond (fs) laser excitation conditions, using the Z-scan technique employing 4 ns, 1064/532 nm and 70 fs, 800/400 nm laser pulses. A noticeable tuning of the NLO character between the synthesized PDI derivatives was observed, revealing the importance of the functionalization of the PDI core by the anchored electron donating units. The largest NLO value was achieved by the incorporation of p-aminoazobenzene at the PDI bay position. The experimental NLO findings and trends were further corroborated with theoretical computations of UV-Vis spectra and NLO response, performed using density functional theory (DFT). It was found that both experiments and simulations satisfactorily convey changes in the NLO response between the studied PDI derivatives. The mechanism that could lead to an efficient tuning of the PDIs' NLO response, is associated with the modification of their electronic character resulting by the proper PDI core functionalization.
Introduction
Perylene diimide (PDI) derivatives represent a versatile family of dyes, renowned for their synthetic adaptability and easily modifiable electronic character.1,2 Indeed, these derivatives have emerged as highly promising molecular materials in organic optoelectronic applications, owing to their tunability and exceptional photophysical properties.3–6 A plethora of PDI derivatives have been deployed for electronics and light-harvesting applications owing to their exceptional stability, strong fluorescence and broad absorption.7–10 Their large two-photon absorption (TPA) cross-section11 makes them ideal NLO materials as well.12,13 Conversely, azobenzenes, belonging to the wider class of diazenes, are π-conjugated compounds composed of two phenyl rings linked by a nitrogen–nitrogen double bond (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), with easily, precisely and facilely adjusted properties via derivatization and incorporation of various functional groups at the phenyl rings.14 For example, different substituents at the phenyl ring of azobenzenes alter the absorption profile, which can be shifted from the UV-Vis to the NIR region of the electromagnetic spectrum. The incorporation of electron donating amine groups at the para-position of the phenyl ring, such as in azoanilines, red-shifts the absorption in comparison with the unsubstituted azobenzene, while, on the other hand, extension of the π-conjugated skeleton enhances the TPA properties.15 Notably, azobenzenes have been employed as ligands for chromophores, such as triarylamines16 and pyrenes,17 among others, enabling the tuning of the NLO properties.
N), with easily, precisely and facilely adjusted properties via derivatization and incorporation of various functional groups at the phenyl rings.14 For example, different substituents at the phenyl ring of azobenzenes alter the absorption profile, which can be shifted from the UV-Vis to the NIR region of the electromagnetic spectrum. The incorporation of electron donating amine groups at the para-position of the phenyl ring, such as in azoanilines, red-shifts the absorption in comparison with the unsubstituted azobenzene, while, on the other hand, extension of the π-conjugated skeleton enhances the TPA properties.15 Notably, azobenzenes have been employed as ligands for chromophores, such as triarylamines16 and pyrenes,17 among others, enabling the tuning of the NLO properties.
With the aforementioned aspects in mind and the rich chemistry of PDIs, which enables their seamless combination with target components, incorporation of azobenzenes in the structure of PDIs is of significant importance. PDI derivatives, among other organic materials,18,19 have been shown to be promising organic materials for NLO applications,13 because of their planar π-aromatic character, their strong electron withdrawing ability (n-type character) and their strong intramolecular charge transfer ability. Moreover, it has also been proved that modification of their ortho, or bay positions can significantly modify their optical and electronic properties, while substitution at the imide position leads to negligible changes due to the existence of nodes at the nitrogen atoms in both HOMO and LUMO orbitals, which electronically decouple the aromatic core from the imide substituents.1,20,21
While the NLO performance of PDI derivatives has been well documented,7,22–25 the combination of the NLO properties of PDI with those of azobenzene and the investigation of the electronic modifications by targeting different functionalization positions of the perylene framework are yet to be realized. The present study aims to provide new knowledge about these aspects, by combining experimental measurements and theoretical calculations, on how functionalization of some newly synthesized PDIs with electron donating units, like azobenzene, tunes their optical characteristics and their third-order non-linear optical properties.
Results and discussion
A. Synthesis and characterization of PDI derivatives A–E
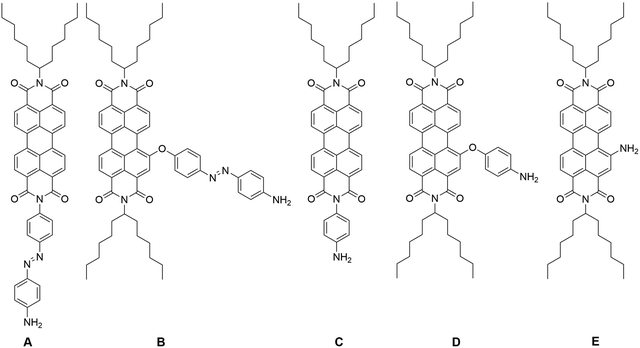
To start with, five different PDI derivatives A–E were targeted (Fig. 1). Azobenzene functionalization of PDI at the imide position, resulting in PDI derivative A, allows the study of the NLO properties of a system composed of two electronically decoupled moieties (vide supra). Functionalization at the bay position of PDI with azobenzene species additionally enhances the aromatic conjugation in PDI derivative B, which may lead to increased TPA.15 The presence of the ether function allows preserving a certain degree of coplanarity between the PDI core and the azobenzene (vide infra), while a C–C direct linkage of PDI and azobenzene would lead to an orthogonal disposition of both moieties, thus disrupting the electronic communication between subunits. Both of these modifications are highly advantageous for various NLO applications. Furthermore, other moieties that extend the aromatic conjugation of perylene, such as a phenyl group at the imide position, yielding PDI derivative C, or at the bay position, furnishing PDI derivative D, as well as incorporating electron-donating amine, yielding PDI derivative E, have also been targeted. Consequently, the overall effects on the NLO properties of PDI and azobenzene can be effectively differentiated, based on (a) the type of the electron-donating groups, (b) the degree of aromatic conjugation, and (c) the PDI functionalization position.The synthesis of compounds A and B is illustrated in Scheme 1. Briefly, condensation of 4-[(4-nitrophenyl)diazenyl]aniline26 with N-(hexylheptyl)perylene-3,4-dicarboxyanhydride-9,10-dicarboxyimide, in the presence of imidazole, affords the intermediate diimide in 32% yield, which was subsequently reduced with sodium sulfide to afford PDI derivative A in 42% yield. On the other hand, PDI derivative B was obtained from N,N′-di(hexylheptyl)-1-bromoperylene-3,4:9,10-tetracarboxydiimide27 and the corresponding Boc-protected aminoazophenol in 17% yield. Interestingly, the Boc protective group was spontaneously removed during the purification process, resulting in the direct formation of the final compound. Full experimental details for the synthesis of PDI derivatives A and B are given in the SI, together with the 1H- and 13C-NMR spectra and HR-mass spectrometry data (Fig. S1–S9). The synthesis of PDI derivatives C, D and E was conducted following literature procedures.28–30
B. Experimental investigation of the NLO response of PDI derivatives A–E
The NLO response of PDI derivatives A–E was studied under nanosecond (ns) and femtosecond (fs) laser excitation conditions, using the Z-scan technique,31,32 employing 4 ns, 1064/532 nm and 70 fs, 800/400 nm laser pulses, respectively. The details concerning the Z-scan technique and the laser sources used are given in the SI.UV-Vis absorption spectra of PDI derivatives A–E
The UV-Vis absorption spectra of PDI derivatives A–E were studied both experimentally and theoretically. For this, the electronic absorption spectra of different concentrations of PDIs A–E were measured and compared with the calculated ones.Experimental investigation. In Fig. 2, some representative UV-Vis absorption spectra of the PDI derivatives A–E dissolved in DMF are depicted (for comparison purposes, all have the same concentration of 0.25 mg mL−1). As can be seen, the absorption spectrum of PDI A is dominated by three strong absorption bands, located at 527, 491 and 460 nm (corresponding to the (0,0), (0,1), and (0,2) electronic transitions, respectively) and a broad absorption band at 404 nm; a similar structure is observed in the UV-Vis spectra of PDI derivatives B–D, with the position and the broadening of each absorption band depending on the nature of the substituent and/or the position of anchoring. For example, substitution with electron donating groups at the bay area of PDI results in red-shifting of the absorption bands due to electronic interactions between the perylene skeleton and the electron donating moieties (compare, e.g., derivative Avs.B, and Cvs.D).33 So, in the case of B, these bands are red-shifted compared to those of A, appearing at 531, 501, 463 and 408 nm, respectively; in the case of C, the corresponding bands are observed at 525, 489 and 459 nm, while for D they appear at 546, 510 and 477 nm (weak shoulder), respectively. Lastly, PDI derivative E exhibits two broad absorption bands at 607 and 423 nm and two weaker absorption bands at 403 and 388 nm.
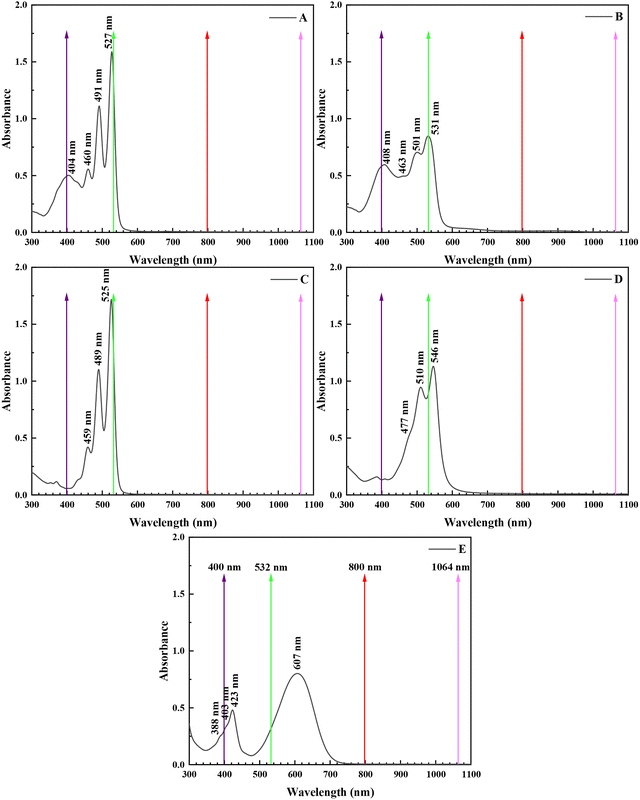 | ||
| Fig. 2 UV-Vis absorption spectra of PDI derivatives A–E obtained in DMF at a concentration of 0.25 mg mL−1. The colored arrows indicate the wavelengths where laser excitation took place. | ||
Theoretical analysis. The UV-Vis absorption spectra of the PDI derivatives A–E were also recorded. The transition energies were computed by employing the time-dependent density functional theory (TD-DFT),34 using the CAM-B3LYP functional, which is known for the satisfactory estimation of the transition energies of other organic dyes, compared with the experimental results.35,36 The effect of DMF as a solvent was computed using the polarizable continuum model.37 All the reported DFT calculations have been performed by using the Gaussian 16 software.38 The obtained results are shown in Table 1. For comparison purposes, the UV-Vis absorption spectra of perylene, p-NH2Azo molecules, unsubstituted PDI, and N,N′-di(hexylheptyl) PDI were also computed.
| Compound | λ (nm)/f | Description |
|---|---|---|
| a Experimental value.15 b Experimental value (see Fig. 2). | ||
| Perylene | 424.5/0.755 | S0 → S1 |
| HOMO → LUMO (99%) | ||
| Unsubstituted PDI | 511.7/1.234 | S0 → S1 |
| HOMO → LUMO (99%) | ||
| 322.79/0.325 | S0 → S3 | |
| HOMO−2 → LUMO (84%) | ||
| N,N′-Di(hexylheptyl) PDI | 512.9/1.288 | S0 → S1 |
| HOMO → LUMO (99%) | ||
| 322.60/0.272 | S0 → S3 | |
| HOMO−2 → LUMO (79%) | ||
| p-NH2Azo | 389.7/1.195 (370)a | S0 → S1 |
| HOMO → LUMO (99%) | ||
| PDI derivative A | 513.2/1.409 (527)b | S0 → S1 |
| HOMO−1 → LUMO (98%) | ||
| 395.04/1.238 (404)b | S0 → S3 | |
| HOMO → LUMO+1 (94%) | ||
| PDI derivative B | 515.8/1.325 (531)b | S0 → S1 |
| HOMO−1 → LUMO (89%) | ||
| HOMO → LUMO (8%) | ||
| 400.8/1.344 (408)b | S0 → S3 | |
| HOMO → LUMO+1 (69.6%) | ||
| HOMO → LUMO (15.7%) | ||
| PDI derivative C | 512.7/1.322 (525)b | S0 → S1 |
| HOMO−1 → LUMO (99%) | ||
| 322.3/0.265 | S0 → S4 | |
| HOMO−4 → LUMO (79%) | ||
| PDI derivative D | 524.9/1.298 (546)b | S0 → S1 |
| HOMO → LUMO (67%) | ||
| HOMO−1 → LUMO (29%) | ||
| 350.1/0.200 | S0 → S3 | |
| HOMO−2 → LUMO (79%) | ||
| PDI derivative E | 567.9/1.003 (607)b | S0 → S1 |
| HOMO → LUMO (98%) | ||
| 376.1/0.374 | S0 → S2 | |
| HOMO−1 → LUMO (85%) | ||
As can be seen in this table, there is a reasonable agreement between the theoretical and experimental excitation energies. The theoretical results reproduce satisfactorily the experimentally observed strong absorption peaks at ca. 530 nm (for A, B and C), the small red shift for D and the larger red shift for E, compared with A, B and C. Similarly, in agreement with the experimental observations, TD-DFT computations show high oscillator strength at ca. 400 nm for A and B, and smaller values for E, D, and C. In order to describe the nature of the process, a description of the involved states and their percentage contribution is given in Table 1. In Fig. S10, the frontier molecular orbitals of PDI A–E involved in the main absorption process are also depicted. As presented, for most of the studied PDIs, the two highest occupied orbitals (HOMO−1 and HOMO) and the two lowest unoccupied orbitals (LUMO and LUMO+1) appear during the single excitation transition process (Fig. S10). So, the results show that the p-NH2Azo group is responsible for the high absorption at ca. 400 nm, found for A and B. By considering the wavelength of the first allowed electronic transition of unsubstituted PDI and N,N′-di(hexylheptyl) PDI, it is ascertained that the absorptions of A, B, and C, determined experimentally at 532 nm, are attributed to the absorption of the PDI π-network. In addition, the incorporation of the two imide units in perylene induces a red shift, ca. 86 nm, to the absorption wavelength, resulting in a more intense HOMO → LUMO transition.
Nonlinear optical response of PDI derivatives A–E
The NLO response of the PDIs A–E was systematically investigated under 4 ns, 532/1064 nm and 70 fs, 800/400 nm laser excitation conditions. For the accurate determination of the different NLO parameters (i.e., the nonlinear absorption coefficient β (and the related Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)), the nonlinear refractive index parameter γ′ (and the related Re
χ(3)), the nonlinear refractive index parameter γ′ (and the related Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)) and the magnitude of the third-order nonlinear susceptibility χ(3)), solutions of the PDIs of different concentrations in DMF were prepared and studied under various laser intensities. For each PDI derivative A–E, special care was taken to maintain the absorbance of the system, at each excitation wavelength, low enough to satisfy the “thin sample approximation” condition, ensuring the validity of the Z-scan technique approximations and therefore the analysis of the Z-scan data. In addition, since Im
χ(3)) and the magnitude of the third-order nonlinear susceptibility χ(3)), solutions of the PDIs of different concentrations in DMF were prepared and studied under various laser intensities. For each PDI derivative A–E, special care was taken to maintain the absorbance of the system, at each excitation wavelength, low enough to satisfy the “thin sample approximation” condition, ensuring the validity of the Z-scan technique approximations and therefore the analysis of the Z-scan data. In addition, since Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) and Re
χ(3) and Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) depend on the concentration of PDI, they were normalized by the corresponding concentration, c, of each solution, providing the Im
χ(3) depend on the concentration of PDI, they were normalized by the corresponding concentration, c, of each solution, providing the Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c and Re
χ(3)/c and Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c values, allowing for easier comparisons. Along the same lines, from the determined values of χ(3) and the known concentration of the samples, the second hyperpolarizability γ of each PDI was calculated, providing the nonlinear optical response per molecule. In addition, for comparison purposes, and for calibration of the experimental setups, a C60-toluene solution, and DMF and toluene, were used for the ns and fs Z-scan measurements, respectively, and the details are given in the SI section. The experimental findings and the determined NLO parameters, for all the excitation conditions employed, are presented in the following.
χ(3)/c values, allowing for easier comparisons. Along the same lines, from the determined values of χ(3) and the known concentration of the samples, the second hyperpolarizability γ of each PDI was calculated, providing the nonlinear optical response per molecule. In addition, for comparison purposes, and for calibration of the experimental setups, a C60-toluene solution, and DMF and toluene, were used for the ns and fs Z-scan measurements, respectively, and the details are given in the SI section. The experimental findings and the determined NLO parameters, for all the excitation conditions employed, are presented in the following.
NLO response of PDI derivatives A–E, under 4 ns, 1064/532 nm laser excitation
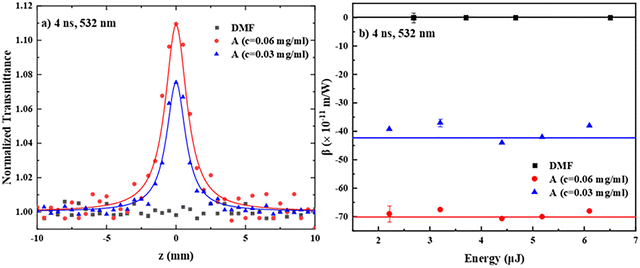
First, the nonlinear absorption of the different PDIs under 4 ns, 532 nm excitation is discussed. In Fig. 3a, some representative open aperture (OA) Z-scans of two different concentrations of PDI derivative A (0.03 and 0.06 mg mL−1) in DMF and the neat solvent, all measured under identical experimental conditions, are illustrated. The solid symbols correspond to the experimental data points, while the continuous lines represent the fitting of the experimental data by eqn (S1). As shown, DMF exhibited a negligible NLO response for the range of laser intensities employed. Therefore, the OA Z-scans of the solutions, which are shown in Fig. 3a, reveal the nonlinear absorption of PDI A straightforwardly, exhibiting a transmission maximum, indicating saturable absorption (SA) behavior (corresponding to a negative sign nonlinear absorption coefficient β, i.e., β < 0). The observed SA behavior is attributed to the resonant excitation conditions occurring, resulting in efficient depletion of the ground state and Pauli blocking mechanism39,40 (see also the absorption spectrum of PDI derivative A in Fig. 2). Similar Z-scan recordings were obtained for the other PDI derivatives, all exhibiting SA behavior (Fig. S11a). From the fitting of the Z-scan recordings with eqn (S1), the β value of each concentration of PDI derivative A in DMF was determined, and then the corresponding values of Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) were calculated using eqn (S4). In Fig. 3b, the dependence of the β values (of PDI derivative A in DMF shown in Fig. 3a) on the incident laser energy is presented. As shown, they were all found not to vary with the laser energy (within the experimental error), as expected for a third-order NLO process, and to scale linearly with the concentration. Similar results were obtained for PDI derivatives B–E (Fig. S11c). The determined values of β, Im
χ(3) were calculated using eqn (S4). In Fig. 3b, the dependence of the β values (of PDI derivative A in DMF shown in Fig. 3a) on the incident laser energy is presented. As shown, they were all found not to vary with the laser energy (within the experimental error), as expected for a third-order NLO process, and to scale linearly with the concentration. Similar results were obtained for PDI derivatives B–E (Fig. S11c). The determined values of β, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) and Im
χ(3) and Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c of all the different concentrations of the PDIs studied are presented in Table S1, while, for simplicity, Table 2 presents only the average values of Im
χ(3)/c of all the different concentrations of the PDIs studied are presented in Table S1, while, for simplicity, Table 2 presents only the average values of Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c of the PDIs of different concentrations. In addition, the wavelength of the S0–1 transition and the ground state absorption cross-section of each PDI derivative are also listed in Table 2.
χ(3)/c of the PDIs of different concentrations. In addition, the wavelength of the S0–1 transition and the ground state absorption cross-section of each PDI derivative are also listed in Table 2.
| Compounds | S0–1 transition (nm)/ground state absorption cross-section (×10−19 cm2 mol−1) | Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−13 esu mL mg−1) χ(3)/c (×10−13 esu mL mg−1) |
Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−13 esu mL mg−1) χ(3)/c (×10−13 esu mL mg−1) |
χ (3)/c (×10−13 esu mL mg−1) | γ (× 10−34 esu) |
|---|---|---|---|---|---|
| PDI derivative A | 527/1.56 | −705 ± 75 | −2040 ± 210 | 2158 ± 224 | 832 ± 86 |
| PDI derivative B | 531/1.25 | −256 ± 26 | −1744 ± 122 | 1764 ± 126 | 856 ± 61 |
| PDI derivative C | 525/1.30 | −509 ± 55 | −2115 ± 239 | 2177 ± 247 | 726 ± 82 |
| PDI derivative D | 546/1.18 | −297.7 ± 28 | −1557 ± 188 | 1584 ± 191 | 686 ± 82 |
| PDI derivative E | 607/0.36 | −146 ± 14 | −549 ± 67 | 569 ± 68 | 220 ± 26 |
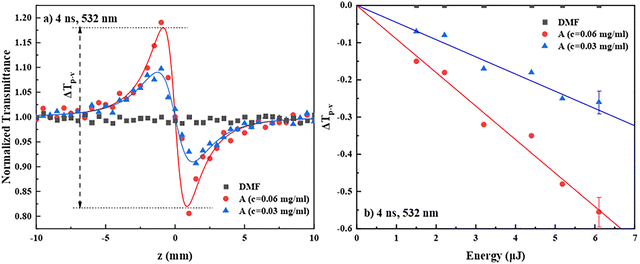
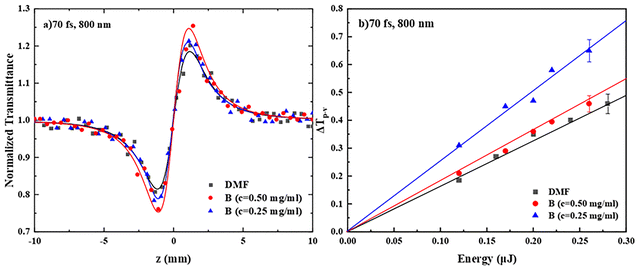
Regarding the nonlinear refraction (NLR) of the PDI derivatives A–E, some representative “divided” Z-scan recordings of two different concentrations of PDI derivative A are presented in Fig. 4a. As can be seen, they exhibited a peak-valley transmittance configuration, indicative of self-defocusing behavior (corresponding to a negative sign nonlinear refractive index parameter γ′, i.e., γ′ < 0). The continuous lines correspond to the fitting of the experimental data (solid points) by eqn (S2). Since the solvent, DMF, exhibited negligible nonlinear refraction, the Z-scans of the solutions reveal the nonlinear refractive response of PDI derivative A directly. In Fig. 4b, the dependence of the values of the ΔTp–v parameter (see, e.g., Fig. 4a) of the two solutions on the incident laser energy is shown. As can be seen, a linear dependence of ΔTp–v on the laser energy was found in both cases, i.e., a typical behavior for a third-order NLO process. All PDIs were found to exhibit the same sign nonlinear refractive response, i.e., self-defocusing (γ′ < 0) (see Fig. S11b and d). From the slopes of the continuous straight lines of Fig. 4b, the values of γ′ and Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) were determined, using eqn (S3) and (S5), respectively, and then the values of Re
χ(3) were determined, using eqn (S3) and (S5), respectively, and then the values of Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c were calculated using the known concentration of the solutions. The average values of Re
χ(3)/c were calculated using the known concentration of the solutions. The average values of Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c, χ(3)/c and γ of PDIs A–E are summarized in Table 2, while the values of γ′, Re
χ(3)/c, χ(3)/c and γ of PDIs A–E are summarized in Table 2, while the values of γ′, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3), Re
χ(3), Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c, χ(3)/c and γ of the different concentration solutions of PDIs studied are presented in Table S1. To understand the NLR response of the different PDI derivatives, several mechanisms can be evoked, the contribution of each depending on the laser pulse duration and the laser intensity used. So, in general, instantaneous bound-electronic response (i.e., Kerr-type nonlinearity) or other non-instantaneous contributions, such as molecular reorientation, thermal effects and free carrier refraction, can be responsible for the observed NLR response. However, under the present 4 ns resonant excitation conditions at 532 nm (see also the absorption spectra in Fig. 2), thermal effects should be, most probably, the dominant mechanism resulting in the observed self-defocusing NLR response.39,40
χ(3)/c, χ(3)/c and γ of the different concentration solutions of PDIs studied are presented in Table S1. To understand the NLR response of the different PDI derivatives, several mechanisms can be evoked, the contribution of each depending on the laser pulse duration and the laser intensity used. So, in general, instantaneous bound-electronic response (i.e., Kerr-type nonlinearity) or other non-instantaneous contributions, such as molecular reorientation, thermal effects and free carrier refraction, can be responsible for the observed NLR response. However, under the present 4 ns resonant excitation conditions at 532 nm (see also the absorption spectra in Fig. 2), thermal effects should be, most probably, the dominant mechanism resulting in the observed self-defocusing NLR response.39,40
For the investigation of the NLO response of the PDI derivatives A–E under 4 ns, 1064 nm laser excitation, similar Z-scan experiments were conducted using the fundamental laser output at 1064 nm. However, although much higher concentrations were used (e.g., up to ∼1 mg mL−1) and higher laser energies were employed (e.g., up to 40 µJ), all PDIs exhibited negligible nonlinear absorption and refraction, suggesting a negligible NLO response under 1064 nm excitation.
From the inspection of the determined values of the NLO parameters of the PDIs listed in Table 2, it is evident that they all exhibit sizeable NLO response under 4 ns, 532 nm excitation. In particular, A and B exhibited the largest, and of similar magnitude (within the experimental error), χ(3)/c and second hyperpolarizability γ values. On the other hand, C and D, having also very similar NLO responses, exhibited relatively lower NLO responses compared to A and B, while E exhibited the lowest NLO response among the PDI derivatives studied. The evaluation of these results and the consideration of the absorption spectra of the different PDI derivatives suggest that the NLO response under 4 ns, 532 nm laser excitation is largely determined by the resonant character of the excitation at this wavelength (see also Fig. 2) and from the ground state absorption cross-section of each PDI as well. So, PDI derivatives A, B, C and D exhibited the largest NLO response, as their excitation at 532 nm is practically full resonant with the corresponding S0-1 electronic transition located at 527, 531, 525 and 546 nm, respectively (see also Fig. 2). In contrast, in the case of PDI derivative E, where the corresponding absorption band is red shifted at 607 nm, the resonant excitation conditions are only partially met (due to the large broadening of this absorption band). Therefore, qualitatively, the closer the laser excitation occurs to the S0-1 transition, the stronger the NLO response of the PDI. Another parameter that should also be considered is the ground state absorption cross-section σ at 532 nm. In that view, from the absorbance and the concentration of each PDI derivative, the extinction coefficient ε, at 532 nm, was determined, and the corresponding σ value was calculated. So, the ground state absorption cross-section σ values for the various PDI derivatives were found to be as follows: A: 1.56, B: 1.25, C: 1.30, D: 1.18, and E: 0.36 (in units of 10−20 cm2 mol−1). It is worth noting that PDI derivative E exhibits the lowest absorption cross-section.
Another interesting finding, resulting from the above results, concerns the influence of the type of anchored group on the PDI core. So, the anchoring of the p-aminoazobenzene group (i.e., PDIs A and B) was found to result in a larger NLO response than that of aniline (i.e., PDIs C and D) or amino (i.e., PDI E) groups. Interestingly, the place of substitution (i.e., at the imide- or bay-position) seems to have a weaker effect on the NLO response.
NLO response of PDI derivatives A–E, under 70 fs, 800/400 nm laser excitation
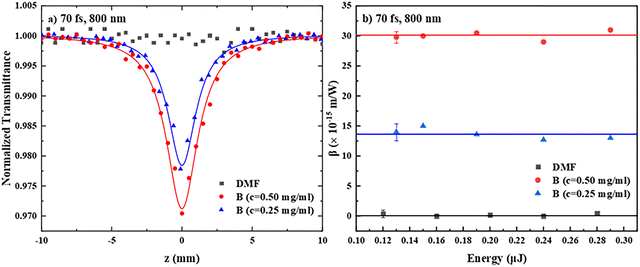
Next, the results concerning the NLO response of the PDI derivatives A–E under 70 fs laser excitation are presented. In this case, the excitation was performed at 800 and 400 nm, in order to study the influence of the non-resonant and resonant excitation conditions, respectively, on the NLO response of the various PDIs.Some representative OA Z-scans of two different concentrations of PDI derivative B in DMF (0.25 and 0.50 mg mL−1) and the neat solvent are presented in Fig. 5a. As shown, DMF exhibited negligible nonlinear absorption. So, the OA Z-scans of the solutions reveal the nonlinear absorption behavior of B, i.e., a transmission minimum, straightforwardly, indicating reverse saturable absorption (RSA) behavior (corresponding to a positive sign nonlinear absorption coefficient β, β > 0). From the absorption spectrum of B (see, e.g., Fig. 2), it can be easily seen that excitation at 800 nm is not resonant with any absorption band; however, when considering the high intensity of the fs laser excitation, TPA becomes very probable and readily occurs; this TPA process is further assisted by the presence of the 400 nm absorption band, which can be attained by the absorption of two photons. Based on these experimental findings, the observed RSA behavior can be attributed to TPA, as has been discussed in detail elsewhere.39 In Fig. 5b, the variation of the β values of the two concentration solutions of PDI derivative B, as shown in Fig. 5a, with the laser energy is depicted. As shown, they were found to be independent of the incident laser energy and scaling linearly with the concentration of B. Similar experiments were performed using different concentrations of A, C, D and E, all in DMF, revealing that all PDI derivatives exhibit RSA behaviour as well (Fig. S12a and c). From the OA Z-scans, the nonlinear absorption coefficient β of each sample was determined following the same procedure as for the analysis followed for the ns measurements. Then, from the determined values of β, the corresponding TPA cross-section of each PDI was calculated, using eqn (S8). The obtained values of Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c and the TPA cross-section at 800 nm of all PDIs A–E are summarized in Table 3; the values of β, Im
χ(3)/c and the TPA cross-section at 800 nm of all PDIs A–E are summarized in Table 3; the values of β, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3), and Im
χ(3), and Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c of all the different concentration solutions studied are presented in Table S2.
χ(3)/c of all the different concentration solutions studied are presented in Table S2.
| λ exc (nm) | Compounds | TPA cross-section (×10−47 m4 s per photon molecule) | Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−16 esu mL mg−1) χ(3)/c (×10−16 esu mL mg−1) |
Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−16 esu mL mg−1) χ(3)/c (×10−16 esu mL mg−1) |
χ (3)/c (×10−16 esu mL mg−1) | γ (× 10−37 esu) |
|---|---|---|---|---|---|---|
| 800 | PDI derivative A | 13.0 ± 1.0 | 21.6 ± 1.2 | — | 21.7 ± 1.2 | 8.4 ± 0.3 |
| PDI derivative B | 22.0 ± 2.0 | 29.4 ± 2.7 | 1.5 ± 0.3 | 30.0 ± 2.1 | 14.4 ± 1.1 | |
| PDI derivative C | 5.8 ± 0.5 | 9.4 ± 1.2 | — | 10.8 ± 1.6 | 3.6 ± 0.5 | |
| PDI derivative D | 11.0 ± 2.0 | 15.8 ± 1.8 | — | 15.8 ± 1.8 | 6.8 ± 1.0 | |
| PDI derivative E | 12.0 ± 0.6 | 18.6 ± 0.6 | — | 18.6 ± 2.1 | 7.3 ± 0.8 |
| λ exc (nm) | Compounds | Ground state absorption cross-section (×10−19 cm2 mol−1) | Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−16 esu mL mg−1) χ(3)/c (×10−16 esu mL mg−1) |
Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c (×10−16 esu mL mg−1) χ(3)/c (×10−16 esu mL mg−1) |
χ (3)/c (×10−16 esu mL mg−1) | γ (× 10−37 esu) |
|---|---|---|---|---|---|---|
| 400 | PDI derivative A | 0.52 | −16.8 ± 0.8 | 87.5 ± 4.6 | 88.7 ± 4.2 | 34.2 ± 1.6 |
| PDI derivative B | 0.94 | −32.5 ± 4.2 | 109.4 ± 8.8 | 119.0 ± 10.1 | 57.8 ± 5.1 | |
| PDI derivative C | 0.04 | −2.2 ± 0.1 | 5.0 ± 0.8 | 6.2 ± 0.8 | 2.0 ± 0.2 | |
| PDI derivative D | 0.17 | −3.4 ± 1.1 | 14.1 ± 0.8 | 14.4 ± 1.4 | 6.1 ± 0.6 | |
| PDI derivative E | 0.26 | −21.1 ± 1.0 | 21.2 ± 4.9 | 29.9 ± 3.5 | 11.6 ± 1.3 |
Next, the results concerning the nonlinear refraction of PDI derivatives A–E under 70 fs, 800 nm excitation are presented and discussed. So, in Fig. 6a, the “divided” Z-scans of the two different concentrations of B shown in Fig. 5a are presented, as an example; they were both found to exhibit a valley-peak transmittance configuration, indicative of self-focusing behavior (corresponding to a positive nonlinear refractive parameter γ′, γ′ > 0). However, similar measurements of neat DMF, performed under identical experimental conditions, have shown that it exhibited significant nonlinear refraction (see, e.g., black line in Fig. 6a) of positive sign (i.e., self-focusing), as well. Therefore, for the determination of the nonlinear refractive index parameter γ′ of the PDIs, DMF's contribution was considered accordingly. More experiments performed on different concentrations of PDIs A, C, D and E have shown that the corresponding “divided” Z-scans were indistinguishable from those of neat DMF (see also Fig. S12b and d). This situation was further confirmed employing up to ten times higher concentrations of A, C, D and E (i.e., up to 2.5 mg mL−1) in DMF. So finally, only the nonlinear refraction of B was possible to be determined accurately.
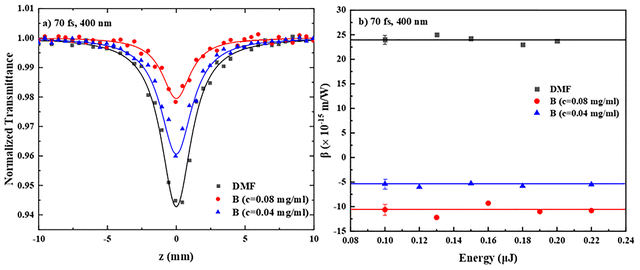
In Fig. 7a, some representative OA Z-scans of two different concentrations of PDI derivative B (0.04 and 0.08 mg mL−1) in DMF and the neat solvent, obtained under 400 nm excitation, are presented. In this case, DMF had a significant NLO response, exhibiting a transmission minimum, indicative of RSA behavior (i.e., β > 0), while all PDIs’ solutions were found to exhibit a smaller transmission minimum, revealing opposite sign nonlinear absorption, i.e., SA. In fact, all PDIs exhibited similar behavior, i.e., negative nonlinear absorption coefficient, β < 0 (see, e.g., Fig. S13a and b). For the accurate determination of the nonlinear absorption coefficient β of A–E, the contribution of DMF was considered accordingly. The variation of the determined β values of the two concentrations of B, as shown in Fig. 7a, with the incident laser energy is presented in Fig. 7b. As can be seen, the β values of the two solutions were found to be independent of the incident laser energy and scaling linearly with the concentration. The average values of Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c of the different concentrations of A–E are summarized in Table 3, while the values of β, Im
χ(3)/c of the different concentrations of A–E are summarized in Table 3, while the values of β, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) and Im
χ(3) and Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c of the different concentrations of the PDIs studied are presented in Table S2.
χ(3)/c of the different concentrations of the PDIs studied are presented in Table S2.
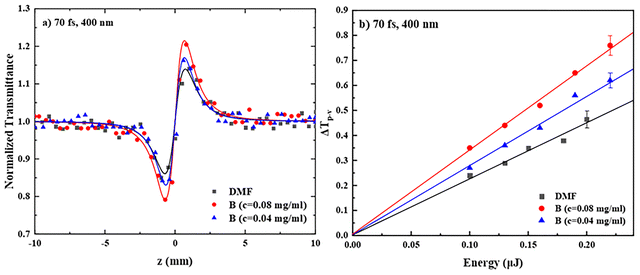
Concerning the nonlinear refraction of PDI derivatives A–E under 400 nm laser excitation, the corresponding “divided” Z-scans were found to exhibit a valley-peak transmittance configuration, indicative of self-focusing behavior (corresponding to a positive nonlinear refractive parameter γ′, γ′ > 0). As an example, the “divided” Z-scans of the two different concentrations of B (of Fig. 7a) in DMF are shown in Fig. 8a. Separate measurements of neat DMF, under identical experimental conditions, have shown that it also exhibits a positive sign nonlinear refraction (i.e., self-focusing). Therefore, for the determination of the nonlinear refractive index parameter γ′, the solvent's contribution was considered accordingly. In Fig. 8b, the variation of the ΔTp–v values of the two different concentrations of B in DMF and neat DMF, as a function of the incident laser energy, is shown. As can be seen, ΔTp–v was found to vary linearly with the incident laser energy, in agreement with a third-order nonlinear optical process. Similar behavior was found for PDIs A, C, D and E (see Fig. S14c and d). Then, the values of γ′ and Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3) were determined using eqn (S3) and (S5), respectively, and the corresponding values of Re
χ(3) were determined using eqn (S3) and (S5), respectively, and the corresponding values of Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c were calculated using the known concentration of each solution. In Table 3, the average values of Re
χ(3)/c were calculated using the known concentration of each solution. In Table 3, the average values of Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c and χ(3)/c of each PDI are presented; the γ′, Re
χ(3)/c and χ(3)/c of each PDI are presented; the γ′, Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3), Re
χ(3), Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(3)/c, χ(3)/c and γ values of the different concentrations studied are summarized in Table S2. Regarding the origin of the NLO refraction of the PDI derivatives under fs excitation, this can be attributed to the instantaneous bound-electronic response of the molecules (i.e., Kerr-type nonlinearity).41
χ(3)/c, χ(3)/c and γ values of the different concentrations studied are summarized in Table S2. Regarding the origin of the NLO refraction of the PDI derivatives under fs excitation, this can be attributed to the instantaneous bound-electronic response of the molecules (i.e., Kerr-type nonlinearity).41
C. Theoretical study of second hyperpolarizability of PDI derivatives A–E
In order to investigate the effect of the structural alterations of the PDI derivatives A–E on their NLO response (structure–property relationship), the static and frequency-dependent electronic second hyperpolarizabilities, γ(0;0,0,0) and γ(−ω;ω,−ω,ω) (hereinafter referred to as γ(0) and γ(ω), respectively), were computed.Computational methods
The energy E(F) of a molecule, placed in a uniform electric field, is given by the following equation:| E(F) = E0 − μiFi − αijFiFj − βijFiFjFk − γijklFiFjFkFl | (1) |
For the computation of the second hyperpolarizability (γ), the following equation was used:
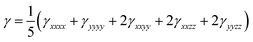 | (2) |
All the static electronic hyperpolarizability components, γijkl, have been computed by employing finite field techniques,42 using eqn (1), by applying a step field (F) of 0.0008 a.u. To ensure the numerical stability, the Romberg method has been used to calculate the (hyper)polarizabilities (γiiii),43,44 by employing field strengths of magnitude 2mF, where m = 0–4 and base field = 0.0002 a.u. For all computations, the energy was converged to 10−11 a.u. The reported hyperpolarizability data have been computed by employing the CAM-B3LYP functional,45 where the latter accounts for the long-range corrections, in connection with the 6-311G and 6-311+G* basis sets. It should be noted that these methods have provided satisfactory hyperpolarizability values for several related compounds.46
All PDI derivatives A–E have been optimized by using the M062-X functional,47 in connection with the 6-311G basis set. This functional has been shown to predict the geometries of π-conjugated systems satisfactorily, due to the appropriate amount (54%) of the included HF exchange.48 Vibrational analysis was employed to confirm that the computed structures correspond to a minimum on the potential energy surface. To all reported hyperpolarizability computations, the structures have been rotated so that their dipole moment coincides with the z-axis. The effect of DMF as a solvent on the static electronic (hyper)polarizabilities was computed using the polarizable continuum model.35 All the reported DFT second hyperpolarizability calculations have been performed by using the Gaussian 16 software.38 For the case of PDI derivatives A–E, the frequency-dependent second hyperpolarizability (γ(−ω;ω,−ω,ω)) for ω = 0.0569 a.u. (λ = 800 nm) has also been calculated with the aid of cubic response functions, as are implemented in the DALTON software.49
As shown in Table 4, although the static hyperpolarizabilities correspond to an excitation frequency, ω → 0, their computation is very useful for a relative and meaningful comparison of γ changes between the different PDIs, since they are good approximations to the values of the dynamic hyperpolarizabilities, in the case of off-resonant excitation. In that context, the present calculations are used to address and shed light on the different issues for the better understanding of the experimental second hyperpolarizability data obtained for PDI derivatives A–E.
Theoretical analysis
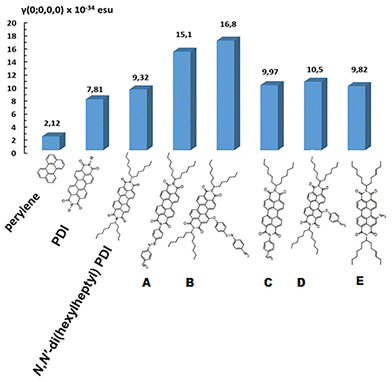
In Fig. 9, the results of γ(0) for PDI derivatives A–E, computed with the CAM-B3LYP/6-311+G* method, are depicted. For comparison, the γ(0) values of perylene, unsubstituted PDI, and N,N′-di(hexylheptyl) PDI are also shown.Electronic second hyperpolarizability γ
In order to study and understand how the derivatization of PDI modifies its polarization character and NLO response, the alteration of the second hyperpolarizability between the PDI derivatives A–E is analyzed in terms of: (a) the group type and (b) the anchoring position.Group type. Three types of functionalization groups were considered: para-aminoazobenzene (p-NH2Azo), aniline (AN) and amine (NH2). It is observed that when the group is anchored on the bay position of the PDI, e.g., derivatives B, D and E, the following trend was found: γ(0)[B] ≫ γ(0)[D] ≥ γ(0)[E]. For an evaluation of the effect of the functionalization groups on the second-order hyperpolarizability of the PDIs, the ratio k(X) = γ(X)/γ(Y) is used, where X = B, D, and E, and Y = unsubstituted PDI. It was found that for B, D and E, this ratio is k(B) = 2.01, k(D) = 1.26, and k(E) = 1.17, respectively.
A similar trend of the γ values is observed when the group is anchored at the imide position, as, e.g., for derivatives A and C, where γ(0)[A] ≫ γ(0)[C], while the ratio k(X): k(X) = γ(X)/γ(Y), where X = A and C and Y = unsubstituted PDI, was found to be: k(A) = 1.81, k(C) = 1.19. From the previous analysis, it is evident that the largest change in the second hyperpolarizability is observed for the p-NH2Azo group, implying its high polarization character and high contribution to the second hyperpolarizability.
Anchoring position. Two positions of group anchoring were examined: the bay and imide positions. It is noted that γ(0)[B] > γ(0)[A] and γ(0)[D] > γ(0)[C]. Similar trends were also observed for the frequency-dependent computed values, whereas γ(ω)[B] > γ(ω)[A], and γ(ω)[C] > γ(ω)[D], ω = 0.05695 a.u. (Table 4). By considering the above defined ratios, k(X), it is also observed that k(B)/k(A) = 1.1 and k(D)/k(C) = 1.06. These findings imply that group (p-NH2Azo, AN) anchoring at the bay position of the PDI (i.e., derivatives B, D, and E) induces greater changes on γ(0), resulting in larger values, compared with those computed when the group is connected at the imide position. From the previous analysis, it is ascertained that the higher alteration on the second hyperpolarizability is achieved by bay anchoring in connection with the p-NH2Azo group.
It is interesting to note that, as observed, the incorporation of the two imide units on the perylene skeleton has a large effect on the second hyperpolarizability value. Therefore, it is seen that γ(0)[Y] = 4.34 × γ(0)[P], where Y is the unsubstituted PDI (see Fig. 9). Furthermore, N,N′-di(hexylheptyl) substitution of PDI has a weaker effect, as the second hyperpolarizability exhibits a smaller enhancement by a factor of 1.3.
Theoretical interpretation of the second hyperpolarizability
In order to get a better insight into the origin of the alteration of γ(0) values and the observed trends between the PDIs A–E, the second hyperpolarizability density was evaluated as well. Hyperpolarizability density is associated with the spatial distribution and characteristics of a molecule's or material's response to a strong electric field. It provides a qualitative way to visualize the electron density fluctuations, responsible for the observed NLO phenomena, thus revealing the regions of the molecule contributing the most to the NLO response. Since hyperpolarizability density analysis can map the electron density of a molecule, which is most susceptible to polarization, it provides a particularly useful way to understand how molecular and electronic structures influence the NLO properties.Since the aromatic core of the PDI lies, e.g., on a ZY plane, only the in-plane diagonal components, γzzzz and γyyyy, of the PDIs are studied, as they are expected to have a larger contribution to γ (see Table S3). For the needs of the analysis, the functions −zρ(3)zzz(r) and −yρ(3)yyy(r) were computed, where the function ρ(3)zzz/yyy(r) is associated with the third-order derivative of the electron density with respect to the field:
These functions provide a way to map the regions of the molecule that contribute in a positive or negative way to its overall second hyperpolarizability γ. Additionally, their integration (i.e., 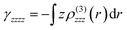 ,
, 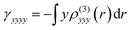 ) allows for the determination of the γzzzz/γyyyy ratio and its comparison with the value obtained by numerical differentiation.
) allows for the determination of the γzzzz/γyyyy ratio and its comparison with the value obtained by numerical differentiation.
The −z/yρ(3)zzz/yyy(r) plots are depicted in Fig. S15. In order to decrease the computational cost, the functions ρ(3)zzz/yyy(r) were computed with the CAM-B3LYP/6-311G method. As shown in Table 4, these γ(0) values are a good approximation to the corresponding dynamic ones, computed far from resonance at λ = 800 nm. Additionally, as provided in Table S4, the γ(0) values computed with the smaller basis set (6-311G) adequately convey the changes and the trends of the second hyperpolarizability between the different PDI derivatives A–E, when compared with the corresponding PDI γ values computed with the larger (6-311+G*) basis set. The calculation of the ρ(3)zzz/yyy(r) functions was performed with the Multiwfn software.50
In general, the computed density plots of γ (see also Fig. S15) were found to fully support and corroborate the previous findings. So, for all PDI derivatives A–E, the positive contribution was found to be larger and mostly distributed along the π network and to a lesser extent to the bay of the PDI core (upon group introduction), thus explaining the computed large and positive γzzzz and γyyyy values of the A–E derivatives.
Bay substitution (e.g., PDI derivatives B, D, and E) imposes large changes on the γzzzz density and even larger on the γyyyy one, expanding the molecular areas that contribute positively to the γ. The largest influence on γzzzz/yyyy densities is observed upon introduction of the trans isomer of the p-NH2Azo group; this can explain the largest second hyperpolarizability found both experimentally and theoretically (i.e., upon excitation at 400 nm) for B. It is interesting to note that for this PDI derivative, a large negative contribution to γzzzz/yyyy density is localized within the region connecting the π-network of PDI and the p-NH2Azo molecular unit. It is also highlighted that the presence of the p-NH2Azo, in its trans configuration, considerably expands the areas of the molecule which contribute positively to γ, compared with those found for D and E. This finding explains the origin of the larger second hyperpolarizability value computed for B, compared with those found for D and E. Moreover, it strengthens our conclusion concerning the influence of the p-NH2Azo group on the polarization properties of the PDIs and the observed changes imposed on γ.
On the other hand, substitution at the imide position with p-NH2Azo or aniline (e.g., PDIs A and C) drastically affects the density of the γzzzz component, by expanding the area of the molecule significantly with a positive contribution. It is seen that the introduction of the trans p-NH2Azo group, at the imide position of the PDI core, expands the area largely with a positive contribution to γzzzz. Similarly to what was observed for derivative B, the largest negative contribution to γzzzz density is localized on the area connecting the π-network of the PDI with the p-NH2Azo molecular unit, whereas a large positive contribution is localized at the terminal aniline group of the p-NH2Azo. Introduction of the aniline group (e.g., PDI C) increases, in a similar way, the positive contribution to the γzzzz density, although at a lower degree compared with derivative A, thus justifying the larger second hyperpolarizability found for A. Overall, it is observed that PDI group anchoring can significantly alter the molecular regions which contribute positively/negatively to the second hyperpolarizability density, thus tuning their overall NLO response.
Structural conformation upon group anchoring. The optimized geometries of the different PDI derivatives are depicted in Fig. S16. It is seen that for A and C, where the group is anchored at the imide position, the PDI core is planar. However, for B, D and E, where the group anchoring occurs at the bay position, the PDI core is twisted at its center, due to steric effects, similar to what was previously reported elsewhere.51,52 All the anchored groups (p-NH2Azo, aniline and NH2), attached either to the bay or to the imide position, are twisted with respect to the π-conjugated PDI core. The degree of rotation depends on both the type of the anchored group and the anchoring position as well. In the case of A and C, the degree of twisting is similar, ca. 61°–62°, while for D, aniline's twisting, with respect to the π-conjugated core, is larger compared with the corresponding of p-aminoazobenzene in B. It is noteworthy that, as expected (vide supra), the ether linkage in B leads to a non-orthogonal arrangement of the PDI core and the azobenzene subunit (dihedral angle 47.5°, Fig. S16). This allows the HOMO of B to spread over the complete π-system, while the LUMO, although mainly located on the PDI, shows some contribution of the azobenzene moiety (Fig. S10).
The observed structural distortions, upon functionalization, influence the distribution of the second hyperpolarizability density (see, e.g., Fig. S15). It is observed that in the case of A and B, where the anchored functional group is the highly polarized p-NH2Azo, distortion results in the formation of two non-overlapping density areas, contributing either positively or negatively to the second hyperpolarizability. The high negative contribution is localized on the phenylene group of p-NH2Azo, anchored either to the imide side, as in A, or to the bay side, as in B, whereas the positive contribution is localized on the terminal aniline group of p-NH2Azo. A similar picture, although to a lesser degree concerning the extent of the γ positive/negative density areas, is observed for C and D, where aniline is the anchored group.
Comparison of the experimental and the theoretical results
As it is known,53 the non-linear optical response of a material can be related to various physical mechanisms that occur at different time scales and contribute to the overall macroscopic NLO response. The relative contribution of each mechanism to the induced NLO response depends on different parameters that can be related to the laser source (e.g., laser intensity, wavelength, CW or pulsed operation, low or high repetition rate, laser pulse duration, etc.), the material itself (e.g., chemical composition, crystal structure, dielectric or metallic character, etc.) and the environment of the atoms/molecules (e.g., solution, thin film, etc.). In the case of fs laser excitation, the NLO response is mainly due to the distortion of the electronic cloud and is usually referred to as instantaneous electronic response and occurs in the time scale of 10−15 s. When longer duration laser pulses are used for excitation, such as, ps or ns, several other mechanisms can take place, e.g., molecular vibrations, intermolecular interactions, thermal diffusion processes, population redistribution within the excited states etc., with the relative contribution of each mechanism on the macroscopic NLO response being mainly determined by the laser pulse duration and the laser repetition rate. So, under ns excitation, although all or some of these physical mechanisms can contribute to the NLO response, population redistribution among the excited states is usually the dominant mechanism and is usually referred to as effective NLO response, and the corresponding NLO parameters as effective ones. Based on the above, the results obtained from the theoretical calculations are comparable with the instantaneous electronic response of the studied PDIs, i.e., to the experimental results obtained under 70 fs, 800 nm laser excitation conditions, i.e., under fs non-resonant excitation.In Fig. 10, the comparison of the experimentally determined and the computed values of the second hyperpolarizability γ is schematically presented. As can be observed, the DFT results, concerning the alterations of the second hyperpolarizability upon side anchoring (bay, imide) and the type of group, are qualitatively in excellent agreement with the experimental results, both following the same trend. For PDI derivatives A and B, where the p-aminoazobenzene group is anchored, the calculations predict larger γ values, compared to those found for C, D and E, in excellent agreement with the reported experimental data. Similarly, the experimentally determined larger NLO response of the bay substituted PDIs B and D, compared to that of the imide substituted ones A and C, is also confirmed by the computations. These findings validate that the computed DFT NLO values can predict successfully the effect of the structure–property relationship on the second hyperpolarizability of the PDI derivatives, as provided by the analysis of the second hyperpolarizability density. Let us also note that the observed discrepancy of the absolute magnitudes between experimental and theoretical γ values originates from the fact that the second hyperpolarizability measurement is performed by applying an oscillating optical field, instead of a static field used for the computations.54,55
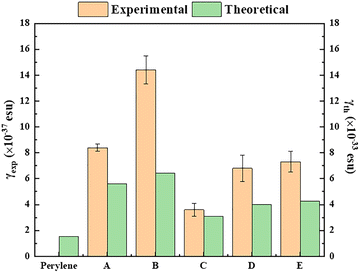 | ||
| Fig. 10 Comparison of the experimentally determined (70 fs/800 nm) second hyperpolarizability values of PDI derivatives A–E with the theoretically calculated ones. | ||
From the results summarized in Table 3, concerning the different NLO parameters of the PDIs A–E, the following conclusions can be drawn:
(a) For the case of 70 fs, 800 nm laser excitation: all PDI derivatives A–E were found to exhibit a similar order of magnitude NLO response (ca. second hyperpolarizability γ, or χ(3)/c), with B exhibiting the largest value, followed by A, E and D (in decreasing order), the last two exhibiting very similar χ(3)/c and γ values, and C exhibiting the lowest response. It is noted that both the experimental results and the theoretical calculations suggest similar trends, concerning the changes of the third-order NLO response between the PDI derivatives studied (see Fig. 10). The values of TPA exhibit a similar trend (see also Table 3), with PDI B exhibiting the largest TPA, with the values for PDIs A, E and D being relatively lower and very similar (within the experimental error) and PDI C exhibiting the lowest TPA value. These findings are well aligned with the non-resonant character of the excitation under 800 nm (as no absorption band was observed in the corresponding absorption spectra of the PDIs shown in Fig. 2).
(b) Effect of the substitution group: under non-resonant excitation conditions, i.e., at 800 nm, the p-aminoazobenzene functionalized PDIs A and B exhibited the largest NLO response, followed by the amino and aniline functionalized PDIs E and D, respectively, in agreement with the results of the theoretical computations. The same trend holds for the NLO response under resonant excitation conditions, i.e., at 400 nm. However, in this case, the differences of the observed NLO response between the different PDIs are relatively more pronounced, as a result of the resonant excitation.
(c) Effect of the position of substitution: the bay functionalized PDIs were found to exhibit larger NLO response than those functionalized at the imide position under both resonant and non-resonant excitation conditions. In more detail, under 800 nm excitation, the bay substituted PDIs B and D were found to exhibit 2–3 times larger NLO response than the imide position substituted counterparts, A and C, while the theoretical results successfully confirm this trend as well. The TPA cross-sections of the PDIs also exhibit similar behaviour, with the TPA values of the bay-substituted PDIs B and D determined to be the larger ones, by a factor of about two. Correspondingly, under 400 nm resonant excitation conditions, the p-aminoazobenzene functionalized PDIs A and B were found to exhibit the largest NLO response, most probably due to the near resonant excitation conditions occurring in this case, as a strong absorption band is located close, at ∼404 and ∼408 nm, respectively (see also Fig. 2). In fact, the NLO response of PDIs A and B was found to be about an order of magnitude larger than that of the aniline substituted PDIs C and D and 3–5 times larger than that of the amino-substituted PDI E. Conversely, PDIs C and D exhibited the lowest NLO response.
Conclusions
In the present work, the NLO response of some newly synthesised PDI derivatives, featuring p-aminoazobenzene (PDI derivatives A and B), aniline (PDI derivatives C and D) and amine (PDI derivative E) groups, at the imide (PDI derivatives A and C) and bay (PDI derivatives B, D and E) positions, was investigated both experimentally and theoretically. The functionalization of the perylene core with these electron donating units allowed assessing the effect of the respective functionalization on their third-order non-linear optical properties. In addition, the effect of the electronic coupling/decoupling of the aromatic substituents of perylene (e.g., by the addition of the phenyl group at the bay or imide positions) on the NLO response was also investigated. The results from DFT theoretical computations reveal the changes in the second hyperpolarizability γ of these PDIs, in excellent agreement with the experimentally determined ones, both demonstrating clearly that the addition of p-aminoazobenzene and the substitution of the perylene core at the bay position lead to stronger NLO response under fs laser excitation. Theoretical analysis shows that the observed NLO alterations between the different PDI derivatives are attributed to changes in the second hyperpolarizability density, caused by group functionalization at either the imide or the bay position. This finding is further corroborated by the experimental results and highlights the importance of the structure–property relationship of the PDIs for the efficient tuning of their NLO properties. It is interesting to note that under non-resonant fs excitation, at 800 nm, the NLO refractive response of the PDIs, except that of derivative A, was insignificant, while under resonant excitation, i.e., 400 nm, the NLO absorptive and refractive responses similarly contributed to the observed NLO response. Under ns laser excitation conditions, where the experimental results cannot be compared with the theoretical predictions, the imide position of p-aminoazobenzene substituted PDI derivative A was found to exhibit the largest NLO response, while the bay substituted PDI derivatives B and D and the imide substituted PDI derivative C exhibited very similar NLO responses.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma01344e.Acknowledgements
A. A. acknowledges that this work was partially performed under the COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). F. F.-L. thanks Grant PID2022-140315NB-I00 funded by MICIU/AEI/10.13039/501100011033 and by ERDF/EU. F. F.-L. is also indebted to the Generalitat Valenciana (CIPROM/2021/059) and the Advanced Materials program by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and Generalitat Valenciana (MFA/2022/028).References
- F. Würthner, Chem. Commun., 2004, 1564–1579 RSC.
- A. Nowak-Król and F. Würthner, Org. Chem. Front., 2019, 6, 1272–1318 Search PubMed.
- C. Huang, S. Barlow and S. R. Marder, J. Org. Chem., 2011, 76, 2386–2407 Search PubMed.
- C. Li and H. Wonneberger, Adv. Mater., 2012, 24, 613–636 Search PubMed.
- E. Kozma and M. Catellani, Dyes Pigm., 2013, 98, 160–179 CrossRef.
- M. Guide, S. Pla, A. Sharenko, P. Zalar, F. Fernández Lázaro, Á. Sastre Santos and T.-Q. Nguyen, Phys. Chem. Chem. Phys., 2013, 15, 18894–18899 RSC.
- X. Zhan, J. Zhang, S. Tang, Y. Lin, M. Zhao, J. Yang, H. L. Zhang, Q. Peng, G. Yu and Z. Li, Chem. Commun., 2015, 51, 7156–7159 Search PubMed.
- F. Fernández Lázaro, N. Zink Lorre and Á. Sastre Santos, J. Mater. Chem. A, 2016, 4, 9336–9346 RSC.
- N. Zink Lorre, E. Font Sanchis, Á. Sastre Santos and F. Fernández Lázaro, Chem. Commun., 2020, 56, 3824–3838 RSC.
- R. Canton-Vitoria, Y. Matsunaga, S. Zhang, M. Xue, M. Osada and R. Kitaura, Nanoscale, 2025, 17, 8084–8100 RSC.
- I. F. A. Mariz, S. Raja, T. Silva, S. Almeida, E. Torres, C. Baleizão and E. Maçôas, Dyes Pigm., 2021, 193, 109470 CrossRef.
- W. Hussain, H. S. Ali, M. S. Iqbal, M. R. Bashir, M. A. Khan, M. Hanif, Y. Sandali, A. Irfan and H. Li, Theor. Chem. Acc., 2024, 143, 27 Search PubMed.
- L. Wang, Y. L. Liu, Q. J. Li, S. H. Chen, D. He and M. S. Wang, J. Phys. Chem. A, 2022, 126, 870–878 Search PubMed.
- F. A. Jerca, V. V. Jerca and R. Hoogenboom, Nat. Rev. Chem., 2022, 6, 51–69 Search PubMed.
- M. Dudek, A. Kaczmarek-Kędziera, R. Deska, J. Trojnar, P. Jasik, P. Młynarz, M. Samoć and K. Matczyszyn, J. Phys. Chem. B, 2022, 126, 6063–6073 CrossRef PubMed.
- E. Piovesan, L. De Boni, E. Ishow and C. R. Mendonça, Chem. Phys. Lett., 2010, 498, 277–280 Search PubMed.
- M. Gascón-Moya, A. Pejoan, M. Izquierdo-Serra, S. Pittolo, G. Cabré, J. Hernando, R. Alibés, P. Gorostiza and F. Busqué, J. Org. Chem., 2015, 80, 9915–9925 CrossRef PubMed.
- Y. Song, J. Sun, X. He, M. Liao, J. Zhao, W. Zeng, S. Zhou and H. Chen, Angew. Chem., Int. Ed., 2023, 62, e202306418 CrossRef PubMed.
- H. Qin, L. Zhao, L. Zheng, Z. Ma, M. Liao, J. Sun, C. Sun and H. Chen, Chem. – Eur. J., 2025, 31, e202403332 CrossRef PubMed.
- X. Shang, J. Ahn, J. H. Lee, J. C. Kim, H. Ohtsu, W. Choi, I. Song, S. K. Kwak and J. H. Oh, ACS Appl. Mater. Interfaces, 2021, 13, 12278–12285 CrossRef PubMed.
- W. Yue, W. Jiang, M. Böckmann, N. L. Doltsinis and Z. Wang, Chem. – Eur. J., 2014, 20, 5209–5213 CrossRef PubMed.
- L. Huang, L. Bin, J. Shen, W. F. Liu, K. Zhou, Y. L. Traskovskis, W. Song, Z. H. Jiang, X. K. Wang and X. K. Ren, Chem. Commun., 2020, 56, 3123–3126 RSC.
- T. Gao, W. F. Zhou, Y. Zhao, L. Shen, W. Y. Chang, R. K. Musendo, E. Q. Chen, Y. L. Song and X. K. Ren, Chem. Commun., 2019, 55, 3012–3014 RSC.
- Y. Yang, Y. Wang, Y. Xie, T. Xiong, Z. Yuan, Y. Zhang, S. Qian and Y. Xiao, Chem. Commun., 2011, 47, 10749–10751 RSC.
- S. L. Oliveira, D. S. Corrêa, L. Misoguti, C. J. L. Constantino, R. F. Aroca, S. C. Zilio and C. R. Mendonça, Adv. Mater., 2005, 17, 1890–1893 CrossRef.
- M. Younis, J. Long, S. Q. Peng, X. S. Wang, C. Chai, N. Bogliotti and M. H. Huang, J. Phys. Chem. Lett., 2021, 12, 3655–3661 CrossRef PubMed.
- Q. Yan and D. Zhao, Org. Lett., 2009, 11, 3426–3429 CrossRef PubMed.
- P. Yan, M. W. Holman, P. Robustelli, A. Chowdhury, F. I. Ishak and D. M. Adams, J. Phys. Chem. B, 2005, 109, 130–137 CrossRef.
- M. Barrejón, S. Pla, I. Berlanga, M. J. Gómez-Escalonilla, L. Martín-Gomis, J. L. G. Fierro, M. Zhang, M. Yudasaka, S. Iijima, H. B. Gobeze, F. D’Souza, Á. Sastre-Santos and F. Langa, J. Mater. Chem. C, 2015, 3, 4960–4969 RSC.
- H. Langhals and S. Kirner, Eur. J. Org. Chem., 2000, 365–380 CrossRef.
- P. Aloukos, K. Iliopoulos, S. Couris, D. M. Guldi, C. Sooambar, A. Mateo-Alonso, P. G. Nagaswaran, D. Bonifazi and M. Prato, J. Mater. Chem., 2011, 21, 2524–2534 RSC.
- N. Karampitsos, D. Kyrginas and S. Couris, Opt. Lett., 2020, 45, 1814–1817 CrossRef.
- S. Vajiravelu, L. Ramunas, G. Juozas Vidas, G. Valentas, J. Vygintas and S. Valiyaveettil, J. Mater. Chem., 2009, 19, 4268–4275 RSC.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 Search PubMed.
- D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135 Search PubMed.
- D. Jacquemin, A. Planchat, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2012, 8, 2359–2372 CrossRef.
- B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 106, 5151–5158 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Rev. B.01, Gaussian Inc., Wallingford, CT, USA, 2016 Search PubMed.
- M. Stavrou, N. Chazapis, E. Nikoli, R. Arenal, N. Tagmatarchis and S. Couris, ACS Appl. Nano Mater., 2022, 5, 16674–16686 CrossRef.
- M. Stavrou, I. Papadakis, T. I. Narayanan and S. Couris, J. Phys. Chem. C, 2021, 125, 16075–16085 CrossRef.
- M. Stavrou, N. Chazapis, V. Georgakilas and S. Couris, Chem. – Eur. J., 2023, 29, e202301959 Search PubMed.
- H. D. Cohen and C. C. Roothaan, J. Chem. Phys., 1965, 43, S34–S39 Search PubMed.
- H. Rutishauser, Numer. Math., 1963, 5, 48–54 CrossRef.
- W. Romberg, K. Nor. Vidensk. Selsk., Forh., 1955, 28, 30–36 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef.
- T. Miletić, A. Fermi, I. Papadakis, I. Orfanos, N. Karampitsos, A. Avramopoulos, N. Demitri, F. De Leo, S. J. A. Pope, M. G. Papadopoulos, S. Couris and D. Bonifazi, Helv. Chim. Acta, 2017, 100 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- D. Jacquemin, A. Femenias, H. Chermette, I. Ciofini, C. Adamo, J.-M. André and E. A. Perpète, J. Phys. Chem. A, 2006, 110, 5952–5959 Search PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani and P. Dahle, et al., The Dalton quantum chemistry program system, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2014, 4, 269–284 Search PubMed.
- T. Lu, J. Chem. Phys., 2024, 161, 082503 CrossRef PubMed.
- S. Gámez-Valenzuela, I. Torres-Moya, A. Sánchez, B. Donoso, J. T. López Navarrete, M. C. Ruiz Delgado, P. Prieto and R. Ponce Ortiz, Chem. – Eur. J., 2023, 29, e202301639 Search PubMed.
- A. Keerthi and S. Valiyaveettil, J. Phys. Chem. B, 2012, 116, 4603–4614 CrossRef.
- G. He, Nonlinear Optics and Photonics, Oxford University Press, Oxford, 2015 Search PubMed.
- Y. Yang, F.-H. Wang, Y.-S. Zhou, L. Yuan and J. Yang, Phys. Rev. A:At., Mol., Opt. Phys., 2005, 71, 013202 CrossRef.
- N. Matsuzawa and D. A. Dixon, J. Phys. Chem., 1992, 96, 6872–6875 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |