 Open Access Article
Open Access ArticleX-ray and neutron diffraction studies of single-crystal cubic Cs2(HSO4)(H2PO4)
Grace
Xiong
 and
Sossina M.
Haile
and
Sossina M.
Haile
 *
*
Department of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: sossina.haile@northwestern.edu
First published on 11th December 2025
Abstract
Superprotonic CsH2PO4 is of interest as an electrolyte for a range of electrochemical devices. To date, the proton position has not been experimentally revealed in the phase of interest. Here, structurally analogous crystals of Cs2(HSO4)(H2PO4) were grown at high temperature, quenched, and then studied by X-ray and neutron diffraction. The compound crystallizes in a CsCl-related structure-type with Cs atoms at the unit cell corners and rotationally disordered (S/P)O4 tetrahedra located at the unit cell centers. At ambient temperature, the cubic phase is metastable for ∼3 h, whereas at 100 K, the cubic phase shows no signs of transformation after 65 h. The neutron diffraction analysis, carried out at 100 K, indicates that the hydrogen resides at the Wycoff 3c position (at the unit cell face center), directly midway between tetrahedral groups. In addition to resolving the hydrogen position, the single crystal studies revealed a significant variation in the cell parameters between individual crystals. Chemical analysis of the crystal used for neutron diffraction studies indicates that cell expansion reflects the presence of Cs vacancies, as has been recently reported for CsH2PO4.
Introduction
Superprotonic solid acids are materials of interest as electrolytes for electrochemical energy devices including fuel-flexible fuel cells, operable on hydrogen,1–3 alcohols,4 or other energy-dense liquids,5 and hydrogen generators using sources such as ammonia and methylcyclohexane.6 These materials are formed from polyanion groups linked together by hydrogen bonds and large counter cations that provide overall charge balance.7 Within this class, CsH2PO4, which is cubic in its high temperature (>501 K), superprotonic phase,8–11 has received the greatest attention for device applications due to its chemical stability in both oxygen-rich and hydrogen-rich environments.12The fast proton transport that characterizes superprotonic behavior in CsH2PO4 and superprotonic solid acids more broadly is known to follow the Grotthuss mechanism.7,13 In this two-step process, protons are transported through the crystal structure by the reorientation of polyhedral anion groups and the hopping of protons between donor and acceptor polyhedra. The overall features of this mechanism have been revealed by both experimental and computational studies. To date, however, there has been no diffraction study that has directly located the proton in superprotonic CsH2PO4, a situation that stands in contrast to that of, for example, superprotonic Rb3H(SeO4)2, for which exquisite single crystal neutron diffraction studies have been performed.14,15 The proton position in cubic CsH2PO4 has instead been inferred from chemical rationalization (the protons must lie between neighboring PO4 polyanion groups) and from experimental studies utilizing techniques such as quasielastic neutron scattering and nuclear magnetic resonance (NMR) spectroscopy;16 the proton position has also been predicted from computational studies,17–19 yet its direct determination remains elusive. The experimental challenge lies in obtaining sufficiently large crystals for neutron diffraction studies, the preferred method for revealing proton positions. Large crystals obtained under ambient conditions typically undergo fracture upon passing through the superprotonic transition20 at which the volume increases by 1.7%.21 The high transition temperature furthermore largely precludes direct growth and characterization of crystals in the superprotonic phase. Moreover, powder neutron diffraction studies require the use of deuterated analogs to eliminate large incoherent backgrounds. However, due to high ionic conductivity, deuterated powders easily recover protons from the ambient environment. Added to this is the challenge that CsH2PO4 requires high steam partial pressure to prevent its decomposition at the temperatures at which it is in the superprotonic phase.9 In the absence of experimental studies that have definitively located protons in superprotonic CsH2PO4, it is difficult to obtain the necessary insight to go beyond a general understanding of the proton transport mechanism and ultimately design materials with superior properties.
In the present work, steps towards addressing this challenge are taken by growing crystals of a compound that is isostructural to cubic CsH2PO4 but has a superprotonic transition that occurs at a sufficiently low temperature that the superprotonic phase can be obtained directly. The compound of choice is Cs2(HSO4)(H2PO4). At ambient temperature, the material crystallizes in a structure with monoclinic symmetry and fixed stoichiometry.22 It undergoes a superprotonic transition that is complete at a temperature of 378 K, with conductivity in the high temperature phase that is comparable to that of CsH2PO4 (Fig. 1).23 At this moderate temperature, aqueous crystal growth is viable, as has been demonstrated for similar compounds.24,25 In the present work, crystals in the cubic phase with compositions close to the target Cs2(HSO4)(H2PO4) are obtained. Exploiting their metastability, single crystal X-ray diffraction studies are performed at several temperatures (ambient, 200 K and 100 K). Significantly, single crystal neutron diffraction studies at 100 K are also achieved, though due to the small crystal size, the proton position is not fully resolved. The methodology reported sets the stage for complete evaluation using larger crystals.
 | ||
Fig. 1 Comparison of the conductivities (σ) of CsH2PO4 (CDP, polycrystalline compact) and Cs2(HSO4)(H2PO4) (CHSP, single crystal, along the b-axis) taken from the studies by Haile et al.8 and Chisholm and Haile,23 respectively. Quoted activation energies, Ea, are those of the superprotonic phases evaluated using the expression 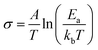 , where A is the pre-exponential constant, T is the temperature, and kb is Boltzmann's constant. , where A is the pre-exponential constant, T is the temperature, and kb is Boltzmann's constant. | ||
Crystal growth and stoichiometry
Single crystals of Cs2(HSO4)(H2PO4) were grown at temperatures at which the cubic phase is stable using a high temperature, high humidity precipitation method adapted from Sanghvi et al.24 The heating profile employed is shown in Fig. 2a. Stoichiometric quantities of the CsH2PO4 and CsHSO4 precursors (approximately 0.1 g in total) were mixed, loaded into a quartz boat (100 mm L × 17 mm W × 10 mm H), placed into a tube furnace, and then heated to 373 K at a rate of 5 K min−1. Following a 30-minute isothermal hold, 0.83 atm of steam, carried by N2 gas, was introduced into the system, inducing deliquescence of the precursors. After the precursors were fully dissolved, the solution was gently heated to 378 K and held under this condition for one hour. The steam partial pressure was then lowered to 0.51 atm. Slow crystallization (induced by slow H2O evaporation) commenced under these conditions. After approximately one week of crystallization, the steam was replaced by dry N2 gas (to prevent steam condensation in the subsequent steps) and the quartz boat sample carrier was removed from the furnace such that the sample was immediately exposed to ambient temperature. The product was a solid mass of crystals, with no residual liquid. Large single crystals of approximately 1 mm in length along each edge, as shown in Fig. 2b, were obtained using this crystallization approach. | ||
| Fig. 2 Growth of cubic Cs2(HSO4)(H2PO4) single crystals: (a) thermal profile used for high-humidity precipitation and (b) optical images of representative crystals. | ||
All crystals used for subsequent characterization were screened by polarized light microscopy (Leica S9i). Consistent with the expected cubic symmetry, high quality crystals were dark under cross-polarization. Preliminary single crystal X-ray diffraction studies (instrumentation details are given below) of screened crystals revealed cubic symmetry and a simple cubic lattice constant of ∼4.90 Å, indicating that the desired phase had been obtained. As discussed in the following, the full structure refinement indicated that cubic Cs2(HSO4)(H2PO4) is isostructural to cubic CsH2PO4, in which Cs cations and rotationally disordered XO4 polyanions adopt a CsCl-related arrangement, consistent with the structure of this compound at elevated (>353 K) temperature.23
Given the wide compositional range over which the cubic superprotonic phase occurs in the CsH2PO4–CsHSO4 system26,27 and the typically incongruent nature of crystal growth from multi-component aqueous solutions (for example, Komornikov et al.28), the possibility that the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio in any crystal studied deviates from the solution ratio of 1
P ratio in any crystal studied deviates from the solution ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is high. This ratio furthermore establishes the proton concentration in the phase. Although neutron diffraction can, in principle, be used to determine the composition of the studied crystal due to the difference in scattering lengths of S and P and the large neutron scattering length of H, the composition of the specific crystal used for the neutron diffraction analysis was independently and directly characterized using a combination of inductively coupled plasma mass spectroscopy (Thermo iCAP Q ICP-MS) and optical emission spectroscopy (Thermo iCAP 7600 ICP-OES). A standard dissolution procedure was used. The crystal, with a mass of 1.78 mg, was dissolved in a solution formed from 300 µL of HNO3 and 100 µL of H2O at room temperature, heated to and held at 338 K for three hours, and then further diluted with 9.6 mL of Millipore water. ICP-MS was used to obtain the Cs and P concentrations in the solution, and ICP-OES was used to obtain the P and S concentrations.
1 is high. This ratio furthermore establishes the proton concentration in the phase. Although neutron diffraction can, in principle, be used to determine the composition of the studied crystal due to the difference in scattering lengths of S and P and the large neutron scattering length of H, the composition of the specific crystal used for the neutron diffraction analysis was independently and directly characterized using a combination of inductively coupled plasma mass spectroscopy (Thermo iCAP Q ICP-MS) and optical emission spectroscopy (Thermo iCAP 7600 ICP-OES). A standard dissolution procedure was used. The crystal, with a mass of 1.78 mg, was dissolved in a solution formed from 300 µL of HNO3 and 100 µL of H2O at room temperature, heated to and held at 338 K for three hours, and then further diluted with 9.6 mL of Millipore water. ICP-MS was used to obtain the Cs and P concentrations in the solution, and ICP-OES was used to obtain the P and S concentrations.
The molar ratio of Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S
S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P was found to be 0.83(6)
P was found to be 0.83(6)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43(1)
0.43(1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.57(1), indicating not only a deviation in the S
0.57(1), indicating not only a deviation in the S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio from that of the starting solution but also a significant deficiency in the Cs content relative to the 1
P ratio from that of the starting solution but also a significant deficiency in the Cs content relative to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cation
1 cation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) polyanion ratio expected for a CsCl-related structure, Table 2. While surprising, such behavior is known to occur in cubic, superprotonic CsH2PO4, where it has been revealed that as much as 22% of the Cs sites can be vacant, with charge compensation occurring via the additional protons present.29 The stoichiometry of the crystal used for neutron studies can thus be described as Cs0.83H1.74(SO4)0.43(PO4)0.57, with an uncertainty in the hydrogen content of 0.14. For notational ease, the stoichiometric description Cs2(HSO4)(H2PO4), though approximate, is retained for all crystals obtained in this work.
polyanion ratio expected for a CsCl-related structure, Table 2. While surprising, such behavior is known to occur in cubic, superprotonic CsH2PO4, where it has been revealed that as much as 22% of the Cs sites can be vacant, with charge compensation occurring via the additional protons present.29 The stoichiometry of the crystal used for neutron studies can thus be described as Cs0.83H1.74(SO4)0.43(PO4)0.57, with an uncertainty in the hydrogen content of 0.14. For notational ease, the stoichiometric description Cs2(HSO4)(H2PO4), though approximate, is retained for all crystals obtained in this work.
Room temperature metastability and X-ray structure determination
Because cubic Cs2(HSO4)(H2PO4) is thermodynamically unstable with respect to its monoclinic form at temperatures below 378 K,23 an assessment of its metastability at the diffraction measurement temperatures was undertaken to provide guidance on the feasibility of complete data collection before initiation of the transformation to the low temperature form. The room temperature metastability was measured by polarized light microscopy (Nikon LV100POL equipped with a CMOS Nikon DS-Fi3 image sensor) using a crystal approximately 1 mm in length along each edge. The selection and screening of the crystal took approximately two hours, a time period that is included in assessing the metastable lifetime. An image of the crystal was captured at the beginning of the measurement under bright field conditions (SI Fig. S1a) and then every hour under cross-polarized light for 24 hours. The imaging settings were selected to prevent pixel saturation, but no color correction was performed. The images were compiled and analyzed using ImageJ.Under cross-polarized light, the crystal, which initially appeared black, gradually displayed visible regions over time, indicative of the transformation to the anisotropic, monoclinic phase, as shown in Fig. 3a (compiled in video format in SI Fig. S1b). The fraction of pixels in which light was recorded was taken as the fraction of the crystal that had converted to the monoclinic phase, as shown in Fig. 3b. Fifty percent conversion of the crystal occurred at 4.7 hours after the crystal was first brought to room temperature, and 95% conversion occurred after 14.3 hours of total room temperature exposure. This extent of room temperature metastability is comparable to that (approximately 12 h) reported by Chisholm et al. for a crystal of Cs2(HSO4)(H2PO4) cooled from the cubic phase and studied by impedance spectroscopy.23 Avrami analysis,30 Fig. S2, suggests that the transformation initiated upon placement in the optical microscope. This is consistent with the complete absence of transmitted light in the first optical image shown in Fig. 3a.
With suitable room temperature metastability established, complete X-ray diffraction data for structure analysis were collected using a Rigaku XtaLab Mo Synergy single crystal diffractometer (Mo Kα radiation, λ = 0.71073 Å) equipped with a Rigaku HyPix Hybrid Photon detector. No absorption correction was applied. A total of 3020 reflections were collected, generating a dataset of 92 independent reflections, from which the unit dimension of 4.9004(4) Å was established. The measurement, including the planning steps, required only about 15 minutes, well within the metastable lifetime of cubic Cs2(HSO4)(H2PO4) at ambient temperature (Fig. 2). Data reduction and finalization were performed using CrysAlisPro.
In the absence of chemical analysis for the small crystal utilized for X-ray diffraction studies, the structure was refined against the cubic structure of CsH2PO4 taking the P site to be partially occupied by S and P at equal levels and the Cs site to be fully occupied. As with cubic CsH2PO4,10 the oxygen was found to reside at a 24l site, with refined coordinates of 0.5, 0.220(2), and 0.373(3). The oxygen occupancy was fixed at 1/6 to match the assumed stoichiometry of Cs2(HSO4)(H2PO4). Because of the limited sensitivity of X-rays to small compositional variations in such a disordered structure, no attempt was made to refine site occupancies. In the final refinement, the displacement parameters of all atoms were refined, including anisotropic displacement parameters for oxygen. The final refinement statistics, with a total of nine refined parameters, were wR(F2) = 0.0670, GooF = 1.020, and R1[F > 4σ(F)] = 0.0189. Refinements were performed using least squares methods as implemented in ShelXL,31 in which the refinement metrics quoted are defined. The complete data collection parameters and refinement statistics are provided in SI Table S1.
Overall, the structure obtained for Cs2(HSO4)(H2PO4), Table 2 and Fig. 4, follows chemical expectations. The X–O bond length is 1.507(11) Å, consistent with typical values of P–O and S–O bond lengths, which vary slightly depending on the hydrogen bonding environment.32,33 The atomic displacement parameters are similar to those reported by Botez for CsH2PO4 at 510 K, though in that work all atomic species were restrained to isotropic behavior and a single displacement parameter was applied across all atom types.10 Here, the thermal ellipsoid of oxygen is directed normal to the X–O bond, as expected (Fig. 4b). Treatment of the displacements of the oxygen atom as anisotropic is further justified by the impact on the refinement statistics; the isotropic refinement gave a significantly higher R1 of 0.0929. A slightly larger displacement parameter for Cs than the other atoms may reflect the presence of cation vacancies.
Low temperature metastability and X-ray structure determination
The sufficient metastability of cubic Cs2(HSO4)(H2PO4) for ambient temperature diffraction studies almost immediately implies suitable metastability for low temperature XRD studies, but not necessarily for much longer neutron diffraction studies. Metastability at 200 K and 100 K was evaluated directly by single crystal XRD (Rigaku Mo Synergy diffractometer, HyPix Hybrid Photon detector), using two different crystals and with the data analyzed in the context of the cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) structure described above. For the measurement at 200 K, the crystal was cooled at a rate of 1 K min−1 using liquid nitrogen, with data additionally collected along the cooling trajectory at 285 K, 265 K, 245 K, 225 K, and 205 K. At each of these temperatures, the crystal was held isothermally for 10 minutes to achieve thermal equilibration prior to the ∼4 minute diffraction data collection. Once the crystal reached the target final temperature (200 K), data were collected every hour over a period of 66 hours. For the 100 K stability measurement, the crystal was cooled at a rate of 3 K min−1 using liquid helium, with one additional measurement at 200 K along the cooling trajectory. Upon reaching 100 K, data were collected every hour for 40 hours. Following this series of measurements, the crystal was heated under dry N2 and diffraction data were collected at 150 K and 200 K.
m) structure described above. For the measurement at 200 K, the crystal was cooled at a rate of 1 K min−1 using liquid nitrogen, with data additionally collected along the cooling trajectory at 285 K, 265 K, 245 K, 225 K, and 205 K. At each of these temperatures, the crystal was held isothermally for 10 minutes to achieve thermal equilibration prior to the ∼4 minute diffraction data collection. Once the crystal reached the target final temperature (200 K), data were collected every hour over a period of 66 hours. For the 100 K stability measurement, the crystal was cooled at a rate of 3 K min−1 using liquid helium, with one additional measurement at 200 K along the cooling trajectory. Upon reaching 100 K, data were collected every hour for 40 hours. Following this series of measurements, the crystal was heated under dry N2 and diffraction data were collected at 150 K and 200 K.
Each diffraction measurement performed as part of these stability studies comprised a complete data collection, suitable for structure refinement. At 200 K, a dataset of 86 independent reflections at each measurement time step was collected. For data collected at 100 K, the dataset at each measurement time step consisted of 54 independent reflections. Further details are provided in SI Table S1. Stability was assessed by monitoring the value of the cubic lattice parameter and of Rint, defined as 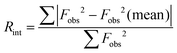 for symmetry equivalent reflections,34 where Fobs is the observed structure factor. As shown in Fig. 5, neither Rint nor the lattice parameter evolved over time at either 200 K or 100 K. Moreover, Rint retained a small value, ∼0.096 at 200 K and ∼0.12 at 100 K, indicating the suitability of the Pm
for symmetry equivalent reflections,34 where Fobs is the observed structure factor. As shown in Fig. 5, neither Rint nor the lattice parameter evolved over time at either 200 K or 100 K. Moreover, Rint retained a small value, ∼0.096 at 200 K and ∼0.12 at 100 K, indicating the suitability of the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group for describing the structures.
m space group for describing the structures.
 | ||
| Fig. 5 Metastability of crystals of cubic Cs2(HSO4)(H2PO4) as reflected in measurements of Rint and cubic lattice parameter at (a), 200 K; and (b) 100 K. | ||
It is to be noted that the lattice parameter measured at 100 K, 4.867(1) Å, is slightly larger than that measured at 200 K, 4.854(3) Å. This is attributed to slight differences in the chemical composition between the two crystals employed rather than any anomalous thermal expansion. The temperature dependent lattice parameters of each individual crystal displayed normal thermal expansion, with coefficients of 4.9(3) × 10−5 and 3.76(9) × 10−5 Å K−1. Because P–O and S–O bond lengths are rather similar,32 it is likely that the compositions differ in terms of the Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion ratio rather than simply the P
anion ratio rather than simply the P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio. In addition to the occurrence of Cs deficiency noted above, cubic CsH2PO4 can also be anion deficient,35 where anion site vacancies are again charge balanced by modification of the overall proton concentration. Across the composition range Cs1±xH2∓xPO4 (i.e., that including both Cs and anion site vacancies), the cubic lattice parameter monotonically increases with decreasing Cs
S ratio. In addition to the occurrence of Cs deficiency noted above, cubic CsH2PO4 can also be anion deficient,35 where anion site vacancies are again charge balanced by modification of the overall proton concentration. Across the composition range Cs1±xH2∓xPO4 (i.e., that including both Cs and anion site vacancies), the cubic lattice parameter monotonically increases with decreasing Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO4.
PO4.
The isothermal data collected at each temperature were combined to create datasets for each of the two temperatures that were then utilized for structure refinement. The complete data collection parameters and refinement statistics are provided in SI Table S1. The resulting crystallographic parameters are reported in SI Table S2. Additional refinement results for these two crystals as measured at ambient temperature and, in the case of the crystal studied isothermally at 100 K, an additional measurement at 200 K are summarized in SI Table S3.
Neutron data collection and structure refinement
Single crystal neutron diffraction data were collected at 100 K using a TOPAZ single-crystal time-of-flight Laue diffractometer at the Spallation Neutron Source at the Oak Ridge National Laboratory. Single crystals were stored and shipped under dry ice to maintain a temperature of 200 K; the time from crystal growth to data collection at the Oak Ridge National Laboratory was approximately one month. Upon arrival at the facility, a clear plate-like crystal with dimensions of 0.6 mm × 0.7 mm × 1 mm was selected and attached to a MiTeGen loop with superglue. A total of 12 crystal orientations, planned using CrystalPlan, were collected with 15 C of proton charge for each orientation; the total collection time was 37.5 hours. A Mantid-based 3D ellipsoidal Q-space integration method was used to obtain peak intensities. Data reduction was performed using the ANVRED3 program and saved in the SHELX HKLF2 format, with a neutron wavelength saved for each reflection. Using a total of 9 unique reflections, the lattice parameter was found to be 4.886(3) Å, with good stability over the course of the measurement (Fig. S3). This lattice parameter is larger than that of the crystal measured by X-ray diffraction at the same temperature, again attributed to the differences in the composition.Structure refinement in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model36 was performed using the stoichiometry determined by ICP-MS/ICP-OES, Table 1. Specifically, the Cs occupancy on the 1a site was fixed at 0.83 and the S and P occupancies on the 1b shared site were fixed at 0.47 and 0.53, respectively. As with the X-ray refinements, the oxygen occupancy was fixed at 1/6. Due to the low number of unique reflections, only an isotropic displacement parameter was refined for oxygen, though the displacement parameters for the Cs, S/P, and O species were (as in the X-ray case) varied independently. Fourier difference maps indicated the hydrogen to be located, as expected, in the vicinity of the 3c site at 1/2 1/2 0 that lies midway between S/P cations and at the center of the cubic unit cell faces. As discussed below, the hydrogen was fixed at the special position and the site occupancy was fixed to match the stoichiometry obtained from chemical analysis (0.58). The uncertainty in this value is 0.05 as derived from the uncertainty in the chemical analysis. In the final refinement, the oxygen position was allowed to vary freely, and all displacement parameters were refined, with the hydrogen displacement parameter constrained to be 1.2 times that of oxygen. The complete data collection and refinement statistics are provided in SI Table S1. The somewhat low goodness of fit (0.785) reflects the very small number of independent reflections, which is, in turn, a result of the rather small crystal available for the measurement. Because distinct crystals, with evidently distinct stoichiometries, were used in the X-ray and neutron data acquisitions, co-refinement with the two sets of 100 K data was not pursued.
m model36 was performed using the stoichiometry determined by ICP-MS/ICP-OES, Table 1. Specifically, the Cs occupancy on the 1a site was fixed at 0.83 and the S and P occupancies on the 1b shared site were fixed at 0.47 and 0.53, respectively. As with the X-ray refinements, the oxygen occupancy was fixed at 1/6. Due to the low number of unique reflections, only an isotropic displacement parameter was refined for oxygen, though the displacement parameters for the Cs, S/P, and O species were (as in the X-ray case) varied independently. Fourier difference maps indicated the hydrogen to be located, as expected, in the vicinity of the 3c site at 1/2 1/2 0 that lies midway between S/P cations and at the center of the cubic unit cell faces. As discussed below, the hydrogen was fixed at the special position and the site occupancy was fixed to match the stoichiometry obtained from chemical analysis (0.58). The uncertainty in this value is 0.05 as derived from the uncertainty in the chemical analysis. In the final refinement, the oxygen position was allowed to vary freely, and all displacement parameters were refined, with the hydrogen displacement parameter constrained to be 1.2 times that of oxygen. The complete data collection and refinement statistics are provided in SI Table S1. The somewhat low goodness of fit (0.785) reflects the very small number of independent reflections, which is, in turn, a result of the rather small crystal available for the measurement. Because distinct crystals, with evidently distinct stoichiometries, were used in the X-ray and neutron data acquisitions, co-refinement with the two sets of 100 K data was not pursued.
| wt% | Molar ratio | |||
|---|---|---|---|---|
| Cs | P | S | Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (P + S) (P + S) |
S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
| 21(1) | 3.1(2) | 2.9(1) | 0.82(6)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0.47(1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.53(1) 0.53(1) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, measured under the conditions indicated. Cs resides in the 1a site (0,0,0), S/P in the 1b site (1/2 1/2 1/2) and O in the 24l site (1/2 x y). Occupancies fixed to the values are given
m, measured under the conditions indicated. Cs resides in the 1a site (0,0,0), S/P in the 1b site (1/2 1/2 1/2) and O in the 24l site (1/2 x y). Occupancies fixed to the values are given
| Parameter | XRD crystal 1 | XRD crystal 2 | XRD crystal 3 | ND crystal 4 |
|---|---|---|---|---|
| Temperature (K) | 298 | 200 | 100 | 100 |
| a (Å) | 4.9004(4) | 4.8552(9) | 4.8664(5) | 4.886(3) |
| Cs(occ) | 1 | 1 | 1 | 0.83 |
| Cs(U11) (Å2) | 0.1584(8) | 0.169(1) | 0.198(1) | 0.140(4) |
| S(occ)/P(occ) | 0.5/0.5 | 0.5/0.5 | 0.5/0.5 | 0.43/0.57 |
| S/P (U11) (Å2) | 0.123(1) | 0.126(1) | 0.147(2) | 0.160(6) |
| O(y) | 0.220(2) | 0.219(2) | 0.220(2) | 0.215(1) |
| O(z) | 0.373(3) | 0.375(3) | 0.369(3) | 0.355(1) |
| P/S–O (Å) | 1.507(11) | 1.493(11) | 1.505(11) | 1.562(4) |
| O(U11) (Å2) | 0.215(15) | 0.24(2) | 0.24(1) | N/A |
| O(U22) (Å2) | 0.128(8) | 0.13(1) | 0.151(8) | N/A |
| O(U33) (Å2) | 0.129(8) | 0.122(7) | 0.14(1) | N/A |
| O(U23) (Å2) | −0.009(7) | 0.017(8) | 0.010(9) | N/A |
| O(Ueq) (Å2) | 0.157(7) | 0.166(9) | 0.181(9) | 0.136(4) |
| H site | N/A | N/A | N/A | 3c |
| H(Ueq) (Å2) | N/A | N/A | N/A | 0.163(4) |
| H(occ) | N/A | N/A | N/A | 0.58 |
Despite the limited neutron data that could be collected, the refinement yielded an excellent result, as shown in Table 2 and Fig. 6. The refined oxygen position is close to that determined from the X-ray analyses. This position may be very slightly inaccurate, however, as the result implies a somewhat elongated P/S–O bond length of 1.562(4) Å, though the lattice parameter is similar to the other refinements. Taking the oxygen to instead lie at 0.5, 0.220, and 0.370, as obtained from the average of X-ray refinements, the P/S–O bond length becomes 1.508 Å, a more physically reasonable value. While it is known that measurements of O–H bond distances can differ between X-ray and neutron structure refinements because of the displacement between the nuclear and electron centers of mass of protons, such an effect is considered unlikely for the P/S–O bond. For example, in the compound Cs3Li(DSO4)4, the X-ray and neutron S–O distances are within 0.01 Å of one another.37 As noted above, co-refinement of the X-ray and neutron data collected at 100 K was not pursued due to the likely compositional differences between the two crystals.
Turning to the hydrogen bond environment, if the proton were to indeed reside at the 3c site, the most plausible bonding configuration would be a linear symmetric bond; other choices for the O–O pair would be anticipated to shift the proton away from the 3c site. The refined oxygen position (with hydrogen at the 3c site) implies an O–H bond length of 1.267(8) Å, which changes only slightly to become 1.249 Å using the X-ray derived oxygen positions. The O⋯O distance is calculated to be 2.498(10) Å using the neutron refined oxygen coordinates and 2.534(10) Å using those from the X-ray refinement. Though the O–H bond lengths from the present neutron refinement are rather long for a bond between an oxygen donor atom and a covalently bonded hydrogen, the O⋯O values are similar to those obtained from analysis of the probability distribution function for O⋯O distances generated by AIMD simulations of cubic CsH2PO4. In particular, Lee and Tuckerman17 reported a value of 2.61 Å (using a lattice parameter of 4.961 Å), whereas Dreßler and Sebastiani19 obtained a value of 2.45 Å (using a lattice parameter of 4.9549 Å20). Lee and Tuckerman further evaluated the geometry of the hydrogen bond and found the O–H⋯O configuration to be linear and asymmetric, with dO–H and dO⋯H distances of 1.02 and 1.54 Å, respectively. Such behavior agrees with the general observation that hydrogen bonds with dO⋯O greater than ∼2.4 Å are typically asymmetric38 (meaning that the hydrogen is displaced from the midpoint between the two oxygen atoms), though linear asymmetric bonds are rare. Very recently, Wang et al.39 studied CsH2PO4 using machine-learned molecular dynamics simulations and concluded the most probable proton position to be slightly displaced from the 3c site, specifically at a 6f site with coordinates (0.5, 0.5, 0.92). These coordinates produce an asymmetric, non-linear bond (∼160°) with bond distances close to those predicted by Lee and Tuckerman.
Motivated by the computational results, additional refinements were performed with the proton positioned on the 6f site. The z-coordinate was fixed to a specific value ranging from 0.92 to 0.99, with all other aspects of the refinement being the same as reported above (isotropic, independent displacement parameters refined for all atoms, except for constraining the hydrogen displacement parameter to be 1.2 times the value of the oxygen displacement parameter, and freely refined oxygen coordinates). The refinement statistics improved monotonically as the hydrogen z-coordinate approached 1, with little impact on the oxygen coordinates or the displacement parameters (Table S3). Ultimately, the best fit to the data was obtained with the hydrogen at the special position, as reported in Table 2. The difference from the computational prediction may be explained by the differences in the composition, CsH2PO4vs. Cs-deficient Cs2(HSO4)(H2PO4), or the metastable nature of the crystals studied here. Alternatively, due to the low number of neutron reflections collected, the possibility that the proton in cubic Cs-deficient Cs2(HSO4)(H2PO4) may, in fact, be slightly displaced from the 3c site cannot be entirely ruled out. Regardless, the neutron diffraction analysis reveals that the proton resides between phosphate groups at physically reasonable locations.
Discussion of lattice and displacement parameter trends
An unexpected observation in this work is the large variation in lattice parameters obtained in the Cs2(HSO4)(H2PO4) crystals, as highlighted in Fig. 7, in which the temperature dependences of cell parameters of each crystal are presented. Shown also is the extrapolated cell parameter of stoichiometric Cs2(HSO4)(H2PO4) assuming thermal expansion that is the average of that measured from the two crystals characterized by low temperature X-ray diffraction (4.377 × 10−5 K−1). While the lattice parameter of crystal 2 closely matches the extrapolated value of stoichiometric Cs2(HSO4)(H2PO4), the cell parameters of the other crystals are conspicuously larger. As is noted, this is likely due to variations in stoichiometry, though not due to differences in SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO4 ratios. In a study of the high temperature behavior of sulfate-rich compounds in the CsH2PO4–CsHSO4 system, Mikheykin et al.40 found the lattice parameters of the high temperature phases (a mixture of co-existing tetragonal and cubic phases) to be largely independent of the composition, with cell parameters varying by only ∼0.1% for a variation in anion chemistry of ∼10%. At ambient temperatures, at which compounds in the CsH2PO4–CsHSO4 system adopt distinct crystal structures, the cell volume varies erratically with anion chemistry, showing perhaps a very slight tendency towards larger volumes with increasing phosphate concentration (Fig. S4).
PO4 ratios. In a study of the high temperature behavior of sulfate-rich compounds in the CsH2PO4–CsHSO4 system, Mikheykin et al.40 found the lattice parameters of the high temperature phases (a mixture of co-existing tetragonal and cubic phases) to be largely independent of the composition, with cell parameters varying by only ∼0.1% for a variation in anion chemistry of ∼10%. At ambient temperatures, at which compounds in the CsH2PO4–CsHSO4 system adopt distinct crystal structures, the cell volume varies erratically with anion chemistry, showing perhaps a very slight tendency towards larger volumes with increasing phosphate concentration (Fig. S4).
 | ||
| Fig. 7 Temperature dependence of the lattice parameters of the Cs2(HSO4)(H2PO4) crystals studied in this work. Thermal expansion coefficients, α, obtained according to Δa/a0 = α(T − T0), with T0 = 298 K. The data for Cs2(HSO4)(H2PO4) correspond to an extrapolation from the high temperature lattice parameter of the stoichiometric material23 based on the expansion coefficients measured here. The differences in cell parameters are attributed to differences in the Cs content. | ||
In contrast to the minimal impact of anion chemistry on cell volumes in the superprotonic phases, variations in the Cs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion ratio are known to have a dramatic impact. In the case of Cs-deficient, cubic Cs1−xH2+xPO4 (α′-CDP), the cell parameter expands with increasing Cs deficiency, by 0.46(3) Å/x.29 The behavior has been interpreted in terms of a weakening of the electrostatic forces that hold the crystal together. Assuming the same level of chemical expansion at low temperature, the crystal examined by neutron diffraction (crystal 4) would be expected to display a lattice parameter of 4.912 Å. This value is larger than the measured lattice parameter of 4.886(3)Å, indicating that the latter is well within the range of what can be expected from compositional variations. Using the measured stoichiometry and lattice parameter of crystal 4 (used for neutron diffraction analysis), along with the extrapolated lattice parameter for stoichiometric Cs2(HSO4)(H2PO4), it is possible to estimate the chemical expansion in the mixed sulfate-phosphate material. The analysis yields 0.31(3) Å/x, somewhat lower than that in the phosphate material. This revised chemical expansion value and the measured lattice parameters of crystals 1 and 3 suggest that the crystals are deficient in Cs by x = 0.005 and 0.010, respectively.
anion ratio are known to have a dramatic impact. In the case of Cs-deficient, cubic Cs1−xH2+xPO4 (α′-CDP), the cell parameter expands with increasing Cs deficiency, by 0.46(3) Å/x.29 The behavior has been interpreted in terms of a weakening of the electrostatic forces that hold the crystal together. Assuming the same level of chemical expansion at low temperature, the crystal examined by neutron diffraction (crystal 4) would be expected to display a lattice parameter of 4.912 Å. This value is larger than the measured lattice parameter of 4.886(3)Å, indicating that the latter is well within the range of what can be expected from compositional variations. Using the measured stoichiometry and lattice parameter of crystal 4 (used for neutron diffraction analysis), along with the extrapolated lattice parameter for stoichiometric Cs2(HSO4)(H2PO4), it is possible to estimate the chemical expansion in the mixed sulfate-phosphate material. The analysis yields 0.31(3) Å/x, somewhat lower than that in the phosphate material. This revised chemical expansion value and the measured lattice parameters of crystals 1 and 3 suggest that the crystals are deficient in Cs by x = 0.005 and 0.010, respectively.
Summary and conclusions
Structure refinement of cubic Cs2(HSO4)(H2PO4) has been carried out using X-ray and neutron diffraction on single crystal samples. Single crystals in the cubic phase were successfully grown using a high temperature, high humidity precipitation technique. The stability of these crystals was evaluated using polarized light optical microscopy and single crystal X-ray diffraction. The metastability at room temperature (∼3 hours) was sufficient for complete X-ray diffraction data acquisition, whereas that at cryogenic temperatures of 100 K and 200 K (>36 hours) was sufficient for neutron diffraction data collection. The neutron diffraction analysis points towards a hydrogen position on the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Wycoff 3c site (0.5, 0.5, 1), i.e., the face center of the cubic unit cell and midway between S/P atoms. The four individual crystals studied exhibited a substantial variation in the lattice parameter, though all could be well-described by a simple cubic structure with Cs on the unit cell corners and P/S at the body center position. The behavior is ascribed to the presence of Cs vacancies that are charge balanced by the incorporation of additional protons, as has recently been observed for CsH2PO4. Access to superprotonic cubic structures under ambient conditions opens up new avenues for experimental studies of proton transport mechanisms, essential for the rational design of next generation materials.
m Wycoff 3c site (0.5, 0.5, 1), i.e., the face center of the cubic unit cell and midway between S/P atoms. The four individual crystals studied exhibited a substantial variation in the lattice parameter, though all could be well-described by a simple cubic structure with Cs on the unit cell corners and P/S at the body center position. The behavior is ascribed to the presence of Cs vacancies that are charge balanced by the incorporation of additional protons, as has recently been observed for CsH2PO4. Access to superprotonic cubic structures under ambient conditions opens up new avenues for experimental studies of proton transport mechanisms, essential for the rational design of next generation materials.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting the conclusions of this article have been included either in the main text or as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma01274k.Acknowledgements
This work was financially supported by the National Science Foundation (OAC-2118201 and DMR-1807234). This work made use of the IMSERC (RRID:SCR_017874) Crystallography facility at Northwestern University, which has received support from the Soft and Hybrid Nanotechnology resource (NSF EECS-2025633) and Northwestern University. Single-crystal neutron diffraction performed on TOPAZ used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory, under contract no. DE-AC05-00OR22725 with UT-Battelle, LLC.References
- D. A. Boysen, T. Uda, C. R. I. Chisholm and S. M. Haile, High-performance solid acid fuel cells through humidity stabilization, Science, 2004, 303(5654), 68–70, DOI:10.1126/science.1090920.
- S. M. Haile, D. A. Boysen, C. R. I. Chisholm and R. B. Merle, Solid acids as fuel cell electrolytes, Nature, 2001, 410(6831), 910–913, DOI:10.1038/35073536.
- D. A. Boysen, S. Cha, C. R. I. Chisholm, K. P. Giapis, S. M. Haile, A. B. Papandrew and K. A. Sasaki, From Laboratory Breakthrough to Technological Realization: The Development Path for Solid Acid Fuel Cells, Electrochem. Soc. Interface, 2009, 18(3), 53–59, DOI:10.1149/2.f06093if.
- T. Uda, D. A. Boysen, C. R. I. Chisholm and S. M. Haile, Alcohol fuel cells at optimal temperatures, Electrochem. Solid-State Lett., 2006, 9(6), A261–A264, DOI:10.1149/1.2188069.
- C. S. Gittleman, H. F. Jia, E. S. De Castro, C. R. I. Chisholm and Y. S. Kim, Proton conductors for heavy-duty vehicle fuel cells, Joule, 2021, 5(7), 1660–1677, DOI:10.1016/j.joule.2021.05.016.
- D. K. Lim, A. B. Plymill, H. Paik, X. Qian, S. Zecevic, C. R. I. Chisholm and S. M. Haile, Solid Acid Electrochemical Cell for the Production of Hydrogen from Ammonia, Joule, 2020, 4(11), 2338–2347, DOI:10.1016/j.joule.2020.10.006.
- A. I. Baranov, Crystals with disordered hydrogen-bond networks and superprotonic conductivity. Review, Crystallogr. Rep., 2003, 48(6), 1012–1037 CrossRef CAS.
- S. M. Haile, C. R. I. Chisholm, K. Sasaki, D. A. Boysen and T. Uda, Solid acid proton conductors: from laboratory curiosities to fuel cell electrolytes, Faraday Discuss., 2007, 134, 17–39, 10.1039/b604311a.
- A. Ikeda and S. M. Haile, The thermodynamics and kinetics of the dehydration of CsH2PO4 studied in the presence of SiO2, Solid State Ionics, 2012, 213, 63–71, DOI:10.1016/j.ssi.2011.09.018 , Article; Proceedings Paper.
- C. E. Botez, J. D. Hermosillo, J. Zhang, J. Qian, Y. Zhao, J. Majzlan, R. R. Chianelli and C. Pantea, High-temperature phase transitions in CsH2PO4 under ambient and high-pressure conditions: A synchrotron X-ray diffraction study, J. Chem. Phys., 2007, 127(19), 194701, DOI:10.1063/1.2804774.
- W. Bronowska and A. Pietraszko, X-ray study of the high-temperature phase transition of CsH2PO4 crystals, Solid State Commun., 1990, 76(3), 293–298, DOI:10.1016/0038-1098(90)90840-8.
- R. B. Merle, C. R. I. Chisholm, D. A. Boysen and S. M. Haile, Instability of sulfate and selenate solid acids in fuel cell environments, Energy Fuels, 2003, 17(1), 210–215, DOI:10.1021/ef0201174.
- P. Zguns, K. Klyukin, L. S. Wang, G. Xiong, J. Li, S. M. Haile and B. Yildiz, Uncovering fast solid-acid proton conductors based on dynamics of polyanion groups and proton bonding strength, Energy Environ. Sci., 2024, 17(15), 5730–5742, 10.1039/d4ee01219d.
- A. Bohn, R. Melzer, R. Sonntag, R. E. Lechner, G. Schuck and K. Langer, Structural stucy of the high and low-temperature phases of the proton conductor Rb3H(SeO4)2, Solid State Ionics, 1995, 77, 111–117, DOI:10.1016/0167-2738(95)00047-a ; Proceedings Paper.
- R. Melzer, T. Wessels and M. Reehuis, The structure of the proton conducting phase of Rb3H(SeO4)2 at 470 K, Solid State Ionics, 1996, 92(1–2), 119–127, DOI:10.1016/s0167-2738(96)00432-8.
- A. Ishikawa, H. Maekawa, T. Yamamura, Y. Kawakita, K. Shibata and M. Kawai, Proton dynamics of CsH2PO4 studied by quasi-elastic neutron scattering and PFG-NMR, Solid State Ionics, 2008, 179(40), 2345–2349, DOI:10.1016/j.ssi.2008.10.002.
- H.-S. Lee and M. E. Tuckerman, The Structure and Proton Transport Mechanisms in the Superprotonic Phase of CsH2PO4: An Ab Initio Molecular Dynamics Study, J. Phys. Chem. C, 2008, 112(26), 9917–9930, DOI:10.1021/jp800342y.
- C. Dressler, G. Kabbe and D. Sebastiani, Proton Conductivity in Hydrogen Phosphate/Sulfates from a Coupled Molecular Dynamics/Lattice Monte Carlo (cMD/LMC) Approach, J. Phys. Chem. C, 2016, 120(36), 19913–19922, DOI:10.1021/acs.jpcc.6b05822.
- C. Dreßler and D. Sebastiani, Effect of anion reorientation on proton mobility in the solid acids family CsHyXO4 (X = S, P, Se, y =1, 2) from ab initio molecular dynamics simulations, Phys. Chem. Chem. Phys., 2020, 22(19), 10738–10752, 10.1039/c9cp06473g , Article.
- K. Yamada, T. Sagara, Y. Yamane, H. Ohki and T. Okuda, Superprotonic conductor CsH2PO4 studied by 1H, 31P NMR and X-ray diffraction, Solid State Ionics, 2004, 175(1–4), 557–562, DOI:10.1016/j.ssi.2004.03.042 ; Proceedings Paper.
- M. W. Louie, M. Kislitsyn, K. Bhattacharya and S. M. Haile, Phase transformation and hysteresis behavior in Cs1−xRbxH2PO4, Solid State Ionics, 2010, 181(3–4), 173–179, DOI:10.1016/j.ssi.2008.11.014.
- C. R. I. Chisholm and S. M. Haile, Structure and thermal behavior of the new superprotonic conductor Cs2(HSO4)(H2PO4), Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 937–946, DOI:10.1107/s0108768199009921.
- C. R. I. Chisholm and S. M. Haile, Superprotonic behavior of Cs2(HSO4)(H2PO4) – a new solid acid in the CsHSO4–CsH2PO4 system, Solid State Ionics, 2000, 136, 229–241, DOI:10.1016/s0167-2738(00)00315-5 ; Proceedings Paper.
- S. Sanghvi and S. M. Haile, A humidity-controlled precipitation technique enabling discovery of Rb3(H1.5PO4)2, J. Solid State Chem., 2021, 296, 121951, DOI:10.1016/j.jssc.2020.121951.
- L. S. Wang, S. V. Patel, S. S. Sanghvi, Y. Y. Hu and S. M. Haile, Structure and Properties of Cs7(H4PO4)(H2PO4)8: A New Superprotonic Solid Acid Featuring the Unusual Polycation (H4PO4)+, J. Am. Chem. Soc., 2020, 142(47), 19992–20001, DOI:10.1021/jacs.0c08870.
- C. R. I. Chisholm, Superprotonic Phase Transitions in Solid Acids: Parameters affecting the presence and stability of superprotonic transitions in the MHnXO4 family of compounds (X = S, Se, P, As; M = Li, Na, K, NH4, Rb, Cs), California Institute of Technology, Pasadena, 2003 Search PubMed.
- Y. Yamane, K. Yamada and K. Inoue, Superprotonic solid solutions between CsHSO4 and CsH2PO4, Solid State Ionics, 2008, 179(13–14), 483–488, DOI:10.1016/j.ssi.2008.03.031.
- V. A. Komornikov, G. V. Zimina, A. G. Smirnova, V. V. Grebenev and V. V. Dolbinina, Synthesis of complex cesium hydrosulfatophosphates, Russ. J. Inorg. Chem., 2012, 57(4), 478–484, DOI:10.1134/s0036023612040134.
- L. S. Wang, S. V. Patel, E. Truong, Y.-Y. Hu and S. M. Haile, Phase Behavior and Superprotonic Conductivity in the System (1–x)CsH2PO4 – xH3PO4: Discovery of Off-Stoichiometric α-[Cs1–xHx]H2PO4, Chem. Mater., 2022, 34(4), 1809–1820, DOI:10.1021/acs.chemmater.1c04061.
- M. Nic; J. Jirat and B. Kosata, IUPAC. Compendium of Chemical Terminology (the “Gold Book”), Blackwell Scientific Publications, 1997 DOI:10.1351/goldbook.
- G. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71(1), 3–8, DOI:10.1107/S2053229614024218.
- S. M. Haile and P. M. Calkins, X-ray diffraction study of Cs5(HSO4)3(H2PO4)2, a new solid acid with a unique hydrogen-bond network, J. Solid State Chem., 1998, 140(2), 251–265, DOI:10.1006/jssc.1998.7884.
- M. Ichikawa, Dependence of the Distortion of the Tetrahedra in Acid Phosphate Groups HnPO4 (n = 1–3) on Hydrogen-Bond Length, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 23–28, DOI:10.1107/s0108768187098355.
- International Tables for Crystallography. Volume G: Definition and exchange of crystallographic data. International Union of Crystallography, 2006. https://www.iucr.org/__data/iucr/cifdic_html/1/cif_core.dic/Idiffrn_reflns_av_R_equivalents.html (accessed).
- G. Xiong, L. S. Wang and S. M. Haile, Phase behavior, crystal structure, and superprotonic conductivity of Cs(H2PO4)1−2y(HPO4)y: phosphate deficient analogs to cubic CsH2PO4 in the (1 − x)CsH2PO4 − xCs2HPO4 system, J. Mater. Chem. A, 2025, 13(25), 19705–19716, 10.1039/d4ta08426h.
- C. B. Hübschle, G. M. Sheldrick and B. Dittrich, ShelXle: a Qt graphical user interface for SHELXL, J. Appl. Crystallogr., 2011, 44, 1281–1284, DOI:10.1107/s0021889811043202.
- W. T. Klooster, R. O. Piltz, T. Uda and S. M. Haile, Structure retinement and chemical analysis of Cs3Li(DSO4)4, formerly ‘Cs1.5Li1.5D(SO4)2’, J. Solid State Chem., 2004, 177(1), 274–280, DOI:10.1016/j.jssc.2003.08.015.
- M. Ichikawa, O–H vs. O⋯O distance correlation, geometric isotope effect in OHO bonds, and its application to symmetric bonds, Acta Crystallogr., Sect. B: Struct. Sci., 1978, 34, 2074–2080, DOI:10.1107/s0567740878007475.
- M. Wang, J. Ding, G. Xiong, N. Zhan, C. J. Owen, A. Musaelian, Y. Xie, N. Molinari, R. P. Adams, S. Haile and B. Kozinsky, Revealing the proton slingshot transport mechanism in solid acid electrolytes with machine learning molecular dynamic, arXiv, 2025, preprint, arXiv:2503.15389 DOI:10.48550/arXiv.2503.15389.
- A. S. Mikheykin, D. Y. Chernyshov, I. P. Makarova, V. V. Grebenev, V. A. Komornikov and E. V. Selezneva, Fast proton conduction in Cs3(HSO4)2(H2PO4) and Cs4(HSO4)3(H2PO4), Solid State Ionics, 2017, 305, 30–35, DOI:10.1016/j.ssi.2017.04.017.
| This journal is © The Royal Society of Chemistry 2026 |



