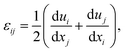Tramp element drag on grain boundaries controlling microstructural and residual stress equilibration in copper thin-films

Abstract

Metallic thin-films are found in a wide range of applications, from energy storage to high-power semiconductors used for green energy technologies. Engineering the growth and treatment of metallic thin-films influences their microstructures and residual stress states, which in turn affect their performance and properties. Here, we uncover the influence of tramp elements on the microstructural equilibration in electroplated Cu thin-films during annealing and evaluate the residual stress states in those Cu thin-films. The residual stress gradients within grains of two Cu thin-films, deposited from different electrolytes, are analysed utilising machine learning (ML) based high-resolution electron backscatter diffraction (HR-EBSD). In order to obtain quantitatively comparable stress mappings for both thin-films, simulated stress-free Kikuchi patterns are chosen as common references for HR-EBSD. Despite vastly different grain sizes after identical annealing treatment, similar stress gradients are present within the grains on both thin-film surfaces. The elemental composition at grain boundaries is analysed with atom probe tomography, revealing that S, Cl and O agglomerate in similar concentrations in the ppm-range at grain boundaries of both thin-films. The methodology corroborates that tramp element drag on grain boundaries during annealing may hinder grain growth from the as-deposited nanocrystalline structure, limiting effective stress relaxation and ultimately triggering failure modes.

---

Introduction

Metallic thin-films are found in a wide range of applications, from electrodes in lithium-ion and solid-state batteries,^1,2 over filters and beam splitters in optical components,³ to sensors and metallisations in microelectronic devices, as well as in high-power semiconductor devices used for green energy technologies.^4–8 In all of these applications, the mechanical, electric and thermal properties of metallic thin-films, which are closely entangled with their microstructure,^9–14 are of pronounced importance.^5,10,15 Microstructural equilibration in metallic thin-films, on the other hand, is largely dependent on their deposition parameters and post-treatment.^7,9,16 Thus, engineering the growth and treatment of metallic thin-films may influence their microstructures and residual stress states,^5,10,17 which in turn affects their performance and properties. Copper (Cu) thin-films are widely utilised as metallisations in microelectronic devices due to the high electrical and thermal conductivity of Cu.^11,18 These metallisations are commonly grown via electro-chemical deposition (ECD), wherein the thin-film grows onto the cathode, i.e. the chip, from organic complexes in electrolyte baths when voltage is applied.¹⁹ In order to control the geometry and growth of these Cu metallisations, various additives are added to the electrolyte bath. During ECD, the elemental components of the electrolyte and the additives may be incorporated into the thin-films as tramp elements.²⁰ Cu thin-films that are deposited via ECD at room temperature usually exhibit nanocrystalline grains after deposition, which subsequently grow due to self-annealing.^7,21,22 The growth rate and equilibration of Cu grains may be influenced by the tramp elements incorporated during ECD,²⁰ as well as the annealing temperature.²³ Hence, tramp elements may be vital for the suppression of uncontrolled grain growth in metallic thin-films and thus for upholding their mechanical integrity, since grain growth is generally related to a decrease in yield strength.^24,25

Furthermore, residual stresses in metallic thin-films play a vital role for their mechanical performance and integrity.^26,27 Therein, thin-films under compressive residual stress exhibit higher hardness, whereas residual stresses of any kind may impact the thin-film's adhesion to the substrate.^7,10,15 Various experimental methods have been established for the measurement of residual stresses in thin-films.^10,28 X-ray diffraction (XRD) yields reliable quantification of global residual stresses,²⁸ however its spatial resolution is limited to the X-ray spot size, which is larger than 100 µm for laboratory devices²⁸ and ∼30 nm for synchrotron radiation.²⁹ In order to analyse residual stress gradients over the thicknesses of thin-films, ion beam layer removal (ILR) can be utilised.^10,30–33 During ILR, a unilaterally fixed beam is fabricated from the sample utilising a focussed ion beam (FIB). Simultaneous scanning electron microscopy (SEM) imaging allows the observation of the deflection of the beam, as the FIB continuously removes layers from its top. By correlating the incremental deflection of the beam with the thickness of the removed layer and the material stiffness, the residual stress in the removed layer can be calculated.^10,30–33 Hence, ILR yields cumulative in-plane residual stress information over the beam width.

While both XRD and ILR are invaluable tools for the quantification of residual stresses in thin-films, the spatial resolution of these methods is limited in mapping stress distributions within individual grains. In this respect, the extraction of strain and stress information based on high-resolution electron backscatter diffraction (HR-EBSD) mappings is gaining momentum,^34–38 wherein the raw Kikuchi diffraction patterns of each pixel are evaluated.³⁹ While conventional EBSD evaluations for crystal orientation indexing rely on Hough transformation of Kikuchi diffraction patterns to increase analysis speed,^40,41 these Hough transformations do not hold the entire angular information that is contained in the raw Kikuchi diffraction patterns and result in indexing difficulties in highly deformed crystals with high dislocation densities.^40–43 Dictionary-based EBSD indexing, on the other hand, utilises the entire diffraction pattern and reliably indexes the crystal orientation by comparing the experimental pattern to a library of simulated ones,^42–44 thereby significantly increasing the indexing accuracy from 0.5°–0.1° for Hough-indexing to less than 0.01° for dictionary-indexing.⁴¹ HR-EBSD takes even more information from the raw diffraction patterns into account and extracts subtle shifts of the Kikuchi bands to determine deformations of the crystal and calculate stress states.³⁹ However, commercial analysis software for HR-EBSD mappings lacks the ability to comparatively quantify residual stresses in different mappings, since arbitrary reference pixels with minimal distortions are chosen from each of the EBSD mappings.³⁹ Hence, the analysis yields mappings of relative stresses utilising cross-correlation between the patterns of each pixel in relation to that reference pixel, which itself may not be entirely stress-free.³⁹ Thus, reference pixels are chosen in each mapping separately, making the analyses of different mappings not directly comparable.³⁹ Furthermore, indexing and strain calculation are usually two consecutive, but separate steps during the HR-EBSD analysis utilising commercial software.⁴⁵

In this study, the influence of tramp elements on the microstructural equilibration in ECD-Cu thin-films during annealing is analysed and the residual stress states in those Cu thin-films are evaluated. In particular, two Cu thin-films with different bulk tramp element concentrations are fabricated from electrolytes with different additive compositions and compared. The resulting different overall bulk tramp element contents in the deposited thin-films lead to pronounced differences in their grain sizes after annealing. Despite these differences, both thin-films exhibit similar residual stress gradients within grains and tramp element concentrations at individual grain boundaries. This convergence indicates a fundamental common mechanism for microstructural equilibration in Cu thin-films during annealing. Therein, the microstructural evolution from the as-deposited nano-crystalline structure is governed by a mechanical balance between tramp element drag on grain boundaries and the driving force for grain growth. To unravel these relationships, we employ a combination of EBSD, ML-based HR-EBSD, ILR and atom probe tomography (APT). Our findings demonstrate that by engineering bulk tramp-element concentrations during deposition, it is possible to tailor the microstructural and residual stress evolution in Cu thin-films during annealing, providing insights into the complex interplay between elemental grain boundary composition, microstructure, and residual stresses in metallic thin-films.

Results

Surface and cross-section microstructure of the investigated Cu thin-films

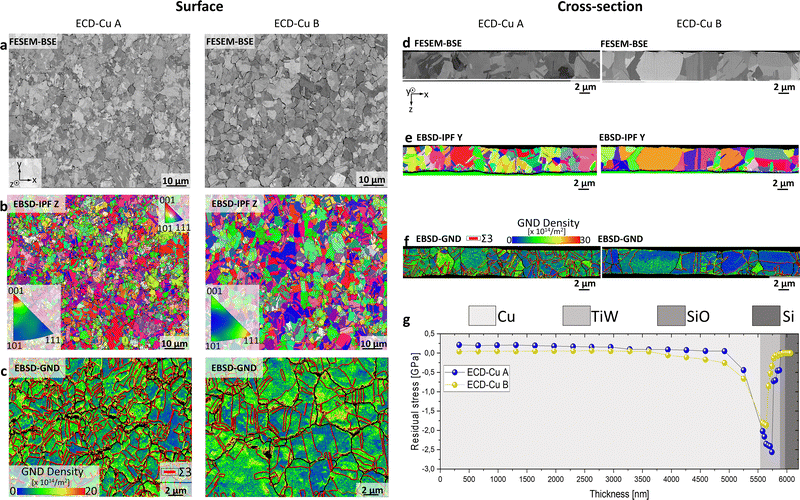
Fig. 1 shows microstructural and residual stress comparisons between two Cu thin-films, ECD-Cu A and B, which are grown from two electrolytes containing different additives. Both electrolyte solutions for A and B are mainly composed of Cu₂SO₄, H₂SO₄ and HCl. For the deposition of thin film ECD-Cu A, a three-component additive system comprising an accelerator, a suppressor and a leveller is utilised.¹² ECD-Cu B differs from ECD-Cu A by the utilisation of a two-component additive system.⁴⁶ The Cu thin-films are grown to a thickness of ∼5 µm on Si wafers with the interlayers of SiO and TiW with thicknesses of 50 nm and 300 nm, respectively. After ECD, both thin-films are annealed for 30 minutes at 400 °C, wherein the as-deposited nano-crystalline grains coarsen. Fig. 1a depicts field emission scanning electron microscopy (FESEM) backscatter electron (BSE) micrographs of both thin-film surfaces after annealing, revealing their polycrystalline microstructures due to the channelling contrast of grains and twins. Both thin-films are composed of polygonal grains, although ECD-Cu B exhibits qualitatively larger grains on average. The crystallography of the thin-film surfaces is discernible from the EBSD-IPF-Z mappings in Fig. 1b. The corresponding IPFs-Z in Fig. 1b reveal a (001)-texture in ECD-Cu A, whereas ECD-Cu B exhibits no similar preferred orientation. Fig. 1c illustrates EBSD geometrically necessary dislocation (GND) mappings of the thin-film surfaces with larger magnifications, which indicate inhomogeneous dislocation distributions within the grains.

Fig. 1 Microstructure and residual stress characterisation of the investigated ECD-Cu thin-films. Left: Microstructural surface characterisation of ECD-Cu A and B which are deposited from two different electrolytes and identically annealed. Right: Cross-sectional microstructures and residual stresses over the thicknesses of both Cu thin-films. (a) FESEM-BSE micrographs of the Cu thin-film surfaces. Grains and twins are discernible due to channelling contrast. Scalebars of 10 µm are valid. (b) EBSD-IPF-Z and EBSD-IPF-Z mappings of the Cu thin-film surfaces in (a). Scalebars represent 10 µm. (c) EBSD-GND density mappings of both Cu thin-film surfaces. GND densities are ranged from 0 to 20 × 10¹⁴ m⁻² and Σ3 twin-boundaries are marked in red. Scalebars of 2 µm are valid. (d) FESEM-BSE micrographs, (e) EBSD-IPF-Y mappings and (f) EBSD-GND mappings of the cross-sections of both Cu thin-films. The cross-sectional EBSD-GND density mappings are ranged from 0 to 20 × 10¹⁴ m⁻² and Σ3 twin-boundaries are marked in red. Scalebars of 2 µm are valid for all cross-sectional micrographs. (g) Residual stress analysis utilising ILR. The residual stresses are plotted in blue for ECD-Cu A and in yellow for B over the film-thickness. The shaded areas represent various layers of the multi-layer system. Cu, TiW, SiO and Si are represented by increasingly darker shadings.

Cross-sectional properties of the thin-films are provided in Fig. 1d–g. FESEM-BSE micrographs of thin-films A and B are depicted in Fig. 1d, EBSD-IPF-Y mappings in Fig. 1e and EBSD-GND mappings in Fig. 1f. The colourations of the EBSD-GND mappings in Fig. 1f indicate gradients in dislocation density over the film-thicknesses. Again, ECD-Cu A exhibits smaller grains than ECD-Cu B, as ECD-Cu A is composed of multiple grains over its thickness, whereas grains in ECD-Cu B span over its thickness mostly or entirely. Correlations of these microstructural differences with residual stresses over thin-film thicknesses are evaluated utilising ILR,¹⁰ the results of which are shown in Fig. 1g. Residual stresses in ECD-Cu A are plotted in blue, those in ECD-Cu B in yellow. The different material layers within the multilayer stack, namely Cu, TiW, SiO and Si, are represented by different background shadings in Fig. 1g. The measured thickness of Cu in both ECD-Cu A and ECD-Cu B is ∼5.6 µm. Both ECD-Cu A and B exhibit similar deflection behaviours in the Cu layers, maintaining relatively neutral stress values between 0 and 0.2 GPa. However, the stress profiles of the two thin-films deviate towards their interfaces of Cu/TiW. ECD-Cu A exhibits more compressive stress, around −2.5 GPa at about 5800 nm, while ECD-Cu B shows only around −1.8 GPa at about 5600 nm. Details about Cu thin-film deposition, FESEM imaging, EBSD mapping and ILR are provided in Methods.

Quantification of grain size and grain configuration on the surface and cross-section of ECD-Cu A and B

Fig. 2 exhibits analyses of the microstructural characteristics of ECD-Cu A and B, quantitatively correlating grain boundary density with grain size. All presented statistical results are based on the micrographs in Fig. 1, wherein ECD-Cu A contains about 525 grains, while ECD-Cu B contains 381 grains on their respective surfaces. Fig. 2a displays the frequency distribution of maximum Feret diameter. ECD-Cu A, plotted in blue, exhibits a significantly narrower grain size distribution with a pronounced peak around 2–3 µm, whereas the grain size distribution in ECD-Cu B, yellow, shows a lower maximum and slightly broader distribution with larger grains extending up to 25–30 µm. The overlaid statistical fit in Fig. 2a confirms that the mean grain size of ECD-Cu A is approximately half that of ECD-Cu B. This substantial difference in grain size may directly impact stress localisation, as smaller grains create more grain boundary interfaces per unit volume where stress discontinuities may develop. Fig. 2b quantifies the neighbour grain count distributions, revealing that grains in ECD-Cu A and B have similar numbers of mean neighbouring grains, namely about 5–7 grains. However, the mean grain density for ECD-Cu A is significantly higher as compared to ECD-Cu B, demonstrating that a larger number of grains is present in the former.

Fig. 2 Analysis of grain sizes and grain configurations in ECD-Cu A and B. The micrographs shown in Fig. 1 are statistically characterised. Properties of ECD-Cu A are plotted in blue and those of ECD-Cu B in yellow. (a) Grain-size distributions on the surfaces of both thin-films and their statistical fits. (b) Neighbour grain count distributions on the thin-film surfaces and respective fits. (c) Twin boundary densities and (d) grain densities in both thin-films, analysed for both their surfaces and cross-sections.

Fig. 2c compares the fractional twin boundary lengths of the two thin-films for both their surface and cross-sectional microstructures. ECD-Cu A exhibits an approximately 30% higher twin boundary density on its surface and nearly twice the density in its cross-section compared to ECD-Cu B. Finally, Fig. 2d displays the grain densities of both thin-films, confirming that ECD-Cu A possesses nearly twice the grain density of ECD-Cu B in both its surface and cross-sectional microstructure. These higher grain and twin densities directly translate to a greater boundary area per unit volume, creating more interfaces where stress discontinuities can develop.

ML-based HR-EBSD workflow for Kikuchi pattern recognition, indexing, local strain and stress analysis

Since Kikuchi patterns are generated by the diffraction of electrons on crystal lattice planes which fulfil the Bragg condition,^47,48 variations in the lattice plane spacing alter the appearance of the resulting Kikuchi patterns. This principle allows the indexing of various crystal orientations. Conventionally, raw Kikuchi patterns are processed utilising Hough transformation, which allow fast indexing.^49,50 However, by Hough transforming raw Kikuchi patterns, subtle details are dismissed, which hold additional information about the state of the diffracting lattice planes. Specifically, mechanical strain changes the spacings of diffracting lattice planes, which in turn alters their Kikuchi patterns. Thus, comparing Kikuchi patterns of strained crystals to stress-free ones allows the calculation of the stress-states in the crystals.⁵¹ Hence, the quantitative stresses and strains in the investigated Cu thin-films are calculated from the displacements between experimental and simulated stress-free Kikuchi patterns.^42,43,52,53 The ML-based workflow processes Kikuchi patterns by performing ML-based dictionary-indexing⁵⁴ and strain calculations.⁵¹ This allows not only the qualitative visualisation of stress distributions within the EBSD mapping, but also the quantitatively comparable calculation of stresses between mappings, since the simulated reference patterns are stress-free and unaltered between mappings.

The ML-model, indicated in Fig. 3a and described in Methods, utilises a convolutional neural network based on the Extreme Inception (Xception)⁵⁵ model, specifically optimised for Kikuchi pattern recognition.⁵⁴ For crystal orientation indexing, the same ML-model architecture is trained for both dictionary-based indexing as well as Hough-based indexing. Out of the two, dictionary-based indexing demonstrates superior performance, converging at 91% model validation accuracy, compared to Hough-based indexing converging at 79% model validation accuracy, as shown in Fig. S1. The improved dictionary-based ML-indexing accuracy enhances the reliability of GND density calculations, enabling more precise quantification of lattice distortion and strain gradients within the grains. Therein, the ML-based workflow enables quantitative stress evaluation through comparison of experimental Kikuchi patterns with simulated stress-free references for dictionary-based HR-EBSD analysis. As strain-induced lattice distortions manifest as measurable shifts in Kikuchi band positions and intensity distributions between experimental and simulated reference patterns, see Fig. 3b, these displacements can be converted to strain tensor components using the cross-correlation relationship shown in Methods.⁵¹ Thus, the ML-based HR-EBSD workflow outputs IPF- and strain mappings based on simulated stress-free reference patterns.

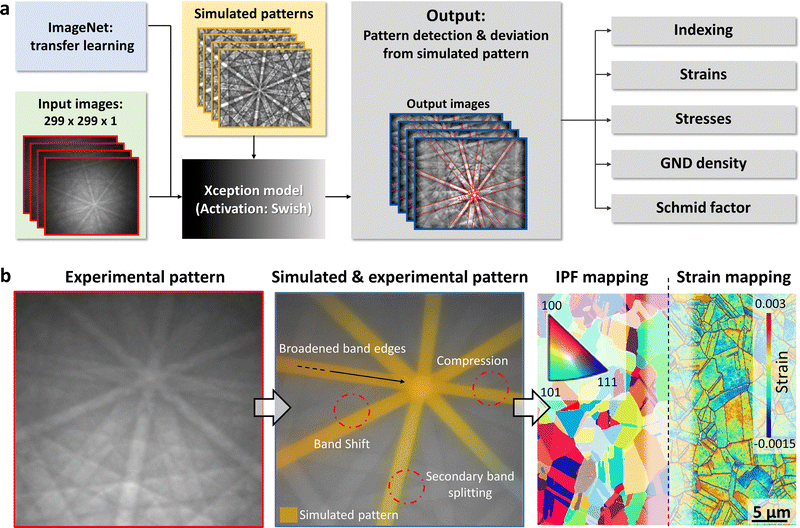Fig. 3 ML-based HR-EBSD analysis utilising simulated stress-free reference patterns. (a) Schematic workflow of the ML-based HR-EBSD analysis, comprising Kikuchi pattern detection and indexing utilising the Xception⁵⁵ model, as described in ref. 54, as well as strain and stress evaluation utilising cross-correlation⁵¹ between simulated and experimental patterns. (b) Comparing experimental (left) to simulated patterns (centre) allow dictionary-based orientation indexing and differences between the patterns, such as broadened band edges, compression of the bands, secondary band splitting and band shifts, are utilised for strain calculation. IPF-Z and strain mappings (right) are the result from the workflow, exemplarily shown for ECD-Cu A.

Microstructural and mechanical analysis of Cu thin-films: Stress, strain and dislocation density with ML-based HR-EBSD analysis

Fig. 4 provides a comprehensive, comparative analysis of microstructural and mechanical characteristics of ECD-Cu A and B, gained from ML-based HR-EBSD of the thin-film surfaces. The analysis leverages advanced Kikuchi pattern recognition, automated indexing and evaluation of Kikuchi pattern displacement enabled by the ML-based workflow depicted in Fig. 3a and further described in Methods. This allows for high-accuracy mappings of stresses, strains and GND densities in both thin-films, shown in Fig. 4b–d, respectively. Notably, ECD-Cu B exhibits lower local stress levels compared to ECD-Cu A, despite similarities in strain and dislocation density distributions, highlighting the influence of microstructural differences on mechanical properties. Fig. 4a presents band contrast micrographs, generated from the ML-based workflow in Fig. 3a, of ECD-Cu A and B. As in Fig. 1, both micrographs reveal polycrystalline microstructures with well-defined grain boundaries, but distinct differences in grain size and morphology are evident. ECD-Cu A displays a finer grain structure with a higher density of grain and twin boundaries, whereas ECD-Cu B is characterised by larger grains and consequently, a lower boundary density. These microstructural differences are critical, as they may influence the mechanical response and defect accommodation mechanisms within each thin-film. The white rectangles in Fig. 4a highlight regions of interest (ROIs) selected for detailed stress, strain and dislocation analysis in Fig. 4b–d. The ML-based HR-EBSD analysis, outlined in Fig. 3, processes the Kikuchi patterns from these ROIs, enabling accurate extraction of crystallographic orientation and band shifting in Kikuchi patterns, which forms the basis for subsequent strain mapping.

Fig. 4 Microstructural and mechanical analysis of thin-films using ML-based HR-EBSD analysis. Mechanical characterisation of ECD-Cu A is shown in the left column and ECD-Cu B in the right column. Selected ROI is marked by a white box. (a) Band contrast micrographs of ECD-Cu A and B. Scalebars of 10 µm are valid for both micrographs. (b) In-plane stress distribution, (c) In-plane strain distribution and (d) GND density distribution shown for the selected ROIs for both thin-films and their histograms, showing the respective pixel counts. Scalebars of 5 µm are valid for all ROI-mappings.

Fig. 4b presents colour-coded maps of local in-plane stress distributions within the ROIs of both thin-film surfaces, alongside respective statistical histograms indicating the pixel counts over the corresponding in-plane stress values. The stress mappings reveal pronounced spatial heterogeneity in both thin-films, with elevated stresses (red) typically concentrated in the vicinity of grain boundaries and triple junctions, and compressive stresses (blue) found within the grain interiors. Despite the stress gradients within grains, both thin-films exhibit similar stress-values overall, which is qualitatively apparent from the stress mappings in Fig. 4b. Note that the stress gradients are calibrated using the same simulated stress-free patterns for both ECD-Cu A and B instead of using different reference pixels from the measured EBSD mappings. The corresponding histograms quantitatively confirm this trend. The mean stresses for ECD-Cu A and B only deviate by 30 MPa and are evaluated to be ∼160 ± 21 MPa and ∼130 ± 17 MPa, respectively. Thus, ECD-Cu B exhibits a coarser grain structure, which reduces the density of grain boundaries, i.e. primary sites for stress concentration, and its overall stress distribution is slightly lower than that of ECD-Cu A. Twin boundaries may significantly influence stress transmission and accommodation mechanisms.^56–59 Hence, the smaller grain size and higher twin boundary density in ECD-Cu A, see Fig. 2, creates a more complex network of grain and twin boundaries, leading to more regions where stress fields interact and potentially concentrate, resulting in the more fragmented stress patterns observed in Fig. 4b. Moreover, the analysis emphasises the effectiveness of the neural network's dictionary-based indexing pathway in regions with complex or noisy diffraction patterns.

Fig. 4c provides the corresponding in-plane strain maps for the ROIs of both thin-films. The colouration represents local strain, with blue indicating compressive strain and red denoting tensile strain. Again, both ECD-Cu A and B display similar spatial patterns, with strain concentrations predominantly localised at grain boundaries and junctions, mirroring the stress distribution. Like for the stress mappings, the statistical histograms reveal that the overall strain distributions are remarkably similar between the two thin-films. The mean strains for ECD-Cu A and B are 0.16 ± 0.02% and 0.13 ± 0.02% respectively. Both thin-films show a span of comparable range from approximately −0.1% to 0.3%. Hence, stresses and strains for ECD-Cu A are slightly higher than for B, but they lie in the same range in both thin-films after microstructural equilibration during ageing.

Fig. 4d displays GND density maps for the ROIs of both thin-films. Both maps exhibit pronounced GND accumulations towards grain boundaries and triple junctions, with significantly lower densities within the grain interiors. The pattern is consistent with the expectation that grain boundaries act as sinks for dislocations. The statistical histogram of the GND density for both thin-films is nearly identical, with peaks around 1.5 × 10¹⁴ m⁻² for thin-film A and 1.2 × 10¹⁴ m⁻² for thin-film B, and distributions spanning from approximately 0.5 × 10¹⁴ to 2.5 × 10¹⁴ m⁻². In addition, the ML-based HR-EBSD workflow allows detailed statistical analysis as a function of orientation, as shown in Fig. S2. Details about the HR-EBSD analyses are provided in Methods.

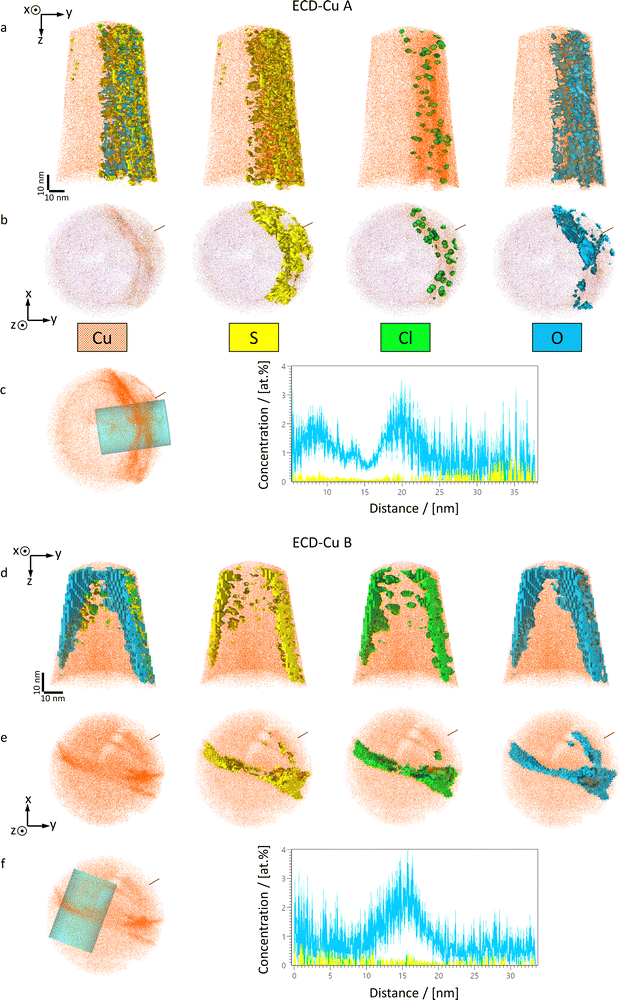
Elemental analysis of grain boundaries in ECD-Cu thin-films utilising APT

As additives are necessary in the electrolytes to control the growth of thin-films during ECD, these additives may be incorporated into the Cu thin-films as tramp elements. In order to evaluate the impact of potential segregation at Cu grain boundaries on the microstructural equilibration of the investigated Cu thin-films during annealing, APT analysis is performed. Fig. 5a and b depict the side- and top-views from the APT analysis of a grain boundary in ECD-Cu A, whereas Fig. 5c and d depict the analysis of a grain boundary in ECD-Cu B. Cu ions are visualised in orange, whereas S, Cl and O iso-concentration surfaces are illustrated in yellow, green and blue, respectively. Details about APT-specimen preparation, APT measurement and analysis are provided in Methods. It should be noted that no transmission Kikuchi diffraction (TKD) is performed on the APT-specimens, since it led to oxidation, as depicted in Fig. S5 and similarly reported in ref. 60. Nonetheless, the grain boundaries are discernible in the top-views in Fig. 5b and d due to their elevated densities of Cu-ions. Furthermore, the grain boundaries are visualised on the detector hit maps in Fig. S4.

Fig. 5 Analysis of tramp element segregation to grain boundaries in ECD-Cu A and B utilising APT. Elemental APT analysis of grain boundary segregation in the investigated Cu thin-films. (a) Side-view (y–z) and (b) top-view (x–y) of ECD-Cu A. (c) Atomic, decomposed concentration profile along the height of the turquoise cylindrical ROI in ECD-Cu A. O is plotted in blue, S in yellow and Cl in green. (d) Side-view (y–z) and (e) top-view (x–y) of ECD-Cu B. Cu ions are shown in orange, S iso-concentration surfaces in yellow, Cl iso-concentration surfaces in green and O iso-concentration surfaces in blue. (e) Atomic, decomposed concentration profile along the height of the turquoise cylindrical ROI in ECD-Cu B. O is plotted in blue, S in yellow and Cl in green. In both specimens, the grain boundaries are discernible by their increased Cu atom density, visible in the top-views. The laser incident direction is indicated by the purple arrow in the top-views in (b) and (e).

For the visualisation of the locations of increased tramp element concentrations, iso-concentration surfaces are shown in Fig. 5 for S, Cl and O. Here, however, iso-concentration surfaces are only utilised for proper visualisation of the location of these elements and not for quantification, as their concentrations are vanishingly small, especially for S and Cl, as quantitatively illustrated in the respective concentration profiles for O, S and Cl in Fig. 5c and f over the respective grain boundaries. The values for the S iso-concentration surfaces are set to 6 ppm for ECD-Cu A and 1 ppm for thin-film B. The iso-values for Cl are set to 1 ppm for ECD-Cu A and 2 ppm for ECD-Cu B, and to 55 ppm and 100 ppm for O, respectively. It should be noted that these values are chosen arbitrarily for proper visualisation. Nonetheless, the concentrations of these tramp elements at the analysed grain boundaries range in the same order of magnitude for both Cu thin-films.

Discussion

This study analyses local residual stress gradients within grains and tramp element concentrations at grain boundaries, as well as how their interplay affects the microstructural equilibration in two ECD-Cu thin-films during annealing, by utilising ML-based HR-EBSD and APT, respectively. Despite being deposited from different electrolyte compositions, both investigated Cu thin-films exhibit similar residual stress gradients within individual grains, as well as comparable tramp element concentrations at grain boundaries after annealing, see Fig. 4 and 5. This observation is particularly striking given the significant differences in their overall grain sizes and cross-sectional stress profiles depicted in Fig. 1 and 2. Specifically, ECD-Cu A demonstrates a mean grain size approximately half that of ECD-Cu B, with nearly twice the grain density on both its surface and its cross-section, as detailed in Fig. 2. The quantitative analysis in Fig. 2 reveals that ECD-Cu A exhibits a significantly narrower grain size distribution with a pronounced peak around 2–3 µm, while ECD-Cu B shows a broader distribution extending up to 25–30 µm.

To accurately quantify the residual stresses on the thin-film surfaces, a ML-based HR-EBSD workflow is utilised. Rather than relying on reference pixels³⁹ within the EBSD mappings, which may undermine the comparability of absolute stress quantification between samples, this workflow employs a dictionary of simulated stress-free Kikuchi diffraction patterns^42,43,53,54 as the reference standard. The developed approach enables direct comparison of experimental patterns against known stress-free references, setting a common zero-value for all EBSD mappings and thus allowing for calibrated, comparable quantitative analysis. The ML-model architecture, based on the Xception model,^55,61,62 indexes raw Kikuchi diffraction patterns with a model validation accuracy of 91%, compared to 79% for Hough-based indexing, as shown in Fig. S1. This enhanced precision is particularly crucial for analysing regions with high GND densities, e.g. near grain boundaries.^53,63–66 The ML-based HR-EBSD workflow also allows the calibrated calculation of residual stresses from the shifts between experimental patterns and simulated stress-free ones, as described in Methods. The ML-based HR-EBSD analysis of ECD-Cu A and B in Fig. 4b yields that, despite their substantial differences in grain sizes, the mean stresses on the surfaces deviate by ∼30 MPa, or ∼18.8%, with mean values of ∼160 ± 21 MPa and ∼130 ± 17 MPa, respectively, indicating that residual stress relief in ECD-Cu A was slightly less effective during annealing. Nonetheless, the residual stress and strain gradients within the grains of both thin-films are similarly distributed, as shown in Fig. 4b and c.

In order to analyse potential tramp element segregation to grain boundaries, APT is utilised. The analyses, shown in Fig. 5, provide direct evidence of agglomeration of S, Cl, and O at grain boundaries in both thin-films, with concentrations in the same order of magnitude and within the same ppm range. Specifically, the iso-concentration surfaces and concentration profiles in Fig. 5b, c, e and f reveal that these elements preferentially segregate to grain boundary regions, where they may hinder grain boundary migration. The similar tramp element concentrations at grain boundaries in both thin-films may explain why their microstructures equilibrate with vastly different grain sizes, discernible in Fig. 1, despite different overall tramp element bulk concentrations, determined via secondary ion mass spectroscopy by Wimmer et al. for the same two thin-films.⁸ It should be noted, the results in ref. 8 reveal that ECD-Cu A exhibits higher overall S, Cl, and O bulk concentrations than ECD-Cu B. However, ECD-Cu A also contains a significantly larger number of grain boundaries to accommodate these tramp element concentrations, as shown in Fig. 1 and 2 of the present study. Hence, the similar tramp element concentrations at grain boundaries, visualised utilising APT in Fig. 5, may represent the point where grain boundary movement is effectively halted by their drag force on the grain boundary.

The similarities in residual stress gradients and tramp element concentrations at grain boundaries, despite substantial differences in grain size distributions and overall microstructures, suggest that the mobility of grain boundaries rather than the initial microstructural configuration is the critical factor governing the microstructural equilibration and residual stress distribution during annealing. The similar residual stress gradients within grains on both thin-film surfaces, despite their different microstructures, illustrated in Fig. 4b, may be attributed to a common mechanism of grain boundary movement cessation. The stresses imposed on grains during boundary migration reach similar magnitudes before being arrested by tramp element drag, resulting in comparable local residual stress states. Hence, as the as-deposited nanocrystalline structure^9,67,68 undergoes annealing, grain growth is progressively decelerated as the tramp elements S, Cl, and O accumulate at grain boundaries. These impurities exert a drag force that opposes grain boundary migration, leading to a mechanical equilibrium where the driving force for grain growth is balanced by the opposing drag from tramp elements. This process may ultimately determine the final microstructure and is reflected in the residual stress state within grains.^67–70 Thus, the mechanism governing microstructural equilibration via grain growth from the nanocrystalline as-deposited structure^9,67,68 appears to be grain boundary mobility modulated by tramp element drag. Hence, higher overall bulk tramp element concentrations lead to a faster arrest of grain boundary movement by tramp element drag, halting grain growth and resulting in smaller grain sizes and slightly higher residual stresses, i.e. less relaxation during annealing.

Complementary to ML-based HR-EBSD, the ILR-based stress analysis reveals different behaviours of the two thin-films, as shown in Fig. 1g. ECD-Cu A exhibits more compressive stress (around −2.5 GPa) near the Cu/TiW interface compared to ECD-Cu B (−1.8 GPa). This difference may reflect the limited recovery and recrystallisation in the finer-grained structure of ECD-Cu A, attributed to the higher overall tramp element content⁸ and resulting in a higher cross-sectional grain boundary density in ECD-Cu A than in ECD-Cu B, illustrated in Fig. 1e. The larger residual stress gradient over ECD-Cu A's cross-section, determined utilising ILR, may be the result of less effective stress relief during annealing due to hindered grain growth and reduced grain boundary mobility compared to ECD-Cu B. Thus, the smaller grain sizes and slightly higher mean residual stress values, from both HR-EBSD and ILR, in ECD-Cu A indicate hindered grain boundary movement by tramp element segregation, which may prevent efficient stress relaxation through microstructural evolution during annealing. This effect may increase farther away from the free surface, i.e., towards the Cu/TiW interface, resulting in the different behaviour during ILR compared to ECD-Cu B.

The findings of this study demonstrate that tramp elements play a decisive role in controlling grain growth in ECD-Cu thin films during annealing, i.e. arresting grain boundary movement, which in turn governs the development and retention of residual stresses. To investigate these intricate relationships, an integrated methodology was employed, combining ML-based HR-EBSD, ILR stress analysis, and APT for comprehensive microstructural characterisation. This approach enables calibrated, comparable quantification of local stress states and direct observation of tramp element segregation at grain boundaries, providing new insights into how electrolyte composition and tramp element incorporation can be strategically leveraged to engineer thin-film microstructures with optimised performance for microelectronic applications and power-semiconductors for green energy applications.

Methods

Samples

The ECD-Cu thin-films are grown at room temperature, to a thickness of 5 µm on oxidised Si wafers. On the SiO₂ covered Si wafer, a TiW adhesion layer is sputtered, followed by a 150 nm Cu seedlayer. A commercial fountain plater is used to electrochemically deposit the investigated Cu layers to the desired thickness. Different additives were used for ECD-Cu A and ECD-Cu B, respectively. Both electrolyte solutions for A and B are mainly composed of Cu₂SO₄, H₂SO₄ and HCl. For the deposition of thin film ECD-Cu A, a three-component additive system comprising an accelerator, a suppressor and a leveller is utilised. After ECD, both thin-films are aged for 30 minutes at 400 °C in forming gas atmosphere, wherein the as-deposited nano-crystalline grains coarsen.

Ion layer removal (ILR)¹⁰

A Zeiss Auriga 40 Crossbeam system is utilised to fabricate a micro-cantilever and perform ILR. To map the local residual stress distribution across the beam's thickness, material is systematically removed in Cu at about 300 nm steps and near the interface and in thin films 15 nm step size increments within a defined 5 × 4 µm² area (ILR region) located near the fixed end using 50 pA and 30 kV. Each removal step is followed by imaging from four beam positions using both secondary electron and backscattered electron detectors. The generated image data is then analysed to obtain a deflection profile followed by finite element simulations to evaluate the residual stresses as a function of thickness.¹⁰

EBSD measurement, analysis and HR-EBSD pattern acquisition

Both conventional EBSD mappings and HR-EBSD pattern collection are performed utilising a Zeiss Gemini 450 FESEM with an Oxford Symmetry detector featuring 1244 × 1024 pixels. Measurements are conducted with 20 kV, 20 nA, a stepsize of 10 nm and a Hough resolution of 96. Oxford Instruments AZtecCrystal 3.1 is utilised to retrieve the grain boundary statistics as shown in Fig. 1 and 2, and the total grain count is subsequently analysed to evaluate grain density. The Kikuchi patterns for HR-EBSD are acquired with the same system utilising 20 kV, 12 nA, a dwell time of 400 ms, a stage tilt of 70° and an EBSD camera mounted at the angle of −7.04°.

ML-based HR-EBSD analysis

The ML-based HR-EBSD analysis is done in three stages: (1) simulation of reference patterns, (2) Xception model and (3) evaluation of strains and stresses. Firstly, the simulation of stress-free theoretical Kikuchi patterns for Cu is performed using the open-source EMsoft software,⁷¹ which is available on GitHub. EMsoft employs dynamical diffraction theory and Monte Carlo methods to generate accurate EBSD master patterns, incorporating experimental parameters, i.e. acceleration voltage of 20 kV, a working distance of 10 mm and a stage tilt of 70°. For this study, the lattice parameters of Cu (face-centred cubic, a = 3.615 Å) were input, and patterns were simulated for ∼22 000 reference orientations. These simulated patterns serve as training data for the model.

Secondly, to enable accurate and efficient analysis of Kikuchi diffraction patterns, we employ the ML-model architecture Xception⁵⁵ from Google. The implementation and adaptation of the Xception model for Kikuchi pattern analysis is carried out as described in Ding et al.⁵⁴ In addition, a transfer learning approach is utilised, which loads the initial convolutional layers with weights pre-trained on ImageNet.⁷² Traditional ReLU activations are replaced with Swish activation functions, providing improved gradient flow and enhanced performance on complex pattern recognition tasks. The model, which consists of three parts – entry, middle and exit flow, extracts the deviations of the experimental patterns with the simulated patterns in order to evaluate the strains and stresses.

The entry flow transforms raw Kikuchi patterns as input data into meaningful feature representations. It begins with two 3 × 3 convolution layers (299 × 299 × 3 → 149 × 149 × 64) extracting basic Kikuchi band features. Three successive Xception blocks employ depth-wise separable convolutions with residual connections, progressively reducing dimensions: Block 1 (75 × 75 × 128) captures low-level Kikuchi bands, Block 2 (38 × 38 × 256) extracts mid-level interplanar relationships, and Block 3 (19 × 19 × 728) identifies high-level crystallographic patterns and symmetry elements. These stages preserve gradient flow and enhance feature abstraction essential for subsequent crystal structure analysis.⁵⁴

The middle flow comprises eight identical residual Xception blocks maintaining 19 × 19 × 728 feature maps. Each block includes three depth-wise separable convolutions with Swish activations, enabling efficient representation of EBSD crystallographic features without altering spatial dimensions. This stage progressively abstracts Kikuchi patterns into higher-level representations, recognising complex multi-band interactions, crystal defects, and subtle orientation differences. Residual connections within each block preserve gradient stability, allowing identity mappings when further transformation is unnecessary. Constant filter depth balances computational efficiency with descriptiveness, ensuring that the network captures both fine-grained and global crystallographic relationships critical for accurate EBSD indexing.⁵⁴

The exit flow converts refined middle-flow features into classification outputs. A transition block applies swish activation and depth-wise separable convolutions, reducing 19 × 19 × 728 maps to 10 × 10 × 1024 via max pooling. Subsequent convolutions generate 5 × 5 × 2048 high-level representations encoding complete orientation and phase characteristics. Global average pooling produces a 2048-dimensional vector, removing spatial bias and minimizing overfitting. An optional 1000-unit dense layer can refine features before final swish-activated classification. Configurable output heads enable phase identification, orientation indexing, or stress analysis. Batch normalisation follows all convolutions, ensuring training stability and consistent crystallographic feature extraction across EBSD datasets.⁵⁴

Lastly, in-plane strain ε_ij on the crystal lattice can be calculated from the deviations of experimental patterns from simulated stress-free ones as,⁵¹

wherein u_i represents displacement-fields derived from pattern distortions. For cubic crystals like Cu, this approach achieves strain measurement error below 0.1%.³⁹

The calculated strain tensors are converted to stress values using Hooke's law for anisotropic materials:⁵¹

σ_ij = C_ijklε_kl

where C_ijkl represents the fourth-order elastic stiffness tensor, i.e. the specific elastic constants of Cu (C₁₁ = 168.4 GPa, C₁₂ = 121.4 GPa, C₄₄ = 75.4 GPa^13,14,73,74).

APT specimen preparation, imaging, measurement and analysis

The APT specimens are prepared from wafer pieces with Cu metallisations from the respective electrolytes. Half-grids are cut from the wafer pieces utilising a Micromac femtosecond laser ablation system, as described in ref. 75. The half-grids are then deoxidised with formic acid in an ultrasonic cleaning bath in order to remove redeposition from the laser ablation and any oxides on the metallisation surfaces. The half-grids are then EBSD-mapped utilising a Tescan Clara FESEM with an Oxford Symmetry detector. EBSD analysis is done with AZtec 6.0, the results of which are shown in Fig. S3. The final APT-specimens are prepared from these half-grids with a FEI Versa 3D HIVAC Ga-FIB. The APT measurements are done utilising a Cameca LEAP 5000 XR at 50 K and a laser pulse energy of 100 pJ. The APT reconstructions and elemental analyses are done with the Cameca IVAS 6 package embedded with AP Suite 6.3 software. All reconstructions are done based on the respective voltage curves. The concentration profiles in Fig. 5c and f are plotted for atomically decomposed O, S and Cl, utilising 0.05 nm binning over the height of the cylindrical ROIs. The mass spectra and detector hit maps of the specimens in Fig. 5 are shown in Fig. S4. TKDs are not done on the APT specimens shown in Fig. 5, as TKD mappings resulted in oxidation of the specimens.⁶⁰ An exemplary reconstruction of an oxidised APT specimen after TKD is shown in Fig. S5. Nonetheless, the respective grain boundaries in Fig. 5 are discernible by their increased ion densities in the top-views.

Author contributions

R.S. did the ML-based HR-EBSD analysis under the supervision of R.B.; C.C. did the data interpretation under the supervision of R.B.; C.C. and M.T. did the APT sample preparation, measurements and analyses in discussion with R.B.; B.S. performed the EBSD, HR-EBSD and ILR measurements; R.S. did the EBSD and ILR analysis under the supervision of R.B.; W.R. fabricated and provided the samples, with support from M.R. and J.Z; R.S. and R.B. planned the HR-EBSD and ILR; C.C., R.S. and R.B. wrote the paper; All authors discussed the results and commented on the paper.

Conflicts of interest

The authors declare no competing interests.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. All code that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma01192b.

Acknowledgements

The authors gratefully acknowledge the financial support under the scope of the COMET program within the K2 Center “Integrated Computational Material, Process and Product Engineering (IC-MPPE)” (Project No 886385). This program is supported by the Austrian Federal Ministries for Economy, Energy and Tourism (BMWET) and for Innovation, Mobility and Infrastructure (BMIMI), represented by the Austrian Research Promotion Agency (FFG), and the federal states of Styria, Upper Austria and Tyrol, P. No: P2.22 (EcoSolder) and P1.12 (NoMaTec). We acknowledge the support from J. Wosik for the HR-EBSD measurements and J. Wagner for the ILR measurements.

References

1. M. Häusler, O. Stamati, C. Gammer, S. Koller, B. Fuchsbauer, B. Schöppl, J. Koutný, F. Mühlbacher, T. Schnabel, D. Schäffer, J. de Looverbosch and R. Brunner, Commun. Mater., 2024, 5, 163.
2. N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264.
3. H. A. Macleod, Thin-Film Optical Filters, CRC Press, 5th edn, 2017.
4. S. P. Murarka, Handbook of Thin Film Deposition, Elsevier, 2018, pp. 329–384.
5. C. Cui, F. Falah Chamasemani, M. Reisinger, P. Imrich, W. Hartner, W. Robl and R. Brunner, npj Mater. Degrad., 2025, 9(1).
6. C. Cui, F. Falah Chamasemani, P. Paulachan, R. Sinojiya, J. Rosc, M. Reisinger, P. Imrich, W. Hartner and R. Brunner, npj Mater. Degrad., 2024, 8(1), 40.
7. R. Huang, W. Robl, H. Ceric, T. Detzel and G. Dehm, IEEE Trans. Device Mater. Reliab., 2010, 10, 47–54.
8. A. Wimmer, M. Smolka, W. Heinz, T. Detzel, W. Robl, C. Motz, V. Eyert, E. Wimmer, F. Jahnel, R. Treichler and G. Dehm, Mater. Sci. Eng., A, 2014, 618, 547–555.
9. C. V. Thompson, Annu. Rev. Mater. Sci., 2000, 30, 159–190.
10. R. J. Sinojiya, P. Paulachan, F. F. Chamasemani, R. Bodlos, R. Hammer, J. Zálešák, M. Reisinger, D. Scheiber, J. Keckes, L. Romaner and R. Brunner, Commun. Mater., 2023, 4(1), 11.
11. A. Wijaya, J. Wagner, B. Sartory, M. Häusler and R. Brunner, Commun. Mater., 2024, 5, 59.
12. S. Bigl, T. Schöberl, S. Wurster, M. J. Cordill and D. Kiener, Surf. Coat. Technol., 2016, 308, 404–413.
13. S. Wurster, S. Bigl, M. J. Cordill and D. Kiener, Microelectron. Eng., 2017, 167, 110–118.
14. S. Bigl, S. Wurster, M. J. Cordill and D. Kiener, Thin Solid Films, 2016, 612, 153–164.
15. L. B. Freund and S. Suresh, Cambridge University Press.
16. M. Stangl, V. Dittel, J. Acker, V. Hoffmann, W. Gruner, S. Strehle and K. Wetzig, Appl. Surf. Sci., 2005, 252, 158–161.
17. A. Wijaya, B. Eichinger, F. F. Chamasemani, B. Sartory, R. Hammer, V. Maier-Kiener, D. Kiener, M. Mischitz and R. Brunner, Mater. Des., 2021, 197, 109188.
18. W. Steinhögl, G. Schindler, G. Steinlesberger and M. Engelhardt, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 66, 75414.
19. M. Paunovic and M. Schlesinger, Fundamentals of Electrochemical Deposition, Wiley, 2nd edn, 2006.
20. T. P. Moffat, D. Wheeler and D. Josell, J. Electrochem. Soc., 2004, 151, C262–C268.
21. N. Alshwawreh, M. Militzer, D. Bizzotto and J. C. Kuo, Microelectron. Eng., 2012, 95, 26–33.
22. H. Lee, W. D. Nix and S. S. Wong, J. Vac. Sci. Technol., B:Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2004, 22, 2369–2374.
23. Q. Wei and L. J. Kecskes, J. Mater. Res., 2005, 20, 2081–2087.
24. P. Haasen, Physikalische Metallkunde, Springer, Berlin Heidelberg, 3rd edn, 1994.
25. G. Gottstein, Physikalische Grundlagen der Materialkunde, Springer, Berlin, Heidelberg, 3rd edn, 2007.
26. A. Akbari, J. P. Riviere, C. Templier, E. Le Bourhis and G. Abadias, Rev. Adv. Mater. Sci., 2007, 15, 111–117.
27. Y.-C. Huang, S.-Y. Chang and C.-H. Chang, Thin Solid Films, 2009, 517, 4857–4861.
28. I. C. Noyan and J. B. Cohen, Springer.
29. H. F. Poulsen, J. Appl. Crystallogr., 2004, 37, 797–804.
30. R. Treml, D. Kozic, J. Zechner, X. Maeder, B. Sartory, H. P. Gänser, R. Schöngrundner, J. Michler, R. Brunner and D. Kiener, Acta Mater., 2016, 103, 616–623.
31. R. Hammer, J. Todt, J. Keckes, B. Sartory, G. Parteder, J. Kraft and S. Defregger, Mater. Design, 2017, 132, 72–78.
32. M. Reisinger, J. Zalesak, R. Daniel, M. Tomberger, J. K. Weiss, A. D. Darbal, M. Petrenec, J. Zechner, I. Daumiller, W. Ecker, B. Sartory and J. Keckes, Mater. Design, 2016, 106, 476–481.
33. R. Schöngrundner, R. Treml, T. Antretter, D. Kozic, W. Ecker, D. Kiener and R. Brunner, Thin Solid Films, 2014, 564, 321–330.
34. C. Ophus, Microsc. Microanal., 2019, 25, 563–582.
35. L. Schretter, J. Eckert and C. Gammer, BIO Web of Conferences, 2024, vol. 129, p. 23006.
36. D. D. Gebhart, L. Schretter, A. Krapf, B. Merle, M. J. Cordill and C. Gammer, JOM, 2025, 1–10.
37. S. H. Mills, C. Gammer, P. Ercius, P. Hosemann and A. M. Minor, Oxford University Press, US, 2024, preprint.
38. A. K. Shukla, C. Ophus, C. Gammer and Q. Ramasse, Microsc. Microanal., 2016, 22, 494–495.
39. T. B. Britton, J. Jiang, R. Clough and E. Tarleton, Ultramicroscopy, 2014, 141, 32–39.
40. A. J. Schwartz, M. Kumar and B. L. Adams, Electron Backscatter Diffraction in Materials Science, Springer, 2nd edn, 2009.
41. Oxford Instruments, 2023, preprint.
42. S. Singh and M. De Graef, 2017, preprint.
43. M. De Graef and P. G. Callahan, J. Appl. Crystallogr., 2013, 46, 1782–1796.
44. Y. H. Chen, S. U. Park, D. Wei, G. Newstadt and M. De Graef, Microsc. Microanal., 2015, 21, 739–752.
45. BLG Vantage, 2024, preprint.
46. R. Huang, Stress and Microstructure Evolution of Electroplated Copper Films, Technische Universität Wien, 2013.
47. J. Kacher and B. L. Adams, et al. , Ultramicroscopy, 2010, 110, 1309–1313.
48. J. Kacher and B. L. Adams, et al., NanoAnalysis, Microsc. Microanal., 2024, 110, 1309–1313.
49. Y. Zhang, et al. , Microsc. Microanal., 2018, 24, 345–352.
50. J. Kacher and B. L. Adams, et al., NanoAnalysis, Microsc. Microanal., 2024, 110, 1309–1313.
51. S. I. Wright, J. Kacher and T. Ruggles, 2021, preprint.
52. P. G. Callahan and M. De Graef, Microsc. Microanal., 2013, 19, 1255–1265.
53. Y.-H. Chen, S. U. Park, D. Wei, G. Newstadt, M. Jackson, J. P. Simmons, M. De Graef and A. O. Hero, Microsc. Microanal., 2015, 21, 739–752.
54. Z. Ding, E. Pascal and M. De Graef, Acta Mater., 2020, 199, 370–382.
55. F. Chollet, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 1251–1258.
56. T. R. Bieler, P. Eisenlohr, C. Zhang, H. J. Phukan and M. A. Crimp, Curr. Opin. Solid State Mater. Sci., 2009, 13, 143–147.
57. Y. M. Wang, F. Sansoz, T. LaGrange, R. T. Ott, J. Marian, T. W. Barbee Jr and A. V. Hamza, Nat. Mater., 2010, 9, 689–693.
58. J. Y. Zhang, G. Liu and J. Sun, Scr. Mater., 2017, 130, 214–219.
59. S. Sinha, S. Ghosh, T. Nowell, B. Luster, J. J. Bhattacharyya and S. R. Agnew, Materialia, 2019, 5, 100230.
60. B. Gault, H. Khanchandani, T. S. Prithiv, S. Antonov and T. Ben Britton, Microsc. Microanal., 2023, 29, 1026–1036.
61. D. Jha, S. Singh, R. Al-Bahrani, W. Liao, A. Choudhary, M. De Graef and A. Agrawal, Microsc. Microanal., 2018, 24, 497–502.
62. A. Foden, D. M. Collins, A. J. Wilkinson and T. B. Britton, Ultramicroscopy, 2019, 207, 112845.
63. P. Lehto, Ultramicroscopy, 2021, 227, 113297.
64. T. M. Rampton, S. I. Wright, M. P. Miles, E. R. Homer, R. H. Wagoner and D. T. Fullwood, Mater. Charact., 2018, 136, 346–356.
65. D. Wallis, L. N. Hansen, T. B. Britton and A. J. Wilkinson, J. Struct. Geol., 2019, 125, 212–221.
66. A. J. Wilkinson, G. Meaden and D. J. Dingley, Ultramicroscopy, 2006, 106, 307–313.
67. Q. Wei and L. J. Kecskes, J. Mater. Res., 2005, 20, 2081–2087.
68. K. Barmak and K. R. Coffey, J. Vac. Sci. Technol., A, 2013, 31, 50818.
69. P. Müllner, C. Solenthaler and R. Spolenak, Acta Mater., 2014, 62, 295–307.
70. M. Hasanuzzaman, S. J. Ray and J. Haider, J. Mater. Sci.: Mater. Electron., 2016, 27, 9609–9615.
71. M. De Graef, M. Jackson, J. Kleingers, C. Zhu, J. Tessmer, W. Lenthe, S. Singh, M. Atkinson, S. Wright and H. Ånes, Zenodo, 2019 DOI:10.5281/zenodo.3489720.
72. J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li and L. Fei-Fei, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2009, pp. 248–255.
73. H. M. Ledbetter and E. R. Naimon, J. Appl. Phys., 1977, 48, 364–365.
74. S. Bigl, S. Wurster, M. J. Cordill and D. Kiener, Materials, 2017, 10, 1–8.
75. M. Tkadletz, N. Schalk, C. Mitterer and C. Czettl, Mater. Today Commun., 2024, 39, 108672.

---

Footnote

† Authors contributed equally.

---