CytroCell: a computational study in aqueous solution and infrared spectroscopic structural characterization

Abstract

A COSMO-RS conductor-like screening model for realistic solvation and molecular dynamics simulations conducted in GROMACS were used to gain insight into the structure and behaviour of CytroCell citrus nanocellulose in aqueous and more complex solutions, including the green solvent dihydrolevoglucosenone. DRIFT spectroscopy was used to investigate the structure of CytroCell nanocellulose solid samples obtained via acoustic cavitation of lemon, orange, and red orange industrial processing waste. The computational and experimental results obtained are relevant to all forthcoming applications of this new family of nanocelluloses sustainably sourced from the citrus industry's main waste product via the CytroCav circular economy process.

---

1 Introduction

Nanocellulose is a renewable and biocompatible nanomaterial with unique chemical and physical properties, including exceptional mechanical strength (high Young's modulus and tensile strength) while maintaining a low density, making it an ideal reinforcing material to improve polymer mechanical properties even at low loadings.¹ Due to its high specific surface area, improved thermal stability, and excellent optical properties, including transparency, nanocellulose has uniquely broad potential for industrial applications in numerous industrial products and devices.²

However, its large-scale production for industrial applications has been mainly constrained by the high expense associated with current manufacturing methods. These are characterised by high energy demand, low efficiency, and substantial waste generation.² Intense research is being devoted to identifying technically and economically viable nanocellulose production routes based on green chemistry principles, including shifting production from wood pulp to cellulose-enriched agro-industrial biowaste.³

First isolated in 2021 via hydrodynamic cavitation (HC) of industrial lemon and grapefruit processing waste,⁴ CytroCell is a unique nanocellulose consisting of submicron cellulose fibers in which a substantial part of the cellobiose units is esterified with citrate groups.⁵ Subsequent investigation showed that CytroCell can be sourced from industrial citrus processing waste (CPW), using either HC or acoustic cavitation (AC) conducted in water only.⁶ Dubbed CytroCav, this new process is promising from the industrial application viewpoint for the lack of effluents, the low energy demand, the small amount of lignin in CPW,⁷ and the unique properties of these new nanocellulose and unique pectin (named IntegroPectin) bioproduct families.

Readily dispersed in water or dissolved in dihydrolevoglucosenone (or Cyrene), the lemon CytroCell nanofibers impart for example pronounced chemical and physical stability alongside vastly enhanced proton conductivity to polymeric membranes suitable for large anion exchange membranes.⁸

Lemon CytroCell obtained via HC consists of rod-like cellulose microfibrils 0.5–3 µm long whose section varies between 110 and 420 nm.⁵ Grapefruit CytroCell obtained via HC consists of longer, ramified microfibrils whose diameter varies from 500 nm to 1 µm,⁵ whereas red orange CytroCell obtained via AC consists of elongated microfibers with a rod-like structure, 0.5–1.0 µm long with a section of about 100–200 nm.⁶

Studying lemon⁴ and red orange⁶ CytroCell using Fourier transform infrared (FTIR) spectroscopy, Pagliaro and co-workers made the hypothesis that in both CytroCell samples the sharp absorption bands at 1742 and 1648 cm⁻¹ are the stretching signals of the free and esterified carboxylic groups of citric acid in cellulose citrate formed as a result of the esterification reaction between the primary alcohol group of cellulose and the residual citric acid present in CPW. In this study, we investigate the structure of CytroCell through two complementary approaches: a computational study in aqueous solution and experimental structural characterization of solid samples using diffuse reflectance infrared Fourier transform (DRIFT) spectroscopy.

The conductor-like screening model for real solvents (COSMO-RS) and molecular dynamics simulations conducted in GROMACS was used to gain insight into the structural and behavioural study of CytroCell in aqueous and more complex solutions. Furthermore, the scope of the molecular dynamics study is expected to expand by incorporating additional solvents, specifically Cyrene, its geminal diol, as well as binary and ternary mixtures of these solvents.

DRIFT spectroscopy was employed as a tool for characterizing CytroCell solid samples obtained from the AC treatment of lemon, orange, and red-orange processing residues, focusing on the degree of esterification and other structural features of the cellulose nanofibers.

Both investigations aim to provide a deeper understanding of the structural properties and potential functional benefits of CytroCell nanocelluloses sustainably sourced from different citrus fruit biowaste, supporting further utilization in diverse practical applications in various industrial and technological contexts.

2 Results and discussion

2.1 Structural basis for cellulose citrate modelling

This section outlines the foundational concepts and design choices for modelling citrate esters of cellulose, integrating the molecular structure of the polymer, the properties of the citrate moiety, and the rationale for the resulting oligosaccharide structures used in this study.

Cellulose is a β-1–4 linked D-glucopyranose (β-Glcp) homopolymer. Most available structures for molecular dynamics simulations are crystalline, typically adopting fibrillar conformations. These structures are generally generated using specialised online platforms^9,10 or dedicated scripts.¹¹ The resulting conformations can be homopolymers or heteropolymers, either linear or branched, with a vast range of possible structures. However, these tools do not allow for the incorporation of non-standard residues, such as glucopyranose units derivatised via esterification with citric acid or related compounds.

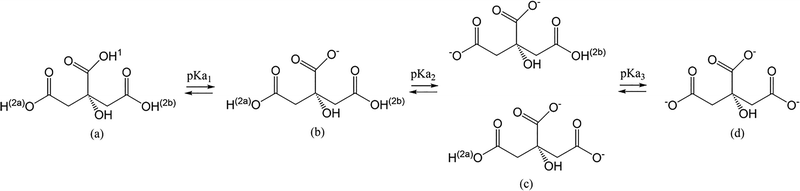
Citric acid is the 2-hydroxypropane-1,2,3-tricarboxylic acid. The three primary dissociation constants (pK_a values) for this triprotic acid are reported as follows: pK_a1 = 3.13, pK_a2 = 4.76, and pK_a3 = 6.40.¹²Fig. 1 shows the structure of the acid and its three deprotonated forms.¹²

Fig. 1 Citric acid and its successive deprotonated forms. (a) Citric acid (fully protonated), (b) citrate monoanion (monodeprotonated form, corresponding to pK_a1), (c) citrate dianions (corresponding to pK_a2) and (d) citrate trianion (corresponding to pK_a3).

The esterification of glucopyranose monomers can occur at various hydroxyl groups, but certain positions are more reactive. The primary hydroxyl group at C6 is often the most reactive and easily esterified due to its greater accessibility and lower steric hindrance.¹³ Secondary hydroxyl groups at C2, C3, and C4 can also be esterified, with their specific reactivity influenced by reaction conditions and steric effects. For this study, esterification was modelled primarily at the C6 position. The conversion of a carboxylic acid to an ester moiety alters the electronic environment, replacing a strongly electron-withdrawing acid group with a moderately electron-withdrawing ester, while the central carboxylic acid remains ionized at pH 6. This modification increases the electron density at the remaining terminal acid group, potentially elevating its apparent pK_a above that of free citrate (∼6.4). The final structure of the monoanionic citrate ester of β-D-glucopyranose used for all subsequent modelling is depicted in Fig. 2.

Fig. 2 Structure of a monoanionic citrate ester of β-D-glucopyranose residue. The atomic numbering shown (C1–C6) is that of the glucopyranosyl ring according to IUPAC carbohydrate nomenclature.

This integrated structural analysis directly informed the calculation of partial charges for force field parametrisation and the design of the oligomeric structures employed in the subsequent COSMO-RS and molecular dynamics simulations, as well as the methods and tools used to construct the models and refine their parameters.

The construction of a cellulose I-β nanofibril was performed using Cellulose-Builder,¹¹ configured with periodic boundary conditions along the chain axis only.

The resulting nanofibril contained 36 chains of 20 β-Glcp endo units each. A monoanionic citrate molecule was then geometry-optimised (Avogadro,¹⁴ MMFF94 force field¹⁵) and its low-energy conformational space was explored using CREST¹⁶ with the partially polarisable GFN2 force field. The optimised structure was validated against a DFT-optimised geometry (B3LYP/6-31G* in GAMESS¹⁷). This optimised citrate fragment was used to esterify the C6 hydroxyl group of selected β-Glcp residues within a single cellulose chain extracted from the nanofibril. Partial charges and geometry for the modified units were refined using the COSMO continuum solvation model in OpenMOPAC,¹² with parameters systematically compared against the GLYCAM06h force field¹⁸ to ensure consistency.

Due to computational constraints, a smaller oligosaccharide model was ultimately derived for the simulation studies, consisting of five β-Glcp residues with two esterified units (40% degree of substitution, Fig. 3, consistent with the experimental results shown in the following section).

Fig. 3 Oligosaccharide used in the molecular dynamics studies (dianionic form).

This structure corresponds to the first five residues of the modified chain, with terminal groups restored and electrical neutrality maintained by adding sodium ions. This model represents an optimal balance between computational feasibility and the study of association phenomena, serving as the basis for all subsequent solubility calculations and molecular dynamics simulations detailed in the following sections.

2.2 Solvation behaviour and supramolecular assembly

2.2.1 Solubility prediction and molecular interactions. The solubility of different charge states of the oligosaccharide (neutral to trianionic) was predicted using COSMO-RS methodology,¹⁹ which combines quantum chemical calculations with statistical thermodynamics to estimate physicochemical parameters without empirical parameter adjustments. In order to better reflect the comparability of the effects of different molecular interactions on solubility, the non-iterative model of the calculation is used: the molar solubility of solute i in pure solvent or mixed solvent (x_i) is calculated according to eqn (1)where μ^pure_i is the chemical potential of solute i, μ^solvent_i is the chemical potential of solute i in solvent, and ΔG_i,fusion represents the Gibbs free energy of fusion. In the following discussion, the value of log(x_i) serves as an indicator of the thermodynamic compatibility between the solute and the solvent (higher values indicate greater solubility or stronger thermodynamic affinity of the compound in the solvent).

Calculations were performed across pure solvents (water, Cyrene; Fig. 4a, dihydrolevoglucosenone or (1R,5S)-7,8-dioxabicyclo-[3.2.1]-octan-2-one, Gemdiol; Fig. 4b. Cyrene's geminal diol or (1S,5R)-6,8-dioxabicyclo-[3.2.1]-octane-4,4-diol) and binary mixtures (water–Cyrene, water–Gemdiol, Cyrene–Gemdiol) at 25 °C.-[3.2.1]-octan-2-one, Gemdiol – Cyrene's geminal diol or ((1S,5R)-6,8-dioxabicyclo-[3.2.1]-octane-4,4-diol, and water) and binary mixtures (water–Cyrene, Gemdiol–Cyrene, and water–Gemdiol) with different molar fractions within these mixtures.

Fig. 4 Structures of Cyrene (a) and Gemdiol (b). In aqueous solution, the carbonyl group of Cyrene undergoes water addition to form the corresponding geminal diol. Equilibrium is established rapidly, with the ratio between the two forms depending on the amount of water present.^20,21

In pure solvents, a remarkable solubility gradient was observed (Table 1), correlating with both solvent properties and solute charge state.

Table 1 Log(x) values obtained from COSMO-RS calculations for the oligosaccharide in its different charge states across the three pure solvents

Pure solvent	Neutral	Monoanion	Dianion	Trianion
Water	8.76	13.70	17.87	32.93
Gemdiol	7.89	6.05	3.89	12.12
Cyrene	5.22	−1.15	−4.89	−9.90

---

• In water (the most polar and protic solvent), the oligosaccharide exhibits the highest solubility across all charge states, with a remarkable increase as ionization progresses: the neutral form shows moderate solubility (8.76), while the trianionic form reaches a significantly higher value (32.93), confirming the strong affinity of highly charged species for water due to favorable electrostatic interactions. This is expected since water is highly polar and protic, efficiently stabilizing ionic species via electrostatic interactions and hydrogen bonding.

• In Gemdiol (solvent with intermediate polarity and protic nature), solubility values are lower than in water, especially for the anionic forms, indicating a reduced ability to stabilise negative charges.

• In Cyrene (polar but aprotic solvent), solubility decreases dramatically, becoming negative for the more highly charged species. The neutral form is moderately soluble (5.22), but the monoanionic, dianionic, and trianionic forms exhibit negative log(x) values, indicating poor solubility. This suggests that cyrene is incompatible with highly charged oligosaccharides, likely due to its limited ability to stabilise ionic species.

The behaviour in binary mixtures revealed complex, charge-dependent solvation phenomena. For the water–Cyrene mixtures the complete set of results is compiled in the heatmap below (Fig. 5), which presents solubility values log(x) as a function of the water fraction in the mixture for the four charge states.

Fig. 5 Heatmap of solubility vs. water fraction for the neutral, monoanionic, dianionic and trianionc structures in a water–Cyrene mixture.

Regardless of the charge state, all compounds exhibit a similar trend at low water fractions: in pure Cyrene, solubility reaches its lowest values for all species. The neutral form, although only slightly soluble, still shows a positive value in pure Cyrene. However, this aprotic solvent fails to stabilize the ionized forms, resulting in increasingly negative log(x) values as the charge increases (from charge 0 to −3, the solubility decreases almost linearly, with a slope of approximately −5).

The addition of water significantly enhanced solubility, though the neutral compound exhibited a distinct co-solvation effect, reaching maximum solubility at ∼75.7% water fraction (interpolated using a polynomial model, order = 4) before decreasing at higher water concentrations (Fig. 6).

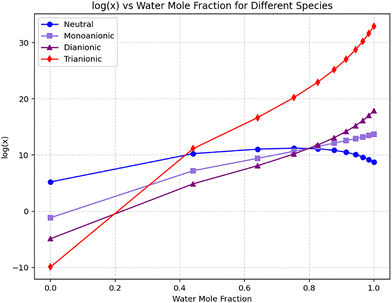Fig. 6 Evolution of solubility as a function of water mole fraction for the neutral, monoanionic, dianionic and trianionc structures in a water–Cyrene mixture.

Water–Gemdiol mixtures showed remarkably similar behaviour to water–Cyrene mixtures at high water fractions (>77%), with Pearson correlation coefficients exceeding 0.99 for all charge states (Table 2), indicating water's dominant role in solvation regardless of cosolvent identity. The slight shift in the monoanion-dianion inversion point (to 77.0% water fraction) suggests competitive hydrogen bonding between Gemdiol and water molecules.

Table 2 Pearson correlation coefficients comparing the behaviour of water–Cyrene and water–Gemdiol mixtures at high water fractions (0.75–1)

Charge state	Neutral	Monoanion	Dianion	Trianion
Pearson correlation coefficient (ρm1,m2)	0.9942	0.9976	0.9996	0.9994

---

Cyrene–Gemdiol mixtures showed intermediate behaviour, with Gemdiol providing significantly better charge stabilization than Cyrene but remaining less effective than water. The trianionic species exhibited the most dramatic solubility enhancement upon Gemdiol addition, rising from near-insolubility in pure Cyrene (log(x) = −9.90) to near-zero values with just 8.8% Gemdiol fraction.

Although Gemdiol provides the necessary proticity for enhanced solubilization, its effect remains weaker than that of water, as evidenced by the lower solubility values observed in pure Gemdiol compared to pure water. This implies that while Gemdiol contributes significantly to hydrogen bonding, it does not replicate the full solvation capacity of water for the charged species.

Predictions of modelling fit experimental results. In the first experimental study showing solubility of lemon CytroCell nanofibers in water and in Cyrene, Fontananova and co-workers showed indeed enhanced solubility in pure water, with good solubility also in Cyrene, provided that the CytroCell nanofibers were further reduced in size via mechanical grinding, followed by immersion in the solvent at room temperature for 24 h followed by 30 min sonication.⁸

2.2.2 Molecular basis of solvation phenomena revealed by MD simulations. Molecular dynamics simulations were employed to provide mechanistic insights into the solubility trends predicted by COSMO-RS. All simulations were performed using GROMACS 2024.5,²² with parameters for the oligosaccharide derived using AmberTools23²³ and cross-validated against the GLYCAM06h force field.¹⁸ The systems (Table 3) were energy-minimized and equilibrated under NVT and NPT ensembles at 298.15 K and 1 bar using stochastic thermostats and barostats to ensure correct ensemble generation.

Table 3 Summary of system compositions

System	Number of oligosaccharide molecules	Number of water molecules	Average^a box volume (nm^3)	Concentration (×10^−2 mol L^−1)
a Average value over 20 ns of simulation run.
A	1	3154	98.325 ± 0.082	1.69
B	2	3105	97.696 ± 0.043	3.40

---

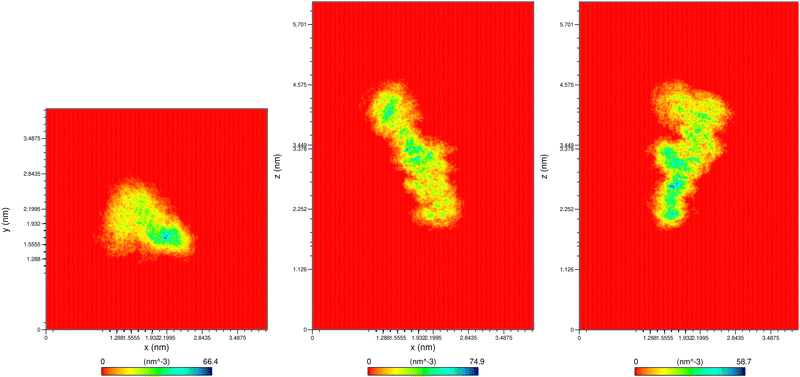
The stability of a single oligosaccharide (A system, Table 3) in aqueous solution was first confirmed. Conformational stability was assessed through 2D density maps (Fig. 7) and RMSD analysis, which converged to a stable value of approximately 0.3 nm, indicating a well-equilibrated system.

Fig. 7 2D Density maps of the A system. Left to right, average over z, y and x.

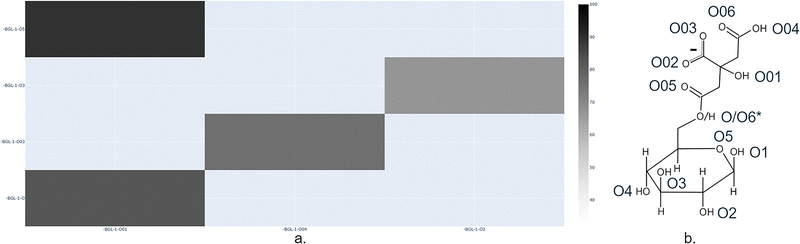
This structural integrity was maintained by an intricate network of intramolecular hydrogen bonds, with an average of 4.41 persistent bonds identified throughout the trajectory. As illustrated in the hydrogen bond occurrence matrix (Fig. 8) over all frames from the MD-Davis python package,²⁴ the most stable interactions involved the citrate groups (BGL-1-O01 and BGL-1-O04 as donors; BGL-1-O03 as acceptor), highlighting their role in stabilizing the molecular conformation.

Fig. 8 (a) Matrix of intramolecular hydrogen-bond stability. Donor groups are represented along the x-axis and acceptor groups along the y-axis. Matrix elements are colour-scaled from lighter shades (least stable H-bonds) to darker shades (most stable H-bonds). (b) Structure of the monoanionic citrate ester of β-D-glucopyranose (BGL), defining the nomenclature employed throughout this figure (and following figures). *Aglycone linkage/free C6 hydroxyl.

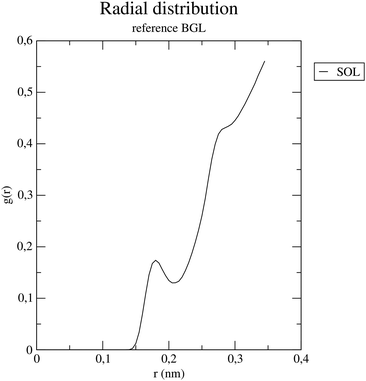
To quantify the solvation structure, radial distribution function (RDF) analysis was performed on A System. The resulting g(r) curve (Fig. 9) revealed a highly structured aqueous environment, with a sharp first peak at 0.165 nm indicating a close and stable first solvation shell, followed by a minimum and a second, broader peak at 0.260 nm, suggesting a more dynamic secondary hydration layer (structured but less stable).

Fig. 9 g(r) curve for the A system with r, distance of water (SOL) from oligosaccharide (BGL).

The dynamics of hydrogen bonding were further characterised through kinetics analysis. The hydrogen bond time autocorrelation function, C(t) (according to the theory of Luzar and Chandler²⁵), was calculated and fitted to a double exponential decay (eqn (2)) to distinguish between fast and slow relaxation processes. Hence, the parameter adjustment shows the coexistence of two hydrogen bond populations.

A₁ and A₂ represent the relative amplitudes of two distinct relaxation processes governing the hydrogen bond autocorrelation decay. Fig. 10 shows the hydrogen bond autocorrelation function C(t) for bulk water (blue) and the water–oligosaccharide system (green), with corresponding fitted τ values.

Fig. 10 Hydrogen bond autocorrelation function C(t), in bulk (blue curve) and in the A system (green curve), with the extracted τ values after double exponential fitting.

This analysis revealed that hydrogen bonds between water and the oligosaccharide exhibited significantly longer lifetimes (〈τ〉_SOL-BGL = 11.66 ps) than those between water molecules in the bulk (〈τ〉_bulk = 5.19 ps). The parameters extracted from the fit—particularly the slower relaxation time τ₂, which increased from 14.33 ps in bulk to 21.13 ps around the solute—demonstrate that water molecules are temporarily “tethered” to the oligosaccharide, especially around the citrate moieties.

Specific citrate oxygen atoms were found to engage in hydrogen bonding for almost 61% of the simulation time (Fig. S6), providing a direct molecular explanation for the high aqueous solubility predicted for the charged species.

The MD methodology confirmed that the aqueous solubility predicted for anionic species stems from a robust and persistent hydration shell, particularly around the charged citrate groups, which significantly reduces water exchange kinetics and stabilises the solute in solution.

2.2.3 Supramolecular assembly and implications. Building upon the understanding of single-molecule solvation, we next investigated how these solvation properties influence intermolecular interactions and potential self-assembly. Molecular dynamics simulations revealed the spontaneous formation of stable supramolecular structures between two oligosaccharide units in aqueous solution (B system, Table 3), providing crucial insights into the balance between solubility and association.

When two dianionic oligosaccharides were placed in proximity (initial separation: 0.663 nm), they rapidly associated into a well-defined suprastructure that persisted throughout the simulation period. This observation is particularly significant given the strong hydration shell identified around individual molecules, suggesting that the same citrate groups that promote solubility through extensive water interactions can also mediate intermolecular association when hydration is compromised or when molecular proximity allows for direct interaction.

The associated oligosaccharides adopted an almost anti-parallel arrangement, as evidenced by minimal deviation between their principal axes of inertia (8.872° for major axes, 30.495° and 29.744° for medium and minor axes, respectively). The center of mass distance between backbones stabilised at 0.49 ± 0.02 nm, indicating tight molecular packing (Fig. 11). Water molecules were totally excluded from the interface, as confirmed by visual examination, 2D density maps and density profiles along each axis.

Fig. 11 2D density maps of the dimer system (B) showing tight association and water exclusion from the interface region.

Furthermore, the solvent-accessible surface area analysis provided quantitative evidence of this association. The measured Solvent Accessible Surface Area (SASA) for the dimer system (20.997 nm²) represented a 22% reduction from the theoretical value expected for two non-interacting oligosaccharides (26.926 nm²), confirming substantial burial of surface area upon association.

This significant reduction in solvent-accessible surface area was primarily driven by the formation of direct intermolecular contacts, most notably a network of hydrogen bonds. Analysis of these interactions revealed exceptionally stable intermolecular connections, particularly between citrate groups (Fig. 12). Intermolecular interactions dominate in terms of half-life, persisting for up to 98% of the simulation time, which indicates exceptionally strong stabilisation of the suprastructure, even though some intramolecular bonds remain, particularly between the free hydroxyl group at position C6 and a hydroxyl group at either position C3 or C4 on the same oligosaccharide.

Fig. 12 Matrix of H-bonds between two oligosaccharide molecules (see Fig. 8 for the nomenclature used in the study).

The charge on the carboxylate groups of the citrate moieties appeared crucial for this stabilisation, facilitating strong electrostatic complementarity between associating units.

Despite this extensive intermolecular association, the suprastructure maintained a well-hydrated exterior. Free hydroxyl groups at positions C2, C3, and C4, along with available donor groups of the esterified moieties, engaged in extensive hydrogen bonding with surrounding water molecules. Radial distribution function analysis confirmed that the hydration shell surrounding the suprastructure was identical in size to that observed around single oligosaccharides, indicating maintained solvation despite the association.

2.2.4 Integrated solvation-assembly model. The combination of COSMO-RS predictions and molecular dynamics simulations has enabled the development of a simplified oligomeric model explaining cellulose citrate behaviour in solution at the molecular level. Although significant limitations must be acknowledged regarding its application to real CytroCell systems, our integrated approach provides valuable insights for solvent selection. It captures fundamental interactions governing solubility and association, particularly the crucial balance between charge-enhanced hydration and intermolecular assembly mediated by citrate groups.

However, these findings must be interpreted with caution when extrapolating to CytroCell, which comprises complex mixtures of polymers and oligomers with heterogeneous substitution patterns and chain lengths. The supramolecular associations observed in our dimer system likely represent simplified analogues of the more intricate networking occurring in real systems, where polydispersity and structural heterogeneity may create additional mechanisms for association or dissolution. Experimental validation is essential to confirm these predictions. To bridge this gap, we employed diffuse reflectance infrared Fourier transform (DRIFT) spectroscopy to directly probe the molecular interactions in cellulose citrate systems, allowing us to compare experimental observations with our computational findings.

2.3 DRIFT investigation

The infrared analysis begins with the study of cellulose infrared spectra, which serve as a reference for interpreting the microcellulose bands in the DRIFT spectra of the considerably more complex CytroCell samples.

The infrared spectra of three cellulose types, wood pulp, native cellulose and microcrystalline cellulose, treated at different pH values, are shown in the SI (Fig. S9). For each cellulose type and each pH, the samples were prepared by adding a sufficient amount of aqueous solution (at the indicated pH) to form a suspension, which was left with agitation for 24 hours. This allows the solvent to penetrate the cellulose fibers and act as a spacer through a swelling process. After this period, the samples were filtered, the solvent was allowed to evaporate under ambient conditions, and the residual solvent was removed by drying in a vacuum oven at room temperature.

The main conclusion drawn from the DRIFT spectra shown in Fig. S9 is that the pH of the solution used for swelling the wood pulp and celluloses does not significantly affect their structure, as no major changes in band shape or maximum band position are observed. For discussion and comparison, the bands observed in the DRIFT spectra of wood pulp and two cellulose types, after exposure to aqueous solutions at pH 7, are shown in Fig. 13.

Fig. 13 DRIFT spectra of cellulose microcrystalline (red line), native cellulose (blue line) and wood pulp (black line), after swelling and solvent evaporation at pH 7. The spectra were normalized to the maxima.

The O–H stretching bands show differences in bandwidth and maximum position when comparing the DRIFT spectra of native cellulose with the other two samples. Specifically, native cellulose exhibits a narrower O–H band with a maximum at ∼3330 cm⁻¹, whereas the maxima for wood pulp and microcrystalline cellulose are at ∼3280 cm⁻¹ (with a noticeable shoulder at ∼3475 cm⁻¹) and ∼3315 cm⁻¹, respectively.

This observation suggests that native cellulose displays a more isotropic hydrogen bonding behavior, with the O–H stretching maximum corresponding to intermolecular hydrogen bonds involving hydroxyl groups of glucose units primarily in amorphous domains.²⁶

In contrast, the broader νO–H bands and the ∼70 cm⁻¹ shift in maximum observed for microcrystalline cellulose indicate different O–H interactions, significantly influencing the band shape.

The DRIFT spectrum of wood pulp closely resembles that of microcrystalline cellulose. However, wood pulp is a more complex material, comprising cellulose (typically 70–80% or less), hemicellulose (20–30%, sometimes higher), lignin (1–2%), and minor constituents.²⁷ Additional bands in the 1730–1710 cm⁻¹ region, attributed to C=O stretching modes, suggest the presence of components other than cellulose, such as lignin or esterified molecules. The band at 1645 cm⁻¹ can be directly associated with adsorbed water, as it is straightforwardly attributed to the δHOH bending mode of water.

Characteristic lignin bands are observed at 1515 cm⁻¹ (νC=C of the aromatic ring) and 1239 cm⁻¹ (νC–O). Hemicellulose contributions are largely overlapped with those of cellulose and lignin, although a feature at ∼1070 cm⁻¹ (νC–O–C) can be specifically attributed to hemicellulose.²⁸

Sample crystallinity can be inferred from the relative intensity of the band at 1280 cm⁻¹, corresponding to C–H bending, which increases with greater crystallinity. Meanwhile, the band at 1200 cm⁻¹, assigned to the C–O–C stretching mode of the pyranose ring, remains unaffected by crystallinity changes.²⁸

By estimating the intensities of the specified bands in the DRIFT spectra, as illustrated in Fig. S10, the crystallinity of cellulose can be evaluated using eqn (3):²⁸

%Cryst. = (1.06 × (I₁₂₈₀/I₁₂₀₀) + 0.19) × 100 (3)

The crystalinity was 47% for native cellulose and wood pulp, and 87% for cellulose microcrystalline.

The CytroCell sample spectra (4000–850 cm⁻¹ region) are presented in Fig. 14, normalized to the νC–O–C band of pyranose rings (at ∼1070 cm⁻¹). The band structure and intensity are very similar for the orange CytroCell samples. While for the lemon samples, the structure remains comparable, but the relative band intensities clearly change.

Fig. 14 DRIFT spectra of CytroCell obtained from lemon (black line), red orange (red line) and sweet orange (blue line). Spectra normalized to the band at ∼1070 cm⁻¹.

In the higher wavenumber region, the spectra are dominated by the stretching modes of OH and CH groups (νOH and νCH), centered at around 3330 and 2925 cm⁻¹, respectively. The shapes of these bands are very similar, suggesting that all samples are likely to exhibit comparable hydrogen bonding behavior. Moreover, this pattern closely resembles the band structure of native cellulose, indicating great variability in the interactions of OH groups within the cellulose microfibril domains. The similarity between cellulose in the CytroCell samples and wood pulp is reflected by the bands observed at 1070 and 1608 cm⁻¹, which are associated with domains containing hemicellulose.

The main differences between the spectra of cellulose and CytroCell samples are observed in the 1800–1500 cm⁻¹ region. As previously mentioned, the feature at 1740 cm⁻¹ in the wood pulp spectrum may indicate the presence of esterified molecules or components other than cellulose. Assuming this is related to the degree of esterification, these bands exhibit significantly higher relative intensity in CytroCell samples, suggesting that the cellulose chains are more extensively esterified than in wood pulp.

In Fig. 14, the bands associated with the stretching modes of carbonyl groups (νC=O), are a very intense band at ∼1740 cm⁻¹, for ester groups, and at ∼1640 cm⁻¹ for acid groups. The asymmetric stretching modes of carboxylates (ν_asCOO⁻) yield several bands in the 1600–1500 cm⁻¹ region. In this region, the relative intensities of the ester-related components are much higher for lemon CytroCell, suggesting a higher degree of esterification.

The band centered at 1440 cm⁻¹ likely arises from overlapping modes: ν_asCOO⁻, ν_sCOO⁻ of the acid groups, and methyl asymmetric deformation (δ_asCH₃) of ester groups. Other bands at ∼1370 and ∼1280 cm⁻¹ are attributed to νC–O–C and δ_sCH₃ modes, respectively, while the very strong band centered at 1070 cm⁻¹ can be assigned to the several overlapped bands (ν(C–O–C)_pyranose + νC–OH + νCC).

The degree of esterification for each sample (percentage of esterified carboxyl groups) was determined through spectral analysis in the 1550–1800 cm⁻¹ region. It was calculated as the ratio of the band areas for esterified carboxyl groups to the total carboxyl groups (eqn (4)) using a method derived from the analysis of pectins:^29,30

The band areas in the sample's spectra, used to estimate the degree of esterification, were determined by decomposing the 850–1800 cm⁻¹ range into a sum of Voigt components using nonlinear least-squares fitting.

Table 4 presents the centers and integrated areas of these components for the three cellulose samples, along with the degree of esterification, as determined in accordance with previous studies.^29,31

Table 4 Positions and areas of the band components identified from the decomposition of DRIFT spectra in the regions 1200–930 cm⁻¹ and 1790–1550 cm⁻¹, along with the degree of esterification (DE), hemicellulose (Hcell) and crystallinity (% Crys)

IR band	Lemon CytroCell		Red orange CytroCell		Sweet orange CytroCell
	Center (cm^−1)	Area	Center (cm^−1)	Area	Center (cm^−1)	Area
ν(C=O)methyl-ester	1754	8.75	1743	12.32	1742	10.82
ν(C=O)ester	1730	23.22	1715	11.17	1715	17.20
ν(C=O)carboxylic acid	1651	25.33	1649	24.36	1648	20.35
ν as(COO^−)	1605	10.65	1603	15.08	1604	18.96
ν(C–O–C)pyranose	1160	14.97	1149	20.77	1144	24.39
	1108	33.12	1099	30.59	1098	18.82
	1068	16.01	1072	10.04	1069	18.44
ν(C–O–C)glycoside	1042	22.05	1049	22.66	1046	18.72
ν(C–OH)pyranose + ν(C–C)pyranose	1014	18.86	1015	21.93	1016	18.75
	971	11.33	971	16.24	970	14.37
DE	—	0.47	—	0.37	—	0.42
Hcell (∝)	—	0.14	—	0.14	—	0.21
Cryst. (%)	—	78	—	90	—	87

---

Assessing the amount of hemicellulose in CytroCell samples based on the infrared spectra is not straightforward because the bands of hemicellulose and other sample components overlap. The most relatively intense characteristic bands of hemicellulose are observed around 1070 cm⁻¹ and near 1600 cm⁻¹, corresponding to νC=O and ν_asCOO⁻ vibrational modes, respectively. Additionally, bands associated with the νC–O stretching and δO–H in-plane bending modes are observed near 1240 cm⁻¹.^30,32–36

Estimates of the relative contents of hemicellulose (Hcell) in the CytroCell samples are presented in Table 4. Values were obtained assuming that the hemicellulose content has a stronger influence on the band components retrieved by deconvolution at ∼1600 cm⁻¹ and ∼1070 cm⁻¹, the relative hemicellulose content by relating the sum of these band areas to the sum of all band areas (eqn (5)):

Using the same approach previously described by eqn (4), the crystallinity of the cellulose in the CytroCell samples was evaluated by comparing the ratio of the intensity at 1278 cm⁻¹ to that at 1205 cm⁻¹ (I₁₂₇₈/I₁₂₀₅). The values obtained (last row in Table 4) show that all the samples exhibit a high degree of crystallinity, comparable to that of microcrystalline cellulose. Although the values obtained fall outside the applicability limits of the method (26–76%²⁸) and should therefore be regarded only as indicative, it is clear that the highest degree of crystallinity was achieved for the CytroCell samples derived from orange.

In summary, the degree of esterification is similar across the three CytroCell samples, ranging from 37% to 47%, with the lemon derived CytroCell exhibiting the highest value and the red orange sample the lowest. Furthermore, based on the proposed simplified method, the submicron CytroCell cellulose from lemon and red orange appears to have comparable hemicellulose content, whereas the sweet orange sample seems to contain a higher amount. Finally, the proportion of the cellulose crystalline phase is similar between the two orange samples, while cellulose in lemon CytroCell shows a lower degree of crystallinity. A comparison of the crystallinity values with the degree of esterification reveals an apparent inverse correlation that is consistent across the three samples. Specifically, a reduction in the degree of esterification appears to be associated with an increase in crystallinity, which may be explained by the reduced steric hindrance and greater availability of hydroxyl groups, favoring tighter molecular packing and the formation of more ordered crystalline domains.

Samples with a higher degree of esterification are expected to show increased solubility due to increased repulsion between carboxylate groups in cellulose citrate ester, expansion in size of the three-dimensional network structure promoting water infiltration, eventually leading to improved swelling capacity,³⁷ while samples with a higher hemicellulose content exhibit decreased solubility. There is no concomitant variation of these two parameters in the CytroCell samples analyzed, making it difficult to predict changes in solubility. However, considering that the lemon CytroCell sample has the highest degree of esterification and the lowest hemicellulose content, it is expected to be the most soluble in aqueous solution.

In brief, these results highlight the unique features of novel nanocellulose CytroCell reproducibly sourced from citrus processing waste using the CytroCav circular economy process, affording in the aqueous phase also the highly bioactive IntegroPectin bioconjugate.³⁸

Including use to enhance the mechanical properties of pectin-based films suitable for therapeutic application,³⁹ to accelerate air lime carbonation,⁴⁰ and to vastly enhance the electrical, chemical and mechanical properties of anion⁸ or proton⁴¹ exchange polymeric membranes for electrochemical applications, this new family of nanocelluloses reproducibly sourced from citrus biowaste at low cost will be employed in many advanced industrial products and devices.

3 Conclusions

The computational and infrared spectroscopic study of CytroCell samples provides important insights into its structural properties and behavior in solution, as well as its structural characteristics in the solid state.

The results of COSMO-RS calculations elucidate the interactions of CytroCell nanofibers not only in aqueous solutions but also in more complex solutions, such as the green solvent Cyrene. A strong preference for charged CytroCell nanofibers for polar solvents, particularly water, is unveiled. Consequently, pH is expected to significantly impact solubility through ionization equilibria. While Cyrene alone is unsuitable for solubilizing ionized forms, binary Cyrene–water mixtures enable tunable solubility control.

Molecular dynamics simulations indicate high stability in water for the oligosaccharide structure comprised of five β-glucopyranose residues, two of which are esterified (in dianionic form) used in the molecular dynamics studies. The radial distribution function (and other analysis of the oligosaccharide–water system) reveals a significant structuring degree of water molecules in the immediate vicinity of the oligosaccharide. The persistent interactions around the oligosaccharide govern the overall system behaviour. Water remains bound to the oligosaccharide longer than it does to other water molecules, reflecting structured and organized interactions stabilized by specific sites on the oligosaccharide.

Due to exceptionally strong stabilisation promoted by the interaction of charged citrate groups, the oligosaccharide units in solution form a suprastructure consisting of two oligosaccharides adopting an almost anti-parallel arrangement and forming a rigid, stable conformation over time. Calculations also indicate that the water shell surrounding the suprastructure is identical in size to that of the oligosaccharide alone, effectively contributing to the overall stabilisation of the suprastructure.

The citrus CytroCell samples were also analyzed using diffuse reflectance infrared Fourier transform spectroscopy. The band pattern of the OH stretching mode suggests that the hydrogen-bonding structures are comparable in all samples and that the molecular chain organization is similar across the samples.

The DRIFT analysis, furthermore, indicates that the cellulose nanofibers exhibit a high degree of esterification, ranging from 37% in red orange CytroCell to 47% in lemon-derived CytroCell. An inverse relationship with crystallinity was observed, where a higher degree of esterification corresponds to a lower degree of crystallinity. On the other hand, the relative hemicellulose content varies from 14% in red orange and lemon CytroCell to 21% in sweet orange CytroCell.

Combining computational and experimental results, solubility is influenced by both the degree of esterification and hemicellulose content. Although these parameters do not vary alongside in the analyzed CytroCell samples, lemon CytroCell, with the highest degree of esterification and lowest hemicellulose content, is expected to exhibit the greatest solubility in aqueous solution.

In general, this approach, applied to CytroCell, by validating simulations against existing data, will enable the extrapolation of unreferenced behaviours for future investigations and applications. Future computational work may use density functional theory to compare simulated IR spectra with experimental data and gain further molecular-level understanding of the CytroCell nanocellulose structure.

4 Experimental section

4.1 Infrared analysis

For infrared analysis, the samples were ground, diluted with FTIR-grade KBr in an appropriate proportion to ensure the validity of the Kubelka–Munk assumptions, and homogenized. The diffuse reflectance infrared Fourier transform (DRIFT) spectra were recorded using a Bruker Vertex 70 FTIR spectrometer equipped with a DLaTGS detector and a Specac diffuse reflectance accessory. The spectra were scanned over the 4000–600 cm⁻¹ range, with a 4 cm⁻¹ resolution, and were the result of 100 co-added scans for the sample, referenced against an equal number of scans for pure KBr as the background. The spectra were converted to Kubelka–Munk units using OPUS software, without further correction. The DRIFT data were processed using Origin software (OriginLab Corporation, Northampton, MA, USA).

Conflicts of interest

The authors declare no competing interests.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary information (SI): Heatmap of solubility vs. water fraction for the neutral, monoanionic, dianionic and trianionic structures in a Water–Gemdiol mixture (Fig. S1). Evolution of solubility as a function of water mole fraction for the neutral, monoanionic, dianionic and trianionic structures in a Water–Gemdiol mixture (Fig. S2). Heatmap of solubility vs. Gemdiol fraction for the neutral, monoanionic, dianionic and trianionic structures in a gemdiol–Cyrene mixture (Fig. S3). Evolution of solubility as a function of Gemdiol mole fraction for the neutral, monoanionic, dianionic and trianionic structures in a Gemdiol–Cyrene mixture (Fig. S4). Matrix of H-bonds between the oligosaccharide and water molecules (Fig. S5). Matrix of H-bonds between the citrate groups and water molecules (Fig. S6). 3D representation of the system B suprastructure (Connoly surface) (Fig. S7). Matrix of H-bonds between the two oligosaccharide and water molecules (Fig. S8). DRIFT spectra of cellulose and wood pulp after swelling and solvent evaporation at different pH's (Fig. S9). Band relative intensity used for calculating crystallinity (Fig. S10). See DOI: https://doi.org/10.1039/d5ma01060h.

Acknowledgements

This work was funded by the Ministero delle Imprese e del Made in Italy under the Piano Operativo della Ricerca “Ricerca e sviluppo sull’idrogeno” financially supported by the European Union – NextGenerationEU – M2C2 Investment 3.5, in the framework of the project PNRR Ricerca e Sviluppo sull’Idrogeno 2022-2025 – Accordo di Programma “Idrogeno” (PRR.AP015.017.002), “Obiettivo 1 – Produzione di idrogeno verde e pulito”, “LA 1.1.6 – Sviluppo di materiali e componenti non contenenti materiali critici per elettrolizzatori anionici (AEM) operanti anche ad elevata pressione differenziale”. The work of G. L. P. was supported by MICS (Made in Italy – Circular and Sustainable) Extended Partnership and received funding from the European Union Next-GenerationEU (PNRR – Mission 4 Component 2, Investment 1.3 – D.D.1551.11-10-2022, PE00000004). The work of G.A. was supported by the SAMOTHRACE (Sicilian Micro and Nano Technology Research and Innovation Center) Innovation Ecosystem using funding from European Union NextGeneration EU (PNRR – Mission 4 Component 2, Investment 1.5 (ECS00000022)).

References

1. Nanocellulose: From Fundamentals to Advanced Materials, ed. J. Huang, A. Dufresne, N. Lin, Wiley-VCH, Weinheim, 2019.
2. R. Ciriminna, G. Angellotti, R. Luque, M. Formenti, C. Della Pina and M. Pagliaro, Learning from hype en route to fulfill the industrial potential of nanocellulose, Carbohydr. Polym. Technol., 2024, 7, 100512,  DOI:10.1016/j.carpta.2024.100512.
3. Y. Ai, L. Zhang, M. Cui, W. Qi, Z. He, J. J. Klemeš and R. Su, Toward cleaner production of nanocellulose: a review and evaluation, Green Chem., 2022, 24, 6406,  10.1039/d2gc01669a.
4. A. Scurria, L. Albanese, M. Pagliaro, F. Zabini, F. Giordano, F. Meneguzzo and R. Ciriminna, Cytrocell: valued cellulose from citrus processing waste, Molecules, 2021, 26, 596,  DOI:10.3390/molecules26030596.
5. S. Al Jitan, A. Scurria, L. Albanese, M. Pagliaro, F. Meneguzzo, F. Zabini, R. Al Sakkaf, A. Yusuf, G. Palmisano and R. Ciriminna, Micronized cellulose from citrus processing waste using water and electricity only, Int. J. Biol. Macromol., 2022, 204, 587,  DOI:10.1016/j.ijbiomac.2022.02.042.
6. R. Ciriminna, G. Angellotti, G. Li Petri, F. Meneguzzo, C. Riccucci, G. Di Carlo and M. Pagliaro, Cavitation as a zero-waste circular economy process to convert citrus processing waste into biopolymers in high demand, J. Bioresour. Bioprod., 2024, 9, 486,  DOI:10.1016/j.jobab.2024.09.002.
7. R. Ciriminna, G. Li Petri, G. Angellotti, E. Fontananova, R. Luque and M. Pagliaro, Nanocellulose and microcrystalline cellulose from citrus processing waste: a review, Int. J. Biol. Macromol., 2024, 281, 135865,  DOI:10.1016/j.ijbiomac.2024.135865.
8. E. Fontananova, R. Ciriminna and D. Talarico, et al., CytroCell@PIL: a new citrus nanocellulose-polymeric ionic liquid composite for enhanced anion exchange membranes, Nano Select, 2025, 6, e70001,  DOI:10.1002/nano.70001.
9. CNRS. Polys glycan builder, CERMAV, 2024, Accessed: 2024.
10. Woods Group, Glycam web. Complex Carbohydrate Research Center, University of Georgia, Athens, GA, 2005–2025, (accessed: September 15, 2025).
11. T. C. F. Gomes and M. S. Skaf, Cellulose-builder: a toolkit for building crystalline structures of cellulose, J. Comput. Chem., 2012, 33, 1338,  DOI:10.1002/jcc.22959.
12. H. Vazquez-Hernandez and R. O. Esquivel, Phenomenological description of the acidity of the citric acid and its deprotonated species: informational-theoretical study, J. Mol. Model., 2023, 29, 253,  DOI:10.1007/s00894-023-05589-2.
13. M. Jäger and A. J. Minnaard, Regioselective modification of unprotected glycosides, Chem. Commun., 2016, 52, 656,  10.1039/c5cc08199h.
14. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4, 1,  DOI:10.1186/1758-2946-4-17.
15. T. A. Halgren, Merck molecular force field. i. basis, form, scope, parameterization, and performance of MMFF94, J. Comput. Chem., 1996, 17, 490,  DOI:10.1002/(SICI)1096-987X(199604)17:5/6%3C490::AID-JCC1%3E3.0.CO;2-P.
16. P. Pracht, S. Grimme and C. Bannwarth, et al., CREST—a program for the exploration of low-energy molecular chemical space, J. Chem. Phys., 2024, 160, 114110,  DOI:10.1063/5.0197592.
17. J. J. P. Stewart, Mopac2016, version 22.234w. Stewart Computational Chemistry, Colorado Springs, CO, 2024.
18. K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, GLYCAM06: a generalizable biomolecular force field. Carbohydrates, J. Comput. Chem., 2008, 29, 622,  DOI:10.1002/jcc.20820.
19. A. Klamt, The COSMO and COSMO-RS solvation models, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338,  DOI:10.1002/wcms.1338.
20. M. De Bruyn, V. L. Budarin, A. Misefari, S. Shimizu, H. Fish, M. Cockett, A. J. Hunt, H. Hofstetter, B. M. Weckhuysen, J. H. Clark and D. J. Macquarrie, Geminal diol of dihydrolevoglucosenone as a switchable hydrotrope: a continuum of green nanostructured solvents, ACS Sustainable Chem. Eng., 2019, 7, 7878,  DOI:10.1021/acssuschemeng.9b00470.
21. A. Misefari, Investigation of the spectroscopic, chemical and physical properties of Cyrene and its hydrate, MSc by research thesis, University of York, 2017. https://etheses.whiterose.ac.uk/id/oai_id/oai:etheses.whiterose.ac.uk:18284.
22. H. Bekker, H. J. C. Berendsen and E. J. Dijkstra, et al., GROMACS – a parallel computer for molecular-dynamics simulations, Physics Computing 92, World Scientific Publishing, Singapore, 1993, pp. 252–256.
23. D. A. Case, H. M. Aktulga and K. Belfon, et al., AmberTools, J. Chem. Inf. Model., 2023, 63, 6183,  DOI:10.1021/acs.jcim.3c01153.
24. D. Maity and D. Pal, MD DaVis: interactive data visualization of protein molecular dynamics, Bioinformatics, 2022, 38, 3299,  DOI:10.1093/bioinformatics/btac314.
25. A. Luzar, Resolving the hydrogen bond dynamics conundrum, J. Chem. Phys., 2000, 113, 10663,  DOI:10.1063/1.1320826.
26. T. Kondo and C. Sawatari, A Fourier transform infra-red spectroscopic analysis of the character of hydrogen bonds in amorphous cellulose, Polymer, 1996, 37, 393,  DOI:10.1016/0032-3861(96)82908-9.
27. K. L. Spence, R. A. Venditti, Y. Habibi, O. J. Rojas and J. Pawlak, The effect of chemical composition on microfibrillar cellulose films from wood pulps: mechanical processing and physical properties, Biores. Technol., 2010, 101, 5961–5968,  DOI:10.1016/j.biortech.2010.02.104.
28. L. M. Ilharco, A. R. Garcia, J. Lopes da Silva and L. F. Vieira Ferreira, Infrared approach to the study of adsorption on cellulose: influence of cellulose crystallinity on the adsorption of benzophenone, Langmuir, 1997, 13, 4126,  DOI:10.1021/la962138u.
29. R. Ciriminna, A. Fidalgo, R. Delisi, A. Tamburino, D. Carnaroglio, G. Cravotto, L. M. Ilharco and M. Pagliaro, Controlling the degree of esterification of citrus pectin for demanding applications by selection of the source, ACS Omega, 2017, 2, 7991,  DOI:10.1021/acsomega.7b01109.
30. M. A. Monsoor, U. Kalapathy and A. Proctor, Improved method for determination of pectin degree of esterification by diffuse reflectance Fourier transform infrared spectroscopy, J. Agric. Food Chem., 2001, 49, 2756–2760,  DOI:10.1021/jf0009448.
31. A. Scurria, M. Sciortino, A. R. Garcia, M. Pagliaro, G. Avellone, A. Fidalgo, L. Albanese, F. Meneguzzo, R. Ciriminna and L. M. Ilharco, Red orange and bitter orange IntegroPectin: structure and main functional compounds, Molecules, 2022, 27, 3243,  DOI:10.3390/molecules27103243.
32. K. V. Berezin, I. T. Shagautdinova, M. L. Chernavina, A. V. Novoselova, K. N. Dvoretskii and A. M. Likhter, The experimental vibrational infrared spectrum of lemon peel and simulation of spectral properties of the plant cell wall, Opt. Spectrosc., 2017, 123, 495,  DOI:10.1134/s0030400x17090089.
33. K. V. Berezin, A. M. Likhter, I. T. Shagautdinova, M. L. Chernavina and A. V. Novoselova, FT-IR and DFT study of lemon peel, Proc. SPIE 10336, Saratov Fall Meeting 2016: Optical Technologies in Biophysics and Medicine XVIII, 103360I (24 March 2017) DOI:10.1117/12.2267975.
34. L. W. Lun, A. A. N. Gunny, F. H. Kasim and D. Arbain, Fourier transform infrared spectroscopy (FTIR) analysis of paddy straw pulp treated using deep eutectic solvent, AIP Conf. Proc., 2017, 1835, 020049,  DOI:10.1063/1.4981871.
35. R. Javier-Astete, J. Jimenez-Davalos and G. Zolla, Determination of hemicellulose, cellulose, holocellulose and lignin content using FTIR in Calycophyllum spruceanum (Benth.) K. Schum. and Guazuma crinita Lam, PLoS One, 2021, 16, e0256559,  DOI:10.1371/journal.pone.0256559.
36. S. G. Kostryukov, H. B. Matyakubov, Y. Y. Masterova, A. S. Kozlov, M. K. Pryanichnikova, A. A. Pynenkov and N. A. Khluchina, Determination of lignin, cellulose, and hemicellulose in plant Materials by FTIR spectroscopy, J. Anal. Chem., 2023, 78, 718,  DOI:10.1134/S1061934823040093.
37. X. Tan, Q. Lv, G. Dong, Z. Zhang, D.-F. Chai, M. Zhao, W. Zhang and J. Li, Insight into the preparation and improved properties of cellulose citrate ester hydrogel slow-release fertilizer, Ind. Crops Prod., 2024, 222, 119517,  DOI:10.1016/j.indcrop.2024.119517.
38. R. Ciriminna, V. Di Liberto, C. Valenza, G. Li Petri, G. Angellotti, L. Albanese, F. Meneguzzo and M. Pagliaro, Citrus IntegroPectin: a family of bioconjugates with large therapeutic potential, ChemFoodChem, 2025, 1, e00014,  DOI:10.1002/cfch.202500014.
39. A. Scurria, M. Pagliaro and G. Pantaleo, et al., CytroCell micronized cellulose enhances the structural and thermal properties of IntegroPectin cross-linked films, ACS Appl. Bio Mater, 2022, 5, 4942,  DOI:10.1021/acsabm.2c00658.
40. P. Guzmán García Lascurain, C. Rodriguez-Navarro, M. Pagliaro, L. Toniolo and S. Goidanich, Cellulose nano- and micro-fibers as air lime carbonation accelerators: FTIR analysis of the carbonation kinetics, Constr. Build. Mater., 2025, 489, 142291,  DOI:10.1016/j.conbuildmat.2025.142291.
41. D. Talarico, E. Fontananova, T. Sibilllano, R. Ciriminna, S. Palermo, F. Galiano, G. Di Profio, A. Figoli, G. Li Petri, G. Angellotti, F. Meneguzzo, C. Giannini and M. Pagliaro, CytroCell@Nafion: enhanced proton exchange membranes, Glob. Chall., 2025, 9, e00338,  DOI:10.1002/gch2.202500338.

---

Footnote

† These authors contributed equally to this work.

---