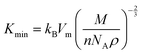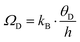DOI:
10.1039/D5MA00961H
(Paper)
Mater. Adv., 2026,
7, 618-640
Compositional tuning and property evolution in cubic Mg-based perovskite and anti-perovskite compounds (MgBO3 and Mg3BO; B = Si, Ge, Sn, Pb): a comparative first-principles study for multifunctional device applications
Received
26th August 2025
, Accepted 10th November 2025
First published on 1st December 2025
Abstract
This study presents a comprehensive and comparative first-principles analysis of cubic-phase perovskite (MgBO3) and anti-perovskite (Mg3BO) compounds, where B = Si, Ge, Sn, Pb, with a focus on their structural, electronic, mechanical, thermodynamical and optical properties. Structural optimization confirms phase stability through tolerance factor evaluation and Birch–Murnaghan equation of state, revealing a systematic increase in lattice constants from Si to Pb due to cationic radius expansion. Formation energy calculations reveal that anti-perovskite compounds exhibit greater thermodynamic stability than their perovskite counterparts, with values decreasing systematically from Si to Pb. The dynamic and thermodynamic stability of MgBO3 perovskites and (Mg3BO) anti-perovskites investigated via phonon dispersion analysis and thermodynamic potential calculations, reveal that anti-perovskites exhibit superior dynamic stability, higher entropy, and enhanced heat capacity making them promising candidates for thermoelectric and high-temperature applications. All compounds satisfy mechanical stability criteria, with elastic moduli decreasing across the series, indicating reduced stiffness. Perovskites exhibit superior ductility and mechanical robustness compared to anti-perovskites, as supported by Cauchy pressure, anisotropy, and Kleinman parameter analyses. Electronic band structure calculations using GGA-PBE, GGA-PBEsol and HSE06 functionals reveal indirect band gaps in perovskites, transitioning from semiconducting to metallic behavior with heavier B-site cations while anti-perovskites display narrow direct band gaps (<0.5 eV). Density of states analysis highlights dominant O-p and B-p orbital contributions near the Fermi level, with most compounds classified as p-type semiconductors, except MgPbO3, which exhibits metallicity. Thermal evaluations identified MgGeO3 and MgSnO3 as the most stable, with Debye parameters and phonon conductivity decreasing with heavier cation substitution. Optical investigations including dielectric function, reflectivity, refractive index, and optical conductivity demonstrate strong tunability across the series. Perovskites show enhanced UV conductivity and low reflectivity, ideal for photodetectors and antireflective coatings, while anti-perovskites excel in visible-light absorption, positioning them as promising candidates for photovoltaics and energy storage. These findings underscore the multifunctional potential and compositional flexibility of Mg-based perovskite and anti-perovskite systems for next-generation optoelectronic, photonic, and memory device applications.
1. Introduction
Perovskite materials, in their normal form, are generally represented by the formula ABX3, where A is a monovalent or divalent cation, B is a tetravalent or pentavalent cation, and X is an anion. When X is oxygen, the resulting compound is known as a perovskite oxide, a class of materials renowned for their unique structural and electronic properties. These oxides possess a broad spectrum of technological applications, including electrocatalysis, sensor devices, spintronics, magneto-resistive devices, and electrode materials.1–3 In addition to the conventional cubic structure, perovskites can also stabilize in alternative structures such as orthorhombic and hexagonal phases, further broadening their functional versatility. If the positions of the A and X elements are interchanged, the resulting compounds form a related class of materials known as anti-perovskites (APs), with a general formula A3BX.4 APs typically exhibit cubic or pseudo-cubic structures, often retaining the same space group (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as their perovskite counterparts. This inversion of cation and anion positions can lead to novel structural and electronic behaviors, enabling a wide variety of physical properties. Depending on their chemical composition, APs may behave as metals, non-metals, semiconductors, or superconductors.5
m) as their perovskite counterparts. This inversion of cation and anion positions can lead to novel structural and electronic behaviors, enabling a wide variety of physical properties. Depending on their chemical composition, APs may behave as metals, non-metals, semiconductors, or superconductors.5
The versatile characteristics of oxide perovskites have long attracted significant interest in basic research, technological development, and commercial applications.6 However, despite extensive investigations into oxide perovskites, certain closely related materials especially oxide Aps have remained relatively underexplored.7 APs are of growing scientific interest due to their potential to exhibit diverse functionalities, including magnetic ordering,8 superconductivity,9 and semiconducting behavior,10 photovoltaic devices,11 energy storage12 all strongly dependent on their atomic configuration. Notably, Sr3SnO has been synthesized via a facile method and found to exhibit superconducting properties.13 Similarly, Ca3XO (X = Pb, Sn) compounds, possessing cubic geometry, have shown enhanced TE power generation performance at room temperature.14 Liang et al.15 explored the optical and thermoelectric (TE) behavior of (Li/Na/K)3OI, revealing strong light absorption that positions these compounds as promising candidates for perovskite solar cell applications. Sharma et al.16 examined Rb-based anti-perovskites and identified several favorable physical properties suitable for renewable energy technologies. In addition, Zhong et al.17 reported that K3AuO possesses exceptionally low thermal conductivity and high carrier concentration, indicating its potential for TE device applications. Zhao et al.18 also investigated RbAuO, contributing further insight into the properties of noble-metal-based oxide APs.
Mg-based perovskites and anti-perovskites are valued for their versatile properties and broad scientific applications. E. O. Chi et al.19 synthesized and characterized Mg-based pnictogen anti-perovskites PnNMg3 (Pn = As, Sb), revealing cubic structures, unusual oxidation states, and ionic bonding consistent with electronic calculations. Yasuhide Mochizuki et al.20 reported that Mg-based anti-perovskites such as Mg3PN featuring direct band gaps and strong optical absorption, are promising earth-abundant semiconductors for light absorption and emission applications. Yangyang Cai et al.21 demonstrated that Mg-based perovskites, particularly a magnesium–manganese double anti-perovskites with in situ quantum wells, achieve 20.2% external quantum efficiency and high luminance in green LEDs, highlighting their potential in lead-free optoelectronics. Ezekiel Oyeniyi et al.22 showed Mg-based anti-perovskites Mg3XN (X = P, As, Sb, Bi) have promising optoelectronic properties with band gap types and spin orbit effects varying by element. MgSiO3 undergoes multiple phase transitions under varying temperature and pressure, including the post-perovskite phase studied by Motohiko Murakami et al.,23 relevant to Earth's mantle dynamics. Ionic vacancy formation and diffusion behavior were detailed by Bijaya B. Karki,24 while Juan Gao25 explored monoclinic and trigonal polymorphs with distinct mechanical properties. Thermoelectric properties were analyzed by Q. Mahmood, high-pressure effects by Lin-Gun Liu,26 and microwave dielectric characteristics by Myung-Eun Song.27 Mg-based perovskites AGeO3 exhibit stable structures, indirect band gaps, and favorable mechanical and thermoelectric properties.28 DFT and transport studies highlight their potential for thermoelectric and optoelectronic uses.29 Luminescence and high-pressure phase analyses reveal unique optical behavior and stability relevant to both applications and geophysics.30 B. B. Dumre et al.31 and Q. Mahmood et al.32 reported that MgSnO3 is mechanically and dynamically stable with high hardness, while the perovskite and ilmenite phases exhibit mechanical stability but dynamic instability, supporting its thermoelectric applications. Xiang-Fu Xu et al.33 demonstrated that compressive strain enhances MgSnO3.'s stability, band gap, and ferroelectric properties, thereby improving its optoelectronic performance.
Despite these advances, experimental studies on oxide APs remain limited, which has motivated theoretical researchers to model and predict their structural, electronic, and transport properties. Such efforts are critical for unlocking their potential in next-generation energy technologies. Currently, there are no detailed theoretical or experimental studies on Mg3BO (B = Si, Ge, Sn, Pb) antiperovskites. In this work, we aim to comprehensively investigate their structural, optical, electronic, and mechanical properties using density functional theory, comparing them with related perovskite structures MgBO3 (B = Si, Ge, Sn, Pb) to assess their potential for multifunctional device applications.
2. Computational details
The DFT-based CASTEP computer software with the generalized gradient approximation GGA+PBE and GGA+PBEsol has been used for first-principles calculations.34,35 For structural optimization and optical property calculations, the GGA-PBE functional was used due to its balanced accuracy and widespread applicability in predicting electronic and optical behavior in semiconductors and insulators.36 For elastic constant and thermodynamic property evaluations, the GGA-PBEsol functional was adopted, as it offers impved accuracy in predicting equilibrium structural parameters and mechanical properties of densely packed solids.37 For band structure calculations, a combination of GGA-PBE, GGA-PBEsol, and the hybrid HSE06 functional was utilized to ensure a comprehensive and accurate description of electronic states. The HSE06 functional, in particular, is known for its superior performance in predicting band gaps by incorporating a portion of exact exchange.38 In the calculation of lattice optimization, the convergence parameters were set as follows: (i) the maximum ionic displacement 0.002 Å, (ii) the maximum stress component 0.10 GPa, (iii) 0.05 eV Å−1 is set for the maximum ionic force. The electromagnetic wave function extension in a plane-wave basis set uses an energy cut-off of 520 eV, and the Brillouin zone is sampled using 8 × 8 × 8 k-points for anti-perovskites calculations and 500 eV cut-off energy with Brillouin zone is sampled using 10 × 10 × 10 k-points for perovskite calculations. This grid size provided a good balance between accuracy and computational cost. The cutoff energy was adjusted until further increases resulted in negligible changes in total energy, ensuring convergence. These parameters ensure the reliability of our calculations. The application of the Broyden has optimized the geometric structure using the Fletcher–Goldfarb–Shanno (BFGS) minimization technique.39 UPPs achieve a substantially softer pseudo-wave function, requiring a significant reduction in plane waves for calculations with the same level of precision.40 Ultrasoft pseudopotentials (UPPs) yield smoother pseudo-wave functions, enabling accurate calculations with fewer plane waves. Elastic constants were computed via first-principles by applying small homogeneous strains (±0.5%) and optimizing internal atomic positions. The resulting stress–strain data were linearly fitted to extract elastic moduli.
3. Result and discussions
3.1 Structural properties
Fig. 1 illustrates the unit cells of perovskite and anti-perovskite structures. In perovskites, Mg occupies the center, O ions the face centers, and B-site cations (Si, Ge, Sn, Pb) the corners; in anti-perovskites, Mg and O positions are reversed. Fig. 1 presents optimized cubic-phase (Pm3m) geometries for MgBO3 and Mg3BO compounds. Demonstrated the total energy for varying volume for investigated compounds using BM-EOS,29| |  | (1) |
The parameter B and V denote the equilibrium bulk modulus and the equilibrium volume of the unit cell, respectively. The bulk modulus (B) is calculated using eqn (2), which relates it to the second derivative of the total energy with respect to volume:| |  | (2) |
The pressure derivative of the bulk modulus, represented as B′, describes how B changes with pressure at constant temperature and is defined by eqn (3):| | 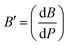 | (3) |
Fig. 2 illustrates the variation in total energy as a function of volume for the perovskites and anti-perovskites compounds, as obtained using the generalized gradient approximation (GGA) method. The computed structural parameters from optimization structures reported in Table 1. The calculated lattice constants increase from Si to Pb, consistent with the rising cationic radius down the group. This expansion in atomic size leads to larger unit cell dimensions. The results align well with existing literature, confirming the accuracy of our computational approach.
 |
| | Fig. 1 Crystal Structure of Mg-based cubic (a) Anti-perovskites & (b) perovskites where cyan atom represent Si, Ge, Sn, Pb and red atom represent oxygen. | |
 |
| | Fig. 2 (a)–(d) Volume optimization of the studied perovskites and anti-perovskites. | |
Table 1 Structural properties of Mg-based perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
|
|
Mg3SiO |
Mg3GeO |
Mg3SnO |
Mg3PbO |
Mg3SiO3 |
Mg3GeO3 |
MgSnO3 |
MgPbO3 |
|
a
0 (Å) |
4.22 |
4.24 |
4.39 |
4.43 |
3.53 |
3.72 |
4.02 |
4.21 |
| Other cal. a0 (Å) |
— |
— |
— |
— |
3.52,131 3.5368 |
3.71,131 3.6968 |
4.02,131 4.0068 |
— |
|
V
0 (Å)3 |
75.39 |
76.70 |
84.72 |
87.49 |
44.11 |
51.69 |
65.10 |
75.12 |
|
B
0 (GPa) |
225.78 |
106.98 |
92.23 |
53.27 |
385.77 |
315.46 |
225.71 |
91.64 |
| Other cal. |
— |
— |
— |
— |
246.2368 |
23068 |
22568 |
— |
|
E
0 (eV) |
−5683.99 |
−8052.27 |
−7562.43 |
−10942.72 |
−3184.94 |
−5549.14 |
−5058.71 |
−8436.05 |
|
t
|
1.02 |
0.97 |
0.93 |
0.91 |
1.02 |
0.97 |
0.93 |
0.91 |
|
H
f (eV) |
−2532.4 |
−2531.85 |
−2530.96 |
−2530.25 |
−33.35 |
−28.72 |
−27.24 |
−23.58 |
| Other cal. |
— |
— |
— |
— |
−2.7068 |
−2.1068 |
−1.9068 |
— |
The bulk modulus, which reflects a material's resistance to compression, is reported in Table 1 and plotted in Fig. 3. For both perovskite and anti-perovskites compounds, the bulk modulus decreases systematically with the variation of the B-site cation from Si to Pb. This trend indicates that as the cation size increases, the material becomes more compressible. The corresponding increase in lattice constant leads to a larger unit cell volume, resulting in a reduced bulk modulus. The bulk modulus of the perovskite compound is notably higher than that of the anti-perovskite counterparts, and the disparity in values gradually diminishes as the B-site cation transitions from silicon (Si) to lead (Pb). The structural parameters of the studied compounds can be adjusted by choosing different cations, making this knowledge crucial for designing devices that can endure mechanical stresses during use.
 |
| | Fig. 3 Variation of bulk modulus of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
Material stability plays a crucial role in device fabrication. We evaluated the structural stability of the studied compounds in their cubic phase using the Goldschmidt tolerance factor41 given by,
| |  | (4) |
where
rMg,
rB and
rO represent the ionic radii of magnesium, the B-site cation (Si, Ge, Sn, Pb), and oxygen, respectively. This factor indicates the geometric fit between cations and anions, helping to reduce lattice strain. For a stable cubic perovskite, the tolerance factor usually lies between 0.90 and 1.04.
42 The results in
Table 1 show that our compounds meet the stability requirements for oxide perovskites. These structural features help improve their optoelectronic performance and are important for designing advanced materials.
43
The formation energy of a compound is a critical thermodynamic parameter that quantifies the energy change associated with the synthesis of a material from its constituent elements in their most stable reference states. It serves as a fundamental indicator of thermodynamic stability, guiding the prediction of phase formation, defect energetics, and material synthesis feasibility.44 Furthermore, the thermodynamic stability is also important for device fabrication which is ensured from the enthalpy of formation calculations using relation,45
| | | ΔHf = Etotal (Mg1BmOn) − lEMg − mEX – nEO | (5) |
where
Etotal represent the total energy and
EMg,
EX,
EO represent the energies of individual elements, where
l,
m,
n represent the number of atoms of Mg, X, and O in the unit cell. Negative Δ
Hf values imply that these compounds can form spontaneously under standard conditions, consistent with the principle that spontaneous processes reduce Gibbs free energy. Since crystal stability depends heavily on strong atomic bonds arising from electron–electron interactions, these negative values reported
Table 1 indicate favorable bonding, contributing to a stable crystal structure.
46
3.2 Dynamical stability
Phonon refers to a quasi-particle that is connected to a progressive elastic wave. Furthermore, the phonon modes are essential for explaining physical phenomena like ferroelectricity,47 phase transitions,48,49 and superconductivity,50 all of which are crucial for the functionality of both well-established and newly developed material technologies. We use the finite displacement method by examining the phonon dispersion curve to identify the dynamic qualities. Phonics frequencies are distinctive and linked to the crystal lattice's vibrational modes.51 A dynamic stable crystal requires positive values for the phonon frequency. Fig. 4 show band gaps between the lower and upper optical modes in all eight compounds. The reason for the gap is that atoms with greater weights cause the acoustic and lower optical modes to overlap, whereas atoms with significantly lower masses cause other upper optical branches to separate from lower optical modes. Because the phonon band gaps only reflect off the surface and do not propagate sound, they can be used in a variety of applications, including sound filters and mirrors.52,53 Evaluating the dynamic stability of a material is essential for determining its viability in practical applications subject to time-dependent external perturbations. The phonon dispersion curve (PDC) serves as a critical indicator of this stability.54,55 In this study, the dynamic behavior of MgBO3 (B = Si, Ge, Sn, Pb) perovskites and MgBO3 (B = Si, Ge, Sn, Pb) anti-perovskite compounds were assessed by calculating their phonon dispersion profiles along the high-symmetry directions (G–F–Q–Z–G) of the Brillouin zone, as illustrated in Fig. 4. A dynamically stable crystal structure is characterized by the absence of imaginary phonon frequencies throughout the Brillouin zone, as their presence signifies lattice instability.54 The phonon dispersion curves (PDCs) of all investigated anti-perovskite compounds MgBO3 (B = Si, Ge, Sn, Pb) show no imaginary frequencies across the Brillouin zone, confirming their dynamic stability.56 This stability is crucial for applications requiring robust thermal and mechanical properties, such as thermoelectric devices and high-temperature optoelectronics.
 |
| | Fig. 4 Phonon dispersion curve of cubic perovskites (a–d) MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites (a′–d′) Mg3BO (B = Si, Ge, Sn, Pb). | |
In contrast, the presence of imaginary modes in the perovskite compounds MgBO3 (B = Si, Ge, Sn, Pb) indicates lattice instability, rendering them dynamically unstable under ambient conditions.57 These instabilities are mirrored in their mechanical profiles, where higher stiffness C11 > 220 GPa and elevated hardness values suggest rigid bonding networks that suppress phonon activity and reduce thermal capacity. Phonon instability in the symmetry points depends on how well the exchange–correlation potential and pseudopotential, which represent the interaction between the core and valence electrons, are demanded.58 This is only a rough estimation, though as the atoms bounce around their equilibrium locations at limited temperatures or may experience more substantial anharmonic motion independently of their ideal crystallographic locations. Even at T = 0 K, the zero-point atomic oscillation plays a role in the internal energy.59 Since dynamic instabilities' imaginary modes are essentially anharmonic, a quantitative description necessitates going beyond the harmonic approximation.60 Therefore, this possibility must be classified using a complete phonon calculation considering the anharmonic effects. But as of right now, this kind of computation still presents significant difficulties.61 Since the calculated phonon dispersion spectra correspond to zero pressure and zero temperature. It's important to remember that the circumstances may differ under pressure or at extremely high temperatures. We also investigated the phonon spectrum up to 80 GPa pressure, but no significant changes were observed. These soft modes often lead to phase transitions, which can be advantageous in applications like ferroelectric memory devices and sensors. Such behavior is reminiscent of the soft phonon modes observed in CsPbCl3, where they facilitate transitions between different crystal phases.62 These dynamics instabilities can be measured by using inelastic-scattering techniques, such as inelastic neutron scattering63 or high energy resolution inelastic X-ray scattering (HERIX).64
We calculated the phonon characteristics to assess the thermodynamic stability. By analyzing these characteristics, we were able to establish the values of the thermodynamic potentials – enthalpy (H), free energy (F), and entropy (S) at a constant temperature. Eqn (6)–(8) represent the impacts of vibrations on enthalpy, free energy, and entropy, respectively,65
| |  | (6) |
| | 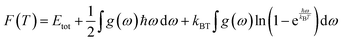 | (7) |
| |  | (8) |
where the phonon density levels are represented by
g(
ω), and the Boltzmann constant is denoted by
kB. As a result, a change in temperature leads to an increase in enthalpy and free energy, while causing a decrease in entropy. The three thermodynamic potentials
H,
F, and
S approach zero as the temperature approaches zero, as depicted in
Fig. 5. This observation aligns well with the third law of thermodynamics. Rising temperatures result in more vibrational modes and configurations, leading to increased entropy. From
Fig. 5, anti-perovskites Mg
3BO (B = Si, Ge, Sn, Pb) compound exhibits higher entropy, enthalpy and free energy than their perovskite counterpart's MgBO
3 (B = Si, Ge, Sn, Pb), making them promising candidates for thermoelectric applications due to their enhanced scattering and entropy-driven transport behavior.
66
 |
| | Fig. 5 (a)–(f) DFT calculated heat capacity, enthalpy, free energy and entropy of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
Fig. 5 depicts the relationship between heat capacity (CP) and temperature (K) for our studied compounds. We observed that heat capacity increases with temperature, which is a typical trend indicating that materials absorb more heat at higher temperatures. Up to 1000 K, the graph shows a gradual increase in heat capacity. Among the compounds, perovskites compounds have the lower heat capacity compare to anti-perovskites compounds across the temperature range, suggesting that it absorbs less heat compared to the other materials at the same temperatures. The anti-perovskite compounds Mg3BO (B = Si, Ge, Sn, Pb) exhibit closely aligned but subtly distinct heat capacity curves, with a progressive increase in heat capacity observed from Si to Pb at the B-site. This trend reflects the increasing atomic mass and lattice softening across the series, which enhances phonon contributions to thermal properties. In contrast, the perovskite counterparts MgBO3 (B = Si, Ge, Sn, Pb), display more pronounced distinctions in their heat capacity profiles. At low temperatures (around 150–300 K), the differences in heat capacity between the compounds are more pronounced. These observations align with theoretical predictions and experimental findings on anti-perovskite systems, where the cubic symmetry and metallic or semi-metallic behavior contribute to smoother thermal transitions.66 The smoother heat capacity curves of anti-perovskites, coupled with their lower hardness and elastic anisotropy, make them promising candidates for thermoelectric and high-temperature applications, where entropy-driven transport and mechanical compliance are advantageous.67 Beyond 600 K, all the curves begin to flatten, indicating that the heat capacities are reaching their upper limits and saturating.
Computed properties create new possibilities for contemporary industrial applications. A precise prediction of a material's mechanical stability can serve as a basis for its development and evaluation in real-world situations.
3.3 Electronics properties
Understanding a material's electronic properties is essential for controlling quantum-scale electron interactions and advancing innovations in materials science, electronics, and photonics. For perovskites and anti-perovskites this entails a detailed analysis of the energy band structure along with precise calculations of the total and partial densities of states (TDOS and PDOS), enabling a deeper comprehension of its electronic behavior and potential device applications. Fig. 6 and 7 illustrated the band profile of MgBO3 (B = Si, Ge, Sn, Pb) and Mg3BO (B = Si, Ge, Sn, Pb) compounds along the Brillouin zone. For the studied cubic-phase, the minimum of the conduction band and the maximum of the valence band are situated at distinct symmetry points within the Brillouin zone. This spatial separation along the Q–Z direction reveals their indirect bandgap nature, thereby classifying them as semiconducting materials. The variation of cation B (Si, Ge, Sn, Pb) shows significant influence on the overall band profile. Our calculations, as illustrated in Fig. 6 demonstrate that as the B-site cation in perovskite MgBO3 (B = Si, Ge, Sn, Pb) progresses from Si to Pb the electronic band gap systematically narrows indicating a transition from semiconducting behavior toward metallicity. This trend is consistently observed across all exchange–correlation functionals employed GGA-PBE, GGA-PBEsol and HSE06 as evidenced by the conduction band minimum shifting progressively closer to the Fermi level. A similar trend was reported by Q. Mohammad et al.68 during their investigation of MgXO3 (X = Si, Ge, Sn) compounds, indicating that our findings are consistent with previously published result. MgSiO3 (2.60 eV) is appropriate for UV-selective optoelectronics and transparent oxide applications,69,70 while MgGeO3 (1.006 eV) andMgSnO3 (0.84 eV) target NIR photodetection and extended-spectrum devices.71 The metallic MgPbO3 can serve as a conducting oxide electrode layer and, more generally, in plasmonic/photonic architectures.72,73 The anti-perovskites compounds studied using three different functional displayed in Fig. 7 Mg3BO (B = Si, Ge, Sn, Pb) possess narrow direct band gaps all below 0.5 eV. Given their narrow band gaps (0.13–0.33 eV), Mg3BO compounds (B = Si, Ge, Sn, Pb) are well-suited for infrared photodetection74 and thermoelectric energy conversion,75 consistent with established design rules for narrow-gap semiconductors.
 |
| | Fig. 6 Band structure of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) compounds using GGA-PBE (a–d), HSE06 (a′–d′) and GGA-PBEsol (a″–d″). | |
 |
| | Fig. 7 Band structure of cubic anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb) compounds using GGA-PBE (a–d), HSE06 (a′–d′) and GGA-PBEsol (a″–d″). | |
As shown in Table 2 and further illustrated in Fig. 8, the calculated band gaps for MgBO3 (B = Si, Ge, Sn, Pb) perovskites and Mg3BO (B = Si, Ge, Sn, Pb) anti-perovskites with HSE06 consistently predicting approximately double the band gap values compared to the semi-local GGA functionals, except for the Pb-based compounds, which exhibit metallic behavior under all approximations due to complete band gap closure. A similar trend of higher band gap values obtained using the HSE06 functional compared to GGA-PBE and GGA-PBEsol has been reported by Min Chul Choi et al.76 and Krishna Kumar Mishra et al.77 These observations reinforce the consistency of our findings with established literature and validate the reliability of our computational approach. The ability to tune the band structures and corresponding band gap values through B-site cation substitution in cubic perovskites and anti-perovskites renders these materials highly promising for diverse optical applications.
Table 2 Calculated bandgap for cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
| Band gap (eV) |
Mg3SiO |
Mg3GeO |
Mg3SnO |
Mg3PbO |
Mg3SiO3 |
Mg3GeO3 |
MgSnO3 |
MgPbO3 |
| GGA-PBE |
0.136 |
0.131 |
0.33 |
0.251 |
2.60 |
1.006 |
0.84 |
0.00 |
| Nature |
Direct |
Direct |
Direct |
Direct |
Indirect |
Indirect |
Indirect |
— |
| GGA-PBEsol |
0.147 |
0.109 |
0.331 |
0.352 |
2.55 |
1.17 |
0.97 |
0.00 |
| HSE06 |
0.279 |
0.294 |
0.346 |
0.00 |
4.04 |
3.05 |
2.12 |
0.00 |
| Other |
— |
— |
— |
— |
Indirect68 |
Indirect68,132 |
Indirect68,114 |
— |
| Reported gap |
— |
— |
— |
— |
2.55,131 2.568 |
1.08,131 3.36,132 1.1068 |
0.83,131 0.8568 |
— |
 |
| | Fig. 8 Calculated bandgap for cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb) using GGA-PBE, HSE06 and GGA-PBEsol functionals. | |
The DOS allows us to calculate the general arrangement of states about energy. The DOS parameter significantly determines the bulk properties of conductive materials, such as heat capacity, magnetization susceptibility, and various transport processes. The total density of states Fig. 9 exhibits trends similar to those in Fig. 6 and 7. An interesting observation from Fig. 9 is that anti-perovskites materials exhibit a more fluctuating behavior of the density of states (DOS) in the valence band than perovskites materials. These fluctuating states in the valence band, often referred to as valence band tail states or localized states significantly impact the optical and electronic properties of materials. Localized energy states in the valence band arise from structural disorder, impurities, or defects present in the material. In LEDs and perovskite solar cells, these localized states can capture photo-generated carriers, thereby reducing radiative recombination and affecting the overall effectiveness of the devices. By controlling the density and energy distribution of these states, researchers can enhance device performance.78,79 Additionally, localized states near the valence band edge in thermoelectric materials significantly affect thermal and electronic transport properties. These states create energy barriers that scatter phonons, thereby reducing thermal conductivity while maintaining a high Seebeck coefficient and electrical conductivity, which are beneficial for thermoelectric applications.80,81
 |
| | Fig. 9 (a)–(f) Optimized DOS & PDOS of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
Analysis of the partial density of states Fig. 9 indicates that O-p states dominate the valence band in perovskites, while B-cation p states contribute most in anti-perovskites near the Fermi level. In all compounds, the conduction band is primarily composed of Mg-s states. The valence band maximum at the Fermi level classifies the materials as P-type semiconductors, except for MgPbO3 which exhibits metallic behavior.
3.4 Mechanical properties
Since MgBO3 (B = Si, Ge, Sn, Pb) and Mg3BO (B = Si, Ge, Sn, Pb) compounds are cubic structure with a high degree of symmetry, the elastic constant reduces to three independent elastic constants: C11, C12, and C44.82 The following is an expression of the conventional mechanical stability conditions in cubic crystals at equilibrium in terms of elastic constants,83,84| | | C44 > 0, C11 > |C12|, C11 + 2C12 > 0. | (9) |
All the investigated compounds satisfy the above criteria indicate mechanically stable to deform forces. The formulations associated with the calculations of bulk modulus (B), shearing modulus (G), young's modulus (E), anisotropy (A), Poisson's ratio (ν), Pugh's ratio (B/G), plasticity measurement (B/C44), Kleinman parameter (ζ) have been computed using the following are given by the following expressions, respectively,85–89| |  | (10) |
| |  | (11) |
| |  | (12) |
| |  | (13) |
| |  | (14) |
| |  | (15) |
| |  | (16) |
| |  | (17) |
The stiffness constant C11 is related to the longitudinal deformation, while C12 and C44 relates to the shearing deformation. As seen from Table 3, C11 decrease linearly with cation changing Si to Pb, implying low resistance of the compound against longitudinal compression. Also, C11 is greater than both of C12 and C44 implying that our investigated compounds have lowest resistance against shear deformation. All the three moduli of elasticity namely the Bulks modulus (B), Young's modulus (E) and the Shear Modulus (G) decrease as cation shifted from Si to Pb as shown in Fig. 10. All the compounds have bulk modulus greater than 40 GPa classified them as hard materials. From the listed value in Table 3 perovskites compounds possesses greater elastic modulus compare to anti-perovskites compounds indicating the perovskites compounds potentiality for strong and flexible electronic applications.
Table 3 Mechanical properties of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
|
|
Mg3SiO |
Mg3GeO |
Mg3SnO |
Mg3PbO |
Mg3SiO3 |
Mg3GeO3 |
MgSnO3 |
MgPbO3 |
|
C
11 (GPa) |
157.58 |
152.95 |
127.76 |
118.25 |
354.32 |
322.62 |
300.01 |
228.79 |
| Other cal. |
— |
— |
— |
— |
41168 |
30068 |
25168 |
— |
|
C
12 (GPa) |
39.04 |
34.94 |
38.64 |
38.26 |
154.37 |
114.28 |
75.56 |
57.83 |
| Other cal. |
— |
— |
— |
— |
16468 |
19568 |
21068 |
— |
|
C
44 (GPa) |
60.45 |
57.53 |
51.15 |
45.51 |
178.73 |
109.86 |
55.01 |
27.68 |
| Other cal. |
— |
— |
— |
— |
20068 |
22068 |
23568 |
— |
|
G (GPa) |
79.31 |
74.37 |
71.71 |
68.94 |
303.55 |
204.85 |
109.09 |
68.16 |
| Other cal. |
— |
— |
— |
— |
16568 |
12468 |
9768 |
— |
|
Y (GPa) |
178.02 |
167.29 |
159.39 |
152.75 |
624.67 |
448.04 |
263.55 |
170.71 |
| Other cal. |
— |
— |
— |
— |
40568 |
31768 |
25468 |
— |
|
B (GPa) |
78.55 |
74.27 |
68.34 |
64.92 |
221.02 |
183.72 |
150.37 |
114.81 |
| Other cal. |
— |
— |
— |
— |
24668 |
23068 |
23568 |
— |
|
C
P (GPa) |
−21.41 |
−22.59 |
−12.51 |
−7.25 |
−24.36 |
4.42 |
20.55 |
30.15 |
|
A
|
1.01 |
0.97 |
1.14 |
1.13 |
1.78 |
1.05 |
0.49 |
0.32 |
|
ν (km s−1) |
0.12 |
0.12 |
0.11 |
0.10 |
0.028 |
0.09 |
0.20 |
0.25 |
|
B/G |
0.99 |
0.99 |
0.95 |
0.94 |
0.72 |
0.89 |
1.37 |
1.68 |
|
ζ
|
0.39 |
0.37 |
0.44 |
0.46 |
0.56 |
0.59 |
0.40 |
0.40 |
| µM |
1.29 |
1.29 |
1.33 |
1.42 |
1.23 |
1.67 |
2.73 |
4.14 |
 |
| | Fig. 10 (a)–(d) Variation of mechanical properties with B cation change in cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
Cauchy's pressure (C12–C44) also accounts for the brittle or ductile nature. A positive C12–C44 implies ductile characteristics whereas negative value of Cauchy's pressure implies brittle nature. All the anti-perovskites compounds have negative Cauchy pressure indicating brittle in nature while except from MgSiO3 all the perovskites’ compounds possess positive Cauchy pressure indicating ductile nature.
Microcracks significantly influence material behavior due to their link with elastic anisotropy (A). This factor, calculated viaeqn (15), quantifies directional stiffness A = 1 denotes isotropy, while deviations indicate anisotropic nature. The computed A values are listed in Table 3. These findings suggest that both class of the selected compounds are anisotropic, whereas MgSiO3, Mg3GeO, MgSiO3 and MgPbO3 exhibits a pronounced degree of anisotropy compared to Mg3SnO, Mg3PbO, MgSnO3 and MgPbO3.
The Pugh (B/G) and Poisson ν ratios are the other crucial parameters employed to determine the mechanical properties, such as brittleness and ductility, of a material. For ductile materials, the necessary criterion is that the B/G and ν values must be greater than 1.75 and 0.26, respectively; otherwise, the material will be brittle.90,91 All the investigating compounds has less value indicating ductile nature.
The Kleinman parameter (ζ) assesses bond rigidity, where ζ = 1 implies strong bonding and ζ = 0 reflects bond flexibility. A value near 0.5 suggests that deformation resistance arises from both bond strength and bending.92 From Table 3, we observed all the compounds except MgSiO3 have ζ less than 0.50 indicates less resistance toward bond bending.
The machinability index (μM) characterizes a machine operation's plastic deformation behavior, cutting performance and overall cost-efficiency. The value can be calculated using following equation93
| |  | (18) |
As shown in
Table 3, MgSnO
3 and MgPbO
3 exhibit machinability index (
μM) values of 2.13, exceeding the critical threshold of 2. This indicates reduced friction and enhanced lubricating behavior, which are advantageous for industrial machining, wear-resistant coatings, and tribological applications. In contrast, all other compounds possess
μM values below 2, suggesting comparatively higher friction and lower lubrication efficiency, limiting their suitability for high-performance cutting or sliding-contact environments.
94
For single and polycrystalline solids, the degree of elastic anisotropy is essential to the evolution of the microscopic behavior of solid materials. Anisotropic nature strongly depends on several elastic constants, C11 in particular.95 Consequently, for the compounds being studied, it is imperative to investigate the directional dependency of the elastic tensor. Improving a solid material's mechanical resistance and applicability under external stress is feasible by examining the degree of elastic anisotropy. Furthermore, accurate characterizations of these characteristics can play a crucial role in fundamental crystal physics and applied engineering sciences for application reasons.96
| |  | (19) |
| |  | (20) |
| |  | (21) |
| |  | (22) |
The Zener anisotropy factor
97AZ deals with the elastic anisotropy of cubic ABO
3 compounds. Shear anisotropy is primarily associated with
AZ. The particular value of
AZ for isotropic compounds is 1.
AG is the new elastic anisotropy (
AG) requirement for cubic compounds developed by Chung and Buessem
et al.98 Anisotropy factor (
A) is often given as a percentage, and a material is considered “isotropic” if
AG = 0. The universal elastic anisotropy factor (
AU) is related to all the components of a material's elasticity tensor and can be determined using the formula given in
eqn (26).
99 The Logarithmic Universal Euclidean anisotropy
100AL is an alternative anisotropy factor for cubic
GR crystals. It is associated with the Voigt and Reuss limits on the bulk modulus.
Table 4 displays all of the values related to
AZ,
AG,
AU, and
AL; the non-zero values of these parameters describe the anisotropic nature of the specified materials. For a cubic compound, the strain along 〈110〉 and the equivalent transverse strain along 〈001〉 and 〈110〉 provide the peak values of Poisson's ratio. Poisson's ratio is as
101 follows:

and

to these directions. The differences in bond strengths and atomic arrangements among different crystallographic orientations account for this variation in Poisson's ratio, indicating the anisotropic nature of the materials under study.
| |  | (24) |
| |  | (25) |
Teter
et al.,
102 Tian
et al.103 and Chen
et al.,
104 have proposed various estimations for the
HV (Vickers hardness) ABO
3.
Table 4 lists the estimated values for these parameters. The estimated
HV values for both alloys show that they are both hard since they are all positive in all estimations. Due to the dearth of scientific data in the literature, these results cannot be directly compared. However, they can provide valuable insights for future experimentation.
Table 4 Calculated values of Vickers hardness (HV), anisotropic parameters and extreme Poisson's ratio for of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
|
|
Mg3SiO |
Mg3GeO |
Mg3SnO |
Mg3PbO |
Mg3SiO3 |
Mg3GeO3 |
MgSnO3 |
MgPbO3 |
|
A
Z
|
2.01 |
1.98 |
2.10 |
2.09 |
2.44 |
2.03 |
1.61 |
1.49 |
|
A
G
|
0.05 |
0.05 |
0.06 |
0.06 |
0.09 |
0.05 |
0.02 |
0.01 |
|
A
U
|
−1.96 |
−1.79 |
−2.44 |
−2.71 |
−3.39 |
−3.21 |
−2.22 |
−2.03 |
|
A
L
|
−1.11 |
−0.99 |
−1.5 |
−1.74 |
−2.54 |
−2.30 |
−1.31 |
−1.16 |
|
V (100, 001) |
0.28 |
0.26 |
0.34 |
0.36 |
0.49 |
0.38 |
0.26 |
0.25 |
|
V (100, 110) |
−0.14 |
−0.15 |
−0.13 |
−0.11 |
−0.13 |
−0.08 |
−0.03 |
0.003 |
|
H
V (Teter) |
11.97 |
11.23 |
10.82 |
10.41 |
45.83 |
30.93 |
16.47 |
10.29 |
|
H
V (Tian) |
20.56 |
19.47 |
19.99 |
19.70 |
74.93 |
44.97 |
17.83 |
10.22 |
|
H
V (Chen) |
23.12 |
21.91 |
22.76 |
22.53 |
79.10 |
44.11 |
18.38 |
9.84 |
3.5 Optical properties
When a material absorbs incoming radiation, electrons are excited from the valence band to the conduction band, generating its optical response. Thus, the optical characteristics of cubic A3SnO (where A = Ca, Sr, and Ba) are closely connected to their electronic band structures and are essential for exploring their practical applications. Fig. 11 illustrate several calculated optical properties as functions of the photon energy. Studying the complex dielectric function, including both its real and imaginary parts, allows for a detailed understanding of these optical properties.
 |
| | Fig. 11 (a)–(g) Optical properties of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
The real part of the dielectric constant ε1(ω), is a key optical parameter for assessing a material's suitability for practical optical applications. Fig. 11(a) presents the calculated real dielectric function of investigated compounds and plotted as a function of the incident photon energy. The value of ε1(ω) is obtained via the Kramers–Kronig relations.38 The static dielectric constant, ε1(0), reflects the material's ability to become polarized in response to incident electromagnetic radiation and reported in Table 5. The increment of real dielectric function in perovskites can be compared with the decreasing Eg and consistent with the Penn's model  .105 The static dielectric function provides insight into the extent of charge recombination, which directly influences the performance of optoelectronic devices. Materials exhibiting higher dielectric constants tend to have lower charge recombination rates, thereby enhancing device efficiency.106 Anti-perovskites exhibiting significantly higher static dielectric values than their perovskite counterparts as shown in Fig. 12. From Table 5, the static dielectric constant of the perovskites is below 10, indicating their suitability for microelectronic applications and high optical transparency.107 In contrast, the anti-perovskites exhibit static dielectric constants exceeding 10, making them promising candidates for energy storage and various optical device applications.108 As the energy increases further, the real part of the dielectric function becomes negative, indicating that the material behaves as a reflective medium in these energy regions. This complete reflection of incident electromagnetic waves signifies the emergence of metallic characteristics in the material. The anti-perovskite compounds exhibit negative values in the real part of the dielectric function starting at approximately 3 eV, whereas the perovskite counterparts begin to show negative values around 13 eV. Additionally, the dielectric function of perovskites is relatively lower in magnitude compared to that of anti-perovskites, indicating distinct optical responses between the two material classes.
.105 The static dielectric function provides insight into the extent of charge recombination, which directly influences the performance of optoelectronic devices. Materials exhibiting higher dielectric constants tend to have lower charge recombination rates, thereby enhancing device efficiency.106 Anti-perovskites exhibiting significantly higher static dielectric values than their perovskite counterparts as shown in Fig. 12. From Table 5, the static dielectric constant of the perovskites is below 10, indicating their suitability for microelectronic applications and high optical transparency.107 In contrast, the anti-perovskites exhibit static dielectric constants exceeding 10, making them promising candidates for energy storage and various optical device applications.108 As the energy increases further, the real part of the dielectric function becomes negative, indicating that the material behaves as a reflective medium in these energy regions. This complete reflection of incident electromagnetic waves signifies the emergence of metallic characteristics in the material. The anti-perovskite compounds exhibit negative values in the real part of the dielectric function starting at approximately 3 eV, whereas the perovskite counterparts begin to show negative values around 13 eV. Additionally, the dielectric function of perovskites is relatively lower in magnitude compared to that of anti-perovskites, indicating distinct optical responses between the two material classes.
Table 5 Static dielectric, refractive and reflectivity of cubic perovskites Mg3BO (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
|
|
Mg3SiO |
Mg3GeO |
Mg3SnO |
Mg3PbO |
Mg3SiO3 |
Mg3GeO3 |
MgSnO3 |
MgPbO3 |
|
ε
1(0) |
23.74 |
27.10 |
29.65 |
34.77 |
3.21 |
3.97 |
4.33 |
6.58 |
| Other cal. |
— |
— |
— |
— |
— |
2.74132 |
— |
— |
| Static refractive index R(0) |
4.87 |
5.20 |
5.46 |
5.91 |
1.79 |
1.99 |
2.08 |
2.56 |
| Other cal. |
— |
— |
— |
— |
— |
2.10132 |
— |
— |
| Extinction (max) |
3.03 |
3.64 |
3.21 |
3.15 |
1.69 |
1.38 |
1.11 |
1.32 |
| Other |
— |
— |
— |
— |
— |
1.32132 |
— |
— |
| Static reflectivity R(0) |
43.5% |
45.9% |
47.9% |
50.8% |
8.07% |
11.01% |
12.3% |
19.2% |
| Other cal. |
— |
— |
— |
— |
— |
6.08%132 |
— |
— |
 |
| | Fig. 12 (a) and (b) Relative change in static dielectric and refractive index of cubic perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
Reflectivity, R(ω), describes the surface characteristics of a material and is defined as the ratio of reflected power to the incident power. Reflectivity R(0), owing to its anti-reflective coating, emerges as a crucial parameter for assessing the suitability of a material for shielding applications. The static reflectivity R(0) measurements yielded values listed in Table 5. Fig. 11(f) shows that perovskites exhibit lower static reflectivity than anti-perovskites, with values increasing as the B-site cation changes from Si to Pb in both material classes. The low reflectivity values observed in the infrared and visible regions indicate that perovskites are more transparent compare to anti-perovskites within these energy ranges, making them promising candidates for antireflective coating applications. With increasing energy, the reflectivity rises, exhibiting slight fluctuations and reaching maximum values within the UV energy range can therefore use as UV shielding.109 Since reflectivity is primarily influenced by free electrons in the material, the sharp increase in reflectivity at certain energies is likely due to enhanced optical conductivity within those energy ranges.
The refractive index, n(ω), characterizes the propagation of electromagnetic radiation through a material and is shown in Fig. 11(b). Both the refractive index n(ω) and the extinction coefficient k(ω) are calculated using the relations. The static refractive index n(0), reported in Table 5, satisfies the relation ε1(0) = n2(0), confirming the accuracy of the calculations.110 Based on the reported values in Table 5 and illustrated in Fig. 12, anti-perovskite compounds exhibit significantly higher static refractive indices compared to their perovskite counterparts, indicating stronger light–matter interaction. This makes them promising candidates for photonic applications such as waveguides, modulators, and optical sensors.111 In contrast, the relatively lower refractive indices of perovskites suggest better transparency, making them suitable for use as window layers in solar cells and other optoelectronic devices.112Fig. 11(b) reveals that n(ω) increases with incident photon energy, reaching a maximum between 0.01361 eV and 2.5 eV, corresponding to the infrared region. We observed that as cation changing from Si to Pb the value rises. Within this range, the material exhibits maximum transparency, which can be tuned by varying the B-site ions (A = Si, Ge, Sn, Pb). Beyond this energy range, n(ω) decreases, indicating reduced transparency and increased absorption of higher-energy radiation. Moreover, the n(ω) curves recorded for compounds closely align with the ε1(ω) curves, especially within the energy ranges corresponding to the observed peaks. The noticed identical nature arises from their inter connectedness via established relationships ε1(0) = n2 − k2.113 Beyond its peak, the refractive index n(ω) drops below 1 at photon energies above 4 eV for anti-perovskites and 16 eV for perovskites implying that the group velocity Vg = c/n of the photons exceeds the speed of light. This decline corresponds to reduced transparency, resulting in increased absorption of high-energy incident radiation by the material.
The optical conductivity of a material fundamentally depends on its ability to produce free carriers when absorbing incident photons, originating from bond disruptions caused by photon–electron interactions.114Fig. 11(d) demonstrates that the optical conductivity and absorption coefficient of the studied materials exhibit similar trends as functions of photon energy, reflecting their interrelated electronic transitions. A closer examination reveals that the perovskite compounds show higher optical conductivity predominantly in the ultraviolet (UV) region. Notably, the peak optical conductivity shifts toward lower photon energies as the B-site cation varies from Si to Pb, indicating tunable electronic structures and band gap narrowing. This tunability makes perovskites attractive candidates for UV photodetectors and optoelectronic devices requiring selective absorption in the UV spectrum.115 In contrast, the anti-perovskite materials exhibit their maximum optical conductivity within the visible energy range, which suggests strong interaction with visible light photons. This characteristic is especially promising for photovoltaic applications and visible-light-driven photocatalysis, where efficient absorption and charge carrier generation are essential.116,117 The enhanced optical conductivity in the visible region can facilitate higher photo response and energy conversion efficiencies, positioning anti-perovskites as potential materials for next-generation solar cells and optoelectronic devices.118
In summary, the optical parameters of the perovskites and anti-perovskites structures can be tailored by altering the cation type (Si, Ge, Sn, Pb), offering promising potential for advanced devices sensitive to infrared radiation.
3.6 Thermodynamics properties
Thermodynamic stability is a fundamental requirement for materials intended for high-temperature applications, necessitating a comprehensive evaluation of their thermal behavior. Thermodynamics governs the principles of energy exchange and heat flow within physical systems, and parameters such as Debye temperature (θD) and acoustic wave velocities serve as critical indicators of thermo-physical performance. Key properties including θD melting temperature (Tm), and minimum thermal conductivity (Kmin) can be derived from longitudinal (V1), transverse (Vt), and average sound velocities (Vm), in conjunction with material density (ρ), as detailed in Table 6. These sound velocities were calculated using established theoretical relations and are presented in Table 6 and illustrated in Fig. 13.| |  | (26) |
| |  | (27) |
| |  | (28) |
The Debye temperature (θD) is a key parameter linking a material's mechanical properties to its thermal behavior, including lattice vibrations, thermal expansion, melting point, specific heat, and thermal conductivity. It represents the upper limit of vibrational modes in a solid and serves as an indicator of lattice stiffness. Although not directly measurable, θD can be reliably estimated from elastic modulus data using the following expressions,119| |  | (29) |
As presented in Table 6 and Fig. 13(c), the Si- and Ge-based compounds exhibit the highest Debye temperatures among the materials studied, indicating stronger interatomic bonding and superior phonon-mediated thermal conductivity.
Table 6 Calculated values of thermal factors of Mg-based perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb)
| Compounds |
ρ (gm cm−3) |
V
1 (km s−1) |
V
t (km s−1) |
V
m (km s−1) |
θ
D (K) |
K
min (W m−1 K−1) |
γ
|
ω
D (THz) |
T
m (K) |
| Mg3SiO |
2.22 |
9.11 |
5.97 |
5.19 |
640.37 |
1.12 |
1.03 |
13.34 |
2481.82 |
| Mg3SiO |
3.21 |
7.35 |
4.81 |
4.35 |
537.07 |
0.94 |
1.03 |
11.19 |
2417.25 |
| Mg3SiO |
3.69 |
6.66 |
4.40 |
4.02 |
440.04 |
0.88 |
1 |
9.17 |
2082.72 |
| Mg3SiO |
6.18 |
5.03 |
3.33 |
3.18 |
350.70 |
0.66 |
0.99 |
7.31 |
1950.33 |
| Mg3SiO |
3.79 |
12.84 |
8.94 |
6.97 |
640.37 |
0.89 |
0.80 |
13.34 |
4252.48 |
| Mg3SiO |
4.78 |
9.77 |
6.54 |
5.54 |
726.35 |
0.74 |
0.95 |
15.14 |
4709.23 |
| Mg3SiO |
4.82 |
7.83 |
4.75 |
4.41 |
539.17 |
0.65 |
1.31 |
11.23 |
4398.78 |
| Mg3SiO |
7.16 |
5.36 |
3.08 |
3.07 |
349.77 |
0.52 |
1.51 |
7.29 |
3442.35 |
 |
| | Fig. 13 (a)–(d) Thermodynamical properties of Mg-based perovskites MgBO3 (B = Si, Ge, Sn, Pb) and anti-perovskites Mg3BO (B = Si, Ge, Sn, Pb). | |
The minimum thermal conductivity (K) of solids typically decreases with increasing temperature and can be estimated using the Clarke model,120
| | 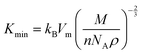 | (30) |
Table 6 and
Fig. 13(d) reveal a pronounced decline in thermal conductivity (
K) as the cation transitions from Si to Pb.
The melting point is a fundamental property of crystalline materials, defined as the temperature at which the solid and liquid phases coexist in equilibrium under standard atmospheric pressure. This parameter plays a critical role in determining the thermal stability, performance, and applicability of materials across various scientific and industrial domains, including alloy design, nanoparticle stability, and high-temperature technologies.121 The melting temperature (Tm) is calculated using the following relation.122
| |  | (31) |
As illustrated in
Table 6 and
Fig. 13(b), the perovskite compounds exhibit notably higher melting temperatures compared to their anti-perovskite counterparts, indicating superior thermal stability. Among the perovskites, MgGeO
3 and MgSnO
3 demonstrate the highest melting points, which reflect their relatively stronger interatomic bonding and enhanced lattice cohesion. This suggests that these materials may be more suitable for high-temperature applications where structural integrity is critical.
The Debye frequency (ωD) is a fundamental parameter for characterizing the thermal behavior of crystalline solids, particularly in relation to specific heat and thermal conductivity. It provides insight into atomic-scale heat transport and significantly influences material performance at low temperatures. The Debye frequency for a given solid is calculated using the following expression.121
| | 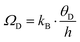 | (32) |
Table 6 and
Fig. 13(d) indicate a notable decline in Debye frequency (
ωD) across both perovskite and anti-perovskite compounds as the cation substitution progresses from Si to Pb, with the exception of MgGeO
3, which exhibits the highest
ωD value. A higher Debye frequency reflects an extended phonon spectrum, contributing to enhanced thermal conductivity and heat capacity. Accordingly, the elevated
ωD of MgGeO
3 correlates with its superior thermal transport properties.
Table 6 and Fig. 13(c) also report the Grüneisen parameter (γ), which characterizes the phonon anharmonicity within the crystal lattice. This parameter is derived from Poisson's ratio using the following relation.120
| |  | (33) |
The Grüneisen parameter plays a critical role in characterizing phonon damping and thermal expansion behavior in crystalline solids. Materials with lower
γ values typically exhibit more harmonic lattice vibrations, which contribute to enhanced phonon-mediated thermal conductivity. As shown in
Table 6, Mg
3PbO, MgSiO
3 and MgGeO
3 possess the lowest
γ values among the compounds studied, indicating their potential for efficient phonon transport. This parameter is fundamental for evaluating the interplay between thermal expansion and specific heat, and is essential for understanding thermo-mechanical properties and lattice dynamics in solid-state systems.
123
Overall thermodynamic properties of Mg-based perovskite and anti-perovskite compounds reveal distinct application potentials across advanced technologies. Mg3SiO, with moderate Debye temperature and low Grüneisen parameter, is suitable for thermoelectric devices and infrared sensors.124 Mg3GeO offers balanced thermal conductivity and phonon transport, making it promising for strain-tuned thermoelectric modules and low-power electronics.125 Mg3SnO, with moderate melting point and phonon conductivity, supports mid-temperature thermoelectric applications.126 Mg3PbO shows the lowest thermal conductivity and Debye frequency but favorable phonon transport due to reduced anharmonicity, making it suitable for phonon filters and low-power dielectric layers.127 Among perovskites, MgSiO3 demonstrates high Debye temperature and melting point with low γ, ideal for UV photodetectors and thermal barrier coatings Springer. MgGeO3, with the highest Debye temperature and melting point, is well-suited for high-performance thermoelectric and memory devices.128 MgSnO3 supports infrared detection and thermoelectric modules due to its strong thermal stability and phonon conductivity.129 Finally, MgPbO3 with high dielectric constant and visible-light absorption, is promising for energy storage and photovoltaic applications.130 These findings highlight the compositional tunability and multifunctional potential of Mg-based compounds in optoelectronics, thermoelectric and energy systems.
4. Conclusion
In this study, we conducted a comparative first-principles investigation of Mg-based cubic perovskite (MgBO3) and anti-perovskite (Mg3BO) compounds, where B = Si, Ge, Sn, Pb, to explore their structural, electronic, mechanical, and optical properties. Structural optimization confirmed phase stability across all compositions, with lattice parameters and unit cell volumes increasing systematically from Si to Pb, consistent with the trend in cationic radii. The more negative formation energies of anti-perovskites indicate stronger thermodynamic favorability, while the decreasing trend across the B-site series reflects reduced cohesive strength with heavier cations. Electronic band structure analysis revealed indirect band gaps in perovskites, transitioning from semiconducting to metallic behavior with heavier B-site cations. Anti-perovskites maintained narrow direct band gaps (<0.5 eV), making them suitable for infrared detection and thermoelectric applications. Density of states analysis further confirmed p-type semiconducting behavior in most compounds, with MgPbO3 displaying metallicity. Mechanical evaluations showed that perovskites possess significantly higher elastic constants, bulk modulus, and Young's modulus, reflecting superior stiffness and ductility. Anisotropy and Kleinman parameters revealed directional dependence and bond flexibility, particularly in systems with heavier cations. MgGeO3 and MgSnO3 demonstrate the highest thermal stability and phonon conductivity among the compounds studied. The decline in thermal performance with heavier cation substitution highlights the role of lattice dynamics. Perovskites outperform anti-perovskites in high-temperature resilience, with select anti-perovskites showing promising phonon transport due to reduced anharmonicity. These findings support the use of Mg-based compounds in thermoelectric, optoelectronic, and energy-related applications. Optical analyses demonstrated Perovskites exhibited low reflectivity and high UV conductivity, making them promising for photodetectors and antireflective coatings. Anti-perovskites showed elevated dielectric constants and strong visible-light absorption, suggesting potential for energy storage and photovoltaic applications. Overall, Mg-based perovskite and anti-perovskite compounds offer complementary advantages: perovskites excel in mechanical robustness and UV-optical performance, while anti-perovskites provide narrow band gaps and enhanced dielectric response. This compositional tunability positions both material classes as versatile candidates for multifunctional engineering applications, including optoelectronics, thermoelectric, and memory devices.
Conflicts of interest
There are no conflicts to declare.
Data availability
The data supporting the findings of this study, including structural parameters, formation energies, electronic band structures, and optical properties of MgBO3 and Mg3BO compounds (B = Si, Ge, Sn, Pb), are available from the corresponding author upon reasonable request. No restrictions apply to data sharing.
Acknowledgements
We thankfully acknowledge the Condensed Matter Physics lab at Jahangirnagar University through their R&D fund allocation program.
References
- Z. Huang,
et al., Interface Engineering and Emergent Phenomena in Oxide Heterostructures, Adv. Mater., 2018, 30, 1802439 CrossRef PubMed.
- A. A. Bokov and Z. G. Ye, Recent progress in relaxor ferroelectrics with perovskite structure, J. Mater. Sci., 2006, 41, 31–52 CrossRef CAS.
- T. Arakawa, H. Kurachi and J. Shiokawa, Physicochemical properties of rare earth perovskite oxides used as gas sensor material, J. Mater. Sci., 1985, 20, 1207–1210 CrossRef CAS.
- M. Oudah,
et al., Superconductivity in the antiperovskite Dirac-metal oxide Sr3−xSnO, Nat. Commun., 2016, 7, 1–6 Search PubMed.
- M. Bilal, S. Jalali-Asadabadi, R. Ahmad and I. Ahmad, Electronic Properties of Antiperovskite Materials from State-of-the-Art Density Functional Theory, J. Chem., 2015, 2015, 495131 CrossRef.
- P. Zubko, S. Gariglio, M. Gabay, P. Ghosez and J. M. Triscone, Interface physics in complex oxide heterostructures, Annu. Rev. Condens. Matter Phys., 2011, 2, 141–165 CrossRef CAS.
- S. V. Krivovichev, Minerals with antiperovskite structure: a review, Z. Kristallogr., 2008, 223, 109–113 CAS.
- Z. Y. Gao, W. Wang, L. Sun and F. Wang, Electronic, magnetic, elastic and thermodynamic properties of antiperovskite metallic compounds Mn3XN (X = Ni, Pd, Pt): a DFT study, Solid State Commun., 2022, 354, 114913 CrossRef CAS.
- N. Hoffmann, T. F. T. Cerqueira, J. Schmidt and M. A. L. Marques, Superconductivity in antiperovskites, npj Comput. Mater., 2022, 8, 1–10 CrossRef.
- M. Bilal, S. Jalali-Asadabadi, R. Ahmad and I. Ahmad, Electronic Properties of Antiperovskite Materials from State-of-the-Art Density Functional Theory, J. Chem., 2015, 2015, 495131 CrossRef.
- M. Xiong, S. Wang and Z. Mao, Regarding the structural, thermodynamic, mechanical, thermoelectric, and optoelectronic properties of anti-perovskite Mg3XN (X = As, Sb, and Bi) through a DFT approach, Phys. B, 2024, 683, 415892 CrossRef CAS.
- C. Guan,
et al., Unlocking the chemical space in anti-perovskite conductors by incorporating anion rotation dynamics, Energy Storage Mater., 2023, 62, 102936 CrossRef.
- S. Venkatesh, A. Baras, J. S. Lee and I. S. Roqan, The magnetic ordering in high magnetoresistance Mn-doped ZnO thin films, AIP Adv., 2016, 6, 035019 CrossRef.
- S. Iqbal,
et al., Electronic and Optical Properties of Ca3MN (M = Ge, Sn, Pb, P, As, Sb and Bi) Antiperovskite Compounds, J. Electron. Mater., 2016, 45, 4188–4196 CrossRef CAS.
- Q. Q. Liang,
et al., First-principles calculations to investigate structural, electronic, optical and thermodynamic properties of anti-perovskite compounds X3OI (X = Na, K, Rb), J. Mater. Res. Technol., 2023, 22, 3245–3254 CrossRef CAS.
- N. Iram,
et al., First-principles investigation on anti-perovskites on Rb3OX (X = Cl, Br, I): promising compounds for high performance photovoltaics and thermoelectric, Mater. Sci. Semicond. Process., 2024, 174, 108168 CrossRef CAS.
- Q. Zhong, Z. Dai, J. Wang, Y. Zhao and S. Meng, Ultra-low lattice thermal conductivity and high thermoelectric efficiency of K3AuO, J. Appl. Phys., 2021, 130(4), 045101 CrossRef CAS.
- Y. Zhao,
et al., Anomalous electronic and thermoelectric transport properties in cubic Rb3AuO antiperovskite, Phys. Rev. B, 2020, 102, 094314 CrossRef CAS.
- E. O. Chi, W. S. Kim, N. H. Hur and D. Jung, New Mg-based antiperovskites PnNMg3 (Pn = As, Sb), Solid State Commun., 2002, 121, 309–312 CrossRef CAS.
- Y. Mochizuki, H. J. Sung, A. Takahashi, Y. Kumagai and F. Oba, Theoretical exploration of mixed-anion antiperovskite semiconductors M3XN (M = Mg, Ca, Sr, Ba; X = P, As, Sb, Bi), Phys. Rev. Mater., 2020, 4, 044601 CrossRef CAS.
- Y. Cai,
et al., Quantum Wells in Magnesium-Manganese Bimetallic Antiperovskites for High Luminescence, ACS Appl. Mater. Interfaces, 2025, 17, 16987–16997 CrossRef CAS.
- E. Oyeniyi, Electronic and optical properties of Mg3XN (X = P, As, Sb, Bi) antiperovskites: the GW/BSE approach, Solid State Commun., 2022, 355, 114927 CrossRef CAS.
- M. Murakami, K. Hirose, K. Kawamura, N. Sata and Y. Ohishi, Post-Perovskite Phase Transition in MgSiO3, Science, 2004, 304, 855–858 CrossRef CAS PubMed.
- B. B. Karki and G. Khanduja, A computational study of ionic vacancies and diffusion in MgSiO3 perovskite and post-perovskite, Earth Planet. Sci. Lett., 2007, 260, 201–211 CrossRef CAS.
- J. Gao,
et al., Effects of pressure on structural, mechanical, and electronic properties of trigonal and monoclinic MgSiO3, Solid State Sci., 2020, 105, 106261 CrossRef CAS.
- L. G. Liu, The high-pressure phases of MgSiO3, Earth Planet. Sci. Lett., 1976, 31, 200–208 CrossRef CAS.
- M. E. Song,
et al., Synthesis and Microwave Dielectric Properties of MgSiO3 Ceramics, J. Am. Ceram. Soc., 2008, 91, 2747–2750 CrossRef CAS.
- Q. Mahmood, M. Yaseen, B. Ul Haq, A. Laref and A. Nazir, The study of mechanical and thermoelectric behavior of MgXO3 (X = Si, Ge, Sn) for energy applications by DFT, Chem. Phys., 2019, 524, 106–112 CrossRef CAS.
- N. Iram,
et al., Insight on thermodynamic and thermoelectric properties of Ge based perovskites AGeO3 (A = Mg, Cd) for energy harvesting applications: a DFT approach, Inorg. Chem. Commun., 2024, 170, 113160 CrossRef CAS.
- C. Xia,
et al., Experimental and theoretical studies on luminescent mechanisms and different visual color of the mixed system composed of MgGeO3: Mn, Eu and Zn2GeO4:Mn, Int. J. Mod. Phys. B, 2020, 34(25), 2050216 CrossRef CAS.
- B. B. Dumre and S. V. Khare, Interrelationship of bonding strength with structural stability of ternary oxide phases of MgSnO3: a first-principles study, Phys. B, 2022, 637, 413896 CrossRef CAS.
- Q. Mahmood, M. Yaseen, B. Ul Haq, A. Laref and A. Nazir, The study of mechanical and thermoelectric behavior of MgXO3 (X = Si, Ge, Sn) for energy applications by DFT, Chem. Phys., 2019, 524, 106–112 CrossRef CAS.
- X. F. Xu,
et al., Tuning mechanical properties, ferroelectric properties and electronic structure in R3c-MgSnO3 by compressive strain: a first-principle study, Phys. B, 2021, 618, 413143 CrossRef CAS.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- D. M. Ceperley and B. J. Alder, Ground State of the Electron Gas by a Stochastic Method, Phys. Rev. Lett., 1980, 45, 566 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew,
et al., Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, Relaxation of Crystals with the Quasi-Newton Method, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- O. Axelsson and I. Gustafsson, Iterative methods for the solution of the Navier equations of elasticity, Comput. Methods Appl. Mech. Eng., 1978, 15, 241–258 CrossRef.
- V. M. Goldschmidt, Die Gesetze der Krystallochemie, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- J. Young and J. M. Rondinelli, Octahedral Rotation Preferences in Perovskite Iodides and Bromides, J. Phys. Chem. Lett., 2016, 7, 918–922 CrossRef CAS PubMed.
- A. E. Maughan, A. M. Ganose, M. A. Almaker, D. O. Scanlon and J. R. Neilson, Tolerance Factor and Cooperative Tilting Effects in Vacancy-Ordered Double Perovskite Halides, Chem. Mater., 2018, 30, 3909–3919 CrossRef CAS.
- Formation enthalpies by mixing GGA and GGA calculations, Phys. Rev. B, 2011, 84, 045115 CrossRef.
- A. A. Emery and C. Wolverton, High-Throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites, Sci. Data, 2017, 4, 1–10 Search PubMed.
- E. Tenuta, C. Zheng and O. Rubel, Thermodynamic origin of instability in hybrid halide perovskites, Sci. Rep., 2016, 6, 1–8 CrossRef PubMed.
- P. Kumar,
et al., Coupled phonons, magnetic excitations, and ferroelectricity in AlFeO3: Raman and first-principles studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134449 CrossRef.
- D. J. Adams and D. Passerone, Insight into structural phase transitions from the decoupled anharmonic mode approximation, J. Phys.: Condens. Matter, 2016, 28, 305401 CrossRef PubMed.
- P. Souvatzis, O. Eriksson, M. I. Katsnelson and S. P. Rudin, The self-consistent ab initio lattice dynamical method, Comput. Mater. Sci., 2009, 44, 888–894 CrossRef CAS.
- T. Cea and F. Guinea, Coulomb interaction, phonons, and superconductivity in twisted bilayer graphene, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2107874118 CrossRef CAS.
- X. Li,
et al., Advances in mixed 2D and 3D perovskite heterostructure solar cells: a comprehensive review, Nano Energy, 2023, 118, 108979 CrossRef CAS.
- N. Arikan, H. Y. Ocak, G. Dikici Yıldız, Y. G. Yıldız and R. Ünal, Investigation of the Mechanical, Electronic and Phonon Properties of X2ScAl (X = Ir, Os, and Pt) Heusler Compounds, J. Korean Phys. Soc., 2020, 76(10), 916–922 CrossRef CAS.
- R. M. Kornreich, M. Kugler, S. Shtrikman and C. Sommers, Phonon Band Gaps, J. Phys. I, 1997, 7, 509–519 CrossRef.
- J. W. Wafula, J. W. Makokha and G. S. Manyali, First-principles calculations to investigate structural, elastic, electronic and thermodynamic properties of NbCoSn and VRhSn Half-Heusler compounds, Results Phys., 2022, 43, 106132 CrossRef.
- M. Tarekuzzaman,
et al., A systematic first-principles investigation of the structural, electronic, mechanical, optical, and thermodynamic properties of Half-Heusler ANiX (A-Sc, Ti, Y, Zr, Hf; X-Bi, Sn) for spintronics and optoelectronics applications, J. Comput. Chem., 2024, 45, 2476–2500 CrossRef CAS PubMed.
- J. Li,
et al., Phononic Weyl pair, phononic Weyl complex, phononic real Chern insulator state, and phononic corner modes in 2D Kekulé-order graphene, Appl. Phys. Rev., 2023, 10, 031416 CAS.
- J. W. Wafula, J. W. Makokha and G. S. Manyali, First-principles calculations to investigate structural, elastic, electronic and thermodynamic properties of NbCoSn and VRhSn Half-Heusler compounds, Results Phys., 2022, 43, 106132 CrossRef.
- A. Bilić and J. D. Gale, Ground state structure of BaZrO3: a comparative first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174107 CrossRef.
- CERN Library Catalogue. https://catalogue.library.cern/legacy/821265/files/0521782856_TOC.pdf.
- I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, The physical significance of imaginary phonon modes in crystals, Electron. Struct., 2022, 4, 033002 CrossRef CAS.
- G. Gao,
et al., Electronic structures, lattice dynamics, and electron–phonon coupling of simple cubic Ca under pressure, Solid State Commun., 2008, 146, 181–185 CrossRef CAS.
- Q. Y. Xie, F. Xiao, Z. Y. Tang, K. W. Zhang and B. T. Wang, Phonon collapse, second-order phase transition, and glassy thermal transport in halide perovskites Cs3Bi2I6Cl3 and Cs3Bi2Br9, Phys. Rev. B, 2025, 111, 024302 CrossRef CAS.
- J. Liu, A. E. Phillips, D. A. Keen and M. T. Dove, Thermal disorder and bond anharmonicity in cesium lead iodide studied by neutron total scattering and the reverse Monte Carlo method, J. Phys. Chem. C, 2019, 123, 14934–14940 CrossRef CAS.
- A. N. Beecher,
et al., Direct Observation of Dynamic Symmetry Breaking above Room Temperature in Methylammonium Lead Iodide Perovskite, ACS Energy Lett., 2016, 1, 880–887 CrossRef CAS.
- B. Luo, X. Wang, E. Tian, G. Li and L. Li, Electronic structure, optical and dielectric properties of BaTiO3/CaTiO3/SrTiO3 ferroelectric superlattices from first-principles calculations, J. Mater. Chem. C, 2015, 3, 8625–8633 RSC.
- S. Uddin,
et al., Theoretical prediction of the mechanical, electronic, optical and thermodynamic properties of antiperovskites A3BO (A = K, Rb and B = Au, Br) using DFT scheme: new candidate for optoelectronic devices application, J. Comput. Electron., 2024, 23, 1217–1237 CrossRef CAS.
- K. Das,
et al., Dynamical stability, vibrational, and optical properties of anti-perovskite A3BX (Ti3TlN, Ni3SnN, and Co3AlC) phases: a first principles study, AIP Adv., 2020, 10, 095226 CrossRef CAS.
- Q. Mahmood, M. Yaseen, B. Ul Haq, A. Laref and A. Nazir, The study of mechanical and thermoelectric behavior of MgXO3 (X = Si, Ge, Sn) for energy applications by DFT, Chem. Phys., 2019, 524, 106–112 CrossRef CAS.
- F. Cao,
et al., Wide Bandgap Semiconductors for Ultraviolet Photodetectors: Approaches, Applications, and Prospects, Research, 2024, 7, 0385 CrossRef CAS PubMed.
- X. Zhou, Z. Lu, L. Zhang and Q. Ke, Wide-bandgap all-inorganic lead-free perovskites for ultraviolet photodetectors, Nano Energy, 2023, 117, 108908 CrossRef CAS.
- H. Wang,
et al., A Review of Perovskite-Based Photodetectors and Their Applications, Nanomaterials, 2022, 12, 4390 CrossRef CAS PubMed.
- V. G. Kravets, A. V. Kabashin, W. L. Barnes and A. N. Grigorenko, Plasmonic Surface Lattice Resonances: A Review of Properties and Applications, Chem. Rev., 2018, 118, 5912–5951 CrossRef CAS PubMed.
- J. Liu,
et al., Recent Advances of Plasmonic Nanoparticles and their Applications, Materials, 2018, 11, 1833 CrossRef PubMed.
- M. I. Saleem, A. K. K. Kyaw and J. Hur, Infrared Photodetectors: Recent Advances and Challenges Toward Innovation for Image Sensing Applications, Adv. Opt. Mater., 2024, 12, 2401625 CrossRef CAS.
- M. Y. Toriyama, A. N. Carranco, G. J. Snyder and P. Gorai, Material descriptors for thermoelectric performance of narrow-gap semiconductors and semimetals, Mater. Horiz., 2023, 10, 4256–4269 RSC.
- M. C. Choi, W. Yang, Y. W. Son and S. Y. Park, First principles study of dielectric properties of ferroelectric perovskite oxides with extended Hubbard interactions, npj Comput. Mater., 2025, 11, 1–11 CrossRef.
- K. K. Mishra, Evaluating the Potential of Ca3SbBr3 Halide Perovskite for Photovoltaics: A Structural, Mechanical, and Optoelectronic Study Using GGA-PBE and HSE06 Functionals, Phys. Solid State, 2024, 66, 464–475 CrossRef CAS.
- Y. Luo and A. J. Flewitt, Understanding localized states in the band tails of amorphous semiconductors exemplified by a –Si:H from the perspective of excess delocalized charges, Phys. Rev. B, 2024, 109, 104203 CrossRef CAS.
- L. Zhang,
et al., Enhanced efficiency and stability in organic light-emitting diodes by employing a p–i–n–p structure, Appl. Phys. Lett., 2016, 109, 173302 CrossRef.
- M. Upadhyaya, C. J. Boyle, D. Venkataraman and Z. Aksamija, Effects of Disorder on Thermoelectric Properties of Semiconducting Polymers, Sci. Rep., 2019, 9(1), 1–11 CrossRef CAS PubMed.
- R. A. Street, Localized state distribution and its effect on recombination in organic solar cells, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075208 CrossRef.
- R. K. Pingak,
et al., Structural, Electronic, Elastic, and Optical Properties of Cubic BaLiX3 (X = F, Cl, Br, or I) Perovskites: An Ab initio DFT Study, Indones. J. Chem., 2023, 23, 843–862 CrossRef CAS.
- S. Goumri-Said and M. B. Kanoun, Theoretical investigations of structural, elastic, electronic and thermal properties of Damiaoite PtIn2, Comput. Mater. Sci., 2008, 43, 243–250 CrossRef CAS.
- Z. J. Wu,
et al., Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- M. J. Mehl, J. E. Osburn, D. A. Papaconstantopoulos and B. M. Klein, Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 10311 CrossRef CAS PubMed.
- P. Wachter, M. Filzmoser and J. Rebizant, Electronic and elastic properties of the light actinide tellurides, Phys. B, 2001, 293, 199–223 CrossRef CAS.
- C. Jasiukiewicz and V. Karpus, Debye temperature of cubic crystals, Solid State Commun., 2003, 128, 167–169 CrossRef CAS.
- Z. Sun, S. Li, R. Ahuja and J. M. Schneider, Calculated elastic properties of M2AlC (M = Ti, V, Cr, Nb and Ta), Solid State Commun., 2004, 129, 589–592 CrossRef CAS.
- M. J. Mehl, Pressure dependence of the elastic moduli in aluminum-rich Al–Li compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 2493 CrossRef CAS PubMed.
- V. V. Brazhkin,
et al., Mechanical Properties of the Superhard Polymeric and Disordered Phases Prepared From C60, C70, and C2N under High Pressure, Rev. High Pressure Sci. Technol., 1998, 7, 989–991 CrossRef CAS.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- S. Das,
et al., First-principles calculations to investigate structural, mechanical, electronic, magnetic and thermoelectric properties of Ba2CaMO6 (M = Re, Os) cubic double perovskites, Phys. B, 2022, 626, 413554 CrossRef CAS.
- Z. Li,
et al., First-principles investigations of structural, elastic, thermodynamic and electronic properties of Pt3Hf compound under pressure, IOP Conf. Ser.: Mater. Sci. Eng., 2020, 733, 012030 CAS.
- S. Uddin,
et al., Theoretical prediction of the mechanical, electronic, optical and thermodynamic properties of antiperovskites A3BO (A = K, Rb and B = Au, Br) using DFT scheme: new candidate for optoelectronic devices application, J. Comput. Electron., 2024, 23, 1217–1237 CrossRef CAS.
- S. K. Mitro, K. M. Hossain, R. Majumder and M. Z. Hasan, Effect of the negative chemical pressure on physical properties of doped perovskite molybdates in the framework of DFT method, J. Alloys Compd., 2021, 854, 157088 CrossRef CAS.
- R. Majumder, S. K. Mitro and B. Bairagi, Influence of metalloid antimony on the physical properties of palladium-based half-Heusler compared to the metallic bismuth: a first-principle study, J. Alloys Compd., 2020, 836, 155395 CrossRef CAS.
- C. M. Zener and S. Siegel, Elasticity and Anelasticity of Metals, J. Phys. Colloid Chem., 2002, 53, 1468 CrossRef.
- D. H. Chung and W. R. Buessem, The Elastic Anisotropy of Crystals, J. Appl. Phys., 1967, 38, 2010–2012 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Universal elastic anisotropy index, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- K. M. Bal and A. Collas, Are Elastic Properties of Molecular Crystals within Reach of Density Functional Theory? Accuracy, Robustness, and Reproducibility of Current Approaches, Cryst. Growth Des., 2024, 24, 3714–3725 CrossRef CAS.
- R. H. Baughman, J. M. Shacklette, A. A. Zakhidov and S. Stafström, Negative Poisson's ratios as a common feature of cubic metals, Nature, 1998, 392(6674), 362–365 CrossRef CAS.
- D. M. Teter, Computational Alchemy: The Search for New Superhard Materials, MRS Bull., 1998, 23, 22–27 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- D. R. Penn, Wave-Number-Dependent Dielectric Function of Semiconductors, Phys. Rev., 1962, 128, 2093 CrossRef CAS.
- D. Abdullah and D. C. Gupta, Analyzing the structural, optoelectronic, and thermoelectric properties of InGeX3 (X = Br) perovskites via DFT computations, Sci. Rep., 2024, 14, 1–16 CrossRef PubMed.
-
Y.-L. Cheng and C.-Y. Lee, Porous Low-Dielectric-Constant Material for Semiconductor Microelectronics, in Nanofluid Flow in Porous Media, ed. M. Sheikholeslami Kandelousi, S. Ameen, M. S. Akhtar and H.-S. Shin, IntechOpen, London, 2018 Search PubMed.
- S. Li,
et al., Energy Storage and Dielectric Properties of PbHfO3 Antiferroelectric Ceramics, ACS Appl. Energy Mater., 2022, 5, 12174–12182 CrossRef CAS.
- M. Hassan, A. Shahid and Q. Mahmood, Structural, electronic, optical and thermoelectric investigations of antiperovskites A3SnO (A = Ca, Sr, Ba) using density functional theory, Solid State Commun., 2018, 270, 92–98 CrossRef CAS.
- S. Ullah,
et al., First Principal Investigations to Explore the Half-metallicity, Structural, Mechanical, and Optoelectronic Properties of Sodium-Based Fluoroperovskites NaYF3 (Y = Sc and Ti) for Applications in Spintronics and Optoelectronics, Inorg. Chem. Commun., 2024, 163, 112369 CrossRef CAS.
- J. Ramanna, N. Yedukondalu, K. Ramesh Babu and G. Vaitheeswaran, Ab initio study of electronic structure, elastic and optical properties of anti-perovskite type alkali metal oxyhalides, Solid State Sci., 2013, 20, 120–126 CrossRef CAS.
- H. J. Snaith, Perovskites: The Emergence of a New Era for Low-Cost, High-Efficiency Solar Cells, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- S. A. Rouf, M. I. Hussain, U. Mumtaz, A. M. Majeed and H. T. Masood, A density functional theory study of the structural, electronic, and optical properties of XGaO3 (X = V, Nb) perovskites for optoelectronic applications, J. Comput. Electron., 2021, 20, 1484–1495 CrossRef CAS.
- R. Larbi, I. Candan, A. Cakmak, O. Sahnoun and M. Sahnoun, First principle calculations of structural, electronic, and optical properties of XSnO3 (X: Ca, Mg, Sr) perovskite oxides, J. Phys.: Condens. Matter, 2024, 37, 075703 CrossRef PubMed.
- H. Wang,
et al., A Review of Perovskite-Based Photodetectors and Their Applications, Nanomaterials, 2022, 12, 4390 CrossRef CAS PubMed.
- M. Irshad,
et al., Photocatalysis and perovskite oxide-based materials: a remedy for a clean and sustainable future, RSC Adv., 2022, 12, 7009–7039 RSC.
- L. M. Herz, Charge-Carrier Dynamics in Organic-Inorganic Metal Halide Perovskites, Annu. Rev. Phys. Chem., 2016, 67, 65–89 CrossRef CAS PubMed.
- M. S. de Lima,
et al., Visible Light-Driven Photocatalysis and Antibacterial Performance of a Cu-TiO2 Nanocomposite, ACS Omega, 2024, 9, 47122–47134 CrossRef CAS PubMed.
- O. L. Anderson, A simplified method for calculating the debye temperature from elastic constants, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
- D. R. Clarke, Materials selections guidelines for low thermal conductivity thermal barrier coatings, Surf. Coat. Technol., 2003, 163–164, 67–74 CrossRef CAS.
- M. Tarekuzzaman,
et al., DFT analysis of structural, electronic, optical, and thermodynamic properties of LiXI3 (where X = Ca, Sr, Ba) halide perovskites for optoelectronics, Sci. Rep., 2025, 15, 1–23 CrossRef PubMed.
- M. A. Rehman, J. Rehman and M. B. Tahir, Density functional theory study of structural, electronic, optical, mechanical, and thermodynamic properties of halide double perovskites Cs2AgBiX6 (X = Cl, Br, I) for photovoltaic applications, J. Phys. Chem. Solids, 2023, 181, 111443 CrossRef CAS.
- M. A. Hadi, M. S. Ali, S. H. Naqib and A. K. M. A. Islam, New ternary superconducting compound LaRu2As2: physical properties from density functional theory calculations, Chin. Phys. B, 2017, 26, 037103 CrossRef.
- Z. Ullah,
et al., “Remarkable Thermoelectric and Magnetic Properties of Anti-Perovskite MgCNi3: A Pathway to Advanced Energy Conversion and Spintronics”, J. Supercond. Novel Magn., 2025, 38, 1–13 CrossRef.
- M. U. Khandaker,
et al., Newly predicted halide perovskites Mg3AB3 (A = N, Bi; B = F, Br, I) for next-generation photovoltaic applications: a first-principles study, RSC Adv., 2025, 15, 5766–5780 RSC.
- T. Hu,
et al., Thermoelectric properties of lead-free anti-perovskites X3BN (B = Bi, Sb, X = Mg, Ca, Sr): a theoretical study based on first-principles calculations and machine learning interatomic potential, AIP Adv., 2024, 14, 045119 CrossRef CAS.
- Z. Ullah,
et al., Remarkable Thermoelectric and Magnetic Properties of Anti-Perovskite MgCNi3: A Pathway to Advanced Energy Conversion and Spintronics, J. Supercond. Novel Magn., 2025, 38, 1–13 CrossRef.
- L. Zhang,
et al., Advances in the Application of Perovskite Materials, Nano-Micro Lett., 2023, 15(1), 1–48 CrossRef CAS.
- M. U. Khandaker,
et al., Newly predicted halide perovskites Mg3AB3 (A = N, Bi; B = F, Br, I) for next-generation photovoltaic applications: a first-principles study, RSC Adv., 2025, 15, 5766–5780 RSC.
- L. Zhang,
et al., Advances in the Application of Perovskite Materials, Nano-Micro Lett., 2023, 15(1), 1–48 CrossRef CAS.
- M. Yasukawa,
et al., Thermoelectric properties and figure of merit of perovskite-type Ba1−xLaxSnO3 with x = 0.002–0.008, Solid State Commun., 2013, 172, 49–53 CrossRef CAS.
- N. Iram,
et al., Insight on thermodynamic and thermoelectric properties of Ge based perovskites AGeO3 (A = Mg, Cd) for energy harvesting applications: a DFT approach, Inorg. Chem. Commun., 2024, 170, 113160 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Mst.
Shamima Khanom
b,
Prianka
Mondal
*ab,
Mst.
Shamima Khanom
b,
Prianka
Mondal
 c,
Akash Kumer
Paul
b and
Farid
Ahmed
b
c,
Akash Kumer
Paul
b and
Farid
Ahmed
b
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) as their perovskite counterparts. This inversion of cation and anion positions can lead to novel structural and electronic behaviors, enabling a wide variety of physical properties. Depending on their chemical composition, APs may behave as metals, non-metals, semiconductors, or superconductors.5
m) as their perovskite counterparts. This inversion of cation and anion positions can lead to novel structural and electronic behaviors, enabling a wide variety of physical properties. Depending on their chemical composition, APs may behave as metals, non-metals, semiconductors, or superconductors.5


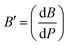





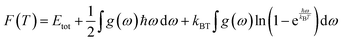




















 and
and  to these directions. The differences in bond strengths and atomic arrangements among different crystallographic orientations account for this variation in Poisson's ratio, indicating the anisotropic nature of the materials under study.
to these directions. The differences in bond strengths and atomic arrangements among different crystallographic orientations account for this variation in Poisson's ratio, indicating the anisotropic nature of the materials under study.


 .105 The static dielectric function provides insight into the extent of charge recombination, which directly influences the performance of optoelectronic devices. Materials exhibiting higher dielectric constants tend to have lower charge recombination rates, thereby enhancing device efficiency.106 Anti-perovskites exhibiting significantly higher static dielectric values than their perovskite counterparts as shown in Fig. 12. From Table 5, the static dielectric constant of the perovskites is below 10, indicating their suitability for microelectronic applications and high optical transparency.107 In contrast, the anti-perovskites exhibit static dielectric constants exceeding 10, making them promising candidates for energy storage and various optical device applications.108 As the energy increases further, the real part of the dielectric function becomes negative, indicating that the material behaves as a reflective medium in these energy regions. This complete reflection of incident electromagnetic waves signifies the emergence of metallic characteristics in the material. The anti-perovskite compounds exhibit negative values in the real part of the dielectric function starting at approximately 3 eV, whereas the perovskite counterparts begin to show negative values around 13 eV. Additionally, the dielectric function of perovskites is relatively lower in magnitude compared to that of anti-perovskites, indicating distinct optical responses between the two material classes.
.105 The static dielectric function provides insight into the extent of charge recombination, which directly influences the performance of optoelectronic devices. Materials exhibiting higher dielectric constants tend to have lower charge recombination rates, thereby enhancing device efficiency.106 Anti-perovskites exhibiting significantly higher static dielectric values than their perovskite counterparts as shown in Fig. 12. From Table 5, the static dielectric constant of the perovskites is below 10, indicating their suitability for microelectronic applications and high optical transparency.107 In contrast, the anti-perovskites exhibit static dielectric constants exceeding 10, making them promising candidates for energy storage and various optical device applications.108 As the energy increases further, the real part of the dielectric function becomes negative, indicating that the material behaves as a reflective medium in these energy regions. This complete reflection of incident electromagnetic waves signifies the emergence of metallic characteristics in the material. The anti-perovskite compounds exhibit negative values in the real part of the dielectric function starting at approximately 3 eV, whereas the perovskite counterparts begin to show negative values around 13 eV. Additionally, the dielectric function of perovskites is relatively lower in magnitude compared to that of anti-perovskites, indicating distinct optical responses between the two material classes.