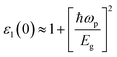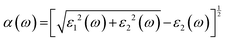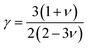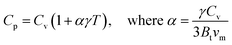Open Access Article
Open Access ArticleTuning the opto-electronic properties of BaTiO3 by S substitution towards energy harvesting applications: a DFT insight using the VASP code
U.
Ahmed
ab,
M. M.
Hossian
 a,
M. M.
Uddin
a,
N.
Jahan
a,
M. M.
Uddin
a,
N.
Jahan
 a and
M. A.
Ali
a and
M. A.
Ali
 *a
*a
aAdvanced Computational Materials Research Laboratory (ACMRL), Department of Physics, Chittagong University of Engineering and Technology (CUET), Chattogram-4349, Bangladesh
bDepartment of Materials Science and Engineering, Rajshahi University of Engineering and Technology, Bangladesh
First published on 4th November 2025
Abstract
This study explored the structural, electrical, optical, mechanical, and thermal properties of sulfur-substituted barium titanate perovskites (BaTiO3−xSx) using first-principles density functional theory (DFT) calculations, implemented in the Vienna Ab initio Simulation Package (VASP). Sulfur (S) substitution at oxygen (O) sites led to the formation of BaTiO2S, BaTiOS2, and BaTiS3. The formation energy, tolerance factors, and AIMD simulation ensured the structural stability of these phases. The band structure calculation revealed a reduction of band gap from 3.069 eV (BaTiO3) to 1.55, 1.02, and 0.35 eV for BaTiO2S, BaTiOS2, and BaTiS3, respectively. The optical properties calculations revealed that the S substitution enhances the absorption coefficient, improving the optical properties in the visible range. The reduction of the band gap, which enhances the optical properties, has been explained in terms of the partial density of states (PDOS). The mechanical stability of the BaTiO3−xSx compounds was confirmed by calculating the elastic constants. The changes in chemical bonding due to S substitution result in a variation in the elastic moduli. The effect of S substitution on the thermal properties was also studied, and a significant decrease in lattice thermal conductivity was explained in terms of phonon scattering. The results obtained for BaTiO2S and BaTiOS2 ordered cells were also cross-checked by performing calculations in supercell structures. The reduced band gap and high absorption coefficient of BaTiO2S and BaTiOS2 suggest a possible use in solar energy harvesting, whereas BaTiS3 could be a potential thermoelectric material (with low lattice thermal conductivity).
1. Introduction
The rise in energy consumption and the growing concern over climate change have motivated a shift from coal, oil, and gas. Such a shift, imperative due to the environmental impacts brought about by the extraction and combustion of fossil fuels, is, therefore, of utmost importance.1,2 Greenhouse gases from fossil fuel combustion have given rise to global warming and subsequent climate change.3 Addressing these issues requires looking into alternative energy sources while making sure to remain environmentally friendly.4 Solar energy is therefore the most promising of the renewable energy options due to its abundance and wide availability.5 Solar energy captured by photovoltaic technology is very popular nowadays. The PV market is currently dominated by crystalline silicon solar cells because of their high durability and efficiency. However, the high cost of producing high-purity silicon and the intricate manufacturing processes pose significant challenges.6 A viable substitute for silicon solar cells is perovskite solar cells.7 Perovskites are substances that resemble the naturally occurring mineral perovskite in terms of their crystal structure. Their general formula is ABX3, in which X is an anion and A and B are cations.8,9 Perovskites have garnered considerable attention in solar energy conversion, owing to their exceptional optoelectronic properties and potential for high power conversion efficiencies.10 Perovskites, in particular, can perform well despite flaws and defects. The power conversion efficiency of perovskite solar cells has risen recently and is now on par with silicon solar cells.11 Perovskite oxides and halide–fluoride systems have recently been revitalized as viable thermoelectric materials due to advances in quantum and solid-state physics. Perovskites with semiconductor-like behavior have a good figure of merit, making them suitable for application in energy conversion and thermoelectric devices.12,13 However, environmental factors like light, humidity, and high temperatures can affect their performance and speed up the degradation processes; their long-term stability is a significant obstacle to their widespread commercialization.14,15BaTiO3 is one of the classical ferroelectric perovskite materials, and it possesses a unique group of properties.16 Due to its large dielectric constant, BaTiO3 finds application in capacitor devices, and due to its piezoelectricity, it is applied in sensors and actuators.17 It has a high Curie temperature, the temperature at which the material starts losing its ferroelectric properties and turning into a paraelectric material. BaTiO3 undergoes a series of phase transitions depending on temperature that influence its properties. When cooled, it passes through tetragonal, orthorhombic, and rhombohedral ferroelectric phases with spontaneous polarization in various crystallographic directions.18 Mishra et al.19 synthesized the cubic phase from the tetragonal phase and studied the bandgap of BaTiO3. For example, the band gap is 3.18 eV for the tetragonal phase and 3.12 eV for the cubic phase. The band gap of BaTiO3 is around 3.2 eV,20 and it lies in the ultraviolet region of the electromagnetic spectrum. BaTiO3 is transparent in the visible spectrum, but it strongly absorbs UV light due to its band gap.21 The refractive index and absorption coefficient of the compound have been determined by optical transmission measurements.22
The electronic structure and optical properties of BaTiO3 make it suitable for application in several sectors. However, the large band gap (3.12 eV) limits its applications in energy harvesting technology, especially in photovoltaic solar cells.23 Doping in materials has been a popular approach to reducing the bandgap. Gillani et al.24 claim that Mg doping in SrZrO3 makes it a strong candidate for optoelectronic applications by altering the electronic structure, imposing a direct bandgap at the Γ-point, and strengthening the Mg–O interactions that significantly impact their optical properties. Fe doping is especially promising for lead-free CsSnCl3, according to Kholil et al.25 Fe doping in CsSnCl3 and CsPbCl3 narrows the bandgap and adds donor states, enhancing absorption, conductivity, and optoelectronic performance. Adhikari et al.26 investigated the effect of Mn2+ doping in CsPbCl3 perovskite nanocrystals, which is regulated by alkylamine hydrochloride (RNH3Cl), which functions as a chlorinating and growth-promoting agent to facilitate dopant incorporation, size control, and emission tuning. Tanwar et al.27 synthesized Eu-doped BaTiO3 using a solid-state method, which was demonstrated to have low overpotential, high stability, and increased electrocatalytic activity in the oxygen evolution reaction, offering a less expensive substitute for catalysts based on noble metals. Lou et al.28 found that Li+ doping in BaTiO3 improves electric polarization and the internal electric field, optimizing electron transport properties and increasing the efficiency of perovskite solar cells by up to 14.3%. Yao et al.29 reported that the effects of internal stress and grain size refinement, through Nd3+ doping of BaTiO3, result in a tetragonal-to-cubic phase transition, modification of the Ti valence state, and an increase in permittivity, while exhibiting typical ferroelectric behavior.
Chalcogen anions such as sulfur (S) significantly contribute to bandgap reduction30. Li et al.31 observed that sulfur anion doping in nanocubic NaTaO3 results in a modulation of the band structure and lattice distortion, which greatly enhances visible light photocatalytic activity and charge carrier mobility, making it a viable option for solar oxidative pollution degradation. Jia et al.32 demonstrate, using DFT, that sulfur doping in LaBO3 (B = Fe, Co, Ni) perovskites promotes the formation of oxygen vacancies by lowering the lattice relaxation energy, thereby improving electrical conductivity and providing a general technique to enhance the functionalities of perovskites. Sulfur-doped oxide perovskites, such as LaCoO3, show great potential for energy conversion and storage using Zn–air batteries because they exhibit improved conductivity and spin-state transitions that increase oxygen electrocatalysis, according to Ran et al.33 Ech-Chargy et al.34 found that when sulfur is added to KTaO3 in amounts up to 12.5%, it lowers the bandgap from 3.86 eV to 1.24 eV and causes a direct bandgap transition. Hasina et al.35,36 also investigated S-substituted KTaO3 and RbTaO3, which form KTaO2S and RbTaO2S, respectively, and are suitable for solar energy conversion and optoelectronic applications due to their reduced band gaps. This higher sulfur content not only enhances the material's ability to absorb visible light but also alters the electronic structure, making it better suited for photocatalytic hydrogen production. Ahmed et al.37 studied the effect of sulfur doping in CsTaO3, which narrows the bandgap during phase changes, thereby improving the sample's absorption in the visible region and making it an efficient solar absorber with dynamic stability. Bennett et al.38 employed first-principles simulations to study the effect of S substitution in BaZrO3, which results in a lower band gap of BaZrS3, and exhibits unique dielectric behavior due to variations in atomic mass, size, and covalency. Zhang et al.39 demonstrated that only S, among all the anion dopants in SrTiO3, effectively narrows the band gap by strongly mixing the S 3p and O 2p states, thereby improving the absorption of visible light.
Prior studies indicate that S incorporation in the perovskite structure significantly reduces the bandgap. However, what causes the bandgap to decrease when S is substituted? Sulfur substitution at oxygen sites is considered an attractive pathway due to this ion's initially favorable radius and chemical compatibility. The larger radius of the S2− ion compared to O2− forces lattice distortions, while its lower electronegativity enhances Ti–S covalent interactions and orbital hybridization, effectively narrowing the band gap and concomitantly increasing optical absorption in the visible range. The S-3p orbitals’ energetic proximity to the upper valence band compared to the O-2p orbitals is one explanation. When S and O are exchanged, these S-3p orbitals can mix to form mid-gap states just above the valence band. The presence of a characteristic spectral signal near the absorption edge—often referred to as the “tail”—that extends into the visible spectrum has demonstrated the availability of these states. According to this behavior, S doping into O causes an enlarged valence band, which lowers the bandgap and improves the material's receptivity to visible light.40 Thus, an expectation has grown among us that the S doping in BaTiO3 could lower the band gap and make it suitable for use in solar cells as an absorbing layer. Furthermore, the more massive sulfur atom enhances phonon scattering, which in turn reduces lattice thermal conductivity and is good for thermoelectric performance. All these factors make sulfur substitution a promising approach to engineer the optoelectronic and thermal properties of BaTiO3−xSx-based perovskites for energy applications. These are the prime motivations for this study.
Using DOS analysis, charge density mapping, and electronic band structure predictions, a thorough examination was conducted to determine the causes underlying this bandgap narrowing. The primary objective is to replace O with S to bring the bandgap of BaTiO3 into the visible range. Achieving a high conversion efficiency in solar energy applications requires a bandgap close to the Shockley–Queisser limit41. Additionally, in semiconducting materials, bandgap narrowing enhances electrical conductivity, which is crucial for developing multifunctional materials with low energy costs.
In light of these factors, we investigate anion doping as a means of adjusting the electronic properties of the oxide perovskite BaTiO3. To achieve this, a DFT-based simulation was performed to understand the impact of substituting S anions for O anions in BaTiO3. The results show that adding S significantly reduces the bandgap, thereby improving optical absorption and ensuring higher mechanical and thermal stability, suitable for solar energy applications. These S-doped perovskites have an advantage in applications where thermal insulation is required to reduce lattice thermal conductivity.
Thus, in this paper, we examine the physical properties of the BaTiO3−xSx series, including structural, electronic, optical, mechanical, and thermal properties, to explore their potential uses in various technologies. The electronic structure calculations indicate that these materials are suitable for use in solar cell technologies. The optical parameters, such as dielectric functions, absorption coefficient, and reflectivity, are considered in relation to solar applications. Mechanical strength and stability are evaluated through elastic constants, while thermal conductivity is analyzed to assess their suitability for thermoelectric applications. It is noted that the opto-electronic properties have been calculated using the hybrid functional, and the properties for BaTiO2S and BaTiO2S have been counter-checked by both ordered cell structures and super-cell structures.
2. Computational methodology
The density functional theory (DFT) calculations for the investigation of BaTiO3−xSx were performed using the Vienna ab initio Simulation Package (VASP) using the projector augmented wave (PAW) basis.42 The Perdew–Burke–Ernzerhof (PBE) functional, in conjunction with the generalized gradient approximation (GGA), was used to address the exchange–correlation interactions in solving the Kohn–Sham equations iteratively towards the ground-state electronic structure.43 For accurate electronic band structure analysis, the hybrid Heyd–Scuseria–Ernzerhof (HSE06) functional was employed.44 Valence electron configurations included Ba (5s2 5p6 6s2), Ti (3p6 3d2 4s2), O (2s2 2p4), and S (3s2 3p4). The energy convergence and ionic convergence criteria were set to 1 × 10−6 eV and −2 × 10−2 eV Å−1, respectively, for structural optimization. A plane-wave kinetic energy cutoff of 600 eV was used, and the Brillouin zone was sampled using Monkhorst–Pack k-point meshes of 6 × 6 × 6 for the cubic unit cells, with adjustments for tetragonal geometries (e.g., 6 × 6 × 5 and 5 × 5 × 6). By updating the charge density and calculating an effective potential to solve for a new wave function, the SCF iteration is carried out until convergence is reached.45 VASPKit was used for post-processing analysis of the calculations, including density of states (DOS), band structure, and optical and mechanical properties.46 To calculate the thermal properties, the phono3py and phonopy packages were utilized, which leverage third-order force constants and the Boltzmann transport equation under the relaxation time approximation.47 To perform ab initio molecular dynamics (AIMD), the Cambridge serial total energy package (CASTEP) code has been used.483. Results and discussion
3.1 Structural properties and stability
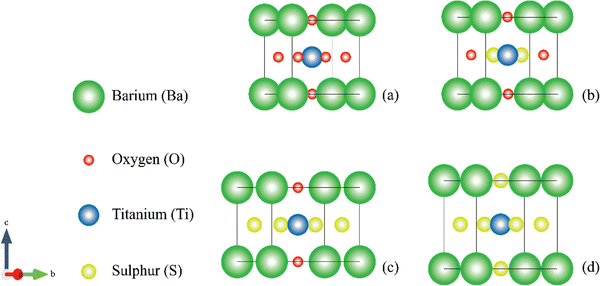
The pristine BaTiO3 [Fig. 1(a)] crystallizes in the perovskite structure (ABX3), with Ba occupying the A-site, Ti at the B-site, and O at the anion sites. The cubic phase (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) is stable at high temperatures and the atoms are arranged as follows: O is located at the center of the face (0, 0.5, 0.5), Ba is at the corner position (0, 0, 0), and Ti is at the center of the unit cell at coordinates (0.5, 0.5, 0.5)19,49,50. Upon substituting O with S, the phase shifts from the cubic to tetragonal phase (P4/mm). The following are the atomic positions of BaTiO2S [Fig. 1(b)] and BaTiOS2 [Fig. 1(c)], respectively: Ba (0, 0, 0), Ti (0.5, 0.5, 0.5), O (0.5, 0, 0.5), and S (0, 0.5, 0.5) and Ti (0, 0, 0), Ba (0.5, 0.5, 0.5), S (0.5, 0, 0.5), and O (0.5, 0.5, 0). When three S atoms are added to the parent molecule, BaTiS3 [Fig. 1(d)] is created, having the space group and Wyckoff positions of BaTiO3, but the lattice parameter was extended due to S's larger ionic radius. The GGA–PBE approximation was employed to optimize the lattice parameter and unit cell volume. With the increase of S content, the volume of the unit cell increases from 65.6 Å3 to 113.2 Å3. The optimized lattice parameters for the cubic and tetragonal phases are summarized in Table 1.
m) is stable at high temperatures and the atoms are arranged as follows: O is located at the center of the face (0, 0.5, 0.5), Ba is at the corner position (0, 0, 0), and Ti is at the center of the unit cell at coordinates (0.5, 0.5, 0.5)19,49,50. Upon substituting O with S, the phase shifts from the cubic to tetragonal phase (P4/mm). The following are the atomic positions of BaTiO2S [Fig. 1(b)] and BaTiOS2 [Fig. 1(c)], respectively: Ba (0, 0, 0), Ti (0.5, 0.5, 0.5), O (0.5, 0, 0.5), and S (0, 0.5, 0.5) and Ti (0, 0, 0), Ba (0.5, 0.5, 0.5), S (0.5, 0, 0.5), and O (0.5, 0.5, 0). When three S atoms are added to the parent molecule, BaTiS3 [Fig. 1(d)] is created, having the space group and Wyckoff positions of BaTiO3, but the lattice parameter was extended due to S's larger ionic radius. The GGA–PBE approximation was employed to optimize the lattice parameter and unit cell volume. With the increase of S content, the volume of the unit cell increases from 65.6 Å3 to 113.2 Å3. The optimized lattice parameters for the cubic and tetragonal phases are summarized in Table 1.
| Compounds | a (Å) | c (Å) | V (Å3) | Formation energy | T F | μ | Ref. |
|---|---|---|---|---|---|---|---|
| BaTiO3 | 4.032 | — | 65.6 | −3.2288 | 1.061702 | 0.4235 | This study |
| 4.01 | — | 64.37 | −3.477 | — | — | 49 | |
| BaTiO2S | 4.136 | 4.842 | 82.8 | −2.4916 | 1.037539 | 0.4678 | This study |
| BaTiOS2 | 5.018 | 3.887 | 97.9 | −2.1509 | 1.016459 | 0.5122 | This study |
| BaTiS3 | 4.837 | — | 113.2 | −1.6675 | 0.997909 | 0.5566 | This study |
To confirm the stability of these materials, the tolerance (TF) factor and octahedral factor (µ) established by Goldschmidt have been calculated. The equations are given below:
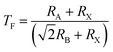 | (1) |
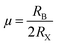 | (2) |
The chemical endurance of the semiconductor BaTiO3−xSx perovskite has been further assessed by computing its formation energy (F.E.). An overview of the formula is provided below, as provided in ref. 54
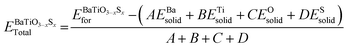 | (3) |
In the given equation, the variables A, B, C, and D correspond to the number of Ba, Ti, O, and S atoms in the unit cell. The terms  , EBaSolid, ETiSolid, EOSolid, and ESSolid represent the total energy of the BaTiO3−xSx perovskite material and the corresponding solid-state energies of Ba, Ti, O, and S. The formation energy's negative sign validated their stability; Table 1 presents the calculated formation energy values. Since BaTiO3 has already been experimentally synthesized, the calculated structural parameter, formation energy, and tolerance factor bolster the stability of the S-doped BaTiO3−xSx compounds.
, EBaSolid, ETiSolid, EOSolid, and ESSolid represent the total energy of the BaTiO3−xSx perovskite material and the corresponding solid-state energies of Ba, Ti, O, and S. The formation energy's negative sign validated their stability; Table 1 presents the calculated formation energy values. Since BaTiO3 has already been experimentally synthesized, the calculated structural parameter, formation energy, and tolerance factor bolster the stability of the S-doped BaTiO3−xSx compounds.
The total energy of BaTiO3−xSx increases (becomes less negative) as sulfur concentration rises due to compositional and bonding factors. Replacing O with S weakens the Ti–X (X = O, S) bond and reduces the lattice cohesive energy because sulfur has a larger ionic radius and lower electronegativity than oxygen. The decrease in formation energy (less negative) with S substitution indicates that the oxides are more energetically favorable and stable, while S-containing compositions are less stable compared to the oxide ones. However, S-containing compositions are still stable due to their negative formation energy.
Ab initio molecular dynamics (AIMD) calculations at 300 K for 10 ps were performed using an NVT ensemble to verify the thermal and structural stability of BaTiO3, BaTiO2S, BaTiOS2, and BaTiS3 under ambient conditions. Fig. 2 illustrates how the total energy of these four compounds changed over time during the simulation. The energy profile for BaTiO3 is shown in Fig. 2(a), fluctuating between −3621.61 eV and −3616.49 eV, with an average of −3619.05 eV and a very low root-mean-square deviation of 0.0707%. Consistent with the well-established knowledge of BaTiO3's stability, this minimal change in average energy indicates its exceptional thermal stability. The results for BaTiO2S are displayed in Fig. 2(b), where the energy varies within a slightly narrower range (−3461.45 eV to −3456.85 eV) and exhibits a slightly smaller deviation of 0.0664%, suggesting that partial substitution of S does not impact the material's thermal stability or structural integrity. Conversely, Fig. 2(c) shows an additional minor decrease in energy fluctuation to 0.0627% with fully substituted BaTiOS2, with extreme total energies of −3299.01 eV and −3303.15 eV. Such a smooth energy curve would indicate strong dynamic stability, achieved by increasing phonon scattering to prevent structural failure. Finally, panel (d) presents the AIMD results for BaTiS3, which exhibits the lowest fluctuations (0.0547%) among the four systems. Despite complete chalcogenide substitution, the system's energy stabilizes at −3144.36 eV to −3140.92 eV, reflecting excellent thermal resistance. Overall, there are no sudden energy jumps or discontinuities during the simulation, and all four compounds show very minimal energy drift (<0.08%). This dynamic resilience arises because the negative formation energies and the prevailing Ti–anion covalency keep bonding cohesive as local geometries relax. In a nutshell, the anion substitution creates a more flexible environment (lower elastic moduli, higher polarizability), yet it cannot eliminate those bonding interactions that impart structural integrity under the influence of thermal agitation in ambient conditions.55 These materials are among the most promising options for optoelectronic and thermoelectric applications, as they demonstrate both dynamic and thermal stability at room temperature.
 | ||
| Fig. 2 Ab initio molecular dynamics (AIMD) of (a) BaTiO3, (b) BaTiO2S, (c) BaTiOS2, and (d) BaTiS3 compounds. | ||
3.2 Electronic properties
To comprehend the electronic properties of the BaTaO3−xSx compounds, the electronic band structure (EBS), density of states (DOS), and charge density were computed to investigate the effects of sulfur (S) substitution. Electronic properties were calculated using both the GGA–PBE and HSE06 functionals. For semiconducting materials, local functionals such as GGA–PBE underestimate the bandgap.56,57 To accurately predict the bandgap of semiconducting materials, a nonlocal functional (hybrid) HSE06, which incorporates 25% exact exchange and provides more accurate bandgap predictions, was utilized.58–61 Gaussian smearing was used, and the smearing value was set to 0.1 eV. The estimated bandgap values are presented in Table 2. Fig. 3 presents the EBS of BaTaO3−xSx compounds, where energy zero (Ef) was set to the Fermi level. The band structure of BaTiO3 [Fig. 3(a)] exhibits an indirect bandgap, with the valence band maximum (VBM) located at the R-point and the conduction band minimum (CBM) at the G-point. This is consistent with previous theoretical and experimental studies.23 The calculated bandgap of BaTiO3 is 3.0691 eV, which agrees with known values for its cubic phase.19 Upon substituting oxygen (O) atom(s) with sulfur (S) in BaTiO2S and BaTiOS2 [Fig. 3(b) and (c)], the band structure shows significant modifications, and the band gaps are also reduced to 1.5501 eV and 1.0221 eV. The bandgap remains indirect, with the VBM and CBM located at A and G points, respectively. In BaTiS3 [Fig. 3(d)], where all O atoms are replaced by S, the band structure shows an indirect bandgap of 0.3542 eV. The VBM and CBM are located at R and G. The bandgap of the BaTiO3−xSx series decreases systematically with increasing S content, from 3.0691 eV for BaTiO3 to 0.3542 eV for BaTiS3. Sulfur's larger atomic size elongates the Ti–S bonds compared to the Ti–O bonds, thereby increasing lattice strain. Consequently, the conduction band minimum (CBM) is lowered, and orbital overlap is diminished. Moreover, the lower electronegativity of S shifts the valence band maximum (VBM) upward, thereby enhancing the charge-transfer efficiency. The electronic structure was gradually altered, and the band gap narrowed as a result of orbital hybridization and bond interactions influenced by these atomic variations. The Shockley–Queisser limit states that 1.4 eV is the ideal band gap for a single-junction solar cell operating under standard solar illumination.62 This value maximizes the theoretical light-to-electricity conversion efficiency. Achieving the highest possible light-to-electricity conversion efficiency requires this range of band gap.62–64 Thus, BaTiO2S exhibits a close value of 1.5501 eV, which is promising for solar cell use. These possible changes in the electronic properties could benefit solar cells. The band gap was calculated for BaTiO2S and BaTiOS2 using both the GGA and HSE06 functionals in the 112 (tetragonal) supercell (SC) method. The results from both approaches are consistent, as shown in Table 2, supporting the accuracy of the findings.| Compounds | Approach | Bandgap (eV) | Ref. |
|---|---|---|---|
| BaTiO3 | GGA–PBE | 1.7002 | This study |
| HSE06 | 3.0691 | This study | |
| Experimental | 3.12 | 23 | |
| BaTiO3 (SC) | GGA–PBE | 1.7053 | This study |
| HSE06 | 3.1064 | This study | |
| BaTiO2S | GGA–PBE | 0.6157 | This study |
| HSE06 | 1.5501 | This study | |
| BaTiO2S (SC) | GGA–PBE | 0.6133 | This study |
| HSE06 | 1.5501 | This study | |
| BaTiOS2 | GGA–PBE | 0.2570 | This study |
| HSE06 | 1.0221 | This study | |
| BaTiOS2 (SC) | GGA–PBE | 0.2456 | This study |
| HSE06 | 1.0234 | This study | |
| BaTiS3 | GGA–PBE | 0 | This study |
| HSE06 | 0.3542 | This study | |
| BaTiS3 (SC) | GGA–PBE | 0 | This study |
| HSE06 | 0.3307 | This study |
From the study of DOS of BaTiO3−xSx, the alteration of the electronic structure can be seen due to successive S substitution. The contribution of the 2p state in the valence band (VB) is shown by the perfect alignment of the first peak in the total density of states (TDOS) with the 2p state of oxygen (O). Meanwhile, the first peak of the conduction band in the TDOS corresponds to the 3d state of titanium (Ti). The contribution of the 2p state of O decreases when sulfur (S) is substituted; however, a decrease in the band gap is observed due to hybridization between the 3p states of S, the 2p state of O, and the 3d state of Ti. Fig. 4(a) depicts the DOS for BaTiO3, where the valence band (VB) region is dominated by strong O 2p states in the region from −6 to −1 eV, while the conduction band shows sharp Ti 3d character above 2 eV, jointly accounting for the indirect bandgap value of 3.07 eV for the material. This configuration is drastically changed when sulfur is added to BaTiO2S [Fig. 4(b)]. The S 3p states become distinct peaks around −1 eV, which hybridize with the remaining O 2p and Ti 3d orbitals to cause the VB maximum to shift upward and the bandgap to decrease to 1.55 eV. The VB edge near Ef is nearly controlled by the S 3p orbitals in the case of BaTiOS2 [Fig. 4(c)], which severely weakens the original O 2p contributions and further sharpens the gap down to 1.02 eV because of higher Ti 3d–S 3p interactions. The electronic structure of fully substituted BaTiS3 can be seen in Fig. 4(d); the VB now only contains S 3p states, which greatly overlap with Ef, while the CB shows strong mixing between the Ti 3d and S 3p orbitals, resulting in a significantly smaller gap of 0.35 eV, which is near metallic. The observed band-gap narrowing with an increase in S quantity is a consequence of the anion electronic structure: S-3p states lie at higher energy than O-2p states and hence, by stronger S-3p/Ti-3d hybridization, raise the valence-band maximum. The projected density of states shows increasing S-3p at the top of the valence band as the value of x increases, while the electron charge density mapping illustrates enhanced shared electron density along Ti–S bonding directions, also signaling an increase in covalency. Both of these effects lower the photon energies at which optical transitions can occur, resulting in the progressive redshift of the absorption observed as one proceeds down the BaTiO3 → BaTiO2S → BaTiOS2 → BaTiS3 series.
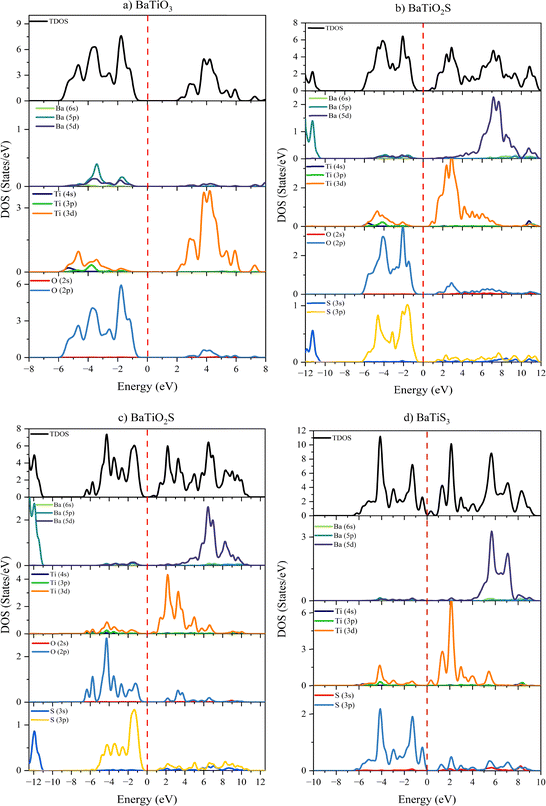 | ||
| Fig. 4 The density of states (TDOS and PDOS) for (a) BaTiO3, (b) BaTiO2S, (c) BaTiOS2, and (d) BaTiS3 compounds. | ||
The band gap narrowing from UV (3.07 eV in BaTiO3) through the visible region (1.02–1.55 eV in BaTiO2S/BaTiOS2) to near-IR (0.35 eV in BaTiS3) demonstrates that the S acts primarily to uplift the VB to higher energy due to S 3p state insertion while maintaining the basic Ti 3d character of the CB. Since their ideal band gaps (around the Shockley–Queisser limit of 1.4 eV) suggest that they are highly beneficial in visible-light harvesting applications, these intermediate compositions are of particular interest. Of course, pure BaTiO3 and BaTiS3 terminate this tunability for UV and IR technologies, respectively. Through controlled S substitution, materials for particular optoelectronic applications can be designed with the help of this orbital-level understanding of the DOS evolution.
The charge density distributions of pure BaTiO3 and its S-doped derivatives, BaTiO2S, BaTiOS2, and BaTiS3, were studied to gain a better understanding of changes in chemical bonding and electronic localization as S substitution increases. The screened hybrid HSE06 functional was employed to accurately capture nonlocal exchange effects, which are critical for modelling charge density in systems with mixed ionic–covalent bonding. The investigations were conducted across various crystallographic planes to determine how charge delocalization and bonding properties change with increasing S concentration. This is demonstrated by charge density contour plots in Fig. 5, which show the slow transition from ionic–covalent bonding in BaTiO3 (Ti–O) to weaker, more ionic interactions in S-doped compounds (Ti–S). The addition of S causes a significant alteration in those surrounding the Ti–S and Ba–S bonds, where charge buildup is indicative of increased orbital hybridization and electronic localization. Fig. 5(a) illustrates the charge density of BaTiO3 along the (110) plane. This indicates a higher degree of covalent bonding character due to the intensive and symmetric charge buildup between the Ti and O atoms. The relatively high charge density values within the Ti–O bond and the concentrated charges surrounding the O atoms indicate a situation in which the high electronegativity of O virtually controls the bond's polarity. Conversely, Ba atoms have nearly minimal charge interaction with their environment, suggesting that their lattice interactions are ionic. When S replaces one O atom in BaTiO2S [Fig. 5(b) and (c)], the charge distribution starts to change, especially around the S atoms. In contrast to Ti–O, the charge density contours of the Ti–S bonds are broader and less intense, indicating weaker covalent bonding and stronger ionic interactions. This shift is explained by S's higher atomic radius and lower electronegativity compared to O. The localized effect of partial anionic substitution is evident in the more diffuse charge density surrounding S and the development of bonding asymmetry between Ti–O and Ti–S. As illustrated in Fig. 5(d) and (e), the effect becomes more pronounced as the substitution of BaTiOS2 increases. Two S atoms have now coordinated the Ti atom, and the charge density will continue to delocalize in these regions. Compared to Ti–O in BaTiO3 or BaTiO2S, the Ti–S bonding seems weaker and more spatially stretched, and has notably lower peak charge densities.
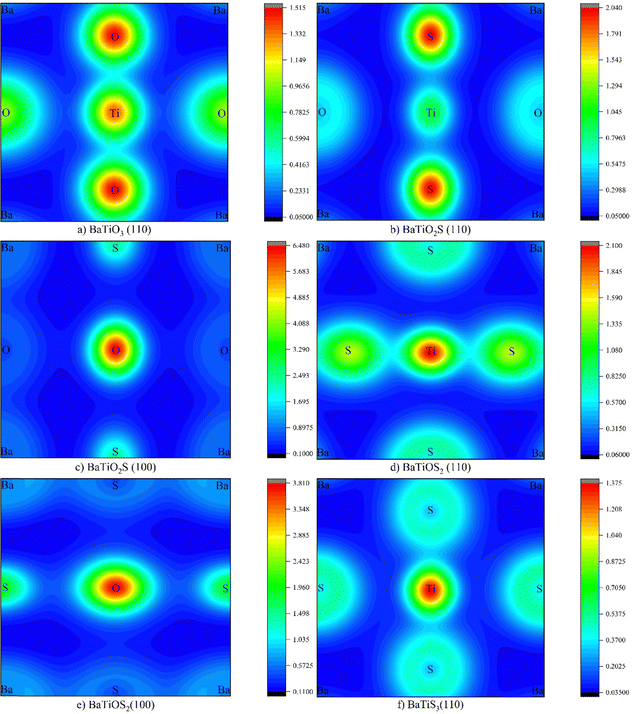 | ||
| Fig. 5 2D Charge density plots for (a) BaTiO3 (110), (b) BaTiO2S (110), (c) BaTiO2S (100), (d) BaTiOS2 (110), (e) BaTiOS2 (100), and (f) BaTiO3 (110). | ||
In addition to weakening covalent bonds, this slow delocalization of charge also indicates structural and electrical changes in the bonding environment surrounding the Ti center as the anionic framework shifts. Finally, the (110) charge density map of totally substituted BaTiS3 [Fig. 5(f)] exhibits an even and extremely low charge accumulation around the Ti–S bonds, with wider contours and a lack of bonding directivity. In contrast to its oxygen-rich counterparts, the S-rich combination exhibits a fundamental shift in its electronic structure, validating the previously observed ionic nature of bonding. The dielectric behavior, band structure, and possible catalytic activity of BaTiO3 are all significantly impacted by the change from strong localized covalent bonding with Ti–O to a weaker, more ionic attachment of Ti to S.
3.3 Optical properties
The optical properties of a material are crucial for selecting suitable materials for optoelectronic and photovoltaic applications. They indicate the material's efficacy when interacting with light. The absorption coefficient is the most important optical measure, as it indicates how a substance absorbs light.65 Electronic transitions in semiconductors are typically classified into two categories: intra-band transitions and inter-band transitions. Since interband transitions are crucial for establishing optical and transport features, they are typically given priority. However, because it allows the material to behave in a completely metallic manner within its band structure, the intra-band transition is also quite significant.66 To explore how S substitution influences light–matter interaction, the optical properties of the BaTiO3−xSx system were comprehensively studied. Key optical parameters were calculated using first-principles methods based on the HSE06 hybrid functional, providing detailed insight into optoelectronic behavior.| ε(ω) = ε1(ω) + iε2(ω) |
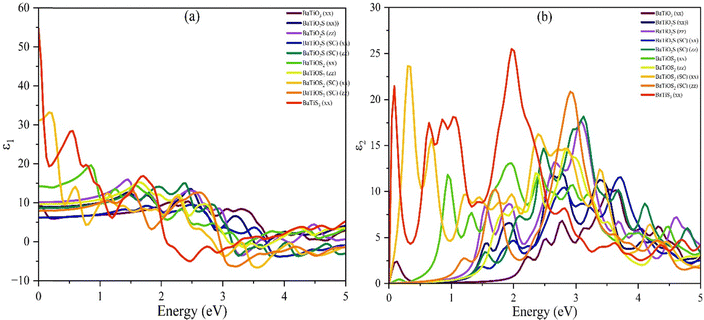 | ||
| Fig. 6 Dielectric constant of BaTiO3−xSx compounds: (a) real dielectric constant and (b) imaginary dielectric constant. | ||
In Fig. 6(a), the real part of the dielectric function (ε1(ω)) is related to photon energy. Of all compounds studied, BaTiS3 has the greatest static dielectric constant (ε1(ω) at 0 eV) with a value of 54.68 due to the relatively higher polarizability of S atoms compared with O atoms. This indicates that they can polarize more effectively in the presence of an external electric field. Again, both BaTiO2S (SC) and BaTiOS2 (SC) exhibit a higher ε1(ω) than pristine BaTiO3, with values of 10.1, 31.124, and 9.6, respectively, suggesting that partial replacement of S might increase dielectric screening. Further along, anisotropy in the xx and zz components is striking in the S-doped systems, as their anisotropic dielectric behavior is due to structural asymmetry and local distortions caused by S incorporation. The imaginary part of the dielectric function (ε2(ω)), which encompasses interband transitions and optical absorption characteristics, is presented in Fig. 6(b). Strong absorption peaks of BaTiS3 [25.5] are found within the low-energy region (0.5–2.5 eV), signifying that those strong optical transitions, facilitated by its narrower band gap and modified electronic structure, are anticipated. Reinforced maximum ε2(ω) values for BaTiOS2 [17.7] and BaTiO2S [20.8], especially in the supercell configurations, further indicate heightened light absorption within the visible spectrum. Such enhancement is attributed to S-induced alterations in the density of states and transition matrix elements, which enable efficient photon-induced electronic excitations. On the other hand, the ε2(ω) values of BaTiO3, with the highest value of 10.3, are considerably lower, appropriate for a wide band gap, resulting in a decreased optical activity within the same energy range. It is very evidently clear now that S substitution enhances, in addition to the dielectric response, optical absorption. However, the scope of their investigation is limited to the significant increase in either ε1(ω) or ε2(ω), particularly BaTiS3 and BaTiOS2 (SC). Such indications suggest that S-doped BaTiO3-based perovskites are promising materials for high-permittivity devices and optoelectronic applications, such as capacitors, photovoltaics, and photodetectors. The Penn model provides an empirical formulation for describing the dielectric function of semiconductors. The approximation of a nearly free-electron model simplifies the complexity of scattering processes in a semiconductor. The method enables us to calculate the dielectric constant, a crucial quantity for investigating a material's response to electromagnetic radiation, thereby enhancing our understanding of how a semiconductor behaves optically and its electronic structure.69 The values described earlier meet those mentioned by the Penn model, to which the following equation is valid:70
At higher energies, however, the dielectric function tends to turn negative, revealing metallic behavior due to electron transition.5
Fig. 7(a) depicts the absorption coefficient α(ω), which relates to the material's ability to absorb incoming photons between 0–5 eV energies. BaTiO3 shows a fairly high absorption onset around 3.1 eV, consistent with a large optical band gap. However, the presence of S substitution significantly redshifts the absorption edge for all doped compounds, particularly for BaTiO2S (SC), BaTiO2S (SC), and BaTiS3, indicating considerable band gap narrowing and increased absorption capacity in the visible range. BaTiO2S [5.45 × 105] demonstrates a shift of the absorption edge toward lower photon energies (∼2.7 eV), characteristic of band gap reduction and enhanced absorption in the visible range. The absorption further increases in the BaTiOS2 [7.25 × 105] and BaTiOS2 (SC) [9.04 × 105] structures, exhibiting stronger and broader absorption features that extend well into the visible spectrum (1.5–3.5 eV). For all the systems under consideration, BaTiS3 shows an exceptionally high absorption intensity of more than 9.16 × 105 cm−1 in the visible region, strongly indicating its highest potential for photon harvesting. BaTiS3 and BaTiOS2 (SC) display strong absorption bands in the 1.8–3.1 eV range, corresponding to S 3p → Ti 3d transitions enabled by the S-modified density of states near the Fermi level. Additionally, there is a clear anisotropy in the spectra for α(ω), especially in the supercell configurations, where the optical response differs significantly between the xx and zz crystallographic directions. This anisotropic behavior arises from the symmetry-breaking effect of the S substitutions and the lattice distortions, which change the electronic dipole transition probabilities.
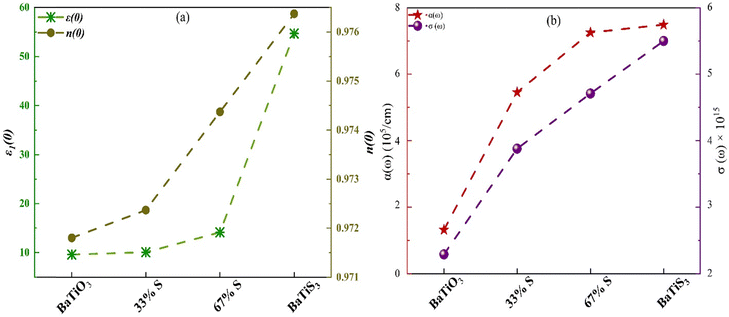
Fig. 10 illustrates the progressive changes in several key optical parameters of these materials as the S concentration increases in BaTiO3, BaTiO2S, BaTiOS2, and BaTiS3. Fig. 10(a) shows that the static dielectric constant ε1(0) and refractive index n(0) both increase with S substitution, justifying enhanced polarizability and further engagement of light with matter. Fig. 10(b) depicts the maximum values of the absorption coefficient α(ω) and optical conductivity σ(ω) in the visible region (1.6–3.1 eV); both display an increasing trend with higher S content, indicating that S enhances light absorption and carrier excitation. The onset of visible-range optical absorption and enhancements in ε(0), n(0), and the extinction coefficient have two interconnected origins: (i) the reduced electronic band gap discussed above, which enables low-energy interband transitions (particularly S-3p → Ti-3d), and (ii) the increased polarizability of S anions that raises the real part of the dielectric function. These electronic changes collectively increase the joint density of states and transition matrix elements within the visible energy range (1.6–3.1 eV). These trends collectively illustrate the favorable effects of S doping in tailoring the optical properties of BaTiO3-based compounds for visible-light optoelectronic applications.
3.4 Mechanical properties
This section discusses the mechanical characteristics of crystalline solids, which reflect their diverse reactions to various applied loads. This provides insights for predicting potential applications across different fields based on physical properties such as stiffness, fracture toughness, mechanical stability, elastic moduli, ductility, brittleness, hardness, and elastic anisotropy. The independent elastic constants were initially derived from strain-stress tests conducted in this study, thereby structuring the research on mechanical characteristics.76 Crystal strain is related to its elastic stiffness, as it indicates structural and mechanical stability, as well as bonding characteristics. This behavior, however, is sometimes very hard to model because often accurate means to determine stress and damage model matching strain are needed. To assess the elastic properties of polycrystalline materials, the upper and lower values of the elastic moduli were calculated using Hill's approximation of the elastic constants.77 The calculated elastic constants for S-doped BaTiO3−xSx compounds are given in Table 3. The stability criteria for these cubic and tetragonal structures are given below:78| For cubic: C11 − C12 > 0, C11 + 2C12 > 0, and C44 > 0. |
| For tetragonal: C11 > |C12|, 2 × C132 < C33(C11 + C12), C44 > 0, and C66 > 0. |
| Compound | C 11 | C 12 | C 13 | C 44 | C 33 | C 66 |
|---|---|---|---|---|---|---|
| BaTiO3 | 226.272 | 83.112 | — | 107.999 | — | — |
| BaTiO2S | 209.216 | 141.030 | 39.128 | 53.414 | 181.020 | 145.780 |
| BaTiO2S (SC) | 213.182 | 142.649 | 39.659 | 54.225 | 179.827 | 146.004 |
| BaTiOS2 | 155.566 | 37.002 | 53.476 | 68.558 | 247.394 | 35.335 |
| BaTiOS2 (SC) | 149.992 | 35.326 | 52.184 | 67.586 | 248.307 | 34.589 |
| BaTiS3 | 120.038 | 50.407 | — | 38.189 | — | — |
| BaTiS3 (SC) | 119.071 | 47.135 | — | 35.655 | — | — |
From Table 3, it can be seen that BaTiO3−xSx compounds meet their specific aforementioned criteria, confirming their mechanical stability.
Mechanical properties of BaTiO3−xSx compounds regarding their supercell (SC) arrangements have been calculated and presented in Table 4. These properties include bulk modulus (B), shear modulus (G), Young's modulus (Y), B/G ratio, Poisson's ratio (ν), Vickers hardness (Hv), and B/C44 ratio. The bulk modulus (B) defines the material's resistance to change in volume under the application of pressure.79 The shear modulus (G) connects the rigidity of a material and its resistance to shape change; some relate it to hardness.80 Young's modulus (Y) is the principal mechanical parameter characterizing the resistance of a material to elastic deformation under uniaxial tensile stress.81
| Compound | B | G | Y | B/G | ν | (Hv)Chen | (Hv)Tian | B/C44 |
|---|---|---|---|---|---|---|---|---|
| BaTiO3 | 131 | 92 | 223 | 1.429 | 0.216 | 15.37 | 15.02 | 1.21 |
| BaTiO2S | 112 | 67 | 168 | 1.66 | 0.258 | 9.86 | 10.16 | 2.11 |
| BaTiO2S (SC) | 113 | 68 | 170 | 1.66 | 0.25 | 10.01 | 10.29 | 2.10 |
| BaTiOS2 | 91 | 60 | 147 | 1.53 | 0.232 | 10.16 | 10.22 | 1.33 |
| BaTiOS2 (SC) | 89 | 59 | 144 | 1.52 | 0.230 | 10.18 | 10.21 | 1.32 |
| BaTiS3 | 73 | 36 | 95 | 2.00 | 0.286 | 4.29 | 5.37 | 1.93 |
| BaTiS3 (SC) | 72 | 36 | 92 | 1.99 | 0.285 | 4.23 | 5.31 | 1.98 |
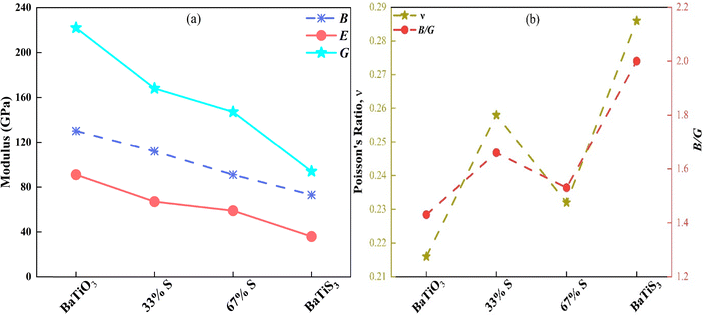
With increasing sulfur content, the bulk modulus (B) decreases. The maximum bulk modulus, 131 GPa, is exhibited by BaTiO3, suggesting strong interatomic bonding. In contrast, BaTiS3 shows a much lower value of 73 GPa, indicating reduced bonding due to S substitution. This softening in mechanical behavior is evidenced by the progressive decline in shear modulus (G) and Young's modulus (Y), which resist shape deformation and subsequently overall stiffness from BaTiO3 to BaTiS3. S weakens the bonding strength in the lattice due to its larger atomic size and lower electronegativity compared to oxygen. The effect of sulfur doping on bulk modulus, shear modulus, and Young's modulus is illustrated in Fig. 11(a). The B/G ratio indicates ductility; much higher values suggest very ductile behavior. BaTiO3 is relatively low at 1.43, similar to a brittle material; however, BaTiS3 has a significantly higher B/G value of 2.00, indicating a considerable improvement in ductility for a fully S-substituted compound. This trend suggests that Poisson's ratio also reflects the transition from brittle to ductile behavior with increased S content (ν). The value is 0.216 for BaTiO3, but for BaTiS3, the increase brings it to 0.286. Additionally, a higher Poisson's ratio indicates better plastic deformation capability and reduced brittleness. In principle, S doping therefore enhances the material's mechanical flexibility. The correlation between Poisson's ratio and the B/G ratio is illustrated in Fig. 11(b). Hardness testing is the fundamental basis in materials science, since hardness provides direct insight into resistance to deformation and wear, rendering it essential for assessing appropriateness for specific applications. Different hardness models enhance our comprehension of the in-ground mechanical behavior of materials, hence facilitating their selection and design for specialized applications. In this work, hardness predictions were made for BaTiO3−xSx compounds using established approaches given by Tian et al.82 and Chen et al.83 Among the compounds studied, BaTiO3 was found to be much harder than the other three.
S substitution leads to an increase in the B/C44 ratio, which gauges elastic anisotropy and bonding properties. BaTiO2S and BaTiOS2 show intermediate values (∼2.1 and ∼1.1.3, respectively), while BaTiS3 reaches ∼1.1.9. In contrast, BaTiS3 has a relatively low B/C44 ratio (1.21). This pattern suggests that the nature of interatomic interactions is altered and elastic anisotropy is enhanced by sulfur substitution. Sulfur substitution decreases the average bond stiffness since, on average, Ti–S bonds are softer than Ti–O bonds. The reduced stiffness arises from increased Ti–anion bond lengths and from more polarizable S ions, reducing resistance to deformation but enhancing mechanical compliance—an effect that is consistent with the observed increase in the B/C44 ratio84 and with the CDM indicating more delocalized bonding for Ti–S. Overall, the findings demonstrate that S dopants consistently exert a stochastic effect, stressing the material to the point of damaging its mechanical stiffness while increasing its ductility and elastic anisotropy. S-substituted BaTiS3 compounds will benefit from these mechanical modifications and enhanced optical characteristics, making them suitable for various applications in optoelectronic materials.
3.5 Thermal properties
Debye temperature (ΘD) is fundamental for characterizing solids’ vibrational properties and thermal behavior. On the other hand, it is related to the material's stiffness and sound velocity and tells us about lattice vibrations and phonon transport. The term “Debye temperature” was given in honor of Dutch physicist Peter Debye. It is the scale of temperature at which all possible atomic modes of vibration in a crystalline solid are excited.85 Elevated ΘD values indicate a more robust handling of atoms and a slight solidity in the structure.86 The densities (ρ) and the longitudinal (νl), transverse (νt), average sound velocities (νm) and Debye temperatures (ΘD) of BaTiO3−xSx compounds are computed and displayed in Table 5. BaTiO3 has strong interatomic bonding and stiffness, as evidenced by its maximum sound velocities (νl = 6710 m s−1, νt = 4038 m s−1, and νm = 4465 m s−1) and a ΘD of 555 K. Sound velocities and Debye temperatures steadily decrease as S gradually replaces O in the lattice (BaTiO2S → BaTiOS2 → BaTiS3). The higher atomic mass of S, accompanied by the weaker bonding environment, is the reason for this decrease. Conversely, BaTiS3 exhibits the lowest Debye temperature (350 K) and sound velocities (νm = 3329 m s−1), indicating a lower lattice and phonon energy scale. From the trend, it can be said that substitution enervates the lattice while lowering the Debye temperature and acoustic phonon velocities, which in turn affect these materials’ anharmonic properties and thermal conductivity.| Compound | ρ (kg m−3) | ν l (m s−1) | ν t (m s−1) | ν m (m s−1) | Θ D (K) |
|---|---|---|---|---|---|
| BaTiO3 | 6240 | 6710 | 4038 | 4465 | 555 |
| BaTiO2S | 5000 | 6353 | 3670 | 4074 | 476 |
| BaTiOS2 | 4230 | 6158 | 3637 | 4030 | 445 |
| BaTiS3 | 4130 | 5451 | 2986 | 3329 | 350 |
The melting temperature of the BaTiO3−xSx compounds was calculated using Tm = [553 + (5.911)C11] for the cubic phase and Tm = 3C11 + 1.5C33 + 354 for the tetragonal phase.87,88 From Table 6, it can be observed that the melting temperature (Tm) decreases from BaTiO3 (1890.5 K) to BaTiOS2 (1192 K), indicating a decrease in thermal stability with an increase in S concentration in the lattice. The comparatively higher Tm values for BaTiO3 imply strong bonding and, thus, thermal resistance, whereas the lower values for sulfur-rich compounds may suggest weak lattice cohesion.
| Compounds | T m (K) | γ | K ph (W mK−1) | C v | C P | S (J K−1 mol−1) |
|---|---|---|---|---|---|---|
| BaTiO3 | 1890.5 | 1.35 | 5.48 | 98.6 | 99.1 | 108.57 |
| BaTiO2S | 1253 | 1.54 | 3.92 | 92.2 | 92.6 | 110.06 |
| BaTiOS2 | 1192 | 1.42 | 1.23 | 106.2 | 107.2 | 138.67 |
| BaTiS3 | 1262 | 1.69 | 1.18 | 83.7 | 83.8 | 149.91 |
The Grüneisen parameter (γ), which measures both anharmonicity and thermal expansion aspects, exhibits a decreasing trend from 1.35 in BaTiO3 to 1.69 in BaTiS3, as shown in Table 6. This increase demonstrates how phonon–phonon scattering is enhanced by the rise in S content, leading to a decrease in lattice thermal conductivity. The Grüneisen parameter (γ) was calculated using the following formula, where ν is Poisson's ratio.
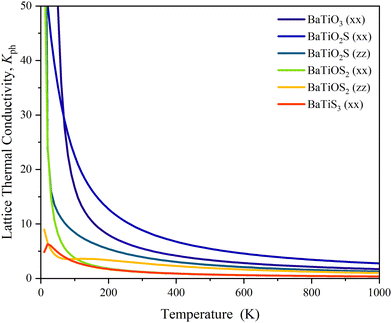
The ability of a solid material to transfer heat through the vibrations of its atoms (phonons) is known as lattice thermal conductivity. From Fig. 12, it can be seen that the highest Kph is found in BaTiO3, which shows effective phonon transport because of its strong bonding and low anharmonicity. It starts above 50 W m−1 K−1 at low temperatures and stays around 1.713 W m−1 K−1 at 1000 K. BaTiO2S exhibits decreased thermal conductivity (∼25 W m−1 K−1 at 50 K) upon partial S substitution, with the xx direction being marginally less conductive than the zz direction. This is an indication of increased phonon scattering from mass disorder and lattice distortion. Both components decrease more significantly for BaTiOS2, particularly in the xx direction, which at high temperatures drops around 0.367 W m−1 K−1, suggesting strong phonon localization and anisotropy. With values falling below 5 W m−1 K−1 even at low temperatures and approaching the amorphous limit 0.363 W m−1 K−1 by 1000 K, the fully substituted BaTiS3 exhibits the lowest and almost isotropic Kph. This is attributed to high lattice anharmonicity and strong phonon scattering due to S's heavier mass and weaker bonding. Lattice thermal conductivity at 300 K is given in Table 6.
The evaluation of thermal properties, including conductivity and heat capacity, is made possible by the scattering or decay processes. For more in-depth insights into the underlying phonon transport mechanisms in the BaTiO3−xSx series, the phonon lifetimes as a function of phonon frequency were considered (Fig. 13). There seems to be a correlation observed between the phonon lifetime distribution and the lattice thermal conductivity that is calculated (Fig. 12).89 Phonon lifetimes, which go up to 1 ps or more in cleaner BaTiO3 along the phonon frequency around a mid-frequency region of 7–12 THz, indicate less strong phonon–phonon scattering and thus longer phonon mean free paths, leading to a higher value of lattice thermal conductivity. On the partial substitution of O with S, the phonon lifetimes get shorter in BaTiO2S and BaTiOS2, particularly in the ranges of low and mid frequencies [Fig. 13(b) and (c)]. The enhanced scattering rates, with peak values above 0.20 and 0.35 ps−1, respectively, may suggest increased phonon anharmonicities through mass disorder and bonding heterogeneities introduced by S atoms. The trend continues in fully substituted BaTiS3 [Fig. 13(d)], where the shortest phonon lifetimes are mostly below 0.4 ps and maximum scattering rates of nearly 0.40 ps−1 are found, particularly in the low-frequency acoustic phonon region below 5 THz. These acoustic phonons mainly carry heat on a crystalline scale, and their strong damping suppresses lattice thermal conductivity. So, in connection with these phenomena, the observed progressive reduction in phonon lifetimes moving from BaTiO3 to BaTiS3 aligns with the change in lattice thermal conductivity across the series as presented in Fig. 13. This conclusion affirms that an S substitution in BaTiO3 indeed serves to modulate phonon dynamics by increasing phonon scattering, subsequently reducing lattice thermal conductivity. The figure of merit of thermoelectric materials depends directly on the electrical conductivity and inversely on the lattice thermal conductivity. The electronic properties section reveals the enhancements of electrical conductivity (by reducing the band gap), and this section reveals a reduction of lattice thermal conductivity. This combined effect could increase the thermoelectrical properties of S-rich compositions (BaTiS3). The tunable thermal transport properties of the BaTiO3−xSx system may find use in advanced heat management systems for microelectronic and optoelectronic devices.
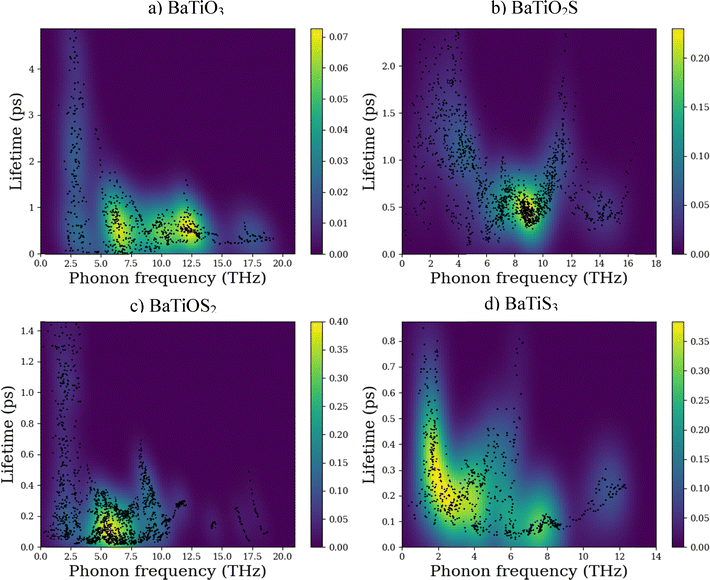 | ||
| Fig. 13 Lifetime vs. phonon frequency curve for (a) BaTiO3, (b) BaTiO2S, (c) BaTiOS2, and (d) BaTiS3 compounds. | ||
The dramatic decrease in lattice thermal conductivity upon S substitution (Kph: 5.48 → 1.18 W m−1 K−1) is explained by two primary mechanisms. First, the greater mass of S (relative to O) reduces phonon group velocities through decreasing mean sound velocities (νm from 4465 → 3329 m s−1) and reduced Debye temperatures (ΘD from 555 → 350 K). Second, the increased lattice anharmonicity—represented by the higher Grüneisen parameter (γ rises from 1.35 → 1.69)—and mass/force-constant disorder introduced by mixed anions greatly increase phonon–phonon and impurity scattering, shortening the phonon mean free paths and lowering κ. The accompanying vibrational entropy increase also favors stronger phonon scattering and anharmonicity in S-rich compounds.
 | ||
| Fig. 14 Gibbs free energy, entropy, and specific heat at constant volume for (a) BaTiO3, (b) BaTiO2S, (c) BaTiOS2, and (d) BaTiS3 compounds. | ||
The red curves represent the Gibbs free energy, which decreases as the temperature rises. The compounds’ enhanced thermodynamic favorability at higher temperatures, due to entropy contributions, is reflected in this trend. Compared to its S-substituted counterparts, BaTiO3 shows the highest thermodynamic stability at low temperatures, as evidenced by its most negative G values. The G values become less negative as the S content increases, indicating a slight decrease in thermal stability as S replaces O. This aligns with the lower stiffness and weaker bonding of the mechanical properties.
Entropy (blue curves) increases smoothly with temperature for all materials. Because S atoms contribute additional atomic mass and vibrational degrees of freedom, the entropy magnitude is slightly higher in S-rich compositions (BaTiOS2 and BaTiS3). BaTiO3 exhibits a somewhat lower value of ∼215 J K−1 mol−1 at 1000 K, whereas BaTiS3 reaches about 225 J K−1 mol−1. This indicates that S substitution enhances the system's configurational entropy and vibrational disorder.
At low temperatures, the specific heat at constant volume (green curves) rises quickly, and at higher temperatures (above 600 K), it saturates near the Dulong–Petit limit (∼125 J K−1 mol−1). This behavior aligns with Debye theory, which posits that as the vibrational modes fill up, Cv tends to stabilize. Despite compositional differences, the Cv curves for all four compositions converge at high temperatures, suggesting comparable high-temperature phonon contributions. Although slight variations exist at low temperatures, BaTiS3 displays a marginally higher Cv rise at early temperatures, likely due to S-induced low-frequency vibrational modes. Specific heat at constant pressure (Cp) was calculated using the formulas below:90
According to thermal analysis, S substitution in the BaTiO3−xSx compounds systematically lowers thermal conductivity by 40–60% while increasing vibrational entropy and heat capacity by 25–30% and 15–20%, respectively, due to improved phonon scattering and bond anharmonicity brought about by softer Ti–S bonds. The combination of ultralow thermal conductivity (∼1.5 W m−1 K−1 in BaTiOS3), high entropy, and strong anharmonicity makes S-rich phases particularly promising for thermoelectric applications where phonon suppression is crucial, as well as for thermal management in optoelectronic devices requiring temperature-stable operation, even though S incorporation slightly reduces thermodynamic stability (less negative formation energies). These patterns show how controlled S doping can engineer thermal transport properties without sacrificing structural integrity, providing a materials design pathway for energy conversion and heat regulation technologies.
4. Conclusions
The effect of S substitution on the mechanical, thermal, and opto-electronic properties of BaTiO3 perovskite was thoroughly investigated by the DFT method, wherein substitution of O by S converts BaTiO3 into BaTiO2S, BaTiOS2, and eventually BaTiS3. All compounds exhibit negative formation energies and acceptable values of tolerance factors, and negligible fluctuation of energy (AIMD studies) confirmed the thermodynamical stability of the studied compositions. Partial substitution creates tetragonal distortions due to mixed Ti–O and Ti–S bonding, with the cubic-like phase becoming the ground-state structure in BaTiS3. Due to the significantly higher energy of S 3p orbitals compared to O 2p orbitals, sulfur doping effectively reduces the bandgap from the ultraviolet (3.06 eV) to the visible range (1.55 eV and 1.02 eV), thus rendering the compounds more suitable for solar and photocatalytic applications. The sulfur-incorporated absorbance edge undergoes a redshift with an increase in absorption coefficient (9.16 × 105 cm−1 in BaTiS3), dielectric constant, refractive index, extinction coefficient (∼0.55), and optical conductivity (up to ∼1015 S m−1) in the visible-light range, bolstering suitability for photonic applications, photovoltaic absorbers, minimal photon loss, and excellent carrier transport capabilities. With increased S content, the elastic modulus and stiffness decrease, but ductility improves with higher B/G ratios (1.43 to 2.00) and Poisson's ratios (0.216 to 0.286), suggesting weakening of the Ti–S bonds and increased ductility. Hardness concurrently diminishes, indicating that sulfur-rich compositions are softer and more easily processed. As the atomic mass of S grows and lattice stiffness diminishes, the Debye temperature decreases from 555 K to 350 K for BaTiO3 to BaTiS3. The lattice vibration thermal conductivity, kph, drops substantially from 5.48 W m−1 K−1 to 1.18 W m−1 K−1 at 300 K due to increased phonon scattering caused by mass disorder and bond anharmonicity. Consequently, S doping results in higher specific heat and entropy, reflecting increased vibrational activity and thermal stability. Thus, S doping provides a controlled approach for engineering BaTiO3−x based perovskites with distinct properties in thermal, mechanical, and optoelectronic domains, thereby enhancing their potential in diverse areas.Author contributions
U. Ahmed: data curation, investigation, visualization, formal analysis, and writing – original draft. M. M. Hossain: formal analysis, validation, writing – review and editing. M. M. Uddin: validation, writing – review and editing. N. Jahan: validation, writing – review and editing. M. A. Ali: conceptualization, methodology, formal analysis, validation, project administration, writing – review and editing, and supervision.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The datasets generated during the current study are available from the corresponding authors upon reasonable request.Acknowledgements
The authors are grateful to the DRE, CUET, for providing financial support for this project [CUET/DRE/2023-24/Phy/014]. This work has been carried out in the ACMRL, which was established with a research grant (grant number: 21-378 RG/PHYS/AS_G-FR3240319526) from UNESCO-TWAS and the Swedish International Development Co-operation Agency (SIDA).References
- M. R. Mohaghegh, M. Heidari, S. Tasnim, A. Dutta and S. Mahmud, Latest advances on hybrid solar–biomass power plants, Energy Sources, Part A, 2021, 47(1), 4901–4924 CrossRef.
- J. Zeghlouli, G. Christophe, A. Guendouz, C. El Modafar, A. Belkamel and P. Michaud, et al., Optimization of bioethanol production from enzymatic treatment of argan pulp feedstock, Molecules, 2021, 26(9), 2516 CrossRef CAS PubMed.
- S. Mukherjee, S. Bin Mujib, D. Soares and G. Singh, Electrode materials for high-performance sodium-ion batteries, Materials, 2019, 12(12), 1952 CrossRef CAS PubMed.
- Y. Nasr, H. El Zakhem, A. E. A. Hamami, M. El Bachawati and R. Belarbi, Comprehensive Review of Innovative Materials for Sustainable Buildings’ Energy Performance, Energies, 2023, 16(21), 7440 CrossRef.
- S. Mahmud, U. Ahmed, M. A. U. Z. Atik, M. M. Hossain, M. M. Uddin and M. A. Ali, Novel Cs2AuIMIIIF6 (M = As, Sb) double halide perovskites: sunlight and industrial waste heat management device applications, Phys. Chem. Chem. Phys., 2025, 27(9), 4686–4703 RSC.
- M. A. C. Teixeira, H. R. Ramos, A. Aguiar and O. e de, Perspectives of New Alternative Materials to Silicon for the Production of Photovoltaic Solar Cells, Rev. Nac. Geren. Cid., 2021, 9(71), 48–61 Search PubMed.
- M. Llanos, R. Yekani, G. P. Demopoulos and N. Basu, Alternatives assessment of perovskite solar cell materials and their methods of fabrication, Renewable Sustainable Energy Rev., 2020, 133, 110207 CrossRef CAS.
- W. Zhang, G. E. Eperon and H. J. Snaith, Metal halide perovskites for energy applications, Nat. Energy, 2016, 1(6), 16048 CrossRef CAS.
- T. Islam, R. Jani, S. M. Al Amin, K. M. Shorowordi, S. S. Nishat and A. Kabir, et al., Simulation studies to quantify the impacts of point defects: An investigation of Cs2AgBiBr6 perovskite solar devices utilizing ZnO and Cu2O as the charge transport layers, Comput. Mater. Sci., 2020, 184, 109865 CrossRef CAS.
- S. Khatoon, S. Kumar Yadav, V. Chakravorty, J. Singh, R. Bahadur Singh and M. S. Hasnain, et al., Perovskite solar cell's efficiency, stability and scalability: A review, Mater. Sci. Energy Technol., 2023, 6, 437–459 CAS.
- J. Diekmann, P. Caprioglio, M. H. Futscher, V. M. Le Corre, S. Reichert and F. Jaiser, et al., Pathways toward 30% Efficient Single-Junction Perovskite Solar Cells and the Role of Mobile Ions, Sol. RRL, 2021, 5(8), 2100219 CrossRef CAS.
- P. Kumari, V. Srivastava, R. Khenata, S. A. Dar and S. H. Naqib, A first-principles prediction of thermophysical and thermoelectric performances of SrCeO3 perovskite, Int. J. Energy Res., 2022, 46(3), 2934–2946, DOI:10.1002/er.7354 . Available from: .
- R. Yadav, A. Srivastava, R. Sharma, J. A. Abraham, S. A. Dar and A. K. Mishra, et al., The study of optical and thermoelectric behaviour of thalium based flouropervoskite (TlSiF3) for photovoltaic and renewable energy applications by DFT, J. Solid State Chem., 2022, 313, 123266, DOI:10.1016/S0022459622003917.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer and T. Leijtens, et al., Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber, Science, 2013, 342(6156), 341–344 CrossRef CAS.
- Y. Yuan, J. Chae, Y. Shao, Q. Wang, Z. Xiao and A. Centrone, et al., Photovoltaic Switching Mechanism in Lateral Structure Hybrid Perovskite Solar Cells, Adv. Energy Mater., 2015, 5(15) DOI:10.1002/aenm.201500615.
- D. Popovici, M. Okuyama and J. Akedo, Barium Titanate-Based Materials – a Window of Application Opportunities, Ferroelectrics – Material Aspects, InTech, 2011 Search PubMed.
- R. E. Newnham, Structure–Property Relationships in Perovskite Electroceramics, 2013, pp. 91–8 Search PubMed.
- M. Acosta, N. Novak, V. Rojas, S. Patel, R. Vaish and J. Koruza, et al., BaTiO3-based piezoelectrics: Fundamentals, current status, and perspectives, Appl. Phys. Rev., 2017, 4(4) DOI:10.1063/1.4990046.
- V. Mishra, A. Sagdeo, V. Kumar, M. K. Warshi, H. M. Rai and S. K. Saxena, et al., Electronic and optical properties of BaTiO3 across tetragonal to cubic phase transition: An experimental and theoretical investigation, J. Appl. Phys., 2017, 122(6) DOI:10.1063/1.4997939.
- J. Chen, H. Deng, D. Zheng, Y. Pan, S. Si and Y. Zhang, et al., Band gap narrowing and electrical properties of (1 − x)BaTiO3−xSrFe0.5Nb0.5O3 lead-free ceramics, J. Mater. Sci.: Mater. Electron., 2021, 32(8), 10151–10159 CrossRef CAS.
- J. M. V. Cunha, M. A. Barreiros, M. A. Curado, T. S. Lopes, K. Oliveira and A. J. N. Oliveira, et al., Perovskite Metal–Oxide–Semiconductor Structures for Interface Characterization, Adv. Mater. Interfaces, 2021, 8(20), 2101004 CrossRef CAS.
- J. Xu, D. P. Durisin and G. W. Auner, Optical properties of pulsed-laser deposited BaTiO3 thin films, In Photon Processing in Microelectronics and Photonics IV, ed. J. Fieret, P. R. Herman, T. Okada, C. B. Arnold, F. G. Bachmann, W. Hoving, et al., 2005, p. 305 Search PubMed.
- S. H. Wemple, Polarization fluctuations and the optical-absorption edge in BaTiO3. Phys. Rev. B. 1970;2(7):2679–2689 Search PubMed.
- S. S. A. Gillani, R. Ahmad, M. Rizwan, M. Rafique, G. Ullah and C. B. Cao, et al., Effect of magnesium doping on band gap and optical properties of SrZrO3 perovskite: A first-principles study, Optik, 2019, 191, 132–138 CrossRef CAS.
- M. I. Kholil, M. T. H. Bhuiyan, M. A. Rahman, M. S. Ali and M. Aftabuzzaman, Effects of Fe doping on the visible light absorption and bandgap tuning of lead-free (CsSnCl3) and lead halide (CsPbCl3) perovskites for optoelectronic applications, AIP Adv., 2021, 11(3) DOI:10.1063/5.0042847.
- S. Das Adhikari, S. K. Dutta, A. Dutta, A. K. Guria and N. Pradhan, Chemically Tailoring the Dopant Emission in Manganese-Doped CsPbCl3 Perovskite Nanocrystals, Angew. Chem., Int. Ed., 2017, 129(30), 8872–8876, DOI:10.1002/ange.201703863.
- N. Tanwar, S. Upadhyay, R. Priya, S. Pundir, P. Sharma and O. P. Pandey, Eu-doped BaTiO3 perovskite as an efficient electrocatalyst for oxygen evolution reaction, J. Solid State Chem., 2023, 317, 123674, DOI:10.1016/S002245962200799X.
- X. Luo, Y. Li, K. Liu and J. Zhang, Electron transport enhancement of perovskite solar cell due to spontaneous polarization of Li+-doped BaTiO3, Solid State Sci., 2020, 108, 106387, DOI:10.1016/S1293255820312590.
- Z. Yao, H. Liu, Y. Liu, Z. Wu, Z. Shen and Y. Liu, et al., Structure and dielectric behavior of Nd-doped BaTiO3 perovskites, Mater. Chem. Phys., 2008, 109(2–3), 475–481, DOI:10.1016/S0254058407007626.
- B. Mouhib, S. Dahbi, A. Douayar, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, Theoretical investigations of electronic structure and optical properties of S, Se or Te doped perovskite ATiO3 (A = Ca, Ba, and Sr) materials for eco-friendly solar cells, Micro and Nanostructures, 2022, 163, 107124, DOI:10.1016/S0749603621003256.
- F. F. Li, D. R. Liu, G. M. Gao, B. Xue and Y. S. Jiang, Improved visible-light photocatalytic activity of NaTaO3 with perovskite-like structure via sulfur anion doping, Appl. Catal., B, 2015, 166–167, 104–111, DOI:10.1016/S0926337314006699.
- T. Jia, Y. Hao and H. Hao, Sulfur-doping effects on oxygen vacancy formation in LaBO3 (B = Fe, Co, and Ni) perovskites, Phys. Chem. Chem. Phys., 2024, 27(3), 1585–1592, 10.1039/D4CP03834G.
- J. Ran, T. Wang, J. Zhang, Y. Liu, C. Xu and S. Xi, et al., Modulation of Electronics of Oxide Perovskites by Sulfur Doping for Electrocatalysis in Rechargeable Zn–Air Batteries, Chem. Mater., 2020, 32(8), 3439–3446, DOI:10.1021/acs.chemmater.9b05148.
- Z. Ech-charqy, A. El Badraoui, A. Elkhou, M. Ziati and H. Ez-Zahraouy, Effect of sulfur doping on the electronic structures, optical and photocatalytic properties of KTaO3 perovskites: DFT calculations, Chem. Phys., 2025, 596, 112759, DOI:10.1016/S0301010425001600.
- H. Akter, M. A. Ali, M. M. Hossain, M. M. Uddin and S. H. Naqib, Oxysulfide perovskites: reduction of the electronic band gap of RbTaO3 by sulfur substitution, Phys. Scr., 2024, 99(4), 045950, DOI:10.1088/1402-4896/ad31f3.
- H. Akter, M. M. Hossain, M. M. Uddin, S. H. Naqib and M. A. Ali, Effects of S substitution on the structural, optoelectronic, and thermomechanical properties of KTaO3 through density functional theory, J. Phys. Chem. Solids, 2024, 190, 112021, DOI:10.1016/S0022369724001562.
- U. Ahmed, H. Akter, A. Hossain, M. M. Hossian, M. M. Uddin and S. H. Naqib, et al., Anion (S) substitution as a pathway for tuning the physical properties of CsTaO3, New J. Chem., 2025, 49(18), 7682–7699 RSC.
- J. W. Bennett, I. Grinberg and A. M. Rappe, Effect of substituting of S for O: The sulfide perovskite BaZrS3 investigated with density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(23), 235115, DOI:10.1103/PhysRevB.79.235115.
- C. Zhang, Y. Jia, Y. Jing, Y. Yao, J. Ma and J. Sun, Effect of non-metal elements (B, C, N, F, P, S) mono-doping as anions on electronic structure of SrTiO3, Comput. Mater. Sci., 2013, 79, 69–74, DOI:10.1016/S0927025613003236.
- B. Wang, P. D. Kanhere, Z. Chen, J. Nisar, B. Pathak and R. Ahuja, Anion-doped NaTaO3 for visible light photocatalysis, J. Phys. Chem. C, 2013, 117(44), 22518–22524 CrossRef CAS.
- S. Dahbi, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, The new eco-friendly lead-free zirconate perovskites doped with chalcogens for solar cells: Ab initio calculations, Opt. Mater., 2020, 109, 110442 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- J. Yang, L. Z. Tan and A. M. Rappe, Hybrid functional pseudopotentials, Phys. Rev. B, 2018, 97(8), 085130 CrossRef CAS.
- H. Ehrenreich and M. H. Cohen, Self-consistent field approach to the many-electron problem, Phys. Rev., 1959, 115(4), 786–790 CrossRef.
- V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35(35), 353001 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert and K. Refson, et al., First principles methods using CASTEP, Z. Kristallogr. Cryst. Mater., 2005, 220(5–6), 567–570, DOI:10.1524/zkri.220.5.567.65075/html.
- C. Srilakshmi, R. Saraf, V. Prashanth, G. M. Rao and C. Shivakumara, Structure and Catalytic Activity of Cr-Doped BaTiO3 Nanocatalysts Synthesized by Conventional Oxalate and Microwave Assisted Hydrothermal Methods, Inorg. Chem., 2016, 55(10), 4795–4805, DOI:10.1021/acs.inorgchem.6b00240.
- N. Inoue, T. Okamatsu, A. Ando, H. Takagi, T. Hashimoto and C. Moriyoshi, et al., Structural Characteristics of (Ba0.94Gd0.06)(Ti0.97Mg0.03)O3 in Cubic Structure Determined by High-Energy Synchrotron-Radiation Powder Diffraction, Jpn. J. Appl. Phys., 2009, 48(9), 09KF03, DOI:10.1143/JJAP.48.09KF03.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A:Found. Crystallogr., 1976, 32(5), 751–767 CrossRef.
- A. E. Fedorovskiy, N. A. Drigo and M. K. Nazeeruddin, The Role of Goldschmidt’s Tolerance Factor in the Formation of A2BX6 Double Halide Perovskites and its Optimal Range. Small, Methods, 2020, 4(5), 1900426 CAS.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Formability of ABX3 (X = F, Cl, Br, I) halide perovskites, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64(6), 702–707 CrossRef CAS.
- M. W. Qureshi, X. Ma, G. Tang and R. Paudel, Ab initio predictions of structure and physical properties of the Zr2GaC and Hf2GaC MAX phases under pressure, Sci. Rep., 2021, 11(1), 3260 CrossRef CAS PubMed.
- S. Nakamura, Y. Tsuji and K. Yoshizawa, Molecular Dynamics Study on the Thermal Aspects of the Effect of Water Molecules at the Adhesive Interface on an Adhesive Structure, Langmuir, 2021, 37(50), 14724–14732, DOI:10.1021/acs.langmuir.1c02653.
- F. Rahman, M. M. Ali, M. A. Ali, M. M. Uddin, S. H. Naqib and M. M. Hossain, DFT approach into the physical properties of MTe3 (M = Hf, Zr) superconductors: A comprehensive study, AIP Adv., 2023, 13(8) DOI:10.1063/5.0160012.
- M. A. Ali, M. Anwar Hossain, M. A. Rayhan, M. M. Hossain, M. M. Uddin and M. Roknuzzaman, et al., First-principles study of elastic, electronic, optical and thermoelectric properties of newly synthesized K2Cu2GeS4 chalcogenide, J. Alloys Compd., 2019, 781, 37–46 CrossRef CAS.
- J. Feng and B. Xiao, Effective masses and electronic and optical properties of nontoxic MASnX3 (X = Cl, Br, and I) perovskite structures as solar cell absorber: A theoretical study using HSE06, J. Phys. Chem. C, 2014, 118(34), 19655–19660 CrossRef CAS.
- J. Gao, W. Zeng, B. Tang, M. Zhong and Q. J. Liu, Optical, electronic, and mechanical properties of p-type conductive oxide BaBiO3: A density functional theory study, Chem. Phys. Lett., 2020, 761, 138054 CrossRef CAS.
- S. Park, B. Lee, S. H. Jeon and S. Han, Hybrid functional study on structural and electronic properties of oxides, Curr. Appl. Phys., 2011, 11(3 Suppl.), S337–S340 CrossRef.
- R. Schira and C. Latouche, DFT and hybrid-DFT calculations on the electronic properties of vanadate materials: Theory meets experiments, New J. Chem., 2020, 44(27), 11602–11607 RSC.
- W. Shockley and H. J. Queisser, Detailed balance limit of efficiency of p-n junction solar cells, J. Appl. Phys., 1961, 32(3), 510–519 CrossRef CAS.
- B. Ehrler, E. Alarcón-Lladó, S. W. Tabernig, T. Veeken, E. C. Garnett and A. Polman, Photovoltaics reaching for the shockley-queisser limit, ACS Energy Lett., 2020, 5(9), 3029–3033 CrossRef CAS.
- Y. Xu, T. Gong and J. N. Munday, The generalized Shockley-Queisser limit for nanostructured solar cells, Sci. Rep., 2015, 5(1), 13536 CrossRef PubMed.
- S. Azam, S. Goumri-Said, S. A. Khan and M. B. Kanoun, Electronic, optical and thermoelectric properties of new metal-rich homological selenides with palladium–indium: Density functional theory and Boltzmann transport model, J. Phys. Chem. Solids, 2020, 138, 109229 CrossRef CAS.
- F. Chiker, B. Abbar, B. Bouhafs and P. Ruterana, Interband transitions of wide-band-gap ternary pnictide BeCN2 in the chalcopyrite structure, Phys. Status Solidi B, 2004, 241(2), 305–316 CrossRef CAS.
- M. Hilal, B. Rashid, S. H. Khan and A. Khan, Investigation of electro-optical properties of InSb under the influence of spin-orbit interaction at room temperature, Mater. Chem. Phys., 2016, 184, 41–48 CrossRef CAS.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175(1), 1–14 CrossRef CAS.
- V. K. Rashenov, M. G. Foigel and R. A. Alarashi, Dielectric Function of a Model Semiconductor, Phys. Status Solidi, 1972, 54(1), 355–368 CrossRef.
- D. R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev., 1962, 128(5), 2093–2097 CrossRef CAS.
- M. A. Rahman, R. Khatun, R. Ferdous, D. Chandra Roy, M. Z. Hasan and A. Irfan, et al., First-principles calculations to investigate structural, elastic, electronic, optical and thermal properties of La-based ternary intermetallic superconductors LaM2Si2 (M = Co, Cu, Rh, Pd, Ag, Ir, Pt, Au), J. Mater. Res. Technol., 2023, 26, 3840–3862 CrossRef CAS.
- P. R. Varadwaj and H. M. Marques, Physical and optoelectronic features of lead-free A2AgRhBr6 (A = Cs, Rb, K, Na, Li) with halide double perovskite composition, J. Mater. Chem. C, 2020, 8(37), 12968–12983 RSC.
- A. Bafekry, M. Shahrokhi, A. Shafique, H. R. Jappor, M. M. Fadlallah and C. Stampfl, et al., Semiconducting chalcogenide alloys based on the (Ge, Sn, Pb) (S, Se, Te) formula with outstanding properties: A first-principles calculation study, ACS Omega, 2021, 6(14), 9433–9441 CrossRef CAS PubMed.
- H. H. Hegazy, G. M. Mustafa, A. Nawaz, N. A. Noor, A. Dahshan and I. Boukhris, Tuning of direct bandgap of Rb2ScTlX6(X = Cl, Br, I) double perovskites through halide ion substitution for solar cell devices, J. Mater. Res. Technol., 2022, 19, 1271–1281 CrossRef CAS.
- A. El Amrani, A. Bekhtari, A. El Kechai, H. Menari, L. Mahiou and M. Maoudj, et al., Determination of the suitable refractive index of solar cells silicon nitride, Superlattices Microstruct., 2014, 73, 224–231 CrossRef CAS.
- M. H. Mia, U. Ahmed, S. K. Saha and M. A. Ali, Unveiling mechanical, electronic, and optical properties of newly synthesized Mo2VAlC2 and Mo2V2AlC3 o-MAX phases via first-principles calculations, J. Mater. Res. Technol., 2025, 36, 2468–2484 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349–354 CrossRef.
- F. Mouhat and F. X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104 CrossRef.
- A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. K. Mao, Synthesis of novel transition metal nitrides IrN2 and OsN2, Phys. Rev. Lett., 2006, 96(15), 155501, DOI:10.1103/PhysRevLett.96.155501.
- M. Hebbache, Shear modulus and hardness of crystals: Density functional calculations, Solid State Commun., 2000, 113(8), 427–432, DOI:10.1016/S0038109899005141.
- I. R. Storch, R. De Alba, V. P. Adiga, T. S. Abhilash, R. A. Barton and H. G. Craighead, et al., Young's modulus and thermal expansion of tensioned graphene membranes, Phys. Rev. B, 2018, 98(8), 085408, DOI:10.1103/PhysRevB.98.085408.
- Y. Tian, B. Xu and Z. Zhao, Microscopic theory of hardness and design of novel superhard crystals, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19(9), 1275–1281 CrossRef CAS.
- M. A. Hossain, M. S. Ali and A. K. M. A. Islam, Rare earth rhodium borides RRh3B (R = Y, Zr, and Nb): mechanical, thermal and optical properties, Eur. Phys. J. B, 2012, 85(12), 396 CrossRef.
- C. Toher, J. J. Plata, O. Levy, M. De Jong, M. Asta and M. B. Nardelli, et al., High-throughput computational screening of thermal conductivity, Debye temperature, and Grüneisen parameter using a quasiharmonic Debye model, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(17), 174107 CrossRef.
- F. W. De Wette and A. D. Kulkarni, Phonon dispersion, phonon specific heat, and Debye temperature of high-temperature superconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(22), 14922–14925 CrossRef CAS PubMed.
- Z. Ali, I. Khan, I. Ahmad, M. S. Khan and S. J. Asadabadi, Theoretical studies of the paramagnetic perovskites MTaO3 (M = Ca, Sr and Ba), Mater. Chem. Phys., 2015, 162, 308–315 CrossRef CAS.
- M. E. Fine, L. D. Brown and H. L. Marcus, Elastic constants versus melting temperature in metals, Scr. Metall., 1984, 18(9), 951–956 CrossRef CAS.
- Z. Tong, Y. Zhang, A. Pecchia, C. Y. Yam, L. Zhou and T. Dumitrică, et al., Predicting the Lattice Thermal Conductivity in Nitride Perovskite LaWN3 from ab initio Lattice Dynamics, Adv. Sci., 2023, 10(9), 2205934 CrossRef CAS.
- O. Delaire, A. F. May, M. A. McGuire, W. D. Porter, M. S. Lucas and M. B. Stone, et al., Phonon density of states and heat capacity of La3−xTe4, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(18), 184302 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |