Precise measurement of ultrathin film thickness via a neutron capture reaction

Abstract

Accurate measurement of ultrathin film thickness is of significant importance in both scientific research and industrial applications. In this study, a neutron capture reaction was successfully employed to measure the thickness of ultrathin Cu films (∼nm) as well as applied to determine the thickness of materials in the semiconductor industry, specifically Si₃N₄ films. The method was demonstrated to be non-destructive and applicable to several different films. Finally, a methodology is proposed to guide the experimental design for thickness measurement. This suggests that the nondestructive method provides a novel approach for measuring thin film thicknesses ranging from the nanoscale to the microscale.

---

Introduction

Nanometer-scale thin film materials exhibit significant grain boundary effects, size effects, and quantum effects, resulting in unique optical, mechanical, electromagnetic, and gas-sensing properties.¹ Consequently, they have broad application prospects in areas such as high-density magnetic recording materials,² optical devices,³ optoelectronic materials,⁴ solar cell materials,⁵ hydrogen storage materials,⁶ efficient catalysts, and superconducting materials.^7,8 Various methods are employed for measuring thin films depending on their characteristics. Common methods include transmission electron microscopy (TEM), X-ray reflectometry (XRR), beta-ray transmission, and laser interferometry.^9–11 These techniques possess broad applicability and distinctive advantages. For instance, XRR enables rapid and nondestructive analysis of single- and multi-layer thin films.^12–14 Previous studies have experimentally and computationally validated the effectiveness and accuracy of NDP for measuring nanometer-scale thin films.¹⁵ This method calculates thin film thickness by measuring the energy loss of charged particles with a specific initial energy generated from neutron nuclear reactions as they pass through the film. The underlying principles are illustrated in Fig. 1.

Fig. 1 Schematic of thin film thickness measurement using nuclear reactions to calculate the film thickness based on the energy lost by particles in the material.¹⁵

Neutron Depth Profiling (NDP) is a near-surface material analysis technique. It was first proposed in 1972 by Ziegler et al.¹⁶ for determining the concentration of boron impurities in substrates and subsequently applied to the semiconductor field. NDP is based on the (n,p) or (n,α) reactions that occur when light element isotopes such as Li, Be, and B capture neutrons, releasing charged particles with specific kinetic energies. By measuring the energy distribution of the emitted particles, the depth profile of the target element can be accurately determined.¹⁷ NDP is non-destructive to the analyzed samples,¹⁸ and the influence of the substrate material on the measurements is minimal. This technique plays a crucial role in the fields of semiconductors, high-temperature alloys, and energy materials.^19–21

Here, the NDP technique provides an innovative approach for measuring the thickness of a set of ultrathin Cu films (∼tens of nanometers). The nondestructive measurement of the thickness of protective Si₃N₄ films on the surface of boro-phospho-silicate glass was carried out. Additionally, the nondestructive measurement of the thickness of single-layer Si₃N₄ films was done using a special experimental design. Finally, a methodology was proposed to assist the experimental design.

Experimental setup

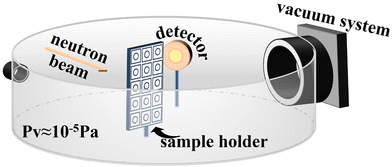
This experiment was conducted using the Neutron Depth Profiling (NDP) system at the China Advanced Research Reactor (CARR). The detection system primarily consists of an α detector, a preamplifier, and a digital multichannel analyzer. A Canberra PD300-16-100 AM detector was used, which has a full width at half maximum (FWHM) of 13.6 keV for the 5.486 MeV α particles from ²⁴¹Am.²² The vacuum level can reach 3.4 × 10⁻⁵ Pa.²³ The angle between the neutron beam incidence direction and the sample plane is approximately 45°, and the angle between the silicon detector detection direction and the sample plane is approximately 90°.²⁴ The experiment was conducted in the cold neutron channel of the CARR reactor with an irradiation flux of approximately 10⁹ cm⁻² s⁻¹. The structure of the device is shown in Fig. 2.

Fig. 2 Schematic view inside the vacuum system of the NDP instrument.

Samples prepared

In the experiment, the thin film materials measured were Cu and Si₃N₄. Two Cu thin films were prepared by first depositing a 10 nm thick LiF layer on a SiO₂ substrate using evaporation coating. Subsequently, Cu layers with thicknesses of 30 nm and 50 nm were deposited on top of the LiF layer, followed by another 10 nm LiF layer on the surface of the Cu film, forming a Cu/LiF/Cu sandwich structure. The Li content in the layers is composed of natural Li. The thickness of the Cu films was calculated by measuring the different energy losses of ³H and ⁴He particles generated from the reactions between Li in the two LiF layers and neutrons.

Furthermore, this measurement method was extended to more comprehensive thin film thickness measurements. Si₃N₄ thin films, known for their high hardness, high elastic modulus, excellent thermal stability, and superior electrical insulation, are indispensable in the fields of microelectronics, semiconductors, and optoelectronics.^25–27

Firstly, a set of Si₃N₄ thin films were uniformly deposited on the surface of Boro-phospho-silicate Glass to provide protection. Secondly, a single-layer Si₃N₄ thin film sample (Silson Ltd., Insight Park, Welsh Road East, Southam Warwickshire, CV 47 1NE, England) was measured. This sample had dimensions of 10 mm × 10 mm and a thickness of approximately one micron. In the experiment, the single-layer Si₃N₄ film was placed before the B₄C material so that the neutrons can pass through the Si₃N₄ film and react with ¹⁰B in B₄C. The energy of the emitted particles was measured after they passed through the film, utilizing the nuclear reaction between ¹⁰B and neutrons. Details of the thin film samples can be found in the SI.

Results

The experimental energy spectra of Cu thin film samples of different thicknesses are shown in Fig. 2. For thinner films (30 nm and 50 nm), the ³H particles (2727 keV) generated by the nuclear reaction do not lose sufficient energy after passing through the sample to be useful for analysis. Therefore, we selected ⁴He particles (2055 keV) for the calculations. The specific method for particle selection will be discussed later in the article.

For the 30 nm Cu film, the energies of the ⁴He particles before and after passing through the film were 2055.51 keV and 2038.19 keV, respectively. This means that the ⁴He particles lost 17.32 keV of energy while passing through the film. Through calculations (see Thickness calibration), the thickness of the Cu film was determined to be 28 nm.

For the 50 nm thick Cu film, the energies of the ⁴He particles before and after passing through the film were 2055.15 keV and 2027.11 keV, respectively. The ⁴He particles lost 28.04 keV of energy while passing through the film, resulting in a calculated thickness of 48 nm for this film sample (Fig. 3(a)).

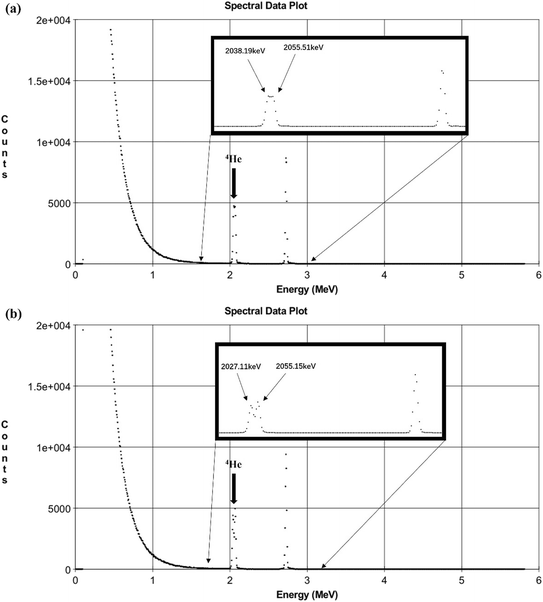Fig. 3 (a) NDP measurement of the LiF(10 nm)/Cu(30 nm)/LiF(10 nm) energy spectrum and (b) NDP measurement of the LiF(10 nm)/Cu(50 nm)/LiF(10 nm) energy spectrum.

These experiments were conducted under the current CARR-NDP experimental conditions. The calculated results show a small deviation from the reference thicknesses, indicating that this method is still capable of accurately measuring the thickness of thin films in the tens-of-nanometers range.

For the first set of Si₃N₄ thin film samples (Si₃N₄ films covering the surface of boro-phospho-silicate glass), we obtained the experimental results as shown in Fig. 4. After ¹⁰B reacted with neutrons, ⁷Li and ⁴He particles were produced. To obtain the energy information of ⁷Li particles, background subtraction is necessary. Hence, ⁴He particles were used in the calculations, which have relatively clean background conditions. In the boro-phospho-silicate glass, B is doped to a certain depth, resulting in a continuous flat energy peak in the spectrum. For measuring the thickness of the Si₃N₄ thin film on the surface, we only need to consider the nuclear reactions of surface ¹⁰B with neutrons. By differentiating, we can obtain the energy of the emitted ⁴He particles from the surface layer.²⁸

Fig. 4 (a) NDP measurement of the boro-phospho-silicate glass#1 energy spectrum of surface-covered Si₃N₄ films. (b) NDP measurement of the boro-phospho-silicate glass#2 energy spectrum of surface-covered Si₃N₄ films.

The initial energy of the ⁴He particles produced from the ¹⁰B-neutron reaction is 1472 keV. In sample #1, the remaining energy of the particles was 1464.12 keV, resulting in a calculated Si₃N₄ film thickness of 23 nm. In sample #2, the remaining energy of the particles was 1465.45 keV, giving a calculated thickness of 21 nm for the Si₃N₄ film. These calculated results align with the expected values from the sample sources, demonstrating the ability to measure the thickness of individual layers in multilayer thin films.

For the second set of single-layer Si₃N₄ thin films, the films were placed over the surface of the B₄C material. The thickness was calculated using the energy information of the ⁴He particles produced from the ¹⁰B-neutron reactions. Under these experimental conditions, the single-layer Si₃N₄ thin film remained undamaged, making this method suitable for the non-destructive measurement of precious thin films. The experimental energy spectrum is shown in Fig. 5.

Fig. 5 Experimental measurement results of the single-layer Si₃N₄ film.

After passing through the Si₃N₄ thin film, the energy of the ⁴He particles attenuated to 1063.71 keV. Given that the initial energy of the produced ⁴He particles was 1472 keV, they lost 408.29 keV of energy after traversing the single-layer Si₃N₄ film. This energy loss corresponds to a calculated thickness of 936 nm for the single-layer Si₃N₄ film.

Discussion

The NDP experiment measured the thickness of five thin film samples, including Cu and Si₃N₄ materials. For the Cu thin film samples, there were two different thicknesses (50 nm and 30 nm), with measured results of 48 nm and 28 nm, respectively. The largest measurement deviation was observed in the 30 nm thick film, reaching 6.7%. This deviation is closely related to the peak overlap in the spectra, which introduced significant errors during peak analysis and fitting, leading to larger measurement discrepancies. For thinner films, selecting ¹⁰B as the neutron-reactive nuclide and using the α particles it produces with an energy of 1472 keV for thickness calculations can reduce such measurement deviations.

Relevant information on data processing is provided in the SI. Potential uncertainty in NDP measurements include small-angle scattering of charged particles, energy straggling of charged particles, detector geometry acceptance angles, and electronic devices (electronic noise, dead time, etc.). Since this study does not require consideration of the total peak area statistical count, related statistical errors are negligible. Therefore, only two main points need to be considered: 1. Errors arising during data fitting. However, in the experimental fitting process, all fitting models achieved R² values above 0.99, ensuring high accuracy; 2. Errors during SRIM calculations. The uncertainty in calculating the stopping power of materials using SRIM is less than 2%.

The choice of nuclide for neutron reactions is crucial for accurately measuring thickness. In the Cu thin film experiments, ³H particles, which have a higher initial energy (2727 keV) and lower mass, lose less energy in Cu thin films compared to ⁴He particles, according to the Bethe–Bloch formula. Since the measured Cu thin films are at the nanometer scale, the 2727 keV ³H particles do not lose significant energy in the film. Given the energy resolution of the detection system, ³H particles, which experience smaller energy losses, are prone to peak overlap. Analyzing these overlapped peaks involves complex fitting. Theoretically, particles directly captured by the detector without passing through the thin film sample do not experience significant energy straggling. Thus, in this experiment, the broadening of energy peaks is influenced by two factors: 1. Energy loss of emitted particles traveling through a high vacuum environment to the detector; 2. The inherent energy resolution of the detection system.

Therefore, the energy peak of particles emitted from the film's surface (without passing through the film) should be “narrow and tall,” while the peak for particles passing through the entire film sample should be broader with lower counts per channel. Based on these conclusions, the overlapped peak can be separated into two peaks—one before and one after passing through the film. The difference in peak energy values can then be used to calculate the film sample's thickness.

Although this fitting process can accurately describe the energy information of emitted particles, it still introduces some fitting uncertainty. Therefore, appropriate nuclides should be selected based on the film's thickness and material to produce emitted particles with suitable energies after nuclear reactions.

Nuclides with high neutron reaction cross-sections include ³He, ⁶Li, ⁷Be, ¹⁰B, ¹⁴N, ¹⁷O, ²²Na, ³³S, ³⁵Cl, and ⁴⁰K. Some of these nuclides present issues such as radioactivity and low natural abundance. Thus, we selected materials containing specific nuclides, such as those containing ⁶Li and ¹⁰B. For these two nuclides, information on their energy losses in Cu and graphene films of different thicknesses was provided to guide the selection of appropriate materials in practical measurements. The nuclear reactions for these two nuclides with neutrons are as follows:

⁶Li + n → ³H(2727 keV) + ⁴He(2055 keV)

¹⁰B + n → ⁴He(1472 keV) + ⁷Li(840 keV)[93.7%]

¹⁰B + n → ⁴He(1777 keV) + ⁷Li(1013 keV)[6.3%]

Among the generated particles, the following specific particles were selected to complete the thickness measurement of most thin materials: ³H (2727 keV), ⁴He (2055 keV), ⁴He (1472 keV), and ⁷Li (840 keV). Tables 1 and 2 present the calculated results of these four energetic charged particles in Cu and graphene.

Table 1 Residual energy of some charged particles after passing through Cu films of different thicknesses

keV	5 nm	10 nm	50 nm	100 nm	200 nm	500 nm	1000 nm
^3H (2727 keV)	2726.4	2725.9	2721.4	2715.8	2704.6	2670.9	2614.6
^4He (2055 keV)	2052.1	2049.4	2026.9	1999.1	1942.7	1771.2	1475.4
^4He (1472 keV)	1468.9	1465.9	1441.7	1411.4	1350.5	1165.2	850.9
^7Li (840 keV)	835.6	831.3	796.9	754.6	672.6	447.1	150.9

---

Table 2 Residual energy of some charged particles after passing through graphene films of different thicknesses

keV	5 nm	10 nm	50 nm	100 nm	200 nm	500 nm	1000 nm
^3H (2727 keV)	2726.7	2726.4	2724.3	2721.5	2716.1	2699.6	2672.2
^4He (2055 keV)	2053.4	2051.9	2039.4	2023.7	1992.4	1897.0	1732.9
^4He (1472 keV)	1470.2	1468.4	1453.9	1435.8	1399.3	1288.2	1095.5
^7Li (840 keV)	836.2	832.6	803.4	767.3	696.8	502.7	248.4

---

From the tables, it is evident that regardless of whether it is the Cu film, which has a high stopping power, or the graphene film, which has a relatively low stopping power, the ³H particle with an initial energy of 2727 keV exhibits strong penetration capabilities. Significant energy loss occurs only when it traverses films with thicknesses on the order of hundreds of nanometers. Conversely, for films with thicknesses in the micrometer range, some particles lose almost all their energy, or their remaining energy falls within the low-energy background range of the spectrum, making it difficult to clearly separate the energy peaks. Therefore, for such thicker films, ³H (2727 keV) particles are more suitable for relevant calculations.

The ⁷Li (840 keV) particle, which has the lowest energy, shows significant energy loss in films with thicknesses ranging from a few nanometers to several tens of nanometers. Theoretically, such particles lose more energy over the same distance in the target material. This is reflected in the spectrum as a larger change in channel number after traveling the same distance. Therefore, using ⁷Li (840 keV) particles for thickness measurement provides better resolution (this measurement method's resolution can be expressed as nm keV⁻¹ or nm per channel, where channel refers to the number of channels). Thus, such high-mass, low-initial-energy particles are suitable for high-resolution measurements of thinner films.

For ⁴He particles with two initial energies, there is measurable energy loss across various thickness ranges (≥10 nm) in both materials, which can be used to calculate the film's thickness. Even after significant energy loss, these particles retain some residual energy. For example, a ⁴He particle with 2055 keV still has over 1000 keV of energy after traversing films with thicknesses in the hundreds of nanometers to micrometer range. Under these conditions, the energy peaks are not interfered with by the low-energy background, making it easier to separate the peaks clearly and calculate the thickness, thereby reducing calculation errors during data processing.

The energy loss of particles should neither be too large nor too small. On one hand, if the particles lose most of their energy, the remaining energy reaching the detector will be very low, causing the energy peak to fall into the low-energy background range and increasing the errors during background subtraction and peak fitting. On the other hand, minimal energy loss may result in peak overlap (as seen in the experiment with 2727 keV ³H particles traversing a 30 nm Cu film), which also affects the results. Considering the energy resolution of the detection system, the energy loss of charged particles is typically controlled within a range of a few hundred keV.

Experimental methods

NDP measurement. NDP spectra were acquired using a “cold” neutron depth profiling facility at the CARR. In the experiments, a Φ10 mm neutron beam was employed, so the measured film thickness represents an area-averaged value. The roughness of the film contributes to the broadening of the energy. On the other hand, the degree of broadening can also be used to evaluate the roughness of the film. The working principle is based on the nuclear reaction between ⁶Li (natural lithium Li with a relative abundance of 7.5 at%) and a neutron according to eqn (1):

⁶Li + n → ⁴He(2055.55 keV) + ³H(2727.92 keV) (1)

The ³H and ⁴He particles generated in the sample are emitted with a specific energy, 2727.92 and 2055.55 keV, respectively. During this process, the particles lose some energy due to their interaction with the sample, but because the experimental chamber has a high vacuum, the energy loss of the particles is negligible, except for the energy lost during their interaction with the sample. Therefore, the thickness of the thin film sample can be determined by analyzing the disparity in energy deposition of emitted particles within the detector, which occurs as a result of the LiF films situated on both sides of the sample.

Thickness calibration. In this study, we used TRIM for relevant calculations, simulating the residual energy of particles generated by nuclear reactions as they traverse film samples of varying thicknesses. The data were fitted using the three-parameter Weibull function, which is defined as follows:

The fitting parameters can be found in the SI. The relationship between the residual energy of the particles and the thickness of the film samples was fitted using a quadratic function. The fitting results are as follows.

The relationship between the residual energy (E) of He particles and the thickness (X) of Cu films is described using the following equation:

X = 3321.8 − 1.444E − 8.52 × 10⁻⁵E²

The relationship between the residual energy (E) of He particles and the thickness (X) of Si₃N₄ films is described using the following equation:

X = 3239.53 − 2.233E + 2.27 × 10⁻⁵E²

Conclusion

Experimental success in measuring film thickness using a neutron capture reaction and application of the method to the semiconductor field was demonstrated. The novel method has been demonstrated to allow non-destructive measurement of film thicknesses ranging from the nanoscale to the microscale. Additionally, a method to optimize the experiment and improve the accuracy of the results was proposed.

However, several aspects of the method still require further improvement. Firstly, in data analysis, the presence of overlapping peaks in the energy spectra can complicate the determination of peak values, potentially increasing errors. Therefore, accurately resolving overlapping peaks is crucial. This issue can be mitigated by altering experimental conditions, such as changing the reacting nuclide. Secondly, this paper only provides basic calculations and theoretical explanations for nuclide selection. In the future, these should be integrated into a user-friendly computational program to simplify the calculation process.

Author contributions

Liang Zhao: article planning, article writer, and experimental measurement; Caijin Xiao: provided the overall idea of the article, provided relevant arguments, reviewed the article, and experimental measurement; Yonggang Yao: reviewed and revised the article and experimental measurement; Xiangchun Jin: reviewed and revised the article. Xiaoyu Xu, Wei Wang, Yu Zhang, Guojian Guo, and Wenxu Zhong reviewed and revised the article.

Conflicts of interest

The authors declare no competing financial interest.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the SI includes sample information and all results of SRIM fitting. See DOI: https://doi.org/10.1039/d5lf00213c.

Acknowledgements

This work was supported by the Continuous-Support Basic Scientific Research Project (BJ22003001).

References

1. Z.-H. Sheng, L. Shao, J.-J. Chen, W.-J. Bao, F.-B. Wang and X.-H. Xia, Catalyst-Free Synthesis of Nitrogen-Doped Graphene via Thermal Annealing Graphite Oxide with Melamine and Its Excellent Electrocatalysis, ACS Nano, 2011, 5(6), 4350–4358.
2. L. Zhou, J. Mao, Y. Ren, S.-T. Han, V. A. L. Roy and Y. Zhou, Recent Advances of Flexible Data Storage Devices Based on Organic Nanoscaled Materials, Small, 2018, 14(10), 1703126.
3. M. D. Scanlon, E. Smirnov, T. J. Stockmann and P. Peljo, Gold Nanofilms at Liquid-Liquid Interfaces: An Emerging Platform for Redox Electrocatalysis, Nanoplasmonic Sensors, and Electrovariable Optics, Chem. Rev., 2018, 118(7), 3722–3751.
4. L. Hu, M. Chen, W. Shan, T. Zhan, M. Liao, X. Fang, X. Hu and L. Wu, Stacking-Order-Dependent Optoelectronic Properties of Bilayer Nanofilm Photodetectors Made from Hollow ZnS and ZnO Microspheres, Adv. Mater., 2012, 24(43), 5872–5877.
5. J. S. Kang, J.-Y. Kim, J. Yoon, J. Kim, J. Yang, D. Y. Chung, M.-C. Kim, H. Jeong, Y. J. Son, B. G. Kim, J. Jeong, T. Hyeon, M. Choi, M. J. Ko and Y.-E. Sung, Room-Temperature Vapor Deposition of Cobalt Nitride Nanofilms for Mesoscopic and Perovskite Solar Cells, Adv. Energy Mater., 2018, 8(13), 1703114.
6. T. N. Borodina, D. O. Grigoriev, D. V. Andreeva, H. Möhwald and D. G. Shchukin, Polyelectrolyte Multilayered Nanofilms as a Novel Approach for the Protection of Hydrogen Storage Materials, ACS Appl. Mater. Interfaces, 2009, 1(5), 996–1001.
7. T.-C. Chou, C.-H. Huang, R.-A. Doong and C.-C. Hu, Architectural Design of Hierarchically Ordered Porous Carbons for High-Rate Electrochemical Capacitors, J. Mater. Chem. A, 2013, 1(8), 2886–2895.
8. J. Feng, X. Sun, C. Wu, L. Peng, C. Lin, S. Hu, J. Yang and Y. Xie, Metallic Few-Layered VS2 Ultrathin Nanosheets: High Two Dimensional Conductivity for in-Plane Supercapacitors, J. Am. Chem. Soc., 2011, 133(44), 17832–17838.
9. C. Jeynes and J. L. Colaux, Thin film depth profiling by ion beam analysis, Analyst, 2016, 141(21), 5944–5985.
10. G. Dollinger, M. Boulouednine and T. Faestermann, et al., Depth microscopy for thin film analysis, Nucl. Instrum. Methods Phys. Res., Sect. A, 1993, 334(1), 187–190.
11. L. Bu, S. Gao and W. Wang, et al., Film-Depth-Dependent Light Absorption and Charge Transport for Polymer Electronics: A Case Study on Semiconductor/Insulator Blends by Plasma Etching, Adv. Electron. Mater., 2016, 2(12), 1600359.
12. C. Tian, C. Maheu and X. Huang, et al., Evaluating the electronic structure and stability of epitaxially grown Sr-doped LaFeO 3 perovskite alkaline O 2 evolution model electrocatalysts, RSC Appl. Interfaces, 2025, 2(1), 122–129.
13. Z. Alinia, D. Miao and T. Baumgartner, et al., Self-assembly of phosphole-lipids in 2D films: the influence of π-interactions and steric constraints, RSC Appl. Interfaces, 2025, 2(2), 460–471.
14. L. Johnston, J. Obenlüneschloß and M. F. K. Niazi, et al., Assessing the potential of non-pyrophoric Zn (DMP) 2 for the fast deposition of ZnO functional coatings by spatial atomic layer deposition, RSC Appl. Interfaces, 2024, 1(6), 1371–1381.
15. L. Zhao, C. Xiao and Y. Yao, et al., Measurement of Nanoscale Film Thickness Using Neutron Depth Profiling Technique, ACS Appl. Mater. Interfaces, 2023, 15(29), 35639–35647.
16. J. F. Ziegler, G. W. Cole and J. E. E. Baglin, Technique for determining concentration profiles of boron impurities in substrates, J. Appl. Phys., 1972, 43(9), 3809–3815,  DOI:10.1063/1.1661816.
17. G. P. Lamaze, H. Chen-Mayer and J. K. Langland, et al., Neutron depth profiling with the new NIST cold neutron source, Surf. Interface Anal., 1997, 25(3), 217–220,  DOI:10.1002/(SICI)1096-9918(199703)25:3<217::AID-SIA226>3.0.CO;2-3.
18. S. Lv, T. Verhallen and A. Vasileiadis, et al., Operando monitoring the lithium spatial distribution of lithium metal anodes, Nat. Commun., 2018, 9(1), 2152.
19. G. P. Lamaze, H. H. Chen-Mayer and A. Gerouki, et al., Analysis of lithium transport in electrochromic multilayer films by neutron depth profiling, Surf. Interface Anal., 2000, 29(9), 637–641,  DOI:10.1002/1096-9918(200009)29:9<637::AID-SIA909>3.0.CO;2-2.
20. J. F. M. Oudenhoven, F. Labohm and M. Mulder, et al., In situ neutron depth profiling: a powerful method to probe lithium transport in micro-batteries, Adv. Mater., 2011, 23(35), 4103–4106,  DOI:10.1002/adma.201101819.
21. D. Fink, J. P. Biersack and H. Liebl, Ion implantation: equipment and techniques, Spring, Berlin, 1983, p. 318, ISBN: 978-3-642-68779-2.
22. T. Chanjuan, X. Caijin and Y. Yonggang, et al., Neutron depth profiling system at CARR, Appl. Radiat. Isot., 2019, 148, 102–107,  DOI:10.1016/j.apradiso.2019.02.003.
23. C. Shi, C. Xiao and Y. Yao, et al., Inverse iteration algorithm for neutron depth profiling, J. Radioanal. Nucl. Chem., 2018, 317(1), 81–85,  DOI:10.1007/s10967-018-5786-4.
24. L. Zhao, C. J. Xiao and Y. G. Yao, et al., Current status and development trends of neutron depth profiling, Nucl. Tech., 2023, 46(7), 070001.
25. R. Grün, The crystal structure of β-Si3N4: structural and stability considerations between α-and β-Si3N4, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35(4), 800–804.
26. M. H. Bocanegra-Bernal and B. Matovic, Dense and near-net-shape fabrication of Si3N4 ceramics, Mater. Sci. Eng., A, 2009, 500(1–2), 130–149.
27. A. Saleem, R. Iqbal and A. Hussain, et al., Recent advances and perspectives in carbon-based fillers reinforced Si3N4 composite for high power electronic devices, Ceram. Int., 2022, 48(10), 13401–13419.
28. T. Z. Hossain and P. M. Zeitzoff, Determination of boron by the neutron depth profile (NDP) technique for VLSI processing application, J. Radioanal. Nucl. Chem., 1987, 113, 379–382.

---