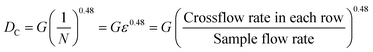Tunable single-column deterministic lateral displacement device by adjustable crossflow

Abstract

Conventional deterministic lateral displacement (DLD) devices are popular for continuous size-based separation of micro-particles at a high resolution through a tilted array of periodically placed micro-posts. However, the conventional DLD devices lack tunability of the critical size of particle sorting (D_C). In a conventional DLD device, the D_C is fixed by the device geometry. Further, many rows and columns of micro-posts are required in the device array to provide adequate spatial separation between large and small particles after lateral bumping of large particles, which leads to large device area and potentially small throughput/area. In this work, we present a novel tunable single-column DLD device where tunability was demonstrated by adjusting crossflow applied perpendicularly to the main flow direction. Our device consists of only 8 bumping obstacles with a device area of 0.83 mm × 0.24 mm = 0.2 mm² (without inlet/outlet ports). The ability to tune the critical size D_C from below 5 μm to above 10 μm in a single structure is demonstrated with a separation efficiency of ∼99.9% and the throughput/area is 45 μL min⁻¹ mm⁻². Further, at very high flow rates (Re > 10), the resolution degrades due to a three-dimensional fluid flow pattern.

---

1. Introduction

Particle sorting plays a crucial role in various applications,¹ such as – chemical² and biological³ processing, clinical diagnostics,^4,5 environmental analysis,⁶ quality control and regulation enforcement in manufacturing cosmetic products.⁷ Deterministic lateral displacement (DLD) is a well-known size-based particle sorting technology for its simple operation, robustness, deterministic physics, and high resolution,⁸ first reported by Huang et al. in 2004.⁹ DLD technique has shown the ability to separate particles in a wide range of sizes spreading from nanometers¹⁰ to micrometers.¹¹ In medical applications, it has also been vastly used to separate biological cells, such as blood cells,^12–15 circulating tumor cells (CTCs),^16–21 DNA^9,22 and exosomes.¹⁰ In the DLD method, particle separation happens due to the flow bifurcation^9,12 around a set of obstacles (“posts”). Migration of particles follows either the average fluid flow direction or the axis direction of the posts, determined by the “critical size (D_C)” of the device. The particles larger than the critical size “bump” at the posts and follow the micro-array inclination (lateral displacement), whereas smaller particles follow the macroscale fluid flow direction (zigzag mode). The critical diameter of particle sorting (D_C) is determined by the array geometry, specifically the gap size between two posts and the tilt angle (ε)²³ of the micro-array. Hence the critical size cannot be changed.

Further, to increase throughput of conventional DLD devices, the number of columns in the DLD array is increased, but at the same time, the number of rows also needs to be increased since each column requires 1/ε rows. Hence, the area of a DLD device increases as the square of the throughput, thus decreasing the throughput per area. To increase throughput per area, Liang et al. (2020) introduced a “single-column” DLD device²⁴ where the array of posts is replaced by a single vertical channel with a series of protrusions on one side. A crossflow right after protrusion, set by a series of carefully designed fluidic resistors, sets the critical size, above which large particles were harvested at the end of the vertical channel.

Both the conventional and single-column DLD devices have a critical size for particle harvesting which is set by the fabrication. There have been several attempts to make the critical diameter (D_C) of conventional DLD devices tunable. One of the very early demonstrations of tunability in DLD device was achieved by stretching a PDMS device.²⁵ However, its elastomeric flexibility makes a PDMS device suffer in high-pressure applications.²⁶ In several studies, dielectrophoresis (DEP) has been coupled with DLD to achieve wide ranges of critical size tuning.^27–30 However, complex theoretical analysis, complicated fabrication and implementation, high voltage, heating, etc. make this hybrid technique difficult to use in practice. Numerical and experimental studies used non-Newtonian viscoelastic fluids as buffer solution for tuning the D_C.^31,32 In one study, acoustic vibrations were passed to PDMS micropillars to switch the trajectory of 2 and 7 μm particles.³³ In moderate Reynolds number regime, Dincau et al. (2018) observed streamline evolution and micro vortices³⁴ in the wake of micro-posts, which shifted the particles trajectory. They were able to switch 10 and 20 μm particles from zigzag mode to displacement mode by increasing Reynolds number by a factor of 6 and 7, respectively.³⁴ Tottori and Nisisako demonstrated tuning of D_C by exploiting temperature-controlled swelling and shrinking of hydrogel pillars. However, the characterization of hydrogel pillars and the temperature control need to be very precise to achieve error-free tuning of D_C.³⁵

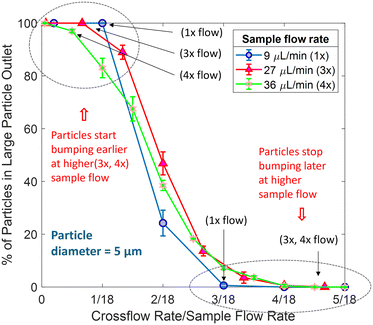
In this paper, we demonstrate the first ability to tune the critical diameter D_C of a single-column deterministic lateral displacement device. Particles with diameter below D_C remain in a vertical streamtube of fluid as it moves down through a device, and particles with diameter above D_C are “bumped” by an asymmetric obstacle into an adjacent streamtube so that they leave the initial streamtube of fluid. Tunability is achieved by applying an externally adjustable crossflow set by syringe pumps, applied individually to each row of bumping obstacles. Fig. 1 presents a schematic diagram of a single-column DLD device with four bumping obstacles tuned by different crossflows (left side I₂ = right side I₃) while keeping the vertical sample flow I₁ fixed. When I₂ = I₃, the right cross-channels withdraw the same volume of fluid introduced in the left cross-channels. Hence, both the fluid segmentation and thus the critical size D_C are identical at each bump. Here, D_C is double the width of the first streamtube adjacent to the bumping obstacle at the protruding bumping site and it can be tuned by changing the crossflow rate. When crossflow rate (I₂ = I₃) is increased for a certain sample flow rate (I₁), D_C also increases, because a larger volume of fluid is drawn out from the central channel through the right-sided cross channels. At the same time, a larger volume of fresh buffer is introduced into the central channel through the left cross channels to keep the amount of fluid same there and to replace sample fluid with fresh buffer. In a conventional DLD with triangular posts, the critical diameter, D_C can be determined by the well-known experimental fit as follows^36–38

where, G is the gap size between adjacent posts and N is the row periodicity . G and N are both fixed by the device geometry. In our tunable single column DLD device, the ratio of the flow rates is the equivalent of ε and hence 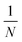. Thus, the expected critical size is
Since we can control the ratio of flowrates by adjusting crossflow, we are not limited by the device geometry (meaning arrangement of obstacles), and our device is tunable with fewer bumps arranged in a single-column channel, enabling high throughput per area.

Fig. 1 Schematic diagram of a tunable single-column DLD device with four bumping obstacles. Sample with particles enters vertically with a flowrate of I₁. The cross channels on the left side introduce fresh buffer each at a flowrate of I₂, and the cross channels on the right side withdraw fluid from the main channel at a flowrate of I₃, where I₂ = I₃. The streamlines at the bumping sites which bifurcate the flow between the main channel and the right-sided cross channels are called segmentation streamlines. At the bumping site, a particle (blue) smaller than D_C will not bump and will go to the small particle outlet. Whereas a particle (red) larger than D_C will bump and be pushed towards the next streamline and continue to travel through the main channel.

In this study, we perform two sets of experiments in the moderate Reynolds number regime (5 < Re < 30). The Reynolds number (Re), in a DLD array is defined as³⁹

where, ρ is the density of water at room temperature, u is the average velocity of the fluid in the gap, L₀ is the characteristic length of the gap (in our case, hydraulic diameter of a rectangular channel), and η is the dynamic viscosity of water. In the first set of experiments, we separate 5, 8.2 and 10 μm particles from each other with ∼100% efficiency at a throughput of 45 μL min⁻¹ mm⁻². In the second set of experiments, we explore the effect of increasing Re on the tuning performance of our single-column DLD device and propose a mechanism for its degradation.

2. Materials and methods

2.1 Device design

The design of a single-column DLD device follows the design of conventional multi-column DLD arrays: (i) in a conventional DLD array, from one row to the next, the carrier fluid in each gap divides in the next gap, with most staying in the current column and some fraction going to the next column, because of the “tilt” of the array axis vs. the average fluid flow direction.⁹ This fraction is set by the number of rows before fluid at one position in a gap is in the same position at the next adjacent gap – the inverse of the so called “tilt angle”, ε. (ii) In a “single column” DLD device, the “effective tilt” (bifurcation of the vertical flow) is set by the amount of fluid injected into the main vertical column from a side channel. Similarly, the same amount of fluid also flows out the opposite side. This is described in detail in the first (non-tunable) single column DLD²⁴ published by Liang et al. (2020). In that paper, this fraction was set by fluidic resistors (determined by the device fabrication). In this paper, the dimensions of cross channels and the protrusion length of bumping obstacles are based on prior work on single-column DLD.²⁴ However, the hydraulic resistance of cross channels does not matter since the horizontal flow component is determined by flowrate-controlled syringe pumps, making the critical size tunable. The channel height is chosen to have a moderate aspect ratio (height/width on the order of 1) for ease of microfabrication.

Our tunable single-column DLD device consists of 8 bumping obstacles. The width of the central bumping column is 38 μm, and the narrowed gap region at each of the bumping sites is 18 μm wide. The protrusion width of each triangular bumping obstacle (parameter “b” in Fig. 2) is 20 μm. The width of the cross channels on both sides on the central column is 16 μm. The device is 826 μm long, 238 μm wide, and 28 μm high (not including the inlet/outlet ports).

Fig. 2 The 8-bump design of the tunable single-column DLD device used in our experiments.

It is fundamental to the operation of a DLD array that the critical diameter depends on the shape and arrangement of the posts (bumping obstacles).^36,37 The triangular shape of posts instead of circular posts allow larger gaps for the same critical size, hence reducing clogging and enabling higher throughput for a given pressure gradient.⁴⁰ Thus, for our single-column devices, we have used triangular posts.

2.2 Device fabrication and experimental setup

We fabricated our device on 500 μm thick silicon wafer using standard microfabrication technique. A SAMCO RIE800iPB reactive-ion etcher was used to etch the channels to a depth of 28 μm and the angle between the vertical wall and the channel floor was approximately 90°. The inlets and outlets were 300 μm through-holes obtained by etching through the silicon wafer from the backside. After performing standard chemical cleaning of silicon wafer, we sealed the device with a polyolefin sealing tape (9795RR, 3M, USA). The device was mounted to an acrylic manifold with stainless steel microtubes.

An inverted microscope was used for imaging the particle movement. Images and videos were captured with 10× Nikon Plan Fluor objective (0.30 NA and 16 mm WD) and ORCA-Flash4.0 digital camera C11440 from Hamamatsu Photonics. We have used three flowrate-controlled syringe pumps (Chemyx Fusion 200) which can be used in either ‘infusion’ or ‘withdraw’ mode. At the sample inlet, we used one syringe pump in ‘infusion’ mode. For the eight fresh buffer inlets, we have mounted a 10-syringe expansion rack on a Fusion 200 syringe pump and operated it in ‘infusion’ mode. At the small particle outlets, we used another syringe pump with a 10-syringe expansion rack in the ‘withdraw’ mode.

2.3 Preparation of experimental samples

Device functionality for various flowrates was confirmed by observing the trajectories of three sizes of fluorescent particles, which are Thermo Scientific™ Fluoro-Max Dye Green Aqueous Fluorescent Polymer Microsphere, 5 and 10 μm (10 mL), and, DiagPoly™ Green Fluorescent Polystyrene Particles, 8.2 μm (1 mL). We have diluted these particles in 0.1% Tween 20 surfactant in DI water to achieve a concentration of 700 to 1000 particles per microliter of sample.

3. Results and discussion

3.1 Experiments

3.1.1 Tuning of the critical size. In our first experiment, we ran samples containing 5, 8.2 and 10 μm particles through the sample inlet of our device at a fixed sample (vertical) flow rate of 9 μL min⁻¹ in each channel which gives a channel Reynolds number of 7.4 at the narrowed bumping region. When we varied the crossflow rates from 0 to 4.5 μL min⁻¹, all the 5 μm particles stop bumping at the crossflow rate of 1.5 μL min⁻¹ and go to small particle outlets. However, the 8.2 and 10 μm particles still bump at the obstacles and reach the large particle outlet (Fig. 3a). Since, there are 8 rows of cross channels in our device, a crossflow rate of 1.5 μL min⁻¹ at each cross channel fully replaces the sample fluid by the 6th row (6 × 1.5 μL min⁻¹ = 9 μL min⁻¹). Hence, at crossflow rate of 1.5 μL min⁻¹, we have large particles in the fresh buffer at the large particle outlet. As we increase the crossflow rate to 2.5 μL min⁻¹, all the 8.2 μm particles go to small particle outlet along with 5 μm particles. However, the 10 μm particles still end up in the large particle outlet (Fig. 3b).

Fig. 3 At sample flow rate of 9 μL min⁻¹, fluorescent images showing separation between a) 5 μm and 8.2 μm particles at crossflow rate of 1.5 μL min⁻¹; b) 8.2 μm and 10 μm particles at crossflow rate of 2.5 μL min⁻¹. The channel Reynolds number is 7.4. As we increase the crossflow, larger volume of fluid leaves the central column through the small particle outlets on the right-side. The streamtubes entering the small particle outlets get wider at higher cross flow. The critical diameter, D_C also increases. As a result, smaller particles stop bumping and end up in small particle outlets. The higher we increase the crossflow, the sooner the smaller particles go to small particle outlet. The dotted structures show the approximate position of the channels.

Finally, when we increase the crossflow rate to 3.5 μL min⁻¹, ∼99% of the 10 μm particles stop bumping and end up in small particle outlets as well. Fig. 4 represents the recovery curves of 5, 8.2 and 10 μm particles at sample flow rate of 9 μL min⁻¹. The x-axis is presented as the ratio of crossflow rate to sample flow rate.

Fig. 4 Experimental results showing the fraction of 5, 8.2 and 10 μm particles in the large particle outlet at various for sample flow rate of 9 μL min⁻¹. The vertical bars indicate variation in the percentage of particle concentration in the large particle outlet during the transition in the traveling modes of particles.

In this work, the channel area (without inlet/outlet ports) is: 0.83 mm × 0.24 mm = 0.2 mm². Hence, a sample flow rate of 9 μL min⁻¹ gives a throughput per area of 45 μL min⁻¹ mm⁻².

3.1.2 High flow rate effects. To understand the separation performance of our device at higher flow rates, next we performed a series of experiments with 5 μm particles at various sample flow rates and hence various moderate Reynolds numbers (5 < Re < 30), and we vary the crossflow rates in each case to see bumping behaviour of 5 μm particles (Fig. 5). As we increased the sample flow rates, the sharpness of the recovery curves of 5 μm particles in the large particle outlet was reduced. Particles showed a tendency to begin bumping earlier (lower crossflow) and stop bumping at a larger crossflow rate when sample flow increased. When sample flow rate is 9 μL min⁻¹, all the 5 μm particles stop bumping at crossflow rate of 1.5 μL min⁻¹. Here, . 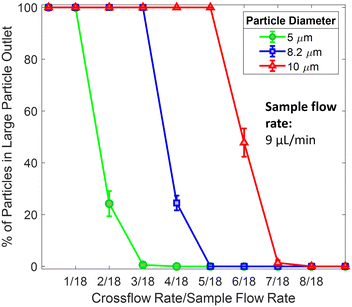But when we triple the sample flow rate (27 μL min⁻¹), the 5 μm particles do not fully stop bumping at tripled crossflow rate of 4.5 μL min⁻¹. Rather they show a ‘mixed mode’, where some particles still go to the large particle outlet, and the rest of the 5 μm particles go to small particle outlets. To stop all the 5 um particles from going to the large particle outlet, we need to increase the . As the sample flow rate increases, the sharpness of the recovery curve reduces.

Fig. 5 Experimental results showing the fraction of 5 μm particles in the large particle output for various sample and crossflow rates. The X-axis is shown as the ratio of crossflow to sample flow rates. Here, the channel Reynolds numbers are 7.4, 22 and 29.4 in the ascending order of sample flow rates. The vertical bars indicate variation in the percentage of particle concentration in the large particle outlet during the transition in the traveling modes of particles.

3.2 Three-dimensional analysis of streamlines in COMSOL

To understand this compromised resolution of recovery curves at higher sample flow rates, we performed 3-dimensional streamline analysis of our tunable single-column DLD device. We ran a grid-independency test for COMSOL with various default sizes of mesh, and the results here are obtained after we see no variation with increasing mesh fineness. We make the simplifying assumption that unless bumping against a wall, particles follow the streamlines. This is justified by the fact that for Re = 22 (or lower), fluid flow is still laminar.⁴¹

The critical diameter of particle sorting (D_C) is twice the width of the streamtube at the bumping site that leaves the main channel and enters the small particle outlet. The streamline which divides the flow at the junction of main channel and the small particle outlet is called the segmentation streamline. 3D simulations allow us visualizing the segmentation streamlines across channel height at the bumping site.⁴² In Fig. 6, we show the segmentation streamlines at the bumping site across height for sample flowrates of 9 μL min⁻¹ (Re = 7.4) and 27 μL min⁻¹ (Re = 22) while keeping the constant. The width of the corresponding streamtubes varies from the center of the channel to the channel floor and the channel ceiling at the bumping site. i.e. across the height of the device. This means that the maximum “critical size” of particles that go to the “small particle outlet” is larger near the top and bottom of the channel than in the middle.

Fig. 6 COMSOL 3D simulations of segmentation streamlines at the bumping site for two Reynolds numbers in the moderate regime. The top panels (dashed outlined) show the device top view, while the bottom panels present cross-sectional views along the flow direction at an angled perspective. Coordinate axes: x = crossflow, y = sample flow, z = channel height (28 μm). The in both cases. (a) Sample flow = 9 μL min⁻¹ (Re = 7.4), crossflow = 1.5 μL min⁻¹. (b) Sample flow = 27 μL min⁻¹ (Re = 22), crossflow = 4.5 μL min⁻¹. In the top views, Magenta streamlines are taken 1 μm above the channel floor; blue streamlines are at mid-height. With higher crossflow, the segmentation streamtube width shows greater variation between mid-height and near the floor/ceiling.

However, this variation is more pronounced at the higher Reynolds number. At sample flow of 9 μL min⁻¹ (Re = 7.4) and crossflow of 1.5 μL min⁻¹, all the segmentation streamtubes are wider than 2.5 μm (Fig. 6a). Hence the predicted bumping radius (r_C) at all heights within the device is larger than the radius of 5 μm particles. As a result, none of the 5 μm particles bump at the obstacle anymore and they simply go to the small particle outlet. However, at sample flow of 27 μL min⁻¹ (Re = 22) and crossflow of 4.5 μL min⁻¹ ( is same as previous case), the width of the segmentation streamtubes at the bumping site is narrower than 2.5 μm at mid-height of the device (Fig. 6b), wider nearer the top and bottom of the channel (device ceiling and floor). This explains why at high flow rates, some of the 5 μm particles (the ones near the middle of the channel) “bump” and go the “large particle outlet”, whereas those near the top and bottom of the channel, where the bumping radii are large, do not “bump” and go to the “small particle outlet”. The 5 μm particles travel in a “mixed” bumping mode at larger sample flow rates, as observed in Fig. 5.

In Fig. 7, we plot the width of segmentation streamtubes (predicted bumping radius) across height for various Reynolds numbers ranging from 0.001 to 29, with . We can see that, the width of streamtubes from mid-height to floor (or ceiling) of the channel is minimum and the plots of streamtubes at different depths are similar, with the streamtubes collapsing on top of each other when Re ≤ 1. Whereas, when Re > 1, the variation in the width of the segmentation streamtubes increases as we go higher Reynolds numbers. For example, at sample flow of 9 μL min⁻¹ (Re = 7.4) and , we demonstrated the separation of 5 μm particles from 8.2 μm particles (Fig. 4). However, at sample flow 1.5 μL min⁻¹ (Re = 1.2) and same cross- to sample flow rate ratio, 6.5 μm particles could potentially be separated from 8 μm particles (according to the predicted bumping radii in Fig. 7). Separation resolution could be improved by two-fold, but throughput would be compromised by six-fold.

Fig. 7 COMSOL simulations of the variance of the width of segmentation streamtubes across channel height for different sample flow rates and hence different Reynolds numbers while we keep fixed at . The interaction region of 5 μm particles are showed as grey horizontal dotted lines based on the corresponding radius of 2.5 μm.

The enhanced variation in the width of segmentation streamtubes (at high Re) across height of the channel depends on the velocity fields of fluid molecules at the bumping site and near the small particle outlet, because velocity field directions are tangent to streamlines. At high flow rates, nonlinear effects³⁹ (inertial) cause flow patterns to differ from their low velocity conditions. That is exhibited in Fig. 6 (6a. low velocity vs. 6b. high velocity). Reducing channel height while keeping the channel width constant would lead to smaller hydraulic diameter which is also the characteristic length in our calculation of Reynolds number. The ratio of volume to surface forces would be reduced to lower the inertial effects.³⁹

3.3 Discussion

This work addresses two major challenges in deterministic lateral displacement (DLD): the tunability of the critical diameter (D_C) combined with a high throughput per area.

Table 1 provides a quantitative comparison of our device against other size-based particle separation methods operating in a similar dynamic size range (sizes of red and white blood cells). Here, throughput represents the total sample flow rate. Particle size is presented in diameters. Separation efficiency has been defined as the yield or the percentage of large particles that are successfully collected in the intended outlet (large particle outlet). The device area and throughput per area are determined without including the inlet/outlet ports for our device, single-column DLD with fixed D_C (ref. 24) and hydrodynamic filtration (HDF) device.⁴³ Compared to a previous high-throughput but non-tunable DLD device,⁴⁴ our design achieves tunable D_C with more than a 2.5-fold increase in throughput per area and over a 6-fold improvement in size resolution, all with higher separation efficiency. Although tunable DLD devices based on hydrogel pillars³⁵ have shown D_C adjustability, to date they exhibit ∼2× lower size resolution and ∼2.5 orders of magnitude lower throughput per area. Our device shares some functional features with both hydrodynamic filtration (HDF) devices⁴³ and single-column non-tunable DLD device,²⁴ where particles follow streamtubes into channels when their radii are smaller than the streamtube width near a bump or wall. However, unlike those approaches, D_C in our device is not fixed by the channel geometry, and our device provides tunability to crossflow control and achieves more than 2.5× higher size resolution. Further, the “large particle outlet” of our device is not contaminated by some “small particles” which inevitably remain in the central channel at each stage, as in HDF.

Table 1 Performance comparison between different microfluidic cell sorters (particle sizes are diameters)

Technology	Fundamental principle	Small particle	Large particle	Ratio of particle sizes separated (small/large)	Separation efficiency	Throughput (μL min^−1)	Device area (mm^2)	Throughput/area (μL min^−1 mm^−2)	Tunability of DC
Clot formation-inhibited DLD^44	• Array with circular posts operating at Re ∼ 10	RBC	PC3 (17 μm)	0.29	86%	1470	85	17.3	No
Tunable conventional DLD^35	• Hydrogel micropillars	Beads (2.1 μm)	Beads (7.3 μm)	0.28	99.99%	8.3	60	0.14 (device temperature is 24 °C)	Yes. At 35 °C, 7.3 μm particles shift from displacement to zigzag mode
	• Swelling/shrinking of pillar width based on device temperature to adjust the gap between pillars
Hydrodynamic filtration^43	• Rectangular microchannel passively splitting flow into side channels	RBC (<3 μm)	Leukocytes (>8 μm)	0.38	99.99% (2 rounds of filtration)	20	0.6	33	No
	• Flow ratios set by channel geometry
Single-column DLD with fixed critical size^24	• Rectangular channel consisting of bumps on one side	Beads (4.8 μm)	Beads (9.9 μm)	0.48	99.99%	30	0.56	53.5	No
	• DC determined by a crossflow after each bump, fixed by the fluidic resistors of side channels
This work	• Single-column tunable DLD consisting of side channels and adjustable crossflow after each bump	Case 1: beads (5 μm)	Case 1: beads (8.2 μm)	0.61	99.99%	9	0.2	45	Yes
	• Critical size is set by the adjustable crossflow	Case 2: beads (8.2 μm)	Case 2: beads (10 μm)	0.82

---

We have discussed in the introduction that, the in our tunable single-column DLD device is the equivalent of the tilt angle (row shift fraction), ε, which is , where N is the row periodicity in conventional DLD devices. In Fig. 8, we plotted data comparing the critical size (D_C) vs. row shift fraction (for the same gap size, G) for a conventional DLD and the effective row shift fraction for new device in this work. While qualitative agreement is good, there is about ≤15% deviation between our experimental data for tunable single-column DLD device and the empirical fit for conventional DLDs. The discrepancy may arise from the Reynolds number effects. Our data were obtained at Re = 7.4, whereas the empirical fit^23,37,38 for conventional DLDs with triangular posts was obtained for Re < 1.

Fig. 8 Comparison of the plots of “critical diameter, D_C vs. the (effective) row shift fraction, ε” for conventional DLD devices^36,37 (empirical fit) and tunable single-column DLD device (experimental data presented in Fig. 4). The effective row shift fraction in the new device is 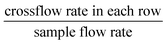, whereas for conventional DLDs, the row shift fraction, . Here, N is the row periodicity in conventional DLDs.

In this work, we have experimentally demonstrated tuning of the critical size by greater than a factor of 2. The width of the narrow “gap” in our device which gives rise to the “bumping” of large particles to adjacent streamtubes (which is the physical mechanism of the particle separation in DLD) is 18 μm. Theoretically, the maximum achievable critical size can be just below this gap size,³⁶ though we limited experiments to 10 μm (upper size limit) to avoid clogging. The lower bound of critical size tuning depends on smaller crossflow rates. However, in our single-column device, using smaller crossflow rates (for the same vertical flow) require more rows (larger N) to separate large and small particles (as in convention DLD arrays), and hence more syringe pumps. Thus, right now we are limiting our interest to devices with N < 10. A single-column DLD device with 8 rows of cross channels, an 18 μm gap and a sample flow of 9 μL min⁻¹ would require at least 1.1 μL min⁻¹ per cross-channel to fully replace the sample with buffer at the large particle outlet. Numerical simulation (not shown here) shows that this would limit the minimum achievable critical size to 4.8 μm.

Apart from limiting the maximum tunable size during experiments to minimize device clogging, the sample was prepared with anti-clogging additives (section 2.3), and was filtered through 20 μm cell strainers.¹³ Further, integrated pre-filters were added to the inlet channel design of our device to remove cell aggregates in sample.⁴⁵ In a conventional DLD array⁴⁶ with a width of 40 mm, a throughput of 70 mL h⁻¹ has been reported, which corresponds to approximately 67 μL h⁻¹ for a single-column device with a 38 μm width. In contrast, our single-column DLD device, with an inlet width of only 38 μm, achieved a sample throughput of 2 mL h⁻¹ containing roughly 1000 particles per μL, operating continuously for 7 hours without clogging. Future work is aimed at extending this concept to multiple integrated vertical channels in parallel and ultimately to a tunable deterministic lateral displacement device.

Conclusion

In summary, we have demonstrated a novel tunable single-column deterministic lateral displacement device where we performed particle separation in the 5–10 μm range with ∼99.9% efficiency by applying an adjustable crossflow. It achieves very high throughput/area due to small device dimensions. The separation performance degrades with increasing Reynolds number (increasing sample throughput) due to an increased variation in critical size across the depth of the device at the bumping site.

Author contributions

Miftahul Jannat Rasna: conceptualization (equal), data curation, formal analysis, investigation, methodology, software, validation (equal), visualization (equal), writing – original draft writing. James C. Sturm: conceptualization (equal), funding acquisition, project administration, resources, supervision, validation (equal), visualization (equal), writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

Significant images, data and modelling results have been presented in the manuscript. The importance of protruding obstacles in our device to ‘bump’ large particles is described in supplementary information (SI). Ref. 24 and 43 in this article's reference list are cited in the SI. More image data and COMSOL models can be made available to readers. Please contact the authors if required.

Supplementary information is available. See DOI: https://doi.org/10.1039/d5lc00786k.

Acknowledgements

The authors gratefully acknowledge Howard A. Stone and Nan Hu of the Department of Mechanical and Aerospace Engineering at Princeton University for helpful discussion on fluid mechanics, and the staff of the Princeton Micro/Nanofabrication and Packaging labs.

Notes and references

1. C. Alix-Panabières and K. Pantel, Challenges in circulating tumour cell research, Nat. Rev. Cancer, 2014, 14(9), 623–631.
2. D. R. Reyes, D. Iossifidis, P.-A. Auroux and A. Manz, Micro total analysis systems. 1. Introduction, theory, and technology, Anal. Chem., 2002, 74(12), 2623–2636.
3. M. Toner and D. Irimia, Blood-on-a-chip, Annu. Rev. Biomed. Eng., 2005, 7(1), 77–103.
4. M. Watanabe, H. Kenmotsu, R. Ko, K. Wakuda, A. Ono, H. Imai, T. Taira, T. Naito, H. Murakami, M. Abe, M. Endo, T. Nakajima, Y. Koh and T. Takahashi, Isolation and molecular analysis of circulating tumor cells from lung cancer patients using a microfluidic chip type cell sorter, Cancer Sci., 2018, 109(8), 2539–2548.
5. A. Farahinia, W. Zhang and I. Badea, Recent Developments in Inertial and Centrifugal Microfluidic Systems along with the Involved Forces for Cancer Cell Separation: A Review, Sensors, 2023, 23(11), 5300.
6. E. L. Tóth, E. Holczer, P. Földesy, K. Iván and P. Fürjes, Microfluidic Particle Sorting System for Environmental Pollution Monitoring Applications, Procedia Eng., 2016, 168, 1462–1465.
7. V. Sogne, F. Meier, T. Klein and C. Contado, Investigation of zinc oxide particles in cosmetic products by means of centrifugal and asymmetrical flow field-flow fractionation, J. Chromatogr. A, 2017, 1515, 196–208.
8. T. Salafi, Y. Zhang and Y. Zhang, A Review on Deterministic Lateral Displacement for Particle Separation and Detection, Nano-Micro Lett., 2019, 11(1), 77.
9. L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Continuous Particle Separation Through Deterministic Lateral Displacement, Science, 2004, 304(5673), 987–990.
10. B. H. Wunsch, J. T. Smith, S. M. Gifford, C. Wang, M. Brink, R. L. Bruce, R. H. Austin, G. Stolovitzky and Y. Astier, Nanoscale lateral displacement arrays for the separation of exosomes and colloids down to 20 nm, Nat. Nanotechnol., 2016, 11(11), 936–940.
11. S. H. Au, J. Edd, A. E. Stoddard, K. H. K. Wong, F. Fachin, S. Maheswaran, D. A. Haber, S. L. Stott, R. Kapur and M. Toner, Microfluidic Isolation of Circulating Tumor Cell Clusters by Size and Asymmetry, Sci. Rep., 2017, 7(1), 2433.
12. J. A. Davis, D. W. Inglis, K. J. Morton, D. A. Lawrence, L. R. Huang, S. Y. Chou, J. C. Sturm and R. H. Austin, Deterministic hydrodynamics: Taking blood apart, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(40), 14779–14784.
13. C. I. Civin, T. Ward, A. M. Skelley, K. Gandhi, Z. Peilun Lee, C. R. Dosier, J. L. D'Silva, Y. Chen, M. Kim, J. Moynihan, X. Chen, L. Aurich, S. Gulnik, G. C. Brittain, D. J. Recktenwald, R. H. Austin and J. C. Sturm, Automated leukocyte processing by microfluidic deterministic lateral displacement, Cytometry, Part A, 2016, 89(12), 1073–1083.
14. N. Tottori and T. Nisisako, Degas-Driven Deterministic Lateral Displacement in Poly(dimethylsiloxane) Microfluidic Devices, Anal. Chem., 2019, 91(4), 3093–3100.
15. K. K. Zeming, R. Vernekar, M. T. Chua, K. Y. Quek, G. Sutton, T. Krüger, W. S. Kuan and J. Han, Label-Free Biophysical Markers from Whole Blood Microfluidic Immune Profiling Reveal Severe Immune Response Signatures, Small, 2021, 17(12), 2006123.
16. K. Loutherback, J. L. D'Silva, L. Liu, A. Wu, R. H. Austin and J. C. Sturm, Deterministic separation of cancer cells from blood at 10 mL/min, AIP Adv., 2012, 2(4), 042107.
17. Z. Liu, F. Huang, J. Du, W. Shu, H. Feng, X. Xu and Y. Chen, Rapid isolation of cancer cells using microfluidic deterministic lateral displacement structure, Biomicrofluidics, 2013, 7(1), 011801.
18. M. Aghaamoo, A. Aghilinejad, X. Chen and J. Xu, On the design of deterministic dielectrophoresis for continuous separation of circulating tumor cells from peripheral blood cells, Electrophoresis, 2019, 40(10), 1486–1493.
19. Y. Song, Y. Shi, M. Huang, W. Wang, Y. Wang, J. Cheng, Z. Lei, Z. Zhu and C. Yang, Bioinspired Engineering of a Multivalent Aptamer-Functionalized Nanointerface to Enhance the Capture and Release of Circulating Tumor Cells, Angew. Chem., Int. Ed., 2019, 58(8), 2236–2240.
20. N. Tottori and T. Nisisako, Particle/cell separation using sheath-free deterministic lateral displacement arrays with inertially focused single straight input, Lab Chip, 2020, 20(11), 1999–2008.
21. Z. Liu, Y. Huang, W. Liang, J. Bai, H. Feng, Z. Fang, G. Tian, Y. Zhu, H. Zhang, Y. Wang, A. Liu and Y. Chen, Cascaded filter deterministic lateral displacement microchips for isolation and molecular analysis of circulating tumor cells and fusion cells, Lab Chip, 2021, 21(15), 2881–2891.
22. Y. Chen, E. S. Abrams, T. C. Boles, J. N. Pedersen, H. Flyvbjerg, R. H. Austin and J. C. Sturm, Concentrating Genomic Length DNA in a Microfabricated Array, Phys. Rev. Lett., 2015, 114(19), 198303.
23. D. W. Inglis, J. A. Davis, R. H. Austin and J. C. Sturm, Critical particle size for fractionation by deterministic lateral displacement, Lab Chip, 2006, 6(5), 655–658.
24. W. Liang, R. H. Austin and J. C. Sturm, Scaling of deterministic lateral displacement devices to a single column of bumping obstacles, Lab Chip, 2020, 20(18), 3461–3467.
25. J. P. Beech and J. O. Tegenfeldt, Tuneable separation in elastomeric microfluidics devices, Lab Chip, 2008, 8(5), 657–659.
26. C. Rein, M. Toner and D. Sevenler, Rapid prototyping for high-pressure microfluidics, Sci. Rep., 2023, 13(1), 1232.
27. S. Chang and Y.-H. Cho, A continuous size-dependent particle separator using a negative dielectrophoretic virtual pillar array, Lab Chip, 2008, 8(11), 1930–1936.
28. J. P. Beech, P. Jönsson and J. O. Tegenfeldt, Tipping the balance of deterministic lateral displacement devices using dielectrophoresis, Lab Chip, 2009, 9(18), 2698–2706.
29. J. P. Beech, K. Keim, B. D. Ho, C. Guiducci and J. O. Tegenfeldt, Active Posts in Deterministic Lateral Displacement Devices, Adv. Mater. Technol., 2019, 4(9), 1900339.
30. V. Calero, P. Garcia-Sanchez, C. Honrado, A. Ramos and H. Morgan, AC electrokinetic biased deterministic lateral displacement for tunable particle separation, Lab Chip, 2019, 19(8), 1386–1396.
31. G. D'Avino, Non-Newtonian deterministic lateral displacement separator: theory and simulations, Rheol. Acta, 2013, 52(3), 221–236.
32. Y. Li, H. Zhang, Y. Li, X. Li, J. Wu, S. Qian and F. Li, Dynamic control of particle separation in deterministic lateral displacement separator with viscoelastic fluids, Sci. Rep., 2018, 8(1), 3618.
33. H. Fukunaga, N. Tottori, S. Sakuma, T. Hayakawa and Y. Yamanishi, Tunable Particle Separation Through Acoustic Deterministic Lateral Displacement Micropillar Arrays, IEEE 37th International Conference on Micro Electro Mechanical Systems (MEMS), 2024, pp. 1142–1145,  DOI:10.1109/MEMS58180.2024.10439594.
34. B. M. Dincau, A. Aghilinejad, T. Hammersley, X. Chen and J.-H. Kim, Deterministic lateral displacement (DLD) in the high Reynolds number regime: high-throughput and dynamic separation characteristics, Microfluid. Nanofluid., 2018, 22(6), 59.
35. N. Tottori and T. Nisisako, Tunable deterministic lateral displacement of particles flowing through thermo-responsive hydrogel micropillar arrays, Sci. Rep., 2023, 13(1), 4994.
36. J. D'Silva, High-Throughput Microfluidic Capture of Rare Cells from Large Volumes of Blood, PhD dissertation, Princeton University, New Jersey, USA, 2016.
37. K. Loutherback, Microfluidic Devices for High Throughput Cell Sorting and Chemical Treatment, PhD dissertation, Princeton University, New Jersey, USA, 2011.
38. J. A. Davis, Microfluidic separation of blood components through deterministic lateral displacement, PhD dissertation, Princeton University, New Jersey, USA, 2008.
39. H. Bruus, Theoretical Microfluidics, Oxford University Press, 2007, vol. 18.
40. K. Loutherback, K. S. Chou, J. Newman, J. Puchalla, R. H. Austin and J. C. Sturm, Improved performance of deterministic lateral displacement arrays with triangular posts, Microfluid. Nanofluid., 2010, 9(6), 1143–1149.
41. S. Manoorkar and J. F. Morris, Particle motion in pressure-driven suspension flow through a symmetric T-channel, Int. J. Multiphase Flow, 2021, 134, 103447.
42. W. Liang, Biological Cell Preparation and On-Chip Particle Sorting Systems at High Flow Rate, PhD dissertation, Princeton University, New Jersey, USA, 2022.
43. M. Yamada and M. Seki, Hydrodynamic filtration for on-chip particle concentration and classification utilizing microfluidics, Lab Chip, 2005, 5(11), 1233–1239.
44. J. D'Silva, R. H. Austin and J. C. Sturm, Inhibition of clot formation in deterministic lateral displacement arrays for processing large volumes of blood for rare cell capture, Lab Chip, 2015, 15(10), 2240–2247.
45. D. W. Inglis, M. Lord and R. E. Nordon, Scaling deterministic lateral displacement arrays for high throughput and dilution-free enrichment of leukocytes, J. Micromech. Microeng., 2011, 21(5), 054024.
46. R. Campos-González, A. M. Skelley, K. Gandhi, D. W. Inglis, J. C. Sturm, C. I. Civin and T. Ward, Deterministic Lateral Displacement: The Next-Generation CAR T-Cell Processing?, SLAS Technol., 2018, 23(4), 338–351.

---