A comprehensive toolkit for manipulation and analysis of sprouting capillary networks based on magnetic ordering of multiple EC-coated microcarriers and their use in tissue modelling and drug testing

Abstract

Despite significant developments in endothelial-cell (EC) manipulation techniques, an in vitro model of a functional microvasculature with controlled local interconnectivity (<1 mm length scale) under well-defined global architecture (∼1 cm length scale) is still lacking. Here, we report the generation of such controlled multi-scale vascular networks via manipulation of tens of sprouting EC microcarriers. We exploit magnetic patterning to assemble superparamagnetic microbeads coated with human umbilical vein endothelial cells (HUVECs) into ordered arrays and establish effective growth rules governing the directionality of sprouting and the development of interconnections between the neighboring beads depending on the applied bead–bead spacing. The microcarrier-based approach offers a range of advantages over conventional EC-manipulation techniques including: (i) expedited sprouting, (ii) spatial control over the interconnections, (iii) reduction in cell consumption by even >100×, and (iv) a native high-throughput format. We co-develop a multiparametric morphometric analysis tool and demonstrate high-content assessment of drug-induced vascular remodeling in 3D tumor microenvironments. Overall, we propose a uniquely precise and standardized vascular tissue-engineering and imaging toolkit with applications, e.g., in angiogenesis/anastomosis research as well as high-throughput drug testing including personalized therapies.

---

Introduction

Precise modeling and design of human tissues or organs in vitro requires incorporation of a functional vascular system, a branched network of vessels enabling the supply of nutrients to the cultured cells, thus preventing necrosis, otherwise caused by hypoxia and malnutrition.¹ In the case of minimal tissues engineered for use in preclinical research e.g. in drug testing, it is critical to provide a microvasculature of well-controlled and reproducible morphology to warrant consistent results. Currently, the most commonly used methods of producing tissues with embedded microvasculature rely on the spontaneous self-organization of randomly dispersed endothelial cells (ECs) into capillaries inside an external hydrogel matrix.² However, owing to the initial random dispersion of ECs in the hydrogel, the resulting microcapillary networks are also random and difficult to control.^3–8 Generation of such random vasculatures is inefficient in terms of cell consumption and often results in a large fraction of disconnected or otherwise non-functional vessels.^4,5,8

Here, we demonstrate how the spatial organization of the microvasculature can be precisely controlled at both the microscopic and the mesoscopic level (respectively ∼1 mm and ∼1 cm) via directed-assembly of EC-microcarriers into ordered quasi-2D arrays. We exploit the use of magnetic hedgehog-like templates—arrays of permanent neodymium micromagnets arranged underneath a cell culture chamber—to guide the assembly of the highly monodisperse EC-coated superparamagnetic microcarriers into a variety of pre-designed patterns. The patterns are embedded inside a layer of fibroblast-laden hydrogel matrix and, under culture, ‘sprout’, branch and eventually interconnect to form a functional, lumenized vasculature penetrating the matrix. The large-scale architecture of the vasculature is determined by the initial distribution of the microcarriers and can be controlled via the design of the magnetic templates. Noteworthy, despite the planar (quasi-2D) arrangement of the microcarriers in the hydrogel, the endothelial cells as well as fibroblasts (and, optionally, cancer cells) self-organize inside the local 3D microenvironment into tissue-like structures.

We stress that the main goal of this work is to demonstrate a new EC-manipulation tool warranting utmost precision of the EC-patterning under retained high angiogenic potential, i.e., resulting in the formation of a functional, physiologically relevant vasculature. While multiple methods have been previously proposed to allow assembly of cells (including ECs) into controlled patterns^9,10 e.g., arrays of EC-aggregates, in most cases these patterns did not translate into the formation of a functional (e.g., branched, lumenized) microvasculature^9,10 or otherwise suffered from significant polydispersity.

Indeed, the currently available methods of EC patterning, such as extrusion bioprinting^11–16 typically suffer from limited angiogenic potential of the fabricated constructs. EC-spheroid-based bioprinting¹⁷ provides some improvements in this respect, but faces unresolved issues of nozzle clogging or spheroid deformation and breakup during printing. More recent advances include aspiration-assisted bioprinting^18–21 which eliminates clogging but the precision and/or reproducibility remain limited by the natural polydispersity of the spheroids, where the coefficient of variation (CV) in the spheroid diameter can easily reach CV > 20%.^22,23 Another class of approaches exploits seeding of ECs inside confined spaces, such as engineered porous structures²⁴ or planar patterns including micropillar arrays.²⁵ However, in those cases the morphology of the resulting vasculature is set by the geometry of the scaffold rather than via physiological processes of sprouting and anastomosis. Therefore, such strategies remain not optimally suited to modeling of tissue vascularization.

A number of alternative approaches have been proposed, of which perhaps the most promising is the use of magnetically labelled single-ECs or magnetically ‘doped’ EC-aggregates and their magnetic assembly into quasi-2D patterns of controlled architecture.^26–28 However, magnetic single-EC aggregation has been applied to generate rather small EC-assemblies with little sprouting potential (no demonstrated vessel formation^26–28). Furthermore, the magnetic assembly of single ECs typically turns out excessively time-consuming, where aggregation of only around 100 cells takes up to several hours.^27,29 The magnetic EC-spheroid manipulation, on the other hand, remains hampered by the aforementioned spheroid polydispersity as well as the necessity of extremely high magnetic nanoparticle loading.²⁷ In both methods, the introduction of magnetic nanoparticles inside the cells or into the spheroids^27,28 is also generally disadvantageous in drug tests, due to the possibility of altering cell behavior (though no cytotoxic or cytostatic effects have been reported²⁷). Finally, the actual assembly of functional (e.g., lumenized) vascular networks has never yet been demonstrated with any type of magnetic assembly approaches.

Compared to the previously reported magnetic EC-assembly methods^3,26–28,30 our approach is unique in that—rather than manipulating magnetically-tagged individual ECs or EC spheroids—it relies on the use of EC-coated magnetic microcarriers. The presence of a pre-formed EC monolayer at the surface of the microcarriers offers important advantages. In particular, (i) it warrants efficient sprouting and vascularization of the neighborhood of the microcarrier, and (ii) provides ultra-high precision in EC-patterning. The unique precision is warranted by the monodispersity of the microcarriers (CV 1–2%) combined with layering of ECs only on the microcarrier surfaces and centering of the microcarriers exactly at the micromagnet axis (this, as we show, requires the use of strong neodymium micromagnets). Those features remain substantial, e.g., in quest for highest possible accuracy and throughput of preclinical drug testing assays, and facilitate highly reproducible morphometric measurements. To this end, we further develop a numerical workflow that we introduced previously in the case of single EC-microcarriers³¹ and extend it to analyze the cases with multiple interacting microcarriers. The new software allows for multi-parametric morphological and topological characterization of the system with multiple sprouting and interconnecting microvasculatures.

The use of multiple EC-coated microbeads as sprouting and interconnecting microvasculatures has been proposed previously as a possible route towards tissue vascularization,^32–34 but no specific methods of controlled assembly of the EC-microcarriers into larger patterns have been elucidated. Here, for the first time, we propose the use of superparamagnetic microparticles coated with ECs as the sprouting ‘seeds’ which can be pre-assembled into controlled spatial patterns via external magnetic fields. Our method, apart from the abovementioned high precision of EC patterning and warranted high angiogenic potential, also offers a range of additional advantageous features: (i) reduced consumption of ECs as compared to the vasculogenesis-based approaches (since ECs are present only at the microcarrier surfaces rather than dispersed in the bulk hydrogel), (ii) development of well-defined vasculature with controlled local connectivity, and (iii) the possibility of parallel tracking of multiple microvasculatures developing in nearly identical conditions (warranted by the precise microbead arrangement). We use transparent polycarbonate (PC) plates to host the permanent micromagnets which allows for direct monitoring of the process of magnetic assembly of the EC-coated microbeads in situ and facilitates manual correction of defects. The method is simple and does not include the use of any expensive equipment such as a bioprinter or a discharge device.²⁸

We use our system to establish a critical bead-bead spacing below which the neighboring microvasculatures become interconnected, and above which they remain disconnected, even at late times of culture. In the latter case, they can be treated as practically independent biological experiments, which allows ensemble-averaging of the morphological characteristics of the sprouts. We show that the microvascular arrays co-cultured, e.g., with cancer cells (HeLa in our case), can efficiently serve as a high-throughput platform for the functional high-content screening of various anti-angiogenic compounds in full 3D microenvironment.³⁵ In this respect, our system allows automated extraction of a range of morphological and network-topological parameters, such as directionality and connectivity, unavailable with more conventional angiogenesis or vasculogenesis assays.^36–39 In particular, our high-content analyses are capable of differentiating between the impact of different drugs, here Taxol and sorafenib—which we both use as model inhibitors of vascular endothelial growth factor (VEGF) or/and VEGF-receptor, respectively (Taxol additionally being a cytostatic)—on the microvascular morphologies at various stages of development, i.e., just after sprouting or later after maturation and interconnection. Hence, in the future, our platform could be used to provide detailed insights into the mechanisms of action of drugs in various types of vascularized microenvironments.

We validate our method using both human umbilical vein endothelial cells (HUVECs) as well as human induced pluripotent stem cells (hiPSC)-derived endothelial cells. Via tight control over the bead-bead spacing, our method allows for the assembly of ordered arrays of mature microcapillary networks which can be used as a robust high-content screening platform for testing of anticancer therapeutics or different anti- and pro-angiogenic agents. Importantly, our platform could not only expedite the development of personalized treatments, but also serve as a standardized model system for studying the basics of angiogenesis or various microphysiological processes of healthy and diseased states involving cell migration such as, e.g., metastasis.

Results

Magnetic assembly of the EC-carrier microarrays

To achieve rapid and functional vascularization of hydrogel sheets with precise control over the vascular topology we assemble mesoscopic magnetic EC microcarriers (>200 μm in diameter) into ordered arrays using external magnetic templates with well-defined and strong magnetic-field “hotspots”. Our system comprises two parts: (i) a PC plate with a micro-milled array of holes accommodating cylinder-shaped strong neodymium micromagnets and (ii) a culture chamber fabricated in polydimethylsiloxane (PDMS) with a bottom wall made of a sufficiently thin cover glass (Fig. 1A and S1A). During the process of magnetic assembly of the EC-microcarriers inside the PDMS chamber, the magnetic template is placed underneath the chamber and both parts are tightly aligned (Fig. 1B). The EC-coated paramagnetic microparticles, serving as the EC-microcarriers, are then suspended in fibrinogen solution and poured into the PDMS culture chamber. We observe fast (lasting few seconds) spontaneous migration of the EC-coated microbeads towards the hotspots generated above the micromagnets, resulting in the formation of an ordered microbead-array (Fig. 1C). We estimate the efficiency of this spontaneous assembly process to be around 80% meaning that we observe on the average around 80% occupied and 20% non-occupied hotspots; the misplaced beads are then manually corrected using titanium fine-tip tweezers (Fig. S1B). In the future, one could imagine further automation of the process, e.g., via its combination with microcarrier-printing. However, even without such automated pre-positioning, our method has an important advantage in that the microbeads remain very efficiently immobilized at their equilibrium positions. This feature, in turn, allows reproducible generation of multiple (nearly) identical microbead-arrays using a single template, which is of great relevance in tissue modeling for use, e.g., in drug testing. In particular, such precise templating allows to differentiate between the intrinsic (biological) complexity of the system and the variations in system geometry.

Fig. 1 Generation of ordered arrays of microparticles over the substrate using magnetic-field patterning. A) Sketch of the experimental setup: a PDMS culture chamber with the glass bottom coverslip and a PC chip hosting the micromagnets. B) Illustration of the assembled device with the PDMS chip placed above the PC chip (left) and magnetic microbead localized precisely above the micromagnet. d – distance between the beads, D_bead – bead diameter, H – distance between the microbead and micromagnet, H_mag – micromagnet height, D_mag – micromagnet diameter. C) Scheme illustrating generation of ordered arrays of microparticles coated with endothelial cells. Left: PC chip hosting the micromagnets and the PDMS chamber filled with magnetic EC-coated microbeads suspended in non-crosslinked fibrin mixed with thrombin. Right: Fibrin crosslinks after 10 min leaving enough time for the magnetic self-assembly to take place. D) Results of the numerical calculation of the radial component F_mag,r of the magnetic force F_mag acting at a probe microparticle depending on its radial displacement r from the micromagnet axis for the experimentally relevant spacing H = 90 μm. Positive direction of the force is outward (i.e., negative values correspond to magnetic attraction). E) Images of PDSM culture chambers with EC-coated magnetic microbeads seeded at different densities in the fibrin hydrogel (spacing between the beads: 500 and 1500 μm respectively). Scale bar 1 cm. F) Confocal images of the array of HUVEC-GFP-coated microbeads visualized at day 2, 5, 7 and 9 of culture. Scale bar 1000 μm.

We note that, in general, it is not obvious that the beads would necessarily tend to align perfectly at the axes of the micromagnets. In fact, the equilibrium XY-position of each bead may depend on the details of the shape of the micromagnet, as well as the distance in the Z-direction separating the bead and the micromagnet. To check the equilibrium positions of the beads in our case, we performed direct numerical calculations of the magnetic field distribution around a cylindrical micromagnet using COMSOL Multiphysics 6.1 with the AC/DC Module. We set the diameter of the microbead (D_bead = 265 μm) and the dimensions of the micromagnet (D_mag = 200 μm, H_mag = 500 μm) to reflect the experimental conditions. We also fixed the spacing H between the upper micromagnet surface and lower microparticle surface to be equal to the thickness of the cover glass used in the experiment, H = 90 μm. The results (Fig. 1D) confirm that the radial component F_mag,r (in the XY-plane) of the magnetic force F_mag acting at a probe magnetic microparticle is always attractive (has negative value), i.e., it is directed towards the symmetry axis of the micromagnet (the Z-axis), which accordingly sets a unique and well-defined equilibrium position of the microparticle to be at the Z-axis, i.e., at a radial distance r = 0 from the axis. We further also checked (Fig. S1C) that this feature (attraction to the Z-axis) actually holds for all tested Z-spacings in the range H ∈ [50, 110] μm corresponding to typical ultra-thin cover-glass thicknesses (used as the chamber bottom). Accordingly, the microparticle pattern assembled above multiple micromagnets can be expected to perfectly reproduce the micromagnet pattern. For comparison, we have performed analogical calculations for the case with the magnetic hotspot generated by a ‘pin-holder’ device consisting of an iron micro-cylinder or a ‘pin’, magnetized by another large permanent magnet placed underneath, as proposed previously by the Honda group.²⁸ In particular, in the case of small H values (below 70 μm), we found the equilibrium condition (zero radial force) to be not at the Z-axis but rather at a distance r = r₀, with r₀ depending on H (e.g. r₀ ≈ 70 μm for H = 50 μm), that is along a circular region of radius r₀ centered around the Z-axis. This means that in the case of magnetized pins the equilibrium positions may become ‘degenerated’, i.e., distributed anywhere along the circular region above the pin (Fig. S1C). In the case of a microparticle array assembled above such magnetized pins, this would lead to random perturbations in the spacing between the neighboring microparticles. The use of permanent cylindrical micromagnets that we exercise here eliminates this perturbations and provides for highly precise patterning independently of H.

Next, we demonstrate experimentally that the system can be indeed used to precisely control the spacing between the EC-coated microparticles (Fig. 1E). To this end, we fabricate several different magnetic templates with varying micromagnet spacing. We carefully move the assembled microparticle arrays into the cell culture incubator for 15 min allowing the fibrin hydrogel to fully crosslink. Next, we remove the PC magnetic templates, place the PDMS culture chambers in the P60 petri dishes and culture the arrays for up to 2 weeks allowing EC-coated microbeads to produce vascular sprouts (Fig. 1F). At pre-determined time-points (typically day 2, day 5, day 7, day 9), we remove the arrays from the incubator to acquire confocal fluorescence images of the arrays of HUVEC-coated microparticles. Noteworthy, imaging of the sprouts, which typically grow not at the bottom but deeper in the hydrogel, is facilitated via the use of an ultrathin (≤110 μm) bottom of the culture chamber. The hydrogel slabs hosting the arrays can also be easily isolated from the open-top PDMS chambers (Fig. S1D) which demonstrates compatibility of our platform with downstream cell- and tissue characterization techniques (e.g., genomic analysis) which, however, we leave as future work, here focusing mostly on the morphometric and functional analyses.

Initial distribution of EC-coated microbeads governs the final topology of microvascular networks

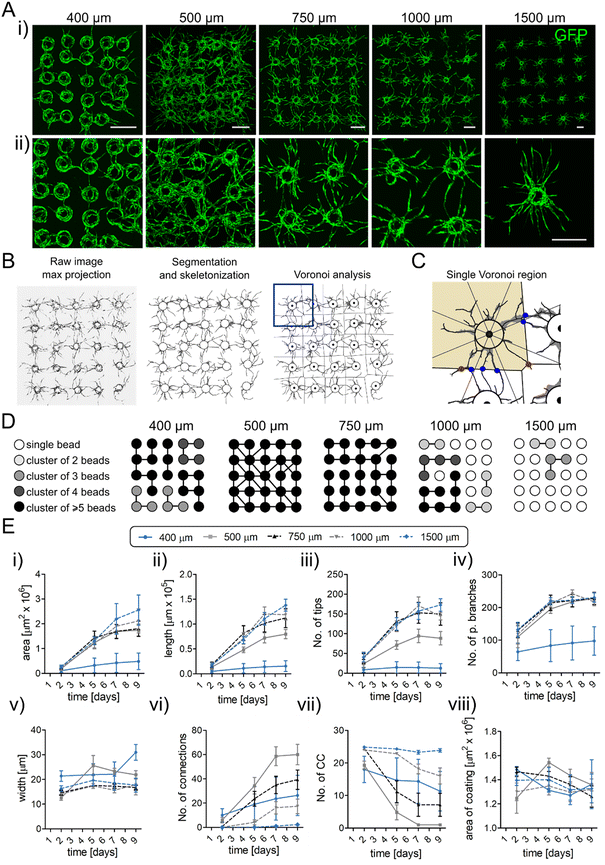
To demonstrate the application of microbead arrays in fabrication of spatially controlled and physiologically relevant microvasculature, we designed magnetic templates hosting the 5 × 5 arrays of micromagnets with a predetermined different micromagnet spacing d, i.e., d = 400, 500, 750, 1000 and 1500 μm, and studied the angiogenic sprouting behavior of the generated microvascular arrays (Fig. 2A). We used GFP-expressing HUVECs (GFP HUVECs) as the vascular precursor cells, and normal human dermal fibroblasts (NHDFs) as the stromal cells, where the latter supported HUVEC morphogenesis, e.g., via secretion of pro-angiogenic growth factors and extracellular matrix proteins.^38,40 To perform complex morphometric analysis of the sprouting networks we adapted and modified a custom image processing tool that we developed previously for the analysis of single sprouting beads.³¹ The current modified software can not only automatically detect and analyze the sprouting behavior of the individual beads forming the N × N array but also detect the interconnections and analyze the directionality of sprouting (see Methods). Our image analysis workflow starts with the generation of a maximum intensity projection of an acquired confocal 3D scan, followed by segmentation of the image and its skeletonization necessary to compute the basic morphological and network-topological metrics such as: area, length and width of the sprouts, number of tips and primary branches, as well as the interconnectivity (Fig. 2B). In particular, as the measure of the interconnectivity, we use (i) the total number of interconnections between the neighboring beads (Fig. 2B and C), and (ii) the total number of connected components, i.e., the number of interconnected groups of beads. We approximate the number of interconnections as the number of intersections of the sprouts with the borders of the Voronoi cell drawn around a given microcarrier under an additional requirement that the intersections are not along the tip segments of the sprouts. In such a way we eliminate the majority of sprouts that terminate just beyond the Voronoi border without reaching the neighboring bead (or anastomosing with its sprouts), i.e., those not forming the actual interconnections.

Fig. 2 Distribution of the EC-coated microbeads in hydrogel (bead-bead spacing) affects the architecture and morphological properties of the microvascular networks. A) (i) Representative images of the arrays of microparticles coated with GFP-tagged HUVEC cells and seeded at different densities (d = 400, 500, 750, 1000 and 1500 μm respectively) imaged at day 7. Each array consists of 25 EC-coated microbeads of the same size (265 μm in diameter). (ii) High magnification images of arrays showing the differences in morphology of the developed microvascular networks depending on the spacing d between the microbeads. Scale bar 500 μm. B) Image processing workflow. From left to right: Generation of the maximum projection image, segmentation and skeletonization, Voronoi analysis of connectivity. C) Illustration of a single Voronoi region. Points of interconnections between the beads are marked in blue. Points that intersect the Voronoi cell but do not result in a formation of interconnections are displayed in red. The image is divided into 8 zones to analyze the directionality of the vascular sprouting. D) Visualization of the number and size of bead-clusters connected via capillaries at various d as acquired from a single representative image for each d at day 7. Lines between the beads indicate the direct vascular connections. E) Morphometric analysis of the arrays: (i) total area of the sprouts, (ii) total length, (iii) number of tips, (iv) number of primary branches, (v) width of the capillaries, (vi) number of established vascular connections, (vii) number of connected components and (viii) area under the masks (i.e., the cells coating the beads). The numbers of the arrays in the assay (biological repetitions) were as follows: spacing 400 μm, n = 3; 500 μm, n = 5; 750 μm, n = 7; 1000 μm, n = 6; 1500 μm, n = 7). Symbols in the graphs indicate the mean values, and error bars are the standard error of the mean (SEM). Statistical significance in E was analyzed using a two-way ANOVA with Bonferroni post hoc test. See Table S1 for detailed statistics for (E). Numerical values that underlie the graphs are shown in SI data file.

We observed that the applied bead-to-bead spacing d in the array had a significant impact not only on the overall complexity of the network but also on the actual type of morphology of the developing endothelium (Fig. 2A, D and E). At the largest spacing, d = 1500 μm, d/D_bead ⋍ 5.7, we observed the neighboring microvasculatures developing practically independently (Fig. 2D), i.e., hardly developing any mutual interconnections at the endpoint of the applied culture period (day 9). The measured dynamics of sprouting remained well aligned with the case of completely isolated beads, i.e., single beads cultured in separate wells, which we studied previously.³¹ At a smaller spacing of d = 1000 μm, yet still significantly exceeding the bead size, d/D_bead ⋍ 3.8, we observed occasional development of individual interconnections (Fig. 2D). The total length and area of the sprouts in this case seemed slightly reduced as compared to the case d = 1500 μm, yet only at the later stages of development (days 7–9) (Fig. 2E). At an intermediate spacing d = 750 μm, d/D_bead ⋍ 2.8, we observed a rapid increase in the number of interconnections, starting already at day 5, with an average of around 40 interconnections per matrix achieved at day 9, corresponding to exactly 1.0 interconnection per each pair of the neighboring beads (Fig. 2E). We note, however, that not all of the nearest neighbors were interconnected in this case (Fig. 2D). This is because some of the beads developed multiple interconnections with their neighbors while others remained disconnected. We observed further decrease in the area of the sprouts at days 7–9 (Fig. 2E). At the spacing d = 500 μm, d/D_bead ⋍ 1.9, we observed a maximum of 60 interconnections per matrix at day 9, that is around 1.5 interconnection per pair of neighboring beads (Fig. 2E). In this case, we typically observed all the nearest neighbors to be interconnected, thus resulting in a fully interconnected vascular mesh (Fig. 2D). At the same time, as compared to the cases with the larger spacings, we observed a significant decrease in the total length of the sprouts and an even more significant decrease in the number of free tips (Fig. 2E). Since the number of primary branches remained unaltered for the bead spacings in the range d = 500–1500 μm (Fig. 2E), the above result quantifies an important effect, namely that the developing of interconnections prevents further growth or branching around the interconnected regions. In fact, each interconnection corresponds to the elimination of a tip, while the growth (and branching) of the sprouts happens predominantly at the tips. Finally, at the smallest studied distances d = 400 μm, d/D_bead ⋍ 1.5, we observed a significant change in the overall morphology of the developing endothelium (Fig. 2E), which included merging of the endothelial cell monolayers (or multilayers) covering the neighboring beads, with scarce actual sprouts. The significantly reduced sprouting manifested itself, e.g., in a strongly diminished number of primary branches and free tips, even at the early stages of development (Fig. 2E). Also, the total area of the sprouts and their total length were multi-fold reduced as compared to the cases with larger spacings (Fig. 2E). In particular, the reduction factor for the area and length at day 9 were around 5 and 9, respectively, as compared to the case with d = 1500 μm (Fig. 2E). The changes in the microvascular morphology in the case d = 400 μm can be attributed to the lack of available space for the development of the sprouts. This trend remains in line with the previously observed cases of ECs growing in porous media, e.g., in the interstitial spaces between close-packed hydrogel microbeads.²⁴

Overall, upon decreasing the bead–bead spacing from d = 1500 μm down to d = 500 μm we find little change in the microvascular morphology, especially at early times of culture, up to day 5. At d = 500 μm, at later times, we observed more and more interconnections, reduced number of growing tips, and finally the formation of a fully percolated network. In fact, the case d = 500 μm appears critical in that it corresponds to the maximal observed connectivity, wherein further decrease in the spacing down to d = 400 μm leads to severely suppressed sprouting and a tendency towards the formation of a space-filling endothelium.

Next, we re-analyzed the acquired confocal images in terms of the impact of the neighboring beads on the direction of angiogenic sprouting. We divided the beads into three subgroups depending on their position in the array: (i) ‘center’ (3 × 3 inner subarray, with each bead having 8 nearest neighbors), (ii) ‘edges’ (the beads at the sides of the array, corners excluded, each bead having 5 nearest neighbors) and (iii) ‘corners’ (each bead having 3 nearest neighbors), see Fig. 3A, and we analyzed the dominant sprouting directions separately for each group depending on the bead–bead spacing d. In particular, we employed the Voronoi division and measured the mass distribution in the angular octants co-aligned with the principal- and diagonal directions of the (square) array, separately for each EC-coated microbead (Fig. 3A). The results from the 4 different edge- and corner regions were pooled together, i.e., transformed to a common coordinate system. For edges, the principal direction (0 degrees) was set as perpendicular to the edge; for corners, as parallel to one of the neighboring edges and such that the matrix diagonal set the 45 degree direction, see Fig. 3A. For the bead–bead spacings d = 400 μm and d = 500 μm we observed that, at day 7, in the edge and corner groups the octants with the largest endothelial mass were directed always outside the matrix (Fig. 3A). For the microbeads located in the center of the array the directions with larger endothelial mass were the diagonals 45°, 135°, 225° and 315°, i.e., the directions pointing towards the further (diagonal) neighbors (Fig. 3A). In contrast, for the spacings d = 750 μm and larger we observed isotropic distributions in all directions (Fig. 3A). We additionally quantified this result via the coefficient of variation (CV), i.e., the standard deviation divided by the mean, of the probability values in different octants for various spacings and culture times (Fig. 3B and S2). As expected, for d ≥ 750 μm in all subgroups we found CV values around or below 10% at days 7–9 reflecting isotropic distributions. For d = 500 μm we observed strong anisotropy in the case of edge and corner beads, with CV around 35–40% at day 7 and 45–50% at day 9, but yet little anisotropy for the central beads (CV ∼ 15%). Similar or even slightly elevated values were observed for d = 400 μm. In addition, in the cases d = 400 μm and 500 μm we observed gradual growth of the anisotropy level at corners and edges during days 5–9 of culture. In contrast, for d ≥ 750 μm, we observed a relatively constant level at those times. In all studied cases, the elevated anisotropy levels at day 2 can be attributed to the small amount of sprouts at such early culture times.

Fig. 3 Analysis of directionality of the sprouting microcapillary networks. A) Radar charts illustrating the angular (azimuthal) distribution of the area occupied by capillaries at day 7 of culture. EC-coated microbeads were classified into 3 groups based on the number of neighbors': center (8 neighbors), edges (5 neighbors) and corner (3 neighbors). Asymmetrical results from corner and bar regions were transformed to a common coordinate system, with all regions oriented to match the region indicated with a dotted frame (e.g. top bar is transformed by −90 degrees, etc.). The numbers of the arrays in the assay (biological repetitions) were as follows: spacing 400 μm, n = 3; 500 μm, n = 5; 750 μm, n = 7; 1000 μm, n = 6; 1500 μm, n = 7). B) Coefficient of variation of the radar charts for EC-coated center-, edge- and corner microbeads at different indicated time-points, as a quantitative measure of the angular anisotropy of sprouting. Numerical values that underlie the graphs are shown in SI data file.

Altogether, we find that the sprouts grow initially isotropically in all directions until the interconnections with the nearest neighbors (in the principal directions) are firmly established. In the case d = 500 μm, this starts to happen around day 5 (Fig. 2E vi and 3B), after which the growth continues towards the regions of the remaining free space. Accordingly, the excess sprout area in those directions (Fig. 3A) can be treated as an artifact of the anisotropy of the Voronoi cells. To eliminate this geometric bias, we additionally measured the angular dependence of sprout coverage. To this end, we calculated the area of the sprouts divided by the area of the Voronoi cell subsection in each octant. We evaluated this quantity for the central beads at day 7, corresponding to the region with an almost fully interconnected, mature network, where no (or little) further growth was observed. We found the sprout coverage to be again isotropic (Fig. S3), which accordingly supports the picture of homogeneous penetration of all available space by the developing microvasculature until all interconnections have been established.

Generation of complex geometries using magnetic force-based patterning of EC-coated microbeads

Vascularized tissue-specific models often require incorporation of microvasculature of a highly specific pre-defined architecture. To address this issue we microfabricated (PC)holders with several different micromagnet patterns (Fig. 4A): (i) a hepatic lobule-like structure, (ii) a hierarchically branched vascular tree, (iii) parallel lines and (iv) a 3 × 3 array of empty squares (such structures could serve as arrays of ‘vascular beds’⁴¹). Next, we used these magnetic templates to guide the assembly of HUVEC-GFP-coated microbeads. For the most efficient vascularization of the whole pattern, we used the optimal spacing d = 500 μm, warranting rapid development of interconnections between all (or nearly all) adjacent beads. Fig. 4B shows the generated vascular structures imaged at day 1 and day 7 of culture. In the latter case, we observe systematic development of vascular interconnections between the neighboring beads which can be readily seen in the high-magnification images (Fig. 4D). The demonstrated freedom of arranging the beads into arbitrary 2D patterns under well-defined and optimized adjacent bead–bead spacing constitutes an important step towards precision-engineering of interconnections in vascularized tissues, e.g., for future applications in perfusable organ-on-chip devices^5,6,42 or in fabrication of vascularized wound dressings.

Fig. 4 Complex patterns assembled from the EC-coated microbeads suspended in a fibrin hydrogel. A) Different magnetic templates used for the generation of different patterns. From the top: A model of liver lobule vasculature, a vascular tree with the hierarchical branching, parallel lines and an array of square-shape microcapillary beds. Scale bar 1000 μm. B) Confocal images of GFP-HUVEC-coated microbeads patterned using different magnetic templates described above and imaged at day 1 and 7 of culture. Bottom panel shows high magnification images of the selected areas. Scale bar 500 μm.

Biological and morphological characterization of the engineered microvascular networks

To test whether the engineered microvascular networks exhibit proper physiological characteristics, we investigated the 3D structural integrity of the microvessels and verified the presence of characteristic marker proteins of healthy blood vessels. Immunofluorescence analysis showed abundant expression of CD31 (Fig. 5A) and laminin (Fig. 5B) in the microvascular arrays cultured for 7 days. The high magnification images (Fig. 5A and B) visualizing the vascular connections between the HUVEC RFP-coated microbeads clearly display the mature morphology of the capillaries with the deposition of basement membrane by ECs around the perivascular extracellular matrix. Those results indicate vessel stabilization, high vessel integrity and characteristic elongated morphology of ECs co-aligned with the longitudinal direction of the capillary-like structures. Cross-sectional images of the engineered microcapillaries show the presence of a continuous lumen along the vessels, enclosed by ECs (Fig. 5A and B). Moreover, we observed formation of apparently toroidal lumens around individual EC-coated microbeads (Fig. 5C) and the formation of tubular vascular connections between those toroidal lumens (Fig. 5D) resulting in the formation of a continuously lumenized structure. Last but not least, we found continuous cell–cell junctions lining the intersection of the ECs, as shown by the presence of the adherent junction protein, CD31 (Fig. 5E). Overall, our results show that engineered arrays of microcapillary network-like structures supported by the microbeads display characteristic morphological and biochemical features of microvessels found in vivo.

Fig. 5 Arrays of HUVEC-coated microbeads form vessel-like structures characteristic of mature capillaries. A and B) Confocal images of arrays of HUVEC-RFP-coated microbeads seeded at 500 μm spacing and immunostained for (A) CD31 and (B) laminin. Right panels show high magnification images of selected areas (selection 1 and 2 i–iii) and their orthogonal cross-sections along the planes indicated with the dashed lines (a and b) showing lumen formation. C) Image of a representative HUVEC-RFP-coated microbead stained for CD31. Images in panels (i–iii) show the selected Z-slices visualizing the formation of lumens around the beads. D) Image of two neighboring HUVEC-coated microbeads immunostained for CD31. Bottom panel shows a single Z-slice illustrating the formation of a capillary tube connecting the two lumenized areas forming around the neighboring microbeads. E) Formation of tight junctions (indicated with arrows) between the HUVEC cells forming capillaries in the microbead-array assay. In all panels (A–E) Hoechst dye was used to visualize nuclei. Scale bar 100 μm.

EC-coated beads accelerate the formation of microvascular networks

Next, we benchmarked the performance of the magnetically assembled arrays of EC-coated microcarriers (d = 500 μm) against the situation with ECs randomly dispersed in the fibrin gel, where the latter remains the most common method of producing microvasculature in vitro.¹ Our goal was to establish whether the strategy based on the use of multiple hydrogel-embedded EC microcarriers can accelerate the formation of microvascular networks as compared to the more conventional approach, and what are the possible morphological differences in the generated capillary networks. First, we calculated the average number of HUVECs on the cell-coated beads (Fig. 6A and B) and used the same number of ECs (per hydrogel volume) in both assays. Next, we imaged the growing vascular networks in both cases at day 2, 5 and 7 of culture. We observed that, after a week of culture, the arrays of EC-coated microbeads formed significantly larger and more complex vascular networks (Fig. 6C). In particular, we found higher values of microvascular area and increased width of capillaries (Fig. 6D). In the assay with dispersed ECs the width of capillaries did not change during the 7 days of culture, which may be attributed to slow cell aggregation and, in particular, to the lack of any pre-formed cell aggregates. As a result, the cells remained dispersed and did not form any bigger vascular structures. To quantify the complexity of the microvascular networks in the two cases, we defined the connectivity coefficient Con(t) as the decrease in the total number of connected components N_CC(t) normalized to the situation with final fully connected network, that is we defined Con(t) = [N_CC(0) − N_CC(t)]/[N_CC(0) − 1]. In the case of EC-coated microbead arrays we found a rapid increase in Con(t), reaching the maximal values close to Con(t) = 1 already at day 5 of culture, corresponding to the formation of a fully interconnected vascular network (Fig. 6D). In the case of dispersed ECs the values of Con(t) remained close to 0 at all times.

Fig. 6 EC-coated microbeads accelerate the formation of vascular networks in 3D in vitro models and warrants formation of 3D capillary networks. A) Representative image of a single GFP-HUVEC-coated microbead. Cell nuclei were visualized with Hoechst dye. Scale bar 100 μm. B) Quantification of the number of HUVECs used to coat one microbead (n = 14). C) Images illustrating vascular network formation using conventional 3D in vitro assay where ECs are (i) randomly dispersed in external hydrogel, here fibrin, and a (ii) microbead array model. In both cases the initial number of HUVECs (per hydrogel volume) was the same. Confocal images were acquired at days 2, 5 and 7 of culture. Scale bar 500 μm. D) Analysis of the (i) the total area, (ii) the width of the capillaries, (iii) and the connectivity index, Con(t) and (iv) of the arrays of HUVEC-coated beads seeded at 500 μm spacing and dispersed HUVECs as described in C). Dispersed cells, n = 4; cell-coated beads n = 6. E) Comparison of size distribution of cell-coated micromagnets and cell aggregates; n = 75, data from 3 arrays. F) Cell coated microbeads and aggregates of magnetically labelled cells assembled using a micromagnet array under fibrin hydrogel. Images show time evolution of the endothelial cell structures in the two cases. In the case with cell aggregates (i) the cells gradually spread without forming well-defined elongated structures, while the elongated capillary-like structures can only be distinguished in the case with microcarriers (ii). Scale bar 500 μm. G) Comparison of the 3D images of a single aggregate (i) vs. a single microcarrier (ii) at day 3 of culture. Note a clear 3D distribution of cells at the depth of around 141 μm in the case of the microcarrier (ii), with capillaries growing at a significant distance from the substrate inside the fibrin gel, and a flat pancake-like morphology in the case of the aggregate (i), whose thickness is only around 32 μm and which remains fully attached to the substrate. Scale bar 250 μm. Error bars around the mean indicate the standard error of the mean (SEM). * p < 0.05, *** p < 0.001. Statistical significance was analyzed using a two-tailed unpaired t-test (B and E) and one-way ANOVA with Turkey post hoc test (D). Numerical values that underlie the graphs are shown in SI data file.

We believe that the slow development of the microvasculature in the case of dispersed ECs was a result of scarce cell–cell interactions caused by low initial cell concentration in the hydrogel and the absence of any pre-assembled EC monolayers. In fact, according to the literature, this strategy is successful only at sufficiently high concentration of the ECs in the hydrogel, i.e., of the order 0.5–2 × 10⁷ cells per mL.^5,8,43 In our experiments, we used 0.35 × 10⁵ cells per mL, which reflects the number of cells coating the microbeads in 5 × 5 microbead arrays. This demonstrates that the approach based on the use of microcarriers as microvascular ‘seeds’ allows for the formation of highly interconnected microvascular networks with endothelial cell consumption around 2 orders of magnitude lower as compared to the conventional approach based on the dispersed ECs.

We further investigated whether the observed high angiogenic potential could be directly attributed to use of EC-coated microcarriers or whether it could be achieved with direct magnetic patterning of magnetically-tagged ECs. For this purpose, we suspended the magnetically-labelled fluorescently-tagged HUVECs—without microcarriers—in the fibrin gel and used a micromagnet template to arrange the cells into clusters. We compared the results of this assay with the results obtained via the assembly of HUVEC-coated microcarriers, while using the same micromagnet template.

We found that, the assembly of magnetically labelled ECs leads to the formation of cell clusters of much higher polydispersity as compared to the case with the microcarriers (Fig. 6E). Moreover, the resulting EC-aggregates do not sprout but rather gradually extend the surface coverage, not producing physiologically relevant tubular vessels. This is contrary to the case with microcarriers (Fig. 6F) which produced visible ‘sprouting’ microvessels, interconnecting into a capillary network. Eventually, we observed that the clusters assembled from magnetically labelled cells (Fig. 6G) remained strictly two-dimensional, i.e., pancake-shaped and strongly flattened against the substrate, even after several days in culture. We assume that such flattening is related to cell sedimentation caused by both gravity as well as the magnetic field during the assembly process at day 0. In contrast, in the case with microcarriers (Fig. 6G), the cells grow in three dimensions and produce tubular structures (microcapillaries) extending into the external fibrin gel with no direct contact with the substrate.

Based on our findings, we conclude that the strategy based on EC-coated microcarriers not only accelerates formation of microvascular networks but also plays a key role in supporting the formation of 3D microvascular networks. The method based on direct magnetic manipulation of magnetically labelled ECs provides cellular structures resembling segmented 2D monolayer rather branched 3D network.

Drug screening studies

To demonstrate the potential use of our device in anti-cancer and anti-angiogenic drug screening studies, we co-seeded fluorescently tagged human cervical cancer cells HeLa GFP with EC-coated microbeads and stromal cells (fibroblasts) thus creating a cancer-like microenvironment. We used HUVEC RFP to enable co-visualization of both cancer cells and ECs in the system. The microvascular arrays were allowed to develop for 4–5 days prior to drug exposure and then were treated with different concentrations of either Taxol (100 or 1000 nM) or sorafenib (1 or 10 μM). Both drugs are known to affect vasculature, however they exhibit different mechanisms of action.^44,45 Taxol affects microtubule dynamics and inhibits EC proliferation and migration. It also has been shown to downregulate VEGF expression.⁴⁵ Sorafenib is a tyrosine kinase inhibitor and acts on signal transduction pathways such as Ras–Raf–MEK–ERK pathway.⁴⁴ As the control, we used arrays subject to the 0.01% DMSO corresponding to the amount of DMSO used in the applied doses of the drugs. To understand the kinetics of drug penetration into the hydrogel, we first estimated the time of diffusion of a small-molecular drug through the hydrogel layer. Considering that the size of sorafenib and Taxol molecules (∼1 nm) is 3–4 orders of magnitude smaller than typical fibrin gel pore size (the latter being of the order 5–10 μm according to literature,^46,47 the diffusion through hydrogel can be assumed to be similar to the diffusion through pure water phase. Given molecular mass of sorafenib M = 464 daltons the diffusion coefficient of sorafenib can be estimated as D₀ ~ 5 × 10⁻⁶ cm² s⁻¹ based on comparison with model molecules of comparable M.⁴⁸ Based on the diffusion equation Δx² = 2D₀t, we estimate that the layer of hydrogel of thickness Δx = 2 mm subject to sorafenib dissolved in the culture medium (administered on top of the hydrogel layer) should become homogenously equilibrated with the sorafenib molecules within around t = 4000 s–1 hour. Accordingly, since our drug treatments last 48 hours, we conclude that any possible delays in the drug responses due to the diffusion through hydrogel are safely negligible. The above analysis relies on the assumption that the drug-fibrin electrostatic interactions are weak. We have not verified this assumption directly, yet we note that the drug molecules that we test here, sorafenib and Taxol, are neutral.

We used microvascular arrays consisting of either (i) well-separated microvasculatures (d = 1500 μm) (Fig. 7A) or (ii) those forming a fully interconnected network (d = 500 μm) (Fig. 7C). Such two-way approach enables the assessment of the action of the drugs both in terms of (i) inhibition of the sprouting potential as well as (ii) disintegration of the existing vasculature. We analyzed the acquired images of the arrays before the drug treatment (time t₀; that is day 4 or 5 of culture depending on experiment) and at 48 h post-treatment (time t₁) (Fig. 7A and C and S4) and quantified the relative change in the macrovascular network area, length, number of tips, width of capillaries, number of connected components and number of primary branches, as well as (in the cases with d = 500 μm) network connectivity.

Fig. 7 Application of microvascular arrays in anticancer drug screening studies. A and C) Images of the arrays of fluorescently tagged HUVEC-coated microbeads co-cultured with HeLa cells (not visualized) and seeded at (A) d = 1500 μm and (C) d = 500 μm spacing. At day 5 Taxol (100 or 1000 nM) or sorafenib (1 or 10 μM) were administered to the structures; t₀ – day 5 of culture, before drug exposure; t₁ – day 7 of culture, 48 h after drug application. High magnification images (upper and middle panels) show selected areas of the arrays just before drug application (t₀) and 48 h after drug exposure (t₁). Scale bars 250 μm. Bottom panels show whole arrays. Scale bar 1500 μm in A and 500 μm in C. B) Morphometric analysis of the fold change in (i) the total area, (ii) the total length, (iii) the number of tips, and (iv) the width of capillaries at t₁ relative to t₀ for d = 1500 μm. Control, n = 6; Taxol (T) 100 nM, n = 6; Taxol (T) 1000 nM, n = 6; sorafenib (S) 1 μM, n = 6; sorafenib (S) 10 μM, n = 5. D) Morphometric analysis of the fold-change in (i) the total area, (ii) the total length, (iii) the number of tips, (iv) the width of capillaries and (v) the number of connections at t₁ relative to t₀ for d = 500 μm. Control, n = 6; Taxol (T) 100 nM, n = 6; Taxol (T) 1000 nM, n = 6; sorafenib (S) 1 μM, n = 5; sorafenib (S) 10 μM, n = 6. Error bars around the mean value indicate the standard error of the mean (SEM). * p < 0.05, ** p < 0.01, *** p < 0.001. E) Selected frames of the arrays of RFP-tagged HUVEC-coated microbeads co-cultured with HeLa GFP cells illustrating the migration of cancer cells into the microcapillaries. For full movies see Videos S1 and S2. Scale bar 250 μm, high magnification images 50 μm. Statistical significance was analyzed using one-way ANOVA with Turkey post hoc test. Numerical values that underlie the graphs are shown in SI data file.

In general, the two tested compounds affected the morphology of microvascular networks in a slightly different manner.

In the case d = 1500 μm, as shown in Fig. 7A, we observed that the treatment with both drugs, applied at the highest concentrations, resulted in a significant reduction of the total area of the sprouts (Fig. 7B) as compared to control. In the case of Taxol, we also observed a significant reduction of the length (Fig. 7A and B) at both lower and higher concentration. However, in the case of sorafenib we observed a rather peculiar effect in that the lower concentration (1 μM) had apparently much stronger effect on the length than the higher concentration (10 μM). Regarding the number of tips (Fig. 7A and B), only the higher dose of Taxol and lower dose of sorafenib led to the expected reduction. In general, the reduction in the number of tips can be interpreted as the effect of either tip retraction or less frequent branching (or both). However, again, the effect was absent in the case of higher dose of sorafenib. The apparently weaker effects of sorafenib at the higher dose can be explained in terms of a very rapid capillary disintegration, in fact happening so fast that the cells have no time to migrate, thus effectively ‘quenching’ the skeleton, as acquired from image processing (see Fig. S5). We stress however that the effect on the area in this case remains very strong (p < 0.01). Next, we also found the number of primary branches to be unaffected by the drugs, at least at the significance level p < 0.05, at any concentration (Fig. S4C and D). This is reasonable as the drugs were administered only after the primary branches were already formed, i.e., when the number of primary branches normally reached a plateau (Fig. 2E).

In the case d = 500 μm, as shown in Fig. 7D, the results for the area and length were similar to the case d = 1500 μm (Fig. 7B). In the case of sorafenib treatments, we also observed higher numbers of tips as compared to the case d = 1500 μm (Fig. 7B). We can attribute this effect to the drug-induced disintegration or ‘cutting’ of the pre-existing capillary connections. Further, similar to the case d = 1500 μm, we observed no significant effect on the number of primary branches (Fig. S5D), except for the case of the higher dose of sorafenib for which we found a significant increase as compared to control. Again, we interpret this result as an artifact of endothelial cell damage and the associated protein (GFP) aggregation, resulting in the numerical classification of the detected morphological irregularities as additional ‘sprouts’. Finally, as expected, we found that all treatments led to the reduction in the number of connections (Fig. 7D) and a change in the number of connected components (Fig. S4B), a signature of vessel ‘cutting’ and/or retraction. The effect was significantly stronger in the case of Taxol, for which we observed that the retraction of EC sprouts led to significant increase of the width of the sprouts and clearly visible retraction-bulb phenotype (Fig. 7C and D).

In this study, we did not investigate the effect of Taxol and sorafenib on cancer HeLa cell proliferation and viability in much detail. Nevertheless, we performed a basic analysis of the cancer cell mass approximated via the projected area of the visible cells. This parameter showed no profound effect on the cancer-cell number after 48 h of treatment (Fig. S4E and F), apart from a visible reduction in the case of sorafenib (10 μM). Those results are in line with the previous results obtained in 3D models.^6,42,49–51

We note that the main aim of the proof-of-concept drug screens presented in this study was to demonstrate the possibility of recreating a possibly complete model of the tumor microenvironment, e.g., including cancer cells, fibroblasts and vasculature. We leave a more detailed study aimed at dissecting the differences in mechanisms of action of chosen drugs in mono- vs. co-culture as a future work. Finally, we also note that the presented approach follows previous literature regarding drug tests exploiting vascularized 3D tumor-on-chip systems which typically also include only the co-culture setting.^6,42

Finally, we also demonstrate that our model can be used to study the migration of cancer cells inside the microcapillaries in real-time. For this purpose, we performed time-lapse imaging of an array of HUVEC-RFP-coated microbeads co-seeded with HeLa GFP cells (Fig. 7E). We observed that individual cancer cells often migrate into close proximity to the neighboring capillaries, trying to integrate with the microvascular network (Fig. 7E). The possibility of direct tracking of cancer cells migrating inside (or outside) the capillary vessels in realistic microenvironments may be of significant interest to studies focusing on the metastatic potential of cancers forming solid tumors. The platform can be also applied to study the migration behavior of non-cancer cells, including tracking of individual endothelial cells or their different populations (Fig. S6) to assess e.g. their mobility or/and sprouting phenotype.

In conclusion, our platform can be successfully used for the screening of drugs in well-controlled cancer microenvironments, providing (i) detailed and robust readouts in terms of the anti-angiogenic effects acquired from morphological changes in the tumor-associated microvasculature and (ii) insights into the interactions between tumor cells and the associated vascular network.

Validation of the model with hiPSC

The recent advances in iPSC technology have made patient- and disease-specific human cells widely available as the sources for personalized drug screening tests, toxicology studies or disease models. To assess the future potential of our angiogenesis assay in personalized precision medicine, we also generated the arrays of EC-coated microparticles using hiPSC-derived ECs (hiPSC-ECs). Commercially available hiPSCs were first differentiated to an intermediate mesoderm stage and then to the final endothelial lineage (Fig. 8A). We performed flow cytometry (Fig. 8B) and immunofluorescence (Fig. 8C) analysis on day 7 of the protocol to evaluate the EC differentiation. We observed that approximately 80% of cells were positive for CD31 (78.5%) and CD34 (82.2%) endothelial cell markers (Fig. 8B). This was consistent with immunocytochemistry analysis showing von Willebrand factor (vWF) immunofluorescence in ECs cytoplasm and strong CD31 staining, visualizing the tight junctions between cells (Fig. 8C). We coated microparticles with hiPSC-ECs and seeded them into arrays using our magnetic field-based micropatterning method. To ensure proper coating of the beads with hiPSC-ECs and to warrant cell adhesion to microbead surface, we pre-coated the microbeads with ACF Cell Attachment Substrate. During the first two days of culture, we observed intense sprouting of ECs from the beads followed by rapid invasion of individual ECs into the fibrin hydrogel (Fig. 8D and E). The observations were qualitatively similar for two different sources of hiPSC-ECs. The hiPSC-ECs formed dense networks in the fibrin gel but failed to form mature tubular capillary structures.

Fig. 8 Generation of the arrays of hiPSC-ECs-coated microbeads. A) Bright-field images at different time points (day 1 to 7) of hiPSC-EC differentiation. Scale bar 25 μm. B) Flow-cytometry scatter plots and histograms of generated hiPSC-ECs stained for CD45, CD31 and CD34. C) Immunostaining of hiPSC-ECs for CD31 (red) and vVW factor (green). Hoechst dye (blue) was used to visualize nuclei. Scale bar 25 μm. D) Images of the arrays of hiPSC-EC-coated microbeads seeded at 500 μm spacing visualized at day 2 and 3 of culture. F-actin (red) was used to visualize the morphology of hiPSC-EC sprouts. Nuclei were stained with Hoechst dye (blue). Scale bar 500 μm. E) High magnification images of selected hiPSC-EC-coated microbeads immunostained for F-actin (red), CD31 (green) and Hoechst (blue) at day 2 and 3 of culture. Scale bar 250 μm.

We can therefore conclude that the behavior of the ECs, including their propensity towards the formation of monolayers or towards sprouting, may strongly depend on the specific cell type and origin (HUVECs vs. hiPSC-ECs).³⁹ Furthermore, hiPSC-ECs, unlike the well-established primary cells such as HUVECs, are strongly heterogeneous, which may result in different (e.g., patient-specific) angiogenic sprouting behavior.³⁹ Thus, to fully assess the potential of hiPSC-ECs in the generation of microvascular arrays and to possibly use such types of cells in drug tests warranting reproducible results, it is essential to optimize the endothelial cell differentiation protocols and source the representative cell batches from multiple donors. Such efforts are crucial for harnessing the full potential of hiPSC-ECs in developing reliable microvascular models for drug testing and personalized therapies.

Conclusions

In this work, we develop magnetic field-driven pre-patterned microvascular arrays and demonstrate their applications in engineering of cancer microenvironments and phenotypic testing of anti-angiogenic or cytostatic compounds. Potential further applications extend to the development of personalized therapies via the use of iPSC-derived ECs. Our technology, based on the use of EC-coated superparamagnetic microbead-arrays, allows for fast formation of biologically mature and lumenized capillary networks of pre-designed architecture under minimal consumption of the endothelial cells. The control over the initial architecture set by the distance between the EC-microcarriers plays a critical role in the formation of the microvasculature and impacts the final morphology while also warrants reproducible culture conditions (including spatial restrictions) around the individual microcarriers.

We demonstrate that the effect of model drugs on the arrayed microvasculatures can be precisely monitored in terms of detailed morphological metrics which besides total area and length of the sprouts also include, e.g., (i) the number of branches and their width (ii) the number of tips and (iii) the connectivity of microvasculature. The fully automated multiparametric morphometric analysis enables better understanding of the impact of the drugs on the tumor microvasculature, which would not be possible based on a single parameter (e.g., only the area or length of the sprouts) as often employed in conventional angiogenesis assays.^6,49,52,53 For example, our analysis does not show any significant impact of Taxol treatment on the area of the microvasculature, while the length and the number of vascular connections are significantly reduced and the width of the capillaries increases. Those type of effects were not reported in previous studies based on the sole microvascular area analysis in Taxol-treated samples.⁴⁹ Here we show that—only taken together—the multiple parameters give a full account of the changes in the morphometric phenotype of drug-treated capillaries. Furthermore, we find a significantly different morphological mechanism of action in the case of sorafenib, i.e., predominantly capillary thinning and ‘overdose’ effects where increasing the drug concentration (from 1 μM to 10 μM in our case) leads to unchanged or even elevated characteristics such as sprout length or the number of tips. Given those observation it would be of great importance to develop strategies that could allow for better understanding of the relation between in vitro drug screening assays and clinical data. Nevertheless, for now, direct comparison seems particularly difficult since the endpoints of clinical trials addressing most anticancer drug efficacy studies in solid tumors are usually limited to such parameters as progression free survival or overall patients survival, while lacking systematic analysis of tumor-related angiogenesis (i.e. tumor vessels morphology) based on e.g. histopathological data. The latter type of data is more available in preclinical studies, such as those involving mouse models, however, it is still limited to one or two parameters describing the effect of the drug on the tumor vascularization. The most common parameters include microvessel area and density, and according to the available reports, in mouse models there is no clear correlation between the effect of sorafenib on the tumor microvasculature and the concentration of the administered compound.⁵⁴ On the other hand, observations from 2D cell models (e.g. HUVECs on Matrigel⁵⁵) show a clear correlation between the applied drug dose and the anti-angiogenic effect. Overall, the scarcity of histopathological clinical data and the lack of evidence from preclinical models underline the importance of developing precise 3D vascularized in vitro models to more adequately predict and better understand the mechanism of action and efficacy of the anti-angiogenic and anti-cancer compounds. Moreover, having demonstrated the compatibility of our platform with hiPSC derived ECs, we believe that it could be successfully applied in personalized drug screening studies in the future. To this end, further studies would require a larger number of hiPSC donors to work out optimal culture protocols. We also believe that our approach could be of great value in terms of screening of the pro-angiogenic therapeutics to support wound healing and/or optimize tissue restoration therapies. With the presented open-top design of the culture chambers, our vascular microtissues can be easily extracted for use in further analysis including gene expression and/or spatial proteomics.

In summary, we have presented a novel platform comprising human vascularized microtissues of highly organized and controlled architecture suitable for precise morphometric analysis of vascular networks and drug screening applications. Our pre-patterned EC-microcarrier arrays allow for generation of spatially controlled microvasculature of high biological relevance, and as such facilitate precise, reproducible morphological analyses including high-content phenotypic drug screens at the microtissue level.

In terms of possible future organ-on-chip applications, we foresee that the platform could be further integrated with microfluidic channels allowing for direct perfusion of the microcapillary networks whose connectivity could be controlled via microcarrier patterning. We present a vision of such a device in Fig. 9, wherein several independent vascular paths between the opposing microfluidic channels are readily provided via on-chip magnetic assembly of the EC-coated microbeads. Combination of such controlled vascularization strategy, e.g., with generation of lateral gradients of active compounds (drugs etc.) inside the hydrogel could be further exploited towards high-throughput screening. We leave the demonstration of such functionalities as a future work.

Fig. 9 Scheme illustrating integration of EC-coated superparamagnetic microbead-arrays with microfluidic chip allowing for flow generation over forming microcapillary networks.

Methods

Device design and fabrication

The device was composed two layers. The bottom layer was 25 mm × 25 mm polycarbonate (PC) chip with embedded array of cylinder-shaped neodymium micromagnets grade N48, of diameter D_mag = 200 μm, H_mag = 500 μm. The upper layer was a 30 mm × 30 mm PDMS chip (SYLGARD™ 184 Silicone Elastomer Kit, Dow Corning Corporation, Michigan, United States) with a culture chamber of the dimensions 10 mm × 10 mm bonded to a 24 mm × 24 mm #0 glass coverslip (85–115 μm; ISO 8255-1:2017) (THORLABS, Mölndal, Sweden; catalog no. CG00C2) as the bottom wall. Before bonding, the glass coverslip and the PDMS chip were rinsed in 70% ethanol and dried under the biological safety cabinet. To accommodate an array of neodymium cylinder-shaped micromagnets in the PC chip, first, the array of holes was fabricated on its surface using CNC micromilling according to the chosen design. Subsequently, the PC chip was placed on top of a large neodymium magnet. The chip was observed under a stereoscopic microscope and micromagnets were manually positioned inside the holes using non-magnetic titanium fine tip tweezers. The spacing between the micromilled holes determined the spacing between the neodymium micromagnets. During the magnetic assembly of EC-microcarriers the device was assembled in such a way that the PDMS chip was mounted on top of the PC chip, tightly aligned with UHU patafix paste to avoid any displacements, and placed under the stereoscopic microscope for inspection and possible corrections.

Numerical simulations

Numerical simulations were performed using COMSOL Multiphysics 6.1 with the AC/DC Module. The simulations were based on the “magnetic fields, no currents” interface to model the magnetic field distributions. The program solves Maxwell's equation ∇·B = 0, where B is the magnetic field defined as B = μ₀μ_rH + B_r, where μ₀ and μ_r correspond to vacuum and relative permeabilities, B_r is remanent magnetic field, and H is the magnetic field strength. Values of μ_r for materials used in this study, i.e., air, NeFeB, and iron, are 1, 1.05, and 4000, respectively. For the domains not being sources of the field, B_r is 0. For the domains acting as permanent magnets, B_r was set to 1.4 T, a value corresponding to N48 grade magnets. H is defined as H = −∇V_m, where V_m is the magnetic scalar potential. A zero-flux boundary condition n·B = 0 was set on the external edges of the system. Two geometries were constructed for the study, as depicted in Fig. S7.

Geometry 1: this model simulated the magnetic field distribution over a ferromagnetic wire with a diameter of 200 μm and a height of 500 μm. A cylindrical permanent magnet (20 mm diameter × 5 mm height) was placed beneath the wire. The permanent magnet served as the source of the magnetic field, while the wire acted as a conduit to guide and concentrate the magnetic field over a localized area.

Geometry 2: this model simulated a permanent NeFeB micromagnet (with dimensions of the wire used in the previous configuration) that generates a magnetic field autonomously.

Both geometries were constructed using a 2D axisymmetric representation to optimize computational efficiency and accurately model the physical setup. To improve the accuracy of the solution in the vicinity of the magnetized wire or micromagnet we introduced an additional fine meshed air domain.

Cell culture

GFP-HUVECs and RFP-HUVECs (Angio-Proteomie, Boston, MA, USA; catalog no. cAP-0001GFP and cAP-0001RFP) were cultured in endothelial cell growth medium 2 (EGM-2) medium supplemented with EGM-2 bulletkit (Lonza, Basel, Switzerland; catalog no. CC-3156 & CC-4176) and were used at passages 3 through 5. NHDF (Promocell, Heidelberg, Germany; catalog no. C-12302) were cultured in Dulbecco's modified Eagle medium (DMEM) (Thermo Fisher Scientific, Waltham, MA, USA; catalog no. 10566016) supplemented with 10% fetal bovine serum (FBS), glutamax, 1% penicillin–streptomycin. NHDF were used between passages 2 and 7. GFP-HeLa cells (GeneTarget Inc, San Diego, CA, USA; catalog no. SC034-Puro) were cultured in DMEM supplemented with 10% FBS, glutamax, 1% penicillin–streptomycin and 0.1 mM Mem non-essential amino acid solution (Merck KGaA, Darmstadt, Germany catalog no.7145). All cells were cultured in 5% CO₂ at 37 °C humidified atmosphere and media were replaced every 2 days.

hiPSC culture and differentiation into endothelial cells

The hiPSC lines were cultured in accordance with National Institute of Molecular Genetics, Italy guidelines and applicable Italian regulations. Ethical approval and informed consent were not required, as the study involved only a commercially available established human cell line. Commercial hiPSC lines derived from healthy donors (ThermoFisher Scientific, Waltham, MA, USA; catalog no. A18944) were cultured and expanded using TeSR E8 complete medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 05990 and 05991) at 37 °C, 5% CO₂ and closely monitored daily. The endothelial differentiation kit (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08005) was employed for the iPSC differentiation into endothelial cells (EC). Briefly, iPSCs were dissociated with gentle cell dissociation reagent (StemCell Technologies, Vancouver, BC, Canada; catalog no. 07174) at 37 °C for 8 min. A single-cell suspension was obtained pipetting up and down 3–4 times and the cells were collected and centrifuged at 300g for 5 min. The hiPSCs were then resuspended in fresh Tesr-E8 medium supplemented with 10 μM RevitaCell (Thermo Fisher Scientific, Waltham, MA, USA; catalog no. A2644501) and 2 × 10⁵ cells per well were seeded on pre-coated Matrigel (Corning, NY, USA; catalog no. 354277) 6-well plates. After 24 hours of incubation at 37 °C, the medium was replaced with STEMdiff Mesoderm Induction Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 05221). Starting from day 3, cells were maintained in STEMdiff Endothelial Induction Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08006), and the medium was changed every 48 h. By day 7, cells were enzymatically detached using Accutase (StemCell Technologies, Vancouver, BC, Canada; catalog no. 07920) and seeded on 6-well plates pre-coated with ACF cell attachment substrate (StemCell Technologies, Vancouver, BC, Canada; catalog no. 07130) in complete STEMdiff Endothelial Expansion Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08008 and 08009). A seeding density of 1 × 10⁴ cells per cm² was used to achieve cell confluency between days 3 and 5 post-seeding. Immunofluorescence and flow cytometry were performed on day 7 of the protocol to evaluate the EC differentiation.

Coating of the beads with endothelial cells

Coating of the beads with HUVECs was performed as described previously.³¹ Briefly, fluorescently tagged HUVECs were mixed with monodispered polystyrene superparamagnetic microcarrier beads of diameter 265 μm, SD = 3.4 μm (CV = 1.3%; microParticles GmbH, Berlin, Germany; catalog no. PS-MAG-AR111) at the concentration of approximately ∼500 cells per bead in a small volume of warm EGM-2 medium and placed in the incubator for 4 hours at 37 °C and 5% CO₂, gently shaking the tube every 20 min. After 4 hours, beads were transferred to a culture flask with fresh EGM-2 medium and placed overnight in the incubator at 37 °C and 5% CO₂. The following day beads were seeded in a culture chamber of the device.

For hiPSC-EC microcarrier beads were pre-coated with ACF Cell Attachment Substrate (StemCell Technologies, Vancouver, BC, Canada; catalog no. 07130) for 2 h at RT with agitation. Subsequently, the beads were transferred to a new Eppendorf tube, washed 3 times with PBS for 5 min, resuspended in complete STEMdiff Endothelial Expansion Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08008 and 08009) and mixed with hiPSC-EC for 2 hours at 37 °C and 5% CO₂, gently shaking the tube every 20 min. After 2 hours, beads were transferred to a culture flask with fresh complete STEMdiff Endothelial Expansion Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08008 and 08009) and placed for 2 hours in the incubator at 37 °C and 5% CO₂. The same day hiPSC-EC coated beads were seeded in the culture chamber of the device.

Seeding the device and generation of the arrays

EC-coated beads were gently washed with fresh medium, appropriate for the used cells, and resuspended in freshly prepared 2.5 mg ml⁻¹ fibrinogen solution (Sigma-Aldrich, St. Louis, MO, USA; catalog no. 341573). Precisely, for each array, 25 microbeads were resuspended in 180 μl of 2.5 mg mL⁻¹ fibrinogen solution, and poured into the culture chamber of the PDMS chip. For HUVECs the fibrinogen solution was additionally mixed with 100 000 hDFs. The role of hDFs was to enhance the angiogenic behavior of HUVECs and to form a dense network of stromal cells surrounding developing microcapillaries (Fig. S8). After positioning the PDMS chip containing the polystyrene microparticles above the PC chip containing the array of cylinder-shape neodymium micromagnets, fibrinogen solution was aspirated to an Eppendorf tube, mixed with 20 μl of 6.25 U mL⁻¹ thrombin solution (Sigma-Aldrich, St. Louis, MO, USA; catalog no. T4648) and poured back into the culture chamber of the PDMS chip allowing hydrogel the hydrogel to crosslink (1–2 minutes). The array generation process consisted of two stages. Immediately after pouring the hydrogel solution containing the microparticles into the PDMS culture chamber, approximately the 80% of microparticles self-assembled over the magnetic hotspots. The remaining microparticles were manually positioned using non-magnetic titanium fine-tip tweezers. Fibrin/bead solution was allowed to clot for 5 minutes at room temperature and then at 37 °C and 5% CO₂ for 30 minutes. Finally, 0.8 mL of medium was added to the culture chamber of each PDMS chip. For HUVECs complete EGM-2 supplemented with 10 ng mL⁻¹ human recombinant VEGF-165 (StemCell Technologies, Vancouver, BC, Canada; catalog no.78073) was used. Arrays of hiPSC-EC-coated beads were cultured in complete STEMdiff Endothelial Expansion Medium (StemCell Technologies, Vancouver, BC, Canada; catalog no. 08008 and 08009) without heparin. The medium was changed every other day.

For generation of arrays of EC-aggregates, HUVECs were preincubated for 1 hour with paramagnetic nanoparticles (diameter = 270 nm; microParticles GmbH, Berlin, Germany; catalog no. PS-MAG-AL43).

Drug exposure studies

Arrays of RFP-tagged HUVECs were cocultured with NHDFs and GFP-tagged Hela cells to mimic the cancer microenvironment. The ratio of NHDFs and HeLa cells was 1 : 10. For screening assays, after 4–5 days of culture arrays were exposed to 100 nM and 1000 nM Taxol (Merck KGaA, Darmstadt, Germany, catalog no. PHL89806) or 1 μM and 10 μM sorafenib (Merck KGaA, Darmstadt, Germany, catalog no. SML2653) for 48 h. The morphometric analyses were performed on days 4–5 before adding a drug, and after 48 h of exposure. Compounds were dissolved in dimethyl sulfoxide (DMSO) and added to the medium with less than 0.01% DMSO. The controls were treated with 0.01% DMSO.

FACS analysis

hiPSC-derived ECs were detached, washed, and incubated at RT for 20 min with the following fluorochrome-conjugated antibodies: CD34 Pe-Cy5 (Beckman Coulter, Brea, CA, USA; catalog no. A07777), CD31 BUV737 (BD Biosciences, Franklin Lakes, NJ, USA; catalog no. 748320), and CD45 BV421 (Biolegend, San Diego, CA, USA; catalog no. 368521). Then, cells were washed and resuspended in PBS supplemented with 5% FBS and 2 mM EDTA. The samples were acquired by BD FACSymphony A5 instrument and data were analyzed by FlowJo software v10.8.1.

Immunofluorescence staining

Cells and fibrin blocks were fixed with 4% paraformaldehyde (PFA) for 15 min. Samples were blocked for 30 min with blocking buffer (2% bovine serum albumin [BSA], 2% normal goat serum, and 0.5% Triton X-100 in PBS) at room temperature before overnight incubation at 4 °C with primary antibodies. The following primary antibodies were used: anti-CD31 (Abcam, Cambridge, MA, USA; catalog no. ab24590), anti-Von Willebrand factor (Abcam, Cambridge, MA, USA; catalog no. ab11713), anti-laminin (Sigma-Aldrich, St. Louis, MO, USA; catalog no. L9393). The following day, the samples were washed 3 times for 5 min in PBS and incubated with appropriate fluorescent-conjugated secondary antibodies for 2 h at RT. Primary and secondary antibodies were applied in the blocking buffer. Alexa Fluor 568 Phalloidin (Thermo Fisher Scientific, Waltham, MA, USA; catalog no. A12380) was applied together with secondary antibodies. To visualize nuclei Hoechst dye 2 mg ml⁻¹ (Thermo Fisher Scientific, Waltham, MA, USA; catalog no. H21491) was used at working dilution 1 : 1000.

Isolation of microvascular arrays from the chip

To isolate microvascular arrays, the fibrin blocks containing microparticles were first washed with PBS and then PDMS chip was disassembled manually in such a way that the fibrin block with the array of microparticles remained on the surface of the coverslip. Arrays were transferred into PBS-containing Petri dish using a laboratory spatula.

Image acquisition and analysis

Fluorescence microscopy was performed using Nikon A1 confocal microscope (Nikon Instruments, Inc, Melville, NY, USA) equipped with a PLAN APO 10×/0.45 or 60×/1.20 objectives. Images were collected using NIS-Elements Advanced Research software (Nikon Instruments, Inc, Melville, NY, USA) in the nd2 format, in 16-bit single-channel, with a typical resolution of 1.25 μm pix⁻¹ with respective metadata.

For the morphometric analysis of microvascular networks, we modified a previously developed Python-based segmentation protocol dedicated to morphometric analysis of a single sprouting microbead³¹ to operate in a system composed of multiple microbeads. The segmentation pipeline followed the workflow illustrated in Fig. 2B. Briefly, the images were first max-pooled on the Z-directional slices (taking the maximum intensity value across the stack) and treated with a Gaussian blur followed by adaptive thresholding using the OpenCV2 library.⁵⁶ After the generation of a binary mask representing endothelial cells, two morphological operations—closing and opening—were performed to connect elements from the adaptive threshold output and to eliminate noise. Next, an additional smoothing step was performed, filling small holes of perimeter smaller than 250 μm. Finally, some disconnected elements of the network were removed which amounted to 3% of the total area, thus almost eliminating any background noise while not significantly affecting the network morphology.

Next, the centers of microcarriers were identified. Part of this task was performed manually, and the results were used to train and apply the YOLO v7 machine learning architecture.⁵⁷ The trained software automatically detected the remaining microbead centers in our datasets. The final outputs were reviewed and corrected manually, if necessary. The binarized images were then skeletonized and masked with circles corresponding to the locations of the micro-carriers. Processed images were then used to generate a graph representation, allowing for the calculation of morphological metrics including the total area of the sprouts (i.e., with the masked areas excluded), the total length of the sprouts, the number of tips (connected to at least one micro-carrier), the number of connected components, and the average width of the sprouts (equal to the total area divided by the total length).

Connected component (CC) can be defined as a group of connected bright pixels, with each pixel having in its Moore neighborhood another bright pixel, where Moore neighborhood is defined as the 8 pixels adjacent to a given pixel. In the case of microbead arrays, we limited the definition of CC only to the groups of connected pixels whose area was comparable to the area of a single sprouting bead, A₁ = A_tot/N, where A_tot is the total area of the network (including the area of the cells at the beads) and N = 5 × 5 = 25. We only counted those CCs that fulfill the condition for their area: A_CC > 0.6A₁.

Additionally, we evaluated network connectivity by counting the number of intersections between the network (excluding the tip segments) and the Voronoi cells centered at the microcarriers (Fig. 2C). Voronoi division was also employed to assess the directionality of growth of the capillaries around the individual microcarriers. For each Voronoi cell, and thus for each microcarrier, we measured mass distribution in octants aligned with the directions of a wind rose. The micro-carrier population was classified based on the number of nearest neighbors: corner (3 neighbors), bar (5 neighbors), and center (8 neighbors). Asymmetrical results for corner and bar regions were transformed to a common coordinate system, with all regions oriented to the right (e.g. top bar is transformed by −90 degrees, etc.).

Analysis of the angular area distribution

The circular histograms (radar-charts) presented in Fig. 3A and S2 and S3 consist each of eight bins that evenly divide the range (−π, π) in the polar coordinate system. The radius of each circular ‘slice’ was calculated so that its area was proportional to the vascular network mass in the corresponding angular range. The areas for a given day were normalized by the total area of the vascular network on day 7 averaged over the group of beads with the corresponding location within the matrix (center, edges, or corner). This allowed us to capture the evolution of angular mass distribution with respect to some reference point.

Coefficient of variation of the angular area distribution (Fig. 3B) was calculated as the standard deviation of the areas of the octants for each day, divided by its mean value.

At small bead-to-bead distances (d = 400, 500 μm), where the network becomes dense, the histograms calculated using the above method may reflect the shape of Voronoi cells rather than the rate of sprouting. This is because the shape of the Voronoi cells is close to a square so that the octagonal division results in Voronoi-cell subsections of different areas (see Fig. 2C). Therefore, to address the rate of sprouting more precisely, we also calculated a normalized histogram (for the case d = 500 μm at day 7), in which the network area within each octant was divided by the area of the corresponding Voronoi-cell subsection. We applied this approach only for the central beads (3 × 3 subarray), where the Voronoi cells were indeed nearly square-shaped (see Fig. S3).

Statistical analysis

Directly measured quantitative data were expressed as the mean ± SEM. The statistical methods (one-way analysis of variance followed by Tukey's post hoc test, and two-way analysis of variance followed by Bonferoni post hoc test, two-tailed unpaired t-test) and p-values were defined in the figure legends or Table S1. The statistical analyses were performed using GraphPad Prism 5 and Microsoft Excel software. The results of the statistical analysis are available in the following sheets of the Table S1. Numerical values that underlie the graphs are shown in SI data file.

Author contributions

Conceptualization: KOR, AW, PS, JG. Methodology: KOR, AW, FM, KG, MCG, CB, RR, PS, JG. Experimental investigations: KOR, AW, KG, FM, MCG. Data analyses: KOR, AW, MCG, FM. Writing – original draft: KOR, AW, FM, KG, MCG, JG, PS. Review & editing: KOR, AW, JG. Project administration: KOR, PS, JG. Funding acquisition: KOR, KG, JG.

Conflicts of interest

KOR, KG, and JG are the authors of a pending patent application regarding the method of magnetic assembly of microcarriers. KOR and JG are shareholders of Living Networks sp. z o. o. There are no other conflicts to declare.

Data availability

The data that support the findings of this study are available in the supplementary information (SI) of this article. Code is available to upon request.

Supplementary information: supplementary figures file and Video S1 and S2. The results of the statistical analysis are available in Table S1. Numerical values that underlie the graphs are shown in SI data file. See DOI: https://doi.org/10.1039/d5lc00664c.

Acknowledgements

Preparation of this article was supported by Sonatina (Grant No. 2020/36/C/NZ1/00238 awarded to KOR), Opus (Grant No. 2022/45/B/ST8/03675 awarded to JG) and Sonata (Grant No. 2019/35/D/ST5/03613 awarded to KG) from the Polish National Science Center (NCN).

References

1. V. S. Shirure, C. C. W. Hughes and S. C. George, Engineering Vascularized Organoid-on-a-Chip Models, Annu. Rev. Biomed. Eng., 2021, 23, 141–167.
2. J. J. Tronolone and A. Jain, Engineering new microvascular networks on-chip: ingredients, assembly, and best practices, Adv. Funct. Mater., 2021, 31(14), 2007199.
3. J. A. Kim, J. H. Choi, M. Kim, W. J. Rhee, B. Son and H. K. Jung, et al., High-throughput generation of spheroids using magnetic nanoparticles for three-dimensional cell culture, Biomaterials, 2013, 34(34), 8555–8563.
4. J. S. Jeon, S. Bersini, J. A. Whisler, M. B. Chen, G. Dubini and J. L. Charest, et al., Generation of 3D functional microvascular networks with human mesenchymal stem cells in microfluidic systems, Integr. Biol., 2014, 6(5), 555–563.
5. X. L. Wang, D. T. T. Phan, A. Sobrino, S. C. George, C. C. W. Hughes and A. P. Lee, Engineering anastomosis between living capillary networks and endothelial cell-lined microfluidic channels, Lab Chip, 2016, 16(2), 282–290.
6. D. T. T. Phan, X. L. Wang, B. M. Craver, A. Sobrino, D. Zhao and J. C. Chen, et al., A vascularized and perfused organ-on-a-chip platform for large-scale drug screening applications, Lab Chip, 2017, 17(3), 511–520.
7. J. Paek, S. E. Park, Q. Z. Lu, K. T. Park, M. Cho and J. M. Oh, et al., Microphysiological Engineering of Self-Assembled and Perfusable Microvascular Beds for the Production of Vascularized Three-Dimensional Human Microtissues, ACS Nano, 2019, 13(7), 7627–7643.
8. J. Yu, S. Lee, J. Song, S. R. Lee, S. Kim and H. Choi, et al., Perfusable micro-vascularized 3D tissue array for high-throughput vascular phenotypic screening, Nano Convergence, 2022, 9(1), 16.
9. L. Koch, A. Deiwick and B. Chichkov, Capillary-like Formations of Endothelial Cells in Defined Patterns Generated by Laser Bioprinting, Micromachines, 2021, 12(12), 1538.
10. W. Zhu, X. Qu, J. Zhu, X. Ma, S. Patel and J. Liu, et al., Direct 3D bioprinting of prevascularized tissue constructs with complex microarchitecture, Biomaterials, 2017, 124, 106–115.
11. X. F. Cui and T. Boland, Human microvasculature fabrication using thermal inkjet printing technology, Biomaterials, 2009, 30(31), 6221–6227.
12. Y. S. Zhang, A. Arneri, S. Bersini, S. R. Shin, K. Zhu and Z. Goli-Malekabadi, et al., Bioprinting 3D microfibrous scaffolds for engineering endothelialized myocardium and heart-on-a-chip, Biomaterials, 2016, 110, 45–59.
13. F. Maiullari, M. Costantini, M. Milan, V. Pace, M. Chirivì and S. Maiullari, et al., A multi-cellular 3D bioprinting approach for vascularized heart tissue engineering based on HUVECs and iPSC-derived cardiomyocytes, Sci. Rep., 2018, 8(1), 13532.
14. H. G. Yi, Y. H. Jeong, Y. Kim, Y. J. Choi, H. E. Moon and S. H. Park, et al., A bioprinted human-glioblastoma-on-a-chip for the identification of patient-specific responses to chemoradiotherapy, Nat. Biomed. Eng., 2019, 3(7), 509–519.
15. E. P. Chen, Z. Toksoy, B. A. Davis and J. P. Geibel, 3D Bioprinting of Vascularized Tissues for in vitro and in vivo Applications, Front. Bioeng. Biotech., 2021, 9, 664188.
16. R. Hooper, C. Cummings, A. Beck, J. Vazquez-Armendariz, C. Rodriguez and D. Dean, Sheet-based extrusion bioprinting: a new multi-material paradigm providing mid-extrusion micropatterning control for microvascular applications, Biofabrication, 2024, 16(2), 025032.
17. V. Mironov, R. P. Visconti, V. Kasyanov, G. Forgacs, C. J. Drake and R. R. Markwald, Organ printing: Tissue spheroids as building blocks, Biomaterials, 2009, 30(12), 2164–2174.
18. B. Ayan, D. N. Heo, Z. F. Zhang, M. Dey, A. Povilianskas and C. Drapaca, et al., Aspiration-assisted bioprinting for precise positioning of biologics, Sci. Adv., 2020, 6(10), eaaw5111.
19. B. Ayan, N. Celik, Z. F. Zhang, K. Zhou, M. H. Kim and D. Banerjee, et al., Aspiration-assisted freeform bioprinting of pre-fabricated tissue spheroids in a yield-stress gel, Commun. Phys., 2020, 3, 183.
20. M. Dey, M. H. Kim, M. Dogan, M. Nagamine, L. Kozhaya and N. Celik, et al., Chemotherapeutics and CAR-T Cell-Based Immunotherapeutics Screening on a 3D Bioprinted Vascularized Breast Tumor Model, Adv. Funct. Mater., 2022, 32(52), 2203966.
21. M. H. Kim, Y. P. Singh, N. Celik, M. Yeo, E. Rizk and D. J. Hayes, et al., High-throughput bioprinting of spheroids for scalable tissue fabrication, Nat. Commun., 2024, 15(1), 10083.
22. L. De Moor, I. Merovci, S. Baetens, J. Verstraeten, P. Kowalska and D. V. Krysko, et al., High-throughput fabrication of vascularized spheroids for bioprinting, Biofabrication, 2018, 10(3), 035009.
23. B. C. Casali, M. P. Baptista, B. C. Pachane, A. A. Cortez, W. F. Altei and H. S. Selistre-de-Araújo, Blockage of αvβ3 integrin in 3D culture of triple-negative breast cancer and endothelial cells inhibits migration and discourages endothelial-to-mesenchymal plasticity, Biochem. Biophys. Rep., 2024, 38, 101686.
24. M. Schot, M. Becker, C. A. Paggi, F. Gomes, T. Koch and T. Gensheimer, et al., Photoannealing of Microtissues Creates High-Density Capillary Network Containing Living Matter in a Volumetric-Independent Manner, Adv. Mater., 2024, 36(28), e2308949.
25. W. Song, A. Chiu, L. H. Wang, R. E. Schwartz, B. Li and N. Bouklas, et al., Engineering transferrable microvascular meshes for subcutaneous islet transplantation, Nat. Commun., 2019, 10, 4602.
26. S. Yamamoto, M. M. Hotta, M. Okochi and H. Honda, Effect of vascular formed endothelial cell network on the invasive capacity of melanoma using the in vitro 3D co-culture patterning model, PLoS One, 2014, 9(7), e103502.
27. R. Z. Lin, W. C. Chu, C. C. Chiang, C. H. Lai and H. Y. Chang, Magnetic reconstruction of three-dimensional tissues from multicellular spheroids, Tissue Eng., Part C, 2008, 14(3), 197–205.
28. K. Ino, M. Okochi and H. Honda, Application of magnetic force-based cell patterning for controlling cell-cell interactions in angiogenesis, Biotechnol. Bioeng., 2009, 102(3), 882–890.
29. V. H. B. Ho, K. H. Müller, A. Barcza, R. J. Chen and N. K. H. Slater, Generation and manipulation of magnetic multicellular spheroids, Biomaterials, 2010, 31(11), 3095–3102.
30. N. Demri, S. Dumas, M. L. Nguyen, G. Gropplero, A. Abou-Hassan and S. Descroix, et al., Remote Magnetic Microengineering and Alignment of Spheroids into 3D Cellular Fibers, Adv. Funct. Mater., 2022, 32(50), 2204850.
31. K. O. Rojek, A. Wrzos, S. Zukowski, M. Bogdan, M. Lisicki and P. Szymczak, et al., Long-term day-by-day tracking of microvascular networks sprouting in fibrin gels: From detailed morphological analyses to general growth rules, APL Bioeng., 2024, 8(1), 016106.
32. N. E. Friend, A. Y. Rioja, Y. P. Kong, J. A. Beamish, X. Hong and J. C. Habif, et al., Injectable pre-cultured tissue modules catalyze the formation of extensive functional microvasculature in vivo, Sci. Rep., 2020, 10(1), 15562.
33. M. Sofman, A. Brown, L. G. Griffith and P. T. Hammond, A modular polymer microbead angiogenesis scaffold to characterize the effects of adhesion ligand density on angiogenic sprouting, Biomaterials, 2021, 264, 120231.
34. A. Y. Rioja, E. L. H. Daley, J. C. Habif, A. J. Putnam and J. P. Stegemann, Distributed vasculogenesis from modular agarose-hydroxyapatite-fibrinogen microbeads, Acta Biomater., 2017, 55, 144–152.
35. Y. Iwata, W. D. Klaren, C. S. Lebakken, F. A. Grimm and I. Rusyn, High-Content Assay Multiplexing for Vascular Toxicity Screening in Induced Pluripotent Stem Cell-Derived Endothelial Cells and Human Umbilical Vein Endothelial Cells, Assay Drug Dev. Technol., 2017, 15(6), 267–279.
36. M. N. Nakatsu, R. C. A. Sainson, S. Pérez-dei-Pulgar, J. N. Aoto, M. Aitkenhead and K. L. Taylor, et al., VEGF regulate blood vessel diameter through vascular endothelial growth fact or receptor 2 in an in vitro angiogenesis model, Lab. Invest., 2003, 83(12), 1873–1885.
37. L. Martineau and C. J. Doillon, Angiogenic response of endothelial cells seeded dispersed versus on beads in fibrin gels, Angiogenesis, 2007, 10(4), 269–277.
38. C. M. Ghajar, X. Chen, J. W. Harris, V. Suresh, C. C. W. Hughes and N. L. Jeon, et al., The effect of matrix density on the regulation of 3-D capillary morphogenesis, Biophys. J., 2008, 94(5), 1930–1941.
39. J. R. Bezenah, Y. P. Kong and A. J. Putnam, Evaluating the potential of endothelial cells derived from human induced pluripotent stem cells to form microvascular networks in 3D cultures, Sci. Rep., 2018, 8, 2671.
40. A. C. Newman, M. N. Nakatsu, W. Chou, P. D. Gershon and C. C. W. Hughes, The requirement for fibroblasts in angiogenesis: fibroblast-derived matrix proteins are essential for endothelial cell lumen formation, Mol. Biol. Cell, 2011, 22(20), 3791–3800.
41. S. Zhang, Z. P. Wan and R. D. Kamm, Vascularized organoids on a chip: strategies for engineering organoids with functional vasculature, Lab Chip, 2021, 21(3), 473–488.
42. A. Sobrino, D. T. Phan, R. Datta, X. Wang, S. J. Hachey and M. Romero-Lopez, et al., 3D microtumors in vitro supported by perfused vascular networks, Sci. Rep., 2016, 6, 31589.
43. E. Hirth, W. J. Cao, M. Peltonen, E. Kapetanovic, C. Dietsche and S. Svanberg, et al., Self-assembled and perfusable microvasculature-on-chip for modeling leukocyte trafficking, Lab Chip, 2024, 24(2), 292–304.
44. D. A. Murphy, S. Makonnen, W. Lassoued, M. D. Feldman, C. Carter and W. M. F. Lee, Inhibition of tumor endothelial ERK activation, angiogenesis, and tumor growth by sorafenib (BAY43-9006), Am. J. Pathol., 2006, 169(5), 1875–1885.
45. G. Bocci, A. Di Paolo and R. Danesi, The pharmacological bases of the antiangiogenic activity of paclitaxel, Angiogenesis, 2013, 16(3), 481–492.
46. R. Mooney, B. Tawil and M. Mahoney, Specific Fibrinogen and Thrombin Concentrations Promote Neuronal Rather Than Glial Growth When Primary Neural Cells Are Seeded Within Plasma-Derived Fibrin Gels, Tissue Eng. Part A, 2010, 16(5), 1607–1619.
47. C. L. Chiu, V. Hecht, H. Duong, B. Wu and B. Tawil, Permeability of Three-Dimensional Fibrin Constructs Corresponds to Fibrinogen and Thrombin Concentrations, Biores. Open Access, 2012, 1(1), 34–40.
48. S. Miyamoto and K. Shimono, Molecular Modeling to Estimate the Diffusion Coefficients of Drugs and Other Small Molecules, Molecules, 2020, 25(22), 5340.
49. V. S. Shirure, Y. Bi, M. B. Curtis, A. Lezia, M. M. Goedegebuure and S. P. Goedegebuure, et al., Tumor-on-a-chip platform to investigate progression and drug sensitivity in cell lines and patient-derived organoids, Lab Chip, 2018, 18(23), 3687–3702.
50. M. Feodoroff, P. Mikkonen, L. Turunen, A. Hassinen, L. Paasonen and L. Paavolainen, et al., Comparison of two supporting matrices for patient-derived cancer cells in 3D drug sensitivity and resistance testing assay (3D-DSRT), SLAS Discovery, 2023, 28(4), 138–148.
51. P. Shen, Y. Jia, W. Zhou, W. Zheng, Y. Wu and S. Qu, et al., A biomimetic liver cancer on-a-chip reveals a critical role of LIPOCALIN-2 in promoting hepatocellular carcinoma progression, Acta Pharm. Sin. B, 2023, 13(11), 4621–4637.
52. H. S. Dorward, A. Du, M. A. Bruhn, J. Wrin, J. V. Pei and A. Evdokiou, et al., Pharmacological blockade of aquaporin-1 water channel by AqB013 restricts migration and invasiveness of colon cancer cells and prevents endothelial tube formation, J. Exp. Clin. Cancer Res., 2016, 35, 36.
53. H. W. Chung and J. B. Lim, High-mobility group box-1 contributes tumor angiogenesis under interleukin-8 mediation during gastric cancer progression, Cancer Sci., 2017, 108(8), 1594–1601.
54. S. M. Wilhelm, C. Carter, L. Y. Tang, D. Wilkie, A. McNabola and H. Rong, et al., BAY 43-9006 exhibits broad spectrum oral antitumor activity and targets the RAF/MEK/ERK pathway and receptor tyrosine kinases involved in tumor progression and angiogenesis, Cancer Res., 2004, 64(19), 7099–7109.
55. R. Hujanen, T. Salo, K. K. Eklund and A. Salem, Ex Vivo Evaluation of Antiangiogenic Drugs in Oral Cancer: Potential Implications for Targeting Vasculogenic Mimicry, Anticancer Res., 2024, 44(6), 2377–2392.
56. G. Bradski, The OpenCV library, Dr. Dobb's Journal of Software Tools, 2000, 25(11), 120 , 122–125.
57. C. Y. Wang, H. Y. M. Liao and I. H. Yeh, Designing Network Design Strategies Through Gradient Path Analysis, J. Inf. Sci. Eng., 2023, 39(3), 975–995.

---