Electroporation of spheroids using an electric field gradient: a tool to study intensity-dependent permeabilization
Théo
Le Berre
 *a,
Julien
Marchalot
*a,
Julien
Marchalot
 a,
Guilhem
Rival
a,
Guilhem
Rival
 b,
Laure
Franqueville
b,
Laure
Franqueville
 a,
Rabia
Önbaş
c,
Charlotte
Riviere
a,
Rabia
Önbaş
c,
Charlotte
Riviere
 cde,
Gabriel
Marcellier
cde,
Gabriel
Marcellier
 f,
Frédéric
Prat
fg and
Marie
Frénéa-Robin
f,
Frédéric
Prat
fg and
Marie
Frénéa-Robin
 a
a
aEcole Centrale de Lyon, INSA Lyon, Universite Claude Bernard Lyon 1, CNRS, Ampère, UMR5005, 69130 Ecully, France. E-mail: theo.le-berre@ec-lyon.fr
bINSA Lyon, LGEF, UR682, 69621 Villeurbanne, France
cUniv Lyon, Université Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, F69622, Villeurbanne, France
dInstitut Universitaire de France (IUF), France
eInstitut Convergence PLAsCAN, Centre de Cancérologie de Lyon, INSERM U1052CNRS UMR5286, Université de Lyon, Université Claude Bernard Lyon 1, Centre Léon Bérard, Lyon, France
fDept of endoscopy, Beaujon hospital, Clichy, AP-HP, France
gUniversité Paris-cité, France
First published on 26th November 2025
Abstract
Electroporation (EPN) is the process by which cell membranes become transiently or permanently permeable upon exposure to pulsed electric fields of suitable intensity and duration. Depending on the pulse parameters, permeabilization can be reversible or irreversible, enabling a wide range of biomedical applications. To improve our understanding of EPN effects on tissues and select efficient treatments and parameters, relevant in vitro tumour models are required. Three-dimensional (3D) cell spheroids have emerged as valuable systems, as they more accurately replicate tumour microenvironment and cell-to-cell interactions than conventional 2D cultures. In this work, we present a new microdevice designed for the culture and gradual electroporation of a population of several hundred uniformly sized spheroids, allowing the systematic study of electroporation over a wide range of electric field intensities within a single experiment. Gradual permeabilization of HT-29 colorectal cancer cell spheroids was performed using a standard electrochemotherapy protocol, and electroporation efficiency was assessed by analysing propidium iodide (PI) uptake. Spheroids were treated with electric fields ranging from 800 V cm−1 to 3400 V cm−1. In toto analysis of PI distribution within spheroids by confocal microscopy revealed highly heterogeneous permeabilization patterns throughout the spheroid volume, for all intensities investigated, even at the highest one of 3400 V cm−1. This study introduces a robust 3D in vitro assay for the systematic evaluation of electroporation-based treatments, providing new insights into the influence of electric field heterogeneity, electrical protocol, and estimation of molecular uptake in the spheroid volume.
Introduction
Classical in vitro models like cell suspensions or 2D cell layers fail to recapitulate 3D cellular interactions that can be observed in vivo. In this regard, 3D aggregates like spheroids are considered a more relevant in vitro model for drug screening, as they do present cohesion and communication between cells, as well as gradients of nutrients and dioxygen.1–3 The spheroid model can also be refined with the introduction of more than one cell type to form a microenvironment, or use primary cells derived from patients' tumours to form tumoroids.4Spheroids and tumoroids have raised interest to mimic avascular tumours, and as such, can help to understand the impact of different treatments and drugs on tumour cells behaviour.5
Electroporation (EPN) is a phenomenon that occurs when exposing cells to a pulsed electric field (PEF) above a certain threshold, provoking the permeabilization of the membrane.6 Depending on the number of pulses, their duration, and their intensity, the permeabilization can be reversible or irreversible. In the last decades, different treatments based on EPN have been developed, making it a viable tool in human and veterinary oncology.7
Irreversible electroporation (IRE) has been used as a non-thermal ablation method since the early 2000s,8,9 with eighty to a hundred 100 μs high-intensity square pulses10 and a repetition frequency of 1 Hz. It induces cell death locally while preserving the overall structure of the targeted area. It is thus an interesting therapy for solid deep-seated tumours localised near vital structures. Clinical studies have shown the efficacy of this therapy on kidney, pancreas, liver, and prostate tumours.7 Beyond oncology, IRE has also been used to treat cardiac arrhythmia.11
Electrochemotherapy (ECT) takes advantage of the reversible membrane permeabilization caused by PEF12 to deliver chemotherapeutic molecules into tumour cells. Studied since the late 1980s, ECT usually uses around eight 100 μs square pulses, whose intensity is set lower than IRE,13 and is shown to potentiate the cytotoxicity of drugs otherwise unable to penetrate cells. In addition to bleomycin and cisplatin as the drugs of choice,14,15 calcium ECT has recently been introduced as an alternative modality.16,17 The main clinical results for ECT have been achieved in melanoma, Kaposi's sarcoma, basal cell carcinoma, as well as some breast and renal cell carcinoma.7 The same principle can also be used to facilitate the delivery of other therapeutic agents into cells, such as DNA or immunomodulatory drugs for therapies known as gene electrotransfer (GET)18 and electroimmunotherapy.19 Another therapeutic strategy is the use of EPN to induce the so-called “fusogenic” state, allowing adjacent cells to merge into a single fused cell. The effect on the immune system can be interesting in oncology as the electrofusion of dendritic cells with cancer cells has a demonstrable anti-tumour effect both in vitro and in vivo.20 Those PEF-based therapies are less mature than IRE and ECT, but are promising solutions for the local treatment of tumours.7 The development of new EPN-based cancer treatment procedures involves drug screening to identify the most promising molecules and the concentrations to be used, as well as optimisation of electroporation parameters such as pulse duration and intensity.21–24 EPN on spheroids is usually performed with parallel electrodes in cuvettes and with commercially available electroporators.17 The experimental steps of spheroid handling, like pipetting, may lead to damage and a random localisation in the cuvette causing a variation in the electric field perceived by each spheroid. The microfluidic-based approach is thus interesting to study electroporation on in vitro models while minimising sample manipulation and improving electric field distribution. The electroporation and monitoring of single cells passing through a microfluidic channel has for example been described,22,25 as well as the use of specifically designed micro-chambers for culture and electroporation,26,27 however they do not allow the production and electroporation of identical 3D aggregates arranged in an array. Without studying EPN specifically, microsystems have been recently designed for the culture and impedance monitoring of an array of spheroids.28 A microfluidic platform specifically designed by our team for culture, electroporation, and observation of spheroids with regular size and shape has been recently described.29 This device enables electroporation of three hundred spheroids under similar conditions.
Here, we present a new microfluidic device derived from our previous work and designed to measure the impact of electroporation on a spheroid population in relation to the electric field intensity, to study the effect of the electric field parameters on the spheroids in a single experiment, thus allowing an assessment of the intensity-dependent effect of EPN on spheroids for a given protocol in a single experiment.
Three experiments are presented in this article, the first being a comparison of measured and expected electrode potentials to assess the validity of the numerical model describing the chamber. The second is the electroporation of a HT-29 spheroid array in the presence of fluorophores, performed in triplicate to assess the repeatability of the procedure. Finally, a more detailed study on HT-29 spheroids using confocal microscopy describes the distribution of permeabilization in the aggregate volume as a function of electric field intensity.
Methods
Design and fabrication of the microsystem
The system presented in Fig. 1 contains a microfluidic chamber with a volume of approximately 200 μL, delimited by a 1 mm silicone seal (Grace Bio-Labs, Merck) and two glass slides on top and bottom. The lower glass slide is fully coated with ITO (indium tin oxide glass slide, 120 to 160 nm, Sigma-Aldrich) while the upper is gold-coated (100 nm thickness on a 50 nm layer of chromium, Neyco, France) and wet-etched. The chamber contains a micro-structured hydrogel scaffold, 500 μm thick, featuring 269 wells, each with a diameter of 200 μm and a depth of 300 μm. The upper glass slide is pierced at two points with a Microblaster® (Comco Inc) and air-plasma bonded (plasma cleaner, Harrick Plasma) to a similarly pierced PDMS spacer to allow the introduction of microfluidic capillaries. The gold layer coating on the upper slide is structured to form eight independent electrodes above the hydrogel, as presented in Fig. 1d. Electrical connexions are provided by spring contacts (spring finger, TE connectivity and rounded test probe, RS Pro) mounted on custom-made printed circuit boards (PCB). Eight variable resistors (0–10 kΩ) (RS components) are added to control the electrical potential on each electrode, as presented in Fig. 1c. A PMMA structure is used to host the PCB and ensure water-tightness.Both the printed circuit boards (PCB) and the gold electrode were etched using wet etching method, with ferric chloride for the PBC and successive baths of gold etchant and chrome etchant (Sigma-Aldrich) for the gold electrode. AZ 5214 photoresist (Merck) was used as the masking material, and the UV KUB 2 (Kloe) was employed for exposure. The structure of the device was manufactured from 3 mm and 5 mm thick plates of PMMA processed with laser etching and cutting (Speedy 400, Trotec). PMMA pieces were assembled with M3 bolds and chemical bonding with dichloromethane (Sigma-Aldrich). The silicone seal was cut using a silhouette cameo cutting machine from a 0.5 mm silicone sheet; two seals were stacked to form the 1 mm joint.
Distribution of the electric field in the chamber
The distribution of the electric field was computed with the FEM software COMSOL using a combination of the AC/DC module, “Electric Current” (ec) study in steady state,30,31 the “Electric Currents in Layered Shells” (ecls) module and the “Electric circuit” (cir) module. The geometry is presented in Fig. 1e. The chamber was modelled as a box empty of spheroids, with the electrical properties of the EPN buffer, namely a conductivity of 309 μS cm−1 and a relative permeability of 78. Eight different resistors labelled R1 to R8 were defined through the cir module and linked to the eight upper electrodes. The lower electrode model was defined through the ecls module to take into account the electric losses in the ITO layer, of conductivity 7.1 × 105 S m−1 for a thickness of 134 nm, which significantly influences the potential and electric field distribution in the chamber. The electrical ground was set at the far edge of the lower electrode to be close to the actual electrical contact in the circuit. The norm of the electric field was plotted along a line perpendicular to the electrodes, at the height of the centre of the spheroids, 300 μm from the lower electrode. The general principle of the simulation is visible in Fig. 1c and e.The overall principle of this model is to build a function with ten numerical inputs (eight resistors, the input voltage and the conductivity of the solution), to achieve the desired distribution of electric field within the chamber. The data of interest is the electric field distribution on a longitudinal axis at the level of the spheroids in their medium. It represents the electric field intensity to which the spheroids will be exposed during electroporation. These data will be used for resistor tuning. Fig. 1e presents the distribution of electric field, for a given resistor setting (Fig. 1f).
As the electroporation protocol used have a low total energy, no rise in temperature was considered during treatment.
Electric resistor tuning method
Given a set of values for the resistors, and a conductivity for the solution in the chamber, the electric field computed is a linear function of the input voltage Vin. Thus, this voltage can be removed from the input data through normalization: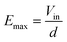 | (1) |
In the tuning program, only the relative electric field was considered, as a percentage of Emax. The conductivity of the chamber was set at the measured conductivity of the solution used for electroporation at ambient temperature, 309 μS cm−1.
A target curve was set for the norm of the relative electric field at spheroid height. The COMSOL LiveLink for Matlab was used to calculate an optimized set of resistor values using the fminsearch command, based on the Nelder–Mead algorithm (Matlab optimization toolbox) so as to minimize the sum of squared errors between the target value and the computed value, evaluated on discrete points distributed each half millimetre along the chamber. The resulting curve was close to an interpolation of the target values, and the resistors are tuned accordingly on the PCB.
Validation of the device
The accuracy of the numerical model was evaluated through a direct measure of the potential on each electrode when the device was submitted to a known voltage, with the chamber filled with a solution of known conductivity.The device was mounted with a chamber containing the electroporation buffer at room temperature, whose conductivity was measured using a conductivity meter (Mettler Toledo, Seven Compact). The device was submitted to an AC signal of 3 VRMS (500 kHz) using an arbitrary waveform generator (Agilent 33250A). The potential on each electrode was measured using manual probes, the values were read on an oscilloscope (Agilent DSO5012A). The frequency was chosen to avoid the double-layer influence appearing at low frequency (typically below 10 kHz), which is not present in the numerical model.
Cell culture in the hydrogel scaffold
HT-29 colorectal cancer cells (ATCC HTB-38, USA) were cultured at 37 °C in a 5% CO2 humidified atmosphere in T-25 flasks in a culture medium composed of high glucose Dulbecco's modified Eagle's medium (DMEM, Dutscher), 10% heat-inactivated foetal bovine serum (FBS, Dutscher), 1% penicillin/streptomycin (Dutscher) and 1% MEM non-essential amino acids (NEAA, Dutscher).The moulded hydrogel (2% agarose D5 standard DNA grade, Euromedex) was grafted on an ITO-coated slide previously functionalized with (3-aminopropyl)triethoxysilane (3-APTS, Sigma-Aldrich) solution (1% APTS and 5 mM acetic acid in deionized water). The whole moulding and grafting process are described elsewhere.29,32
A volume of 200 μL of a 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cell per mL cell suspension was deposited on the micro-structured hydrogel scaffold bonded to an ITO coated slide. The latter was placed in a petri dish for 10 minutes on an orbital agitator to ensure cell seeding into the micro-wells homogenously. The excess solution was then removed and the cell-seeded hydrogel was placed in the incubator for 3 to 7 days to form spheroids.
000 cell per mL cell suspension was deposited on the micro-structured hydrogel scaffold bonded to an ITO coated slide. The latter was placed in a petri dish for 10 minutes on an orbital agitator to ensure cell seeding into the micro-wells homogenously. The excess solution was then removed and the cell-seeded hydrogel was placed in the incubator for 3 to 7 days to form spheroids.
A specific mould was designed for this experiment, to ensure the placement of the hydrogel on the bottom electrode, and thus precise and repeatable positioning of the spheroids in the chamber. The design and a picture of the mould are presented in SI material.
Electroporation protocol
For electroporation, the medium needs to be changed from culture medium to a less conductive Hepes-based EPN buffer to minimize the current delivered in the system and protect the thin electrodes from degradation. The change was made by rinsing three times for 5 minutes to allow complete diffusion of the solution into the hydrogel.The EPN buffer is composed of 10 mM of Hepes (Merck), 1 mM of magnesium chloride hexahydrate (MgCl2 (6H2O), Merck) and 250 mM of saccharose (Roth) dissolved in deionized water. A few drops of 10 M sodium hydroxide (NaOH, Merck) are added while monitoring pH to adjust it to 7.1.
The third rinsing bath was performed adding propidium iodide (PI, 20 μM, Merck) to the buffer. PI is commonly used to label cells having lost their membrane integrity, meaning dead or electroporated cells, as already described in the literature.24,29,33–35
The EPN protocol used was similar to the classical ECT protocol described in the guidelines,13 the electroporation was performed with a commercial device (Electrocell B15, Leroy Biotech), with 8 monopolar square pulses of 100 μs length, and a repetition frequency of 1 Hz. The current was monitored by the equipment, which enabled to check the proper delivery of the pulses. The input voltage for each experiment was fixed at 380 V. For convenience, this electrical protocol will be referred to as one ESOPE protocol in the rest of this paper (in reference to the European Standard Operating Procedures on Electrochemotherapy13).
After EPN, the ITO-coated slide was dipped for 5 minutes into a phosphate-buffered saline buffer (PBS w/o Ca Mg, Dutscher) containing fluorescein diacetate (FDA, Merck) at a concentration of 12 μM to label living cells in green, and then dipped in PBS alone for 2 minutes to wash the excess of FDA.
During each rising bath after the addition of fluorophores, samples were protected from light.
Fluorescence imaging
After EPN and exposition to PBS with FDA, the hydrogel was observed under a fluorescence microscope (AxioImager M1, Colibri 5 light source, Zeiss) with 2.5× magnification. A 10 images z-stack was acquired for each area of the sample, with the first and last focal length being respectively just below and above the spheroids. The wavelength of PI excitation is 555 nm, used at maximum intensity, with an acquisition time of 350 ms. For the FDA channel, the wavelength is 475 nm, used at maximum intensity, with an acquisition time of 20 ms. The images for each area were assembled using the stitching function of the Zen (Zeiss) software, taking as a baseline the middle-stack FDA-channel image. The resulting image is a recomposed 2-channel/10 images z-stack of the whole population of spheroids.This recomposed 2-channel/10 images z-stack was converted with ImageJ software into one image per channel of max intensity projection (MIP) of the z-stacks, giving a 2-channel image of the whole population of spheroids. Regions of interest (ROI) were defined using the particle analysis feature of ImageJ, and the median intensity of the fluorophores per spheroids was then measured on the MIP images of the two channels. The position of the spheroids is considered known based on the mould.
The array being organized in columns, it is considered that each spheroid in a column was exposed to the same electric field. The dataset is thus sorted into 23 columns of approximately 12 spheroids each.
Confocal imaging
After fluorescence microscopy imaging, the samples were rinsed in PBS, 3 times for 5 minutes, and fixed with paraformaldehyde (3.7% PFA in PBS, Merk) for 20 minutes, then rinsed in PBS again. To optimize optical sectioning with confocal microscopy, the spheroids were clarified to uniformize the refractive indexes in the volume with a solution of glycerol (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 in PBS), as previously described.29 The imaging was done on a Leica SP5 confocal microscope, using 3 μm slices and ×25 magnification (NA 0.95). As FDA tends to bleach quickly with temperature and exposition to light, only the PI signal was measured at this stage.
20 in PBS), as previously described.29 The imaging was done on a Leica SP5 confocal microscope, using 3 μm slices and ×25 magnification (NA 0.95). As FDA tends to bleach quickly with temperature and exposition to light, only the PI signal was measured at this stage.
Images were acquired on five columns, regularly placed across the chamber. Four spheroids were imaged per column, as well as four spheroids from a live sample. Acquisition parameter were set to reach near saturation with the most intense signal. The data was processed with ImageJ software.
Protocol
A preliminary experiment was performed to measure the intensity and background noise of FDA and PI signals on live spheroids with fluorescence microscopy. This control group was thus cultured using the previously described protocol, in the absence of the electric field.A second experiment was conducted to measure the repeatability of exposure to the electric fields using small spheroids. Three arrays of spheroids cultured for 3 days (approximately 100 μm in diameter) were electroporated with a linear gradient of electric field in the presence of PI, as described previously. The electric field was tuned to reach 20% to 90% of Emax, with an input voltage of 380 V, which corresponds to intensities ranging from 900 V cm−1 to 3400 V cm−1 approximately. The three curves representing PI uptake versus position were acquired with fluorescence microscopy (×2.5 magnification) and compared to assess repeatability.
Finally, EPN was performed on an array of larger spheroids (approximately 200 μm in diameter), cultured for 6 days with the same setup. PI and FDA uptake were acquired with fluorescence microscopy (×2.5 magnification). This array was then fixed, clarified and imaged by confocal microscopy (×25 magnification, NA 0.95) in order to localize the PI uptake within the spheroid volume depending on the electric field intensity.
Results
Device validation
The desired shape of the electric field in the chamber is a linear gradient along the spheroid array, from the minimum possible value on one side of the grid to the maximum value on the other. Fig. 2 presents the target values for the relative electric field, along with the computed relative electric field in the chamber, and the corresponding resistor values, in Table 1, resulting from the tunning program. | ||
| Fig. 2 Computed ratio of electric field in the chamber after resistor tuning, target values used are represented as red crosses. Spheroid column's positions are represented as blue vertical lines. | ||
| No. | R (Ω) | Computed solution V/Vin (%) | Experimental measure lean V/Vin (%) | Error (%) |
|---|---|---|---|---|
| 1 | 5 | 99.8% | 99.9% | 0.1% |
| 2 | 976 | 80.8% | 80.7% | −0.1% |
| 3 | 1236 | 74.3% | 74.6% | 0.4% |
| 4 | 2171 | 63.8% | 64.3% | 0.8% |
| 5 | 2877 | 55.6% | 56.6% | 1.9% |
| 6 | 5142 | 44.3% | 46.3% | 4.2% |
| 7 | 5389 | 38.5% | 41.1% | 6.3% |
| 8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
26.5% | 30.4% | 12.7% |
Table 1 presents the computed and measured relative potential on each electrode for this configuration. The solution used was the same EPN buffer as for the experiment, with a conductivity of 309 μS cm−1, and the input voltage for the measure (Vin) was 3 VRMS (500 kHz).
The proximity of the eight potentials expected and measured is the indication of the accuracy of the numerical model, as the electric field derives from the voltage.
Control group
Fig. 3 presents the PI and FDA intensities of the untreated spheroid population, serving as a negative control.The mean noise values of FDA and PI are 4865 ± 1006 and 560 ± 230, respectively, in arbitrary units.
Repeatability of the procedure
Populations of small spheroids (approximately 100 μm in diameter) were exposed to one ESOPE protocol using the linear gradient previously described. The electric field computed estimation is presented in Fig. 2.The three plots of PI intensity with respect to the position x are presented in Fig. 4a–c. Data are fitted to a logistic sigmoid shaped functions in order to quantify repeatability:
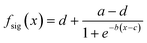 | (2) |
The main differences between those three experiments are an intensity offset and more importantly a horizontal offset. The variations in intensity results from different factors such as the bleaching of fluorophores, the precise time of exposition or the temperature. As the variation of signal is studied, it is relevant to work on normalized dataset. On the other hand, the horizontal offset results from misplacements during the manual mounting of the device. It can be measured through c-value, whose standard deviation is 260 μm. The electric field values at spheroids' positions across the chamber with different placement errors are represented in Fig. 4e. Since the electric field was tuned to be linear, this result in a nearly constant error across the chamber.
We can notice that the last column is highly sensitive to this error, which was to be expected as it is close to the edge effect in the electric field visible in Fig. 2. To avoid unacceptable uncertainties, the data from the last column will be removed from the dataset. For the 22 first columns, the error in electric field evaluation resulting from a misplacement is nearly constant and its mean value is 96 ± 20 V cm−1. For the sake of simplicity, we will consider from now on a single maximalised error value across the chamber of ±116 V cm−1 when evaluating the electric field at a given location.
Gradual permeabilization of a population of spheroids
Fig. 5a presents the superimposed MIP images of FDA and PI channels for the population of 200 μm spheroids exposed to an ESOPE protocol. The brightness and contrast are adjusted arbitrarily for readability purposes. Fig. 5b presents FDA and PI intensities with respect to position (the data for the plot being extracted from the unmodified version of Fig. 5a).Fig. 5c presents the PI data from the same dataset, with respect to the electric field intensity. The noise previously determined on the untreated sample (560 u.a.) is subtracted to the measured PI values. Fig. 6 presents 3D reconstructions from confocal images of one spheroid per condition, evenly spaced in the chamber. Section and orthogonal views of all four spheroids imaged per condition are presented in Fig. 7.
 | ||
| Fig. 6 3D reconstructions of PI repartition in the spheroids (maximum image projection of z-stacks). The data was obtained through ×25 confocal imaging. All electric fields are evaluated ±116 V cm−1. | ||
Discussion
Data interpretation
As PI dye enters into cells that have lost their membrane integrity, temporary or not, it stains cells that have been both reversibly or irreversibly electroporated, as well as dead cells. Meanwhile, FDA is converted into green fluorescent fluorescein by living cells through enzymatic cleavage by esterases present in their cytoplasm.36 Thus, similarly to viability assays also using PI and FDA, the only-green cells are alive, and the only-red cells are dead, but reversibly electroporated cells are visible in both the red and the green channels. The FDA channel assesses the qualitative viability of the procedure, while the PI channel provides a quantitative measure of permeabilization.37 As permeabilization can be reversible or irreversible, the two effects are bound to superimpose in the PI signal.The balance between IRE and reversible electroporation is expected to depend on the electrical protocol used. In our case, Fig. 5b shows that even at 3400 V cm−1, we are far from complete irreversible electroporation, since the FDA signal remains high. These findings suggest that the PI uptake mainly results from reversible electroporation.
It has to be noted that this measure represents the state of spheroids immediately after electroporation, and does not presume of long-term survival. A proper study of IRE and reversible electroporation comparison would require putting spheroids back into culture immediately after treatment and doing a live/dead assay after a few days.
This result is however, consistent with the literature, as it was reported that HT-29 spheroids exposed to a 5000 V cm−1 electric field during an ESOPE protocol were not irreversibly electroporated.38 It has been shown in the same work that a 1000 V cm−1 ESOPE electroporation protocol allows for the effective permeabilization of HT-29 spheroids, as the addition of bleomycin or calcium results in an efficient electrochemotherapy. Such a protocol is close to the lowest electric field our cell populations have been exposed to (see column no. 2 in Fig. 5c). A PI signal significantly higher than the noise value is indeed measured, as can be seen in Fig. 5b, showing that permeabilization is present at this intensity. The intensity of the signal is however, weak compared to spheroids treated at higher electric field intensity.
Electroporation is considered a threshold phenomenon at the cellular scale, the occurrence of which is assessed through fluorophore uptake in suspensions of single cells, and expressed as a proportion of cells electroporated with respect to the whole population. The transition from untreated to a fully electroporated population of cells is rather sharp in terms of electric field intensity.37 It is to be noted that the electroporation threshold depends, among other things, on the cellular type, medium conductivity, and the exact electrical protocol used.21
In a 3D-cell construct, the phenomenon cannot be considered to occur above a precise threshold, as every cell in the spheroid is not exposed to the same electric field intensity, as can be seen in the sections displayed in Fig. 7 for conditions α and β, where distribution of PI uptake shows a higher rate of electroporation at the periphery of the aggregate, and a lower uptake in the centre, which is consistent with the literature.29,35 The uptake of PI is thus not a binary electroporation indicator, but a local indicator of the proportion of cells electroporated in the aggregate. If we can assume that a bleomycin electrochemotherapy at 1000 V cm−1 is sufficient to stop spheroid growth, it is mainly a treatment of proliferating cells in the peripheral layers, and not a full treatment of the whole spheroid volume. However, the distribution of the electric field is not the only factor affecting the uptake and the distribution of molecules within spheroids treated at very high electric fields, like in conditions γ and ε in Fig. 6 and 7. In fact, with the intensity plots resulting from fluorescence microscopy only (see Fig. 4 and 5), it could be assumed that the spheroids undergo a shift from peripheral to more homogeneous electroporation as the electric field at the centre reaches the cellular threshold, leading to a uniform PI uptake.
On the contrary, as one can see in Fig. 6 and 7, PI uptake over the spheroid volume remains highly inhomogeneous even at very high electric fields. While the centre of the spheroids does reach a value significantly above the noise, expressing local electroporation, peripheral layers also tend to get brighter. This result is consistent with recent work studying the exposition of spheroids to IRE protocols of different intensities through PI uptake.35
The 3D reconstructions presented in Fig. 6 show that some cells present a high PI uptake, which results in a higher global measure of PI when averaged on ×2.5 fluorescent images (standard epifluorescence). This explains the slow increase in global PI signal per spheroid, from lightly permeabilized to highly electroporated aggregates that can be seen in Fig. 5c. Two explanations, not mutually exclusive, can be suggested for those brighter cells.
Firstly, as mentioned before, PI stains dead cells. As such, a high electric field might cause irreversible electroporation for some cells, mainly in the peripheral layers, where the field is highest. However, we can notice in Fig. 5b that the FDA signal is nearly constant from column 9 to column 22, suggesting that the increase in PI signal is not mainly caused by cell death. On the other hand, although we may consider that those brighter cells are alive, the higher uptake of PI suggests that cells are more permeabilized, and/or for a longer time, at a high electric field. This is coherent with the observations made by Gabriel and Teissié,39 showing on single cells that the global uptake of PI is intensity-dependent. This assertion was later linked to a cellular model by Krassowska,40 interpreting it as an increase in the number of pores created in the membrane by the electric field. It is interesting to note that while electroporation can be numerically modelled at cellular scale, through approaches describing the development of membrane defects,40–46 and can be described at tissue scale by considering a non-linear static distribution of the electric field in a conductive medium,30,47–52 no numerical model can describe the special distribution of electric field inside a spheroid, where geometry, arrangement and properties cannot be assimilated to an homogenised medium.
To the best of our knowledge, the only simple approach able to describe electroporation in a volume while considering phenomena at the level of cells is based on the equivalent electrical circuit of a cell, where one uses the local density of intracellular and extracellular currents to define a homogenized transmembrane potential at the macroscopic scale.53 This approach might be relevant to model the electroporation of spheroids, as suggested recently by Gidel et al.54 This model is however, based on the assumption that all cells in an aggregate behave similarly, and is not designed to describe electroporation. Adaption would be necessary to model heterogeneous electroporation of the volume.
Overall, this measure of global PI uptake of a spheroid during electroporation is a valuable experimental result to understand the effect of cell-to-cell interaction on the distribution of the electric field in a volume, as well as the properties of aggregates.
An adaptable tool to study electroporation
The device described in this work allows for the controlled application of a variable electric field into a microfluidic chamber. While the application presented deals with the reversible permeabilization of monotypic cell spheroids, the model, the electric field, or the medium in the chamber is directly adaptable. Indeed, the microdevice presented in this paper enables cell seeding in a similar manner to protocols classically used to form 3D spheroids. It is hence fully compatible with co-culture models as well as the use of primary cell culture. Thus, many different uses can be envisioned, including the incorporation of cancer-associated cells such as fibroblasts or immune cells, as well as extracellular matrix.Considering that a spheroid is an incomplete model of a real tumour, and lacking most of all microvascularization, one cannot directly transpose values measured in vitro with this microsystem to an in vivo application. However, it is possible to compare any given protocol to a well-known and experienced protocol, such as the ECT classical ESOPE protocol used in this work, or an IRE protocol composed of 80 to 100 high intensities 100 μs mono-polar pulses, both with decades of clinical feedback.7,55,56 If another protocol allows for a complete electroporation at a lower electric field intensity than a classical protocol in vitro, we may assume that it will permeabilize the cells at a lower intensity in vivo as well.
The newly developed device could be efficient when it comes to comparing experimentally, from one spheroid population to another, the effect of parameter changes during electroporation by changing the electrical protocol upstream of the device. The main parameters that could be studied this way are the number of pulses, their length, waveform, and the frequency of repetition.
Exposure to a gradient of electric fields acts as an intensity–efficiency scan in a single experiment. The data collected could also contribute to the validation of numerical models of aggregate electroporation.
Another direct use of this device centres around ECT, as the drugs used in a procedure may vary depending on the pathology, and their effect is not immediate, we can assume that the exact final intensity–efficiency relation will depend on the type of drug used. In the same way as homogeneous electrochemotherapy on a spheroid population,29,38 it would be interesting to use this device as a drug-screening tool. For example, by treating small spheroids, following their growth afterwards, and ending with a live/dead staining. By cross-referencing the results with a permeabilization assessment protocol as presented here, one could measure the proportion of permeabilized cells necessary for the procedure to be efficient on a given in vitro model. Other microsystems described in the literature allow for the creation of concentration gradients,57 an interesting future direction for this device, when used for drug screening, could be to evaluate both the effect of the electric field and the concentration of the drug in the same experiment, with the two gradients orthogonally oriented.
We can assume that GET could also benefit from that approach, as the device could enable the measurement of the transfection rate with respect to the electric field. Finally, the in vitro model can be complexified to be more realistic or to measure more accurately the impact of the model on the procedure, from monoculture spheroids to co-culture spheroids, organoids, or tumour slices extracted from patients.
Limits
Together with its benefits, there are some drawbacks; the first of all being that the accessible window of the electric field is somewhat limited. As it is calculated as a proportion of a theoretical maximum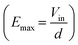 , it is difficult at this point to expand it more than it is, from 20% to 90% of Emax, as it would require increasing the resistor values. Since the potential on each electrode can be roughly described by a voltage divider between a portion of the chamber and the corresponding resistor, a significantly higher value is needed to reach 10% of Emax, probably resulting in a significant divergence between the numerical model and the experiment, for the higher the resistor value, the higher the relative error, as can be seen in Table 1. Secondly, in this work, the permeabilization is linked to PI uptake, while neglecting for the most part the PI signal caused by cellular death through irreversible electroporation. In further experiments, it would be interesting to evaluate the actual contribution of cell death in the PI signal with an exposition to the fluorophore after the resealing of membranes. On a different note, the device is only adapted to in vitro models of rather small size. The chamber area being constant, a change in spheroid size would affect their number, and thus the number of spheroids treated at each intensity. This would result in a loss in statistical strength. It implies that a significant change in electrode geometry and device design is necessary to perform gradual electroporation on bigger spheroids. The materials used for the electrodes are also to be considered. As ITO electrode can be damaged if it is connected to the anode, the device is not adapted to bipolar square protocols, and is limited in overall peak intensity. The maximum input voltage successfully tested with our device was 400 V, meaning a maximum electric field intensity of 3600 V cm−1 (result not presented in this work). Lastly, some aspects of electroporation only appear on in vivo experiments, such as the vascular lock effect,7 and are therefore not covered by this work, and cannot be studied with this device.
, it is difficult at this point to expand it more than it is, from 20% to 90% of Emax, as it would require increasing the resistor values. Since the potential on each electrode can be roughly described by a voltage divider between a portion of the chamber and the corresponding resistor, a significantly higher value is needed to reach 10% of Emax, probably resulting in a significant divergence between the numerical model and the experiment, for the higher the resistor value, the higher the relative error, as can be seen in Table 1. Secondly, in this work, the permeabilization is linked to PI uptake, while neglecting for the most part the PI signal caused by cellular death through irreversible electroporation. In further experiments, it would be interesting to evaluate the actual contribution of cell death in the PI signal with an exposition to the fluorophore after the resealing of membranes. On a different note, the device is only adapted to in vitro models of rather small size. The chamber area being constant, a change in spheroid size would affect their number, and thus the number of spheroids treated at each intensity. This would result in a loss in statistical strength. It implies that a significant change in electrode geometry and device design is necessary to perform gradual electroporation on bigger spheroids. The materials used for the electrodes are also to be considered. As ITO electrode can be damaged if it is connected to the anode, the device is not adapted to bipolar square protocols, and is limited in overall peak intensity. The maximum input voltage successfully tested with our device was 400 V, meaning a maximum electric field intensity of 3600 V cm−1 (result not presented in this work). Lastly, some aspects of electroporation only appear on in vivo experiments, such as the vascular lock effect,7 and are therefore not covered by this work, and cannot be studied with this device.
Conclusions
The work presented here is the conception, tuning, and utilization of a microsystem for in vitro treatment and observation of multicellular spheroids model, when submitted to an electric field of gradually increasing intensity across the chamber. This allows for the precise plot of permeabilization depending on intensity, in a single experiment. The strength of the data collected resides in the important number – usually more than 200 – of spheroids treated simultaneously. Given that the device can deliver virtually any electroporation signal to any in vitro model, this kind of experiment could help nurture existing models on several levels: first of all, it is a tool to investigate the exact role of each parameter, such as waveform, duration, number of pulses, and repetition frequency, and enables the study of specialized protocols. It is also a useful drug scanning device, as the efficiency of a drug can be plotted precisely with respect to the electric field. But one could look at the system from another angle, as the device could be used to improve the in vitro model itself. For example, by measuring the impact of a change in an in vitro model on the outcome of an electroporation experiment, like the addition of elements of the microenvironment to a spheroid through co-culture, or the comparison of different cell lines on a given protocol. The repartition of electrodes also allows for impedance measurement in specific areas of the chamber, which could bring interesting new data for analysing the phenomena. Generally speaking, we believe that this microsystem can be a useful and adaptable tool in the overall research on electroporation.Author contributions
T. Le Berre: conceptualization, investigation, data curation, visualization, writing – original draft, writing – review and editing. J. Marchalot: conceptualization, writing – original draft, writing – review and editing, supervision. G. Rival: conceptualization, writing – original draft, writing – review and editing, supervision. L. Franqueville: resources, writing – original draft, writing – review. R. Onbas: data curation, visualization, writing – original draft, writing – review. C. Rivière: conceptualization, writing – original draft, writing – review and editing, resources. G. Marcellier: writing – original draft, writing – review. F. Prat: writing – original draft, writing – review, funding acquisition. M. Frénéa-Robin: conceptualization, writing – original draft, writing – review and editing, supervision.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article, including raw fluorescence, confocal images and 3D rendering, as well as the numerical model used are available from Recherche Data Gouv at https://doi.org/10.57745/1A0GQZ.Acknowledgements
We gratefully acknowledge the financial support from ITMO Cancer Aviesan within the framework of the 2021–2030 Cancer Control Strategy, on funds administrated by Inserm, and financial support from the CNRS through the MITI interdisciplinary program. We also gratefully thank Matthieu Bartholin, from the Ampère Laboratory, for his help in the fabrication of the final device.References
- I. Dufau, C. Frongia, F. Sicard, L. Dedieu, P. Cordelier, F. Ausseil, B. Ducommun and A. Valette, Multicellular Tumor Spheroid Model to Evaluate Spatio-Temporal Dynamics Effect of Chemotherapeutics: Application to the Gemcitabine/CHK1 Inhibitor Combination in Pancreatic Cancer, BMC Cancer, 2012, 12(1), 15, DOI:10.1186/1471-2407-12-15.
- L. Wasungu, J.-M. Escoffre, A. Valette, J. Teissie and M.-P. Rols, A 3D in Vitro Spheroid Model as a Way to Study the Mechanisms of Electroporation, Int. J. Pharm., 2009, 379(2), 278–284, DOI:10.1016/j.ijpharm.2009.03.035.
- M. T. Santini and G. Rainaldi, Three-Dimensional Spheroid Model in Tumor Biology, Pathobiology, 1999, 67(3), 148–157, DOI:10.1159/000028065.
- J. Pape, M. Emberton and U. Cheema, 3D Cancer Models: The Need for a Complex Stroma, Compartmentalization and Stiffness, Front. Bioeng. Biotechnol., 2021, 9, 660502, DOI:10.3389/fbioe.2021.660502.
- Z. Wen, Q. Liao, Y. Hu, L. You, L. Zhou and Y. Zhao, A Spheroid-Based 3-D Culture Model for Pancreatic Cancer Drug Testing, Using the Acid Phosphatase Assay, Braz. J. Med. Biol. Res., 2013, 46(7), 634–642, DOI:10.1590/1414-431X20132647.
- E. Neumann and K. Rosenheck, Permeability Changes Induced by Electric Impulses in Vesicular Membranes, J. Membr. Biol., 1972, 10(1), 279–290, DOI:10.1007/BF01867861.
- B. Geboers, H. J. Scheffer, P. M. Graybill, A. H. Ruarus, S. Nieuwenhuizen, R. S. Puijk, P. M. van den Tol, R. V. Davalos, B. Rubinsky, T. D. de Gruijl, D. Miklavčič and M. R. Meijerink, High-Voltage Electrical Pulses in Oncology: Irreversible Electroporation, Electrochemotherapy, Gene Electrotransfer, Electrofusion, and Electroimmunotherapy, Radiology, 2020, 295(2), 254–272, DOI:10.1148/radiol.2020192190.
- R. V. Davalos, I. L. M. Mir and B. Rubinsky, Tissue Ablation with Irreversible Electroporation, Ann. Biomed. Eng., 2005, 33(2), 223–231, DOI:10.1007/s10439-005-8981-8.
- B. Rubinsky, G. Onik and P. Mikus, Irreversible Electroporation: A New Ablation Modality — Clinical Implications, Technol. Cancer Res. Treat., 2007, 6(1), 37–48, DOI:10.1177/153303460700600106.
- M. Bower, L. Sherwood, Y. Li and R. Martin, Irreversible Electroporation of the Pancreas: Definitive Local Therapy without Systemic Effects, J. Surg. Oncol., 2011, 104(1), 22–28, DOI:10.1002/jso.21899.
- S. McBride, S. Avazzadeh, A. M. Wheatley, B. O'Brien, K. Coffey, A. Elahi, M. O'Halloran and L. R. Quinlan, Ablation Modalities for Therapeutic Intervention in Arrhythmia-Related Cardiovascular Disease: Focus on Electroporation, J. Clin. Med., 2021, 10(12), 2657, DOI:10.3390/jcm10122657.
- C. Domenge, S. Orlowski, B. Luboinski, T. D. Baere, G. Schwaab, J. Belehradek and L. M. Mir, Antitumor Electrochemotherapy: New Advances in the Clinical Protocol, Cancer, 1996, 77(5), 956–963, DOI:10.1002/(SICI)1097-0142(19960301)77:5<956::AID-CNCR23>3.0.CO;2-1.
- J. Gehl, G. Sersa, L. W. Matthiessen, T. Muir, D. Soden, A. Occhini, P. Quaglino, P. Curatolo, L. G. Campana, C. Kunte, A. J. P. Clover, G. Bertino, V. Farricha, J. Odili, K. Dahlstrom, M. Benazzo and L. M. Mir, Updated Standard Operating Procedures for Electrochemotherapy of Cutaneous Tumours and Skin Metastases, Acta Oncol., 2018, 57(7), 874–882, DOI:10.1080/0284186X.2018.1454602.
- M. Okino and H. Mohri, Effects of a High-Voltage Electrical Impulse and an Anticancer Drug on in Vivo Growing Tumors, Jpn. J. Cancer Res., 1987, 78(12), 1319–1321 CAS.
- G. Serša, B. Štabuc, M. Čemažar, B. Jančar, D. Miklavčič and Z. Rudolf, Electrochemotherapy with cisplatin: potentiation of local cisplatin antitumour effectiveness by application of electric pulses in cancer patients, Eur. J. Cancer, 1998, 34(8), 1213–1218, DOI:10.1016/S0959-8049(98)00025-2.
- J. Rudno-Rudzińska, W. Kielan, M. Guziński, M. Płochocki, A. Antończyk and J. Kulbacka, New Therapeutic Strategy: Personalization of Pancreatic Cancer Treatment-Irreversible Electroporation (IRE), Electrochemotherapy (ECT) and Calcium Electroporation (CaEP) – A Pilot Preclinical Study, J. Surg. Oncol., 2021, 38, 101634, DOI:10.1016/j.suronc.2021.101634.
- S. K. Frandsen, H. Gissel, P. Hojman, J. Eriksen and J. Gehl, Calcium Electroporation in Three Cell Lines: A Comparison of Bleomycin and Calcium, Calcium Compounds, and Pulsing Conditions, Biochim. Biophys. Acta, Gen. Subj., 2014, 1840(3), 1204–1208, DOI:10.1016/j.bbagen.2013.12.003.
- C. Rosazza, S. Haberl Meglic, A. Zumbusch, M.-P. Rols and D. Miklavcic, Gene Electrotransfer: A Mechanistic Perspective, Cancer Gene Ther., 2016, 16(2), 98–129, DOI:10.2174/1566523216666160331130040.
- C. Y. Calvet and L. M. Mir, The Promising Alliance of Anti-Cancer Electrochemotherapy with Immunotherapy, Cancer Metastasis Rev., 2016, 35(2), 165–177, DOI:10.1007/s10555-016-9615-3.
- L. Rems, M. Ušaj, M. Kandušer, M. Reberšek, D. Miklavčič and G. Pucihar, Cell Electrofusion Using Nanosecond Electric Pulses, Sci. Rep., 2013, 3(1), 3382, DOI:10.1038/srep03382.
- J. C. Weaver, K. C. Smith, A. T. Esser, R. S. Son and T. R. Gowrishankar, A Brief Overview of Electroporation Pulse Strength–Duration Space: A Region Where Additional Intracellular Effects Are Expected, Bioelectrochemistry, 2012, 87, 236–243, DOI:10.1016/j.bioelechem.2012.02.007.
- M. B. Sano, C. B. Arena, M. R. DeWitt, D. Saur and R. V. Davalos, In-Vitro Bipolar Nano- and Microsecond Electro-Pulse Bursts for Irreversible Electroporation Therapies, Bioelectrochemistry, 2014, 100, 69–79, DOI:10.1016/j.bioelechem.2014.07.010.
- J. Dermol-Černe, T. Batista Napotnik, M. Reberšek and D. Miklavčič, Short Microsecond Pulses Achieve Homogeneous Electroporation of Elongated Biological Cells Irrespective of Their Orientation in Electric Field, Sci. Rep., 2020, 10(1), 9149, DOI:10.1038/s41598-020-65830-3.
- D. C. Sweeney, M. Reberšek, J. Dermol, L. Rems, D. Miklavčič and R. V. Davalos, Quantification of Cell Membrane Permeability Induced by Monopolar and High-Frequency Bipolar Bursts of Electrical Pulses, Biochim. Biophys. Acta, Biomembr., 2016, 1858(11), 2689–2698, DOI:10.1016/j.bbamem.2016.06.024.
- T. Geng and C. Lu, Microfluidic Electroporation for Cellular Analysis and Delivery, Lab Chip, 2013, 13(19), 3803–3821, 10.1039/C3LC50566A.
- Y. Xu, H. Yao, L. Wang, W. Xing and J. Cheng, The Construction of an Individually Addressable Cell Array for Selective Patterning and Electroporation, Lab Chip, 2011, 11(14), 2417, 10.1039/c1lc20183b.
- S. Bian, Y. Zhou, Y. Hu, J. Cheng, X. Chen, Y. Xu and P. Liu, High-Throughput in Situ Cell Electroporation Microsystem for Parallel Delivery of Single Guide RNAs into Mammalian Cells, Sci. Rep., 2017, 7(1), 42512, DOI:10.1038/srep42512.
- W. Wang, Y. Liu, X. Huang, F. Liang, H. Luo, Z. Mao, J. Shi, L. Wang, J. Peng and Y. Chen, Diffusion-Based Culture and Real-Time Impedance Monitoring of Tumor Spheroids in Hydrogel Microwells of a Suspended Membrane under Microfluidic Conditions, Talanta, 2024, 278, 126473, DOI:10.1016/j.talanta.2024.126473.
- P. Bregigeon, C. Rivière, L. Franqueville, C. Vollaire, J. Marchalot and M. Frénéa-Robin, Integrated Platform for Culture, Observation, and Parallelized Electroporation of Spheroids, Lab Chip, 2022, 22(13), 2489–2501, 10.1039/D2LC00074A.
- D. Miklavcic, M. Snoj, A. Zupanic, B. Kos, M. Cemazar, M. Kropivnik, M. Bracko, T. Pecnik, E. Gadzijev and G. Sersa, Towards Treatment Planning and Treatment of Deep-Seated Solid Tumors by Electrochemotherapy, J. Geophys. Res. Planets, 2010, 9(1), 10, DOI:10.1186/1475-925X-9-10.
- P. A. Garcia, R. V. Davalos and D. Miklavcic, A Numerical Investigation of the Electric and Thermal Cell Kill Distributions in Electroporation-Based Therapies in Tissue, PLoS One, 2014, 9(8), e103083, DOI:10.1371/journal.pone.0103083.
- C. Rivière, A. Prunet, L. Fuoco and H. Ayari, Plaques de Micropuits En Hydrogel Biocompatible, Patent (France) FR3079524A1, 2019.
- V. Novickij, P. Ruzgys, A. Grainys and S. Šatkauskas, High Frequency Electroporation Efficiency Is under Control of Membrane Capacitive Charging and Voltage Potential Relaxation, Bioelectrochemistry, 2018, 119, 92–97, DOI:10.1016/j.bioelechem.2017.09.006.
- Z. Zhang, T. Zheng and R. Zhu, Single-Cell Individualized Electroporation with Real-Time Impedance Monitoring Using a Microelectrode Array Chip, Microsyst. Nanoeng., 2020, 6(1), 81, DOI:10.1038/s41378-020-00196-0.
- A. Collin, H. Bruhier, J. Kolosnjaj, M. Golzio, M.-P. Rols and C. Poignard, Spatial Mechanistic Modeling for Prediction of 3D Multicellular Spheroids Behavior upon Exposure to High Intensity Pulsed Electric Fields, AIMS Bioeng., 2022, 9(2), 102–122, DOI:10.3934/bioeng.2022009.
- B. Rotman and B. W. Papermaster, Membrane Properties of Living Mammalian Cells as Studied by Enzymatic Hydrolysis of Fluorogenic Esters, Proc. Natl. Acad. Sci. U. S. A., 1966, 55(1), 134–141, DOI:10.1073/pnas.55.1.134.
- J. Teissié and M. P. Rols, An Experimental Evaluation of the Critical Potential Difference Inducing Cell Membrane Electropermeabilization, Biophys. J., 1993, 65(1), 409–413, DOI:10.1016/S0006-3495(93)81052-X.
- S. K. Frandsen, L. Gibot, M. Madi, J. Gehl and M.-P. Rols, Calcium Electroporation: Evidence for Differential Effects in Normal and Malignant Cell Lines, Evaluated in a 3D Spheroid Model, PLoS One, 2015, 10(12), e0144028, DOI:10.1371/journal.pone.0144028.
- B. Gabriel and J. Teissié, Direct Observation in the Millisecond Time Range of Fluorescent Molecule Asymmetrical Interaction with the Electropermeabilized Cell Membrane, Biophys. J., 1997, 73(5), 2630–2637, DOI:10.1016/S0006-3495(97)78292-4.
- W. Krassowska and P. D. Filev, Modeling Electroporation in a Single Cell, Biophys. J., 2007, 92(2), 404–417, DOI:10.1529/biophysj.106.094235.
- A. Steinchen, D. Gallez and A. Sanfeld, A Viscoelastic Approach to the Hydrodynamic Stability of Membranes, J. Colloid Interface Sci., 1982, 85(1), 5–15, DOI:10.1016/0021-9797(82)90229-6.
- I. P. Sugár, A Theory of the Electric Field-Induced Phase Transition of Phospholipid Bilayers, Biochim. Biophys. Acta, Biomembr., 1979, 556(1), 72–85, DOI:10.1016/0005-2736(79)90420-6.
- C. Taupin, M. Dvolaitzky and C. Sauterey, Osmotic Pressure-Induced Pores in Phospholipid Vesicles, Biochemistry, 1975, 14(21), 4771–4775, DOI:10.1021/bi00692a032.
- K. A. DeBruin and W. Krassowska, Modeling Electroporation in a Single Cell. I. Effects of Field Strength and Rest Potential, Biophys. J., 1999, 77(3), 1213–1224, DOI:10.1016/S0006-3495(99)76973-0.
- T. Kotnik, F. Bobanović and D. Miklavčič, Sensitivity of Transmembrane Voltage Induced by Applied Electric Fields—A Theoretical Analysis, Bioelectrochem. Bioenerg., 1997, 43(2), 285–291, DOI:10.1016/S0302-4598(97)00023-8.
- C. Poignard, A. Silve and L. Wegner, Different Approaches used in Modeling of Cell Membrane Electroporation, [Research Report] RR-8940, Inria Bordeaux Sud-Ouest, 2016, hal-01349523v2f Search PubMed.
- D. Sel, D. Cukjati, D. Batiuskaite, T. Slivnik, L. M. Mir and D. Miklavcic, Sequential Finite Element Model of Tissue Electropermeabilization, IEEE Trans. Biomed. Eng., 2005, 52(5), 816–827, DOI:10.1109/TBME.2005.845212.
- R. E. Neal, P. A. Garcia, H. Kavnoudias, F. Rosenfeldt, C. A. Mclean, V. Earl, J. Bergman, R. V. Davalos and K. R. Thomson, In Vivo Irreversible Electroporation Kidney Ablation: Experimentally Correlated Numerical Models, IEEE Trans. Biomed. Eng., 2015, 62(2), 561–569, DOI:10.1109/TBME.2014.2360374.
- D. Miklavcic, S. Corovic, G. Pucihar and N. Pavselj, Importance of Tumour Coverage by Sufficiently High Local Electric Field for Effective Electrochemotherapy, EJC Suppl., 2006, 4(11), 45–51, DOI:10.1016/j.ejcsup.2006.08.006.
- D. Miklavčič, L. M. Mir and P. Thomas Vernier, Electroporation-Based Technologies and Treatments, J. Membr. Biol., 2010, 236(1), 1–2, DOI:10.1007/s00232-010-9287-9.
- A. G. Pakhomov, D. Miklavcic and M. S. Markov, Advanced Electroporation Techniques in Biology and Medicine, CRC Press, 2010, DOI:10.1201/EBK1439819067.
- A. Ivorra, B. Al-Sakere, B. Rubinsky and L. M. Mir, In Vivo Electrical Conductivity Measurements during and after Tumor Electroporation: Conductivity Changes Reflect the Treatment Outcome, Phys. Med. Biol., 2009, 54(19), 5949 CrossRef PubMed.
- D. Voyer, A. Silve, L. M. Mir, R. Scorretti and C. Poignard, Dynamical Modeling of Tissue Electroporation, Bioelectrochemistry, 2018, 119, 98–110, DOI:10.1016/j.bioelechem.2017.08.007.
- F. Gidel, D. Voyer and C. Poignard, In-Silico Electrical Modeling of Cell Aggregates, IEEE Trans. Magn., 2020, 56(3), 1–4, DOI:10.1109/TMAG.2019.2952156.
- U. Probst, I. Fuhrmann, L. Beyer and P. Wiggermann, Electrochemotherapy as a New Modality in Interventional Oncology: A Review, Technol. Cancer Res. Treat., 2018, 17, 153303381878532, DOI:10.1177/1533033818785329.
- K. N. Aycock and R. V. Davalos, Irreversible Electroporation: Background, Theory, and Review of Recent Developments in Clinical Oncology, Bioelectricity, 2019, 1(4), 214–234, DOI:10.1089/bioe.2019.0029.
- X. Wang, Z. Liu and Y. Pang, Concentration Gradient Generation Methods Based on Microfluidic Systems, RSC Adv., 2017, 7(48), 29966–29984, 10.1039/C7RA04494A.
| This journal is © The Royal Society of Chemistry 2026 |





