Aging grade estimation of Z3CN20-09M steel from nuclear power plants using LIBS based on fiber laser ablation combined with mutual information-random forest
Qi
Yang
a,
Jinna
Mei
*d,
Sijie
Feng
a,
Yuhua
Hang
d,
Weizhe
Ma
a,
Chengjun
Li
a,
Huaiqing
Qin
a,
Fangjie
Shi
d,
Zhimin
Lu
abc,
Chao
Ye
e and
Shunchun
Yao
 *abc
*abc
aGuangdong Province Key Laboratory of Heat and Mass Transfer and Low-Carbon Conversion, Ministry of Education, South China University of Technology, Guangzhou, 510640, China. E-mail: epscyao@scut.edu.cn
bSchool of Electric Power Engineering, South China University of Technology, Guangzhou 510641, China
cGuangdong Engineering Technology Center for High-Efficiency and Low-Pollution Conversion of Energy, Guangzhou, 510641, China
dSuzhou Nuclear Power Research Institute, Suzhou 215004, China
eInstitute of Clean Energy, Yangtze River Delta Research Institute, Northwestern Polytechnical University, Taicang 215400, China
First published on 8th December 2025
Abstract
Estimating the aging state of the main pipeline steel Z3CN20-09M during its service life is critical for the safe operation of nuclear power plants. This study proposes an innovative approach combining fiber laser-based laser-induced breakdown spectroscopy (FL-LIBS) with mutual information-random forest (MI-RF) to estimate the aging grade of Z3CN20-09M steel. The spectral characteristics corresponding to ten distinct aging grades of the steel were analyzed. Considering the surface elemental inhomogeneity of alloy steels, the impact of various spectral characterization scales (SCS) on the classification accuracy of the RF-based model was investigated. The model's performance was further optimized through the application of the MI feature extraction method. Finally, the robustness of the model was evaluated under conditions of limited training data. The results demonstrate significant inhomogeneity in the distribution of elemental concentrations across the surface of the Z3CN20-09M samples. The RF model achieved optimal performance at an SCS of 1.2 mm. By extracting the first 1476 high-scoring features via mutual information, the classification accuracy of the prediction set rose to 99.0%, with notable enhancements in both precision and recall. Finally, the robustness of the MI-RF model was verified even when the number of samples obtained was insufficient. These findings indicate that the combination of FL-LIBS with MI-RF provides a promising approach for the in situ, rapid estimation of the aging state of essential metal components in nuclear facilities.
1 Introduction
Duplex stainless steel (DSS) Z3CN20-09M is the material of choice for the primary loop main pipeline, the ‘aorta’, of pressurized water reactors (PWR) due to its unique dual-phase microstructure. The blend of austenitic and ferritic phases provides a superior combination of high mechanical strength, toughness, and corrosion resistance.1 However, the material endures harsh service conditions during operation, including elevated temperatures and severe corrosion. The primary failure mechanism is thermal aging, which is caused by the spinodal decomposition of the ferrite phase and the precipitation of the G-phase. Over time, the microstructure and mechanical properties progressively degrade, ultimately resulting in thermal aging embrittlement.2,3 This deterioration markedly diminishes material efficacy and endangers the secure functioning of nuclear power facilities. The aging grade of the steel is a crucial factor for evaluating the operational health and longevity of nuclear plants. Conventional aging evaluation techniques, including pipe cutting sampling, are inefficient and result in irreversible damage to the original metal components. Non-destructive methods such as X-ray and ultrasonic testing can identify existing flaws but do not offer early warning. Consequently, the development of an in situ, rapid, and predictive diagnostic approach for aging failures is critically important.Laser-induced breakdown spectroscopy (LIBS) is an emerging atomic emission spectroscopy method, recognized as a promising tool for future material analysis. Due to its distinctive benefits, including minimal sample preparation, simultaneous multi-element detection, and in situ analysis, LIBS has found widespread applications across various fields.4–7 It has been shown that the matrix properties of the material can significantly influence the laser–sample interaction mechanism and the plasma evolution process, leading to variations in the spectral characteristics. Consequently, using spectral characteristics to monitor changes in material properties has proven to be an effective approach. Tsuyuki et al. employed the intensity ratio of the Ca II 396.8 nm and Ca I 422.6 nm spectral lines to assess the hardness of concrete. Their findings demonstrated a positive correlation between the velocity of the plasma-induced shockwave and the material's hardness, as well as between the shockwave velocity and the plasma ionization rate.8 Abdel-Salam et al. similarly reported a strong correlation between the intensity ratio of Zr II 404.56 nm and Zr I 428.22 nm with the hardness of ferrous alloys. They argued that spectral line ratios of trace elements more accurately reflect material properties than those of major elements.9 Labutin et al. investigated the correlation between the hardness of aluminum alloys and plasma characteristics, identifying strong linear relationships between hardness and parameters including spectral intensity, plasma temperature, and ablation mass. This capability has been successfully applied to diagnose failures in boiler heating surface materials.10 Yao et al. established correlations between the spectral line ratio Fe II 275.57/Fe I 278.81 and the spheroidization grade of pearlite in 20 G steel, enabling accurate identification through LIBS.11 Meanwhile, Li et al. discovered strong linear relationships between the intensity ratios of alloy elements Cr and Mo to the base element Fe and both aging grades and material hardness.12 Furthermore, our recent study used a portable high-frequency fiber laser as the excitation source for the LIBS system (fiber laser-based laser-induced breakdown spectroscopy, FL-LIBS) and found a linear relationship between the spectral properties (Cr and Fe spectral line intensities and intensity ratios) and the aging grade of the metallic material Z3CN20-09M from nuclear applications.13 These studies affirm FL-LIBS as an effective method for evaluating the properties of metallic materials.
Although it has been demonstrated that the spectral characteristics can effectively reflect variations in material matrix properties, accurately assessing the aging grade with traditional univariate models remains challenging. In practice, the aging mechanism of steel is highly complex. As aging progresses, both the microstructure and mechanical properties undergo significant changes. Additionally, limitations in measurement conditions, coupled with the heterogeneity of steel composition, impose greater demands on the adaptability and robustness of the model.14 Therefore, multivariate analysis methods, which can integrate LIBS spectral data with multidimensional features, are more suitable for improving the accuracy and reliability of aging state assessments. Common algorithms applied in LIBS analysis, such as partial least squares (PLS),15,16 principal component analysis (PCA),17,18 and support vector machines (SVM),19–21 often face challenges in terms of robustness when applied to real problems, such as uneven element distribution on the steel surface or increased outliers.22 Random forest (RF) is an effective ensemble learning technique recognized for its adaptability and high performance on extensive, noisy datasets. It has been widely employed in classification and regression tasks based on LIBS.23–28 Meanwhile, LIBS full-spectrum data contain many redundant signals, which can adversely reduce stability and prediction accuracy of model. Relying solely on manual filtering and combining spectral variables has notable limitations. Mutual information (MI) can effectively capture the complex relationships between features and target variables, enhancing both model performance and feature interpretability. Its efficiency in managing high-dimensional data and adaptability to diverse data types have made it widely applicable in the field of LIBS.29–31 While above studies have applied LIBS combined with RF to analyze samples with significant elemental composition differences, the samples in this study have relatively uniform elemental contents, differing mainly in microstructure and mechanical properties. To our knowledge, there has been no research exploring the use of LIBS in combination with RF for such samples. Furthermore, the application of LIBS coupled with MI-RF to assess the aging grade of nuclear-grade metallic materials has been scarcely addressed in prior research.
In this paper, an aging grade estimation method based on the combination of MI-RF and FL-LIBS was proposed for Z3CN20-09M material. Given the inherent fluctuations in LIBS spectral signals and the uneven distribution of elements across the surface of Z3CN20-09M, this study explores the effect of various spectral characterization scales (SCS) on model performance. Then, MI feature selection was employed to refine the input variables for aging grade evaluation model based on RF. Finally, since laser ablation on the sample surface may have an impact on the material surface and the detection area is usually limited in real measurements. Therefore, we investigate the effect of different numbers of ablation paths on the performance of aging grade evaluation model.
2 Experimental
2.1 Samples
A comprehensive account of sample preparation is available in our prior research and is briefly outlined below.13 Ten raw samples were provided by the Suzhou Nuclear Power Research Institute, sourced from China and France. All samples comply with the RCC-M standard established by the French Society for Design and Construction Rules for Nuclear Island Components (AFCEN),32 with their precise chemical compositions detailed in Table 1. The materials from the two production regions have the same elemental composition, with only certain differences in concentration levels. Compared with the French samples, the Z3CN20-09M steel produced in China has relatively lower contents of C, N, S, Cr and Mo, while having higher contents of Ni and Mn.| C | Cr | Ni | Si | Mn | S | P | Mo | N | Fe | |
|---|---|---|---|---|---|---|---|---|---|---|
| China | 0.018 | 19.8 | 9.03 | 1.27 | 1.17 | 0.004 | 0.023 | 0.055 | <0.02 | Bal. |
| France | 0.027 | 20.19 | 8.92 | 1.27 | 1.13 | 0.014 | 0.023 | 0.21 | 0.031 | Bal. |
The raw samples underwent accelerated aging studies at a temperature of 400 °C. Samples were subjected to heating for 500, 1000, 3000, 6000, and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hours to achieve diverse aging characteristics.33 The Charpy V-notch impact energy is a crucial parameter for evaluating the aging state of Z3CN20-09M steel, according to the aging management standards for main pipeline steel.34 The Charpy V-notch impact energy was measured at six different points on the surface for each sample, with the average values displayed in Table 2. The samples were qualitatively categorized into six aging grades by using both aging time and the average Charpy V-notch impact energy. The artificial aging treatments were performed in strict adherence to established standards to guarantee consistency and reliability. In addition, the division of the sample dataset is also listed in the table. There are a total of six samples in the training set, covering six different aging grades, which can ensure the model's comprehensive representational capacity in multi-class classification tasks. The remaining four samples were classified as the testing set.
000 hours to achieve diverse aging characteristics.33 The Charpy V-notch impact energy is a crucial parameter for evaluating the aging state of Z3CN20-09M steel, according to the aging management standards for main pipeline steel.34 The Charpy V-notch impact energy was measured at six different points on the surface for each sample, with the average values displayed in Table 2. The samples were qualitatively categorized into six aging grades by using both aging time and the average Charpy V-notch impact energy. The artificial aging treatments were performed in strict adherence to established standards to guarantee consistency and reliability. In addition, the division of the sample dataset is also listed in the table. There are a total of six samples in the training set, covering six different aging grades, which can ensure the model's comprehensive representational capacity in multi-class classification tasks. The remaining four samples were classified as the testing set.
| No. | Origin | Aging time (h) | Charpy V-impact power (J) | Aging grade | Assigned set |
|---|---|---|---|---|---|
| 1# | France | 0 | 303.25 | 1 | Testing |
| 2# | China | 0 | 369.83 | 1 | Training |
| 3# | France | 500 | 263.00 | 2 | Training |
| 4# | China | 500 | 337.33 | 2 | Testing |
| 5# | France | 1000 | 151.25 | 3 | Testing |
| 6# | China | 1000 | 286.33 | 3 | Training |
| 7# | France | 3000 | 133.50 | 4 | Training |
| 8# | China | 6000 | 122.67 | 5 | Training |
| 9# | France | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
113.75 | 6 | Training |
| 10# | China | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
107.67 | 6 | Testing |
2.2 FL-LIBS set up
Fig. 1 illustrates the FL-LIBS experimental configuration employed to predict the aging grade of Z3CN20-09M. The Q-switched fiber laser operated at 1064 nm with a pulse duration of 120 ns as an ablation source was set to a frequency of 25 kHz and a power setting of 30%. The laser beam focused on the sample surface with a plano-convex lens. Plasma emission was collected laterally and analyzed using a time-integrated spectrometer (AvaSpec-ultras2048-4, Avantes, wavelength: 225–836 nm, resolution: 0.1–0.22 nm). The elevated repetition rate of the fiber laser caused the plasma excitation frequency to surpass the spectrometer's minimum integration time (1.05 ms), making sequential acquisition modes unfeasible. As a result, the spectrometer performed in an internally triggered, continuous acquisition mode with an integration time of 40 ms. Samples were placed on a motorized X–Y stage, designed to traverse in a linear path at a constant velocity of 3 mm s−1. Before the collect of spectra, each sample's surface was sanded and polished using 800 grit sandpaper, followed by an alcohol wipe. This guarantees that the acquired spectra are protected from oxide interference and more precisely represent the matrix characteristics of the material. Five ablation paths were measured for each training set, with each path being 12 millimeters in length. As a result, 100 spectra were obtained from each ablation path, yielding a total of 500 spectra per sample. However, considering that ideal acquisition conditions are often compromised in real-world testing environments due to physical constraints (e.g., equipment layout), a different and more constrained strategy was adopted for the test set. For each test set sample, only 50 spectra were acquired randomly from its surface. A total of 200 spectra were collected for the entire test set. All obtained spectrum data were normalized by the total intensity of the spectrometer channels to reduce the impact of noise and spectral drift.3 Methods
3.1 Aging grade classification model based on random forests
RF is an enhancement of the bagging algorithm that integrates multiple decision trees utilizing ensemble learning principles. For each input sample, every decision tree functions as an independent classifier, resulting in N classification outcomes from a forest of N trees. The RF algorithm synthesizes these results through majority voting, assigning the category with the highest vote tally as the definitive output. Owing to its robust noise resilience, parallel computing potential, and ease of implementation, RF has been extensively utilized in LIBS-based classification modeling.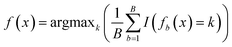 | (1) |
This study utilized the RF model to classify Z3CN20-09M steel samples into various age grades. The optimization of critical parameters, specifically the quantity of trees and random variables, was executed utilizing a grid search methodology. During the optimization phase, a grid search approach was employed. The search began with an initial value of 50 trees, and this value was then progressively increased with a step size of 50, up to a maximum of 500 trees. Therefore, the set of tree values evaluated during optimization was [50, 100, 150, 200, 250, 300, 350, 400, 450, 500], comprising a total of 10 distinct values. The optimum range for the leaf was determined between 1 and 5. Consequently, each RF model was trained using 50 distinct parameter combinations to optimize classification accuracy.
3.2 Mutual information feature extraction
The MI between two random variables quantifies the degree of dependency between them. The MI is defined as: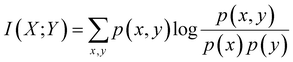 | (2) |
In simpler terms, a higher mutual information (MI) value between a feature and a label class signifies a stronger correlation, indicating that the feature is more likely to be associated with that class. In contrast, a lower MI value denotes a weaker correlation. Notably, MI can capture nonlinear relationships between variables and is not dependent on distributional assumptions, rendering it highly adaptable. In the context of LIBS spectral data, where spectral variables and labels seem independent, MI effectively identifies the correlation between spectral features and class labels. This facilitates the selection of the most significant spectral features for classification tasks, thereby improving model performance and interpretability.
3.3 Model evaluation
The performance of the classification model was evaluated using three key metrics: accuracy, precision, and recall. Among these, accuracy is calculated using the following formula: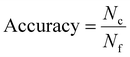 | (3) |
Based on the sample information, the dataset was qualitatively divided into six categories, making it a multi-class classification problem. The evaluation of multi-class classification can be transformed into multiple binary classification evaluations, with the final metric being the average of all binary evaluations. The definitions and calculations of precision and recall are introduced below using binary classification as an example.
Precision, also referred to as the positive predictive value, measures the proportion of true positive predictions among all samples predicted as positive. It is calculated using the following formula:
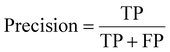 | (4) |
Recall, also known as sensitivity or true positive rate, represents the proportion of true positive samples correctly identified by the model. Its formula is given by:
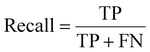 | (5) |
All machine learning models and data processing were implemented using MATLAB (R2024a).
4 Results and discussion
4.1 Spectral characteristics analysis
Z3CN20-09M is a duplex stainless steel that consists of both ferrite and austenite. Its spectral composition is complex, involving thousands of characteristic spectral lines. We present representative spectra of samples with different aging grades in Fig. 2, which correspond to sample numbers 2#, 3#, 6#, 7#, 8# and 9#. The spectrometer can accurately identify the characteristic spectral lines of the sample elements, including the matrix element Fe and the alloying elements Cr and Mn. The spectra of various aging grades following identical pretreatment are very similar, and materials from different origins exhibit no significant differences. Consequently, directly discerning the aging grades of the samples through the observation of the spectral images of the materials proves challenging.Due to the high-alloy composition of the material Z3CN20-09M, the elemental distribution on material's surface after synthetic processing is often uneven. When the FL-LIBS system scans the sample surface, the laser is focused on different areas with each measurement, and the acquired spectral data represents the composition of the localized elements in those specific regions. The inhomogeneity of the surface distribution of the material may result in significant discrepancies in the spectrum data acquired by focusing the laser onto different areas. To assess the impact of elemental distribution on the spectral properties, the peak intensities of characteristic spectral lines from the matrix element Fe I 275.01 nm and the alloying element Cr I 262.05 nm were selected as indices for visualizing the distribution of elemental concentrations across the sample surface.
The specifics are illustrated in Fig. 3. Each pixel in the image corresponds to an individual spectrum, and there is continuity between these pixel points. The spatial resolution is determined by the product of the spectrometer's integration time and the translation stage's velocity, which is 0.12 mm. The image reveals notable variations in the peak intensities of the characteristic spectral lines across different regions of spectral acquisition, indicating that the spectral characteristics used for analysis are highly sensitive to both the material composition and the variability in laser–material interaction. This variability presents a challenge in directly correlating the peak intensities of these spectral lines with material properties.
 | ||
| Fig. 3 Spatial distribution of intensity of characteristic spectral lines on sample surface: (a) 2# – Cr I 262.05 nm; (b) 2# – Fe I 275.01 nm; (c) 9# – Cr I 262.05 nm; (d) 9# – Fe I 275.01 nm. | ||
To verify the applicability of the spectral line intensity ratios to characterize the aging grades of samples from different origins, the correlation between peak spectral line intensity ratios and aging grades was analyzed for the matrix element Fe and the alloying element Cr. As shown in Fig. 4, for samples of the same origin, Fe I 282.88/Cr I 262.05 and Fe I 283.82/Cr I 262.05 demonstrate a strong correlation with aging grade, consistent with the findings of our previous study.13 However, for samples with the same aging grade but from different origins, although similar trends are observed, there is a significant numerical difference in the spectral line intensity ratios between the two sets of samples. This occurs because variations in the elemental concentrations of samples from different origins affect the degree of performance change during thermal aging. Elements such as C and N significantly enhance solid solution strengthening, while the impurity element S tends to segregate near grain boundaries, increasing material brittleness. Cr and Mo are ferrite-stabilizing elements; lower concentrations of these elements result in a reduced ferrite phase content. In contrast, Ni and Mn stabilize austenite, and higher concentrations of these elements reduce ferrite phase content.35 While a reduction in ferrite content can mitigate aging-induced embrittlement in duplex stainless steels, it simultaneously increases the alloy's resistance to thermal aging. These compositional changes are expected to alter the interaction mechanisms between the laser and the material, leading to matrix effects. As a result, distinct spectral properties emerge under different aging states. Consequently, the linear model may misclassify samples from different origins, limiting the practical application of this method in practice.
 | ||
| Fig. 4 Correlations between aging grades and line intensity ratios of matrix element to alloying element with the error bars. | ||
As indicated above, direct linear modeling between spectral characteristics (spectral line intensities and intensity ratios) and aging grade is affected by the fluctuations in spectral intensities within the collection area and variations in the material matrix result in a weak linear relationship between spectral characteristics (spectral line intensities and intensity ratios) and aging grade. Thus, linear models are not adequate for the purpose of evaluating aging grades. Additionally, linear models struggle to effectively differentiate between samples from different origins, making them less suitable for practical applications. Therefore, RF as an advanced supervised nonlinear classification learning method that can fully exploit the complex nonlinear relationships and feature interactions in the spectral data, is attempted to be used for the assessment of the aging grade of Z3CN20-09M material.
4.2 Effects of different spectral characterization scales (SCS) on RF models
The analysis indicates that the intensity of spectral lines from the same element, obtained along the ablation route during the FL-LIBS system's scanning of the sample surface, exhibits noticeable fluctuation. This fluctuation primarily arises from variations in the laser pulse, small changes in the interaction between the laser and the sample, and the uneven distribution of elemental concentrations on the sample surface. As a result, it is challenging to accurately represent the overall elemental composition of the sample surface by relying solely on spectral data from one or a few positions. To enhance the representativeness of the sample as characterized by the spectral data, averaging the spectral data collected along the entire scanning path is a common pre-processing approach. However, using a single spectrum as a representative for the entire sample fails to capture the inhomogeneity of elemental distribution and overlooks the uncertainty inherent in the spectral signal. Therefore, optimizing the spatial scale for spectral characterization is essential to better represent the material's properties.Based on the experimental parameter settings, it can be concluded that the minimum unit length for the spectral characterization scale (SCS) is 0.12 mm. Subsequently, data with different SCS are obtained by altering the average number of spectra along the scanning path. This procedure is illustrated in Fig. 5(a). Spectral data for samples with varying aging grades were collected at SCS values of 0.12 mm, 0.60 mm, 1.2 mm, 2.4 mm, 3 mm, and 12 mm. These values correspond to averaging the spectral data at intervals of 1, 5, 10, 20, 25, and the full spectrum along the ablation path, respectively. Separate RF classification models were constructed for each SCS using the corresponding training set data. The specific modeling procedure is illustrated in Fig. 5(b). The results showing the influence of key parameters of the RF model on classification accuracy are presented in Fig. 6. The RF models based on different SCS exhibit significant differences in classification accuracy, with the model achieving the highest overall accuracy when the SCS is 1.2 mm.
 | ||
| Fig. 5 RF model optimized based on different SCS: (a) data acquisition process for different SCS; (b) modeling process. | ||
The results of the best classification accuracies for the RF models with different SCS values are summarized in Fig. 7. The classification accuracy initially increases with SCS, but then decreases as the SCS continues to rise. The optimal classification accuracy of 90.5% for the prediction set was achieved with an SCS of 1.2 mm, a tree parameter of 50, and a random variable of 2. The specific performance of these predictive models is detailed in Table 3. These findings indicate that the classification model with an SCS of 1.2 mm exhibits the highest stability in both accuracy and recall for the projected sample set, outperforming all other models. This suggests that this model offers greater reliability in terms of detection capabilities.
| SCS (mm) | Accuracy (%) | Precision (%) | Recall (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 4# | 5# | 10# | Average | 1# | 4# | 5# | 10# | Average | ||
| 0.12 | 50.5 | 0 | 58.8 | 73.3 | 100.0 | 58.0 | 0 | 80.0 | 22.0 | 100.0 | 50.5 |
| 0.60 | 73.5 | 73.1 | 91.3 | 94.7 | 100.0 | 89.8 | 38.0 | 84.0 | 72.0 | 100.0 | 76.0 |
| 1.20 | 90.5 | 93.6 | 90.2 | 89.1 | 100.0 | 93.2 | 88.0 | 92.0 | 82.0 | 100.0 | 90.5 |
| 2.40 | 76.0 | 92.9 | 83.3 | 100.0 | 100.0 | 94.1 | 26.0 | 100.0 | 78.0 | 100.0 | 76.0 |
| 3.00 | 75.5 | 93.9 | 54.9 | 100.0 | 100.0 | 87.2 | 92.0 | 100.0 | 100.0 | 100.0 | 75.5 |
| 12.0 | 58.0 | 43.2 | 57.5 | 33.3 | 100.0 | 58.5 | 82.0 | 46.0 | 4.0 | 100.0 | 58.0 |
To rationally explain the reason for the differences in the classification accuracy of models based on different SCSs, an attempt was first made to correlate the data from different SCS values with the distribution of elemental concentrations on the sample surface. As previously discussed, samples subjected to thermal aging experience elemental segregation, which alters the matrix properties of the material. Consequently, the spectral intensities of samples with different aging grades are influenced by matrix effects. To establish a reference, we use the average spectral intensity of the characteristic spectral lines from a sample that has not undergone thermal aging treatment. This is because the elemental distribution on the surface of an unaged sample is primarily determined by the material processing, and the fluctuation in spectral intensity is not influenced by the matrix property changes that occur during thermal aging. Subsequently, if the spectral intensity of the characteristic spectral lines in the surface region of a thermally aged sample exceeds the reference value, this region is considered significantly affected by the matrix effect. The greater the influence of matrix effect, the more obvious the spectral differences, leading to higher classification accuracy. Based on this, the rate of spectral difference characterization affected by thermal aging is defined as follows:
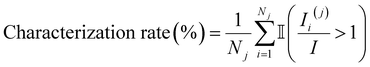 | (6) |
The unaged (2#) and aged (6# and 8#) samples of the same origin in the training set were analyzed to investigate the characterization rate of different SCS values influenced by matrix effects. For each sampling region, a peak intensity ratio was calculated under different SCS conditions by dividing the local element peak intensity of the test sample by the average surface element intensity of the unaged sample. Regions where this ratio exceeded 1 were classified as ‘significantly affected by matrix effects’. The overall proportion of these ‘significantly affected’ regions relative to the total number of sampling regions was then determined, with the results presented in Fig. 8. The analysis shows that when the SCS value is 1.2 mm, the spectral intensity changes caused by the inhomogeneous distribution of elements can be maximally preserved while eliminating the influence of systematic factors on the spectral fluctuations. The characterization rates for samples 6# and 8# are 40% and 30%, respectively, which are higher than those observed for the other SCS values. This indicates that different SCS values have varying abilities to integrate information across regions, resulting in differences in the characterization rate. A higher characterization rate suggests that the SCS can better capture the aging properties of the sample. Therefore, spectral data at this optimal SCS are more representative, leading to improved classification accuracy for the model.
The inter-pulse spectral signal stability of all training set samples at different SCS values was further analyzed. The relative standard deviation (RSD) values of the peak intensities of the characteristic spectral lines for the matrix element Fe and the alloying element Cr along the ablation paths were employed as assessment metrics, and the results are presented in Fig. 9. The analysis demonstrates that the RSD values of the spectral signals along the ablation path generally decrease as the SCS increases. Specifically, when the SCS is 0.12 mm or 0.6 mm, the spatial resolution of the spectral acquisition is higher, making it more sensitive to the fluctuation in the elemental concentration on the sample's surface, resulting in larger RSD values. At the same time, the spectral data characterizing the same sample contains more irrelevant information, which negatively impacts the classification accuracy of the model. In contrast, the increase in the number of average spectra improves the stability of the spectral signals when the SCS are 2.4 mm and 3.0 mm. However, larger SCS values also reduce the number of spectra used to characterize the same sample. As shown in Fig. 7, when the SCS increases further, the classification accuracy for the training set remains at 100%, but the accuracy of the prediction set drops significantly. This phenomenon occurs because the number of variables remains constant while the number of samples decreases, leading to sparse data points in the high-dimensional feature space (as shown in Table 4), which results in overfitting of the RF classification model.
| Scale (mm) | Number of spectra corresponding to each training set sample | Training set data matrix dimensions (number of dependent variables × number of independent variables) |
|---|---|---|
| 0.12 | 500 | 3000 × 4096 |
| 0.60 | 100 | 600 × 4096 |
| 1.20 | 50 | 300 × 4096 |
| 2.40 | 25 | 150 × 4096 |
| 3.00 | 20 | 120 × 4096 |
| 12.00 | 5 | 30 × 4096 |
In summary, optimizing the SCS of the spectra helps to strike a balance between local and global information, enabling the spectral data to accurately represent the overall composition of the sample while preserving the local distribution details. This optimization significantly reduces the signal uncertainty and enhances the robustness and accuracy of the analytical model. Additionally, the RSD values of the peak intensities of the characteristic spectral lines for the same element across different ablation paths at the same SCS exhibit significant variation. It is presented in the form of error bars in Fig. 9. This further emphasizes the inhomogeneity of the elemental concentration distribution on the surface of the Z3CN20-09M sample, which aligns with the imaging results presented in Fig. 3.
To further enhance the model's classification accuracy, the MI feature extraction method was employed to screen spectral variables, identifying the subset with the optimal predictive performance by traversing all variables in the spectrum. The baseline model adopted is a classification model with a SCS of 1.2 mm, as it attained the maximum classification accuracy in the previous analysis. MI scores between spectral feature variables and aging grades were calculated, and the variables were ranked in descending order. Features with high MI scores were progressively added to the model until all variables were included. The classification accuracy from the training set cross-validation was used as the evaluation criterion to identify the best variable combination. As shown in Fig. 10, the RF model achieves the maximum classification accuracy of 99% when the top 1476 features, ranked by the highest mutual information scores with the aging grade, are selected.
 | ||
| Fig. 10 MI-RF model classification results: (a) the effect of different variable numbers on the model classification accuracy; (b) the confusion matrix of the best MI-RF classification results. | ||
The MI-RF model's performance is summarized in Table 5. Compared to the RF model, the MI-RF model shows significant improvements in classification accuracy, precision, and recall following feature extraction. This indicates that MI successfully identified the variables within the full-spectrum data that exhibit the strongest correlation with the material's aging characteristics. As a result, the MI-RF model achieves high-precision classification of Z3CN20-09M material across various aging grades.
| Model | Accuracy (%) | Precision (%) | Recall (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 4# | 5# | 10# | Average | 1# | 4# | 5# | 10# | Average | ||
| MI-RF | 99.0 | 100.0 | 98.0 | 100.0 | 100.0 | 99.5 | 96.0 | 100.0 | 100.0 | 100.0 | 99.0 |
| RF | 90.5 | 93.6 | 90.2 | 89.1 | 100.0 | 93.2 | 88.0 | 92.0 | 82.0 | 100.0 | 90.5 |
To further validate the superiority and necessity of the selected MI-RF model, a rigorous comparative study was conducted. We benchmarked the MI-RF model against three other highly representative dimensionality reduction methods: PCA-RF (Principal Component Analysis, a linear feature extraction method), LASSO-RF (L1 Regularization, a linear feature selection method), and RFE-RF (Recursive Feature Elimination, a non-linear feature selection method). To ensure a fair comparison, all methods utilized the same training and validation sets, and all employed RF as the final classifier. Each method was optimized by traversing its number of features (or principal components) to find the best model performance. The final comparative results are presented in Table 6.
| Model | Number of features in the input model | Accuracy (%) | Total building time (s) |
|---|---|---|---|
| PCA | 4 | 55.5% | 92.01 |
| LASSO | 72 | 73.0% | 13.17 |
| RFE | 738 | 97.0% | 3674.93 |
| MI | 1476 | 99.0% | 48.56 |
These empirical results demonstrate that MI is the optimal choice for this task. The poor performance of linear methods (PCA-RF: 55.5% and LASSO-RF: 73.0%) confirms the highly non-linear relationship between the spectra and aging grade, which MI is designed to capture. Furthermore, when compared to the other high-performing non-linear method (RFE-RF), the MI-RF model achieved both a higher classification accuracy (99.0% vs. 97.0%) and a vastly superior computational efficiency (48.56 s vs. 3674 s), proving it is the most accurate, robust, and practical solution.
4.3 Model robustness test
The distribution of surface elements concentration in the steel utilized for the main pipes of nuclear power plants is inherently non-uniform in real-world applications. To develop a reliable aging grade classification model, it is essential to capture comprehensive spectral information from the steel surface. However, the potential effects of laser-induced ablation marks on material properties, coupled with the limitations of on-site equipment arrangement, render the acquisition of an optimal data amount hard. Therefore, it is essential to analyze the robustness of the established MI-RF classification model to determine its adaptability in the presence of spectral signal fluctuations and limited data.In this case, the spectral data collection range is constrained by reducing the number of laser ablation paths on the sample surface, which further limits the quantity of training set samples. The model is constructed according to the SCS of 1.2 mm. The classification accuracy of the MI-RF model is evaluated across varying numbers of ablation paths, with results compared to those of the RF model under identical SCS settings. The number of spectra used to characterize the same sample remained constant for both models. Furthermore, the RF models, after adjusting the number of training set samples, underwent the same optimization process described earlier to ensure the best classification results. The results are illustrated in Fig. 11. The model's classification accuracy decreases as the quantity of spectral data points in the training set decreases. However, the MI-RF model demonstrates superior stability and accuracy compared to the RF model without feature extraction. Specifically, the classification accuracy of the MI-RF model decreased by only 13.6%, remaining within an acceptable range (not less than 85%), whereas the RF model fluctuated by 34.8%, reaching only 59% accuracy with just one ablation path. The specific comparison results of the two models are shown in Table 7. These results indicate that the MI-RF model maintains reliable generalization performance despite sparse data. Additionally, the MI-RF model exhibits significant resilience to spectral data variability, enabling accurate aging grade prediction even with a limited number of spectral data points. Therefore, the MI-RF model can still yield precise diagnostic outcomes despite constraints imposed by the arrangement of measurement points in real applications. Furthermore, Fig. 11 illustrates the duration necessary for spectral data collection across different numbers of ablation paths. The FL-LIBS system takes 20 seconds to collect spectral data from five ablation paths. When only one ablation path is measured, the acquisition time is reduced to 4 seconds. This demonstrates that the combination of the FL-LIBS system and the MI-RF classification model holds significant potential as a rapid and portable in situ diagnostic solution for the aging state of critical metal components in nuclear power plants.
 | ||
| Fig. 11 Effect of different number of ablation paths on the classification accuracy of MI-RF and RF models. | ||
| Model | Ablation path number | Precision (%) | Recall (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 4# | 5# | 10# | Average | 1# | 4# | 5# | 10# | Average | ||
| MI-RF | 5 | 100.0 | 98.0 | 100.0 | 100.0 | 99.5 | 96.0 | 100.0 | 100.0 | 100.0 | 99.0 |
| 4 | 87.3 | 97.7 | 100.0 | 100.0 | 96.3 | 96.0 | 86.0 | 100.0 | 100.0 | 95.5 | |
| 3 | 86.0 | 90.0 | 100.0 | 100.0 | 94.0 | 74.0 | 90.0 | 94.0 | 100.0 | 89.5 | |
| 2 | 94.1 | 86.8 | 95.6 | 100.0 | 94.2 | 64.0 | 92.0 | 86.0 | 100.0 | 85.5 | |
| 1 | 98.0 | 65.3 | 95.8 | 100.0 | 89.8 | 96.0 | 98.0 | 46.0 | 100.0 | 85.0 | |
| RF | 5 | 93.6 | 90.2 | 89.1 | 100.0 | 93.2 | 88.0 | 92.0 | 82.0 | 100.0 | 90.5 |
| 4 | 78.6 | 62.0 | 100.0 | 100.0 | 85.2 | 88.0 | 98.0 | 24.0 | 100.0 | 77.5 | |
| 3 | 100.0 | 51.5 | 100.0 | 100.0 | 87.9 | 74.0 | 100.0 | 100.0 | 100.0 | 71.0 | |
| 2 | 77.1 | 83.1 | 100.0 | 100.0 | 90.1 | 54.0 | 98.0 | 54.0 | 100.0 | 76.5 | |
| 1 | 28.8 | 100.0 | 100.0 | 100.0 | 82.2 | 30.0 | 80.0 | 26.0 | 100.0 | 59.0 | |
5 Conclusions
In this paper, it is demonstrated that the combination of FL-LIBS and MI-RF provides a rapid and robust approach for estimating the aging grade of Z3CN20-09M steel in nuclear power plants. The inhomogeneity of the elemental concentration distribution on the sample surface was characterized using the FL-LIBS system, highlighting the necessity of optimizing the SCS. To address the challenges posed by the inherent signal fluctuations of LIBS systems and the uneven distribution of elemental concentrations on the sample surface, an MI-RF classification model was developed. The performance of the model was evaluated under various SCS settings. When the SCS was set to 1.2 mm, the MI-RF model achieved a peak accuracy of 99.0%. Finally, the stability and generalization capability of the MI-RF model were further validated under conditions of limited training data. These findings show that the combination of FL-LIBS and MI-RF holds significant potential for application in assessing the aging state of Z3CN20-09M in nuclear power plants.Author contributions
Qi Yang: conceptualization, methodology, formal analysis, writing – original draft. Jinna Mei: resources, supervision. Sijie Feng: validation, investigation. Yuhua Hang: resources, supervision. Weizhe Ma: validation, writing – review & editing. Chengjun Li: validation. Huaiqing Qin: validation, writing – review & editing. Fangjie Shi: supervision, project administration. Zhimin Lu: supervision, project administration. Chao Ye: supervision. Shunchun Yao: conceptualization, supervision, project administration, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. All authors declare that no conflict of interest exists.Data availability
Data will be made available on request.Acknowledgements
This work was supported by the National Natural Science Foundation of China [No. U22B20119], National Natural Science Foundation of China [No. 22403032], Natural Science Foundation of Guangdong Province for Distinguished Youth [No. 2021B1515020071], Fundamental Research Funds for the Central Universities [No. 2023ZYGXZR090], Foundation of State Key Laboratory of High-efficiency Utilization of Coal and Green Chemical Engineering [No. 2022-K72]. The authors would like to gratefully thank Suzhou Nuclear Power Research Institute Co., Ltd for providing experimental samples and support for the paper research.Notes and references
- F. Xue, Z. X. Wang, G. G. Shu, W. W. Yu, H. J. Shi and W. X. Ti, Nucl. Eng. Des., 2009, 239, 2217–2223 CrossRef CAS.
- H. Jiang, S. Hong, C. Jang and J. G. Lee, Mater. Des., 2014, 56, 517–521 CrossRef.
- K. Chandra, V. Kain, V. Bhutani, V. S. Raja, R. Tewari, G. K. Dey and J. K. Chakravartty, Mater. Sci. Eng., A, 2012, 534, 163–175 CrossRef CAS.
- J. Wu, H. Yu, Y. Qiu, Z. Zhang, T. Liu, F. Xue, W. W. Yu, X. W. Li and A. C. Qiu, J. Phys. D: Appl. Phys., 2019, 52, 014006 CrossRef.
- S. W. Hudson, J. Craparo, R. De Saro and D. Apelian, Metall. Mater. Trans. B, 2017, 48, 2731–2742 CrossRef CAS.
- S. Balakrishnan, V. M. Reddy, A. Mehta, N. J. Vasa and R. Nagarajan, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 399 CrossRef.
- S. C. Yao, J. B. Zhao, Z. Z. Wang, Y. Deguchi, Z. M. Lu and J. D. Lu, Spectrochim. Acta, Part B, 2019, 149, 249–255 CrossRef.
- K. Tsuyuki, S. Miura, N. Idris, K. H. Kurniawan, T. J. Lie and K. Kagawa, Appl. Spectrosc., 2006, 60, 61–64 CrossRef CAS PubMed.
- Z. Abdel-Salam, M. Abdelhamid, S. M. Khalil and M. A. Harith, The 7th International Conference on Laser Applications – ICLA 2009, AIP Conf. Proc., 2009, 1172, 49–52 CrossRef CAS.
- T. A. Labutin, A. M. Popov, D. N. Sychev and N. B. Zorov, Advanced Laser Technologies 2007, Proc. SPIE, 2008, 7022, 70221C CrossRef.
- S. C. Yao, M. R. Dong, J. D. Lu, J. Li and X. Dong, Laser Phys., 2013, 23, 125702 CrossRef.
- J. Li, J. D. Lu, Y. Dai, M. R. Dong, W. L. Zhong and S. C. Yao, Appl. Surf. Sci., 2015, 346, 302–310 CrossRef CAS.
- Q. Yang, J. N. Mei, W. Z. Ma, S. J. Feng, Y. H. Hang, Z. Y. Yu, F. J. Shi, H. Q. Qing, C. Ye and Z. M. Lu, At. Spectrosc., 2025, 45, 462–472 Search PubMed.
- J. W. Huang, M. R. Dong, S. Z. Lu, W. B. Li, J. D. Lu, C. Y. Liu and J. H. Yoo, J. Anal. At. Spectrom., 2018, 35, 720–729 RSC.
- Z. Wang, T. B. Yuan, S. L. Lui, Z. Y. Hou, X. W. Li, Z. Li and W. D. Ni, Front. Phys., 2012, 7, 708–713 CrossRef.
- J. M. Liu, D. Wu, C. L. Fu, R. Hai, X. Yu, L. Y. Sun and H. B. Ding, Plasma Sci. Technol., 2019, 21, 034017 CrossRef CAS.
- H. X. Yang, H. B. Fu, H. D. Wang, J. W. Jia, M. W. Sigrist and F. Z. Dong, Chin. Phys. B, 2016, 25, 065201 CrossRef.
- Q. Q. Wang, K. Liu, H. Zhao, C. H. Ge and Z. W. Huang, Front. Phys., 2013, 7, 701–707 CrossRef.
- J. Y. Zhou, L. B. Guo, M. S. Zhang, W. H. Huang, G. D. Wang, A. J. Gong, Y. C. Liu and H. Sattar, Anal. Chim. Acta, 2024, 1309, 342674 CrossRef CAS PubMed.
- J. J. Lin, J. F. Yang, Y. T. Huang, X. M. Lin and C. J. Che, J. Anal. At. Spectrom., 2023, 38, 1501–1511 RSC.
- S. Z. Lu, M. R. Dong, J. W. Huang, W. B. Li, J. D. Lu and J. Li, Spectrochim. Acta, Part B, 2018, 140, 35–43 CrossRef CAS.
- R. L. Somorjai, B. Dolenko and R. Baumgartner, Bioinformatics, 2003, 19, 1484–1491 CrossRef CAS PubMed.
- X. Y. Jin, G. Yang, X. X. Sun, D. M. Qu, S. C. Li, G. Y. Chen, C. S. Li, D. Tian and L. Yao, J. Anal. At. Spectrom., 2023, 38, 243–252 RSC.
- X. M. Lin, H. R. Sun, X. Gao, Y. T. Xu, Z. X. Wang and Y. Wang, Spectrochim. Acta, Part B, 2021, 180, 106200 CrossRef CAS.
- T. L. Zhang, L. Liang, K. Wang, H. S. Tang, X. F. Yang, Y. X. Duan and H. Li, J. Anal. At. Spectrom., 2014, 29, 2323–2329 RSC.
- S. F. Hu, J. M. Ding, Y. Dong, T. L. Zhang, H. S. Tang and H. Li, RSC Adv., 2024, 14, 16358–16367 RSC.
- T. L. Zhang, D. H. Xia, H. S. Tang, X. F. Yang and H. Li, Chemometr. Intell. Lab. Syst., 2016, 157, 196–201 CrossRef CAS.
- L. W. Sheng, T. L. Zhang, G. H. Niu, K. Wang, H. S. Tang, Y. X. Duan and H. Li, J. Anal. At. Spectrom., 2015, 30, 453–458 RSC.
- Y. Ding, W. J. Chen, J. Chen, L. Y. Yang, Y. F. Wang, X. Q. Zhao, A. Hu, Y. Shu and M. L. Zhao, Anal. Sci., 2023, 40, 399–411 CrossRef PubMed.
- M. G. Li, H. Fu, Y. Du, X. Huang, T. L. Zhang, H. S. Tang and H. Li, J. Anal. At. Spectrom., 2022, 37, 1099–1108 RSC.
- F. Q. Ruan, L. Hou, T. L. Zhang and H. Li, Analyst, 2021, 143, 1023–1031 RSC.
- C. Heng, J. M. Grandemange and A. Morel, Nucl. Eng. Des., 1987, 98, 265–277 CrossRef.
- S. L. Li, Y. L. Wang, H. L. Zhang, S. X. Li, K. Zheng, F. Xue and X. T. Wang, J. Nucl. Mater., 2013, 433, 41–49 CrossRef CAS.
- GB/T 7714-2015, Guidelines for Aging Management of Pipelines in Nuclear Power Plants, 2015 Search PubMed.
- M. G. Pujar, R. Dayal, S. N. Malhotra and T. P. S. Gill, J. Mater. Eng. Perform., 2005, 14, 327–342 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |






