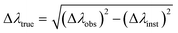Improving the quantitative accuracy of one-point calibration LIBS based on magnetic confinement of self-absorption correction
Received
19th September 2025
, Accepted 21st October 2025
First published on 22nd October 2025
Abstract
Laser-induced breakdown spectroscopy (LIBS) is widely applied in elemental quantitative analysis due to its rapid response, in situ detection, and simultaneous multi-element measurement capabilities. However, self-absorption effects, especially in high-concentration samples or under resonant transition conditions, often cause nonlinearity in calibration curves, significantly compromising the accuracy of quantitative analysis. To address this issue, this study proposed a combined approach integrating magnetic field confinement with one-point calibration LIBS (OPC-LIBS) to mitigate self-absorption effects and thereby improve quantitative accuracy. Six certified standard aluminum alloy samples were selected to evaluate the method. The impact of the applied field on plasma properties and analytical performance was studied for both the major matrix element (Al) and trace alloying constituents (Mg, Cu, Fe, and Ni). The experimental results demonstrated that magnetic field confinement enhanced spectral intensity and electron temperature, while increasing electron density—a signature of plasma confinement. This led to a more stable and uniform plasma, which effectively decreased self-absorption. In terms of quantitative performance, magnetically confined OPC-LIBS exhibited higher linearity and accuracy compared to conventional OPC-LIBS. Moreover, the linearity and accuracy varied among different elements. Under optimal conditions, the coefficient of determination (R2) between the predicted and certified concentrations of Al and Fe increased from 86.67% and 97.57% to 98.89% and 99.85%, while the average relative error (ARE) decreased from 0.21% and 8.99% to 0.05% and 2.99%, and the root mean square error of calibration (RMSEC) dropped from 0.20 wt% and 0.1 wt% to 0.05 wt% and 0.02 wt%, respectively. These results confirm the synergistic advantage of combining magnetic field confinement with OPC-LIBS for self-absorption correction and precise quantitative analysis, providing an effective technical pathway for high-precision elemental detection in complex matrices.
1 Introduction
As a newly developed technique under optical emission spectroscopy (OES), laser-induced breakdown spectroscopy (LIBS), also referred to as laser-induced plasma spectroscopy (LIPS), has attracted growing interest. Due to its minimal sample preparation requirements, in situ, real-time, remote, and simultaneous multi-element analysis capabilities, as well as stable operation in complex or harsh environments, LIBS has gained widespread attention in recent years.1,2 At present, LIBS technology is practically applied in various fields such as deep-sea exploration,3 coal quality assessment,4 metallurgical process monitoring,5 and planetary exploration (e.g., Mars missions).6
However, achieving accurate quantitative results with LIBS remains challenging, primarily due to matrix effects, plasma instability, self-absorption, and challenges in obtaining and creating calibration standards.7,8 Calibration-free LIBS (CF-LIBS), based on the local thermodynamic equilibrium (LTE) assumption, is one of the most widely used quantitative analysis strategies1 and has been successfully applied to element quantification in alloys, pigments, soils, rocks, aerosols, and other samples.9 However, the accuracy of CF-LIBS heavily depends on the plasma being optically thin and thermodynamically uniform, conditions that are often difficult to meet in practical applications. In particular, the commonly occurring self-absorption effect in plasma leads to weakened spectral line intensities and impaired linearity of Boltzmann plots, thereby reducing quantitative accuracy.9,10 To address these challenges, researchers have proposed various experimental enhancement methods11–14 and algorithmic correction approaches14–19 to suppress self-absorption and improve quantitative accuracy. Among these methods, the one-point calibration LIBS (OPC-LIBS) technique, proposed by Cavalcanti et al. in 2013, has attracted wide attention for its simplicity and efficiency, using a single standard sample.20
In recent years, several research groups have attempted to combine OPC-LIBS with other enhancement techniques to further improve its performance. For example, Borduchi et al.18 used OPC-LIBS to calibrate the emission intensities of Ca, Mg, and Fe in soybean leaves, achieving prediction accuracies above 92%. Wang et al.13 combined high-repetition-rate laser ablation spark discharge spectroscopy (HRR LA-SIBS) with OPC-LIBS, substantially reducing quantitative errors of Al, Mg, Cu, Cr, Mn, and Zn in aluminum alloys. Chen et al.21 combined target-enhanced orthogonal double-pulse LIBS with an improved OPC method, achieving relative errors below 4% in quantifying bismuth brass samples. Moreover, Zeng et al.14 further combined OPC-LIBS with target-enhanced orthogonal double-pulse technology, integrating Saha–Boltzmann calculations and Stark broadening analysis, successfully controlling the relative quantitative errors of Al and Mg in aluminum alloys to about 0.02%. These studies demonstrate that through appropriate experimental enhancements and algorithmic corrections, self-absorption effects can be effectively suppressed and quantitative accuracy significantly improved.
Magnetic field confinement is simple, low cost, and a promising approach to control the plasma. Under a steady magnetic field, charged particles in the plasma undergo spiral or circular motion along magnetic field lines due to the Lorentz force, which results in compressing the plume, increasing particle collision rates, and prolonging plasma lifetime. Crucially for quantitative analysis, this confinement can promote more uniform spatial distribution of the plasma and lessen the effects of self-absorption.11,22 Previous studies have confirmed that magnetic field confinement can significantly enhance emission intensity; for example, Shen et al.23 reported enhancement factors of 2 in the aluminum atomic line and 6 to 8 in the copper atomic line with magnetic field confinement. Li et al.24 investigated copper plasma enhancement under a 0.67 T magnetic field, reporting copper atomic line enhancement factors of 3 to 4 and copper ionic line enhancement factors of up to 6 to 8 and Guo et al.25 achieved a remarkable 22- and 24-fold enhancements in cobalt and chromium lines, respectively, compared to enhancement factors of 11 and 12 achieved by spatial confinement alone. Although extensive research has focused on signal enhancement rather than analytical accuracy, it has often been conducted under optimized conditions (such as low pressure) that yield large gains. The application of magnetic confinement to enhance quantitative calibration approaches, such as OPC-LIBS, remains largely unexplored. The plasma stabilization provided by a magnetic field is not an end in itself but as a means of establishing a stronger basis for advanced calibration. By generating a more stable and spatially uniform plasma, magnetic confinement can effectively reduce self-absorption and matrix effects, thereby enhancing quantitative accuracy.
In this study, a systematic approach combining magnetic confinement with OPC-LIBS for the analysis of major and trace elements (Al, Mg, Cu, Fe, and Ni) in aluminum alloys is presented. The combined method's success based on its ability to improve analytical figures of merit is evaluated. Systematic comparative analyses were conducted under both conventional LIBS and magnetically confined LIBS conditions, focusing on the spectral line intensities, plasma parameters (electron temperature and electron density), self-absorption degree, and most importantly, the quantitative accuracy of OPC-LIBS. The results confirm that magnetic confinement enhances the emission intensity while simultaneously reducing self-absorption, which significantly enhances the validity and precision of the one-point calibration approach.
2 Method
2.1. One-point calibration LIBS
Cavalcanti provided a detailed description of the OPC-LIBS method.20 First, the matrix-matched standards samples can be quantified using CF-LIBS based on the Boltzmann plot equation with and without magnetic field confinement, stated as:where xi and yi are the coordinates in the Boltzmann plot.| | 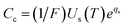 | (6) |
where Iij, gi, Ei, Aij, Te, Us(T), C, F, and kB are line intensity, statistical weight of the upper level, upper-level energy, transition probability, plasma temperature, partition function, concentration of the species, experimental parameter, and Boltzmann constant, respectively. Eqn (1)–(3) indicate that a linear regression technique in the xiyi plane can be used to estimate Te and qs. The Te and normalized relationship of concentrations (the sum of the concentrations of all species present in the sample) can be used to determine the experimental parameter F, and the concentration (Cc) of each element in the standard sample can be calculated using eqn (6). The calculated concentrations (Cc) of elements obtained with CF-LIBS may differ from the certified values Ccert. This difference suggests that the data points in the Boltzmann plot may deviate from their expected positions, due to uncertainties in the xiyi plane values.
OPC-LIBS is a simple technique, and it can correct the Boltzmann plots by reducing the uncertainty of transition probabilities, variations in spectrum acquisition efficiency, and possible self-absorption effects. A new Δyi and a correction parameter Pλ need to be calculated:
| |  | (7) |
| | 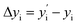 | (8) |
By using
eqn (7) and
(8), measuring
eqn (9) and modifying
eqn (3) we obtain:
Eqn (10) can be used to draw a new Boltzmann plot for OPC-LIBS. The correction parameter (Pλ) can be used to eliminate the uncertainty of the transition probability and the variations in spectral acquisition efficiency.20 In OPC-LIBS, self-absorption can be corrected to some extent by the correction parameter Pλ. The offsets corrected by Pλ originate from three sources: the uncertainty of transition probabilities, variations in spectrum acquisition efficiency, and potential self-absorption effects. While the first two sources are independent of elemental concentration, self-absorption is concentration-dependent. This implies that Pλ inherently accounts for self-absorption to some extent. Self-absorption is closely related to line width (FWHM), which in turn depends on element concentrations when self-absorption is present. Therefore, the influence of the first two sources and the self-absorption effect in the OPC-LIBS algorithm can be reasonably removed. However, self-absorption must still be corrected unless the self-absorption of the target lines can be ignored, or the target lines have the same extent of self-absorption.
2.2. Magnetic field confined one-point calibration LIBS (OPC-LIBS)
Self-absorption is a major hurdle in the application of CF-LIBS and OPC-LIBS. It can affect the concentrations of elements, and it directly related to the FWHM of line intensities.12 To reduce the self-absorption effect, magnetic field confinement LIBS is combined with OPC-LIBS. According to self-absorption theory, the self-absorption coefficient (SA) can be expressed as follows:26| | | (SA)1/2 = (Δλo)/(Δλ) = (IΔλ)/(I0Δλ0) | (11) |
Δλ and I can be measured from line width and intensity, while Δλ0 and I0 are the theoretical values of line width and intensity, unaffected by self-absorption.
Rearranging eqn (11):
Δλ0 can be measured using electron density Ne.
where
w and
Nrefe are the electron impact parameter and reference electron number density, which is generally 10
16 cm
—3;
Ne can be calculated as follows:.
27| | | Ne = 8.02 × 1012(ΔλHα/α1/2)3/2 | (14) |
Δ
λHα and
α1/2 are the FWHM of the
Hα line and is the half width of the reduced Stark profile, which is described by Griem.
28 The self-absorption in the
Hα line can be ignored because it comes from water in LIBS spectra.
I0 can be written by combining
eqn (12) and
(14):
| | | I0 = (Δλ)2(ΔλHα)−3(α1/2)3{Nrefe/(1.604 × 1013ω)}2 | (15) |
Considering eqn (15):
| | | Q = (α1/2)3{Nrefe/(1.604 × 1013ω)}2 | (17) |
Eqn (15) can be written as:
where the term
Q is constant, while
Wλ contains two variables, which are directly associated with the FWHM of the calculated spectral line (Δ
λ) and the FWHM of the
Hα line. The self-absorption in the
Hα line can be ignored but in the calculated spectral line (Δ
λ) it cannot be ignored. In this work, the magnetic field is used to correct the parameter
Wλ. And,
Pλ can be expressed as:
where
Ri is a correction factor for the uncertainty of the transition probability and the differences in spectral acquisition efficiency, (
WλQi) is a correction factor for self-absorption correction (SAC), and
Wλ can be calculated for the standard samples. Thus, we can define another correction parameter
Pconfinedλ:
| | | Pconfinedλ = Ri/Qi = PλQi | (20) |
The yi intercept for thick lines can be written as:
| | | yi = ln((WλIij)/Pconfinedλ) | (21) |
Eqn (21) can be used to calculate a new parameter with magnetic field confinement Pconfinedλ. It should be noted that any spectral line can be utilized with this parameter. In this work, we will apply OPC-LIBS under magnetic field confinement to all spectral lines.
3 Experimental setup
The experimental setup for magnetically confined LIBS is illustrated in Fig. 1. A Nd:YAG laser (Continuum Surelite II, wavelength 1064 nm, repetition rate 10 Hz, pulse duration 10 ns) was used as the excitation source to generate laser-induced plasma on aluminum alloy samples in ambient air. The laser beam was focused onto the sample surface using a K9 lens with a focal length of 125 mm, producing a focal spot diameter of approximately 500 µm. The single-pulse laser energy was set to 30 mJ. Samples were mounted on a three-dimensional motorized translation stage (PI M-410.DG) with a minimum step size of 0.1 µm and repeat positioning accuracy of 0.2 µm to ensure that each laser pulse ablated a fresh surface area. To achieve magnetic confinement, two rectangular permanent magnets sized 60 mm × 45 mm were arranged parallel and fixed on a non-magnetic steel frame, with a fixed separation of 2.9 cm. The magnetic field intensity was controlled by adjusting the gap between the magnet poles and measured in the plasma plume region using a Gauss–Tesla meter (HT20). The magnetic field strength was set at 0.4 T in this study to optimize signal enhancement and repeatability. Plasma emission was collected by a convex lens with a focal length of 100 mm and transmitted via optical fiber to a spectrometer (Andor Me5000) covering a spectral range of 200–975 nm with a spectral resolution of 0.05 nm. The detection system was equipped with an ICCD (Andor DH334T, 1024 × 1024 pixels). The gate width and delay time were set to 3 µs and 1 µs, respectively, to capture emission signals during the plasma's thermal steady-state phase. Wavelength calibration of the spectrometer was performed before experiments using a mercury lamp. Synchronization between the laser and ICCD was controlled by a digital delay pulse generator (Stanford DG645) featuring four pulse outputs and eight delay control outputs. For each set of experimental conditions, signals from 30 independent laser pulses were collected and averaged to reduce the influence of laser energy fluctuations on LIBS signal stability. Data analysis was conducted using Origin 2022 software and the NIST atomic database. The spectral data were used to evaluate the performance of the magnetically confined OPC-LIBS method in terms of signal enhancement and measurement repeatability, and to further carry out quantitative analysis.
 |
| | Fig. 1 Experimental setup for magnetically confined LIBS. | |
4 Results and discussion
4.1. Emission spectra
Fig. 2 presents the comparison of emission spectra from aluminum alloy sample E311 under conditions with and without magnetic confinement. The experiments demonstrated that applying a steady magnetic field of 0.4 T significantly enhanced the emission intensities of multiple elements, including Mg, Cu, Al, Fe, Zn, and Ni. This enhancement effect is primarily attributed to the magnetic field's regulation of various dynamic processes within the plasma plume, such as increased electron impact ionization, radiative recombination, and recombination of charged particles. Under the influence of the external magnetic field, these processes become more active, effectively suppressing the rapid expansion of the plasma plume and significantly limiting its spatial spread. Meanwhile, the collision frequency and energy transfer efficiency among particles are improved, resulting in an overall enhancement of spectral line intensities and signal quality.29 Furthermore, due to the Lorentz force, charged particles (electrons and ions) in the plasma moving perpendicular to the magnetic field undergo trajectory deflection, causing spatial charge separation. This effect induces currents that drive the plasma to expand synchronously in both radial and axial directions.30 Such behavior further optimizes the plasma's spatial structure and excitation uniformity, providing a more stable plasma environment conducive to subsequent high-precision spectral analysis.
 |
| | Fig. 2 Emission spectra of aluminum alloy with and without magnetic confinement. | |
4.2. Plasma parameters
The electron temperature (Te) and electron density (Ne) play crucial roles in the ionization and excitation processes within the plasma plume and serve as important physical parameters to reveal the enhancement mechanism of LIBS signals under magnetic confinement. In this study, Te and Ne were calculated using the Boltzmann plot method and Stark broadening method, in sample E311, respectively, to comprehensively characterize the plasma's physical state. The Boltzmann plot method is based on the relationship between the population distribution of excited atomic energy levels and the electron temperature, while the Stark broadening method uses spectral line broadening to characterize the degree of ionization in the plasma. To ensure the accuracy of parameter extraction, the plasma must satisfy the local thermodynamic equilibrium (LTE) and optically thin conditions. Under these assumptions, the population of excited states follows the Boltzmann distribution, expressed as:31,32| | | ln(Iλ/gA) = −Em/kBTe + ln(N(T)/U(T)) | (22) |
where, λ is the wavelength, I is the peak intensity, g is the statistical weight, A is the transition probability, E is the energy of the level, kB is the Boltzmann constant, Te is the plasma temperature, N(T) is the total plasma density, and U(T) is the partition function. Under no magnetic confinement, the electron temperatures Te of Al, Mg, Cu, Fe, and Ni in sample E311 were 5112 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 K, 8858 K, 5831 K, and 8995 K, respectively. After applying a steady magnetic field of 0.4 T, the Te values increased to 5448 K, 11
947 K, 8858 K, 5831 K, and 8995 K, respectively. After applying a steady magnetic field of 0.4 T, the Te values increased to 5448 K, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 K, 10
489 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091 K, 7344 K, and 9670 K, respectively. This trend indicates that magnetic confinement significantly enhanced the plasma excitation intensity. The main reasons are the Joule heating effect and adiabatic compression induced by the magnetic field, which promote energy accumulation and frequent collisions among particles.33
091 K, 7344 K, and 9670 K, respectively. This trend indicates that magnetic confinement significantly enhanced the plasma excitation intensity. The main reasons are the Joule heating effect and adiabatic compression induced by the magnetic field, which promote energy accumulation and frequent collisions among particles.33
The electron density Ne was calculated from the Stark broadening of the 656.27 nm line, using eqn (14) from ref. 27. To exclude instrumental broadening effects, all spectral line full widths at half maximum (FWHM) were corrected as follows:
| | 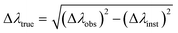 | (23) |
where Δ
λobs is the measured linewidth and Δ
λinst is the instrumental broadening, taken as 0.10 nm. The corrected FWHM was used to calculate
Ne for
Hα. In sample E311,
Ne without magnetic field was approximately 3.89 × 10
17 cm
−3. After applying magnetic field confinement,
Ne increased to 4.18 × 10
17 cm
−3. This increase of
Ne under magnetic field confinement is attributed to increased collisional and recombination processes between charged particles.
34 The combined effect formed a denser, more uniform, stable plasma with higher excitation efficiency, thereby improving the spectral quality and analytical accuracy of LIBS.
4.3. Effect of magnetic confinement on self-absorption
Self-absorption is a critical factor affecting the accuracy of quantitative analysis in LIBS, especially for high-precision detection of elements in complex matrices. This phenomenon leads to the weakening of emission line intensities and a reduction in the linearity of calibration curves, ultimately causing deviations in concentration determination. To quantitatively evaluate the degree of self-absorption, the self-absorption coefficient (SA) is introduced. The value of SA ranges from 0 to 1, with smaller values indicating more severe self-absorption. SA can be calculated using the following equation:26| | | SA1/2 = {(Δλ/ωs)(1/Ne)}1/α | (24) |
where, Δλ is the full width at half maximum (FWHM) of the spectral line, Ne is the electron density which can be calculated using eqn (14), and α is typically set to −0.54.12 In this study, characteristic emission lines of Al(I) 396.15 nm, Mg(I) 285.21 nm, Cu(I) 324.77 nm, Fe(I) 373.48 nm, and Ni(I) 358.79 nm were selected for self-absorption analysis. FWHM and SA values were calculated and compared under both magnetic and non-magnetic confinement conditions across six aluminum alloy samples. Fig. 3 presents the SA variations of these elements in samples E311, E312a, E313, E314, E315, and E316. The results demonstrate that SA values increased to varying degrees under magnetic confinement, indicating narrower spectral lines12 and reduced self-absorption effects. This improvement can be primarily attributed to the constraining effect of the magnetic field on the plasma. Firstly, the external magnetic field applies Lorentz forces that suppress the lateral expansion of the plasma plume, resulting in a denser and more stable morphology.29 This enhances plasma excitation uniformity and reduces electron density gradients, thereby lowering the probability of self-absorption. Secondly, the magnetic field increases the kinetic energy of charged particles in the plasma, particularly in the outer regions, leading to a localized temperature rise. This reduces the likelihood of reabsorption of emitted radiation by the outer layers, further mitigating the probability of self-absorption.11 The introduction of the magnetic field optimizes the spatial distribution of excited-state particles, improving both the intensity and the sharpness of emission lines. These effects work synergistically to suppress self-absorption.
 |
| | Fig. 3 Comparison of SA for Al(I) 396.15 nm, Mg(I) 285.21 nm, Cu(I) 324.75 nm, Fe(I) 373.48 nm, and Ni(I) 358.79 nm in samples E311 (a), E312a (b), E313 (c), E314 (d), E315 (e), and E316 (f) under conditions with and without magnetic confinement. | |
4.4. Quantitative analysis accuracy of trace elements
Magnetic field confinement can improve the accuracy of compositional analysis using calibration curves in LIBS signals.22 To verify the impact of the magnetic field on enhancing the accuracy of quantitative analysis, six certified aluminum alloy standards were selected, and both OPC-LIBS and magnetically confined OPC-LIBS methods were employed to quantitatively analyze major and trace elements—Al, Mg, Cu, Fe, and Ni. The selected characteristic spectral lines are listed in Table 1, with corresponding level energies, transition probabilities, and degeneracies obtained from NIST. We considered E311 as the standard sample, while E312a, E313, E314, E315, and E316 were considered as unknown samples and tested. Fig. 4(a) and (b) show the Boltzmann plots of the five major and trace elements in sample E311 under non-magnetic and magnetic confinement conditions, respectively. The results indicate that, compared with conventional OPC-LIBS, the data points from magnetically confined OPC-LIBS exhibit significantly better alignment with the fitted Boltzmann lines. The Te was first calculated by using the Boltzmann plot for each element, and then an averaged value, was determined with and without magnetic field confinement, respectively. Data points almost fall on the fitted line, and all plots for different elements are approximately parallel.13 The linear regression coefficients (R2) are markedly improved and approach unity. Table 2 summarizes the quantitative analysis results of aluminum alloy samples. Compared with the OPC-LIBS method without magnetic confinement, the relative errors (REs) were notably reduced when magnetic confinement was applied. Under optimal conditions, the AREs of Al and Fe elements decreased from 0.21% and 8.99% to 0.05% and 2.99%, respectively, listed in Table 3. These results demonstrate that the introduction of the magnetic field effectively enhances plasma spatial confinement and thermal stability, possibly suppresses self-absorption effects, and improves the uniform distribution of excited-state particles, resulting in improved calibration curves.22 Furthermore, when combined with self-absorption correction, the yi coordinate values increased as shown in Fig. 4(b) compared with Fig. 4(a), which means that the self-absorption was effectively corrected.35 Consequently, the Boltzmann plots display improved linear fitting characteristics.
Table 1 Analytical spectral lines selected for OPC-LIBS with and without magnetic field confinement
| Element |
Spectral lines (nm) |
| Al(I) |
308.22, 309.27, 394.40, 396.15 |
| Mg(I) |
285.21, 383.82, 552.84 |
| Cu(I) |
324.75, 327.41, 510.58, 578.27 |
| Fe(I) |
382.94, 492.04, 357.61, 371.99, 610.32 |
| Ni(I) |
339.30, 361.94, 547.68, 617.68 |
 |
| | Fig. 4 Boltzmann plots of elements (Al, Mg, Cu, Fe, and Ni) in sample E311 obtained using OPC-LIBS (a) and magnetically confined OPC-LIBS (0.4 T) (b), at a delay time of 1 µs. | |
Table 2 Quantitative results of Al alloy samples using OPC-LIBS with and without magnetic field confinement
| Sample |
Technique |
Element concentrations (wt%) |
| Al |
RE (%) |
Mg |
RE (%) |
Cu |
RE (%) |
Fe |
RE (%) |
Ni |
RE (%) |
| E312a |
Reference value |
92.719 |
— |
1.37 |
— |
2.45 |
— |
1.23 |
— |
1.09 |
— |
|
|
OPC-LIBS (0 T) |
92.562 |
0.17 |
1.32 |
3.65 |
2.41 |
1.47 |
1.21 |
1.63 |
1.12 |
2.75 |
|
|
OPC-LIBS (0.4 T) |
92.704 |
0.02 |
1.39 |
1.31 |
2.43 |
0.65 |
1.24 |
0.81 |
1.08 |
0.92 |
| E313 |
Reference value |
92.742 |
— |
0.897 |
— |
1.52 |
— |
0.908 |
— |
2.02 |
— |
|
|
OPC-LIBS (0 T) |
91.915 |
0.19 |
0.961 |
7.13 |
1.49 |
1.97 |
0.947 |
4.29 |
1.87 |
7.43 |
|
|
OPC-LIBS (0.4 T) |
92.704 |
0.04 |
0.849 |
5.35 |
1.53 |
0.66 |
0.895 |
1.43 |
1.98 |
1.98 |
| E314 |
Reference value |
91.86 |
— |
1.80 |
— |
3.33 |
— |
1.61 |
— |
0.624 |
— |
|
|
OPC-LIBS (0 T) |
91.99 |
0.14 |
1.87 |
3.89 |
3.22 |
3.30 |
1.66 |
3.11 |
0.723 |
15.87 |
|
|
OPC-LIBS (0.4 T) |
91.81 |
0.05 |
1.79 |
0.56 |
3.47 |
4.20 |
1.58 |
1.86 |
0.595 |
4.65 |
| E315 |
Reference value |
92.445 |
— |
2.26 |
— |
0.927 |
— |
1.87 |
— |
0.153 |
— |
|
|
OPC-LIBS (0 T) |
94.229 |
0.23 |
2.41 |
6.64 |
0.987 |
6.47 |
1.67 |
10.70 |
0.147 |
3.92 |
|
|
OPC-LIBS (0.4 T) |
91.405 |
0.04 |
2.21 |
2.21 |
0.968 |
4.42 |
1.91 |
2.14 |
0.144 |
5.88 |
| E316 |
Reference value |
91.78 |
— |
0.074 |
— |
5.55 |
— |
0.115 |
— |
2.25 |
— |
|
|
OPC-LIBS (0 T) |
91.48 |
0.33 |
0.114 |
54.05 |
5.37 |
3.24 |
0.144 |
25.22 |
2.41 |
7.11 |
|
|
OPC-LIBS (0.4 T) |
91.86 |
0.09 |
0.092 |
24.32 |
5.51 |
0.72 |
0.125 |
8.70 |
2.14 |
4.88 |
| E311 |
Standard |
92.708 |
— |
0.428 |
— |
4.51 |
— |
0.454 |
— |
1.55 |
— |
Table 3 ARE (%), RMSEC (wt%), and R2 analyzed by OPC-LIBS with and without Magnetic Field Confinement
| Elements |
ARE (%) |
RMSEC (wt%) |
R
2
|
| 0 T |
0.4 T |
0T |
0.4 T |
0 T |
0.4 T |
| Al |
0.21 |
0.05 |
0.20 |
0.05 |
0.8667 |
0.9889 |
| Mg |
15.07 |
6.75 |
0.08 |
0.03 |
0.9875 |
0.9980 |
| Cu |
3.29 |
2.13 |
0.10 |
0.07 |
0.9962 |
0.9982 |
| Fe |
8.99 |
2.99 |
0.10 |
0.02 |
0.9757 |
0.9985 |
| Ni |
7.42 |
3.66 |
0.11 |
0.05 |
0.9817 |
0.9954 |
As a result of application of magnetically confined OPC-LIBS to correct the self-absorption method, the calibration curves of Al, Mg, Cu, Fe, and Ni between predicted and certified values are shown in Fig. 5(a–e). A clear improvement in the linearity of calibration curves is observed upon the introduction of magnetic confinement. Under optimal conditions, the coefficient of determination (R2) between the predicted and certified concentrations of Al and Fe increased from 86.67 and 97.57% to 98.89% and 99.85%, while RMSEC dropped from 0.20 wt% and 0.10 wt% to 0.05 wt% and 0.02 wt%, respectively, as shown in Table 3. To evaluate the accuracy of predicted values, AREs (%) were calculated for all five elements in each sample, which were significantly reduced with magnetically confined OPC-LIBS to correct self-absorption, as shown in Fig. 5(f). These notable enhancements in performance parameters demonstrated that magnetically confined OPC-LIBS for self-absorption correction is effective in improving the accuracy of OPC-LIBS, especially for high-concentration and trace elements in complex matrix samples. The improvement in accuracy of the OPC-LIBS method is attributed to magnetically confined LIBS with SAC, in which the plasma plume is compressed and elongated along the magnetic field lines, forming a denser and more stable emission zone. This confinement effectively suppresses excessive plasma expansion and energy dissipation, thereby enhancing emission intensity, possibly mitigating self-absorption, and promoting a state closer to LTE.36 This advancement offers an effective pathway for high-precision detection of major and trace elements in complex metallic matrices and lays a solid foundation for the practical application of LIBS in fields such as in situ material composition analysis, industrial process monitoring, and advanced manufacturing.
 |
| | Fig. 5 Comparison between predicted and certified concentrations of Al (a), Mg (b), Cu (c), Fe (d), and Ni (e), and the quantitative AREs of all five elements (f) in Al alloys using OPC-LIBS with and without magnetic confinement. | |
5 Conclusion
To address the adverse effects of self-absorption on the accuracy of quantitative analysis in laser-induced breakdown spectroscopy (LIBS), this study proposes an improved method by integrating magnetic confinement with one-point calibration LIBS (OPC-LIBS). To assess the technique, aluminum standard alloy samples were selected to systematically compare the spectral intensity, plasma parameters, self-absorption characteristics, and analytical performance of major and trace elements Al, Mg, Cu, Fe, and Ni under conventional LIBS and magnetically confined LIBS conditions. The results from spectral analysis showed that the application of a magnetic field significantly enhanced plasma emission intensity, electron temperature, and electron density, indicating a more uniform excitation and improved spectral quality. This caused the plasma to become more consistent and stable, which possibly reduced self-absorption. Comparison of the quantitative performance between OPC-LIBS and magnetically confined OPC-LIBS revealed that the latter exhibits superior precision. Moreover, the linearity and accuracy varied among different elements. Under optimal conditions, the R2 between the predicted and certified concentrations of Al and Fe elements increased from 86.67 and 97.57% to 98.89% and 99.85%, while the AREs decreased from 0.21% and 8.99% to 0.05% and 2.99%, and the RMSEC dropped from 0.20 wt% and 0.10 wt% to 0.05 wt% and 0.02 wt%, respectively. These results demonstrate that the proposed method significantly enhances the quantitative analytical capability of LIBS for trace elements in complex metallic matrices. In summary, magnetic confinement not only optimizes plasma physical parameters by improving spatial confinement and thermal stability, but also complements the quantitative calibration mechanism of OPC-LIBS. This synergistic effect effectively suppresses self-absorption, enhances signal stability, and improves quantitative accuracy. The proposed approach provides a solid theoretical foundation and technical support for high-sensitivity and high-precision detection of trace elements in complex metal materials, offering broad application prospects.
Authors contributions
Rana Muhammad Shahbaz: methodology, formal analysis, writing- original draft. Qiuyun Wang: investigation, writing-review & editing. Hailong Yu: software, data curation, investigation, writing-review & editing. Yinping Dou: formal analysis, writing-review & editing. Xun Gao: resources, supervision, project administration, funding acquisition, writing-review & editing. Jingquan Lin: resources, writing-review & editing.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Data will be made available on request.
Acknowledgements
This study was supported by the Natural Science Foundation of China (No. 62335016) and the Natural Science Foundation of Jilin province (No. 20220101035JC).
References
- A. Ciucci, M. Corsi, V. Palleschi, S. Rastelli, A. Salvetti and E. Tognoni, Appl. Spectrosc., 1999, 53, 960–964 CrossRef CAS.
- J. Dong, L. Liang, J. Wei, H. S. Tang, T. L. Zhang, X. F. Yang, K. Wang and H. Li, J. Anal. At. Spectrom., 2015, 30, 1336–1344 RSC.
- C. H. Liu, J. J. Guo, Y. Tian, C. Zhang, K. Cheng, W. Q. Ye and R. E. Zheng, Sensors, 2020, 20, 7341 CrossRef CAS PubMed.
- K. Liu, C. He, C. W. Zhu, J. Chen, K. P. Zhan and X. Y. Li, TrAC, Trends Anal. Chem., 2021, 143, 116357 CrossRef CAS.
- J. M. Li, M. L. Xu, Q. X. Ma, N. Zhao, X. Y. Li, Q. M. Zhang, L. Guo and Y. F. Lu, Talanta, 2019, 194, 697–702 CrossRef CAS PubMed.
- X. Wan, C. H. Li, H. P. Wang, W. M. Xu, J. J. Jia, Y. J. Xin, H. Z. Ma, P. P. Fang and Z. C. Ling, At. Spectrosc., 2021, 42, 294–298 CrossRef CAS.
- J. J. Yan, Z. Q. Hao, R. Zhou, Y. Tang, P. Yang, K. Liu, W. Zhang, X. Y. Li, Y. F. Lu and X. Y. Zeng, Anal. Chim. Acta, 2019, 1082, 30–36 CrossRef CAS PubMed.
- P. Yang, G. R. Fu, J. Wang, Z. Luo and M. Y. Yao, J. Anal. At. Spectrom., 2022, 37, 1948–1960 RSC.
- T. Q. Li, Z. Y. Hou, Y. T. Fu, J. L. Yu, W. L. Gu and Z. Wang, Anal. Chim. Acta, 2019, 1058, 39–47 CrossRef CAS.
- E. Tognoni, G. Cristoforetti, S. Legnaioli and V. Palleschi, Spectrochim. Acta, Part B, 2010, 65, 1–14 CrossRef.
- J. H. Li, J. Wu, M. X. Shi, Y. Qiu, Y. Zhou, H. Sun, X. Y. Guo, D. Wu, Y. H. Hang, H. L. Yang and X. W. Li, J. Anal. At. Spectrom., 2024, 39, 1235–1247 RSC.
- Z. Xiong, Z. Q. Hao, X. Y. Li and X. Y. Zeng, J. Anal. At. Spectrom., 2019, 34, 1606–1610 RSC.
- Y. R. Wang, Y. Q. Chen, R. H. Li, J. Kang and J. K. Gao, J. Anal. At. Spectrom., 2021, 36, 314–321 RSC.
- H. L. Zeng, R. H. Li and Y. Q. Chen, Appl. Opt., 2024, 63, 338–344 CrossRef CAS PubMed.
- L. C. Leva Borduchi, C. R. Menegatti, D. M. Bastos Pereira Milori, H. J. Izário Filho and P. R. Villas-Boas, J. Anal. At. Spectrom., 2023, 38, 1155–1163 RSC.
- J. L. Li, Q. Yang, J. Q. Yao, X. Y. He and F. J. Wang, Anal. Chim. Acta, 2023, 1238, 340613 CrossRef CAS.
- X. Bai, R. Hai, Z. L. He, X. Y. Wang, J. P. Mu, H. C. Wu, C. Li, D. Wu, G. L. Xu, Z. H. Hu, F. Ding and H. Bin Ding, Spectrochim. Acta, Part B, 2023, 206, 106724 CrossRef CAS.
- L. C. L. Borduchi, D. M. B. P. Milori, M. C. Meyer and P. R. Villas-Boas, Spectrochim. Acta, Part B, 2022, 198, 106561 CrossRef CAS.
- C. Aragón and J. A. Aguilera, Anal. Chim. Acta, 2018, 1009, 12–19 CrossRef.
- G. H. Cavalcanti, D. V. Teixeira, S. Legnaioli, G. Lorenzetti, L. Pardini and V. Palleschi, Spectrochim. Acta, Part B, 2013, 87, 51–56 CrossRef CAS.
- S. L. Chen, R. H. Li and Y. Q. Chen, Appl. Opt., 2023, 62, 4512–4517 CrossRef CAS.
- M. R. Khan, S. U. Haq, Q. Abbas and A. Nadeem, Spectrochim. Acta, Part B, 2023, 200, 106612 CrossRef CAS.
- X. K. Shen, Y. F. Lu, T. Gebre, H. Ling and Y. X. Han, J. Appl. Phys., 2006, 100, 053303 CrossRef.
- C. Li, X. Gao, Q. Li, C. Song and J. Q. Lin, Plasma Sci. Technol., 2015, 17, 919–922 CrossRef.
- L. B. Guo, W. Hu, B. Y. Zhang, X. N. He, C. M. Li, Y. S. Zhou, Z. X. Cai, X. Y. Zeng and Y. F. Lu, Opt. Express, 2011, 19, 14067–14075 CrossRef CAS.
- A. M. El Sherbini, T. M. El Sherbini, H. Hegazy, G. Cristoforetti, S. Legnaioli, V. Palleschi, L. Pardini, A. Salvetti and E. Tognoni, Spectrochim. Acta, Part B, 2005, 60, 1573–1579 CrossRef.
- S. S. Harilal, C. V. Bindhu, R. C. Issac, V. P. N. Nampoori and C. P. G. Vallabhan, J. Appl. Phys., 1997, 82, 2140–2146 CrossRef CAS.
-
H. R. Griem and W. L. Barr, Spectral Line Broadening by Plasmas, 1974, vol. 3 Search PubMed.
- V. N. Rai, H. S. Zhang, F. Y. Yueh, J. P. Singh and A. Kumar, Appl. Opt., 2003, 42, 3662 CrossRef CAS.
- X. K. Shen, J. Sun, H. Ling and Y. F. Lu, J. Appl. Phys., 2007, 102, 093301 CrossRef.
- C. A. Bye and A. Scheeline, Appl. Spectrosc., 1993, 47, 2022–2030 CrossRef CAS.
- H. Amamou, A. Bois, B. Ferhat, R. Redon, B. Rossetto and P. Matheron, J. Quant. Spectrosc. Radiat. Transfer, 2002, 75, 747–763 CrossRef CAS.
- A. M. El Sherbini, H. Hegazy and T. M. El Sherbini, Spectrochim. Acta, Part B, 2006, 61, 532–539 CrossRef.
- M. Akhtar, A. Jabbar, N. Ahmed, S. Mahmood, Z. A. Umar, R. Ahmed and M. A. Baig, Appl. Phys. B, 2019, 125, 1–11 Search PubMed.
- Z. L. Hu, J. F. Nie, Z. Y. Ouyang, D. Zhang, Y. C. Liu, Y. W. Chu and L. B. Guo, Opt. Lett., 2023, 48, 1–4 CrossRef CAS PubMed.
- L. M. John and K. K. Anoop, RSC Adv., 2023, 13, 29613–29624 RSC.
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab and
Jingquan
Lin
ab
*ab and
Jingquan
Lin
ab
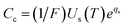

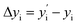
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 K, 8858 K, 5831 K, and 8995 K, respectively. After applying a steady magnetic field of 0.4 T, the Te values increased to 5448 K, 11
947 K, 8858 K, 5831 K, and 8995 K, respectively. After applying a steady magnetic field of 0.4 T, the Te values increased to 5448 K, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 489 K, 10
489 K, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091 K, 7344 K, and 9670 K, respectively. This trend indicates that magnetic confinement significantly enhanced the plasma excitation intensity. The main reasons are the Joule heating effect and adiabatic compression induced by the magnetic field, which promote energy accumulation and frequent collisions among particles.33
091 K, 7344 K, and 9670 K, respectively. This trend indicates that magnetic confinement significantly enhanced the plasma excitation intensity. The main reasons are the Joule heating effect and adiabatic compression induced by the magnetic field, which promote energy accumulation and frequent collisions among particles.33