Systematic evaluation of plasma and reactor parameters in non-thermal dielectric barrier discharge plasma ammonia synthesis

Abstract

Dielectric barrier discharge (DBD) plasmas provide an electrified, nonequilibrium route to ammonia synthesis that can be directly powered by renewable electricity. However, the coupled effects of reactor geometry, operating conditions, and microdischarge on plasma characteristics and process performance remain poorly understood. Here, we present a comprehensive study of N₂–H₂ conversion in a DBD reactor, systematically varying the barrier thickness (1.0–2.0 mm and empty-cell reference), electrode and discharge gaps, applied voltage, gas composition, flow rate, and pulse timing parameters. Integrated diagnostics, including Lissajous power analysis, microdischarge statistics, optical emission spectroscopy of N₂, N₂⁺, and NH, and colorimetric NH₃ quantification, are combined with statistical correlation and machine-learning (Random Forest) analyses. We show that the reactor geometry governs the microdischarge charge and energy distributions through capacitive coupling, while the residence time and pulse timing regulate the excitation partitioning across the electronic, ionic, and dissociative channels. Gas composition further determines the balance between nitrogen excitation and radical generation pathways. Ammonia yields correlate most strongly with NH(A → X) emission intensity and scale with microdischarge dynamics, linking discharge structure directly to nitrogen activation efficiency. This parameter-mapped framework provides mechanistic design rules for tuning plasma reactors and advances the development of sustainable, decentralised ammonia synthesis under mild conditions.

---

Green foundation

1. This work advances green chemistry by establishing mechanistic design rules for electrified, catalyst-free ammonia synthesis under mild, atmospheric-pressure conditions. It enables direct conversion of N₂ and H₂ using renewable electricity, offering a fossil-free alternative to the Haber–Bosch process.

2. We demonstrate that optimising plasma microdischarge behaviour in dielectric-barrier discharge (DBD) reactors can double the nitrogen activation efficiency while operating below 100 °C and 1 bar. A systematic correlation among the reactor geometry, pulse timing, and excitation channels provides a quantitative framework to minimise energy losses and guide low-energy plasma process design.

3. Further greening could be achieved by coupling the plasma reactor with renewable H₂ generation or plasma-catalyst hybrids to enhance yield at lower power densities. Integration with life-cycle and techno-economic assessments will advance scalability toward carbon-neutral ammonia production.

Introduction

Ammonia sits at the nexus of food, fuels, and net-zero ambitions. It is indispensable for fertilizers and increasingly recognised for its potential value as a hydrogen carrier, yet its production still relies on the Haber–Bosch process, which consumes 1%–2% of global energy and emits more CO₂ than any other single industrial chemistry.¹ Because Haber–Bosch is bound to high temperatures, pressures, and fossil-derived hydrogen, new sustainable routes to ammonia are urgently required.² Therefore, electrified nitrogen fixation has emerged as a central grand challenge in catalysis and green chemistry.^3–5

Non-thermal plasmas (NTPs) offer a distinctive pathway for small-scale, delocalised ammonia synthesis as they operate fundamentally out of equilibrium, with “hot” electrons coexisting alongside a comparatively “cold” bulk gas.⁵ This disparity allows electrical work to be funnelled into vibrational, electronic, and radical channels rather than getting dissipated as heat.^3,6,7 For nitrogen, NTPs can generate vibrationally excited nitrogen, N₂(v), electronically excited N₂*, atomic nitrogen, ions, and radicals, all sustained at near-ambient conditions. In an N₂–H₂ mixture, these non-equilibrium ensembles can interact with catalytic surfaces via, for example, non-thermal Eley–Rideal⁸ and hot-precursor mechanisms⁹ or homogeneous reactions,^10,11 and when persistent, they can even drive apparent conversions beyond the thermal equilibrium limit at modest bulk temperatures.^12,13

Dielectric barrier discharges (DBDs) have gained attention recently, particularly with respect to ammonia synthesis, because they combine operational simplicity at atmospheric pressure with a microdischarge-driven mode of energy deposition.^14–21 Microdischarges, which are short-lived, filamentary discharges in the plasma initiated by a streamer breakdown, occur on nanosecond timescales with high local fields and electron densities, and they are central to the plasma chemical kinetics.²⁰ Microdischarges are primarily generated in the bulk plasma gap; however, discharge filaments have also been observed at the entrances of macropores, interparticle voids, or micro- to millimetre-scale channels in structured catalysts. The formation of microdischarges inside porous catalysts is highly dependent on pore size, dielectric properties, and local field enhancement, and they are not typically believed to form within conventional nano- or micro-porous catalyst architectures, where pore dimensions and local field screening prevent breakdown.^22–26 The statistics of microdischarge formation are regulated by the dielectric barrier's material and thickness, electrode geometry, and discharge gap. These parameters determine charge accumulation, local field distributions, and ultimately the spatiotemporal distribution of microdischarges.^20,25–27 In turn, these features sculpt the electron energy distribution function (EEDF), partition energy flow into internal modes, and define the spectrum of reactive species delivered to the catalyst surface.²⁸ Establishing mechanistic connections between microdischarge characteristics, such as dynamics, vibrational, and electronic excitation, and plasma chemical process performance, remains an open frontier that has been identified as a key priority in recent community roadmaps.^5,20,21

Converging theory and experiments have suggested that vibrational activation of N₂ can, in some plasma systems, lower the effective barrier for N≡N dissociation and thereby promote ammonia synthesis.^7,29–31 Kinetic modelling and microkinetic analyses show that elevating the population of N₂(v) selectively lowers the effective barrier for dissociation on metal surfaces, without proportionally accelerating the subsequent hydrogenation sequence, thus biasing rate control toward the N–N bond-activation step, which is rate-determining in thermal catalysis.³¹ Correlations between vibrational excitation and NH₃ formation have been reported under certain conditions.³¹ However, recent analyses^32,33 caution that the significance of N₂(v) in atmospheric-pressure DBDs may be substantially reduced due to the high reduced electric field (E/N), rapid V–T quenching, and limited survival of high-v states.^7,30 As a result, vibrational pathways may play a secondary or system-dependent role compared with electronic, ionic, and dissociative channels in typical DBD regimes. Taken together, these studies underscore the importance of characterising both internal-mode excitation and microdischarge behaviour when seeking to rationally optimise plasma-enabled NH₃ synthesis.

Plasmas offer a second advantage: they can circumvent classical scaling relations that constrain thermal catalysis^7,34 because a significant fraction of the input energy can be channelled into non-thermal electronic and vibrational activation pathways rather than uniformly into gas heating. Although DBDs can still exhibit appreciable gas heating through V–T relaxation, collisions, and exothermic chemistry, this partial decoupling of internal excitation from bulk gas temperature can reshape the reaction kinetics, enabling forward–reverse rate asymmetry and apparent yields that surpass equilibrium-limited values. This opportunity has been demonstrated for Ru catalysts in DBD reactors, motivating systematic efforts to map the operating regimes where non-thermal promotion is strongest.³⁵

Despite rapid progress,^19,21,36,37 the literature remains fragmented, as many studies vary a single parameter (e.g. gas ratio, voltage, or catalyst) and report only subsets of diagnostics. Controlled, multi-parameter studies that couple reactor configuration properties with electrical driving modes and integrated diagnostics are required in order to reveal how plasma structure governs catalytic function. As in many other fields, machine learning tools have recently been increasingly applied in plasma science, particularly for addressing computationally expensive simulations and complex parameter optimisation. Neural network approaches have been applied to predict product densities in pulsed discharge systems,³⁸ enabling efficient extraction of operating parameters from experimental data with relative errors below 10⁻³. Deep neural networks have also been employed to simulate atmospheric dielectric barrier discharges³⁹ and CO₂ conversion plasmas,⁴⁰ reducing computational time from hours to seconds while maintaining high accuracy. For ammonia synthesis, artificial neural networks have successfully correlated operational parameters with synthesis rates and energy yields.⁴¹ While these studies primarily focused on predicting macroscopic outcomes, our work advances the field by integrating machine learning with multi-modal plasma diagnostics—combining electrical measurements, optical emission spectroscopy, and chemical analysis—to reveal mechanistic connections between microdischarge characteristics, excited-state distributions, and ammonia formation efficiency.

Here, we perform a systematic analysis of N₂–H₂ plasma characteristics and parameters in a DBD reactor to understand their relationship to ammonia yield. We vary dielectric barrier thickness, electrode and discharge gaps, applied voltage amplitude, gas composition, and flow rate to isolate the most significant features for ammonia yield. Each condition is characterised by a set of complementary characterisation techniques, including time-resolved electrical measurements (to assess total power and microdischarge statistics), optical emission spectroscopy of N₂, N₂⁺ and NH, and colorimetric NH₃ quantification. Statistical correlation analysis is used to identify which plasma descriptors (microdischarge total charge, energy per microdischarge, and distribution of molecular excited states) best correlate with ammonia production and energy efficiency. By systematically decoupling reactor geometry from operating mode and linking discharge structure to process performance, we establish mechanistic design rules for out-of-equilibrium nitrogen activation.

Results and discussion

Electrical diagnostics and microdischarge behaviour

To gain a fundamental and generalisable understanding of how reactor geometry and process parameters control plasma-driven ammonia synthesis, we systematically varied eight geometrical and process parameters (Fig. 1), namely: pellet thickness (P), electrode gap (EG), discharge gap (DG), applied voltage, total gas-flow rate, nitrogen-to-hydrogen mixing ratio (N₂: H₂), and pulse-timing parameters (DT and ST) (further details in SI Table S1; Fig. S1 and S2). The full factorial combination of these levels would result in ca. 13 000 combinations, rendering the problem intractable. Therefore, a partial factorial design of experiments was implemented, yielding several hundred operating points (including repetitions) that are systematically analysed in the following sections. Fig. 2 summarises how these parameters influence the electrical diagnostics and microdischarge behaviour of the DBD plasma (see SI section S1 for full experimental details). Representative Lissajous plots (Fig. 2A) show the characteristic charge–voltage loops, while current–voltage traces (Fig. 2B) resolve the nanosecond-scale microdischarge spikes within each AC half-cycle.

Fig. 1 Schematic overview of the dielectric-barrier discharge (DBD) plasma reactor, and the full experimental parameter matrix. Eight geometrical and process parameters were systematically varied, namely, pellet thickness (P, 0–2 mm), electrode gap (EG, 3.5–5.5 mm), discharge gap (DG, 1.5–3.5 mm), applied voltage (19–21 kV), gas flow (20–40 mL min⁻¹), nitrogen-to-hydrogen mixing ratio (N₂: H₂ = 1 : 1, 1 : 2, 2 : 1), and pulse timing combinations (DT and ST = 75–80 and 200–475). These variations produced several hundred operating points, summarised in SI Table S1. To identify statistically significant dependencies, both Spearman rank correlations (to capture monotonic trends) and random forest regressions (to capture nonlinear and interaction effects) were applied to all parameter–response pairs.

Fig. 2 Discharge characteristics as a function of geometry and process settings. (A) Lissajous figure for the empty reactor, showing the capacitor-like charge–voltage relationship across a dielectric layer of MACOR® on high-voltage with a ground electrode of 1.2 mm thickness, in an otherwise empty cell. (B) Representative zoomed-in current–voltage waveform of a single envelope, revealing microdischarge spikes during AC (half-)cycles. (C) Distribution of total charge of microdischarges per envelope across all experimental conditions at constant DG as a function of dielectric barrier thickness. (D) Distribution of total charge of microdischarges per envelope across all experimental conditions at constant EG as a function of DG. (E) Distribution of median energy of microdischarges across all experimental conditions at constant DG as a function of dielectric barrier thickness. (G) Statistical relationships between all geometrical/process inputs and discharge outputs (mean median energy and mean total charge) obtained from Spearman and random forest analyses. The colour indicates the correlation sign and strength (Spearman ρ); bubble size represents random forest feature importance; and numbers to the right denote model R². Asterisks (*) indicate statistically significant correlations (p < 0.05, two-tailed Spearman test).

The dielectric barrier thickness is varied by introducing pellets P of given thickness (made of MACOR®, the same material as the reactor components). The gap geometry (EG, DG) tunes both the charge and energy of microdischarges. To understand their effects, two cases must be distinguished, as the reactor geometry influences the external electric field applied across the discharge gap differently (SI Fig. S1). When maintaining a constant-EG, increasing the barrier thickness raises the reactor capacitance, thereby amplifying the electric field within the discharge gap. However, when the DG is constant, the increased distance between the electrodes outweighs the effect of higher capacitance, leading to an overall decrease in the external field strength. Although the field inside the discharge gap results from the superposition of external and internal fields generated by charged plasma species, making the geometric field relationship inherently complex, these two configurations must be analysed separately to capture the distinct directionality of external forcing.

Experimentally, we observed that increasing the barrier thickness at constant DG decreases the total microdischarge charge, and simultaneously increases the median microdischarge energy (Fig. 2C and E). Conversely, under constant EG, increasing the barrier thickness (and thus reducing the DG) decreases both the total charge and median energy (Fig. 2D and F). This behaviour indicates that, for constant DG, thicker barriers distribute less total charge among fewer (but more energetic) filaments, whereas for constant electrode gap, fewer energetic microdischarges carrying less overall charge are produced as a result of weakened superposition of external and internal fields.

To generalise these relationships, we performed a statistical analysis linking geometric and process inputs to electrical outputs (total charge and median energy of microdischarges). Monotonic trends independent of linearity were captured using Spearman rank correlation (quantified by the Spearman coefficient ρ), and nonlinear or coupled effects were identified using random forest (RF) regression. Details of data preprocessing, cross-validation, and model tuning are provided in the SI, section S1.5. The resulting correlation map (Fig. 2G) reveals that sustain-time (ST) frequency and gap geometry dominate energy deposition (|ρ| ≈ 0.5; RF importance ≈ 0.7), while applied voltage strongly influences total charge. Increasing voltage increases both total charge and per-discharge energy due to higher input power and a stronger external field, whereas reducing the ST parameter directly shortens the energy-accumulation window (energy and charge are calculated per single pulse envelope).

The mechanistic origin of the observed geometric effects is less straightforward. Generally, decreasing the discharge-gap distance (or the electrode spacing, with a corresponding change in dielectric barrier thickness) enhances the external field due to higher reactor capacitance.^42,43 The actual field distribution, however, is also shaped by space charges generated through electron-molecule collisions,^9,44,45 and further modified by reactive fragments that contribute to the local potential landscape.^20,44,46 Nevertheless, these dependencies show that geometric control alone, as demonstrated here in the catalyst-free configuration, can effectively modulate the microdischarge regime and energy dissipation, enabling plasma-structure tuning. We note, however, that introducing catalyst loading, packing structure, or additional dielectric materials would modify the effective geometry experienced by the discharge and represent an additional layer that must be considered in plasma–catalytic systems.

Optical emission spectroscopy and excitation pathways

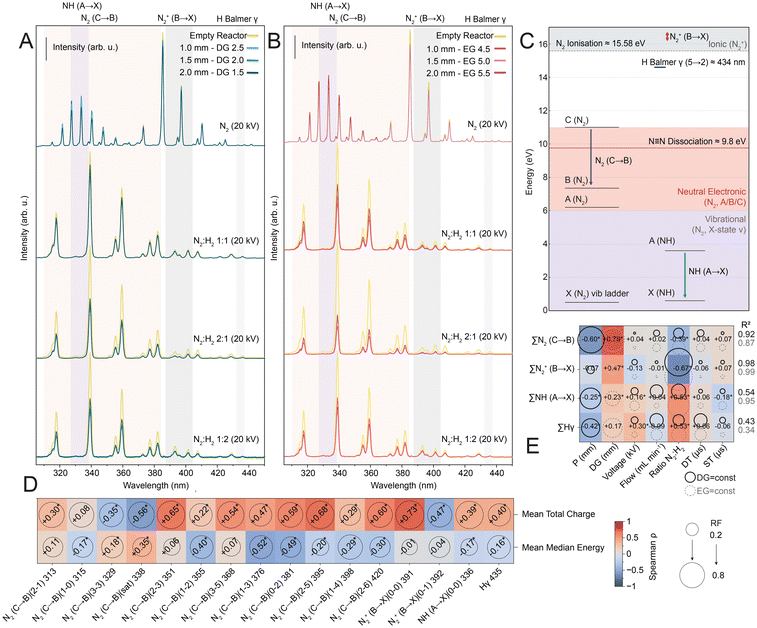
We next employed optical emission spectroscopy (OES) to elucidate how the electrical plasma characteristics described above partition energy among internal excitation channels. Representative spectra recorded under pure N₂ and mixed N₂–H₂ feeds at different ratios (for constant EG and DG with varying P) are shown in Fig. 3A and B. OES provides a window into the electronically and vibrationally excited states within the discharge, as the emitted photons reflect relaxation from molecules, ions, and radicals formed under the prevailing electron energy distribution function (EEDF).^45,47,48 A spectrum for pure H₂ is provided in SI Fig. S8.

Fig. 3 Optical emission spectroscopy (OES) signatures and their statistical interpretation. (A and B) Representative emission spectra for (A) constant EG and (B) constant DG under different gas mixtures (N₂: H₂ = 1 : 1, 2 : 1, 1 : 2) for different pellet thicknesses P and for the empty reactor, with reference spectra for pure N₂. (C) Schematic of the electronic and vibrational energy levels of N₂(C → B), N₂⁺(B → X), NH(A → X), and H (Balmer) transitions probed by OES, also indicated in (A and B). (D) Spearman correlations between discharge-derived quantities (mean total charge and mean median energy), and the intensity of each individual spectral line obtained via Gaussian integration (see SI Table S2 for more details), revealing which discharge properties most strongly influence which excited-state populations. Tile color encodes Spearman ρ. (E) Combined analysis of geometrical/process inputs versus summed integrated OES band intensities (N₂(C–B), N₂⁺(B–X), NH(A–X), H Balmer). Bubble size indicates the random forest importance, and right-hand values indicate the model R². The figure highlights how voltage and gas composition jointly govern the excitation of nitrogen and hydrogen species.

In nitrogen plasmas, emissions arise from a dense manifold of electronic levels, 27 primary states, ranging from the ground X¹Σ⁺ to the z¹Δg level at 14.3 eV, each containing multiple vibrational and rotational sublevels.^43,44 Under the low effective electron temperatures (≈ 1–5 eV) typical of dielectric-barrier discharges, excitation is dominated by triplet states. The metastable N₂(A³Σ_u⁺) serves as a long-lived reservoir that can be collisionally promoted to higher triplet states, B³Π_g, C³Π_u, producing the observed UV–visible bands.^49,50 To describe these transitions consistently, we adopt the spectroscopic notation species: “(Upper → Lower) (v′–v″) λ” (see SI section 2 and Tables S2 and S3 for more details on energy levels, notation, and assignments). For example, N₂(C–B)(2–1) 313 nm denotes a photon emitted as neutral nitrogen relaxes from the excited C³Π_u to the B³Π_g state (both electronically excited) while changing vibrational level from v′ = 2 to v″ = 1. Fig. 3C schematically depicts these electronic systems and their associated neutral and ionic transitions.

Within our spectral window, four distinct emission families dominate, each linked to a specific excitation pathway. Neutral N₂ bands arise from the C–B system (C³Π_u → B³Π_g; commonly called the “second positive system”⁵¹), ionic N₂⁺ B–X transitions (B²Σ_u⁺ → X²Σ_g⁺; the “first negative system”), NH radical emission A–X (i.e., A³Π → X³Σ⁻ ), and atomic hydrogen contributes the Balmer series. The feature near 434 nm, often associated with Hγ, may also include contributions from the N₂(C–B)(0–4) transition (λ = 434.36 nm), and we therefore treat it as a composite peak rather than a purely hydrogen emission. These nitrogen-containing emission families represent distinct electronic excitation pathways of increasing energy cost: neutral excitation (N₂ C–B), ionisation (N₂⁺ B–X), and dissociation leading to radical (NH A–X).

All four families can clearly be observed in all spectra in Fig. 3A and B, with the neutral N₂(C–B) features appearing most intense within our detection window. We note that OES intensities convolve excited-state populations, radiative probabilities, quenching, and detector sensitivity; therefore, ‘dominance’ refers only to measured emission strength, not to the full distribution of electronically or vibrationally excited species. Systematic variation of input parameters reveals pronounced intensity redistributions among manifolds (Fig. 3E). As expected, the N₂/H₂ ratio exerts the strongest influence: higher nitrogen content directs energy into electronically excited N₂ species. Notably, both NH and H emission intensities also positively correlate with the N₂/H₂ ratio, despite reduced absolute H₂ concentration, suggesting that nitrogen addition enhances hydrogen dissociation through energy transfer from long-lived N₂ metastable states (A³Σ⁺_u) and modification of the electron energy distribution function toward energies favorable for H₂ dissociation. Geometric effects further modulate excitation. For a constant discharge gap, increasing the barrier thickness strengthens the NH emission while H features diminish, whereas nitrogen bands remain largely unchanged. For a constant electrode gap, however, increasing the discharge gap enhances the fraction of ionised N₂⁺ species.

To determine whether these spectral changes arise directly from the tuneable inputs or indirectly through modified discharge behaviour, we compared random forest models trained on (i) process parameters alone and (ii) parameters plus microdischarge descriptors (total charge and median energy) (SI Fig. S9–S11). The results show that microdischarge characteristics strongly affect predictions of optical-band intensities (SI Fig. S9), with the total charge being a more influential feature than the median energy, particularly for NH and H species. Comparing both models reveals little change in the importance of total flow rate and N₂/H₂ ratio, moderate shifts for dielectric thickness and discharge gap, and pronounced changes for applied voltage and waveform parameters (DT/ST) once microdischarge features are included. These findings indicate that total flow and gas composition act as direct “tuning knobs” for active-species distributions, while most other parameters influence chemistry indirectly through their impact on microdischarges. The effect of the N₂/H₂ ratio stems from direct modification of reaction kinetics, whereas the flow rate, although minimally affecting discharge characteristics due to large disparities in convective and electron timescales,^52,53 modulates residence time and thus reaction probability.^53,54 Reactor geometry has a dual effect by shaping the external electric field that governs microdischarges and by defining the flow residence time that controls reaction kinetics.

To connect spectral fine structure with discharge physics, we further correlated the integrated area of each emission line with the electrical descriptors. The Spearman analysis (Fig. 3D) reveals non-uniform trends: for N₂(C–B), most peak intensities increase with total charge, except the dominant 329 nm line, which decreases. In contrast, ionic N₂⁺ bands show opposite trends; while both NH and H features increase total charge, they decrease with median microdischarge energy. By combining electrical and spectroscopic analyses, we thus reveal how reactor geometry and process parameters govern the excitation partitioning underlying non-thermal N₂ activation in N₂–H₂ plasmas. Reactor geometry and flow parameters act as simple yet powerful levers to bias the discharge toward electronic, ionising, or dissociative pathways, thus bridging plasma physics and process chemistry in plasma-driven ammonia synthesis. In the following section, we link electronically, ionically, and dissociatively dominated regimes, characterised by enhanced N₂(C–B), N₂⁺, and NH emission, respectively, to ammonia yields, establishing a mechanistic bridge between plasma structure, reactive-species generation, and catalytic function.

From plasma descriptors to ammonia formation

To establish how plasma excitation pathways relate to ammonia formation, we correlated the integrated optical-emission features with measured NH₃ concentrations. As shown in Fig. 4A, the aggregate neutral N₂(C–B) emission exhibits the highest (though moderate) correlation with NH₃ yield (ρ = +0.43), whereas the NH(A–X) band exhibits the highest random forest predictive power (≈ 0.8). Interestingly, neither the absolute intensity of N₂⁺(B–X) nor the N₂⁺/N₂ ratio correlates strongly with yield. Testing the effect of different families of excited states normalised on the total intensity of spectra revealed that although all of the species concentrations have high predictive power, only NH and H species show a monotonic increase with the increase of ammonia concentration (SI Fig. S12), whereas the relationships between ammonia and different nitrogen species concentrations are more complex.

Fig. 4 Linking plasma parameters and spectroscopy to ammonia formation. (A) Statistical relationships between OES features and measured NH₃ concentrations. Tile colour = Spearman ρ, bubble size = RF importance, R² per row indicates predictive power. The strong contributions of N₂⁺(B–X) and NH(A–X) emissions demonstrate that excitation of reactive N–H intermediates correlates with NH₃ yield. (B) Per-peak intercorrelation matrix (Spearman) among all detected emission lines. (C) Geometrical and process parameters as inputs versus NH₃ production as output. Colour encodes correlation and bubble size indicates RF importance. The analysis shows that the generation of NH₃ depends most strongly on the applied voltage and gas flow, as well as ST, pointing towards pulsed plasma as a practical optimisation parameter.

Electronically excited and ionised species have long been proposed to participate directly or indirectly in nitrogen activation. Van't Veer et al. showed that microdischarges with higher local fields enhance N₂⁺(B–X) and NH(A–X) emission, with these features scaling positively with NH₃ production in a DBD reactor.²⁰ Kinetic modelling by Mehta et al.^7,9,35 revealed that electronically excited N₂ and N₂⁺ lower the effective N≡N dissociation barrier on metal surfaces, enabling non-thermal Eley–Rideal-type N insertion pathways. These models, however, assume catalytic surfaces (typically Ru or Fe) and may not directly translate to barrier-only discharges such as ours, where ion-driven channels likely influence gas-phase radical formation rather than surface activation.

Vibrational activation can be regarded as one of the most energy-efficient routes to weaken the N≡N bond, but its quantitative contribution remains contested. Rouwenhorst et al. reported that higher N₂⁺/N₂ emission ratios correlate with improved yields, and interpreted this as evidence that high-energy electrons co-populate vibrationally excited ground-state N₂(X,v) levels.³¹ However, this interpretation is indirect, since OES cannot detect N₂(X,v) transitions directly; the observed N₂(C–B) and N₂⁺(B–X) transitions are purely electronic. Bayer et al. combined modelling with time-resolved OES and concluded that only highly excited vibrational states (ν ≥ 8–10) survive long enough near catalytic surfaces to contribute to turnover before vibrational relaxation quenches them.³⁰ Whether such populations are sustained under atmospheric DBD conditions and contribute to NH₃ in meaningful quantities thus remains an open question.

Across the literature, three activation regimes are distinguished. These are difficult to disentangle experimentally, and likely often co-exist. However, they are not (yet) hierarchically ranked in importance. Firstly, vibrationally assisted dissociation, energetically efficient but experimentally elusive; its contribution depends on sustaining high-ν populations at the surface.^7,30 Secondly, electronic and ionic activation, clearly observable via OES; here, radical formation is enhanced and this mechanism likely dominates in dielectric-barrier reactors without catalysts.⁴⁸ Thirdly, ion-mediated radical chemistry, N₂⁺ and H₂ collisions forming NH⁺ or NH* intermediates that recombine or relax to NH₃; its contribution is inferred from correlated NH(A–X) and Hγ emissions. While the relative importance of these channels remains under debate, especially comparing catalytic to non-catalytic plasmas, the consensus is that optimal operation requires balancing neutral excitation with ionising and dissociative events rather than maximising any single pathway.

Since direct measurement of N₂(X,v) is not feasible here, the N₂⁺(B–X)/N₂(C–B) ratio is commonly adopted as a qualitative indicator of a “harder” electron-energy distribution function (EEDF).^20,31 The same electrons energetic enough to ionise N₂ can also populate high-v states of N₂(X,v) and drive dissociative channels leading to NH(A–X) and H Balmer emission. This ratio, although influenced by Franck–Condon factors, quenching, and collection geometry, is thus taken as a proxy of discharge regimes with greater ionisation and dissociation capacity.^20,31 In our experiments, the relatively weak correlation of N₂⁺ intensity with NH₃ yield therefore suggests that ionisation alone is not rate-determining but that mixed electronic-ionic regimes favouring simultaneous H formation and (thus) NH are most productive (Fig. 4A, SI Fig. S12).

The interdependence matrix of OES peaks (Fig. 4B) provides further nuance. The NH(A–X) intensity, an indirect yet robust indicator of gas-phase N–H bond-formation capacity, is strongly negatively correlated with specific lines such as N₂(C–B)(3–3) 329 nm and N₂⁺(B–X)(0–1) 392 nm, but positively correlated with several higher-v″ N₂(C–B) transitions. A similar pattern is observed for the H Balmer emission. This anticorrelation does not imply NH₃ dissociation; rather, it reflects competition for nitrogen excitation pathways. When a larger fraction of electron energy is channelled into dissociation and radical formation (producing NH and H), fewer neutral or ionic excited states are populated radiatively. The resulting redistribution signifies that nitrogen previously emitting as N₂(C–B) or N₂⁺(B–X) is being consumed or diverted toward NH formation. Consistent with this, NH and H emissions correlate positively with measured NH₃ concentration, indicating that enhanced radical generation promotes net synthesis. The positive association with higher-v″ N₂(C–B) transitions further suggests that partial vibrational excitation of electronically excited N₂ accompanies or facilitates NH formation. This is consistent with stepwise excitation mechanisms in which moderately energetic electrons concurrently promote vibrational and dissociative channels. NH(A–X) emission provides a useful qualitative indicator of productive N–H chemistry, as NH radicals arise from reactions between N and H atoms generated via electron-impact dissociation and energy-transfer pathways. Both kinetic modelling and laser-induced fluorescence measurements have shown that NH is a key intermediate linking N and H radical pools to subsequent NH₂ and NH₃ formation.^55–57 Accordingly, increased NH emission is consistent with enhanced access to N–H bond-forming channels, although it does not directly quantify absolute radical concentrations. Although gas-phase indicators correlate strongly with NH₃ formation, they may not capture the full reaction network. Because NH₃ is more readily dissociated by electron impact than N₂, wall-mediated pathways can provide additional stabilisation routes even on non-catalytic surfaces. These contributions are not reflected in OES signals and may help explain residual variability in NH₃ yield. The present study focuses on gas-phase plasma characteristics, but the role of surface pathways represents an important direction for future mechanistic work.

Fig. 4C maps how reactor geometry and operating parameters correlate with (Spearman) or predict (RF) ammonia production. NH₃ concentration increases with applied voltage and, interestingly, also with total gas flow, but decreases with the ST parameter. The positive correlation with voltage is readily explained by its influence on discharge characteristics: higher voltage increases both the number and energy of microdischarges (Fig. 2G), raising electron energy and thus excitation and reaction rates. The negative correlation with ST aligns with its role in reducing total charge and median microdischarge energy (Fig. 2G), thereby lowering effective electron energy. The modest positive dependence on flow suggests that enhanced gas renewal or improved heat removal can offset the reduced residence time, an effect previously noted for atmospheric DBDs operating near power-density limits.⁵³ Overall, these trends indicate that voltage, flow, and pulse timing jointly define the operational window for efficient nitrogen activation, requiring sufficient field strength to initiate ionisation and N–H formation, but short plasma lifetimes to avoid over-fragmentation and recombination.

Absolute yield and energy efficiency, however, need not coincide. Fig. 5A–E compare NH₃ energy efficiency (kWh per g NH₃) across all operating variables. Feature-importance analysis (Fig. 5F) identifies flow rate and reactor geometry as the primary determinants of efficiency, while timing parameters (DT/ST) and voltage play secondary roles. This ranking agrees with the constant-discharge-gap case but contrasts with the constant-electrode-gap configuration (Fig. 4C), where voltage dominates yield. The divergence arises because efficiency normalises yield by energy consumption: parameters that increase discharge energy (narrow gaps, high voltage) enhance yield but diminish efficiency, whereas higher flow directly contributes to throughput in the numerator of the efficiency metric. Retraining both models on identical data subsets and comparing the permutation importance (see SI Table S4) confirmed that this “rank inversion” originates from intrinsic physical trade-offs rather than sampling bias.

Fig. 5 Energy-efficiency analysis of plasma ammonia synthesis. (A–E) Experimental mean ± standard deviation plots of NH₃ production efficiency (kWh per g NH₃) versus each varied input: applied voltage, gas-flow rate, N₂: H₂ ratio, DT, and ST. (F) Random forest summary of feature importance for predicting energy efficiency from all input variables. Efficiency improves primarily with optimised gas flow and applied voltage, while timing parameters (DT/ST) and pellet geometry play secondary roles.

Taken together, these results establish a simple set of design rules for optimising plasma-driven ammonia synthesis. In this work, we employ a catalyst-free DBD configuration to provide a clean mechanistic baseline, as catalyst loading can introduce additional geometric and dielectric effects that complicate interpretation. Prior studies have shown that catalyst performance in DBD reactors is highly metal-dependent; some catalysts perform worse than plasma-only operation, while others improve yields, reflecting the fundamentally different reaction environment of non-thermal plasmas.^58–60 Moreover, operating without a catalyst means that bulk discharge behaviour is largely unaffected by catalyst presence, meaning that catalyst-free operation offers a robust platform for isolating how geometry, pulse timing, and gas composition govern microdischarge statistics and excitation pathways. Building on this plasma–intrinsic baseline, these design rules can later be extended to plasma–catalytic systems:

(i) Applied voltage and waveform time constants govern the balance between microdischarge integral charge and its energy, parameters directly related to electron energy distribution and the mixture of electronic, ionic, and dissociative channels that dictate NH₃ yield. (ii) Flow rate and gas composition have a more direct effect on the distribution of active species through other mechanisms, such as residence time, microkinetics, and heat transfer, directing energy into transient ionisation and N–H bond formation rather than bulk heating or product breakdown. (iii) Reactor geometry exerts dual control, modifying both electrical capacitance and residence time, to tune energy delivery and reactive throughput. (iv) Flow rate (or, by inference, pulsed plasma) serves as a practical handle for overall NH₃ production energy efficiency, improving gas renewal and suppressing back-reaction losses.

Conclusions

This study quantitatively links plasma microphysics to macroscopic ammonia synthesis in dielectric-barrier discharge (DBD) reactors. By systematically varying geometry and operating modes and combining electrical, spectroscopic, and statistical analyses, we show how microdischarge behaviour governs excitation partitioning and nitrogen activation efficiency. Three main insights emerge:

(1) Excited-state competition: no single emission feature predicts ammonia formation, reflecting interconnected excitation and reaction pathways. NH(A–X) correlates most strongly with NH₃ yield, while inter-peak analysis reveals competition for electron energy between neutral and ionic N₂ channels.

(2) Geometry–composition coupling: reactor geometry, together with gas composition, defines the excitation balance. Geometry modulates both capacitance and residence time, while composition and flow act as kinetic levers through stoichiometry and renewal rate.

(3) Yield-efficiency trade-off: parameters that raise discharge power (high voltage, narrow gaps) increase NH₃ concentration but reduce energy efficiency, whereas higher flow enhances throughput and efficiency.

In essence, reactor geometry and operating mode act as low-complexity yet powerful tuning knobs that shift plasma behaviour from radiative, power-dense regimes toward energetically optimised operation emphasising productive ion–radical chemistry. By mapping these dependencies quantitatively, we establish a framework in which microdischarge statistics, optical descriptors, and reactor-scale metrics converge to guide the rational design of sustainable, electrically driven nitrogen-fixation systems.

Author contributions

Conceptualisation: R. D., C. V.; data curation: R. D., C. V.; formal analysis: D. L., C. V.; funding acquisition: C. V.; methodology: R. D., D. S., A. B., D. L., C. V.; project administration: C. V.; resources: C. V.; supervision: C. V.; validation; D. L., A. B., C. V.; visualisation; R. D., D. S., D. L., C. V.; writing – original draft: D. L., C. V.; and writing – review & editing: R. D., D. S., A. B., D. L., C. V.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data are available either in the supplementary information (SI) or from the authors upon reasonable request. Supplementary information is available. The supplementary information contains additional details on the experimental methods, as well as results (mediation analyses, and additional correlations). See DOI: https://doi.org/10.1039/d5gc05784a.

Acknowledgements

The authors gratefully acknowledge the Israeli Innovation Authority for grant number 81158, supporting this work. Joseph Lefkowitz and Carmel Rothschild (Technion) are both gratefully acknowledged for lending equipment. Caterina Suzanna Wondergem is acknowledged for proofreading.

References

1. C. Smith, A. K. Hill and L. Torrente-Murciano, Energy Environ. Sci., 2020, 13, 331–344.
2. J. R. Chan, S. G. Lambie, H. J. Trodahl, D. Lefebvre, M. Le Ster, A. Shaib, F. Ullstad, S. A. Brown, B. J. Ruck, A. L. Garden and F. Natali, Phys. Rev. Mater., 2020, 4, 115003.
3. K. H. R. Rouwenhorst, H. G. B. Burbach, D. W. Vogel, J. Núñez Paulí, B. Geerdink and L. Lefferts, Catal. Sci. Technol., 2021, 11, 2834–2843.
4. J. Hong, S. Prawer and A. B. Murphy, ACS Sustainable Chem. Eng., 2018, 6, 15–31.
5. M. L. Carreon, J. Phys. D: Appl. Phys., 2019, 52, 483001.
6. K. H. R. Rouwenhorst, S. Mani and L. Lefferts, ACS Sustainable Chem. Eng., 2022, 10, 1994–2000.
7. P. Mehta, P. Barboun, F. A. Herrera, J. Kim, P. Rumbach, D. B. Go, J. C. Hicks and W. F. Schneider, Nat. Catal., 2018, 1, 269–275.
8. R. Michiels, N. Gerrits, E. C. Neyts and A. Bogaerts, J. Phys. Chem. C, 2024, 128, 11196–11209.
9. P. Mehta, P. Barboun, D. B. Go, J. C. Hicks and W. F. Schneider, ACS Energy Lett., 2019, 4, 1115–1133.
10. J. Li, S. Li and L. Li, Chem. –Eur. J., 2025, 31, e02088.
11. J. H. van Helden, P. J. van den Oever, W. M. M. Kessels, M. C. M. van de Sanden, D. C. Schram and R. Engeln, J. Phys. Chem. A, 2007, 111, 11460–11472.
12. J. Qian, Q. An, A. Fortunelli, R. J. Nielsen and W. A. Goddard III, J. Am. Chem. Soc., 2018, 140, 6288–6297.
13. J. Fuller, A. Fortunelli, W. A. Goddard III and Q. An, Phys. Chem. Chem. Phys., 2019, 21, 11444–11454.
14. X. Xu and M. J. Kushner, J. Appl. Phys., 1998, 84, 4153–4160.
15. X. Xu, Thin Solid Films, 2001, 390, 237–242.
16. V. Shahed Gharahshiran and Y. Zheng, J. Energy Chem., 2024, 96, 1–38.
17. H. Hosseini, RSC Adv., 2023, 13, 28211–28223.
18. C. Piferi, R. Barni, H. E. Roman and C. Riccardi, Appl. Sci., 2021, 11, 2079.
19. K. H. R. Rouwenhorst, Y. Engelmann, K. van ‘t Veer, R. S. Postma, A. Bogaerts and L. Lefferts, Green Chem., 2020, 22, 6258–6287.
20. K. van ‘t Veer, Y. Engelmann, F. Reniers and A. Bogaerts, J. Phys. Chem. C, 2020, 124, 22871–22883.
21. B. S. Patil, A. S. R. van Kaathoven, F. J. J. Peeters, N. Cherkasov, J. Lang, Q. Wang and V. Hessel, J. Phys. D: Appl. Phys., 2019, 53, 144003.
22. Z. Chen, S. Jaiswal, A. Diallo, S. Sundaresan and B. E. Koel, J. Phys. Chem. A, 2022, 126, 8741–8752.
23. F. P. Abramo, G. Giorgianni, S. Perathoner, G. Centi, F. Gallucci and S. Abate, Chem. Eng. J., 2025, 512, 162608.
24. Q. Z. Zhang and A. Bogaerts, Plasma Sources Sci. Technol., 2018, 27, 035009.
25. Y. R. Zhang, E. C. Neyts and A. Bogaerts, J. Phys. Chem. C, 2016, 120, 25923–25934.
26. Y. R. Zhang, E. C. Neyts and A. Bogaerts, Plasma Sources Sci. Technol., 2018, 27, 055008.
27. K. Hensel, V. Martišovitš, Z. Machala, M. Janda, M. Leštinský, P. Tardiveau and A. Mizuno, Plasma Processes Polym., 2007, 4, 682–693.
28. S. Chen, Y. Wang, Q. Li, K. Li, M. Li and F. Wang, Phys. Chem. Chem. Phys., 2022, 25, 3920–3929.
29. A. Miyake, N. Shirai and K. Sasaki, J. Appl. Phys., 2024, 135, 213301.
30. N. Bayer, S. Raskar, I. V. Adamovich, P. J. Bruggeman and A. Bhan, Plasma Sources Sci. Technol., 2024, 32, 125005.
31. K. H. R. Rouwenhorst, H. H. Kim and L. Lefferts, ACS Sustainable Chem. Eng., 2019, 7, 17515–17522.
32. N. Gerrits and A. Bogaerts, EES Catal., 2025, 3, 733–742.
33. J.-J. Qiao, Q. Yang, L.-C. Wang, M. Albrechts, I. Tsonev, A. Bogaerts and Q. Xiong, Plasma Sources Sci. Technol., 2025, 34, 065008.
34. J. van Turnhout, K. Rouwenhorst, L. Lefferts and A. Bogaerts, EES Catal., 2025, 3, 669–693.
35. P. Mehta, P. M. Barboun, Y. Engelmann, D. B. Go, A. Bogaerts, W. F. Schneider and J. C. Hicks, ACS Catal., 2020, 10, 6726–6734.
36. D. Panchal, Q. Lu, K. Sakaushi and X. Zhang, Chem. Eng. J., 2024, 498, 154920.
37. X. Zeng, S. Zhang, X. Hu, C. Zhang, K. Ostrikov and T. Shao, Faraday Discuss., 2023, 243, 473–491.
38. J. Pan, Y. Liu, S. Zhang, X. Hu, Y. Liu and T. Shao, Energy Convers. Manage., 2023, 277, 116620.
39. Y.-T. Zhang, S.-H. Gao and Y.-Y. Zhu, J. Appl. Phys., 2023, 133, 053303.
40. X.-C. Wang and Y.-T. Zhang, J. Appl. Phys., 2023, 133, 143301.
41. X. Wang, X. Du, K. Chen, Z. Zheng, Y. Liu, X. Shen and C. Hu, ACS Sustainable Chem. Eng., 2023, 11, 4543–4554.
42. S. Zhang, Z. Chen, B. Zhang and Y. Chen, Molecules, 2019, 24, 3933.
43. H. Ghomi, M. Gasemkhani and S. Rostami, Vacuum, 2009, 83, S193–S195.
44. K. Vodlan, B. Likozar and M. Huš, Chem. Eng. J., 2025, 509, 161459.
45. P. Ganji, R. Zaplotnik, G. Primc, M. Mozetič and A. Vesel, Energy Fuels, 2025, 39, 14413–14436.
46. Y. Feng, Y. Cai, Y. Wang, T. Li, S. Luo, W. Liang, S. Zheng, T. Xie, Q. Y. Yang, X. Yong, R. Zhou, D. Liu and X. Tu, Chem. Eng. J., 2025, 510, 161553.
47. K. Shao and A. Mesbah, JACS Au, 2024, 4, 525–544.
48. Y. Wang, M. Craven, X. Yu, J. Ding, P. Bryant, J. Huang and X. Tu, ACS Catal., 2019, 9, 10780–10793.
49. B. R. Arnold, S. D. Roberson and P. M. Pellegrino, J. Phys. Chem. A, 2014, 118, 10456–10463.
50. B. S. Truscott, M. W. Kelly, K. J. Potter, M. Johnson, M. N. R. Ashfold and Y. A. Mankelevich, J. Phys. Chem. A, 2015, 119, 12962–12976.
51. J. Han, W. Park, J. Kim, K. H. Lim, G. H. Lee, S. In, J. Park, S. J. Oh, S. K. Nam, D. Y. Sung and S. Y. Moon, Spectrochim. Acta, Part A, 2023, 304, 123389.
52. Z. Fan, H. Yan, Y. Wang, Y. Liu, H. Guo and C. Ren, Phys. Plasmas, 2018, 25, 053517.
53. J. A. Andersen, M. C. Holm, K. van ‘t Veer, J. M. Christensen, M. Østberg, A. Bogaerts and A. D. Jensen, Chem. Eng. J., 2023, 457, 1385–8947.
54. J. Hong, S. Pancheshnyi, E. Tam, J. J. Lowke, S. Prawer and A. B. Murphy, J. Phys. D: Appl. Phys., 2018, 50, 154005.
55. B. N. Bayer, P. J. Bruggeman and A. Bhan, ACS Catal., 2023, 13, 2619–2630.
56. Y. Matsumoto, J. Iwamoto and K. Honma, Phys. Chem. Chem. Phys., 2012, 14, 12938.
57. N. Liu, X. Mao, C. Kondratowicz, T. Y. Chen, B. Mei, Z. Wang, Y. Xu, H. Zhong, Z. Shi, A. Morozov, A. Dogariu and Y. Ju, ACS Energy Lett., 2024, 9, 2031–2036.
58. J. Shah, F. Gorky, P. Psarras, B. Seong, D. A. Gómez–Gualdrón and M. L. Carreon, ChemCatChem, 2020, 12, 1200–1211.
59. Y. Zhang, J. Niu, S. Chen, Y. Chen, H. Chen and X. Fan, J. Phys. D: Appl. Phys., 2024, 57, 323001.
60. B. S. Patil, N. Cherkasov, N. V. Srinath, J. Lang, A. O. Ibhadon, Q. Wang and V. Hessel, Catal. Today, 2021, 362, 2–10.

---