Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cutting the overpotential of electrochemical hydrogenations for enhanced hydrogenation efficiency
Jannelle Casanova ,
Keyvan Malaie
,
Keyvan Malaie and
Uwe Schröder
and
Uwe Schröder *
*
Institute of Biochemistry, Faculty of Natural Sciences and Mathematics, University of Greifswald, Felix-Hausdorff-Straße 4, 17489, Greifswald, Germany. E-mail: uwe.schroeder@uni-greifswald.de
First published on 15th December 2025
Abstract
Electrochemical hydrogenations (ECH) of biogenic platform molecules offer a sustainable alternative to catalytic hydrogenations, but their efficiency is often limited by high overpotentials and competition with the hydrogen evolution reaction (HER). In this study, we demonstrate that hydrogenations of levulinic acid and furfural can be carried out efficiently at electrode potentials positive to the reversible hydrogen electrode (RHE) and close to the thermodynamic standard potential of the respective redox processes, thereby overcoming a central barrier to the energetic feasibility of ECH. Using platinized platinum electrodes, we exploit the hydrogen underpotential deposition (Hupd) region, where adsorbed hydrogen monolayers form, to catalyse reductive transformations under mild conditions. Electrolysis experiments reveal that hydrogenation commences already in the Hupd region, achieving Coulomb efficiencies up to 76% for levulinic acid and 53% for furfural hydrogenation at +0.015 V vs. RHE—among the highest values reported at low substrate concentrations. These findings establish the Hupd region as a previously overlooked window for efficient electrochemical hydrogenations, highlighting a promising strategy to reduce energy demand, suppress HER, and advance the integration of biogenic feedstocks into electrochemical valorisation processes.
Green foundation1. This paper addresses the energy efficiency (as one of the key principles of green chemistry) of electrochemical hydrogenations. The manuscript highlights the possibility to carry out electrochemical hydrogenations relatively close to their thermodynamic standard potential and at electrode potentials positive to the reversible hydrogen electrode (RHE).2. Compared to electrochemical hydrogenations that are typically performed at electrode potentials between −1.5 to −2 V, the cell voltage and thus the energy consumption can be practically halved, thus considerably improving the energy efficiency. 3. Next steps in the development will focus on the electrochemical conversion rates. This can, of course, not be achieved via increased overpotentials but rather requires an optimization of the electrocatalyst. Future work should focus on the development of tailored electrocatalysts that maximize hydrogen availability in the underpotential region while enhancing turnover frequencies to reach industrially relevant productivity. |
Introduction
Biogenic organic compounds are the foundation of a biobased economy and of a transition of the chemical industry away from petrochemical resources.1 In contrast to petrochemicals, they are typically highly functionalized, such as by oxygen-containing functional groups. The selective modification or removal of these groups, e.g., via hydrogenation reactions, is an important step to integrate biogenic compounds into the existing processing infrastructure of the chemical industry. Hydrogenations (in this article, this general term is also used synonymously for hydrodeoxygenation or hydrogenolysis reactions in which oxygen functions are removed reductively) can be achieved chemically (catalytically) or electrochemically (electrocatalytically). In addition to their general compliance with the principles of green chemistry,2–5 electrochemical hydrogenations offer several advantages over conventional, catalytic hydrogenations. They can thus be carried out under mild reaction conditions (ambient temperature and atmospheric pressure6–10) and can be performed highly dynamically, making them very suitable for buffering fluctuations in renewable electricity.The use of electrical energy to carry out chemical processes inevitably raises the question of energy efficiency. In an electrochemical process, the energy efficiency is determined (i) by the applied cell voltage, which should be as close to the thermodynamic value as possible, and (ii) by the Coulomb (or Faraday) efficiency of the reaction, which takes into account the contribution of competing side reactions. Both are very different parameters, but as we will see later, they can be closely connected. In addition to the selection of a suitable counter electrode reaction, the cell voltage is governed by the overpotentials of the electrode reactions necessary to overcome kinetic barriers and to perform the electrochemical process at a target rate.
The reference system for electrochemical hydrogenations is the H2/2H+ redox couple or the hydrogen evolution reaction, HER. Compared to the HER, which at catalysts like platinum requires only low overpotentials (i.e., ≪100 mV@10 mA cm−2),11 electrochemical hydrogenations are usually carried out at potentials much more negative than the formal potential of the H2/2H+ system. Thus, the hydrogenation of biogenic platform chemicals such as levulinic acid or furfurals is often performed at reduction potentials of as high as −1 to −2 V (ref. 12–17) versus the Reversible Hydrogen Electrode, RHE. The application of negative electrode potentials leads to two effects: (i) an increasing share of the HER as a side reaction, reducing the Coulomb efficiency of hydrogenation, and (ii) an increasing cell voltage. The HER can be reduced to a certain extent by using electrode materials with a high HER overpotential, such as lead12,18 or copper, or by using high reactant concentrations.19 The high cell voltage, however, remains a problem and provokes a debate on the energetic feasibility of electrochemical hydrogenations as compared to an electrochemical water splitting and subsequent catalytic hydrogenation. Thus, considering a typical overpotential of the anodic oxygen evolution reaction, OER, for acidic conditions of 300 mV@10 mA cm−2 (ref. 20) and a respective overpotential of the HER of 50 mV, the cell voltage of a hydrogen-producing water electrolysis system would be 1.58 V (ΔE = 1.23 V + 0.3 V + 0.05 V = 1.58 V) – neglecting mass transfer and ohmic losses. An electrochemical hydrogenation of a typical organic oxygenate at a cathode potential of −1.5 V (against RHE) and under otherwise identical conditions would result in a cell voltage of 3.03 V – representing an increase of the cell voltage and consequently of the energy consumption by 91% compared to the electrochemical hydrogen generation.
In order to make electrochemical hydrogenations energetically competitive with water electrolysis, the overpotentials need to be reduced drastically. Here, a recently presented opportunity would be the use of electrochemical membrane reactors, as proposed by the group of Berlinguette,21,22 allowing to reduce the cathode potential and HER side reaction. This is already a great improvement.
Despite recent progress in the efficiency of electrochemical hydrogenations, a central question that needs to be addressed is: Do electrochemical hydrogenations fundamentally require a reduction potential more negative than the potential of the H2/2H+ couple?
Reported standard potentials for typical hydrogenation reactions are slightly more positive than that of the H2/2H+ couple (e.g., E° (furfural/furfuryl alcohol) = 0.19 V vs. RHE, E° (furfuryl alcohol/methyl furan) = 0.13 V vs. RHE, E° (levulinic acid/valeric acid) = 0.54 V vs. RHE (ref. 23)); yet, the respective redox processes are strongly kinetically controlled and dependent on the underlying hydrogenation mechanism. In this communication, we show that efficient electrochemical hydrogenations can be achieved at a potential positive to the reversible hydrogen potential, and without the use of co-solvents. Hereby, we exploit the ability of noble metals like platinum to form monolayers of adsorbed hydrogen at potentials positive to the formal potential of the H2/2H+ – often referred to as underpotential hydrogen deposition, Hupd. We show that this potential region can be utilized to catalyse hydrogenation reactions with high energy and Coulomb efficiency using levulinic acid (LA) and furfural (FF) as model compounds.
Results and discussion
Fig. 1A illustrates a typical voltammogram of platinum in an acidic (perchloric acid) solution. Of particular relevance for the electrochemical hydrogenation are the areas of the hydrogen evolution reaction (HER, E < 0 V vs. RHE), and the hydrogen underpotential deposition region (HUPD, 0.4 V > E > 0 V). In the hydrogen underpotential deposition region, three reduction peaks can be recognized, which belong to the reductive hydrogen underpotential deposition at the different platinum crystal surfaces (with the corresponding reoxidation peaks in the oxidative scan). The two main redox systems in Fig. 1A are denominated as strongly bound Hupd1 (Ef = 0.225 V), corresponding to the Pt(100) facet and weakly bound Hupd2 (Ef = 0.115 V) for the Pt(110) facet.24–27 Hereby, the extent and strength of the hydrogen adsorption in the HUPD region is impacted by surface distortions,28 defect sites,29 as well as a competitive adsorption of e.g., hydroxide.30,31Fig. 1B now highlights the changes that occur in the Pt voltammogram upon addition of a reducible organic component such as furfural. On the one hand, the more positive Hupd1 system completely disappears. The disappearance of Hupd systems has been observed before and is caused by the adsorption of the organic component at the metal surface, preventing the proton reduction.25,32–40 This behaviour has frequently been used to quantify the adsorption of organic compounds at platinum surfaces.34,37,41,42 Surprisingly, the Hupd2 system behaves completely differently: whereas the reduction current increases significantly, the oxidative peak vanishes.35
Nevertheless, the resulting voltammetric curve has the typical appearance of a reductive electrocatalytic process. Similar observations can also be made for other organic molecules, such as levulinic acid (Fig. 2). In the case of levulinic acid, the catalytic behaviour is only weakly pronounced at room temperature (Fig. 2A) and may thus be overlooked. At increasing temperature (Fig. 2B), however, it becomes significantly enhanced.
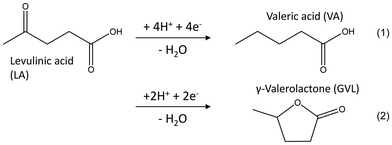
In order to elucidate the underlying electrocatalytic reactions, we performed 1-hour electrolysis experiments using 10 mM levulinic acid solutions, exposed to different electrode potentials within the HUPD and HER region. Fig. 3A illustrates that the hydrogenation of levulinic acid to the typical hydrogenation products, valeric acid (VA) and γ-valerolactone (GVL) (see eqn (1) and (2)), takes place at all tested electrode potentials, and thus commences already at potentials positive to the formal potential of the H2/2H+ couple and thus the HER. The potentials highlighted in this range (0.015 VRHE to 0.115 VRHE) correspond to the Pt(110) facet as shown in the deconvoluted CV in Fig. 1A. As the applied potential is swept towards more positive potentials, the ratio of the involved facets shifts from Pt(110) to Pt(100). This also results in the shift of Hupd2- to Hupd1-dominated Pt surface, decreasing the product formation rate as shown in Fig. 3A.
Particularly interesting is the comparison of the electrolysis results close to the hydrogen formal potential (i.e., of the applied potentials of +0.015 V and −0.085 V). Whereas the overall rate of the hydrogenation product formation is comparable for both potentials, the Coulomb efficiency differs extremely. At the negative potential, the dominance of the HER leads to CE values of the electro-organic hydrogenation of barely 5% – clearly underlining why platinum is generally not considered as a catalyst for electrochemical hydrogenations. Most remarkably, a shift of only 100 mV from −0.085 – across the hydrogen formal potential – to an electrode potential of +0.015 V leads to a steep increase of the Coulomb efficiency to 76.3%, reflecting the strong dominance of the electroorganic reaction over the HER. As we kept the applied potential above 0 VRHE, the 2H* → H2(g) is suppressed, and hydrogenation of organics is greatly preferred. The value also represents one of the highest hydrogenation efficiencies reported so far,14,17 especially taking into account the low educt concentration level. The difference in the Coulomb efficiency between the Hupd and the HER region can also be expressed by the difference in the respective current densities, which are multiple times higher at −0.085 V as compared to 0.015 V – at similar product formation rates, which are solely due to the increasing share of the hydrogen evolution reaction at the negative reduction potential. Fig. 3 also illustrates that the Coulomb efficiency – being highest at a potential of 0.015 V, decreases to values around 50% at more positive potentials. This seems unexpected since the hydrogen evolution as a main side reaction should be ruled out at these potentials. Considering the generally high carbon balance of our experiments (see Tables S1 to S5), product losses or unknown side reactions have most likely only a minor effect. Control experiments of our electrolysis reactor in the absence of the organic precursor, however, show a constant reduction current even in the Hupd region (see Fig. S4). This reduction current may be attributed to (i) an electrochemical reduction of the electrolyte anion (perchlorate) and (ii) the reduction of oxygen that is being formed in the anodic counter reaction and that may diffuse through the membrane in the course of the electrolysis. Especially at the two depicted positive reaction potentials, the low hydrogenation rate of the organic reactant in relation to these side reactions can most likely be made responsible for the lowering of the CE.
It is worth noting that the ratio of the hydrogenation products – the 4H-product VA and the 2H-product GVL (see eqn (1) and (2)) differs for the individual potentials – with a clear trend from the 4H reduction at +0.115 V (83% VA, 17% GVL) to a 2H reduction at −0.085 V (15% VA, 85% GVL). Whether this is an effect of the applied electrode potential or more indirectly of the increasing reaction rates has to be clarified. Nonetheless, it has been reported that elimination of the ketone moiety via hydrolysis is more kinetically and thermodynamically favoured over ring closure (of cyclized intermediate angelicalactone) for VA and GVL formation, respectively. This hints at the confirmation of separate pathways for GVL and VA formation from LA instead of a two-step hydrogenation process.17,43
The rate of valeric acid hydrogenation in the Hupd region is concentration-dependent. In voltammetric experiments (Fig. 4), the reduction current densities increase significantly upon an increase in the LA concentration. Thus, increasing the LA concentration from 10 to 100 mM resulted in a threefold current increase. The corresponding product formation rates confirm a threefold increase of the product formation rate from 6.4 µmol cm−2 h−1 at 10 mM LA concentration (Fig. 3A) to 19.8 µmol cm−2 h−1 at 100 mM LA concentration (Fig. 5A) at 0.015 V and one-hour electrolysis. With 71.8%, the maximum Coulomb efficiency of the electrolysis of 100 mV LA (Fig. 5B) was similar to 10 mM LA and slowly decreased with the duration of the electrolysis, which is typical for batch experiments.
During the experiment, the reaction slowly shifted towards the 2H product formation, γ-valerolactone. Thus, the γ-valerolactone-to-valeric acid ratio increased from 1.2 (after one hour) to 1.6 (after four hours). We also performed exemplary electrolysis experiments using furfural as a starting material. As Fig. 6 illustrates, furfural can also be hydrogenated at +0.015 V vs. RHE, with the major reaction products being furfuryl alcohol (FA) and methyl furan (MF). Hereby, as expected, reaction rate and Coulomb efficiency increase with increasing furfural concentration, and a maximum CE of 48% was achieved. The difference between the CE of FF and the LA hydrogenation is significant but cannot be explained at the moment. With 3.17 µmol cm−2 h−1, the overall product formation rate was very similar to the hydrogenation of levulinic acid under identical conditions (here, 10 mM substrate solution, 20 °C; see also Fig. S2).
ECH of both LA and FF seems to favour the initial 4H- over 2H-product formationin acidic medium. The ratio between the products shifts as the potential becomes less positive, suggesting parallel pathways for the two products formations. These observations are supported by studies using the 2H product as precursors, only generating traces of the 4H-product at longer reaction times or higher temperatures.44
Although the elucidation of the ECH mechanism was not the target of our study, our findings are consistent with the literature17,44–48 that the ECH on Pt follows a hydrogen atom transfer (HAT) mechanism. Thus, the product formation takes place in the potential window of the adsorbed hydrogen formation, with a reaction rate increasing towards potentials at which higher Hads concentrations and less strong hydrogen binding energies prevail. As a second aspect, the potential dependence of the ECH of the studied model compounds seems independent of the standard reduction potentials of the respective starting materials (0.54 V for levulinic acid and 0.19 V for furfural), speaking against a direct reduction mechanism.
It is interesting to notice that the Hupd region of platinum has frequently been used to study the interaction of organic molecules with the electrode material and potential mechanisms of electrochemical hydrogenations42,47,49–51 – without, however, recognizing the actual potential of this potential region for energy-efficient electrochemical hydrogenations. The findings in these studies confirm a clear distinction of the involved Pt facets on the electrohydrogenation process, with the selective involvement of the Pt(110) step. This can be discussed based on the H-adsorption energies of the individual Pt facets, where the Pt(110) possesses the lowest apparent H-adsorption energy38,52 (possibly due to differences in the repulsion of the adsorbed hydrogen at the individual facets28 or a competition of the hydrogen adsorption with hydroxide or water adsorption27), making adsorbed H at this site accessible for hydrogenation.47 As a side remark, the Pt(111) terrace, in the form of Pt[2(111) × (111)],53 is also regarded as Pt(110) step. It is crucial to note that in the presence of these two Pt crystal lattices, one may appear as one over the other in the literature.54
Conclusions
In this communication we highlighted the opportunity to perform electrochemical hydrogenations close to their thermodynamic standard potentials and at potentials positive to the potential of the hydrogen system. Hereby, operating the electrochemical hydrogenations in the Hupd potential range of electrocatalysts like platinum offers two advantages: on the one hand, the considerably lower dominance of the hydrogen evolution reaction in this potential range increases the Coulomb (or Faraday) efficiency of the electrocatalytic hydrogenation, even at low substrate concentrations. Equally important, it drastically reduces the voltage of the electrolysis process. Compared to hydrogenations being performed at a potential of e.g., −1.5 V (and using water oxidation as the counter reaction), operating the process in the Hupd region halves cell the voltage and thus the energy consumption of the process. This can make electrocatalytic hydrogenations economically more competitive with respect to competing conventional hydrogenation approaches.Overall, this study identifies the Hupd region as a powerful and previously underutilized operational window for electrochemical hydrogenations, offering a pathway toward more energy-efficient valorization of biogenic feedstocks. The results presented here are, however, only a first proof of concept. There is a clear need to increase the current densities of the proposed electrochemical hydrogenation. We could already illustrate for the levulinic acid hydrogenation that without any catalyst or reactor optimization, the reaction rate could be improved from 3.2 µmol cm−2 h−1 (10 mM/20 °C) to 6.34 µmol cm−2 h−1 (10 mM/50 °C) and 19.8 µmol cm−2 h−1 (100 mM/50 °C). Further improvement is, however, necessary to reach the reaction rates of conventional electrochemical hydrogenations performed at negative potential values (see Table S4). This can, of course, not be achieved via increased overpotentials but rather requires an optimization of the electrocatalyst. Future work should focus on the development of tailored electrocatalysts that maximize hydrogen availability in the underpotential region while enhancing turnover frequencies to reach industrially relevant productivity. This, however, requires a precise mechanistic investigation of the rate-determining steps of the reaction.
Experimental section
Electrode preparation
All electrochemical experiments were conducted using platinized (Ptblack) platinum electrodes. Base material was polycrystalline platinum sheets (99.99%, Mateck, Germany, 3 cm long, 2 cm wide and 0.1 mm thick, wire connected, which in the electrochemical experiments were immersed into the electrolyte solutions by 2 cm to reach a total exposed geometric surface area of 8 cm−2). The electrode was first cleaned with deionized (DI) water and acetone and finally washed with DI water and left to dry in a normal air atmosphere. Before platinization, the platinum was conditioned by repetitive CV cycling between −0.250 to +1.20 V vs. Ag/AgCl (Sensortechnik Meinsberg, Germany) in 0.5 M H2SO4 at a scan rate of 100 mV s−1 until a stable CV is observed. Platinization was carried out in a single cell according to literature:14 platinum black was deposited on bare Pt sheets using an aqueous solution containing 3.5% H2PtCl6·6H2O and 0.005% Pb(II) acetate. Hereby, the role of lead lies in a lowering of the energetic barrier of the platinum electrodeposition and thus in an enhanced Pt electrodeposition.55 The platinization was conducted galvanostatically by applying a reductive current density of −30 mA cm−2 on each side (by turning the electrode by 180 degrees to achieve an even Pt deposition on both electrode sides) of the electrode for a total coating time of 2 minutes. The as-treated electrode was first dried in the air, and finally conditioned with CV until a stable CV was observed.Electrochemical experiments
All electrochemical experiments were conducted using three-electrode cell arrangements consisting of the respective Pt working electrode (WE), a Ag/AgCl (saturated KCl) reference electrode (RE), and a Pt sheet as a counter electrode (CE). The potentiostat was an SP50e instrument (BioLogic, France). All potentials in this paper are converted vs. RHE. Unless stated otherwise, the experiments are carried out at room temperature (22 °C ± 2 °C) in an H-cell separated using cation exchange membranes (Fumasep FKE-50, Fumatech, Germany). Each half of the cell was filled with 50 mL 0.1 M HClO4 electrolyte (pH 1.09) with the WE and the RE positioned in one side and the CE in the other side. The chamber containing the WE/RE was pre-purged with nitrogen gas, stirred at 300 rpm, and sealed upon addition of the reactant. All electrolysis experiments were performed potentiostatically. CV peaks and diagrams were analyzed using OriginPro 2024, academic version (OriginLab, USA). Deconvolution of peaks in the H region was done using OriginPro Multiple Peak fit function.All experiments were typically repeated as tree independent replicates. A comprehensive overview of the resulting experimental data is provided in Tables S1 to S5.
HPLC analysis
Reaction performance parameters were calculated from quantitative data obtained from reversed-phase high-performance liquid chromatography (RP-HPLC) (Agilent, USA) equipped with a diode array detector and a refractive index detector (RID). The stationary phase used was a Synergi Hydro-RP column (4 µm particle size; 80 Å pore size; 250 mm by 4.6 mm) in an isocratic 1 mL min−1 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 DI water
50 DI water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetonitrile (ACN) mobile phase run at 25 °C for 15 minutes. Analytical standards of the educts and potential products were used to quantify the concentrations before and after the reaction. Product formation rate, yield (Y), coulombic efficiency (CE), carbon balance (Cbal), and conversion (C) were calculated as reaction performance parameters as shown below:
acetonitrile (ACN) mobile phase run at 25 °C for 15 minutes. Analytical standards of the educts and potential products were used to quantify the concentrations before and after the reaction. Product formation rate, yield (Y), coulombic efficiency (CE), carbon balance (Cbal), and conversion (C) were calculated as reaction performance parameters as shown below:
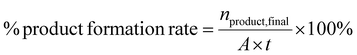 | (1) |
 | (2) |
 | (3) |
 | (4) |
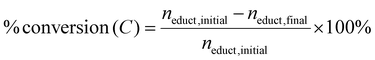 | (5) |
AFM imaging
Surface topographies of the bare Pt and the Pt/Pt(poly) electrodes were investigated with an atomic force microscope (AFM) using a DualScope DS 95-50 scanner coupled with a DualScope C-26 controller (DME Nanotechnologie GmbH, Germany).Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5gc05348j.Acknowledgements
This study is funded under the NSF-DFG Echem project: Future Fuels and Chemicals from Electrocatalytic Upgrading: Advancing Kinetic Understanding using Operando Spectroscopic Approaches and Quantum Chemical Modeling; funding by: Deutsche Forschungsgemeinschaft; funding code: SCHR 753/12-1.References
- B. Kamm, P. R. Gruber and M. Kamm, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH, Weinheim, 2016, pp. 1–38 Search PubMed.
- F. Harnisch and U. Schröder, ChemElectroChem, 2019, 6, 4126–4133 CrossRef.
- H. J. Schäfer, C. R. Chim., 2011, 14, 745–765 CrossRef.
- D. Pollok and S. R. Waldvogel, Chem. Sci., 2020, 11, 12386–12400 RSC.
- B. A. Frontana-Uribe, R. D. Little, J. G. Ibanez, A. Palma and R. Vasquez-Medrano, Green Chem., 2010, 12, 2099–2119 RSC.
- M. C. Leech, A. D. Garcia, A. Petti, A. P. Dobbs and K. Lam, React. Chem. Eng., 2020, 5, 977–990 RSC.
- D. S. P. Cardoso, B. Šljukić, D. M. F. Santos and C. A. C. Sequeira, Org. Process Res. Dev., 2017, 21, 1213–1226 CrossRef.
- A. Wiebe, T. Gieshoff, S. Möhle, E. Rodrigo, M. Zirbes and S. R. Waldvogel, Angew. Chem., Int. Ed., 2018, 57, 5594–5619 CrossRef PubMed.
- S. Möhle, M. Zirbes, E. Rodrigo, T. Gieshoff, A. Wiebe and S. R. Waldvogel, Angew. Chem., Int. Ed., 2018, 57, 6018–6041 CrossRef.
- M. Yan, Y. Kawamata and P. S. Baran, Chem. Rev., 2017, 117, 13230–13319 CrossRef PubMed.
- J. N. Hansen, H. Prats, K. K. Toudahl, N. Mørch Secher, K. Chan, J. Kibsgaard and I. Chorkendorff, ACS Energy Lett., 2021, 6, 1175–1180 CrossRef PubMed.
- P. Nilges, T. R. Dos Santos, F. Harnisch and U. Schröder, Energy Environ. Sci., 2012, 5, 5231–5235 RSC.
- P. Nilges and U. Schröder, Energy Environ. Sci., 2013, 6, 2925–2931 RSC.
- T. Lenk, V. Rueß, J. Gresch and U. Schröder, Green Chem., 2023, 3077–3085 RSC.
- S. Jung and E. J. Biddinger, Energy Technol., 2018, 6, 1370–1379 CrossRef.
- A. S. May and E. J. Biddinger, ACS Catal., 2020, 10, 3212–3221 CrossRef.
- Y. Zhang and Y. Shen, Appl. Catal., B, 2024, 343, 123576 CrossRef.
- J. Tafel and B. Emmert, Z. Elektrochem. Angew. Phys. Chem., 1911, 17, 569–572 CrossRef.
- T. R. Dos Santos, P. Nilges, W. Sauter, F. Harnisch and U. Schröder, RSC Adv., 2015, 5, 26634–26643 RSC.
- J. Li, W. Tian, Q. Li and S. Zhao, ChemSusChem, 2024, 17, e202400239 CrossRef.
- R. S. Delima, M. D. Stankovic, B. P. MacLeod, A. G. Fink, M. B. Rooney, A. Huang, R. P. Jansonius, D. J. Dvorak and C. P. Berlinguette, Energy Environ. Sci., 2021, 15, 215–224 RSC.
- R. S. Sherbo, A. Kurimoto, C. M. Brown and C. P. Berlinguette, J. Am. Chem. Soc., 2019, 141, 7815–7821 CrossRef PubMed.
- S. A. Akhade, N. Singh, O. Y. Gutiérrez, J. Lopez-Ruiz, H. Wang, J. D. Holladay, Y. Liu, A. Karkamkar, R. S. Weber, A. B. Padmaperuma, M.-S. Lee, G. A. Whyatt, M. Elliott, J. E. Holladay, J. L. Male, J. A. Lercher, R. Rousseau and V.-A. Glezakou, Chem. Rev., 2020, 120, 11370 CrossRef PubMed.
- R. Gómez, J. M. Orts, B. Álvarez-Ruiz and J. M. Feliu, J. Phys. Chem. B, 2004, 108, 228–238 CrossRef.
- M. Deblois, J. Lessard and G. Jerkiewicz, Electrochim. Acta, 2005, 50, 3517–3523 CrossRef.
- X. Yang, J. Nash, N. Oliveira, Y. Yan and B. Xu, Angew. Chem., Int. Ed., 2019, 58, 17718–17723 CrossRef PubMed.
- I. T. McCrum and M. J. Janik, ChemElectroChem, 2016, 3, 1609–1617 CrossRef.
- J. Liu, A. Hagopian, I. T. McCrum, K. Doblhoff-Dier and M. T. M. Koper, J. Phys. Chem. C, 2024, 128, 15019–15028 CrossRef.
- I. T. McCrum and M. J. Janik, J. Phys. Chem. C, 2017, 121, 6237–6245 CrossRef.
- M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Catal. Today, 2013, 202, 105–113 CrossRef.
- M. J. Janik, I. T. McCrum and M. T. M. Koper, J. Catal., 2018, 367, 332–337 CrossRef.
- M. W. Breiter, J. Electrochem. Soc., 1962, 109, 42–48 CrossRef.
- V. S. Bagotzky, Y. B. Vassilyev, J. Weber and J. N. Pirtskhalava, Electroanal. Chem. Interfacial Electrochem., 1970, 27, 31–46 CrossRef.
- J. O. M. Bockris and K. T. Jeng, J. Electroanal. Chem., 1992, 330, 541–581 CrossRef.
- L. H. S. Gasparotto, J. F. Gomes and G. Tremiliosi-Filho, J. Electroanal. Chem., 2011, 663, 48–51 CrossRef.
- M. Lukaszewski, M. Soszko and A. Czerwiński, Int. J. Electrochem. Sci., 2016, 11, 4442–4469 CrossRef.
- N. Singh, U. Sanyal, J. L. Fulton, O. Y. Gutiérrez, J. A. Lercher and C. T. Campbell, ACS Catal., 2019, 9, 6869–6881 CrossRef.
- R. Rizo, E. Herrero, V. Climent and J. M. Feliu, Curr. Opin. Electrochem., 2023, 38, 101240 CrossRef.
- K. Zhao, N. Xiang, Y. Q. Wang, J. Ye, Z. Jin, L. Fu, X. Chang, D. Wang, H. Xiao and B. Xu, Nat. Energy, 2025, 10, 725–736 CrossRef.
- A. T. Hubbard, R. M. Ishikawa and J. Katekaru, J. Electroanal. Chem., 1978, 86, 271–288 CrossRef.
- M. P. Soriaga and A. T. Hubbard, Electroanal. Chem., 1984, 167, 79–95 CrossRef.
- M. D. Obradović, J. Lessard and G. Jerkiewicz, J. Electroanal. Chem., 2010, 649, 248–256 CrossRef.
- O. A. Abdelrahman, A. Heyden and J. Q. Bond, ACS Catal., 2014, 4, 1171–1181 CrossRef.
- X. H. Chadderdon, D. J. Chadderdon, J. E. Matthiesen, Y. Qiu, J. M. Carraher, J. P. Tessonnier and W. Li, J. Am. Chem. Soc., 2017, 139, 14120–14128 CrossRef.
- B. Zhao, M. Chen, Q. Guo and Y. Fu, Electrochim. Acta, 2014, 135, 139–146 CrossRef.
- Q. X. Cai, J. G. Wang, Y. G. Wang and D. Mei, Am. Inst. Chem. Eng. J., 2015, 61, 3812–3824 CrossRef.
- M. A. Quiroz, F. Córdova, E. Lamy-Pitara and J. Barbier, Electrochim. Acta, 2000, 45, 4291–4298 CrossRef CAS.
- M. J. Taylor, L. Jiang, J. Reichert, A. C. Papageorgiou, S. K. Beaumont, K. Wilson, A. F. Lee, J. V. Barth and G. Kyriakou, J. Phys. Chem. C, 2017, 121, 8490–8497 CrossRef PubMed.
- T. Mebrahtu, G. M. Berry and M. P. Soriaga, J. Electroanal. Chem., 1988, 239, 375–386 CrossRef.
- D. S. Mekazni, R. M. Arán-Ais, J. M. Feliu and E. Herrero, J. Electroanal. Chem., 2022, 922, 116697 CrossRef.
- G. Jerkiewicz, M. Deblois, Z. Radovic-Hrapovic, J. P. Tessier, F. Perreault and J. Lessard, Langmuir, 2005, 21, 3511–3520 CrossRef PubMed.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- S. Taguchi and J. M. Feliu, Electrochim. Acta, 2007, 52, 6023–6033 CrossRef.
- V. Climent and J. M. Feliu, Adv. Electrochem. Sci. Eng. Nanopatterned Nanoparticle-Modified Electrodes Vol. 17, 2017, pp. 1–57 Search PubMed.
- M. Saitou, Surf. Coat. Technol., 2006, 201, 3611–3614 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |