Room-temperature chromatographic H₂/D₂ separation via a solid dihydrogen complex with balanced thermodynamics and kinetics

Abstract

To meet the growing demand for hydrogen isotopes, the development of efficient and practical methods for isotope separation for dihydrogen is essential to replace the current cryogenic distillation method operating at 20 K. One of the most promising alternatives is chemical affinity quantum sieving (CAQS), which exploits differences in adsorption enthalpy (|ΔΔH°|) arising from variations in zero-point vibrational energy (ZPVE) between isotopologues. However, low |ΔΔH°| values of materials have prevented effective separation under ambient conditions. In addition, designing materials with a high |ΔΔH°| value is challenging. Herein, we report the largest |ΔΔH°| value of 5.0 kJ mol⁻¹ observed in the solid-state dihydrogen complex [Mn(PCy₃)₂(CO)₃][BARF], exceeding that of all previously known materials. Quantum chemical calculations and statistical analyses were employed to elucidate the origin of this separation ability. Furthermore, we demonstrated H₂/D₂ separation at ambient temperature using gas chromatography. This work presents a novel strategy to enhance the efficiency of isotope separation, thereby enabling H₂/D₂ separation at room temperature.

---

Green foundation

1. Our work advances green chemistry by replacing cryogenic isotope distillation (20 K) with a room-temperature adsorption method. A preliminary estimation indicated that pressure swing adsorption (PSA) using our material could achieve H₂/D₂ separation with only ∼1/10 of the energy cost of distillation, thereby enabling a sustainable, low-energy pathway.

2. Specifically, we demonstrated that [Mn(PCy₃)₂(CO)₃][BARF] exhibited the largest enthalpy difference (ΔΔH° = 5.0 kJ mol⁻¹) reported to date, achieving a separation factor of α = 4.2 at 213 K. Moreover, this compound displayed rapid adsorption–desorption kinetics at room temperature, thereby enabling the first chromatographic isotope separation under ambient conditions.

3. This work could be made greener by designing recyclable column materials and scaling up to industrial PSA processes. Furthermore, by integrating quantum chemical calculations and data science-driven screening, we can propose molecules with α > 5 above 200 K, thereby enabling even lower-energy separations and elevating the sustainability of hydrogen isotope supply chains.

Introduction

Hydrogen isotopes such as deuterium (D) and tritium (T) play important roles across a wide range of research and industrial applications. D has been used as an NMR solvent, tracer,¹ and moderator in nuclear reactors. Recently, D has been used for the termination of silicon surfaces of the transistors,² polymer optical fibers,³ as well as organic light-emitting diodes (OLEDs).⁴ In the future, D and T will serve as fuels for nuclear fusion reactors.⁵ Thus, the demand for the hydrogen isotopes will increase further. T also contaminates water in nuclear waste, and its removal will be important from an environmental point of view. The separation of hydrogen isotopes could be one of the greatest challenges to be addressed.

For heavy water (D₂O) extraction, the Girdler sulfide (GS) process—which utilizes the equilibrium reaction of H₂O + HDS ⇄ HDO + H₂S—has been used industrially.⁶ However, this process contains toxic H₂S and gives small separation factors. Recently, new approaches have been proposed, such as penetration into graphene or hexagonal boron nitride,^7,8 and metal–organic frameworks (MOFs).⁹ For the separation of isotopologues of dihydrogen molecules (H₂, HD, D₂, HT, DT and T₂), distillation at 20 K is used in industry, which is also energy-intensive and gives a small separation factor.

In the last decade, “quantum sieving” has attracted much attention as a new method for the isotope separation of dihydrogen molecules. Beenakker et al. proposed the concept of “kinetic quantum sieving” (KQS) in 1995.¹⁰ The KQS process utilizes the difference in the diffusion rates within small pores arising from the variation in thermal de Broglie wavelengths of hydrogen isotopes. Its mechanism has been validated by experimental studies using organic cages,¹¹ and MOFs.¹² However, KQS requires a low temperature (<77 K) and then high energy consumption for cooling is inevitable. Another mechanism for H₂/D₂ separation was independently reported in MOFs with open-metal sites by FitzGerald et al. in 2013¹³ and by Oh et al. in 2014.¹⁴ This phenomenon was named “chemical affinity quantum sieving (CAQS)”.¹⁵ The CAQS process utilizes the difference in the zero-point vibrational energy (ZPVE) and resultant adsorption enthalpy . The ΔΔH° value of these compounds is so small (<2 kJ mol⁻¹) that the operating temperature is <100 K. In 2017, Weinrauch et al. reported a new CAQS candidate, Cu-MFU-4l, which demonstrated efficient isotope separation at elevated temperatures (≈200 K) through the use of open-metal sites of Cu(I) ions.¹⁶ This material exhibited the largest |ΔH°| (32.6 and 35.0 kJ mol⁻¹ for H₂ and D₂, respectively) among extensive MOF libraries, resulting in a significant enthalpy difference (ΔΔH° = 2.4 kJ mol⁻¹). This pronounced isotope effect arises from orbital interactions (specifically σ-donation and π-back donation) between H₂ and Cu(I) open-metal sites, known as the “Kubas interaction”.^16,17 The separation factor—defined as the ratio of the equilibrium constant for D₂ and H₂ adsorption (α ≡ K_D2/K_H2)—was 2.1 at 203 K for Cu-MFU-4l. Since the discovery of CAQS behaviour in Cu-MFU-4l, materials with a higher separation factor have not been reported,^18,19 underscoring the significant challenge of designing MOFs capable of engaging in strong interactions with hydrogen molecules.

In light of this information, we focused on dihydrogen complexes—the original Kubas-type materials. The first metal dihydrogen complex was reported by Kubas and co-workers in 1984,²⁰ and hundreds of compounds have been reported so far.^20–28 Bender et al. reported a difference in adsorption enthalpy between H₂ and D₂ for the dihydrogen complex W(CO)₃(PCy₃)₂(η²-H₂) in THF.²⁴ However, dihydrogen complexes had not been considered as candidates for CAQS until our recent study. Recently, we demonstrated that solid-state [Mn(dppe)₂(CO)][BARF] (dppe = 1,2-bis(diphenylphosphino)ethane, BARF = tetrakis(3,5-bis(trifluoromethyl)phenyl)borate; hereafter abbreviated as Mn-dppe) exhibited promising CAQS property at room temperature (α = 2.0 at 313 K).²⁸ This compound showed higher absolute values of adsorption enthalpy (|ΔH°| = 50.2 and 54.4 kJ mol⁻¹ for D₂ and H₂, respectively) and a larger difference in adsorption enthalpy (ΔΔH° = 4.2 kJ mol⁻¹) than previously reported dihydrogen complexes. A further increase in α would be expected at lower temperatures, but Mn-dppe exhibited very slow adsorption kinetics at <313 K, preventing evaluation of separation performance. We summarized the reported H₂/D₂ selectivity in CAQS materials in Fig. 1.

Fig. 1 Summary of CAQS materials. Selectivity was estimated by (a) thermal desorption spectroscopy and (b) adsorption isotherms (K_D2/K_H2).

Herein, we report a new CAQS material candidate, [Mn(PCy₃)₂(CO)₃][BARF] (PCy₃ = tricyclohexylphosphine; hereafter abbreviated as Mn-PCy3),²⁹ which improved the kinetics while maintaining a good K_D2/K_H2. This compound showed a similar |ΔH°| to Cu-MFU-4l (27.0 and 32.0 kJ mol⁻¹ for H₂ and D₂, respectively) but a much larger difference in the adsorption enthalpy (ΔΔH° = 5.0 kJ mol⁻¹). In addition, Mn-PCy3 showed much faster adsorption kinetics than Mn-dppe, enabling adsorption measurements down to 213 K, giving α = 4.2 at 213 K, thereby combining a higher working temperature with high H₂/D₂ selectivity. We discussed the origin of these thermodynamic phenomena through quantum chemical calculations, and propose designing guidelines for high-performance CAQS materials. Finally, we demonstrated the gas-chromatography separation of H₂/D₂ mixture using a column packed with Mn-PCy3, taking advantage of its high separation factor and good kinetics.

Results and discussion

H₂ and D₂ adsorption isotherms

We measured H₂ and D₂ adsorption to solid-state Mn-PCy3 between 213 K and 273 K. The adsorption isotherms are shown in Fig. 2(b) and (c). All isotherms were well reproduced by the Langmuir equation, as follows:where V, V_max, K and p represent the volume of adsorbate, saturated volume of the adsorbate, adsorption equilibrium constant and gas pressure, respectively. We fitted the isotherms with two parameters, K and V_max. V_max was globally refined across all data, whereas K was refined for each temperature. We obtained V_max of 10.56 cm³(STP) g⁻¹ for H₂ and D₂ adsorption (Table S1 and S2). By assuming the molecular weight of Mn-PCy3 (1563.06 g mol⁻¹), the estimated V_max was 14.3 cm³(STP) g⁻¹ given that one H₂ or D₂ molecule bonds to one Mn(I) site. Thus, we estimated that 74% of Mn(I) sites were used, indicating that many of the Mn(I) open-metal sites were accessible. Previously, we reported that solid-state Mn-dppe quantitatively adsorbs H₂ (H₂/Mn = 0.97) despite its monomeric nature. Weller and co-workers also reported the reversible adsorption/desorption behaviour of CH₂Cl₂ and xenon to [Rh(Cy₂PCH₂PCy₂)(NBD)][BARF].³⁰ They proposed that the non-covalent interactions with the CF₃ group in the BARF anion had important roles for gas permeation into crystals.

Fig. 2 Structure and hydrogen adsorption properties of Mn-PCy3. (a) Molecular structure. (b) H₂ and (c) D₂ adsorption isotherms. Solid lines were regression curves using the Langmuir equation. (d) van't Hoff plots using the Langmuir model.

The thermodynamic parameters were evaluated using the van't Hoff equation, as follows:

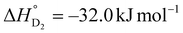where ΔH° is the standard molar enthalpy change of adsorption, ΔS° is the standard molar entropy change of adsorption, and R is the ideal gas constant. The van't Hoff plots for H₂ and D₂ adsorptions in Mn-PCy3 are shown in Fig. 2(d). The obtained parameters have been summarized in Table S3 together with those of Cu-MFU-4l. ΔH° of Mn-PCy3 (, ) was similar to that of Cu-MFU-4l (, ). Conversely, their difference () in Mn-PCy3 (5.0 kJ mol⁻¹) was much higher than that of Cu-MFU-4l (2.4 kJ mol⁻¹). This finding suggested that Mn-PCy3 showed a higher separation factor than Cu-MFU-4l at the same temperature. The α values, defined as K_D2/K_H2, are shown in Fig. 3. Solid lines represent the α value estimated from the fitted ΔH° and ΔS°. Mn-PCy3 showed much larger α than Cu-MFU-4l due to the larger |ΔΔH°| value. It is noteworthy that α of Mn-PCy3 at 273 K was 2.2, which was nearly the same as that of Cu-MFU-4l at 203 K (2.1). This value increased as the temperature decreased, reaching 4.2 at 213 K.

Fig. 3 Temperature dependence of the H₂/D₂ separation factor (α ≡ K_D2/K_H2) in Cu-MFU-4l, Mn-dppe and Mn-PCy3. Solid lines are regression curves using the van't Hoff equation.

Quantum chemical calculations

We performed quantum chemical calculations to reveal the origin of the separation ability of H₂ and D₂ in Mn-PCy3, Mn-dppe and Cu-MFU-4l. First, we estimated the thermodynamic parameters of H₂ and D₂ adsorption. For the calculation, we used the cationic fragment ([Mn(PCy₃)₂(CO)₃]⁺ (Mn-PCy3⁺) (Fig. S1(a)), [Mn(dppe)₂(CO)]⁺ (Mn-dppe⁺) (Fig. S1(b)) and Zn₃Cu₂ cluster as a partial structure of Cu-MFU-4l (Fig. S1(c)). The following equations were used to evaluate and at 298.15 K and 1 bar:where comp-H₂ and H₂ represent the H₂ adduct of the complexes and free H₂ molecule, respectively. Hereafter, element symbols for hydrogen are shown in bold (H), while isotopologues are shown in regular font (H and D) to avoid misreading.

We calculated the thermodynamic parameters of Mn-PCy3, Mn-dppe and Cu-MFU-4l, and then performed structural optimization using various functionals and basis sets. We also estimated the α values at 298.15 K using eqn (7). These have been summarized in Tables S4–S6. At any level of the calculation we examined, and α were nearly independent and showed good agreement with the experimental trend. This result supported the validity of the calculations. For a more detailed discussion, we used the results of the quantum chemical calculations with wB97X-D functional and def2-TZVP for Mn, aug-cc-pVDZ for H₂, and 6-31G for other atoms’ basis sets, which showed good agreement with experimental thermodynamic parameters. We also calculated the α for other pairs of isotopes of hydrogen molecules (HD, HT, DT and T2) (Table S7).

In the CAQS mechanism, differences in the zero-point vibrational energy serve as the driving force for isotope separation. Therefore, it is essential to discuss molecular vibrations derived from adsorbed hydrogen molecules. Fig. 4(a)–(c) show the partial vibrational density of states (p-vDOS) derived from adsorbed hydrogen molecules, estimated through quantum chemical calculations. The motion of the H₂ molecule can be described by the six normal modes presented in Fig. 4(d). For all three samples, the vibrational frequencies followed the order: H–H stretching (ν(H–H)) > M–H asymmetric stretching (ν_asym(M–H)) > symmetric stretching (ν_sym(M–H)) > in-plane bending ≈ out-of-plane bending > rotation (libration). This order is consistent with the vibrational frequencies reported by Kubas and colleagues, determined from FT-IR spectra of a series of complexes.³¹

Fig. 4 Partial vibrational density of state (p-vDOS) of the H (or D) atom of the dihydrogen molecule in (a) Cu-MFU-4l, (b) Mn-PCy3 and (c) Mn-dppe. Red and blue lines represent p-vDOS of H₂ and D₂ adducts, respectively. (d) The six vibrational modes related to H₂ molecules.

The bending and rotation modes possess relatively low vibrational energies (<800 cm⁻¹) and are highly split due to the coupling with other modes. At room temperature, these modes are likely to be thermally excited in part by considering the Boltzmann distribution, so the contribution from these modes can be less than that from stretching modes. Therefore, we focused on three modes: ν(H–H), ν_asym(M–H), and ν_sym(M–H). For ν(H–H), the trend was Cu-MFU-4l > Mn-PCy3 ≈ Mn-dppe, whereas for ν_asym(M–H) and ν_sym(M–H), the trend was Cu-MFU-4l < Mn-PCy3 ≈ Mn-dppe. In general, there is a trade-off between the strengths of the M–H bond and the H–H bond.²¹ These results indicated that the strengths of the M–H bond followed the trend Cu-MFU-4l < Mn-PCy3 ≈ Mn-dppe. Conversely, the trend of |ΔH°| values was Cu-MFU-4l ≈ Mn-PCy3 < Mn-dppe. That is, the |ΔH°| value of Mn-PCy3 was much smaller than that of Mn-dppe despite similar M–H bond strengths. This was probably due to the more rigid structure of Mn-dppe with the five-membered chelate ring structure, resulting in a smaller structural relaxation energy upon H₂ desorption.

Statistical analyses of vibrational energy and isotope selectivity

We wished to elucidate the underlying factors contributing to the isotope selectivity observed in hydrogen adsorption systems. Hence, we performed statistical analyses on the vibrational frequencies associated with adsorbed H₂ and D₂ molecules. To clarify the correlation between these vibrational frequencies and isotope separation performance, we selected the structures of 20 dihydrogen complexes from the Cambridge Crystal Structure Database (CCDC) or modified versions thereof (Fig. S2), and performed quantum chemical calculations to determine ΔΔH° and ΔΔG°. The α at 298.15 K was calculated using eqn (7) and has been summarized in Table S8.

The vibrational frequencies of ν(H–H), ν_asym(M–H), and ν_sym(M–H) were also evaluated by the quantum chemical calculations. These have been summarized in Fig. S3–S22 and Table S9. The sum of these vibrational frequencies was calculated separately for H₂- and D₂-derived modes and evaluated as a single descriptor against K_D2/K_H2.

As shown in Fig. 5a and b, H₂ and D₂ vibrational frequency sums exhibited strong positive correlations with K_D2/K_H2. The Pearson correlation coefficient was 0.945 for the H₂ vibrational sum and 0.943 for the D₂ vibrational sum. These results suggested that the ν(H–H), ν_asym(M–H), and ν_sym(M–H) had a dominant role in the thermodynamic differentiation between H₂ and D₂. Based on regression analyses, we derived a quantitative relationship between isotope selectivity and vibrational energy, K_D2/K_H2 = (1.98 × 10^–3) × ∑ν(H₂) − 9.63, where ∑ν(H₂) represents the sum of ν(H–H), ν_asym(M–H), and ν_sym(M–H) in cm⁻¹. This simple linear expression captured the essence of how vibrational contributions correlated with isotope separation efficiency and could serve as a predictive model for screening new candidate materials. This enables the prediction of separation performance without the need for comparative isotopic experiments, thereby accelerating material discovery.

Fig. 5 (a) Correlation between the sum of the three vibrational frequencies and K_D2/K_H2@298 K for (a) H₂-derived modes and (b) D₂-derived modes and K_D2/K_H2. The structures corresponding to the data point labels are shown in the SI. The red lines represent regression lines.

An additional and important observation from our study was that the top-ranked complexes in terms of α values were cationic first-row transition metal dihydrogen complexes. In general, there is a trade-off between H–H bond strength and M–H bond strength,²¹ but the principal factor weakening the H–H bond is π-backdonation. The cationic nature and first-row transition metal character contribute to lowering d-orbital energy levels, which, in turn, enhances σ-donation and suppresses the π-backdonation components in the M–H bonding interaction. As a result, the observed complexes exhibited higher overall vibrational frequencies. This insight offers a valuable design principle for the future development of high-performance isotope separation materials.

Adsorption kinetics and chromatographic separation

Adsorption kinetics were examined by monitoring gas pressure during isotherm measurements. Fig. 6 shows the temperature dependence of the adsorption kinetics of H₂ and D₂ in Mn-PCy3. At 273 K, adsorption kinetics were well represented by single-exponential behaviour, and reached equilibrium within ∼20 s. This was much faster than that of Mn-dppe, which reached equilibrium in ∼1 h. The exact cause was not clear, but in situ PXRD measurements revealed a difference between the two: Mn-dppe gradually became amorphous upon H₂ adsorption, whereas Mn-PCy3 showed almost no change in PXRD patterns during the same process (Fig. S2). This finding suggested that, in Mn-dppe, the diffusion of H₂ molecules within the crystal impacted the crystalline lattice, suggesting that some factors hindered H₂ diffusion, whereas there was little resistance to H₂ diffusion in Mn-PCy3. Therefore, the difference in molecular packing in the crystal was considered to influence the difference in kinetics.

Fig. 6 Adsorption kinetics of (a and b) H₂ and (c and d) D₂ in Mn-PCy3. (b) and (d) are the magnification of T < 100 s.

With decreasing temperature, the adsorption kinetics gradually became slower and comprised at least two components. The origin of this phenomenon was not revealed. However, it is noteworthy that the adsorption rate was always faster for H₂ than for D₂, indicating that an isotope effect was also observed in the adsorption kinetics. Such a kinetic isotope effect in a CAQS material has not been reported.

By utilizing the large α value and fast adsorption kinetics at ambient temperature, we conducted an experiment on the separation of H₂/D₂ by gas chromatography. A 6.35 mm ∅ (4 mm inner diameter) stainless-steel column of ∼90 cm was filled with 8.75 g of Mn-PCy3. Ar was the carrier gas (8 mL min⁻¹) and H₂/D₂ (8 mL min⁻¹, 50 : 50 (v/v)) flowed for 60 s (between 30 s to 90 s). The gases from the column were detected by a mass spectrometer. The results are shown in Fig. 7. At all temperatures, H₂ was clearly detected before D₂, indicating that D₂ was retained more strongly on the column due to its larger K_D2 (i.e., longer mean residence time on the complexes at the same temperature). The time difference of each gas exiting the column increased with decreasing temperature. This can be attributed to a higher separation factor at lower temperatures. On the other hand, the lower the temperature, the broader were the respective peak widths. This was probably due to the decrease in adsorption/desorption rate caused by the decrease in temperature (Fig. 6). In the breakthrough experiment (Fig. 7(b)), H₂ broke through before D₂ at room temperature. This is the first successful chromatographic separation of hydrogen isotopes at ambient temperature. It is also noteworthy that all chromatographic measurements were conducted using the same batch of samples, indicating that these chromatographic separations could be repeatedly performed by purging H₂ and D₂ gases with Ar flow at room temperature.

Fig. 7 Gas chromatograph of a 1 : 1 H₂/D₂ (v/v) mixture using a packed column of Mn-PCy3. (a) Sixty-second pulse-flow experiment. (b) Continuous flow (breakthrough) experiment.

Conclusions

We showed that Mn-PCy3 possessed a higher affinity for D₂ than H₂. The difference in the adsorption enthalpy between H₂ and D₂ adsorption was estimated to be 5.0 kJ mol⁻¹, which is the highest among any known material. Our preliminary estimation indicated that pressure swing adsorption using our material could achieve H₂/D₂ separation with only ∼1/10 of the energy cost of distillation (see page 20 and 21 in the SI). The mechanism of this phenomenon was reasonably explained by the isotopic difference in the ZPVE. We demonstrated the chromatographic H₂/D₂ separation at ambient temperature. Thus, with its high isotopic selectivity and gas permeability, Mn-PCy3 is a promising material to produce high-purity deuterium and to capture tritium from a low-concentration hydrogen gas mixture by repeating adsorption/desorption at room temperature.

Author contributions

T. K. and T. Y. wrote the manuscript together with H. I., R. T, R. S. and S. T. The synthesis and measurements of isotherms were performed by T. K., T. Y., K. U. and S.-i. N. Quantum chemical calculations were performed by N. K., K. U., H. X. and N. K., S. T directed the project.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting the conclusions reached from our study have been included as part of the supplementary information (SI). Supplementary information: experimental details, experimental and calculated thermodynamic parameters, partial vibrational density of states of a series, thermodynamic parameters, and vibrational frequencies of dihydrogen complexes. See DOI: https://doi.org/10.1039/d5gc04476f.

Acknowledgements

This work was supported by JSPS KAKENHI (23H02054, 21H04696, 19H02729), Adaptable and Seamless Technology Transfer Program Through Target-driven R&D from Japan Science and Technology Agency (JPMJTR20T9), Institute for Quantum Chemical Exploration, ENEOS Hydrogen Trust Fund, and KIOXIA Corporation.

References

1. T. Tani and Y. Ishikawa, Sci. Total Environ., 2023, 903, 166792.
2. J. W. Lyding, K. Hess and I. C. Kizilyalli, Appl. Phys. Lett., 1996, 68, 2526–2528.
3. J. Stone and C. A. Burrus, Bell Syst. Tech. J., 1980, 59, 1541–1548.
4. H. Tsuji, C. Mitsui and E. Nakamura, Chem. Commun., 2014, 50, 14870–14872.
5. T. S. Pedersen, Nat. Commun., 2016, 7, 13493.
6. H. K. Rae, ACS Symp. Ser., 1978, 68, 1–26.
7. M. Lozada-Hidalgo, S. Hu, O. Marshall, A. Mishchenko, A. N. Grigorenko, R. A. W. Dryfe, B. Radha, I. V. Grigorieva and A. K. Geim, Science, 2016, 351, 68–70.
8. S. Yasuda, H. Matsushima, K. Harada, R. Tanii, T. Terasawa, M. Yano, H. Asaoka, J. S. Gueriba, W. A. Diño and K. Fukutani, ACS Nano, 2022, 16, 14362–14369.
9. Y. Su, K.-i. Otake, J. J. Zheng, S. Horike, S. Kitagawa and C. Gu, Nature, 2022, 611, 289–294.
10. J. J. M. Beenakker, V. D. Borman and S. Yu. Krylov, Chem. Phys. Lett., 1995, 232, 379–382.
11. M. Liu, L. Zhang, M. A. Little, V. Kapil, M. Ceriotti, S. Yang, L. Ding, D. L. Holden, R. Balderas-Xicohténcatl, D. He, R. Clowes, S. Y. Chong, G. Schütz, L. Chen, M. Hirscher and A. I. Cooper, Science, 2019, 366, 613–620.
12. D. Denysenko, M. Grzywa, M. Tonigold, B. Streppel, I. Krkljus, M. Hirscher, E. Mugnaioli, U. Kolb, J. Hanss and D. Volkmer, Chem. – Eur. J., 2011, 17, 1837–1848.
13. S. A. FitzGerald, C. J. Pierce, J. L. C. Rowsell, E. D. Bloch and J. A. Mason, J. Am. Chem. Soc., 2013, 135, 9458–9464.
14. H. Oh, I. Savchenko, A. Mavrandonakis, T. Heine and M. Hirscher, ACS Nano, 2014, 8, 761–770.
15. I. Savchenko, A. Mavrandonakis, T. Heine, H. Oh, J. Teufel and M. Hirscher, Microporous Mesoporous Mater., 2015, 216, 133–137.
16. I. Weinrauch, I. Savchenko, D. Denysenko, S. M. Souliou, H.-H. Kim, M. Le Tacon, L. L. Daemen, Y. Cheng, A. Mavrandonakis, A. J. Ramirez-Cuesta, D. Volkmer, G. Schütz, M. Hirscher and T. Heine, Nat. Commun., 2017, 8, 14496.
17. B. R. Barnett, et al. , J. Am. Chem. Soc., 2021, 143, 14884–14894.
18. Y. Si, X. He, J. Jiang, Z. Duan, W. Wang and D. Yuan, Nano Res., 2021, 14, 518–525.
19. L. Li, C. Ji, W. Wang, F. Wu, Y.-X. Tan and D. Yuan, Inorg. Chem. Front., 2022, 9, 1674–1680.
20. G. J. Kubas, R. R. Ryan, B. I. Swanson, P. J. Vergamini and H. J. Wasserman, J. Am. Chem. Soc., 1984, 106, 451–452.
21. G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205.
22. R. H. Morris, Coord. Chem. Rev., 2008, 252, 2381–2394.
23. G. J. Kubas, in Metal Dihydrogen and σ-Bond Complexes, ed. J. P. Fackler Jr., Kluwer Academic/Plenum Publishers, New York, 2001, pp. 33–51.
24. B. R. Bender, G. J. Kubas, L. H. Jones, B. I. Swanson, J. Eckert, K. B. Capps and C. D. Hoff, J. Am. Chem. Soc., 1997, 119, 9179–9190.
25. D. G. Abrecht and B. Fultz, J. Phys. Chem. C, 2012, 116, 22245–22252.
26. K. Uchida, N. Kishimoto, S.-i. Noro, H. Iguchi and S. Takaishi, Dalton Trans., 2021, 50, 12630–12634.
27. K. Uchida, S. Tanaka, S. Adachi, H. Iguchi, R. Sakamoto and S. Takaishi, RSC Adv., 2024, 14, 11452–11455.
28. T. Kitayama, T. Yamauchi, K. Uchida, S. Tanaka, R. Toyoda, H. Iguchi, R. Sakamoto, H. Xue, N. Kishimoto, T. Yoshida, T. Uruga, S.-i. Noro and S. Takaishi, Dalton Trans., 2025, 54, 2621–2627.
29. A. Toupadakis, G. J. Kubas, W. A. King, B. L. Scott and J. Huhmann-Vincent, Organometallics, 1998, 17, 5315–5323.
30. A. J. Martínez-Martínez, N. H. Rees and A. S. Weller, Angew. Chem., Int. Ed., 2019, 58, 16873–16877.
31. G. J. Kubas, C. J. Unkefer, B. I. Swanson and E. Fukushima, J. Am. Chem. Soc., 1986, 108, 7000–7009.

---